A Comparative Study on the Parameter Identification of an Equivalent Circuit Model for an Li-ion Battery Based on Different Discharge Tests
Abstract
:1. Introduction
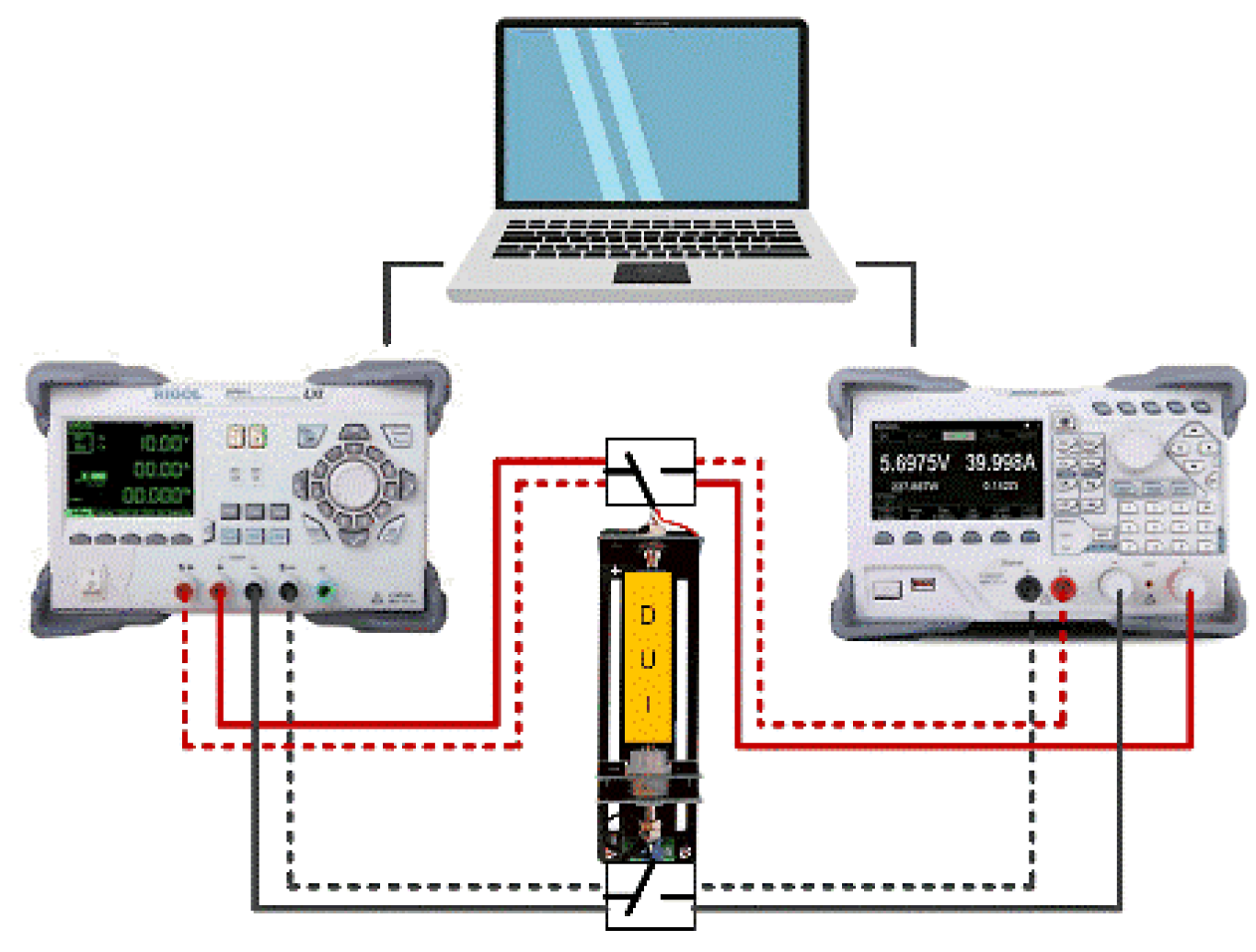
2. Experiment
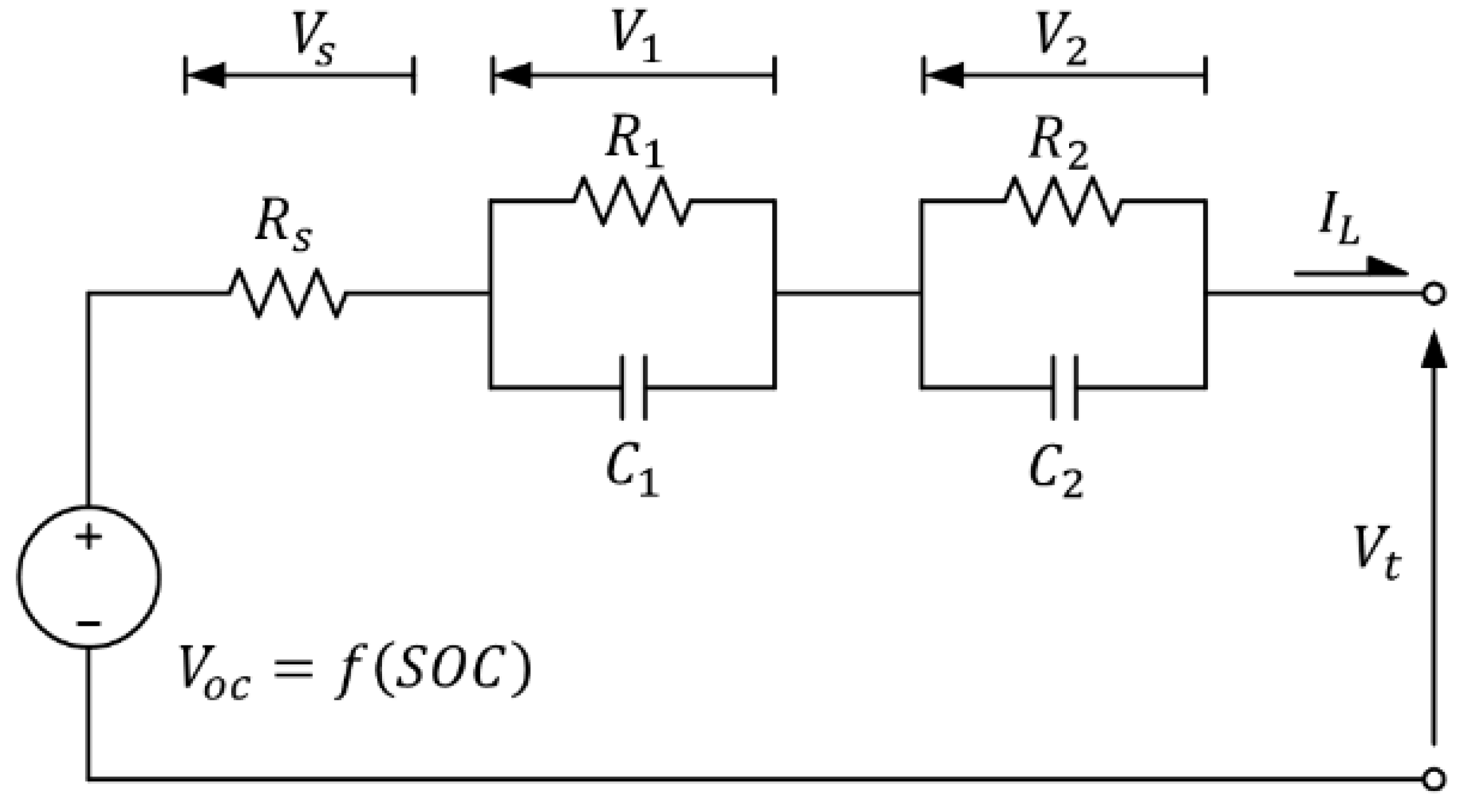
3. Battery Model and Parameter Identification
3.1. Multiple Linear Regression (MLR)
3.2. Exponential Curve Fitting (ECF)
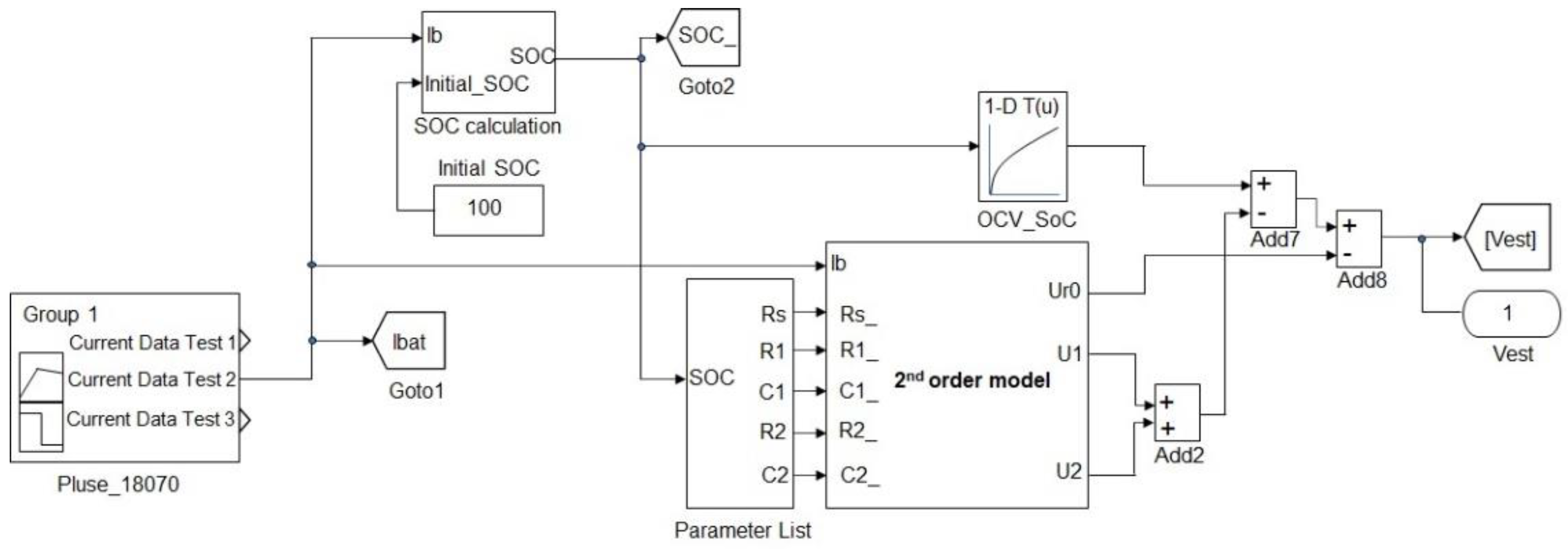
3.3. Simulink Design Optimization Tool (SDOT)
4. Results and Discussion
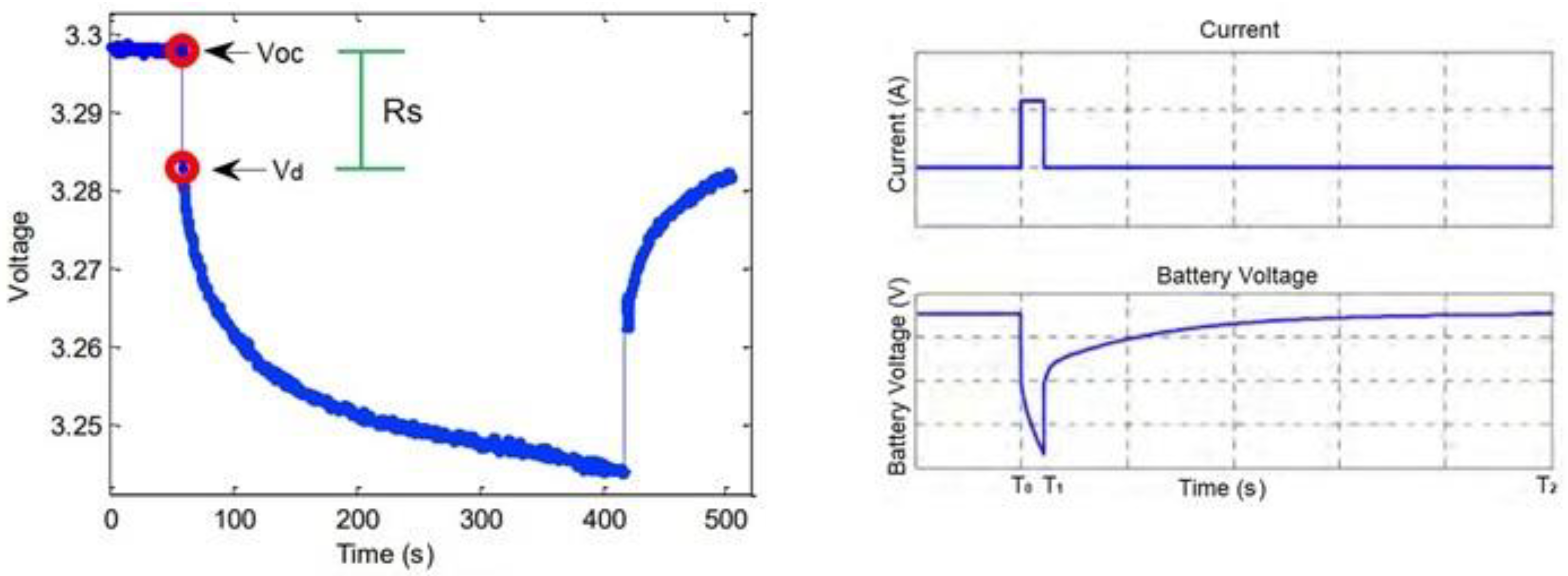
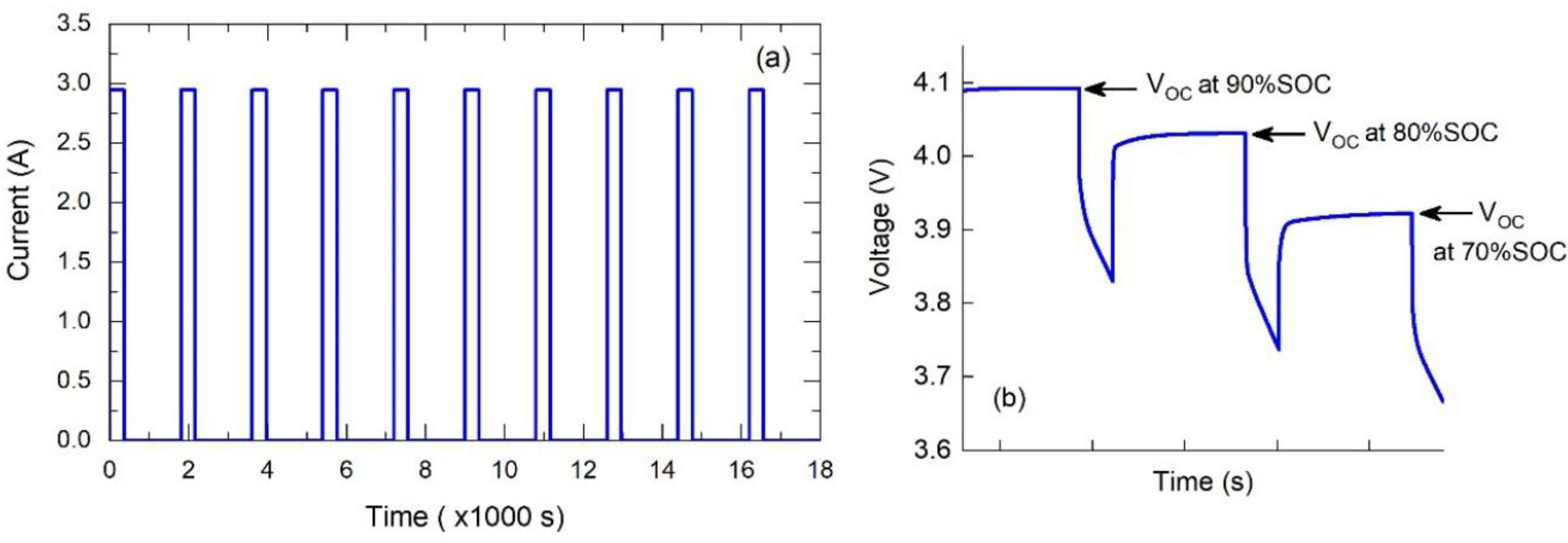
4.1. Pulse Discharge Test
4.1.1. Pulse Discharge Test
4.1.2. Constant Current Discharge Test
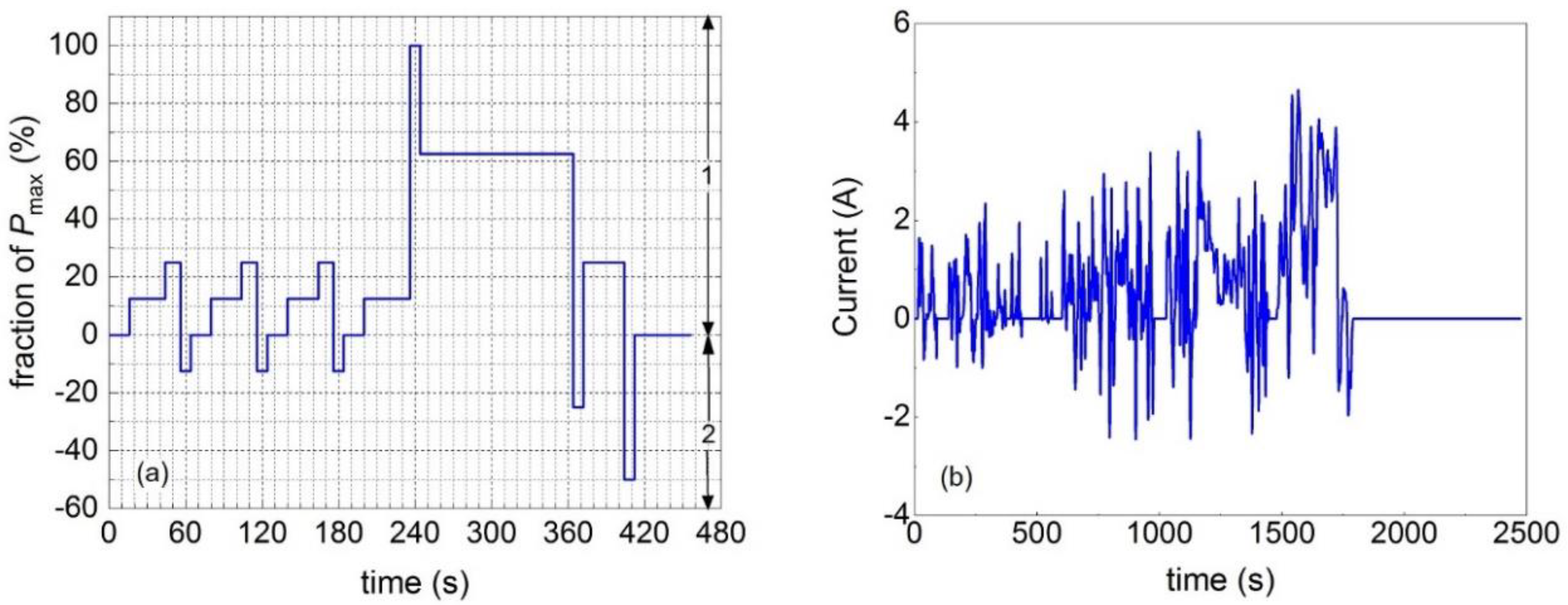
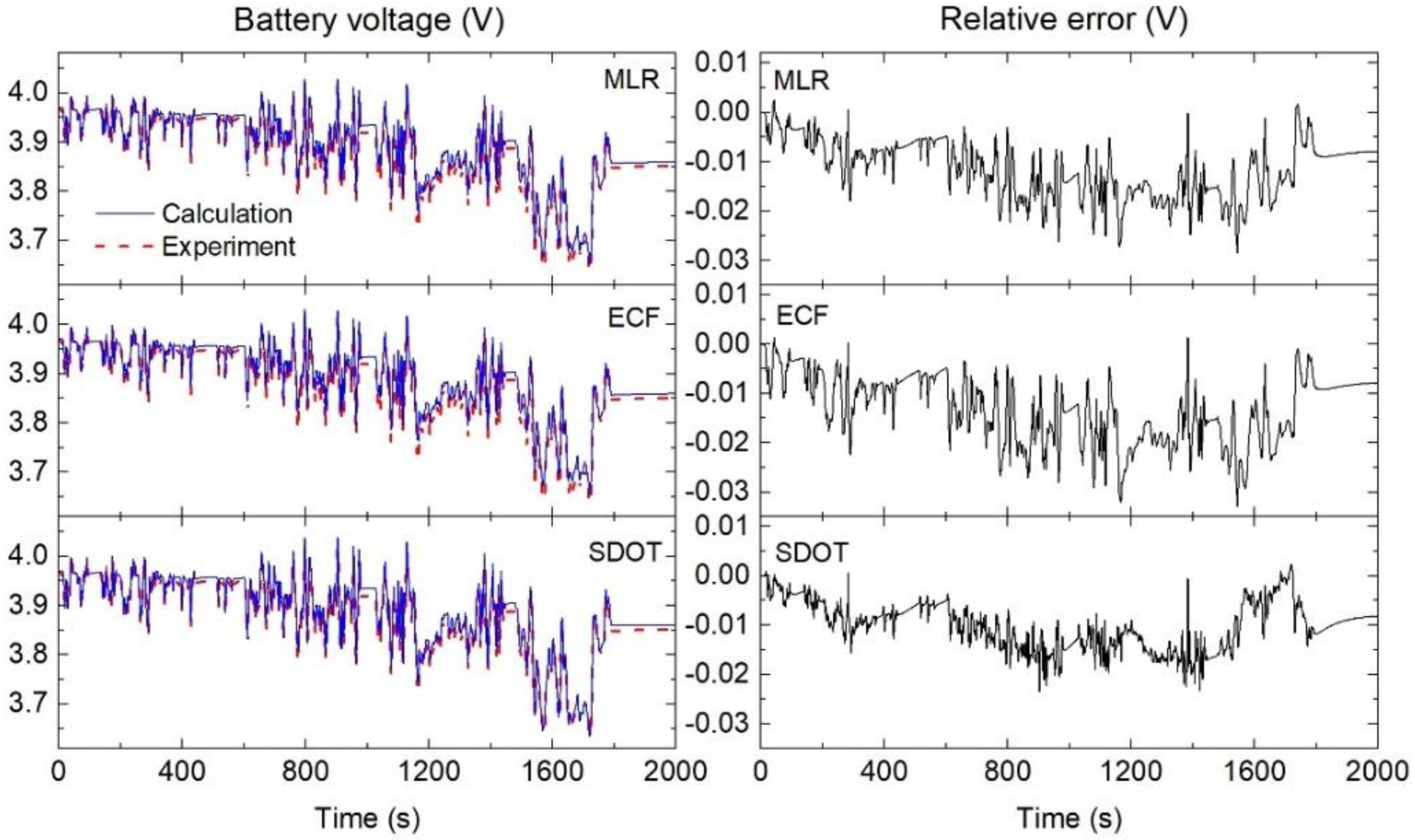
4.1.3. Dynamic Discharge Tests for EVs
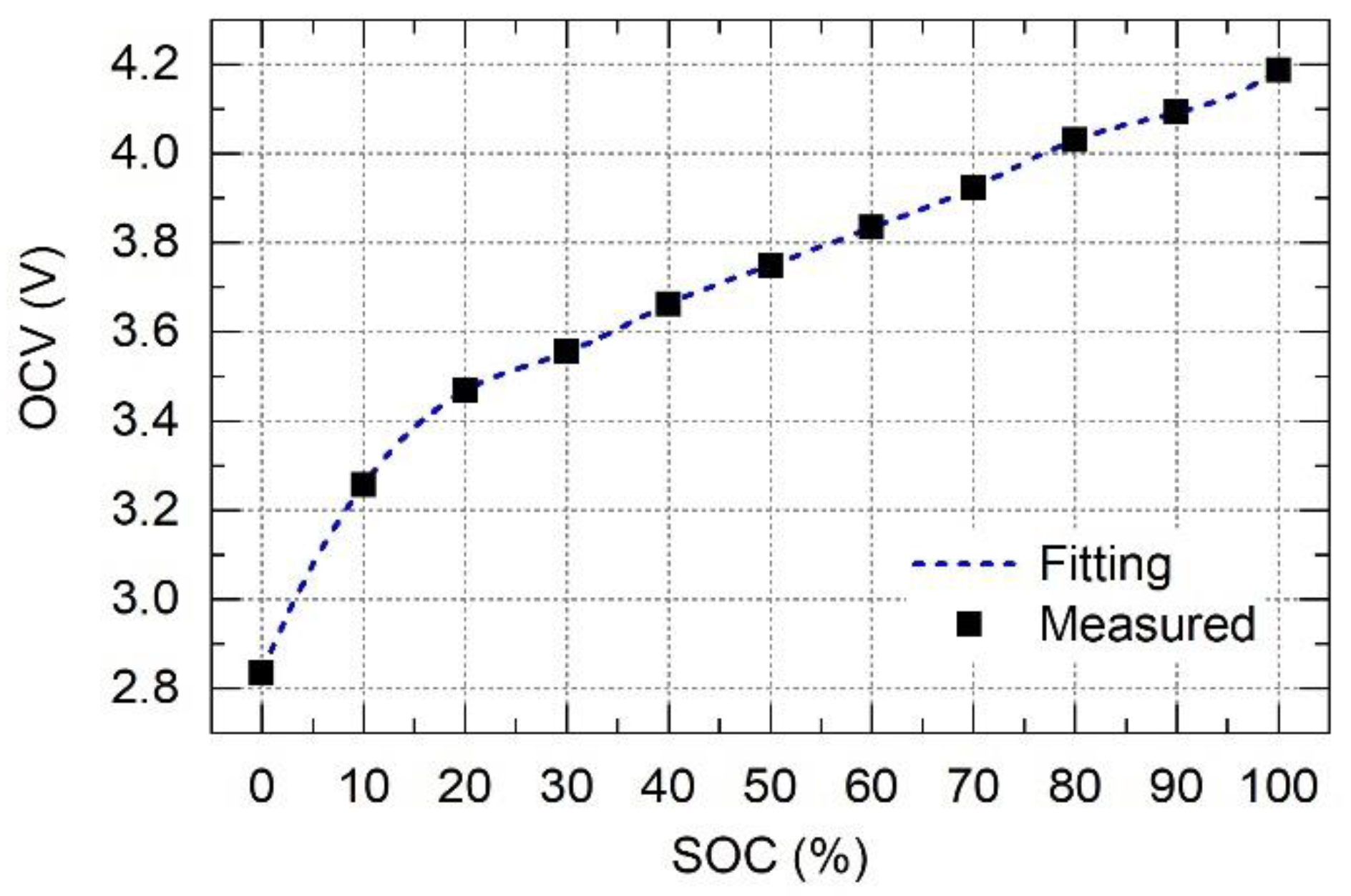
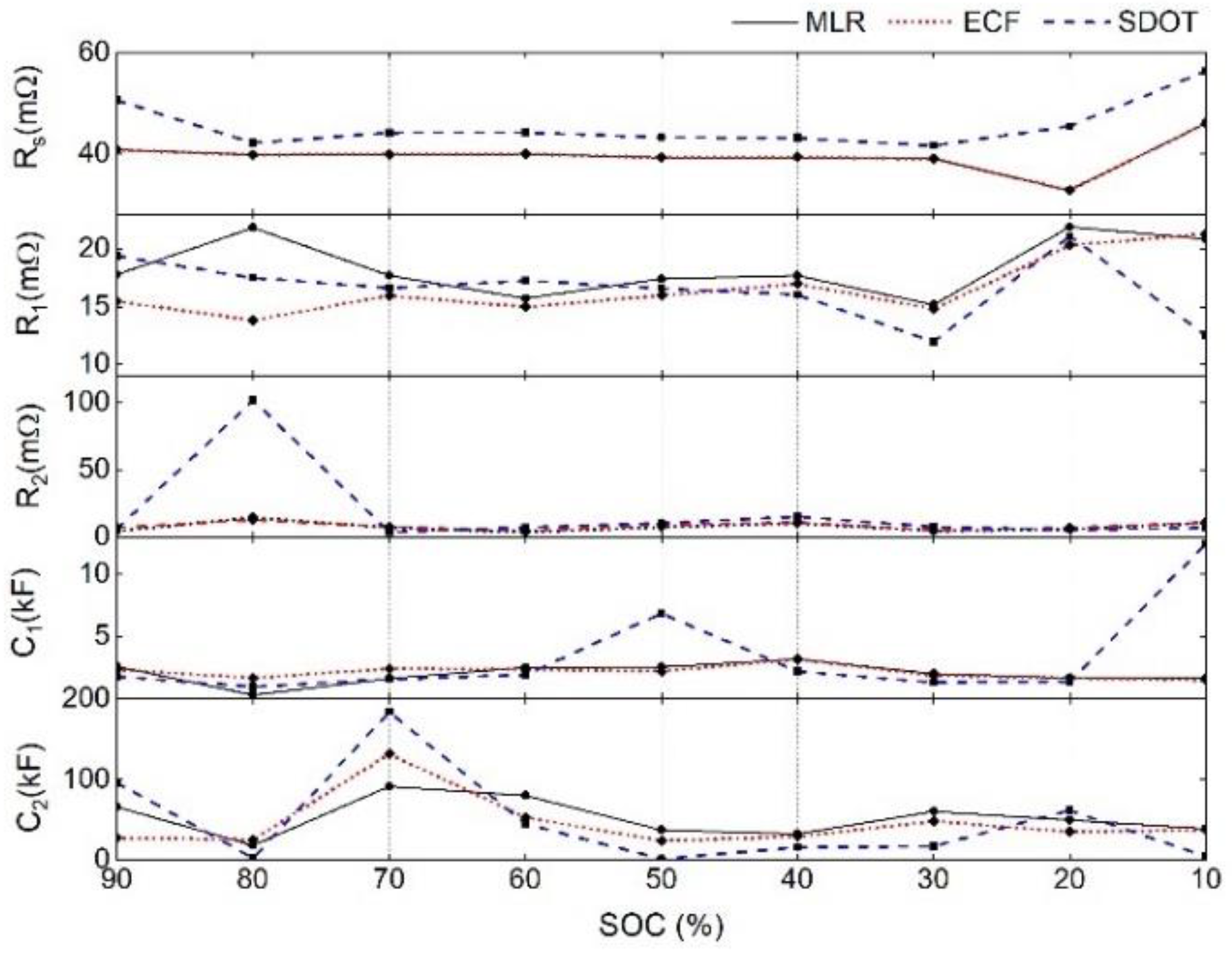
4.2. Identify the Model Parameters
4.3. Simulated Terminal Voltage for the Dynamic Discharge Tests
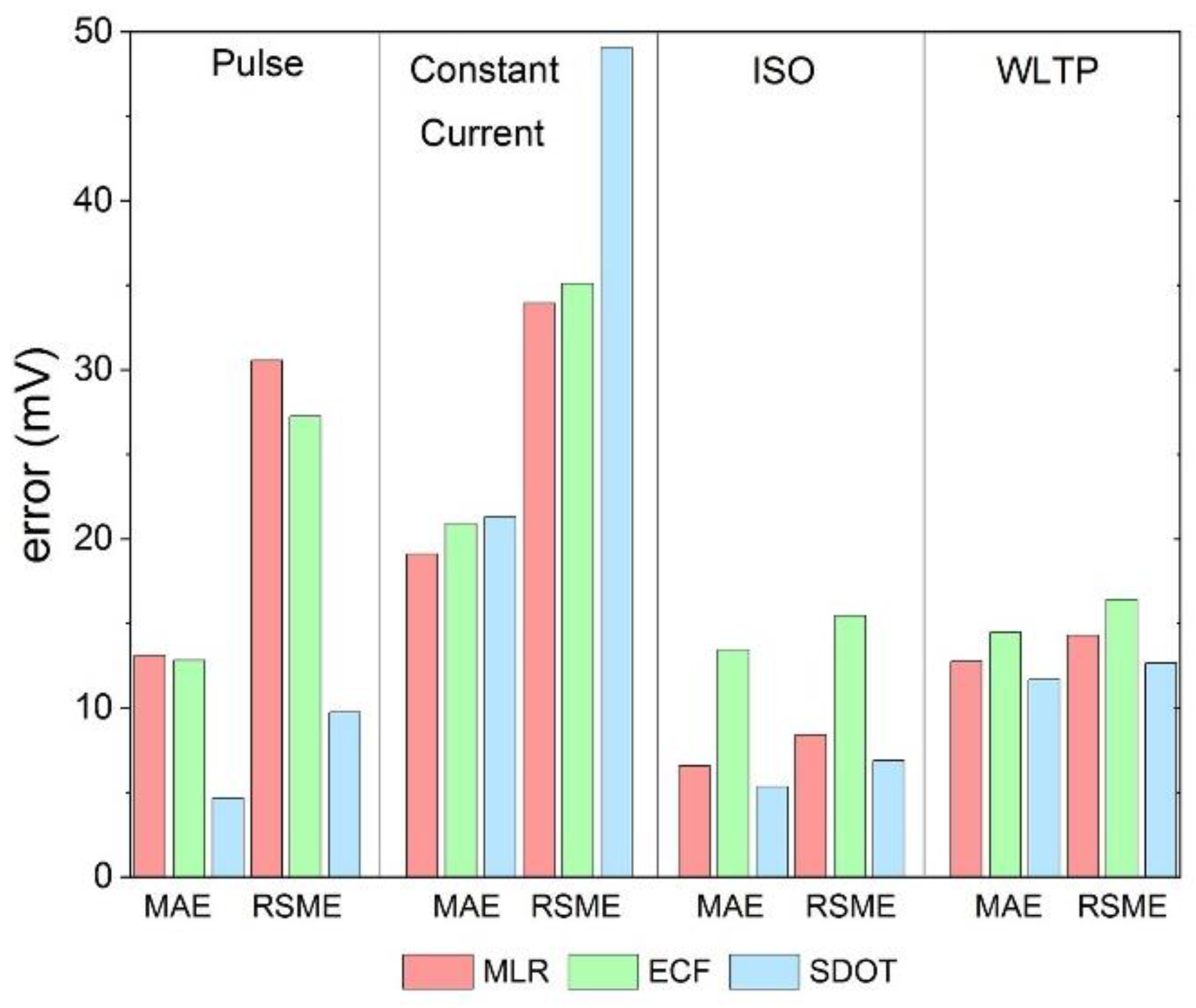
- For the pulse test, the MAE (RMSE) of the predicted voltage is 12.8 (31.5), 12.2 (27.9) and 4.2 (10.1) mV for MLR, ECF and SDOT, respectively. The errors of SDOT are around three times less than the other two methods, but it took a longer time to calculate.
- For the CC test, the MAEs of the three methods are comparable (19.1 mV(MLR) 20.2 mV(ECF) 21.9 mV(SDOT)), but the RMSE value of SDOT is obviously higher than the others (34.2 mV(MLR) 35.3 mV(ECF) 47.8 mV(SDOT)). This excess RMSE of SDOT is caused by a large error between the calculated and measured voltages at a low SOC when the nonlinearity is dominated (see Figure 10).
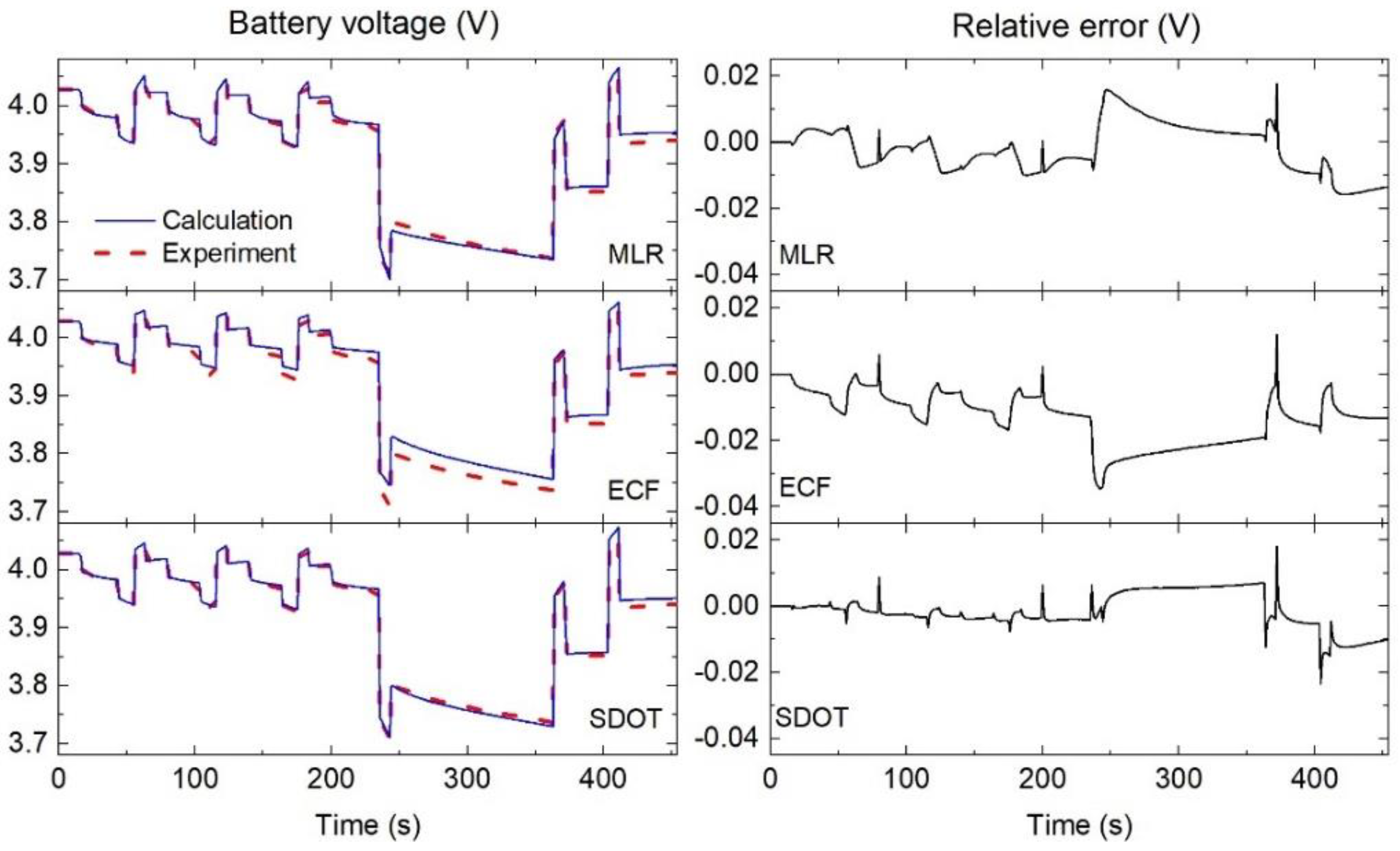
- The results under the dynamic ISO and WLTP discharge tests have a similar tendency. The SDOT is the best method providing the smallest error, followed by the MLR and ECF estimations, respectively. As can be seen in the figure, MLR and SDOT produce a comparable error, for example, the MAE for ISO is 6.1 mV (4.5 mV) and WLTP is 11.4 mV (10.2 mV) for MLR (SDOT).
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Böttiger, M.; Paulitschke, M.; Bocklisch, T. Systematic Experimental Pulse Test Investigation for Parameter Identification of an Equivalent Based Lithium-Ion Battery Model. Energy Procedia 2017, 135, 337–346. [Google Scholar] [CrossRef]
- Masoudinejad, M. Open-Loop Dynamic Modeling of Low-Budget Batteries with Low-Power Loads. Batteries 2020, 6, 50. [Google Scholar] [CrossRef]
- Yong, J.Y.; Ramachandaramurthy, V.K.; Tan, K.M.; Mithulananthan, N. A Review on the State-of-the-Art Technologies of Electric Vehicle, Its Impacts and Prospects. Renew. Sustain. Energy Rev. 2015, 49, 365–385. [Google Scholar] [CrossRef]
- Cuma, M.U.; Koroglu, T. A Comprehensive Review on Estimation Strategies Used in Hybrid and Battery Electric Vehicles. Renew. Sustain. Energy Rev. 2015, 42, 517–531. [Google Scholar] [CrossRef]
- Mayer, B.; Schier, M.; Friedrich, H.E. Stand-Alone Battery Thermal Management for Fast Charging of Electric Two Wheelers—Integrated Busbar Cooling. World Electr. Veh. J. 2019, 10, 37. [Google Scholar] [CrossRef] [Green Version]
- Wei, P.; Fan, M.Q.; Chen, H.C.; Yang, X.R.; Wu, H.M.; Chen, J.; Li, T.; Zeng, L.W.; Li, C.M.; Ju, Q.J.; et al. Enhanced Cycle Performance of Hollow Polyaniline Sphere/Sulfur Composite in Comparison with Pure Sulfur for Lithium–Sulfur Batteries. Renew. Energy 2016, 86, 148–153. [Google Scholar] [CrossRef]
- Ruiz, V.; Pfrang, A.; Kriston, A.; Omar, N.; Van den Bossche, P.; Boon-Brett, L. A Review of International Abuse Testing Standards and Regulations for Lithium Ion Batteries in Electric and Hybrid Electric Vehicles. Renew. Sustain. Energy Rev. 2018, 81, 1427–1452. [Google Scholar] [CrossRef]
- Madani, S.; Schaltz, E.; Knudsen Kær, S. An Electrical Equivalent Circuit Model of a Lithium Titanate Oxide Battery. Batteries 2019, 5, 31. [Google Scholar] [CrossRef] [Green Version]
- Baczyńska, A.; Niewiadomski, W.; Gonçalves, A.; Almeida, P.; Luís, R. Li-NMC Batteries Model Evaluation with Experimental Data for Electric Vehicle Application. Batteries 2018, 4, 11. [Google Scholar] [CrossRef] [Green Version]
- Meng, J.; Stroe, D.-I.; Ricco, M.; Luo, G.; Teodorescu, R. A Simplified Model-Based State-of-Charge Estimation Approach for Lithium-Ion Battery with Dynamic Linear Model. IEEE Trans. Ind. Electron. 2019, 66, 7717–7727. [Google Scholar] [CrossRef] [Green Version]
- Jiang, J.; Liang, Y.; Ju, Q.; Zhang, L.; Zhang, W.; Zhang, C. An Equivalent Circuit Model for Lithium-Sulfur Batteries. Energy Procedia 2017, 105, 3533–3538. [Google Scholar] [CrossRef]
- Lu, L.; Han, X.; Li, J.; Hua, J.; Ouyang, M. A Review on the Key Issues for Lithium-Ion Battery Management in Electric Vehicles. J. Power Sources 2013, 226, 272–288. [Google Scholar] [CrossRef]
- Technologies in Battery Management System—A Review. Available online: http://www.ijstr.org/final-print/feb2020/Technologies-In-Battery-Management-System-a-Review.pdf (accessed on 6 February 2022).
- Li, X.; Li, J.; Xu, L.; Ouyang, M.; Han, X.; Lu, L.; Lin, C. Online Management of Lithium-Ion Battery Based on Time-Triggered Controller Area Network for Fuel-Cell Hybrid Vehicle Applications. J. Power Sources 2010, 195, 3338–3343. [Google Scholar] [CrossRef]
- Yang, N.; Zhang, X.; Li, G. State of Charge Estimation for Pulse Discharge of a LiFePO4 Battery by a Revised Ah Counting. Electrochim. Acta 2015, 151, 63–71. [Google Scholar] [CrossRef]
- How, D.N.T.; Hannan, M.A.; Hossain Lipu, M.S.; Ker, P.J. State of Charge Estimation for Lithium-Ion Batteries Using Model-Based and Data-Driven Methods: A Review. IEEE Access 2019, 7, 136116. [Google Scholar] [CrossRef]
- Yang, F.; Li, W.; Li, C.; Miao, Q. State-of-Charge Estimation of Lithium-Ion Batteries Based on Gated Recurrent Neural Network. Energy 2019, 175, 66–75. [Google Scholar] [CrossRef]
- Chen, L.; Wang, Z.; Lu, Z.; Li, J.; Ji, B.; Wei, H.; Pan, H. A Novel State-of-Charge Estimation Method of Lithium-Ion Batteries Combining the Grey Model and Genetic Algorithms. IEEE Trans. Power Electron. 2018, 33, 8797–8807. [Google Scholar] [CrossRef] [Green Version]
- Chandran, V.; Patil, C.K.; Karthick, A.; Ganeshaperumal, D.; Rahim, R.; Ghosh, A. State of Charge Estimation of Lithium-Ion Battery for Electric Vehicles Using Machine Learning Algorithms. World Electr. Veh. J. 2021, 12, 38. [Google Scholar] [CrossRef]
- Klein, R.; Chaturvedi, N.A.; Christensen, J.; Ahmed, J.; Findeisen, R.; Kojic, A. Electrochemical Model Based Observer Design for a Lithium-Ion Battery. IEEE Trans. Control Syst. Technol. 2013, 21, 289–301. [Google Scholar] [CrossRef]
- Zhang, X.; Lu, J.; Yuan, S.; Yang, J.; Zhou, X. A Novel Method for Identification of Lithium-Ion Battery Equivalent Circuit Model Parameters Considering Electrochemical Properties. J. Power Sources 2017, 345, 21–29. [Google Scholar] [CrossRef]
- Zhou, Y.; Huang, M. On-Board Capacity Estimation of Lithium-Ion Batteries Based on Charge Phase. J. Electr. Eng. Technol. 2018, 13, 733–741. [Google Scholar]
- Uddin, K.; Perera, S.; Widanage, W.; Marco, J. Characterising Li-Ion Battery Degradation through the Identification of Perturbations in Electrochemical Battery Models. World Electr. Veh. J. 2015, 7, 76–84. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Zhang, L.; Xu, D.; Zhang, P.; Zhang, G. A Simplified Fractional Order Equivalent Circuit Model and Adaptive Online Parameter Identification Method for Lithium-Ion Batteries. Math. Probl. Eng. 2019, 2019, 6019236. [Google Scholar] [CrossRef]
- Zhang, Q.; Shang, Y.; Li, Y.; Cui, N.; Duan, B.; Zhang, C. A Novel Fractional Variable-Order Equivalent Circuit Model and Parameter Identification of Electric Vehicle Li-Ion Batteries. ISA Trans. 2020, 97, 448–457. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Guo, H.; Li, S. Comparison Study on the Battery Models Used for the Energy Management of Batteries in Electric Vehicles. Energy Convers. Manag. 2012, 64, 113–121. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, P.; Liu, Y.; Cheng, Z. Variable-Order Equivalent Circuit Modeling and State of Charge Estimation of Lithium-Ion Battery Based on Electrochemical Impedance Spectroscopy. Energies 2021, 14, 769. [Google Scholar] [CrossRef]
- De Sutter, L.; Nikolian, A.; Timmermans, J.-M.; Omar, N.; Van Mierlo, J. Online Multi Chemistry SoC Estimation Technique Using Data Driven Battery Model Parameter Estimation. World Electr. Veh. J. 2018, 9, 16. [Google Scholar] [CrossRef] [Green Version]
- Vilsen, S.B.; Stroe, D.-I. Battery State-of-Health Modelling by Multiple Linear Regression. J. Clean. Prod. 2021, 290, 125700. [Google Scholar] [CrossRef]
- Zhang, R.; Xia, B.; Li, B.; Cao, L.; Lai, Y.; Zheng, W.; Wang, H.; Wang, W.; Wang, M. A Study on the Open Circuit Voltage and State of Charge Characterization of High Capacity Lithium-Ion Battery under Different Temperature. Energies 2018, 11, 2408. [Google Scholar] [CrossRef] [Green Version]
- Tudoroiu, R.-E.; Zaheeruddin, M.; Tudoroiu, N.; Radu, S.-M. SOC Estimation of a Rechargeable Li-Ion Battery Used in Fuel Cell Hybrid Electric Vehicles—Comparative Study of Accuracy and Robustness Performance Based on Statistical Criteria. Part II: SOC Estimators. Batteries 2020, 6, 41. [Google Scholar] [CrossRef]
- Wen, F.; Duan, B.; Zhang, C.; Zhu, R.; Shang, Y.; Zhang, J. High-Accuracy Parameter Identification Method for Equivalent-Circuit Models of Lithium-Ion Batteries Based on the Stochastic Theory Response Reconstruction. Electronics 2019, 8, 834. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Mi, C.C.; Fu, Y.; Xu, J.; Gong, X. Online Battery State of Health Estimation Based on Genetic Algorithm for Electric and Hybrid Vehicle Applications. J. Power Sources 2013, 240, 184–192. [Google Scholar] [CrossRef]
- Xia, B.; Lao, Z.; Zhang, R.; Tian, Y.; Chen, G.; Sun, Z.; Wang, W.; Sun, W.; Lai, Y.; Wang, M.; et al. Online Parameter Identification and State of Charge Estimation of Lithium-Ion Batteries Based on Forgetting Factor Recursive Least Squares and Nonlinear Kalman Filter. Energies 2017, 11, 3. [Google Scholar] [CrossRef] [Green Version]
- Sun, X.; Ji, J.; Ren, B.; Xie, C.; Yan, D. Adaptive Forgetting Factor Recursive Least Square Algorithm for Online Identification of Equivalent Circuit Model Parameters of a Lithium-Ion Battery. Energies 2019, 12, 2242. [Google Scholar] [CrossRef] [Green Version]
- BSI Standard Publication. Electrically Propelled Road Vehicles—Test Specification for Lithium-Ion Traction Battery Packs and Systems—Part 2: High-Energy Applications; BSI Standards Limited 2012: London, UK, 2012. [Google Scholar]
- United Nations. Addendum 15: Global Technical Regulation No. 15—Worldwide Harmonized Light Vehicles Test Procedure; UNECE: Geneva, Switzerland, 2014. [Google Scholar]



| Item | Specification |
|---|---|
| Capacity | Nominal 3200 mAh/Minimum 3100 mAh |
| Nominal voltage | 3.67 V |
| Maximum charge voltage | 4.2 ± 0.05 V |
| Maximum charge current | 1.0C (3100 mA) |
| Maximum discharge current | 10 A |
| Standard charge | CC 0.5C (1550 mA)/CV 4.2 V/Cut-off 50 mA |
| Standard discharge | CC 0.2C (620 mA)/Cut-off 2.5 V |
| Operating temperature | Charge 0–45 °C/Discharge −20–60 °C |
| No. of Testing | 1 | 2 | 3 | 4 | 5 | Average |
|---|---|---|---|---|---|---|
| Capacity (mAh) | 2969 | 2943 | 2946 | 2952 | 2954 | 2951 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Poopanya, P.; Sivalertporn, K.; Phophongviwat, T. A Comparative Study on the Parameter Identification of an Equivalent Circuit Model for an Li-ion Battery Based on Different Discharge Tests. World Electr. Veh. J. 2022, 13, 50. https://doi.org/10.3390/wevj13030050
Poopanya P, Sivalertporn K, Phophongviwat T. A Comparative Study on the Parameter Identification of an Equivalent Circuit Model for an Li-ion Battery Based on Different Discharge Tests. World Electric Vehicle Journal. 2022; 13(3):50. https://doi.org/10.3390/wevj13030050
Chicago/Turabian StylePoopanya, Piyawong, Kanchana Sivalertporn, and Teeraphon Phophongviwat. 2022. "A Comparative Study on the Parameter Identification of an Equivalent Circuit Model for an Li-ion Battery Based on Different Discharge Tests" World Electric Vehicle Journal 13, no. 3: 50. https://doi.org/10.3390/wevj13030050
APA StylePoopanya, P., Sivalertporn, K., & Phophongviwat, T. (2022). A Comparative Study on the Parameter Identification of an Equivalent Circuit Model for an Li-ion Battery Based on Different Discharge Tests. World Electric Vehicle Journal, 13(3), 50. https://doi.org/10.3390/wevj13030050






