Abstract
The effectiveness of inductive power transfer (IPT) presents a serious challenge for improving the global recharge system performance. An electric vehicle (EVs) needs to be charged rapidly and have maximum power when it is charged with wireless technology. Based on various research, the performance of this recharge system is attached to several points and the frequency resonance is one of those parameters that can influence. In this paper, we try to explore the relationship between the obtained power and the signal input frequency for charging a lithium battery, solve the class imbalance problem and understand the maximum allowed frequency. To obtain the results, a mathematical model was first created to demonstrate the relationship, then the dynamic model was validated and tested using the Matlab Simulink platform. The performance of the worldwide wireless recharging system in terms of frequency variation is depicted in a summary graph.
1. Introduction
Many established automobile manufacturers and new dedicated companies have made significant efforts in recent years to change traditional vehicles into Electric Vehicles (EVs), which provide a green and reliable answer [1]. This solution has necessitated the development of a reliable and simple charging method [2]. The traditional recharge mechanism at home or in station parks does not satisfy consumers since it requires a long time to recharge. Waiting for a place to recharge the vehicle on a highway is not always a good idea for a driver [3]. Several engineers and researchers looked at this issue to come up with solutions [4]. Others characterized a portable recharge system as the photovoltaic recharge approach, and some proposals were centered on establishing super-fast recharge stations that require only 45 min to fully recharge the Electric Vehicles (EVs) [4]. Each solution has its own set of benefits and drawbacks, with the main issue remaining the recharge time and capacity, particularly for photovoltaic solutions. In terms of recharge time, drivers choose the super-fast recharge station; nevertheless, this is not always recommended, especially in terms of battery safety and endurance [5]. For that, the researchers seek to introduce another solution such as the wireless charging system which uses the inductive power transfer (IPT) [6]. This solution has become a potential alternative for charging at home and on the road. In the previous three decades, this innovation was extensively researched for systems ranging from 1 kW to 50 kW, and it has demonstrated significant energy and performance increases while operating safely and dependably [7]. This machinery can be applied to the charge of the battery of an EV (Electric Vehicle) for which daily recharging is mandatory [8,9]. Different methods of control were proposed for IPT systems and resonant converters for improving the recharge phase and decreasing the recharge time. Those methods try to contribute to the control of power frequency [10], control of phase shift and frequency [11], intelligent load detection [12], control of power flow [13], and modifying the battery technologies [14]. A self-oscillating phase shift control, which matches the switching activity to the resonant current, is proposed in [15] to regulate the IPT systems. The system components of an EV are based on the high-frequency block [16,17]. High-frequency designs require more amp-turns in the transmission coils and receiving coils, increasing conduction losses [18]. When the order is intended at lower frequencies, such as 10 kHz [18], high-power systems also require physically larger inductors and capacitors. When the system operates at higher rates, such as 65 kHz, the size of the inductors and capacitors can be lowered. Switching losses in converters using standard Silicon MOSFETs [19], on the other hand, grow dramatically at 65 kHz. Due to switching frequency and power handling constraints, these losses limit the switching circuit and magnetic pad components that can be used. The frequency of low-power systems was standardized at 65 kHz [19]. High-power systems, on the other hand, lack such standardization.
We provide and enhance the mathematical model, as well as results for the wireless charger and higher frequency block, in this regard. The position of the electrical receiver in relation to the transmitter, as well as the consequences for frequencies and practical validation, will be investigated. To acquire the necessary findings, the Matlab Simulink platform will be used. This paper’s expanded plan is divided into four chapters. The first will be linked to the introduction, while the second will be linked to the notion of a high-frequency wireless charging system. In the third section, the model of the static and dynamic wireless charging system is revealed. The fourth section will cover the system’s control system as well as the conclusion.
2. Wireless Charging System Presentation and Modelisation
2.1. The Position of the Frequency Controller
This research looks at the wireless charging system (wr), which is made up of two components: fixed transmitters and a moving receiver separated by a vacuum. The transmitter unit creates a high alternating magnetic flux. This magnetic flux is connected to the receiving coil and converted to electrical energy, which can then be utilized to charge an EV battery [20,21]. The charging system’s essential parameter is the amount of energy received that is brought to the cell [20]. The quantity of energy emitted, the distance between the transmit coil and the receive coil, and the alignment between the transmit coil and the receive coil all influence the received power. The component of EV and the location of the high-frequency block are shown in Figure 1a [21,22].
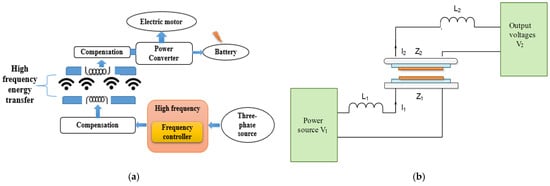
Figure 1.
Wireless charging system: (a) Block diagram of the wireless power transfer; (b) Simplified diagram of the wireless transfer system.
2.2. Model of the Wireless Charging System
2.2.1. Static Modeling
Figure 1b shows a simplified illustration of this power transfer system. The input and output voltages of this IPT are denoted by V1 and V2 as it is in Equation (6) [23]. The mutual inductance coupling model can be depicted from Equation (1), as it is in relation with the impedance formulation [22].
With
The mutual inductance “M”, the angular frequency “ω” and the primary and secondary currents are used to specify the induced and reflected voltages in this model. The magnetic coupling coefficient is related to mutual inductance by Equation (2).
Zr is the reflected impedance from the secondary to the primary, and it is expressed in Equation (3).
Zs is the secondary impedance part which depends on the selected compensation topology and then the current flowing in the secondary winding is in Equation (4).
The primary and secondary resonant frequencies are the same, according to Equation (5).
with I1 being the primary current, I2 is the secondary current. The primary and secondary inductance and capacitance are presented by (C1, C2), (L1, L2).
Equation (6) shows the voltages and power between the primary and secondary windings:
With V1, P1 as the primary voltage and power, V2, P2 are the secondary voltage and power.
Remark: this modeling method was based on two assumptions. The first one supposes that the transmission is perfect and ideal, where no magnetic loss exists and secondly no power loss is present.
2.2.2. Dynamic Modeling
The form of the transmitted magnetic flux is shown in Figure 2 for both primary and secondary coil positions. Even though the space between the coils’ centers is small, the amount of transferred flux will be large, and the energy will be higher [17]. The percentage ratio presents an essential element that should be considered to supervise the amount of the receiver power [21,23].
Figure 2.
The form of the transmitted magnetic flux for both primary and secondary coil positions.
In Equation (7), we observe the proportional flux expression of the first coil as a function of the linked physical factors. The notion that the flux transmission lines are linear is the basis for this equation. However, if the two coils are jumbled in the mobile example, we should observe that the obtained flux () in the secondary coil “connected to the vehicle” is stated as a purpose of the first established flux, as in Equation (7).
We indicate N number of turns, “” is the length of the solenoid, I current, S the surface, B the magnetic field, and the magnetic constant.
The new dynamic model method of the wireless charging system is based on two parameters, k, and Tt. k is the percentage of the obtained flux in the secondary coil is given by Equation (8).
The secondary parameter, “Tt” is the energy transfer time. The vehicle speed will affect the quantity of the received flux and power as the secondary coil is in movement. The transmitted time between the two coils is seen in Equation (9) The flux transferred is related to numerous characteristics such as the distances among coils (noted by “Dcoil”) and the vehicle (noted by “Vs > 0”) [24]. We note that even though the vehicle speed is high, the coming output power from the wireless generator is minima as the inverse for the lowest rate.
with Vs > 0.
Based on this linear relation and Equation (7) it is possible to express the portioned outputted voltage in the secondary coil as compared in Equation (10). The speed (Vs)is the relation between the static model and the dynamic model we observe that V2 in the dynamic model according to Tt and Tt = f (Vs).
“R2” is the Resistance of the secondary coil.
We note that the inductance « L » factor is related to the coil form; in this application, the shape is spiral based on the flat model. So « L » can be expressed as Equation (11).
where w is the width of winding, r is the average winding radius and N is the number of turns.
3. Results and Discussion
To improve the efficiency of the wireless charging system, we need to increase the frequency in the transmitter part, but there is a maximum limit for this phase. For this reason and based on [25,26], these simulation results show us the maximum allowable limit of the frequency. These were used to begin the simulation stage. The transmitter power is 10 kW for 500 V as an alternative input signal. The transmitter and receiver parameters are given in Table 1. The marge of switching frequencies started by 10 kHz, 30 kHz,50 kHz, and 65 kHz for the first, second, third, and fourth cases. We simulated this system for 3 s using the Simulink platform. For the control in the wireless charge system, we previously carried out some research about this subject and found that generally, the control will only be on the transmitter part. The receiver must always have the maximum flux possible and its control is related to the battery state of charge. For the transmitter part, the control has two sides. Firstly, this element will be controlled according to the reactive power value if it is acceptable or not by the grid to assure the overall grid stability. From the other side, the control of the transmitter can be made by controlling the final inverter frequency if it is on the allowed region or not. Because there is a specific region of frequency pulsation that must be guaranteed to optimize the transmitter function bloc [27].

Table 1.
Transmitter and receiver parameters.
The initial simulation phase is used to test the prior description and dynamic model. The results are achieved using a 50 kHz prototype, as shown in Figure 3. To validate the dynamic model description for the wireless charging system. This figure shows the two coils.

Figure 3.
Real prototype for the wireless transfer system.
Figure 4 shows the experimental setup in which the two coils were connected to the filter’s output to minimize any problem of instability, in parallel across the AC bus line composed of an aluminum bar 35VDC was used as the giving voltage [28].
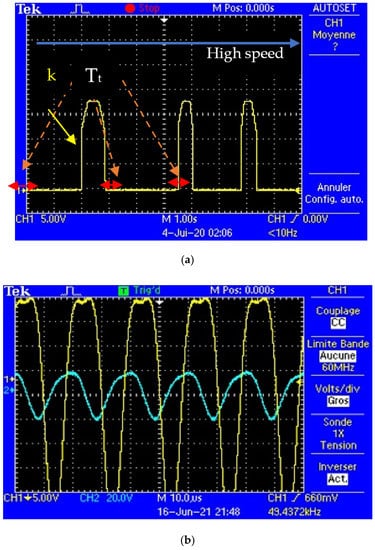
Figure 4.
(a) The effect of speed on the time required for energy to be transferred; (b) Input and output voltage of each coil receiver and transmitter.
The moveable coil is moved in a different direction with various speeds, and the result is depicted in Figure 4. Figure 4a depicts the wireless charging system’s test results as measured “Tt” from this prototype. The Tt drops as the speed increases, while the voltage at the DC bus terminal remains constant, according to this chart. Figure 4b shows the input and output voltage of each coil receiver and transmitter we observe that the frequency is high and that the output voltage is proportional to the input voltage. This confirms the dynamic mathematical model of a wireless charging system. in which the obtained power is higher for a lower speed. As a result, the findings suggest that this recharge mechanism be used at reduced levels.
Figure 5 and Figure 6 present the magnetic flux, and the corresponding obtained Power for all the measured frequency values. There is a deformation on the flux signal for the high-frequency values as “fr > 50 kHz”, which influences the quality of the obtained Power where a chattering phenomenon appears on the signal forms. The maximum density of the magnetic flux should not exceed 2187 Wb. So, the frequency limit in the interval [50 kHz 65 kHz], but this frequency hurts the wireless power transfer system.
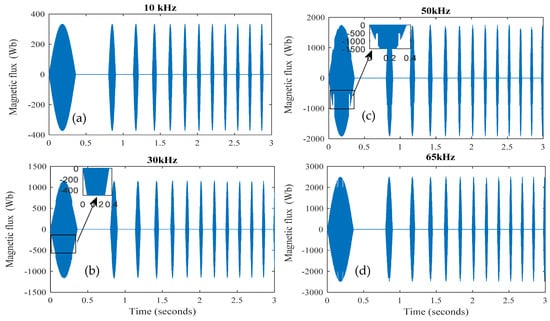
Figure 5.
Magnetic flux in relation to the resonance frequency: (a) 10 kHz; (b) 30 kHz; (c) 50 kHz; (d) 65 kHz.
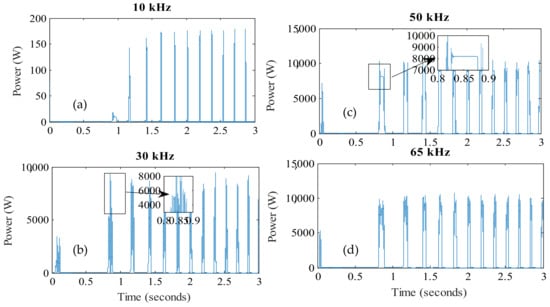
Figure 6.
The frequency effect on the Power: (a) 10 kHz; (b) 30 kHz; (c) 50 kHz; (d) 65 kHz.
The high-frequency system follows the controller regulator and reaches the desired output power of 10 kW at a resonant frequency of 50 kHz with an error of +/−100 Hz. The results of the simulations make to verify that the increase in frequency rate has a positive effect on the gain. In this case, we placed 70 transmitter coils, and this means that there is 150 cm between each transmitter coil and coil diameter 50 cm. The coils dimension is given in Figure 7.
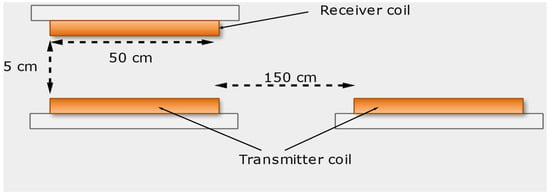
Figure 7.
Coil dimension and position.
In this part, we will attempt to expose the outcomes of the state of charge (SOC) of the battery in the car as a function of frequency, as shown in Figure 8.
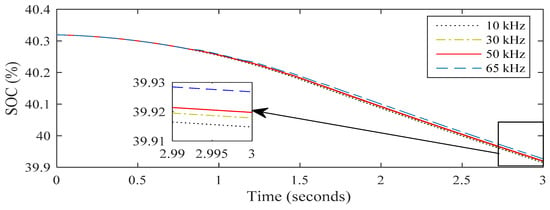
Figure 8.
Variation SOC according to the frequency.
For obtaining these results, the assumption was made that the car will be running for a distance of 0.5 km of the road in four various frequencies, 10 kHz, 30 kHz, 50 kHz, and 65 kHz.
We began with a depleted battery., where the SOC is 40.32%. In Figure 9, we can see that for the same number of coils, obtaining 39.92 percent battery SOC takes only 3 s at 10 kHz.
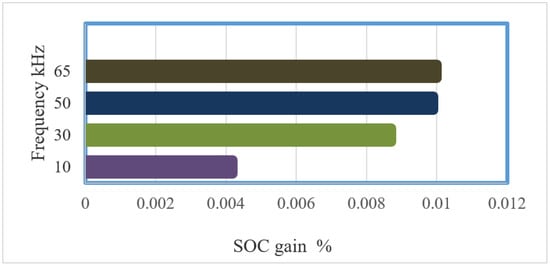
Figure 9.
SOC gain concerning the resonance frequency with consumption.
Though, for 30 kHz, we need 3 s to reach 39.925% of battery SOC. For 50 kHz and 65 kHz, the SOC value reaches only 39.93% of SOC. As a result, charging the car at a low frequency is not suggested. Adequately, we can estimate that the energy gain from each rate for 10 kHz and 30 kHz is 4 × 10−3%, 8.7 × 10−3%, 50 kHz, or more the gain estimate is 9.9 × 10−3%, 10 × 10−3%.
Figure 9 shows the SOC gain for each value of the tested frequency. It is obvious that when the resonance frequency increase, the SOC gain will be better. Between 10 kHz and 65 kHz, we had twice the SOC gain. This validates the influence of the resonance frequency on the recharge period. Based on Figure 9, Table 2 demonstrates the gain SOC for this case in 3 s and 10 h.

Table 2.
Estimated gain for 3 s and 10 h without consumption.
Figure 10 shows the wireless recharge system performances according to the tested marge of frequency. As explained before, four frequency cases are tested as 10 kHz, 30 kHz, 50 kHz, and 65 kHz. Five factors are presented in this scheme as the efficiency parameter, which is calculated using the relationship between the recharge time and the amount of the established Power. In this case, the best performance is attached to the marge of 30 to 50 kHz. However, on the derived Power, without a taken account of the quality of the electrical signal, the 65 kHz seems the best. This is validated by the estimated gain value, which is the highest for this case. According to the literature, the most used frequency is 30 kHz; however, compared to the highest frequency marge, the energetic global performance can be estimated less than the obtained one. Based on this statistic, it is clear that the resonance frequency of this recharge system can affect the global performances and can expand or drop this recharging method uses in the private or public recharge wireless stations.
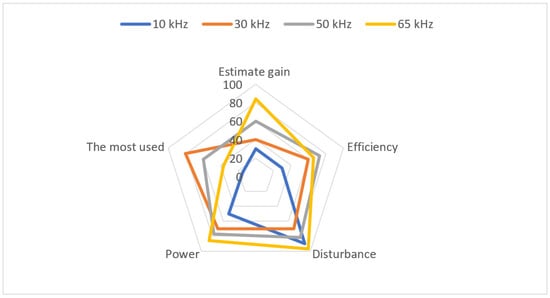
Figure 10.
Statistic with four frequencies.
4. Conclusions
According to this analysis and research, the wireless recharge system efficacy depends on several parameters, and the resonance frequency has a severe effect on its performance. Based on the mathematical analysis and using the Simulink software, the results prove that even the resonance frequency increases the output power increase from this recharge system. The high-frequency margin, on the other hand, was shown in this investigation to reduce the output electrical signal clarity. Actually, in this instance, the signal will have a detrimental impact on the employed converters, causing a slew of electronic issues. For this recharge approach, this research suggests employing a frequency range of more than 30 kHz and less than 50 kHz. With these results, future endeavors will be based on finding the optimum frequency value for a better relationship between those parameters using intelligent control methods based on PSO or BFO algorithms.
Author Contributions
N.M., F.A. and M.A. have contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the University of Business and Technology, Saudi Arabia.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| M | Mutual inductance (H) |
| ω | Oscillation angular frequency (rad/s) |
| k | Magnetic coupling constant |
| L2 | Secondary inductance (H) |
| L1 | Primary inductance (H) |
| Z2 | Primary impedance (Ω) |
| Zs | Secondary impedance (Ω) |
| I1 | Primary current (A) |
| I2 | Secondary current (A) |
| V1 | Primary voltage (V) |
| V2 | Secondary voltage (V) |
| N | Number of turns |
| Magnetic constant | |
| L | Inductance (H) |
| P1 | Primary power |
| P2 | Secondary power |
References
- Salah, W.A.; Albreem, M.A.M.; Alsayid, B.; Zneid, B.A.; Alkhasawneh, M.; Al–Mofleh, A.; Sneineh, A.A.; Abu Al-Aish, A. Electric vehicle technology impacts on energy. Int. J. Power Electron. Drive Syst. 2019, 10, 1–9. [Google Scholar] [CrossRef]
- Ten Have, S.Y.; Gkiotsalitis, K.; Geurs, K.T. Investigating the future of ultrafast charging: A choice experiment in The Netherlands. World Electr. Veh. J. 2020, 11, 70. [Google Scholar] [CrossRef]
- Chakrabarty, M.; Sarkar, D.; Basak, R. A comprehensive literature review report on basic issues of power system restoration planning. J. Inst. Eng. Ser. B 2020, 101, 287–297. [Google Scholar] [CrossRef]
- Kumaresan, J.; Govindaraju, C. PV-tied three-port DC–DC converter-operated four-wheel-drive hybrid electric vehicle (HEV). Electr. Eng. 2020, 102, 2295–2313. [Google Scholar] [CrossRef]
- Fotouhi, A.; Auger, D.J.; Propp, K.; Longo, S.; Wild, M. A review on electric vehicle battery modelling: From Lithium-ion toward Lithium-Sulphur. Renew. Sustain. Energy Rev. 2016, 56, 1008–1021. [Google Scholar] [CrossRef] [Green Version]
- Bi, Z.; Kan, T.; Mi, C.C.; Zhang, Y.; Zhao, Z.; Keoleian, G.A. A review of wireless power transfer for electric vehicles: Prospects to enhance sustainable mobility. Appl. Energy 2016, 179, 413–425. [Google Scholar] [CrossRef] [Green Version]
- Naoui, M.; Flah, A.; Ben Hamed, M.; Sbita, L. Review on autonomous charger for EV and HEV. In Proceedings of the International Conference on Green Energy Conversion Systems (GECS), Hammamet, Tunisia, 23–25 March 2017; pp. 1–6. [Google Scholar]
- Kraiem, H.; Flah, A.; Mohamed, N.; Alowaidi, M.; Bajaj, M.; Mishra, S.; Sharma, N.K.; Sharma, S.K. Increasing electric vehicle autonomy using a photovoltaic system controlled by particle swarm optimization. IEEE Access 2021, 9, 72040–72054. [Google Scholar] [CrossRef]
- Madawala, U.K.; Neath, M.; Thrimawithana, D.J. A power-frequency controller for bidirectional inductive power transfer systems. IEEE Trans. Ind. Electron. 2013, 60, 310–317. [Google Scholar] [CrossRef]
- Zahid, Z.U.; Dalala, Z.M.; Zheng, C.; Chen, R.; Faraci, W.E.; Lai, J.S.J.; Lisi, G.; Anderson, D. Modeling and control of series-series compensated inductive power transfer system. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 111–123. [Google Scholar] [CrossRef]
- Berger, A.; Agostinelli, M.; Vesti, S.; Oliver, J.A.; Cobos, J.A.; Huemer, M. A Wireless charging system applying phase-shift and amplitude control to maximize efficiency and extractable power. IEEE Trans. Power Electron. 2015, 30, 6338–6348. [Google Scholar] [CrossRef]
- Wang, Z.H.; Li, Y.P.; Sun, Y.; Tang, C.S.; Lv, X. Load detection model of voltage-fed inductive power transfer system. IEEE Trans. Power Electron. 2013, 28, 5233–5243. [Google Scholar] [CrossRef]
- Miller, J.M.; Onar, O.C.; Chinthavali, M. Primary-side power flow control of wireless power transfer for electric vehicle charging. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 147–162. [Google Scholar] [CrossRef]
- Li, Y.; Vilathgamuwa, M.; Wikner, E.; Wei, Z.; Zhang, X.; Thiringer, T.; Wik, T.; Zou, C. Electrochemical model-based fast charging: Physical constraint-triggered PI control. IEEE Trans. Energy Convers. 2021, 8969, 3208–3220. [Google Scholar] [CrossRef]
- Namadmalan, A. Self-oscillating tuning loops for series resonant inductive power transfer systems. IEEE Trans. Power Electron. 2016, 31, 7320–7327. [Google Scholar] [CrossRef]
- Huang, M.; Li, X.; Lei, Y.; Gu, J. Structural damage identification based on modal frequency strain energy assurance criterion and flexibility using enhanced Moth-Flame optimization. Structures 2020, 28, 1119–1136. [Google Scholar] [CrossRef]
- Chopra, S. Contactless Power Transfer for Electric Vehicle Charging Application. Master’s Thesis, Delft University, Delft, The Netherlands, 2011. [Google Scholar]
- Mohamed, N.; Aymen, F.; Mouna, B.H. Inductive charger efficiency under internal and external parameters variation for an electric vehicle in motion. Int. J. Powertrains 2019, 8, 343–358. [Google Scholar] [CrossRef]
- Rosu, S.G. A dynamic wireless charging system for electric vehicles based on DC/AC converters with SiC MOSFET-IGBT switches and resonant gate-drive. In Proceedings of the 42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; pp. 4465–4470. [Google Scholar]
- Khutwad, S.R.; Gaur, S. Wireless charging system for electric vehicle. In Proceedings of the 2016 International Conference on Signal Processing, Communication, Power and Embedded System (SCOPES), Paralakhemundi, India, 3–5 October 2016; pp. 441–445. [Google Scholar]
- Mohamed, N.; Aymen, F.; Alqarni, M.; Turky, R.A.; Alamri, B.; Ali, Z.M.; Abdel, S.H.E. A new wireless charging system for electric vehicles using two receiver coils. Ain Shams Eng. J. 2021. [Google Scholar] [CrossRef]
- Mohamed, N.; Aymen, F.; Ali, Z.M.; Zobaa, A.F.; Aleem, S.H.E.A. Efficient power management strategy of electric vehicles based hybrid renewable energy. Sustainability 2021, 13, 7351. [Google Scholar] [CrossRef]
- Dominic Savio, A.; Vimala Juliet, A. Development of multiple plug-in electric vehicle mobile charging station using bidirectional converter. Int. J. Power Electron. Drive Syst. 2020, 11, 785–791. [Google Scholar] [CrossRef]
- Mohamed, N.; Flah, A.; Ben Hamed, M. Wireless charging system for a mobile hybrid electric vehicle. In Proceedings of the 2018 International Symposium on Advanced Electrical and Communication Technologies (ISAECT), Rabat, Morocco, 21–23 November 2018; pp. 1–5. [Google Scholar]
- Allamehzadeh, H. Wireless power transfer (WPT) fundamentals with resonant frequency-dependent parameters, energy transfer efficiency, and green technology applications. In Proceedings of the 2021 IEEE 48th Photovoltaic Specialists Conference (PVSC), Fort Lauderdale, FL, USA, 20–25 June 2021; pp. 36–40. [Google Scholar]
- Ishida, H.; Furukawa, H.; Kyoden, T. Scheme for providing parity-time symmetry for low-frequency wireless power transfer below 20 kHz. Electr. Eng. 2021, 103, 35–42. [Google Scholar] [CrossRef]
- Lin, C.H.; Amir, M.; Tariq, M.; Shahvez, M.; Alamri, B.; Alahmadi, A.; Siddiqui, M.; Beig, A.R. Comprehensive analysis of ipt v/s CPT for wireless EV charging and effect of capacitor plate shape and foreign particle on CPT. Processes 2021, 9, 1619. [Google Scholar] [CrossRef]
- Mohamed, N.; Aymen, F.; Lassaad, S.; Mouna, B.H. Practical validation of the vehicle speed influence on the wireless recharge system efficiency. In Proceedings of the 6th IEEE International Energy Conference (ENERGYCon), Gammarth, Tunisia, 28 September–1 October 2020; pp. 372–376. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).