Abstract
In a recent trend, electric vehicles (EV) have been facing various power quality issues, so fuel cells (FC) are considered the best choice for integrating EV technology to enhance performance. A fuel cell electric vehicle (FCEV) is a type of EV that uses a fuel cell combined with a small battery or super-capacitor to power its on-board electric motor. However, the power obtained from the FC system is much less and is not enough to drive the EV. So, another energy source is required to deliver the demanded power, which should contain high voltage gain with high conversion efficiency. The traditional converter produces a high output voltage at a high duty cycle, which generates various problems, such as reverse recovery issues, voltage spikes, and less lifespan. High switching frequency and voltage gain are essential for the propulsion of FC-based EV. Therefore, this paper presents an improved radial basis function (RBF)-based high-gain converter (HGC) to enhance the voltage gain and conversion efficiency of the entire system. The RBF neural model was constructed using the fast recursive algorithm (FRA) strategy to prune redundant hidden-layer neurons. The improved RBF technique reduces the input current ripple and voltage stress on the power semiconductor devices to increase the conversion ratio of the HGC without changing the duty cycle value. In the end, the improved RBF with HGC achieved an efficiency of 98.272%, vehicle speed of 91 km/h, and total harmonic distortion (THD) of 3.12%, which was simulated using MATLAB, and its waveforms for steady-state operation were analyzed and compared with existing methods.
1. Introduction
For the past few years, conventional automobiles have used petroleum products, which leads to more environmental pollution and has become a major concern globally. To overcome the environmental pollution problems, EVs with renewable energy sources (RES) such as solar, FCs, and combined systems have been introduced [1,2]. Hence, EVs inevitably became the most ideal technological solution in the automobile industry sector [3]. These EVs need an electric power source to supply power to the motor that runs the vehicle. This power source comprises a battery that needs to be charged when the power is completely discharged [4]. This means that battery-powered electric vehicles have a limited driving range, after which the batteries need to be charged. So, in this research, a fuel cell was selected as a better substitute for batteries to overcome the above-mentioned factors. A fuel cell can generate electric current as long as hydrogen is supplied [5]. Fuel cells (FC) are a suitable solution for transportation applications because of their compactness and hydrogen usage, which is utilized as an alternative fuel that does not emit CO2. A single FC system in a vehicle is not sufficient to satisfy the dynamically varying motor power demands. FCs provide good proficiency and presentation for the duration of the steady-state process, but the response time of FCs in the course of transient conditions is unsatisfactory [6,7]. So, to overcome these challenging factors, the FC system should be connected to a high-gain converter that has a good transient and steady-state response to come across the total power necessity of the EV in both conditions [8].
Generally, the main purpose of applying a converter is to control the source side independently and to transmit energy from the supply side to deliver to the grid with higher voltage levels. Nevertheless, the fundamental boost converter can encounter some drawbacks. For example, high voltage can be attained by increasing the duty cycle [9,10]. However, due to reasons such as saturation, reverse recovery problems, and low conversion efficiency, the conversion ratio cannot be increased. Moreover, a proper DC-DC boost converter should have some beneficial features, for example, low power losses, high voltage-gain ratio, a low number of elements and stress across the power switch, and lower volume/weight [11,12]. The problem of CO2 emissions and global warming can be reduced by focusing on the usage of renewable energy in vehicles [13]. Out of the available renewable energy sources, a fuel cell is the only source that has reasonable efficiency and can be used in vehicles. However, the main disadvantage of a fuel cell is its slow response time [14]. Therefore, fuel cells are used during steady-state vehicle operation, whereas for transient conditions like starting, acceleration, and braking, batteries and super-capacitors can supply or absorb energy [15].
In the paper by [16], the sensor and proposed system were appropriate for small autonomous surface vehicles (ASV), accomplishing their responsibilities in local water or constrained harbor zones. The sensor recognition range was too little, so it was valuable for oceanic vessels only. Consequently, for this research, oceanic applications were considered out of scope [17]. So, in this research, the cases covered by this investigation assume that the ASV is executing an autonomic mission in some roadside applications. In addition, to further validate the performance and highlight the benefit of the proposed algorithm, a case study is conducted where the improved RBF algorithm is applied to supply the reference for predictive energy management of EV, and FRA is applied with the help of the future speed information supplied by different speed prediction algorithms, including the proposed algorithm. The motor speed is compared to evaluate the predictor’s performance, and the detailed comparison results indicate that the proposed algorithm is more effective in supplying future information for predictive EMSs and facilitating improvement of EVs.
- In this paper, a bidirectional high-gain converter with improved RBF is projected that could incorporate DC at various levels of voltages and similarly control the voltage level to the DC bus and vice versa.
- To control the output voltage of the high-gain converter, an improved RBF controller is designed to change the duty cycle.
- An improved RBF with HGC is designed using MATLAB/SIMULINK, and its performance parameters of speed, power loss, input/output voltage waveforms, and THD for steady-state operation are analyzed.
The structure of the paper is as follows: Section 2 describes the literature review of the existing methods. Section 3 explains the problem statement of the research work. Section 4 elaborates on the improved RBF method, and Section 5 describes the results and discussion, as well as a comparative analysis of existing and proposed methods. Section 6 presents the conclusions of this research paper.
2. Literature Review
Navamani et al. [18] demonstrated various high-gain (HG) cells, and the cell’s performance was analyzed by combining it with a quadratic boost converter. HG cells reduce the voltage stress across the active switch. This allows the usage of an active switch with low resistance and thus reduces the conduction loss of the switch. Three state-switching cells were combined with a voltage multiplier cell to increase the output voltage. The suggested converter was working at a high duty cycle value, which was used to attain a high ratio, but it cannot produced an intense reduction in the performance of efficiency.
Lakshmi and Hemamalini [19] demonstrated a single-stage high-gain DC-DC converter with coordinated control that helped to provide constant DC voltage to the DC loads even though the inverter was disconnected from the DC bus. The operation of three switches with two different duty ratios was the main advantage of this converter to accomplish the coordinated control of MPPT and DC voltage regulation. However, the disadvantage of the proposed coordinated control strategy was that the DC voltage regulation was not possible at the DC link during the fault/disconnection of the DC-DC converter.
Upadhyay and Kumar [20] presented a high-gain cascaded converter that had two-stage boosting with effective overall gain in the form of a quadratic quadruple boost (QQB) factor. The converter achieved high voltage gain with a low duty ratio, which was necessary for the efficient operation of a boost converter. The two-stage converter was operated at a duty ratio of 0.5 to achieve a better voltage gain, whereas maintaining the coupled inductor turned the ratio into less than two. However, a detailed analysis of the proposed converter in terms of soft-switching and integration was not considered in this paper.
Revathi et al. [21] demonstrated a non-isolated high-gain DC-DC converter to improve the voltage gain and conversion efficiency of the system. The proposed converter used the interleaved technique with a uniform phase shift between the interleaved legs, and the converter was constructed from an interleaved boost converter (IBC) to reduce the input current ripple. However, the switching losses of the semiconductor devices occurred due to the deployed hard-switching technique, especially when high currents were involved.
Amir et al. [22] presented a high-gain boost and buck-boost converter with a modular control strategy to improve the voltage gain and conversion efficiency. The proposed modular structure allowed for an increase in the number of switched-capacitor cells to obtain reduced voltage stress on the switching components with a higher voltage gain. The proposed converter operated at a lower duty cycle, which resulted in significantly improved efficiency compared to existing converters. Even though it produced high voltage gain, it was not essentially feasible with a conventional boost converter.
Mebarki et al. [23] demonstrated a controller for a freestanding hybrid power system that provides electricity to an electric vehicle. To charge the EV, a direct torque control (DTC) technique was used to coordinate three sources of power. This strategy achieved effective control of the stator flux and torque by selecting the space voltage vectors optimally in each sample cycle. However, although hydrogen cells are now used to power hybrid autos, they are still not a viable fuel source for all applications.
Hassan Fathabadi [24] proposed a three-phase PWM six-switch DC/AC inverter to design novel PV/battery combinations. In the suggested hybrid power source system, solar energy was used as a renewable energy source to extend PHEVs’ cruise range. The power efficiency curve clearly showed that the proposed battery/PV hybrid power source had a power efficiency of 91% around the traction motor’s rated output. However, the vehicle’s battery charge level may be insufficient at providing the requisite power to its electric motors at times.
Padmagirisan and Sankaranarayanan [25] demonstrated a hybrid electric vehicle with solar photovoltaic batteries and a powertrain controller (HEV). The lower-level controllers were then switched between using a high-level control algorithm based on different operating conditions like high state of charge, low state of charge, maximum battery current, and heavy load. The suggested controller’s major goal was to improve battery management, load regulation, and maximum power extraction from photovoltaic panels whenever possible. However, only a limited quantity of energy can be stored in the battery using this method, limiting the driving range significantly.
Zhiyu Huang et al. [26] presented the modeling and energy management of a photovoltaic–fuel cell–battery hybrid electric vehicle. To maximize solar energy utilization under fast-changing power demand, solar energy variance, and varied degrees of battery state of charge, a fuzzy logic control-based energy management strategy (EMS) was proposed. Under the EMS regulation, this system proved to be successful and adaptable in a variety of scenarios, and it achieved better fuel economy than a widely used power-following control technique. However, modeling and simulating the power electrical system produced from that structure to examine the possibility of deploying such a vehicular power system in the real world remains an unsolved problem.
Esfandiari et al. [27] demonstrated remote control energy management to examine the performance of a campus solar electric vehicle charging station in various temperature situations. A vehicle charging station consisting of a PV array with a lithium-ion battery was designed using a measured solar resource and vehicle energy use, as well as locational, mechanical, and electrical restrictions. This notion, however, is unlikely to come to fruition because EV charging would take place at night.
A lot of studies have been discussed about fuel cell electric vehicles, which are popular and effective. Still, there is a gap in describing the progress and developments in fuel cell electric vehicles due to the problem in powertrain structures, restricted capacity, and fuel cell components, which reduces traveling ranges and vehicle speed. Furthermore, EVs take more time to recharge and fast-charging stations consume higher costs. These inherent problems, combined with a lack of recharging infrastructure, highly inhibit the wide-scale adoption of EVs. So, this research identifies the essential methods and challenges of a fuel cell-operated vehicle under different load profiles. The power source required to operate a vehicle is very high. As it is not possible to run a vehicle with one single fuel cell, it is necessary to stack the fuel cell in a series or in parallel to get the maximum power productivity to increase the vehicle speed. This research achieves higher efficiency through high-tech sensors and driving schemes which allows them to activate securely in a quicker manner.
3. Problem Statement
- Converters have a high voltage ratio, which leads to huge losses in electrical components, and voltage stress occurs at converting stages.
- Once the capacitor is exploited, more current transfers through the switches, which creates damage to the circuit. So, the efficiency of the converter can be decreased by this process.
- Furthermore, charging the vehicle battery has more impact on increasing the total harmonic distortion rather than the power losses.
4. Proposed Method
Many automotive establishments are working on developing fuel cell-powered hybrid electric vehicles because they offer reduced loss and improved efficiency. This paper presents HGC converter topologies used to interface the fuel cell to the motor controllers in HEVs. The aim is to present a simple HGC converter topology with a coordinated control, called an improved RBF, that can regulate both the output voltage and the input current simultaneously.
Figure 1 shows the general block diagram for the FC-integrated high-gain converter. Generally, traditional converters working at risky duty cycle values attain better voltage gain. Executing the circuit at a risky ratio produces interference, high conduction losses, and reverse recovery issues at the switches. So, this research suggests an HGC that functions at a low value of duty cycle. This HGC needs a distinct signal for controls to decrease the operational complication. In the Results and Discussion section, the steady-state analysis is designated and tested by MATLAB simulation. The overall control structure of the research is shown below in Figure 2.
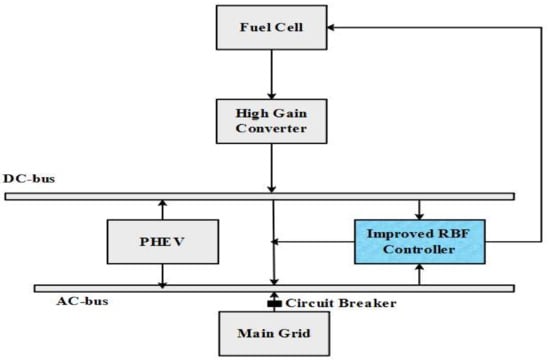
Figure 1.
Block diagram for the FC-integrated high-gain converter.
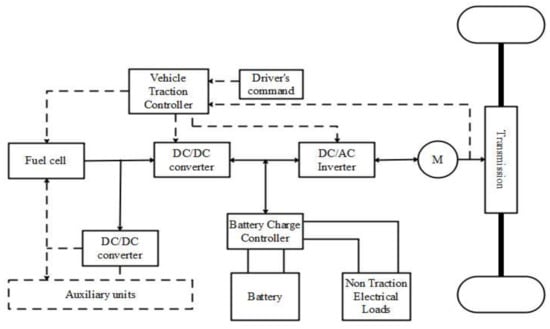
Figure 2.
Overall control structure.
The following characteristic operating points of the drive system are offered to supplement the powertrain’s summary evaluation during energy flow on selected instantaneous vehicle acceleration and deceleration phases.
- During vehicle acceleration, the initial energy input from the battery is visible until the fuel cell starts producing energy.
- During braking, the fuel cell operation is shut down and the energy is recovered to the high-voltage battery.
- Larger amounts of energy are utilized from both the battery and the fuel cell sources depending on the vehicle’s acceleration rate.
- The high-voltage battery meets the energy requirements of the on-board systems when the vehicle is stationary.
4.1. High-Gain Converter
This HGC topology contains two half-bridge diodes on the high voltage side and two full-bridge diodes on the low voltage side of the transformers. The designated topology delivers the selection to associate various resources at dissimilar voltage ranges. When an FC-dependent EV increases the speed, the HGC works in boost operation mode and maintains the voltage at the preferred range. As soon as the EV operates in braking mode, the HGC functions in buck mode to incriminate the loading components [6,7,8,9].
Figure 3 illustrates the HGC topology, which contains three capacitors, three inductors, four switches, four diodes, and resistive load. In this topology, MOSFETs are exploited as switches, which are established by the duty cycle value produced by the proposed technique. The ratio of the DC voltage is enhanced without the help of isolated transformers. While associating with a traditional converter, this HGC topology provides less stress on switches, which increases its consistency in real-world applications.
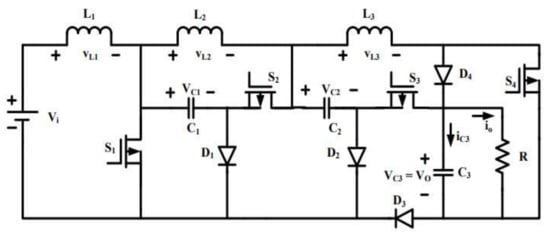
Figure 3.
Circuit diagram of a high-gain converter.
4.2. Modeling of the Fuel Cell
In this research, an FC was utilized for the design of experimental inputs/outputs to make them appropriate for the real-time model. This designed circuit consisted of a converter, battery charger, and DC load. Those components helped to measure the output of the FC. The equivalent modeling of the fuel cell is shown in Figure 4.
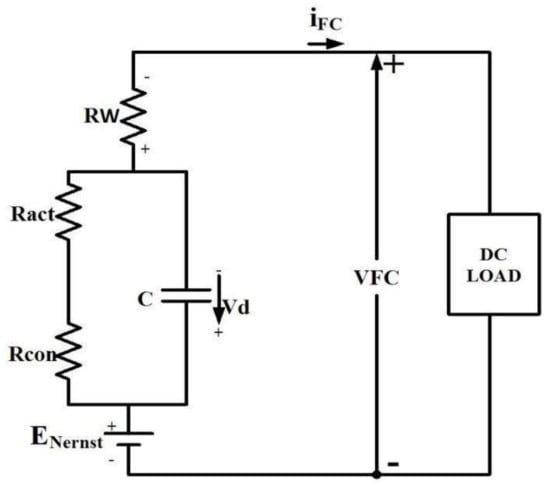
Figure 4.
Equivalent circuit of a fuel cell.
From the diagram, where represents the actual value of resistance; signifies the output voltage of every piece; characterizes the resistance concentration loss; VFC and IFC represents the voltage and current across the fuel cell, respectively; and signifies the resistance coefficient. The excess ratio of oxygen is referred to as (), which works as a significant component in an FC regulator. Equations (1) and (2) describe the demanded stack current () separately.
where the mass of hydrogen is referred to as , the mass of oxygen is designated as , F is as the Faraday constant, and n represents the cell count. represents the hydrogen movement, and the stack is signified as . The connection between the movement of oxygen and the stack is necessary to provide the existing demand, which is stated in Equation (3).
where the oxygen excess ratio is stated as . signifies the movement of the cathode oxygen, and characterizes the flow of oxygen disbursed, which is completely based on Equation (2). The steady-state equation is exhibited as Equation (4):
where the stack current of the FC is stated as and , are tuned parameters. In physical security information management (PSIM) archives, non-linear resistors are available. Therefore, the logarithmic and exponential terms of Equation (4) are modeled by nonlinear resistors RNL1 and RNL2.
4.3. Backpropagation Algorithm
In this research, ANN was deliberated and trained by the backpropagation (BP) method, which uses Levenberg–Marquardt (LM) [28]. Here, the BPNN utilized current as the input and DC voltage as the output, which produced a duty cycle value to regulate the converter switches to attain better results [29]. The working principle of BPNN is managed in four layers. A demonstration of each layer is shown in the next steps.
The input/output signal matrix is characterized in the following Equations (5) and (6).
where x represents the input signal and y is referred to as the output. Primarily, the assumed inputs are managed in the BPNN’s first layer, which computes the z value, which is provided in the following layer. This layer controls the max/min values of x and y, which are described in Equation (7).
where is the gain that is given in Equation (8).
is given as an input to the next layer. During the training process, bias and weight are designed. The hidden layer output is expressed in Equation (9).
The result produced from the layer is assumed as the input for layer two. and are referred to as weight and bias, respectively. is designated as the hidden layer two output, which is expressed as Equation (10).
Finally, from the output layer, an equivalent duty cycle value is attained. The layer input is exposed as inverse planning to accomplish the preferred output. The result of layer is managed and sustained as input to the FC, which is specified in Equation (11).
Hence, by means of the above-mentioned scheme, an equivalent value for a high-gain converter is attained.
4.4. Radial Basis Function Network Algorithm
RBFN is a type of feed-forward neural network that develops a radial network for convenient working operation [30]. This method functions identically to the backpropagation process, which is described clearly in [31].
Here, the voltage/current is provided as an input to RBFN, which is utilized to calculate the duty cycle value for the output. RBFN is assigned to produce a duty cycle value for a high-gain converter. Figure 5 illustrates the three layers that are used for the operation of RBFN.
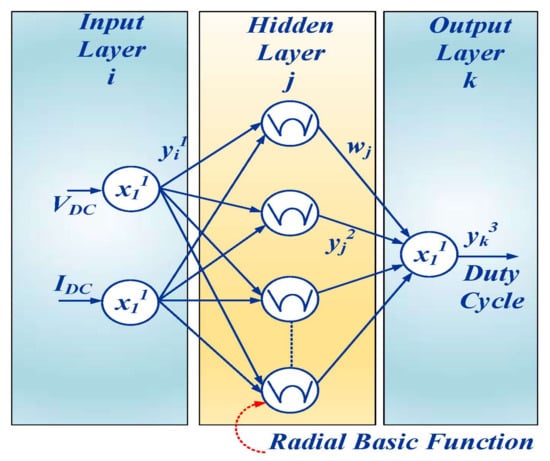
Figure 5.
Radial basis function network (RBFN).
The input layer consists of two neurons that are directly transferred to successive layers. The net i/o of this layer is stated in Equation (12).
where represents the hidden layer, and is stated as an input layer that contains the motor speed as and the produced speed as . characterizes the input layer with a sum of nodes, and the output is signified as , which is drawn to node .
In RBFN, the hidden layer neurons achieve a Gaussian state, which is utilized as a membership function. The net i/o of this layer is stated in Equation (13).
where the Gaussian function mean is specified as and represents the standard deviation.
k is denoted as the single neuron that is computed by the output layer (duty cycle). defines the received signs with a linear objective, and represents the output layer function, which is mentioned in Equations (14) and (15).
The controlled learning procedure is executed when RBFN is modified to train the model. To choose the RBF inputs, the trained function should be transformed into a polynomial structure. The structure of the polynomial model can be efficiently detected by choosing significant polynomial terms using the fast recursive algorithm (FRA) technique with less complication. Therefore, the input assortment problem is formulated as Equation (16).
where specifies the output variable, states the input variable vector, ε(t) represent the model error at and n represents the mapping terms. Nonlinear mapping and the linear coefficients are specified as and . For assumed N training models, the system is stated in Equation (17).
is formed by mapping functions; , where is referred as output vector. states the linear parameters. In this, the mapping functions are nominated by means of the subsequent polynomial Equation (18):
where 0 , 0, and = 10, = 3.
At that time, the inputs of RBF could be recognized by choosing the substantial polynomial expressions with the help of FRA.
A general RBF is expressed as a linear exemplary similar to Equation (16), as follows,
where the additional parameters are the radial basis activation function for the hidden nodes, which is often chosen as a Gaussian function. is the centers, and denotes the RBF widths. Similar to Equation (17), the RBF neural model is formulated in the matrix form as shown in Equation (20).
where the output matrix of the hidden layer is stated as , , . Figure 6 shows the flowchart for the proposed method.
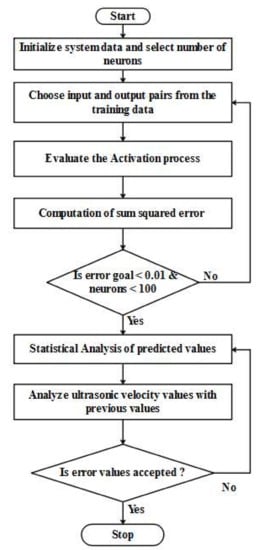
Figure 6.
Flowchart for the proposed method.
Improved RBF Neural Model
The presentation of the RBF design is associated with the number of nodes present in the hidden layer. For that reason, the establishment of RBF is observed as an optimization issue that can be influenced by weight and hidden layer nodes. FRA is exploited to create a precise and compacted RBF to enhance the speed of the vehicle. By means of improved RBF-FRA, the nodes present in the hidden layer are designated, conferring a total impact of the output hidden layer node.
Predicted residual sums-of-squares (PRESS) errors are utilized as a key to choose hidden nodes and mechanically interrupt the assortment process [32]. The nodes of the hidden layer are designated through the condensed PRESS error values. Thus, the total impact is reformed to the resulting Equation (21).
where sample number is represented as , a maximum quantity of hidden layer nodes is designated as , and model error values are stated as and .
5. Results and Discussion
Mathematical Laboratory (MATLAB) version R2018a was employed to perform the simulation procedures and develop the mathematical computing. All computational simulations were performed on a Windows machine with Intel Dual Core 4 GHz as the processor and 4 GB of RAM.
FCs are one of the most important components used in the widespread deployment of EVs. The designed battery charger should be highly efficient, low in cost, and must have minimal pressure on the network. High power factor correction is required, and the power dissipated in the switching elements must be minimized. To accomplish extraordinary competence, an isolated configuration topology needs to be established by eliminating a time interval with the high-frequency converter. Because of the number of elements, isolated topologies require more constituents than non-isolated structures. In calculation, the supplementary components and the converter are directly associated with the growing space and price of the entire structure. The simulation diagram of the improved RBF technique with isolated topologies is shown in Figure 7. The specifications of fuel cell-operated vehicles are shown in Table 1.
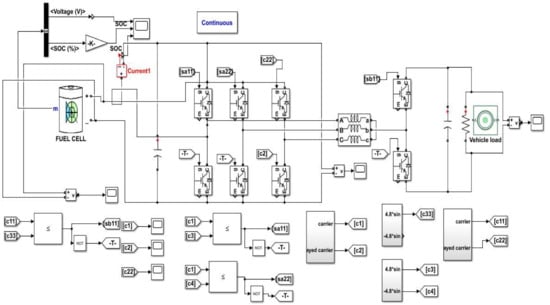
Figure 7.
Simulink model for the proposed method with a high-gain converter.

Table 1.
Specifications of a fuel cell.
The major constituents present in this simulation model are the fuel cell, PHEV, and improved RBF controller. Primarily, the battery delivers the crucial energy to drive the vehicle; therefore, it is exploited as the chief source. If the car is stopped, the regeneration process starts to charge the battery while the state of charge (SOC) of the FC is less than the original level, which is handled by the improved RBF controller.
The most important goal of battery operation is to re-establish a rechargeable power scheme to process the peripheral transmission system. To avoid the probable destruction of the costly apparatus of the power system, the converters should produce a higher gain and more reliable voltage. This investigation delivers a simulation model to examine dissimilar inverter configurations to identify the most suitable converter organization for battery presentation. The SOC approximation of the FC prevents the system from unexpected disturbances and protects the batteries from being overcharged/discharged, which might destroy the interior prearrangement of the FC. Figure 8 and Figure 9 show the performance measures of EV at the time of discharging and charging conditions.
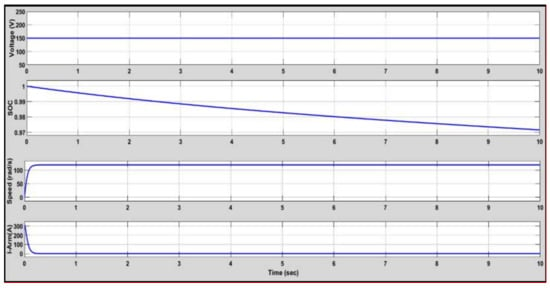
Figure 8.
Performance measures of the EV while discharging.
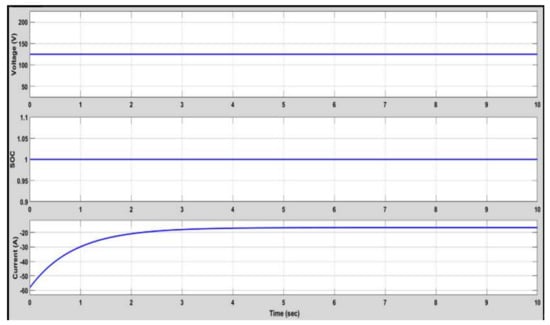
Figure 9.
Performance measures of the EV while charging.
From Figure 8 and Figure 9, it can be determined that the SOC of the battery was developed when the improved RBF organized the charging/discharging characteristics. The SOC approximation of the FC prevents the system from unexpected disturbance and protects the batteries from being overcharged/discharged, which might destroy the internal arrangement of the FC. This motor-powered speed designates the speed values in RPM, which is run by the engine of the motor. Table 2 indicates the specification for the battery charger.

Table 2.
Battery charger specifications.
If the car experiences a signal in the road, the SOC of the FC will be checked and it will start to charge through an isolated bidirectional converter with the help of the improved RBF to fulfill the charge. Figure 10 shows the performance of the high-gain converter.
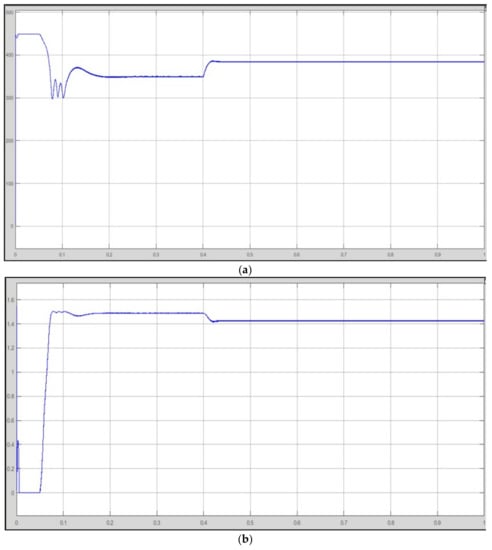
Figure 10.
Performance of the high-gain converter: (a) voltage and (b) current.
The proposed charger configuration maintained better performance for the converter and was capable of accomplishing an ultra-wide output voltage range. The designed HGC achieved DC-link voltage regulation to charge the pack of 100 V and 420 V while maintaining good conversion efficiency, proximity to the unity power factor, and small THD. The proposed HGC converter efficiently optimized the wide load conditions. Integrating the resonant inductor and magnetizing inductor into a single magnetic core helped to reduce the power loss and size of the converter.
Figure 11 clearly denotes the voltage and current performance for the EV. This proposed structure correspondingly provided low swells in the resulting DC voltage. As a result, an insulated high-gain converter was exploited to confirm the good power quality features existing with the unity power factor. The proposed isolated converter topology was implemented and its performances were replicated in MATLAB with resistive load. The outcomes from the HGC were used to validate that topology and successfully enhanced the power quality features for definite circumstances.
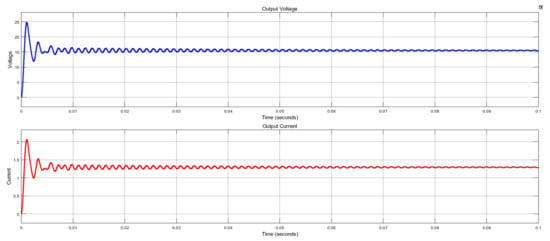
Figure 11.
Voltage and current measurement for EVs.
HGC characteristically contains a power factor correction (PFC) stage that completely depends on the converter connected through a huge loading capacitor and line current that is monitored by an isolation transformer. Some of the existing strategies operate well, particularly where the power is desirable to produce various voltage supports, and an extensive raid period is essential. These designs mostly use more inductors in the dynamic PFC phase, where some of the inductors are required to manage the whole power supply.
The recommended high-gain converter was associated with the PFC configurations in terms of several constraints, which are quantified in Table 3. Consequently, it was apparent that the projected PFC converter delivered better performance with better stability, low ripple voltage, and condensed switch voltage strain, and provided satisfactory charging instances at the load side. Table 4 provides the performance comparison in terms of THD, power loss, and efficiency for the proposed and existing converter topologies.

Table 3.
Detailed behavior of the proposed high-gain converter.

Table 4.
Comparison table of the converter topology.
Figure 12 shows the Simulink diagram of the power factor correction (PFC). Table 5 shows the comparison table for each converter strategy with the proper PFC value. From Table 5, it can be confirmed that the isolated converter achieved a PFC value close to unity.
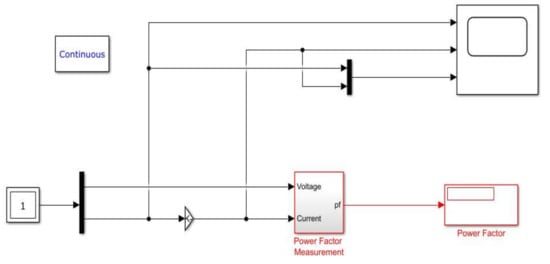
Figure 12.
Power factor correction.

Table 5.
Comparison table of the converter topology with PFC.
In this research, an onboard PHEV battery charger based on isolated converter topology was proposed. The maximum efficiency of the proposed HGC topology was utilized to enhance the charger. The proposed topology charged the extremely depleted FC packs, whose voltage might have gone down to 100 V. This topology contained both features, i.e., boosting and slaying the input voltage, and was also utilized in the front-end power factor correction stage. Both steady-state analysis and AC small-signal modeling of the topology in the HGC application were carried out. Strategic techniques were used to confirm the continuous mode process and to restrict the voltage and current ripples. The simulation output validated that the proposed charger is capable of sustaining an extensive voltage range while maintaining the LLC converter, which functions at its determined efficacy point.
Even though the motor inductances were dissimilar for different incorporated stations, the incorporated charger had equivalent charging presentation, as suggested by the improved RBF technique. Figure 13 shows the THD analysis for the improved RBF. Table 6 shows a comparison among the existing topologies. Table 6 clearly shows that the improved RBF achieved better results in all performances.
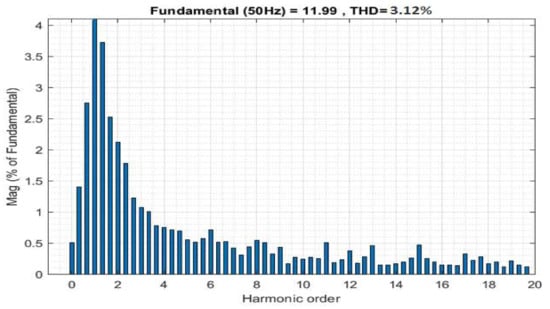
Figure 13.
THD analysis.

Table 6.
Comparison table of existing topologies.
The energy for propulsion in a hybrid vehicle comes from two sources. In the tested vehicle, the range of the propulsion power source was determined in the intervals of each stage of the test route. The fuel cell power consumption circumstances in the vehicle drive indicated areas of battery-only operation as well as areas of dual power source cooperation. The battery provided propulsion energy at low vehicle speeds, such as 0–10 km/h. The fuel cell began to work in the power generation process at higher vehicle speeds. The instantaneous maximum values of the powertrain energy demand and the average values in each speed window with a 10 km/h interval both increased as the vehicle speed increased.
Some speed ranges recorded lower energy consumption due to individual driving parameters; however, the justification for these results can be found in the temporary driving conditions. For example, the lowest average energy values were obtained in the speed range of 41–50 km/h, which occurred only in transition states between acceleration and deceleration to the urban speed range’s maximum speed. Similar energy recovery values were reported for both the urban and rural parts throughout a wide range of speed ranges, illustrating the versatility of the energy recovery at different speeds.
The speed of the vehicle with improved RBF was exploited more compared to other techniques. Figure 14 shows the comparative analysis of the proposed method. It indicates that the improved RBF controller achieved a maximum speed of 91 (km/h), which is much better than the remaining implemented existing techniques.
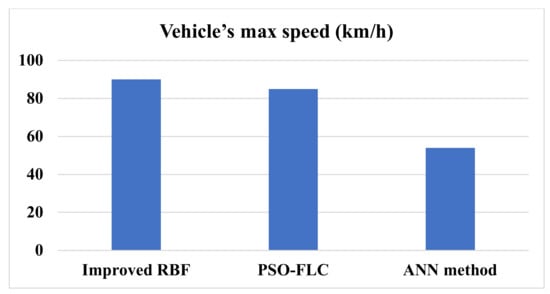
Figure 14.
Comparative analysis of the proposed method.
Adjacently, two modernization processes—autonomous vehicle growth and electric power transition—are occurring in self-propelled production. Meanwhile, most of the EVs contain a smaller assortment when compared with gas-based cars and it is considered as rechargeable autonomous cars which are not feasible for all the applications. This apprehension encourages investigating the effects that automation has on vehicle range. The research on ASV [16,17] execute the simulation results for roadside applications which are explained in the comparison table.
In a recent trend, more experimentations are being done on autonomous vehicles, which generally use electricity to run. The simulated results for vehicle speed with various algorithms are shown in Figure 15. Figure 15 clearly shows the comparative analysis for the autonomous surface vehicle’s speed when it is exploited with the same specifications used in a normal EV.
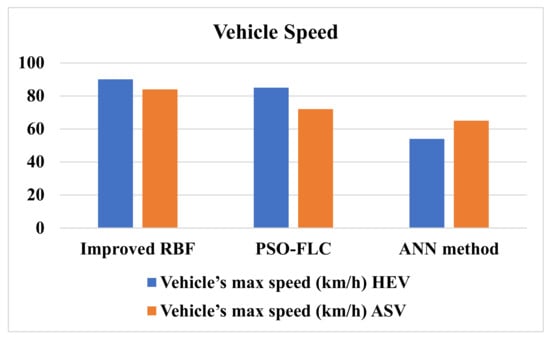
Figure 15.
Comparative analysis of vehicle type.
A case study was undertaken in this work to test the performance of velocity prediction using the prediction algorithm for the energy management of a parallel EV. There was a clutch between the engine and the motor, as seen in the overall control structure diagram. Between the motor and the final differential reducer, a dual clutch transmission (DCT) was used. Improved RBF was used to regulate the control output in a receding horizon according to the projected speed and was used as a benchmark to evaluate the performance of the suggested technique to validate the speed predictor’s performance. Furthermore, improved RBF was used in this study to solve the local optimal control in the receding horizon optimization technique. The improvement achieved with the prediction approach could be quantified and compared this way. Note that when using the improved RBF algorithm with the specific speed predictor, the consumption of fuel economy optimality is determined by dividing the result by the current speed. According to the findings, normal RBF and BP achieved optimality at 89.41% and 88.82%, respectively. However, the improved RBF yielded the greatest results: 92.39%, indicating that it had a significant impact on EV operation, demonstrating the significance of the suggested method’s more exact speed prediction.
6. Conclusions
In this work, improved RBF was proposed for a high-gain converter with continuous input and output current, which was introduced to achieve better efficiency and speed of EVs. Performance parameters like power loss, efficiency, and THD analysis were established to prove the high efficiency of the proposed topology in FC-connected systems. The converter not only allowed the usage of a battery with lesser cost, but also created the probability of regulating the voltage of the inverter to decrease the system losses. From the simulation results, it can be concluded that the proposed method with isolated converter topology provides the least amount of losses, estimated at around 0.042 KW. The efficiency was estimated as 98.272% with a THD of 3.12%, which is much better than the remaining existing converters. So, the improved RBF with a high-gain converter was selected as the topology most suitable for EV applications. It should be noted that due to the presence of the inductor on the input and output of the converter, the proposed high-gain converter offers better implementation when used in FC-type applications. The simulation results in MATLAB Simulink verify the theoretical concepts and derived equations and waveforms. In the future, this research can be further extended through the various types of isolated and non-isolated topologies with different optimization techniques to improve the efficiency of its performance.
Author Contributions
The paper investigation, resources, data curation, writing—original draft preparation, writing—review and editing, and visualization were done by B.G. and H.S. The paper conceptualization, methodology, software, validation, and formal analysis were done by H.K.J. Supervision, project administration, and final approval of the version to be published were conducted by W.-C.L. and P.B.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yoo, E.; Kim, M.; Song, H.H. Well-to-wheel analysis of hydrogen fuel-cell electric vehicle in Korea. Int. J. Hydrog. Energy 2018, 43, 19267–19278. [Google Scholar] [CrossRef]
- Han, X.; Li, F.; Zhang, T.; Zhang, T.; Song, K. Economic energy management strategy design and simulation for a dual-stack fuel cell electric vehicle. Int. J. Hydrog. Energy 2017, 42, 11584–11595. [Google Scholar] [CrossRef]
- Thompson, S.T.; James, B.D.; Huya-Kouadio, J.M.; Houchins, C.; DeSantis, D.A.; Ahluwalia, R.; Wilson, A.R.; Kleen, G.; Papageorgopoulos, D. Direct hydrogen fuel cell electric vehicle cost analysis: System and high-volume manufacturing description, validation, and outlook. J. Power Sources 2018, 399, 304–313. [Google Scholar] [CrossRef]
- Eberle, U.; Müller, B.; Helmolt, R.V. Fuel cell electric vehicles and hydrogen infrastructure: Status 2012. Energy Environ. Sci. 2012, 5, 8780–8798. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, H.; Ravey, A.; Péra, M.C. An integrated predictive energy management for light-duty range-extended plug-in fuel cell electric vehicle. J. Power Sources 2020, 451, 227780. [Google Scholar] [CrossRef]
- Wang, H.; Gaillard, A.; Hissel, D. Online electrochemical impedance spectroscopy detection integrated with step-up converter for fuel cell electric vehicle. Int. J. Hydrog. Energy 2019, 44, 1110–1121. [Google Scholar] [CrossRef]
- Nassif, G.G.; de Almeida, S.C. Impact of powertrain hybridization on the performance and costs of a fuel cell electric vehicle. Int. J. Hydrog. Energy 2020, 45, 21722–21737. [Google Scholar] [CrossRef]
- Hong, B.K.; Kim, S.H. Recent advances in fuel cell electric vehicle technologies of Hyundai. ECS Trans. 2018, 86, 3. [Google Scholar] [CrossRef]
- Cipollone, R.; Battista, D.D.; Marchionni, M.; Villante, C. Model based design and optimization of a fuel cell electric vehicle. Energy Procedia 2014, 45, 71–80. [Google Scholar] [CrossRef][Green Version]
- Gaikwad, S.D.; Ghosh, P.C. Sizing of a fuel cell electric vehicle: A pinch analysis-based approach. Int. J. Hydrog. Energy 2020, 45, 8985–8993. [Google Scholar] [CrossRef]
- Lipman, T.E.; Elke, M.; Lidicker, J. Hydrogen fuel cell electric vehicle performance and user-response assessment: Results of an extended driver study. Int. J. Hydrog. Energy 2018, 43, 12442–12454. [Google Scholar] [CrossRef]
- Tanç, B.; Arat, H.T.; Conker, C.; Baltacioğlu, E.; Aydin, K. Energy distribution analyses of an additional traction battery on hydrogen fuel cell hybrid electric vehicle. Int. J. Hydrog. Energy 2020, 45, 26344–26356. [Google Scholar] [CrossRef]
- Lee, D.Y.; Elgowainy, A.; Kotz, A.; Vijayagopal, R.; Marcinkoski, J. Life-cycle implications of hydrogen fuel cell electric vehicle technology for medium-and heavy-duty trucks. J. Power Sources 2018, 393, 217–229. [Google Scholar] [CrossRef]
- Oldenbroek, V.; Verhoef, L.A.; Wijk, A.J.V. Fuel cell electric vehicle as a power plant: Fully renewable integrated transport and energy system design and analysis for smart city areas. Int. J. Hydrog. Energy 2017, 42, 8166–8196. [Google Scholar] [CrossRef]
- Robledo, C.B.; Oldenbroek, V.; Abbruzzese, F.; Wijk, A.J.V. Integrating a hydrogen fuel cell electric vehicle with vehicle-to-grid technology, photovoltaic power and a residential building. Appl. Energy 2018, 215, 615–629. [Google Scholar] [CrossRef]
- Stateczny, A.; Kazimierski, W.; Gronska-Sledz, D.; Motyl, W. The empirical application of automotive 3D radar sensor for target detection for an autonomous surface vehicle’s navigation. Remote Sensing 2019, 11, 1156. [Google Scholar] [CrossRef]
- Stateczny, A.; Burdziakowski, P.; Najdecka, K.; Domagalska-Stateczna, B. Accuracy of trajectory tracking based on nonlinear guidance logic for hydrographic unmanned surface vessels. Sensors 2020, 20, 832. [Google Scholar] [CrossRef]
- Navamani, J.D.; Jegatheesan, R.; Vijayakumar, K. Reliability study of high gain DC-DC converters based on RRPP I-IIA configuration for shipboard power system. Sādhanā 2018, 43, 71. [Google Scholar] [CrossRef]
- Lakshmi, M.; Hemamalini, S. Nonisolated high gain DC–DC converter for DC microgrids. IEEE Trans. Ind. Electron. 2017, 65, 1205–1212. [Google Scholar] [CrossRef]
- Upadhyay, P.; Kumar, R. A high gain cascaded boost converter with reduced voltage stress for PV application. Sol. Energy 2019, 183, 829–841. [Google Scholar] [CrossRef]
- Revathi, B.S.; Mahalingam, P.; Gonzalez-Longatt, F. Interleaved high gain DC-DC converter for integrating solar PV source to DC bus. Sol. Energy 2019, 188, 924–934. [Google Scholar] [CrossRef]
- Amir, A.; Amir, A.; Selvaraj, J.; Rahim, N.A.; Abusorrah, A.M. Conventional and modified MPPT techniques with direct control and dual scaled adaptive step-size. Sol. Energy 2017, 157, 1017–1031. [Google Scholar] [CrossRef]
- Mebarki, N.; Rekioua, T.; Mokrani, Z.; Rekioua, D. Supervisor control for stand-alone photovoltaic/hydrogen/battery bank system to supply energy to an electric vehicle. Int. J. Hydrog. Energy 2015, 40, 13777–13788. [Google Scholar] [CrossRef]
- Fathabadi, H. Novel battery/photovoltaic hybrid power source for plug-in hybrid electric vehicles. Sol. Energy 2018, 159, 243–250. [Google Scholar] [CrossRef]
- Padmagirisan, P.; Sankaranarayanan, V. Powertrain control of a solar photovoltaic-battery powered hybrid electric vehicle. Front. Energy 2019, 13, 296–306. [Google Scholar] [CrossRef]
- Huang, Z.; Zhang, C.; Zeng, T.; Lv, C.; Chan, S.H. Modeling and energy management of a photovoltaic-fuel cell-battery hybrid electric vehicle. Energy Storage 2019, 1, e61. [Google Scholar] [CrossRef]
- Esfandyari, A.; Norton, B.; Conlon, M.; McCormack, S.J. McCormack. Performance of a campus photovoltaic electric vehicle charging station in a temperate climate. Sol. Energy 2019, 177, 762–771. [Google Scholar] [CrossRef]
- Yilmaz, A.S.; Özer, Z. Pitch angle control in wind turbines above the rated wind speed by multi-layer perceptron and radial basis function neural networks. Expert Syst. Appl. 2009, 36, 9767–9775. [Google Scholar] [CrossRef]
- Assareh, E.; Biglari, M. A novel approach to capture the maximum power from variable speed wind turbines using PI controller, RBF neural network and GSA evolutionary algorithm. Renew. Sustain. Energy Rev. 2015, 51, 1023–1037. [Google Scholar] [CrossRef]
- Saravanan, S.; Babu, N.R. RBFN based MPPT algorithm for PV system with high step up converter. Energy Convers. Manag. 2016, 122, 239–251. [Google Scholar] [CrossRef]
- Babu, N.R.; Arulmozhivarman, P. Forecasting of wind speed using artificial neural networks. Int. Rev. Model. Simul. 2012, 5, 2276–2280. [Google Scholar]
- Deng, J.; Li, K.; Irwin, G.W. A two-stage algorithm for automatic construction of rbf neural models. In Proceedings of the MELECON 2010–2010 15th IEEE Mediterranean Electrotechnical Conference, IEEE, Valletta, Malta, 26–28 April 2010; pp. 166–171. [Google Scholar]
- Musavi, F.; Edington, M.; Eberle, W.; Dunford, W.G. Evaluation and efficiency comparison of front end AC-DC plug-in hybrid charger topologies. IEEE Trans. Smart Grid 2012, 3, 413–421. [Google Scholar] [CrossRef]
- Cheng, H.; Wang, Z.; Yang, S.; Huang, J.; Ge, X. An Integrated SRM Powertrain Topology for Plug-In Hybrid Electric Vehicles with Multiple Driving and On-board Charging Capabilities. IEEE Trans. Transp. Electrif. 2020, 6, 578–591. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).