Bidirectional Converter for Plug-In Hybrid Electric Vehicle On-Board Battery Chargers with Hybrid Technique
Abstract
1. Introduction
- A novel technique called NN–IPSO is proposed to determine the best suitable converter topology for battery charger management.
- The stability of the system is improved using NN–IPSO, which interfaces the battery with an isolated converter topology.
2. Literature Review
Summary
3. Proposed Method
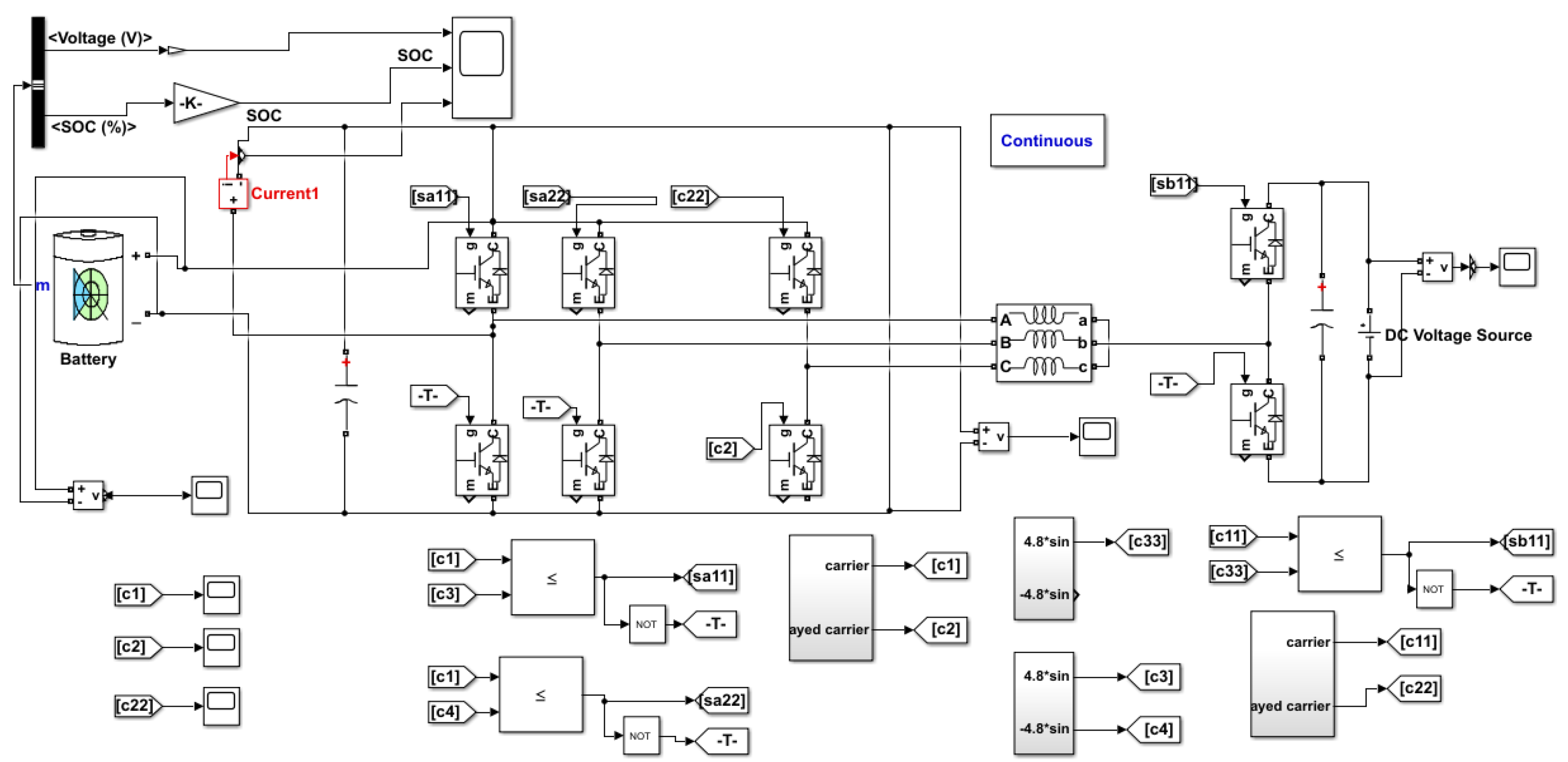
3.1. Setup of the Bidirectional Converter
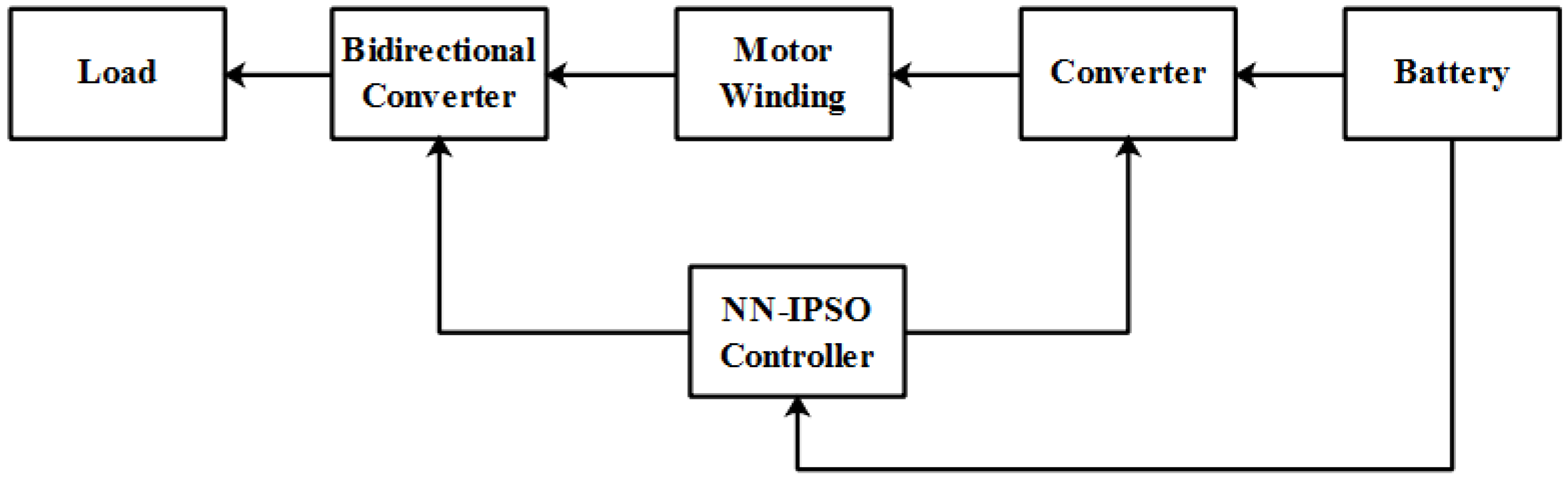
- Integration of the traction inverter with the charging system.
- Integration of the charging system detector with the motor winding inductance, considerably decreasing the system’s mass. Furthermore, it has little effect on the rotor-side converter or the operation of common EV motors.
- The capacity to block faults in both directions.
- The ability to recharge at lower or higher voltages than the voltage supply.
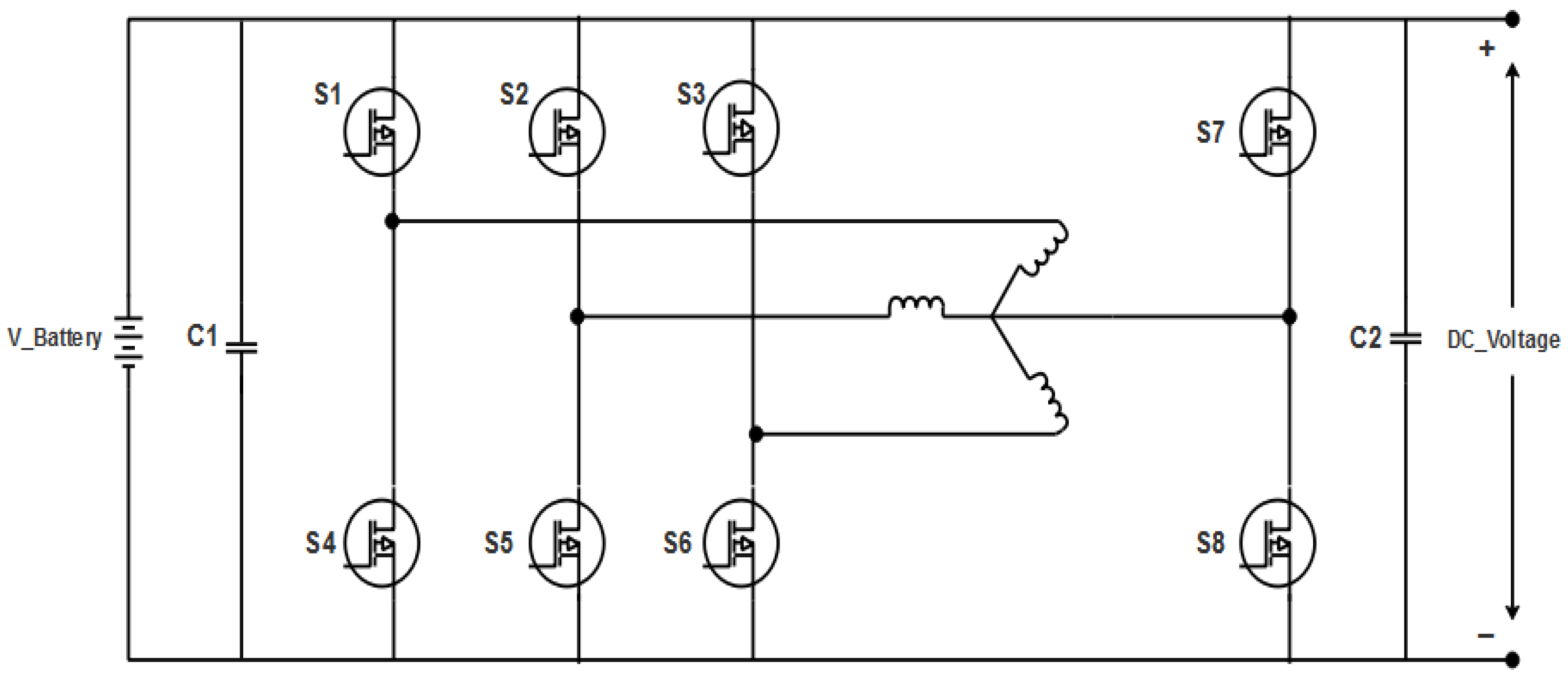
- The circuit illustration of the isolated converter is displayed in Figure 1.
- Whenever the signal is high, the switches S1 and S2 are continuously activated; whenever the voltage is low, the switches S1, and S2 are switched off.
- This switching method allows the propagation of the antiparallel transistors of the switching devices relating to phase.
- Similarly, whenever the signal is high, switches S3 and S4 should be engaged; whenever the voltage is low, switches S3 and S4 should be shifted to off; switches S5 and S6 should always be triggered whenever the signal is high; and switches S5 and S6 should always be switched off if the voltage is low.
- The remaining switches have a 50% duty cycle and a constant current. Only when the topmost bidirectional switch of a half-bridge is fully triggered (with j = 1, 3, or 5), and the voltage of the cycle linked is optimistic, is the voltage level at the winding also optimistic.
- When the bottom switch (with k = 2, 4, or 6) is fully triggered under identical conditions, the voltage is zero. If the phase voltage is low, the direction of the voltage is the aspect of the voltage in the previous circumstances.
- Whenever the topmost switch on every limb of the converter is active, the signal applied to the respective winding is also high, and whenever the bottom switch is triggered, it is negligible. If another minimum or maximum switch is turned on at the same time, the voltage supplied to the associated windings is zero. The PHEV uses a battery with a voltage range of 200 V–400 V.
3.2. Block Diagram of the Proposed Method
3.3. NN Process
3.3.1. Particle Swarm Optimization (PSO)
3.3.2. Improved PSO Parameters
- The NN reduces the computational requirements of the modulation technique and makes the implementation faster.
- The duty cycle of the PWM signal is independent of the carrier signal voltages and frequencies.
- For the training process, the NN obtains the input voltage, capacitors [32], and load demand.
- After receiving the input, the NN generates an output voltage whose value corresponds to the duty cycle of the PWM signal input. The inverse proportionality principle states that if an inverter receives a periodic input signal—such as a clock—its average output voltage will be inversely proportional to the input signal’s duty cycle.
- If the condition is YES, the NN obtains the reference vector’s amplitude and angle to determine the duty cycles of various space vectors that can be utilized to create PWM pulses to drive the converter.
- If the condition is NO, the duty cycle of the input signal is once again processed in the training section to update the duty cycle value.
- The output duty cycle of the NN is given as input to IPSO to update the velocity and position.
- While evaluating the fitness values of IPSO, the duty cycle value is updated, and is given as the switching pulse for the converter.
3.3.3. Steps for Generating the Switching Pulse
- For a particular modulation index, NN–IPSO has been effectively applied in electronic systems circuitry to produce the appropriate switching frequency of a PWM inverter.
- It accepts the standard vector’s magnitude and position to estimate the duty cycles of multiple space vectors in industrial domains that can be used to generate PWM pulses for conversion operation.
- The amplitude of the output voltage is minimally affected by even substantial departures from the ideal switching pattern. Since notch angles continue to coincide, this is a useful characteristic.
- As a result, the Neural Network’s converter may only be designed to reliably recreate the ideal switching angles within the modulation index range from 0 to 0.95.
- The inverter must be adjusted to vary the size and frequency of the AC output voltage, because the DC bus voltage must be constant.
- The analysis of the two voltage waveforms is the fundamental premise of PWM—a changeable voltage with the same frequencies as the inverter, known as the reference voltage, and a high-frequency signal with a triangular waveform, known as the carrier voltage.
- The amplitude of the triangular carrier waveform is fixed. The reference constant valuation magnitude can be modified.
- The inverter output frequency is just like the standard square wave; the standard wave frequency can be changed to modify the inverter output frequencies. The entire switching frequency is still substantial in the PWM output waveform.
- The number of pulses used every half-cycle determines the sequence of harmonics in the PWM waveform.
- PWM provides more capability in terms of THD reduction, dimension and cost savings, and extra operational characteristics of the inverter, including active filtering and reactive power management.
4. Results and Discussion
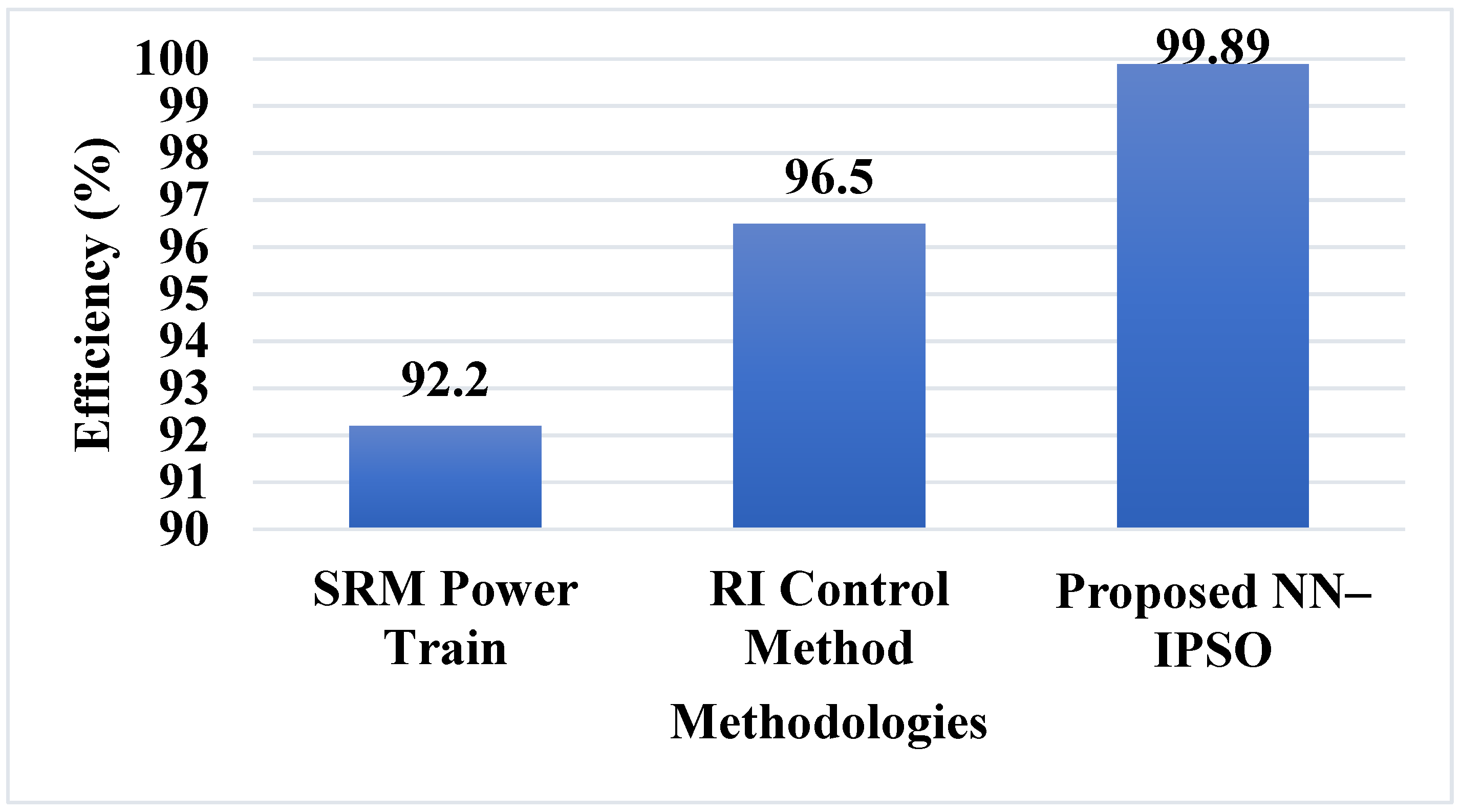
Comparative Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bai, Y.; Li, J.; He, H.; Santos, R.C.D.; Yang, Q. Optimal design of a hybrid energy storage system in a plug-in hybrid electric vehicle for battery lifetime improvement. IEEE Access 2020, 8, 142148–142158. [Google Scholar] [CrossRef]
- Zhou, S.; Chen, Z.; Huang, D.; Lin, T. Model prediction and rule based energy management strategy for a plug-in hybrid electric vehicle with hybrid energy storage system. IEEE Trans. Power Electron. 2020, 36, 5926–5940. [Google Scholar] [CrossRef]
- Kumar, D.; Nema, R.K.; Gupta, S. A comparative review on power conversion topologies and energy storage system for electric vehicles. Int. J. Energy Res. 2020, 44, 7863–7885. [Google Scholar] [CrossRef]
- Mozhi, S.A.; Raja, S.C.; Saravanan, M.; Nesamalar, J.J.D. Energy management of hybrid energy storage system in PHEV with various driving mode. In Artificial Intelligent Techniques for Electric and Hybrid Electric Vehicles; Chitra, A., Sanjeevikumar, P., Holm-Nielsen, J.B., Himavathi, S., Eds.; Scrivener Publishing: Beverly, MA, USA; Wiley: Hoboken, NJ, USA, 2020; pp. 103–113. [Google Scholar]
- Habib, S.; Khan, M.M.; Abbas, F.; Ali, A.; Faiz, T.M.; Ehsan, F.; Tang, H. Contemporary trends in power electronics converters for charging solutions of electric vehicles. CSEE J. Power Energy Syst. 2020, 6, 911–929. [Google Scholar]
- Yadlapalli, R.T.; Kotapati, A.; Kandipati, R.; Koritala, C.S. A review on energy efficient technologies for electric vehicle applications. J. Energy Storage 2022, 50, 104212. [Google Scholar] [CrossRef]
- Rathore, V.; Siddavatam, R.P.R.; Rajashekara, K. An Isolated Multilevel DC-DC Converter Topology with Hybrid Resonant Switching for EV Fast Charging Application. IEEE Trans. Ind. Appl. 2022, 58, 5546–5557. [Google Scholar] [CrossRef]
- Fouladi, E.; Baghaee, H.R.; Bagheri, M.; Gharehpetian, G.B. Smart V2G/G2V charging strategy for PHEVs in AC microgrids based on maximizing battery lifetime and RER/DER employment. IEEE Syst. J. 2020, 15, 4907–4917. [Google Scholar] [CrossRef]
- Aluisio, B.; Bruno, S.; De Bellis, L.; Dicorato, M.; Forte, G.; Trovato, M. DC-microgrid operation planning for an electric vehicle supply infrastructure. Appl. Sci. 2019, 9, 2687. [Google Scholar] [CrossRef]
- Chen, M.; Ma, S.; Wan, H.; Wu, J.; Jiang, Y. Distributed control strategy for DC microgrids of photovoltaic energy storage systems in off-grid operation. Energies 2018, 11, 2637. [Google Scholar] [CrossRef]
- Sahoo, S.K.; Sinha, A.K.; Kishore, N.K. Control techniques in AC, DC, and hybrid AC–DC microgrid: A review. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 6, 738–759. [Google Scholar] [CrossRef]
- Wang, P.; Wang, D.; Zhu, C.; Yang, Y.; Abdullah, H.M.; Mohamed, M.A. Stochastic management of hybrid AC/DC microgrids considering electric vehicles charging demands. Energy Rep. 2020, 6, 1338–1352. [Google Scholar] [CrossRef]
- Azeem, O.; Ali, M.; Abbas, G.; Uzair, M.; Qahmash, A.; Algarni, A.; Hussain, M. A comprehensive review on integration challenges, optimization techniques and control strategies of hybrid AC/DC Microgrid. Appl. Sci. 2021, 11, 6242. [Google Scholar] [CrossRef]
- Kim, I.; Lee, S.; Park, J.-W. Design and Control of OBC-LDC Integrated Circuit with Variable Turns Ratio for Electric Vehicles. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; pp. 885–890. [Google Scholar]
- Fan, Y.; Li, W.; Liu, B.; Jin, M.; Ren, X.; Xu, C.; Diao, L. Evaluation Model of Loop Stray Parameters for Energy Storage Converter of Hybrid Electric Locomotive. IEEE Access 2020, 8, 212589–212598. [Google Scholar] [CrossRef]
- Baek, J.; Youn, H.-S. Full-bridge active-clamp forward-flyback converter with an integrated transformer for high-performance and low cost low-voltage DC converter of vehicle applications. Energies 2020, 13, 863. [Google Scholar] [CrossRef]
- Bak, Y.; Kang, H.-S. Control Methods for Performance Improvement of an Integrated On-Board Battery Charger in Hybrid Electric Vehicles. Electronics 2021, 10, 2506. [Google Scholar] [CrossRef]
- Chen, J.; Yang, C.; Tang, S.; Zou, J. A High Power Interleaved Parallel Topology Full-Bridge LLC Converter for Off-Board Charger. IEEE Access 2021, 9, 157790–157799. [Google Scholar] [CrossRef]
- Bayati, M.; Abedi, M.; Farahmandrad, M.; Gharehpetian, G.B.; Tehrani, K. Important Technical Considerations in Design of Battery Chargers of Electric Vehicles. Energies 2021, 14, 5878. [Google Scholar] [CrossRef]
- Yuan, J.; Dorn-Gomba, L.; Callegaro, A.D.; Reimers, J.; Emadi, A. A review of bidirectional on-board chargers for electric vehicles. IEEE Access 2021, 9, 51501–51518. [Google Scholar] [CrossRef]
- Ramos, L.A.; Van Kan, R.F.; Mezaroba, M.; Batschauer, A.L. A Control Strategy to Smooth Power Ripple of a Single-Stage Bidirectional and Isolated AC-DC Converter for Electric Vehicles Chargers. Electronics 2022, 11, 650. [Google Scholar] [CrossRef]
- Elshaer, M.; Bell, C.; Hamid, A.; Wang, J. DC–DC Topology for Interfacing a Wireless Power Transfer System to an On-Board Conductive Charger for Plug-In Electric Vehicles. IEEE Trans. Ind. Appl. 2021, 57, 5552–5561. [Google Scholar] [CrossRef]
- Nam, V.; Tinh, D.; Choi, W. A Novel Hybrid LDC Converter Topology for the Integrated On-Board Charger of Electric Vehicles. Energies 2021, 14, 3603. [Google Scholar] [CrossRef]
- Zinchenko, D.; Blinov, A.; Chub, A.; Vinnikov, D.; Verbytskyi, I.; Bayhan, S. High-Efficiency Single-Stage On-Board Charger for Electrical Vehicles. IEEE Trans. Veh. Technol. 2021, 70, 12581–12592. [Google Scholar] [CrossRef]
- Kanimozhi, G.; Natrayan, L.; Angalaeswari, S.; Paramasivam, P. An Effective Charger for Plug-In Hybrid Electric Vehicles (PHEV) with an Enhanced PFC Rectifier and ZVS-ZCS DC/DC High-Frequency Converter. J. Adv. Transp. 2022, 2022, 7840102. [Google Scholar] [CrossRef]
- He, C.; Wang, Z.; Yang, S.; Huang, J.; Ge, X. An Integrated SRM Powertrain Topology for Plug-In Hybrid Electric Vehicles with Multiple Driving and On-board Charging Capabilities. IEEE Trans. Transp. Electrif. 2020, 6, 578–591. [Google Scholar]
- Viana, C.; Lehn, P.W. A drivetrain integrated DC fast charger with buck and boost functionality and simultaneous drive/charge capability. IEEE Trans. Transp. Electrif. 2019, 5, 903–911. [Google Scholar] [CrossRef]
- Lee, F.C.; Li, Q.; Nabih, A. High frequency resonant converters: An overview on the magnetic design and control methods. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 9, 11–23. [Google Scholar] [CrossRef]
- Attia, H. Artificial neural network based unity power factor corrector for single phase DC-DC converters. Int. J. Electr. Comput. Eng. 2020, 10, 4145. [Google Scholar] [CrossRef]
- Sabanci, K.; Balci, S. Development of an expression for the output voltage ripple of the DC-DC boost converter circuits by using particle swarm optimization algorithm. Measurement 2020, 158, 107694. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, Y.; Chan, T.H.T.; Li, X.; Zhao, S. A Particle Swarm Optimization Algorithm with Sigmoid Increasing Inertia Weight for Structural Damage Identification. Appl. Sci. 2022, 12, 3429. [Google Scholar] [CrossRef]
- Anandhi, P.; Harikrishnan, S.; Kumar, V.J.S.; Lai, W.-C.; Mahmoud, A.E.D. The Enhanced Energy Density of rGO/TiO2 Based Nanocomposite as Electrode Material for Supercapacitor. Electronics 2022, 11, 1792. [Google Scholar] [CrossRef]
- Lai, W.-C.; Jian, R.; Xiaoning, X. DC-DC Converter and Rectifier with Resonator for Underwater Wireless Power Transfer Module. In Proceedings of the 2020 IEEE International Conference on Consumer Electronics-Taiwan (ICCE-Taiwan), Taoyuan, Taiwan, 28–30 September 2020. [Google Scholar]
- Lai, W.-C. DC-DC Converter and Rectifier with Resonator for Solar and Wireless Charging in Advanced Driver Assistance Systems. In Proceedings of the 2019 IEEE 4th International Future Energy Electronics Conference (IFEEC), Singapore, 25–28 November 2019. [Google Scholar]
- Girirajan, B.; Shekhar, H.; Lai, W.-C.; Jagannathan, H.K.; Divakarachar, P.B. High Gain Converter with Improved Radial Basis Function Network for Fuel Cell Integrated Electric Vehicles. World Electr. Veh. J. 2022, 13, 31. [Google Scholar] [CrossRef]




| Components | Ratings |
|---|---|
| Battery voltage | |
| Capacitance C1, C2 Inductance L1, L2 | |
| DC voltage | |
| Flux linkage | |
| Resistance | |
| Rotational friction coefficient | |
| Rotational inertia | |
| Switching frequency |
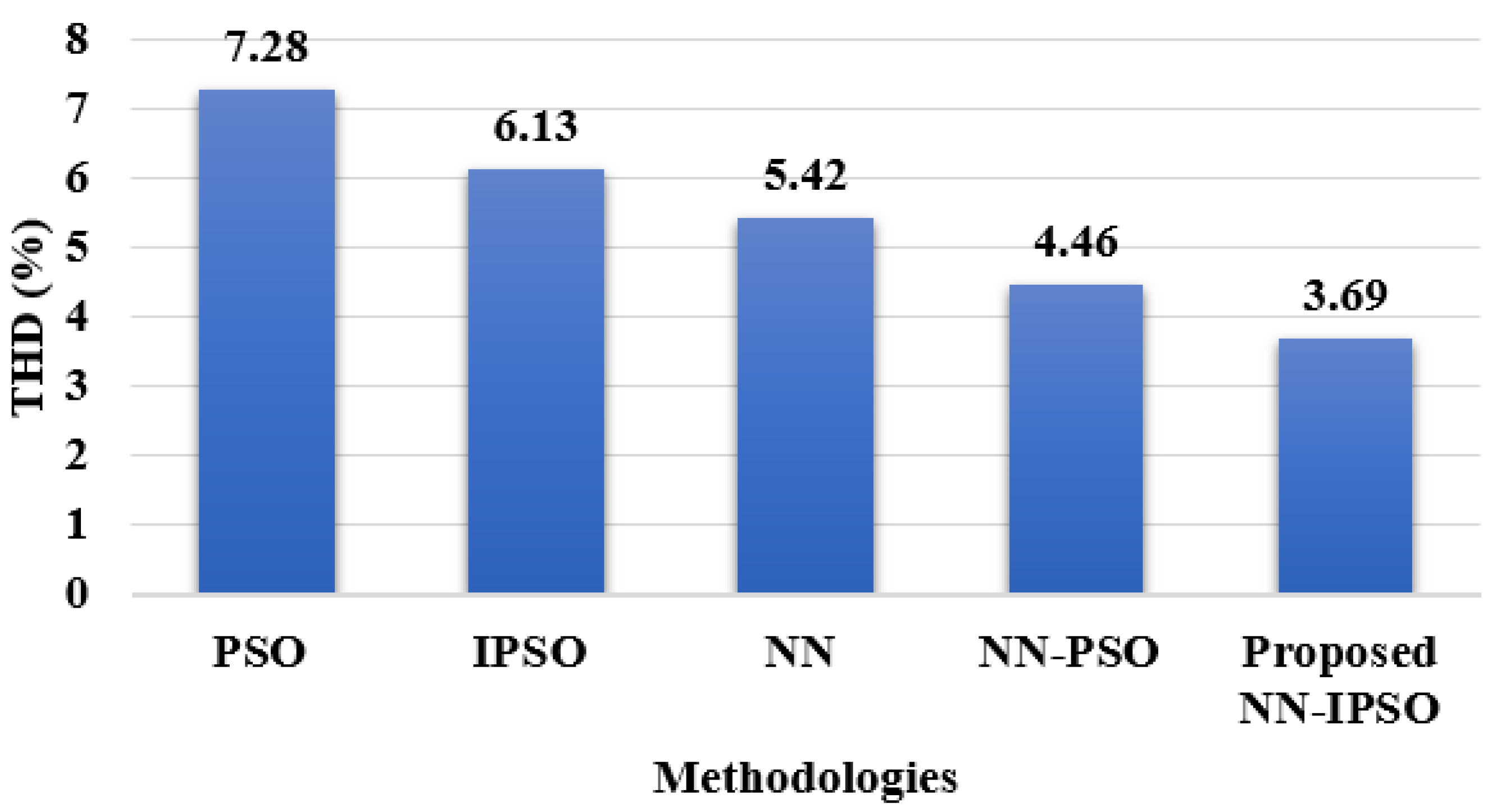
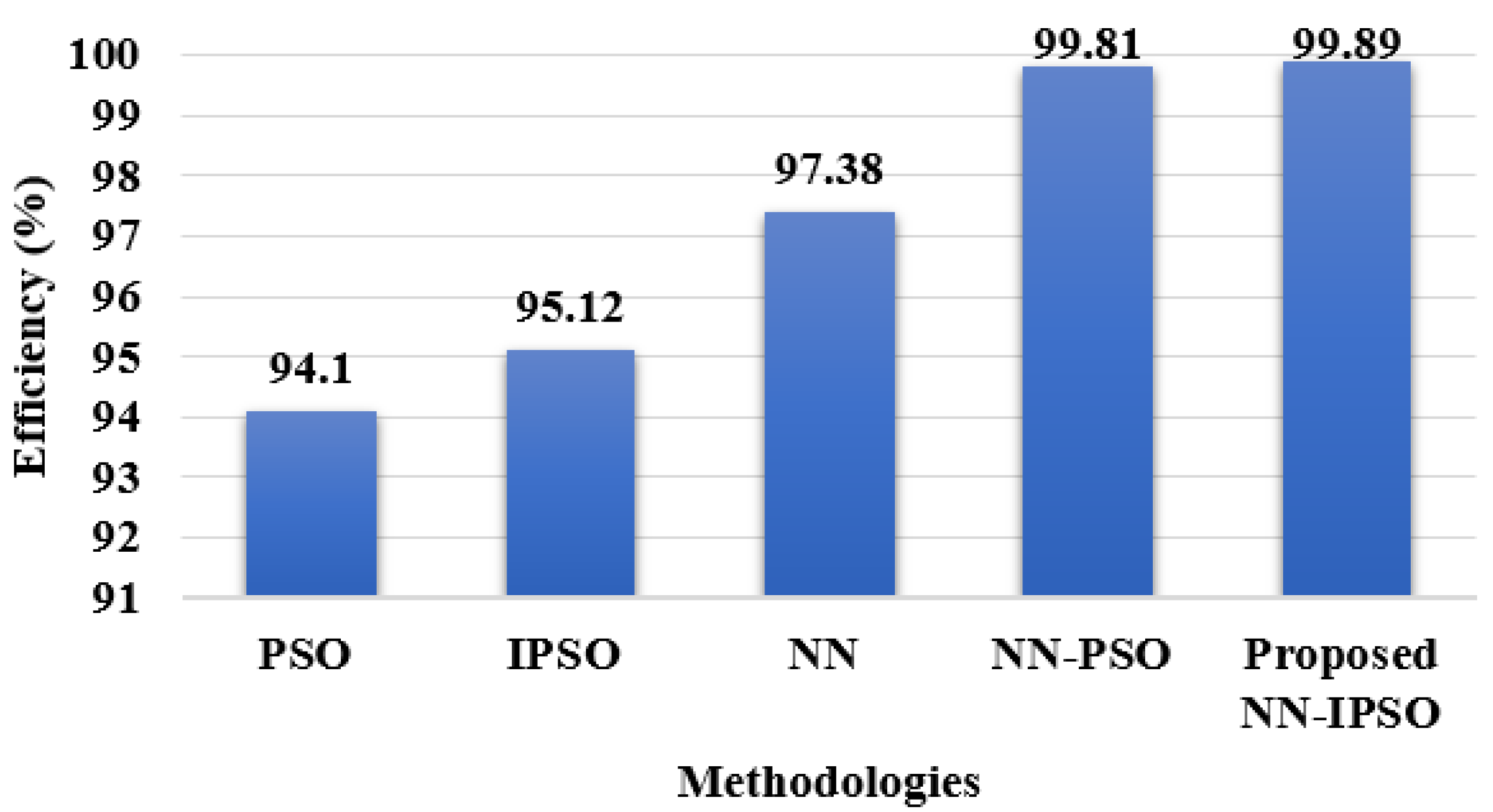
| Isolated Topology | THD % | Efficiency % | Power Loss (KW) |
|---|---|---|---|
| PSO controller | 7.28 | 94.10 | 0.163 |
| IPSO controller | 6.13 | 95.12 | 0.129 |
| NN controller | 5.42 | 97.38 | 0.105 |
| NN–PSO controller | 4.46 | 99.81 | 0.091 |
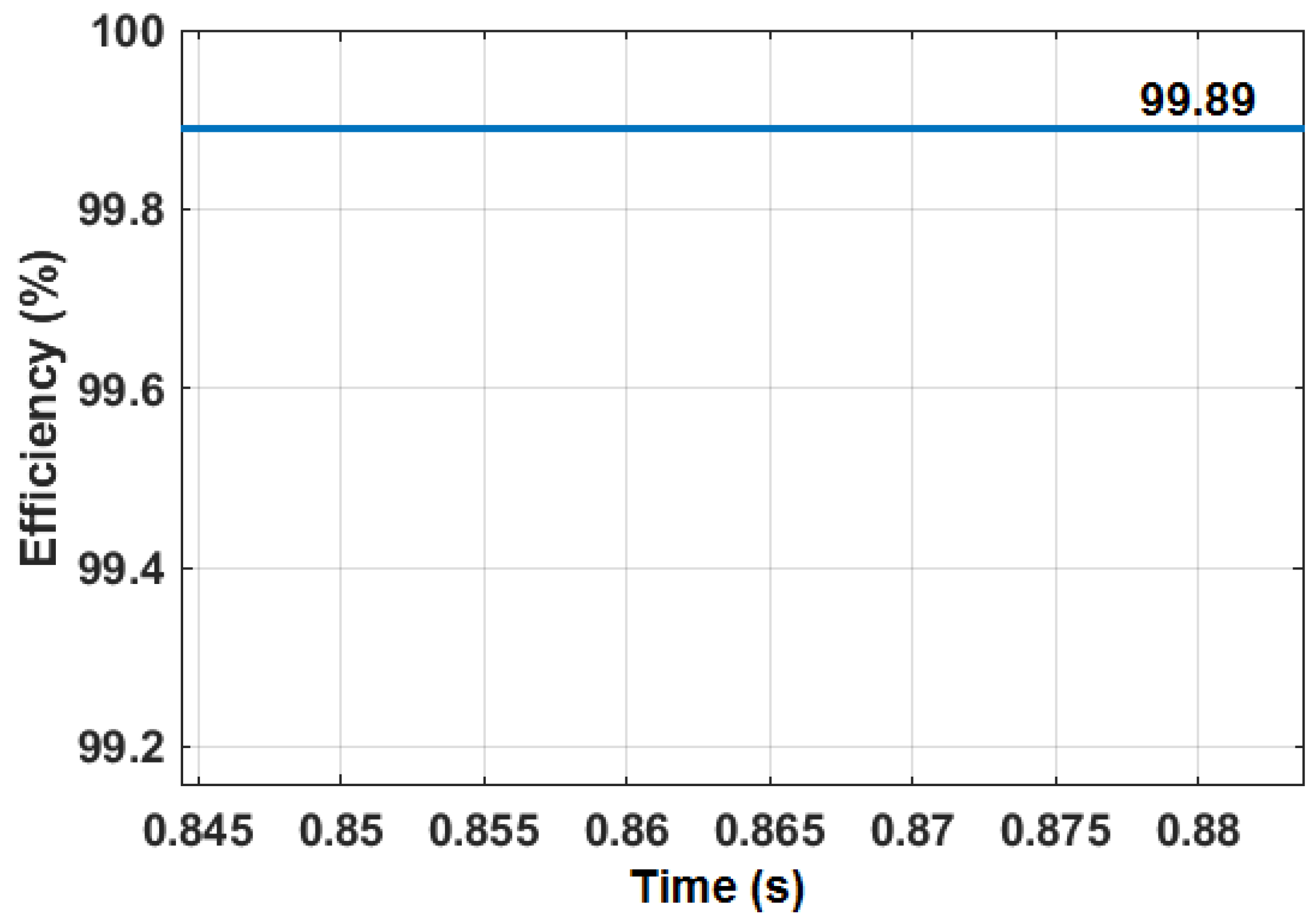
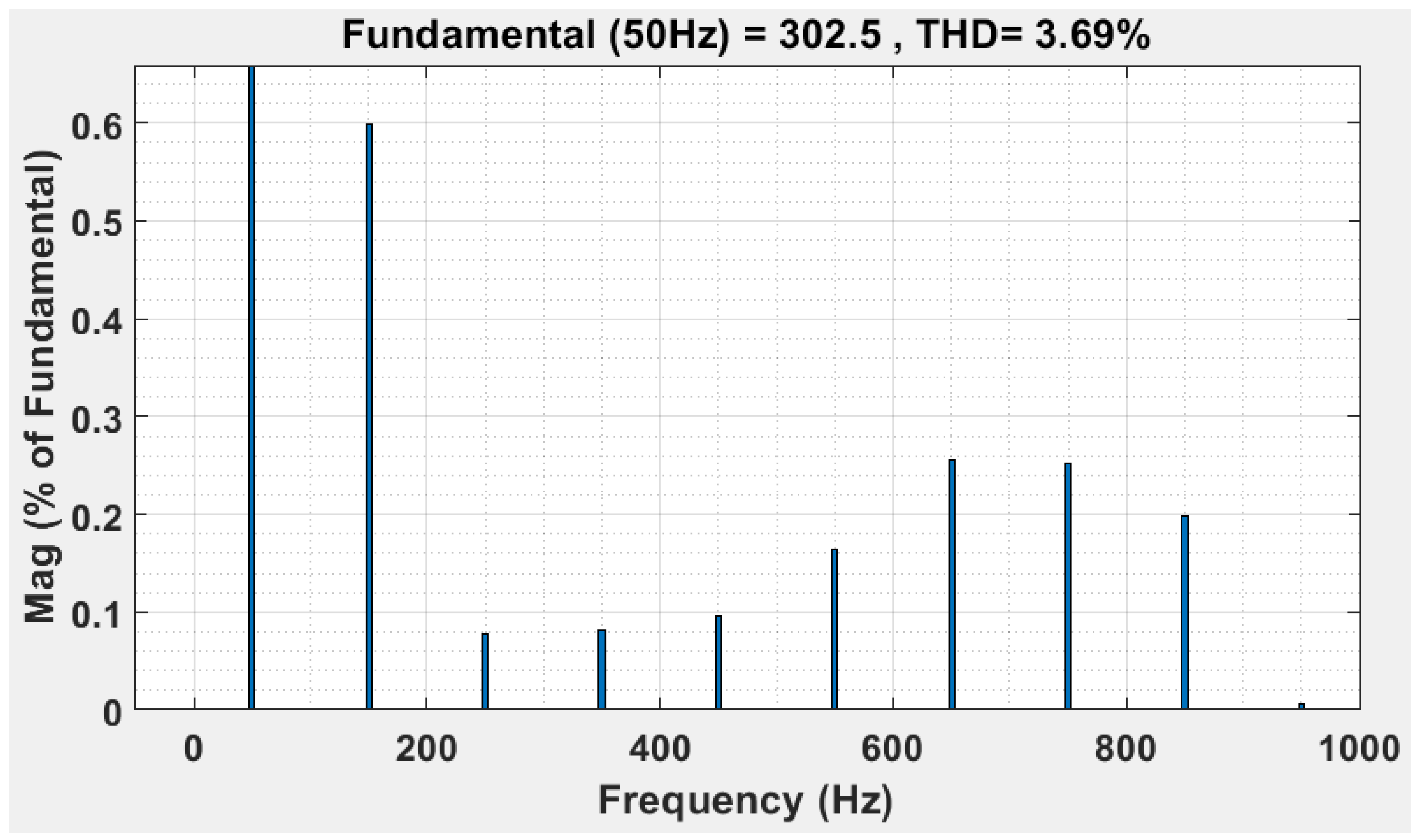
| Proposed NN–IPSO controller | 3.69 | 99.89 | 0.083 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anjinappa, G.; Prabhakar, D.B.; Lai, W.-C. Bidirectional Converter for Plug-In Hybrid Electric Vehicle On-Board Battery Chargers with Hybrid Technique. World Electr. Veh. J. 2022, 13, 196. https://doi.org/10.3390/wevj13110196
Anjinappa G, Prabhakar DB, Lai W-C. Bidirectional Converter for Plug-In Hybrid Electric Vehicle On-Board Battery Chargers with Hybrid Technique. World Electric Vehicle Journal. 2022; 13(11):196. https://doi.org/10.3390/wevj13110196
Chicago/Turabian StyleAnjinappa, Gopinath, Divakar Bangalore Prabhakar, and Wen-Cheng Lai. 2022. "Bidirectional Converter for Plug-In Hybrid Electric Vehicle On-Board Battery Chargers with Hybrid Technique" World Electric Vehicle Journal 13, no. 11: 196. https://doi.org/10.3390/wevj13110196
APA StyleAnjinappa, G., Prabhakar, D. B., & Lai, W.-C. (2022). Bidirectional Converter for Plug-In Hybrid Electric Vehicle On-Board Battery Chargers with Hybrid Technique. World Electric Vehicle Journal, 13(11), 196. https://doi.org/10.3390/wevj13110196