1. Introduction
In the development of an electric race car, the battery pack sizing is directly related to the ultimate performance of the vehicle, often reflecting a trade-off between vehicle range and mass. As a result, most electric race cars are limited mainly by the energy capacity of the battery rather than the total power capability of the drivetrain. This compromise is especially valid for Formula Student vehicles, which are power-limited to 80 kW by regulations and have a small battery capacity, often of less than 7 kWh. Indeed, preliminary lap time simulations indicate that an energy capacity of approximately 10 kWh would be required to finish the endurance event at the maximum regulatory power level. Thus, the optimal use of this energy can produce significant lap time improvements over simple constant power or torque limitation strategies. Furthermore, while highly skilled drivers can approximate an optimal strategy using lift and coast techniques, Formula Student relies on amateur drivers. Thus, automated torque control and energy-saving methods are preferable.
The need to optimize the energy consumption of racing vehicles powered by an internal combustion engine (ICE) has been long understood, with associated trade-offs among fuel consumption, fuel mass, range, and available power [
1]. Numerous approaches have addressed this challenge, including optimising vehicle speed with the driving path [
2]. However, most real-time applications of power optimisation have remained mainly independent of the driving path [
3,
4,
5]. In order to minimise lap time and simultaneously reduce energy consumption, the controller must use energy when it contributes most to acceleration. As drag squares with speed, this occurs at lower velocities [
6]. This challenge is exacerbated by drag forces from the aerodynamic packages commonly used in motorsport competitions.
A number of different control approaches could be used for an energy management system, for example proportional integral derivative (PID) control, linear quadratic regulation (LQR), and model predictive control (MPC). PIDs are commonly used in motorsport, industrial, and mobility applications. It is computationally efficient and intuitive to tune in single-input single-output (SISO) applications. However, it is typically unstable or difficult to tune in multiple-input multiple-output (MIMO) plants [
7]. LQR uses a fixed horizon to calculate a single optimal solution to the quadratic control problem, described by a cost function. However, this approach only computes a single optimal solution. Furthermore, it poorly adapts to nonlinear conditions, which prevents the ability of the controller to rely on superposition to interpret the system dynamics, thus limiting the performance and dramatically increasing the computational cost of the controller [
8]. In addition, because the LQR solution is computed only once, it is susceptible to plant model inaccuracies and does not adapt well to changing conditions [
9].
Specifically for motorsport applications, energy management control systems have been reported in the literature using dynamic programming and convex optimization [
10,
11,
12], nonlinear programming [
13], and artificial neural networks (ANNs) [
14]. In addition, optimal controls have been applied to motorsports for thermal and current prediction [
15] and electrical overloading (EOL) of the battery pack and electric motors for increased vehicle performance [
16]. On the other hand, model predictive controller (MPC) approaches have been of significant interest to driverless researchers. They have recently been shown to work in driverless systems at 10–50 ms sample rates, indicating the feasibility of this control methodology for real-time onboard systems [
17,
18]. Furthermore, MPC has also been used in grid-based energy management systems [
19], fast charging methods in battery electric vehicles to reduce lithium plating [
20], and to estimate the battery state of power [
21,
22]. However, real-time MPC-based energy management solutions focused on reducing computational costs are still needed, which can be accomplished through the linearization of models, a reduced number of states, and appropriate quadratic programming solvers [
23,
24]. In addition, control methodologies have been employed in powertrain and energy management strategies for motorsport applications such as Formula (1) [
4,
23,
25]. However, although MPC approaches have been used in several research areas, the published literature still lacks a predictive algorithm for energy management of purely electric race vehicles.
This paper describes a model-based predictive torque control system for energy management in motorsport applications. It introduces a novel feedback control methodology for energy-limited race vehicles that uses a model-based control algorithm to reduce energy use in an optimal manner when consumption is greater than the target. Furthermore, this real-time algorithm is adaptive to unforeseen changes in race conditions, such as a safety car or driver change, as it repeatedly re-targets the optimal solution [
8].
The proposed methodology is compared against a torque-limited approach with the same energy consumption, resulting in an 11.4% improvement in elapsed time to complete the course of a 150 m straight-line acceleration. A representative manoeuvre in a Formula Student track layout was also investigated—the manoeuvre was extracted from a real endurance event at the Michigan, USA, competition. The MPC approach reduced the elapsed time by 13.5%, as well as responding to energy deficit conditions by reducing torque in an optimal manner.
The remainder of this paper is organized as follows. The next section addresses the development of a state-space linearized vehicle model and its verification against a transient model using the commercial software AVL VSM™. Then, the MPC is presented in
Section 3 alongside design considerations for the number of prediction and control horizons and the definition of set points and signal weight. Next, results are presented in
Section 4 for three scenarios: straight-line acceleration, Formula Student manoeuvre, and a reduced prediction and control horizons scenario to verify the algorithm stability. Finally, this work is summarized and concluded in
Section 5.
2. Vehicle Model
Designed to reduce the computational cost of the controller, the plant model is based on a simplified vehicle longitudinal dynamics model using first-principles (Equation (
1)). It expresses a lumped mass being accelerated by a thrust force—torque from the electric motors, drive ratio, and tire rolling radius—which is resisted by aerodynamic drag, rolling resistance, and road gradient forces. Equation (
2) expresses the power output based on the battery pack voltage
v and torque of the motors.
where
V is the vehicle velocity,
E is the energy available in the battery pack, and
is the total motor torque—from the four in-hub motors. The remaining parameters are described in
Table 1 alongside the values used to populate the model.
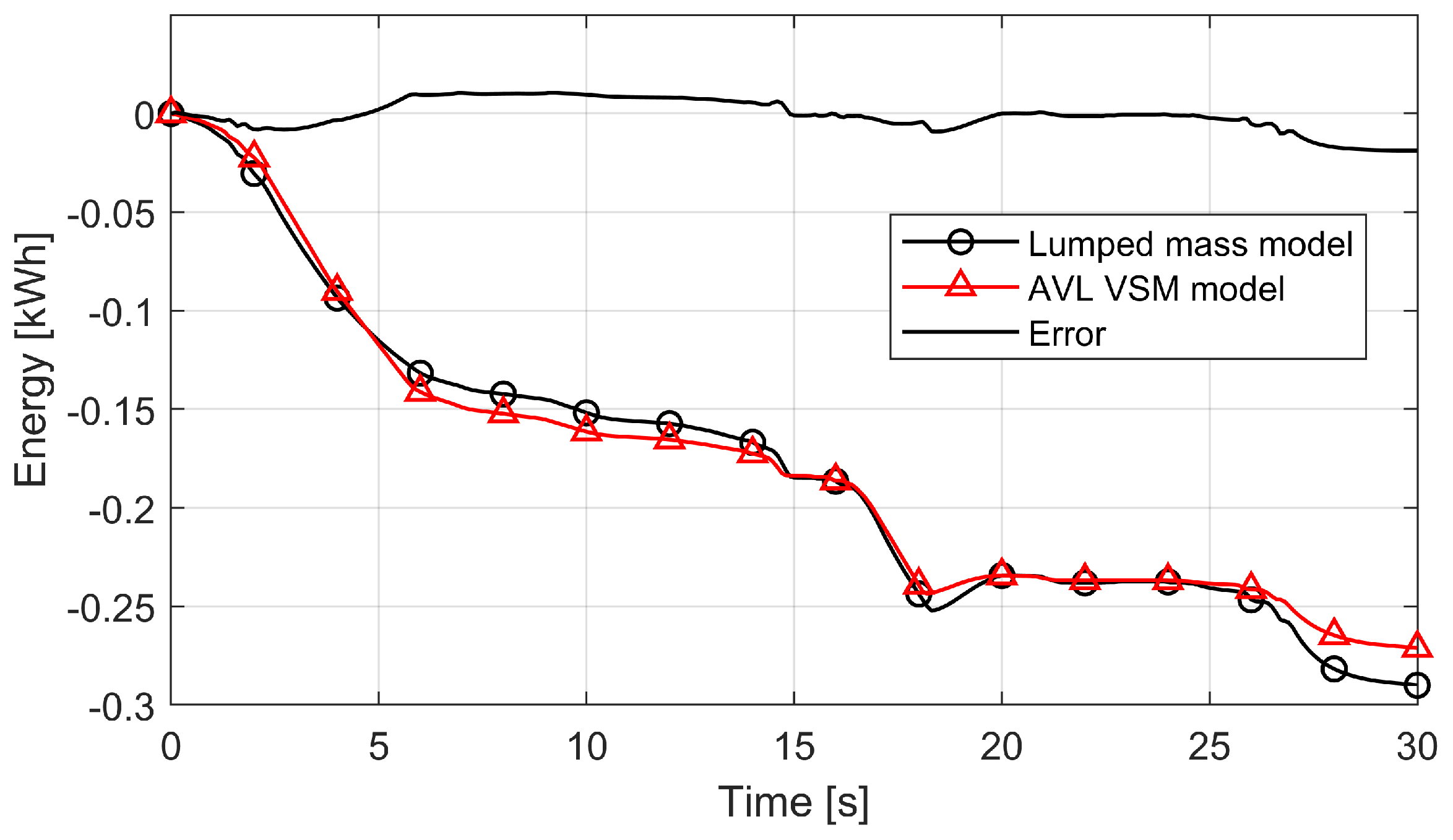
To verify the fidelity of the simplified lumped model in comparison to the real dynamics of the system, a transient model was created using the AVL VSM™ software. The energy consumption was then compared to the lumped model resulting in a root-mean-squared error (RMSE) of
kWh (
Figure 1). The comparison was based on a Formula Student manoeuvre over medium-speed corners from a Formula Student endurance event in Michigan, USA.
Identified Linear Time-Invariant Model
MPC-based control methodologies generally rely on linear time-invariant (LTI) state-space representations of systems [
19]. However, real-world dynamical systems are very rarely purely linear [
8], and in fact, the lumped mass vehicle model used in this paper is time invariant and nonlinear: as drag forces square with velocity, the outputs remain independent of absolute time. The representation of a LTI assumes the state-space format of Equations (
3) and (
4).
In the first equation,
x is the state vector of the system,
is the state matrix,
is the input matrix, and
u is the input vector of the plant. In the second equation, the output vector
y is a function of the output matrix
, the feed-through matrix
, and the state and input vectors. The
,
,
, and
matrices are a function of the plant dynamics and were determined through the process of system identification (
Appendix A).
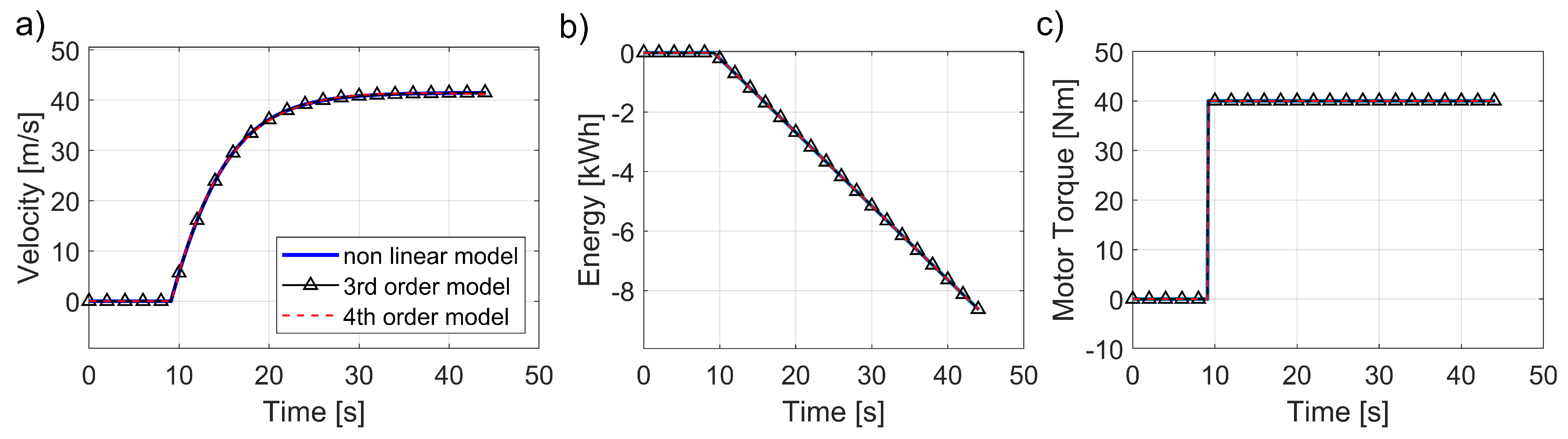
With the help of the MathWorks System Identification Toolbox™, a third- and a fourth-order linearized plant were developed. The process consists of evaluating the system response to a given set of inputs and identifying the set of parameters of the state-space model that better approximate the system response compared to the nonlinear plant. Hence, these models are called identified linear time-invariant (IDLTI) models [
26]. In this work, three step inputs of magnitudes similar to those expected in real-world conditions were used for the system identification.
Figure 2 compares both models with the nonlinear plant.
Because the second derivative of Equation (
1) is relatively small, this vehicle model is considered only slightly nonlinear [
8]. Even then, the linearization process introduces inaccuracies to the model, and thus, the comparison between the linearized model against the nonlinear plant needs to be evaluated. This was accomplished by a normalized root-mean-squared error (NRMSE) cost function (Equation (
5)):
where
y is the validation data output,
is the output of the model, and
is a percentage. Values of 100% indicate a perfect fit, whereas a fit of at least greater than 75% is recommended for stable control [
7]. The 3rd-order model achieved an NRMSE greater than 98%, whilst the 4th-order linearized model had a 99% fit with the corresponding results of the nonlinear plant. Because of the negligible difference of the model fit, the third-order model was selected to reduce the computational costs.
3. MPC Design
In this work, a dynamic optimization problem was created to control a single-input multiple-output plant. The model predictive controller calculates a minimal cost over a receding prediction horizon using a defined plant model at a repeating time step. It uses two horizon values in its calculation. The first is the prediction horizon
P, or number of steps into the future the model predicts and optimizes for. This allows the controller to avoid constraints, as well as make decisions while understanding the long-term implications of the control action, such as in plants with a negative short-term response and positive long-term response or in plants with a long delay period [
27]. The second horizon is the control horizon, which predicts the next
M control moves in the future. Only the first of these control moves is implemented; the rest are discarded. This is typically a small number, between two and five [
7,
27]. The MPC algorithm calculates an optimal solution to a quadratic control problem. However, it calculates a minimal cost over a receding prediction horizon using a defined plant model at a repeating time step, as shown in
Figure 3 [
27].
The manipulated variables
u are held within established limits, as can measured outputs
y, allowing the MPC to consider the physical constraints of the system. As the optimal output is recomputed at every time step
k, the MPC tends to incur relatively high computational costs compared to the PID and LQR controllers. However, as real-time controllers gain computational power, MPCs have been recently able to be used in high-frequency real-time applications [
3,
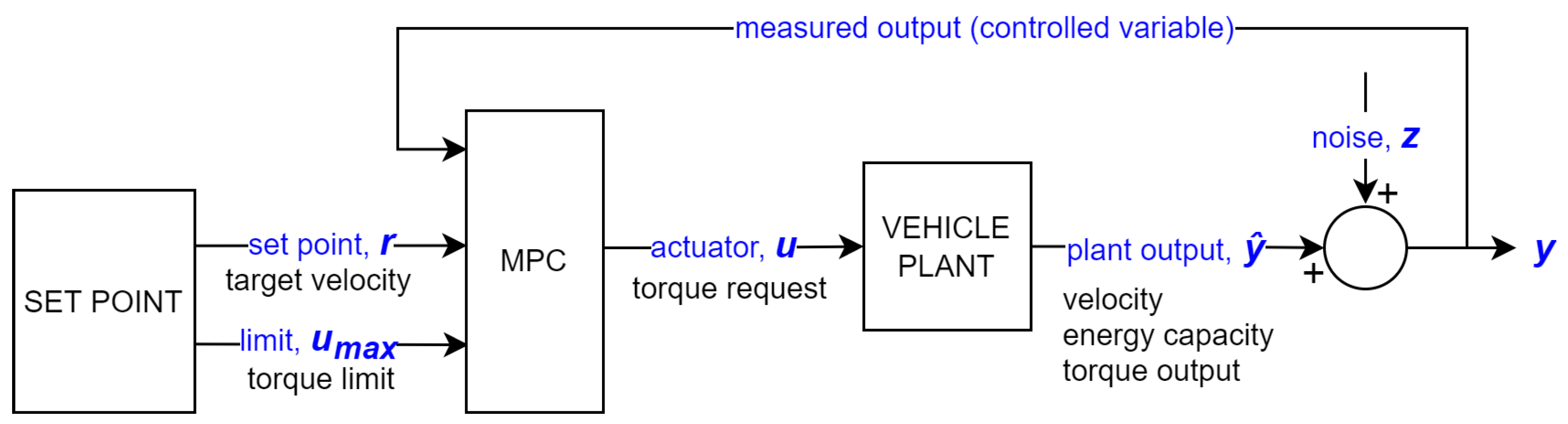
7]. The MPC design is illustrated in
Figure 4. The set point block diagram gives the controller the hard limits of the motor torque,
, and the target velocity set point,
r. The MPC then optimizes the energy consumption based on the feedback of the battery energy capacity, torque output, and actual velocity compared to the target velocity. The implementation of the controller was realized using the MathWorks MPC Designer Toolbox™.
3.1. Horizons
The MPC calculates an optimal solution to a quadratic control problem. The minimal cost is computed over a receding prediction horizon using a defined plant model at a repeating time step. Two horizons are therefore implemented—visualized previously in
Figure 3:
prediction and
control horizons. In general, longer horizons increase controller stability, but come at a higher computational cost because of the increased number of optimized solutions it computes. If control horizons can be lowered without affecting the controller’s response, this is typically taken as an indication that the prediction and control horizon times are adequate [
27]. In this work, a
prediction horizon of ten time steps and a
control horizon of two time steps were used.
The relation between the cost function and the number of horizons used by the MPC is dictated by how close the evaluation of the cost function is to the design constraints—in this work: energy consumption and target velocity. A longer prediction horizon is needed to find the optimal solution if the evaluation of the cost function is close to those constraints. On the other hand, if the cost function is not reaching those limits, it is possible to reduce the number of the prediction and control horizons without major effects on the optimal solution, which is advantageous to reduce the computational costs. In order to investigate the instabilities caused by reducing the predictive and control horizons, these values were reduced to five and one, respectively, further discussed in the Results Section.
3.2. Set Point and Control Signal Weighting
The MPC uses five set points: torque request (N.m); rate of change of the torque request (N.m/Δt); manoeuvre target velocity (km/h); target energy consumption (kWh); and finally, the torque output (N.m) to meet the energy consumption and target velocity constraints. Each set point is weighted differently in the MPC cost function. Multiple weight schemes were tested by trial and error for this implementation with the help of the MPC Designer Toolbox™. In general, the driver’s torque request carries less weight than the velocity term. This is partially because the units used in the torque request are generally larger than those seen in the velocities. The controller attempts to meet the torque request until the cost weighed against that of the other set points grows too high. The energy term carried greater weight because the deviation from the set point occurs over smaller absolute numbers when compared to torque and velocity. This term reduced the torque limits as the energy use exceeded the targets. Similarly, as speed rises over the predetermined set point, the cost increases, and the controller reduces the torque. The set point weighting parameters used in this work are described in
Table 2.
4. Results and Discussion
The purpose of the MPC controller presented in this paper is to optimize torque delivery during acceleration events. Two scenarios were investigated: (1) straight line wide-open throttle acceleration event over 150 m, and (2) cornering manoeuvre of positive torque request over 150 m—that is, the torque demand is always positive; no braking or coasting is involved.
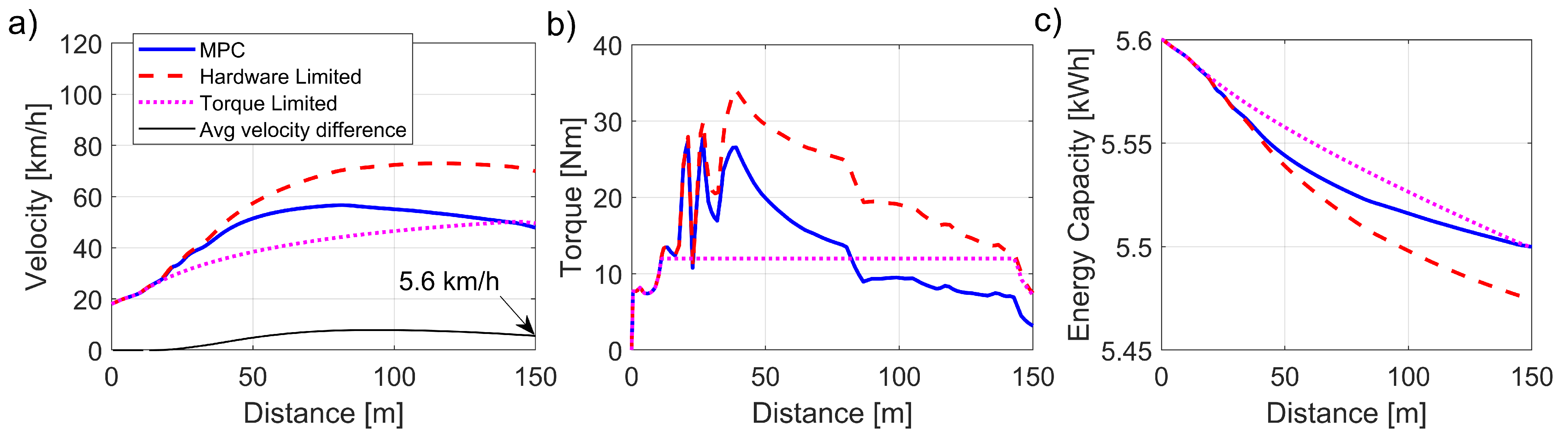
In the first scenario, the vehicle accelerates from a low-speed corner onto a straight line, and the length of the straight represents the longest continuous straight a Formula Student car is likely to encounter in an endurance event. In
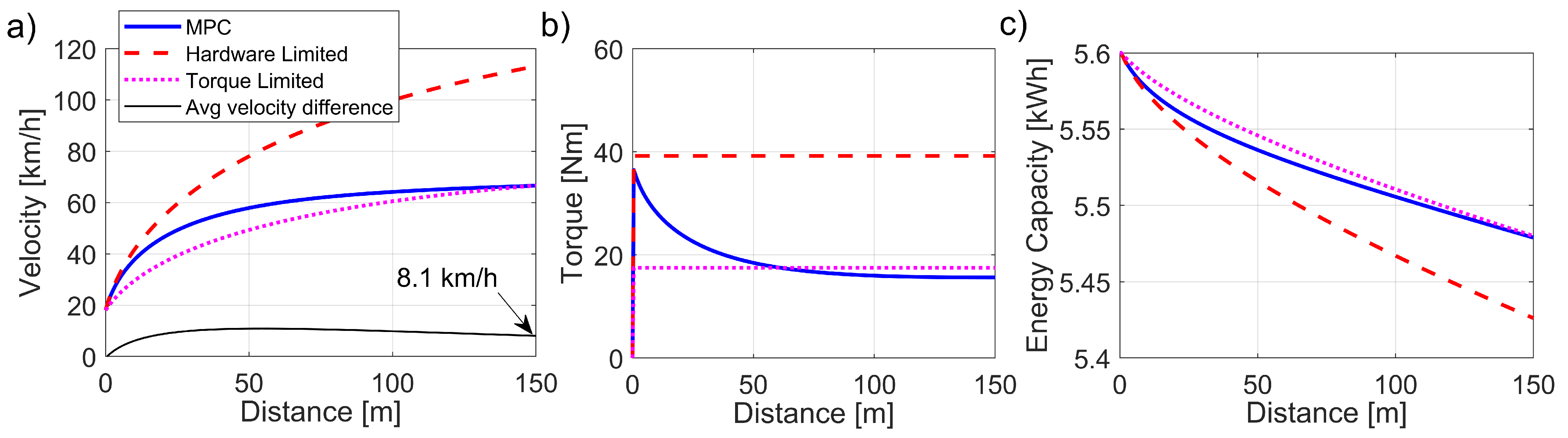
Figure 5, the MPC controller receives an arbitrated constant torque request of
, which is the maximum torque output of the motors (hardware limit). The system response is then compared between a torque-limited approach with an equivalent energy usage.
As expected, the MPC torque set point decreased with distance to optimize the energy consumption as shown in
Figure 5b). This is explained as the most efficient use of the energy in an acceleration manoeuvre occurs at low speeds, as the thrust force is resisted by the least amount of the drag force, which increases with the square of the velocity (
part of Equation (
1)). Compared to the torque-limited approach, an average velocity improvement of 8.1 km/h was observed using the MPC strategy, resulting in a time improvement of
seconds (11.4%) for the same energy consumed.
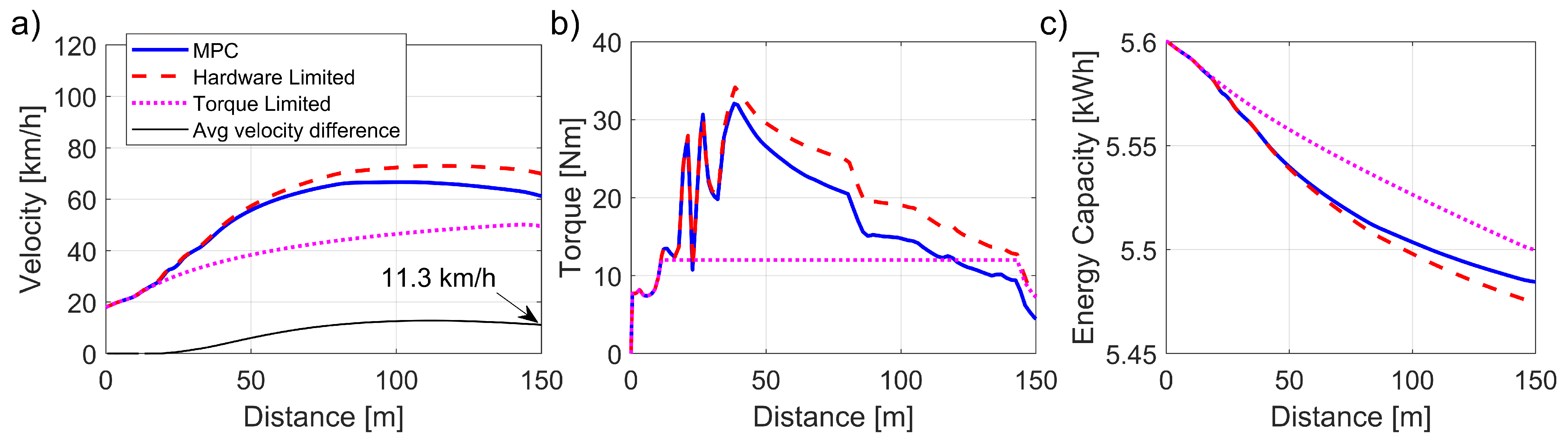
In the second scenario, the manoeuvre input was the same torque request used in the vehicle model verification (
Figure 1).
Figure 6 compares the MPC approach with the torque-limited approach. The MPC results in an average velocity of 42.5 km/h, 5.6 km/h faster than the equivalent energy used by the torque-limited system. This yields a
second or a 13.5% lap time improvement over the course of 150 m.
In order to investigate the instabilities caused by reducing the predictive horizon, it was reduced to five and the control horizon reduced to a single time step. The results are shown in
Figure 7, while the controller was less able to restrict energy use, no instability or boundary violations in the controller were observed, indicating that, with this controller and plant, reducing the control and prediction horizons is a viable method to lower the computational cost if shorter time steps are desired.
5. Conclusions
The MPC torque limiter met the preliminary requirements of the system: it provided significant improvements in lap time and energy use while balancing the immediate torque demand and associated energy use against the overall state of energy in the system. Furthermore, torque safety was maintained by using the hard constraints allowed by the MPC methods. Therefore, model predictive control methods show significant promise for energy-limited race cars, especially Formula Student-class electric vehicles—which are required by the competition rules to be driven by amateur drivers. This controller benefits such drivers since it decreases cockpit workload during competition events, eliminating the need for drivers to use lift and coast techniques to save energy.
Many control architectures are possible to solve a given set of control requirements. While this controller housed the energy management function of the controller within the torque controller, future explorations of this method should consider a low-frequency energy management hypervisor to evaluate the energy state of the system and estimated energy use per lap using a plant model generated from a lap time simulation as suggested by [
3]. This offloads the computational cost of energy management to a very low-frequency controller, freeing up computational headroom to increase the frequency of the torque converter. The actuators of the hypervisor can include the weighting, set points, and limitations of the torque controller. The torque controller can then be expanded to include a thermal winding load of the torque request, as well as the battery pack thermal load.
This paper outlined how an MPC-based control algorithm can be implemented in electric motorsport powertrain optimization and provides a starting point for additional control algorithm development in Formula Student vehicles. Furthermore, it addresses the gap identified in the literature where an MPC-based energy management algorithm was applied for a fully electric race car. However, further validations are needed to investigate the robustness of the controller under real-world conditions.