Cooperative Control for Dual Permanent Magnet Motor System with Unified Nonlinear Predictive Control
Abstract
:1. Introduction
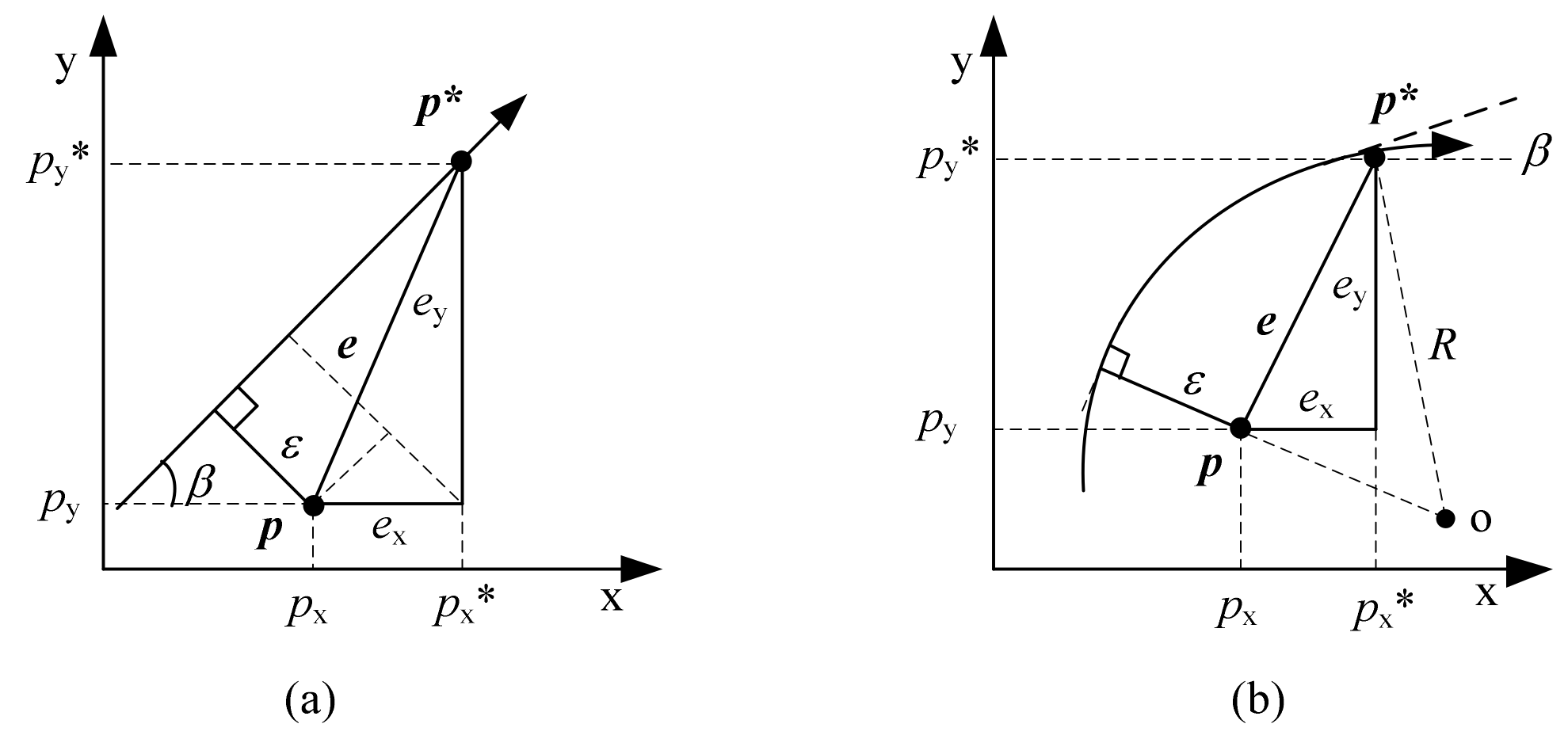
2. Contour Errors of Traditional Dual Motor System
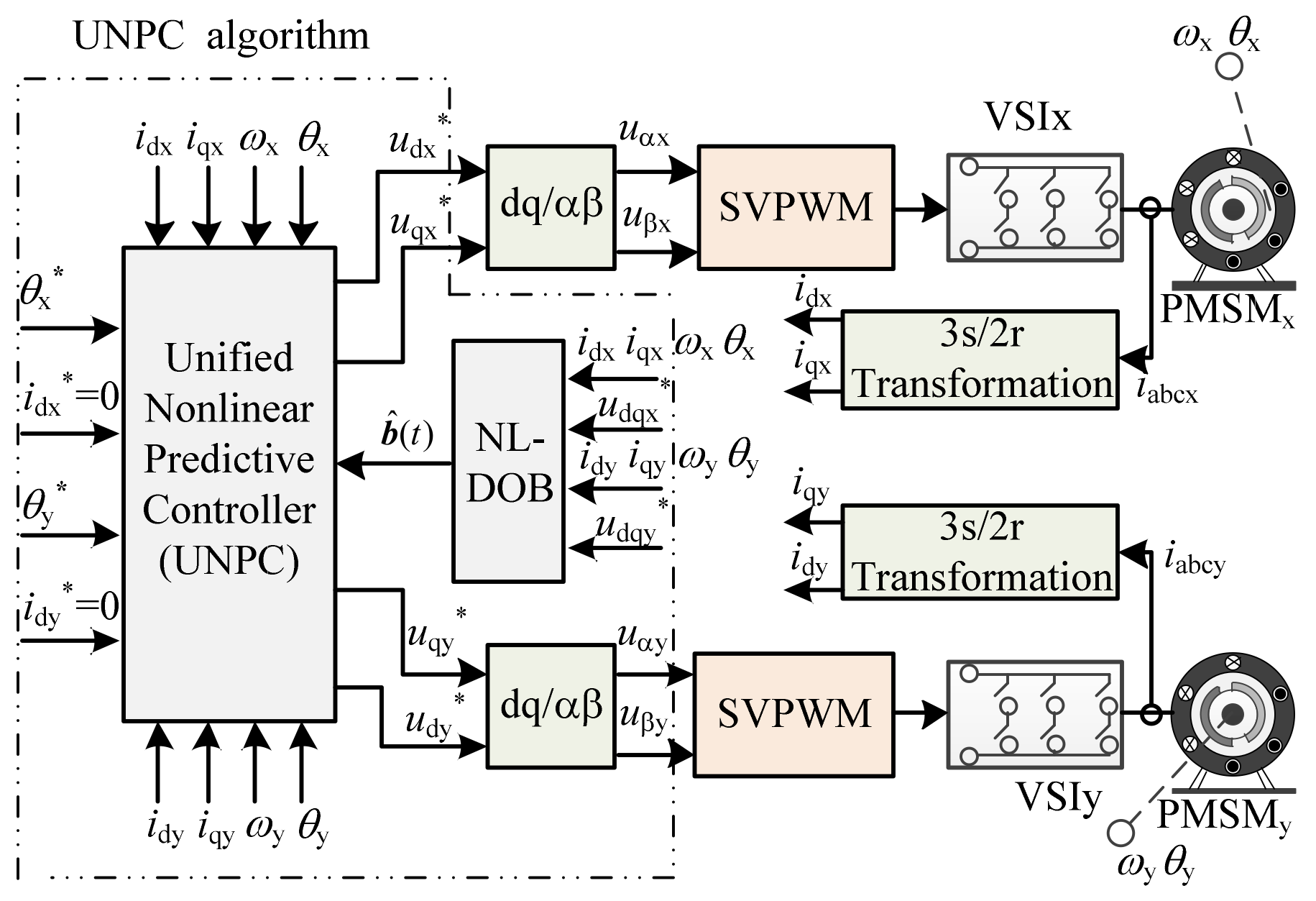
3. Design of UNPC System
3.1. Mathematical Model of PMSM Systems
3.2. Design of Nonlinear Disturbance Observer
3.3. Design of Unified Nonlinear Predictive Controller
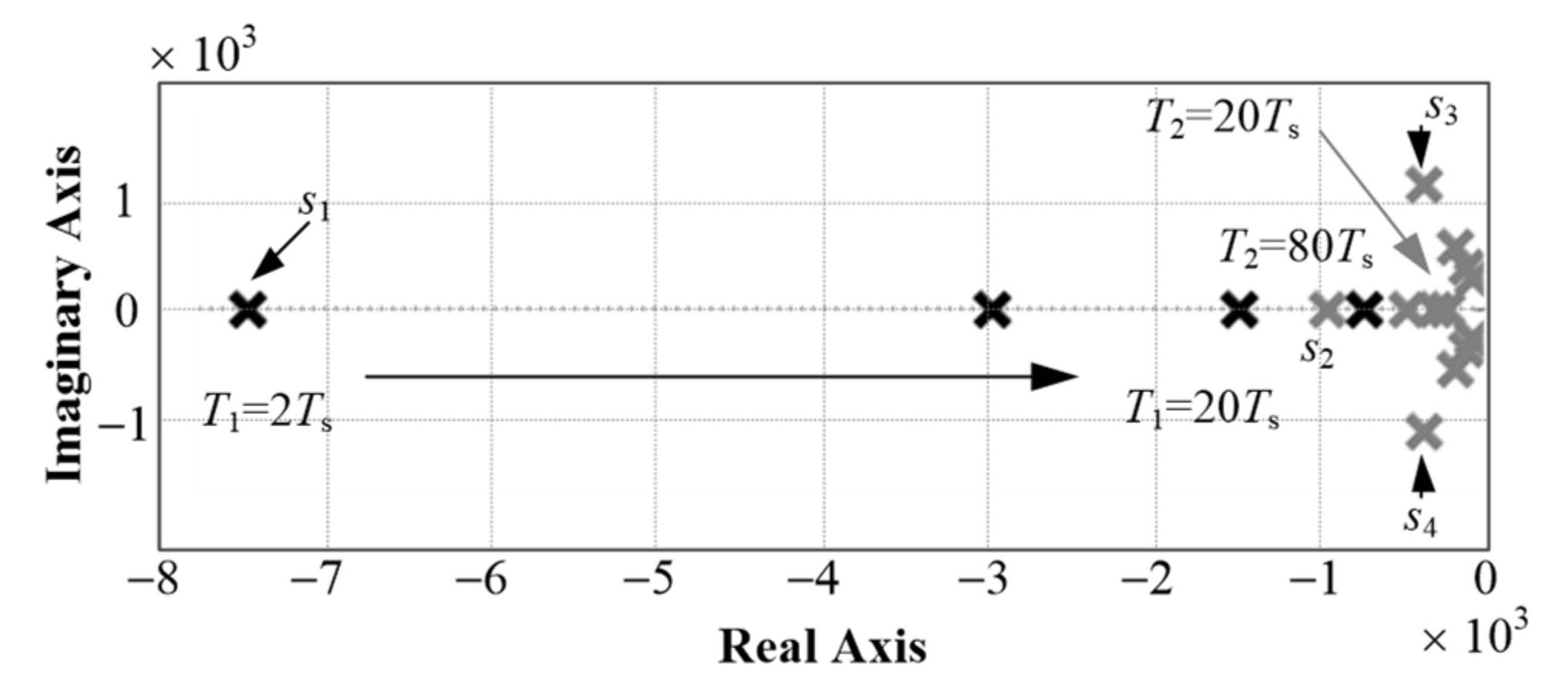
4. Stability Analysis and Parameters Tuning
- (1)
- With the increasing in the T1 and T2, the poles s1, s2, and s3,4 will continue to approach the imaginary axis, the dynamic response speed of the system will slow down, and the stability of the system will deteriorate;
- (2)
- The position poles s3,4 are closer to the imaginary axis than the pole s2. That is, when the T2 changes, the poles s3,4 will play a dominant role in the position tracking performance.
- (3)
- With the increasing in T1 and T2, the position poles s3,4 are closer to the imaginary axis than the current pole s1, that is, the position response speed is slower than the current response speed of the PMSM control system. Thus, the corresponding requirement is T2 > T1.
5. Experimental Verification
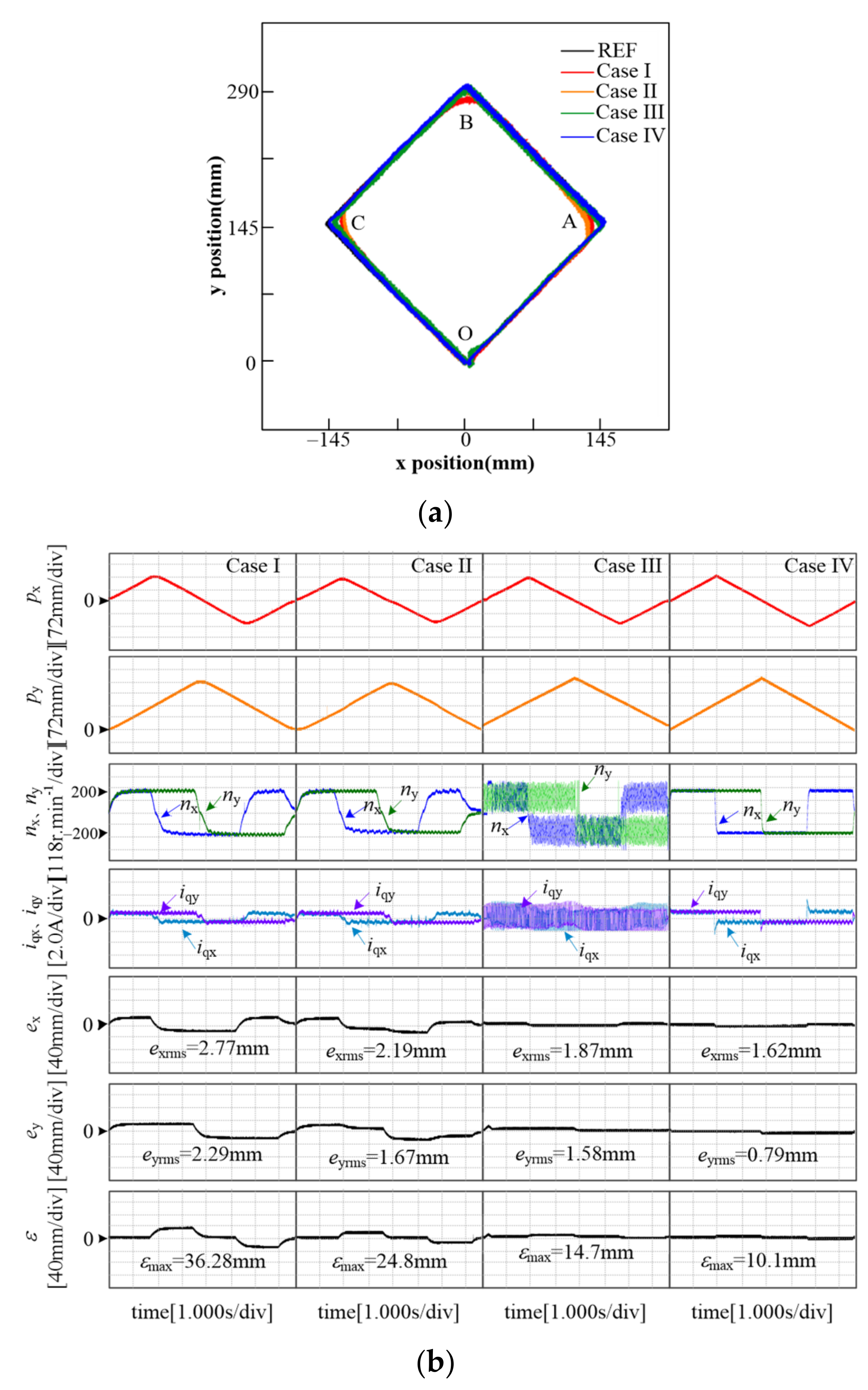
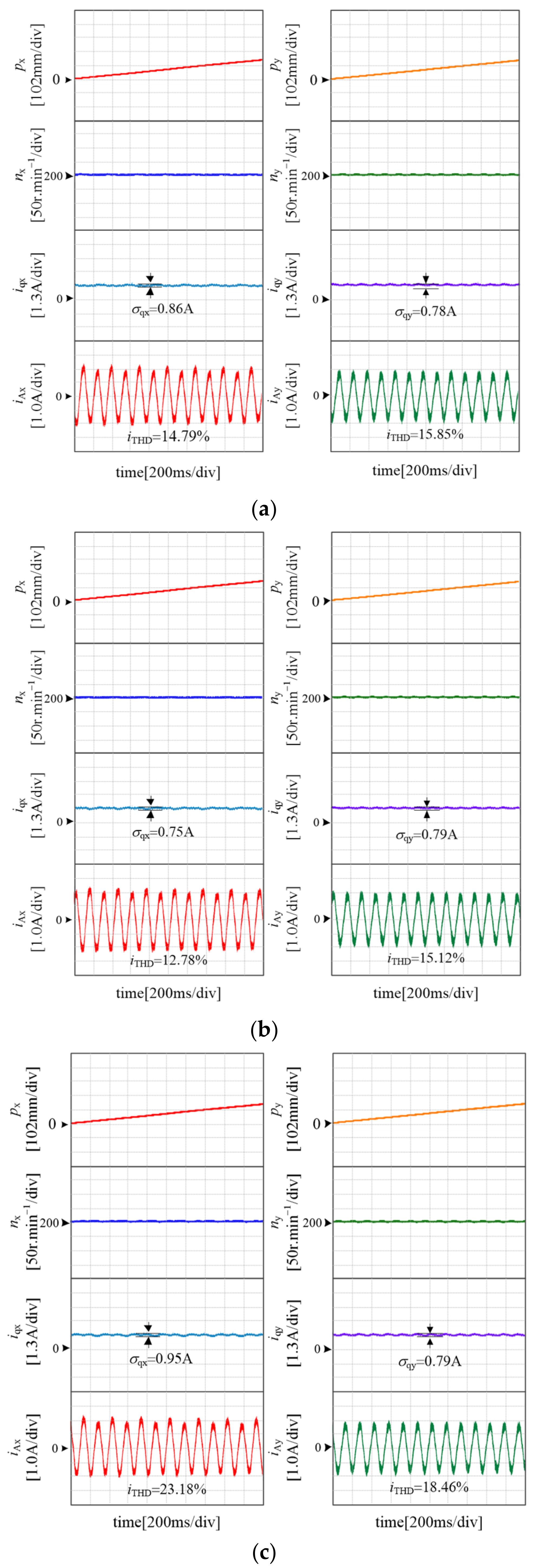
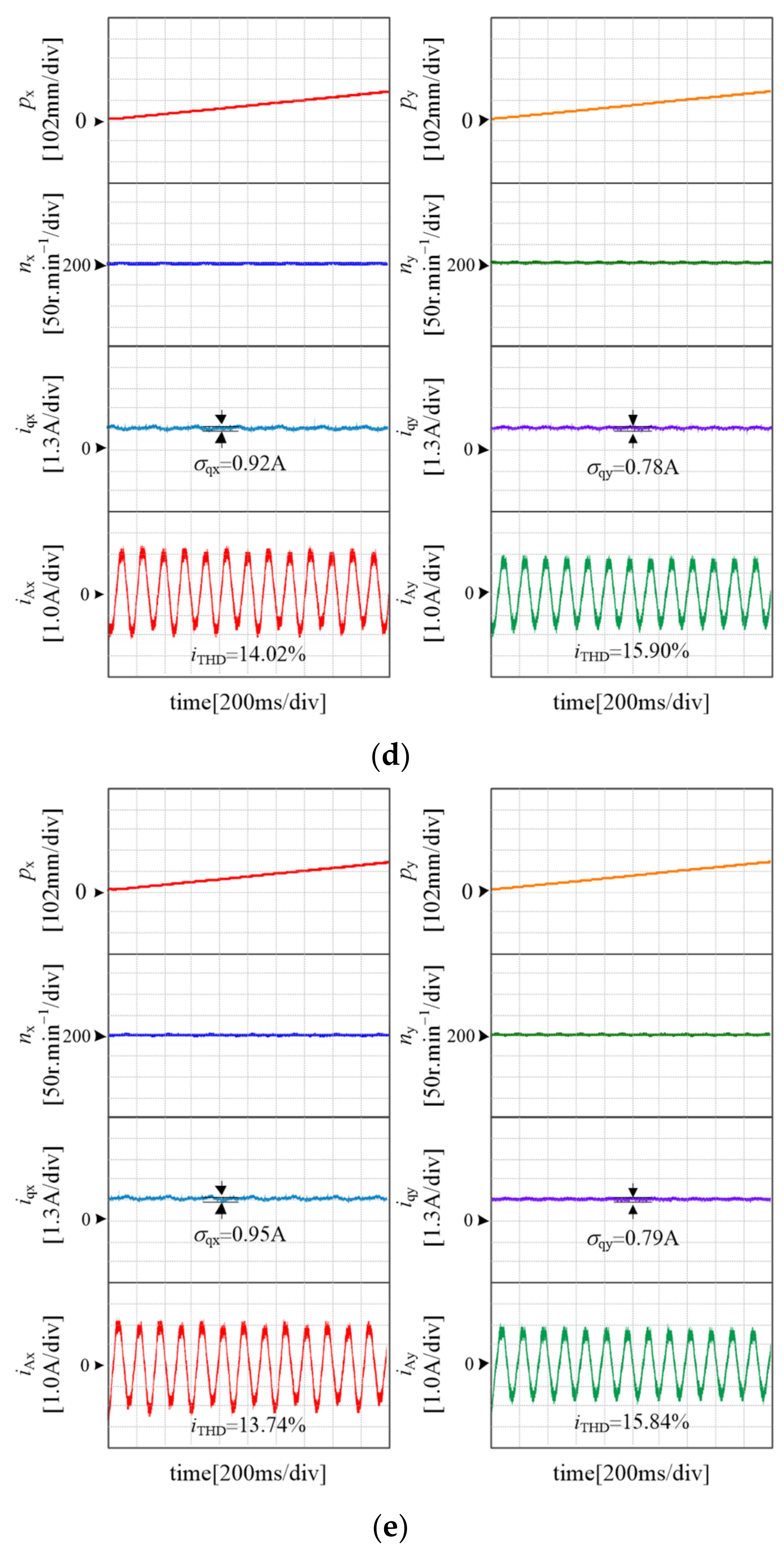
5.1. Linear Trajectory Comparative Experiments
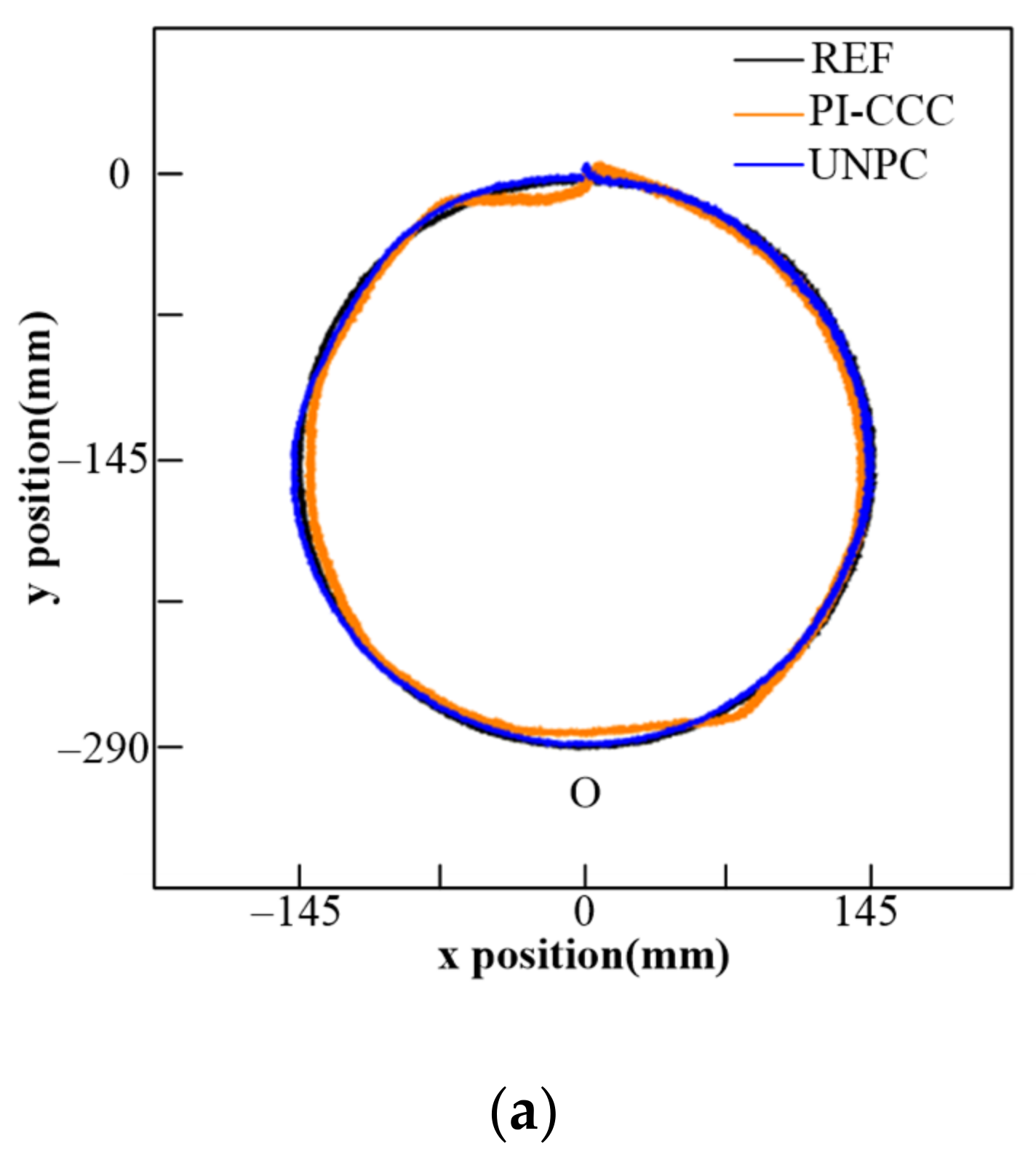
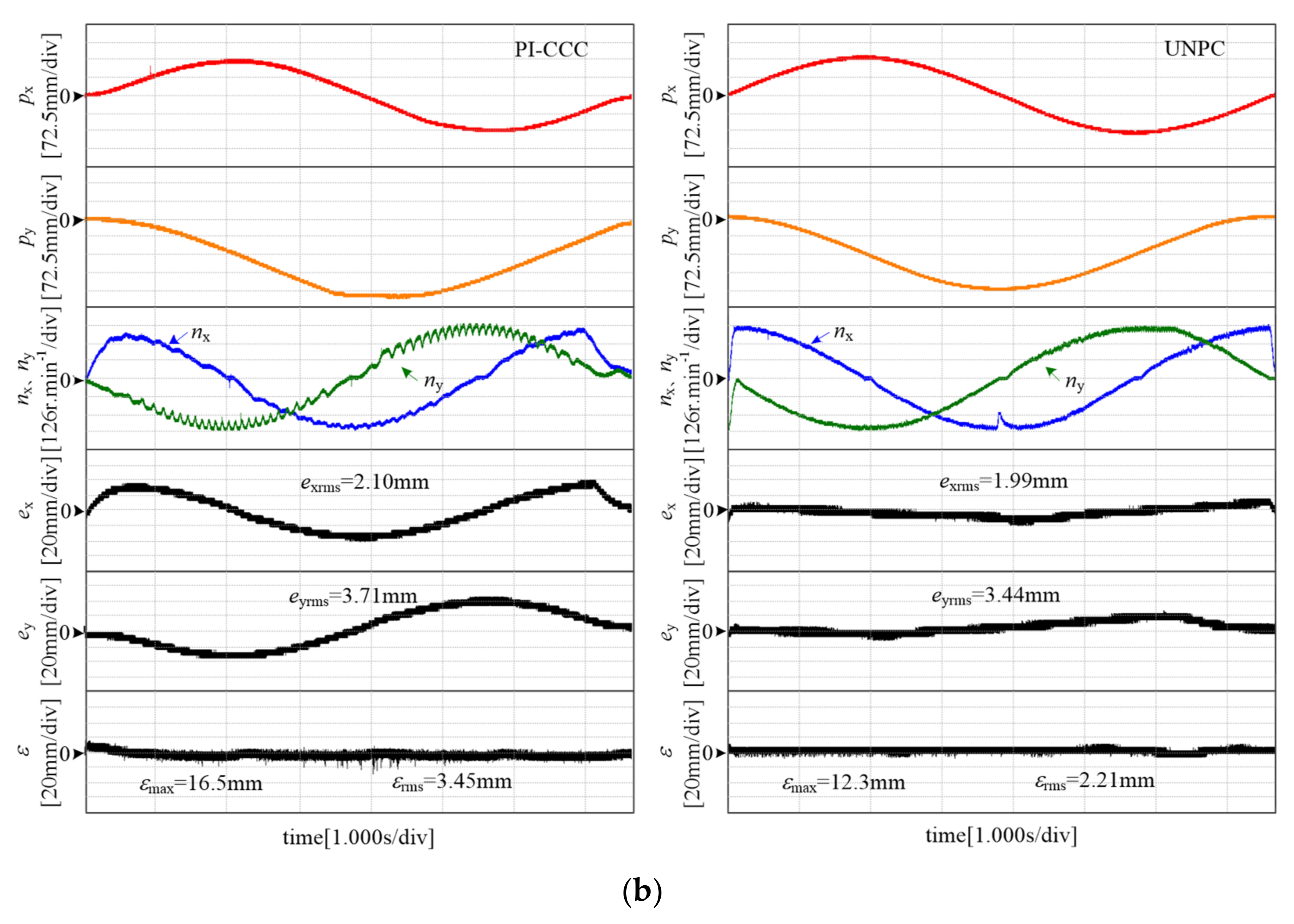
5.2. Circular Trajectory Experiments
5.3. Motor Parameters Mismatch Experiment
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Liu, M.; Gu, F.; Huang, J.; Wang, C.; Cao, M. Integration design and optimization control of a dynamic vibration absorber for electric wheels with in-wheel motor. Energies 2017, 10, 2069. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.; Liang, J.; Shi, T. Speed Synchronous Control of Multiple Permanent Magnet Synchronous Motors Based on an Improved Cross-Coupling Structure. Energies 2018, 11, 282. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; Cheng, Y.; Wang, Y. Research on a Multi-Motor Coordinated Control Strategy Based on Fuzzy Ring Network Control. IEEE Access 2020, 8, 39375–39388. [Google Scholar] [CrossRef]
- Hanifzadegan, M.; Nagamune, R. Contouring Control of CNC Machine Tools Based on Linear Parameter-Varying Controllers. IEEE/ASME Trans. Mechatron. 2016, 21, 2522–2530. [Google Scholar] [CrossRef]
- Lie, T.; Landers, R.G. Multiaxis contour control—The state of the art. IEEE Trans. Control Syst. Technol. 2013, 21, 1997–2010. [Google Scholar]
- Corapsiz, M.F.; Erenturk, K. Trajectory tracking control and contouring performance of three-dimensional CNC. IEEE Trans. Ind. Electron. 2016, 63, 2212–2220. [Google Scholar] [CrossRef]
- Lou, Y.; Meng, H.; Yang, J.; Li, Z.; Gao, J.; Chen, X. Task Polar Coordinate Frame-Based Contouring Control of Biaxial Systems. IEEE Trans. Ind. Electron. 2014, 61, 3490–3501. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, C.; Zhu, Y. Dynamical Model Based Contouring Error Position-Loop Feedforward Control for Multiaxis Motion Systems. IEEE Trans. Ind. Inf. 2019, 15, 4686–4695. [Google Scholar] [CrossRef]
- Li, M.; Zhu, Y.; Yang, K.; Hu, C.; Mu, H. An Integrated Model-Data-Based Zero-Phase Error Tracking Feedforward Control Strategy with Application to an Ultraprecision Wafer Stage. IEEE Trans. Ind. Electron. 2017, 64, 4139–4149. [Google Scholar] [CrossRef]
- Chu, Z.; Chen, G.; Cui, J.; Wang, S.; Sun, F. Classifier-Based Approximator for Friction Compensation in High Accelerated Positioning System. IEEE Trans. Ind. Electron. 2021, 68, 4090–4098. [Google Scholar] [CrossRef]
- Amthor, A.; Zschaeck, S.; Ament, C. High Precision Position Control Using an Adaptive Friction Compensation Approach. IEEE Trans. Autom. Control 2010, 55, 274–278. [Google Scholar] [CrossRef]
- Koren, Y. Cross-coupled biaxial computer for manufacturing systems. ASME J. Dyn. Syst. Meas. Control 1980, 102, 265–272. [Google Scholar] [CrossRef]
- Koren, Y.; Lo, C.C. Advanced controllers for feed drives. CIRP Ann. 1992, 41, 689–698. [Google Scholar] [CrossRef]
- Xu, W.; Hou, J.; Li, J.; Yuan, C.; Simeone, A. Multi-Axis Motion Control Based on Time-Varying Norm Optimal Cross-Coupled Iterative Learning. IEEE Access 2020, 8, 124802–124811. [Google Scholar] [CrossRef]
- Yang, X.; Seethaler, R.; Zhan, C.; Lu, D.; Zhao, W. A Model Predictive Contouring Error Precompensation Method. IEEE Trans. Ind. Electron. 2020, 67, 4036–4045. [Google Scholar] [CrossRef]
- Lam, D.; Manzie, C.; Good, M.C. Model Predictive Contouring Control for Biaxial Systems. IEEE Trans. Control Syst. Technol. 2013, 21, 552–559. [Google Scholar] [CrossRef]
- Shi, T.; Zhang, X.; Zhou, Z.; Xia, C. Precise Contour Control of Biaxial Motion System Based on MPC. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 1711–1721. [Google Scholar] [CrossRef]
- Tang, L.; Landers, R.G. Predictive contour control with adaptive feed rate. IEEE/ASME Trans. Mechatron. 2012, 17, 669–679. [Google Scholar] [CrossRef]
- Zhang, X.; Shi, T.; Wang, Z.; Geng, Q.; Xia, C. Generalized Predictive Contour Control of the Biaxial Motion System. IEEE Trans. Ind. Electron. 2018, 65, 8488–8497. [Google Scholar] [CrossRef]
- Wei, Y.; Wei, Y.; Sun, Y.; Qi, H.; Guo, X. Prediction Horizons Optimized Nonlinear Predictive Control for Permanent Magnet Synchronous Motor Position System. IEEE Trans. Ind. Electron. 2020, 67, 9153–9163. [Google Scholar] [CrossRef]
- Errouissi, R.; Ouhrouche, M.; Chen, W.; Trzynadlowski, A.M. Robust Nonlinear Predictive Controller for Permanent-Magnet Synchronous Motors with an Optimized Cost Function. IEEE Trans. Ind. Electron. 2012, 59, 2849–2858. [Google Scholar] [CrossRef]
- Chen, W.; Ballance, D.; Gawthrop, P.; Gribble, J. Nonlinear PID predictive controller. Proc. Inst. Elect. Eng.—Control Theory Appl. 1999, 146, 603–611. [Google Scholar] [CrossRef] [Green Version]
- Isidori, A. Nonlinear Control Systems: An Introduction, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]

| Parameters | Symbol | Value | Units |
|---|---|---|---|
| Rated power | PN | 2.3 | kW |
| Rated torque | TN | 15 | Nm |
| Number of pole–pairs | p | 2 | - |
| Stator resistance | Rs | 0.635 | Ω |
| Stator inductance | Ls | 4.025 | mH |
| Permanent magnet flux | ψf | 0.5 | Wb |
| Inertia | Jm | 0.00272 | kgm2 |
| Friction coefficient | B | 0.002 | - |
| Movement of the end | Θi | 0.145 | m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Z.; Xu, Z.; Zhang, G.; Geng, Q. Cooperative Control for Dual Permanent Magnet Motor System with Unified Nonlinear Predictive Control. World Electr. Veh. J. 2021, 12, 266. https://doi.org/10.3390/wevj12040266
Zhou Z, Xu Z, Zhang G, Geng Q. Cooperative Control for Dual Permanent Magnet Motor System with Unified Nonlinear Predictive Control. World Electric Vehicle Journal. 2021; 12(4):266. https://doi.org/10.3390/wevj12040266
Chicago/Turabian StyleZhou, Zhanqing, Zhengchao Xu, Guozheng Zhang, and Qiang Geng. 2021. "Cooperative Control for Dual Permanent Magnet Motor System with Unified Nonlinear Predictive Control" World Electric Vehicle Journal 12, no. 4: 266. https://doi.org/10.3390/wevj12040266
APA StyleZhou, Z., Xu, Z., Zhang, G., & Geng, Q. (2021). Cooperative Control for Dual Permanent Magnet Motor System with Unified Nonlinear Predictive Control. World Electric Vehicle Journal, 12(4), 266. https://doi.org/10.3390/wevj12040266






