Simulating Electric Vehicle Diffusion and Charging Activities in France and Germany †
Abstract
1. Introduction
How is it possible to combine the modeling of PEV adoption, charging behavior, and load-shifting potentials in energy-system analysis for France and Germany?
2. Related Work
3. Method: A Hybrid Modelling Approach
3.1. Plug-In Electric Vehicle (PEV) Diffusion and Adoption
3.1.1. Bass Diffusion Model
3.1.2. Binary Logistic PEV Adoption Model
3.1.3. Hybrid PEV Diffusion Modeling Approach
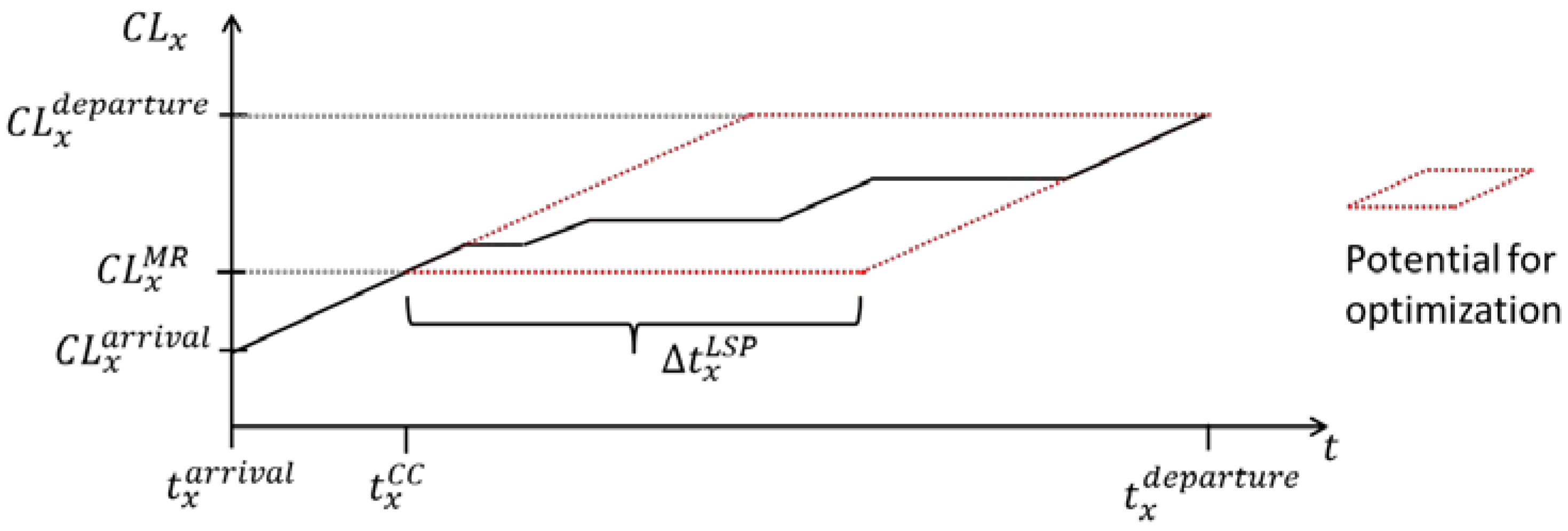
3.2. PEV Charging
4. Results
4.1. PEV Diffusion and Adoption
4.2. PEV Charging
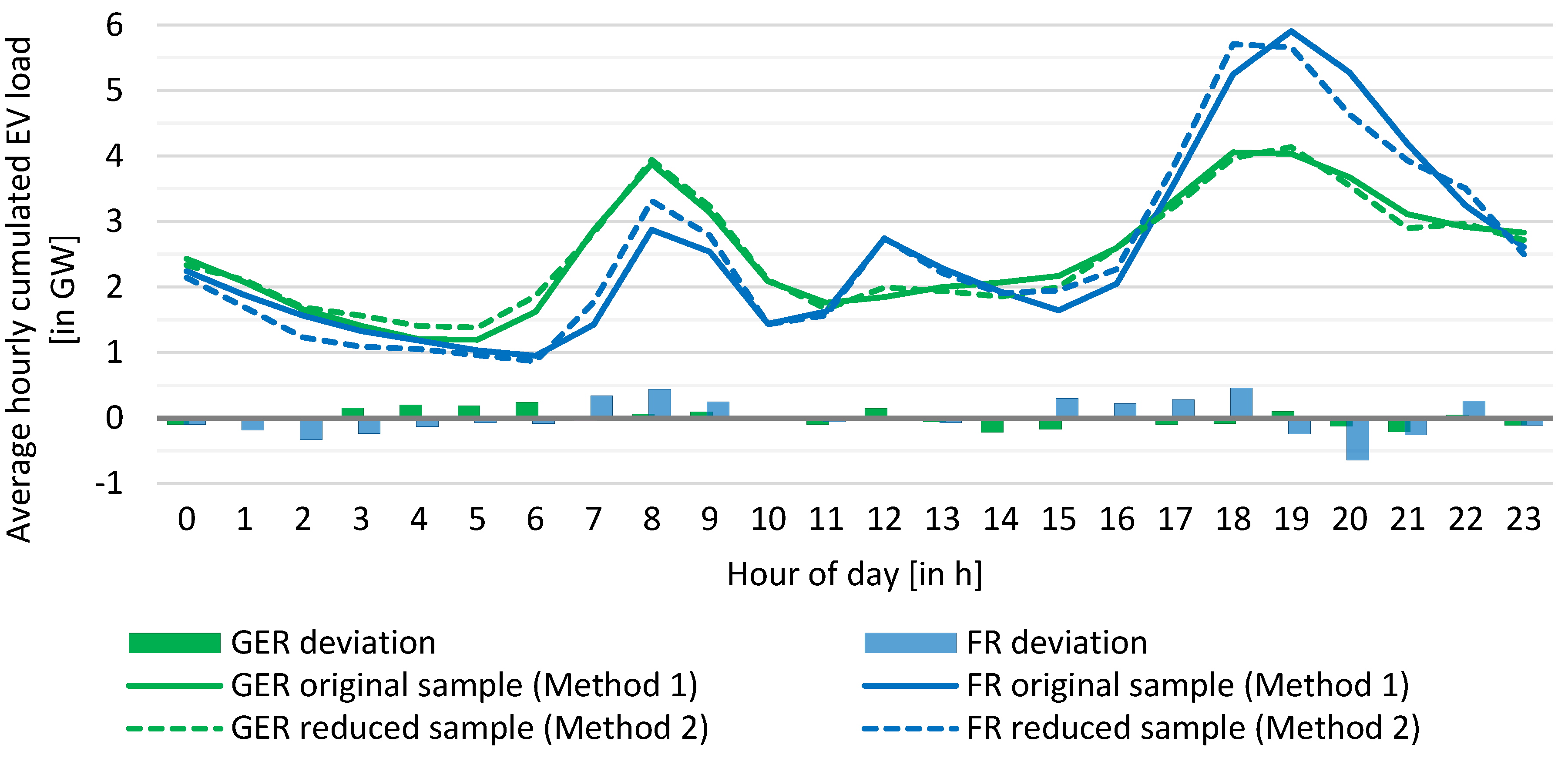
4.3. Effects of Re-Sampling Approach
5. Discussion
5.1. Hybrid Diffusion and Adoption Model for PEV
5.2. Sensitivity Analysis for PEV Charging
5.3. Limitations
6. Conclusions and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Stern, N. The Economics of Climate Change; Cambridge University Press: Cambridge, UK, 2007; ISBN 9780511817434. [Google Scholar]
- Europäische Kommission. Langfristige Strategie—Zeithorizont 2050. Available online: https://ec.europa.eu/clima/policies/strategies/2050_de (accessed on 26 February 2019).
- Europäische Kommission. Greenhouse Gas Emission Statistics-Emission Inventories. Available online: https://ec.europa.eu/eurostat/statistics-explained/pdfscache/1180.pdf (accessed on 26 February 2019).
- Eurostat. Statistics Explained—Greenhouse Gas Emission Statistics: Emission Inventories. Available online: https://ec.europa.eu/eurostat/statistics-explained/index.php/Greenhouse_gas_emission_statistics (accessed on 31 October 2019).
- Jochem, P. A CO2 Emission Trading Scheme for German Road Transport: Assessing the Impacts Using a Meso Economic Model with Multi-Agent Attributes. Ph.D. Thesis, Karlsruher Institut für Technologie, Karlsruhe, Germany, 2009. [Google Scholar]
- Creutzig, F.; Jochem, P.; Edelenbosch, O.Y.; Mattauch, L.; van Vuuren, D.P.; McCollum, D.; Minx, J. Transport: A roadblock to climate change mitigation? Science 2015, 350, 911–912. [Google Scholar] [CrossRef] [PubMed]
- Jochem, P.; Rothengatter, W.; Schade, W. Climate change and transport. Transp. Res. Part D. Transp. Environ. 2016, 45, 1–3. [Google Scholar] [CrossRef]
- Europäische Kommission. Reducing CO2 Emissions from Passenger Cars. Available online: https://ec.europa.eu/clima/policies/transport/vehicles/cars_en (accessed on 26 February 2019).
- Jochem, P. Electric Mobility & Energy Systems: A Techno-Economic Impact Analysis of Electric Vehicles on the Energy Systems. Ph.D. Thesis, Karlsruher Institut für Technologie, Karlsruhe, Germany, 2016. [Google Scholar]
- Wu, Y.; Yang, Z.; Lin, B.; Liu, H.; Wang, R.; Zhou, B.; Hao, J. Energy consumption and CO2 emission impacts of vehicle electrification in three developed regions of China. Energy Policy 2012, 48, 537–550. [Google Scholar] [CrossRef]
- Will, C.; Jochem, P.; Pfahl, S.; Fichtner, W. Economic and sustainability-potential of carbon-neutral charging services for electric vehicle customers. In Proceedings of the 30th International Electric Vehicle Symposium & Exhibition, EVS30, Stuttgart, Germany, 9–11 October 2017. [Google Scholar]
- IEA. Global EV Outlook. Available online: https://www.connaissancedesenergies.org/sites/default/files/pdf-actualites/globalevoutlook2018.pdf (accessed on 31 October 2019).
- Egbue, O.; Long, S. Barriers to widespread adoption of electric vehicles: An analysis of consumer attitudes and perceptions. Energy Policy 2012, 48, 717–729. [Google Scholar] [CrossRef]
- Richardson, D.B. Electric vehicles and the electric grid: A review of modeling approaches, Impacts, and renewable energy integration. Renew. Sust. Energy Rev. 2013, 19, 247–254. [Google Scholar] [CrossRef]
- Keles, D.; Bublitz, A.; Zimmermann, F.; Genoese, M.; Fichtner, W. Analysis of design options for the electricity market: The German case. Appl. Energy 2016, 183, 884–901. [Google Scholar] [CrossRef]
- Jochem, P.; Gómez Vilchez, J.J.; Ensslen, A.; Schäuble, J.; Fichtner, W. Methods for forecasting the market penetration of electric drivetrains in the passenger car market. Transp. Rev. 2018, 38, 322–348. [Google Scholar] [CrossRef]
- Al-Alawi, B.M.; Bradley, T.H. Review of hybrid, plug-in hybrid, and electric vehicle market modeling Studies. Renew. Sustain. Energy Rev. 2013, 21, 190–203. [Google Scholar] [CrossRef]
- Gnann, T.; Stephens, T.S.; Lin, Z.; Plötz, P.; Liu, C.; Brokate, J. What drives the market for plug-in electric vehicles?:—A review of international PEV market diffusion models. Renew. Sustain. Energy Rev. 2018, 93, 158–164. [Google Scholar] [CrossRef]
- Coffman, M.; Bernstein, P.; Wee, S. Electric vehicles revisited: A review of factors that affect adoption. Transp. Rev. 2016, 37, 79–93. [Google Scholar] [CrossRef]
- Rezvani, Z.; Jansson, J.; Bodin, J. Advances in consumer electric vehicle adoption research: A review and research agenda. Transp. Res. Part D. Transp. Environ. 2015, 34, 122–136. [Google Scholar] [CrossRef]
- Kühl, N.; Goutier, M.; Ensslen, A.; Jochem, P. Literature vs. Twitter: Empirical insights on customer needs in e-mobility. J. Clean. Prod. 2019, 213, 508–520. [Google Scholar] [CrossRef]
- Jensen, A.F.; Cherchi, E.; Mabit, S.L.; Ortúzar, J.D.D. Predicting the Potential Market for Electric Vehicles. Transp. Sci. 2016, 51, 395–789. [Google Scholar] [CrossRef]
- McCollum, D.L.; Wilson, C.; Pettifor, H.; Ramea, K.; Krey, V.; Riahi, K.; Bertram, C.; Lin, Z.; Edelenbosch, O.Y.; Fujisawa, S. Improving the behavioral realism of global integrated assessment models: An application to consumers’ vehicle choices. Transp. Res. Part D Transp. Environ. 2017, 55, 322–342. [Google Scholar] [CrossRef]
- Schühle, F. Die Marktdurchdringung der Elektromobilität in Deutschland: Eine Akzeptanz- und Absatzprognose; Hampp: München, Germany, 2014; ISBN 978-3-95710-000-9. [Google Scholar]
- Wolinetz, M.; Axsen, J. How policy can build the plug-in electric vehicle market: Insights from the REspondent-based Preference And Constraints (REPAC) model. Technol. Forecast. Soc. Chang. 2017, 238–250. [Google Scholar] [CrossRef]
- Hardman, S.; Jenn, A.; Tal, G.; Axsen, J.; Beard, G.; Daina, N.; Figenbaum, E.; Jakobsson, N.; Jochem, P.; Kinnear, N.; et al. A review of consumer preferences of and interactions with electric vehicle charging infrastructure. Transp. Res. Part D. Transp. Environ. 2018, 62, 508–523. [Google Scholar] [CrossRef]
- Gnann, T.; Plötz, P. A review of combined models for market diffusion of alternative fuel vehicles and their refueling infrastructure. Renew. Sust. Energy Rev. 2015, 47, 783–793. [Google Scholar] [CrossRef]
- García-Villalobos, J.; Zamora, I.; San Martín, J.I.; Asensio, F.J.; Aperribay, V. Plug-in electric vehicles in electric distribution networks: A review of smart charging approaches. Renew. Sust. Energy Rev. 2014, 38, 717–731. [Google Scholar] [CrossRef]
- Habib, S.; Kamran, M.; Rashid, U. Impact analysis of vehicle-to-grid technology and charging strategies of electric vehicles on distribution networks—A review. J. Power Sources 2015, 277, 205–214. [Google Scholar] [CrossRef]
- Mwasilu, F.; Justo, J.J.; Kim, E.-K.; Do, T.D.; Jung, J.-W. Electric vehicles and smart grid interaction: A review on vehicle to grid and renewable energy sources integration. Renew. Sust. Energy Rev. 2014, 34, 501–516. [Google Scholar] [CrossRef]
- Hu, J.; Morais, H.; Sousa, T.; Lind, M. Electric vehicle fleet management in smart grids: A review of services, optimization and control aspects. Renew. Sust. Energy Rev. 2016, 56, 1207–1226. [Google Scholar] [CrossRef]
- Chen, J.; Huang, X.; Tian, S.; Cao, Y.; Huang, B.; Luo, X.; Yu, W. Electric vehicle charging schedule considering user’s charging selection from economics. IET Gener. Transm. Distrib. 2019, 13, 3388–3396. [Google Scholar] [CrossRef]
- Korkas, C.D.; Baldi, S.; Yuan, S.; Kosmatopoulos, E.B. An Adaptive Learning-Based Approach for Nearly Optimal Dynamic Charging of Electric Vehicle Fleets. IEEE Trans. Intell. Transport. Syst. 2018, 19, 2066–2075. [Google Scholar] [CrossRef]
- Clairand, J.-M.; Rodriguez-Garcia, J.; Alvarez-Bel, C. Smart Charging for Electric Vehicle Aggregators Considering Users’ Preferences. IEEE Access 2018, 6, 54624–54635. [Google Scholar] [CrossRef]
- Bass, F.M. A New Product Growth for Model Consumer Durables. Manag. Sci. 1969, 15, 215–227. [Google Scholar] [CrossRef]
- Hulot, N. Plan Climat. Available online: http://www.gouvernement.fr/action/plan-climat (accessed on 15 March 2018).
- Levenberg, K. A method for the solution of certain non-linear problems in least squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef]
- Marquardt, D.W. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- KIT Scientific Publishing. Cross-border Mobility for Electric Vehicles: Selected Results from One of the First Cross-Border Field Tests in Europe; Jochem, P., Schäuble, J., Fichtner, W., Eds.; KIT Scientific Publishing: Karlsruhe, Germany, 2016. [Google Scholar]
- Ensslen, A.; Babrowski, S.; Jochem, P.; Fichtner, W. Existe-il des différences d’acceptation des véhicules électriques entre la France et l’Allemagne?—Premiers résultats de l’analyse scientifique du test de flotte Cross Border Mobility for Electric Vehicles (CROME). In Proceedings of the 11ème séminaire francophone Est-Ouest de socio-économie des transports, Karlsruhe, Germany, 24–25 May 2012. [Google Scholar]
- Ensslen, A.; Paetz, A.-G.; Babrowski, S.; Jochem, P.; Fichtner, W. On the Road to an Electric Mobility Mass Market—How Can Early Adopters be Characterized? In Markets and Policy Measures in the Evolution of Electric Mobility; Fornahl, D., Hülsmann, M., Eds.; Springer International Publishing: Cham, Switzerland, 2016; ISBN 978-3-319-24227-9. [Google Scholar]
- ENTD. Enquête Nationale Transports et déplacements. Available online: http://www.statistiques.developpement-durable.gouv.fr/transports/s/transport-voyageurs-deplacements.html (accessed on 10 May 2016).
- MiD. Mobilität in Deutschland 2008. Available online: http://www.mobilitaet-in-deutschland.de/mid2008-publikationen.html (accessed on 10 May 2016).
- Ensslen, A.; Ringler, P.; Jochem, P.; Keles, D.; Fichtner, W. About business model specifications of a smart charging manager to integrate electric vehicles into the German electricity market. In Proceedings of the 14th IAEE European Conference, Rome, Italy, 28–31 October 2014. [Google Scholar]
- Ensslen, A.; Ringler, P.; Dörr, L.; Jochem, P.; Fichtner, W. Incentivizing smart charging: Modeling charging tariffs for electric vehicles in German and French electricity markets. Energy Res. Soc. Sci. 2018, 42, 112–126. [Google Scholar] [CrossRef]
- Babrowski, S.; Heinrichs, H.; Jochem, P.; Fichtner, W. Load shift potential of electric vehicles in Europe. J. Power Sources 2014, 255, 283–293. [Google Scholar] [CrossRef]
- Ministère de la Transition Écologique et Solidaire. Parc au 1er janvier 2011 à 2017 par département, région, source d’énergie et classe de puissance administrative. Available online: http://www.statistiques.developpement-durable.gouv.fr/fileadmin/documents/Themes/Transports/Vehicules_routiers/Parc/2017/parc-vehicules-routiers-2017-2pr2.xls (accessed on 25 January 2018).
- KBA Website. Kraftfahrt-Bundesamt-Umwelt-Bestand an Pkw. Available online: https://www.kba.de/DE/Statistik/Fahrzeuge/Bestand/Umwelt/2017_b_umwelt_dusl.html?nn=663524 (accessed on 25 January 2018).
- Bourbon, J.-C. Le développement des voitures électriques met le réseau sous tension. Available online: https://www.la-croix.com/Economie/France/Le-developpement-voitures-electriques-reseau-sous-tension-2017-02-03-1200822315 (accessed on 23 February 2018).
- Die Bundesregierung. Regierungsprogramm Elektromobilität. Available online: https://www.bmbf.de/files/programm_elektromobilitaet%281%29.pdf (accessed on 25 January 2018).
- Leurent, F.; Windisch, E. Triggering the development of electric mobility: A review of public policies. Eur. Transp. Res. Rev. 2011, 3, 221–235. [Google Scholar] [CrossRef]
- Jenn, A.; Tal, G.; Fulton, L. A multi-model approach to generating international electric vehicle future adoption scenarios. In Proceedings of the 30th International Electric Vehicle Symposium & Exhibition, EVS30, Stuttgart, Germany, 9–11 October 2017. [Google Scholar]
- Sultan, F.; Farley, J.U.; Lehmann, D.R. A Meta-Analysis of Applications of Diffusion Models. J. Mark. Res. 1990, 27, 70. [Google Scholar] [CrossRef]
- ZSW. Data Service. Available online: https://www.zsw-bw.de/en/media-center/data-service.html#c6700 (accessed on 18 October 2019).
- Zimmermann, F.; Bublitz, A.; Keles, D.; Fichtner, W. Cross-border Effects of Capacity Remuneration Mechanisms. The Swiss Case; KIT: Karlsruhe, Germany, 2019. [Google Scholar]
- Hauff, K.; Pfahl, S.; Degenkolb, R. Taxation of Electric Vehicles in Europe: A Methodology for Comparison. WEVJ 2018, 9, 30. [Google Scholar] [CrossRef]
- Mersky, A.C.; Sprei, F.; Samaras, C.; Qian, Z. Effectiveness of incentives on electric vehicle adoption in Norway. Transp. Res. Part D Transp. Environ. 2016, 46, 56–68. [Google Scholar] [CrossRef]
- Sierzchula, W.; Bakker, S.; Maat, K.; van Wee, B. The influence of financial incentives and other socio-economic factors on electric vehicle adoption. Energy Policy 2014, 68, 183–194. [Google Scholar] [CrossRef]
- Jenn, A.; Springel, K.; Gopal, A.R. Effectiveness of electric vehicle incentives in the United States. Energy Policy 2018, 119, 349–356. [Google Scholar] [CrossRef]



| PEV Stock | France | Germany | ||
|---|---|---|---|---|
| End 2009 | - | [47] | 3032 | [48] |
| End 2010 | 3368 | 4404 | ||
| End 2011 | 6167 | 8670 | ||
| End 2012 | 12,805 | 13,582 | ||
| End 2013 | 22,217 | 23,208 | ||
| End 2014 | 33,595 | 36,175 | ||
| End 2015 | 54,282 | 48,688 | ||
| End 2016 | 79,856 | 54,997 | ||
| Mid 2017 [1] | 101,799 | 92,731 | ||
| Expectation 2030 | 6,000,000 [49] | 6,000,000 [50] | ||
| Total vehicle stock (M) * | 32,675,972 [47] | 45,803,560 [48] | ||
| Parameter | France | Germany | ||
|---|---|---|---|---|
| Mean | Std. Dev. | Mean | Std. Dev. | |
| 0.32 | 0.004 | 0.31 | 0.0015 | |
| 2008.22 | 5.82 | 2010.01 | 1.05 | |
| R2 | ~1 | ~1 | ||
| France | Germany | ||||
|---|---|---|---|---|---|
| Original Sample | Reduced Sample | Original Sample | Reduced Sample | ||
| PEV adopters charging in sample | 4942 | 967 | 4487 | 930 | |
| Represented number of PEV adopters charging | 5.9 mn | 6.0 mn | 5.5 mn | 5.1 mn | |
| Charging events of sampled PEV adopters | 8873 | 1700 | 8590 | 1756 | |
| Represented charging events | 11.8 mn | 12.2 mn | 10.4 mn | 9.5 mn | |
| Plug-in time | Mean | 10.36 h | 9.94 h | 9.93 h | 10.59 h |
| Std. Dev. | 7.23 h | 7.76 h | 7.75 h | 7.24 h | |
| Median | 9.67 h | 11.64 h | 11.42 h | 9.58 h | |
| Active charging time | Mean | 1.56 h | 1.35 h | 1.39 h | 1.70 h |
| Std. Dev. | 2.18 h | 2.32 h | 2.39 h | 2.19 h | |
| Median | 0.82 h | 0.77 h | 0.79 h | 0.82 h | |
| Load-shifting potential | Mean | 8.80 h | 8.59 h | 8.53 h | 8.88 h |
| Std. Dev. | 7.12 h | 7.59 h | 7.58 h | 7.16 h | |
| Median | 7.81 h | 9.09 h | 8.66 h | 7.89 h | |
| Energy charged per charging event | Mean | 5.77 kWh | 4.99 kWh | 5.15 kWh | 6.31 kWh |
| Std. Dev. | 8.07 kWh | 8.60 kWh | 8.86 kWh | 8.12 kWh | |
| Median | 3.04 kWh | 2.84 kWh | 2.92 kWh | 3.04 kWh | |
| Total energy charged per day | 60.82 GWh | 60.82 GWh | 59.96 GWh | 59.96 GWh | |
| Total energy directly charged per day | 1.65 GWh | 2.26 GWh | 2.06 GWh | 2.92 GWh | |
| Total energy flexibly charged per day | 59.16 GWh | 58.56 GWh | 57.90 GWh | 57.04 GWh | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ensslen, A.; Will, C.; Jochem, P. Simulating Electric Vehicle Diffusion and Charging Activities in France and Germany. World Electr. Veh. J. 2019, 10, 73. https://doi.org/10.3390/wevj10040073
Ensslen A, Will C, Jochem P. Simulating Electric Vehicle Diffusion and Charging Activities in France and Germany. World Electric Vehicle Journal. 2019; 10(4):73. https://doi.org/10.3390/wevj10040073
Chicago/Turabian StyleEnsslen, Axel, Christian Will, and Patrick Jochem. 2019. "Simulating Electric Vehicle Diffusion and Charging Activities in France and Germany" World Electric Vehicle Journal 10, no. 4: 73. https://doi.org/10.3390/wevj10040073
APA StyleEnsslen, A., Will, C., & Jochem, P. (2019). Simulating Electric Vehicle Diffusion and Charging Activities in France and Germany. World Electric Vehicle Journal, 10(4), 73. https://doi.org/10.3390/wevj10040073





