Abstract
Resource pricing in cloud computing has become one of the main challenges for cloud providers. The challenge is determining a fair and appropriate price to satisfy users and resource providers. To establish a justifiable price, it is imperative to take into account the circumstances and requirements of both the provider and the user. This research tries to provide a pricing mechanism for cloud computing based on game theory. The suggested approach considers three aspects: the likelihood of faults, the interplay among virtual machines, and the amount of energy used, in order to determine a justifiable price. In the game that is being proposed, the provider is responsible for determining the price of the virtual machine that can be made available to the user on each physical machine. The user, on the other hand, has the authority to choose between the virtual machines that are offered in order to run their application. The whole game is implemented as a function of the resource broker component. The proposed mechanism is simulated and evaluated using the CloudSim simulator. Its performance is compared with several previous recent mechanisms. The results indicate that the suggested mechanism has successfully identified a more rational price for both the user and the provider, consequently enhancing the overall profitability of the cloud system.
1. Introduction
Over the past few decades, cloud computing has emerged as a new technology in the information technology industry [1]. This technology provides users with many resources and services based on user demand [2]. Cloud Computing (CC) services are offered in three categories: infrastructure as a service, platform as a service (PaaS), and software as a service (SaaS). Google Docs, Google App Engine, and Amazon Elastic Compute Cloud (Amazon Ec2) are examples of the most popular cloud computing services [3]. The complete list of abbreviations is provided in Abbreviations at the back matter. The concept of CC has become increasingly popular among users due to its remarkable features, such as its exceptional computing power, its affordability advantages, and its remarkable adaptability. Users have the ability to utilize cloud computing resources without the need to invest in costly hardware and software. Instead, they can simply pay for rental services based on the terms outlined in the Service Level Agreement (SLA) provided by the cloud service providers [4]. The SLA is formulated as a formal commitment between the user and the provider to compensate the users if the provider fails to provide the expected level of service [5].
Despite the advancements in cloud computing technology over the years, there remain numerous challenges that must be confronted. The services provided by the cloud providers are not free, and customers have to pay a fee based on the amount of resources and the length of time they are used. The cloud pricing plan has a significant impact on the system’s economic benefits. Pricing policies in the cloud are in two fixed and dynamic types. Fixed pricing is a tactic wherein a price is set and upheld for services throughout a particular timeframe. This price can be determined based on hours of resource usage, gigabytes of data storage, etc. Usage-based and subscription-based are examples of fixed pricing strategies [2]. In the context of dynamic pricing, individuals are charged for the services they receive in accordance with the specific features of the service, the characteristics of the user, and the interplay between the supply and demand within the market. Although a dynamic pricing strategy imposes more computational overhead, it also has more economic benefits [6].
Resource allocation and pricing have consistently posed significant challenges for researchers in the cloud, owing to its intricate, extensive, and fiercely competitive landscape. Cloud providers aim to enhance their resource utilization while ensuring customer satisfaction and loyalty in order to maximize their revenue.
The aim of this study is to introduce a just pricing approach derived from game theory. The suggested approach determines the price by considering the users’ resource usage and the expenses incurred by the providers, such as the costs of purchasing and maintaining resources. Additionally, the proposed pricing method takes into account some novel factors that significantly influence the operational costs in cloud computing. These factors include the amount of power consumed for each user’s request, the likelihood of successful job execution, and the interactions between virtual machines when they are allocated on the same resource. The game-based pricing method also considers the market supply and demand to provide a more precise and fairer price.
Game theory offers a structured framework for mathematically representing and articulating decision problems involving multiple agents. This theory provides a platform to examine different strategies of decision-making agents and determine their optimal decisions [7]. Various formats have been proposed to model a decision problem in this theory, two of the most widely used being static and dynamic games. A game is defined as a trio of decision-making factors, their set of possible strategies, and the profit functions of each one. In games that are static, the decision-makers lack knowledge of each other’s decisions. In simpler terms, their decisions can be presumed to occur simultaneously. However, in dynamic games, the agents’ decisions have an order, and the decision-maker in each stage of the game is aware of the decisions of other agents in the previous stages.
Dynamic games are commonly depicted using a decision tree, wherein each node defines a decision state and each edge signifies a potential action in that state for a player. The optimal decision for each player is determined by finding a situation where no player is willing to change his decision if the other players’ decisions are stable. This situation is called the Nash equilibrium point [7]. To tackle dynamic games, we begin by addressing the sub-games at the lowest level in the tree. Through solving these sub-games, we eventually reach the tree’s root. This way of solving a tree is called backward induction.
Therefore, the main contributions of this research can be stated as follows:
- Providing a comprehensive model for cloud pricing based on dynamic games in game theory.
- Taking into account a broader range of factors that impact the price, including energy usage, the likelihood of a job being successfully completed, and the influence of one job on the execution of others. For instance, if a CPU-intensive task is run during a time when the cloud is experiencing a high computational load, it can result in higher costs for the service provider. This aspect should be taken into consideration when determining the pricing.
- A comprehensive comparison of the proposed method compared to related tasks with different scenarios.
The remaining part of the paper is structured in the following manner: Section 2 presents a thorough examination of the most recent literature on pricing methods. Section 3 provides a detailed description of the proposed game-based pricing method and the preliminaries required. The experimental results and performance evaluation of the proposed method are discussed in Section 4. The performance of the proposed method is evaluated in comparison with other recent pricing methods based on the simulation study. Finally, Section 5 concludes the paper with a summary.
2. Related Work
In this section, a review of related works about pricing models in cloud computing environments is presented. Previous studies, including [4,8], have presented and contrasted various pricing techniques within the domain of cloud computing. Auction-based pricing, also known as dynamic pricing, is a widely used pricing mechanism for cloud services [9,10,11,12].
In [13], the authors proposed the online extended consensus revenue estimate mechanism for conducting a recurrent, multiunit, and single-price auction in the Infrastructure as a Service (IaaS) cloud resource setting. This mechanism is both envy-free and truthful, and it is capable of generating profits that are close to optimal. It incorporates a system for dynamically determining reserve prices based on the Power Usage Effectiveness (PUE) of the data center and the costs of electricity. Through the use of simulation-based assessment, its efficacy has been proven across a range of market conditions, surpassing the conventional uniform price auction. The authors also investigated the importance of prior knowledge in maximizing profit by considering the execution time of virtual machines. A small-scale experimental study involving ten users has confirmed the truthfulness of this mechanism in a real-world testing environment.
In [9], a double-auction pricing model named Combinatorial Double Auction Resource Allocation (CDARA) was proposed to balance profit between user and provider. In [10], the CDARA model has been improved. In order to achieve a higher level of fairness, this model takes into account not only the price but also other parameters related to the quality of service during the resource allocation process. If the provider does not meet the required service quality, it imposes penalties on providers and diminishes their reputation. In [11], the resource allocation problem was formulated as a linear programming model to maximize the total profit of users and providers using a combinatorial double auction-based pricing mechanism. In [12], a QoS-based auction method was proposed, which attempts to dynamically determine the price based on the quality of service parameters (such as availability) to increase the provider’s profit.
Performance-based pricing is another approach in which cloud providers are paid based on the actual consumption of their resources. For example, Lucani et al. proposed a pricing model according to the CPU capacity consumed by the user application [14]. They considered the number of CPU cores and the selected CPU frequency in the pricing model. Similarly, another study conducted by Aldossary et al. put forth a pricing policy that takes into account the quantity of energy consumed as well as the real usage of resources per unit, including memory, network, and disk. For this purpose, a mathematical approach has been used to calculate energy consumption and resource usage [15].
The distinction between customers and using incentive mechanisms has always been the focus of pricing methods. For example, Chi et al. proposed a fairness-aware pricing model to increase the profitability of cloud infrastructure providers [16]. They offered lower prices to the customers whose requested resources could be allocated efficiently to encourage them to use cloud services more. Using algorithms from financial option theory, Sharma et al. proposed a pricing architecture for cloud services. A commonly used equation, known as the compound–Moore’s law, was put forward to calculate the cost using factors like the properties of resources, the rate of inflation, and the decline in value. They also used a genetic algorithm and fuzzy logic-based approach to measure the potential loss of cloud providers [17].
The law of supply and demand in marketing is another basis for determining cloud service prices. Cong et al. proposed a dynamic model that determines the price for cloud services according to the real supply-and-demand relationship. They employed closed-loop control mechanisms to dynamically modify the price for cloud services. They also considered penalties for SLA violations by the provider and rewards for users who are not sensitive to delay [5]. Similarly, in [18], the authors also proposed a value-based pricing solution that uses a hedonic regression model to estimate how much a customer is willing to pay for the cloud service.
The amount of energy consumed is another important factor that has been considered recently in pricing methods for achieving a fairer price and making computation greener [15,19]. For instance, Qiu et al. have introduced a pricing solution based on greediness in order to decrease energy usage in cloud computing and transition towards environmentally friendly cloud computing [19]. They showed that the price of resources should be proportional to their energy consumption.
Several dynamic pricing models have been conducted based on game theory [20,21,22,23,24,25]. In [20], the authors suggested a framework for the cloud computing market to make the market uniform and competitive, whereby users can purchase resources from different companies and flexibly exchange their idle resources. Then, a static game-based pricing method is proposed to mathematically model the pricing problem and develop an optimal strategy for the user and cloud provider.
In a study of price competition in a diverse cloud market, the authors examined the rivalry between cloud service providers (CSPs) and cloud users [21]. They devised a two-stage non-cooperative game, where CSPs established prices to maximize their revenue in the first stage. By using an iterative algorithm, they obtained Nash equilibrium prices and analyzed the convergence properties. In the second stage, cloud users opted for services based on performance and price, employing an evolutionary game approach. The result demonstrated that the rate of arrival or resource capacity had a more substantial impact on the CSP side, influencing equilibrium prices and utilities, as opposed to the cloud user side, which affected user cost and arrival rates.
In [26], a framework was introduced that acts as an intermediary between multiple cloud platforms to facilitate the processing of large-scale data streams. This framework offers cloud services for streaming big data processing to users. The process includes renting computer resources from various cloud services and providing users with different service interfaces. To increase income and reduce potential harm, a strategy called Pricing–Repurchasing is created. This strategy involves forming long-term rental agreements with customers. The Pricing–Repurchasing problem was mathematically formulated as a two-stage leader–follower game (Stackelberg), and the equilibrium was thoroughly analyzed. The simulations were conducted to evaluate the effectiveness of the pricing strategy, demonstrating that it generates more revenue for the intermediary than other approaches.
The authors in [22] formulated the problem of setting prices for cloud web services with a collaborative game theory approach. They concluded that cloud platforms can co-exist if they adopt the same pricing strategy.
In [27], the authors explored the issue of maximizing revenue in the context of SaaS and IaaS providers. They depicted this issue by viewing it as a Stackelberg game and examining the presence and uniqueness of the game equilibrium. Furthermore, examining the influence of resource prices on the users’ desire to utilize the service was conducted, and a dynamic pricing strategy was proposed to maximize the revenue for both SaaS and IaaS providers. By performing simulations, the results demonstrate that the proposed strategy surpasses fixed pricing and auction-based pricing mechanisms in terms of revenue maximization and resource utilization.
Ref [28] roposed a pricing strategy that aims to achieve fairness for cloudlet resources. The goal is to find a middle ground that satisfies the needs and desires of both Cloudlet Infrastructure Providers (CIPs) and maximizes overall profits [28]. They introduced a model based on game theory that considers the initial quotes, idle resource rates of CIPs, and the overall profit of the Cloudlet Federation (CLF). The strategy for adjusting prices takes into consideration demand-side psychology and the rate at which the game process converges. The research demonstrates the existence of a solution that achieves Nash equilibrium and introduces an algorithm, known as the game pricing approach based on selection times, to solve the model. The results indicate significant improvements in total profit (more than 20%) and resource utilization (over 50%) than existing methods.
A study in cloud manufacturing examined three resource-sharing strategies: independence, alliance, and co-operation with a cloud platform operator [29]. The research examined how these strategies affected meeting client needs. The findings, represented as a two-stage Stackelberg game, showed that when suppliers formed an alliance, the system profit decreased compared to when they shared independently. This contrasted with the platform operator’s preferences. The analysis also highlighted the complexities involved in task and profit allocation when multiple suppliers were involved. Suppliers with lower prices had the advantage in tasks and profits based on varying marginal prices. These findings guide suppliers in choosing appropriate resource-sharing strategies in cloud manufacturing.
In [30], a hybrid approach was used to optimize fair prices of resources through a stock market-based technical analysis and maximize resource utilization using Stackelberg output volume in a cloud service provider pool. The experiment incorporates three price rebalancing methods: exponential moving average, pivot point analysis, and relative strength index. The proposed approach ensures higher revenues and improved utilization rates for service providers while subscribers benefit from fair prices and enhanced resource availability. Overall, this solution offers advantages to both service providers and subscribers as it optimizes revenue, enhances resource utilization, and guarantees equitable pricing and resource availability.
As mentioned above, cloud pricing policies can be categorized as fixed and dynamic. In selected methods, the price cannot be well adapted based on the supply and demand of the cloud market. Therefore, lower economic profit and customer satisfaction are expected for fixed pricing strategies compared to dynamic ones.
Therefore, the purpose of this paper is to introduce a pricing method based on dynamic game theory. This method aims to enhance the fairness of the estimated price and simultaneously maximize the profit of the provider and the satisfaction of the customer. The proposed method is modeled using a dynamic game framework. The game is defined between the provider and the user. The effect of other cloud providers and market conditions is seen as the relation of supply and demand in the proposed method. The proposed approach takes into account a wide range of factors that affect the price, including energy consumption, the quantity and duration of resource usage, depreciation, and maintenance expenses, in order to achieve a price that is as fair as possible. Furthermore, virtual machines’ performance interference effects and failure probability of cloud resources are incorporated into the proposed pricing method as two new influencing factors.
3. System Model
The system model adopted in this study is introduced in this section. This study aims to propose a game-based pricing model; by using it, a cloud provider can set a fair price for their services and increase its economic profits while attracting customers. The cloud environment consists of physical machines (), and each one can host multiple virtual machines. Each physical machine is defined by three characteristics: processing power, amount of memory, and price coefficient. The purpose of defining the price coefficient is to take into consideration the price difference when using different machines in the model. In addition, the system model incorporates a resource broker for the cloud environment. This particular component is responsible for resource management and serves as an intermediary between the cloud user and the cloud provider. The cloud broker component receives the user request, which includes the required amount of resources, the task’s volume (measured in million instructions), the task’s deadline, and the user’s total budget. Therefore, a user request can be described by the following Quadruple.
The cloud user who is a player in the dynamic game of the proposed method is identified by their request. The cloud broker identifies the balance of the competition among participants and assigns the appropriate virtual machine to the user’s inquiry at a reasonable cost. The general model of the system is shown in Figure 1.
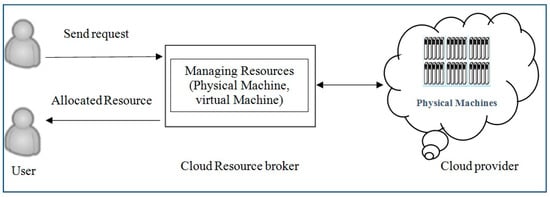
Figure 1.
The architecture of cloud computing system.
4. The Proposed Game-Based Pricing Method
As mentioned, the proposed pricing method is formulated using a dynamic game. The details of the proposed pricing method are described in this section by introducing the game model, the game’s player and their action space, and the game’s payoff functions. It describes how the game tree (extensive form) is constructed by the cloud broker and how a proper virtual machine with a fair price is allocated to the user by finding the Nash equilibrium of the game.
4.1. The Game’s Components
The game consists of two players. The first player is the user, and the second is the cloud service provider. The possible actions (action set) for each player are defined as follows: The first player can select between different virtual machines offered by the provider (). The price of each virtual machine depicted will be provided, and the set of actions available to the second player is the range , where represents the highest price that the user is willing to pay for the service.
The user decides so they can get the required quality of service at the lowest cost. However, the cloud provider chooses the proper price such that it can maximize its profit. Therefore, the utility (payoff) functions of the players can be defined as follows:
Definition 1.
The Cloud Provider’s (CP) usefulness for action of the cloud provider and action of the user is calculated using Equation (1).
where parameter indicates the probability that the user’s task faces a failure during its execution and does not complete successfully; parameter is calculated based on the following equations:
In Equation (3), the parameter signifies the quantity of users who are requesting the service at the price and represents the maximum market demand in terms of the number of customers for the cloud services when the price is set to zero. Figure 2 illustrates the relationship between demand and price. When the number of users applying for cloud resources is high, the provider can also raise the bid price. Conversely, when the number of applicants decreases, the price should also be lowered to attract more customers [17]. The parameter is considered for this purpose and is calculated using Equation (3). The value of the , and parameters can be determined by studying the demand-and-supply relationship for the cloud services in the market. It should be noted that the value of the parameter is less than zero (). The parameter is a coefficient to make a difference in the cost of using expensive hardware over the low-cost one. Parameter indicates the duration of the resource usage. The cost of using the resource would be higher if the duration of resource usage is longer. The parameter specifies the price for a virtual machine with the default processing power and memory amount. If the user requests a virtual machine with different processing power or memory amounts, the price of the virtual machine should be adjusted according to the amount of resources consumed. This adjustment is completed by the use of parameter . The value of the parameter is calculated based on Equation (4). This parameter assists in determining the price by considering the quantity of resources used. The more requested resources will cost more. The and parameters represent the weight of two memory and processing element resources in the final price of the virtual machine and can be set by the cloud provider.
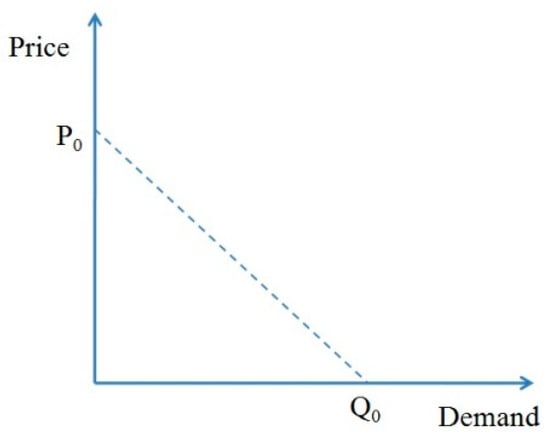
Figure 2.
The relationship between price and demand.
Definition 2.
The utility of the user (customer) corresponding to action of the cloud provider and action of the user themself is computed based on Equation (5):
where the parameter indicates the money that is available to the user and parameter represents all costs required to provide the service (the user’s final payment amount). The parameter is computed based on the following equation:
Parameter indicates the expenses corresponding to the energy consumed by virtual machine ( ) for performing the user’s job. This parameter is calculated based on Equation (7):
where shows the power consumption rate of the machine.
4.2. Constructing the Game Tree
As previously stated, the game being proposed consists of a single decision step for every player. Consequently, the game possesses a tree structure with a depth of two. The starting point of this tree is a decision node assigned to the user, with each subsequent branch signifying a potential action that the user can take. At this decision node, the user should select a virtual machine among different candidate virtual machines offered by the cloud provider. It is assumed that the cloud would offer one virtual machine on each physical machine if possible (for example, if enough resources are available on that physical machine to create the requested virtual machine). The nodes placed at depth one are the decision nodes for the cloud provider. Each node corresponds to a situation in which the provider should decide on the price () of the offered virtual machine. The structure of the game tree is shown in Figure 3. To create the comprehensive representation (tree) of the suggested game, there are two primary stages involved. Initially, the action set of the initial player (user) needs to be established by identifying the potential virtual machines. Following that, the next step entails deciding the feasible actions for the provider and, ultimately, calculating the anticipated payoffs for both players.
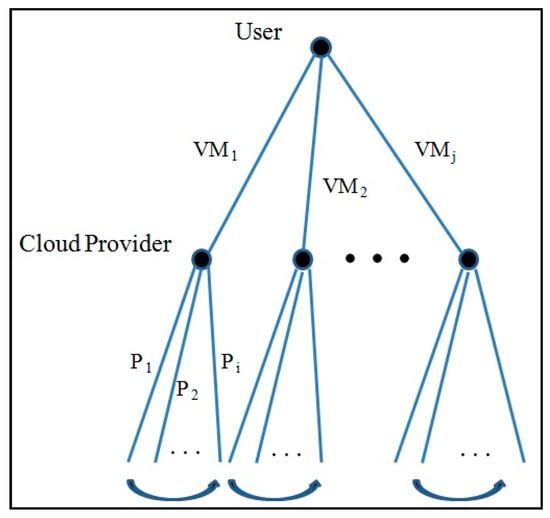
Figure 3.
The tree of the proposed game.
4.2.1. Step One: Finding the Candidate Virtual Machines
In the process of constructing the game tree, the proposed method checks each physical machine to see whether it is possible to create the requested virtual machine of the user on it. This checking is necessary to constitute the action set of the first player (user). Creation of the requested virtual machine might not be possible on all physical machines due to the lack of available resources or the adverse effect of other virtual machines on the performance. Running multiple virtual machines at the same time on a single physical machine can have a negative impact on their performance, as they share resources [31]. It would be advantageous to consider these effects in order to achieve optimal resource allocation, enhance system efficiency, and ensure a fair price.
In cases where multiple virtual machines placed on the same physical machine are responsible for executing programs with high consumption of a particular resource, such as CPU and memory, these effects would be more serious [32]. In such cases, the over-utilized resource could become a bottleneck or a breakpoint for the system and eventually lead to service degradation. In such instances, the resource that is being excessively used could potentially become a hindrance or a stopping point for the system, ultimately resulting in a decline in service quality. According to research conducted and documented in [33], the time it takes to complete a task that requires a significant amount of processing power or memory can be twice as long or even worse if another task that also demands a lot of processing power or memory is using the same physical resource at the same time. Building upon the findings of [33], the proposed approach takes these conflicts into consideration and excludes the physical machines that are unable to promptly execute the user’s task from the process of constructing the tree. Additionally, physical machines that do not have enough available resources are also eliminated from the tree construction process.
4.2.2. Step Two: Constructing the Cloud Provider’s Sub-Games
At this step, the proposed method constructs the second depth of the game tree. The resource broker is in charge of constructing and solving the game. It calculates the provider’s payoff for selecting various prices at each decision point according to Equation (1). As an increase in the price leads to a lower demand for the resource, choosing higher prices does not necessarily mean more profit for the cloud provider.
According to Equation (1), in order to compute the provider’s benefit for each action, it is necessary to calculate the corresponding penalty for each action as well. The proposed approach considers this penalty for cloud providers due to the probability of unsuccessful execution of the user’s task and SLA violation. Considering this probability leads to better resource allocation since the provider tends to improve its profit. Execution of users’ tasks may fail due to various reasons, such as resource breakdown and system overload [34]. In the event of an error or a malfunction, the provider should be obliged to compensate the user for violating the SLA. The proposed approach employs a failure probability model presented in [35] in order to minimize the penalty paid by the provider.
This model helps to predict the failure probability of a task execution on a physical machine with a high accuracy (up to 90%).
At this stage, we estimate the energy cost required to complete the user’s task on each virtual machine, as stated in Equation (7). Because large-scale computing systems such as clouds have increased energy consumption rates, a significant portion of their operating costs are related to paying electricity bills [36,37]. Given that high energy consumption imposes high expenses on the cloud providers, the proposed model considers energy consumption an influential factor in resource allocation and pricing mechanisms.
4.3. Finding the Sub-Game Perfect Nash Equilibrium of the Game
The backward induction method is employed in order to resolve the game and uncover the sub-game perfect Nash equilibrium [38]. First, the lower level (provider level) sub-games are solved. It should be determined which actions the provider (final mover) should take in each possible circumstance to maximize its profit. Second, the upper level (user level) sub-game should be solved. By finding a solution to this sub-game, the actions that would lead to the Nash equilibrium for both players will be established.
Lower-level sub-games: In each sub-game, the optimal price for the corresponding candidate virtual machine should be determined so that the cloud provider’s profit is maximized. Therefore, the derivative of the provider’s payoff function concerning variable should be found. This derivative is equal to zero, and the equation is solved for . First, the extended form of the provider’s payoff function is written as follows:
Now
Therefore, the optimal price in each possible circumstance can be finally calculated as follows:
Upper-level sub-game: After finding out the optimal reaction of the second player () to the user’s moves in the sub-games at a lower level, the sub-game at a higher level can be resolved. At this step, the best response of the user to the cloud provider’s action would also be determined. Knowing the price selected by the provider for each candidate virtual machine, the resource broker can calculate the amount of the user’s profit for each action and choose the most proper virtual machine for the user. To determine the user’s earnings, the resource broker utilizes Equations (5)–(7). Therefore, the best response of the user to action of the provider can be determined as follows:
The action pair is a Nash equilibrium because both players’ action is the best response to each other.
The steps involved in the proposed method, executed by the Grid’s Resource Broker, are illustrated in Algorithm 1. The proposed method first collects information about the physical machine conditions. Then, to handle each request, it determines on which physical machine the desired virtual machine can be created for the successful execution of the request. In the next step, the dynamic game tree is constructed as described in Section 4.2. In the initial phase of game resolution, it determines the optimum cost for every potential virtual machine based on Equation (8). At this stage, it seeks to increase the profit of the cloud provider. In the second stage of solving the game, he chooses the best virtual machine for the user’s request based on Equation (9). At this stage, the user’s profit is expected to increase.
| Algorithm 1. Resource Broker |
 |
5. Experimental Results: Performance Evaluation of the Proposed Method
The performance of the suggested pricing model has been assessed by comparing it to the approaches presented by Chi et al. [16] and Dabbagh et al. [39]. These two past works have been chosen as competitors due to their proximity in assumptions and goals. The proposed method in [16] seeks to increase the efficiency of cloud resources to guarantee the profit of the cloud provider in this way. At the same time, by reducing the price for customers whose requests for the cloud can easily be met, it also seeks to satisfy the user. In the method that has been suggested, users whose requests are not easily met will experience an increase in price. In this work, the relationship between supply and demand in the market has been considered. However, the impact of energy consumption on the price has not been taken into account in comparison to the suggested approach. The method presented in [39] seeks to increase the profit of the cloud provider by increasing resource efficiency and reducing energy consumption. In this work, energy consumption has been considered an important factor in the current costs of the cloud. The method presented in this article only considers the problem from the point of view of the cloud provider and does not take into account user satisfaction, the relationship between supply and demand, and the effect of price on it, as well as the chance of success in executing a request.
The proposed model was implemented using the NetBeans integrated development environment and the CloudSim 4.0 simulator [40]. In the simulation, the cloud provider has several physical machines with various hardware characteristics. One hundred user requests have been considered to be submitted to the system through the simulation period. The implementation parameters are considered the same as shown in Table 1.

Table 1.
Implementation Parameters.
Each physical machine is a powerful server that consists of several computing elements. Therefore, multiple virtual machines can be assigned to one physical machine simultaneously. Physical machines are seen as diverse and therefore possess varying resource attributes, as illustrated in Table 1. The resource broker, which is in charge of constructing the game tree and resolving it, possesses comprehensive knowledge regarding the physical machines and their attributes. Furthermore, the broker maintains a continuously updated inventory of the resources accessible on each physical machine. Having such information helps the broker determine all the candidate virtual machines. An example of a user’s request is shown in Table 2. During the simulation period, it is important to mention that none of the 100 user requests under consideration should be submitted to the system. A number of the requests that are submitted to the system follow a simple linear supply-and-demand model.

Table 2.
A user request example.
5.1. Evaluation of the Proposed Method in Terms of Users’ Profit
Users’ profits are defined as the amount of money left over from their budget after their request is met by the system. In order to ensure a more equitable assessment, the mean quantity is presented in Figure 4. Since the number of users who submit their requests to the system can be different based on the supply-and-demand model and the pricing method applied, the average amount of profit per user would be a better comparison criterion. It is calculated based on the following equation:
where indicates the total number of requests submitted to the system and fulfilled during the simulation time. The other parameters are described in the previous sections.
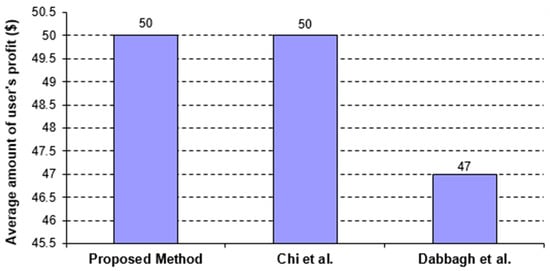
Figure 4.
Comparison of the proposed method with [16,39] from the viewpoint of average profit per user.
As can be seen, the average amount of profits users gain by the proposed approach, and the method proposed by [16] are the same. However, with this difference based on the supply-and-demand model employed, the total number of requests submitted to the system during the simulation period is 94, 98, and 85 for the proposed method, and the approaches proposed by [16] and [39], respectively. It should also be noted that 93, 86, and 85 requests from the submitted ones have been fulfilled during the simulation period, respectively.
The method proposed by [16] has primarily focused on enhancing the users’ profitability, which has led to noteworthy advancements in this aspect, as depicted in Figure 4. Their method usually offers the lowest price per time unit for the virtual machines; however, considering the conflicts between virtual machines and heterogeneity in resources by the proposed method results in better mapping of the jobs and thus usually a lower execution time. This is why the final cost for users is reduced in the proposed method and the users experience almost the same profit in the proposed method and the one proposed by [16].
5.2. Evaluation of the Proposed Method in Terms of Provider’s Profit
Considering conflicts between virtual machines, heterogeneity in resources, and energy consumption costs helps the broker reduce the operational costs of the cloud provider and increase the success rate in performing users’ requests. As mentioned in the earlier section, the broker considers these parameters while creating the game tree and determining the players’ utility for every potential action. By carefully considering different factors while allocating users’ requests to virtual machines and setting a price for those virtual machines, the cloud provider can not only increase its revenue but also its profit. The total revenue of the provider is calculated using the following formula:
where indicates the total number of requests submitted to the system and fulfilled during the simulation time. The cloud provider’s utility () is calculated based on Equation (1) and represents the financial penalty paid by the cloud for the request if it fails to perform successfully. It is assumed that in the case of violating SLA, the provider must refund the total funds received to the user. Since the operating costs of the system can be changed with different policies for mapping and executing requests, the provider’s profit is also calculated by reducing the expenses from revenue (Equation (12)).
The parameter “” denotes the expenses that correspond to the energy consumption required for executing the request. These expenses are calculated using Equation (7). The performance of the proposed approach, in comparison to other methods, is displayed in Figure 5 and Figure 6. These figures showcase the provider’s total revenue and profit from different perspectives.
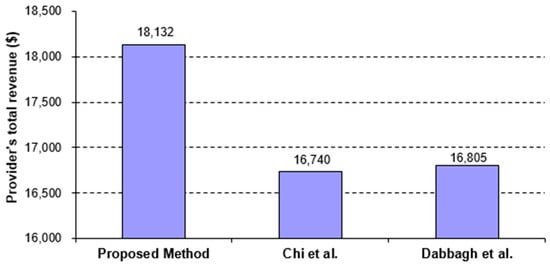
Figure 5.
Comparison of the proposed method with [16,39] from the viewpoint of the provider’s total revenue.
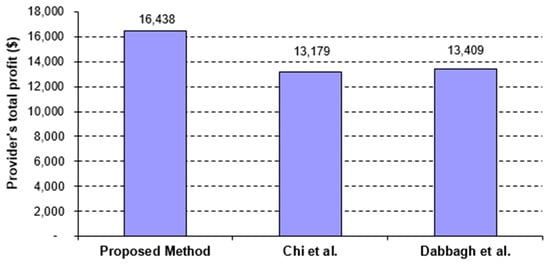
Figure 6.
Comparison of the proposed method with [16,39] from the viewpoint of the provider’s total profit.
As shown in Figure 6, the proposed method is more successful in performing users’ requests with lower energy consumption. This conclusion is based on the fact that the results shown in Figure 6 are obtained according to Equation (12) by deducting the costs related to energy consumption from the cloud revenue (i.e., the results shown in Figure 5). The mapping obtained from the Nash equilibrium point results in reduced energy consumption and sometimes a reduced response time to user requests. This leads to more profit for the cloud provider.
5.3. Comparing the Number of Submitted and Unanswered Requests
The proposed method has offered a higher price to the users than the method presented in [16] and a lower price than the method presented in [39]. As a result, the number of requests submitted to the system during the simulation period must be a number between the input loads for the other two methods (you can see this issue in the results presented for the number of submitted requests in Section 5.1). The reason for this higher price could be the inclusion of operational costs in the utility functions of the players. On the other hand, considering the heterogeneity of hardware resources and conflicts between virtual machines in constructing the game tree leads to better job mappings and thus resource utilization. The strategy of Nash equilibrium assists the cloud provider in making the most advantageous decision when selecting a suitable virtual machine for the user’s request and offering it to the user at a fair price. Assigning efficient virtual machines to user requests has resulted in more requests being submitted to the system and answered within the simulation interval. Figure 7 shows the total number of submitted and responded-to requests during the simulation interval. As can be seen, the proposed method has the highest number of answered requests than the other competitive methods. Offering a higher price by the method presented in [39] ended up reducing the number of submitted requests. Therefore, the system was able to answer all the requests. In contrast, the price reduction in the method presented in [19] has led to an increase in the number of requests, and due to the lack of proper allocation of requests to virtual machines, we see a higher number and rate of unanswered requests compared to other methods.
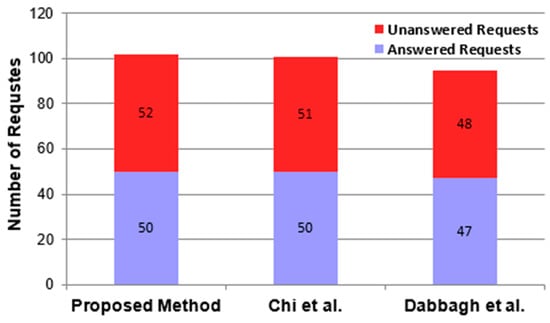
Figure 7.
Comparison of the proposed method with [16,39] from the viewpoint of the number of users’ requests that can be met.
5.4. Comparison under Different System Loads
A good pricing algorithm should perform well in different system loads. The algorithm must respond appropriately to the decreases and increases in demand. During the simulation period, the consideration of different system loads leads to a variation in the number of requests that should be submitted in each simulation run. Figure 8 and Figure 9 depict the mean profit of users as well as the overall profit of the cloud provider when faced with varying system loads, respectively.
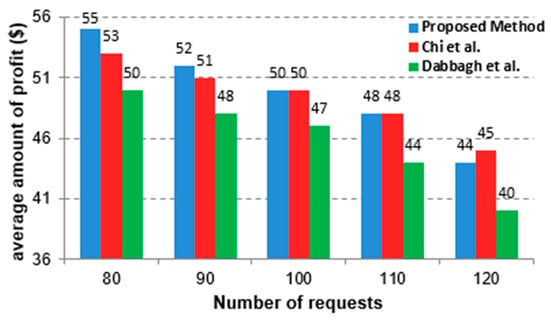
Figure 8.
Comparison of the proposed method with [16,39] under different system loads from the viewpoint of average user’s profit.
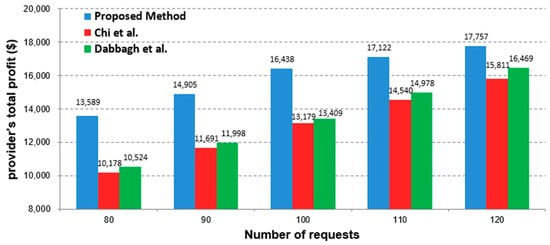
Figure 9.
Comparison of the proposed method with [16,39] under different system loads from the viewpoint of the provider’s total profit.
As can be seen, the performance of the proposed method is better than the two other methods in terms of both average user profit and total provider profit for different loads. The superiority of the proposed method in lighter loads compared to other competitors is also more evident. The reason for this behavior is that in a light workload, the options ahead to allocate the appropriate resource to a request are more, and the maneuverability of the proposed method is higher. Since the proposed method has a more comprehensive view of the factors influencing the finding of a good resource and its appropriate price, compared to the other two methods, increasing the number of options ahead will naturally lead to better performance as expected. The method presented in [16] increases the profit of users due to offering a lower price so that at the highest system load, it has the best performance in this regard among different methods; still, on the other hand, it results in the lowest profit for the cloud provider. On the other hand, the proposed method, considering more parameters that are effective on cloud operating costs and resource efficiency, while providing a fairer price, has also followed a more appropriate mapping of tasks. Therefore, in all cases, both the profit of the user and the profit of the cloud provider have increased.
The experiments that were conducted demonstrate that taking into account a wide range of factors in the pricing model for cloud services can contribute to creating more equitable and lucrative prices for both users and cloud providers. Acceptance of a task with a high chance of failure due to the penalties it can bring to the provider should be considered in the pricing model. It should be acknowledged that the factors taken into account in this study (specifically, the likelihood of achievement, the level of energy utilized, and the potential disruption among tasks) might not be readily and promptly accessible. As mentioned, many researchers have investigated and predicted these factors, but usually, determining the amount of their effects is associated with computational overhead and inaccuracy.
6. Conclusions
Since the advent of clouds, choosing the right price for the services offered by this large-scale computing system has been a challenge. Considering all the various factors such as supply and demand, operating costs such as electricity bills, the possibility of a resource failure and the resulting financial and operational losses, and heterogeneity of resources in terms of the ability to execute different programs in a comprehensive pricing model is an issue that is less common in the past related work.
In this paper, we propose an approach based on game theory that offers a formal framework for examining various factors that are effective in resolving resource allocation and pricing issues. The proposed approach models these problems as a dynamic game between cloud user and provider. Since it is ultimately the user who decides whether or not to rent a resource from the cloud, we consider the user to be the leader of the game and the player who has priority in the decision. Various factors have been considered in the players’ profit functions to help bring the model closer to the real situation. The resource broker, who is responsible for resource allocation and management processes, constructs and solves the game tree. The simulation results demonstrate that the proposed method is superior in reducing the operating costs for the cloud provider, even though it offers a reasonable price for renting resources to users compared to previous related methods. Paying attention to a more comprehensive set of factors affecting the execution costs of running a job by a cloud has helped the proposed method perform better than related works. However, a more precise assessment of the impact of these factors can enhance the effectiveness of the proposed approach. Extensive research has been conducted to ascertain the level of mutual influence between jobs in their execution, anticipate the energy consumption of the jobs, and assess the likelihood of successful execution. Nevertheless, further investigation in this area is still necessary.
Author Contributions
Conceptualization, H.S. and J.H.J.; methodology, H.S. and J.H.J.; software, H.S.; validation, H.S., J.H.J. and H.G.A.; formal analysis, H.S.; investigation, J.H.J.; resources, H.G.A.; data curation, H.S.; writing—original draft preparation, H.S., J.H.J. and H.G.A.; writing—review and editing, H.S. and J.H.J.; visualization, H.S.; supervision, H.S.; project administration, J.H.J.; funding acquisition, J.H.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are simulated and generated during the experiment.
Acknowledgments
Javad Hassannataj Joloudari is grateful for the financial support of MDPI Publisher, which was provided for refereeing in MDPI journals by receiving 20 vouchers.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
Abbreviations explains the abbreviations utilized in this study. Abbreviations List of abbreviations used in this study.
| Abbreviations | Meaning |
| CC | Cloud Computing |
| SLA | Service Level Agreement |
| PaaS | Platform as a service |
| SaaS | Software as a service |
| Amazon Ec2 | Amazon Elastic Compute Cloud |
| IaaS | Infrastructure as a Service |
| PUE | Power Usage Effectiveness |
| CDARA | Combinatorial Double Auction Resource Allocation |
| QoS | Quality of Service |
| CSPs | Cloud service providers |
| CIPs | Cloudlet Infrastructure Providers |
| CLF | Cloudlet Federation |
| CP | Cloud Provider |
| Virtual machine |
References
- Teng, F.; Magoulès, F. A new game theoretical resource allocation algorithm for cloud computing. In Advances in Grid and Pervasive Computing: Proceedings of the 5th International Conference, GPC 2010, Hualien, Taiwan, 10–13 May 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 321–330. [Google Scholar]
- Mazrekaj, A.; Shabani, I.; Sejdiu, B. Pricing schemes in cloud computing: An overview. Int. J. Adv. Comput. Sci. Appl. 2016, 7, 80–86. [Google Scholar] [CrossRef]
- Tang, L.; Chen, H. Joint pricing and capacity planning in the IaaS cloud market. IEEE Trans. Cloud Comput. 2014, 5, 57–70. [Google Scholar] [CrossRef]
- Luong, N.C.; Wang, P.; Niyato, D.; Wen, Y.; Han, Z. Resource management in cloud networking using economic analysis and pricing models: A survey. IEEE Commun. Surv. Tutor. 2017, 19, 954–1001. [Google Scholar] [CrossRef]
- Cong, P.; Li, L.; Zhou, J.; Cao, K.; Wei, T.; Chen, M.; Hu, S. Developing user perceived value-based pricing models for cloud markets. IEEE Trans. Parallel Distrib. Syst. 2018, 29, 2742–2756. [Google Scholar] [CrossRef]
- Zhao, Y.; Huang, Z.; Liu, W.; Peng, J.; Zhang, Q.A. combinatorial double auction-based resource allocation mechanism with multiple rounds for geo-distributed data centers. In Proceedings of the 2016 IEEE International Conference on Communications (ICC), Kuala Lumpur, Malaysia, 22–27 May 2016; pp. 1–6. [Google Scholar]
- Webb, J.N. Game Theory: Decisions, Interaction and Evolution; Springer: London, UK, 2007. [Google Scholar]
- Kumar, D.; Baranwal, G.; Raza, Z.; Vidyarthi, D.P. A survey on spot pricing in cloud computing. J. Netw. Syst. Manag. 2018, 26, 809–856. [Google Scholar] [CrossRef]
- Samimi, P.; Teimouri, Y.; Mukhtar, M. A combinatorial double auction resource allocation model in cloud computing. Inf. Sci. 2016, 357, 201–216. [Google Scholar] [CrossRef]
- Baranwal, G.; Vidyarthi, D.P. A fair multi-attribute combinatorial double auction model for resource allocation in cloud computing. J. Syst. Softw. 2015, 108, 60–76. [Google Scholar] [CrossRef]
- Tafsiri, S.A.; Yousefi, S. Combinatorial double auction-based resource allocation mechanism in cloud computing market. J. Syst. Softw. 2018, 137, 322–334. [Google Scholar] [CrossRef]
- Lu, Y.; Zheng, X.; Li, L.; Xu, L.D. Pricing the cloud: A QoS-based auction approach. Enterp. Inf. Syst. 2020, 14, 334–351. [Google Scholar] [CrossRef]
- Toosi, A.N.; Vanmechelen, K.; Khodadadi, F.; Buyya, R. An auction mechanism for cloud spot markets. ACM Trans. Auton. Adapt. Syst. (TAAS) 2016, 11, 1–33. [Google Scholar] [CrossRef]
- Lučanin, D.; Pietri, I.; Holmbacka, S.; Brandic, I.; Lilius, J.; Sakellariou, R. Performance-based pricing in multi-core geo-distributed cloud computing. IEEE Trans. Cloud Comput. 2016, 8, 1079–1092. [Google Scholar] [CrossRef]
- Aldossary, M.; Djemame, K. Energy consumption-based pricing model for cloud computing. In Proceedings of the 32nd UK Performance Engineering Workshop, Bradford, UK, 8–9 September 2016; pp. 16–27. [Google Scholar]
- Chi, Y.; Li, X.; Wang, X.; Leung, V.C.; Shami, A. A fairness-aware pricing methodology for revenue enhancement in service cloud infrastructure. IEEE Syst. J. 2015, 11, 1006–1017. [Google Scholar] [CrossRef]
- Sharma, B.; Thulasiram, R.K.; Thulasiraman, P.; Buyya, R. Clabacus: A risk-adjusted cloud resources pricing model using financial option theory. IEEE Trans. Cloud Comput. 2014, 3, 332–344. [Google Scholar] [CrossRef]
- Wu, C.; Toosi, A.N.; Buyya, R.; Ramamohanarao, K. Hedonic pricing of cloud computing services. IEEE Trans. Cloud Comput. 2018, 9, 182–196. [Google Scholar] [CrossRef]
- Qiu, C.; Shen, H.; Chen, L. Towards green cloud computing: Demand allocation and pricing policies for cloud service brokerage. IEEE Trans. Big Data 2018, 5, 238–251. [Google Scholar] [CrossRef]
- Shang, S.; Jiang, J.; Wu, Y.; Huang, Z.; Yang, G.; Zheng, W. DABGPM: A double auction Bayesian game-based pricing model in cloud market. In Proceedings of the Network and Parallel Computing: IFIP International Conference, NPC 2010, Zhengzhou, China, 13–15 September 2010; pp. 155–164. [Google Scholar]
- Do, C.T.; Tran, N.H.; Huh, E.N.; Hong, C.S.; Niyato, D.; Han, Z. Dynamics of service selection and provider pricing game in heterogeneous cloud market. J. Netw. Comput. Appl. 2016, 69, 152–165. [Google Scholar] [CrossRef]
- Shi, B.; Huang, Y.; Wang, J.; Xiong, S. A game-theoretic analysis of pricing strategies for competing cloud platforms. In Proceedings of the 2016 IEEE 22nd International Conference on Parallel and Distributed Systems (ICPADS), Wuhan, China, 13–16 December 2016; pp. 653–660. [Google Scholar]
- Niu, D.; Feng, C.; Li, B. A theory of cloud bandwidth pricing for video-on-demand providers. In Proceedings of the 2012 Proceedings IEEE INFOCOM, Orlando, FL, USA, 25–30 March 2012; pp. 711–719. [Google Scholar]
- Xiao, P.; Tang, Z. Game theory–based resource pricing model in cloud platforms. Int. J. Commun. Netw. Distrib. Syst. 2015, 14, 256–271. [Google Scholar] [CrossRef]
- Lee, I. Pricing and profit management models for SaaS providers and IaaS providers. J. Theor. Appl. Electron. Commer. Res. 2021, 16, 859–873. [Google Scholar] [CrossRef]
- Li, H.; Dong, M.; Ota, K.; Guo, M. Pricing and repurchasing for big data processing in multi-clouds. IEEE Trans. Emerg. Top. Comput. 2016, 4, 266–277. [Google Scholar] [CrossRef]
- Zhu, Z.; Peng, J.; Liu, K.; Zhang, X. A game-based resource pricing and allocation mechanism for profit maximization in cloud computing. Soft Comput. 2020, 24, 4191–4203. [Google Scholar] [CrossRef]
- Ye, H.; Feng, B.; Li, X. A game-based approach for cloudlet resource pricing for cloudlet federation. J. Supercomput. 2023, 79, 1–21. [Google Scholar] [CrossRef]
- Cao, X.; Bo, H.; Liu, Y.; Liu, X. Effects of different resource-sharing strategies in cloud manufacturing: A Stackelberg game-based approach. Int. J. Prod. Res. 2023, 61, 520–540. [Google Scholar] [CrossRef]
- Godhrawala, H.; Sridaran, R. A dynamic Stackelberg game based multi-objective approach for effective resource allocation in cloud computing. Int. J. Inf. Technol. 2023, 15, 803–818. [Google Scholar] [CrossRef]
- Koh, Y.; Knauerhase, R.; Brett, P.; Bowman, M.; Wen, Z.; Pu, C. An analysis of performance interference effects in virtual environments. In Proceedings of the 2007 IEEE International Symposium on Performance Analysis of Systems & Software, San Jose, CA, USA, 25–27 April 2007; pp. 200–209. [Google Scholar]
- Su, K.; Xu, L.; Chen, C.; Chen, W.; Wang, Z. Affinity and conflict-aware placement of virtual machines in heterogeneous data centers. In Proceedings of the 2015 IEEE Twelfth International Symposium on Autonomous Decentralized Systems, Taichung, Taiwan, 25–27 March 2015; pp. 289–294. [Google Scholar]
- Shim, Y.C. Inter-VM performance interference aware static VM consolidation algorithms for cloud-based data centers. Recent Adv. Electr. Eng. 2015, 1, 18–25. [Google Scholar]
- Sutaria, V.; Prasad, V.K.; Bhavsar, M. Fault Prediction and Mitigation in Cloud Computing. Int. J. Adv. Res. Comput. Sci. 2017, 8, 1042–1050. [Google Scholar]
- Saadatfar, H.; Fadishei, H.; Deldari, H. Predicting job failures in AuverGrid based on workload log analysis. New Gener. Comput. 2012, 30, 73–94. [Google Scholar] [CrossRef]
- Kenga, M.D.; Omwenga O, V.O.; Ogao, P.J. Energy consumption in cloud computing environments. In Pan African Conference on Science, Computing and Telecommunications (PACT); Strathmore University: Nairobi, Kenya, 2017; pp. 1–15. [Google Scholar]
- Aldossary, M.; Djemame, K.; Alzamil, I.; Kostopoulos, A.; Dimakis, A.; Agiatzidou, E. Energy-aware cost prediction and pricing of virtual machines in cloud computing environments. Future Gener. Comput. Syst. 2019, 93, 442–459. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, C.; Xin, X. Stackelberg Game-Based Resource Allocation with Blockchain for Cold-Chain Logistics System. Computers. Mater. Contin. 2023, 75, 2429–2442. [Google Scholar]
- Dabbagh, M.; Hamdaoui, B.; Guizani, M.; Rayes, A. Exploiting task elasticity and price heterogeneity for maximizing cloud computing profits. IEEE Trans. Emerg. Top. Comput. 2015, 6, 85–96. [Google Scholar] [CrossRef]
- Calheiros, R.N.; Ranjan, R.; Beloglazov, A.; De Rose, C.A.; Buyya, R. CloudSim: A toolkit for modeling and simulation of cloud computing environments and evaluation of resource provisioning algorithms. Softw. Pract. Exp. 2011, 4, 23–50. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).