FLAME-VQA: A Fuzzy Logic-Based Model for High Frame Rate Video Quality Assessment
Abstract
:1. Introduction
1.1. Background and Motivation
1.2. Contributions
- Our study involved an in-depth analysis of the dataset, revealing intricate relationships between four key video properties (video frame rate, compression rate, spatial information, and temporal information) and user subjective ratings;
- We developed a fuzzy logic-based video quality assessment model (FLAME-VQA) capable of assessing the quality for a wide range of streaming scenarios based on the four video properties;
- The model incorporates an inference system that effectively tackles uncertainty and vagueness in the data. By employing fuzzy clustering and membership functions, our model enables more human-like decision-making;
- The proposed model successfully bridges the gap between objective and subjective evaluation and paves the way for more refined multimedia delivery systems that cater to users’ preferences and expectations.
1.3. Paper Structure
2. Related Works
- Inference systems of developed models primarily rely on machine learning, neural networks, fuzzy logic, or a combination of these techniques;
- Models based on neural networks are content-domain-dependent and require application-specific training [41];
- Video-related parameters, such as video frame rate, compression, and spatio-temporal properties, have been identified as crucial factors influencing the human perception of video quality;
- Online video databases serve as excellent starting points for developing VQA models, offering rich, diverse, and subjectively rated video content, and adhering to international standards for conducting research in this field;
- Given the abundance of diverse video content and streaming scenarios in various network contexts, it is challenging to create a universal VQA model.
3. Dataset Properties
3.1. The Video Sequences
3.2. The Subjective Experiment
4. Fuzzy Logic in User Experience Assessment
4.1. Applicability of Fuzzy Logic
4.2. The Model Development Process
- Fuzzification. This step entails transforming crisp input and output values into fuzzy sets that describe the variable states. The grouping of the values into the fuzzy sets allows for handling uncertainty and vagueness in the data;
- Defining a rule-based system to operate with the fuzzy states. These rules are typically in the form of “IF [condition] THEN [conclusion]” and use linguistic variables to express relationships between inputs and outputs. For instance, an example rule could be “IF [video fps IS low] AND [video compression IS high] THEN [quality IS bad]”;
- Defuzzification. The final step involves converting the fuzzy output (e.g., quality IS bad) back into a crisp result. This process produces a clear and quantitative assessment based on the inference system of the model.
4.2.1. Fuzzification of the Scalars
4.2.2. A Set of Fuzzy Rules and Defuzzification to the Scalar Result
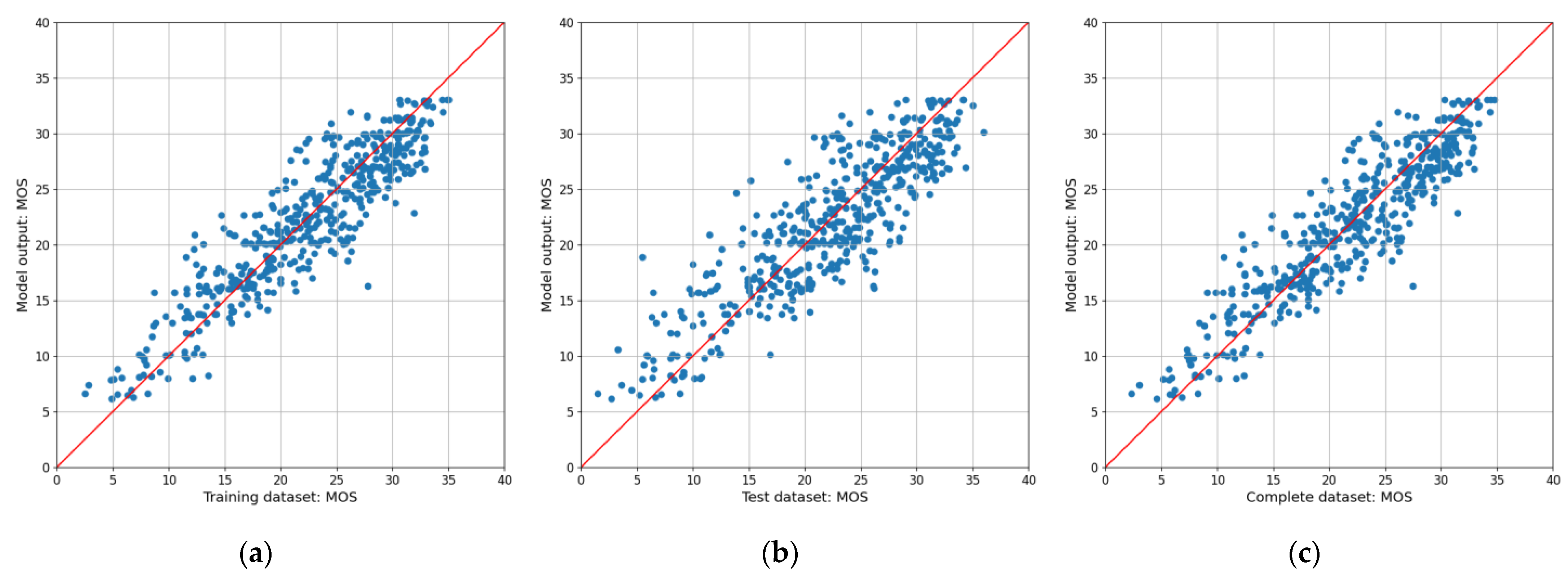
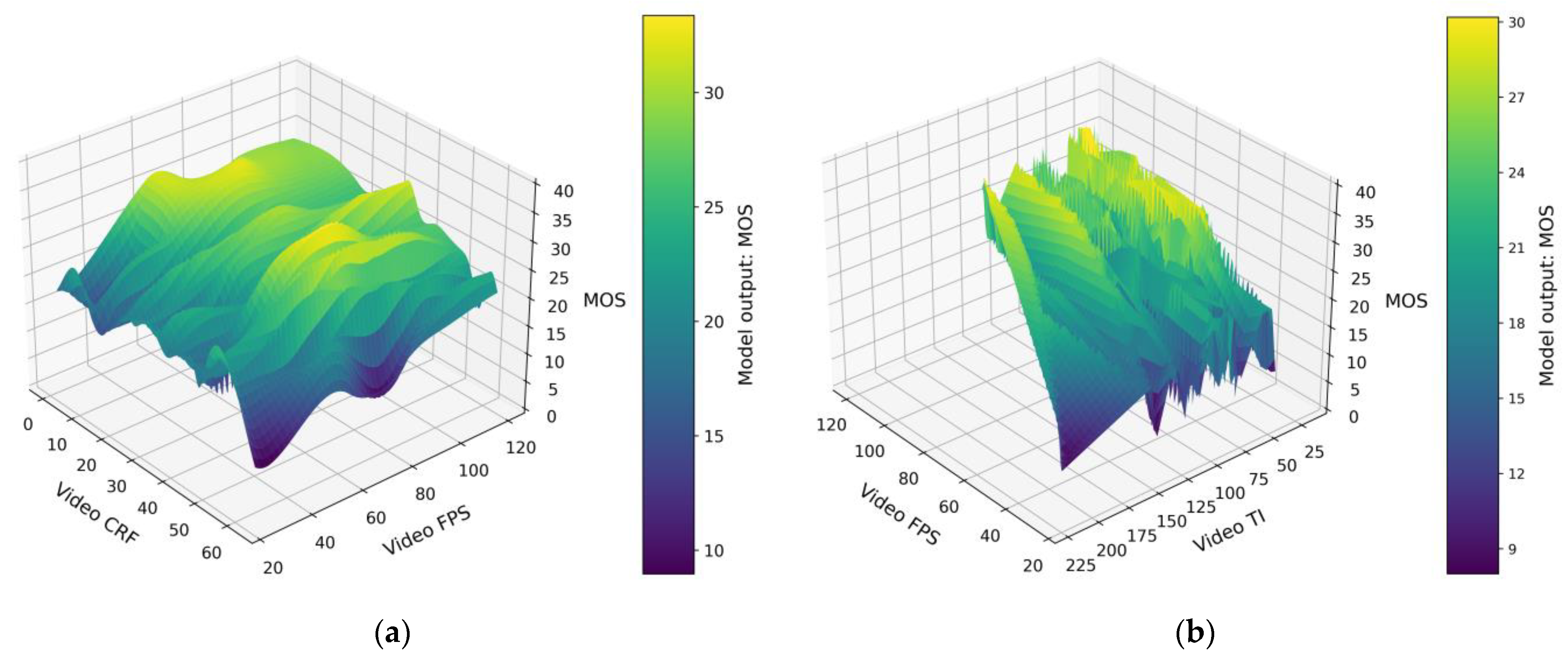
5. Results and Discussion
5.1. Evaluation of the Model Output
5.2. Comparative Performance Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Rule Number | IF Video fps = l/m/h AND Video crf = l/m/h AND Video si = l/m/h AND Video ti = l/m/h | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| FPS | CRF | SI | TI | B | P | F | G | E | ||
| 1 | High | Low | Low | Medium | 1 | 0.4 | ||||
| 2 | High | Low | Low | High | 1 | 0.3 | ||||
| 3 | High | Low | Low | Low | 0.6 | 1 | ||||
| 4 | High | Low | Medium | High | 0.5 | 1 | ||||
| 5 | Medium | Low | Low | High | 1 | 0.3 | ||||
| 6 | High | Low | Medium | Medium | OR | 1 | ||||
| High | Low | High | Medium | |||||||
| High | Medium | Low | Medium | |||||||
| 7 | High | Medium | Low | Low | OR | 1 | 0.4 | |||
| High | High | Low | Medium | |||||||
| 8 | High | Medium | Low | High | 1 | 0.8 | ||||
| 9 | High | Medium | Medium | Low | 1 | 0.5 | ||||
| 10 | High | Medium | Medium | Medium | 1 | 1 | ||||
| 11 | High | Medium | Medium | High | 1 | 0.6 | ||||
| 12 | Low | Low | Low | High | 0.7 | 1 | ||||
| 13 | Medium | Low | Medium | High | 0.6 | 1 | ||||
| 14 | Low | Low | High | High | OR | 0.5 | 1 | |||
| Medium | Low | High | High | |||||||
| 15 | High | High | Low | Low | 0.5 | 0,1 | ||||
| 16 | Low | Medium | Medium | Low | 0.35 | 1 | ||||
| 17 | Low | Low | Medium | Medium | OR | 0.3 | 1 | |||
| Low | Low | Medium | High | |||||||
| Medium | Low | Medium | Medium | |||||||
| 18 | High | Medium | High | Low | OR | 0.2 | 1 | |||
| High | High | Medium | High | |||||||
| 19 | Low | Low | Low | Low | OR | 1 | ||||
| Low | Low | Low | High | |||||||
| Medium | Low | Low | Low | |||||||
| Medium | Medium | Medium | Low | |||||||
| Medium | High | Medium | Low | |||||||
| High | High | Medium | Low | |||||||
| 20 | Low | Low | Low | Medium | OR | 1 | 0.3 | |||
| Medium | Medium | Low | Medium | |||||||
| 21 | Low | Low | High | Medium | OR | 1 | 0.2 | |||
| High | High | High | Low | |||||||
| 22 | Low | Medium | High | High | 1 | 0.7 | ||||
| 23 | Low | High | Medium | Low | OR | 1 | 0.5 | |||
| Medium | Medium | High | High | |||||||
| 24 | Medium | Low | Low | Medium | OR | 1 | 0.1 | |||
| High | High | Medium | Medium | |||||||
| 25 | Medium | Low | High | Medium | 1 | 0.05 | ||||
| 26 | Medium | Medium | Low | High | 1 | 0.8 | ||||
| 27 | Medium | High | Low | Medium | 1 | 1 | ||||
| 28 | Medium | Medium | Medium | Medium | 0.7 | 1 | ||||
| 29 | Low | Medium | Low | High | 0.5 | 1 | ||||
| 30 | Low | Medium | Medium | Medium | 0.4 | 1 | ||||
| 31 | Medium | High | Low | Low | OR | 0.3 | 1 | |||
| Medium | Medium | High | Medium | |||||||
| Medium | High | Medium | Medium | |||||||
| Medium | High | High | High | |||||||
| 32 | Low | Medium | Low | Low | 1 | 0.3 | ||||
| 33 | Low | Medium | Low | Medium | OR | 1 | ||||
| Low | High | Low | Medium | |||||||
| Low | High | Medium | Medium | |||||||
| Low | High | High | High | |||||||
| Medium | Medium | Low | Low | |||||||
| Medium | High | High | Medium | |||||||
| 34 | Low | Medium | High | Medium | OR | 1 | 0.5 | |||
| Medium | Medium | High | Low | |||||||
| Medium | High | High | Low | |||||||
| 35 | Low | High | High | Medium | 1 | 0.2 | ||||
| 36 | Low | Medium | High | Low | OR | 0.6 | 1 | |||
| Low | High | Low | Low | |||||||
| Low | High | High | Low | |||||||
References
- Zeng, Q.; Chen, G.; Li, Z.; Jiang, H.; Zhuang, Y.; Hai, J.; Pan, Q. An Innovative Resource-Based Dynamic Scheduling Video Computing and Network Convergence System. In Proceedings of the 2023 International Wireless Communications and Mobile Computing (IWCMC), Marrakesh, Morocco, 19–23 June 2023; pp. 174–181. [Google Scholar]
- Ericsson. Ericsson Mobility Report. Available online: https://www.ericsson.com/en/reports-and-papers/mobility-report (accessed on 15 July 2023).
- Hubspot. The Video Marketing Playbook Trends & Tips to Create a Video Strategy in 2023. Available online: https://blog.hubspot.com/marketing/video-marketing-report (accessed on 27 July 2023).
- Sultan, M.T.; Sayed, H. El QoE-Aware Analysis and Management of Multimedia Services in 5G and Beyond Heterogeneous Networks. IEEE Access 2023, 11, 77679–77688. [Google Scholar] [CrossRef]
- Ramachandra Rao, R.R.; Borer, S.; Lindero, D.; Göring, S.; Raake, A. PNATS-UHD-1-Long: An Open Video Quality Dataset for Long Sequences for HTTP-Based Adaptive Streaming QoE Assessment. In Proceedings of the 2023 15th International Conference on Quality of Multimedia Experience (QoMEX), Ghent, Belgium, 20–22 June 2023; pp. 252–257. [Google Scholar]
- Ellawindy, I.; Shah Heydari, S. Crowdsourcing Framework for QoE-Aware SD-WAN. Futur. Internet 2021, 13, 209. [Google Scholar] [CrossRef]
- Matulin, M.; Mrvelj, Š. Modelling User Quality of Experience from Objective and Subjective Data Sets Using Fuzzy Logic. Multimed. Syst. 2018, 24, 645–667. [Google Scholar] [CrossRef]
- Mrvelj, Š.; Matulin, M. Impact of Packet Loss on the Perceived Quality of UDP-Based Multimedia Streaming: A Study of User Quality of Experience in Real-Life Environments. Multimed. Syst. 2016, 24, 33–53. [Google Scholar] [CrossRef]
- Madhusudana, P.C.; Yu, X.; Birkbeck, N.; Wang, Y.; Adsumilli, B.; Bovik, A.C. Subjective and Objective Quality Assessment of High Frame Rate Videos. IEEE Access 2021, 9, 108069–108082. [Google Scholar] [CrossRef]
- Lin, L.; Zheng, Y.; Chen, W.; Lan, C.; Zhao, T. Saliency-Aware Spatio-Temporal Artifact Detection for Compressed Video Quality Assessment. IEEE Signal Process. Lett. 2023, 30, 693–697. [Google Scholar] [CrossRef]
- Uhrina, M.; Bienik, J.; Vaculik, M.; Voznak, M. Subjective Video Quality Assessment of VP9 Compression Standard for Full HD Resolution. In Proceedings of the 2016 International Symposium on Performance Evaluation of Computer and Telecommunication Systems (SPECTS), Montreal, QC, Canada, 24–27 July 2016; pp. 1–5. [Google Scholar]
- Chennagiri, P.; Yu, X.; Birkbeck, N.; Wang, Y.; Adsumilli, B.; Bovik, A. LIVE YouTube High Frame Rate (LIVE-YT-HFR) Database. Available online: https://live.ece.utexas.edu/research/LIVE_YT_HFR/LIVE_YT_HFR/index.html (accessed on 3 July 2023).
- Madhusudana, P.C.; Birkbeck, N.; Wang, Y.; Adsumilli, B.; Bovik, A.C. Capturing Video Frame Rate Variations via Entropic Differencing. IEEE Signal Process. Lett. 2020, 27, 1809–1813. [Google Scholar] [CrossRef]
- Alata, M.; Molhim, M.; Ramini, A. Optimizing-of-Fuzzy-C-Means-Clustering-Algorithm-Using-GA. Int. J. Comput. Electr. Autom. Control. Inf. Eng. 2008, 2, 670–675. [Google Scholar] [CrossRef]
- Gupta, P.; Bampis, C.G.; Glover, J.L.; Paulter, N.G.; Bovik, A.C. Multivariate Statistical Approach to Image Quality Tasks. J. Imaging 2018, 4, 117. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image Quality Assessment: From Error Visibility to Structural Similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Wang, Z.; Simoncelli, E.P.; Bovik, A.C. Multiscale Structural Similarity for Image Quality Assessment. In Proceedings of the Thrity-Seventh Asilomar Conference on Signals, Systems & Computers, Pacific Grove, CA, USA, 9–12 November 2003; Volume 2, pp. 1398–1402. [Google Scholar]
- Zhang, L.; Zhang, L.; Mou, X.; Zhang, D. FSIM: A Feature Similarity Index for Image Quality Assessment. IEEE Trans. Image Process. 2011, 20, 2378–2386. [Google Scholar] [CrossRef] [PubMed]
- Soundararajan, R.; Bovik, A.C. Video Quality Assessment by Reduced Reference Spatio-Temporal Entropic Differencing. IEEE Trans. Circuits Syst. Video Technol. 2013, 23, 684–694. [Google Scholar] [CrossRef]
- Bampis, C.G.; Gupta, P.; Soundararajan, R.; Bovik, A.C. SpEED-QA: Spatial Efficient Entropic Differencing for Image and Video Quality. IEEE Signal Process. Lett. 2017, 24, 1333–1337. [Google Scholar] [CrossRef]
- Alizadeh, M.; Sharifkhani, M. Subjective Video Quality Prediction Based on Objective Video Quality Metrics. In Proceedings of the 2018 4th Iranian Conference on Signal Processing and Intelligent Systems (ICSPIS), Tehran, Iran, 25–27 December 2018; pp. 7–9. [Google Scholar]
- Schiffner, F.; Moller, S. Direct Scaling & Quality Prediction for Perceptual Video Quality Dimensions. In Proceedings of the 2018 Tenth International Conference on Quality of Multimedia Experience (QoMEX), Cagliari, Italy, 29 May–1 June 2018; pp. 1–3. [Google Scholar]
- Pinson, M.H.; Choi, L.K.; Bovik, A.C. Temporal Video Quality Model Accounting for Variable Frame Delay Distortions. IEEE Trans. Broadcast. 2014, 60, 637–649. [Google Scholar] [CrossRef]
- García-Pineda, M.; Segura-García, J.; Felici-Castell, S. A Holistic Modeling for QoE Estimation in Live Video Streaming Applications over LTE Advanced Technologies with Full and Non Reference Approaches. Comput. Commun. 2018, 117, 13–23. [Google Scholar] [CrossRef]
- Lebreton, P.; Kawashima, K.; Yamagishi, K.; Okamoto, J. Study on Viewing Time with Regards to Quality Factors in Adaptive Bitrate Video Streaming. In Proceedings of the 2018 IEEE 20th International Workshop on Multimedia Signal Processing (MMSP), Vancouver, BC, Canada, 29–31 August 2018; pp. 1–6. [Google Scholar]
- Ghadiyaram, D.; Pan, J.; Bovik, A.C. A Subjective and Objective Study of Stalling Events in Mobile Streaming Videos. IEEE Trans. Circuits Syst. Video Technol. 2019, 29, 183–197. [Google Scholar] [CrossRef]
- Wang, C. IPTV Video Perception Quality Based on Packet Loss Distribution. In Proceedings of the 2023 3rd International Conference on Consumer Electronics and Computer Engineering (ICCECE), Guangzhou, China, 6–8 January 2023; pp. 502–506. [Google Scholar]
- Bampis, C.G.; Li, Z.; Katsavounidis, I.; Bovik, A.C. Recurrent and Dynamic Models for Predicting Streaming Video Quality of Experience. IEEE Trans. Image Process. 2018, 27, 3316–3331. [Google Scholar] [CrossRef]
- Bampis, C.G.; Krasula, L.; Li, Z.; Akhtar, O. Measuring and Predicting Perceptions of Video Quality Across Screen Sizes with Crowdsourcing. In Proceedings of the 2023 15th International Conference on Quality of Multimedia Experience (QoMEX), Ghent, Belgium, 20–22 June 2023; pp. 13–18. [Google Scholar]
- Xian, W.; Chen, B.; Fang, B.; Guo, K.; Liu, J.; Shi, Y.; Wei, X. Effects of Different Full-Reference Quality Assessment Metrics in End-to-End Deep Video Coding. Electronics 2023, 12, 3036. [Google Scholar] [CrossRef]
- Zhou, W.; Min, X.; Li, H.; Jiang, Q. A Brief Survey on Adaptive Video Streaming Quality Assessment. J. Vis. Commun. Image Represent. 2022, 86, 103526. [Google Scholar] [CrossRef]
- Kim, W.; Kim, J.; Ahn, S.; Kim, J.; Lee, S. Deep Video Quality Assessor: From Spatio-Temporal Visual Sensitivity to A Convolutional Neural Aggregation Network. In Proceedings of the European Conference on Computer Vision (ECCV), Glasgow, UK, 23–28 August 2018. [Google Scholar]
- Ghosh, M.; Singhal, C. MO-QoE: Video QoE Using Multi-Feature Fusion Based Optimized Learning Models. Signal Process. Image Commun. 2022, 107, 116766. [Google Scholar] [CrossRef]
- Banjanin, M.K.; Stojčić, M.; Danilović, D.; Ćurguz, Z.; Vasiljević, M.; Puzić, G. Classification and Prediction of Sustainable Quality of Experience of Telecommunication Service Users Using Machine Learning Models. Sustainability 2022, 14, 17053. [Google Scholar] [CrossRef]
- Nguyen, D.; Pham Ngoc, N.; Thang, T.C. QoE Models for Adaptive Streaming: A Comprehensive Evaluation. Futur. Internet 2022, 14, 151. [Google Scholar] [CrossRef]
- Gao, Y.; Min, X.; Zhu, Y.; Zhang, X.-P.; Zhai, G. Blind Image Quality Assessment: A Fuzzy Neural Network for Opinion Score Distribution Prediction. IEEE Trans. Circuits Syst. Video Technol. 2023, 1, 1–16. [Google Scholar] [CrossRef]
- Yu, X.; Ying, Z.; Birkbeck, N.; Wang, Y.; Adsumilli, B.; Bovik, A.C. Subjective and Objective Analysis of Streamed Gaming Videos. IEEE Trans. Games 2023, 1–14. [Google Scholar] [CrossRef]
- Cao, Y.; Min, X.; Sun, W.; Zhai, G. Subjective and Objective Audio-Visual Quality Assessment for User Generated Content. IEEE Trans. Image Process. 2023, 32, 3847–3861. [Google Scholar] [CrossRef]
- Da, P.; Song, G.; Shi, P.; Zhang, H. Perceptual Quality Assessment of Nighttime Video. Displays 2021, 70, 102092. [Google Scholar] [CrossRef]
- Ramachandra Rao, R.R.; Göring, S.; Raake, A. AVQBits—Adaptive Video Quality Model Based on Bitstream Information for Various Video Applications. IEEE Access 2022, 10, 80321–80351. [Google Scholar] [CrossRef]
- Lodha, I. Subjective and No-Reference Quality Metric of Domain Independent Images and Videos. Comput. Graph. 2021, 95, 123–129. [Google Scholar] [CrossRef]
- Mackin, A.; Zhang, F.; Bull, D.R. A Study of Subjective Video Quality at Various Frame Rates. In Proceedings of the 2015 IEEE International Conference on Image Processing (ICIP), Quebec City, QC, Canada, 27–30 September 2015; pp. 3407–3411. [Google Scholar]
- MSU Graphics & Media Lab. MSU Quality Measurement Tool. Available online: https://www.compression.ru/video/quality_measure/ (accessed on 3 August 2023).
- Mukherjee, D.; Han, J.; Bankoski, J.; Bultje, R.; Grange, A.; Koleszar, J.; Wilkins, P.; Xu, Y. A Technical Overview of VP9—The Latest Open-Source Video Codec. In Proceedings of the SMPTE 2013 Annual Technical Conference & Exhibition, Hollywood, CA, USA, 22–24 October 2013; pp. 1–17. [Google Scholar]
- ITU-R. Methodology for the Subjective Assessment of the Quality of Television Pictures, Document ITU-R Recommendation BT.500-11. 2000. Available online: https://www.itu.int/rec/R-REC-BT.500-11-200206-S/en (accessed on 15 July 2023).
- Zadeh, L.A. Fuzzy Sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Bezdek, J.C.; Ehrlich, R.; Full, W. FCM: The Fuzzy c-Means Clustering Algorithm. Comput. Geosci. 1984, 10, 191–203. [Google Scholar] [CrossRef]
- Ishibuchi, H.; Yamamoto, T. Rule Weight Specification in Fuzzy Rule-Based Classification Systems. IEEE Trans. Fuzzy Syst. 2005, 13, 428–435. [Google Scholar] [CrossRef]
- Ross, T.J. Fuzzy Logic with Engineering Applications, 4th ed.; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar]
- Zhang, F.; Mackin, A.; Bull, D.R. A Frame Rate Dependent Video Quality Metric Based on Temporal Wavelet Decomposition and Spatiotemporal Pooling. In Proceedings of the 2017 IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 300–304. [Google Scholar]
- Netflix VMAF—Video Multi-Method Assessment Fusion. Available online: https://github.com/Netflix/vmaf (accessed on 12 August 2023).

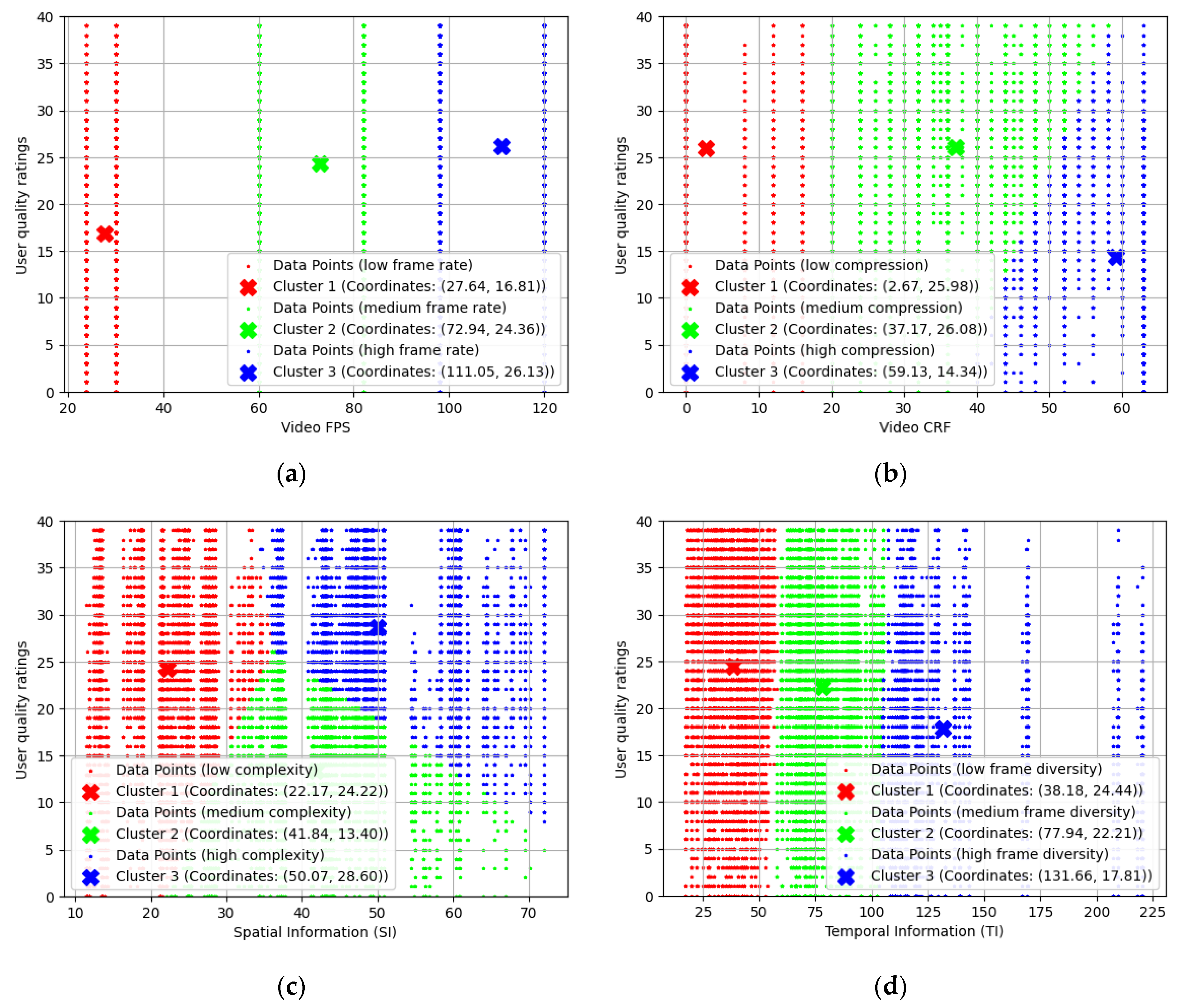


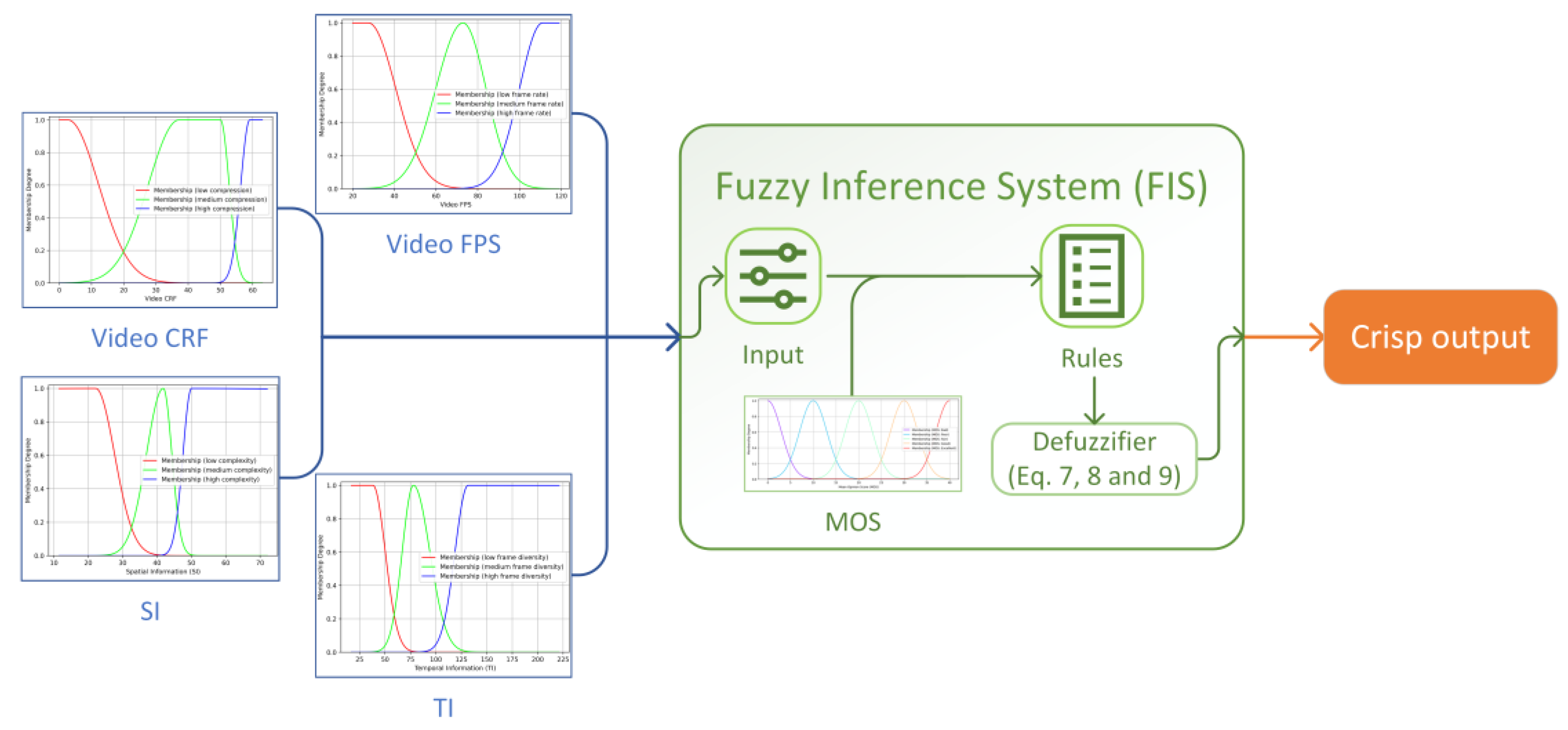
| Model Parameter | Fuzzy Cluster | Function Type and Properties |
|---|---|---|
| Video FPS | High frame rate | Gauss2: (11, 111, 1 121) |
| Medium frame rate | Gauss2: (13, 72.94, 11, 72.94) | |
| Low frame rate | Gauss2: (−1, −1, 13, 27.64) | |
| Video CRF | High compression | Gauss2: (2.8, 59.13, 1, 64) |
| Medium compression | Gauss2: (9.5, 37.17, 2.7, 50) | |
| Low compression | Gauss2: (−1, −1, 9.5, 2.67) | |
| Video SI | High complexity | Gauss2: (2.5, 50.07, 1, 81) |
| Medium complexity | Gauss2: (4.9, 41.84, 2.5, 41.84) | |
| Low complexity | Gauss2: (−1, −1, 5.5, 22.17) | |
| Video TI | High frame diversity | Gauss2: (12.8, 131.7, 1, 226) |
| Medium frame diversity | Gauss2: (11, 77.94, 16, 77.94) | |
| Low frame diversity | Gauss2: (−1, −1, 12, 38.18) | |
| MOS | Bad | Gauss: (3, 0) |
| Poor | Gauss: (3, 10) | |
| Fair | Gauss: (3, 20) | |
| Good | Gauss: (3, 30) | |
| Excellent | Gauss: (3, 40) |
| Metric | Training Data | Test Data | Complete Dataset |
|---|---|---|---|
| R2 | 0.827 | 0.7447 | 0.8253 |
| MSE | 8.7819 | 13.6213 | 8.7605 |
| RMSE | 2.9634 | 3.6907 | 2.9598 |
| SROCC | 0.8977 | 0.8455 | 0.8961 |
| PCC | 0.9096 | 0.8632 | 0.9086 |
| Model Name | SROCC | PCC |
|---|---|---|
| PSNR | 0.695 | 0.6685 |
| SSIM [16] | 0.4494 | 0.4526 |
| MS-SSIM [17] | 0.4898 | 0.4673 |
| FSIM [18] | 0.5251 | 0.5008 |
| ST-RRED [19] | 0.5531 | 0.5107 |
| SpEED [20] | 0.4861 | 0.4449 |
| FRQM [50] | 0.4216 | 0.452 |
| VMAF [51] | 0.7303 | 0.7071 |
| DeepVQA [32] | 0.3463 | 0.3329 |
| GSTI [13] | 0.7909 | 0.791 |
| AVQBits|M3 [40] | 0.7118 | 0.7805 |
| AVQBits|M1 [40] | 0.4809 | 0.5528 |
| AVQBits|M0 [40] | 0.4947 | 0.5538 |
| AVQBits|H0|s [40] | 0.7324 | 0.7887 |
| AVQBits|H0|f [40] | 0.674 | 0.7242 |
| FLAME-VQA | 0.8961 | 0.9086 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mrvelj, Š.; Matulin, M. FLAME-VQA: A Fuzzy Logic-Based Model for High Frame Rate Video Quality Assessment. Future Internet 2023, 15, 295. https://doi.org/10.3390/fi15090295
Mrvelj Š, Matulin M. FLAME-VQA: A Fuzzy Logic-Based Model for High Frame Rate Video Quality Assessment. Future Internet. 2023; 15(9):295. https://doi.org/10.3390/fi15090295
Chicago/Turabian StyleMrvelj, Štefica, and Marko Matulin. 2023. "FLAME-VQA: A Fuzzy Logic-Based Model for High Frame Rate Video Quality Assessment" Future Internet 15, no. 9: 295. https://doi.org/10.3390/fi15090295
APA StyleMrvelj, Š., & Matulin, M. (2023). FLAME-VQA: A Fuzzy Logic-Based Model for High Frame Rate Video Quality Assessment. Future Internet, 15(9), 295. https://doi.org/10.3390/fi15090295







