FREDY: Federated Resilience Enhanced with Differential Privacy

Abstract

Federated Learning is identified as a reliable technique for distributed training of ML models. Specifically, a set of dispersed nodes may collaborate through a federation in producing a jointly trained ML model without disclosing their data to each other. Each node performs local model training and then shares its trained model weights with a server node, usually called Aggregator in federated learning, as it aggregates the trained weights and then sends them back to its clients for another round of local training. Despite the data protection and security that FL provides to each client, there are still well-studied attacks such as membership inference attacks that can detect potential vulnerabilities of the FL system and thus expose sensitive data. In this paper, in order to prevent this kind of attack and address private data leakage, we introduce FREDY, a differential private federated learning framework that enables knowledge transfer from private data. Particularly, our approach has a teachers–student scheme. Each teacher model is trained on sensitive, disjoint data in a federated manner, and the student model is trained on the most voted predictions of the teachers on public unlabeled data which are noisy aggregated in order to guarantee the privacy of each teacher’s sensitive data. Only the student model is publicly accessible as the teacher models contain sensitive information. We show that our proposed approach guarantees the privacy of sensitive data against model inference attacks while it combines the federated learning settings for the model training procedures.

1. Introduction

Conventional machine learning methods demand the data for training to be located on one machine or on a central server. These methods collect a great amount of data from various devices (smartphones, laptops, IoT devices, etc.) and transfer them to a high-end central server or a super strong computer, for training. However, data owners are not often willing to share their data, because it is sensitive information, which is subject to the GDPR rules. Thus, applying Machine Learning (ML) models on data without revealing the data itself is a major task, which many researchers have tried to address during recent years.

Federated Learning (FL) [1] came as the solution. FL aims to train a shared ML model across multiple devices (clients) on local data. A federated learning system is comprised of a server and several clients. Initially, the server sends a copy of a global ML model to its clients and then each client trains the ML model on its local data. Afterwards, the clients of the FL system send back to the server the trained models and the server updates the global model by performing weight aggregation (e.g., average across trained weights). The global model is the result model of the federated learning system. That said, each client keeps its sensitive data private and does not share them with external parties such as cloud servers, as the ML models are trained locally.

However, the potential for privacy breaches still exists when models are uploaded by clients in federated learning. While the architecture of FL ensures that client nodes do not openly share data, providing a certain level of privacy protection, there remains a vulnerability wherein a malicious actor could exploit the models to extract sensitive information. Furthermore, there is a risk of compromising the integrity of communication during the exchange of model parameters, which opens the door to various attacks within the FL framework, including data and model poisoning attacks. The preservation of privacy in federated learning is primarily pursued through three distinct techniques: differential privacy (DP) as outlined in [2], homomorphic encryption as detailed in [3], and secure multiparty computation as described in [4]. Numerous effective strategies, including works such as [5,6,7,8,9,10], have been developed to bolster client privacy.

The realm of privacy attacks on machine learning models encompasses a spectrum of techniques that exploit inherent vulnerabilities within data protection mechanisms. Among these, model inversion attacks [11,12] endeavor to reconstruct confidential attributes from the model’s outputs while attribute inference attacks [13] seek to infer sensitive attributes of individuals from the outputs of a machine learning model. Attackers exploit the model’s predictions to deduce sensitive information not explicitly included in the input. The pernicious model stealing attack vector [14,15] involves unauthorized replication of a target model by means of black-box querying, potentially engendering concerns of intellectual property infringement. Data poisoning attacks [16,17], on the other hand, engender deliberate model degradation through the introduction of malicious data instances. Lastly, watermarking attacks [18] involve inserting subtle changes into the input data to create a unique “watermark” that can be later detected in the model’s outputs. This is often used to identify data leakage or unauthorized model usage. These multifarious attacks collectively underscore the compelling exigency for robust privacy preservation methodologies to fortify the integrity of machine learning models against these pervasive threats.

As an intricate facet of privacy attacks in the domain of machine learning, black-box membership inference attacks [19,20,21] hold a prominent position. Membership inference attacks aim to determine whether a specific record or a data point has been used in the training procedure of a machine learning model. In cases when the training dataset of a machine learning model contains sensitive data such as medical records, these kinds of attacks can be extremely harmful. Particularly, the adversarial has access to model’s predictions, and based on their statistical distribution it decides whether a record is part of a model’s training data or not. There are several approaches about training an adversarial for model inference attacks [22,23,24,25,26,27], with [28] being a solid baseline in the area. The authors of [28] propose the first membership inference attack model on several classification models in the context of machine learning. They show that an attacker can determine whether a data point has been used to train a network or not based on the probabilistic output of the network on that data record (also known as black-box access to the target ML model).

To protect the privacy of training data, the authors of [29] propose PATE (Private Aggregation of Teacher Ensembles). In this framework, initially, an ensemble of teacher models is trained on private and sensitive data. Then, a student model, which is later released to the public, is trained with supervised learning on public, unlabeled, insensitive data, whose labels are generated by noisy aggregating the teacher outputs on those public data. That said, the student model does not depend on any of the training data points and thus the privacy of the training data is protected. However, PATE treats teachers as individuals and does not consider the federated learning scenario, a scenario where the server-aggregated model can be vulnerable to adversarials and expose data information.

In this paper, we introduce FREDY, a federated learning framework which uses knowledge transfer from private data. FREDY exploits both the data privacy from FL, as the data remain private and locally in each client of the FL system, and the data leakage protection from PATE [29]. Particularly, FREDY has a teachers–student scheme. The teachers are trained in a federated form, acting as clients of an FL system, and then knowledge is transferred from teachers to student by noisy aggregating the teachers’ outputs on the student’s public data. Finally, the student model is publicly available and can successfully respond to user queries without the risk of data leakage when it is being attacked from adversarials such as model inference attacks. Our proposed FREDY model architecture is evaluated in the widely used benchmark datasets CIFAR10 [30] and MNIST [31], achieves data privacy and prevents data leakage against possible attackers while it combines the federated learning settings.

FREDY leverages the synergy between federated learning and differential privacy to bolster resilience in data-driven applications. By combining these two powerful techniques, FREDY enhances the robustness and privacy of the model training process. Federated learning allows FREDY the training of models collaboratively across distributed data sources, such as different institutions or devices, without centralizing sensitive information. This decentralized approach enhances resilience by minimizing the risk of a single point of failure and enabling the system to continue functioning even if certain participants experience disruptions. Differential privacy, on the other hand, introduces noise into the model training process, making it extremely challenging for attackers to reverse-engineer individual data points. FREDY applies differential privacy during the aggregation of teachers’ outputs, thereby safeguarding the privacy of individual contributions while still enabling knowledge transfer to the student model. This ensures that the sensitive information of each participant remains protected and contributes to a collective resilient model. Together, these two techniques create a synergistic effect. Federated learning’s collaborative nature distributes the training process, while differential privacy adds a layer of noise that prevents adversaries from extracting sensitive information. This combination not only enhances the system’s overall resilience by diversifying data sources, but also fortifies the privacy of participant data. FREDY thus offers a robust and privacy-conscious framework that strengthens resilience through the seamless integration of federated learning and differential privacy.

The contributions of this paper are twofold:

• We introduce FREDY, a knowledge transfer federated learning framework which offers PATE’s privacy-preserving technique in a federated learning setting. From a federated learning standpoint, multiple teachers are trained in a federated manner and then the FL server queries the teachers and aggregates their outputs in order to label public data and thus train a student model on these data. We evaluate FREDY on two benchmark datasets, namely CIFAR10 and MNIST.
• We implement a membership inference attack model and perform inference attacks to several student models that are trained with different noise addition values, showing its robustness and the privacy preservation ability of our proposed method.

The remainder of the paper is organized as follows. Section 2 describes the related work in the field of federated learning and knowledge transfer frameworks from private data. Section 3 provides the architecture of FREDY following with experimental results in Section 4 and discussion in Section 5. Finally, the paper concludes in Section 6.

2. Related Work and Backround

2.1. Federated Learning

Federated Learning [1] adopts a distributed paradigm for the learning process of Machine Learning models, implementing collaborative training among a set of nodes (participants). Each node in FL trains its own local model based on their own data, which are kept private and not disclosed to the peer nodes in the FL system. In this way, FL does not involve any centralized training, but rather the locally trained models are aggregated into a global model at a centralized server. Figure 1 presents the Federated Learning process. The process starts by initiating the training of the initial global model at the central server for n federated rounds. For each round, the server sends a copy of this model to the clients of the FL system, where it is trained using the client’s local data. Then, the updated model weights are sent back to the central server and the global model is updated by aggregating each client’s weights. The most commonly used aggregated function [4,32,33,34,35,36] is the averaging function of the weights, and it is defined as follows:

$$W_t^{global}=\frac{1}{K}\sum _{k=1}^K{W}_t^k,$$

(1)

where $W_t^k$ is the updated weights from the client k and K it the total number of clients at round t. Therefore, through this process, machine learning models can be derived, exploiting the aggregated knowledge of a number of dispersed nodes, without disclosing the data to the peers, thus ensuring data privacy and saving communication overheads.

2.2. Membership Inference Attack Models

The attacker can obtain different amounts of information to attack machine learning models. Usually, the attackers have access to two types of information: the distribution of training data and the target model. In most cases of Membership Inference Attacks, it is assumed that the distribution of training data is available to an attacker. This means that the attacker can obtain a dataset that contains data with the same distribution as the target model’s training data. This assumption is reasonable because the dataset can be obtained through statistics-based synthesis if the data distribution is known [28]. It is assumed that the newly created dataset and the training dataset are disjoint. Knowledge of the target model refers to how the target model is trained (i.e., the learning algorithm) and the architecture and learned parameters of the target model. Based on the adversary knowledge, we can characterize the existing attacks as follows:

• White-box Attack: An adversarial has access to all kinds of information such as the training data distribution, the learned parameters, etc., and uses it to attack a target machine learning model [37,38,39,40,41].
• Black-box Attack: An adversarial has black-box access to a target model meaning that it has information about the training data distribution and the black-box queries on the target model. For example, the attacker queries the target model and obtains only the raw prediction probability of the input data [42,43,44,45,46,47].

The most common way to implement a membership inference attack model is to treat it like a binary classification problem. Given the input data x and access to the target model (e.g., the model’s raw predictions, learned parameters, etc.), an attacker infers whether or not x is in the dataset. In other words, a binary classifier is trained that can distinguish the behavior of training members of a target model from that of non-members. The challenge is how to train such a classifier. In [28], the authors proposed an effective technique called shadow training, which is the first and perhaps most widely used approach. Particularly, the attacker is aware of the architecture of the target model and thus can generate shadow models in order to realize membership inference attacks. These shadow models mirror the behavior of the target model but are trained on known and labeled training data. By utilizing the shadow models which possess ground truth knowledge of membership, the attack model is trained to distinguish between the target model’s behavior on familiar training inputs and its behavior on previously unseen inputs. This enables the attack model to effectively determine whether a specific input was part of the target model’s training dataset or not. Through shadow training, the technique offers a potent means to quantify the extent of membership information leakage in machine learning models.

In this paper, we are focusing on the black-box attack type, where the adversarial has access only to the data distribution and the output predictions when querying a target model. The shadow training attack framework proposed in [28] is applied in our experiments to evaluate the robustness of the proposed FREDY against membership inference attacks.

2.3. Knowledge Transfer Frameworks

The concept of PATE (Private Aggregation of Teacher Ensembles), introduced in [29], revolves around safeguarding the differential privacy of machine learning. The central idea posit that when two independently trained classifiers converge on a classification verdict, the decision itself does not divulge information about any individual training instance. This strategy employs a teachers–student model architecture, specifically designed to uphold the confidentiality of each entity’s data. Numerous teacher models undergo training using distinct datasets, which could be sensitive, like medical records. Conversely, the student model is trained on publicly available data, encompassing labels generated through a noisy (Laplacian) voting process among all teachers. Subsequently, an aggregated teacher assimilates the predictions (votes) from each trained teacher concerning the student’s unlabeled data for each sample and introduces random noise. The resultant most frequently endorsed predictions serve as labels to train the student model. Consequently, the student model, which might eventually become publicly accessible, internalizes consolidated insights drawn from teachers’ private data, founded on their collective input, all while preserving their privacy.

However, while PATE operates within a transfer learning framework, it overlooks the scenario of federated learning, where safeguarding privacy against malicious participants is paramount. In [48], the authors propose an innovative approach called FL-PATE that bridges the PATE transfer learning technique with the principles of federated learning. The FL-PATE framework unfolds in two distinct stages. Initially, teacher models undergo training via federated learning, executed across participant groups, and further fortified with differential privacy measures by introducing Gaussian noise to a dedicated layer within the teacher models, i.e., the last fully connected layer within a ResNet18 network. This strategic noise addition substantially mitigates its impact on model accuracy. Subsequently, the second stage involves training the student model using public datasets, the labels of which result from aggregating the outputs of the teacher models.

Nevertheless, the original concept presented in [29] introduces PATE as a method for maintaining privacy, while FL-PATE employs PATE solely as a transfer learning approach, devoid of its privacy-preserving aspect. This deviation becomes evident through FL-PATE’s utilization of Gaussian noise augmentation on the collective model’s weights during the federated learning training phase, whereas PATE relies on Laplacian noise addition to the consensus of teacher predictions. In light of this, we put forward FREDY, an innovative federated learning framework that harnesses PATE as a central architecture, seamlessly integrating both transfer learning and privacy preservation techniques. That said, FREDY employs PATE’s original Laplacian noise addition on the most voted teacher predictions to achieve privacy protection while simultaneously enhancing transfer learning. This distinctive dual utilization of PATE in FREDY sets it apart from both PATE and FL-PATE, making it a unique and promising approach that encompasses both transfer learning and privacy preservation within the federated learning paradigm.

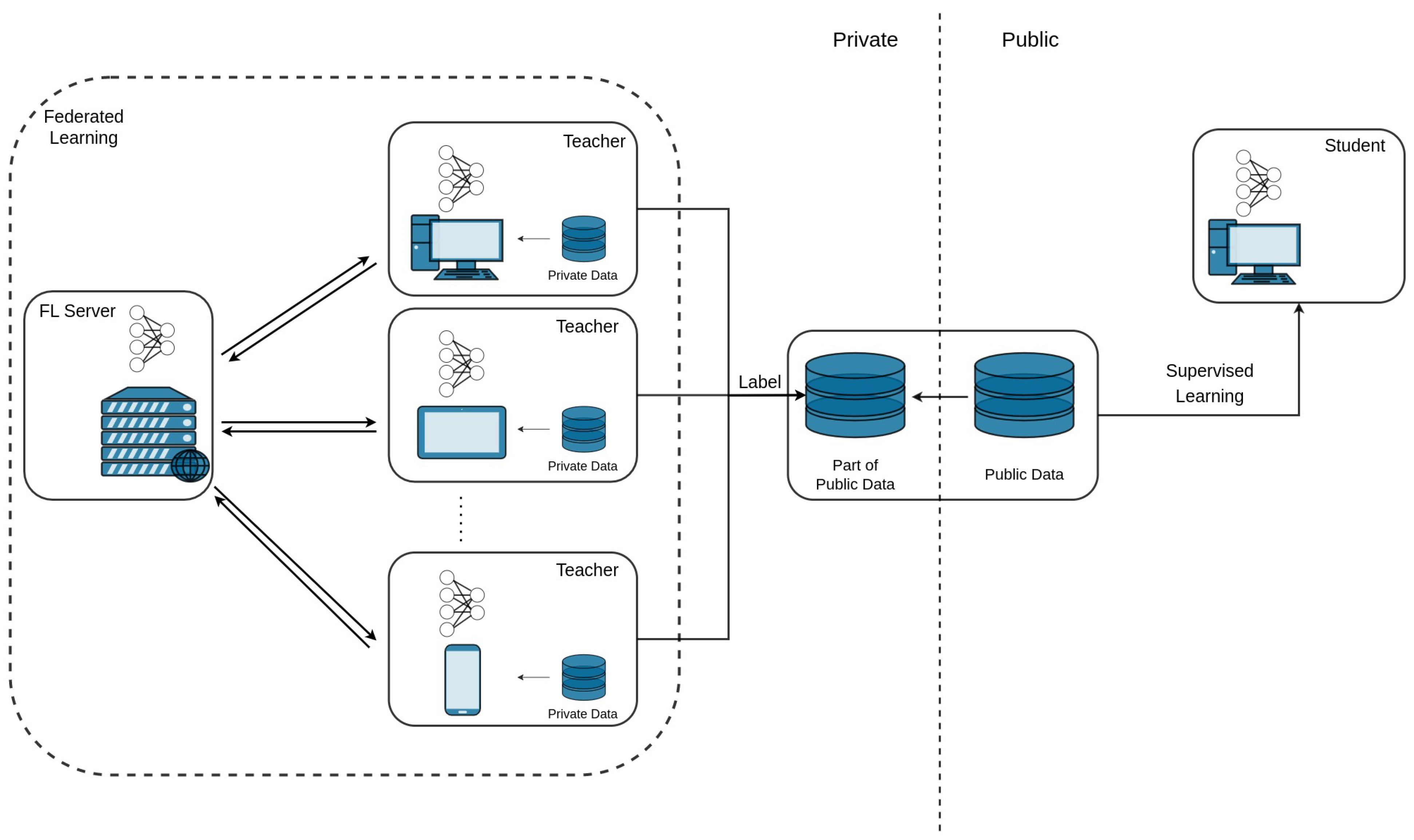
3. Proposed Framework

3.1. Design Overview

As discussed above, FL-PATE addresses the context of federated learning by employing a client-level differential privacy mechanism for teacher model training. In contrast, PATE introduces a vote-level differential privacy mechanism. That said, we introduce FREDY, a novel federated learning framework rooted in the PATE methodology for knowledge transfer, while also incorporating differential privacy measures. Analogous to PATE’s configuration [29], FREDY employs a teachers–student scheme. The teachers undergo training within a federated learning scenario, and, upon the completion of the FL process, each teacher’s model performs inference on the student public data. These predictions from public data are amalgamated and subjected to noise addition to facilitate the training of the student model. A schematic representation of FREDY’s design is presented in Figure 2. Our objective is to cultivate a privacy-preserving model that can tackle intricate real-world tasks. Each teacher’s model is trained on its private, sensitive data. The outcome of this comprehensive procedure is the student model, slated for later public release. The detailed steps of our proposed framework are described in Algorithm 1.

Algorithm 1 Training Procedure of FREDY

Require:  $PublicData$   1: procedure ServerExecution($n,T$)   2:     $Initializeglobalmodelweights{W}_0^{global}$   3:     for $roundr\leftarrow 1,2,\dots ,n$ do   4:         if $r=n$ then  // last round   5:            $W_n^T\leftarrow$TrainTeachers$(r,T,W_{n-1}^{global})$   6:            $Labels\leftarrow$NoisyAgg$\left(PublicData\right)$   7:            $W_{st}\leftarrow$TrainStudent$(Labels,W_0^{global})$   8:            return $W_{st}$   9:         else 10:            $W_r^T\leftarrow$TrainTeachers$(r,T,W_{r-1}^{global})$ 11:            $W_r^{global}\leftarrow \frac{1}{T}{\sum }_{t=1}^T{W}_r^{T_t}$ 12:         end if 13:     end for 14: end procedure 15: procedure TrainTeachers($r,T,W_r^{global}$) 16:     for $teacher{T}_i\leftarrow 1,2,\dots ,T$ in parallel do 17:         $W^{Ti}\leftarrow W_r^{global}$ 18:         for $localepochse\leftarrow 1,2,\dots ,E$ do 19:            $Update{W}^{Ti}usingSGD$ 20:         end for 21:     end for 22:     return $W_r^T$ 23: end procedure 24: procedure TrainStudent($Labels,W_r^{global}$) 25:     $W_{St}\leftarrow W_r^{global}$ 26:     for $localepochse\leftarrow 1,2,\dots ,E$ do 27:         $Update{W}_{St}usingSGDandLabels$ 28:     end for 29:     return $W_{St}$ 30: end procedure

3.2. Teachers Model Training

Each individual teacher model is trained using its proprietary sensitive data, ensuring its confidentiality is maintained. Within the federated learning framework, the server orchestrates the training of these teachers, while the student remains in a state of readiness for the teacher training to conclude. At each iteration of the federated learning procedure, the teachers retrieve the global model (i.e., $W^{global}$) from the FL server. Employing the Stochastic Gradient Descent (SGD) training algorithm [49], they train this global model using their own private-sensitive training set, with a local batch size B, local epochs E and learning rate $\eta$. For each local epoch $e\in E$ of the teacher training procedure, each teacher holds a local model which can described as

$$\Delta W_t^{local}=\eta \ast \nabla J\left(W_t\right),$$

(2)

where $J\left(\right)$ is the loss function of the model and $\eta$ is the learning rate. Then, each client computes the update of the weights as

$$W_{t+1}^{local}=W_t^{local}-\Delta W_t^{local}.$$

(3)

Then, at the final local epoch, the teachers upload their updated weights $W^{local}$ to the server and the global model Sis updated by aggregating the $W^{local}$. We use (1) as the aggregation function of the updated weights from the teachers.

3.3. Student Model Training

At the final round of the FL training process, the teacher models abstain from uploading their weights to the server. Instead, these models are leveraged for making predictions on the student’s publicly available data. Subsequently, the server employs unlabeled public data to engage the teachers in a querying process, followed by the execution of a noisy aggregation method to consolidate the predictions offered by the teachers. The privacy guarantees come from the aggregation mechanism that the server performs on the predictions of the teacher models. Given an unlabeled public sample of data, the server queries the trained teachers on this data point and then it counts the votes (i.e., predictions of the teachers) for each class. Finally, the server injects Laplacian noise to these vote counts and the final aggregated label of the data point for the student’s training is the class with the most counts.

Particularly, suppose we have a C number of classes in our task. For a given class $c\in C$ and an input x, the label count is the number of teachers that assign class c to input x: $Vote{s}_c\left(x\right):\left|\{i:i\in N,T_i\left(x\right)=c\}\right|$, where $T_i$ is the ith teacher and N illustrates the indices of the teacher model set. The final aggregation of teacher model predictions is as follows:

$$NoisyAgg\left(x\right)=arg\underset{c}{max}\left\{Vote{s}_c\left(x\right)+Lap\left(\frac{1}{ϵ}\right)\right\},$$

(4)

where $Vote{s}_c\left(x\right)$ is the label count, $ϵ$ is a privacy parameter and $Lap\left(\beta \right)$ is the Laplacian distribution with location zero and scale $\beta$. The value of the parameter $ϵ$ dictates the level of privacy assurance we can establish. A larger $ϵ$ entails a robust privacy guarantee but comes with the trade-off of potential label accuracy degradation.

Finally, the server employs these predictions to assign labels to the student’s training dataset and then proceeds to train the student model through supervised learning. This approach facilitates the transfer of knowledge from the teachers to the student. Throughout this entire process, only the student model is publicly accessible, with the teachers remaining beyond a user’s reach. The resultant student model trained on public data exhibits heightened resilience against membership inference and model inversion attacks. This robustness stems from the fact that the final training occurs with public data, thus averting direct exposure of the teachers’ private information. Nonetheless, the student model acquires insights from the private data of each teacher, given that its training involves labels derived from the predictions made by the teacher models on the unlabeled data.

4. Experiments

4.1. Datasets

For the experiments, we used the CIFAR-10 [30] and MNIST [31] datasets. The first is a collection of images that are commonly used to train machine learning and computer vision algorithms. It is one of the most widely used datasets for machine learning research. CIFAR-10 consists of 60,000 32 × 32 color (RGB) images in 10 different classes, of which 50,000 are training images and 10,000 are test images. The 10 different classes represent airplanes, cars, birds, cats, deer, dogs, frogs, horses, ships and trucks. There are 6000 images for each of the 10 classes. The MNIST dataset is a collection of 70,000 32 × 32 grayscale hand-written digit images of 10 classes (0–9), of which 60,000 are training images and 10,000 are test images, with 1000 images per digit.

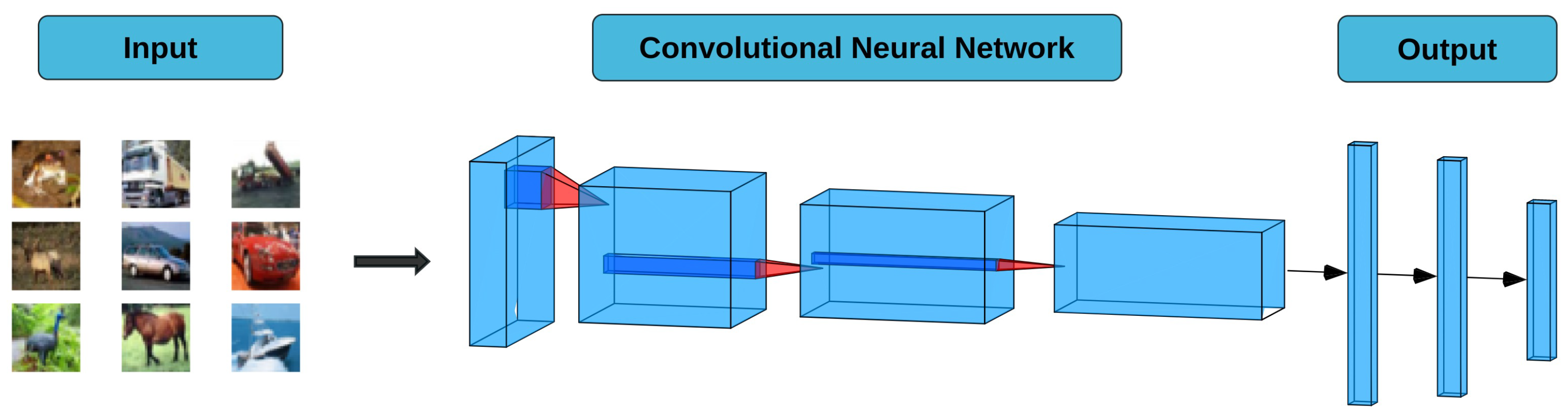
4.2. Models

Both the teacher and student models employed in FREDY’s training are Convolutional Neural Networks (CNNs) comprising three convolutional layers, each employing a 3 × 3 filter. This architecture is augmented by a Max-Pooling layer and a Batch Normalization layer, further accompanied by three fully connected layers. The structure of the above model is described in Figure 3.

Our Membership Inference Attack model is a binary CatBoostClassifier [50], an open-source gradient boosting framework. A CatBoostClassifier uses a decision-tree-based ensemble technique known as gradient boosting to build an ensemble of weak learners, typically decision trees, in a sequential manner.

4.3. Metrics

The metrics used for performance evaluation for the teacher and student models is Accuracy, and those used for the attack model evaluation are Accuracy, Recall, Precision and F1-Score. These metrics are derived from the following four categories: True/False Positive, which refers to the instances where the model correctly/incorrectly identifies a positive class, and True/False Negative, which represents the instances where the model correctly/incorrectly identifies the absence of a class.

That said, having C classes in our classification problem, we can now define the above metrics as follows:

• Accuracy. Number of samples correctly identified as either truly positive or truly negative out of the total number of samples.

  $$\mathrm{Accuracy}=\frac{{\sum }_{c=1}^C(T{P}_c+T{N}_c)}{{\sum }_{c=1}^C(T{P}_c+T{N}_c+F{P}_c+F{N}_c)}.$$
• Precision. Number of samples correctly identified as positive out of the total samples identified as positive.

  $$\mathrm{Precision}=\frac{{\sum }_{c=1}^{C}T{P}_c}{{\sum }_{c=1}^C\left(T{P}_c+F{P}_c\right)}.$$
• Recall. Number of samples correctly identified as positive out of the total actual positives.

  $$\mathrm{Recall}=\frac{{\sum }_{c=1}^{C}T{P}_c}{{\sum }_{c=1}^C\left(T{P}_c+F{N}_c\right)}.$$
• F1-Score. The harmonic average of the precision and recall measures the effectiveness of identification when just as much importance is given to recall as to precision.

  $$\mathrm{F}1-\mathrm{Score}=2\ast \frac{\mathrm{Precision}\ast \mathrm{Recall}}{\mathrm{Precision}+\mathrm{Recall}}.$$

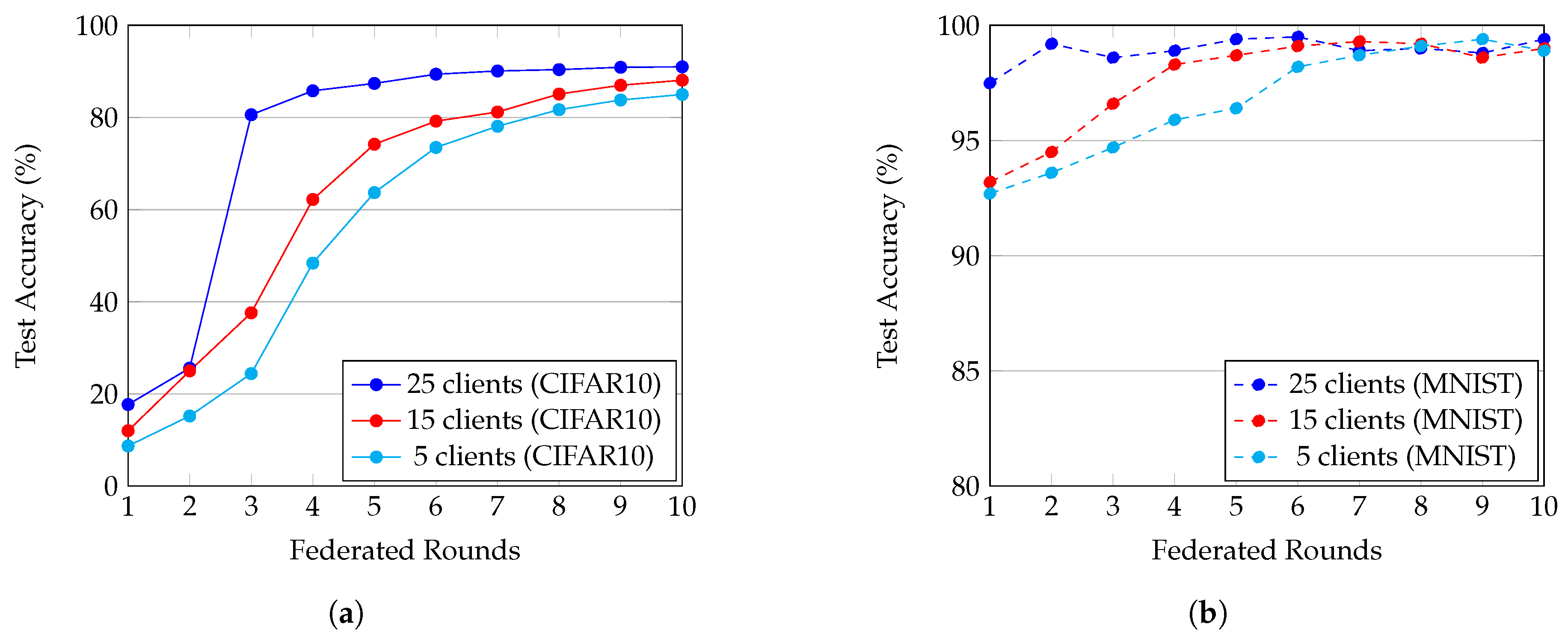
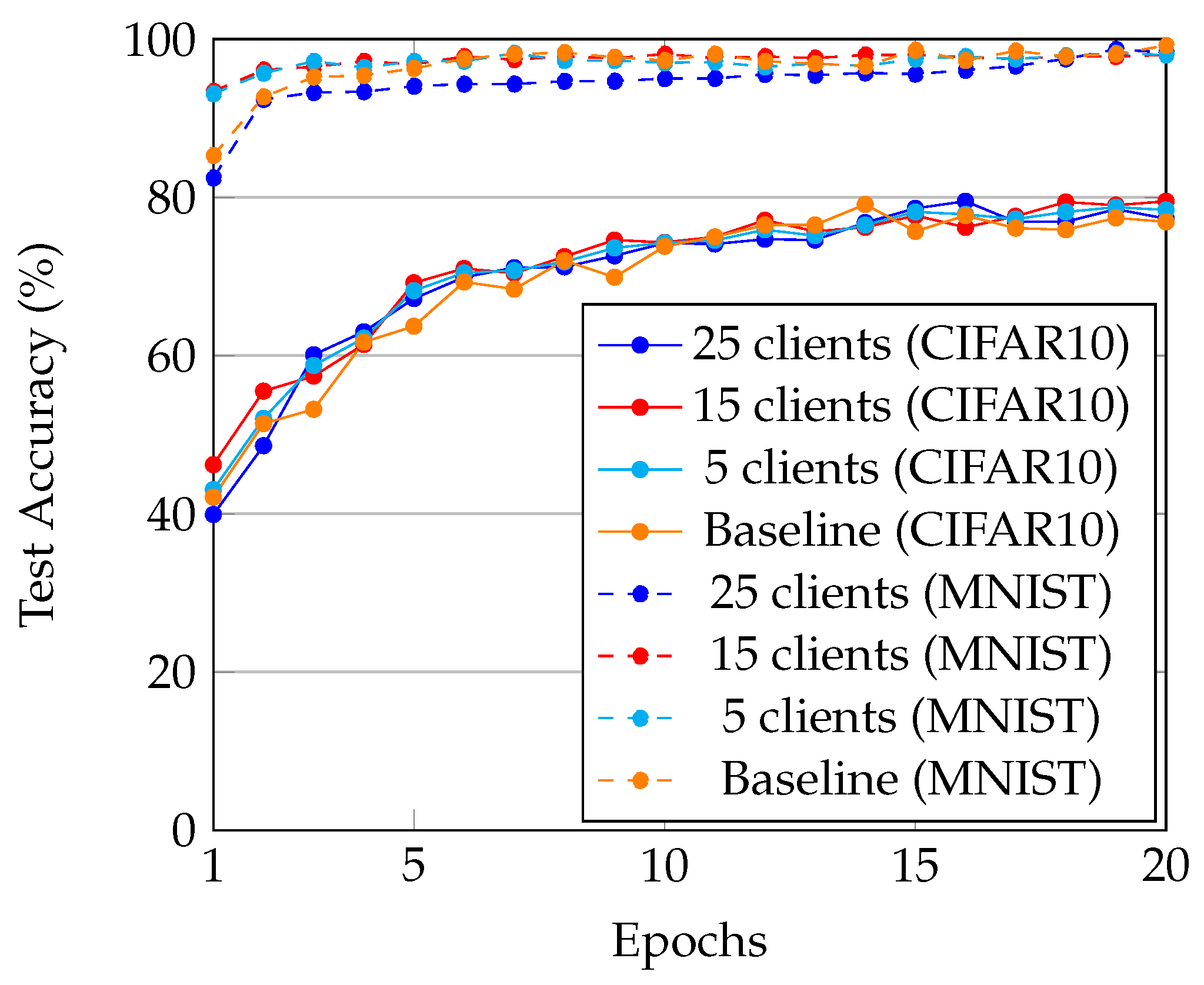
4.4. Performance Evaluation

For training a machine learning model within a Federated Learning configuration among clients, the datasets must be partitioned to ensure distinct data for each Teacher within the FL System. In our approach, both the CIFAR10 and MNIST training datasets are partitioned into T separate subsets. A unique teacher model is trained on each of these sets, where T represents the total number of teachers. As for the CIFAR10 and MNIST test datasets, they serve as the public unlabeled data for student training. Within this context, a segment of labels is derived from the most prevalent predictions made by the teachers concerning these data. Similar to the PATE methodology, we allocate 90% of both test datasets (equivalent to 9000 images) for the student’s training procedure, reserving the remaining 10% (1000 images) for evaluating the entire training process.

We train the teacher models for $n=10$ federated rounds and $E_T=10$ local epochs for each round using the Flower [51] framework. The student model is trained for $E_{ST}=20$. All the models are trained with the Adam Optimizer [52] with learning rate $\eta =0.001$, weight decay $w=1\times {10}^{-5}$ and batch size $B=32$. A summary of FREDY’s hyper-parameter setup is shown in

Table 1. Hyper-parameter configuration.

Hyper-Parameter	Value
Federated rounds (n)	10
Teacher epochs ($E_T$)	10
Student epochs ($E_{ST}$)	20
Learning rate ($\eta$)	$0.001$
Weight decay (w)	$1\times {10}^{-5}$
Batch size (B)	32
Optimizer	$Adam$

.

The baseline models are subjected to supervised learning, devoid of any privacy-preserving techniques, and undergo 20 epochs of training using identical train and test datasets as the student. Consequently, the student model attains accuracy rates of 79% for CIFAR10 and 99.2% for MNIST. These achievements serve as the performance benchmarks for the student models, establishing an upper limit for comparison in subsequent experiments.

As previously mentioned, the initial phase of FREDY entails the server engaging in federated learning to train the teachers, while the student awaits the completion of their training cycles. Our investigation involves three ensembles, comprising 5, 15, and 25 teachers. Consequently, the dataset is partitioned into distinct segments of equal size, yielding 10,000, 3333, and 2000 images for the CIFAR10 dataset, and 12,000, 4000, and 2400 images for the MNIST dataset. Each teacher undergoes 10 federated rounds, encompassing 10 epochs per round. The evolving test accuracy of the aggregated model is showcased in Figure 4, tracing its performance across each federated round during the training of teachers for the three ensembles. By the concluding round, the aggregated model achieves accuracy levels of 91%, 86.1%, and 82% on CIFAR10, and 99.4%, 99%, and 98.9% on MNIST, corresponding to ensembles of 5, 15, and 25 clients, respectively.

In the second phase of FREDY, the FL server proceeds to query the teacher model predictions on the student training data, followed by a noise-infused aggregation of their votes (predictions) to label a specific portion of these data for student training. As previously mentioned, we introduce Laplacian noise with an inversely scaled $ϵ$, spanning values of 1, 0.5, 0.2, 0.1, and 0.01. As $ϵ$ diminishes, a greater degree of random noise is introduced to each query. With access to a dataset containing 9000 samples, a subset of 500, 1000, 2000, or 9000 samples is labeled using the noisy aggregation mechanism for each $ϵ$ value. Figure 5 presents a comparison between the accuracy of the baseline model and the student model, both trained without noise injection, and involving ensembles of 5, 15, and 25 teachers. Notably, it is observed that each model exhibits a nearly identical performance, with an accuracy of ~79% for CIFAR10 and ~99% for the MNIST dataset. This result aligns with our expectations given that individual teachers achieve average test accuracies of ~87%, ~83%, and ~79% for CIFAR10, and ~98.8%, ~98.2%, and ~97.3% for MNIST, corresponding to ensembles of 5, 15, and 25 teachers, respectively. Consequently, these accurate predictions contribute to the student’s effective handling of public, unlabeled data.

In Figure 6, the student test accuracy is illustrated across various scenarios. Specifically, Figure 6a outlines the student test accuracy as the server conducts 500, 1000, 2000, and 9000 queries using the ensemble of 15 teachers with a noise parameter of $ϵ=0.2$. As anticipated, the student accuracy exhibits a decline as the number of queries directed towards the teacher models increases. In the context of 9000 queries, exploring values below 0.1 for $ϵ$ becomes inconsequential, as this introduces excessive noise to the student’s labels, rendering the training process ineffective. Additionally, Figure 7 shows the accuracy of the student model on both datasets varying the number of teacher models during federated learning and the value $ϵ$ of noise per label query. Small values of $ϵ$ on the left of the axis correspond to large noise and large $ϵ$ values on the right to small noise. The number of teacher models needs to be large in order to compensate for the impact of noise injection on student accuracy. Through our analysis, we ascertain that the introduction of Laplacian noise with $ϵ=0.2$ into teacher queries yields significant outcomes. In particular, this approach yields commendable accuracy rates of 75.1% and 93.2% for CIFAR10 and MNIST, respectively, within the student model. Although this represents a slight decrease of ~4% and ~6% compared to the baselines, it is important to note that this trade-off is balanced by the considerable enhancement in privacy preservation achieved across the sensitive data of all 25 teacher models. Finally, as Figure 6b shows, the student model achieves ~25% accuracy with 5 teacher models and ~60% accuracy with 15 teacher models while it achieves almost 70% accuracy with 25 clients and noise parameter $ϵ=0.1$ as the number of teachers increases (i.e., the clients of the FL system), and thus noise injection has less impact on model accuracy. It is worth mentioning that in Figure 6a,b, we report results on CIFAR10 only as it contains RGB images from common objects in real life and thus represents more real-world scenarios.

Furthermore,

Table 2. Shadow attack model inference results.

Model	$\mathit{ϵ}$	Attack Performance
		Accuracy	Recall	Precision	F1-Score
Baseline	-	0.71	0.71	0.78	0.70
FREDY (Ours)	1.0	0.68	0.68	0.69	0.67
	0.5	0.57	0.57	0.57	0.52
	0.2	0.50	0.49	0.49	0.46
	0.1	0.49	0.49	0.49	0.45

shows the attack results of a shadow training membership inference attack on our baseline model and on FREDY’s student model that is trained with 25 teacher models and 2000 queries on CIFAR10, varying the value of $ϵ$, i.e., the noise injection to each query. Compared to the baseline model, FREDY reduces the performance of the membership inference attack to a random guess (i.e., ~25% drop in all metrics) when the value of $ϵ$ is equal to $0.2$ and thus it can successfully protect and keep private each teacher’s sensitive data. We can also observe that when $ϵ=0.1$, the membership inference attack performance is slightly lower, i.e., ~0.005% lower when compared with $ϵ=0.2$; however, the student accuracy degradation on this setting makes this attack performance difference meaningless.

5. Discussion

FREDY offers a versatile solution applicable across diverse domains. In healthcare, FREDY facilitates collaborative medical research by training models on data from different hospitals while preserving patient privacy. Financial institutions can utilize FREDY for fraud detection, pooling transaction data to identify patterns without compromising individual financial details. Smart cities benefit from FREDY’s traffic prediction capabilities, where local districts contribute data to develop accurate models while safeguarding private travel information. In education, FREDY enables personalized learning models by aggregating insights from various schools, enhancing student recommendations while upholding privacy. Collaborative Internet of Things (IoT) systems leverage FREDY to build unified models from sensor data across locations, ensuring data confidentiality while optimizing predictive accuracy. In legal applications, FREDY empowers law firms across jurisdictions to collectively analyze legal documents, enhancing legal insights without disclosing sensitive case information. These diverse use cases highlight FREDY’s prowess in enabling collaborative model development while ensuring stringent data privacy and security measures.

The scalability of FREDY demonstrates a promising trajectory as the number of clients or the size of data increases. FREDY’s inherent architecture leverages the decentralized paradigm of federated learning, allowing it an effective accommodation of a growing number of clients while preserving data privacy. Moreover, FREDY’s knowledge transfer mechanism through noisy aggregation ensures that the burden on individual clients remains manageable, even as the dataset expands. This design not only promotes efficient scalability, but also positions FREDY as a robust solution for large-scale federated environments, facilitating the seamless integration of additional clients or increased data sizes without compromising performance or privacy.

Moreover, FREDY showcases remarkable strengths tailored to distinct contexts. FREDY’s compatibility with homogeneous scenarios where the FedAvg algorithm is employed underscores its adaptability and efficacy. Furthermore, the strategic incorporation of Laplacian noise highlights FREDY’s commitment to striking an optimal balance between privacy preservation and heightened model accuracy, a challenge that is a recurrent theme in various extant works dedicated to privacy-preserving federated learning [19], thus inviting precise configuration of noise parameters.

Additionally, the computational overhead of FREDY in comparison to non-private federated learning methods is an essential aspect that warrants thorough consideration. While FREDY integrates both federated learning and differential privacy, this amalgamation may introduce additional computational demands. The utilization of differential privacy involves the introduction of noise, impacting the efficiency of model training and potentially extending convergence times as shown in

Table 3. Computational overhead of FREDY with respect to student convergence time.

Model	$\mathit{ϵ}$	Queries	Student Convergence Time (s)
Baseline	-	-	32.9
FREDY (ours)	0.2	2000	33.6

. The aggregation of teacher outputs with Laplacian noise, although enhancing privacy, may lead to increased computation during the aggregation process. It is crucial to recognize that FREDY’s enhanced privacy-preserving capabilities inherently involve a computational trade-off. The noise introduced for privacy protection could lead to slower convergence and higher training times when contrasted with non-private federated learning methods. Balancing this trade-off is a nuanced endeavor that requires a careful consideration of the application’s requirements, available computational resources, and desired level of privacy.

6. Conclusions

PATE is a powerful privacy-preserving technique that enables the training of teacher models on local sensitive data whose outputs in public unlabeled data are noisy aggregated, and the final results act as labels and thus train a student model on these public data. Only the student model is released to the public, and therefore each teacher’s sensitive data are kept private. However, PATE trains the teacher models sequentially and does not consider the federated learning scenario. In this paper, we proposed FREDY, a federated learning privacy-preserving framework that uses knowledge transfer from private data. FREDY trains teacher models in a federated manner on local sensitive data using the standard FedAvg algorithm as the aggregation function. At the last round of the federated training procedure, the teacher models do not upload their weights to the server and keep them to perform inference on public unlabeled data. The outputs of each teacher model’s inference are noisy aggregated by adding Laplacian noise and keeping the most voted classes for each public unlabeled data point. The final aggregated labels along with the corresponding public data are used to train a student model. Similar to PATE, only the student model is available to the public community, while the teacher models are kept private. We show that our final student model is not vulnerable to membership inference attacks, making an attack model unable to determine whether a data point is part of the training data of the teacher models or not. In doing so, FREDY fortifies resilience not only against external threats, but also within its internal mechanisms, culminating in a comprehensive approach to maintaining data privacy and model integrity.