Addressing the Gaps of IoU Loss in 3D Object Detection with IIoU

Abstract

Three-dimensional object detection involves estimating the dimensions, orientations, and locations of 3D bounding boxes. Intersection of Union (IoU) loss measures the overlap between predicted 3D box and ground truth 3D bounding boxes. The localization task uses smooth-L1 loss with IoU to estimate the object’s location, and the classification task identifies the object/class category inside each 3D bounding box. Localization suffers a performance gap in cases where the predicted and ground truth boxes overlap significantly less or do not overlap, indicating the boxes are far away, and in scenarios where the boxes are inclusive. Existing axis-aligned IoU losses suffer performance drop in cases of rotated 3D bounding boxes. This research addresses the shortcomings in bounding box regression problems of 3D object detection by introducing an Improved Intersection Over Union (IIoU) loss. The proposed loss function’s performance is experimented on LiDAR-based and Camera-LiDAR-based fusion methods using the KITTI dataset.

1. Introduction

Object detection has become increasingly popular and contributed to the development of various applications in the autonomous vehicular industry, such as obstacle detection, collision avoidance, lane-level detection, parking assistance and pedestrian safety [1,2,3]. In order to perform detection tasks in autonomous vehicles, range sensors such as LiDAR, RADAR, RGB-D, and stereo vision cameras are heavily relied upon [4,5,6]. LiDAR and RADAR emit light pulses and radio waves to detect the presence of an object and provide data in the form of point clouds. In contrast, vision cameras capture 2D image data of the environment along with depth/distance estimation. With rapid development in deep learning, 2D and 3D detections have gathered more interest in the research community [7]. 2D networks are often termed image-based network since it heavily depends on image data to perform localization and classification tasks [8]. The bounding box coordinates of 2D objects are represented as x1, y1, x2, y2. Recently, various architectures such as SSD [9], Faster R-CNN [10], YOLO [11], FFNet [12] and VirConv-S [13] have been proposed in 2D detection challenge and are successfully backed by large-scale datasets such as KITTI [14]. Compared to 2D detection techniques, 3D object detection poses a trivial challenge because the concepts of 2D detection cannot be directly translated to the 3D domain due to its 6 Degrees-of-Freedom (DoF) [15]. 3D object detectors estimate the bounding box coordinates as (x, y, z, l, w, h, $\theta$).

Like 2D object detectors, state-of-the-art 3D object detectors can be classified into single-stage and two-stage detectors based on the presence or absence of Regional Proposal Networks (RPN). In two-stage methods, the first stage extracts feature information generated by RPN and generates Regions of Interest (RoI). The second stage acts as a detector network that operates only on the proposed regions to create accurate predictions. On the other hand, Single-stage detectors serve as a simple and efficient end-to-end pipeline. However, single-stage detectors face a performance drop as compared to two-stage detectors. One of the primary reasons is the sparsity of point clouds, and when the network progressively scales down during the forward pass of the network, crucial spatial information is lost [1]. This causes an inability to predict the bounding box coordinates in 3D space accurately. Architectures such as PointNet [16] and VoxelNet [4] were proposed to increase the performance of single-stage detector networks. VoxelNet divides the 3D space into voxels and then applies PointNet across each voxel, followed by 3D and 2D convolution layers [17]. Following the recent success in the usage of transformers [18] in computer vision, another approach was to utilize transformer structures to address sparse irregularities in processing point cloud information [19].

During training, the predicted bounding boxes are regressed continuously to match the ground truth data [20,21,22]. The detector stage of single and two-stage object detectors use $L_{norm}$ based loss functions such as L1, L2, and smooth-l1 to optimize the bounding box regression problem [10,23]. However, a performance gap exists between IoU-based evaluation metrics and distance-based loss functions. Refs. [17,24,25,26,27] have analyzed this mismatch and demonstrated that similar bounding boxes with different aspect ratios yield the same distance loss while their IoU values remain different. IoU based loss functions [27,28,29] were proposed to address this issue. IoU, as the name suggests, measures the Intersection Over Union area between two bounding boxes. One of the critical differences between IoU losses and distance loss is that IoU considers all the properties of bounding boxes, such as length, width, height, and orientation, and remains scale-invariant, solving scale and range differences between the boxes.

However, IoU loss in 3D object detection brings additional complexity, such as higher DOF and huge 3D space compared to its 2D counterpart, leading to slow convergence and affecting the network performance [30]. During our earlier study [26], we observed that convergence of existing IoU losses and their variations are affected when the boxes have the same centers and aspect ratios but still have varying shapes and orientations. Additionally, objects in 3D space can have arbitrary orientations, and usage of axis-aligned loss functions results in prediction mismatch [31]. To address these drawbacks, an improved loss function 3D IIOU is proposed in this research. This loss function considers orientation as a parameter in the 4th dimension and calculates the center distance between x, y, and z centers individually. The proposed loss function addresses the edge cases when the loss value and the guided regression aid in better convergence. The performance of this loss is evaluated on both single-stage and two-stage 3D object detectors on the KITTI and nuScenes datasets. The research article follows the below structure,

• A background study on various categories of 3D object detectors and their challenges Section 2.
• Section 3 analyzes the shortcomings of IoU losses and Section 4 explains the proposed the loss function.
• Section 5 demonstrates the performance of the proposed loss function in a synthetic dataset.
• Section 6.1 and Section 6.2 provide information on the training networks and dataset utilized in this study
• The performance evaluation on KITTI datasets is carried out in Section 7.

2. Literature Review

Based on the type of input data representation, a 3D object detection network can be broadly classified into three categories: image-based detection network, point cloud-based network, and fusion networks. The following subsections provide a brief survey of current trends in the development of 3D detection networks and challenges faced by each category.

2.1. Image-Based Detection Networks

The success of 2D detection networks [9,11,23] using RGB images gave rise to the development of image-based 3D detection techniques to localize and classify objects in a 3D frame. The main idea is to generate 3D feature maps from the images to estimate 3D bounding boxes, 3D locations, and orientations of an object in 3D space. Image-based methods can be further classified into monocular image and multi-view image methods. As the name suggests, multi-view image methods infer images from different views to create a depth map [32]. Monocular image methods utilize sliding windows to predict object category, bounding box coordinates, and orientation angle of 2D bounding boxes before estimating 3D losses [33]. Since this method only utilizes a monocular RGB camera, it is economical and cheap compared to multi-views or point cloud-based methods. Two primary techniques, feature lifting, and data lifting methods, extract required 3D features from an image. The camera calibration parameters are utilized by feature lifting methods to transform 2D image features to 3D voxel features [34,35]. The data lifting method takes an alternate route by transforming 2D image data to 3D point cloud information, popularly known as pseudo-LiDAR pipeline [36]. However, this method needs to be improved due to limited depth perception, light sensitivity, overlap of multi-objects on crowded scenes, and limited detection range [37].

2.2. LiDAR-Based Detection Networks

Developing LiDAR-based object detection has seen numerous contributions [4,37]. Earlier approaches utilized hand-crafted features when detailed 3D information was available. Since the objects vary in shape and size, this approach becomes tedious. To minimize the complexity, recent developments focus on voxels (grid-like structures), point-based and voxel-point-based. PointRCNN [38] proposes a two-stage detector network similar to RCNN, where a Regional Proposal Network (RPN) has a point-based feature extractor. The approach provides high accuracy in detection, but the network significantly suffers from the amount of power computation and storage. To reduce the model complexity and improve network speed, PointNet [16] and PointNet++ [39] were proposed. PointNet architectures utilize MLPs to independently extract features from each point cloud and create a global feature vector. This vector space represents the entire point cloud information for the particular scene. These networks underperform in the case of sparse point cloud data, which is commonly observed in autonomous platforms. PointPillars [40] uses PointNet to represent the point cloud information in vertical columns known as pillars. An encoder structure operates on the stacked pillars to extract features and are followed by CNN layers. F-ConvNet [41] proposed an end-to-end learning framework that utilizes PointNet to aggregate local points from frustum structures, known as frustum-level feature vectors. This approach addresses the shortcomings of PointNet, which relies on a few foreground points. VoxelNet [4] networks prepossess the point clouds by dividing them into 3D small cubes to address the sparsity issue. These cubes are passed through 2D CNN layers and 3D sparse CNNs to generate feature maps. These feature maps are, in turn, utilized for developing network predictions. This network shows a significant increase in performance in detection tasks but is computationally expensive as it uses CNNs. MGAF-3DSSD [42] network converts voxel-based 3D feature volumes into sparse 2D feature maps to address the unordered sparsity of point clouds. Second [43], an improvement of VoxelNet reduces the number of parameters in 3D sparse convolutional layers while still maintaining the network performance. DOPS [44] incorporates PointNet++ with VoxelNet to gather local geometric features to reduce the noisy data and significantly improve network performance. The Point-GNN [45] down samples the density of point clouds using voxels and represents the LIDAR point clouds in graph structures. LiDAR sensors suffer from sensor interference from other LiDAR and are vulnerable to adverse weather conditions, resulting in poor performance.

2.3. Fusion-Based Detection Networks

Fusion networks can be classified into three types: feature level, decision level, and sensor level. Owing to its superior performance, feature-level fusion is the commonly used approach that extracts and combines different features from point clouds and RGB images [46]. CenterFusion [47] network utilizes a 2D detection network to operate on RGB images to extract feature maps followed by a voxel feature encoder. This differs from the traditional approach by following a center-based method for 3D object detection. The network aims to predict 3D object centers in all dimensions. In cases of noisy data, this approach makes the detection process robust. On the other hand, the PointFusion [48] network utilizes RGB images, point cloud information, and GPS/IMU data for localization tasks. 3D CNN layers are used as voxel encoders, and 3D CNN for feature extraction on images. This network follows a multi-model fusion approach where features from various layers are fused to develop final network prediction. RadarNet [49] introduces early fusion and late fusion mechanisms to gather additional information on the radial velocity of an object and obtain more information. To address the sparsity of the RADAR point cloud, CRF-Net [50] projects the radar point clouds on the image plane and launches vertical lines at a height of 3 m, creating additional point cloud information along the lines. MVF-Net [51], and Part-$A^2$ Net [52] fuse information from multiple cameras and LIDAR sensors using multi-view feature fusion. To address the sparsity when utilizing LiDAR point cloud information, SalsaNet [53] was proposed. STD network [54] uses a sparse to dense feature extraction on dense image features and sparse LiDAR information. PFF3D [55] offers an early-fusion method to extract features from LiDAR and camera data using a single backbone structure. The authors of this research, AVOD-FPN [56], propose an RPN structure utilizing multiple modalities to produce high-recall proposals for small classes. This approach aims to increase the detection performance of small objects. The sequential fusion method proposed in PointPainting [57] involves projecting point clouds onto an image-only segmentation network and adding class scores. Fast-CLOCs [58], as the name suggests, is a high-speed fusion detector system that introduces a 3D detector-cued image detector to address limited computation resources in self-driving vehicles. Frustum-PointPillars [59] explores the pillar representations and adopts an early fusion approach.

2.4. Bounding Box Regression

The success of IoU-based losses on 2D object detection networks [26,29] have widely adapted in 3D detection networks as well [43,60,61]. The shortcomings of IoU have been addressed with a variety of new variations. For instance, [62] proposed using projection area to estimate IoU directly. In this study [63], three new loss variants of IoU, such as 3D distance IoU, 3D Complete IoU, and Efficient IOU, were proposed. 3D Complete IoU estimates the distance between the box centers, and during the optimization stage of loss estimation, the partial derivative of length (l), width (w), and height (h) was considered. Efficient IOU loss calculates IoU loss, distance loss, and aspect ratio loss. However, the orientation of the boxes was not considered. Ref. [64] proposed ODIoU loss to supervise 3D detector using hard targets. Ref. [65] proposed the use of the Manhattan distance instead of the Euclidean distance for all loss equations. Ref. [66] addresses the IoU drawbacks by considering interior overlapping pixels. Ref. [17] addresses the decoupling effect by considering the orientation of the bounding boxes as an additional 4th-dimension parameter in loss estimation. To resolve this issue, ref. [17] proposed the usage of a decoupling rotation parameter to act as a 4th-dimensional parameter with a fixed side length of k. This approach strengthens the IoU loss estimation but fails to address the edge cases of inclusion, where two boxes with centers with the same aspect ratio can still have a different overlap area. Another study, ref. [67], suggested sorting the overlapping vertices by rotation angle and followed by calculating intersection area by dividing them into smaller individual triangles. However, this approach is computationally expensive since there would be numerous bounding box predictions for each object, and it affects the model convergence. Authors of this research [68] proposed the usage of IoU as a constant factor added to L1 loss to address the orientation problem.

3. Analysis on 3D IoU Losses

Given a ground truth (GT) box G = {x_g, y_g, z_g, w_g, h_g, l_g, $\theta$_g} and a prediction (Pred) box P = {x_p, y_p, z_p, w_p, h_p, l_p, $\theta$_p}, whereas, x, y, and z represent the center coordinates along the x, y, and z-axis and l, w and h indicate the length, width and height along their respective axes and $\theta$ denotes the orientation of an object.

The IoU between the boxes [69] are calculated as follows,

$$\mathrm{IoU}={\displaystyle \frac{I(P,G)}{U(P,G)}}={\displaystyle \frac{|P\cap G|}{\left|P\right|+\left|G\right|-|P\cap G|}}$$

(1)

$$L_{IoU}=1-\mathrm{IoU}(\mathrm{P},\mathrm{G})$$

(2)

However, the above IoU loss works well for axis-aligned bounding boxes. However, loss estimation for rotated bounding boxes is more complex cause the boxes can overlap and intersect differently. To address this problem, skewIoU [67] was proposed as follows,

$$\mathrm{skewIoU}={\displaystyle \frac{A_I\ast h_I}{A_G\ast h_G+A_P\ast h_P-A_I\ast h_I}}$$

(3)

In the above Equation (3), I represent the overlap/intersection area. During the loss estimation, boxes with intersection area are sorted in anticlockwise order, and  skewIoU estimates the overall IoU. However, this method also depends on intersection areas like Equation (1), which results in a high loss value of 1 in the event of two boxes located far from each other without any overlap. Sorting the vertices in an anticlockwise direction adds computation time in loss estimation.

To address the shortcomings of IoU loss, GIoU [27] was proposed as follows,

$$L_{GIoU}=1-\mathrm{IoU}+{\displaystyle \frac{|CA-U(P,G\left)\right|}{\left|CA\right|}}$$

(4)

As seen in Equation (4), $L_{GIoU}$ considers a small convex rectangle enclosing both boxes. This loss technique addresses the edge cases when the boxes are away from each other and have zero intersection area. However, when the boxes are inclusive of each other, the IoU term in Equation (4) becomes 1, and convergence slows down, affecting the gradient estimation. A new variation of GIoU called smooth GIoU was proposed to ensure stable convergence in GIoU loss. Ref. [28] introduced a smoothness parameter if GIoU loss reaches a specific threshold value ($\delta$) as shown in Equation (5).

$$\mathrm{Smooth}\left(\mathrm{GIoU}\right)=\left\{\begin{array}{cc}GIo{U}_L{}_1\left(GIoU\right),\hfill & GIoU<\delta \hfill \\ GIo{U}_L{}_2\left(GIoU\right),\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(5)

However, Equation (3) degrades to IoU in case of inclusion and cannot overcome the aspect ratio difference between the boxes. For instance, in Figure 1, the boxes are of different orientations and sizes, but their overlapping and convex areas remain constant. The loss estimation for rotated bounding boxes is more complex cause the boxes can overlap and intersect in different ways [63,67].

To address the problem of overlap and aspect ratio similarity, DIoU and CIoU losses were proposed.

$$L_{DIoU}=1-\mathrm{IoU}+{\displaystyle \frac{d^2(P,G)}{c^2}}$$

(6)

$$L_{CIoU}=1-\mathrm{IoU}+{\displaystyle \frac{d^2(P,G)}{c^2}}+\alpha \mathit{v}$$

(7)

$$v={\displaystyle \frac{4}{pi\ast pi}}{(arctan{\displaystyle \frac{w^G}{h^G}}-arctan{\displaystyle \frac{w^P}{h^P}})}^2$$

(8)

Equation (6) regresses the centers of the bounding boxes in addition to the overlap area. In the minimum rectangle containing the prediction and ground truth boxes, C represents the diagonal distance from the center of each box. This helps in convergence when the boxes are inclusive but with different centers and in cases where the boxes do not overlap. However, $L_{DIoU}$ is scale invariant. To address the scale invariance problem, $L_{CIoU}$ added a new term called $\alpha$ to address the gap in aspect ratio between the boxes. However, as seen in Equation (8), $\alpha$ considers only two aspect ratios, such as w and h. For 3D boxes, a third aspect ratio l exists, which is not utilized in $L_{CIoU}$.

To address this gap in aspect ratio and consider all geometric sides, authors of this research [63] proposed 3D EIoU loss. The representation of the loss function is as follows,

$$L_{EIo{U}_{3D}}=1-\mathrm{IoU}+{\displaystyle \frac{d^2(P,G)}{c^2}}+{\displaystyle \frac{d^2(w^P,w^G)}{c_w^2}}+{\displaystyle \frac{d^2(l^P,l^G)}{c_l^2}}+{\displaystyle \frac{d^2(h^P,h^G)}{c_h^2}}$$

(9)

In Equation (9), in addition to the estimation of the distance between the centers of the boxes, the aspect ratio of the individual sides is taken into consideration, addressing the shortcomings of $L_{DIoU}$ and $L_{CIoU}$. Since this technique does not involve the sorting operation utilized in skewIoU, the loss function’s convergence is also faster. However, the orientation of an object $\theta$ needs to be more used in loss estimation. Two boxes with the same centers and aspect ratio but different orientations can have the same loss value. This requires additional operations in the analysis of the orientation of the objects [68].

The drawbacks of existing IoU loss functions can be summarized as follows:

• Various IoU losses converge to simple IoU in cases of complete overlap of boxes, boxes with the same centers, and the same aspect ratio.
• Axis-aligned IoU losses suffer poor regression for rotated bounding boxes.
• Performance gap due to orientation of the objects.

4. Proposed IIoU Loss

Let $(x_g,y_g,z_g,l_g,w_g,h_g,{\theta }_g)$ and $(x_p,y_p,z_p,l_p,w_p,h_p,{\theta }_p)$ denote 3D ground-truth regression vector and 3D prediction branch vector. We isolated a selected ground truth box as $(x_1,y_1,z_1,l_1,w_1,h_1,{\theta }_1)$ and selected prediction box as $(x_2,y_2,z_2,l_2,w_2,h_2,{\theta }_2)$. Following the common settings [30,43], we set ${\theta }_{t1}$ = sin${\theta }_1$cos${\theta }_2$ and ${\theta }_{t2}$ = cos${\theta }_1$sin${\theta }_2$. ${\theta }_{t1}$ and ${\theta }_{t2}$ were clamped to avoid infinity values. Our proposed IIoU loss has two portions: IoU loss and center loss.

Following the initial settings, IoU values are calculated as follows:

$$I=F(x_1,x_2,l_1,l_2)+F(y_1,y_2,w_1,w_2)+F(z_1,z_2,h_1,h_2)$$

whereas,

$$F(a,a^{\prime },b,b^{\prime })=min(\frac{a+b}{2},\frac{a^{\prime }+b^{\prime }}{2})-max(\frac{a-b}{2},\frac{a^{\prime }-b^{\prime }}{2})$$

(10)

The min and max functionality estimates the intersection area between the two boxes in 3D space, and the overall IoU of two 3D boxes are calculated in (11).

$$U=l_1\ast w_1\ast h_1+l_2\ast w_2\ast h_2-I$$

$$\mathrm{IoU}=I/U$$

(11)

The diagonal length of the minimum convex rectangle enclosing the ground truth and prediction boxes is calculated as follows:

$$Diagonal=F^{\prime }(x_1,x_2,l_1,l_2)+F^{\prime }(y_1,y_2,w_1,w_2)+F^{\prime }(z_1,z_2,h_1,h_2)+F^{\prime }({\theta }_1,{\theta }_2,K,k)$$

(12)

$$F^{\prime }(a,a^{\prime },b,b^{\prime })=(max(\frac{a-b}{2},\frac{a^{\prime }-b^{\prime }}{2})-min(\frac{a+b}{2},\frac{a^{\prime }+b^{\prime }}{2}))$$

(13)

The K value is a hyperparameter since we consider orientation as an additional dimension in distance loss estimation. Estimating intersection area and diagonal distance are adapted from [27] but modified to include all the dimensions for 3D space. Our proposed loss IIoU estimates the Euclidean distance between x, y, and z centers individually to estimate the center loss. The center coordinate of each axis, along with the minimum and maximum edges, are utilized as follows,

$$d^2\left(C{D}_x\right)={(x_1^{cc}-x_2^{cc})}^2+{(y_1^{min}-y_2^{min})}^2+{(z_1^{min}-z_2^{min})}^2+{({\theta }_1^{min}-{\theta }_2^{min})}^2$$

(14)

In the above Equation (14), the Euclidean distance between x centers is calculated. Similarly, we can estimate the Euclidean distance for y and z centers  (line 10 in Algorithm 1). Once the center distance is calculated, the diagonal length is a denominator to minimize the distance between two boxes. The IIoU can be obtained at  line 12 in Algorithm 1.

This approach has a few advantages when compared to traditional IoU losses. Rotation as an additional dimensional parameter simplifies loss calculation when the boxes are not aligned/rotated. For instance, when the boxes are a little tilted, and two axes coincide, Euclidean distance estimation of rotation and other third axis aids in effective loss estimation. Secondly, when the boxes have different orientations but have the same centers, existing losses fail as they are heavily dependent on the centers. Previous studies [26] show that two boxes with the same centers can still have different dimensions. The same observation can be made regarding aspect ratios. All the bounding box parameters in our proposed loss equation are completely differentiable and can be trained on GPU with gradient-based back-propagation. Our Algorithm 1 presents sequential steps carried out in loss estimation.

Algorithm 1 Improved intersection over union loss estimation.

Input:  $B^g$ = $(x_g,y_g,z_g,l_g,w_g,h_g,{\theta }_g)$, $B^p$ = $(x_p,y_p,z_p,l_p,w_p,h_p,{\theta }_p)$. Output:  $L_{IIoU}.$ 1: ▹ IoU calculation: 2: U = $A^g$ + $A^p$ = ($l_g\ast w_g\ast h_g$) + ($l_p\ast w_p\ast h_p$) 3: I = F$(x_g,x_p,l_g,l_p)$ + F$(y_g,y_p,w_g,w_p)$ + F$(z_g,z_p,h_g,h_p)$ 4: ▹ F$(a,a^{\prime },b,b^{\prime })$ = min( $\frac{a+b}{2}$,$\frac{a^{\prime }+b^{\prime }}{2}$) − max( $\frac{a-b}{2}$,$\frac{a^{\prime }-b^{\prime }}{2}$) 5: IoU = I/(U − I ) 6: ▹ Distance Estimation: 7: Diagonal = F’$(x_g,x_p,l_g,l_p)$ + F’$(y_g,y_p,w_g,w_p)$ + F’$(z_g,z_p,h_g,h_p)$ + F’$({\theta }_g,{\theta }_p,c_g,c_p)$ 8: ▹ F’$(a,a^{\prime },b,b^{\prime })$ = (max( $\frac{a-b}{2}$,$\frac{a^{\prime }-b^{\prime }}{2}$) − min( $\frac{a+b}{2}$,$\frac{a^{\prime }+b^{\prime }}{2}$))** 2 9: Distance Estimation = $\frac{Distance\_bt\_centres}{Diagonal}$ 10: $Distance\_bt\_centres=d^2\left(C{D}_x\right)+d^2\left(C{D}_y\right)+d^2\left(C{D}_z\right)$ 11: ▹$d^2\left(C{D}_x\right)={(x_g^{cc}-x_p^{cc})}^2+{(y_g^{min}-y_p^{min})}^2+{(z_g^{min}-z_p^{min})}^2+{({\theta }_g^{min}-{\theta }_p^{min})}^2$ 12: $IIoU=\mathrm{IoU}-\frac{Distance\_bt\_centres}{Diagonal}$ 13: return $IIoU$

5. Simulation Experiment

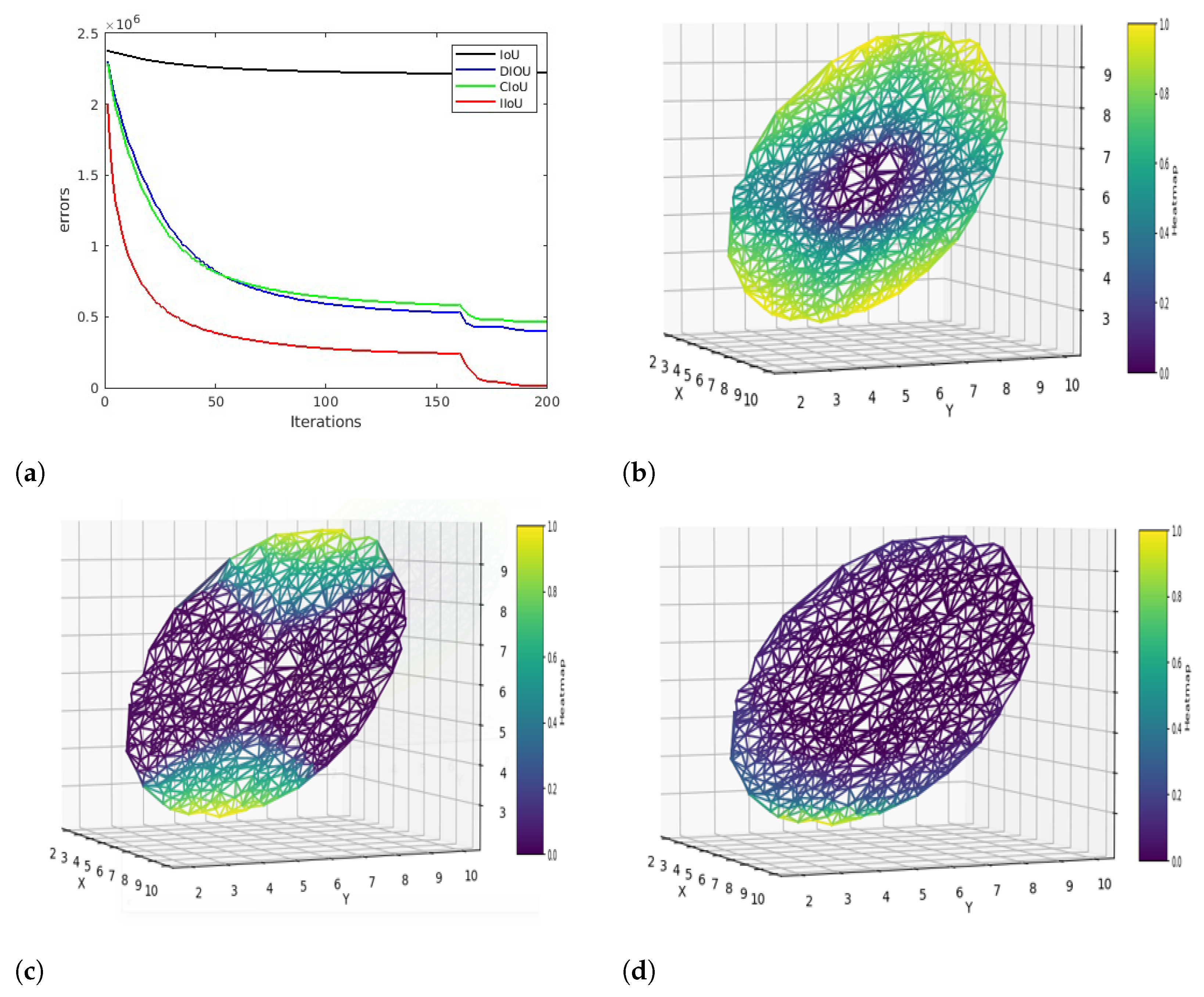
A simulation experiment was conducted to evaluate the performance of the proposed IIoU loss function against the above-explained loss functions. When preparing a synthetic dataset, aspect ratio, scale, and distance between bounding boxes were considered. Seven 3D ground truths centered at (6, 6, 6) were generated with several aspect ratios such as 1:1:1, 0.66:1:1, 1:0.66:1, 1:1:0.66, 2.5:1:1, 1;2.5:1, 1:1:2.5. 3D anchor boxes were uniformly distributed at 1000 points in a circular region with a radius of 4 and a center at (6, 6, 6). A range of 3D anchor boxes were chosen to accommodate overlapping and non-overlapping cases. These volumes are 0.5, 0.67, 0.75, 1, 1.33, 1.5 and 2. For any given point and scale, 3D anchor boxes with the same aspect ratios 1:1:1, 0.66:1;1, 1:0.66:1, 1:1:0.66, 2.5:1;1, 1;2.5:1, 1:1:2.5 were provided. This approach would generate 49,000 (1000 × 7 × 7) anchor boxes for each ground truth box. Since we have seven ground truth boxes, the total number of regression cases will equal 343,000 (1000 × 7 × 7 × 7).

For each case, we simulated bounding box regression using gradient descent Algorithm  2 as follows,

$$B_{n,s}^t=B_{n,s}^{t-1}+\alpha (2-Io{U}_{n,s}^{t-1})\nabla B_{n,s}^t$$

(15)

$B_{n,s}^t$ and $\nabla B_{n,s}^t$ indicate anchor box at iteration t and gradient loss to the same anchor box at iteration t − 1 with a learning rate of $\eta$. For accelerating the convergence of network, we multiply the gradient loss by $2-Io{U}_{n,s}^{t-1}$

At the end of 200th iteration, cumulative loss values of $L_{IoU}$, $L_{DIoU}$, $L_{DIoU}$ and $L_{IIoU}$ are reported as follows: 4.5 × 10${}^8$, 1.51 × 10${}^8$, 1.55 × 10${}^8$, 6.9 × 10${}^7$. $L_{IIoU}$ has the lowest error rate and a better convergence speed, as shown in Figure 2a. Figure 2b–d represents the distribution of regression errors across the x, y, and z axes with a heat map. $L_{IoU}$ suffers a higher error rate throughout the iterations due to inclusions and non-overlapping scenarios. In Figure 2c, we can observe that $L_{DIoU}$ performs better than $L_{IoU}$ but has a higher error rate at the edges. This could be due to a special case of inclusion where the centers of the boxes align, or they have similar aspect ratios. Similarly, we can observe the improved performance of proposed IoU loss, $L_{IIoU}$ from Figure 2d. The proposed loss function was able to regress the boxes more efficiently across all the cases of inclusions, boxes with the same centers, and similar aspect ratios.

Algorithm 2 Simulation experiment on synthetic data.

Input:  ${\left\{{\left\{B_{n,s}\right\}}_{s=1}^S\right\}}_{n=1}^N$ indicates anchor boxes at 1000 points (N) centered at (6, 6, 6) and scattered in a circular space with a radius of 4. S = $7\times 7$ covering 7 different scales and aspect ratios of the anchor boxes. ${\left\{B_i^{gt}\right\}}_{i=1}^7$ is the set of ground truth boxes with center (6, 6, 6) and 7 aspect ratios. $\eta$ corresponds to learning rate. Output:  Regression error $RE\in R^T$ is calculated for each iteration and 200 scattered points.  1: Initiate $RE=0$ and iteration limit of 343,000 (T).  2: for $t=1\to T$ do  3:      for $n=1\to N$ do  4:          for $s=1\to 7$ do  5:             for  $i=1\to 7$ do  6:                 if $\eta \le 80\%T$ then $\alpha =0.1$  7:                 else if $\eta \le 90\%T$ then $\alpha =0.01$  8:                 else $\eta =0.001$  9:                 end if 10:                 $\nabla B_{n,s}^t=\partial L(B_{n,s}^{t-1},B_i^{gt})/\partial B_{n,s}^{t-1}$ 11:                 $B_{n,s}^t=B_{n,s}^{t-1}$ + $\eta (2-Io{U}_{n,s}^{t-1}$) $\nabla B_{n,s}^t$ 12:                 $RE\left(t\right)=RE\left(t\right)+|B_{n,s}^t-B_i^{gt}|$ 13:              end for 14:           end for 15:       end for 16:  end for 17:  return RE

6. Experiments

In this section, we evaluate the performance of our proposed IIoU loss function against other loss functions on the KITTI [14] dataset. We also observe the convergence of different loss functions regarding localization and overall training loss.

6.1. Training Networks

To test the performance of the proposed IIoU in different settings, following the previous studies [17,43,46,67], LiDAR-based and LiDAR-Camera fusion detection networks were experimented with. The conducted experiments were based on OpenPCDet [70].

LiDAR detection network A two-stage detection network, as well as a single-stage detection network, was tested. A single-stage network utilizes a voxel-based 3D backbone structure to convert initial voxel features to feature volumes. The detection layers consist of transformers and 2D convolutions stacked (CT-Stack). The network was trained with Adam optimizer, with a learning rate of 0.00035 and a learning decay of 0.1. We adopted multi-GPU training with a batch size of 4 for 120 epochs. PointPillars is a two-stage network consisting of a voxelization stage and a pillar-based detection stage. PointPillars converts point clouds into voxels and further transforms them into pillars. Using Tesla V100 GPUs, the network was trained with batch size 16 for 40 epochs.

Fusion detection network consists of a 3D point cloud and a 2D image branch as backbone structures, allowing point-to-pixel propagation and the backpropagated gradients from the 2D image branch strengthen the 3D LiDAR branch. Adam optimizer with a learning rate of 0.003 and batch size of 4 was adapted during network training. This network was trained on NVIDIA Tesla P100 GPUs.

6.2. Dataset

To evaluate the performance of the proposed loss function in 3D object detectors, we utilized popular autonomous driving datasets such as KITTI and nuScenes.

6.2.1. KITTI

KITTI [14] dataset consists of 3D point cloud data and RGB images. During the pre-processing, following the existing studies [70], the raw point clouds are clipped into (0, 70.4) m, (−40, 40) m, (−3, 1) m for X, Y, and Z axis ranges with voxel size (0.05, 0.05, 0.1) m, respectively. The training dataset was split into 3712 and 3768 samples for training and validation. Three significant classes in the KITTI dataset, such as car, pedestrian, and cyclist, were focused on. Performance is evaluated in terms of Average Precision (AP) for various IoU thresholds, such as 0.5 and 0.75. 0.5 and 0.75 represent 50% and 75% overlap of detection with ground truth.

6.2.2. nuScenes

The nuScenes [71] dataset contains about 1000 driving sequences, with 700 for training, 150 for validation, and 150 for testing. In this research, we utilized the bicycle class of the nuScenes dataset. Following [70], the dataset is prepossessed with the point cloud range set as (−51.2, 51.2) m for the X and Y axes and (−5, 3) m for the z-axis. The performance of the 3D networks was reported in terms of nuScenes detection score (NDS), Absolute Translation Error (ATE), Angular Scale Error (ASE), Area Orientation Error (AOE), and Average Attribute Error (AAE).

7. Evaluation

The performance of the proposed IIoU was evaluated on both the LiDAR-based detection network and the fusion detector network. Due to testing constraints in the KITTI benchmark test set [14], performance evaluation was carried out on the KITTI val dataset. Three classes of the KITTI dataset, such as 3D car, pedestrian, and cyclist, were evaluated with different IoU thresholds, 0.7, 0.5, and 0.5. The testing thresholds were adapted from previous studies [38,40,43]. The results are displayed in average precision (AP) and mean average precision (mAP), a cumulative average of different APs. This section calculates the relative improvement (R.L.) to IoU loss. The highest prediction result in each category is highlighted in bold.

Table 1. Experimental evaluation of Camera-Fusion 3D detector network trained using $L_{IoU}$, $L_{DIoU}$, and $L_{IIoU}$ losses. Results are reported on the KITTI val dataset.

Loss	3D Car (IoU = 0.7)	3D Pedestrian (IoU = 0.5)	3D Cyclist (IoU = 0.5)	mAP
	Easy Mod Hard	Easy Mod Hard	Easy Mod Hard
$L_{IoU}$	89.20 79.08 77.6	65.75 59.87 56.32	86.22 66.32 63.17	71.50
$L_{DIoU}$	89.20 78.97 77.71	66.56 60.86 57.00	86.27 66.55 64.16	71.92
$L_{IIOU}$	89.20 79.02 77.93	64.54 59.11 55.60	86.64 67.66 65.36	71.67

displays the improved performance of IIoU against IoU and DIoU losses in a 3D fusion network. The initial analysis phase revealed a performance gap between networks trained from scratch and pre-trained model weights [17,46,70]. To conduct a fair evaluation, we trained all the networks from scratch. All the training parameters, including the hyper-parameters, training, and testing environments, were kept constant during the network training and evaluation phase. Table 1 shows that the proposed IIoU performs well for all easy, moderate, and hard categories of the 3D cyclist class. We can observe an R.L. of 3.4% in the hard class.

Table 2. Experimental evaluation of Camera-Fusion 3D detector network trained using $L_{IoU}$, $L_{DIoU}$, and $L_{IIoU}$ losses. AP_40 results are reported on the KITTI val dataset.

Loss	3D Car (IoU = 0.7)	3D Pedestrian (IoU = 0.5)	3D Cyclist (IoU = 0.5)	mAP
	Easy Mod Hard	Easy Mod Hard	Easy Mod Hard
$L_{IoU}$	92.01 82.84 78.01	66.43 59.55 54.62	89.13 66.91 62.31	72.42
$L_{DIoU}$	91.99 82.81 78.01	66.51 60.24 55.15	89.10 67.92 63.75	72.83
$L_{IIOU}$	92.18 82.84 79.80	64.02 58.57 53.67	89.77 69.43 66.06	72.93

measures the A.P. at 40 sampling recall positions. IIoU performs significantly better than IoU and DIoU in the 3D car and cyclist classes. The hard category of the 3D car class shows an R.L. of 2.29%. 3D cyclist shows a R.L. of 0.71%, 3.76%, 6.01% demonstrating a significant performance change for smaller objects. In both Table 1 and Table 2, the 3D cyclist class attains the best performance for the proposed loss function.

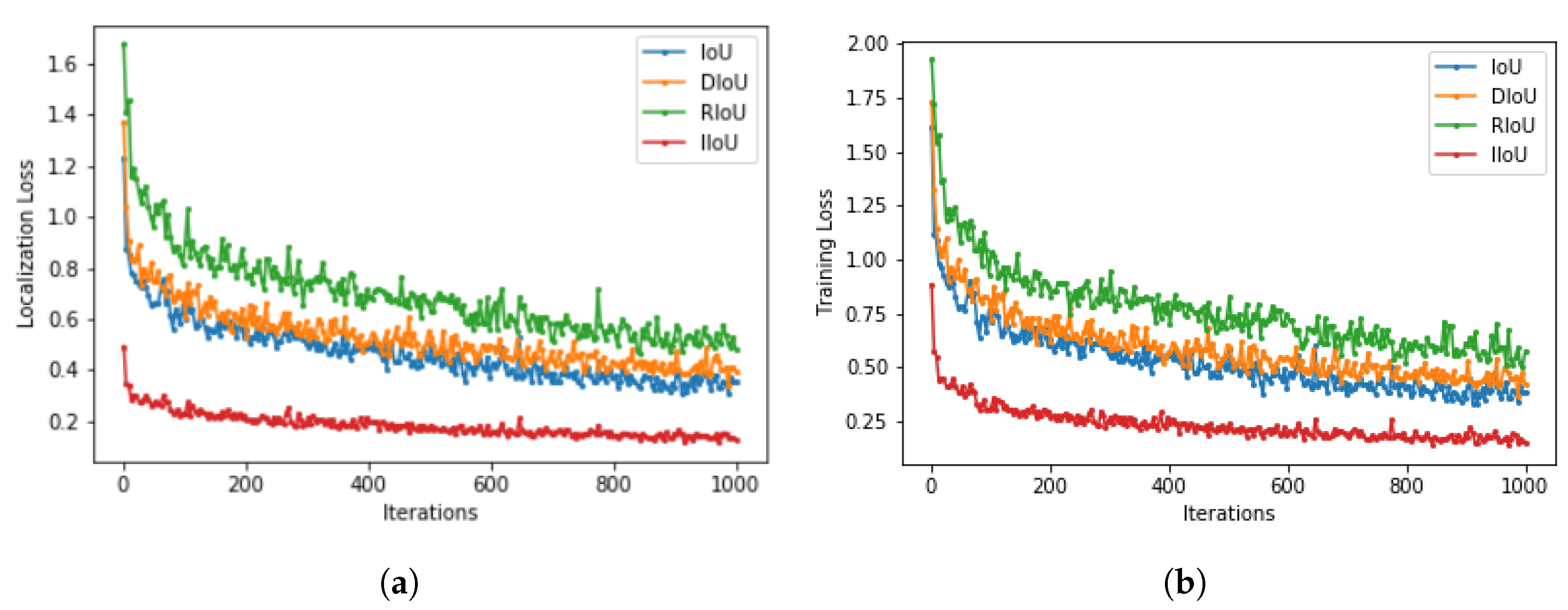
Figure 3 displays the loss convergence of IoU, DIoU, RIoU, and proposed IIoU loss. Figure 3a represents the localization loss estimation at each iteration step. IoU and DIoU almost converge at the same rate. However, the proposed IIoU loss converges much faster and minimizes the loss values. Figure 3b showcases overall training loss. This sums up both classification and localization loss. Better convergence is observed at the proposed IIoU loss compared to IoU, DIoU, and RIoU losses.

Table 3. Experimental evaluation of single stage LiDAR 3D detector network trained using $L_{IoU}$, $L_{DIoU}$, $L_{RIoU}$ and $L_{IIoU}$ losses. Results are reported on the KITTI val dataset.

Loss	3D Car (IoU = 0.7)	3D Pedestrian (IoU = 0.5)	3D Cyclist (IoU = 0.5)	mAP
	Easy Mod Hard	Easy Mod Hard	Easy Mod Hard
$L_{IoU}$	69.96 62.55 62.43	49.96 45.78 43.56	69.51 56.55 52.16	56.94
$L_{DIoU}$	73.65 64.63 64.16	55.35 52.76 48.24	73.43 60.44 55.20	60.87
$L_{RIoU}$	87.6 77.71 76.8	58.45 52.71 47.3	81.22 67.57 62.34	67.96
$L_{IIOU}$	87.39 77.01 75.78	59.99 54.22 48.63	83.56 64.69 63.52	76.27

displays the improved performance of IIoU against IoU, DIoU, and RIoU losses in the 3D LiDAR detection network. The table shows that the DIoU loss performs well across all categories compared to the IoU loss. This is because DIoU loss considers center distance estimation and aids in better localization. However, RIoU loss shows consistent improvement compared to DIoU loss. Our proposed IIoU loss attains higher results in the 3D pedestrian class with an R.L. of 20%, 18.43%, and 11.63%. IIoU loss has the highest mAP of 76.27 when compared to its counterparts.

Table 4. Experimental evaluation of single-stage LiDAR 3D detector network trained using $L_{IoU}$ and $L_{IIoU}$ losses. Results are reported on the nuScenes val dataset.

Loss	NDS	ATE	ASE	AOE	AAE
$L_{IoU}$	0.0244	0.447	0.320	0.964	0.166
$L_{IIoU}$	0.0295	0.324	0.344	0.687	0.186

and

Table 5. Experimental evaluation of two-stage LiDAR 3D detector network trained using $L_{IoU}$ and $L_{IIoU}$ losses. Results are reported on the nuScenes val dataset.

Loss	NDS	ATE	ASE	AOE	AAE
$L_{IoU}$	0.0263	0.219	0.307	0.777	0.312
$L_{IIoU}$	0.0348	0.180	0.274	0.370	0.287

demonstrate the performance of the proposed loss function against IoU loss. NDS is a consolidated metric that captures metrics such as IoU, box location, size, and orientation. As we can observe, the NDS score of the proposed method has improved in both single-stage and two-stage LIDAR networks. Area Orientation Error (AOE) measures the difference in yaw angles between the ground truth and predictions, and ATE measures the Euclidean distance between the centers in 2D. A low AOE and ATE error from the proposed method indicates the network could regress the boxes more accurately. The classification accuracy is measured by AAE, which has improved in the two-stage LIDAR network.

For the next phase of evaluation and to compare our proposed method with other state-of-the-art detectors, the fusion network was trained with the proposed loss function using the KITTI train+val dataset. The total number of training samples was 7480. No additional data split and data augmentation were carried out. The train settings were kept constant throughout the execution across Table 1, Table 2 and Table 3 and

Table 6. Performance evaluation with state-of-the-art detection networks for 3D pedestrian class on KITTI test benchmark set.

Method	Network Type	3D Pedestrian (IoU = 0.5)
		Easy Mod Hard
Point-GNN [45]	LiDAR	51.92 43.77 40.14
Part-A${}^2$ [52]	LiDAR	53.10 43.35 40.06
ine PointPillars [40]	LiDAR	51.45 41.92 38.89
F-ConvNet [41]	LiDAR	52.16 43.38 38.80
MGAF-3DSSD [42]	LiDAR	50.65 43.09 39.65
PFF3D [55]	Camera + LiDAR	43.93 36.07 32.86
AVOD-FPN [56]	Camera + LiDAR	50.46 42.27 39.04
PointPainting [57]	Camera + LiDAR	50.32 40.97 37.84
Fast-CLOCs [58]	Camera + LiDAR	52.10 42.72 39.08
Frustum-PointPillars [59]	Camera + LiDAR	51.22 42.89 39.28
Ours	Camera + LiDAR	53.62 44.42 40.40

. Table 6 provides the evaluation results for the 3D pedestrian class across easy, moderate, and hard categories in the test set. Our proposed loss method achieves optimal performance in easy and hard categories, surpassing many state-of-the-art detectors such as PointGNN [45], Frustum-PointPillars [40] and Part-$A^2$ [52].

Discussion and Limitations: Machine learning, especially deep learning, has shown significant promise in feature extraction and pattern recognition, which could complement our geometric approach. For instance, integrating deep learning-based feature extraction with our IIoU loss could enhance the model’s ability to discern subtle variations in object orientation and position, leading to more accurate predictions. This integration could be in the form of a hybrid model where deep learned features inform the geometric bounding box adjustments, creating a synergy between abstract feature representation and concrete geometric calculation.

Recent research related to deep learning-based object detection comprehensively covered in paper [72], and the advancements in ML-based geometric analysis as discussed by [73], there is a growing trend towards combining geometric computations with ML methodologies for improved performance in spatial understanding tasks. Adopting a similar approach, we propose to extend our IIoU loss framework by incorporating ML elements, such as polynomial fitting or parametric regression models, to refine the bounding box parameters based on learned spatial features. This not only retains the intuitive clarity of our current geometric approach but also leverages the robustness of ML in handling complex patterns. Furthermore, to address the aspect of error control strategies in bounding box estimation, future work can be undertaken to integrate an error feedback mechanism into the algorithm proposed in this paper. This mechanism will utilize ML-based error estimation to adjust the bounding box parameters dynamically, ensuring a more precise and reliable detection outcome. By doing so, the gap between geometric intuitiveness and ML’s adaptive robustness can be addressed, thus enhancing the overall efficacy of our method in 3D object detection tasks.

8. Conclusions

In this research, we analyzed the current challenges in the performance of 3D detection networks regarding bounding box regression and classification problems. A literature study investigated the current trends in developing 3D object detectors. We analyzed the shortcomings of applying axis-aligned IoU losses to rotated bounding boxes. We studied that IoU losses and their variants suffer drawbacks in edge cases of inclusion and objects with the same centers and aspect ratio, affecting the network convergence. To address this issue, we proposed an efficient IIoU loss function that estimates the center distance of the x, y, and z axes individually while considering orientation as a 4th-dimensional parameter. We also carried out a simulation experiment to observe the convergence of loss functions using a synthetic data and loss convergence during the network training phase. Then, the performance of the proposed loss function was explored on the KITTI and nuScenes val datasets using Camera-LiDAR fusion and LiDAR-based 3D networks. Our proposed loss function performs better compared to its counterparts. Performance evaluation was also carried out in the KITTI test set to demonstrate the optimal performance of our approach compared to other state-of-the-art methods. This approach can also be extended to multi-object tracking and object segmentation applications.