A Novel NODE Approach Combined with LSTM for Short-Term Electricity Load Forecasting
Abstract
1. Introduction
- Challenge 1: Insensitivity to the dynamic change of inputs. In LSTM and its variants, time series are input into the discrete LSTM unit in chronological order. Discrete LSTM unit causes LSTM and its variant to be insensitive to the change of inputs and they cannot learn dynamically.However, in real datasets, the input signals constantly change in a nonperiodic manner. This difference in continuity significantly lowers the forecasting accuracy of the LSTM and its variants.
- Challenge 2: Ignores the internal nonperiodic rules of series. Due to the discrete observation interval, LSTM and its variants cannot observe series information on missing observation intervals. However, fine-grained temporal information and internal nonperiodic series interrelationship can be hidden between missing observation intervals, therefore missing the internal nonperiodic rules of series, causing higher forecasting numerical errors.
2. Related Work
2.1. Statistical Method
2.2. Machine Learning Method
2.3. Deep Learning Method
- Saves computing consumption. NODE does not store any intermediate quantities of the forward pass. Therefore, NODE has constant memory cost.
- Highly dynamic and flexible. Due to continuous observation interval, NODE removes hysteresis of LSTM-based models. Thus, the NODE-based model dynamically adapts to drastic change of series to reduce the forecasting error.
- Captures complex nonperiodic patterns. Through learning the law of internal evolution equation, NODE can extrapolate input series to approach expected target series in latent space. In this way, NODE builds continuous temporal connection of time series to capture complex nonperiodic patterns.
3. Background Knowledge
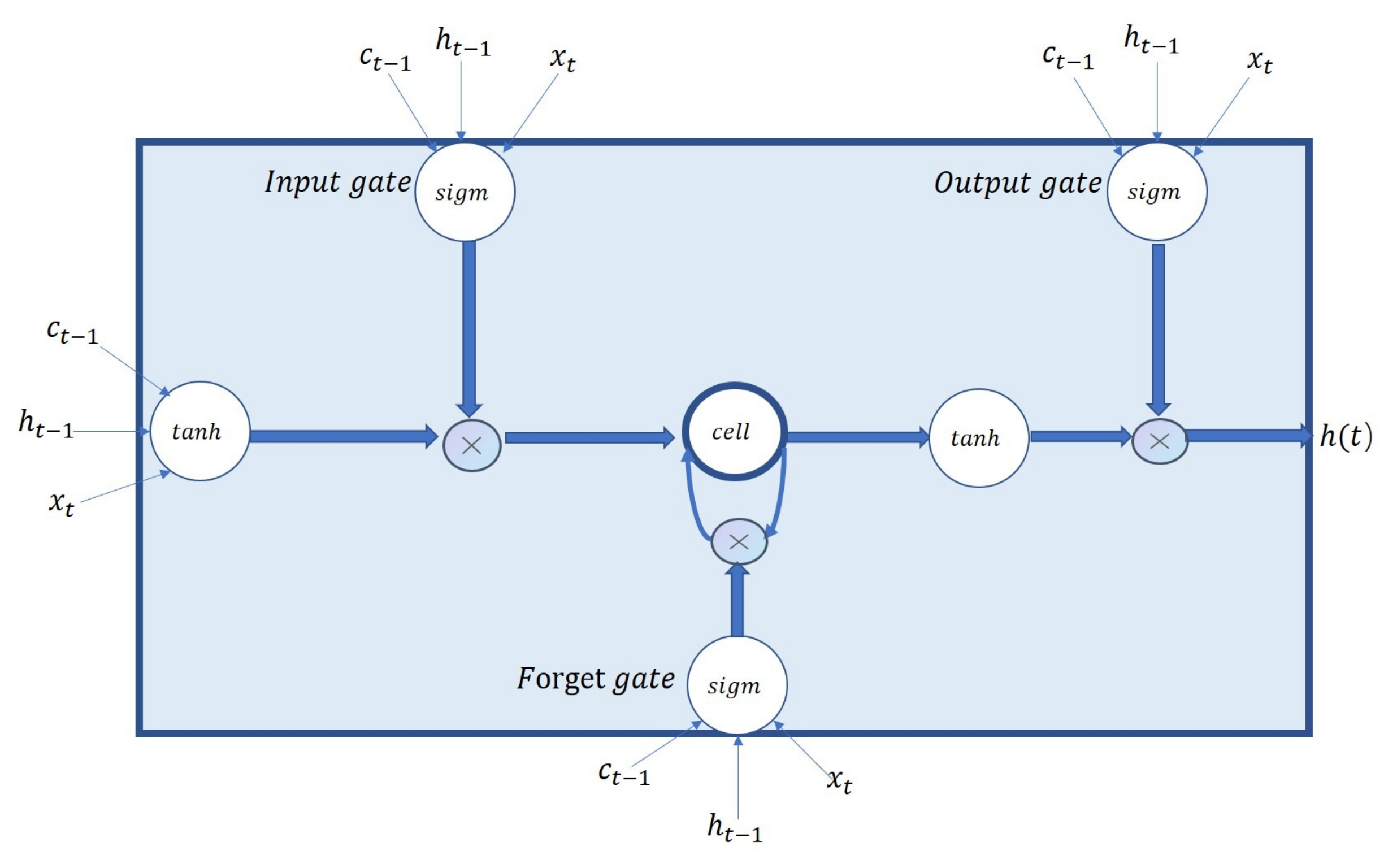
3.1. LSTM
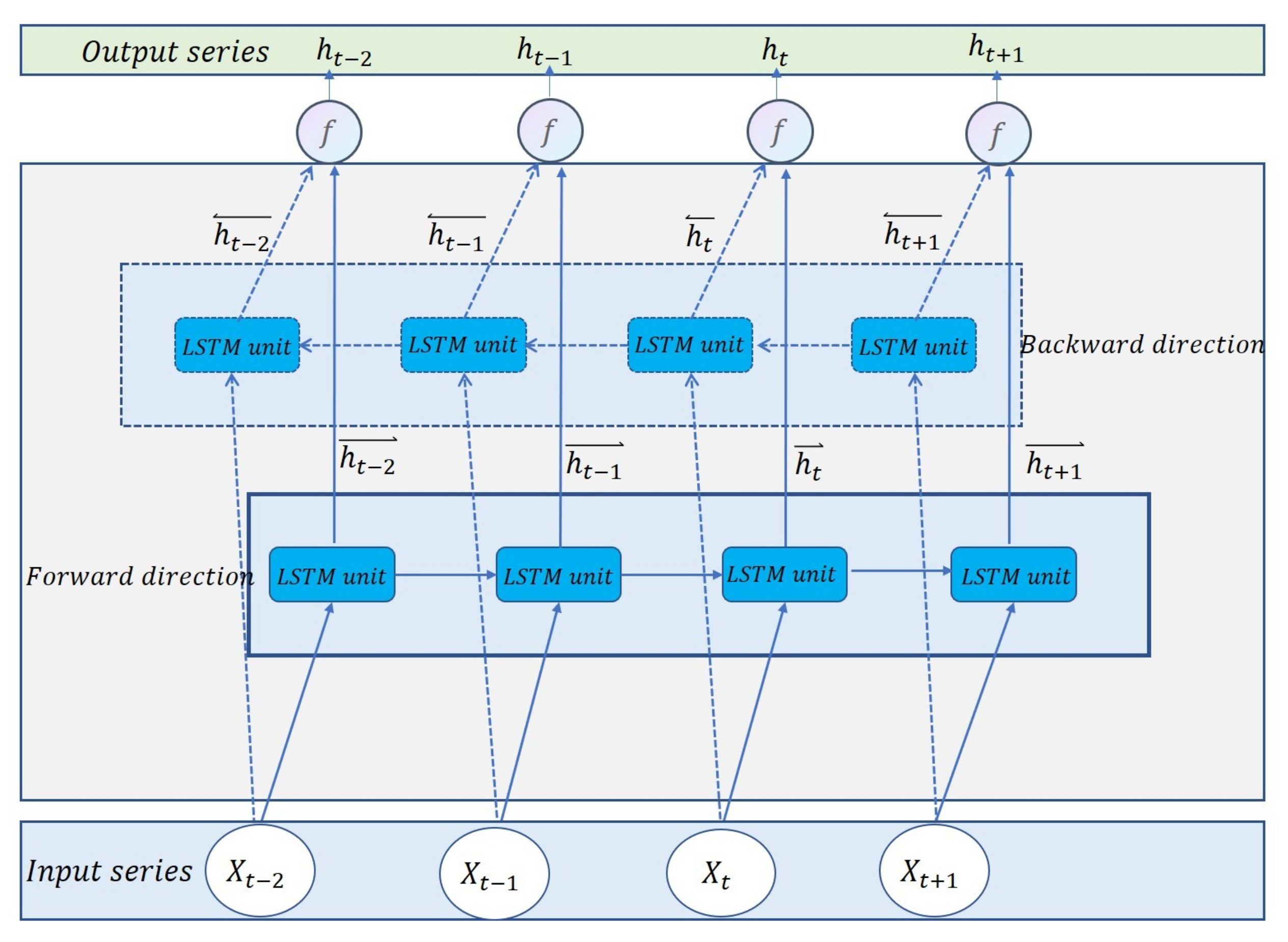
3.2. Bidirection LSTM
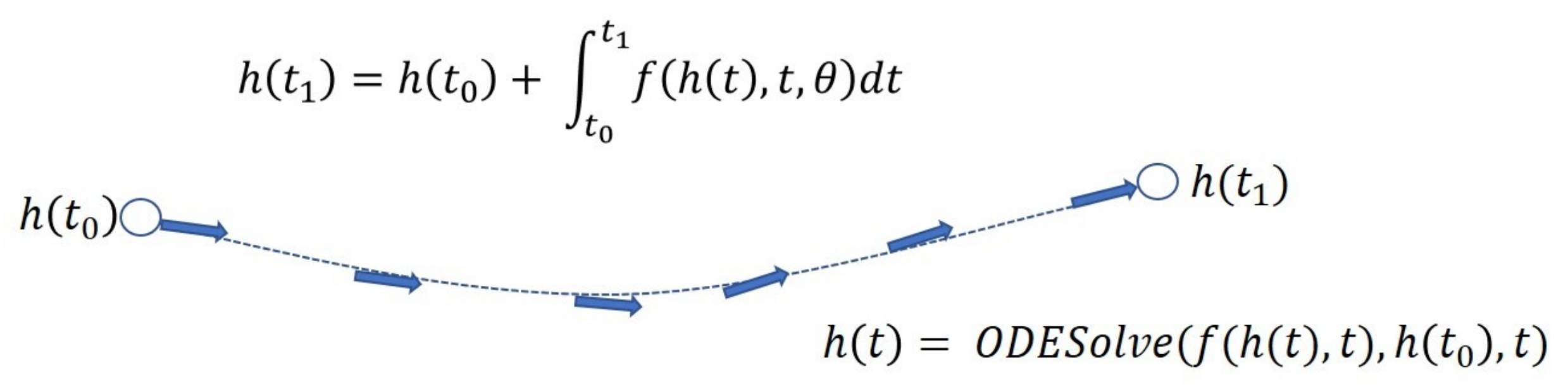
3.3. NODE
4. Data and Methodology
4.1. Data Source and Data Preprocessing
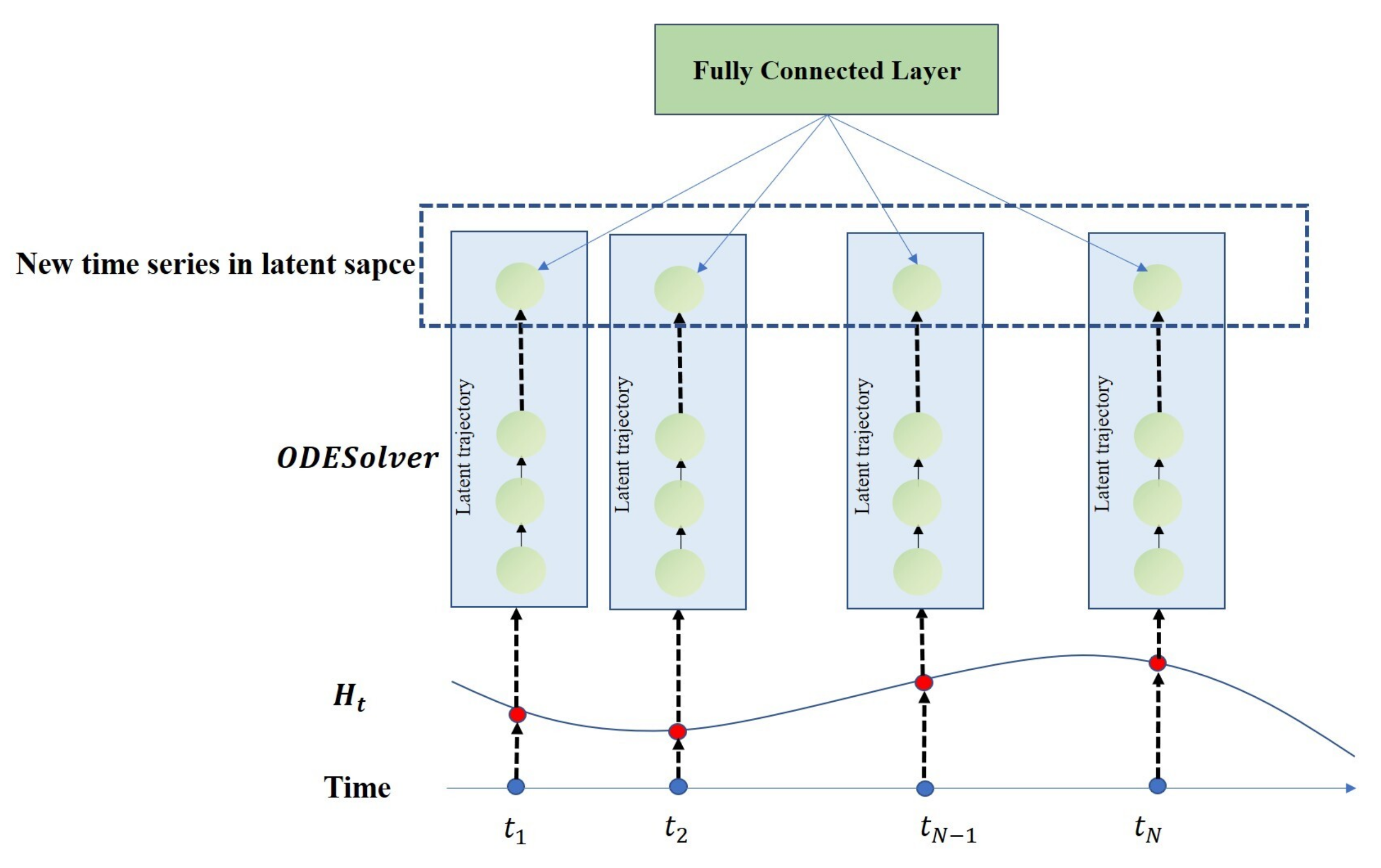
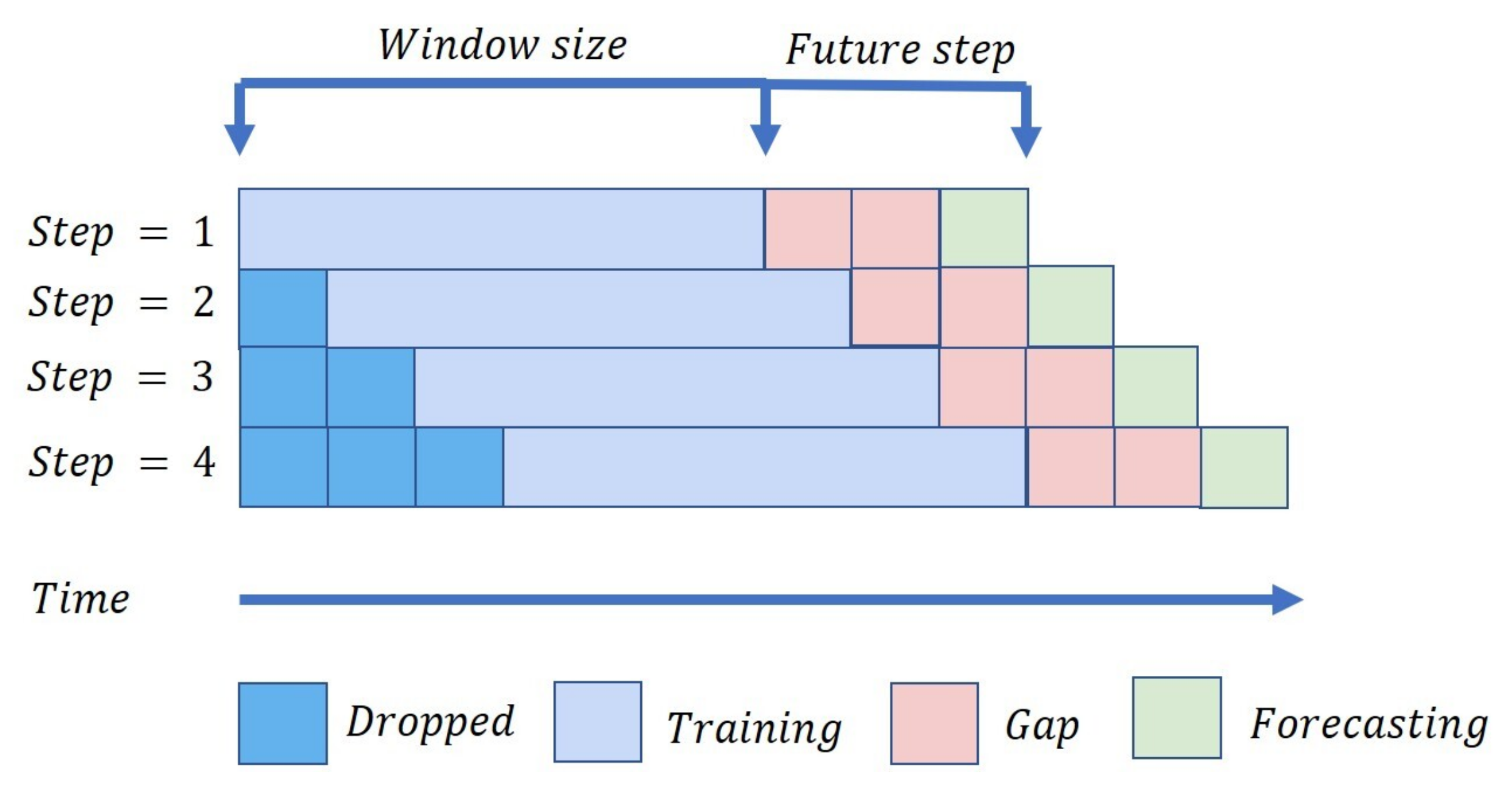
4.2. Forecasting Modeling Method
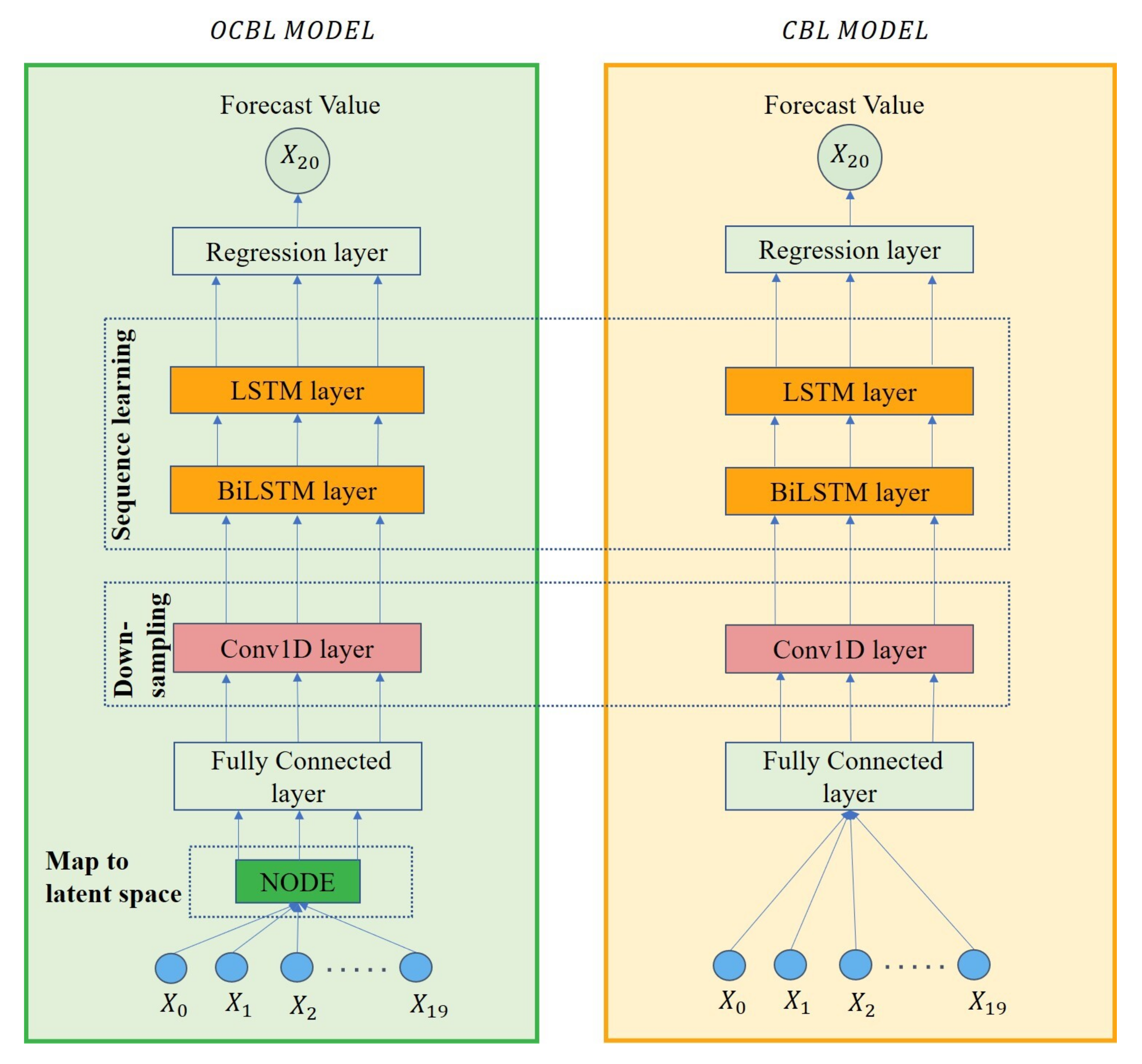
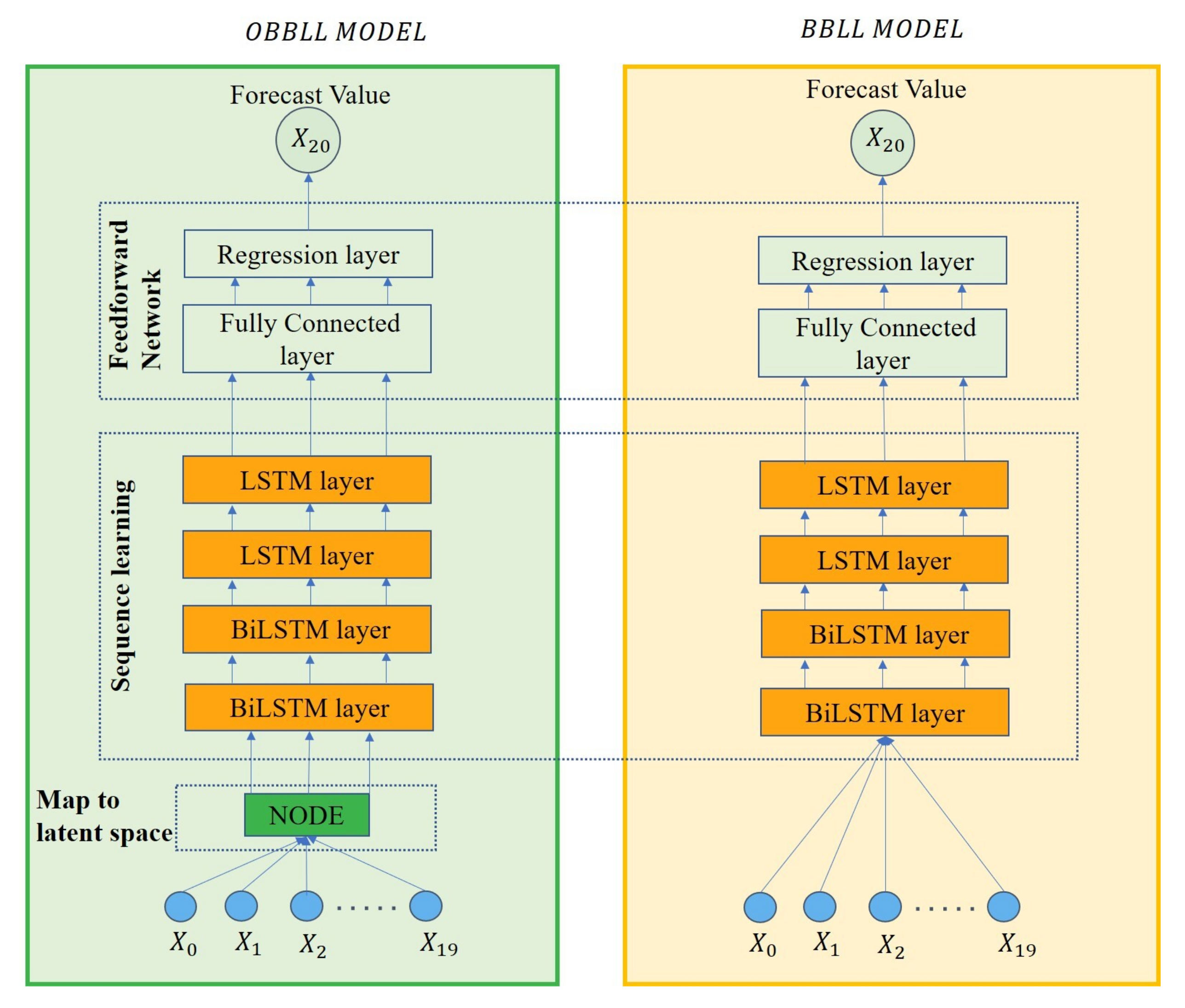
4.3. Forecasting Models
4.4. Model Settings
5. Experimental Results and Analysis
5.1. Comparing Metric
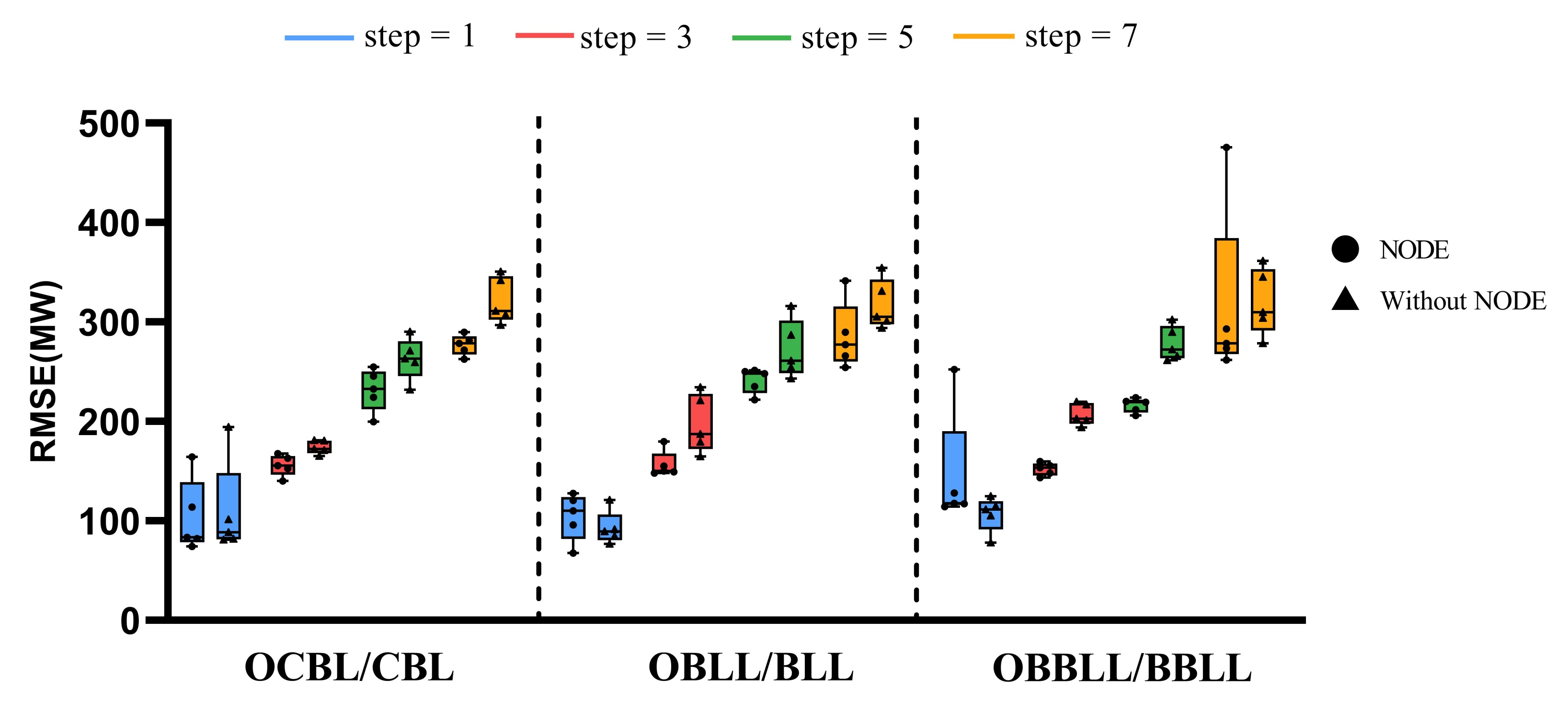
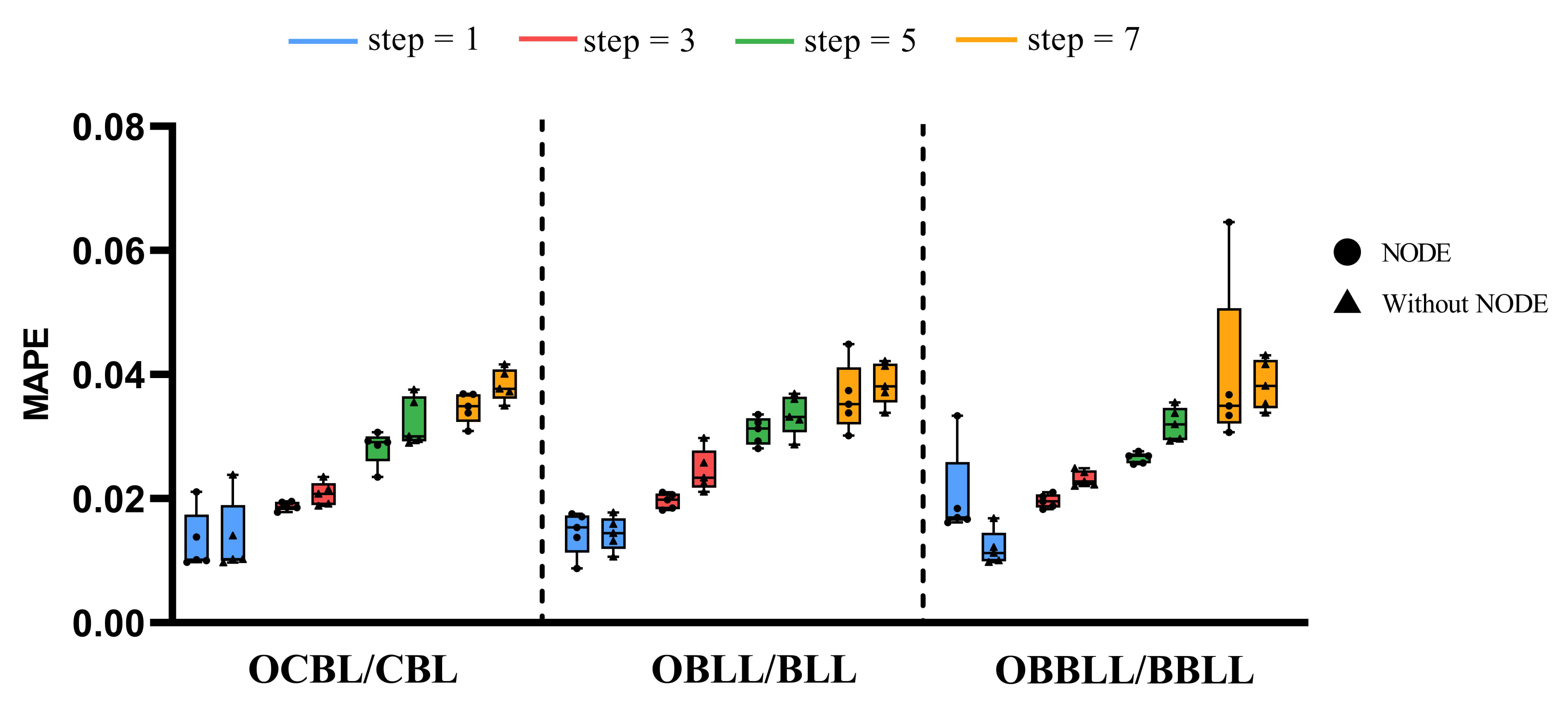
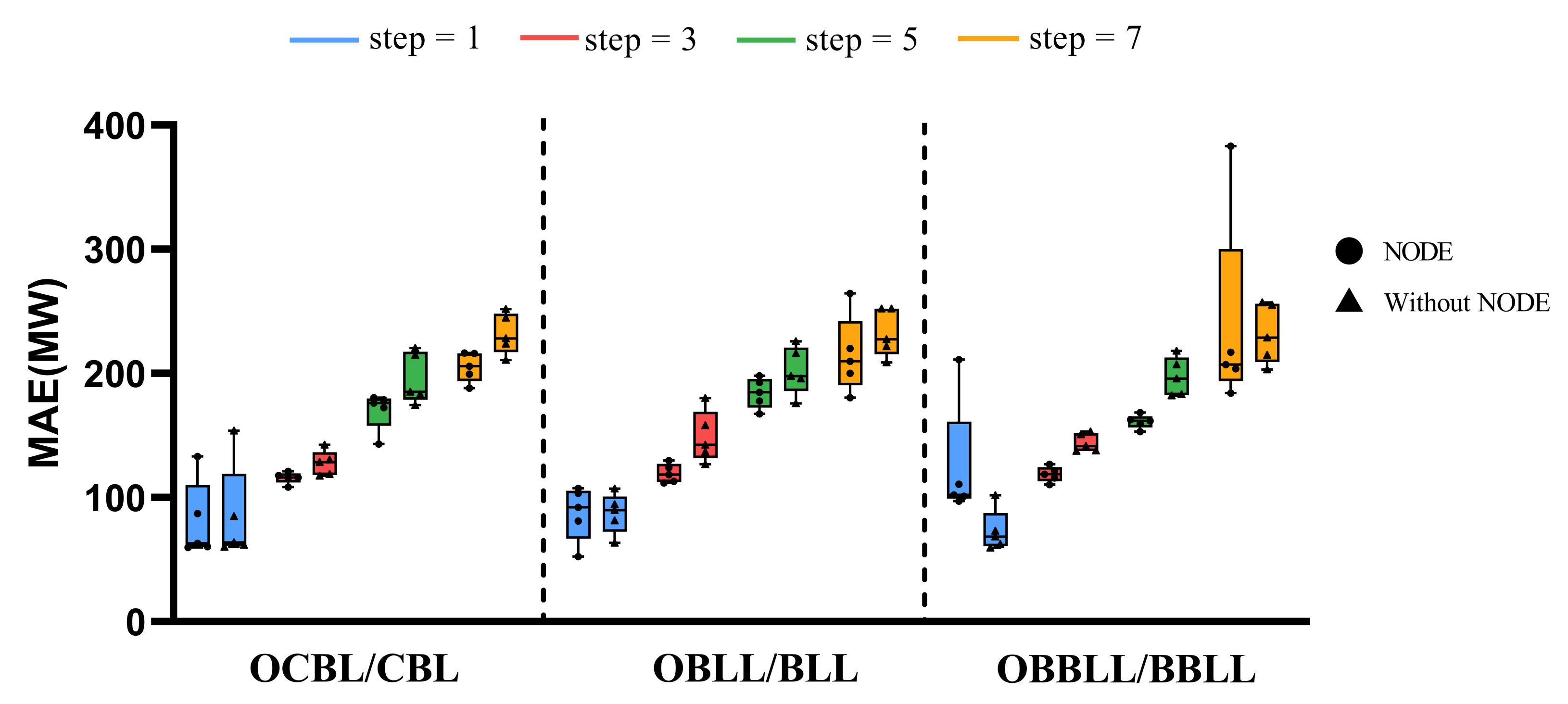
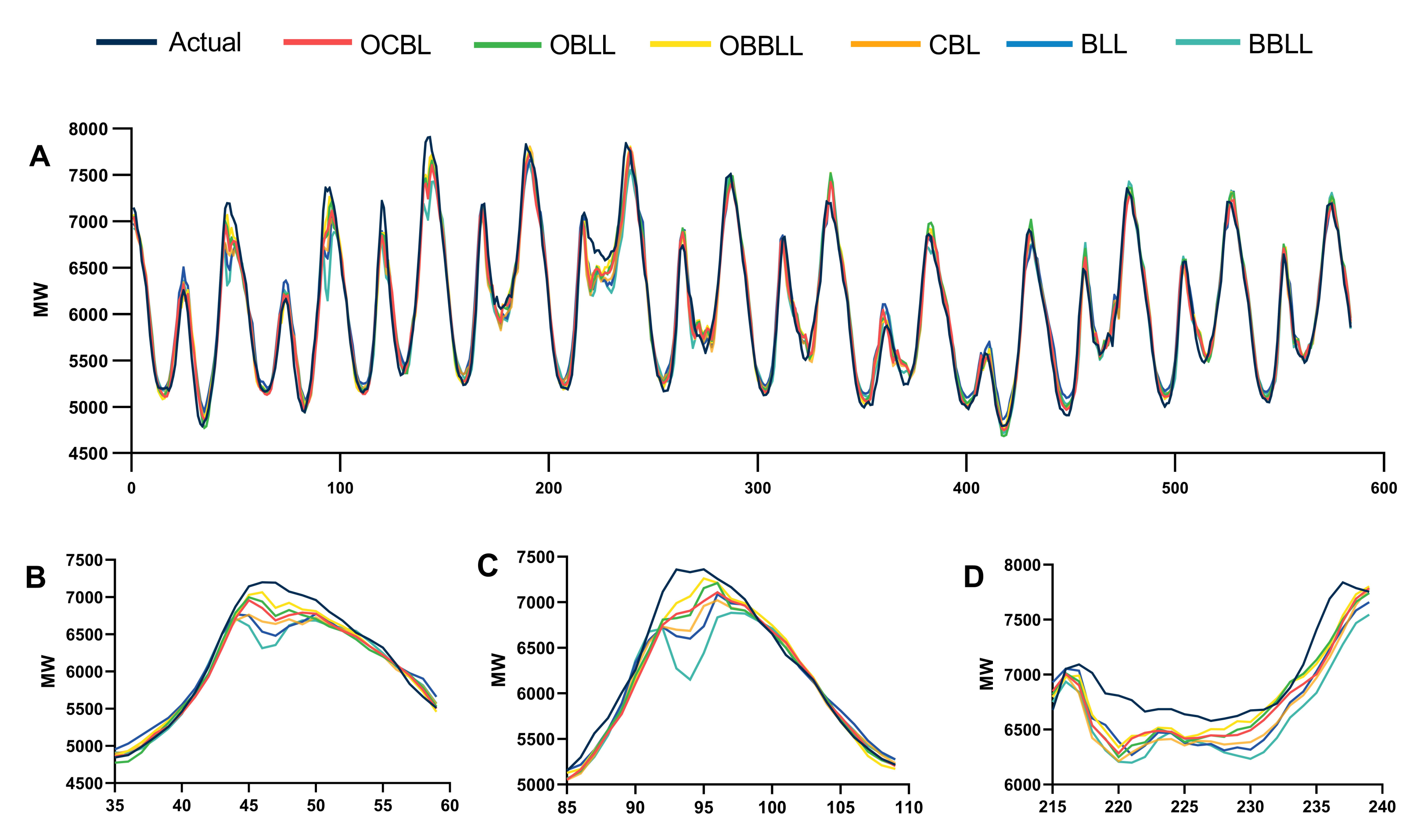
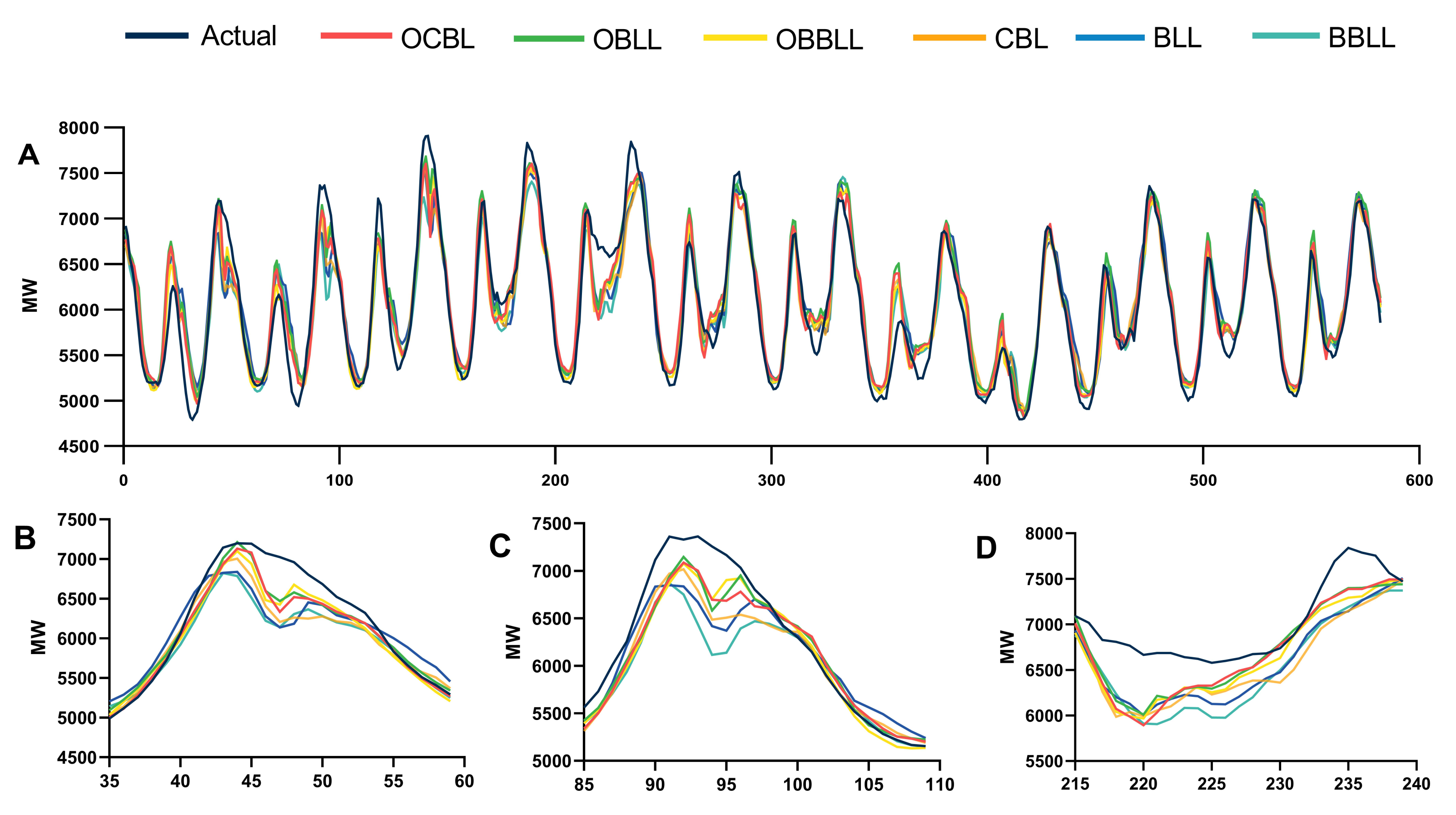
5.2. Forecasting Results Comparison
5.3. Experimental Results Analysis
6. Conclusions
- Multivariate time series dataset is not adopted.
- Other neural networks that can be used to parameterize the derivative of NODE are not used.
- Long-term forecasting was not attempted.
- Other recurrent neural networks, such as GRU and basic RNN, were not attempted.
- Investigate more forms of NODE to balance the computation memory and forecasting accuracy.
- Apply the combination of NODE and LSTM-based models to multivariate time series forecasting.
- Explore NODE interpolation to fill in missing values of time series.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hammad, M.A.; Jereb, B.; Rosi, B.; Dragan, D. Methods and Models for Electric Load Forecasting: A Comprehensive Review. Logist. Sustain. Transp. 2020, 11, 51–76. [Google Scholar] [CrossRef]
- gil Koo, B.; Kim, M.S.; Kim, K.H.; Lee, H.T.; Park, J.; Kim, C.H. Short-term electric load forecasting using data mining technique. In Proceedings of the 2013 7th International Conference on Intelligent Systems and Control (ISCO), Coimbatore, India, 4–5 January 2013; pp. 153–157. [Google Scholar]
- Chen, K.; Chen, K.; Wang, Q.; He, Z.; Hu, J.; He, J. Short-Term Load Forecasting With Deep Residual Networks. IEEE Trans. Smart Grid 2019, 10, 3943–3952. [Google Scholar] [CrossRef]
- Bunn, D.W.; Farmer, E.D. Comparative Models for Electrical Load Forecasting; Wiley: New York, NY, USA, 1986. [Google Scholar]
- Fallah, S.N.; Ganjkhani, M.; Shamshirband, S.; Chau, K.w. Computational Intelligence on Short-Term Load Forecasting: A Methodological Overview. Energies 2019, 12, 393. [Google Scholar] [CrossRef]
- Li, J.; Shui, C.; Li, R.; Zhang, L. Driving factors analysis of residential electricity expenditure using a multi-scale spatial regression analysis: A case study. Energy Rep. 2022, 8, 7127–7142. [Google Scholar] [CrossRef]
- Ghiasi, M.I.; Ahmadinia, E.; Lariche, M.J.; Zarrabi, H.; Simoes, R. A New Spinning Reserve Requirement Prediction with Hybrid Model. Smart Sci. 2018, 6, 212–221. [Google Scholar] [CrossRef]
- Ghiasi, M.I.; Jam, M.I.; Teimourian, M.; Zarrabi, H.; Yousefi, N. A new prediction model of electricity load based on hybrid forecast engine. Int. J. Ambient Energy 2019, 40, 179–186. [Google Scholar] [CrossRef]
- Cho, K.; van Merrienboer, B.; Çaglar, G.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning Phrase Representations using RNN Encoder–Decoder for Statistical Machine Translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Memarzadeh, G.; Keynia, F. Short-term electricity load and price forecasting by a new optimal LSTM-NN based prediction algorithm. Electr. Power Syst. Res. 2021, 192, 106995. [Google Scholar] [CrossRef]
- Chen, T.Q.; Rubanova, Y.; Bettencourt, J.; Duvenaud, D.K. Neural Ordinary Differential Equations. In Proceedings of the NeurIPS, Montreal, QC, Canada, 3–8 December 2018. [Google Scholar]
- Cui, Z.; Ke, R.; Pu, Z.; Wang, Y. Stacked bidirectional and unidirectional LSTM recurrent neural network for forecasting network-wide traffic state with missing values. Transp. Res. Part C Emerg. Technol. 2020, 118, 102674. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Hansen, C.K. Short-term electricity load forecasting with Time Series Analysis. In Proceedings of the 2017 IEEE International Conference on Prognostics and Health Management (ICPHM), Dallas, TX, USA, 19–21 June 2017; pp. 214–221. [Google Scholar]
- Chen, Z.; Chen, Y.; Xiao, T.; Wang, H.; Hou, P. A novel short-term load forecasting framework based on time-series clustering and early classification algorithm. Energy Build. 2021, 251, 111375. [Google Scholar] [CrossRef]
- Li, J.; Lei, Y.; Yang, S. Mid-long term load forecasting model based on support vector machine optimized by improved sparrow search algorithm. Energy Rep. 2022, 8, 491–497. [Google Scholar] [CrossRef]
- Atef, S.; Eltawil, A.B. Assessment of stacked unidirectional and bidirectional long short-term memory networks for electricity load forecasting. Electr. Power Syst. Res. 2020, 187, 106489. [Google Scholar] [CrossRef]
- Guo, X.; Zhao, Q.; Zheng, D.; Ning, Y.; Gao, Y. A short-term load forecasting model of multi-scale CNN-LSTM hybrid neural network considering the real-time electricity price. Energy Rep. 2020, 6, 1046–1053. [Google Scholar] [CrossRef]
- Kuan, L.; Yan, Z.; Xin, W.; Yan, C.; Xiangkun, P.; Wenxue, S.; Zhe, J.; Yong, Z.; Nan, X.; Xin, Z. Short-term electricity load forecasting method based on multilayered self-normalizing GRU network. In Proceedings of the 2017 IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 26–28 November 2017; pp. 1–5. [Google Scholar]
- Han, J.; Yan, L.; Li, Z. A Task-Based Day-Ahead Load Forecasting Model for Stochastic Economic Dispatch. IEEE Trans. Power Syst. 2020, 36, 5294–5304. [Google Scholar] [CrossRef]
- Zhou, Q.G.; Yong, B.; Li, F.; Wu, J.; Xu, Z.; Shen, J.; Chen, H. A novel Monte Carlo-based neural network model for electricity load forecasting. Int. J. Embed. Syst. 2020, 12, 522–533. [Google Scholar]
- Yong, B.; Shen, Z.; Wei, Y.; Shen, J.; Zhou, Q. Short-Term Electricity Demand Forecasting Based on Multiple LSTMs. In Advances in Brain Inspired Cognitive Systems; Ren, J., Hussain, A., Zhao, H., Huang, K., Zheng, J., Cai, J., Chen, R., Xiao, Y., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 192–200. [Google Scholar]
- Han, L.; Peng, Y.; Li, Y.; Yong, B.; Zhou, Q.; Shu, L. Enhanced Deep Networks for Short-Term and Medium-Term Load Forecasting. IEEE Access 2019, 7, 4045–4055. [Google Scholar] [CrossRef]
- Mughees, N.; Ali, S.M.; Mughees, A.; Mughees, A. Deep sequence to sequence Bi-LSTM neural networks for day-ahead peak load forecasting. Expert Syst. Appl. 2021, 175, 114844. [Google Scholar] [CrossRef]
- Szegedy, C.; Ioffe, S.; Vanhoucke, V.; Alemi, A.A. Inception-v4, Inception-ResNet and the Impact of Residual Connections on Learning. In Proceedings of the AAAI, San Francisco, CA, USA, 4–9 February 2017. [Google Scholar]
- Xie, X.; Parlikad, A.K.; Puri, R.S. A Neural Ordinary Differential Equations Based Approach for Demand Forecasting within Power Grid Digital Twins. In Proceedings of the 2019 IEEE International Conference on Communications, Control, and Computing Technologies for Smart Grids (SmartGridComm), Beijing, China, 1–23 October 2019; pp. 1–6. [Google Scholar]
- Lai, G.; Chang, W.C.; Yang, Y.; Liu, H. Modeling Long- and Short-Term Temporal Patterns with Deep Neural Networks. In Proceedings of the The 41st International ACM SIGIR Conference on Research & Development in Information Retrieval, SIGIR’18, Ann Arbor, MI, USA, 8–12 July 2018; Association for Computing Machinery: New York, NY, USA, 2018; pp. 95–104. [Google Scholar] [CrossRef]


| Model | Parameter | Configurations |
|---|---|---|
| OCBL | Number of nodes in parameterized FC layer of NODE | [100, 100] |
| Number of nodes in ouput FC layer of NODE | [10] | |
| Number of nodes in BiLSTM layer | [50] | |
| Number of nodes in LSTM layer | [30] | |
| Number of nodes in FC layers | [100] | |
| Kernel parameter of Conv1D layer | kernel size = 3, filters number = 64 | |
| OBLL | Number of nodes in parameterized FC layer of NODE | [100, 100] |
| Number of nodes in ouput FC layer of NODE | [10] | |
| Number of nodes in BiLSTM layer | [50] | |
| Number of nodes in LSTM layers | [30, 10] | |
| Number of nodes in FC layers | [100, 50, 20] | |
| OBBLL | Number of nodes in parameterized FC layer of NODE | [100, 100] |
| Number of nodes in ouput FC layer of NODE | [10] | |
| Number of nodes in BiLSTM layers | [50, 30] | |
| Number of nodes in LSTM layers | [20, 10] | |
| Number of nodes in FC layers | [100, 20] |
| Model | RMSE (MW) | MAE (MW) | MAPE (%) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 5 | 7 | 1 | 3 | 5 | 7 | 1 | 3 | 5 | 7 | |
| *OCBL | 103.67 | 155.92 | 231.57 | 276.96 | 80.79 | 115.87 | 170.25 | 205.22 | 1.30% | 1.88% | 2.82% | 3.47% |
| CBL | 109.52 | 173.97 | 263.20 | 321.54 | 84.85 | 127.59 | 195.62 | 231.84 | 1.36% | 2.08% | 3.23% | 3.83% |
| *OBBL | 104.35 | 156.59 | 241.33 | 285.82 | 87.39 | 119.51 | 184.16 | 215.02 | 1.45% | 1.96% | 3.09% | 3.63% |
| BBL | 106.78 | 197.39 | 272.31 | 317.13 | 87.26 | 148.85 | 202.27 | 232.57 | 1.44% | 2.45% | 3.35% | 3.85% |
| *OBBLL | 145.98 | 152.18 | 216.27 | 316.55 | 124.51 | 118.83 | 161.14 | 239.11 | 2.03% | 1.96% | 2.66% | 4.01% |
| BBLL | 92.73 | 206.86 | 278.42 | 319.78 | 73.03 | 144.16 | 197.28 | 231.89 | 1.20% | 2.32% | 3.20% | 3.84% |
| Model | RMSE (MW) | MAE (MW) | MAPE (%) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 5 | 7 | 1 | 3 | 5 | 7 | 1 | 3 | 5 | 7 | |
| *OCBL | 88.78 | 161.19 | 193.52 | 235.38 | 67.52 | 122.31 | 140.29 | 172.32 | 1.12% | 2.05% | 2.31% | 2.92% |
| CBL | 82.01 | 155.59 | 231.22 | 304.46 | 60.31 | 114.48 | 172.73 | 228.34 | 1.00% | 1.90% | 2.90% | 3.85% |
| *OBBL | 90.82 | 174.30 | 214.65 | 275.38 | 71.50 | 127.59 | 160.61 | 203.17 | 1.18% | 2.10% | 2.71% | 3.50% |
| BBL | 88.56 | 179.34 | 259.67 | 315.16 | 63.66 | 130.24 | 192.68 | 233.04 | 1.04% | 2.15% | 3.24% | 3.91% |
| *OBBLL | 103.36 | 191.37 | 235.04 | 249.82 | 82.38 | 151.87 | 173.95 | 183.82 | 1.37% | 2.53% | 2.90% | 3.14% |
| BBLL | 87.76 | 193.61 | 250.28 | 281.40 | 64.83 | 139.67 | 175.77 | 195.12 | 1.06% | 2.30% | 2.94% | 3.32% |
| Model | RMSE (MW) | MAE (MW) | MAPE (%) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 5 | 7 | 1 | 3 | 5 | 7 | 1 | 3 | 5 | 7 | |
| *OCBL | 115.46 | 247.68 | 373.69 | 473.87 | 95.91 | 183.20 | 274.13 | 341.78 | 1.56% | 2.94% | 4.36% | 5.37% |
| CBL | 104.32 | 291.99 | 371.35 | 492.39 | 78.63 | 214.72 | 280.55 | 362.72 | 1.24% | 3.36% | 4.50% | 5.75% |
| *OBBL | 142.34 | 262.38 | 381.87 | 481.58 | 112.92 | 196.97 | 288.11 | 358.54 | 1.75% | 3.13% | 4.56% | 5.68% |
| BBL | 111.36 | 281.34 | 473.11 | 588.46 | 84.36 | 208.37 | 372.65 | 453.56 | 1.33% | 3.27% | 5.94% | 7.11% |
| *OBBLL | 136.62 | 244.78 | 367.79 | 445.90 | 106.07 | 181.06 | 275.52 | 318.91 | 1.65% | 2.89% | 4.45% | 5.06% |
| BBLL | 101.98 | 281.06 | 418.97 | 583.49 | 76.59 | 210.93 | 305.48 | 421.33 | 1.21% | 3.32% | 4.83% | 6.61% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, S.; Shen, J.; Lv, Q.; Zhou, Q.; Yong, B. A Novel NODE Approach Combined with LSTM for Short-Term Electricity Load Forecasting. Future Internet 2023, 15, 22. https://doi.org/10.3390/fi15010022
Huang S, Shen J, Lv Q, Zhou Q, Yong B. A Novel NODE Approach Combined with LSTM for Short-Term Electricity Load Forecasting. Future Internet. 2023; 15(1):22. https://doi.org/10.3390/fi15010022
Chicago/Turabian StyleHuang, Songtao, Jun Shen, Qingquan Lv, Qingguo Zhou, and Binbin Yong. 2023. "A Novel NODE Approach Combined with LSTM for Short-Term Electricity Load Forecasting" Future Internet 15, no. 1: 22. https://doi.org/10.3390/fi15010022
APA StyleHuang, S., Shen, J., Lv, Q., Zhou, Q., & Yong, B. (2023). A Novel NODE Approach Combined with LSTM for Short-Term Electricity Load Forecasting. Future Internet, 15(1), 22. https://doi.org/10.3390/fi15010022








