Digitalization of Distribution Transformer Failure Probability Using Weibull Approach towards Digital Transformation of Power Distribution Systems
Abstract
1. Introduction
2. Theoretical Background
2.1. Failure-Rate Model
2.2. Reliability Function
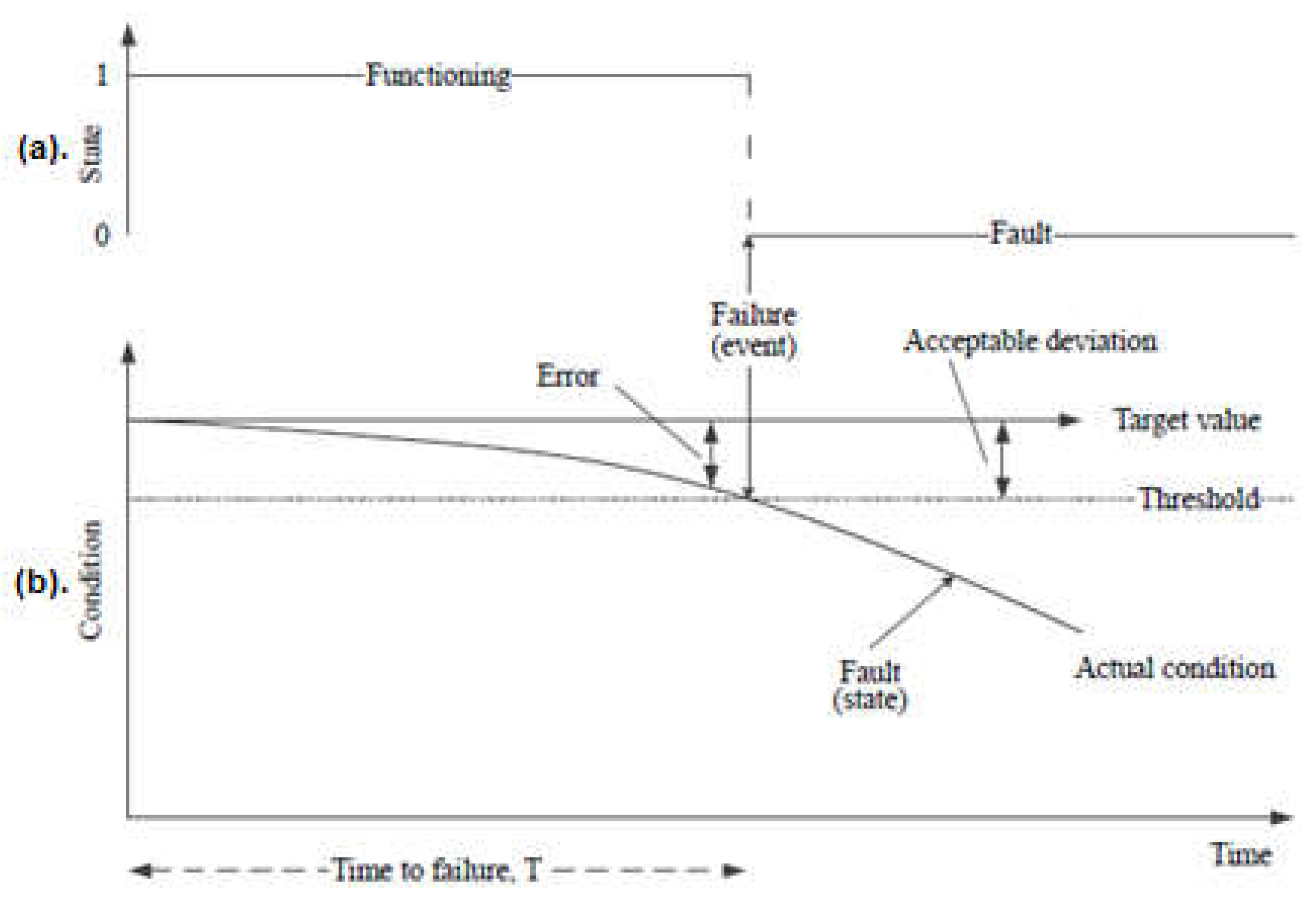
2.3. Bathtub Curve
2.4. Parametric Lifetime Models
2.4.1. Exponential Distribution
2.4.2. Weibull Distribution
2.4.3. Other Parametric Distributions
2.4.4. Goodness of Fit
2.5. Reliability Indices
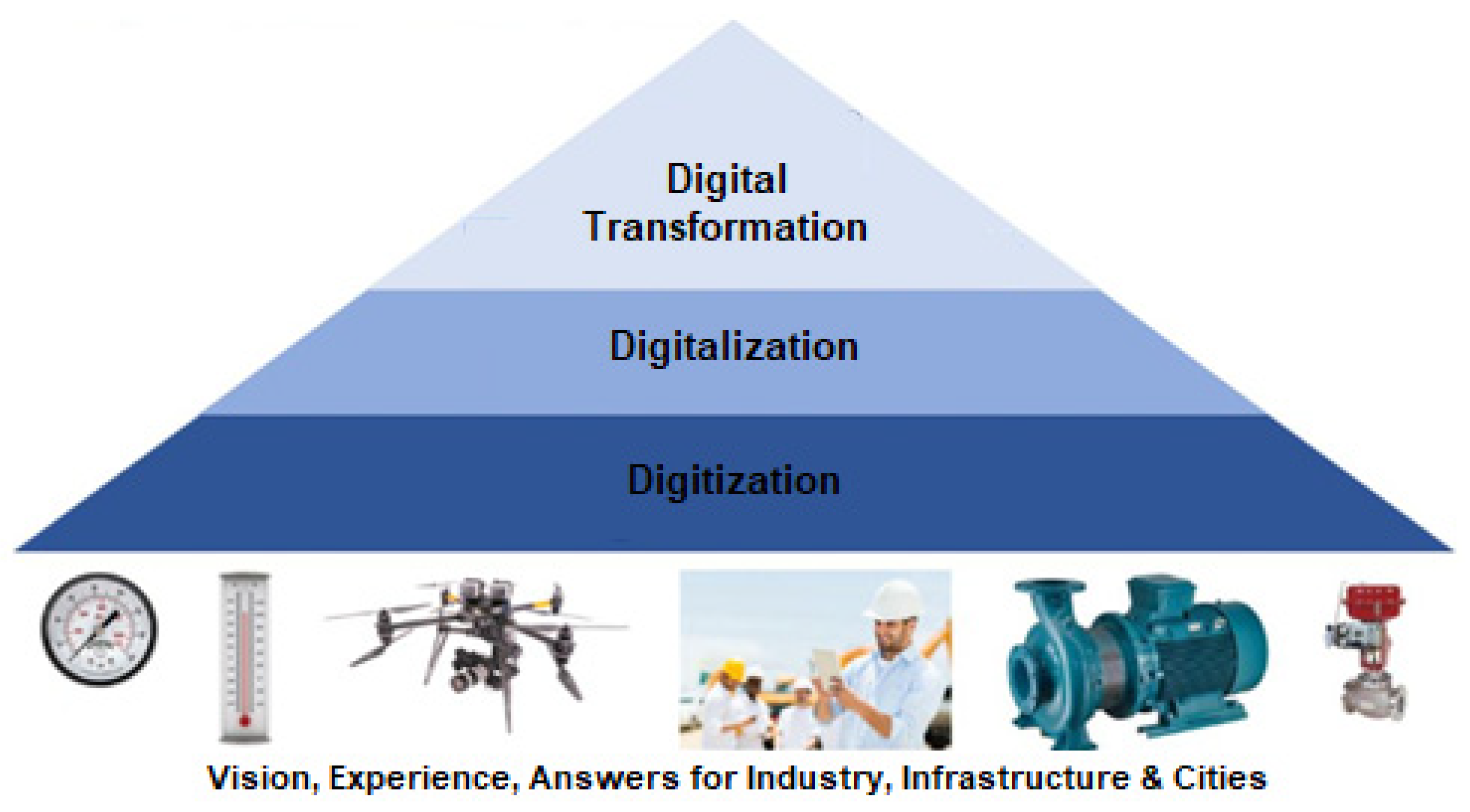
2.6. Digitization, Digitalization, and Digital Transformation
3. Case-Study Methodology and Development
3.1. Use of Case-Study Methodology
3.2. Weibull Cumulative-Distribution Function and Reliability Function
3.3. Methodology and Analysis
4. Results and Discussion
5. Conclusions
Future Works
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bertling, L. Reliability-Centred Maintenance for Electric Power Distribution Systems. Ph.D. Dissertation, Royal Institute of Technology (KTH), Stockholm, Sweden, 2002; p. 449. [Google Scholar]
- Lucas, J.R.; Udayakanthi, M.V.P.G. Identification of Causes of Distribution Transformer Failures and Introduction of Measures to Minimize Failures; Department of Electrical Engineering, University of Moratuwa: Moratuwa, Sri Lanka, 2015. [Google Scholar]
- Mateo, C.; de Cuadra, F. Digitalization of Electricity Distribution Systems. 2021. Available online: https://www.eddie-erasmus.eu/publications-eddie/blogs-eddie/digitalization-of-electricity-distribution-systems/ (accessed on 4 December 2022).
- Fusco, G.; Russo, M.; De Santis, M. Decentralized Voltage Control in Active Distribution Systems: Features and Open Issues. Energies 2021, 14, 2563. [Google Scholar] [CrossRef]
- Corsi, S.; Pozzi, M.; Sforna, M.; Dell’Olio, G. The Coordinated Automatic Voltage Control of the Italian Transmission Grid-Part II: Control Apparatuses and Field Performance of the Consolidated Hierarchical System. IEEE Trans. Power Syst. 2004, 19, 1733–1741. [Google Scholar] [CrossRef]
- Digital Transformation of the Distribution Grid; White Paper; Hitachi Energy: Zurich, Switzerland, 2022.
- Mateo, C.; Postigo, F.; de Cuadra, F.; Gómez, T.; Elgindy, T.; Dueñas, P.; Hodge, B.-M.; Krishnan, V.; Palmintier, B. Building Large-Scale U.S. Synthetic Electric Distribution System Models. IEEE Trans. Smart Grid 2020, 11, 5301–5313. [Google Scholar] [CrossRef]
- Stajnarova, M.; Reyna, A. Consumer Rights in Electricity and Gas Markets; BEUC Position Paper; BEUC: Brussels, Belgium, 2013; pp. 3–20. [Google Scholar]
- Attanayake, A.M.S.R.H.; Ratnayake, R.M.C. Risk-based Inspection and Maintenance Analysis of Distribution Transformers: Development of a Risk Matrix and Fuzzy Logic Based Analysis Approach. In Proceedings of the 2022 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Kuala Lumpur, Malaysia, 7–10 December 2022; pp. 0457–0462. [Google Scholar]
- Attanayake, A.M.S.R.H.; Ratnayake, R.M.C. On the Necessity of Using Supervised Machine Learning for Risk-based Screening of Distribution Transformers: An Industrial Case Study. In Proceedings of the 2022 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Kuala Lumpur, Malaysia, 7–10 December 2022; pp. 0468–0473. [Google Scholar]
- Ronan, E.R.; Sudhoff, S.D.; Glover, S.F.; Galloway, D.L. A Power Electronic-Based Distribution Transformer. IEEE Trans. Power Deliv. 2002, 17, 537–543. [Google Scholar] [CrossRef]
- Perna, S.; Casolino, G.M.; Santis, M.D. Design of a Single-Phase Two-Winding Transformer for Prototyping a Voltage Regulator. In Proceedings of the 2022 IEEE International Conference on Environment and Electrical Engineering and 2022 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Prague, Czech Republic, 28 June–1 July 2022; pp. 1–6. [Google Scholar]
- Reid, M. Introduction to the Field of Reliability Engineering. 2019–2022. Available online: https://reliability.readthedocs.io/en/latest/Introduction%20to%20the%20field%20of%20reliability%20engineering.html (accessed on 6 November 2022).
- Smith, D.J. Reliability, Maintainability, and Risk, 8th ed.; Elsevier Ltd.: Oxford, UK, 2011; p. 463. [Google Scholar]
- Smith, R.; Mobley, R.K. Rules of Thumb for Reliability and Maintenance Engineers, 1st ed.; Elsevier Inc.: Oxford, UK, 2007; pp. 57–78. [Google Scholar]
- Gupta, M.S. What Is Digitization, Digitalization, and Digital Transformation? 2020. Available online: https://www.arcweb.com/blog/what-digitization-digitalization-digital-transformation (accessed on 4 December 2022).
- Calixto, E. Gas and Oil Reliability Engineering Modeling and Analysis, 2nd ed.; Elsevier Inc.: Oxford, UK, 2016. [Google Scholar]
- Chowdhury, A.A.; Koval, D.O. Power Distribution System Reliability: Practical Methods and Applications; Institute of Electrical and Electronics Engineers, Ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009; p. 556. [Google Scholar]
- Jurgensen, J.H. Individual Failure Rate Modeling and Exploratory Failure Data Analysis for Power System Components. Ph.D. Thesis, Royal Institute of Technology (KTH), Stockholm, Sweden, 2018; p. 95. [Google Scholar]
- O’Connor, A.N.; Modarres, M.; Mosleh, A. Probability Distributions Used in Reliability Engineering; The Center for Reliability Engineering University of Maryland: College Park, MD, USA, 2016. [Google Scholar]
- Rausand, M.; Hoyland, A. System Reliability Theory; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2004; p. 644. [Google Scholar]
- Pasha, G.R.; Khan, M.S.; Pasha, A.H. Empirical Analysis of the Weibull Distribution for Failure Data. J. Stat. 2006, 13, 33–45. [Google Scholar]
- Ceylon Electricity Board. Operating Manual—Area Electrical Engineer; Ceylon Electricity Board: Colombo, Sri Lanka, 2016. [Google Scholar]
- Yin, R.K. Case Study Research and Applications, 6th ed.; SAGE Publications, Inc.: Thousand Oaks, CA, USA, 2018; pp. 20–54. [Google Scholar]
- Liu, J.; Wu, Z.; Wu, J.; Dong, J.; Zhao, Y.; Wen, D. A Weibull Distribution Accrual Failure Detector for Cloud Computing. PLoS ONE 2017, 12, e0173666. [Google Scholar] [CrossRef] [PubMed]
- Conti, M.; Orcioni, S. Modeling of Failure Probability for Reliability and Component Reuse of Electric and Electronic Equipment. Energies 2020, 13, 2823. [Google Scholar] [CrossRef]
- General Electric Company. About Weibull Distribution. 2018. Available online: https://www.ge.com/digital/documentation/meridium/Help/V43050/Default/Subsystems/ReliabilityAnalytics/Content/WeibullDistrubution.htm (accessed on 4 December 2022).



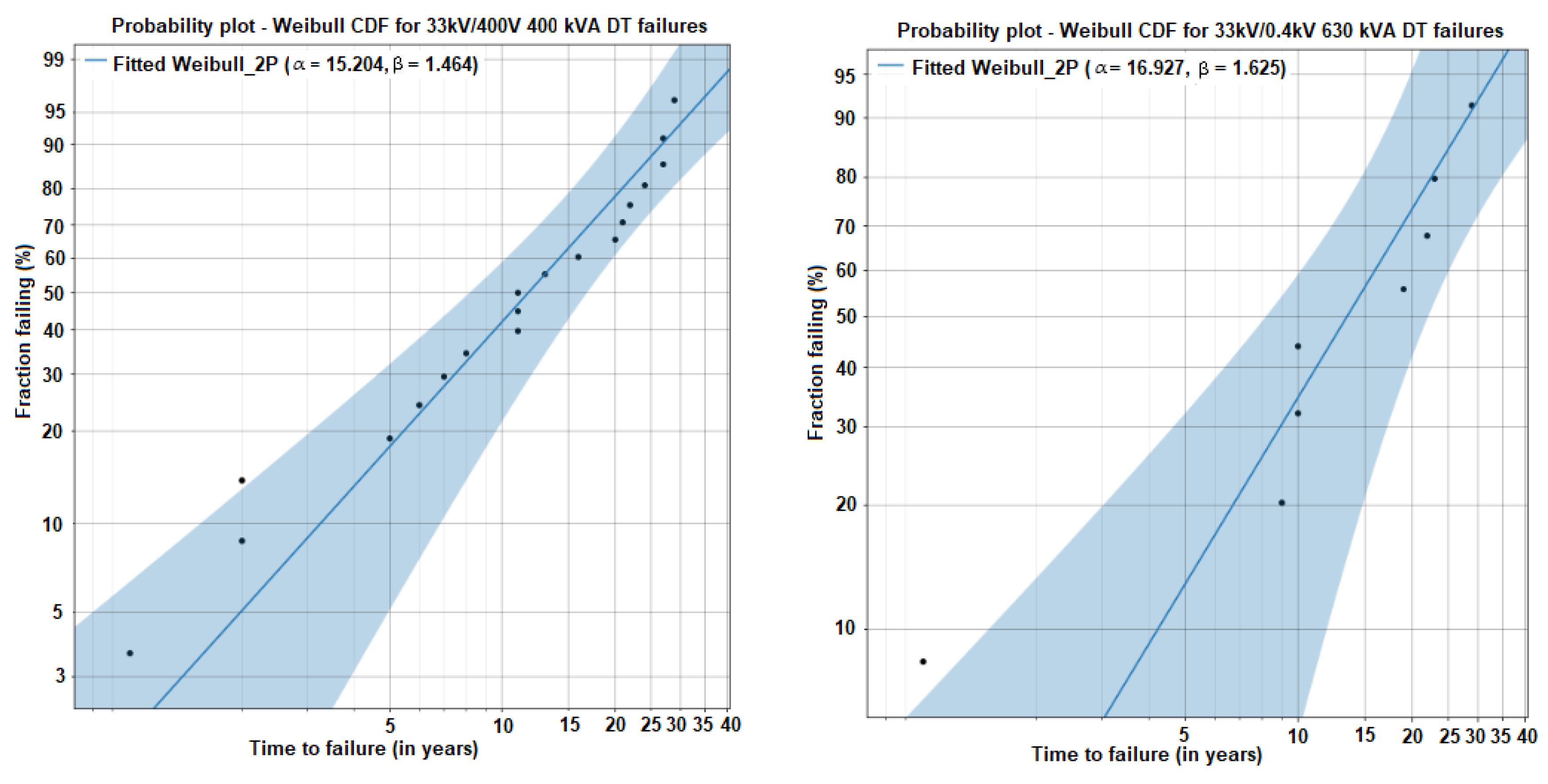


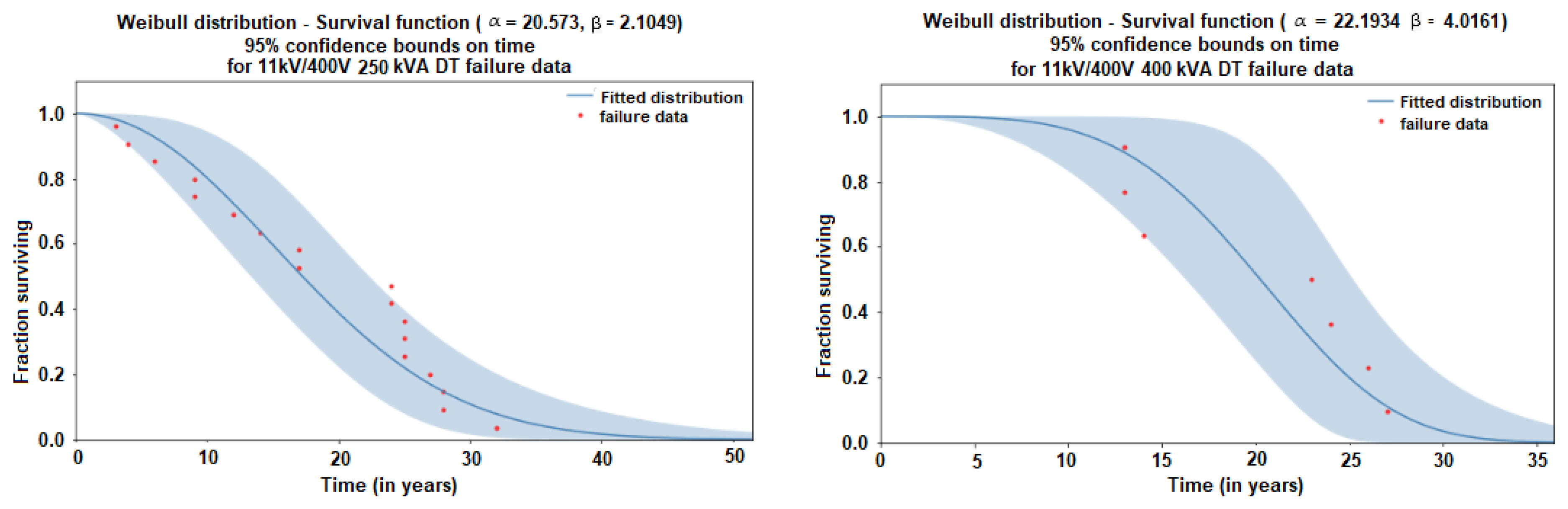
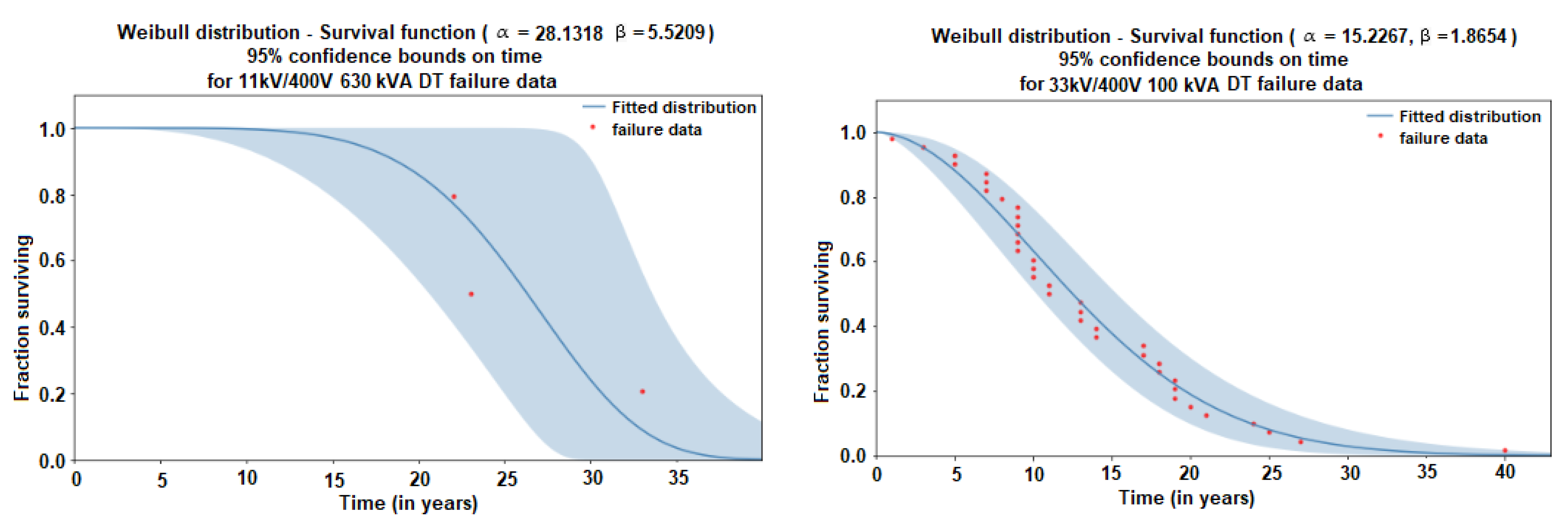
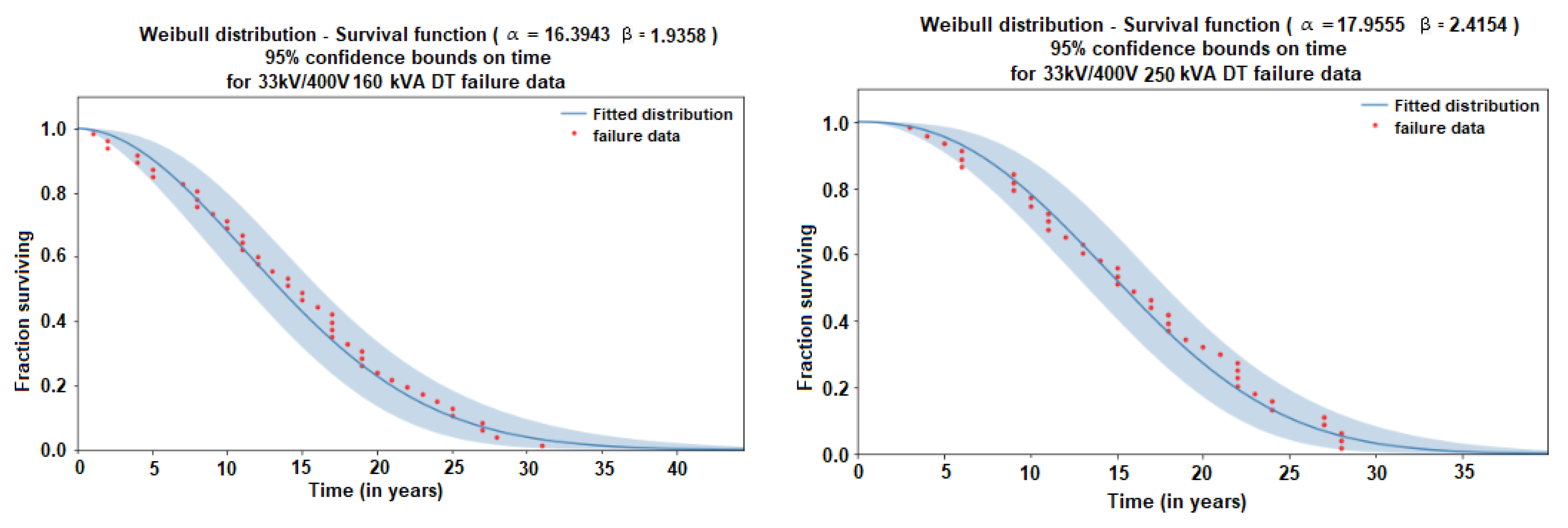
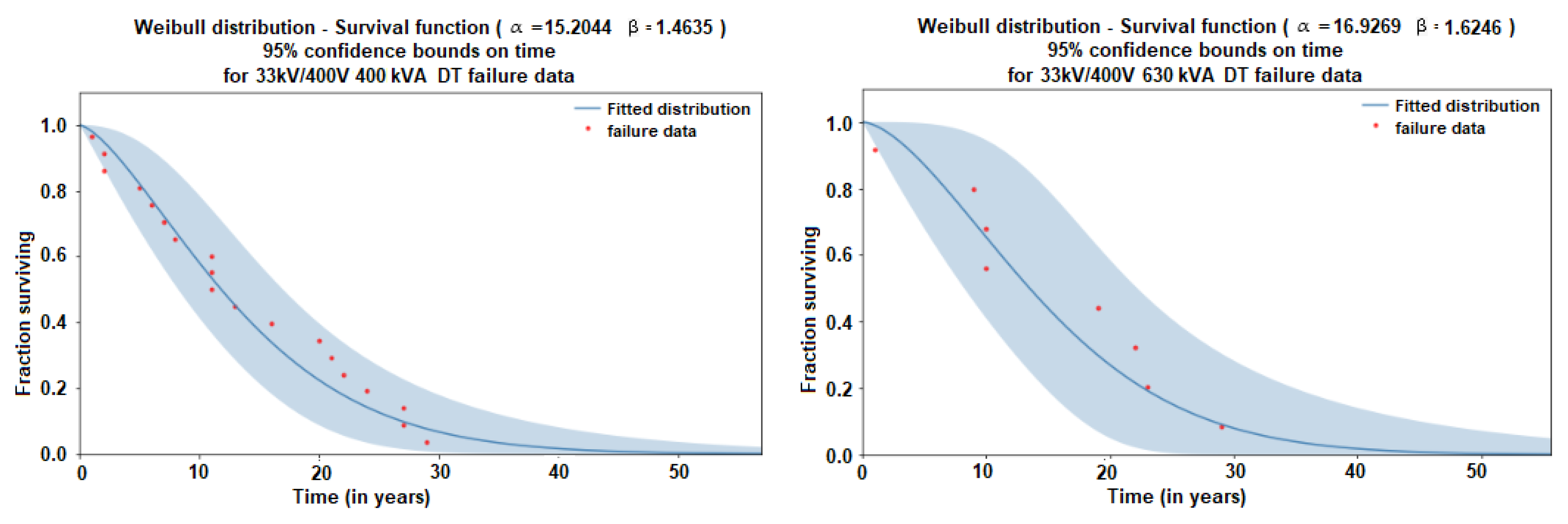

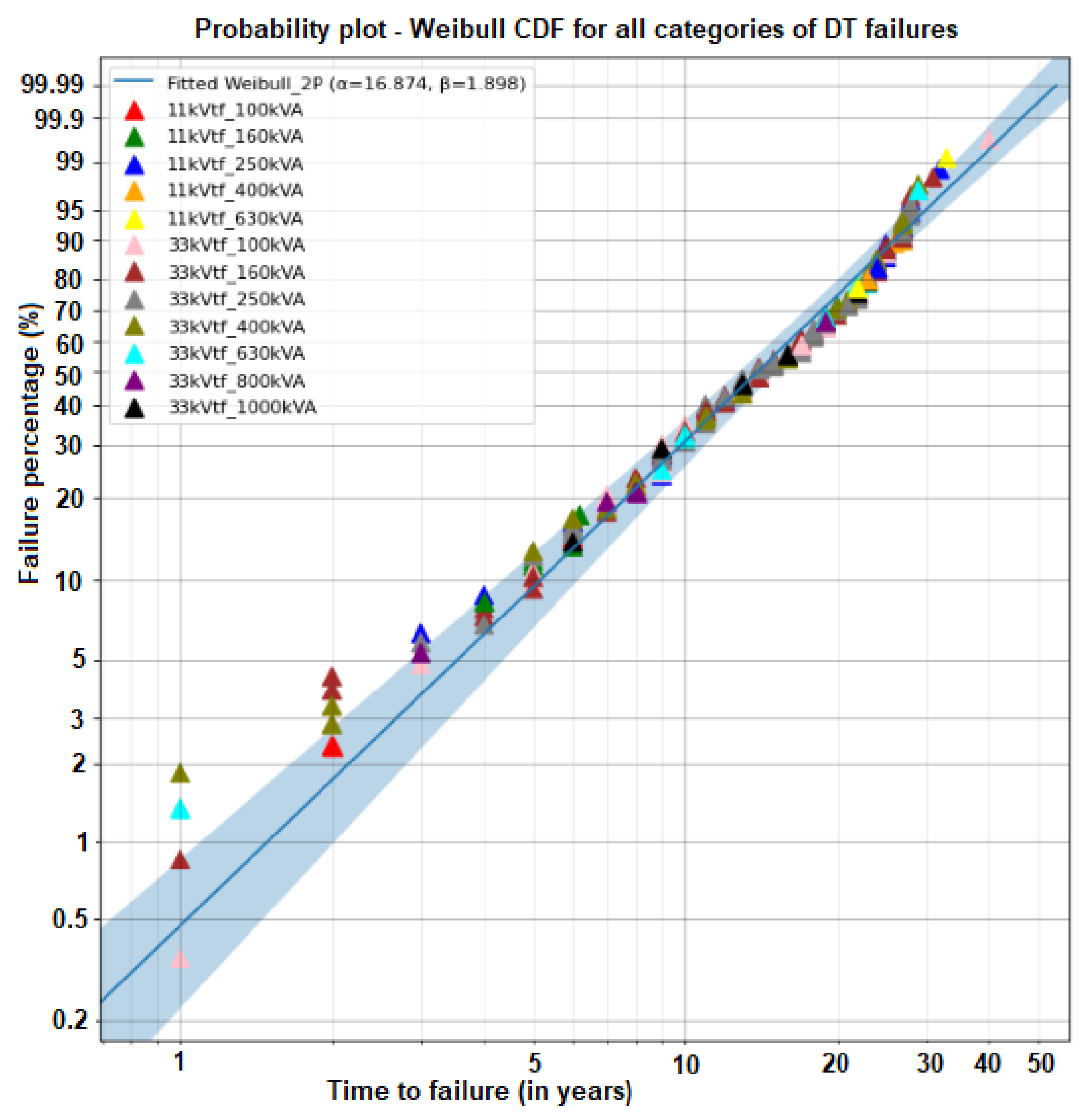
| Apparent power (kVA) category | 100 | 160 | 250 | 400 | 630 |
| Apparent power (kVA) category | 100 | 160 | 250 | 400 | 630 | 800 | 1000 |
| Transformer Category | No. of Failures | Parameter | Point Estimate | Standard Error | Lower CI | Upper CI |
|---|---|---|---|---|---|---|
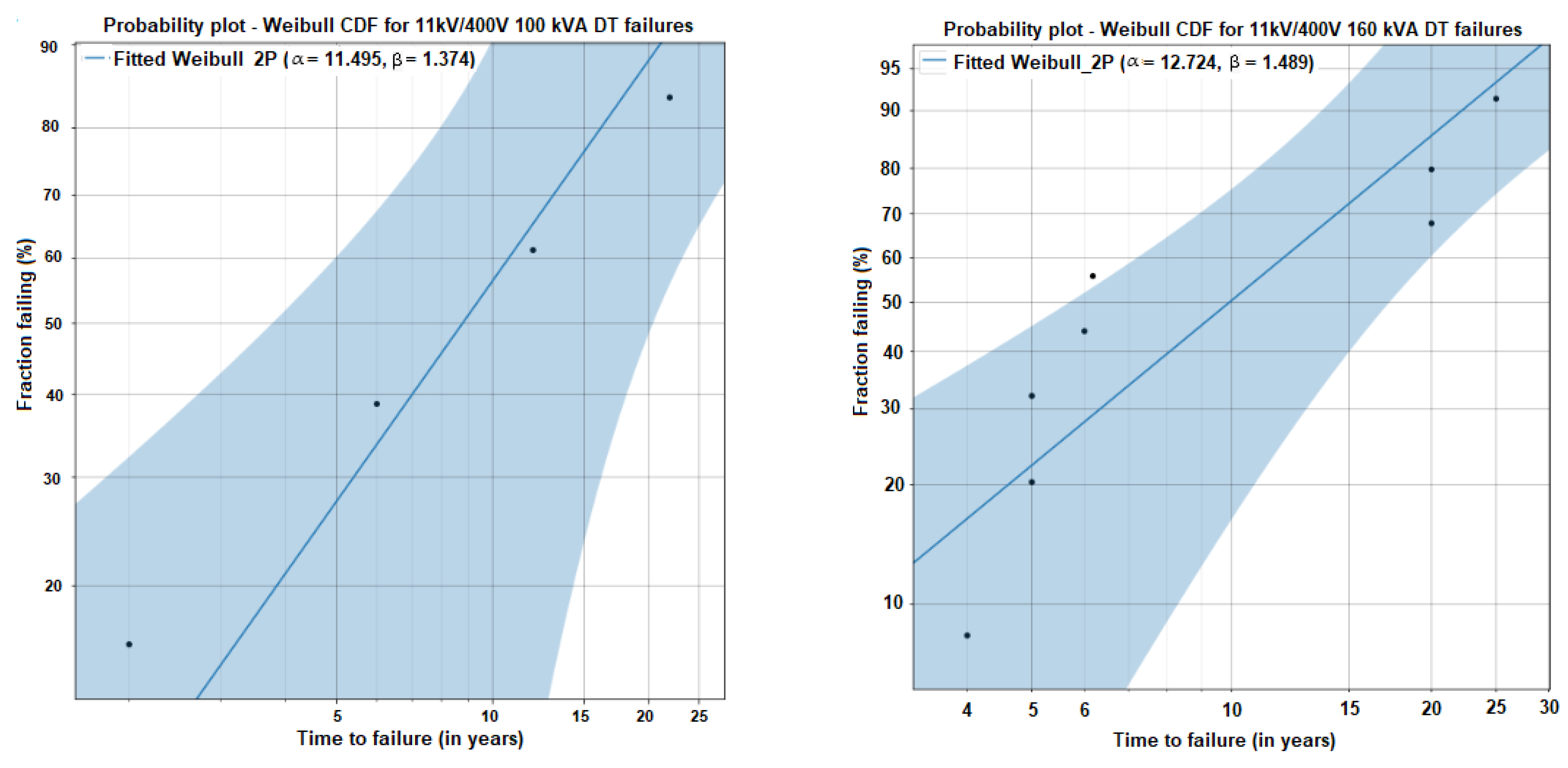
| 11 kV to 400 V 100 kVA | 4 | Alpha | 11.4954 | 4.41194 | 5.41794 | 24.3902 |
| Beta | 1.37384 | 0.555899 | 0.621607 | 3.0364 | ||
| 11 kV to 400 V 160 kVA | 3 | Alpha | 12.7236 | 3.20768 | 7.7628 | 20.8546 |
| Beta | 1.48876 | 0.410304 | 0.86743 | 2.55515 | ||
| 11 kV to 400 V 250 kVA | 18 | Alpha | 20.573 | 2.40769 | 16.3562 | 25.8771 |
| Beta | 2.10485 | 0.426645 | 1.41477 | 3.13153 | ||
| 11 kV to 400 V 400 kVA | 7 | Alpha | 22.1934 | 2.19919 | 18.2758 | 26.9508 |
| Beta | 4.01613 | 1.28084 | 2.14951 | 7.50373 | ||
| 11 kV to 400 V 630 kVA | 3 | Alpha | 28.1318 | 3.12802 | 22.623 | 34.9819 |
| Beta | 5.52089 | 2.44696 | 2.31601 | 13.1607 | ||
| 33 kV to 400 V 100 kVA | 37 | Alpha | 15.2267 | 1.41542 | 12.6905 | 18.2696 |
| Beta | 1.8654 | 0.229805 | 1.46525 | 2.37485 | ||
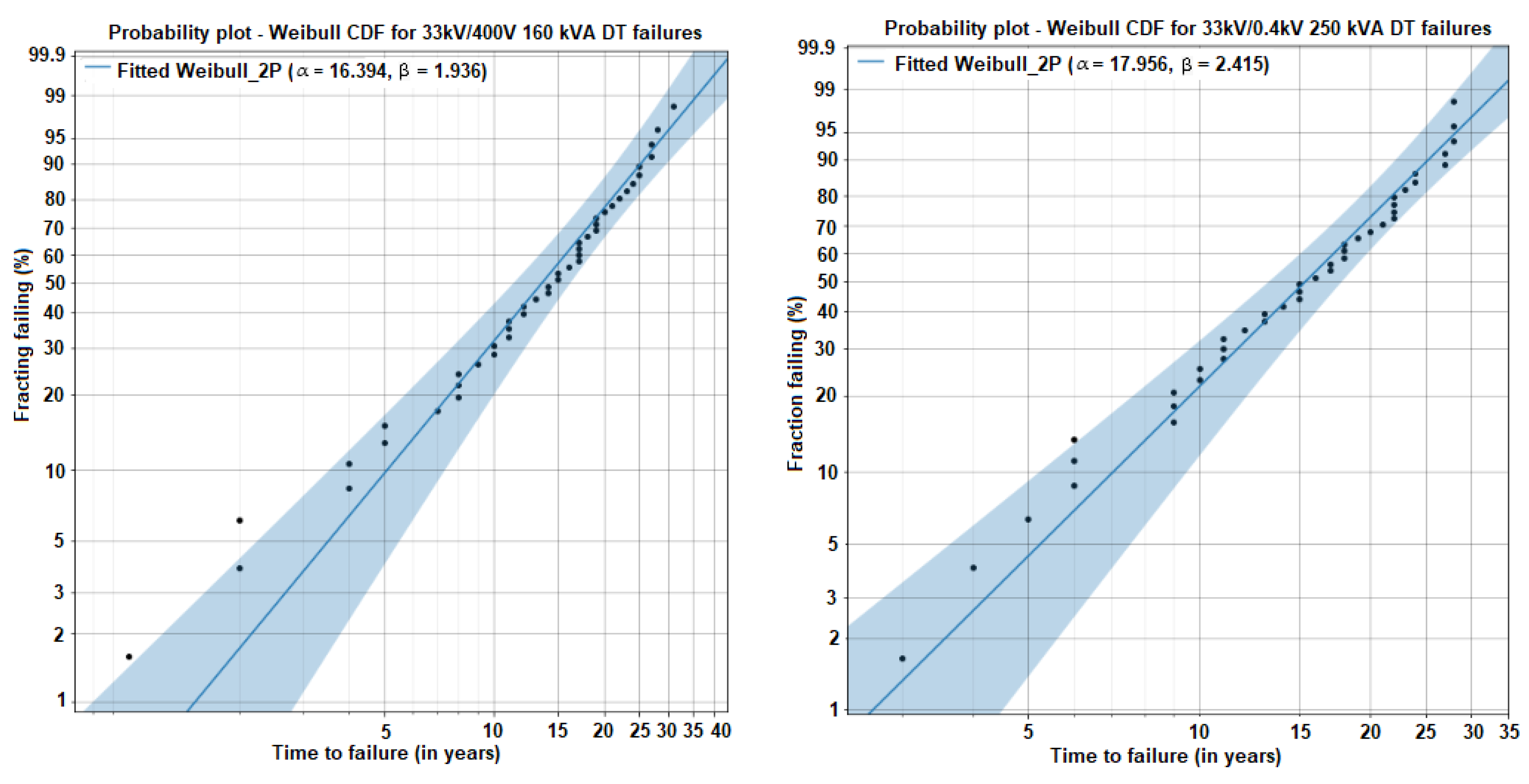
| 33 kV to 400 V 160 kVA | 44 | Alpha | 16.3943 | 1.33623 | 13.9738 | 19.234 |
| Beta | 1.9358 | 0.240369 | 1.51763 | 2.46919 | ||
| 33 kV to 400 V 250 kVA | 42 | Alpha | 17.9555 | 1.20517 | 15.7422 | 20.48 |
| Beta | 2.41537 | 0.303852 | 1.88757 | 3.09075 | ||
| 33 kV to 400 V 400 kVA | 19 | Alpha | 15.2044 | 2.49815 | 11.0183 | 20.981 |
| Beta | 1.46352 | 0.28023 | 1.00557 | 2.13002 | ||
| 33 kV to 400 V 630 kVA | 8 | Alpha | 16.9269 | 3082971 | 10.8641 | 26.3731 |
| Beta | 1.62459 | 0.49219 | 0.897143 | 2.94189 | ||
| 33 kV to 400 V 800 kVA | 4 | Alpha | 10.4237 | 3.3206 | 5.5829 | 19.4618 |
| Beta | 1.66328 | 0.639442 | 0.782936 | 3.53352 | ||
| 33 kV to 400 V 1000 kVA | 6 | Alpha | 16.7628 | 2.74205 | 12.1649 | 23.0986 |
| Beta | 2.62885 | 0.880714 | 1.36332 | 5.06914 |
| Beta Value | Alpha Value | Typical Failure Mode | Interpretation of Cause of Failure |
|---|---|---|---|
| >4 | Low compared with standard values for failed parts (less than 20%) | Old age, rapid wear-out (systematic, regular) | Poor machine/material design |
| Between 1 and 4 | Low compared with standard values for failed parts (less than 20%) | Early wear-out | Poor system design |
| Between 1 and 4 | Low | Early wear-out | Construction problem |
| <1 | Low | Infant mortality | Production problems, design problems, misassembled, quality control, overhaul problems |
| Between 1 and 4 | Between 1 and 4 | Less than manufacturer-recommended preventive maintenance cycle | Inadequate preventive-maintenance schedule |
| Around 1 | Much less | Random failures with definable causes | Inadequate operating procedure |
| Transformer Category | Log Likelihood | AIC | BIC | AD |
|---|---|---|---|---|
| 11 kV to 400 V 100 kVA | −13.1355 | 42.2709 | 29.0435 | 2.91429 |
| 11 kV to 400 V 160 kVA | −26.59 | 59.5801 | 12.7236 | 2.25092 |
| 11 kV to 400 V 250 kVA | −65.1467 | 135.093 | 136.074 | 1.48386 |
| 11 kV to 400 V 400 kVA | −22.1699 | 51.3398 | 48.1316 | 2.2968 |
| 11 kV to 400 V 630 kVA | −9.18554 | NA | 20.5683 | 3.76559 |
| 33 kV to 400 V 100 kVA | −19.3341 | 46.6682 | 42.2517 | 2.17347 |
| 33 kV to 400 V 160 kVA | −151.298 | 306.889 | 310.165 | 0.627865 |
| 33 kV to 400 V 250 kVA | −141.136 | 286.58 | 289.747 | 0.655464 |
| 33 kV to 400 V 400 kVA | −67.2275 | 139.205 | 140.344 | 1.05074 |
| 33 kV to 400 V 630 kVA | −28.8044 | 64.0089 | 61.7678 | 1.92899 |
| 33 kV to 400 V 800 kVA | −12.2087 | 40.4173 | 27.1899 | 2.99284 |
| 33 kV to 400 V 1000 kVA | −19.3341 | 46.6682 | 42.2517 | 2.17347 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Attanayake, A.M.S.R.H.; Ratnayake, R.M.C. Digitalization of Distribution Transformer Failure Probability Using Weibull Approach towards Digital Transformation of Power Distribution Systems. Future Internet 2023, 15, 45. https://doi.org/10.3390/fi15020045
Attanayake AMSRH, Ratnayake RMC. Digitalization of Distribution Transformer Failure Probability Using Weibull Approach towards Digital Transformation of Power Distribution Systems. Future Internet. 2023; 15(2):45. https://doi.org/10.3390/fi15020045
Chicago/Turabian StyleAttanayake, A. M. Sakura R. H., and R. M. Chandima Ratnayake. 2023. "Digitalization of Distribution Transformer Failure Probability Using Weibull Approach towards Digital Transformation of Power Distribution Systems" Future Internet 15, no. 2: 45. https://doi.org/10.3390/fi15020045
APA StyleAttanayake, A. M. S. R. H., & Ratnayake, R. M. C. (2023). Digitalization of Distribution Transformer Failure Probability Using Weibull Approach towards Digital Transformation of Power Distribution Systems. Future Internet, 15(2), 45. https://doi.org/10.3390/fi15020045








