Toward Vulnerability Detection for Ethereum Smart Contracts Using Graph-Matching Network
Abstract
1. Introduction
- We design a novel graph representation ASG for smart contracts in forms of source code and bytecode, which takes advantage of both syntactic information and code structural features.
- We apply a graph-matching network model based on the ASG representation for vulnerability detection in smart contracts. We adopt two different training models, i.e., GNN and GMN, to analyze the difference between their performance.
- We implement two tools called ASGVulDetector and BASGVulDetector for smart contracts in source code and bytecode, respectively, and conduct extensive experiments to evaluate their effectiveness and superiority through comparisons with competitors.
2. Background
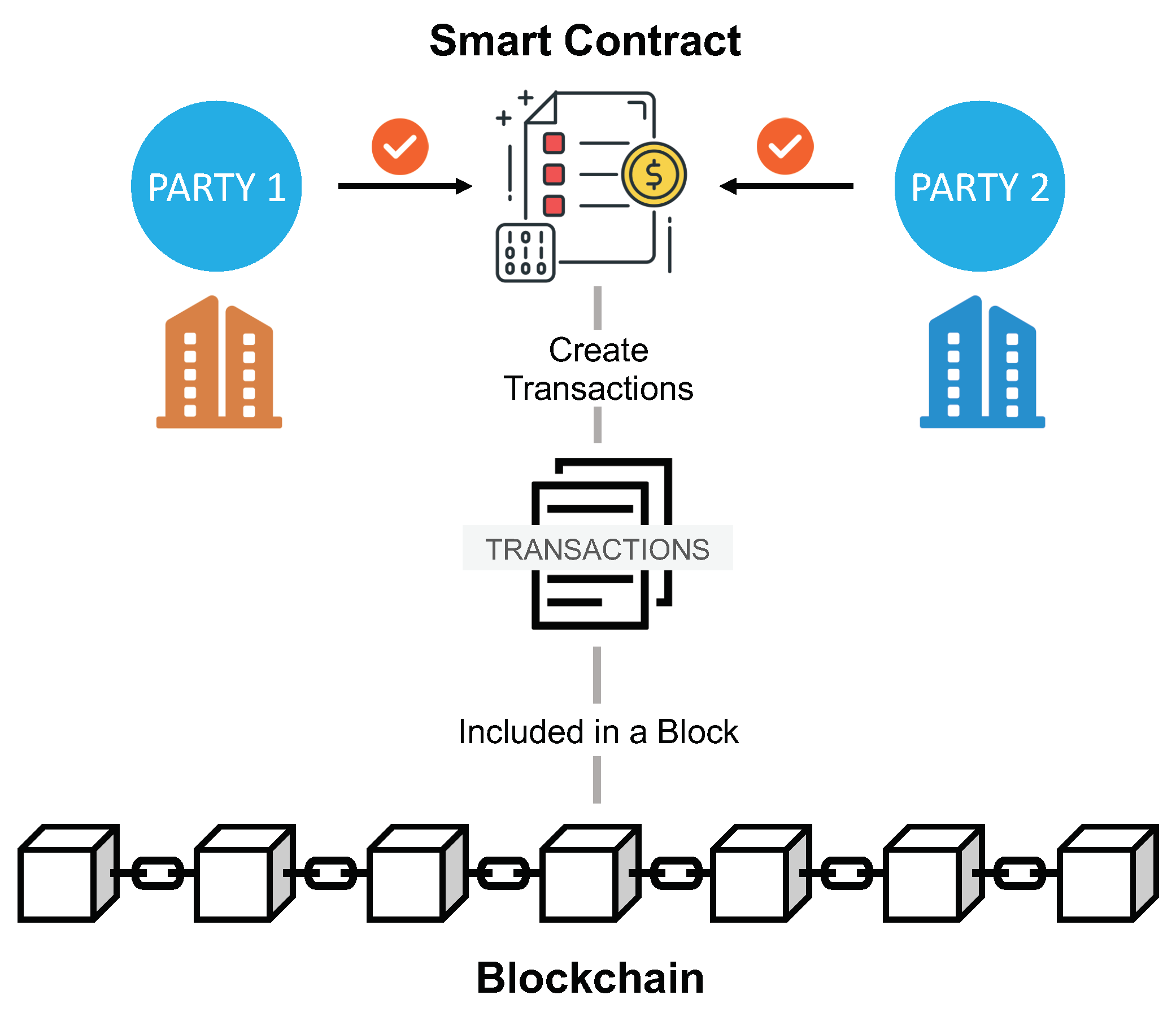
2.1. Smart Contract in a Nutshell
2.2. Four Types of Vulnerabilities in Smart Contracts
2.2.1. Reentrancy
2.2.2. Timestamp Dependency
2.2.3. Block info Dependency
2.2.4. Tx.Origin Attack
2.3. Graph-Matching Network
3. Related Work
4. Methodology
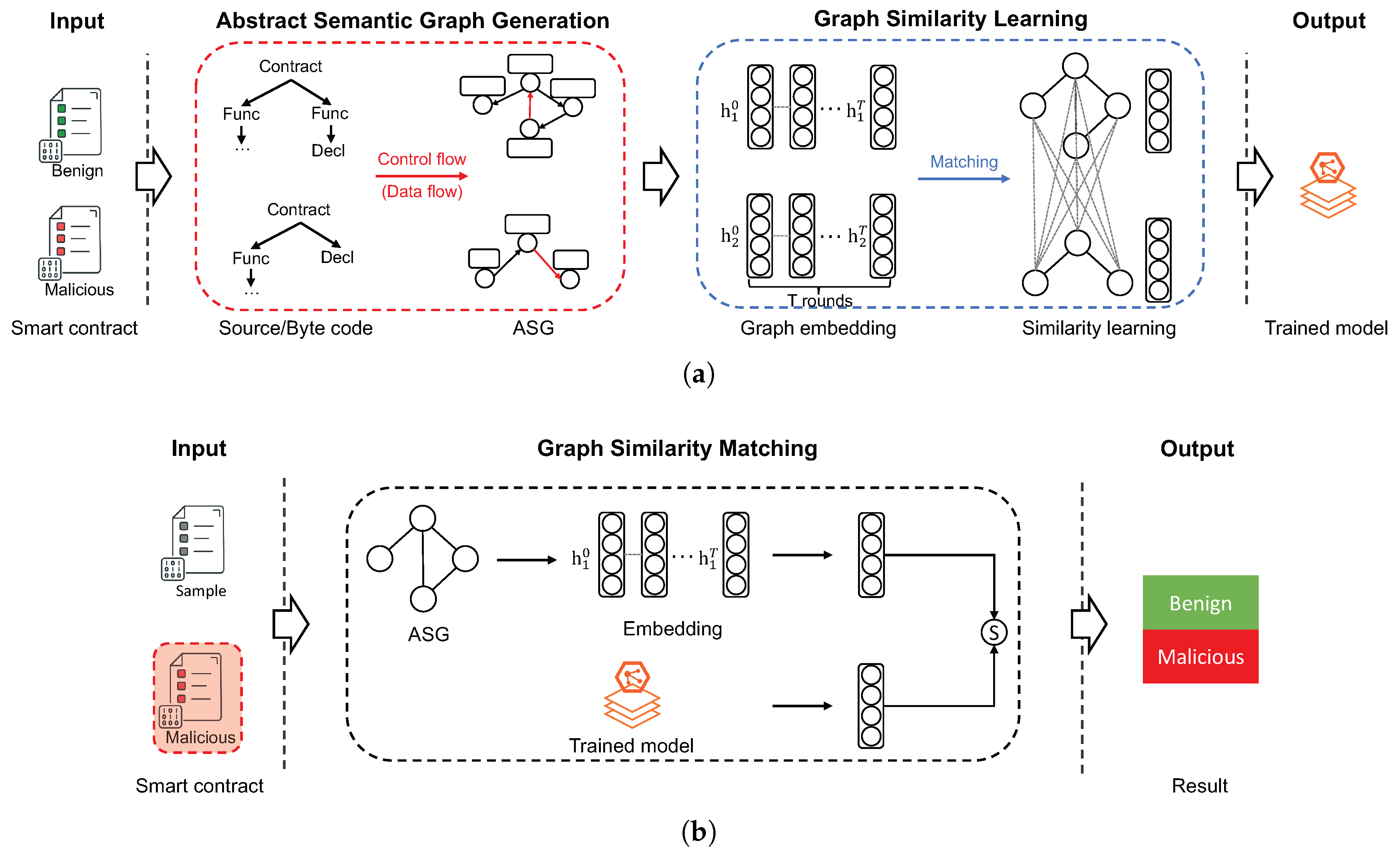
4.1. Framework
4.2. Abstract Semantic Graph Generation
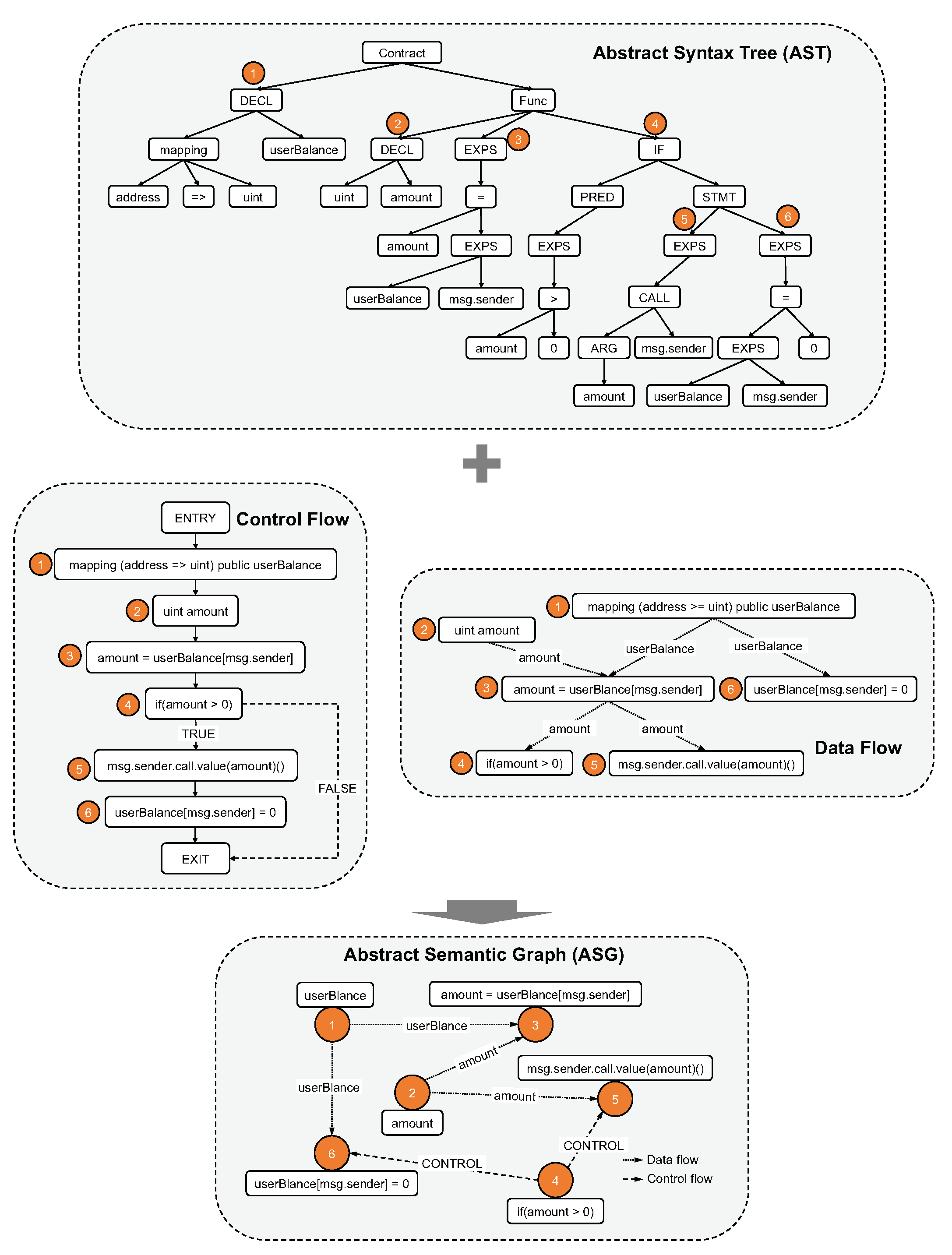
4.2.1. ASG from Source Code
| Algorithm 1 ASG generation from source code. |
| Input: Source code of smart contract, S Output: Abstract semantic graph,
|
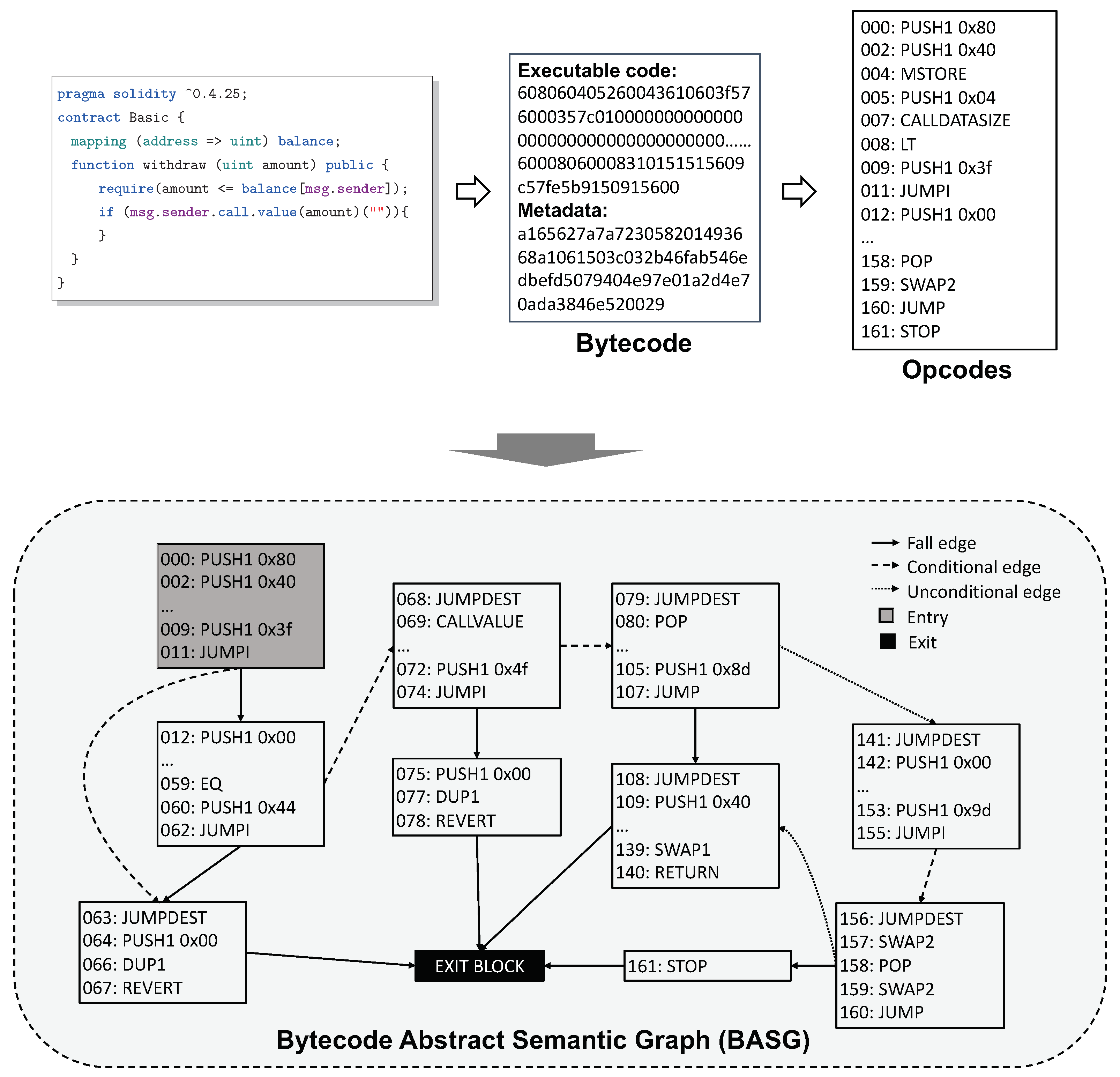
4.2.2. ASG from Bytecode
| Algorithm 2 BASG generation from bytecode. |
| Input: Bytecode of smart contract, B Output: Bytecode abstract semantic graph,
|
4.3. Graph Similarity Learning
4.3.1. Contract Graph Embedding
4.3.2. Graph Matching Network
5. Evaluation
5.1. Experimental Setup
5.2. Performance Evaluation
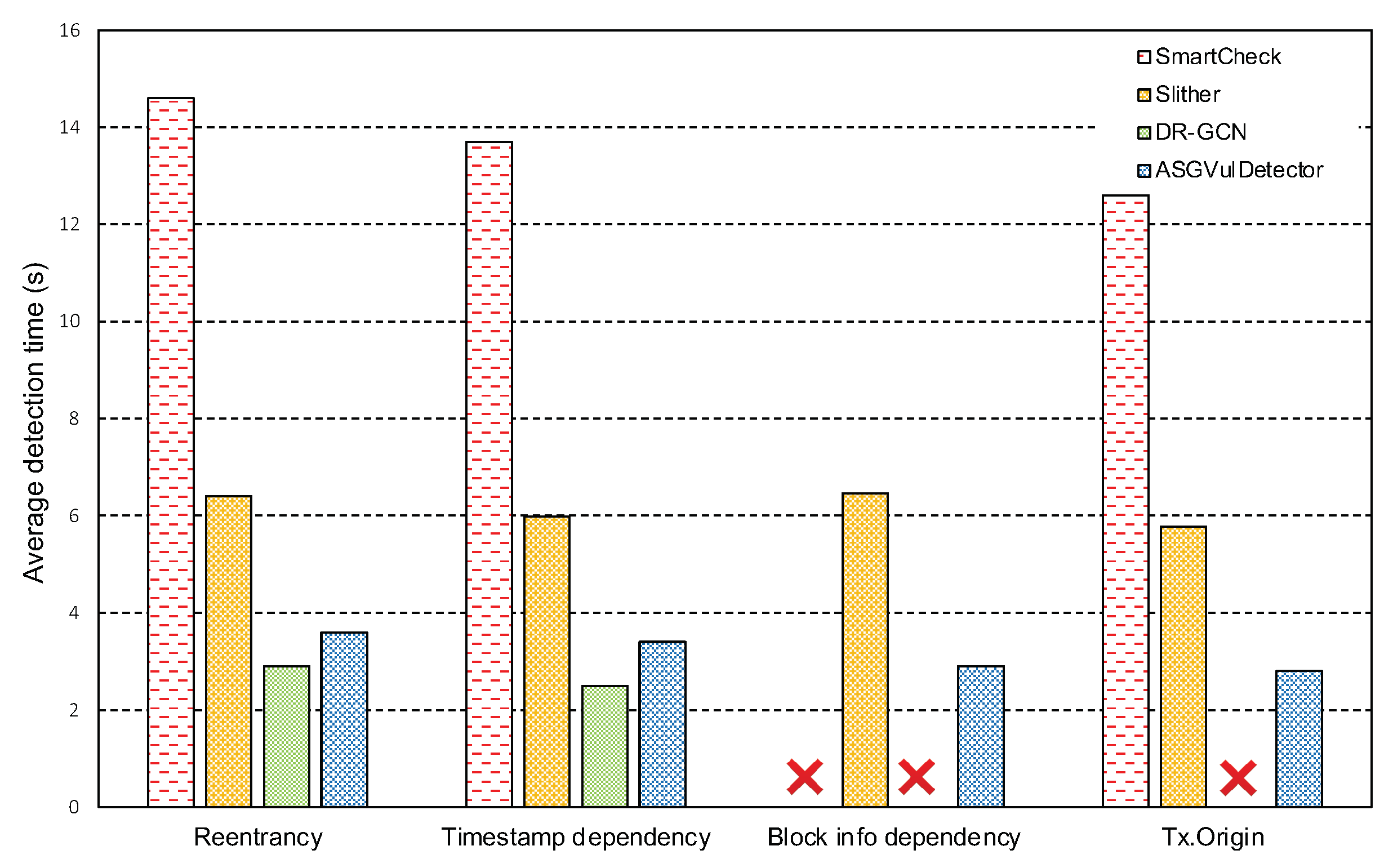
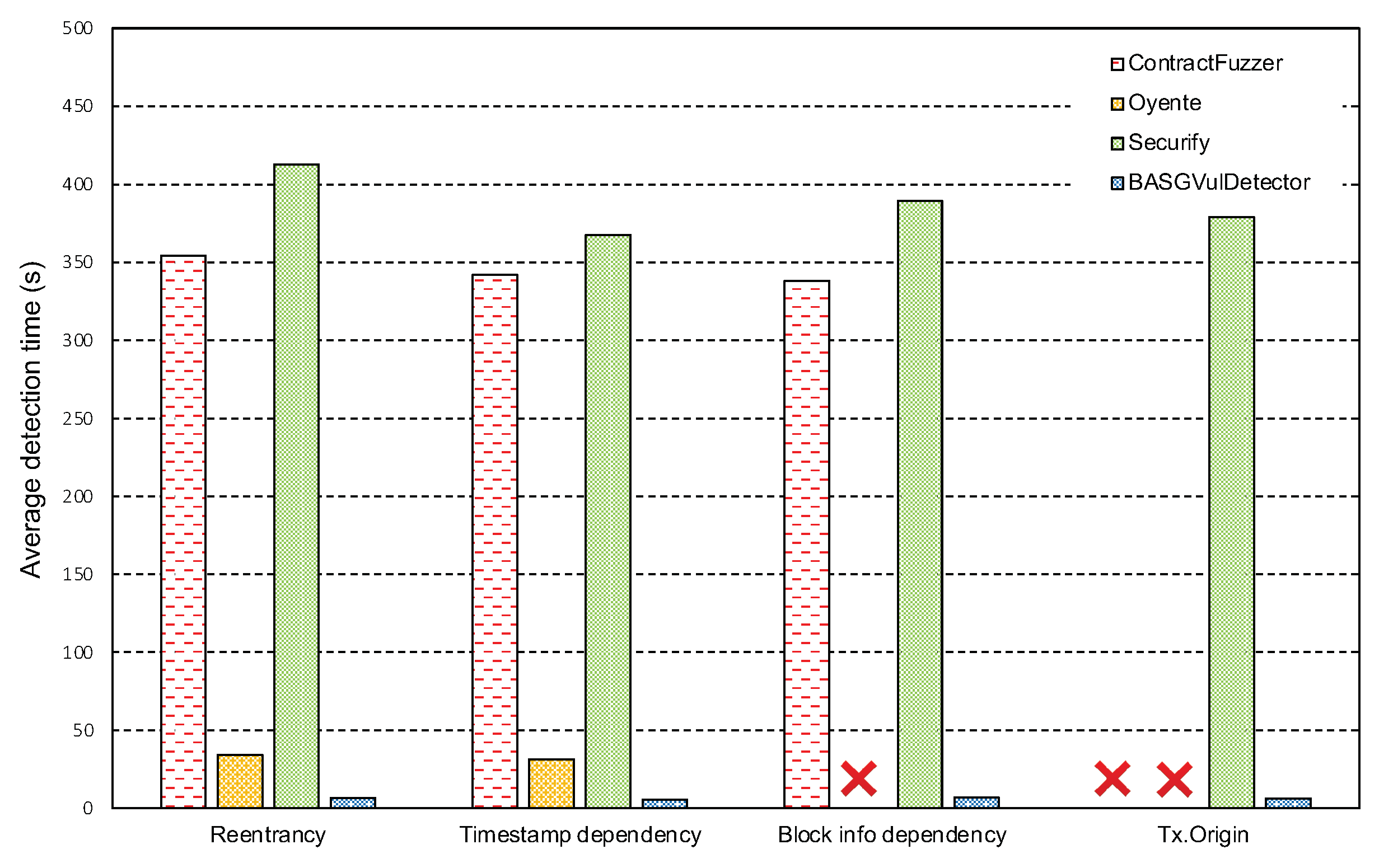
5.3. Detection Time Cost
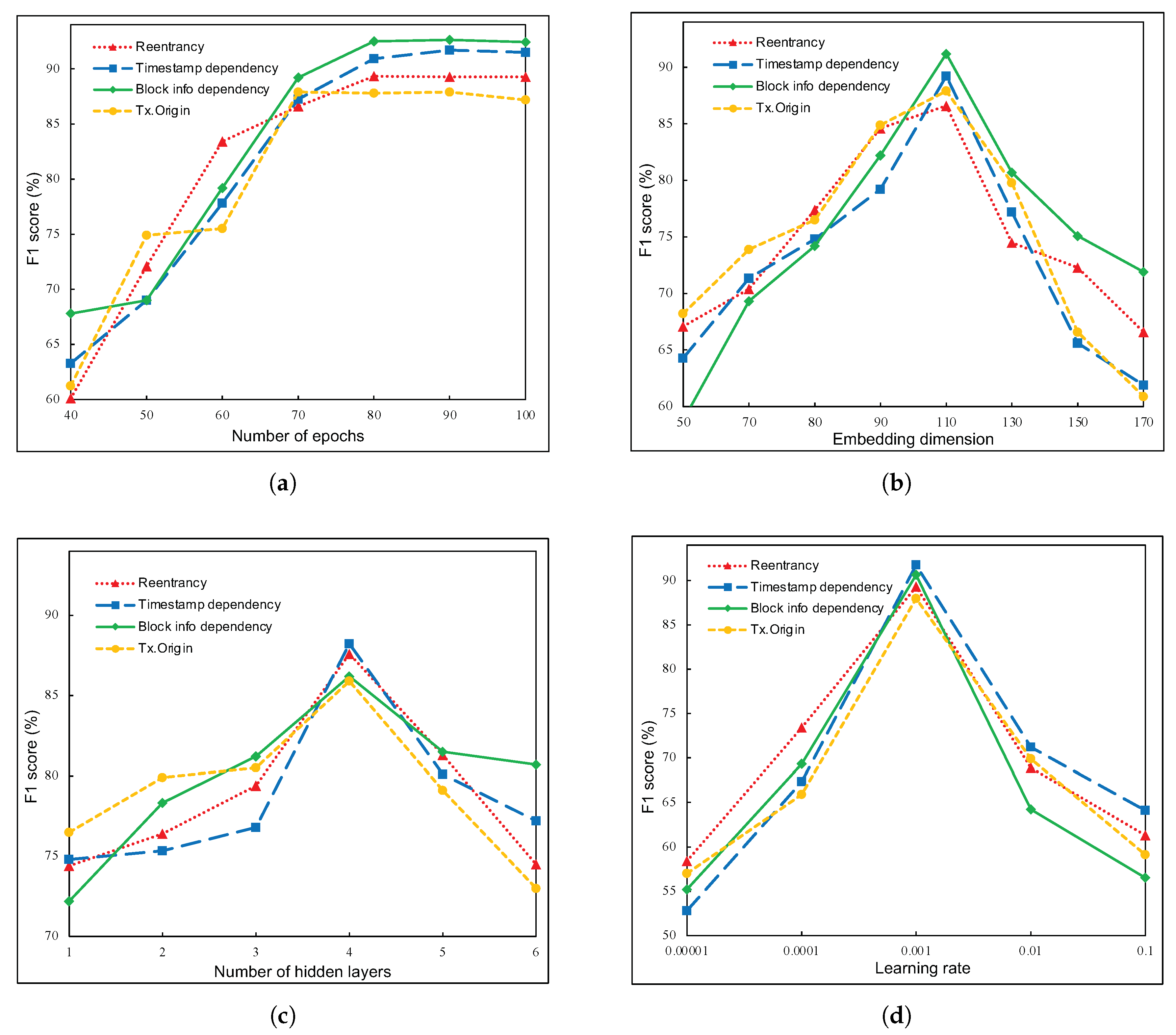
5.4. Impact of GMN Parameters
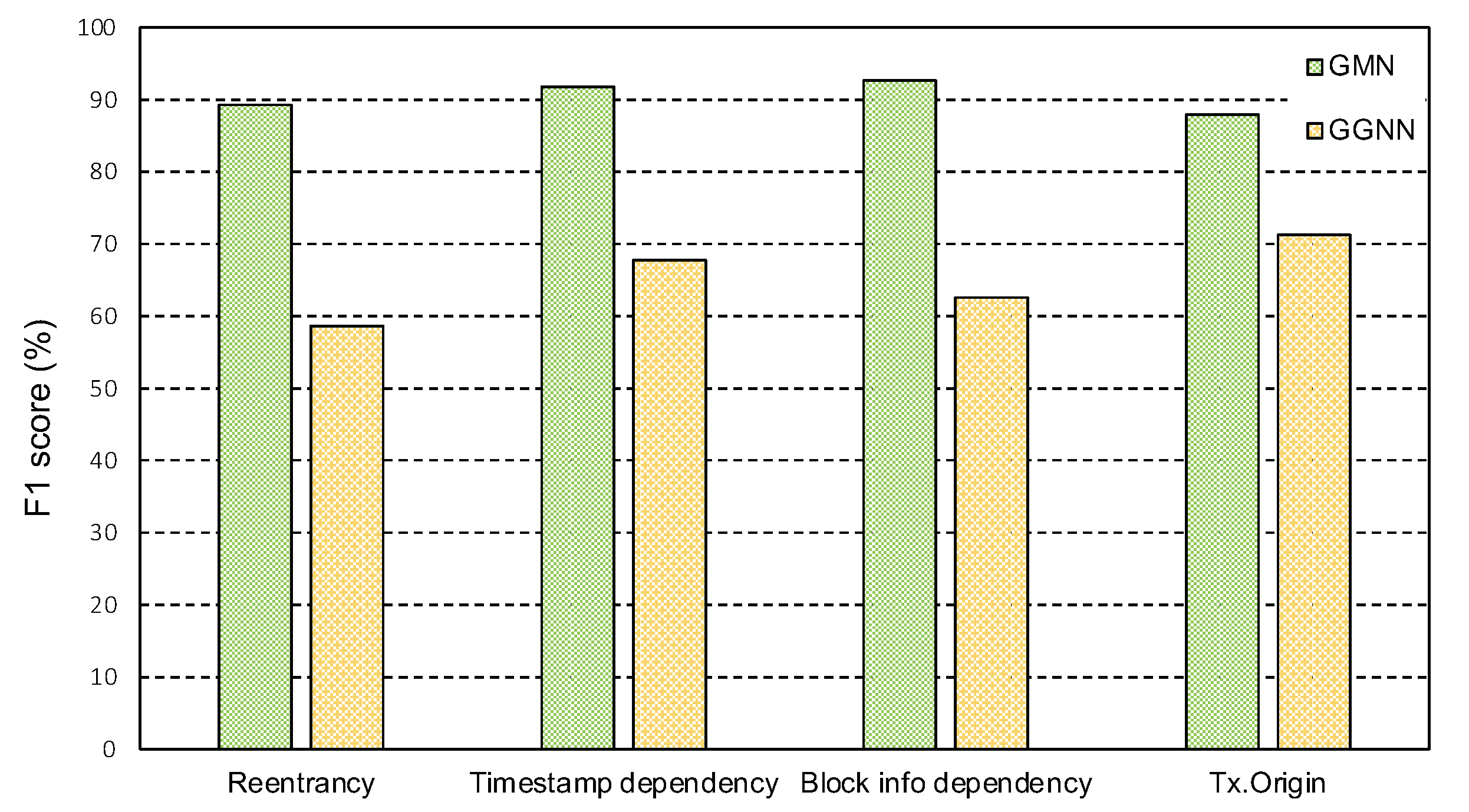
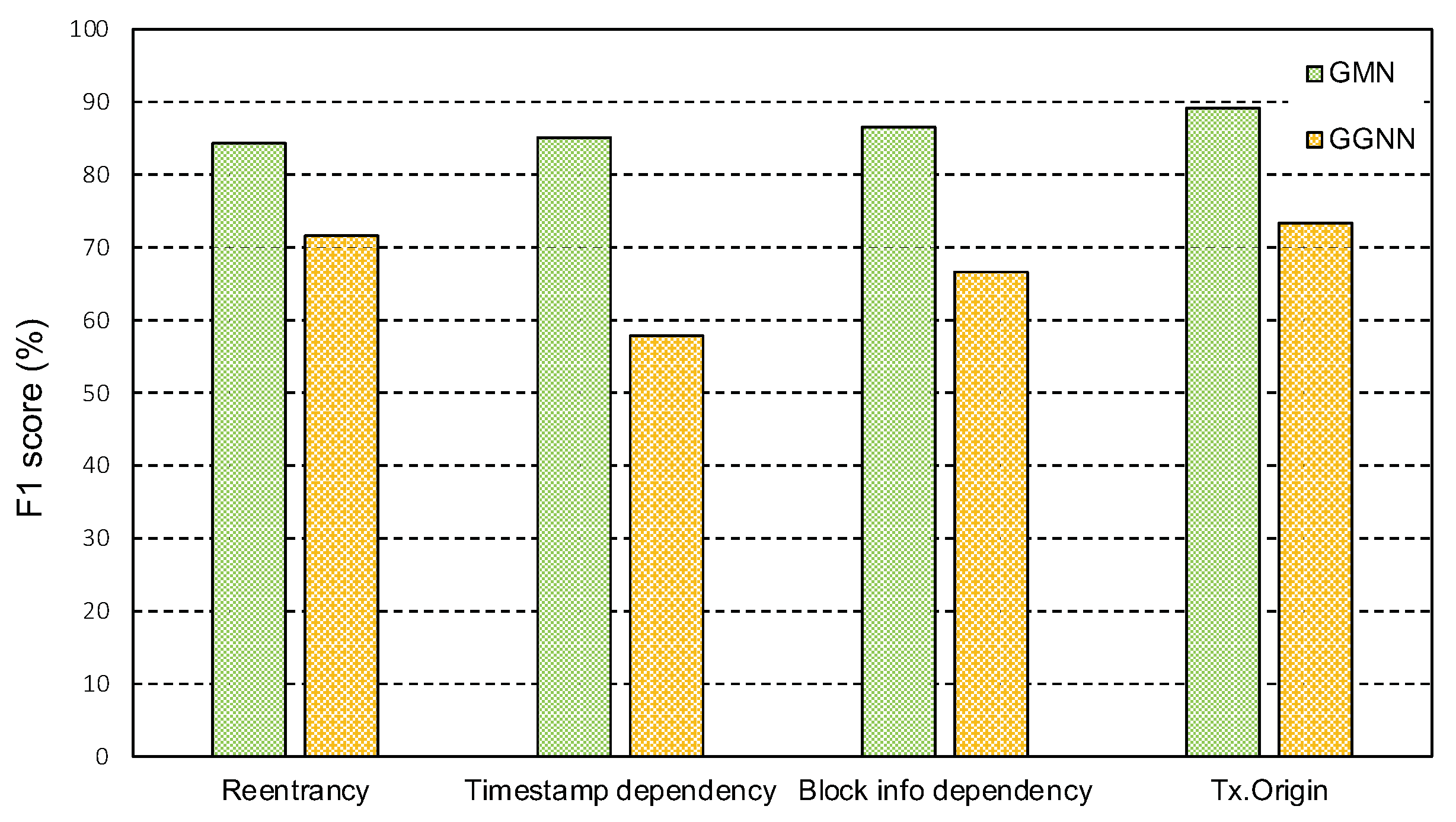
5.5. Impact of Different Models
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ethereum. Ethereum: Blockchain App Platform. Available online: https://www.ethereum.org/ (accessed on 13 April 2022).
- Nick, S. Formalizing and Securing Relationships on Public Networks. First Monday 1997, 2, 1–21. [Google Scholar]
- Khan, S.N.; Loukil, F.; Ghedira-Guegan, C.; Benkhelifa, E.; Bani-Hani, A. Blockchain smart contracts: Applications, challenges, and future trends. Peer-to-Peer Netw. Appl. 2021, 14, 2901–2905. [Google Scholar] [CrossRef] [PubMed]
- Vacca, A.; Sorbo, A.D.; A.Visaggio, C.; Canfora, G. A systematic literature review of blockchain and smart contract development: Techniques, tools, and open challenges. J. Syst. Softw. 2021, 174, 110891. [Google Scholar] [CrossRef]
- Izhar, M.M.; Louis, S.C.; Alana, G.; Elgar, G.; Gabrielle, F.; Ryan, S.; M, K.H.; Marek, L. Understanding a revolutionary and flawed grand experiment in blockchain: The DAO attack. J. Cases Inf. Technol. 2019, 21, 19–32. [Google Scholar]
- Destefanis, G.; Marchesi, M.; Ortu, M.; Tonelli, R.; Bracciali, A.; Hierons, R. Smart contracts vulnerabilities: A call for blockchain software engineering? In Proceedings of the 2018 International Workshop on Blockchain Oriented Software Engineering, Campobasso, Italy, 20 March 2018; pp. 19–25. [Google Scholar]
- Enmei, L.; Wenjun, L. Static analysis of integer overflow of smart contracts in ethereum. In Proceedings of the 2020 4th International Conference on Cryptography, Security and Privacy, Nanjing, China, 10–12 January 2020; pp. 110–115. [Google Scholar]
- Liu, Z.; Qian, P.; Wang, X.; Zhu, L.; He, Q.; Ji, S. Smart Contract Vulnerability Detection: From Pure Neural Network to Interpretable Graph Feature and Expert Pattern Fusion. In Proceedings of the 30th International Joint Conference on Artificial Intelligence, Montreal, QC, Canada, 19–26 August 2021; pp. 2751–2759. [Google Scholar]
- Zhou, L.; Qin, K.; Cully, A.; Livshits, B.; Gervais, A. On the Just-In-Time Discovery of Profit-Generating Transactions in DeFi Protocols. In Proceedings of the 2021 IEEE Symposium on Security and Privacy, San Francisco, CA, USA, 24–27 May 2021; pp. 919–936. [Google Scholar]
- Perez, D.; Livshits, B. Smart Contract Vulnerabilities: Vulnerable Does Not Imply Exploited. In Proceedings of the 30th USENIX Security Symposium, Vancouver, BC, Canada, 11–13 August 2021; pp. 1325–1341. [Google Scholar]
- Jiang, B.; Liu, Y.; Chan, W.K. ContractFuzzer: Fuzzing smart contracts for vulnerability detection. In Proceedings of the 33rd ACM/IEEE International Conference on Automated Software Engineering, Montpellier, France, 3–7 September 2018; pp. 259–269. [Google Scholar]
- Grieco, G.; Song, W.; Cygan, A.; Feist, J.; Groce, A. Echidna: Effective, Usable, and Fast Fuzzing for Smart Contracts. In Proceedings of the 29th ACM SIGSOFT International Symposium on Software Testing and Analysis, Virtual Event, 18–22 July 2020; pp. 557–560. [Google Scholar]
- Wüstholz, V.; Christakis, M. Harvey: A Greybox Fuzzer for Smart Contracts. In Proceedings of the 28th ACM Joint European Software Engineering Conference and Symposium on the Foundations of Software Engineering, Virtual Event, 8–13 November 2020; pp. 1398–1409. [Google Scholar]
- Nguyen, T.D.; Pham, L.H.; Sun, J.; Lin, Y.; Minh, Q.T. sFuzz: An efficient adaptive fuzzer for solidity smart contracts. In Proceedings of the ACM/IEEE 42nd International Conference on Software Engineering, Seoul, Korea, 27 June–19 July 2020; pp. 778–788. [Google Scholar]
- Luu, L.; Chu, D.H.; Olickel, H.; Saxena, P.; Hobor, A. Making Smart Contracts Smarter. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, Vienna, Austria, 24–28 October 2016; pp. 254–269. [Google Scholar]
- Torres, C.F.; Schütte, J.; State, R. Osiris: Hunting for Integer Bugs in Ethereum Smart Contracts. In Proceedings of the 34th Annual Computer Security Applications Conference, San Juan, PR, USA, 3–7 December 2018; pp. 664–676. [Google Scholar]
- Mossberg, M.; Manzano, F.; Hennenfent, E.; Groce, A.; Grieco, G.; Feist, J.; Brunson, T.; Dinaburg, A. Manticore: A User-Friendly Symbolic Execution Framework for Binaries and Smart Contracts. In Proceedings of the 2019 34th IEEE/ACM International Conference on Automated Software Engineering, San Diego, CA, USA, 11–15 November 2019; pp. 1186–1189. [Google Scholar]
- So, S.; Hong, S.; Oh, H. SmarTest: Effectively Hunting Vulnerable Transaction Sequences in Smart Contracts through Language Model-Guided Symbolic Execution. In Proceedings of the 30th USENIX Security Symposium, Vancouver, BC, Canada, 11–13 August 2021; pp. 1361–1378. [Google Scholar]
- Lin, S.W.; Tolmach, P.; Liu, Y.; Li, Y. SolSEE: A Source-Level Symbolic Execution Engine for Solidity. In Proceedings of the 2022 ACM Joint European Software Engineering Conference and Symposium on the Foundations of Software Engineering, Singapore, 14–18 November 2022; pp. 1–6. [Google Scholar]
- Bai, X.; Cheng, Z.; Duan, Z.; Hu, K. Formal Modeling and Verification of Smart Contracts. In Proceedings of the 2018 7th International Conference on Software and Computer Applications, Kuantan, Malaysia, 8–10 February 2018; pp. 322–326. [Google Scholar]
- Tsankov, P.; Dan, A.; Drachsler-Cohen, D.; Gervais, A.; Bünzli, F.; Vechev, M. Securify: Practical Security Analysis of Smart Contracts. In Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security, Toronto, ON, Canada, 15–19 October 2018; pp. 67–82. [Google Scholar]
- Albert, E.; Correas, J.; Gordillo, P.; Román-Díez, G.; Rubio, A. SAFEVM: A safety verifier for Ethereum smart contracts. In Proceedings of the 28th ACM SIGSOFT International Symposium on Software Testing and Analysis, Beijing, China, 15–19 July 2019; pp. 386–389. [Google Scholar]
- Antonino, P.; Roscoe, A.W. Solidifier: Bounded model checking solidity using lazy contract deployment and precise memory modelling. In Proceedings of the 36th Annual ACM Symposium on Applied Computing, Virtual Event, 22–26 March 2021; pp. 1788–1797. [Google Scholar]
- Tikhomirov, S.; Voskresenskaya, E.; Ivanitskiy, I.; Takhaviev, R.; Marchenko, E.; Alexandrov, Y. SmartCheck: Static Analysis of Ethereum Smart Contracts. In Proceedings of the 2018 IEEE/ACM 1st International Workshop on Emerging Trends in Software Engineering for Blockchain, Gothenburg, Sweden, 27 May 2018; pp. 9–16. [Google Scholar]
- Feist, J.; Grieco, G.; Groce, A. Slither: A Static Analysis Framework for Smart Contracts. In Proceedings of the 2019 IEEE/ACM 2nd International Workshop on Emerging Trends in Software Engineering for Blockchain, Montreal, QC, Canada, 27 May 2019; pp. 8–15. [Google Scholar]
- Xue, Y.; Ma, M.; Lin, Y.; Sui, Y.; Ye, J.; Peng, T. Cross-Contract Static Analysis for Detecting Practical Reentrancy Vulnerabilities in Smart Contracts. In Proceedings of the 35th IEEE/ACM International Conference on Automated Software Engineering, Melbourne, VIC, Australia, 21–25 September 2020; pp. 1029–1040. [Google Scholar]
- Zhuang, Y.; Liu, Z.; Qian, P.; Liu, Q.; Wang, X.; He, Q. Smart Contract Vulnerability Detection Using Graph Neural Networks. In Proceedings of the 29th International Joint Conference on Artificial Intelligence, Yokohama, Japan, 11–17 July 2020; pp. 3283–3290. [Google Scholar]
- Alharby, M.; Aldweesh, A.; van Moorsel, A. Blockchain-based Smart Contracts: A Systematic Mapping Study. In Proceedings of the 2018 International Conference on Cloud Computing, Big Data and Blockchain, Fuzhou, China, 15–17 November 2018; pp. 1–6. [Google Scholar]
- Khan, Z.A.; Namin, A.S. Ethereum Smart Contracts: Vulnerabilities and their Classifications. In Proceedings of the 2020 IEEE International Conference on Big Data, Atlanta, GA, USA, 10–13 December 2020; pp. 1–10. [Google Scholar]
- Chen, J.; Xia, X.; Lo, D.; Grundy, J.; Luo, X.; Chen, T. Defining Smart Contract Defects on Ethereum. IEEE Trans. Softw. Eng. 2022, 48, 327–345. [Google Scholar] [CrossRef]
- Fan, W.; Ma, Y.; Li, Q.; He, Y.; Zhao, E.; Tang, J.; Yin, D. Graph Neural Networks for Social Recommendation. In Proceedings of the 2019 World Wide Web Conference, San Francisco, CA, USA, 13–17 May 2019; pp. 417–426. [Google Scholar]
- Zhao, L.; Li, Z.; Al-Dubai, A.Y.; Min, G.; Li, J.; Hawbani, A.; Zomaya, A.Y. A Novel Prediction-Based Temporal Graph Routing Algorithm for Software-Defined Vehicular Networks. IEEE Trans. Intell. Transp. Syst. 2022, 23, 13275–13290. [Google Scholar] [CrossRef]
- Li, Y.; Gu, C.; Dullien, T.; Vinyals, O.; Kohli, P. Graph Matching Networks for Learning the Similarity of Graph Structured Objects. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; pp. 3835–3845. [Google Scholar]
- Allamanis, M.; Brockschmidt, M.; Khademi, M. Learning to represent programs with graphs. In Proceedings of the 2018 International conference on learning representations, Vancouver, BC, Canada, 30 April–3 May 2018; pp. 1–17. [Google Scholar]
- Contro, F.; Crosara, M.; Ceccato, M.; Preda, M.D. EtherSolve: Computing an Accurate Control-Flow Graph from Ethereum Bytecode. In Proceedings of the 29th International Conference on Program Comprehension, Madrid, Spain, 20–21 May 2021; pp. 127–137. [Google Scholar]
- Wood, G. Ethereum: A Secure Decentralised Generalised Transaction Ledger. Available online: https://ethereum.github.io/yellowpaper/ (accessed on 21 April 2022).
- Ferreira, J.F.; Cruz, P.; Durieux, T.; Abreu, R. SmartBugs: A Framework to Analyze Solidity Smart Contracts. In Proceedings of the 35th IEEE/ACM International Conference on Automated Software Engineering, Virtual Event, 21–25 December 2020; pp. 1349–1352. [Google Scholar]
- Ghaleb, A.; Pattabiraman, K. How effective are smart contract analysis tools? evaluating smart contract static analysis tools using bug injection. In Proceedings of the 29th ACM SIGSOFT International Symposium on Software Testing and Analysis, Virtual Event, 18–22 July 2020; pp. 415–427. [Google Scholar]

| Opcode | Normalized Code |
|---|---|
| LOG0-LOG4 | LOGX |
| PUSH1-PUSH32 | PUSHX |
| DUP1-DUP16 | - |
| SWAP1-SWAP16 | - |
| POP | - |
| Opcode | Normalized Operand |
|---|---|
| ADD, MUL, SUB, EXP, SIGNEXTEND | ArithData |
| BLOCKHASH, COINBASE, TIMESTAMP, NUMBER, DIFFICULTY, GASLIMIT | BlockData |
| LT, GT, SLT, SGT, EQ, ISZERO | LogicData |
| MLOAD | MemData |
| SLOAD | StorData |
| BYTE, SHL, SHR, SAR AND, OR, XOR, NOT | BitData |
| Vulnerability | Method | Acc (%) | Rec (%) | Pre (%) | F1 (%) |
|---|---|---|---|---|---|
| Reentrancy | SmartCheck | 55.70 | 74.95 | 62.08 | 67.91 |
| Slither | 70.51 | 85.93 | 75.83 | 80.57 | |
| DR-GCN | 66.21 | 81.78 | 71.08 | 76.06 | |
| ASGVulDetector | 84.96 | 95.37 | 84.17 | 89.42 | |
| Timestamp dependency | SmartCheck | 40.41 | 77.44 | 37.45 | 50.49 |
| Slither | 74.19 | 89.47 | 77.27 | 82.93 | |
| DR-GCN | 50.59 | 84.22 | 47.55 | 60.78 | |
| ASGVulDetector | 87.02 | 94.59 | 89.09 | 91.76 | |
| Block info dependency | SmartCheck | - | - | - | - |
| Slither | 67.77 | 84.46 | 70.43 | 76.81 | |
| DR-GCN | - | - | - | - | |
| ASGVulDetector | 88.99 | 94.01 | 91.30 | 92.63 | |
| Tx.Origin | SmartCheck | 41.12 | 69.34 | 43.69 | 53.60 |
| Slither | 60.96 | 82.09 | 62.97 | 71.27 | |
| DR-GCN | - | - | - | - | |
| ASGVulDetector | 81.18 | 87.58 | 88.35 | 87.97 |
| Vulnerability | Method | Acc (%) | Rec (%) | Pre (%) | F1 (%) |
|---|---|---|---|---|---|
| Reentrancy | ContractFuzzer | 37.94 | 67.12 | 31.36 | 42.75 |
| Oyente | 41.64 | 74.02 | 42.50 | 54.00 | |
| Securify | 53.62 | 77.46 | 54.42 | 63.93 | |
| BASGVulDetector | 80.59 | 92.73 | 80.00 | 85.90 | |
| Timestamp dependency | ContractFuzzer | 32.96 | 82.94 | 28.36 | 40.70 |
| Oyente | 43.24 | 76.62 | 38.45 | 52.55 | |
| Securify | 52.06 | 84.62 | 50.00 | 62.86 | |
| BASGVulDetector | 79.28 | 92.17 | 81.36 | 86.43 | |
| Block info dependency | ContractFuzzer | 30.52 | 58.08 | 28.75 | 38.46 |
| Oyente | - | - | - | - | |
| Securify | 49.40 | 72.15 | 53.75 | 61.60 | |
| BASGVulDetector | 85.04 | 93.66 | 86.09 | 89.71 | |
| Tx.Origin | ContractFuzzer | - | - | - | - |
| Oyente | - | - | - | - | |
| Securify | 47.12 | 71.93 | 51.00 | 59.68 | |
| BASGVulDetector | 81.56 | 86.94 | 89.81 | 88.35 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Liu, D. Toward Vulnerability Detection for Ethereum Smart Contracts Using Graph-Matching Network. Future Internet 2022, 14, 326. https://doi.org/10.3390/fi14110326
Zhang Y, Liu D. Toward Vulnerability Detection for Ethereum Smart Contracts Using Graph-Matching Network. Future Internet. 2022; 14(11):326. https://doi.org/10.3390/fi14110326
Chicago/Turabian StyleZhang, Yujian, and Daifu Liu. 2022. "Toward Vulnerability Detection for Ethereum Smart Contracts Using Graph-Matching Network" Future Internet 14, no. 11: 326. https://doi.org/10.3390/fi14110326
APA StyleZhang, Y., & Liu, D. (2022). Toward Vulnerability Detection for Ethereum Smart Contracts Using Graph-Matching Network. Future Internet, 14(11), 326. https://doi.org/10.3390/fi14110326






