Autonomous Navigation of a Solar-Powered UAV for Secure Communication in Urban Environments with Eavesdropping Avoidance
Abstract
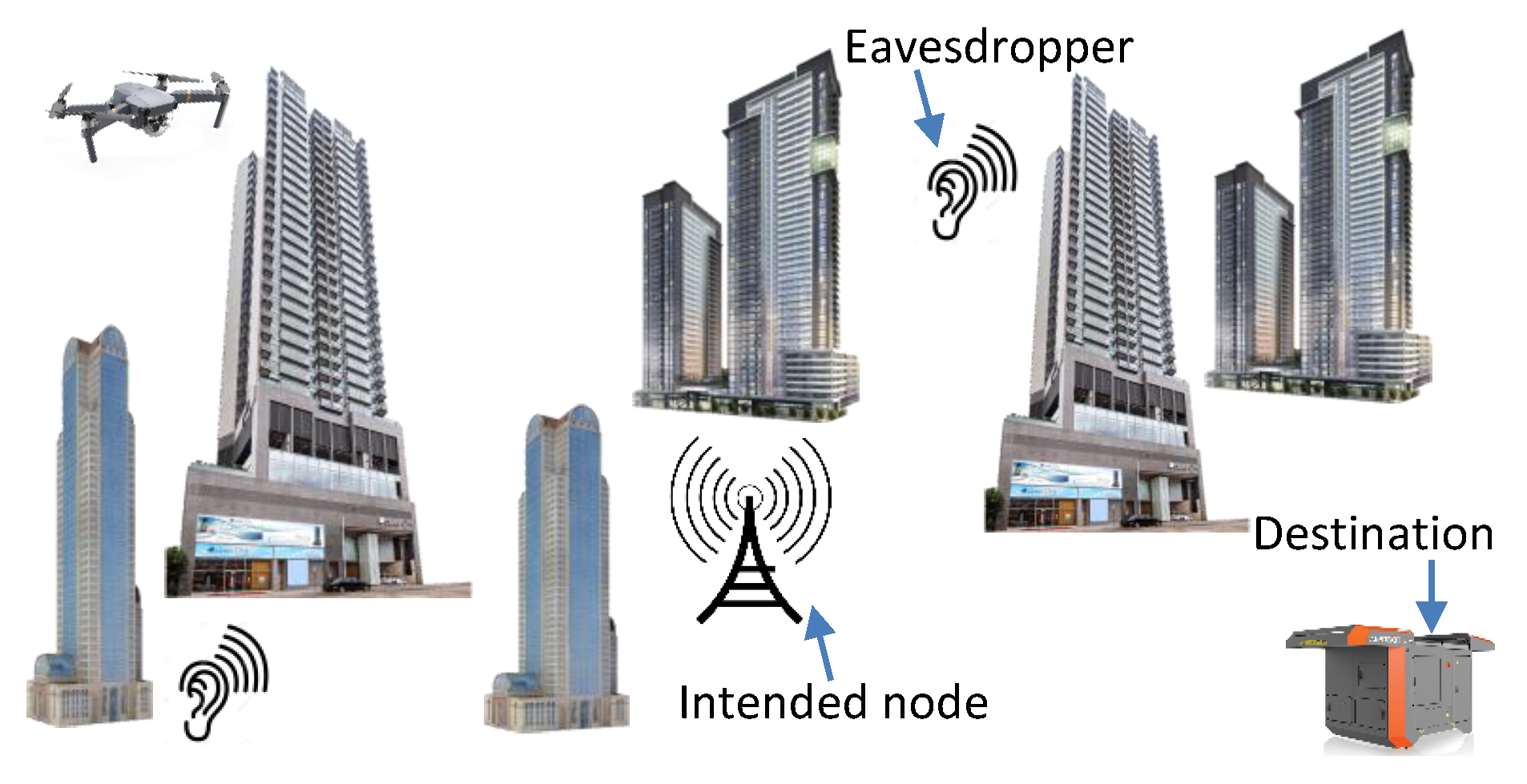
1. Introduction
Related Work
2. Problem Statement
2.1. UAV Model
2.2. Energy Harvesting and Consuming
2.3. No-Fly-Zone (NFZ)
2.4. Line-of-Sight (LoS)
2.5. Secure Communication
2.6. Problem Statement
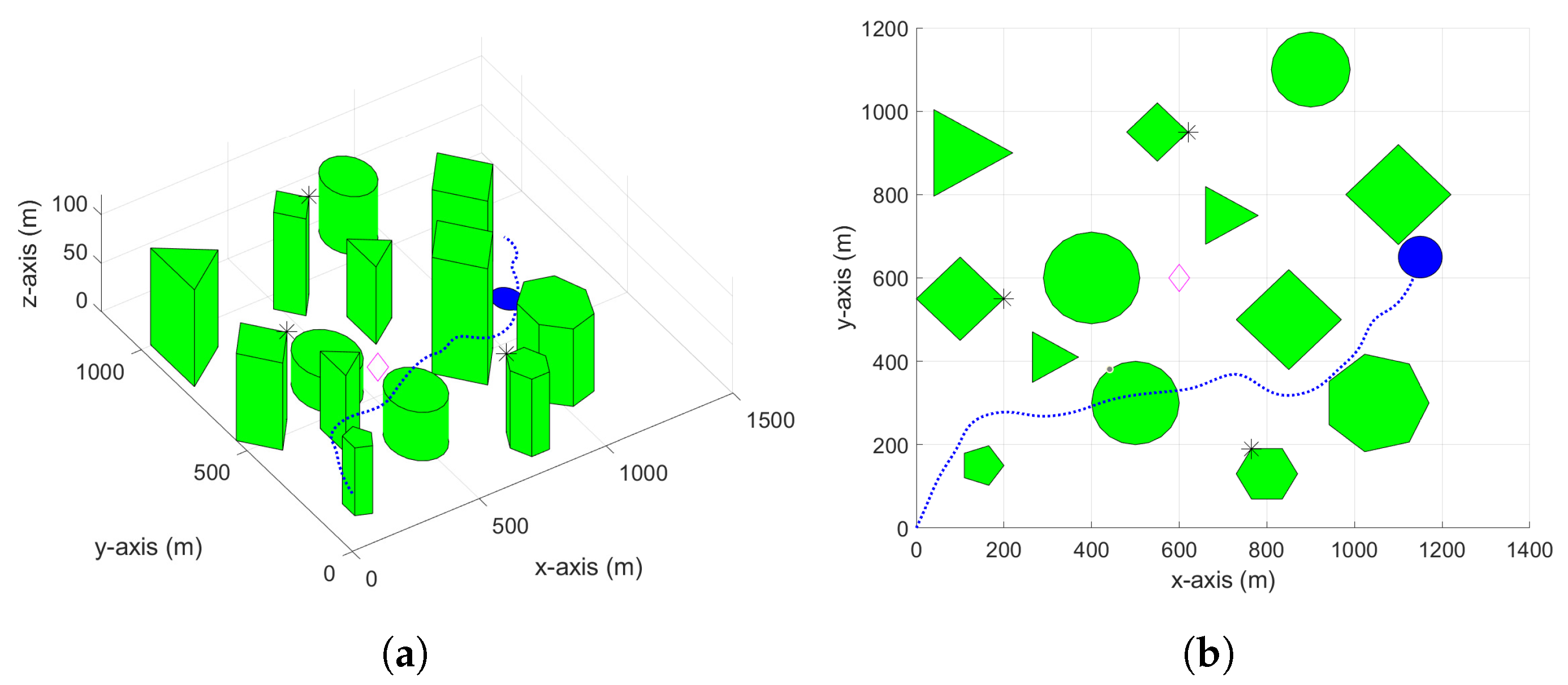
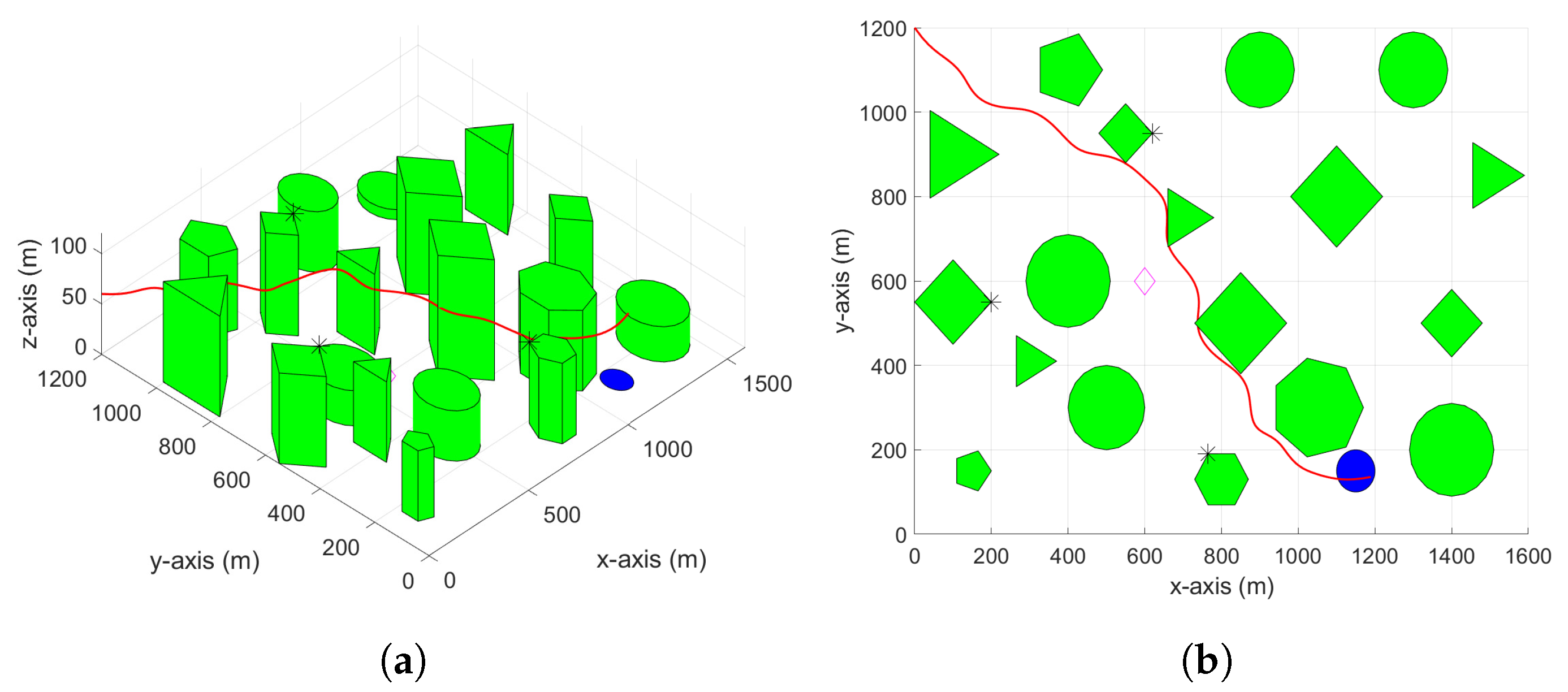
3. RRT-Based Path Planning
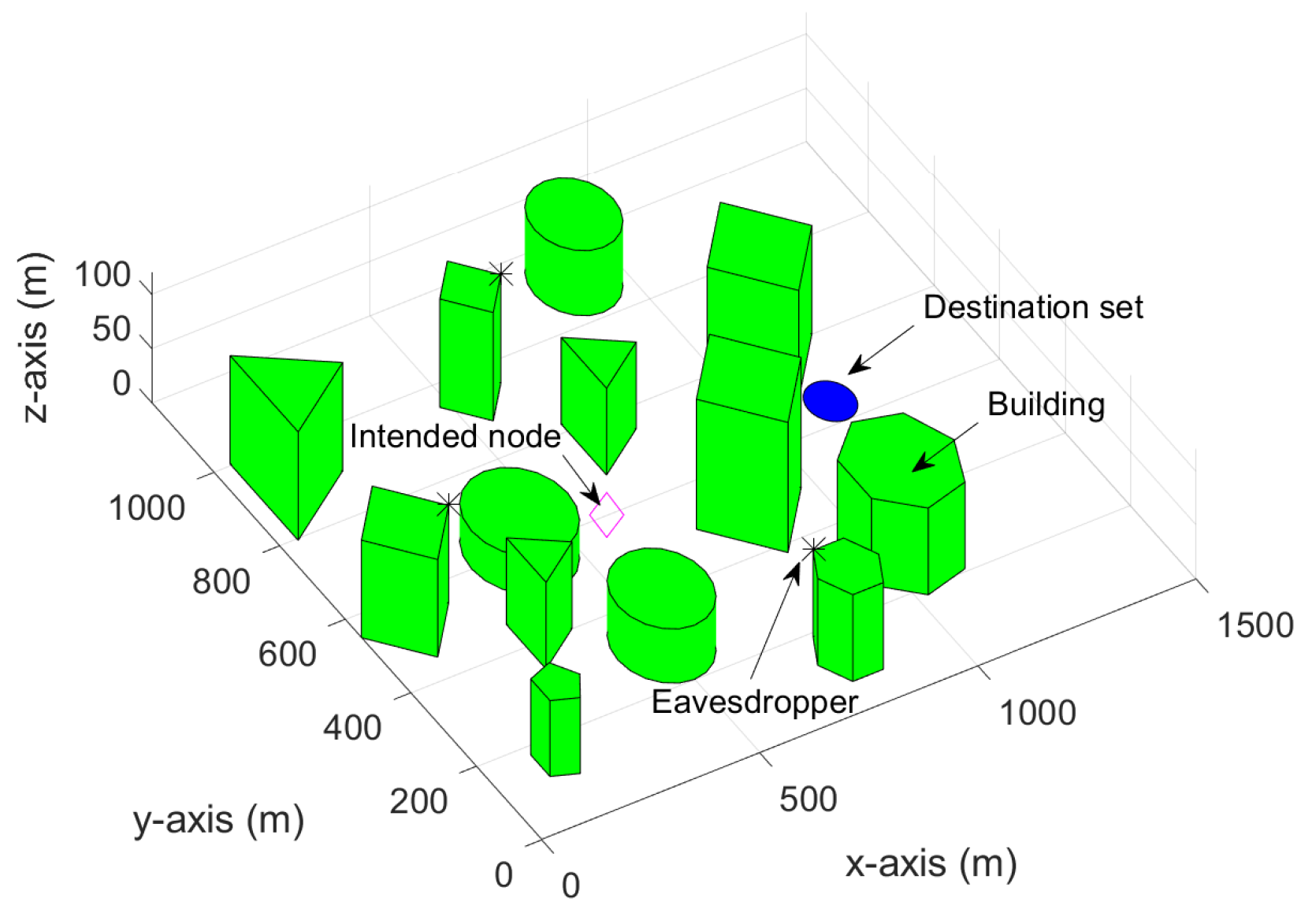
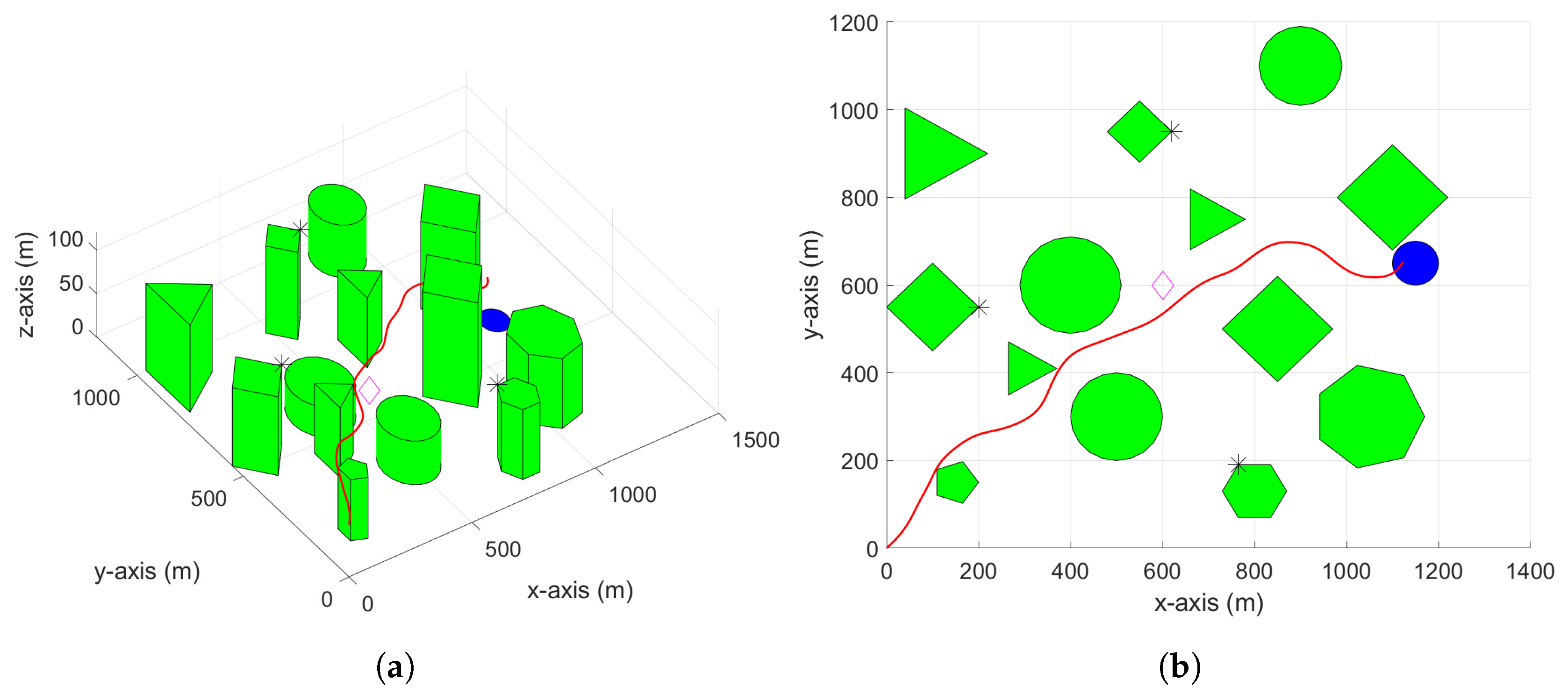
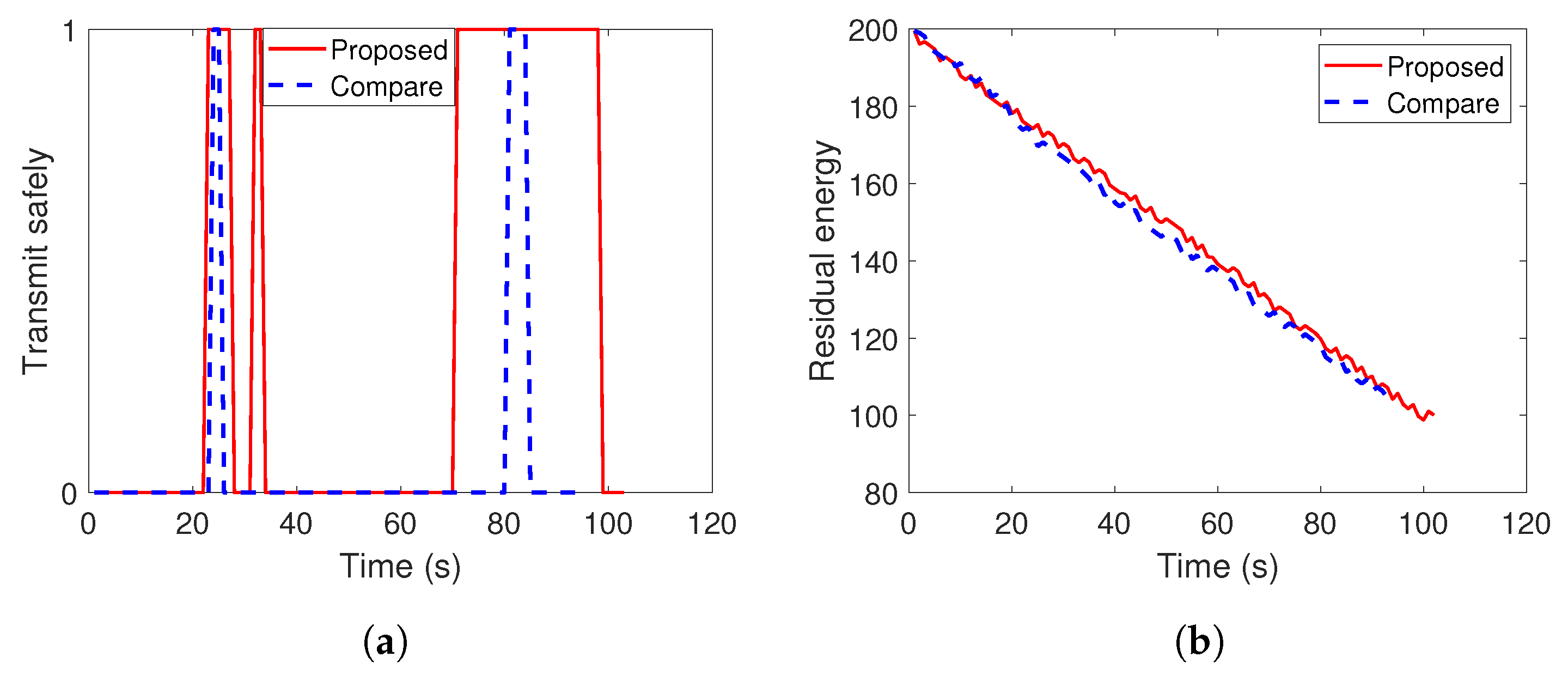
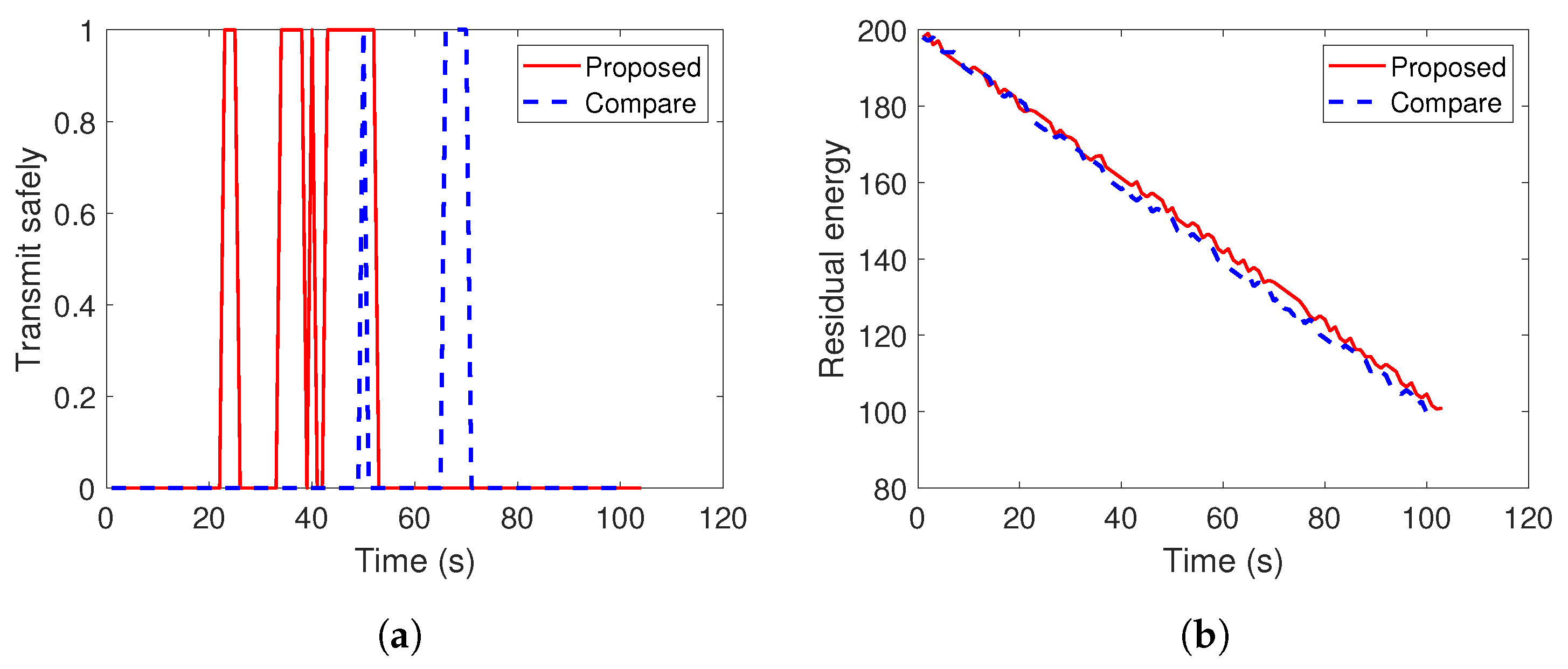
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ghaddar, A.; Merei, A. EAOA: Energy-Aware Grid-Based 3D-Obstacle Avoidance in Coverage Path Planning for UAVs. Future Internet 2020, 12, 29. [Google Scholar] [CrossRef]
- Huang, H.; Savkin, A.V. Towards the internet of flying robots: A survey. Sensors 2018, 18, 4038. [Google Scholar] [CrossRef] [PubMed]
- Savkin, A.V.; Huang, H.; Ni, W. Securing UAV Communication in the Presence of Stationary or Mobile Eavesdroppers via Online 3D Trajectory Planning. IEEE Wirel. Commun. Lett. 2020, 9, 1211–1215. [Google Scholar] [CrossRef]
- Kavallieratos, G.; Katsikas, S.; Gkioulos, V. Cybersecurity and Safety Co-Engineering of Cyberphysical Systems—A Comprehensive Survey. Future Internet 2020, 12, 65. [Google Scholar] [CrossRef]
- Wang, D.; Bai, B.; Zhang, G.; Han, Z. Optimal Placement of Low-Altitude Aerial Base Station for Securing Communications. IEEE Wirel. Commun. Lett. 2019, 8, 869–872. [Google Scholar] [CrossRef]
- Cui, M.; Zhang, G.; Wu, Q.; Ng, D.W.K. Robust Trajectory and Transmit Power Design for Secure UAV Communications. IEEE Trans. Veh. Technol. 2018, 67, 9042–9046. [Google Scholar] [CrossRef]
- Huang, H.; Savkin, A.V.; Ni, W. Energy-Efficient 3D Navigation of a Solar-Powered UAV for Secure Communication in the Presence of Eavesdroppers and No-Fly Zones. Energies 2020, 13, 1445. [Google Scholar] [CrossRef]
- Yuan, X.; Feng, Z.; Ni, W.; Liu, R.P.; Zhang, J.A.; Xu, W. Secrecy Performance of Terrestrial Radio Links under Collaborative Aerial Eavesdropping. IEEE Trans. Inf. Forensics Secur. 2020, 15, 604–619. [Google Scholar] [CrossRef]
- Huang, H.; Savkin, A.V.; Ding, M.; Kaafar, M.A. Optimized deployment of drone base station to improve user experience in cellular networks. J. Netw. Comput. Appl. 2019, 144, 49–58. [Google Scholar] [CrossRef]
- LaValle, S.M.; Kuffner, J.J., Jr. Randomized kinodynamic planning. Int. J. Robot. Res. 2001, 20, 378–400. [Google Scholar] [CrossRef]
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A formal basis for the heuristic determination of minimum cost paths. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Dubins, L.E. On curves of minimal length with a constraint on average curvature, and with prescribed initial and terminal positions and tangents. Am. J. Math. 1957, 79, 497–516. [Google Scholar] [CrossRef]
- Savkin, A.V.; Hoy, M. Reactive and the shortest path navigation of a wheeled mobile robot in cluttered environments. Robotica 2013, 31, 323. [Google Scholar] [CrossRef]
- Savkin, A.V.; Huang, H. Optimal Aircraft Planar Navigation in Static Threat Environments. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 2413–2426. [Google Scholar] [CrossRef]
- Zhang, Y.; Gong, D.W.; Zhang, J.H. Robot path planning in uncertain environment using multi-objective particle swarm optimization. Neurocomputing 2013, 103, 172–185. [Google Scholar] [CrossRef]
- Roberge, V.; Tarbouchi, M.; Labonté, G. Comparison of parallel genetic algorithm and particle swarm optimization for real-time UAV path planning. IEEE Trans. Ind. Inform. 2012, 9, 132–141. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, Y. Operating point optimization of auxiliary power unit using adaptive multi-objective differential evolution algorithm. IEEE Trans. Ind. Electron. 2016, 64, 115–124. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A gravitational search algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Ferguson, D.; Stentz, A. Anytime RRTs. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 5369–5375. [Google Scholar]
- Otte, M.; Frazzoli, E. RRTX: Asymptotically optimal single-query sampling-based motion planning with quick replanning. Int. J. Robot. Res. 2016, 35, 797–822. [Google Scholar] [CrossRef]
- Ko, I.; Kim, B.; Park, F.C. VF-RRT: Introducing optimization into randomized motion planning. In Proceedings of the 2013 9th Asian Control Conference (ASCC), Istanbul, Turkey, 23–26 June 2013; pp. 1–5. [Google Scholar]
- Wang, J.; Meng, M.Q.; Khatib, O. EB-RRT: Optimal Motion Planning for Mobile Robots. IEEE Trans. Autom. Sci. Eng. 2020. [Google Scholar] [CrossRef]
- Li, A.; Wu, Q.; Zhang, R. UAV-enabled cooperative jamming for improving secrecy of ground wiretap channel. IEEE Wirel. Commun. Lett. 2019, 8, 181–184. [Google Scholar] [CrossRef]
- Cai, Y.; Cui, F.; Shi, Q.; Zhao, M.; Li, G.Y. Dual-UAV-enabled secure communications: Joint trajectory design and user scheduling. IEEE J. Sel. Areas Commun. 2018, 36, 1972–1985. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, R.; Zhang, J.; Yang, L. Cooperative Jamming via Spectrum Sharing for Secure UAV Communications. IEEE Wirel. Commun. Lett. 2020, 9, 326–330. [Google Scholar] [CrossRef]
- Kang, Y.; Hedrick, J.K. Linear tracking for a fixed-wing UAV using nonlinear model predictive control. IEEE Trans. Control Syst. Technol. 2009, 17, 1202–1210. [Google Scholar] [CrossRef]
- Li, H.; Savkin, A.V. Wireless sensor network based navigation of micro flying robots in the industrial internet of things. IEEE Trans. Ind. Informatics 2018, 14, 3524–3533. [Google Scholar] [CrossRef]
- Klesh, A.T.; Kabamba, P.T. Solar-powered aircraft: Energy-optimal path planning and perpetual endurance. J. Guid. Control. Dyn. 2009, 32, 1320–1329. [Google Scholar] [CrossRef]
- Matveev, A.S.; Teimoori, H.; Savkin, A.V. A method for guidance and control of an autonomous vehicle in problems of border patrolling and obstacle avoidance. Automatica 2011, 47, 515–524. [Google Scholar] [CrossRef]
- Hoy, M.; Matveev, A.S.; Savkin, A.V. Algorithms for collision-free navigation of mobile robots in complex cluttered environments: A survey. Robotica 2015, 33, 463–497. [Google Scholar] [CrossRef]
- Wu, J.; Wang, H.; Li, N.; Yao, P.; Huang, Y.; Su, Z.; Yu, Y. Distributed trajectory optimization for multiple solar-powered UAVs target tracking in urban environment by Adaptive Grasshopper Optimization Algorithm. Aerosp. Sci. Technol. 2017, 70, 497–510. [Google Scholar] [CrossRef]
- Zhang, G.; Wu, Q.; Cui, M.; Zhang, R. Securing UAV communications via joint trajectory and power control. IEEE Trans. Wirel. Commun. 2019, 18, 1376–1389. [Google Scholar] [CrossRef]
- Friis, H.T. A note on a simple transmission formula. Proc. IRE 1946, 34, 254–256. [Google Scholar] [CrossRef]
- Saeed., R.A.; Recupero., D.R. Path Planning of a Mobile Robot in Grid Space using Boundary Node Method. In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics, Prague, Czech Republic, 29–31 July 2019; pp. 159–166. [Google Scholar]


| Symbol | Meaning |
|---|---|
| Position of the UAV | |
| Linear speed on -plane | |
| Angular speed on -plane | |
| Vertical speed | |
| Heading of the UAV on -plane | |
| Drag of the UAV | |
| Thrust of the UAV | |
| m | The mass of the UAV |
| Energy harvesting power of the UAV | |
| Energy consuming power of the UAV | |
| Residual energy of the UAV | |
| The random tree | |
| The set of paths in |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 20 m/s | 1 rad/s | ||
| 2 m/s | 100 m | ||
| 20 m | V | [0.8, 0, −0.6] | |
| 200 | 20 | ||
| 1 s | T | 150 s | |
| m | 0.5 kg | 1.29 kg/m | |
| A | 0.5 m | 0.011 | |
| 0.1 | 10 | ||
| 0.1 | g | 9.8 kg m | |
| a | [0, 0, 60] | ||
| 1 | 0.8 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, H.; Savkin, A.V. Autonomous Navigation of a Solar-Powered UAV for Secure Communication in Urban Environments with Eavesdropping Avoidance. Future Internet 2020, 12, 170. https://doi.org/10.3390/fi12100170
Huang H, Savkin AV. Autonomous Navigation of a Solar-Powered UAV for Secure Communication in Urban Environments with Eavesdropping Avoidance. Future Internet. 2020; 12(10):170. https://doi.org/10.3390/fi12100170
Chicago/Turabian StyleHuang, Hailong, and Andrey V. Savkin. 2020. "Autonomous Navigation of a Solar-Powered UAV for Secure Communication in Urban Environments with Eavesdropping Avoidance" Future Internet 12, no. 10: 170. https://doi.org/10.3390/fi12100170
APA StyleHuang, H., & Savkin, A. V. (2020). Autonomous Navigation of a Solar-Powered UAV for Secure Communication in Urban Environments with Eavesdropping Avoidance. Future Internet, 12(10), 170. https://doi.org/10.3390/fi12100170






