Integrating Machine Learning with Hybrid and Surrogate Models to Accelerate Multiscale Modeling of Acute Respiratory Infections
Abstract
1. Introduction
2. Related Works
2.1. Hybrid Modeling
2.2. Surrogate Modeling
3. Materials and Methods
3.1. Epidemic Models
- The modeled population represents one large metropolitan area without strong clusterization (i.e., the city districts are well connected with each other).
- The contact patterns of individuals in a given city does not exhibit substantial changes in the course of several years, so the topology of contact networks might be approximately assessed before the outbreak.
- The population size is constant: we do not consider mortality, migration, births.
- The contact network is fixed and not influenced by an epidemic (i.e., network edges are not added or removed during the simulation).
- The individuals do not differ (i.e., have the same transmission rate and latent and infectious periods).
- The modeled infection is caused by a single virus which does not change its characteristics during the simulation.
3.1.1. Network Model
3.1.2. Compartmental Model
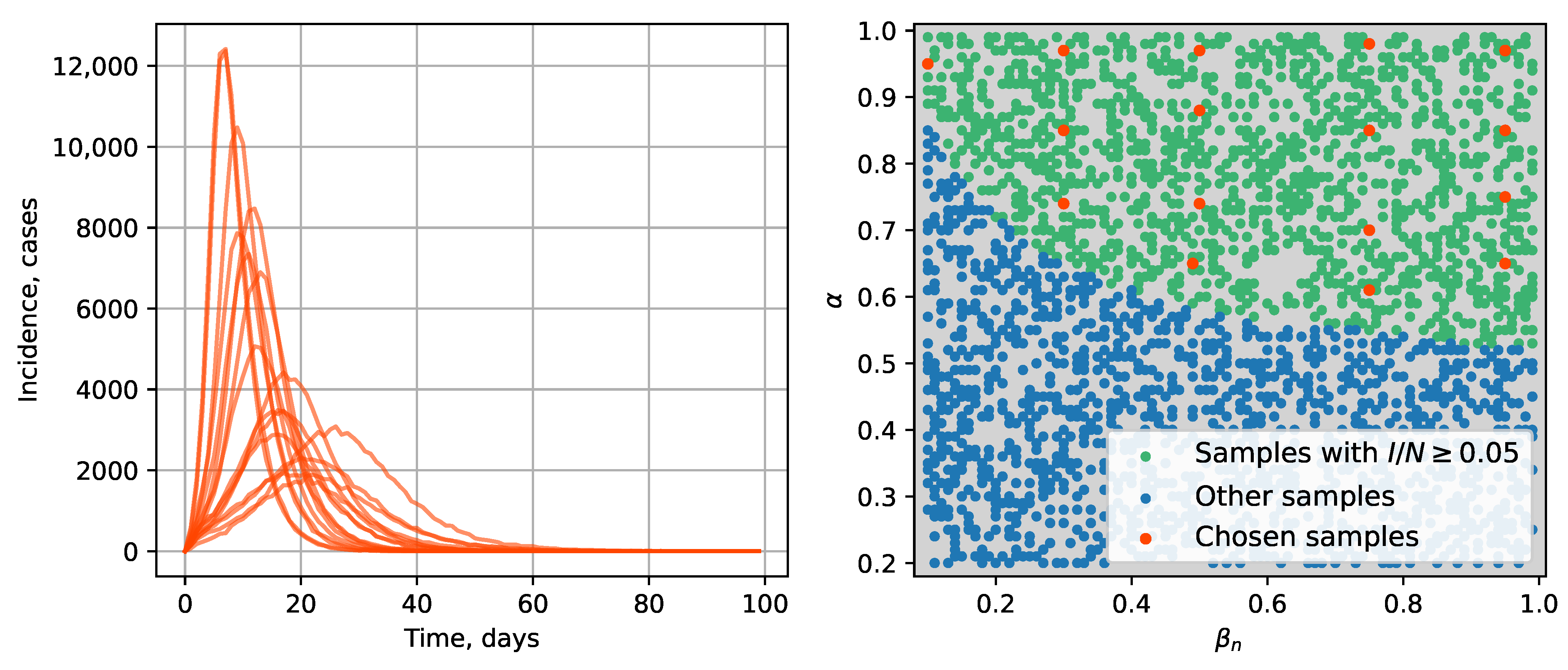
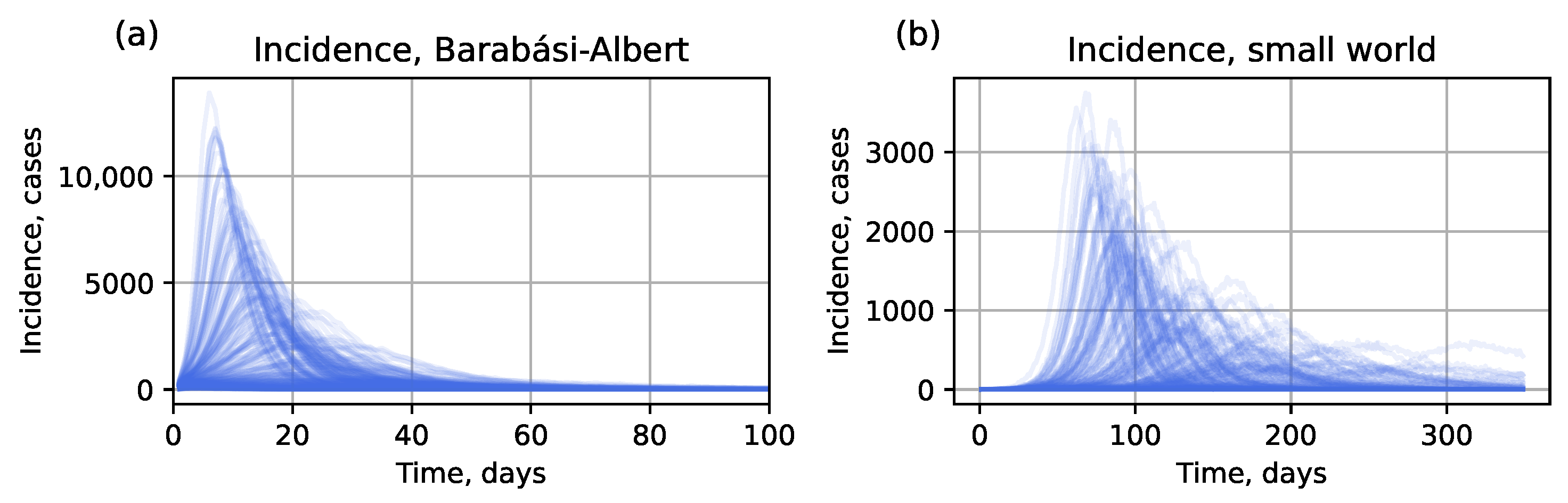
3.2. Data Generation
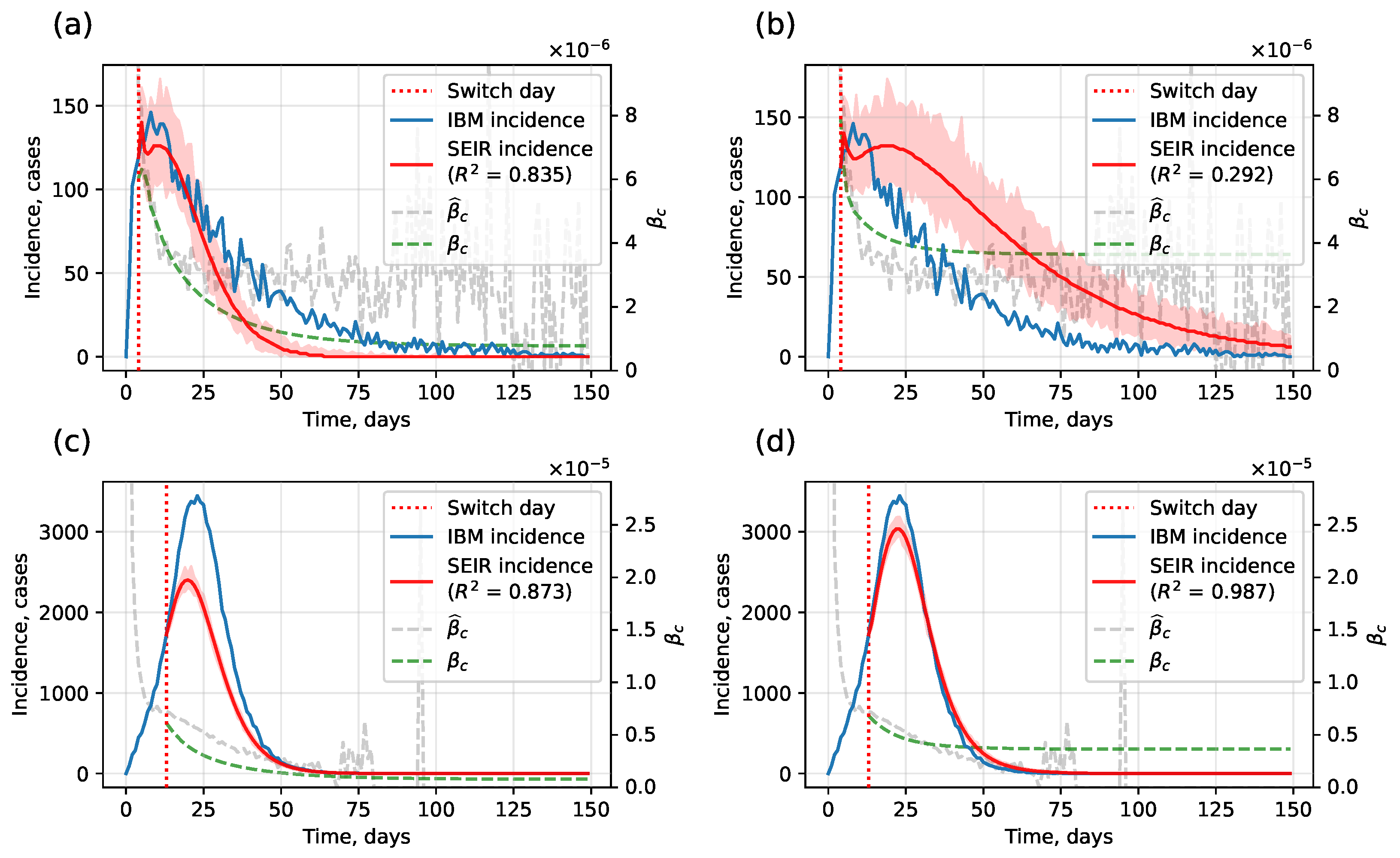
3.3. Hybrid Approach
- Initialize an IBM with parameters .
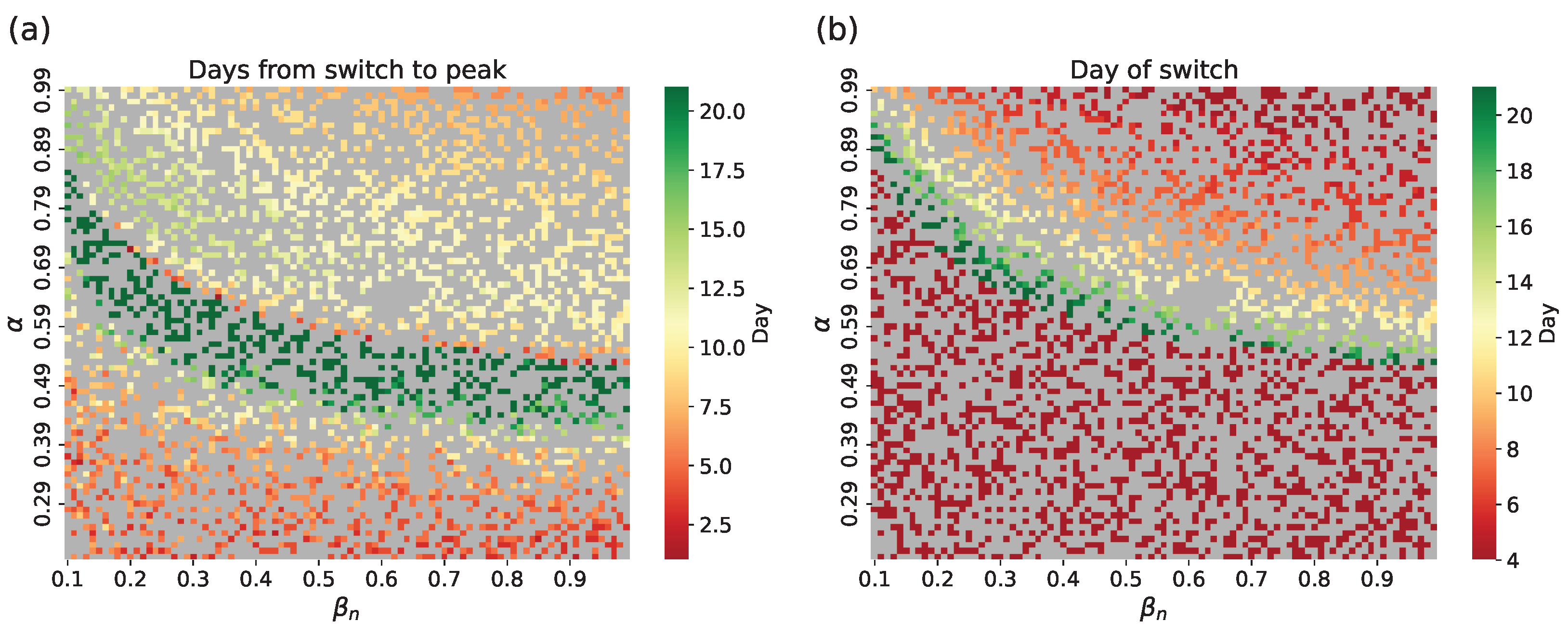
- Identify the switch time when the infected population can be assumed homogeneous, so the perfect mixing assumption is considered to be satisfied, making the SEIR model applicable. The switch time is determined by sufficient infection prevalence to meet the well-mixed assumption; .
- Switch to the SEIR model initialized from compartments and parameters .
- Analytical method. Assuming , find based on the network topology. This method works only for , which limits the accuracy of the hybrid model. In such cases the SEIR submodel is generally unable to closely approximate the IBM [33].
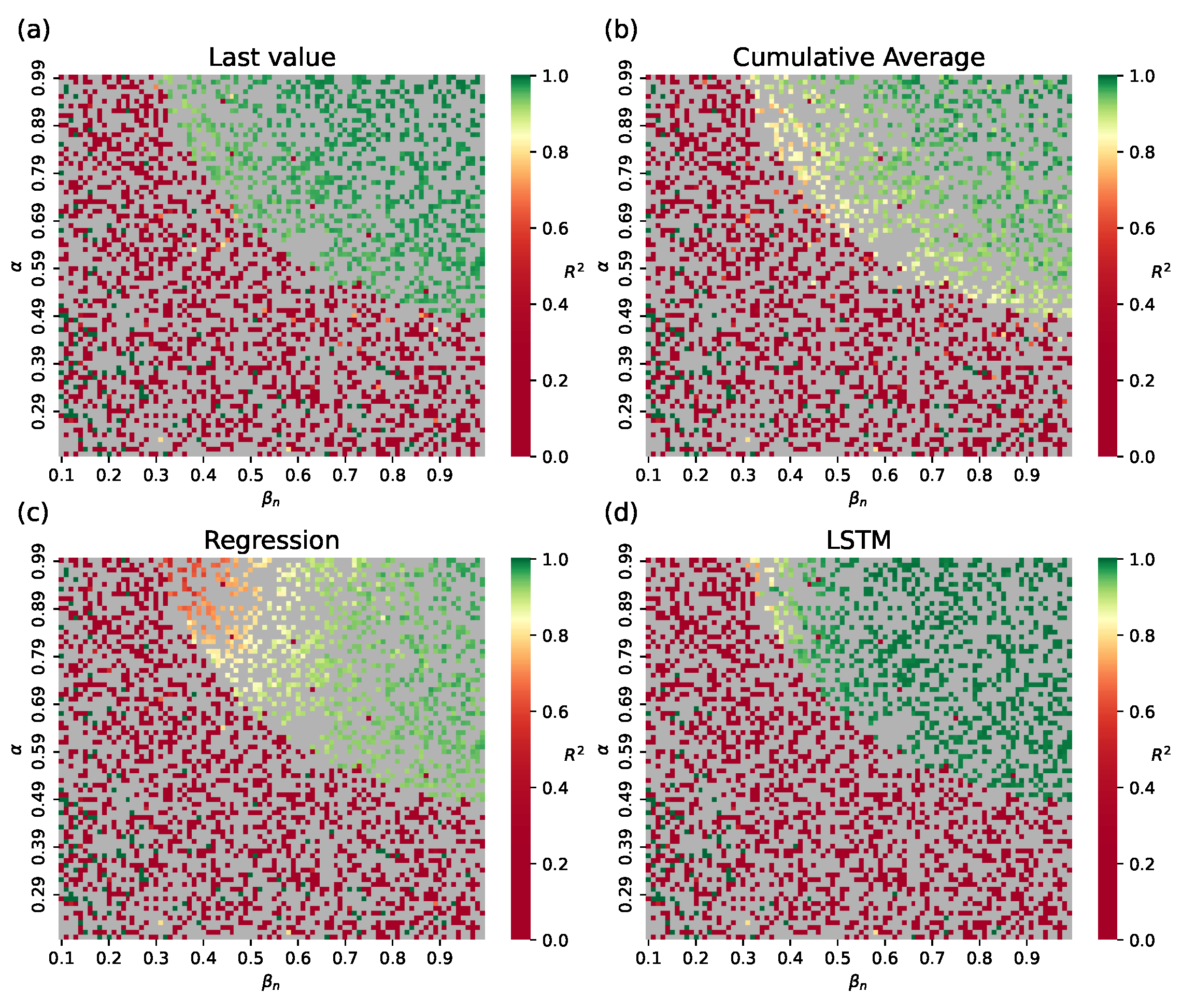
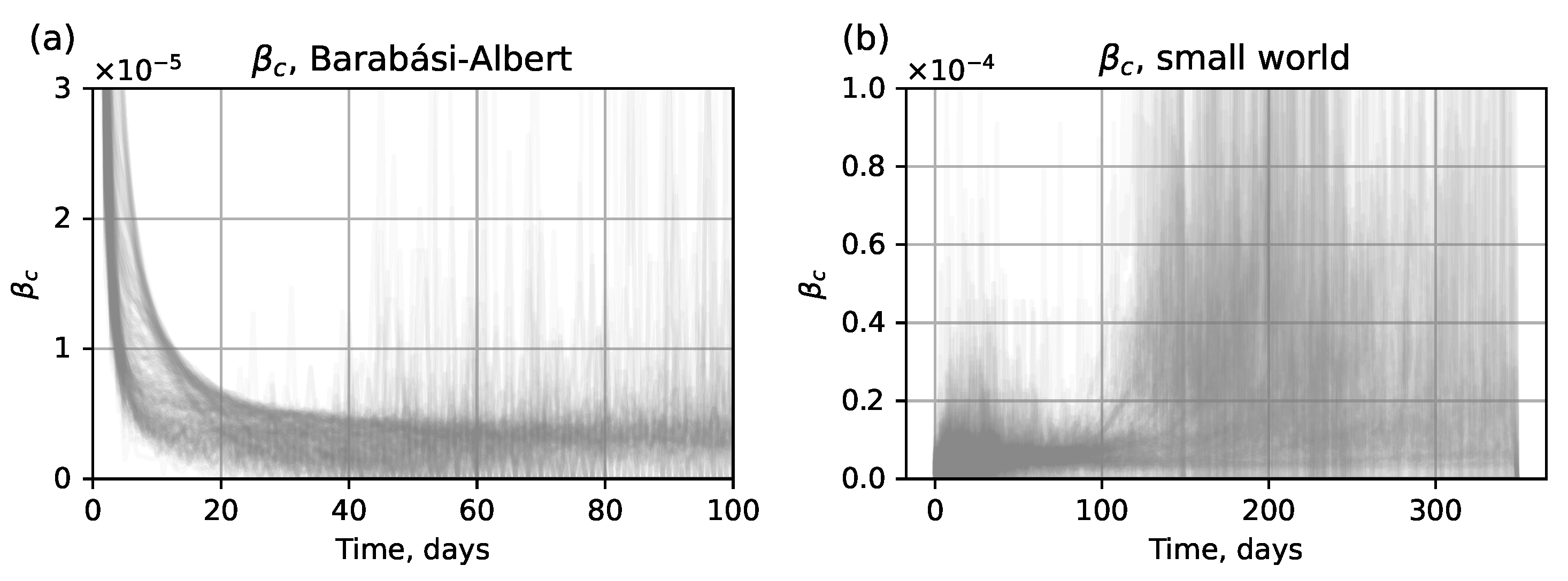
- Numerical method. Assess the value of using the approximate values of derived from the output of the network submodel. The estimated compartmental transmission rate can be found via a formula derived from Equation (1) of the ODE system (1), which givesThe typical form of curves obtained from the test dataset is shown in Figure 4. Here we show for ; however, in an actual simulation run, this data is available only for , before the network submodel is replaced by the SEIR submodel.
- Statistical: Last value observed on the switch day, i.e., ; cumulative average for , or median of trajectories from the train set.
- ML: Polynomial regression (third order with L2 regularization), and a Long Short-Term Memory network (LSTM) trained on .
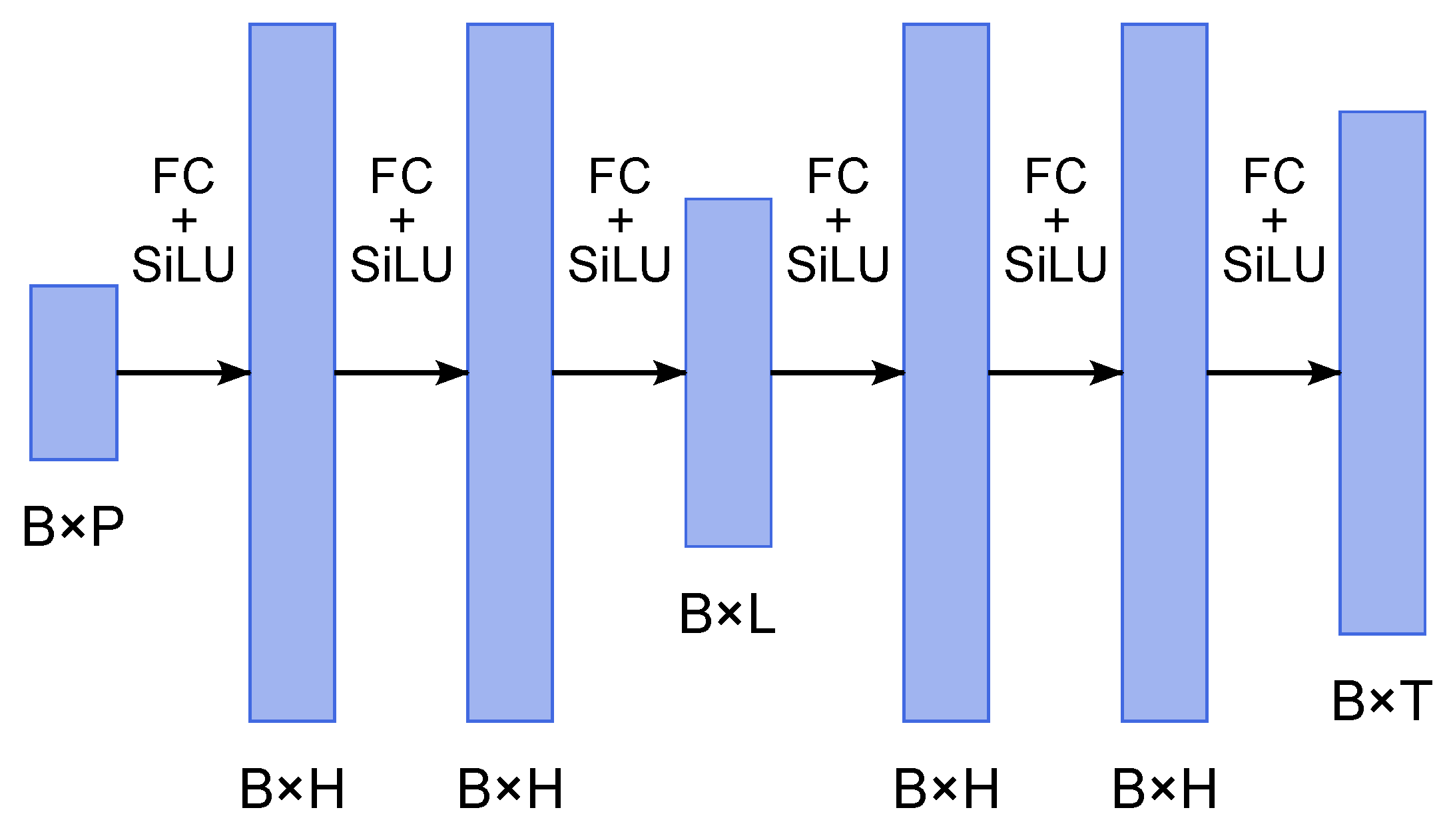
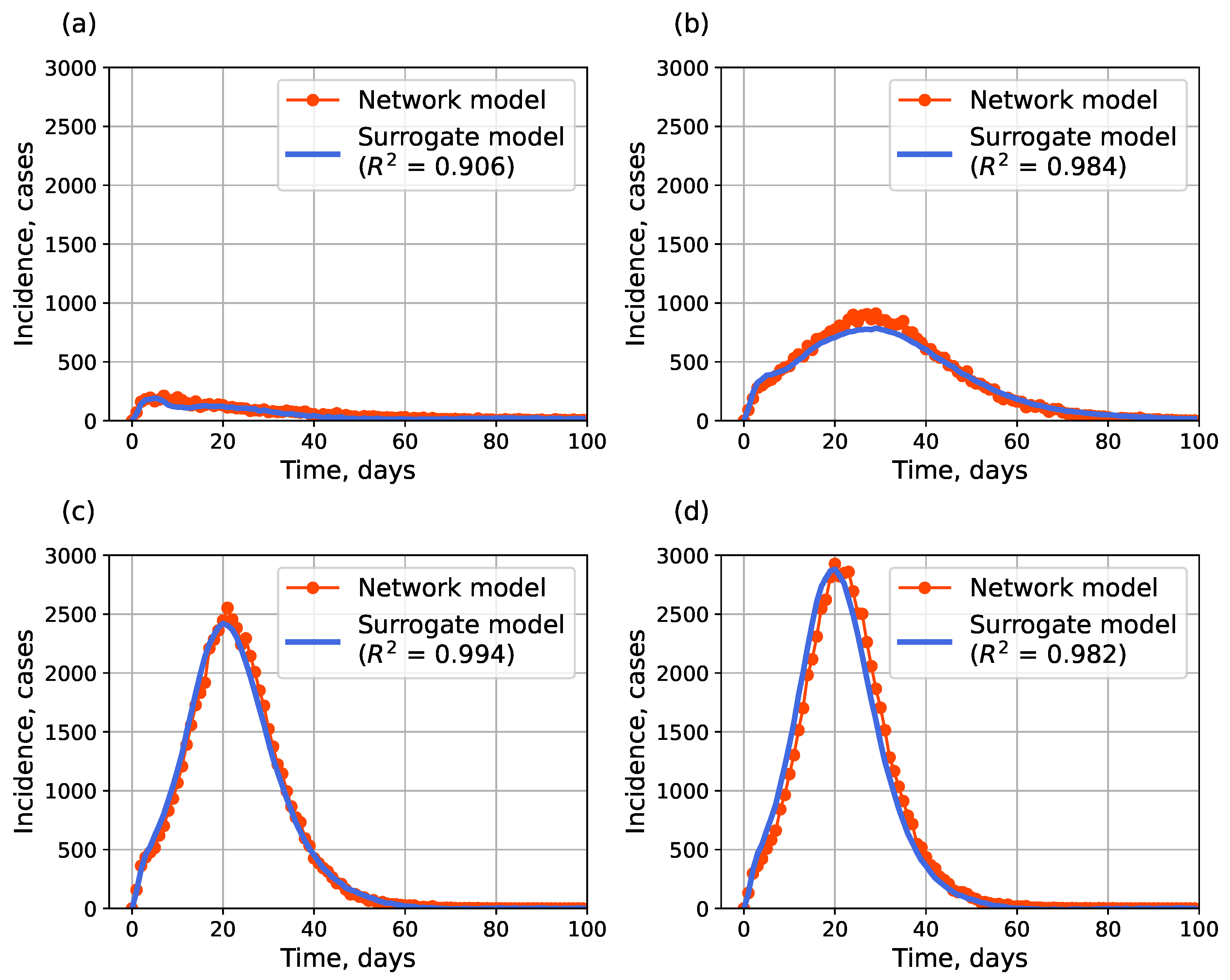
3.4. Surrogate Approach
- Encoder: Three fully connected layers with SiLU activations, mapping inputs of size to latent space , where B is the batch size, P is the number of input parameters, L is the latent dimension;
- Decoder: Three fully connected layers with SiLU activations, mapping the latent space back to time series of size .
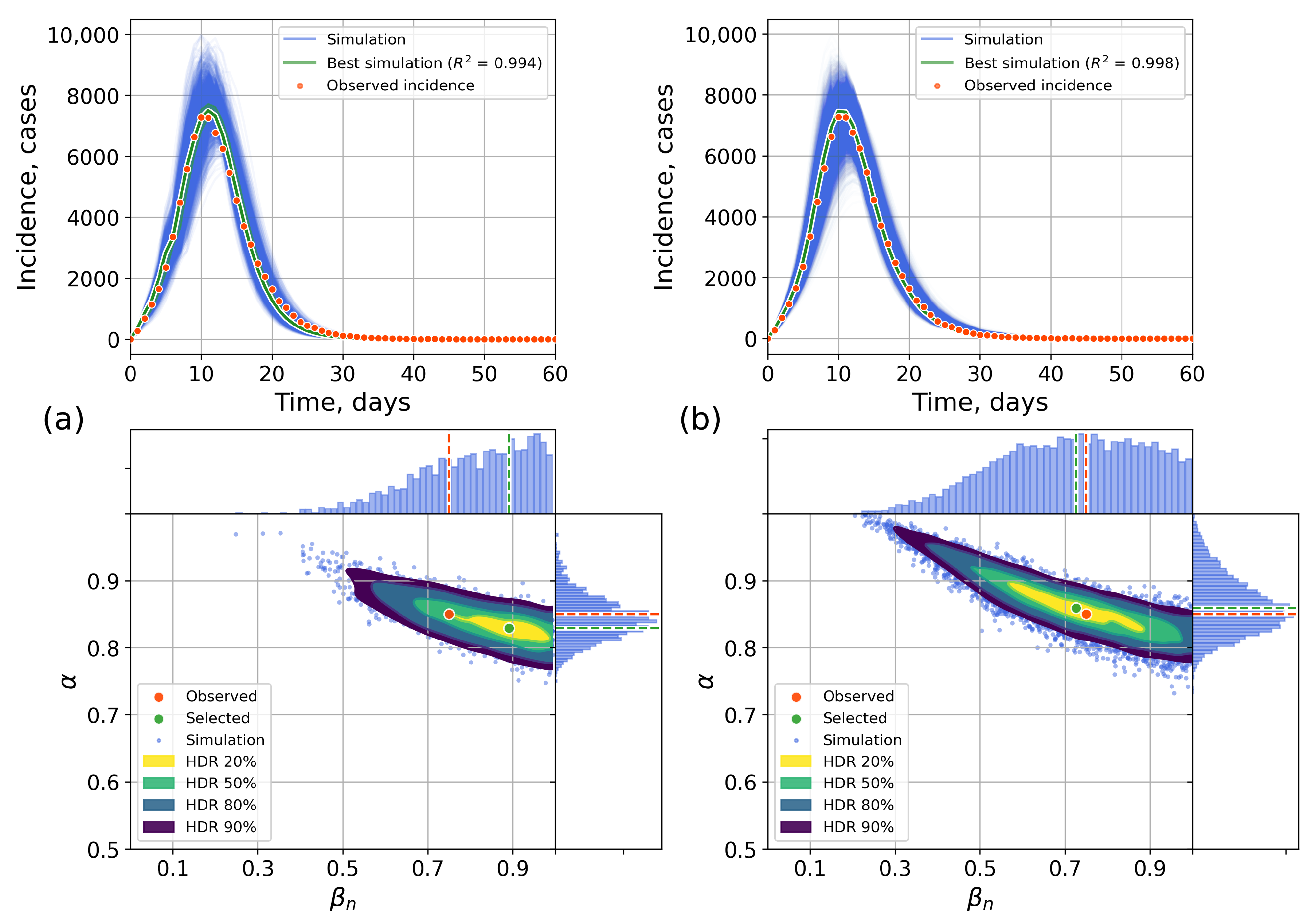
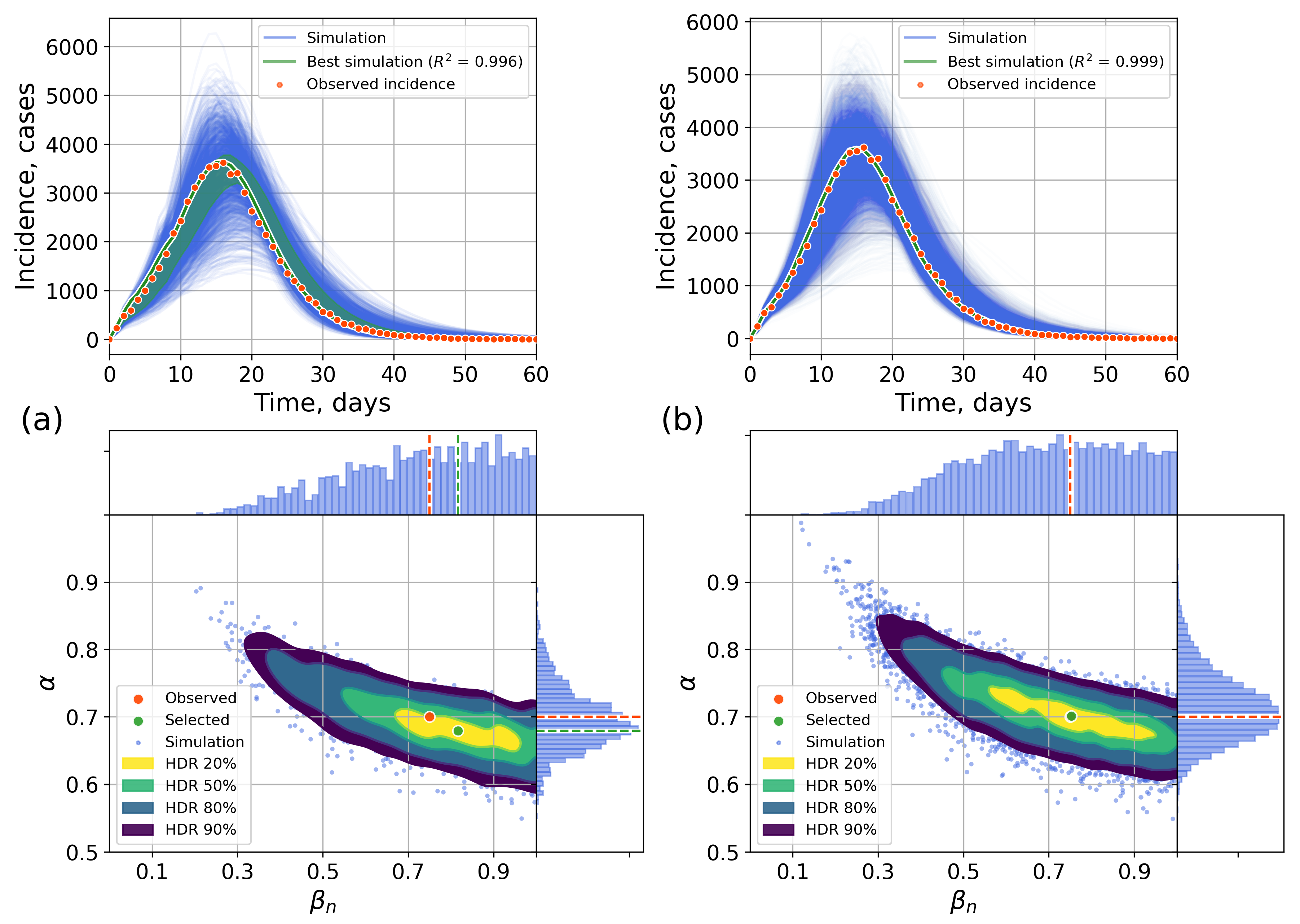
4. Results
4.1. Numerical Experiments with Simulated Data
4.1.1. Hybrid Approach
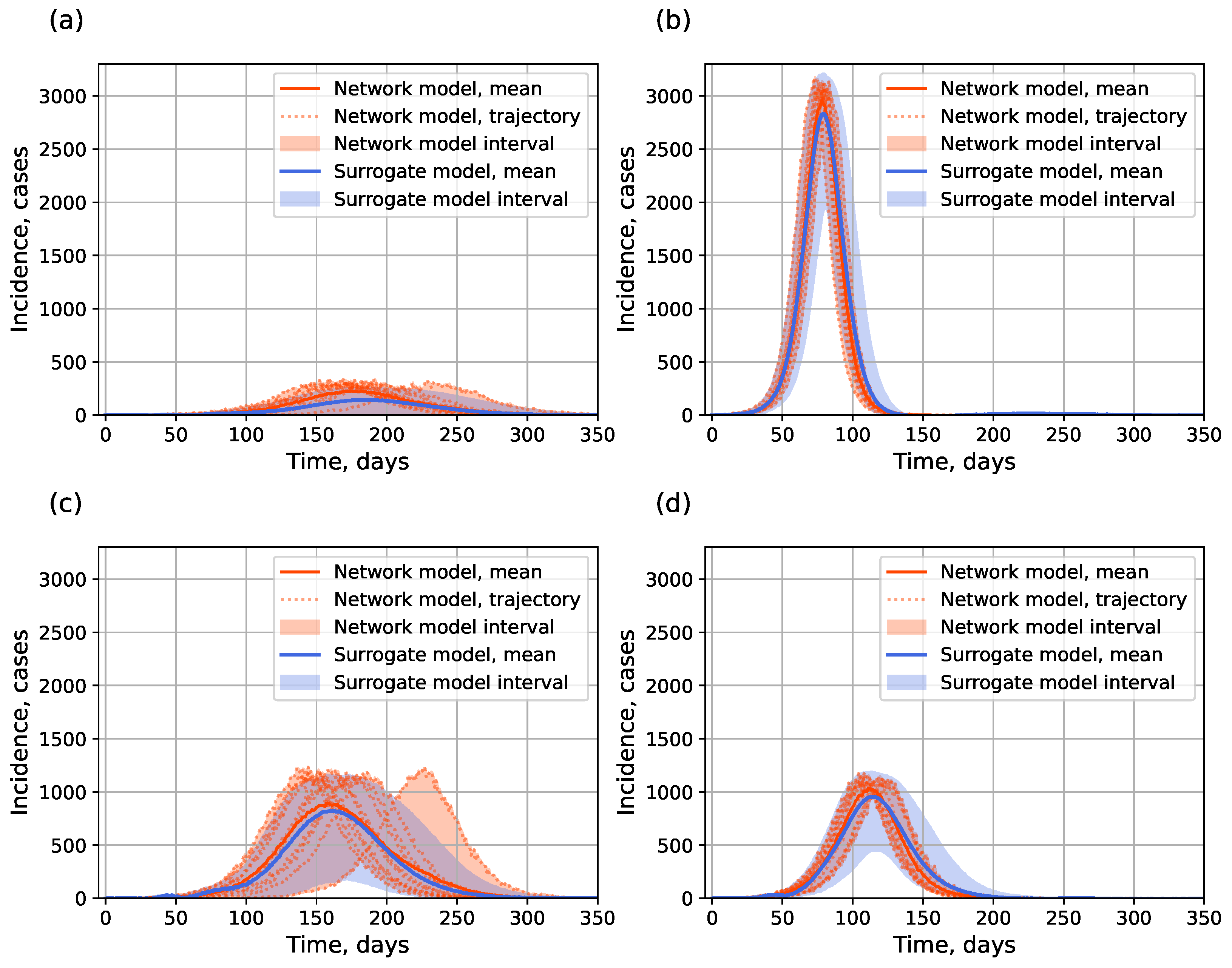
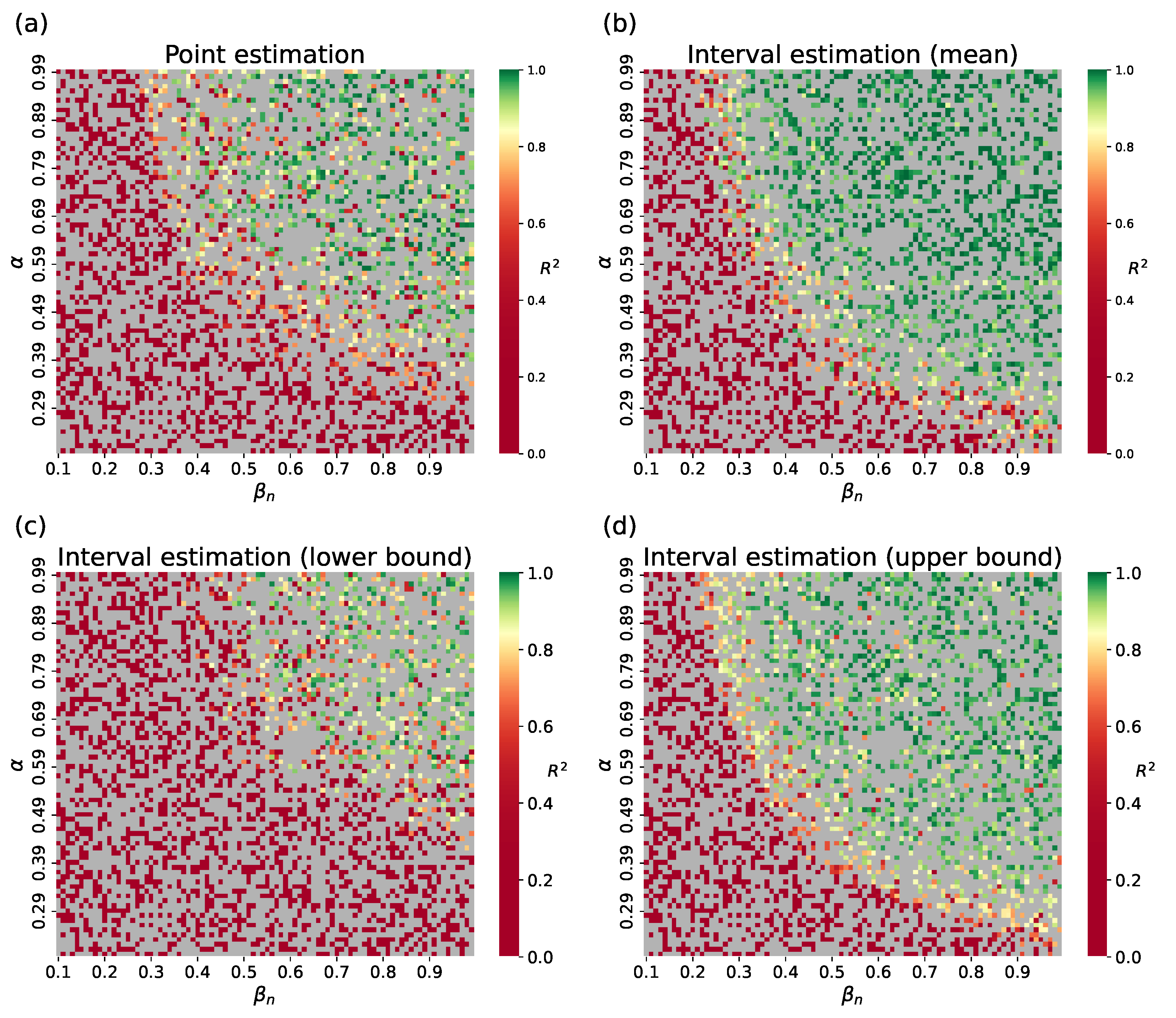
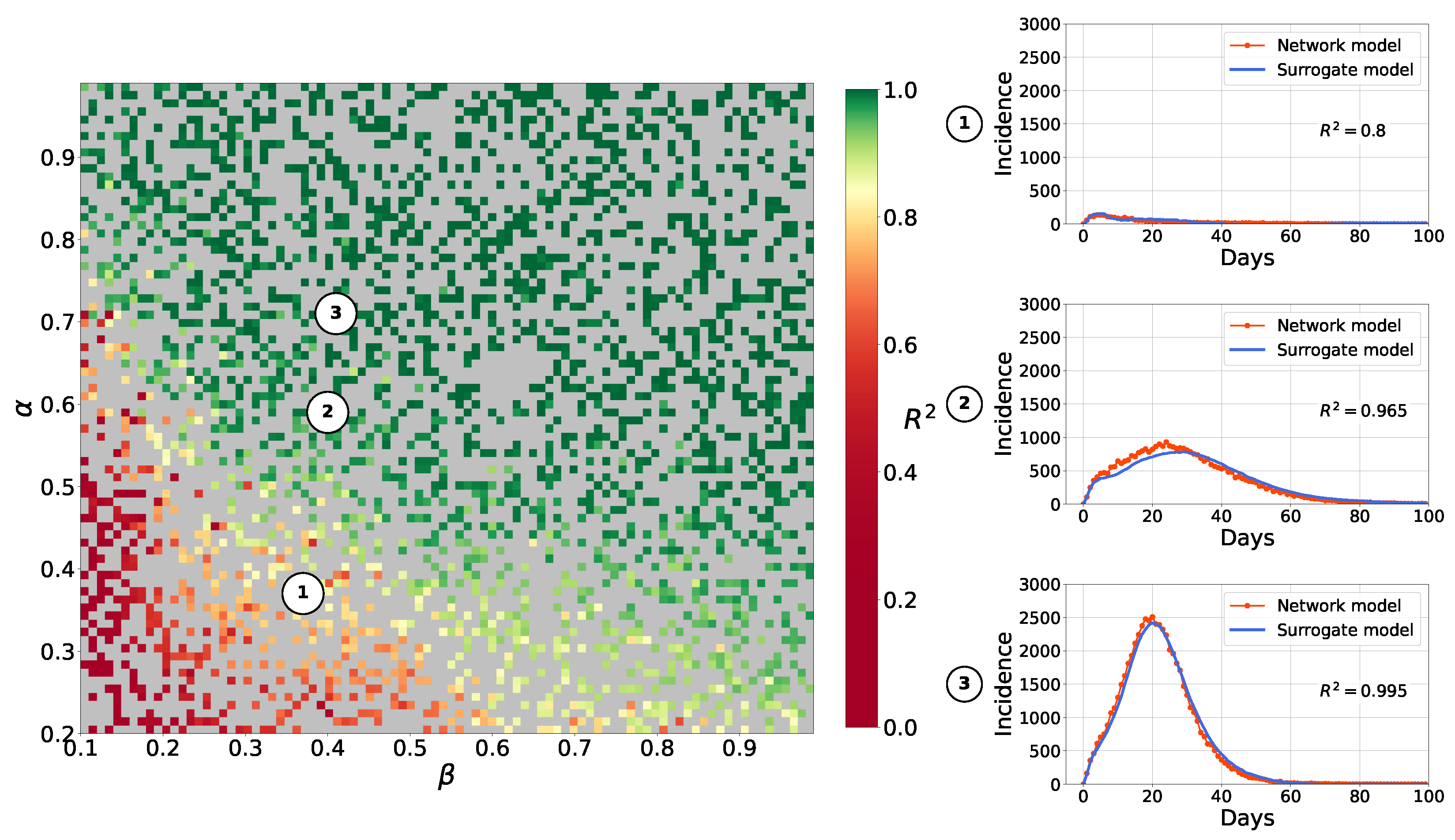
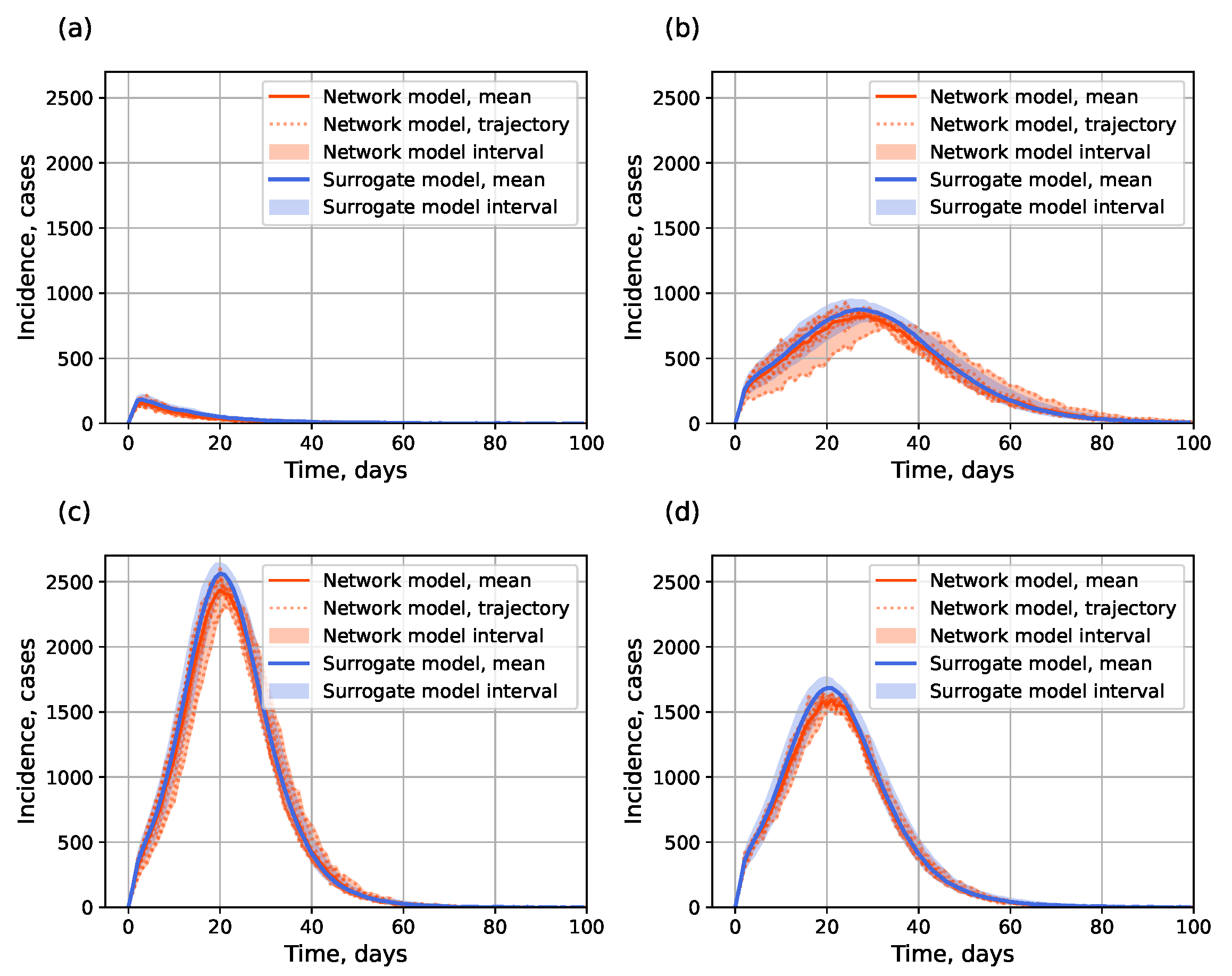
4.1.2. Surrogate Approach
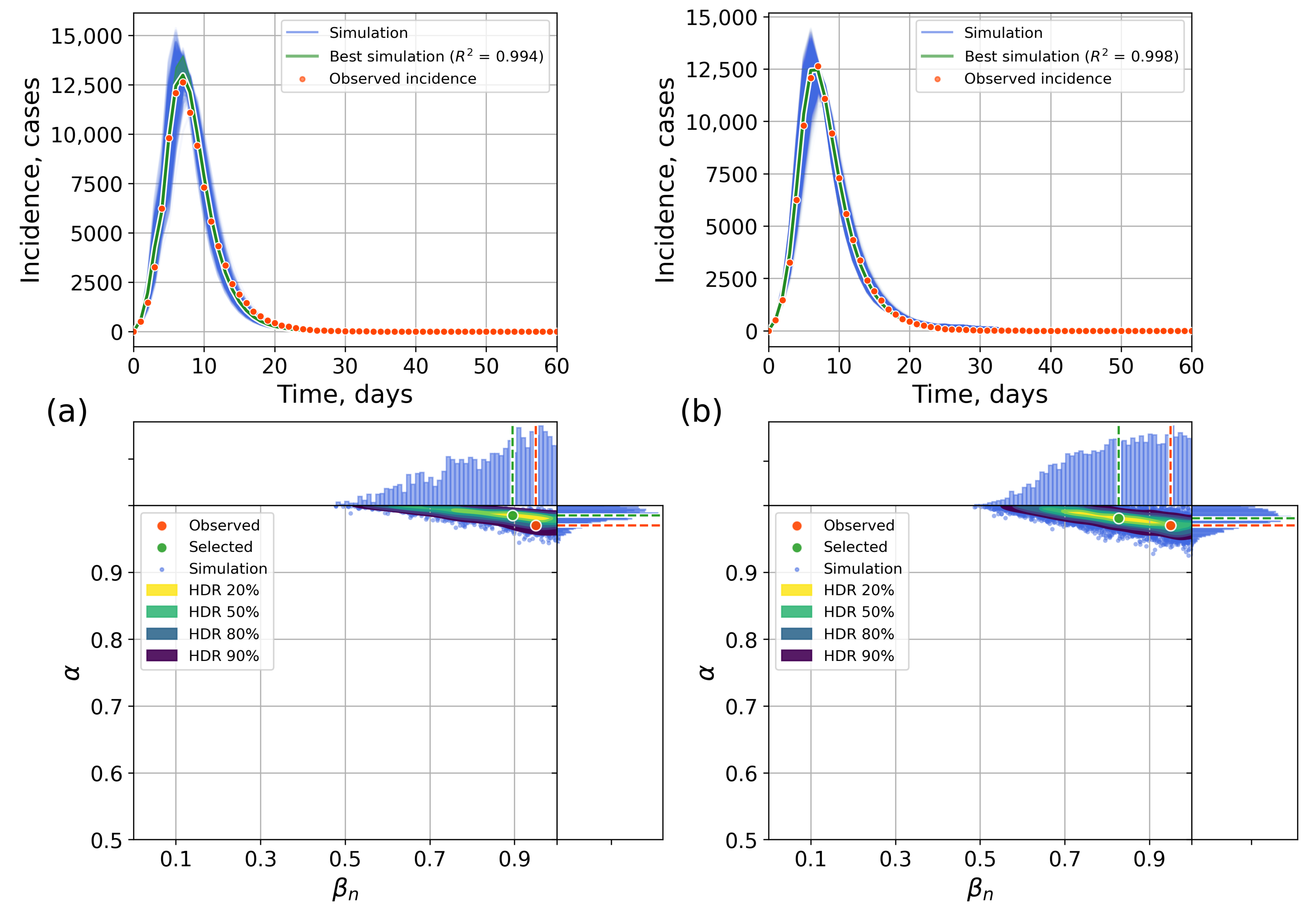
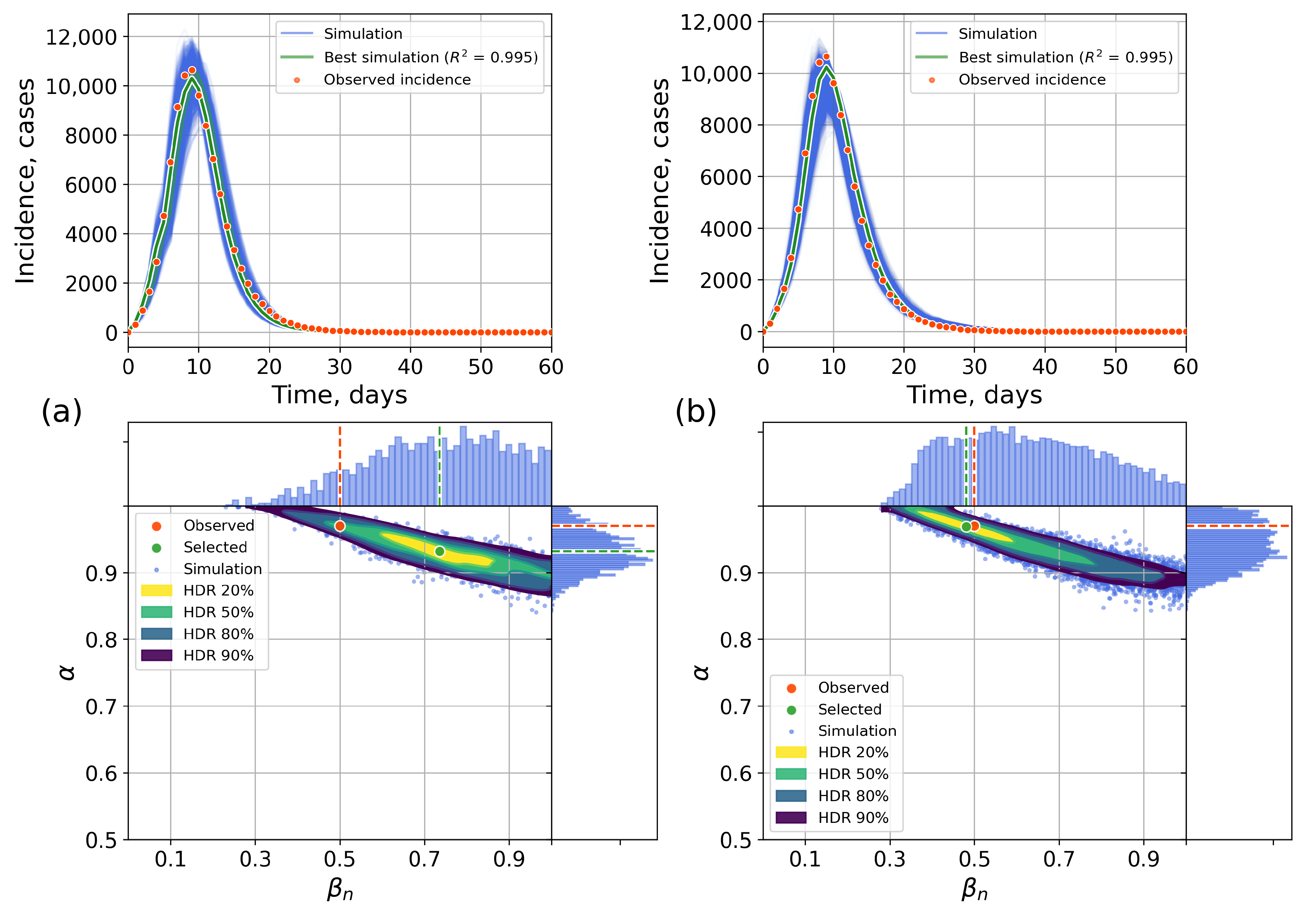
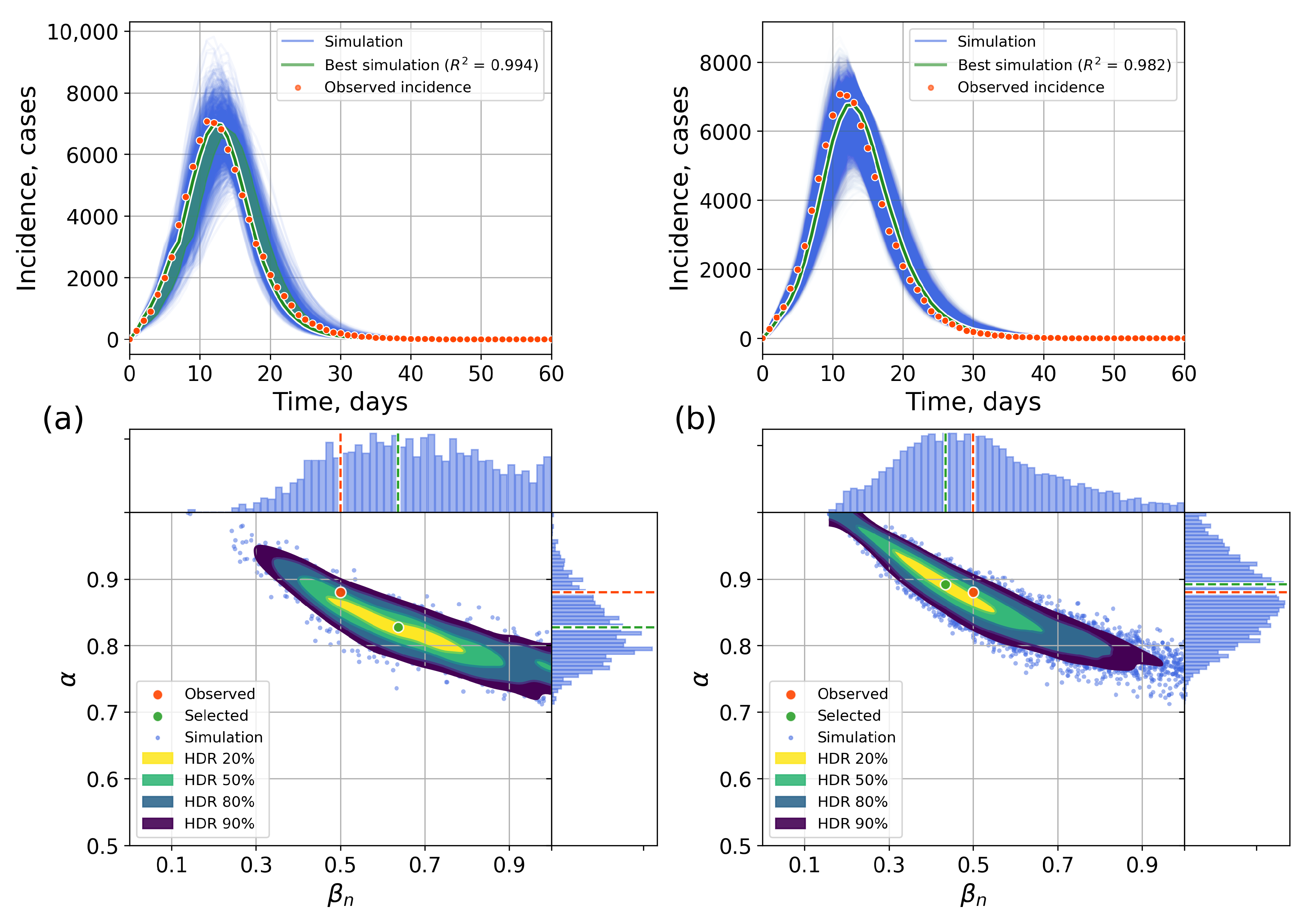
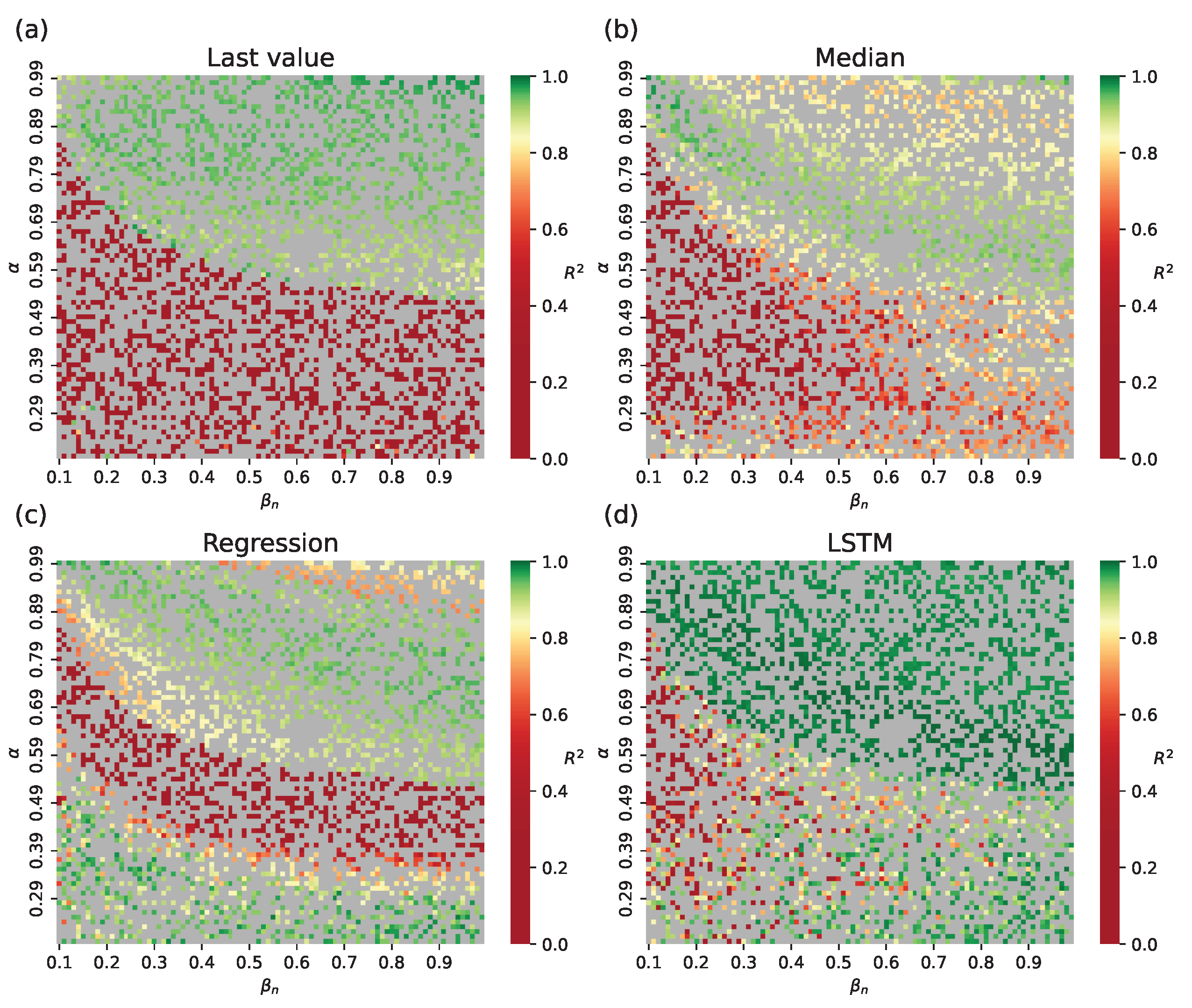
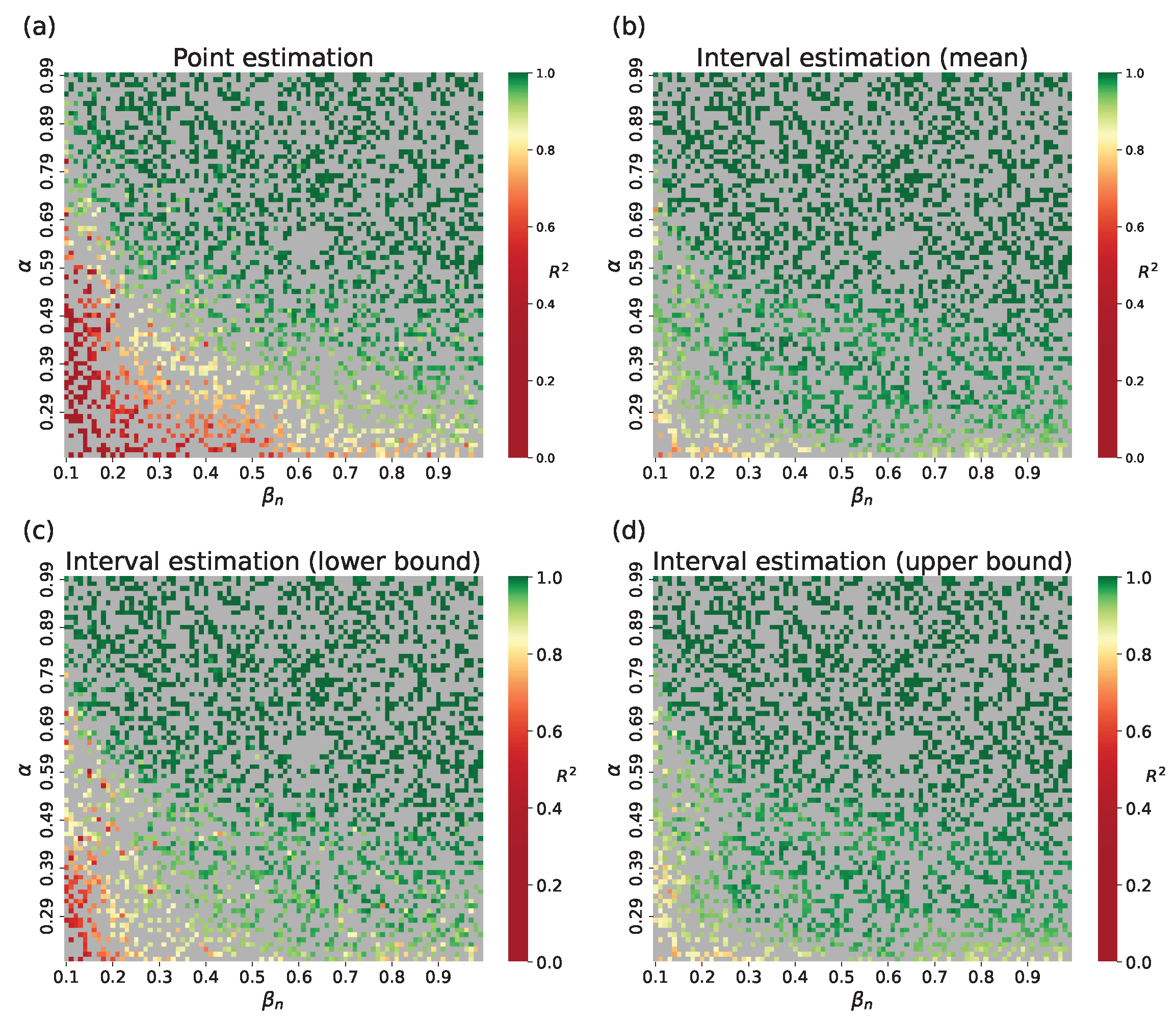
4.2. Parameter Estimation on a Synthetic Incidence Data
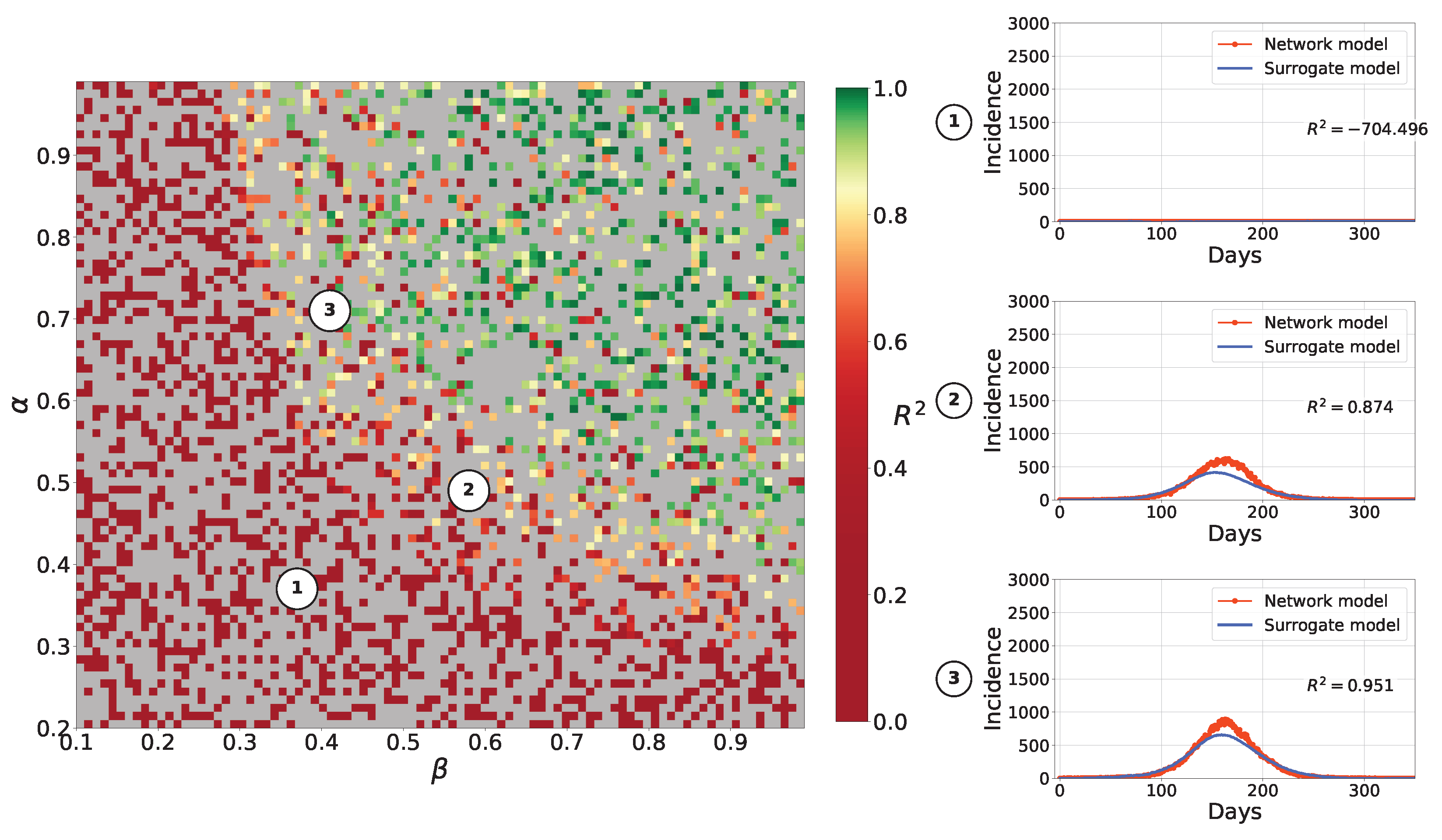
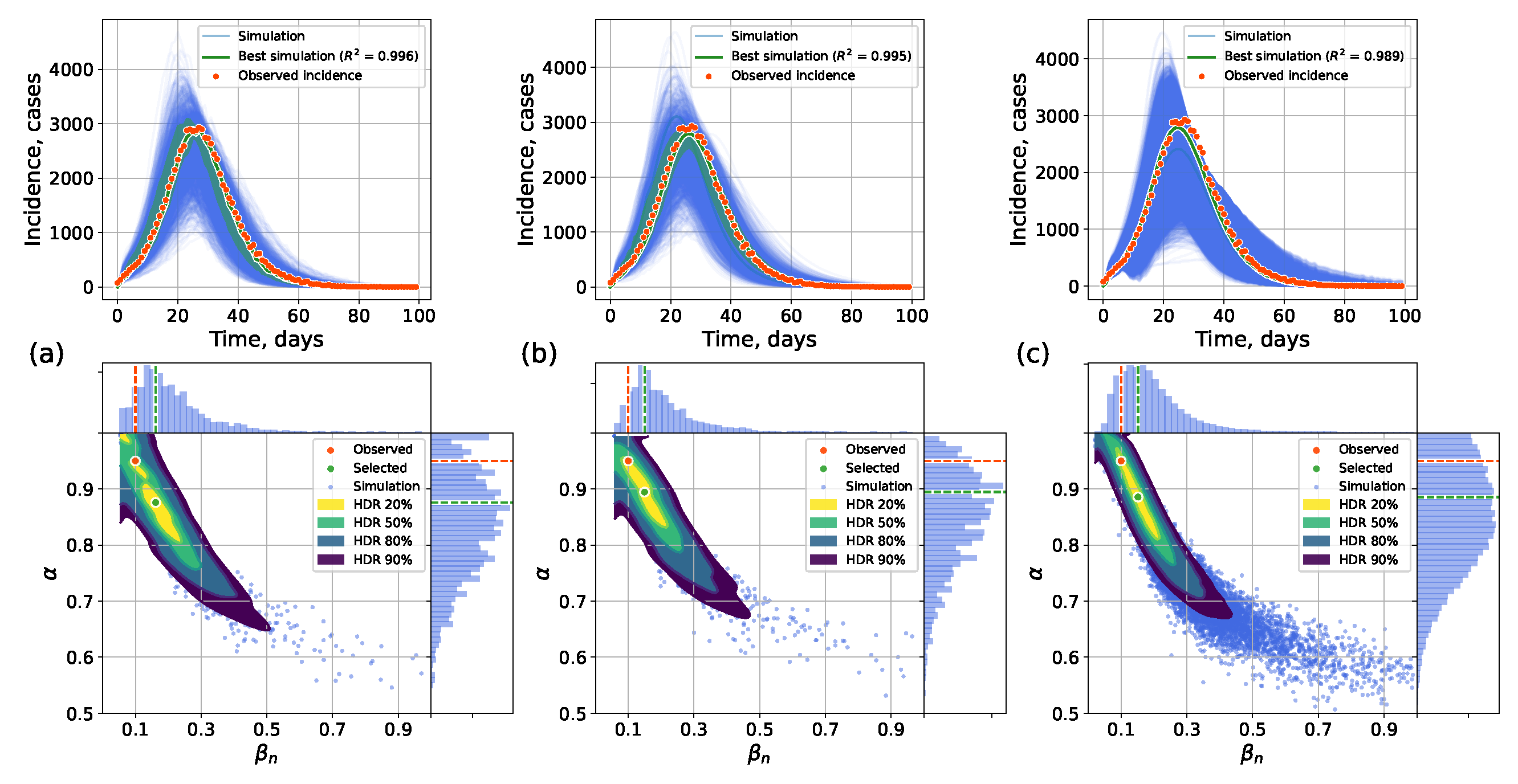
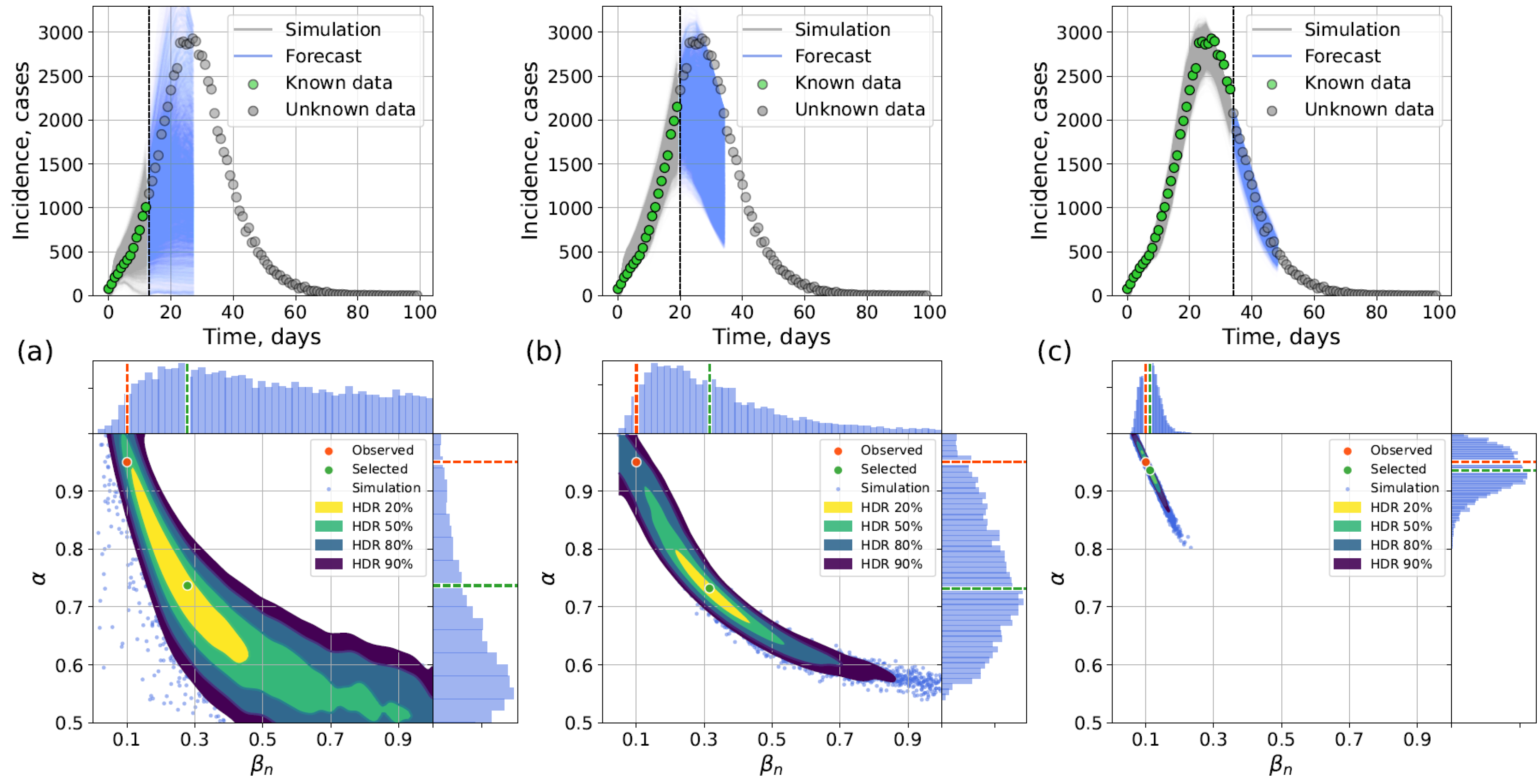
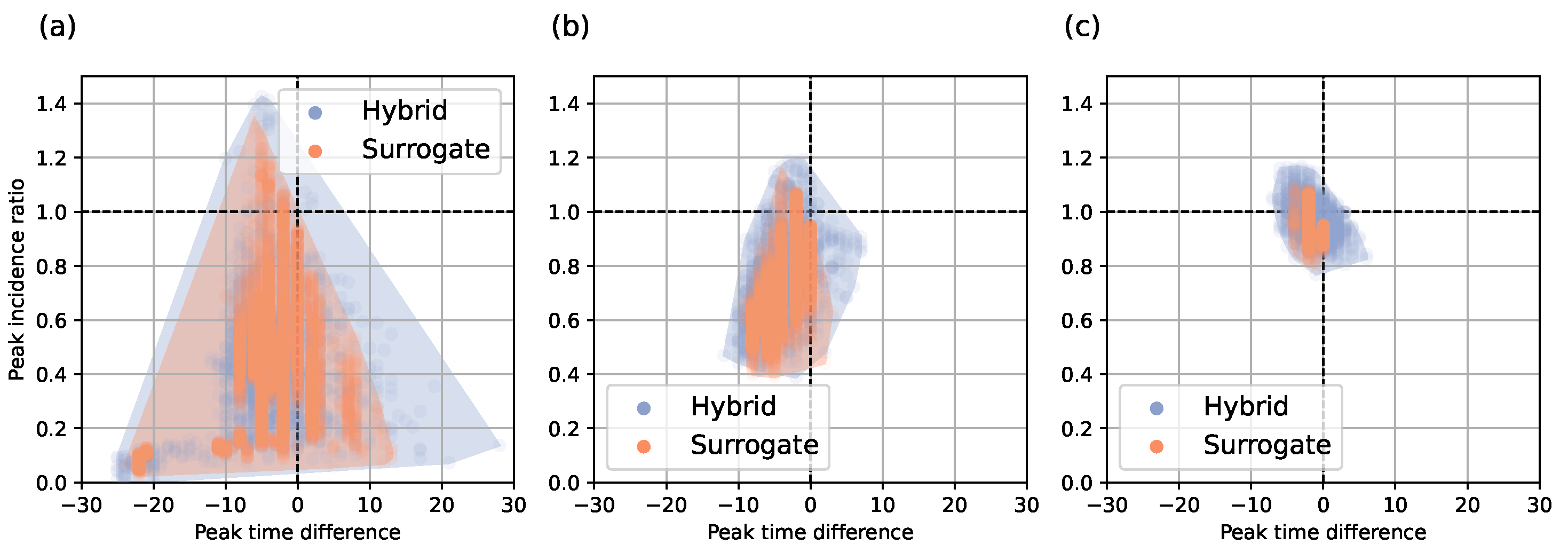
4.2.1. Retrospective Calibration
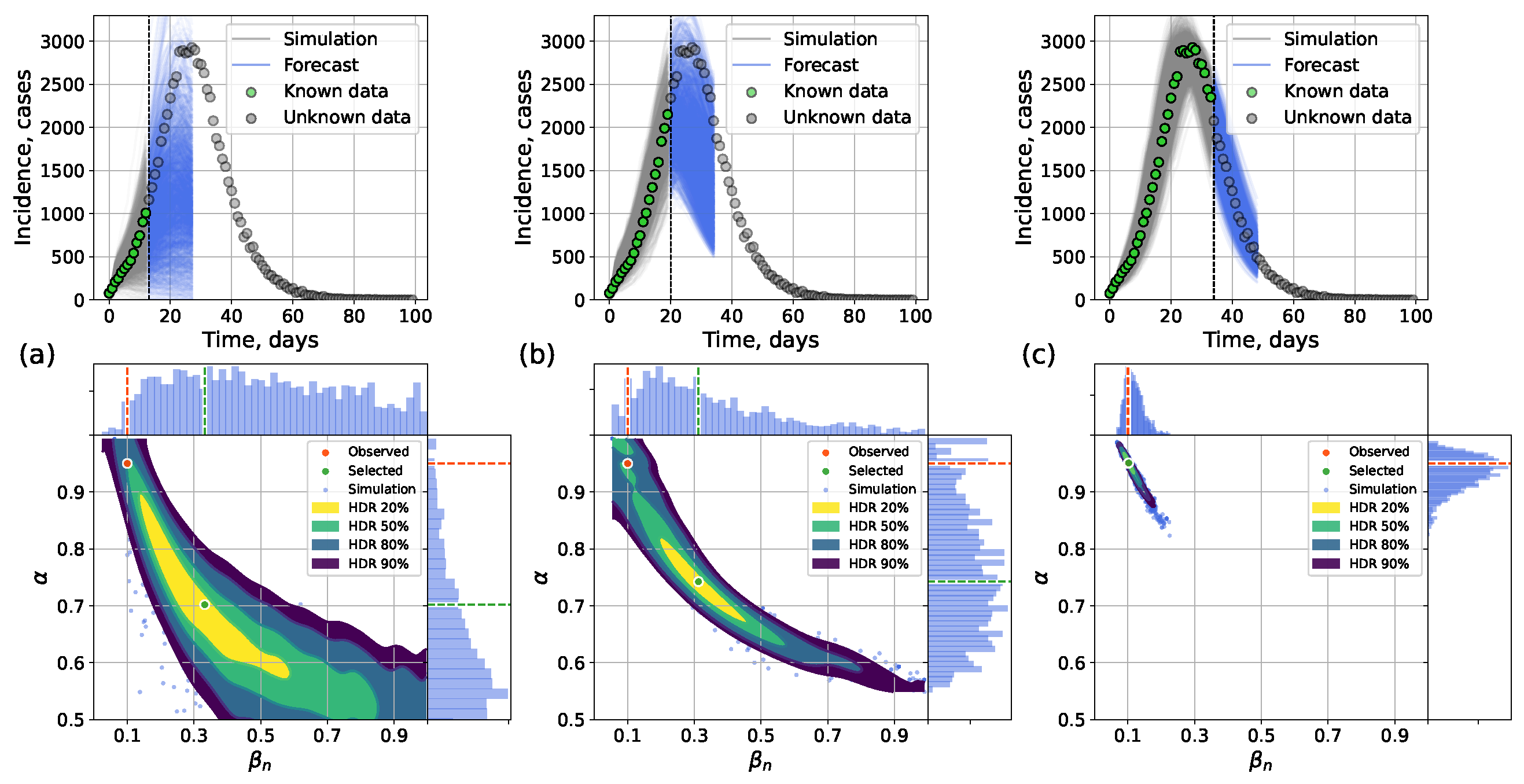
4.2.2. Forecasting Examples
5. Discussion
5.1. Methods Advantages and Drawbacks
- Independence from training data at the outbreak onset with certain estimators. Two statistical estimators, last and cumulative , require only the knowledge of the contact network topology and and values related to the disease properties, all of which are known/can be calculated during epidemic onset. Thus these statistical estimators can be applied immediately, making this approach suitable for early epidemic stages with limited prior information.
- Preservation of explicit stochasticity. Unlike the surrogate approach which produces a single deterministic output (point or interval assessment) for a fixed input parameter set, the hybrid approach is capable of generating multiple trajectories for a fixed input to reflect the influence of random factors, just like the original IBM it aims at replacing—by means of the actual IBM before the switch or via the stochastic SEIR model after the switch.
- Interpretability. It is possible to use different trajectories to analyze the impact of government policies such as lockdowns, or to assess future values.
- Homogeneity assumption. When incidence remains very low, the SEIR submodel is ill-suited, and switching produces poor approximations.
- Computational cost relative to surrogate modeling. Although faster than the pure network model, the hybrid approach is still slower than the surrogate approach.
5.2. Application to Real Epidemic Data
- There exists an incomplete incidence dataset .
- After each time period (day or week) passed, a new measurement is added to the dataset.
- Perform short-term prediction of disease incidence and peak height/time prediction
- Simulate the effect of control measures on the prediction
- Begin with the network model for an entirely new outbreak.
- Once infection prevalence rises sufficiently, employ the hybrid approach with statistical estimation to provide early forecasts.
- After accumulating sufficient simulation data and/or obtaining incidence data from similar cities where the epidemic has already passed, train the surrogate model, which can then take over for large-scale parameter calibration and forecasting.
- Quarantine measures can be simulated by assuming slower transmission due to fewer contacts. On the level of models, it is made by changing in the SEIR part of the hybrid approach and change of in the surrogate approach. In its current implementation, the surrogate does not support a variable , so it can be used only for playing “what-if” scenarios when change in happened before the outbreak (for instance, quarantine measures were introduced before the inception of the virus in the population). This might be changed in its future implementations to allow dynamical adjustment of trajectories during the simulation.
- Real-time vaccination may be considered within a hybrid approach by changing . In a surrogate approach, vaccination is simulated by changing the proportion of immune individuals in the population, i.e., generally, the vaccination campaign is assumed to be finished before the outbreak.
5.3. Study Limitations
- According to the assumptions stated, this study considers a population whose contact patterns can be reasonably approximated by a static, regular network topology. Disease properties are also assumed to be constant. As a result, this study does not cover other important cases, such as several moderately interconnected cities with Barabási–Albert or small-world networks, multiwave epidemics, or co-circulation of multiple virus strains (e.g., different SARS-CoV-2 variants or influenza strains H1N1(pdm09) and H3N2).
- The contact network structure in the city is assumed to be stable over a multi-year period, otherwise establishing a specific topology (Barabasi–Albert or small world) would be infeasible. While this is a simplification compared to real dynamic contact patterns, it is a common assumption in data-driven demographic and epidemic modeling (see, for instance, [58]), because to construct realistic dynamical contact networks, extensive and often unavailable data is required.
- We do not consider asymptomatic cases and under-reporting. While it does not affect the forecasting accuracy, which is our main interest in this study, it will lead to wrong assessment of epidemic indicators, such as effective reproduction number, when the framework is calibrated to real data. This issue will be fixed in the future studies.
- The choice of switch condition in the hybrid approach remains heuristic. Different estimation methods may favor different thresholds: for example, the last method benefits from higher prevalence thresholds, whereas LSTM performs well at earlier switches.
- Calibration with ABC-SMC requires the choice of . A smaller may narrow parameter range, but it requires more simulation time, which may limit our exploration under computational constraints.
- We tested our approaches on synthetic data, whereas real surveillance data may contain noise, delays, under-reporting, and gaps. We plan to address this issue in the future studies by using data imputation and bootstrapping techniques [59].
5.4. Additional Capabilities
5.5. Future Directions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Symbols and Abbreviations
| Symbols | |
| Fraction of non-immune individuals on day t = 0 | |
| Infection transmission rate for compartmental model | |
| Infection transmission rate for network model | |
| Mean latent (exposed) period, days | |
| Mean infectious period, days | |
| t | Time (days) |
| Number of susceptible individuals on day t | |
| Number of exposed individuals on day t | |
| Number of infectious individuals on day t | |
| Number of recovered individuals on day t | |
| Number of new incidence cases on day t | |
| N | Total population size |
| H | Hidden layer size for autoencoder model |
| B | Batch size during training autoencoder model |
| L | Latent vector size in autoencoder model |
| Abbreviations | |
| ABM | Agent-based model |
| AE | Autoencoder |
| ARI | Acute respiratory infection |
| COVID-19 | Coronavirus disease 2019 |
| HDR | Highest density region |
| IBM | Individual-based model |
| LSTM | Long short-term memory |
| ML | Machine learning |
| SEIR | Susceptible–exposed–infected–recovered |
| SIR | Susceptible–infected–recovered |
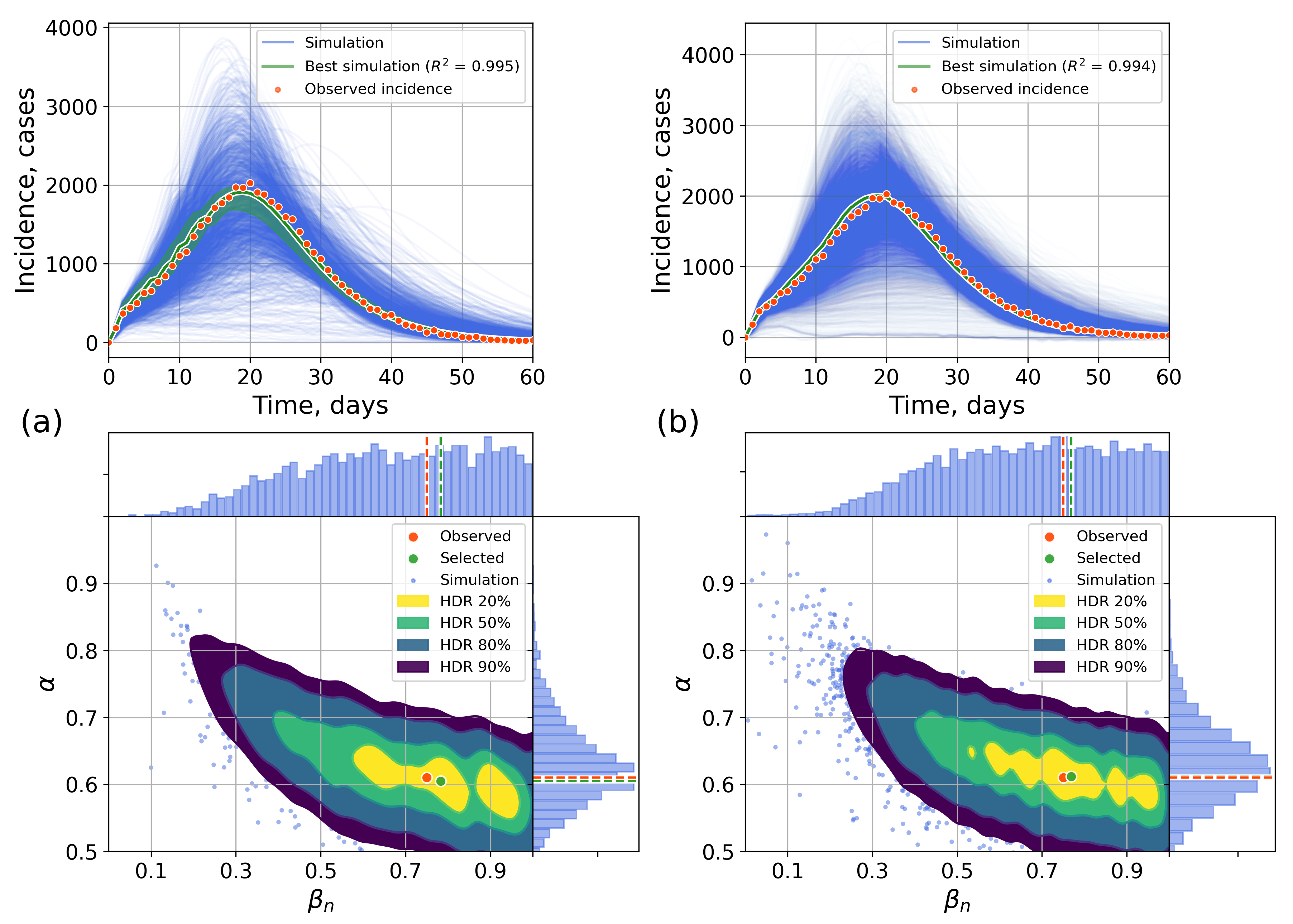
Appendix A. Numerical Experiments, Small-World Topology

Appendix B. Retrospective Calibration, Barabási–Albert Topology
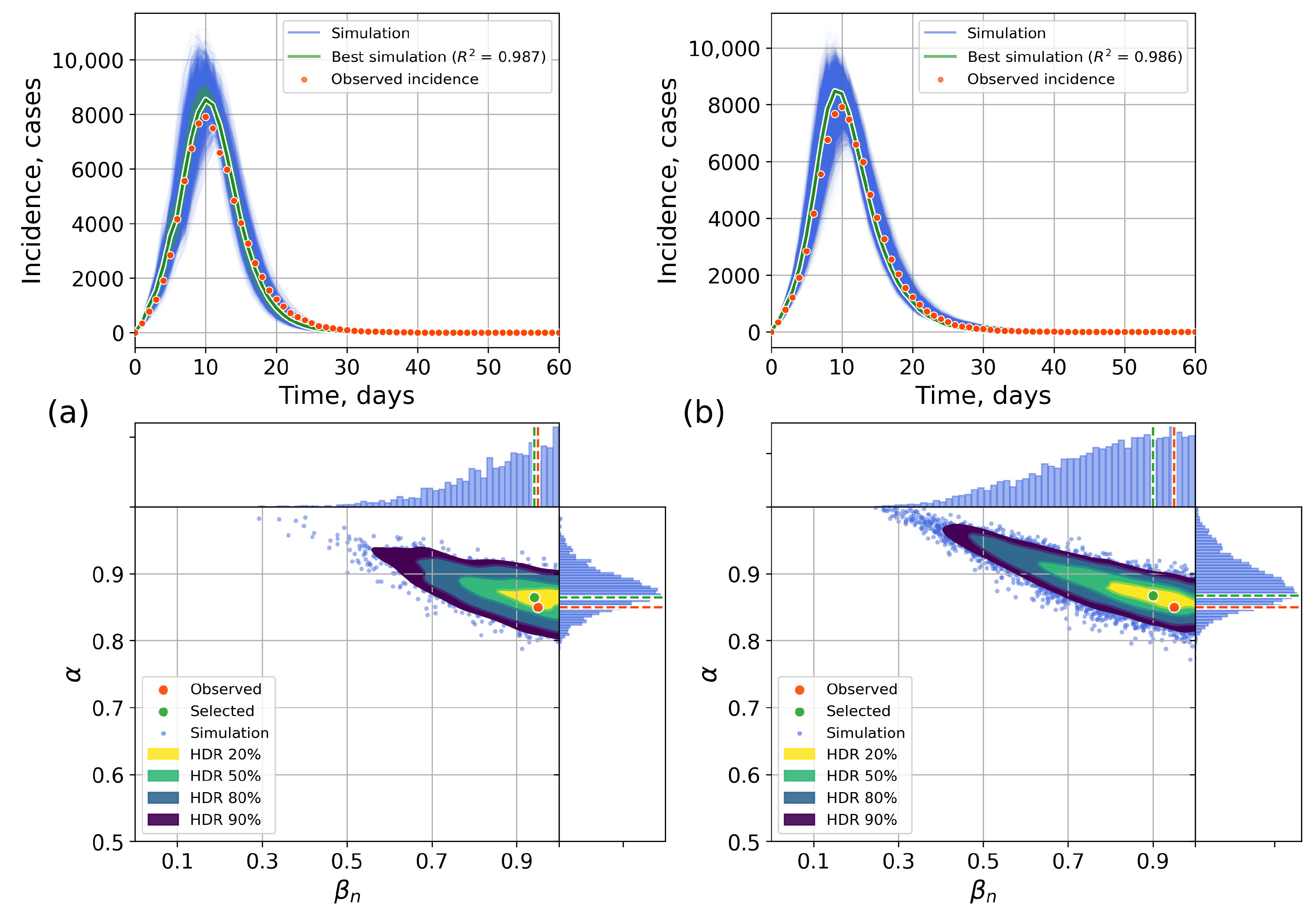
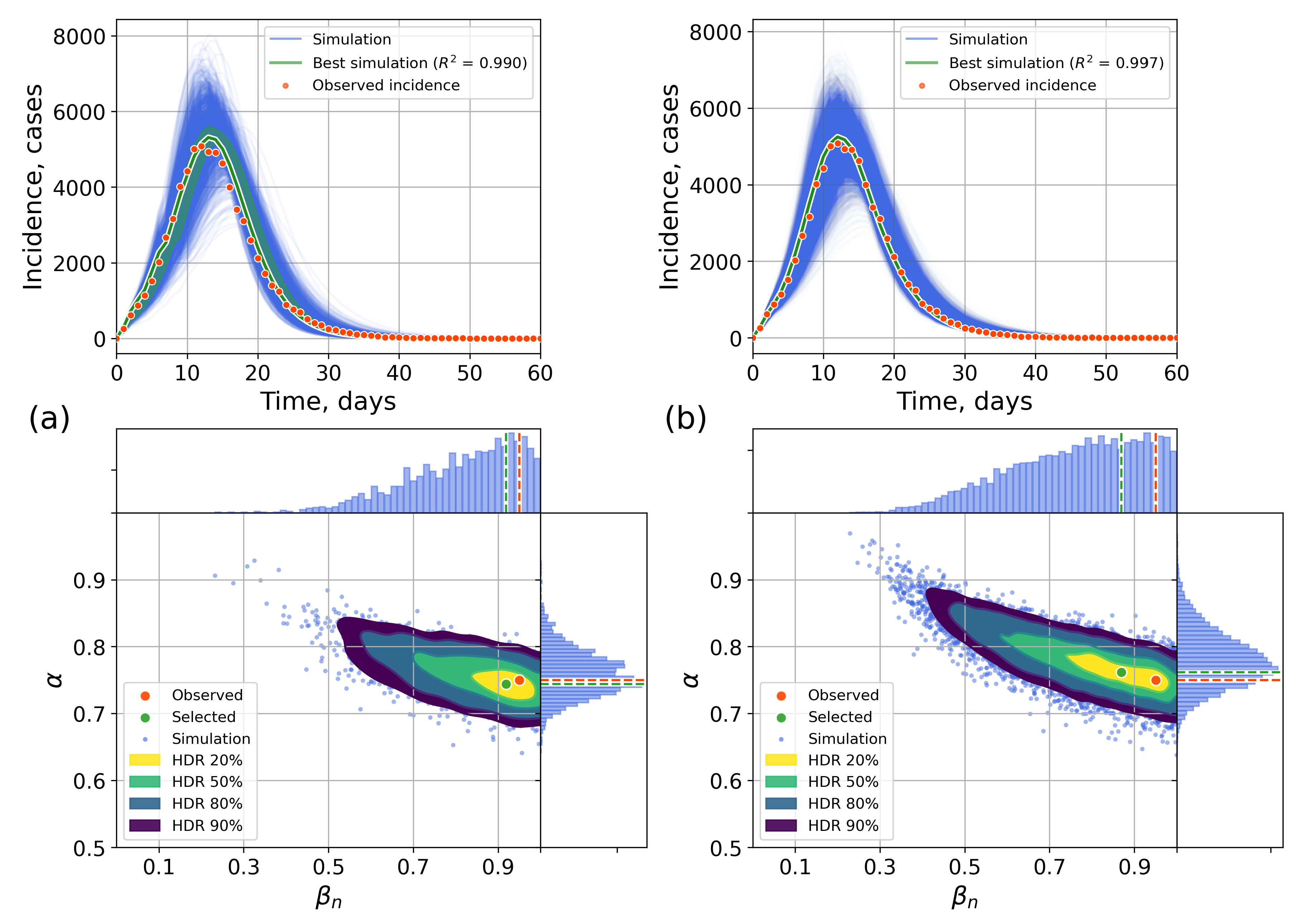

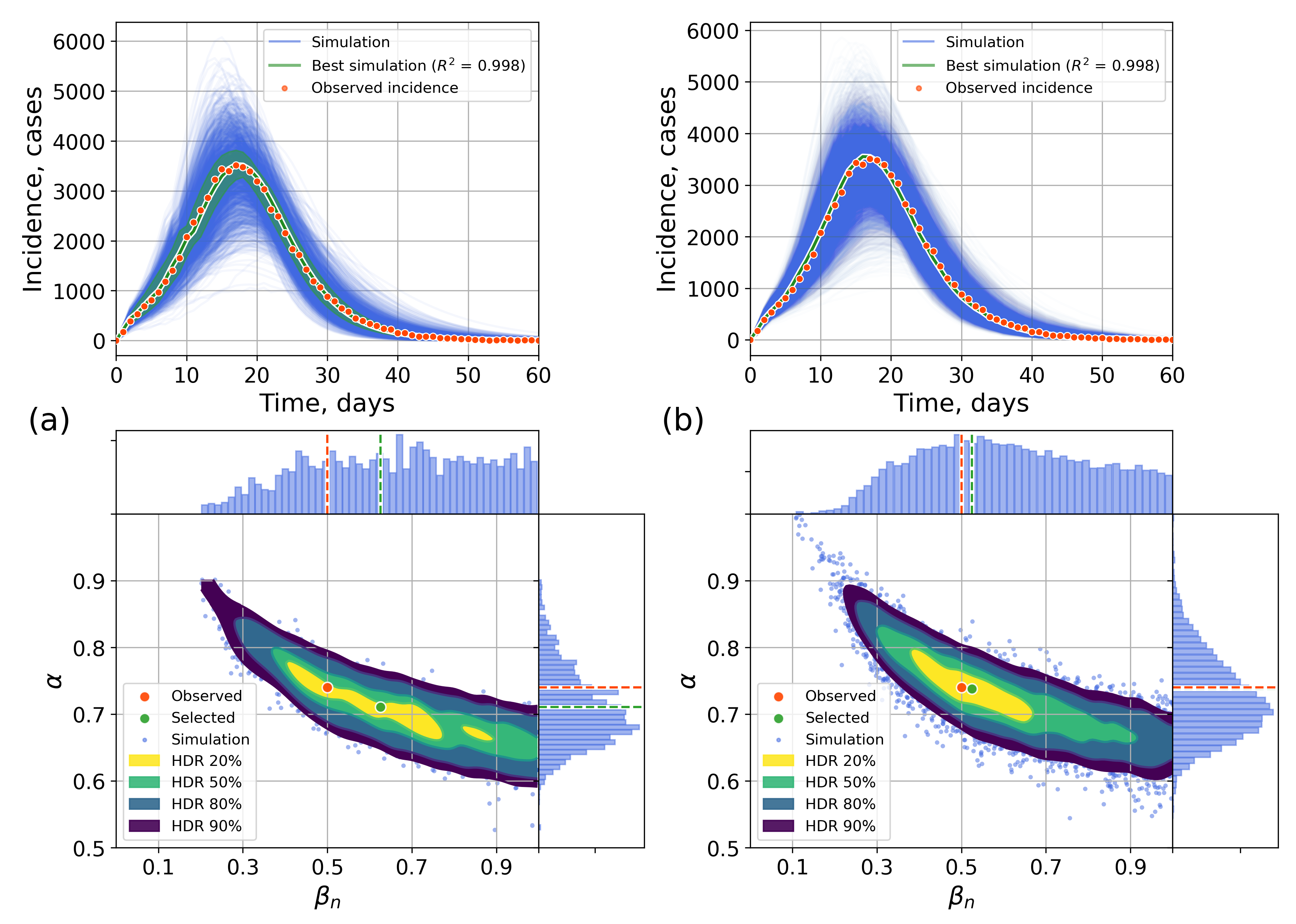
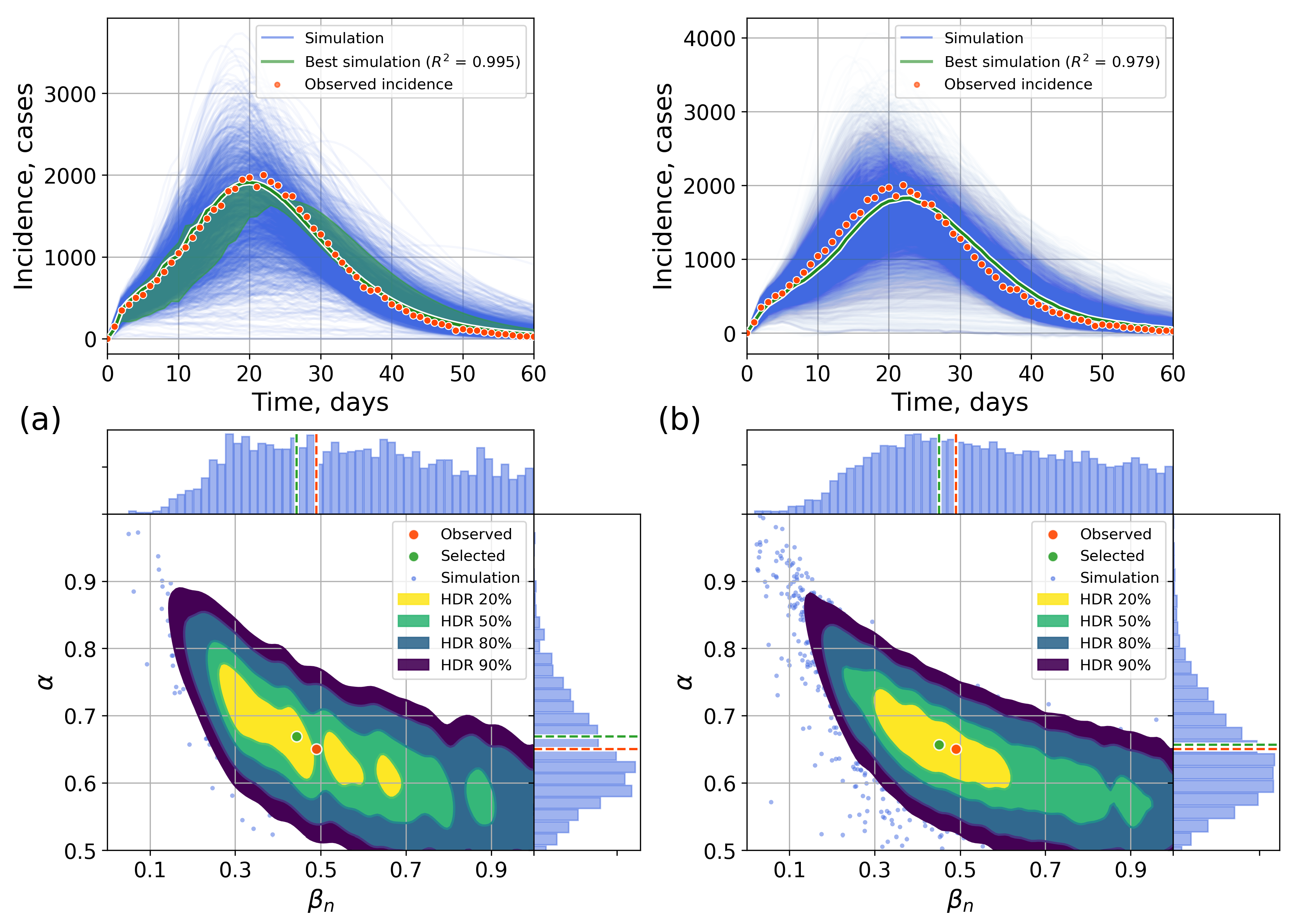
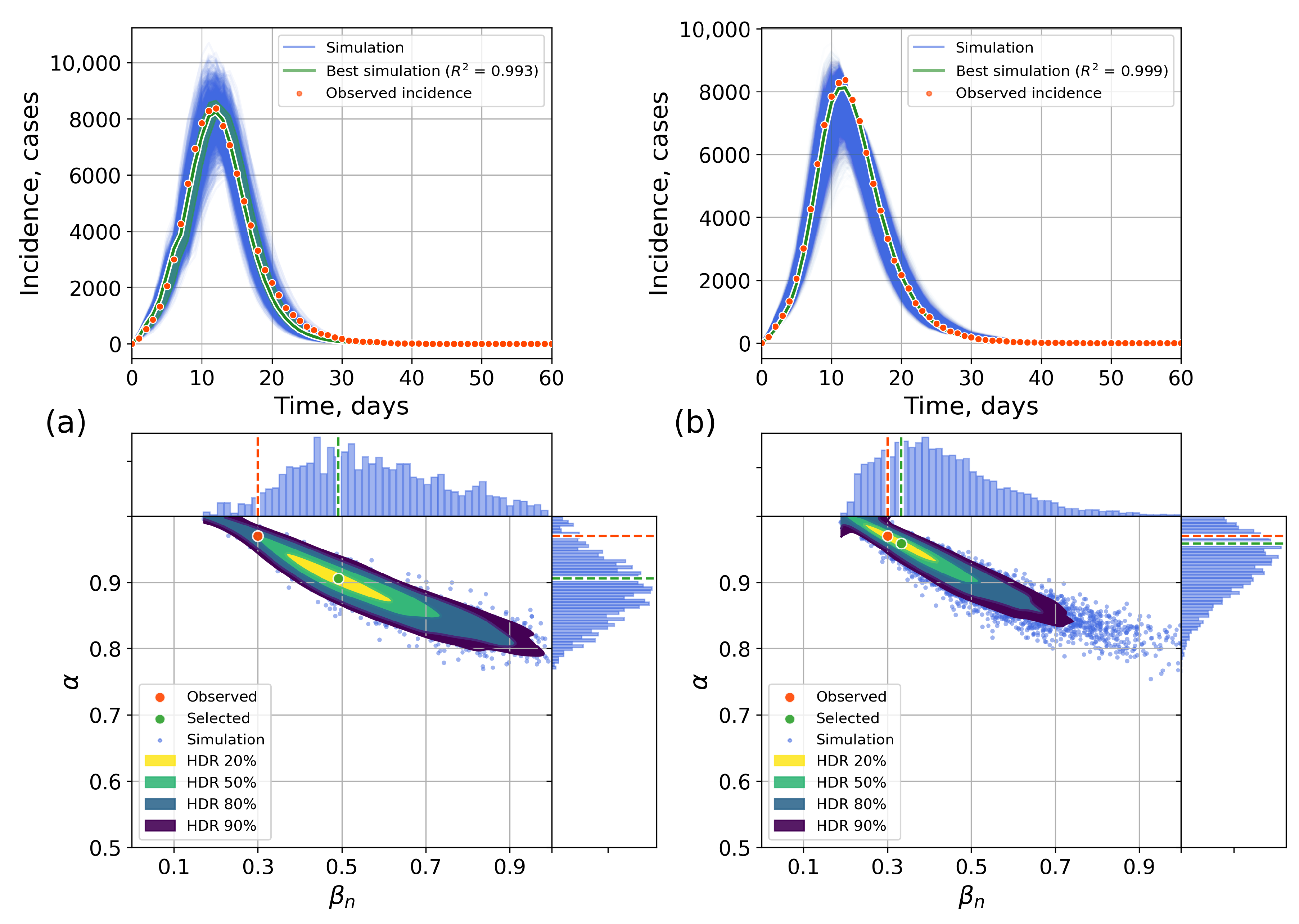
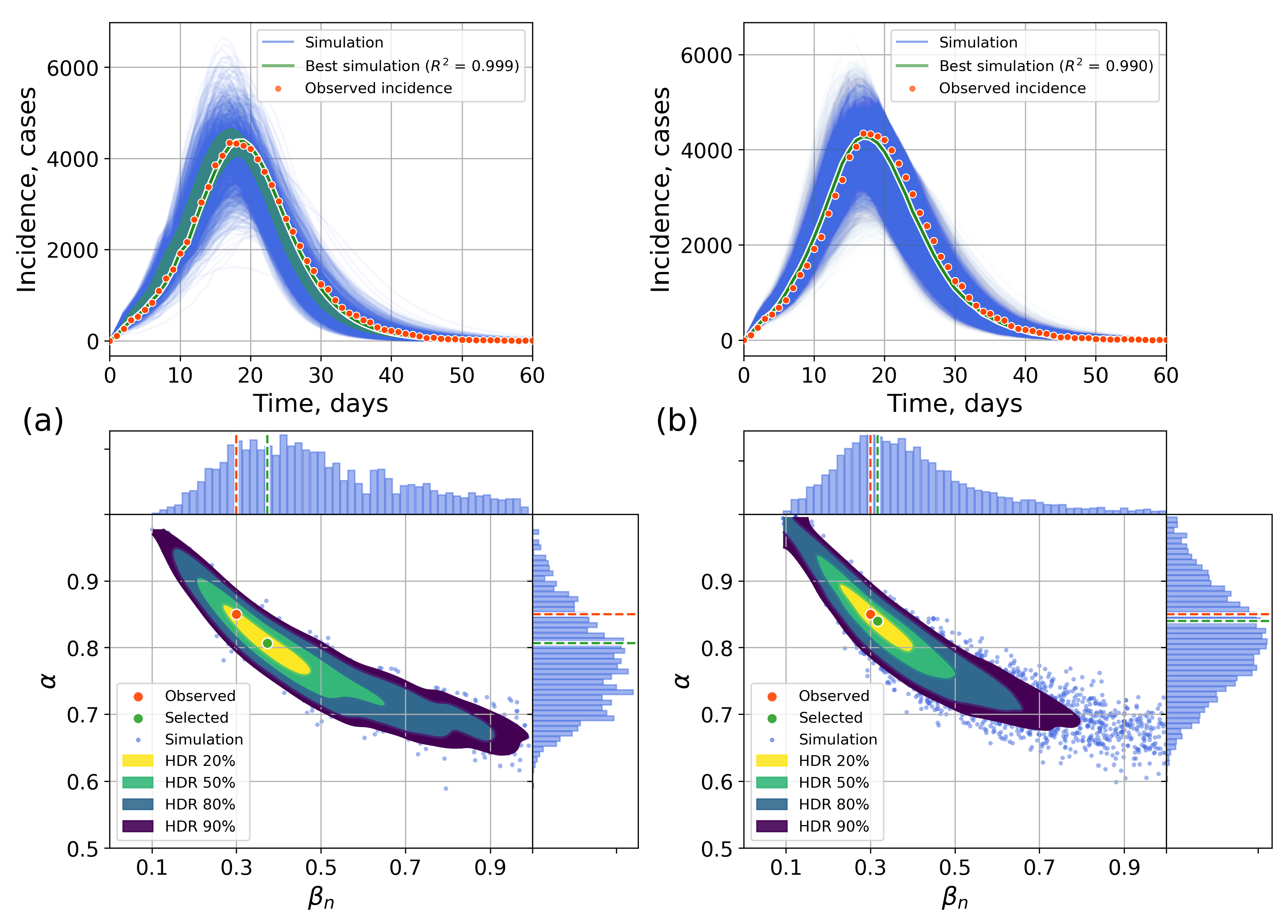
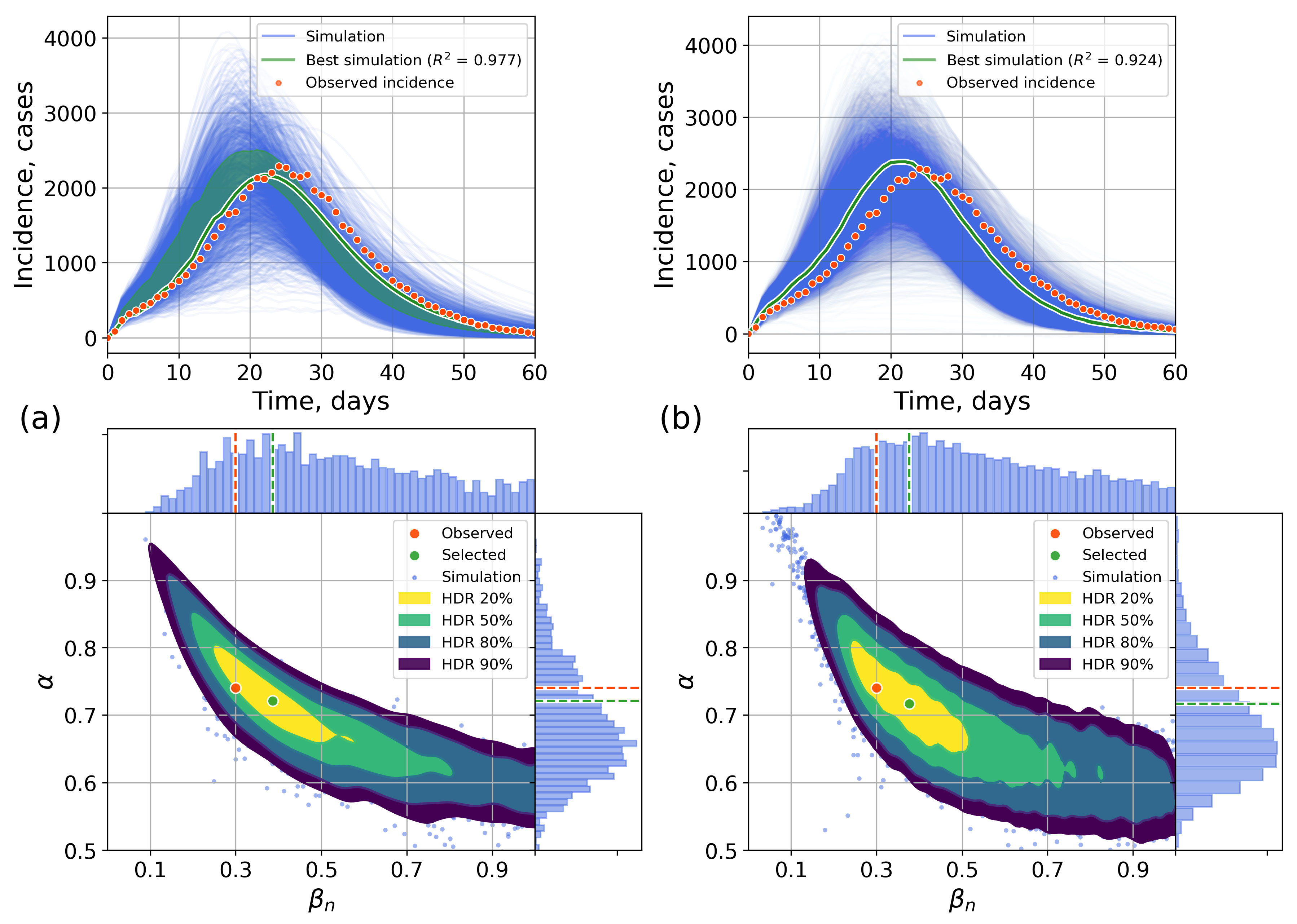
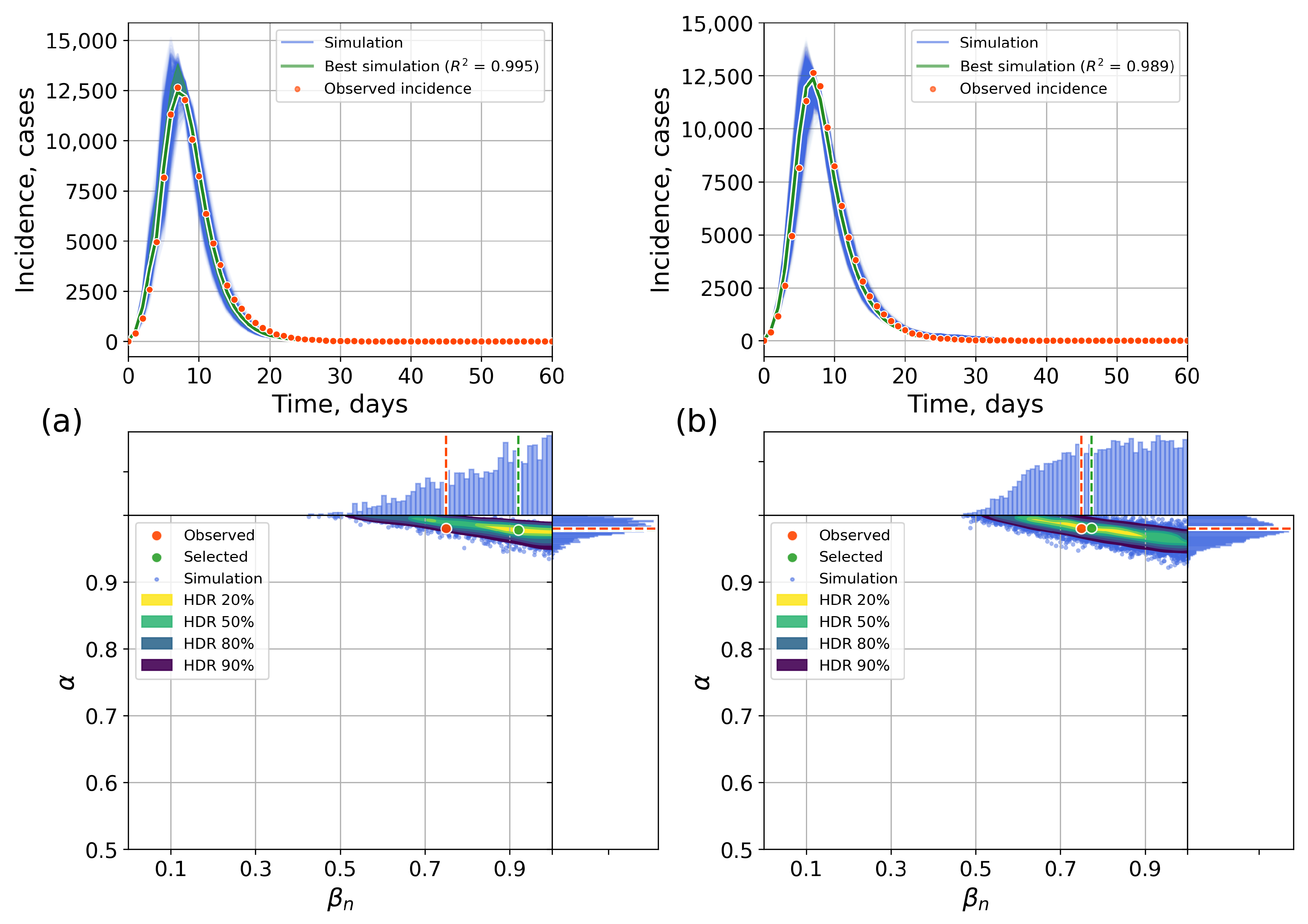
Appendix C. The Network Model Description
- Input:
- –
- A graph with nodes, representing individuals and their contact patterns.
- –
- Disease progression parameters: incubation rate , recovery rate , and a base transmission rate .
- –
- The initial number of infected individuals, .
- –
- The proportion of the population with prior immunity, .
- Output:
- –
- Time series of compartment counts: for .
- –
- (Optional) a detailed event log specifying the state of each node at each time t.
- Simulation procedure:
- Initialization:
- –
- Assign prior immunity: Uniformly at random, assign nodes to the Recovered (R) state.
- –
- Seed initial infection: From the remaining susceptible nodes, uniformly at random assign nodes to the infected (I) state. All the other non-immune nodes are set to Susceptible (S). The Exposed (E) compartment is initially empty.
- –
- Set the initial simulation time .
- Main loop: while :
- –
- For each node in state E, schedule an event time by sampling from .
- –
- For each node in state I, schedule an event time by sampling from .
- –
- For each node in state S with one or more infected neighbors, calculate the cumulative force of infection . Schedule an event time by sampling from .
- –
- Find the next event: Determine , the minimum time among all scheduled events.
- –
- Advance time: Set .
- –
- Execute event: Change the state of the node associated with the event at .
- *
- If : Remove the node from S, add to E. Schedule a new event for it.
- *
- If : Remove the node from E, add to I. Schedule a new event for it.
- *
- If : Remove the node from I, add to R.
- –
- Update the scheduled events list: Remove the executed event from scheduled events.
- Termination: the simulation concludes at time T. The time series is returned.
References
- Chowell, G.; Hyman, J.; Bettencourt, L.; Castillo-Chávez, C. Mathematical and Statistical Estimation Approaches in Epidemiology; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Anderson, R.M.; May, R.M. Infectious Diseases of Humans: Dynamics and Control; Oxford University Press: Oxford, UK, 1991. [Google Scholar] [CrossRef]
- Chowell, G. Fitting dynamic models to epidemic outbreaks with quantified uncertainty: A Primer for parameter uncertainty, identifiability, and forecasts. Infect. Dis. Model. 2017, 2, 379–398. [Google Scholar] [CrossRef] [PubMed]
- Friedman, J.; Liu, P.; Troeger, C.; Carter, A.; Reiner, R.; Barber, R.; Collins, J.; Lim, S.; Pigott, D.; Vos, T.; et al. Predictive performance of international COVID-19 mortality forecasting models. Nat. Commun. 2021, 12, 2609. [Google Scholar] [CrossRef]
- Vega, R.; Flores, L.; Greiner, R. SIMLR: Machine Learning inside the SIR Model for COVID-19 Forecasting. Forecasting 2022, 4, 72–94. [Google Scholar] [CrossRef]
- Bubar, K.; Middleton, C.; Larremore, D.; Gostic, K. A fundamental limit to the effectiveness of traveller screening with molecular tests. Epidemiol. Infect. 2025, 153, e95. [Google Scholar] [CrossRef]
- Leonenko, V.N. When a Pandemic Comes to Town: Combating Propagation of Novel Viruses in Russian Cities Using Statistical and Mathematical Modeling. In Proceedings of the 2024 IEEE 3rd International Conference on Problems of Informatics, Electronics and Radio Engineering (PIERE), Novosibirsk, Russia, 15–17 November 2024; pp. 990–995. [Google Scholar] [CrossRef]
- Mizumoto, K.; Kagaya, K.; Zarebski, A.; Chowell, G. Estimating the asymptomatic proportion of coronavirus disease 2019 (COVID-19) cases on board the Diamond Princess cruise ship, Yokohama, Japan, 2020. Eurosurveillance 2020, 25, 2000180. [Google Scholar] [CrossRef]
- Zhao, S.; Cao, P.; Gao, D.; Zhuang, Z.; Wang, W.; Ran, J.; Wang, K.; Yang, L.; Einollahi, M.R.; Lou, Y.; et al. Modelling COVID-19 outbreak on the Diamond Princess ship using the public surveillance data. Infect. Dis. Model. 2022, 7, 189–195. [Google Scholar] [CrossRef]
- Azimi, P.; Keshavarz, Z.; Cedeno Laurent, J.G.; Stephens, B.; Allen, J.G. Mechanistic transmission modeling of COVID-19 on the Diamond Princess cruise ship demonstrates the importance of aerosol transmission. Proc. Natl. Acad. Sci. USA 2021, 118, e2015482118. [Google Scholar] [CrossRef]
- Huang, L.S.; Li, L.; Dunn, L.; He, M. Taking account of asymptomatic infections: A modeling study of the COVID-19 outbreak on the Diamond Princess cruise ship. PloS ONE 2021, 16, e0248273. [Google Scholar] [CrossRef]
- Kumar, S.; Grefenstette, J.J.; Galloway, D.; Albert, S.M.; Burke, D.S. Policies to reduce influenza in the workplace: Impact assessments using an agent-based model. Am. J. Public Health 2013, 103, 1406–1411. [Google Scholar] [CrossRef] [PubMed]
- Hoertel, N.; Blachier, M.; Blanco, C.; Olfson, M.; Massetti, M.; Rico, M.S.; Limosin, F.; Leleu, H. A stochastic agent-based model of the SARS-CoV-2 epidemic in France. Nat. Med. 2020, 26, 1417–1421. [Google Scholar] [CrossRef] [PubMed]
- Krivorotko, O.; Sosnovskaia, M.; Vashchenko, I.; Kerr, C.; Lesnic, D. Agent-based modeling of COVID-19 outbreaks for New York state and UK: Parameter identification algorithm. Infect. Dis. Model. 2022, 7, 30–44. [Google Scholar] [CrossRef]
- Della Rossa, F.; Salzano, D.; Di Meglio, A.; De Lellis, F.; Coraggio, M.; Calabrese, C.; Guarino, A.; Cardona-Rivera, R.; De Lellis, P.; Liuzza, D.; et al. A network model of Italy shows that intermittent regional strategies can alleviate the COVID-19 epidemic. Nat. Commun. 2020, 11, 5106. [Google Scholar] [CrossRef]
- Chang, S.; Pierson, E.; Koh, P.W.; Gerardin, J.; Redbird, B.; Grusky, D.; Leskovec, J. Mobility network models of COVID-19 explain inequities and inform reopening. Nature 2021, 589, 82–87. [Google Scholar] [CrossRef]
- Elsenbroich, C.; Polhill, J.G. Agent-based modelling as a method for prediction in complex social systems. Int. J. Soc. Res. Methodol. 2023, 26, 133–142. [Google Scholar] [CrossRef]
- Jamshidi, M.; Roshani, S.; Daneshfar, F.; Lalbakhsh, A.; Roshani, S.; Parandin, F.; Malek, Z.; Talla, J.; Peroutka, Z.; Jamshidi, A.; et al. Hybrid deep learning techniques for predicting complex phenomena: A review on COVID-19. AI 2022, 3, 416–433. [Google Scholar] [CrossRef]
- Ning, X.; Guan, J.; Li, X.A.; Wei, Y.; Chen, F. Physics-informed neural networks integrating compartmental model for analyzing COVID-19 transmission dynamics. Viruses 2023, 15, 1749. [Google Scholar] [CrossRef]
- Rama, M.; Santin, G.; Cencetti, G.; Tizzoni, M.; Lepri, B. Forecasting Seasonal Influenza Epidemics with Physics-Informed Neural Networks. arXiv 2025, arXiv:2506.03897. [Google Scholar] [CrossRef]
- Baldo, F.; Iannello, M.; Lombardi, M.; Milano, M. Informed Deep Learning for epidemics forecasting. In PAIS 2022; IOS Press: Amsterdam, The Netherlands, 2022; pp. 86–99. [Google Scholar] [CrossRef]
- Rahmadani, F.; Lee, H. Hybrid deep learning-based epidemic prediction framework of COVID-19: South Korea case. Appl. Sci. 2020, 10, 8539. [Google Scholar] [CrossRef]
- Polcz, P.; Reguly, I.Z.; Tornai, K.; Juhász, J.; Pongor, S.; Csikász-Nagy, A.; Szederkényi, G. Smart epidemic control: A hybrid model blending ODEs and agent-based simulations for optimal, real-world intervention planning. PLoS Comput. Biol. 2025, 21, e1013028. [Google Scholar] [CrossRef]
- Cheng, Y.; Cheng, R.; Xu, T.; Tan, X.; Bai, Y. Machine learning techniques applied to COVID-19 prediction: A systematic literature review. Bioengineering 2025, 12, 514. [Google Scholar] [CrossRef]
- Kraemer, M.U.; Tsui, J.L.H.; Chang, S.Y.; Lytras, S.; Khurana, M.P.; Vanderslott, S.; Bajaj, S.; Scheidwasser, N.; Curran-Sebastian, J.L.; Semenova, E.; et al. Artificial intelligence for modelling infectious disease epidemics. Nature 2025, 638, 623–635. [Google Scholar] [CrossRef]
- Ye, Y.; Pandey, A.; Bawden, C.; Sumsuzzman, D.M.; Rajput, R.; Shoukat, A.; Singer, B.H.; Moghadas, S.M.; Galvani, A.P. Integrating artificial intelligence with mechanistic epidemiological modeling: A scoping review of opportunities and challenges. Nat. Commun. 2025, 16, 581. [Google Scholar] [CrossRef]
- Binder, P.M.; Simpfendorfer, J.; McNeney, B.; Brailsford, S.C. Hybrid Modeling in Health Care—Combining Agent Based and Equation Based Approaches. ANZIAM J. 2012, 53, C313–C329. [Google Scholar] [CrossRef]
- Bobashev, G.V.; Goedecke, D.M.; Yu, F.; Epstein, J.M. A Hybrid Epidemic Model: Combining the Advantages of Agent-Based and Equation-Based Approaches. In Proceedings of the 2007 Winter Simulation Conference, Washington, DC, USA, 9–12 December 2007; pp. 1532–1537. [Google Scholar] [CrossRef]
- Hunter, E.; Mac Namee, B.; Kelleher, J. A Hybrid Agent-Based and Equation Based Model for the Spread of Infectious Diseases. J. Artif. Soc. Soc. Simul. 2020, 23, 14. [Google Scholar] [CrossRef]
- Hunter, E.; Kelleher, J.D. Adapting an agent-based model of infectious disease spread in an Irish county to COVID-19. Systems 2021, 9, 41. [Google Scholar] [CrossRef]
- Liu, X.D.; Wang, W.; Yang, Y.; Hou, B.H.; Olasehinde, T.S.; Feng, N.; Dong, X.P. Nesting the SIRV model with NAR, LSTM and statistical methods to fit and predict COVID-19 epidemic trend in Africa. BMC Public Health 2023, 23, 138. [Google Scholar] [CrossRef]
- Leonenko, V. A Hybrid Modeling Framework for City-Scale Dynamics of Multi-strain Influenza Epidemics. In Proceedings of the Computational Science—ICCS 2022, London, UK, 21–23 June 2022; Groen, D., de Mulatier, C., Paszynski, M., Krzhizhanovskaya, V.V., Dongarra, J.J., Sloot, P.M.A., Eds.; Springer: Cham, Switzerland, 2022; pp. 164–177. [Google Scholar] [CrossRef]
- Koshkareva, M.; Guseva, E.; Sharova, A.; Leonenko, V. Predicting Disease Transmission Rates for Hybrid Modeling of Epidemic Outbreaks: Statistical and Machine Learning Approaches. In Proceedings of the Computational Science—ICCS 2025 Workshops, Singapore, 7–9 July 2025; Paszynski, M., Barnard, A.S., Zhang, Y.J., Eds.; Springer: Cham, Switzerland, 2025; pp. 149–163. [Google Scholar] [CrossRef]
- Kurul, E.; Tunc, H.; Sari, M.; Guzel, N. Deep learning aided surrogate modeling of the epidemiological models. J. Comput. Sci. 2025, 84, 102470. [Google Scholar] [CrossRef]
- Pereira, F.H.; Schimit, P.H.; Bezerra, F.E. A deep learning based surrogate model for the parameter identification problem in probabilistic cellular automaton epidemic models. Comput. Methods Programs Biomed. 2021, 205, 106078. [Google Scholar] [CrossRef]
- Angione, C.; Silverman, E.; Yaneske, E. Using machine learning as a surrogate model for agent-based simulations. PLoS ONE 2022, 17, e0263150. [Google Scholar] [CrossRef]
- Pokharel, G.; Deardon, R. Gaussian process emulators for spatial individual-level models of infectious disease. Can. J. Stat. 2016, 44, 480–501. [Google Scholar] [CrossRef]
- Matveeva, A.; Leonenko, V. Application of Gaussian process regression as a surrogate modeling method to assess the dynamics of COVID-19 propagation. Procedia Comput. Sci. 2022, 212, 340–347. [Google Scholar] [CrossRef] [PubMed]
- Langmüller, A.M.; Chandrasekher, K.A.; Haller, B.C.; Champer, S.E.; Murdock, C.C.; Messer, P.W. Gaussian Process Emulation for Exploring Complex Infectious Disease Models. medRxiv 2025. [Google Scholar] [CrossRef]
- Schmidt, A.; Zunker, H.; Heinlein, A.; Kühn, M.J. Graph Neural Network Surrogates to leverage Mechanistic Expert Knowledge towards Reliable and Immediate Pandemic Response. arXiv 2024, arXiv:2411.06500. [Google Scholar] [CrossRef]
- Vlad, A.I.; Romanyukha, A.A.; Sannikova, T.E. Parameter tuning of agent-based models: Metaheuristic algorithms. Mathematics 2024, 12, 2208. [Google Scholar] [CrossRef]
- Anirudh, R.; Thiagarajan, J.J.; Bremer, P.T.; Germann, T.; Del Valle, S.; Streitz, F. Accurate Calibration of Agent-based Epidemiological Models with Neural Network Surrogates. In Proceedings of the 1st Workshop on Healthcare AI and COVID-19, ICML 2022, Baltimore, MD, USA, 23–24 July 2022; Volume 184, pp. 54–62. [Google Scholar]
- Perumal, R.; Zyl, T.L.v. Surrogate-assisted strategies: The parameterisation of an infectious disease agent-based model. Neural Comput. Appl. 2025, 37, 627–638. [Google Scholar] [CrossRef]
- Norton, K.A.; Bergman, D.; Jain, H.V.; Jackson, T. Advances in surrogate modeling for biological agent-based simulations: Trends, challenges, and future prospects. arXiv 2025, arXiv:2504.11617. [Google Scholar] [CrossRef]
- Panovska-Griffiths, J.; Bayley, T.; Ward, T.; Das, A.; Imeneo, L.; Kerr, C.; Maskell, S. Machine learning assisted calibration of stochastic agent-based models for pandemic outbreak analysis. Res. Sq. 2023. [Google Scholar] [CrossRef]
- Kerr, C.C.; Stuart, R.M.; Mistry, D.; Abeysuriya, R.G.; Rosenfeld, K.; Hart, G.R.; Núñez, R.C.; Cohen, J.A.; Selvaraj, P.; Hagedorn, B.; et al. Covasim: An agent-based model of COVID-19 dynamics and interventions. PLoS Comput. Biol. 2021, 17, e1009149. [Google Scholar] [CrossRef]
- Senichev, S.D.; Fandeev, A.A.; Leonenko, V.N. Accelerating Multiagent Epidemic Modeling with Surrogate-Based Methods. In Proceedings of the 2024 IEEE International Multi-Conference on Engineering, Computer and Information Sciences (SIBIRCON), Novosibirsk, Russia, 30 September–2 October 2024; pp. 220–223. [Google Scholar] [CrossRef]
- Leonenko, V.; Arzamastsev, S.; Bobashev, G. Contact patterns and influenza outbreaks in Russian cities: A proof-of-concept study via agent-based modeling. J. Comput. Sci. 2020, 44, 101156. [Google Scholar] [CrossRef]
- Korzin, A.; Leonenko, V. Lightweight Heterogeneous SEIR Models for Epidemic Surveillance in Russian Cities: Turning Synthetic Populations Into Equations. In Proceedings of the International Conference on Computational Science, Singapore, 7–9 July 2025; pp. 164–175. [Google Scholar]
- Gillespie, D.T. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 1977, 81, 2340–2361. [Google Scholar] [CrossRef]
- Miller, J.C.; Ting, T. Eon (epidemics on networks): A fast, flexible python package for simulation, analytic approximation, and analysis of epidemics on networks. arXiv 2020, arXiv:2001.02436. [Google Scholar] [CrossRef]
- Sergio, A.R.; Schimit, P.H. Optimizing contact network topological parameters of urban populations using the genetic algorithm. Entropy 2024, 26, 661. [Google Scholar] [CrossRef]
- Abramov, A.; Gorik, U.; Velichko, A.; Nelyub, V.; Samoshkin, A.; Gantimurov, A.; Borodulin, A.; Tynchenko, V.S.; Malashin, I. Barabási–Albert-Based Network Growth Model to Sustainable Urban Planning. Sustainability 2025, 17, 1095. [Google Scholar] [CrossRef]
- Hagberg, A.; Swart, P.J.; Schult, D.A. Exploring Network Structure, Dynamics, and Function Using NetworkX; Technical Report; Los Alamos National Laboratory (LANL): Los Alamos, NM, USA, 2008. [Google Scholar]
- Hill, E.M.; Petrou, S.; de Lusignan, S.; Yonova, I.; Keeling, M.J. Seasonal influenza: Modelling approaches to capture immunity propagation. PLoS Comput. Biol. 2019, 15, e1007096. [Google Scholar] [CrossRef] [PubMed]
- Abril-Pla, O.; Andreani, V.; Carroll, C.; Dong, L.; Fonnesbeck, C.J.; Kochurov, M.; Kumar, R.; Lao, J.; Luhmann, C.C.; Martin, O.A.; et al. PyMC: A modern, and comprehensive probabilistic programming framework in Python. PeerJ Comput. Sci. 2023, 9, e1516. [Google Scholar] [CrossRef] [PubMed]
- Baroyan, O.; Rvachev, L.; Ivannikov, Y.G. Modelling and Prediction of Influenza Epidemics in the USSR; Gamelei Institute of Epidemiology and Microbiology: Moscow, Russia, 1977. [Google Scholar]
- Ajelli, M.; Litvinova, M. Estimating contact patterns relevant to the spread of infectious diseases in Russia. J. Theor. Biol. 2017, 419, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Sahatova, K.; Kharlunin, A.; Huaman, I.; Leonenko, V. Accounting for data uncertainty in modeling acute respiratory infections: Influenza in Saint Petersburg as a case study. In Proceedings of the International Conference on Computational Science, Prague, Czech Republic, 3–5 July 2023; pp. 286–299. [Google Scholar]
- Li, B.; Peng, Y.; He, H.; Wang, M.; Feng, T. Built environment and early infection of COVID-19 in urban districts: A case study of Huangzhou. Sustain. Cities Soc. 2021, 66, 102685. [Google Scholar] [CrossRef]
- Shen, Z.; Wang, W.X.; Fan, Y.; Di, Z.; Lai, Y.C. Reconstructing propagation networks with natural diversity and identifying hidden sources. Nat. Commun. 2014, 5, 4323. [Google Scholar] [CrossRef]
- Jiang, J.; Wen, S.; Yu, S.; Xiang, Y.; Zhou, W. K-center: An approach on the multi-source identification of information diffusion. IEEE Trans. Inf. Forensics Secur. 2015, 10, 2616–2626. [Google Scholar] [CrossRef]
- Li, C.; Wang, L.; Sun, S.; Xia, C. Identification of influential spreaders based on classified neighbors in real-world complex networks. Appl. Math. Comput. 2018, 320, 512–523. [Google Scholar] [CrossRef]
- Jiang, J.; Wen, S.; Yu, S.; Xiang, Y.; Zhou, W. Rumor source identification in social networks with time-varying topology. IEEE Trans. Dependable Secur. Comput. 2016, 15, 166–179. [Google Scholar] [CrossRef]
- Aina, Y.A.; Abubakar, I.R.; Almulhim, A.I.; Dano, U.L.; Maghsoodi Tilaki, M.J.; Dawood, S.R. Digitalization and smartification of urban services to enhance urban resilience in the post-pandemic era: The case of the pilgrimage city of Makkah. Smart Cities 2023, 6, 1973–1995. [Google Scholar] [CrossRef]

| Parameter | Description |
|---|---|
| Initial fraction of non-immune individuals | |
| Infection transmission rate (compartmental and network models) | |
| Mean latent (exposed) period, days | |
| Mean infectious period, days | |
| Number of susceptible individuals on day t | |
| Number of exposed individuals on day t | |
| Number of infectious individuals on day t | |
| Number of recovered individuals on day t | |
| N | Total population size |
| T | Simulation time |
| Parameter | Type | Value |
|---|---|---|
| Varied | [0.2, 1] | |
| Varied | [0.1, 1] | |
| Fixed | days | |
| Fixed | days | |
| N | Fixed | individuals |
| Estimation Method | Switch Condition: Percent of the Population | ||||
|---|---|---|---|---|---|
| 3% | 4% | 5% | 6% | 7% | |
| Last Value | |||||
| Cumulative Average | |||||
| Median | |||||
| Regression | |||||
| LSTM | |||||
| Switch day | |||||
| Estimation Method | Switch Condition: Percent of the Population | ||||
|---|---|---|---|---|---|
| 3% | 4% | 5% | 6% | 7% | |
| Last value | |||||
| Cumulative Average | |||||
| Median | |||||
| Regression | |||||
| LSTM | |||||
| Switch day | |||||
| Modeling Approach | Simulation Time | Calibration Time |
|---|---|---|
| Network model | ms | s ≈ 43 h |
| Hybrid approach | ms | s ≈ 25 h |
| Surrogate approach | 0.1 ms | 50 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Korzin, A.; Koshkareva, M.; Leonenko, V. Integrating Machine Learning with Hybrid and Surrogate Models to Accelerate Multiscale Modeling of Acute Respiratory Infections. Viruses 2025, 17, 1541. https://doi.org/10.3390/v17121541
Korzin A, Koshkareva M, Leonenko V. Integrating Machine Learning with Hybrid and Surrogate Models to Accelerate Multiscale Modeling of Acute Respiratory Infections. Viruses. 2025; 17(12):1541. https://doi.org/10.3390/v17121541
Chicago/Turabian StyleKorzin, Andrey, Maria Koshkareva, and Vasiliy Leonenko. 2025. "Integrating Machine Learning with Hybrid and Surrogate Models to Accelerate Multiscale Modeling of Acute Respiratory Infections" Viruses 17, no. 12: 1541. https://doi.org/10.3390/v17121541
APA StyleKorzin, A., Koshkareva, M., & Leonenko, V. (2025). Integrating Machine Learning with Hybrid and Surrogate Models to Accelerate Multiscale Modeling of Acute Respiratory Infections. Viruses, 17(12), 1541. https://doi.org/10.3390/v17121541






