Mathematical Models of HIV-1 Dynamics, Transcription, and Latency
Abstract
:1. Introduction
2. History of Mathematical Models of HIV-1
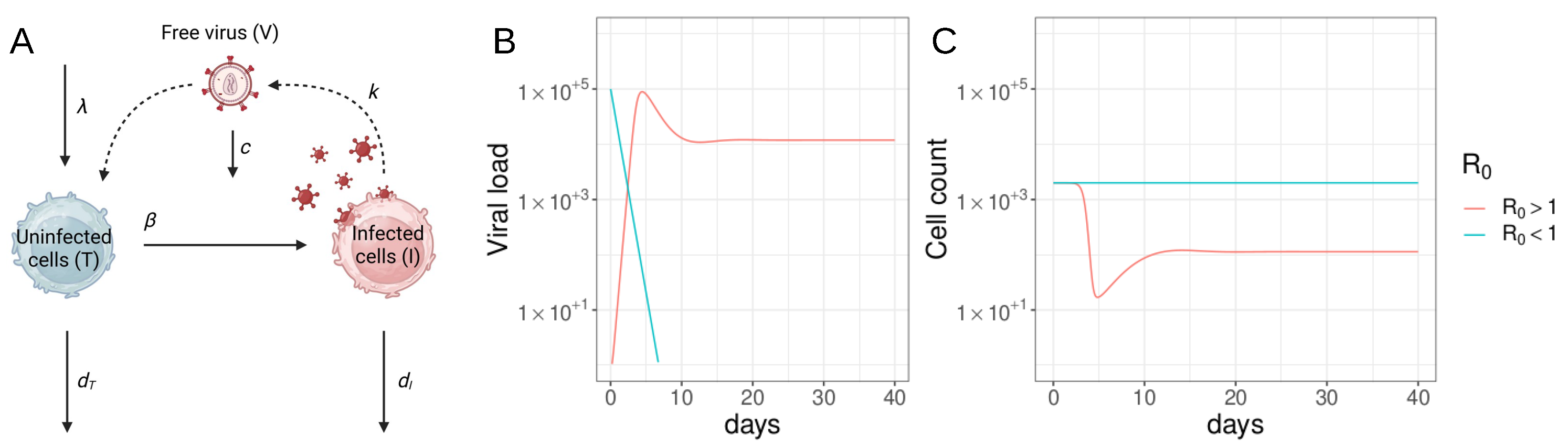
2.1. Viral Dynamics Model
2.1.1. The Basic Viral Dynamics Model
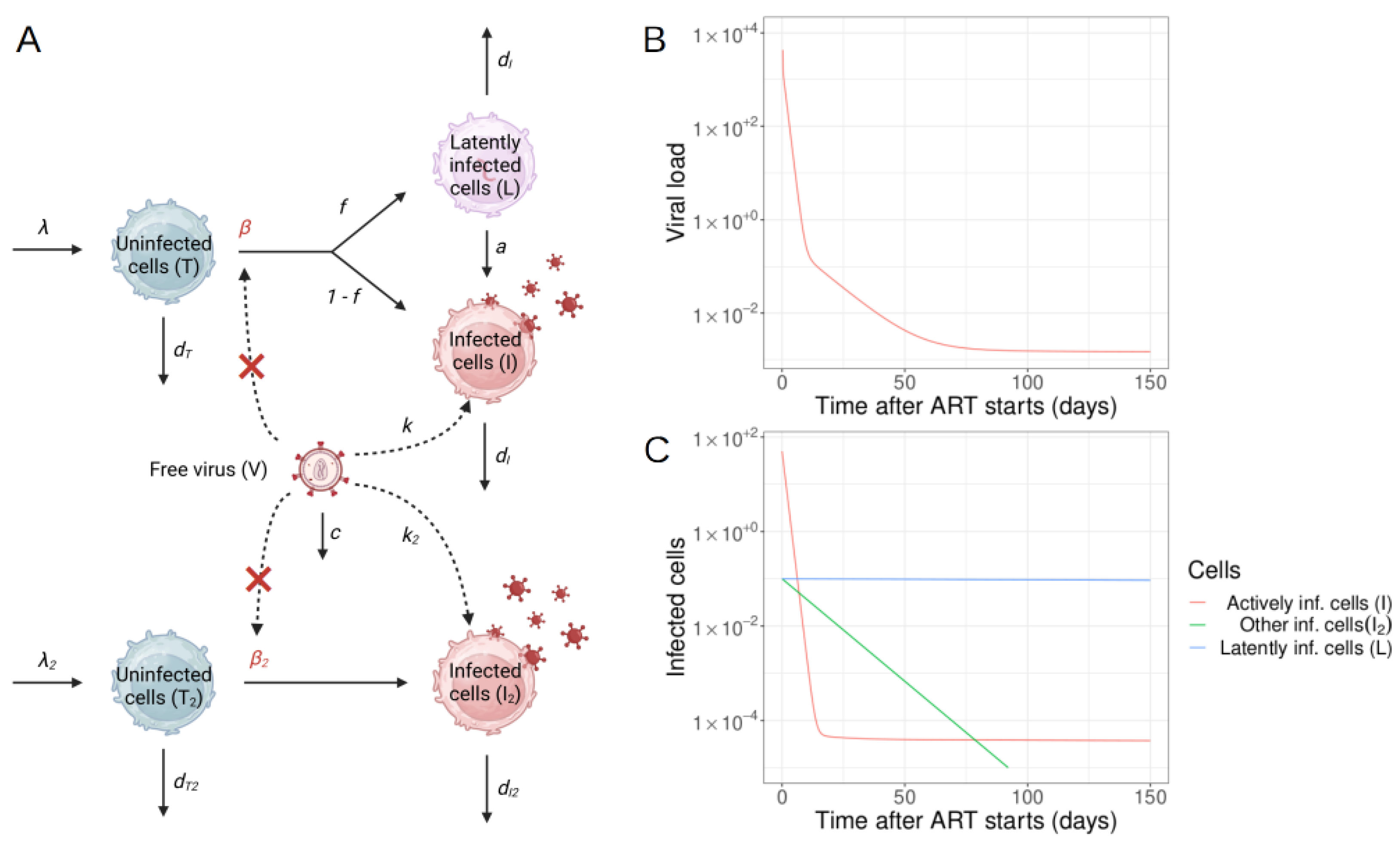
2.1.2. Models of ART
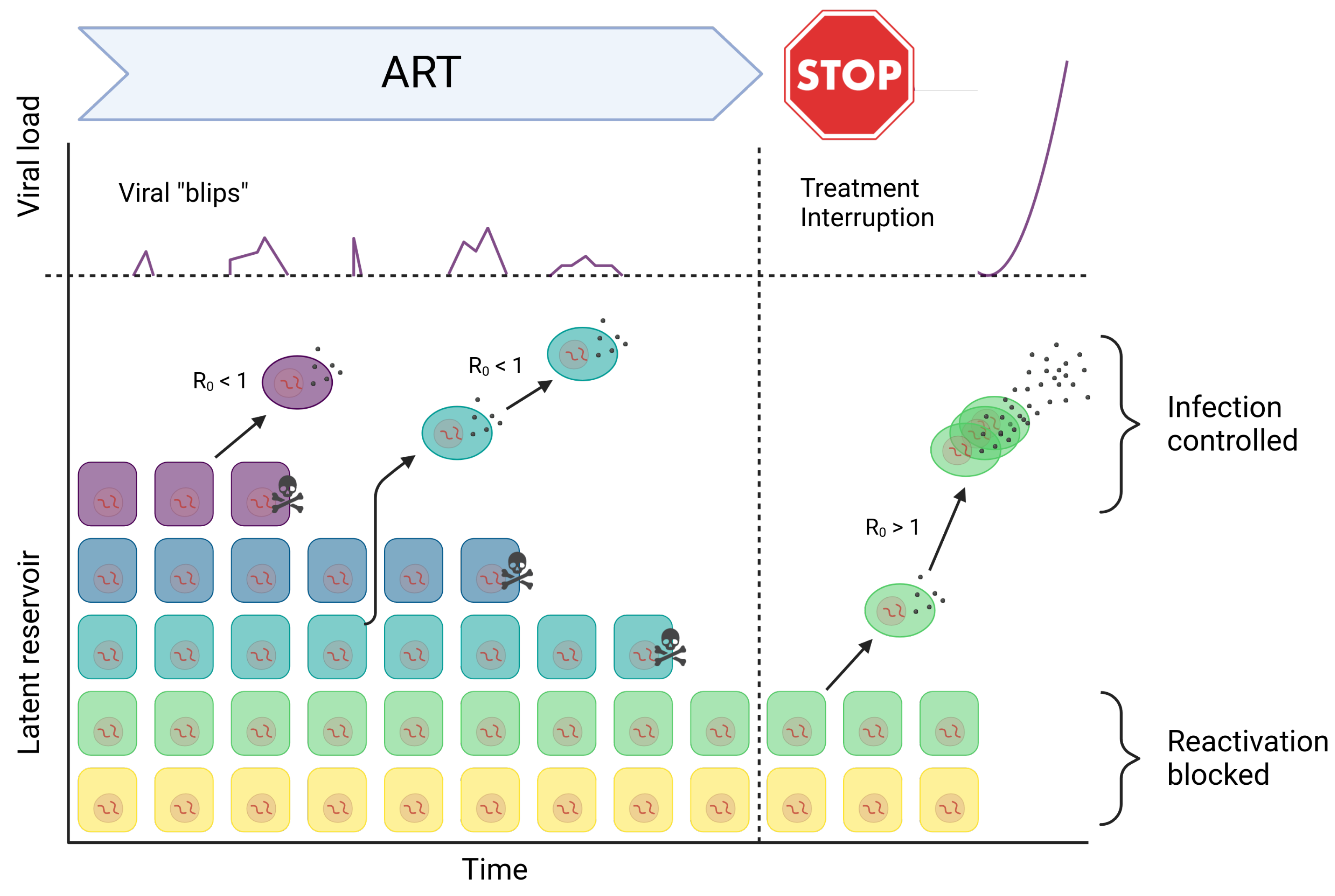
2.2. Mechanisms of Latent Reservoir Persistence
3. Molecular Features Contributing to HIV-1 Latency and Reactivation
3.1. Integration Site
3.2. Chromatin
3.3. Transcription Machinery
4. Transcriptional Bursting and Mathematical Modeling
4.1. Transcriptional Bursting and Gene Expression Noise
4.2. A Stochastic Model to Describe the HIV-1 Transcriptional Circuit
4.3. Incorporating Host and Viral Phases to Model the HIV-1 Transcriptional Circuit
4.4. Two-State HIV-1 Transcriptional Model
4.5. Three-State HIV-1 Transcriptional Model
5. Discussion and Future Perspective
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chun, T.W.; Carruth, L.; Finzi, D.; Shen, X.; DiGiuseppe, J.A.; Taylor, H.; Hermankova, M.; Chadwick, K.; Margolick, J.; Quinn, T.C.; et al. Quantification of latent tissue reservoirs and total body viral load in HIV-1 infection. Nature 1997, 387, 183–188. [Google Scholar] [CrossRef] [PubMed]
- Finzi, D.; Hermankova, M.; Pierson, T.; Carruth, L.M.; Buck, C.; Chaisson, R.E.; Quinn, T.C.; Chadwick, K.; Margolick, J.; Brookmeyer, R.; et al. Identification of a reservoir for HIV-1 in patients on highly active antiretroviral therapy. Science 1997, 278, 1295–1300. [Google Scholar] [CrossRef] [PubMed]
- Finzi, D.; Blankson, J.; Siliciano, J.D.; Margolick, J.B.; Chadwick, K.; Pierson, T.; Smith, K.; Lisziewicz, J.; Lori, F.; Flexner, C.; et al. Latent infection of CD4+ T cells provides a mechanism for lifelong persistence of HIV-1, even in patients on effective combination therapy. Nat. Med. 1999, 5, 512–517. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Abbas, W.; Herbein, G. HIV-1 latency in monocytes/macrophages. Viruses 2014, 6, 1837–1860. [Google Scholar] [CrossRef] [PubMed]
- Mitchell, B.I.; Laws, E.I.; Ndhlovu, L.C. Impact of myeloid reservoirs in HIV cure trials. Curr. HIV/AIDS Rep. 2019, 16, 129–140. [Google Scholar] [CrossRef] [PubMed]
- Veenhuis, R.T.; Abreu, C.M.; Costa, P.A.; Ferreira, E.A.; Ratliff, J.; Pohlenz, L.; Shirk, E.N.; Rubin, L.H.; Blankson, J.N.; Gama, L.; et al. Monocyte-derived macrophages contain persistent latent HIV reservoirs. Nat. Microbiol. 2023, 8, 833–844. [Google Scholar] [CrossRef] [PubMed]
- Wallet, C.; De Rovere, M.; Van Assche, J.; Daouad, F.; De Wit, S.; Gautier, V.; Mallon, P.W.; Marcello, A.; Van Lint, C.; Rohr, O.; et al. Microglial cells: The main HIV-1 reservoir in the brain. Front. Cell. Infect. Microbiol. 2019, 9, 362. [Google Scholar] [CrossRef]
- Wei, X.; Ghosh, S.K.; Taylor, M.E.; Johnson, V.A.; Emini, E.A.; Deutsch, P.; Lifson, J.D.; Bonhoeffer, S.; Nowak, M.A.; Hahn, B.H.; et al. Viral dynamics in human immunodeficiency virus type 1 infection. Nature 1995, 373, 117–122. [Google Scholar] [CrossRef]
- Ho, D.D.; Neumann, A.U.; Perelson, A.S.; Chen, W.; Leonard, J.M.; Markowitz, M. Rapid turnover of plasma virions and CD4 lymphocytes in HIV-1 infection. Nature 1995, 373, 123–126. [Google Scholar] [CrossRef]
- Ramratnam, B.; Bonhoeffer, S.; Binley, J.; Hurley, A.; Zhang, L.; Mittler, J.E.; Markowitz, M.; Moore, J.P.; Perelson, A.S.; Ho, D.D. Rapid production and clearance of HIV-1 and hepatitis C virus assessed by large volume plasma apheresis. Lancet 1999, 354, 1782–1785. [Google Scholar] [CrossRef]
- Perelson, A.S.; Essunger, P.; Cao, Y.; Vesanen, M.; Hurley, A.; Saksela, K.; Markowitz, M.; Ho, D.D. Decay characteristics of HIV-1-infected compartments during combination therapy. Nature 1997, 387, 188–191. [Google Scholar] [CrossRef] [PubMed]
- McMyn, N.F.; Varriale, J.; Fray, E.J.; Zitzmann, C.; MacLeod, H.; Lai, J.; Singhal, A.; Moskovljevic, M.; Garcia, M.A.; Lopez, B.M.; et al. The latent reservoir of inducible, infectious HIV-1 does not decrease despite decades of antiretroviral therapy. J. Clin. Investig. 2023, 133, e171554. [Google Scholar] [CrossRef] [PubMed]
- Rong, L.; Perelson, A.S. Modeling latently infected cell activation: Viral and latent reservoir persistence, and viral blips in HIV-infected patients on potent therapy. PLoS Comput. Biol. 2009, 5, e1000533. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Perelson, A.S. Viral and latent reservoir persistence in HIV-1–infected patients on therapy. PLoS Comput. Biol. 2006, 2, e135. [Google Scholar] [CrossRef] [PubMed]
- Perelson, A.S.; Ribeiro, R.M. Modeling the within-host dynamics of HIV infection. BMC Biol. 2013, 11, 96. [Google Scholar] [CrossRef]
- Conway, J.M.; Meily, P.; Li, J.Z.; Perelson, A.S. Unified model of short-and long-term HIV viral rebound for clinical trial planning. J. R. Soc. Interface 2021, 18, 20201015. [Google Scholar] [CrossRef]
- Conway, J.M.; Coombs, D. A stochastic model of latently infected cell reactivation and viral blip generation in treated HIV patients. PLoS Comput. Biol. 2011, 7, e1002033. [Google Scholar] [CrossRef]
- Hill, A.L. Mathematical Models of HIV Latency. Curr. Top. Microbiol. Immunol. 2018, 417, 131–156. [Google Scholar]
- Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. Ser. Contain. Pap. Math. Phys. Character 1927, 115, 700–721. [Google Scholar]
- Brauer, F. Mathematical epidemiology is not an oxymoron. BMC Public Health 2009, 9, S2. [Google Scholar] [CrossRef]
- Anderson, R.M.; May, R.M. Infectious Diseases of Humans: Dynamics and Control; Oxford University Press: Oxford, UK, 1991. [Google Scholar]
- Nowak, M.; May, R.M. Virus Dynamics: Mathematical Principles of Immunology and Virology: Mathematical Principles of Immunology and Virology; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- Nowak, M.A.; Bonhoeffer, S.; Hill, A.M.; Boehme, R.; Thomas, H.C.; McDade, H. Viral dynamics in hepatitis B virus infection. Proc. Natl. Acad. Sci. USA 1996, 93, 4398–4402. [Google Scholar] [CrossRef] [PubMed]
- Perelson, A.S.; Ribeiro, R.M. Hepatitis B virus kinetics and mathematical modeling. In Seminars in Liver Disease; Thieme Medical Publishers, Inc.: New York, NY, USA, 2004; Volume 24, pp. 11–16. [Google Scholar]
- Dahari, H.; Shudo, E.; Ribeiro, R.M.; Perelson, A.S. Modeling complex decay profiles of hepatitis B virus during antiviral therapy. Hepatology 2009, 49, 32–38. [Google Scholar] [CrossRef] [PubMed]
- Neumann, A.U.; Lam, N.P.; Dahari, H.; Gretch, D.R.; Wiley, T.E.; Layden, T.J.; Perelson, A.S. Hepatitis C viral dynamics in vivo and the antiviral efficacy of interferon-α therapy. Science 1998, 282, 103–107. [Google Scholar] [CrossRef] [PubMed]
- Chatterjee, A.; Guedj, J.; Perelson, A.S. Mathematical modeling of HCV infection: What can it teach us in the era of direct antiviral agents? Antivir. Ther. 2012, 17, 1171. [Google Scholar] [CrossRef]
- Murillo, L.N.; Murillo, M.S.; Perelson, A.S. Towards multiscale modeling of influenza infection. J. Theor. Biol. 2013, 332, 267–290. [Google Scholar] [CrossRef]
- Nuraini, N.; Tasman, H.; Soewono, E.; Sidarto, K.A. A with-in host dengue infection model with immune response. Math. Comput. Model. 2009, 49, 1148–1155. [Google Scholar] [CrossRef]
- Clapham, H.E.; Tricou, V.; Van Vinh Chau, N.; Simmons, C.P.; Ferguson, N.M. Within-host viral dynamics of dengue serotype 1 infection. J. R. Soc. Interface 2014, 11, 20140094. [Google Scholar] [CrossRef]
- Schiffer, J.T.; Swan, D.A.; Magaret, A.; Corey, L.; Wald, A.; Ossig, J.; Ruebsamen-Schaeff, H.; Stoelben, S.; Timmler, B.; Zimmermann, H.; et al. Mathematical modeling of herpes simplex virus-2 suppression with pritelivir predicts trial outcomes. Sci. Transl. Med. 2016, 8, 324ra15. [Google Scholar] [CrossRef]
- Butterworth, E.; Jardine, B.E.; Raymond, G.M.; Neal, M.L.; Bassingthwaighte, J.B. JSim, an open-source modeling system for data analysis. F1000Research 2013, 2, 288. [Google Scholar] [CrossRef]
- Phillips, A.N. Reduction of HIV concentration during acute infection: Independence from a specific immune response. Science 1996, 271, 497–499. [Google Scholar] [CrossRef]
- Stafford, M.A.; Corey, L.; Cao, Y.; Daar, E.S.; Ho, D.D.; Perelson, A.S. Modeling plasma virus concentration during primary HIV infection. J. Theor. Biol. 2000, 203, 285–301. [Google Scholar] [CrossRef] [PubMed]
- Burg, D.; Rong, L.; Neumann, A.U.; Dahari, H. Mathematical modeling of viral kinetics under immune control during primary HIV-1 infection. J. Theor. Biol. 2009, 259, 751–759. [Google Scholar] [CrossRef]
- Diekmann, O.; Heesterbeek, J.A.P.; Metz, J.A. On the definition and the computation of the basic reproduction ratio R 0 in models for infectious diseases in heterogeneous populations. J. Math. Biol. 1990, 28, 365–382. [Google Scholar] [CrossRef] [PubMed]
- Ribeiro, R.M.; Qin, L.; Chavez, L.L.; Li, D.; Self, S.G.; Perelson, A.S. Estimation of the initial viral growth rate and basic reproductive number during acute HIV-1 infection. J. Virol. 2010, 84, 6096–6102. [Google Scholar] [CrossRef]
- McLean, A.R.; Nowak, M.A. Competition between zidovudine-sensitive and. Aids 1992, 6, 71–79. [Google Scholar] [CrossRef]
- Frost, S.; McLean, A.R. Quasispecies dynamics and the emergence of drug resistance during zidovudine therapy of HIV infection. Aids 1994, 8, 323–332. [Google Scholar] [CrossRef] [PubMed]
- Pialoux, G.; Raffi, F.; Brun-Vezinet, F.; Meiffrédy, V.; Flandre, P.; Gastaut, J.A.; Dellamonica, P.; Yeni, P.; Delfraissy, J.F.; Aboulker, J.P. A randomized trial of three maintenance regimens given after three months of induction therapy with zidovudine, lamivudine, and indinavir in previously untreated HIV-1–infected patients. N. Engl. J. Med. 1998, 339, 1269–1276. [Google Scholar] [CrossRef]
- Ribeiro, R.M.; Bonhoeffer, S.; Nowak, M.A. The frequency of resistant mutant virus before antiviral therapy. Aids 1998, 12, 461–465. [Google Scholar] [CrossRef]
- Colgrove, R.; Japour, A. A combinatorial ledge: Reverse transcriptase fidelity, total body viral burden, and the implications of multiple-drug HIV therapy for the evolution of antiviral resistance. Antivir. Res. 1999, 41, 45–56. [Google Scholar] [CrossRef]
- Li, M.; Oliveira Passos, D.; Shan, Z.; Smith, S.J.; Sun, Q.; Biswas, A.; Choudhuri, I.; Strutzenberg, T.S.; Haldane, A.; Deng, N.; et al. Mechanisms of HIV-1 integrase resistance to dolutegravir and potent inhibition of drug-resistant variants. Sci. Adv. 2023, 9, eadg5953. [Google Scholar] [CrossRef]
- Shekhar, K.; Ruberman, C.F.; Ferguson, A.L.; Barton, J.P.; Kardar, M.; Chakraborty, A.K. Spin models inferred from patient-derived viral sequence data faithfully describe HIV fitness landscapes. Phys. Rev. E 2013, 88, 062705. [Google Scholar] [CrossRef] [PubMed]
- Biswas, A.; Haldane, A.; Levy, R.M. Limits to detecting epistasis in the fitness landscape of HIV. PLoS ONE 2022, 17, e0262314. [Google Scholar] [CrossRef] [PubMed]
- Biswas, A.; Haldane, A.; Arnold, E.; Levy, R.M. Epistasis and entrenchment of drug resistance in HIV-1 subtype B. Elife 2019, 8, e50524. [Google Scholar] [CrossRef] [PubMed]
- Anderson, R.W.; Ascher, M.S.; Sheppard, H.W. Direct HIV cytopathicity cannot account for CD4 decline in AIDS in the presence of homeostasis: A worst-case dynamic analysis. J. Acquir. Immune Defic. Syndr. 1998, 17, 245–252. [Google Scholar] [CrossRef] [PubMed]
- Ribeiro, R.M.; Mohri, H.; Ho, D.D.; Perelson, A.S. In vivo dynamics of T cell activation, proliferation, and death in HIV-1 infection: Why are CD4+ but not CD8+ T cells depleted? Proc. Natl. Acad. Sci. USA 2002, 99, 15572–15577. [Google Scholar] [CrossRef]
- Yates, A.; Stark, J.; Klein, N.; Antia, R.; Callard, R. Understanding the slow depletion of memory CD4+ T cells in HIV infection. PLoS Med. 2007, 4, e177. [Google Scholar] [CrossRef]
- Nowak, M.A.; Anderson, R.M.; McLean, A.R.; Wolfs, T.F.; Goudsmit, J.; May, R.M. Antigenic diversity thresholds and the development of AIDS. Science 1991, 254, 963–969. [Google Scholar] [CrossRef]
- Regoes, R.R.; Wodarz, D.; Nowak, M.A. Virus dynamics: The effect of target cell limitation and immune responses on virus evolution. J. Theor. Biol. 1998, 191, 451–462. [Google Scholar] [CrossRef]
- Perelson, A.S.; Neumann, A.U.; Markowitz, M.; Leonard, J.M.; Ho, D.D. HIV-1 dynamics in vivo: Virion clearance rate, infected cell life-span, and viral generation time. Science 1996, 271, 1582–1586. [Google Scholar] [CrossRef]
- Markowitz, M.; Louie, M.; Hurley, A.; Sun, E.; Di Mascio, M.; Perelson, A.S.; Ho, D.D. A novel antiviral intervention results in more accurate assessment of human immunodeficiency virus type 1 replication dynamics and T-cell decay in vivo. J. Virol. 2003, 77, 5037–5038. [Google Scholar] [CrossRef]
- Andrade, A.; Rosenkranz, S.L.; Cillo, A.R.; Lu, D.; Daar, E.S.; Jacobson, J.M.; Lederman, M.; Acosta, E.P.; Campbell, T.; Feinberg, J.; et al. Three distinct phases of HIV-1 RNA decay in treatment-naive patients receiving raltegravir-based antiretroviral therapy: ACTG A5248. J. Infect. Dis. 2013, 208, 884–891. [Google Scholar] [CrossRef] [PubMed]
- Ollerton, M.T.; Berger, E.A.; Connick, E.; Burton, G.F. HIV-1-specific chimeric antigen receptor T cells fail to recognize and eliminate the follicular dendritic cell HIV reservoir in vitro. J. Virol. 2020, 94, 10–1128. [Google Scholar] [CrossRef] [PubMed]
- Cohn, L.B.; Chomont, N.; Deeks, S.G. The biology of the HIV-1 latent reservoir and implications for cure strategies. Cell Host Microbe 2020, 27, 519–530. [Google Scholar] [CrossRef]
- Siliciano, J.D.; Kajdas, J.; Finzi, D.; Quinn, T.C.; Chadwick, K.; Margolick, J.B.; Kovacs, C.; Gange, S.J.; Siliciano, R.F. Long-term follow-up studies confirm the stability of the latent reservoir for HIV-1 in resting CD4+ T cells. Nat. Med. 2003, 9, 727–728. [Google Scholar] [CrossRef]
- Davey, R.T., Jr.; Bhat, N.; Yoder, C.; Chun, T.W.; Metcalf, J.A.; Dewar, R.; Natarajan, V.; Lempicki, R.A.; Adelsberger, J.W.; Miller, K.D.; et al. HIV-1 and T cell dynamics after interruption of highly active antiretroviral therapy (HAART) in patients with a history of sustained viral suppression. Proc. Natl. Acad. Sci. USA 1999, 96, 15109–15114. [Google Scholar] [CrossRef]
- Ruiz, L.; Martinez-Picado, J.; Romeu, J.; Paredes, R.; Zayat, M.K.; Marfil, S.; Negredo, E.; Sirera, G.; Tural, C.; Clotet, B. Structured treatment interruption in chronically HIV-1 infected patients after long-term viral suppression. Aids 2000, 14, 397–403. [Google Scholar] [CrossRef] [PubMed]
- White, J.A.; Simonetti, F.R.; Beg, S.; McMyn, N.F.; Dai, W.; Bachmann, N.; Lai, J.; Ford, W.C.; Bunch, C.; Jones, J.L.; et al. Complex decay dynamics of HIV virions, intact and defective proviruses, and 2LTR circles following initiation of antiretroviral therapy. Proc. Natl. Acad. Sci. USA 2022, 119, e2120326119. [Google Scholar] [CrossRef]
- Spivak, A.M.; Rabi, S.A.; McMahon, M.A.; Shan, L.; Sedaghat, A.R.; Wilke, C.O.; Siliciano, R.F. dynamic constraints on the second phase compartment of HIV-infected cells. Aids Res. Hum. Retroviruses 2011, 27, 759–761. [Google Scholar] [CrossRef]
- Arnaout, R.A.; Martin, A.N.; Wodarz, D. HIV–1 dynamics revisited: Biphasic decay by cytotoxic T lymphocyte killing? Proc. R. Soc. Lond. Ser. Biol. Sci. 2000, 267, 1347–1354. [Google Scholar] [CrossRef]
- Zhang, J.; Perelson, A.S. Contribution of follicular dendritic cells to persistent HIV viremia. J. Virol. 2013, 87, 7893–7901. [Google Scholar] [CrossRef]
- Eriksson, S.; Graf, E.H.; Dahl, V.; Strain, M.C.; Yukl, S.A.; Lysenko, E.S.; Bosch, R.J.; Lai, J.; Chioma, S.; Emad, F.; et al. Comparative analysis of measures of viral reservoirs in HIV-1 eradication studies. PLoS Pathog. 2013, 9, e1003174. [Google Scholar] [CrossRef] [PubMed]
- Crooks, A.M.; Bateson, R.; Cope, A.B.; Dahl, N.P.; Griggs, M.K.; Kuruc, J.D.; Gay, C.L.; Eron, J.J.; Margolis, D.M.; Bosch, R.J.; et al. Precise quantitation of the latent HIV-1 reservoir: Implications for eradication strategies. J. Infect. Dis. 2015, 212, 1361–1365. [Google Scholar] [CrossRef]
- Cory, T.J.; Schacker, T.W.; Stevenson, M.; Fletcher, C.V. Overcoming pharmacologic sanctuaries. Curr. Opin. HIV AIDS 2013, 8, 190. [Google Scholar] [CrossRef] [PubMed]
- Martinez-Picado, J.; Deeks, S.G. Persistent HIV-1 replication during antiretroviral therapy. Curr. Opin. HIV AIDS 2016, 11, 417. [Google Scholar] [CrossRef]
- Lorenzo-Redondo, R.; Fryer, H.R.; Bedford, T.; Kim, E.Y.; Archer, J.; Kosakovsky Pond, S.L.; Chung, Y.S.; Penugonda, S.; Chipman, J.G.; Fletcher, C.V.; et al. Persistent HIV-1 replication maintains the tissue reservoir during therapy. Nature 2016, 530, 51–56. [Google Scholar] [CrossRef] [PubMed]
- Bachmann, N.; Von Siebenthal, C.; Vongrad, V.; Turk, T.; Neumann, K.; Beerenwinkel, N.; Bogojeska, J.; Fellay, J.; Roth, V.; Kok, Y.L.; et al. Determinants of HIV-1 reservoir size and long-term dynamics during suppressive ART. Nat. Commun. 2019, 10, 3193. [Google Scholar] [CrossRef]
- Brodin, J.; Zanini, F.; Thebo, L.; Lanz, C.; Bratt, G.; Neher, R.A.; Albert, J. Establishment and stability of the latent HIV-1 DNA reservoir. Elife 2016, 5, e18889. [Google Scholar] [CrossRef]
- Jones, L.E.; Perelson, A.S. Transient viremia, plasma viral load, and reservoir replenishment in HIV-infected patients on antiretroviral therapy. J. Acquir. Immune Defic. Syndr. 2007, 45, 483. [Google Scholar] [CrossRef]
- Sedaghat, A.R.; Siliciano, R.F.; Wilke, C.O. Low-level HIV-1 replication and the dynamics of the resting CD4+ T cell reservoir for HIV-1 in the setting of HAART. BMC Infect. Dis. 2008, 8, 2. [Google Scholar] [CrossRef]
- Conway, J.M.; Perelson, A.S. Residual viremia in treated HIV+ individuals. PLoS Comput. Biol. 2016, 12, e1004677. [Google Scholar] [CrossRef]
- Kirchhoff, F. HIV life cycle: Overview. Encycl. AIDS 2013, 1–9. [Google Scholar] [CrossRef]
- Vargas, B.; Sluis-Cremer, N. Toward a Functional Cure for HIV-1 Infection: The Block and Lock therapeutic Approach. Front. Virol. 2022, 2, 917941. [Google Scholar] [CrossRef]
- Schröder, A.R.; Shinn, P.; Chen, H.; Berry, C.; Ecker, J.R.; Bushman, F. HIV-1 integration in the human genome favors active genes and local hotspots. Cell 2002, 110, 521–529. [Google Scholar] [CrossRef] [PubMed]
- Ruess, H.; Lee, J.; Guzman, C.; Malladi, V.S.; D’Orso, I. Decoding Human Genome Regulatory Features That Influence HIV-1 Proviral Expression and Fate Through an Integrated Genomics Approach. Bioinform. Biol. Insights 2022, 16, 11779322211072333. [Google Scholar] [CrossRef]
- Chen, H.C.; Martinez, J.P.; Zorita, E.; Meyerhans, A.; Filion, G.J. Position effects influence HIV latency reversal. Nat. Struct. Mol. Biol. 2017, 24, 47–54. [Google Scholar] [CrossRef] [PubMed]
- Jordan, A.; Defechereux, P.; Verdin, E. The site of HIV-1 integration in the human genome determines basal transcriptional activity and response to Tat transactivation. EMBO J. 2001, 20, 1726–1738. [Google Scholar] [CrossRef]
- Burnett, J.C.; Miller-Jensen, K.; Shah, P.S.; Arkin, A.P.; Schaffer, D.V. Control of stochastic gene expression by host factors at the HIV promoter. PLoS Pathog. 2009, 5, e1000260. [Google Scholar] [CrossRef]
- Einkauf, K.B.; Osborn, M.R.; Gao, C.; Sun, W.; Sun, X.; Lian, X.; Parsons, E.M.; Gladkov, G.T.; Seiger, K.W.; Blackmer, J.E.; et al. Parallel analysis of transcription, integration, and sequence of single HIV-1 proviruses. Cell 2022, 185, 266–282. [Google Scholar] [CrossRef]
- Van Lint, C.; Emiliani, S.; Ott, M.; Verdin, E. Transcriptional activation and chromatin remodeling of the HIV-1 promoter in response to histone acetylation. EMBO J. 1996, 15, 1112–1120. [Google Scholar] [CrossRef]
- Verdin, E.; Paras, P., Jr.; Van Lint, C. Chromatin disruption in the promoter of human immunodeficiency virus type 1 during transcriptional activation. EMBO J. 1993, 12, 3249–3259. [Google Scholar] [CrossRef]
- Shukla, A.; Ramirez, N.; DLOrso, I. HIV-1 proviral transcription and latency in the new era. Viruses 2020, 12, 555. [Google Scholar] [CrossRef] [PubMed]
- Lusic, M.; Siliciano, R.F. Nuclear landscape of HIV-1 infection and integration. Nat. Rev. Microbiol. 2017, 15, 69–82. [Google Scholar] [CrossRef] [PubMed]
- Struhl, K.; Segal, E. Determinants of nucleosome positioning. Nat. Struct. Mol. Biol. 2013, 20, 267–273. [Google Scholar] [CrossRef] [PubMed]
- Bartha, I.; Carlson, J.M.; Brumme, C.J.; McLaren, P.J.; Brumme, Z.L.; John, M.; Haas, D.W.; Martinez-Picado, J.; Dalmau, J.; López-Galíndez, C.; et al. A genome-to-genome analysis of associations between human genetic variation, HIV-1 sequence diversity, and viral control. Elife 2013, 2, e01123. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Klatt, A.; Gilmour, D.S.; Henderson, A.J. Negative elongation factor NELF represses human immunodeficiency virus transcription by pausing the RNA polymerase II complex. J. Biol. Chem. 2007, 282, 16981–16988. [Google Scholar] [CrossRef] [PubMed]
- Jadlowsky, J.K.; Wong, J.Y.; Graham, A.C.; Dobrowolski, C.; Devor, R.L.; Adams, M.D.; Fujinaga, K.; Karn, J. Negative elongation factor is required for the maintenance of proviral latency but does not induce promoter-proximal pausing of RNA polymerase II on the HIV long terminal repeat. Mol. Cell. Biol. 2014, 34, 1911–1928. [Google Scholar] [CrossRef] [PubMed]
- Kao, S.Y.; Calman, A.F.; Luciw, P.A.; Peterlin, B.M. Anti-termination of transcription within the long terminal repeat of HIV-1 by tat gene product. Nature 1987, 330, 489–493. [Google Scholar] [CrossRef]
- Bacon, C.; D’Orso, I. CDK9: A signaling hub for transcriptional control. Transcription 2019, 10, 57–75. [Google Scholar] [CrossRef]
- Tantale, K.; Garcia-Oliver, E.; Robert, M.C.; L’hostis, A.; Yang, Y.; Tsanov, N.; Topno, R.; Gostan, T.; Kozulic-Pirher, A.; Basu-Shrivastava, M.; et al. Stochastic pausing at latent HIV-1 promoters generates transcriptional bursting. Nat. Commun. 2021, 12, 4503. [Google Scholar] [CrossRef]
- Mancebo, H.S.; Lee, G.; Flygare, J.; Tomassini, J.; Luu, P.; Zhu, Y.; Peng, J.; Blau, C.; Hazuda, D.; Price, D.; et al. P-TEFb kinase is required for HIV Tat transcriptional activation in vivo and in vitro. Genes Dev. 1997, 11, 2633–2644. [Google Scholar] [CrossRef]
- Kuzmina, A.; Krasnopolsky, S.; Taube, R. Super elongation complex promotes early HIV transcription and its function is modulated by P-TEFb. Transcription 2017, 8, 133–149. [Google Scholar] [CrossRef] [PubMed]
- Chou, S.; Upton, H.; Bao, K.; Schulze-Gahmen, U.; Samelson, A.J.; He, N.; Nowak, A.; Lu, H.; Krogan, N.J.; Zhou, Q.; et al. HIV-1 Tat recruits transcription elongation factors dispersed along a flexible AFF4 scaffold. Proc. Natl. Acad. Sci. USA 2013, 110, E123–E131. [Google Scholar] [CrossRef] [PubMed]
- Lu, H.; Li, Z.; Zhang, W.; Schulze-Gahmen, U.; Xue, Y.; Zhou, Q. Gene target specificity of the Super Elongation Complex (SEC) family: How HIV-1 Tat employs selected SEC members to activate viral transcription. Nucleic Acids Res. 2015, 43, 5868–5879. [Google Scholar] [CrossRef] [PubMed]
- Leyes Porello, E.A.; Trudeau, R.T.; Lim, B. Transcriptional bursting: Stochasticity in deterministic development. Development 2023, 150, dev201546. [Google Scholar] [CrossRef]
- Tantale, K.; Mueller, F.; Kozulic-Pirher, A.; Lesne, A.; Victor, J.M.; Robert, M.C.; Capozi, S.; Chouaib, R.; Bäcker, V.; Mateos-Langerak, J.; et al. A single-molecule view of transcription reveals convoys of RNA polymerases and multi-scale bursting. Nat. Commun. 2016, 7, 12248. [Google Scholar] [CrossRef]
- Sanchez, A.; Golding, I. Genetic determinants and cellular constraints in noisy gene expression. Science 2013, 342, 1188–1193. [Google Scholar] [CrossRef]
- Dar, R.D.; Razooky, B.S.; Singh, A.; Trimeloni, T.V.; McCollum, J.M.; Cox, C.D.; Simpson, M.L.; Weinberger, L.S. Transcriptional burst frequency and burst size are equally modulated across the human genome. Proc. Natl. Acad. Sci. USA 2012, 109, 17454–17459. [Google Scholar] [CrossRef]
- Suter, D.M.; Molina, N.; Gatfield, D.; Schneider, K.; Schibler, U.; Naef, F. Mammalian genes are transcribed with widely different bursting kinetics. Science 2011, 332, 472–474. [Google Scholar] [CrossRef]
- Senecal, A.; Munsky, B.; Proux, F.; Ly, N.; Braye, F.E.; Zimmer, C.; Mueller, F.; Darzacq, X. Transcription factors modulate c-Fos transcriptional bursts. Cell Rep. 2014, 8, 75–83. [Google Scholar] [CrossRef]
- Li, C.; Cesbron, F.; Oehler, M.; Brunner, M.; Höfer, T. Frequency modulation of transcriptional bursting enables sensitive and rapid gene regulation. Cell Syst. 2018, 6, 409–423. [Google Scholar] [CrossRef]
- Raser, J.M.; O’Shea, E.K. Control of stochasticity in eukaryotic gene expression. Science 2004, 304, 1811–1814. [Google Scholar] [CrossRef]
- Dey, S.S.; Foley, J.E.; Limsirichai, P.; Schaffer, D.V.; Arkin, A.P. Orthogonal control of expression mean and variance by epigenetic features at different genomic loci. Mol. Syst. Biol. 2015, 11, 806. [Google Scholar] [CrossRef]
- Wong, V.C.; Bass, V.L.; Bullock, M.E.; Chavali, A.K.; Lee, R.E.; Mothes, W.; Gaudet, S.; Miller-Jensen, K. NF-κB-chromatin interactions drive diverse phenotypes by modulating transcriptional noise. Cell Rep. 2018, 22, 585–599. [Google Scholar] [CrossRef] [PubMed]
- Bartman, C.R.; Hamagami, N.; Keller, C.A.; Giardine, B.; Hardison, R.C.; Blobel, G.A.; Raj, A. Transcriptional burst initiation and polymerase pause release are key control points of transcriptional regulation. Mol. Cell 2019, 73, 519–532. [Google Scholar] [CrossRef] [PubMed]
- Cavallaro, M.; Walsh, M.D.; Jones, M.; Teahan, J.; Tiberi, S.; Finkenstädt, B.; Hebenstreit, D. 3′-5′ crosstalk contributes to transcriptional bursting. Genome Biol. 2021, 22, 1–20. [Google Scholar] [CrossRef]
- Bullock, M.E.; Moreno-Martinez, N.; Miller-Jensen, K. A transcriptional cycling model recapitulates chromatin-dependent features of noisy inducible transcription. PLoS Comput. Biol. 2022, 18, e1010152. [Google Scholar] [CrossRef] [PubMed]
- Brouwer, I.; Kerklingh, E.; van Leeuwen, F.; Lenstra, T.L. Dynamic epistasis analysis reveals how chromatin remodeling regulates transcriptional bursting. Nat. Struct. Mol. Biol. 2023, 30, 692–702. [Google Scholar] [CrossRef] [PubMed]
- Mbonye, U.; Karn, J. The molecular basis for human immunodeficiency virus latency. Annu. Rev. Virol. 2017, 4, 261–285. [Google Scholar] [CrossRef]
- Richter, W.F.; Nayak, S.; Iwasa, J.; Taatjes, D.J. The Mediator complex as a master regulator of transcription by RNA polymerase II. Nat. Rev. Mol. Cell Biol. 2022, 23, 732–749. [Google Scholar] [CrossRef]
- Spudich, J.L.; Koshland, D.E. Non-genetic individuality: Chance in the single cell. Nature 1976, 262, 467–471. [Google Scholar] [CrossRef]
- McAdams, H.H.; Arkin, A. Stochastic mechanisms in gene expression. Proc. Natl. Acad. Sci. USA 1997, 94, 814–819. [Google Scholar] [CrossRef] [PubMed]
- Becskei, A.; Serrano, L. Engineering stability in gene networks by autoregulation. Nature 2000, 405, 590–593. [Google Scholar] [CrossRef] [PubMed]
- Elowitz, M.B.; Levine, A.J.; Siggia, E.D.; Swain, P.S. Stochastic gene expression in a single cell. Science 2002, 297, 1183–1186. [Google Scholar] [CrossRef] [PubMed]
- Arkin, A.; Ross, J.; McAdams, H.H. Stochastic kinetic analysis of developmental pathway bifurcation in phage λ-infected Escherichia coli cells. Genetics 1998, 149, 1633–1648. [Google Scholar] [CrossRef]
- Elowitz, M.B.; Leibler, S. A synthetic oscillatory network of transcriptional regulators. Nature 2000, 403, 335–338. [Google Scholar] [CrossRef]
- Weinberger, L.S.; Burnett, J.C.; Toettcher, J.E.; Arkin, A.P.; Schaffer, D.V. Stochastic gene expression in a lentiviral positive-feedback loop: HIV-1 Tat fluctuations drive phenotypic diversity. Cell 2005, 122, 169–182. [Google Scholar] [CrossRef]
- Gillespie, D.T. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 1977, 81, 2340–2361. [Google Scholar] [CrossRef]
- Morton, E.L.; Forst, C.V.; Zheng, Y.; DePaula-Silva, A.B.; Ramirez, N.G.P.; Planelles, V.; D’Orso, I. Transcriptional circuit fragility influences HIV proviral fate. Cell Rep. 2019, 27, 154–171. [Google Scholar] [CrossRef]
- Lu, Y.; Bohn-Wippert, K.; Pazerunas, P.J.; Moy, J.M.; Singh, H.; Dar, R.D. Screening for gene expression fluctuations reveals latency-promoting agents of HIV. Proc. Natl. Acad. Sci. USA 2021, 118, e2012191118. [Google Scholar] [CrossRef]
- Rouzine, I.M.; Razooky, B.S.; Weinberger, L.S. Stochastic variability in HIV affects viral eradication. Proc. Natl. Acad. Sci. USA 2014, 111, 13251–13252. [Google Scholar] [CrossRef]
- Damour, A.; Slaninova, V.; Radulescu, O.; Bertrand, E.; Basyuk, E. Transcriptional Stochasticity as a Key Aspect of HIV-1 Latency. Viruses 2023, 15, 1969. [Google Scholar] [CrossRef] [PubMed]
- Chavali, A.K.; Wong, V.C.; Miller-Jensen, K. Distinct promoter activation mechanisms modulate noise-driven HIV gene expression. Sci. Rep. 2015, 5, 17661. [Google Scholar] [CrossRef] [PubMed]
- Bass, V.L.; Wong, V.C.; Bullock, M.E.; Gaudet, S.; Miller-Jensen, K. TNF stimulation primarily modulates transcriptional burst size of NF-κB-regulated genes. Mol. Syst. Biol. 2021, 17, e10127. [Google Scholar] [CrossRef] [PubMed]
- Miller-Jensen, K.; Dey, S.S.; Pham, N.; Foley, J.E.; Arkin, A.P.; Schaffer, D.V. Chromatin accessibility at the HIV LTR promoter sets a threshold for NF-κB mediated viral gene expression. Integr. Biol. 2012, 4, 661–671. [Google Scholar] [CrossRef] [PubMed]
- Razooky, B.S.; Cao, Y.; Hansen, M.M.; Perelson, A.S.; Simpson, M.L.; Weinberger, L.S. Nonlatching positive feedback enables robust bimodality by decoupling expression noise from the mean. PLoS Biol. 2017, 15, e2000841. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.; Lei, X.; Ribeiro, R.M.; Perelson, A.S.; Liang, J. Probabilistic control of HIV latency and transactivation by the Tat gene circuit. Proc. Natl. Acad. Sci. USA 2018, 115, 12453–12458. [Google Scholar] [CrossRef]
- Boettiger, A.N.; Levine, M. Synchronous and stochastic patterns of gene activation in the Drosophila embryo. Science 2009, 325, 471–473. [Google Scholar] [CrossRef]
- Shao, W.; Zeitlinger, J. Paused RNA polymerase II inhibits new transcriptional initiation. Nat. Genet. 2017, 49, 1045–1051. [Google Scholar] [CrossRef]
- Gressel, S.; Schwalb, B.; Cramer, P. The pause-initiation limit restricts transcription activation in human cells. Nat. Commun. 2019, 10, 3603. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
D’Orso, I.; Forst, C.V. Mathematical Models of HIV-1 Dynamics, Transcription, and Latency. Viruses 2023, 15, 2119. https://doi.org/10.3390/v15102119
D’Orso I, Forst CV. Mathematical Models of HIV-1 Dynamics, Transcription, and Latency. Viruses. 2023; 15(10):2119. https://doi.org/10.3390/v15102119
Chicago/Turabian StyleD’Orso, Iván, and Christian V. Forst. 2023. "Mathematical Models of HIV-1 Dynamics, Transcription, and Latency" Viruses 15, no. 10: 2119. https://doi.org/10.3390/v15102119
APA StyleD’Orso, I., & Forst, C. V. (2023). Mathematical Models of HIV-1 Dynamics, Transcription, and Latency. Viruses, 15(10), 2119. https://doi.org/10.3390/v15102119





