Early Phase of the COVID-19 Outbreak in Hungary and Post-Lockdown Scenarios
Abstract
1. Introduction
2. Materials and Methods
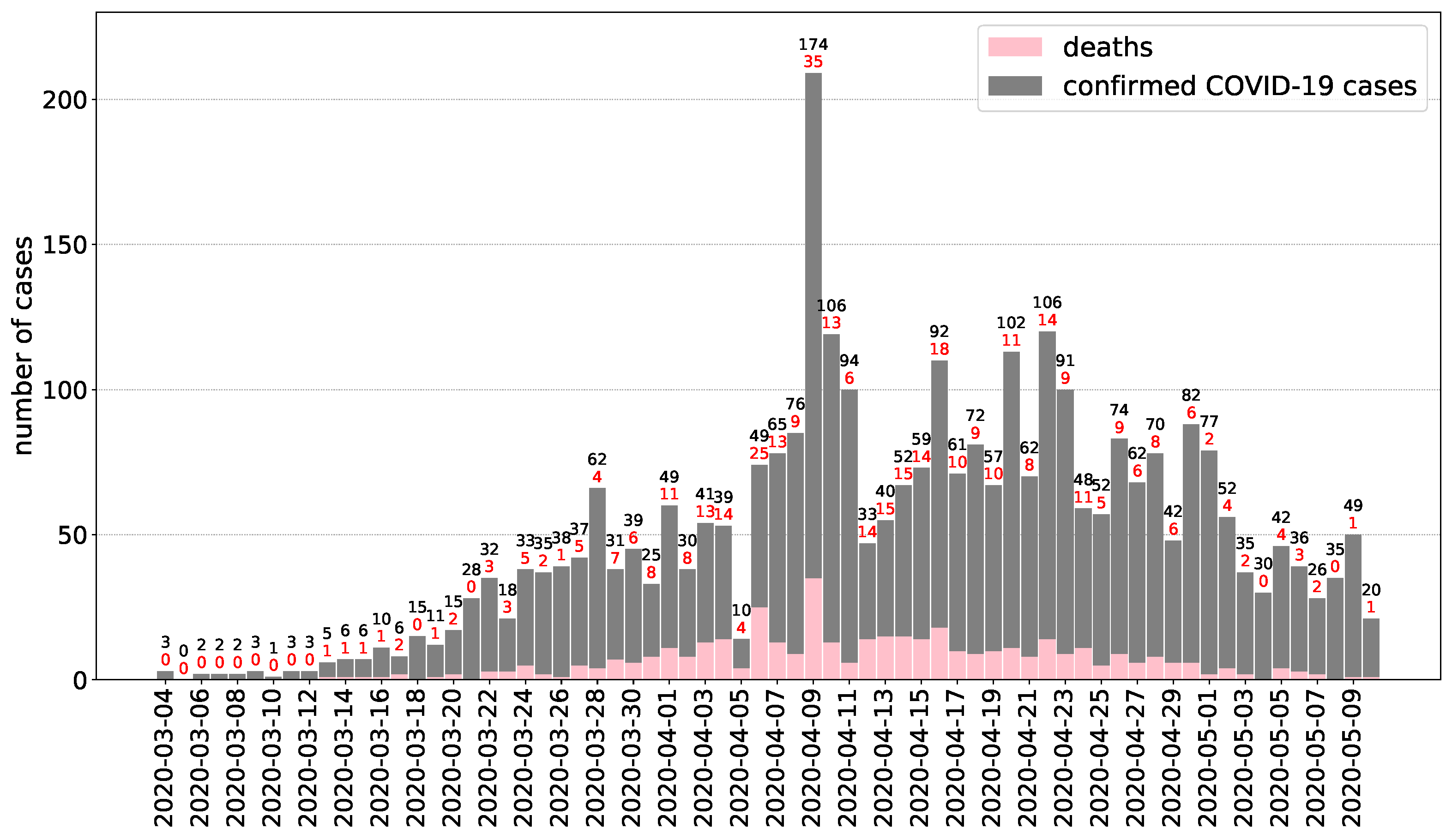
2.1. Epidemiological Report
2.2. Statistical Analysis
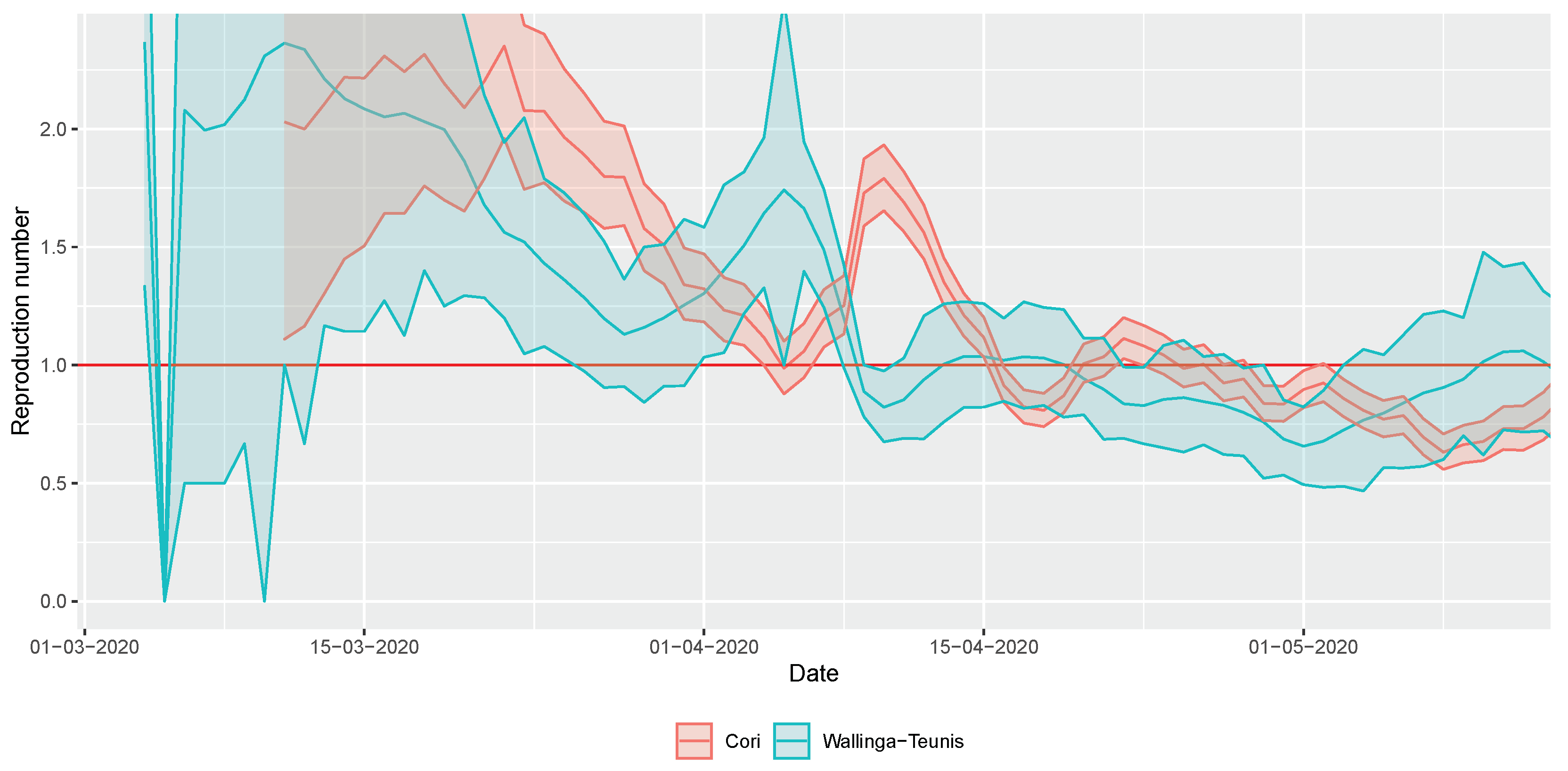
2.2.1. Temporal Variation of the Effective Reproduction Number
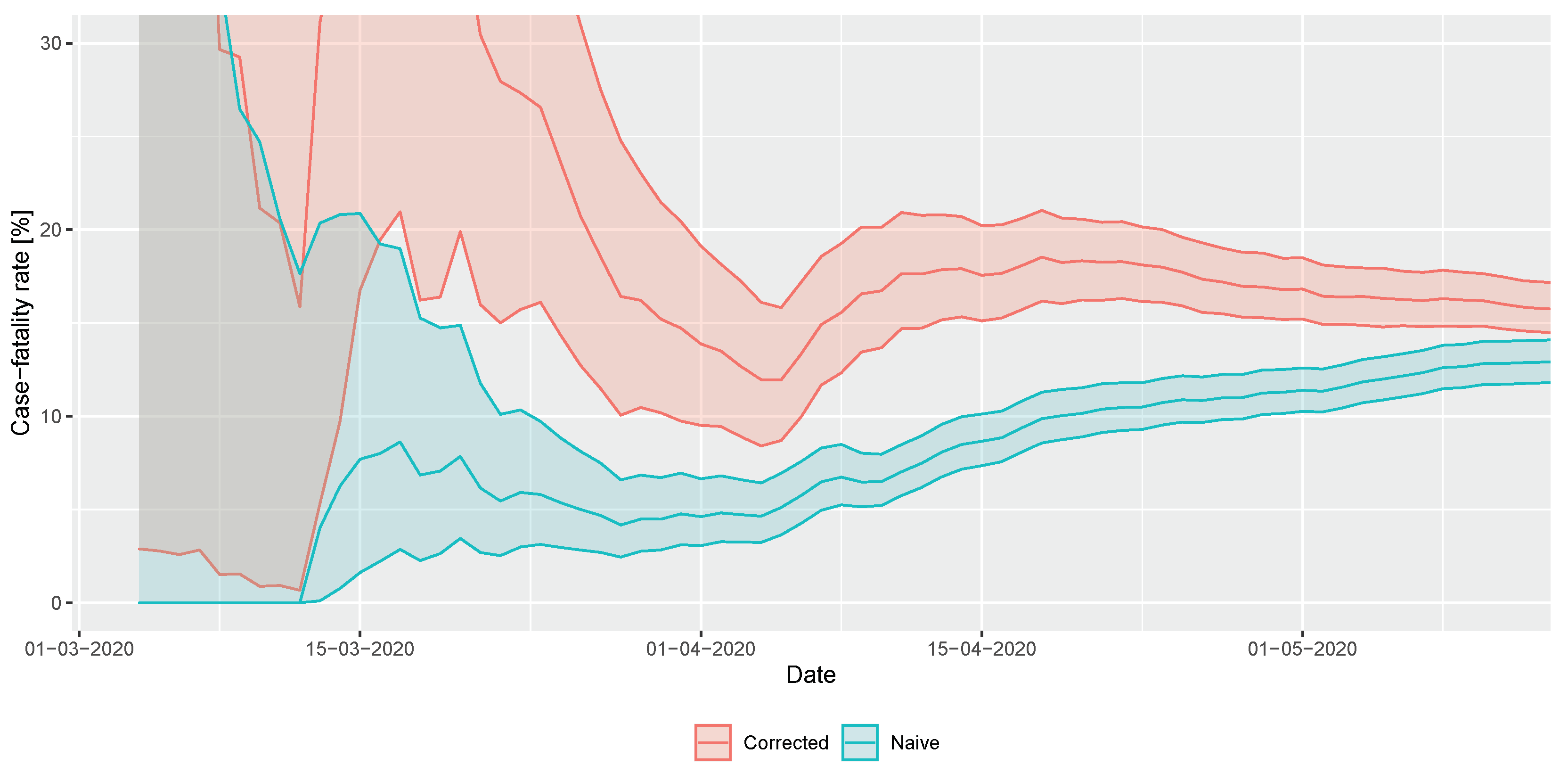
2.2.2. Adjusted Case Fatality Ratio
2.2.3. Estimation of the Ascertainment Rate
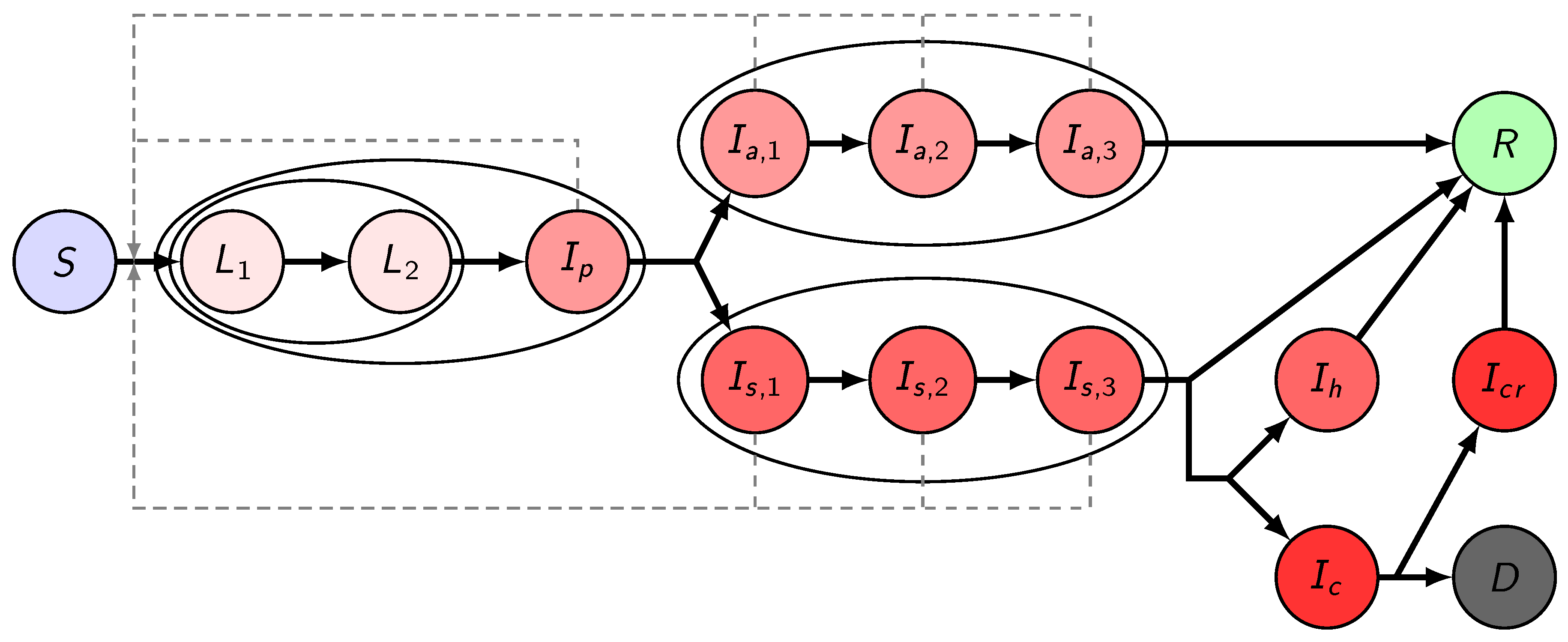
2.3. Transmission Model
2.3.1. The Governing Equations of the Transmission Model
2.3.2. Model Parameters
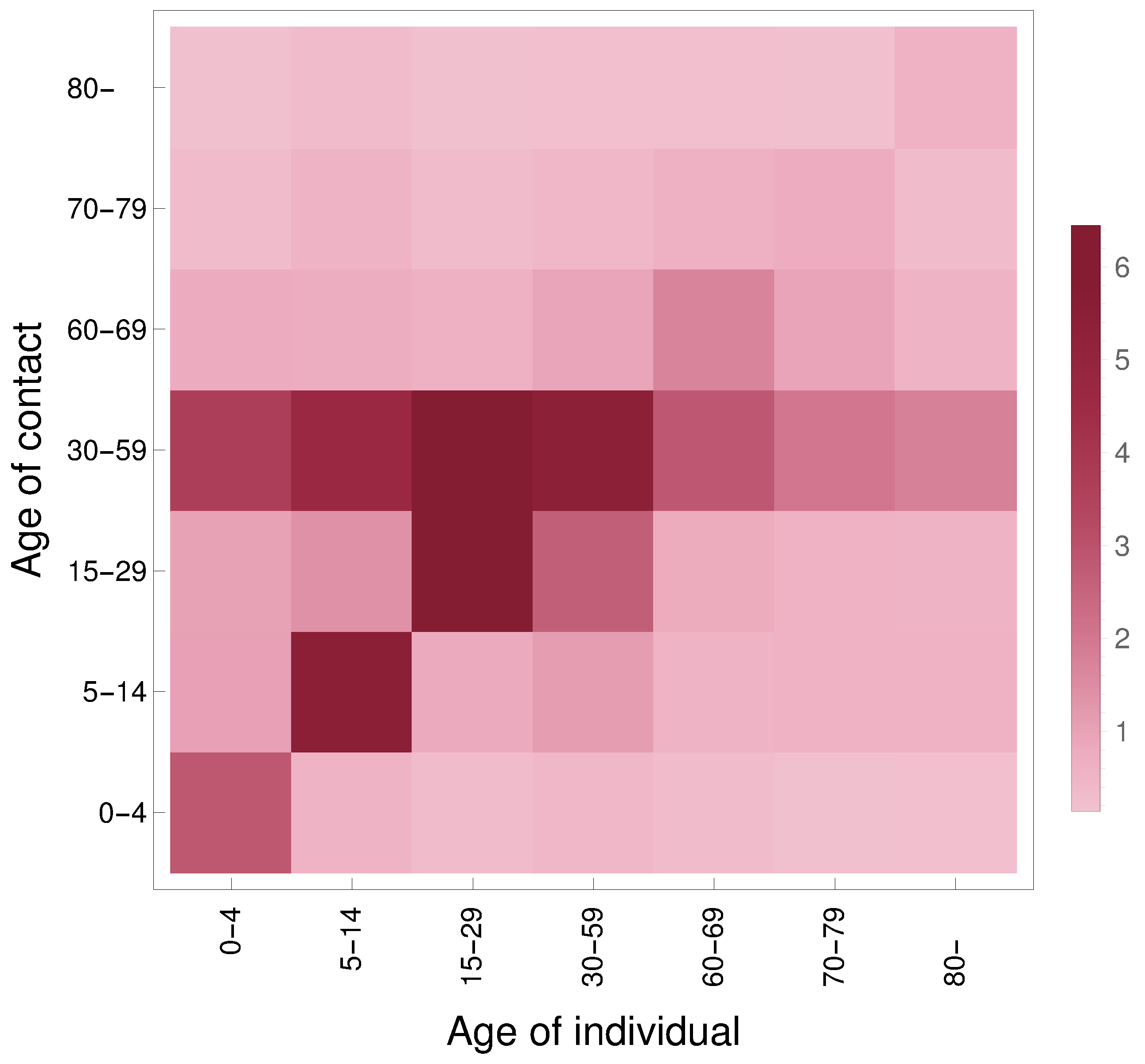
2.3.3. Contact Matrix
2.3.4. Transmission Rates and the Next Generation Matrix
2.3.5. Scenarios
2.3.6. Parameter Uncertainty and Other Limitations
3. Results
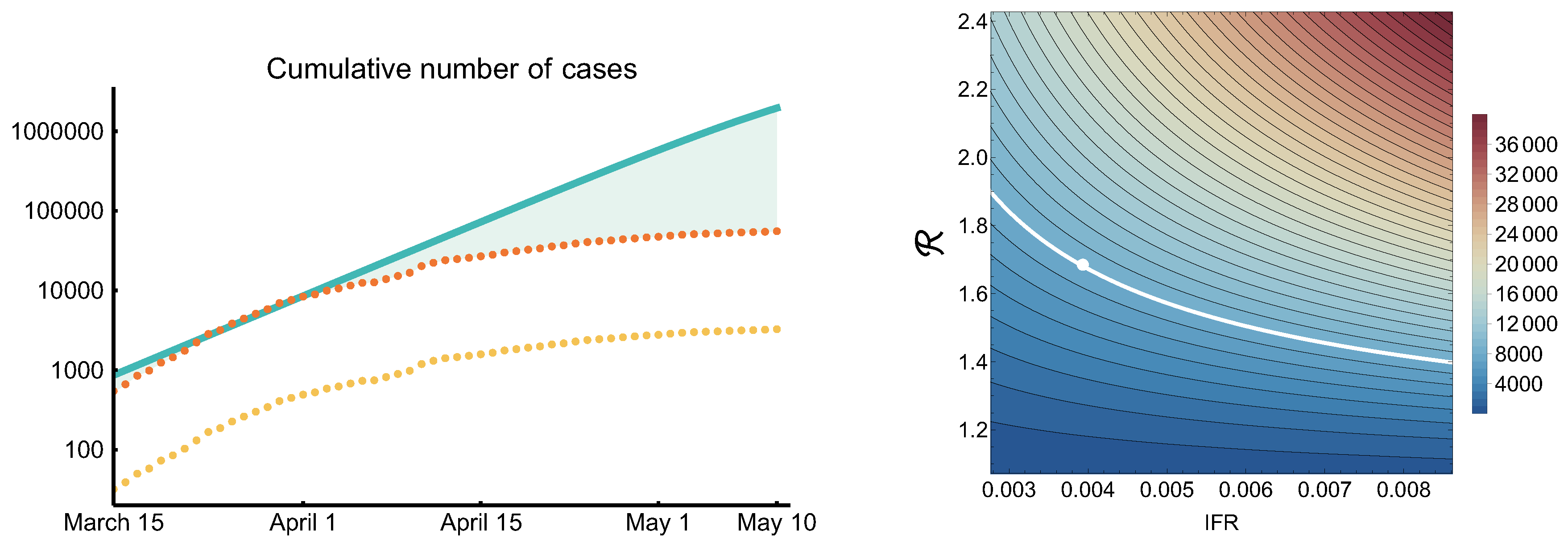
3.1. Epidemiological Report
3.2. Statistical Analysis
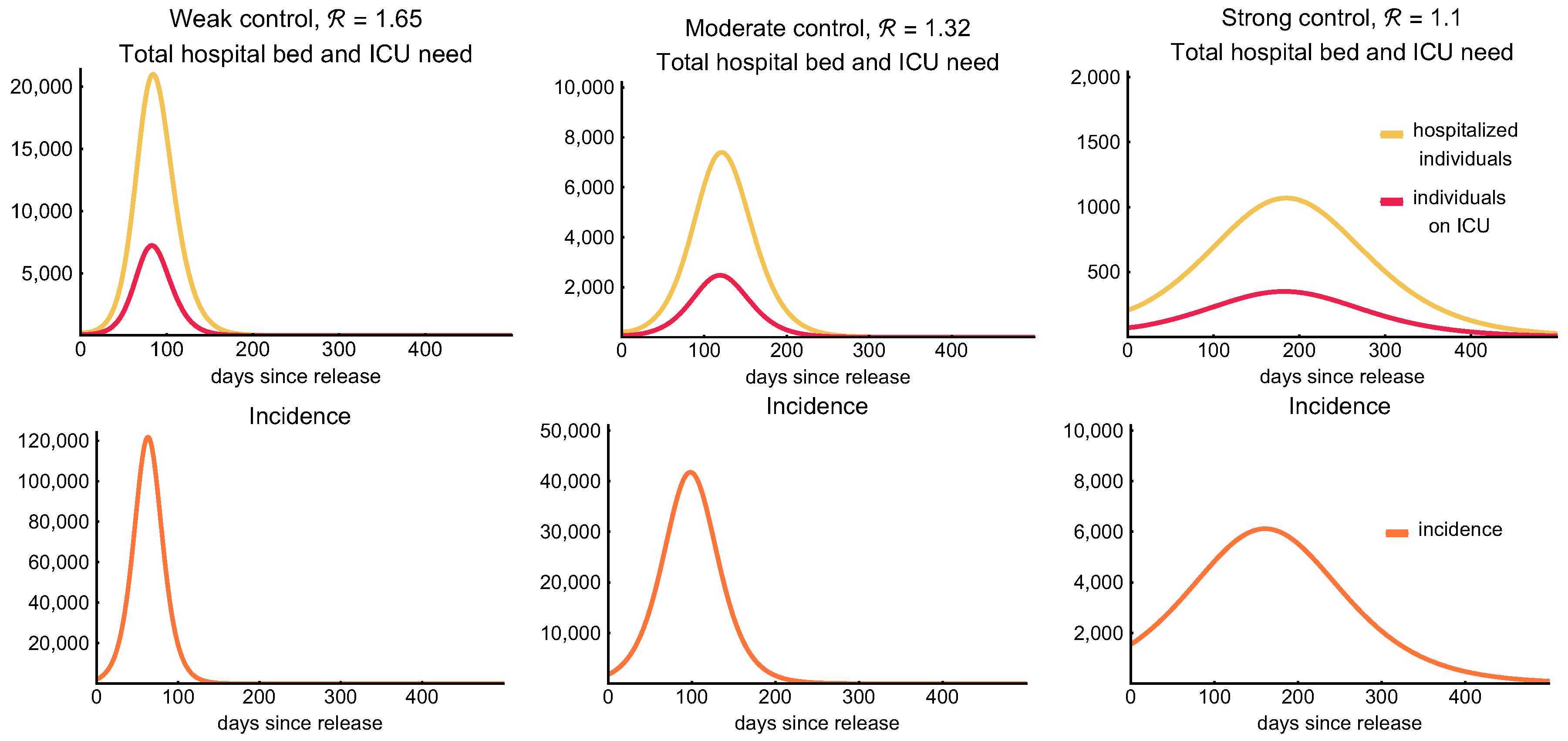
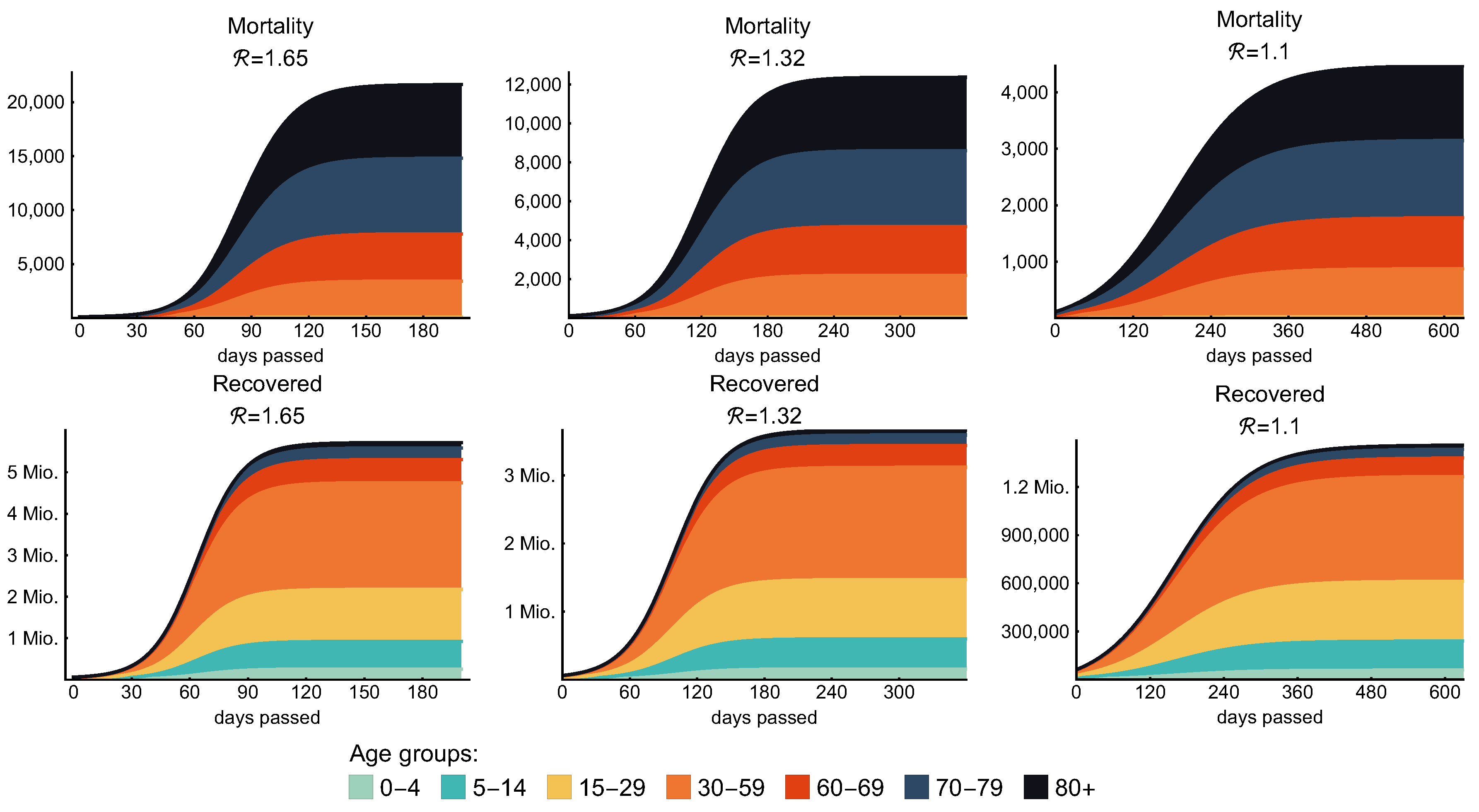
3.3. Post-Lockdown Scenarios
3.4. Age-Dependent Intervention Measures
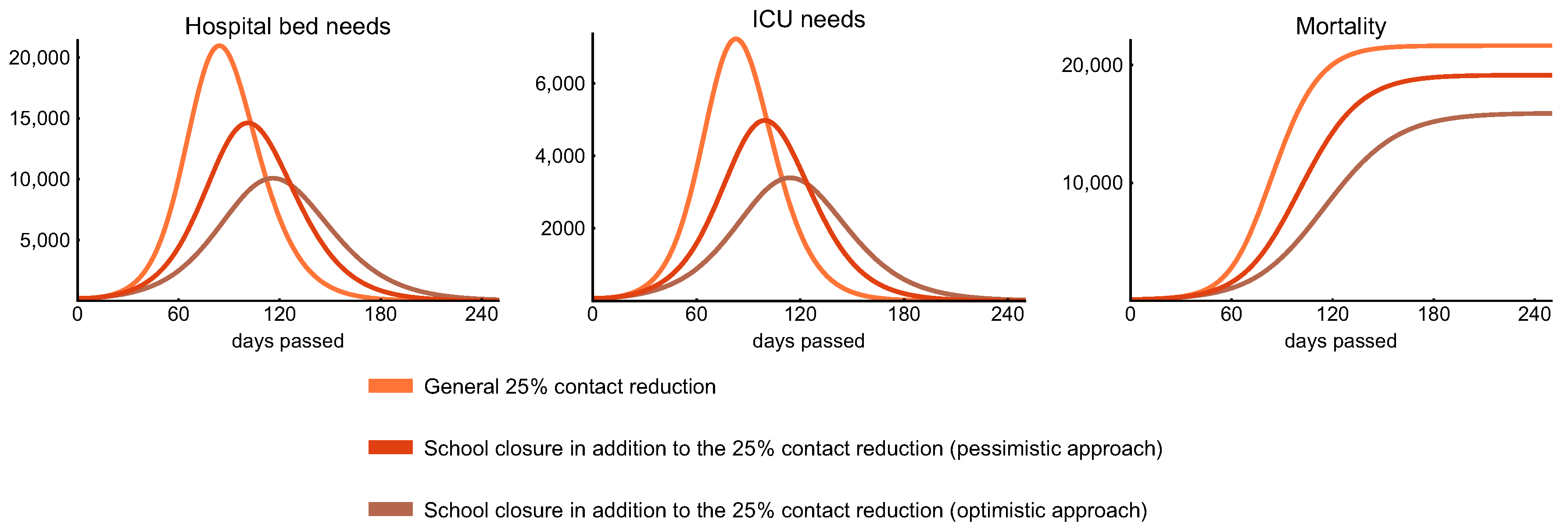
3.4.1. School Closures
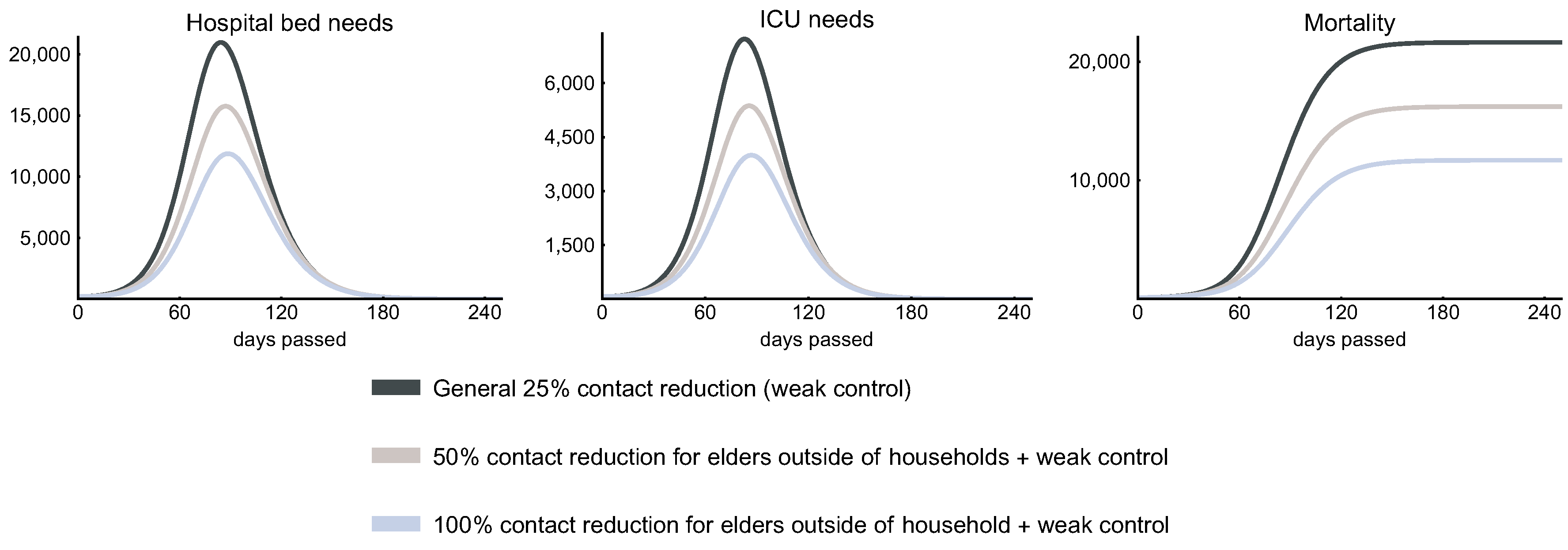
3.4.2. Protection of the Elderly
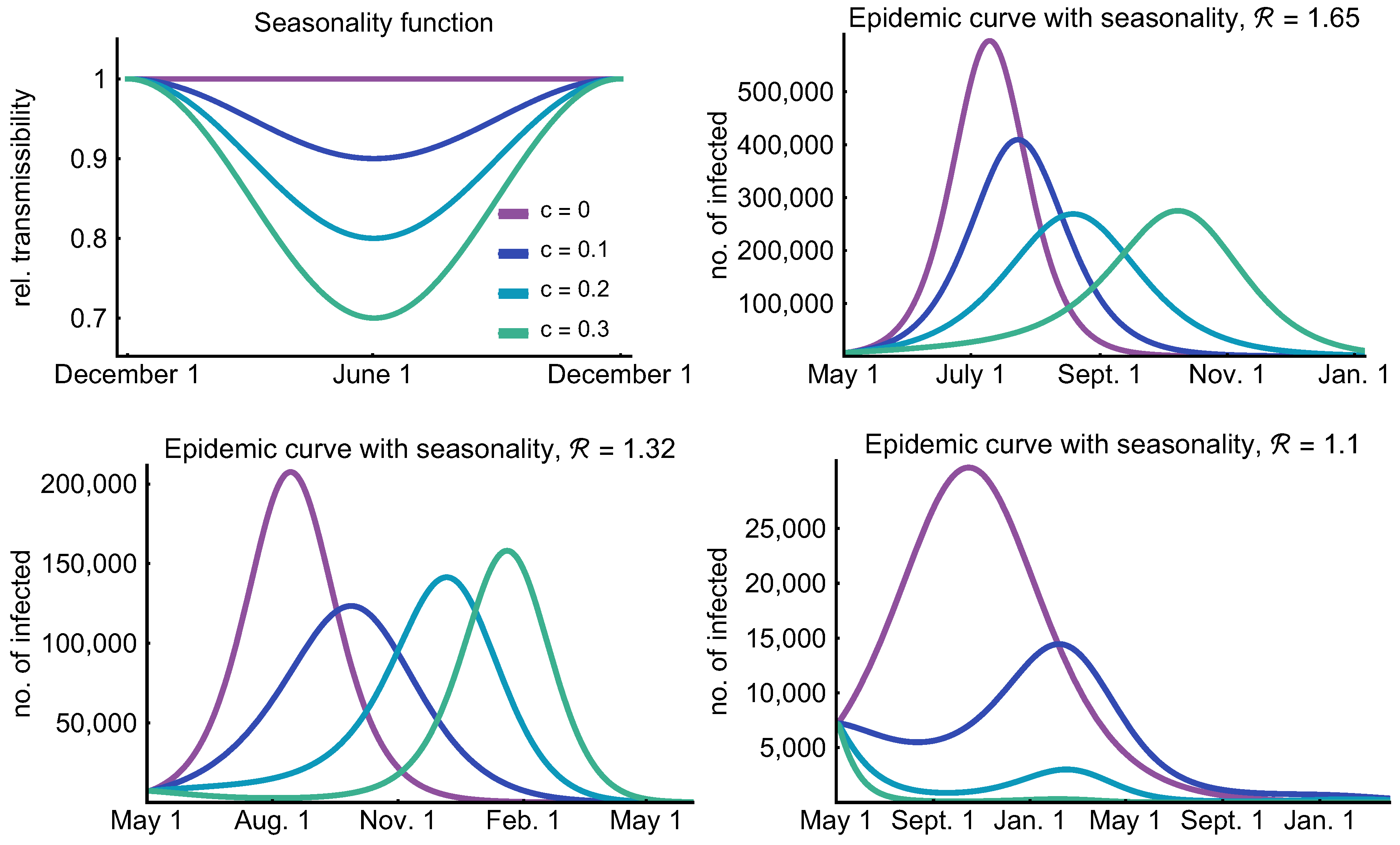
3.5. Role of Seasonality
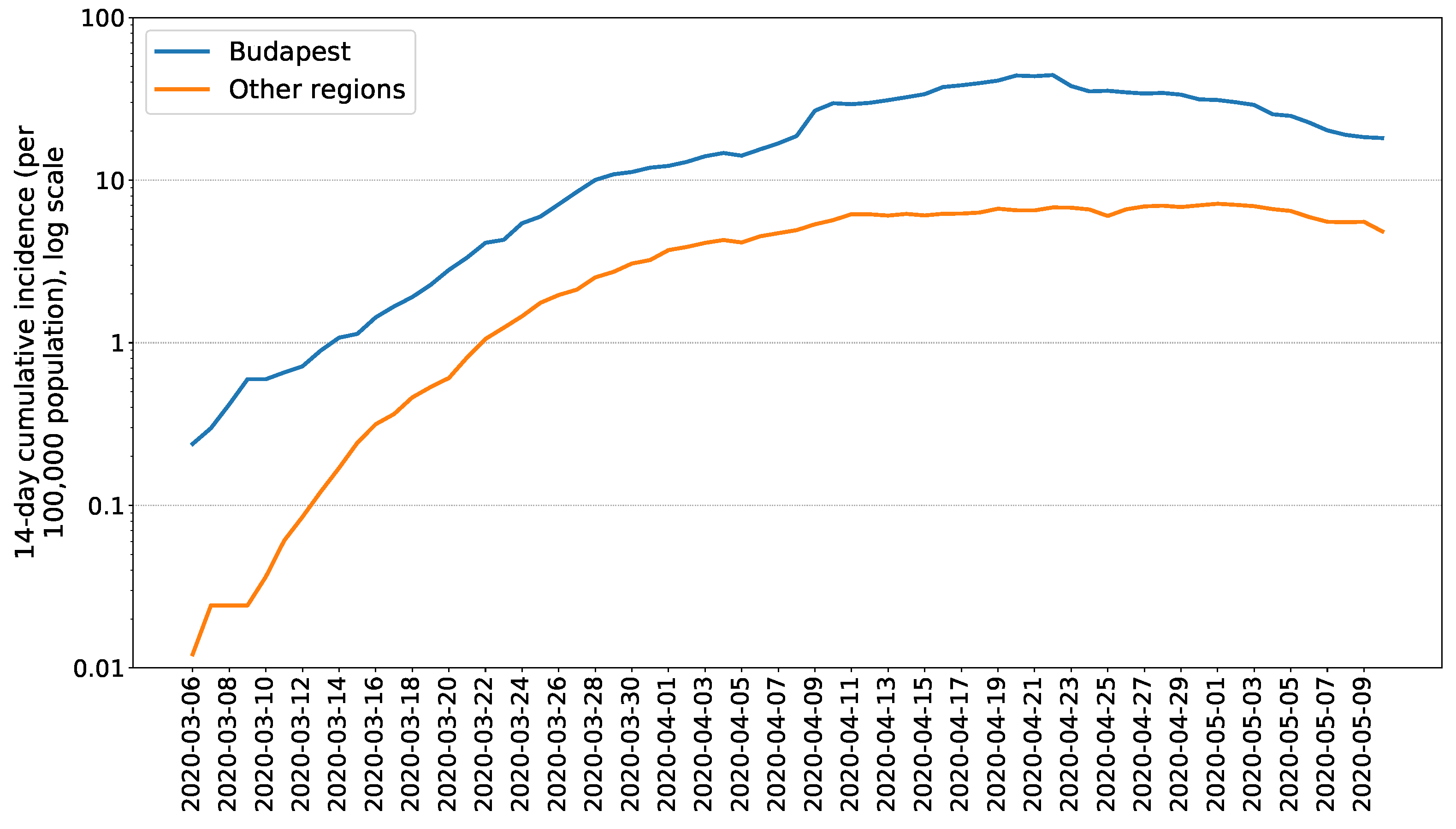
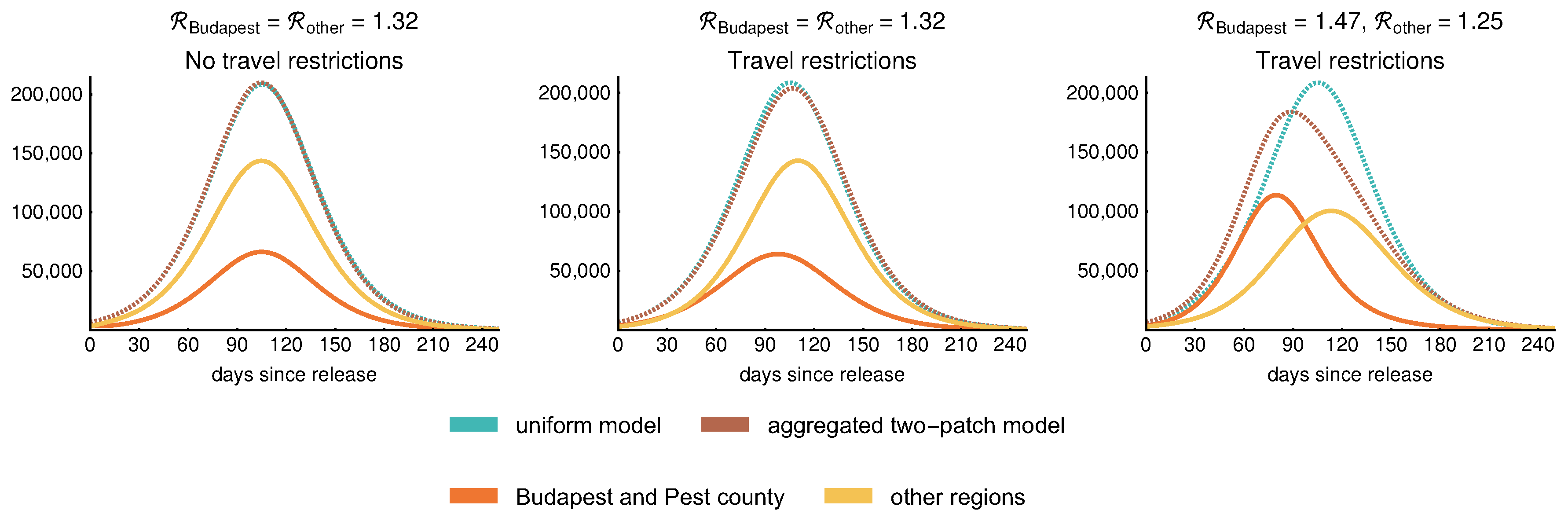
3.6. Spatial Heterogeneity
3.7. Sensitivity of the Peak ICU Demand to Key Parameters
3.8. The Impact of Implemented Measures Since Mid-March
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- WHO. Novel Coronavirus (2019-nCoV): Situation Reports; World Health Organization: Geneva, Switzerland, 2020; Available online: https://www.who.int/emergencies/diseases/novel-coronavirus-2019/situationreports (accessed on 30 June 2020).
- Stoecklin, S.B.; Rolland, P.; Silue, Y.; Mailles, A.; Campese, C.; Simondon, A.; Mechain, M.; Meurice, L.; Nguyen, M.; Bassi, C.; et al. First Cases of Coronavirus Disease 2019 (COVID-19) in France: Surveillance, Investigations and Control Measures, January 2020. Eurosurveillance 2020, 25. [Google Scholar] [CrossRef]
- Deslandes, A. SARS-CoV-2 was already spreading in France in late December 2019. Int. J. Antimicrob. Agents 2020, 106006. [Google Scholar] [CrossRef]
- Böhmer, M.M.; Buchholz, U.; Corman, V.M.; Hoch, M.; Katz, K.; Marosevic, D.V.; Böhm, S.; Woudenberg, T.; Ackermann, N.; Konrad, R.; et al. Investigation of a COVID-19 outbreak in Germany resulting from a single travel-associated primary case: A case series. Lancet Infect. Dis. 2020. [Google Scholar] [CrossRef]
- Sebastiani, G.; Massa, M.; Riboli, E. Covid–19 epidemic in Italy: Evolution, projections and impact of government measures. Eur. J. Epidemiol. 2020, 35, 341–345. [Google Scholar] [CrossRef] [PubMed]
- WHO. Statement on the Second Meeting of the International Health Regulations (2005) Emergency Committee Regarding the Outbreak of Novel Coronavirus (2019-nCoV); World Health Organization: Geneva, Switzerland, 2020; Available online: https://www.who.int/news-room/detail/30-01-2020-statement-on-the-secondmeeting-of-the-international-health-regulations-(2005)-emergency-committee-regarding-the-outbreak-ofnovel-coronavirus-(2019-ncov) (accessed on 30 June 2020).
- WHO. WHO Director-General’s Opening Remarks at the Media Briefing on COVID-19; World Health Organization: Geneva, Switzerland, 2020; Available online: https://www.who.int/dg/speeches/detail/who-directorgeneral-s-opening-remarks-at-the-media-briefing-on-covid-19---11-march-2020 (accessed on 30 June 2020).
- ECDC. Coronavirus Disease 2019 (COVID-19) in the EU/EEA and the UK—Ninth Update; Europen Centre for Disease Prevention and Control: Solna, Sweden, 2020; Available online: https://www.ecdc.europa.eu/sites/default/files/documents/covid-19-rapid-risk-assessment-coronavirusdisease-2019-ninth-update-23-april-2020.pdf (accessed on 30 June 2020).
- Kemenesi, G.; Zeghbib, S.; Somogyi, B.A.; Tóth, G.E.; Bányai, K.; Solymosi, N.; Szabo, P.M.; Szabó, I.; Bálint, Á.; Urbán, P.; et al. Multiple SARS-CoV-2 introductions shaped the early outbreak in Central Eastern Europe: Comparing Hungarian data to a worldwide sequence data-matrix. bioRxiv 2020. [Google Scholar] [CrossRef]
- COVID-19 Announcements of Hungary (Tájékoztató Oldal a Koronavírusról—In Hungarian); Cabinet Office of the Prime Minister: Budapest, Hungary, 2020. Available online: https://koronavirus.gov.hu (accessed on 30 June 2020).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020; Available online: https://www.R-project.org (accessed on 30 June 2020).
- Wickham, H. ggplot2: Elegant Graphics for Data Analysis; Springer: New York, NY, USA, 2016. [Google Scholar] [CrossRef]
- Dowle, M.; Srinivasan, A.; Gorecki, J.; Chirico, M.; Stetsenko, P.; Short, T.; Lianoglou, S.; Antonyan, E.; Bonsch, M.; Parsonage, H.; et al. Data.Table: Extension of ‘Data.Frame’. R package version 1.12.8. 2019. Available online: https://cran.r-project.org/package=data.table (accessed on 30 June 2020).
- Chang, W.; Cheng, J.; Allaire, J.; Xie, Y.; McPherson, J. Shiny: Web Application Framework for R. R Package Version 1.4.0.2. 2020. Available online: https://cran.r-project.org/package=shiny (accessed on 30 June 2020).
- Ferenci, T. Real-Time Epidemiology of COVID–19 in Hungary (A Magyarországi Koronavírus jáRvány Valós Idejű Epidemiológiája—In Hungarian); Óbuda University: Budapest, Hungary, 2020; Available online: https://research.physcon.uni-obuda.hu/COVID19MagyarEpi (accessed on 30 June 2020).
- Ferenci, T. Quantitative, Real-Time Epidemiology of COVID–19 in Hungary (A Magyarországi Koronavírus járváNy Valós Idejű, Kvantitatív Epidemiológiája—In Hungarian); Github: San Francisco, CA, USA, 2020; Available online: https://github.com/tamas-ferenci/COVID19MagyarEpi (accessed on 30 June 2020).
- Cori, A.; Ferguson, N.M.; Fraser, C.; Cauchemez, S. A New Framework and Software to Estimate Time-Varying Reproduction Numbers During Epidemics. Am. J. Epidemiol. 2013, 178, 1505–1512. [Google Scholar] [CrossRef]
- Wallinga, J.; Teunis, P. Different Epidemic Curves for Severe Acute Respiratory Syndrome Reveal Similar Impacts of Control Measures. Am. J. Epidemiol. 2004, 160, 509–516. [Google Scholar] [CrossRef] [PubMed]
- Wallinga, J.; Lipsitch, M. How Generation Intervals Shape the Relationship Between Growth Rates and Reproductive Numbers. Proc. R. Soc. Biol. Sci. 2007, 274, 599–604. [Google Scholar] [CrossRef]
- Cowling, B.J.; Lau, M.S.Y.; Ho, L.-M.; Chuang, S.-K.; Tsang, T.; Liu, S.-H.; Leung, P.-Y.; Lo, S.-V.; Lau, E.H.Y. The Effective Reproduction Number of Pandemic Influenza: Prospective Estimation. Epidemiology 2010, 21, 842–846. [Google Scholar] [CrossRef]
- Lipsitch, M.; Joshi, K.; Cobey, S.E. Comment on “Pan, A.; Liu, L.; Wang, C. et al. Association of Public Health Interventions With the Epidemiology of the COVID–19 Outbreak in Wuhan, China. JAMA. doi:10.1001/jama.2020.6130”; Github: San Francisco, CA, USA, 2020; Available online: https://github.com/keyajoshi/Pan_response (accessed on 30 June 2020).
- Höhle, M. Effective Reproduction Number Estimation; Stockholms Universitet: Stockholm, Sweden, 2020; Available online: https://staff.math.su.se/hoehle/blog/2020/04/15/effectiveR0.html (accessed on 30 June 2020).
- Cauchemez, S.; Boëlle, P.Y.; Thomas, G.; Valleron, A.J. Estimating in real time the efficacy of measures to control emerging communicable diseases. Am. J. Epidemiol. 2006, 164, 591–597. [Google Scholar] [CrossRef] [PubMed]
- Du, Z.; Xu, X.; Wu, Y.; Wang, L.; Cowling, B.J.; Meyers, L.A. Serial Interval of COVID-19 Among Publicly Reported Confirmed Cases. Emerg. Infect. Dis. 2020, 26. [Google Scholar] [CrossRef]
- Riccardo, F.; Ajelli, M.; Andrianou, X.; Bella, A.; Del Manso, M.; Fabiani, M.; Bellino, S.; Boros, S.; Mateo Urdiales, A.; Marziano, V.; et al. Epidemiological characteristics of COVID-19 cases in Italy and estimates of the reproductive numbers one month into the epidemic. medRxiv 2020. [Google Scholar] [CrossRef]
- Nishiura, H.; Linton, N.M.; Akhmetzhanov, A.R. Serial interval of novel coronavirus (COVID-19) infections. Int. J. Infect. Dis. 2020, 93, 284–286. [Google Scholar] [CrossRef]
- Obadia, T.; Haneef, R.; Boëlle, P. The R0 package: A toolbox to estimate reproduction numbers for epidemic outbreaks. BMC Med. Inform. Decis. Mak. 2012, 12, 147. [Google Scholar] [CrossRef] [PubMed]
- Boelle, P.Y.; Obadia, T. R0: Estimation of R0 and Real-Time Reproduction Number from Epidemics. R package Version 1.2-6. 2015. Available online: https://cran.r-project.org/package=R0 (accessed on 30 June 2020).
- Cori, A.; Cauchemez, S.; Ferguson, N.M.; Fraser, C.; Dahlqwist, E.; Demarsh, P.A.; Jombart, T.; Kamvar, Z.N.; Lessler, J.; Li, S.; et al. EpiEstim: Estimate Time Varying Reproduction Numbers from Epidemic Curves. R Package Version 2.2-2. 2020. Available online: https://cran.r-project.org/package=EpiEstim (accessed on 30 June 2020).
- Ghani, A.C.; Donnelly, C.A.; Cox, D.R.; Griffin, J.T.; Fraser, C.; Lam, T.H.; Ho, L.M.; Chan, W.S.; Anderson, R.M.; Hedley, A.J.; et al. Methods for Estimating the Case Fatality Ratio for a Novel, Emerging Infectious Disease. Am. J. Epidemiol. 2005, 162, 479–486. [Google Scholar] [CrossRef]
- Garske, T.; Legrand, J.; Donnelly, C.A.; Ward, H.; Cauchemez, S.; Fraser, C.; Ferguson, N.M.; Ghani, A.C. Assessing the severity of the novel influenza A/H1N1 pandemic. BMJ 2009, 339. [Google Scholar] [CrossRef] [PubMed]
- Nishiura, H.; Klinkenberg, D.; Roberts, M.; Heesterbeek, J.A.P. Early Epidemiological Assessment of the Virulence of Emerging Infectious Diseases: A Case Study of an Influenza Pandemic. PLoS ONE 2009, 4, e06852. [Google Scholar] [CrossRef] [PubMed]
- Jung, S.-M.; Akhmetzhanov, A.R.; Hayashi, K.; Linton, N.M.; Yang, Y.; Yuan, B.; Kobayashi, T.; Kinoshita, R.; Nishiura, H. Real-Time Estimation of the Risk of Death from Novel Coronavirus (COVID-19) Infection: Inference Using Exported Cases. J. Clin. Med. 2020, 9, 523. [Google Scholar] [CrossRef]
- Linton, N.M.; Kobayashi, T.; Yang, Y.; Hayashi, K.; Akhmetzhanov, A.R.; Jung, S.M.; Yuan, B.; Kinoshita, R.; Nishiura, H. Incubation Period and Other Epidemiological Characteristics of 2019 Novel Coronavirus Infections with Right Truncation: A Statistical Analysis of Publicly Available Case Data. J. Clin. Med. 2020, 9, 538. [Google Scholar] [CrossRef]
- Stan Development Team. RStan: The R Interface to Stan. R Package Version 2.19.3. 2020. Available online: http://mc-stan.org (accessed on 30 June 2020).
- Russell, T.; Hellewell, J.; Abbott, S.; Jarvis, C.; van Zandvoort, K.; Flasche, S.; Eggo, R.; Edmunds, J.; Kucharski, A. Using a Delay-Adjusted Case Fatality Ratio to Estimate under-Reporting (2020). CMMID. 2020. Available online: https://cmmid.github.io/topics/covid19/global_cfr_estimates.html (accessed on 30 June 2020).
- Boldog, P.; Tekeli, T.; Vizi, Z.; Dénes, A.; Bartha, F.A.; Röst, G. Risk Assessment of Novel Coronavirus COVID–19 Outbreaks Outside China. J. Clin. Med. 2020, 9, 571. [Google Scholar] [CrossRef]
- Moss, R.; Wood, J.; Brown, D.; Shearer, F.; Black, A.J.; Cheng, A.; McCaw, J.M.; McVernon, J. Modelling the impact of COVID-19 in Australia to inform transmission reducing measures and health system preparedness. medRxiv 2020. [Google Scholar] [CrossRef]
- Di Domenico, L.; Pullano, G.; Sabbatini, C.E.; Boëlle, P.-Y.; Colizza, V. Expected impact of lockdown in Île-de-France and possible exit strategies. medRxiv 2020. [Google Scholar] [CrossRef]
- Barbarossa, M.V.; Fuhrmann, J.; Heidecke, J.; Varma, H.V.; Castelletti, N.; Meinke, J.H.; Krieg, S.; Lippert, T. A first study on the impact of current and future control measures on the spread of COVID-19 in Germany. medRxiv 2020. [Google Scholar] [CrossRef]
- Ferguson, N.M.; Laydon, D.; Nedjati-Gilani, G.; Imai, N.; Ainslie, K.; Baguelin, M.; Bhatia, S.; Boonyasiri, A.; Cucunubá, Z.; Cuomo-Dannenburg, G.; et al. Report 9 – Impact of Non-Pharmaceutical Interventions (NPIs) to Reduce COVID-19 Mortality and Healthcare Demand; Imperial College London: London, UK, 2020; Available online: https://www.imperial.ac.uk/mrc-global-infectious-disease-analysis/covid-19/report-9-impact-ofnpis-on-covid-19 (accessed on 30 June 2020).
- Moghadas, S.M.; Shoukat, A.; Fitzpatrick, M.C.; Wells, C.R.; Sah, P.; Pandey, A.; Sachs, J.D.; Wang, Z.; Meyers, L.A.; Singer, B.H.; et al. Projecting hospital utilization during the COVID-19 outbreaks in the United States. Proc. Natl. Acad. Sci. USA 2020, 117, 9122–9126. [Google Scholar] [CrossRef] [PubMed]
- Weitz, J.S. COVID-19 Epidemic Risk Assessment for Georgia; Github: San Francisco, CA, USA, 2020; Available online: https://github.com/jsweitz/covid-19-ga-summer-2020 (accessed on 30 June 2020).
- He, X.; Lau, E.H.; Wu, P.; Deng, X.; Wang, J.; Hao, X.; Lau, Y.C.; Wong, J.Y.; Guan, Y.; Tan, X.; et al. Temporal dynamics in viral shedding and transmissibility of COVID-19. Nat. Med. 2020. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Guan, X.; Wu, P.; Wang, X.; Zhou, L.; Tong, Y.; Ren, R.; Leung, K.S.M.; Lau, E.H.Y.; Wong, J.Y.; et al. Early Transmission Dynamics in Wuhan, China, of Novel Coronavirus–Infected Pneumonia. N. Engl. J. Med. 2020, 382, 1199–1207. [Google Scholar] [CrossRef]
- Blyuss, K.B.; Kyrychko, Y.N. Effects of latency and age structure on the dynamics and containment of COVID-19. medRxiv 2020. [Google Scholar] [CrossRef]
- Wearing, H.J.; Rohani, P.; Keeling, M.J. Appropriate Models for the Management of Infectious Diseases. PLoS Med. 2005, 2. [Google Scholar] [CrossRef] [PubMed]
- University of Szeged. Hungarian Data Supply Questionnaire (MASZK–Magyar Adatszolgáltató Kérdőív—In Hungarian). Available online: https://covid.sed.hu/tabs/response (accessed on 30 June 2020).
- Bolyai Institute, University of Szeged. Code Basis for COVID 19 Modelling in Hungary; Github: San Francisco, CA, USA, 2020; Available online: https://github.com/zsvizi/covid19hun (accessed on 30 June 2020).
- Cheng, H.-Y.; Jian, S.-W.; Liu, D.-P.; Ng, T.-C.; Huang, W.-T.; Lin, H.-H. Contact Tracing Assessment of COVID-19 Transmission Dynamics in Taiwan and Risk at Different Exposure Periods Before and After Symptom Onset. JAMA Intern Med. 2020. [Google Scholar] [CrossRef]
- Ferretti, L.; Wymant, C.; Kendall, M.; Zhao, L.; Nurtay1, A.; Abeler-Dörner, L.; Parker, M.; Bonsall, D.; Fraser, C. Quantifying SARS-CoV-2 transmission suggests epidemic control with digital contact tracing. Science 2020. [Google Scholar] [CrossRef] [PubMed]
- Docherty, A.B.; Harrison, E.M.; Green, C.A.; Hardwick, H.E.; Pius, R.; Norman, L.; Holden, K.A.; Read, J.M.; Dondelinger, F.; Carson, G.; et al. Features of 16,749 hospitalised UK patients with COVID-19 using the ISARIC WHO Clinical Characterisation Protocol. medRxiv 2020. [Google Scholar] [CrossRef]
- Intensive Care National Audit & Research Center (ICNARC). Report on COVID-19 in Critical Care. 2020. Available online: https://www.icnarc.org/DataServices/Attachments/Download/c5a62b13-6486-ea11-9125-00505601089b (accessed on 30 June 2020).
- Lewnard, J.A.; Liu, V.X.; Jackson, M.L.; Schmidt, M.A.; Jewell, B.L.; Flores, J.P.; Jentz, C.; Northrup, G.R.; Mahmud, A.; Reingold, A.L.; et al. Incidence, clinical outcomes, and transmission dynamics of severe coronavirus disease 2019 in California and Washington: Prospective cohort study. BMJ 2020, 369. [Google Scholar] [CrossRef] [PubMed]
- Parri, N.; Lenge, M.; Buonsenso, D. Children with Covid-19 in Pediatric Emergency Departments in Italy. N. Engl. J. Med. Corresp. 2020. [Google Scholar] [CrossRef] [PubMed]
- Prem, K.; Cook, A.R.; Jit, M. Projecting social contact matrices in 152 countries using contact surveys and demographic data. PLoS Comput. Biol. 2017, 13. [Google Scholar] [CrossRef]
- Diekmann, O.; Heesterbeek, J.A.P.; Roberts, M.G. The construction of next-generation matrices for compartmental epidemic models. J. R. Soc. Interface 2020, 7, 873–885. [Google Scholar] [CrossRef] [PubMed]
- Preliminary Results of the H-UNCOVER Study. (H-UNCOVER Részeredmények: 8276 Tesztből Kettő Lett Pozitív—In Hungarian); Semmelweis University: Budapest, Hungary, 2020; Available online: https://semmelweis.hu/hirek/2020/05/13/h-uncover-reszeredmenyek-8276-tesztbol-ketto-lett-pozitiv (accessed on 30 June 2020).
- Verity, R.; Okell, L.C.; Dorigatti, I.; Winskill, P.; Whittaker, C.; Imai, N.; Cuomo-Dannenburg, G.; Thompson, H.; Walker, P.G.T.; Fu, H.; et al. Estimates of the severity of coronavirus disease 2019: A model-based analysis. Lancet Infect. Dis. 2020, 20, 669–677. [Google Scholar] [CrossRef]
- Streeck, H.; Schulte, B.; Kuemmerer, B.; Richter, E.; Hoeller, T.; Fuhrmann, C.; Bartok, E.; Dolscheid, R.; Berger, M.; Wessendorf, L.; et al. Infection fatality rate of SARS-CoV-2 infection in a German community with a super-spreading event. medRxiv 2020. [Google Scholar] [CrossRef]
- Valenti, L.; Bergna, A.; Pelusi, S.; Facciotti, F.; Lai, A.; Tarkowski, M.; Berzuini, A.; Caprioli, F.; Santoro, L.; Baselli, G.; et al. SARS-CoV-2 seroprevalence trends in healthy blood donors during the COVID-19 Milan outbreak. medRxiv 2020. [Google Scholar] [CrossRef]
- Riou, J.; Althaus, C.L. Pattern of early human-to-human transmission of Wuhan 2019 novel coronavirus (2019-nCoV), December 2019 to January 2020. Eurosurveillance 2020, 25. [Google Scholar] [CrossRef]
- RKI. Epidemiologisches Bulletin 17/2020; Robert Koch Institute: Berlin, Germany, 2020; Available online: https://www.rki.de/DE/Content/Infekt/EpidBull/Archiv/2020/Ausgaben/17_20.pdf (accessed on 30 June 2020).
- Allieta, M.; Allieta, A.; Sebastiano, D.R. COVID-19 outbreak in Italy: Estimation of reproduction numbers over two months toward the Phase 2. medRxiv 2020. [Google Scholar] [CrossRef]
- National Institute for Public Health and the Environment (RIVM), Ministry of Health, Welfare and Sport, Netherlands. Children and COVID-19. 2020. Available online: https://www.rivm.nl/en/novel-coronavirus-covid-19/children-and-covid-19 (accessed on 30 June 2020).
- WHO. Q&A on Coronaviruses (COVID-19); World Health Organization: Geneva, Switzerland, 2020; Available online: https://www.who.int/emergencies/diseases/novel-coronavirus-2019/question-and-answers-hub/q-a-detail/q-a-coronaviruses (accessed on 30 June 2020).
- Jones, T.C.; Mühlemann, B.; Veith, T.; Biele, G.; Zuchowski, M.; Hoffmann, J.; Stein, A.; Edelmann, A.; Corman, V.M.; Drosten, C. An analysis of SARS-CoV-2 viral load by patient age. medRxiv 2020. [Google Scholar] [CrossRef]
- Armitage, R.; Nellums, L.B. COVID-19 and the consequences of isolating the elderly. Lancet Public Health 2020, 5, 256. [Google Scholar] [CrossRef]
- Balcan, D.; Hu, H.; Goncalves, B.; Bajardi, P.; Poletto, C.; Ramasco, J.J.; Paolotti, D.; Perra, N.; Tizzoni, M.; Van den Broeck, W.; et al. Seasonal transmission potential and activity peaks of the new influenza A (H1N1): A Monte Carlo likelihood analysis based on human mobility. BMC Med. 2009, 7, 45. [Google Scholar] [CrossRef]
- KSH. The Salient Targets of Commuters. (Az Ingázás Kiemelt Célpontjai—In Hungarian); Hungarian Central Statistical Office (KSH): Budapest, Hungary, 2016. Available online: http://www.ksh.hu/docs/hun/xftp/idoszaki/pdf/ingazas.pdf (accessed on 30 June 2020).
- Kissler, S.M.; Tedijanto, C.; Lipsitch, M.; Grad, Y. Social distancing strategies for curbing the COVID-19 epidemic. medRxiv 2020. [Google Scholar] [CrossRef]
- Sajadi, M.M.; Habibzadeh, P.; Vintzileos, A.; Shokouhi, S.; Miralles-Wilhelm, F.; Amoroso, A. Temperature, Humidity, and Latitude Analysis to Estimate Potential Spread and Seasonality of Coronavirus Disease 2019 (COVID-19). JAMA Netw. Open 2020, 3. [Google Scholar] [CrossRef] [PubMed]
- Davies, N.G.; Kucharski, A.J.; Eggo, R.M.; Gimma, A.; Edmunds, W.J.; CMMID COVID-19 Working Group. Effects of non-pharmaceutical interventions on COVID-19 cases, deaths, and demand for hospital services in the UK: A modelling study. Lancet Public Health 2020. [Google Scholar] [CrossRef]
- Kucharski, A.J.; Klepac, P.; Conlan, A.J.K.; Kissler, S.M.; Tang, M.L.; Fry, H.; Gog, J.R.; Edmunds, W.J.; CMMID COVID-19 Working Group. Effectiveness of isolation, testing, contact tracing, and physical distancing on reducing transmission of SARS-CoV-2 in different settings: A mathematical modelling study. Lancet Infect. Dis. 2020. [Google Scholar] [CrossRef]
| Duration of | Value | |
|---|---|---|
| Incubation period | days | |
| Latent period | days | |
| Presymptomatic (infectious) period | days | |
| Infectious period of | days | |
| Infectious period of | days | |
| Hospitalization | days | |
| Intensive care | ||
| until transition to or | days | |
| Recovery in | days | |
| Relative infectiousness | ||
| Presymptomatic vs Symptomatic | ||
| Asymptomatic vs Symptomatic | ||
| Age Group | 0–4 | 5–14 | 15–29 | 30–59 | 60–69 | 70–79 | 80– |
|---|---|---|---|---|---|---|---|
| Population | 468,605 | 953,134 | 1,678,211 | 4,087,976 | 1,312,208 | 839,589 | 433,033 |
| Probability/Age Group | 0–4 | 5–14 | 15–29 | 30–59 | 60–69 | 70–79 | 80– | |
|---|---|---|---|---|---|---|---|---|
| Asymptomatic course | ||||||||
| Hospitalization or | ||||||||
| intensive care (from ) | ||||||||
| Intensive care | ||||||||
| (given hospitalization) | ||||||||
| Fatal outcome | ||||||||
| (from ) | ||||||||
| 0.0210 | 0.0231 | 0.0277 | 0.0347 | 0.0462 |
| Scenario | Description | Pointer |
|---|---|---|
| Weak control | general 25% reduction in transmission | Section 3.3 |
| Moderate control | general 40% reduction in transmission | |
| Strong control | general 50% reduction in transmission | |
| School closure | two variants of changing the mixing patterns of schoolchildren | Section 3.4.1 |
| Protection of elderly | 50–100% reduction of contacts outside the household for the elderly | Section 3.4.2 |
| Seasonality | exploring various degrees of seasonal behavior | Section 3.5 |
| Spatial heterogeneity | considering two patches, which are strongly or weakly connected | Section 3.6 |
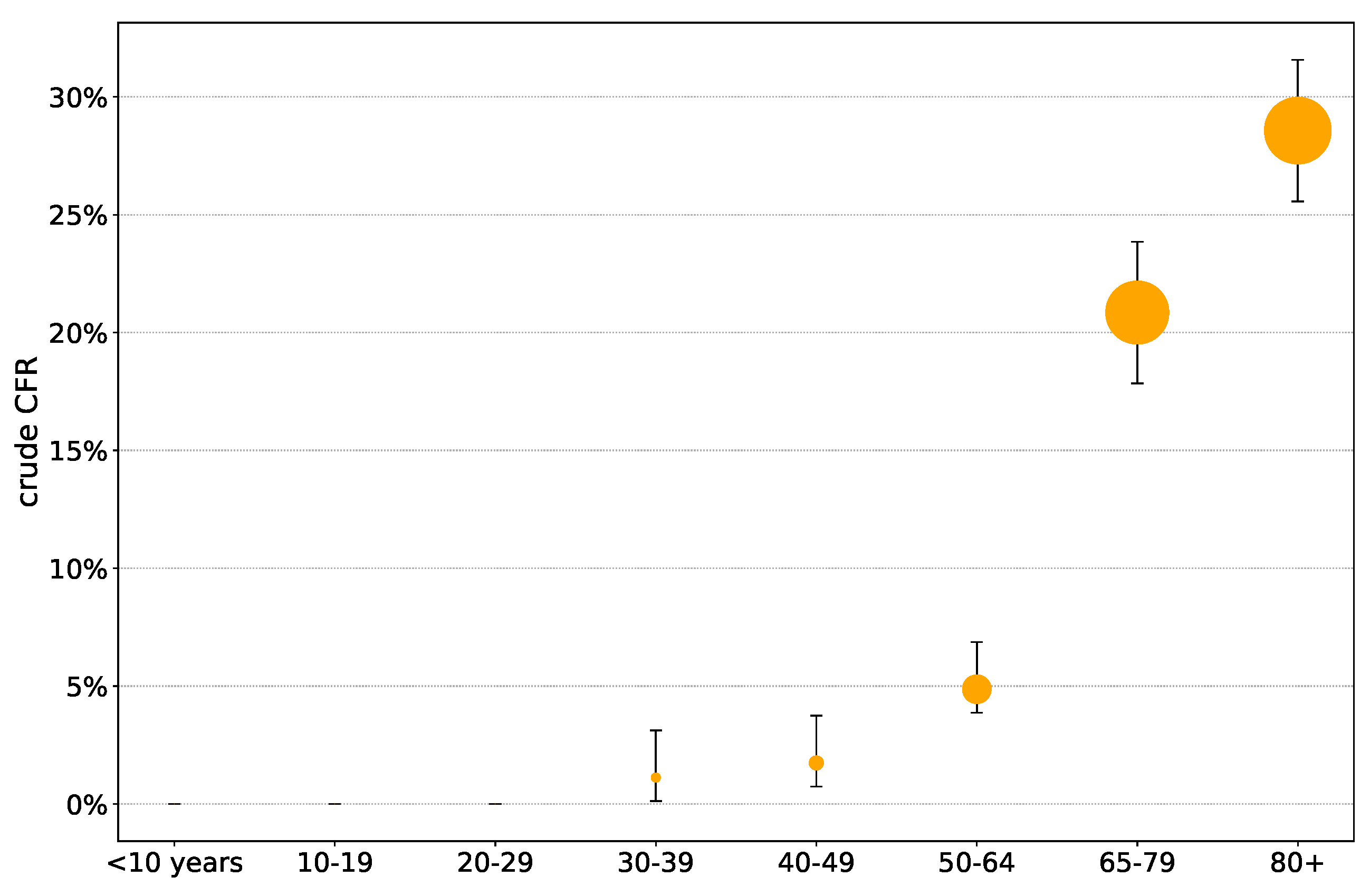
| Age Group (Years) | Number of Confirmed COVID-19 Cases | Morbidity (Per 100,000 Population) | Number of Deaths | Case Fatality Rate (Per 100 Confirmed COVID-19 Cases) |
|---|---|---|---|---|
| <1 | 3 | 3.3 | 0 | 0.0 |
| 1–4 | 10 | 2.6 | 0 | 0.0 |
| 5–14 | 31 | 3.2 | 0 | 0.0 |
| 15–29 | 254 | 15.5 | 0 | 0.0 |
| 30–39 | 267 | 19.9 | 3 | 1.1 |
| 40–49 | 459 | 27.7 | 8 | 1.7 |
| 50–59 | 485 | 38.3 | 15 | 3.1 |
| 60–64 | 233 | 35.4 | 20 | 8.6 |
| 65–69 | 254 | 39.4 | 44 | 17.3 |
| 70–79 | 595 | 69.5 | 133 | 22.4 |
| ≥80 | 693 | 163.3 | 198 | 28.6 |
| Overall | 3284 | 33.1 | 421 | 12.8 |
| IFR | 0.3% | 0.6% | 0.9% | 1.2% |
|---|---|---|---|---|
| Underascertainment (true/reported) | 54.0 | 27.0 | 18.0 | 13.5 |
| Corrected cumulative number of infections by 10 May | 177,242 | 88,621 | 59,081 | 44,310 |
| Transmission Reduction | Reproduction Number | Hospital Bed Need at Peak | ICU Need at Peak | Time to Reach 1000 ICU Beds | Mortality (Pers.) | Recovered (of Tot. Pop.) |
|---|---|---|---|---|---|---|
| 25% | 1.65 | 20,973 | 7225 | 6 weeks | 21,624 | 58.25% |
| 40% | 1.32 | 7400 | 2477 | 10 weeks | 12,374 | 37.37% |
| 50% | 1.1 | 1069 | 350 | - | 4447 | 14.84% |
| 60% | 0.9 | - | - | - | - | - |
| Date | Measure | Reported Number of Cases at the Time of Introduction |
|---|---|---|
| 8 March | Banned visits to health care institutions and long-term care facilities | 9 |
| 9 March | Suspension of Northern Italy flights | 12 |
| 11 March | Emergency notification | 16 |
| 12 March | University closures, no entry for non-Hungarian passengers to Hungary from Italy, China, Korea and Iran | 19 |
| 16 March | School closures | 50 |
| 17 March | Shortened opening time of shops, ban on events | 58 |
| 28 March | Stay at home measures | 408 |
| 4 May | Partial lifting of stay at home measures and opening of restaurants in the countryside (except Pest county where from May 14) | 3065 |
| 18 May | Lifting of stay at home measures and opening of shops and outdoor areas of restaurants in Budapest | 3556 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Röst, G.; Bartha, F.A.; Bogya, N.; Boldog, P.; Dénes, A.; Ferenci, T.; Horváth, K.J.; Juhász, A.; Nagy, C.; Tekeli, T.; et al. Early Phase of the COVID-19 Outbreak in Hungary and Post-Lockdown Scenarios. Viruses 2020, 12, 708. https://doi.org/10.3390/v12070708
Röst G, Bartha FA, Bogya N, Boldog P, Dénes A, Ferenci T, Horváth KJ, Juhász A, Nagy C, Tekeli T, et al. Early Phase of the COVID-19 Outbreak in Hungary and Post-Lockdown Scenarios. Viruses. 2020; 12(7):708. https://doi.org/10.3390/v12070708
Chicago/Turabian StyleRöst, Gergely, Ferenc A. Bartha, Norbert Bogya, Péter Boldog, Attila Dénes, Tamás Ferenci, Krisztina J. Horváth, Attila Juhász, Csilla Nagy, Tamás Tekeli, and et al. 2020. "Early Phase of the COVID-19 Outbreak in Hungary and Post-Lockdown Scenarios" Viruses 12, no. 7: 708. https://doi.org/10.3390/v12070708
APA StyleRöst, G., Bartha, F. A., Bogya, N., Boldog, P., Dénes, A., Ferenci, T., Horváth, K. J., Juhász, A., Nagy, C., Tekeli, T., Vizi, Z., & Oroszi, B. (2020). Early Phase of the COVID-19 Outbreak in Hungary and Post-Lockdown Scenarios. Viruses, 12(7), 708. https://doi.org/10.3390/v12070708






