Significant Differences in RNA Structure Destabilization by HIV-1 Gag∆p6 and NCp7 Proteins
Abstract
1. Introduction
2. Materials and Methods
2.1. Hairpin Construct Synthesis
2.2. Gag Polyprotein Preparation
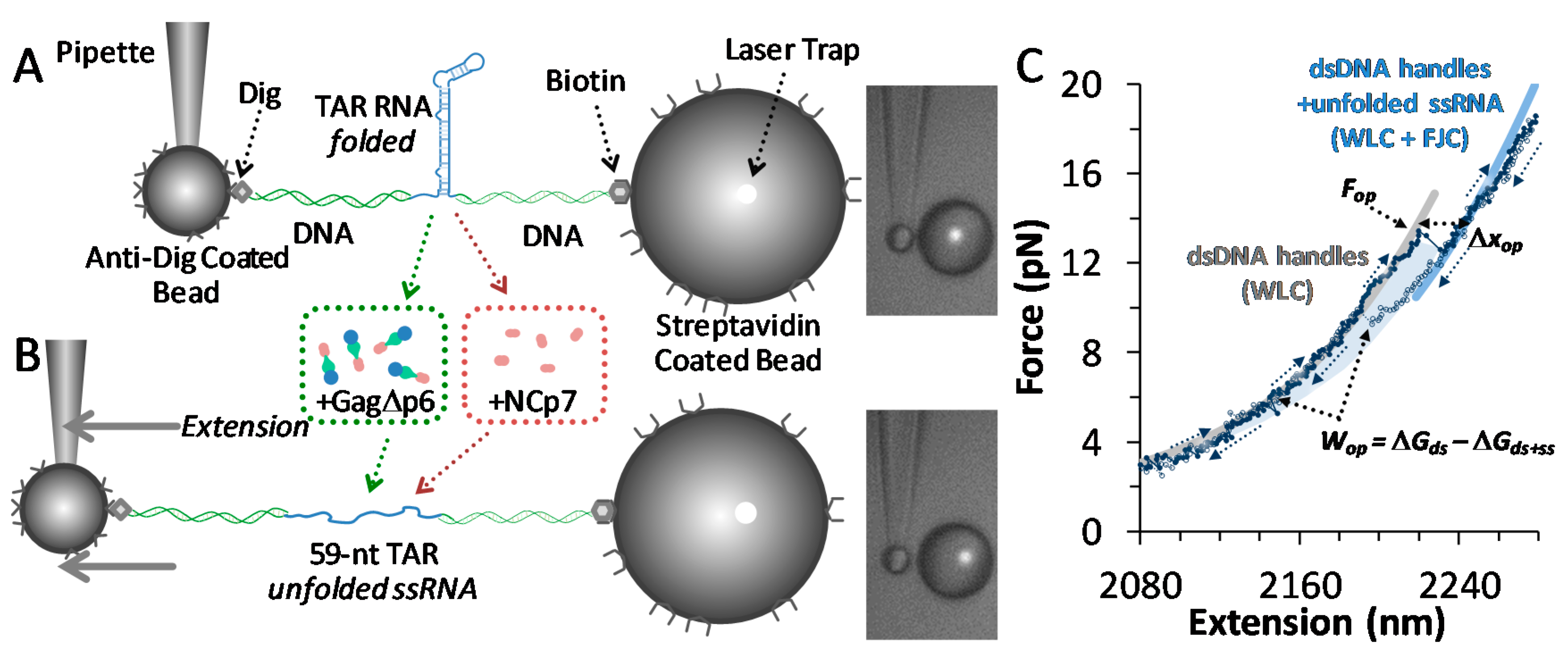
2.3. Single Molecule Optical Tweezers
2.4. Hairpin Energies from Mfold
3. Results
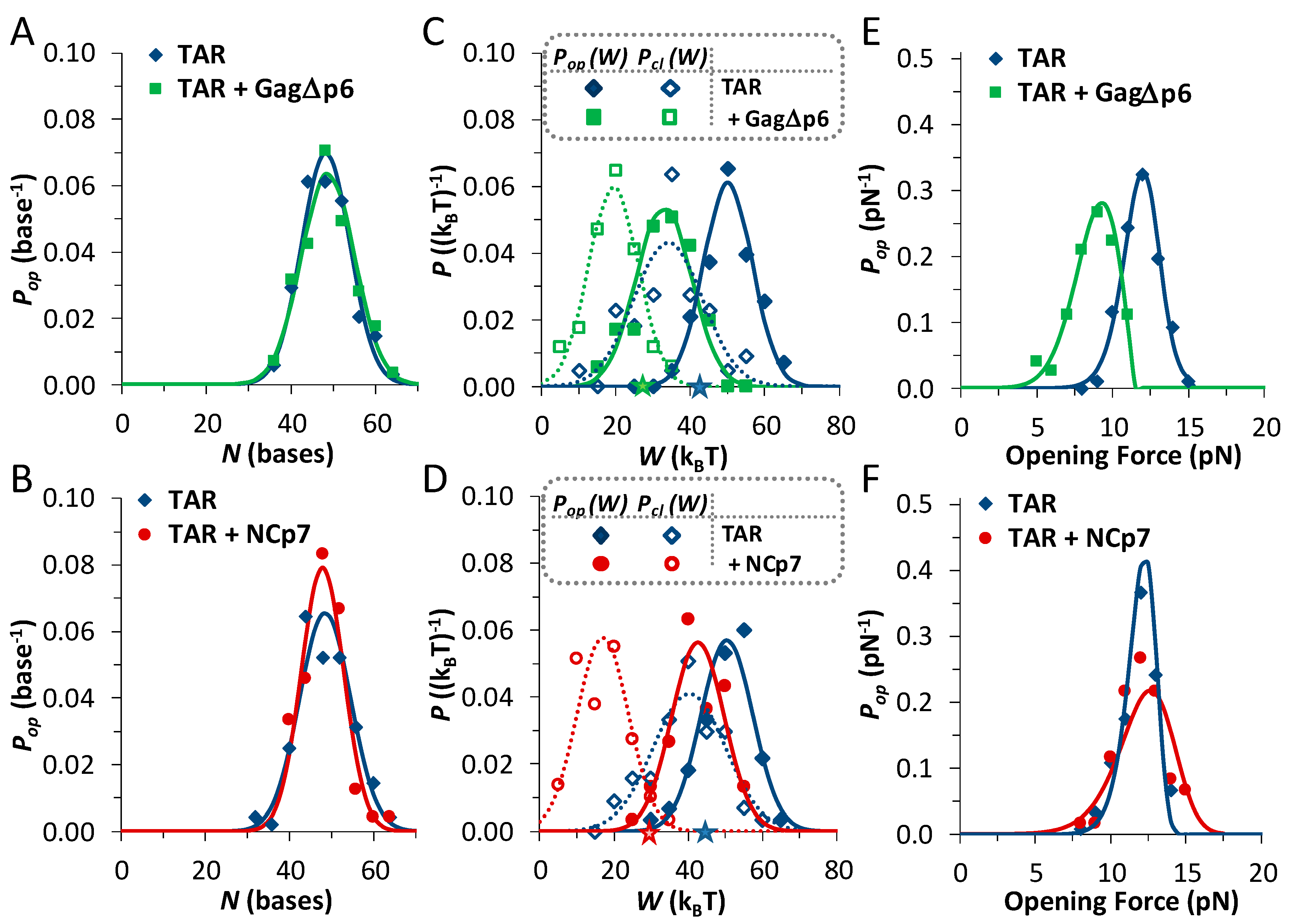
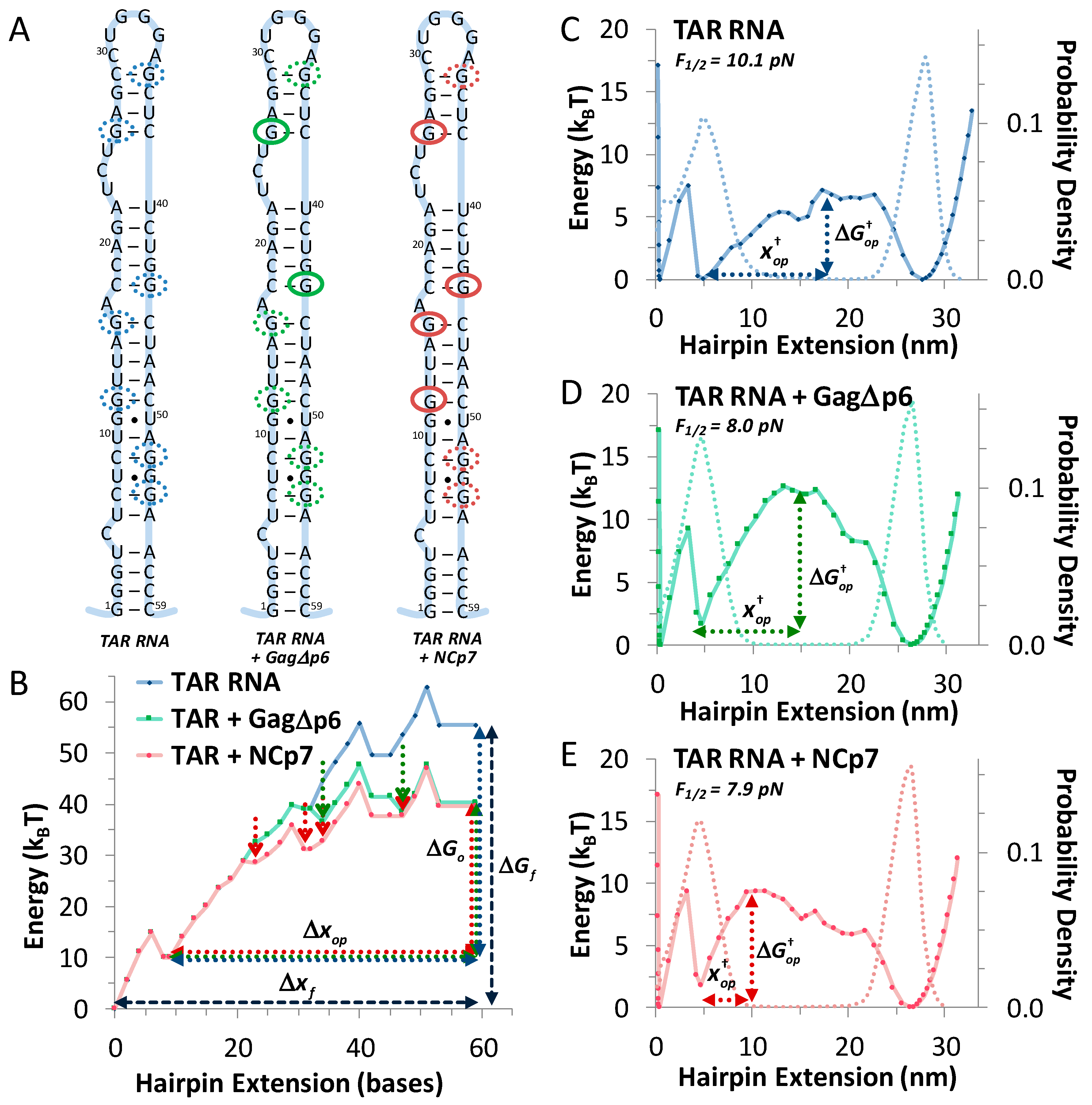
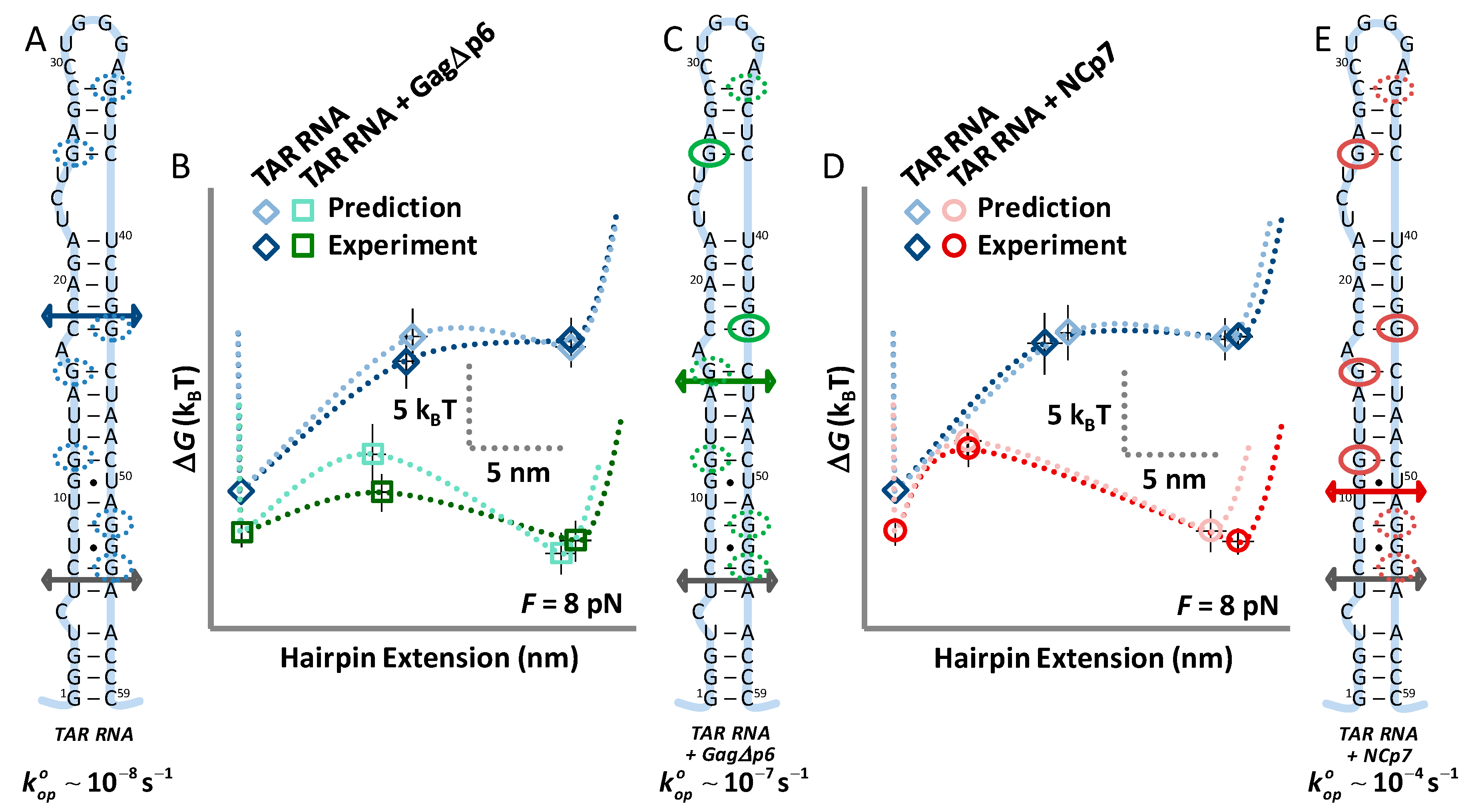
3.1. TAR Hairpin Length Is Unaffected by Gag∆p6
3.2. Gag∆p6 Reduces the Energy of Unfolding
3.3. Gag∆p6 Lowers but Does Not Shift the Energy Barrier
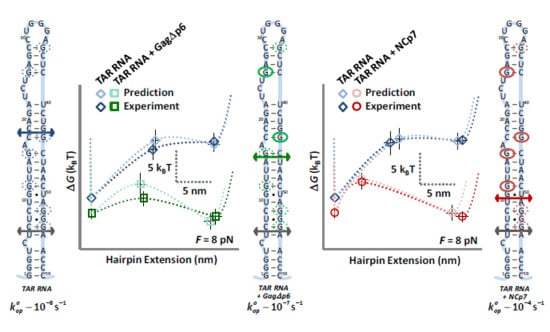
3.4. Landscape Models Locate Gag∆p6 Binding
4. Discussion
4.1. Both NCp7 and Gag∆p6 Chaperone Nucleic Acids
4.2. While NCp7 Strongly Facilitates TAR Opening, Gag∆p6 Does Not
Author Contributions
Funding
Conflicts of Interest
Appendix A. Polymer Models of Elasticity
Appendix B. Equilibrium Energies from Non-Equilibrium Measurements
Appendix C. Kinetic Models and the Transition State
Appendix D. Modeling the Energy Landscape
References
- Cech, T.R.; Zaug, A.J.; Grabowski, P.J. In vitro splicing of the ribosomal RNA precursor of Tetrahymena: Involvement of a guanosine nucleotide in the excision of the intervening sequence. Cell 1981, 27, 487–496. [Google Scholar] [CrossRef]
- Anthony, P.C.; Perez, C.F.; García-García, C.; Block, S.M. Folding energy landscape of the thiamine pyrophosphate riboswitch aptamer. Proc. Natl. Acad. Sci. USA 2012, 109, 1485–1489. [Google Scholar] [CrossRef] [PubMed]
- Greenleaf, W.J.; Frieda, K.L.; Foster, D.A.N.; Woodside, M.T.; Block, S.M. Direct Observation of Hierarchical Folding in Single Riboswitch Aptamers. Science 2008, 319, 630–633. [Google Scholar] [CrossRef] [PubMed]
- Li, P.T.; Bustamante, C.; Tinoco, I., Jr. Unusual mechanical stability of a minimal RNA kissing complex. Proc. Natl. Acad. Sci. USA 2006, 103, 15847–15852. [Google Scholar] [CrossRef]
- Onoa, B.; Dumont, S.; Liphardt, J.; Smith, S.B.; Tinoco, I., Jr.; Bustamante, C. Identifying kinetic barriers to mechanical unfolding of the T. thermophila ribozyme. Science 2003, 299, 1892–1895. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Glucksmann-Kuis, M.A.; Dai, X.; Markiewicz, P.; Rothman-Denes, L.B. E. coli SSB activates N4 virion RNA polymerase promoters by stabilizing a DNA hairpin required for promoter recognition. Cell 1996, 84, 147–154. [Google Scholar] [CrossRef]
- Vo, M.N.; Barany, G.; Rouzina, I.; Musier-Forsyth, K. Mechanistic studies of mini-TAR RNA/DNA annealing in the absence and presence of HIV-1 nucleocapsid protein. J. Mol. Biol. 2006, 363, 244–261. [Google Scholar] [CrossRef]
- Vo, M.N.; Barany, G.; Rouzina, I.; Musier-Forsyth, K. HIV-1 nucleocapsid protein switches the pathway of transactivation response element RNA/DNA annealing from loop-loop “kissing” to “zipper”. J. Mol. Biol. 2009, 386, 789–801. [Google Scholar] [CrossRef]
- Berkhout, B.; Jeang, K.T. Functional roles for the TATA promoter and enhancers in basal and Tat-induced expression of the human immunodeficiency virus type 1 long terminal repeat. J. Virol. 1992, 66, 139–149. [Google Scholar] [CrossRef]
- Levin, J.G.; Guo, J.; Rouzina, I.; Musier-Forsyth, K. Nucleic acid chaperone activity of HIV-1 nucleocapsid protein: Critical role in reverse transcription and molecular mechanism. Prog. Nucleic Acid. Res. Mol. Biol. 2005, 80, 217–286. [Google Scholar] [CrossRef]
- Cruceanu, M.; Gorelick, R.J.; Musier-Forsyth, K.; Rouzina, I.; Williams, M.C. Rapid kinetics of protein-nucleic acid interaction is a major component of HIV-1 nucleocapsid protein’s nucleic acid chaperone function. J. Mol. Biol. 2006, 363, 867–877. [Google Scholar] [CrossRef] [PubMed]
- Darlix, J.-L.; Lapadat-Tapolsky, M.; De Rocquigny, H.; Roques, B.P. First Glimpses at Structure-function Relationships of the Nucleocapsid Protein of Retroviruses. J. Mol. Biol. 1995, 254, 523–537. [Google Scholar] [CrossRef] [PubMed]
- Lapadat-Tapolsky, M.; de Rocquigny, H.; Van Gent, D.; Roques, B.; Plasterk, R.; Darlix, J.-L. Interaction between HIV-1 nucleocapsid protein and viral DNA may have important functions in the viral life cycle. Nucleic Acids Res. 1993, 21, 831–839. [Google Scholar] [CrossRef] [PubMed]
- Lapadat-Tapolsky, M.; Pernelle, C.; Borie, C.; Darlix, J.L. Analysis of the nucleic acid annealing activities of nucleocapsid protein from HIV-1. Nucleic Acids Res. 1995, 23, 2434–2441. [Google Scholar] [CrossRef] [PubMed]
- Thomas, J.A.; Gorelick, R.J. Nucleocapsid protein function in early infection processes. Virus Res. 2008, 134, 39–63. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Mitra, M.; McCauley, M.J.; Thomas, J.A.; Rouzina, I.; Musier-Forsyth, K.; Williams, M.C.; Gorelick, R.J. Aromatic residue mutations reveal direct correlation between HIV-1 nucleocapsid protein’s nucleic acid chaperone activity and retroviral replication. Virus Res. 2013, 171, 263–277. [Google Scholar] [CrossRef]
- De Guzman, R.N.; Wu, Z.R.; Stalling, C.C.; Pappalardo, L.; Borer, P.N.; Summers, M.F. Structure of the HIV-1 Nucleocapsid Protein Bound to the SL3 psi-RNA Recognition Element. Science 1998, 279, 384–388. [Google Scholar] [CrossRef]
- Chen, N.; Morag, A.; Almog, N.; Blumenzweig, I.; Dreazin, O.; Kotler, M. Extended nucleocapsid protein is cleaved from the Gag-Pol precursor of human immunodeficiency virus type 1. J. Gen. Virol. 2001, 82, 581–590. [Google Scholar] [CrossRef]
- Shehu-Xhilaga, M.; Krausslich, H.G.; Pettit, S.; Swanstrom, R.; Lee, J.Y.; Marshall, J.A.; Crowe, S.M.; Mak, J. Proteolytic processing of the p2/nucleocapsid cleavage site is critical for human immunodeficiency virus type 1 RNA dimer maturation. J. Virol. 2001, 75, 9156–9164. [Google Scholar] [CrossRef]
- Rein, A.; Henderson, L.E.; Levin, J.G. Nucleic-acid-chaperone activity of retroviral nucleocapsid proteins: Significance for viral replication. Trends Biochem. Sci. 1998, 23, 297–301. [Google Scholar] [CrossRef]
- Tsuchihashi, Z.; Brown, P.O. DNA strand exchange and selective DNA annealing promoted by the human immunodeficiency virus type 1 nucleocapsid protein. J. Virol. 1994, 68, 5863–5870. [Google Scholar] [CrossRef] [PubMed]
- Belfetmi, A.; Zargarian, L.; Tisne, C.; Sleiman, D.; Morellet, N.; Lescop, E.; Maskri, O.; Rene, B.; Mely, Y.; Fosse, P.; et al. Insights into the mechanisms of RNA secondary structure destabilization by the HIV-1 nucleocapsid protein. RNA 2016, 22, 506–517. [Google Scholar] [CrossRef]
- McCauley, M.J.; Rouzina, I.; Manthei, K.A.; Gorelick, R.J.; Musier-Forsyth, K.; Williams, M.C. Targeted binding of nucleocapsid protein transforms the folding landscape of HIV-1 TAR RNA. Proc. Natl. Acad. Sci. USA 2015, 112, 13555–13560. [Google Scholar] [CrossRef] [PubMed]
- Vogt, V.M.; Simon, M.N. Mass determination of Rous sarcoma virus virions by scanning transmission electron microscopy. J. Virol. 1999, 73, 7050–7055. [Google Scholar] [CrossRef] [PubMed]
- Briggs, J.A.; Simon, M.N.; Gross, I.; Krausslich, H.G.; Fuller, S.D.; Vogt, V.M.; Johnson, M.C. The stoichiometry of Gag protein in HIV-1. Nat. Struct. Mol. Biol. 2004, 11, 672–675. [Google Scholar] [CrossRef] [PubMed]
- Chertova, E.; Chertov, O.; Coren, L.V.; Roser, J.D.; Trubey, C.M.; Bess, J.W., Jr.; Sowder, R.C., II; Barsov, E.; Hood, B.L.; Fisher, R.J.; et al. Proteomic and biochemical analysis of purified human immunodeficiency virus type 1 produced from infected monocyte-derived macrophages. J. Virol. 2006, 80, 9039–9052. [Google Scholar] [CrossRef] [PubMed]
- Roldan, A.; Warren, O.U.; Russell, R.S.; Liang, C.; Wainberg, M.A. A HIV-1 minimal gag protein is superior to nucleocapsid at in vitro annealing and exhibits multimerization-induced inhibition of reverse transcription. J. Biol. Chem. 2005, 280, 17488–17496. [Google Scholar] [CrossRef]
- Guo, J.; Wu, T.; Anderson, J.; Kane, B.F.; Johnson, D.G.; Gorelick, R.J.; Henderson, L.E.; Levin, J.G. Zinc finger structures in the human immunodeficiency virus type 1 nucleocapsid protein facilitate efficient minus- and plus-strand transfer. J. Virol. 2000, 74, 8980–8988. [Google Scholar] [CrossRef]
- Guo, J.; Wu, T.; Kane, B.F.; Johnson, D.G.; Henderson, L.E.; Gorelick, R.J.; Levin, J.G. Subtle alterations of the native zinc finger structures have dramatic effects on the nucleic acid chaperone activity of human immunodeficiency virus type 1 nucleocapsid protein. J. Virol. 2002, 76, 4370–4378. [Google Scholar] [CrossRef][Green Version]
- Levin, J.G.; Mitra, M.; Mascarenhas, A.; Musier-Forsyth, K. Role of HIV-1 nucleocapsid protein in HIV-1 reverse transcription. RNA Biol. 2010, 7, 754–774. [Google Scholar] [CrossRef]
- Wu, T.; Datta, S.A.; Mitra, M.; Gorelick, R.J.; Rein, A.; Levin, J.G. Fundamental differences between the nucleic acid chaperone activities of HIV-1 nucleocapsid protein and Gag or Gag-derived proteins: Biological implications. Virology 2010, 405, 556–567. [Google Scholar] [CrossRef]
- McCauley, M.J.; Furman, L.; Dietrich, C.A.; Rouzina, I.; Nunez, M.E.; Williams, M.C. Quantifying the stability of oxidatively damaged DNA by single-molecule DNA stretching. Nucleic Acids Res. 2018, 46, 4033–4043. [Google Scholar] [CrossRef] [PubMed]
- Campbell, S.; Rein, A. In vitro assembly properties of human immunodeficiency virus type 1 Gag protein lacking the p6 domain. J. Virol. 1999, 73, 2270–2279. [Google Scholar] [CrossRef] [PubMed]
- Campbell, S.; Vogt, V.M. In vitro assembly of virus-like particles with Rous sarcoma virus Gag deletion mutants: Identification of the p10 domain as a morphological determinant in the formation of spherical particles. J. Virol. 1997, 71, 4425–4435. [Google Scholar] [CrossRef] [PubMed]
- Cruceanu, M.; Urbaneja, M.A.; Hixson, C.V.; Johnson, D.G.; Datta, S.A.; Fivash, M.J.; Stephen, A.G.; Fisher, R.J.; Gorelick, R.J.; Casas-Finet, J.R.; et al. Nucleic acid binding and chaperone properties of HIV-1 Gag and nucleocapsid proteins. Nucleic Acids Res. 2006, 34, 593–605. [Google Scholar] [CrossRef]
- Chaurasiya, K.R.; Paramanathan, T.; McCauley, M.J.; Williams, M.C. Biophysical characterization of DNA binding from single molecule force measurements. Phys. Life Rev. 2010, 7, 299–341. [Google Scholar] [CrossRef]
- Greenleaf, W.J.; Woodside, M.T.; Abbondanzieri, E.A.; Block, S.M. Passive all-optical force clamp for high-resolution laser trapping. Phys. Rev. Lett. 2005, 95, 208102. [Google Scholar] [CrossRef]
- Li, P.T.; Collin, D.; Smith, S.B.; Bustamante, C.; Tinoco, I., Jr. Probing the mechanical folding kinetics of TAR RNA by hopping, force-jump, and force-ramp methods. Biophys. J. 2006, 90, 250–260. [Google Scholar] [CrossRef][Green Version]
- McCauley, M.J.; Williams, M.C. Optical tweezers experiments resolve distinct modes of DNA-protein binding. Biopolymers 2009, 91, 265–282. [Google Scholar] [CrossRef]
- Neuman, K.C.; Nagy, A. Single-molecule force spectroscopy: Optical tweezers, magnetic tweezers and atomic force microscopy. Nat. Methods 2008, 5, 491–505. [Google Scholar] [CrossRef]
- Woodside, M.T.; Block, S.M. Reconstructing folding energy landscapes by single-molecule force spectroscopy. Ann. Rev. Biophys. 2014, 43, 19–39. [Google Scholar] [CrossRef] [PubMed]
- Zuker, M. Mfold web server for nucleic acid folding and hybridization prediction. Nucleic Acids Res. 2003, 31, 3406–3415. [Google Scholar] [CrossRef] [PubMed]
- Markham, N.R.; Zuker, M. UNAFold: Software for nucleic acid folding and hybridization. Methods Mol. Biol. 2008, 453, 3–31. [Google Scholar] [CrossRef]
- Woodside, M.T.; Anthony, P.C.; Behnke-Parks, W.M.; Larizadeh, K.; Herschlag, D.; Block, S.M. Direct measurement of the full, sequence-dependent folding landscape of a nucleic acid. Science 2006, 314, 1001–1004. [Google Scholar] [CrossRef] [PubMed]
- Woodside, M.T.; Behnke-Parks, W.M.; Larizadeh, K.; Travers, K.; Herschlag, D.; Block, S.M. Nanomechanical measurements of the sequence-dependent folding landscapes of single nucleic acid hairpins. Proc. Natl. Acad. Sci. USA 2006, 103, 6190–6195. [Google Scholar] [CrossRef]
- Godet, J.; Kenfack, C.; Przybilla, F.; Richert, L.; Duportail, G.; Mely, Y. Site-selective probing of cTAR destabilization highlights the necessary plasticity of the HIV-1 nucleocapsid protein to chaperone the first strand transfer. Nucleic Acids Res. 2013, 41, 5036–5048. [Google Scholar] [CrossRef]
- Grohman, J.K.; Gorelick, R.J.; Lickwar, C.R.; Lieb, J.D.; Bower, B.D.; Znosko, B.M.; Weeks, K.M. A guanosine-centric mechanism for RNA chaperone function. Science 2013, 340, 190–195. [Google Scholar] [CrossRef]
- Wang, W.; Naiyer, N.; Mitra, M.; Li, J.; Williams, M.C.; Rouzina, I.; Gorelick, R.J.; Wu, Z.; Musier-Forsyth, K. Distinct nucleic acid interaction properties of HIV-1 nucleocapsid protein precursor NCp15 explain reduced viral infectivity. Nucleic Acids Res. 2014, 42, 7145–7159. [Google Scholar] [CrossRef]
- Wu, T.; Gorelick, R.J.; Levin, J.G. Selection of fully processed HIV-1 nucleocapsid protein is required for optimal nucleic acid chaperone activity in reverse transcription. Virus Res. 2014, 193, 52–64. [Google Scholar] [CrossRef] [PubMed]
- Cen, S.; Khorchid, A.; Gabor, J.; Rong, L.; Wainberg, M.A.; Kleiman, L. Roles of Pr55(gag) and NCp7 in tRNA(3)(Lys) genomic placement and the initiation step of reverse transcription in human immunodeficiency virus type 1. J. Virol. 2000, 74, 10796–10800. [Google Scholar] [CrossRef]
- Guo, F.; Saadatmand, J.; Niu, M.; Kleiman, L. Roles of Gag and NCp7 in facilitating tRNA(Lys)(3) Annealing to viral RNA in human immunodeficiency virus type 1. J. Virol. 2009, 83, 8099–8107. [Google Scholar] [CrossRef] [PubMed]
- Jones, C.P.; Datta, S.A.; Rein, A.; Rouzina, I.; Musier-Forsyth, K. Matrix domain modulates HIV-1 Gag’s nucleic acid chaperone activity via inositol phosphate binding. J. Virol. 2011, 85, 1594–1603. [Google Scholar] [CrossRef] [PubMed]
- Comas-Garcia, M.; Kroupa, T.; Datta, S.A.; Harvin, D.P.; Hu, W.S.; Rein, A. Efficient support of virus-like particle assembly by the HIV-1 packaging signal. Elife 2018, 7, e38438. [Google Scholar] [CrossRef] [PubMed]
- Webb, J.A.; Jones, C.P.; Parent, L.J.; Rouzina, I.; Musier-Forsyth, K. Distinct binding interactions of HIV-1 Gag to Psi and non-Psi RNAs: Implications for viral genomic RNA packaging. RNA 2013, 19, 1078–1088. [Google Scholar] [CrossRef] [PubMed]
- Williams, M.C.; Rouzina, I.; Wenner, J.R.; Gorelick, R.J.; Musier-Forsyth, K.; Bloomfield, V.A. Mechanism for nucleic acid chaperone activity of HIV-1 nucleocapsid protein revealed by single molecule stretching. Proc. Natl. Acad. Sci. USA 2001, 98, 6121–6126. [Google Scholar] [CrossRef] [PubMed]
- Mekdad, H.E.; Boutant, E.; Karnib, H.; Biedma, M.E.; Sharma, K.K.; Malytska, I.; Laumond, G.; Roy, M.; Real, E.; Paillart, J.C.; et al. Characterization of the interaction between the HIV-1 Gag structural polyprotein and the cellular ribosomal protein L7 and its implication in viral nucleic acid remodeling. Retrovirology 2016, 13, 54. [Google Scholar] [CrossRef]
- Munro, J.B.; Nath, A.; Farber, M.; Datta, S.A.; Rein, A.; Rhoades, E.; Mothes, W. A conformational transition observed in single HIV-1 Gag molecules during in vitro assembly of virus-like particles. J. Virol. 2014, 88, 3577–3585. [Google Scholar] [CrossRef]
- Dick, R.A.; Zadrozny, K.K.; Xu, C.; Schur, F.K.M.; Lyddon, T.D.; Ricana, C.L.; Wagner, J.M.; Perilla, J.R.; Ganser-Pornillos, B.K.; Johnson, M.C.; et al. Inositol phosphates are assembly co-factors for HIV-1. Nature 2018, 560, 509–512. [Google Scholar] [CrossRef]
- Todd, G.C.; Duchon, A.; Inlora, J.; Olson, E.D.; Musier-Forsyth, K.; Ono, A. Inhibition of HIV-1 Gag-membrane interactions by specific RNAs. RNA 2017, 23, 395–405. [Google Scholar] [CrossRef]
- Kenyon, J.C.; Prestwood, L.J.; Lever, A.M. A novel combined RNA-protein interaction analysis distinguishes HIV-1 Gag protein binding sites from structural change in the viral RNA leader. Sci. Rep. 2015, 5, 14369. [Google Scholar] [CrossRef]
- Smyth, R.P.; Despons, L.; Huili, G.; Bernacchi, S.; Hijnen, M.; Mak, J.; Jossinet, F.; Weixi, L.; Paillart, J.C.; von Kleist, M.; et al. Mutational interference mapping experiment (MIME) for studying RNA structure and function. Nat. Methods 2015, 12, 866–872. [Google Scholar] [CrossRef] [PubMed]
- Wilkinson, K.A.; Gorelick, R.J.; Vasa, S.M.; Guex, N.; Rein, A.; Mathews, D.H.; Giddings, M.C.; Weeks, K.M. High-throughput SHAPE analysis reveals structures in HIV-1 genomic RNA strongly conserved across distinct biological states. PLoS Biol. 2008, 6, e96. [Google Scholar] [CrossRef] [PubMed]
- Bouchiat, C.; Wang, M.D.; Allemand, J.F.; Strick, T.; Block, S.M.; Croquette, V. Estimating the persistence length of a Worm-Like Chain molecule from Force-Extension measurements. Biophys. J. 1999, 76, 409–413. [Google Scholar] [CrossRef]
- Odijk, T. Stiff chains and filaments under tension. Macromolecules 1995, 28, 7016–7018. [Google Scholar] [CrossRef]
- Smith, S.B.; Cui, Y.; Bustamante, C. Overstretching B-DNA: The elastic response of individual double-stranded and single-stranded DNA molecules. Science 1996, 271, 795–799. [Google Scholar] [CrossRef] [PubMed]
- Seol, Y.; Li, J.; Nelson, P.C.; Perkins, T.T.; Betterton, M.D. Elasticity of short DNA molecules: Theory and experiment for contour lengths of 0.6–7 microns. Biophys. J. 2007, 93, 4360–4373. [Google Scholar] [CrossRef] [PubMed]
- Wenner, J.R.; Williams, M.C.; Rouzina, I.; Bloomfield, V.A. Salt dependence of the elasticity and overstretching transition of single DNA molecules. Biophys. J. 2002, 82, 3160–3169. [Google Scholar] [CrossRef]
- Baumann, C.G.; Smith, S.B.; Bloomfield, V.A.; Bustamante, C. Ionic effects on the elasticity of single DNA molecules. Proc. Natl. Acad. Sci. USA 1997, 94, 6185–6190. [Google Scholar] [CrossRef]
- Smith, S.; Finzi, L.; Bustamante, C. Direct mechanical measurements of the elasticity of single DNA molecules by using magnetic beads. Science 1992, 258, 1122–1126. [Google Scholar] [CrossRef]
- McCauley, M.J.; Rouzina, I.; Williams, M.C. Specific Nucleic Acid Chaperone Activity of HIV-1 Nucleocapsid Protein Deduced from Hairpin Unfolding. Methods Mol. Biol. 2020, 2106, 59–88. [Google Scholar] [CrossRef]
- Crooks, G.E. Entropy production fluctuation theorem and the nonequilibrium work relation for free energy differences. Phys. Rev. E 1999, 60, 2721–2726. [Google Scholar] [CrossRef] [PubMed]
- Crooks, G.E. Path-ensemble averages in systems driven far from equilibrium. Phys. Rev. E 2000, 61, 2361–2366. [Google Scholar] [CrossRef]
- Bennett, C.H. Efficient estimation of free energy differences from Monte Carlo data. J. Comput. Phys. 1976, 22, 245–268. [Google Scholar] [CrossRef]
- Jarzynski, C. Nonequilibrium Equality for Free Energy Differences. Phys. Rev. Lett. 1997, 78, 2690–2693. [Google Scholar] [CrossRef]
- Dudko, O.K.; Filippov, A.E.; Klafter, J.; Urbakh, M. Beyond the conventional description of dynamic force spectroscopy of adhesion bonds. Proc. Natl. Acad. Sci. USA 2003, 100, 11378–11381. [Google Scholar] [CrossRef] [PubMed]
- Dudko, O.K.; Hummer, G.; Szabo, A. Intrinsic rates and activation free energies from single-molecule pulling experiments. Phys. Rev. Lett. 2006, 96, 108101. [Google Scholar] [CrossRef]
- Dudko, O.K.; Hummer, G.; Szabo, A. Theory, analysis, and interpretation of single-molecule force spectroscopy experiments. Proc. Natl. Acad. Sci. USA 2008, 105, 15755–15760. [Google Scholar] [CrossRef]
- Pierse, C.A.; Dudko, O.K. Distinguishing Signatures of Multipathway Conformational Transitions. Phys. Rev. Lett. 2017, 118, 088101. [Google Scholar] [CrossRef]
- McCauley, M.J.; Rouzina, I.; Williams, M.C. Constructing Free Energy Landscapes of Nucleic Acid Hairpin Unfolding. Methods Mol. Biol. 2018, 1811, 315–332. [Google Scholar] [CrossRef]

| Experiment | Δxop | ΔGop | F½ | |||
|---|---|---|---|---|---|---|
| (bases) | (kBT) | (pN) | (nm) | (kBT) | (s−1) | |
| TAR (OT) | 48.2 ± 0.6 | 42.1 ± 1.5 | 10.6 ± 0.2 | 10.9 ± 0.7 | 28.0 ± 1.4 | (0.7 ± 0.4) × 10−8 |
| TAR (mfold) | 48 ± 1 | 41.5 ± 1.5 | 10.1 ± 0.1 | 11.3 ± 0.9 | 30.7 ± 2.0 | - |
| TAR + Gag∆p6 (OT) | 47.5 ± 0.7 | 28.9 ± 1.5 | 7.7 ± 0.2 | 9.2 ± 0.7 | 18.1 ± 0.9 | (10 ± 6) × 10−8 |
| TAR + Gag∆p6 (mfold) | 48 ± 1 | 26.0 ± 1.5 | 8.0 ± 0.2 | 8.6 ± 1.0 | 20.1 ± 1.5 | |
| TAR + NCp7 (OT) | 48.4 ± 0.5 | 28.3 ± 0.9 | 7.7 ± 0.2 | 4.8 ± 0.6 | 14.3 ± 1.3 | (1.2 ± 0.8) × 10−4 |
| TAR + NCp7 (mfold) | 48 ± 1 | 25.6 ± 1.5 | 7.9 ± 0.1 | 4.7 ± 0.9 | 14.8 ± 1.2 | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
McCauley, M.J.; Rouzina, I.; Li, J.; Núñez, M.E.; Williams, M.C. Significant Differences in RNA Structure Destabilization by HIV-1 Gag∆p6 and NCp7 Proteins. Viruses 2020, 12, 484. https://doi.org/10.3390/v12050484
McCauley MJ, Rouzina I, Li J, Núñez ME, Williams MC. Significant Differences in RNA Structure Destabilization by HIV-1 Gag∆p6 and NCp7 Proteins. Viruses. 2020; 12(5):484. https://doi.org/10.3390/v12050484
Chicago/Turabian StyleMcCauley, Micah J., Ioulia Rouzina, Jasmine Li, Megan E. Núñez, and Mark C. Williams. 2020. "Significant Differences in RNA Structure Destabilization by HIV-1 Gag∆p6 and NCp7 Proteins" Viruses 12, no. 5: 484. https://doi.org/10.3390/v12050484
APA StyleMcCauley, M. J., Rouzina, I., Li, J., Núñez, M. E., & Williams, M. C. (2020). Significant Differences in RNA Structure Destabilization by HIV-1 Gag∆p6 and NCp7 Proteins. Viruses, 12(5), 484. https://doi.org/10.3390/v12050484