Simulations of Phage T7 Capsid Expansion Reveal the Role of Molecular Sterics on Dynamics
Abstract
1. Introduction
2. Materials and Methods
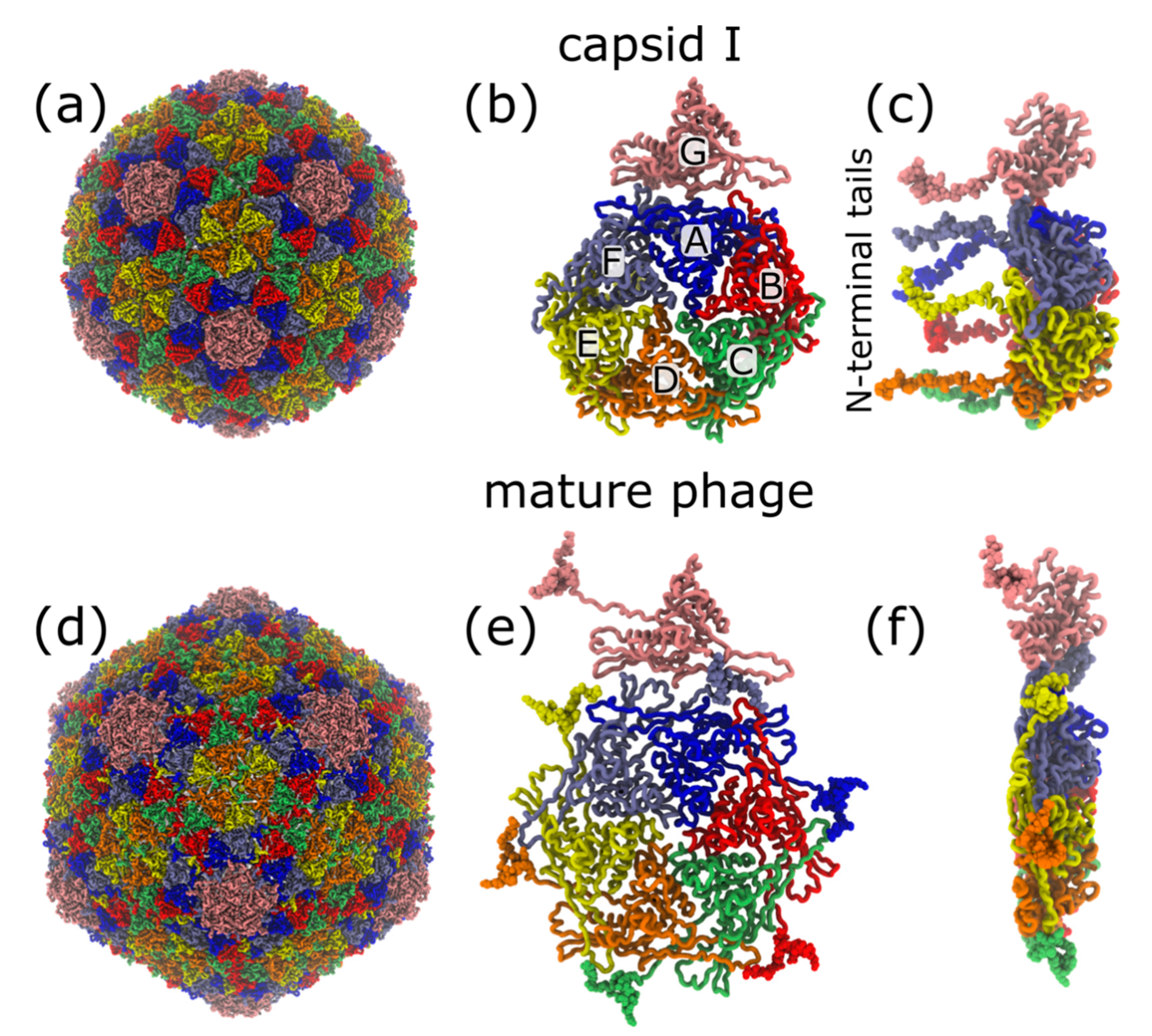
2.1. Structure of Phage T7 and its Capsid I and Capsid II
2.2. Force Field Description
2.3. Simulation Details
3. Results
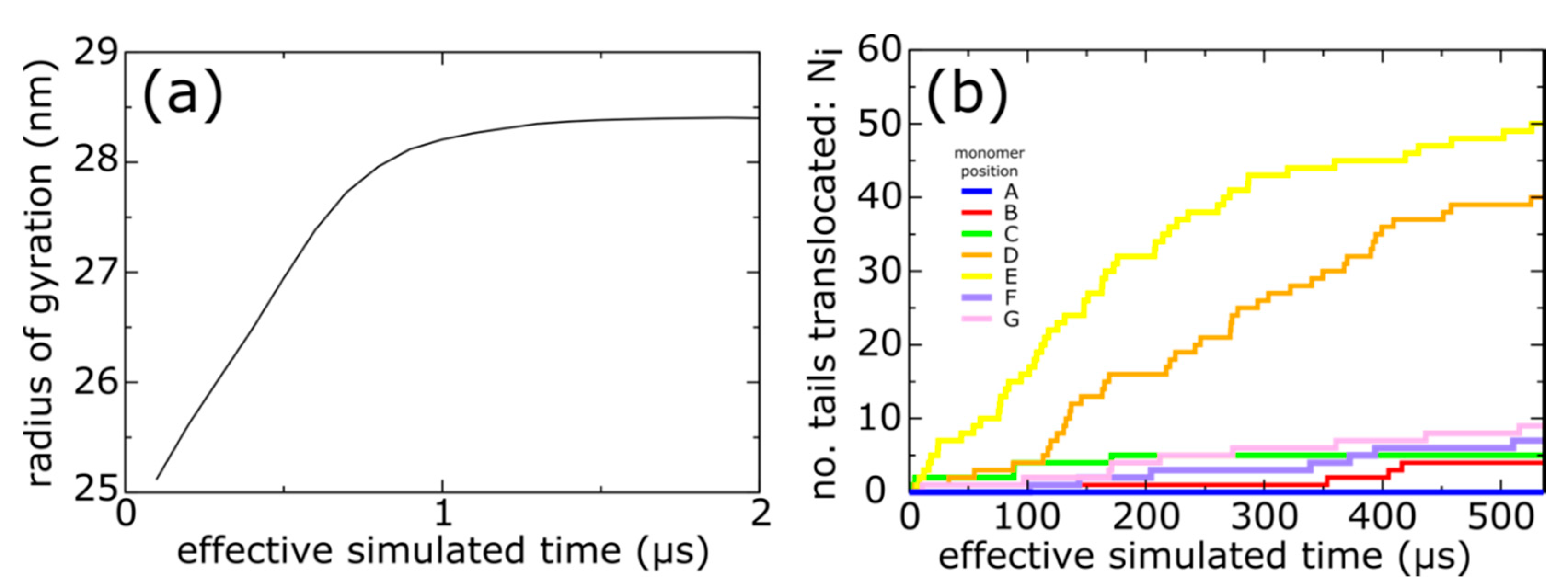
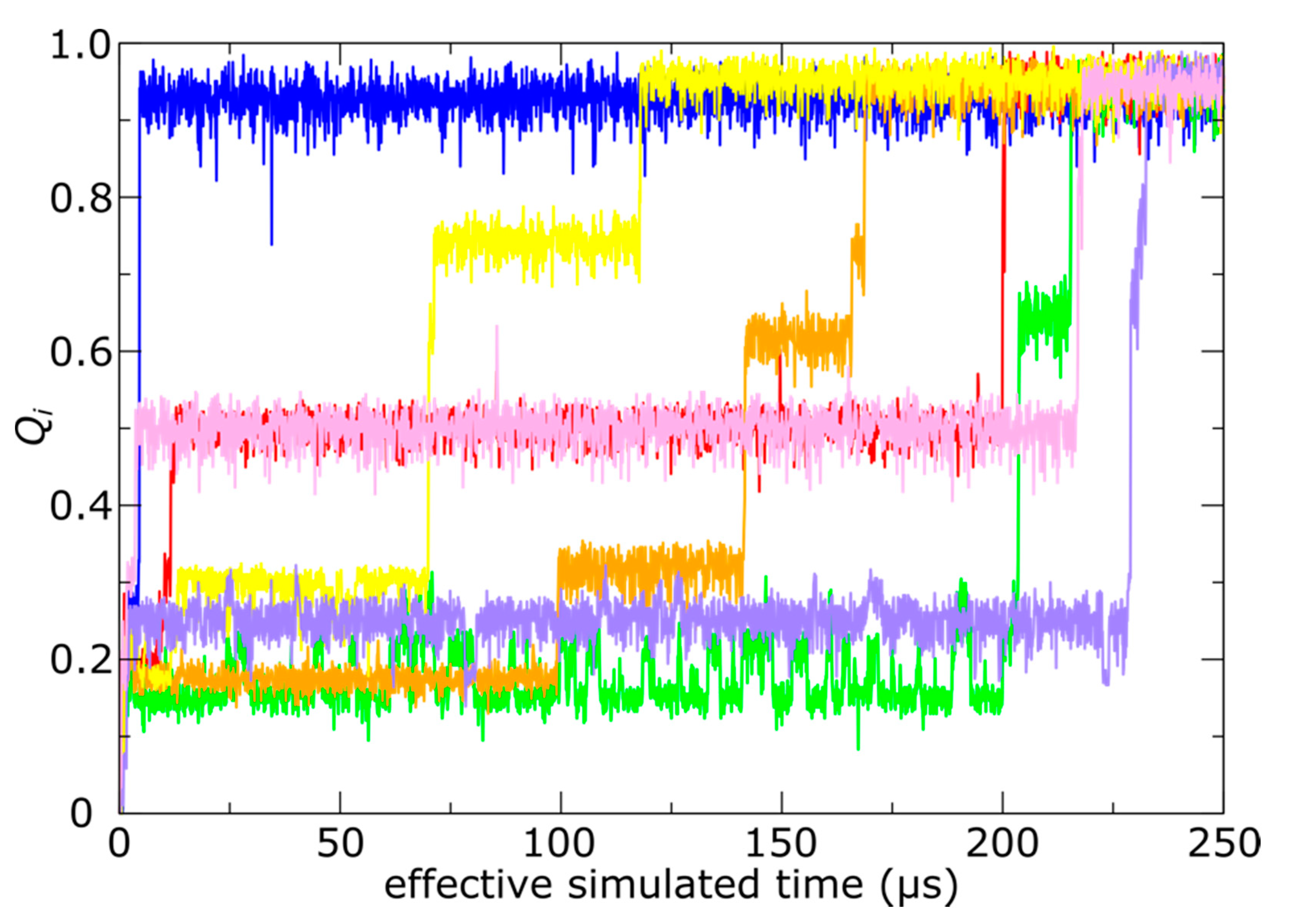
3.1. Molecular Dynamics Simulation of Spontaneous Capsid Expansion
3.2. Simulations Implicate Hierarchical Timescales for Trans-Shell Displacements
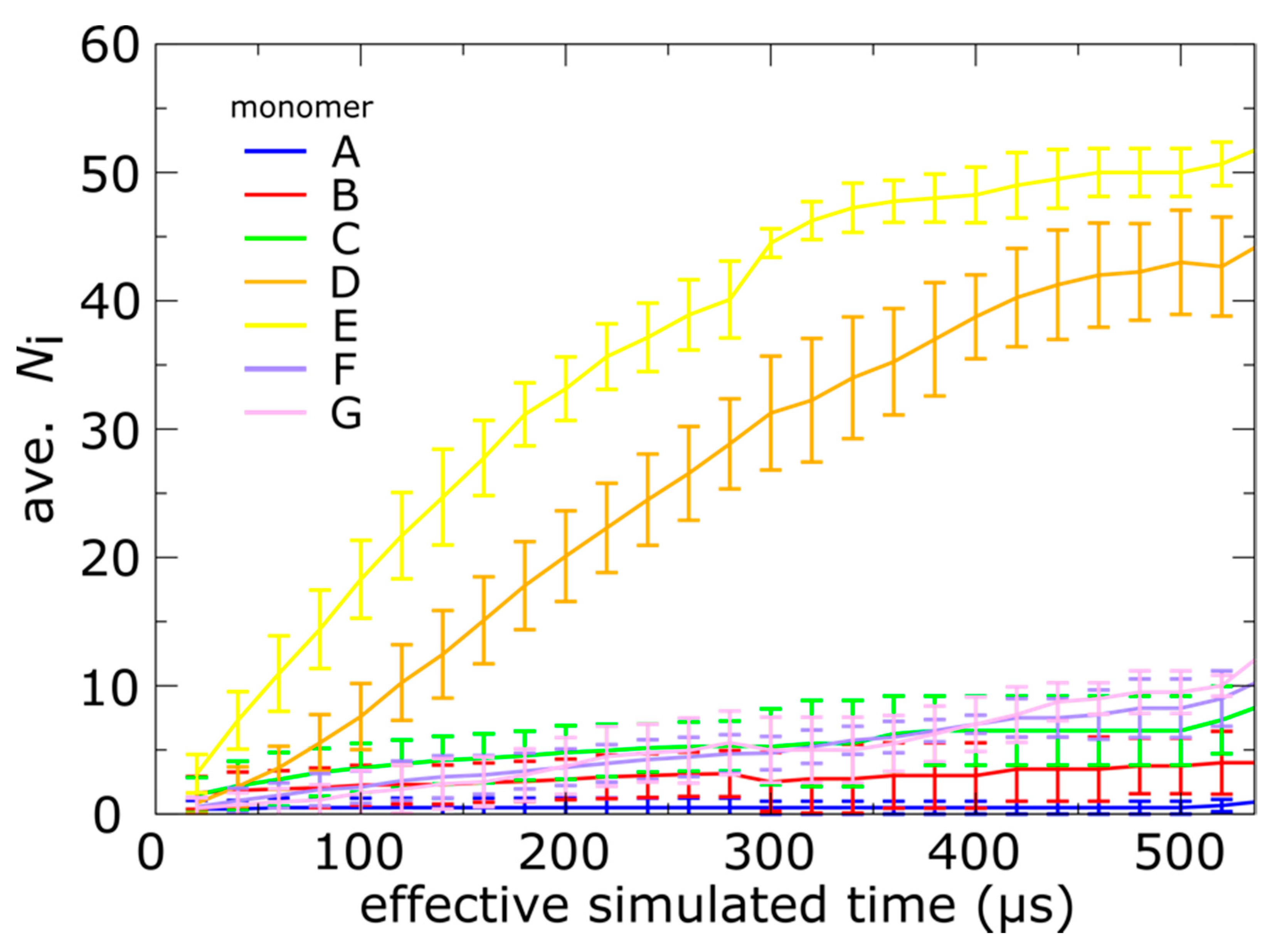
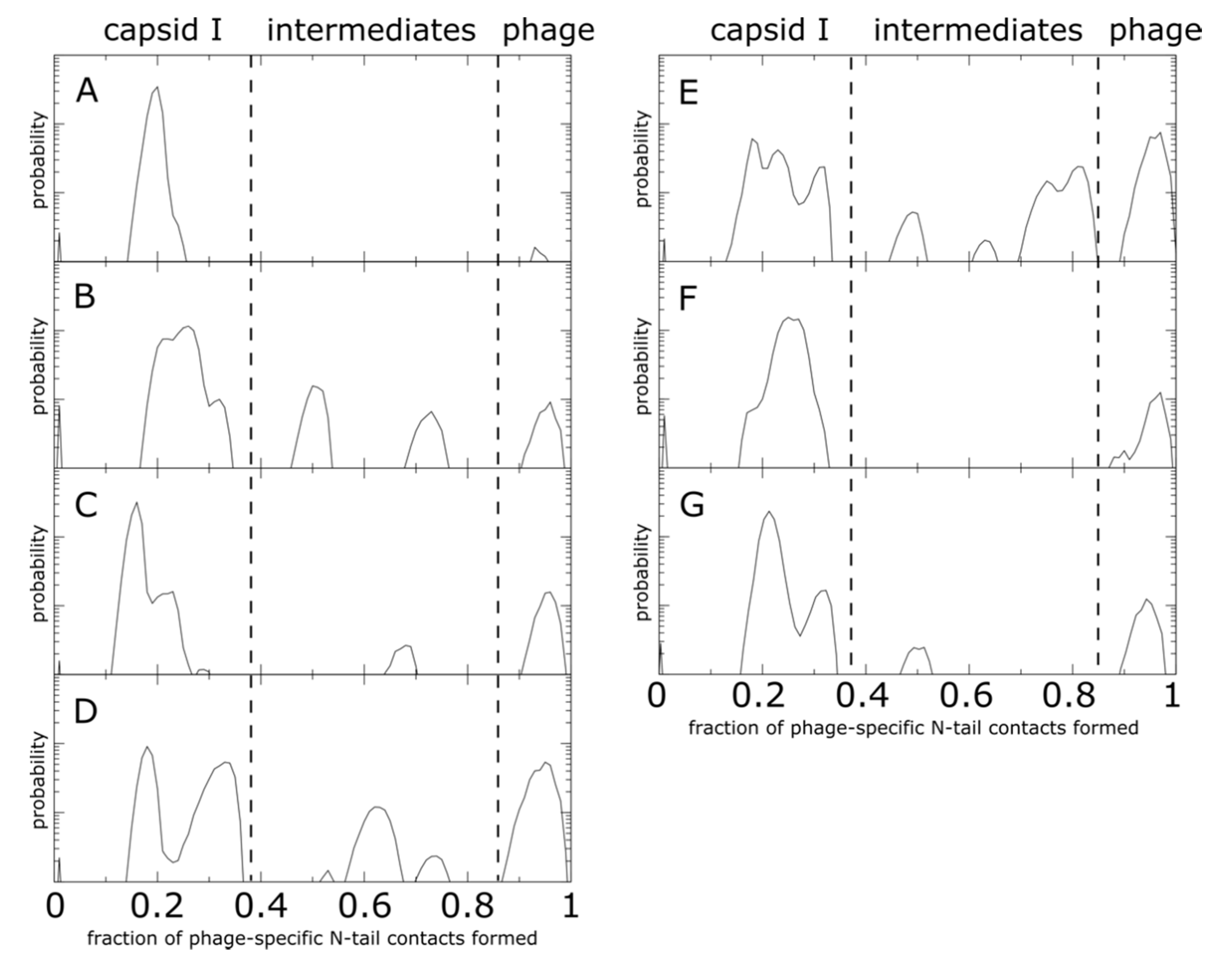
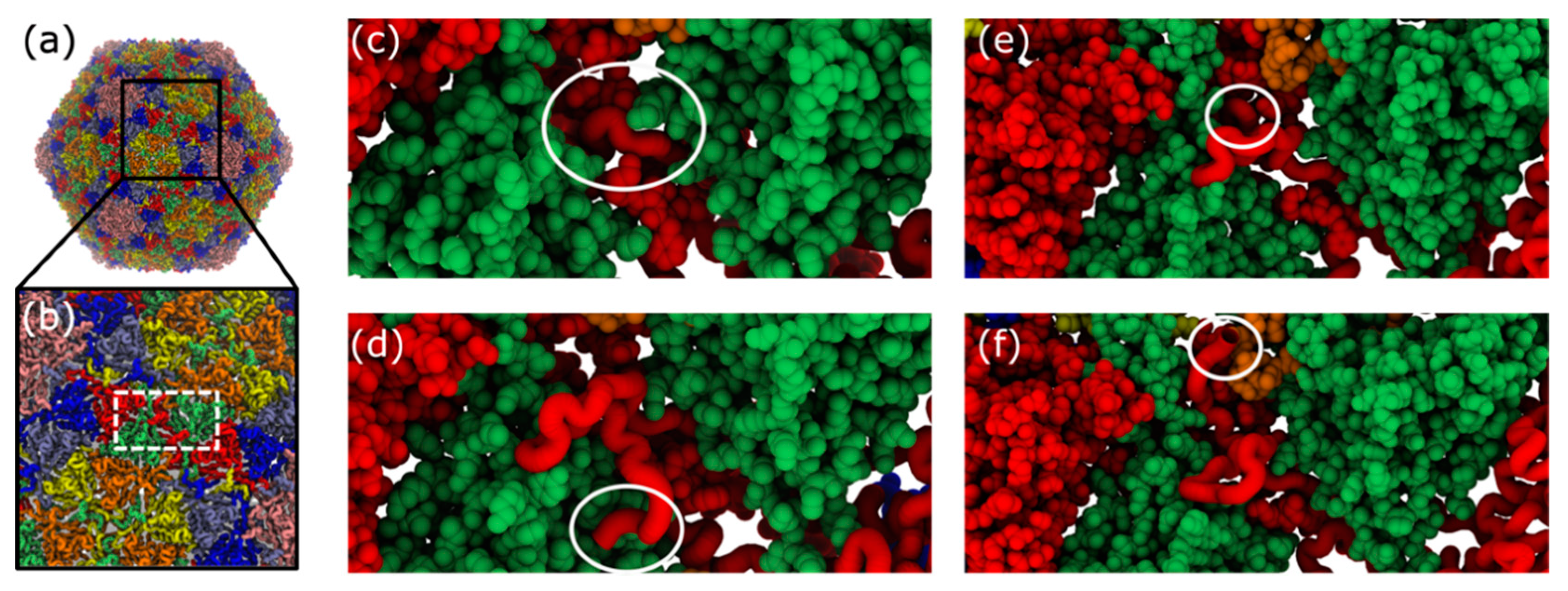
3.3. Capsid Shell Sterics Lead to Multiple Intermediates during N-tail Translocation
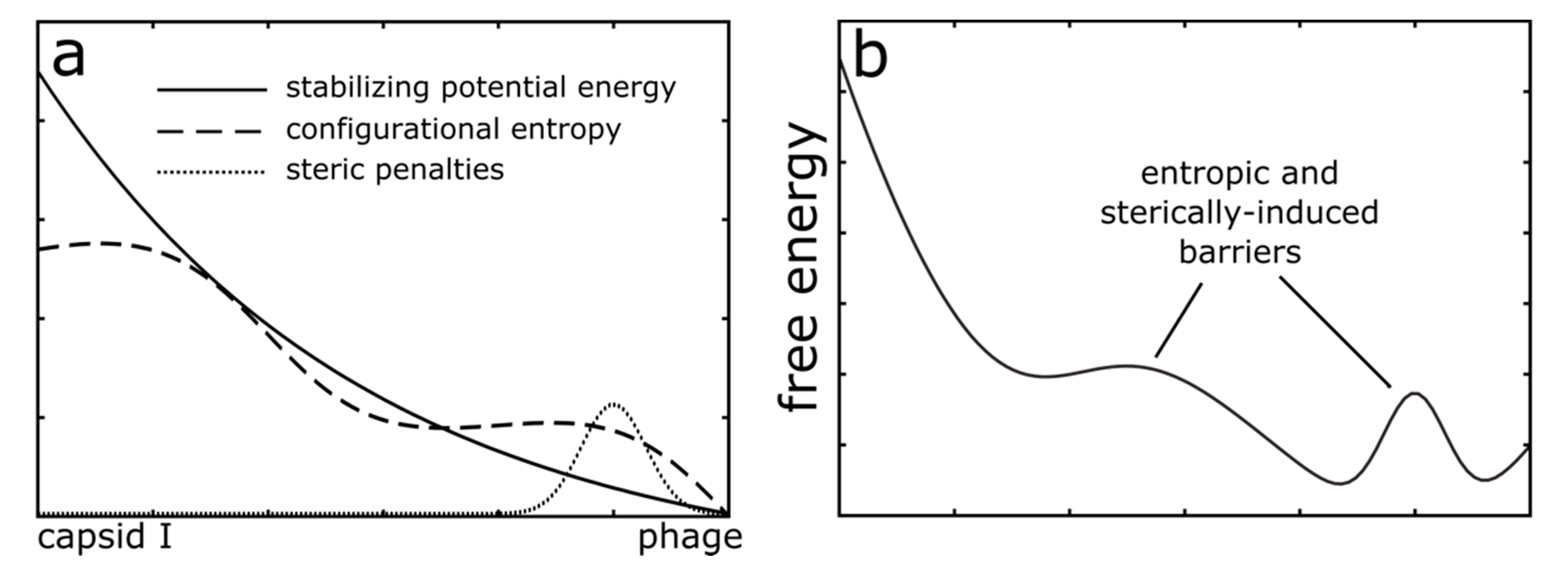
4. Discussion
4.1. Non-Uniformity of Subunit Structure during Expansion
4.2. Interplay of N-Terminal Tails at Different Positions
4.3. The Future of Modeling Capsid Dynamics
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Whitford, P.C.; Onuchic, J.N.; Wolynes, P.G. Energy landscape along an enzymatic reaction trajectory: Hinges or cracks? HFSP J. 2008, 2, 61–64. [Google Scholar] [CrossRef] [PubMed]
- Howard, J. Motor Proteins as Nanomachines: The Roles of Thermal Fluctuations in Generating Force and Motion. In Biological Physics; Seminaire Poincare XII; Birkhauser Basel: Basel, Switzerland, 2011; pp. 33–44. [Google Scholar]
- Milescu, L.S.; Yildiz, A.; Selvin, P.R.; Sachs, F. Maximum likelihood estimation of molecular motor kinetics from staircase dwell-time sequences. Biophys. J. 2006, 91, 1156–1168. [Google Scholar] [CrossRef] [PubMed]
- Weber, G. Energetics of ligand binding to proteins. Adv. Protein Chem. 1975, 29, 1–83. [Google Scholar] [PubMed]
- Rossmann, M.G. Structure of viruses: A short history. Q. Rev. Biophys. 2013, 46, 133–180. [Google Scholar] [CrossRef] [PubMed]
- Harrison, S.C. Protein tentacles. J. Struct. Biol. 2017, 200, 244–247. [Google Scholar] [CrossRef] [PubMed]
- Twarock, R.; Luque, A. Structural puzzles in virology solved with an overarching icosahedral design principle. Nat. Commun. 2019, 10, 4414. [Google Scholar] [CrossRef]
- Liu, Y.; Hill, M.G.; Klose, T.; Chen, Z.; Watters, K.; Bochkov, Y.A.; Jiang, W.; Palmenberg, A.C.; Rossmann, M.G. Atomic structure of a rhinovirus C, a virus species linked to severe childhood asthma. Proc. Natl. Acad. Sci. USA 2016, 113, 8997–9002. [Google Scholar] [CrossRef]
- Sirohi, D.; Chen, Z.; Sun, L.; Klose, T.; Pierson, T.C.; Rossmann, M.G.; Kuhn, R.J. The 3.8 A resolution cryo-EM structure of Zika virus. Science 2016, 352, 467–470. [Google Scholar] [CrossRef]
- Rossmann, M.G. My happy years of collaboration with Fumio Arisaka. Biophys. Rev. 2018, 10, 139–140. [Google Scholar] [CrossRef]
- Delbrück, M.A. A physicist looks at biology. In Phage and the Origins of Molecular Biology; Cairns, J., Stent, G.S., Watson, J.D., Eds.; Cold Spring Laboratory of Quantitative Biology: Cold Spring Harbor, NY, USA, 1966; pp. 9–22. [Google Scholar]
- Levinthal, C. Mossbauer Spectroscopy in Biological Systems. Proceedings 1969, 67, 22–24. [Google Scholar]
- Bryngelson, J.D.; Wolynes, P.G. A Simple Statistical Field-Theory of Heteropolymer Collapse with Application to Protein Folding. Biopolymers 1990, 30, 177–188. [Google Scholar] [CrossRef]
- Bryngelson, J.D.; Wolynes, P.G. Intermediates and Barrier Crossing in A Random Energy-Model (with Applications to Protein Folding). J. Phys. Chem. 1989, 93, 6902–6915. [Google Scholar] [CrossRef]
- Bryngelson, J.D.; Onuchic, J.N.; Socci, N.D.; Wolynes, P.G. Funnels, pathways, and the energy landscape of protein folding: A synthesis. Proteins 1995, 21, 167–195. [Google Scholar] [CrossRef]
- Linke, H.; Hocker, B.; Furuta, K.; Forde, N.R.; Curmi, P.M.G. Synthetic biology approaches to dissecting linear motor protein function: Towards the design and synthesis of artificial autonomous protein walkers. Biophys. Rev. 2020, 12, 1041–1054. [Google Scholar] [CrossRef]
- Hwang, W.; Karplus, M. Structural basis for power stroke vs. Brownian ratchet mechanisms of motor proteins. Proc. Natl. Acad. Sci. USA 2019, 116, 19777–19785. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Wolynes, P.G. Topology, structures, and energy landscapes of human chromosomes. Proc. Natl. Acad. Sci. USA 2015, 112, 6062–6067. [Google Scholar] [CrossRef]
- Di Pierro, M.; Zhang, B.; Aiden, E.L.; Wolynes, P.G.; Onuchic, J.N. Transferable model for chromosome architecture. Proc. Natl. Acad. Sci. USA 2016, 113, 12168–12173. [Google Scholar] [CrossRef]
- Lin, Y.H.; Forman-Kay, J.D.; Chan, H.S. Sequence-Specific Polyampholyte Phase Separation in Membraneless Organelles. Phys. Rev. Lett. 2016, 117, 178101. [Google Scholar] [CrossRef]
- Fujisawa, H.; Morita, M. Phage DNA packaging. Genes Cells 1997, 2, 537–545. [Google Scholar] [CrossRef]
- Serwer, P.; Jiang, W. Dualities in the analysis of phage DNA packaging motors. Bacteriophage 2012, 2, 239–255. [Google Scholar] [CrossRef][Green Version]
- Guo, F.; Liu, Z.; Fang, P.A.; Zhang, Q.; Wright, E.T.; Wu, W.; Zhang, C.; Vago, F.; Ren, Y.; Jakana, J.; et al. Capsid expansion mechanism of bacteriophage T7 revealed by multistate atomic models derived from cryo-EM reconstructions. Proc. Natl. Acad. Sci. USA 2014, 111, E4606–E4614. [Google Scholar] [CrossRef] [PubMed]
- Guo, F.; Liu, Z.; Vago, F.; Ren, Y.; Wu, W.; Wright, E.T.; Serwer, P.; Jiang, W. Visualization of uncorrelated, tandem symmetry mismatches in the internal genome packaging apparatus of bacteriophage T7. Proc. Natl. Acad. Sci. USA 2013, 110, 6811–6816. [Google Scholar] [CrossRef]
- Pajunen, M.I.; Elizondo, M.R.; Skurnik, M.; Kieleczawa, J.; Molineux, I.J. Complete Nucleotide Sequence and Likely Recombinatorial Origin of Bacteriophage T3. J. Mol. Biol. 2002, 319, 1115–1132. [Google Scholar] [CrossRef]
- Studier, F.W.; Dunn, J.J. Organization and expression of bacteriophage T7 DNA. Cold Spring Harb. Symp. Quant. Biol. 1983, 47, 999–1007. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Gr. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Whitford, P.C.; Noel, J.K.; Gosavi, S.; Schug, A.; Sanbonmatsu, K.Y.; Onuchic, J.N. An all-atom structure-based potential for proteins: Bridging minimal models with all-atom empirical forcefields. Proteins 2009, 75, 430–441. [Google Scholar] [CrossRef]
- Levi, M.; Noel, J.K.; Whitford, P.C. Studying ribosome dynamics with simplified models. Methods 2019, 162, 128–140. [Google Scholar] [CrossRef]
- Noel, J.K.; Levi, M.; Raghunathan, M.; Lammert, H.; Hayes, R.L.; Onuchic, J.N.; Whitford, P.C. SMOG 2: A Versatile Software Package for Generating Structure-Based Models. PLoS Comput. Biol. 2016, 12, e1004794. [Google Scholar] [CrossRef]
- May, E.R.; Feng, J.; Brooks, C.L., 3rd. Exploring the symmetry and mechanism of virus capsid maturation via an ensemble of pathways. Biophys. J. 2012, 102, 606–612. [Google Scholar] [CrossRef][Green Version]
- Noel, J.K.; Whitford, P.C.; Onuchic, J.N. The shadow map: A general contact definition for capturing the dynamics of biomolecular folding and function. J. Phys. Chem. B 2012, 116, 8692–8702. [Google Scholar] [CrossRef]
- Nguyen, K.; Whitford, P.C. Steric interactions lead to collective tilting motion in the ribosome during mRNA-tRNA translocation. Nat. Commun. 2016, 7, 10586. [Google Scholar] [CrossRef]
- Duan, Y.; Wu, C.; Chowdhury, S.; Lee, M.C.; Xiong, G.; Zhang, W.; Yang, R.; Cieplak, P.; Luo, R.; Lee, T.; et al. A point-charge force field for molecular mechanics simulations of proteins based on condensed-phase quantum mechanical calculations. J. Comput. Chem. 2003, 24, 1999–2012. [Google Scholar] [CrossRef]
- Hess, B.; Kutzner, C.; van der Spoel, D.; Lindahl, E. GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. J. Chem. Theory Comput. 2008, 4, 435–447. [Google Scholar] [CrossRef]
- Lindahl, E.; Hess, B.; van der Spoel, D. GROMACS 3.0: A package for molecular simulation and trajectory analysis. Mol. Model. Ann. 2001, 7, 306–317. [Google Scholar] [CrossRef]
- Jackson, J.; Nguyen, K.; Whitford, P.C. Exploring the balance between folding and functional dynamics in proteins and RNA. Int. J. Mol. Sci. 2015, 16, 6868–6889. [Google Scholar] [CrossRef]
- Yang, H.; Bandarkar, P.; Horne, R.; Leite, V.B.P.; Chahine, J.; Whitford, P.C. Diffusion of tRNA inside the ribosome is position-dependent. J. Chem. Phys. 2019, 151, 085102. [Google Scholar] [CrossRef]
- Di Pierro, M.; Potoyan, D.A.; Wolynes, P.G.; Onuchic, J.N. Anomalous diffusion, spatial coherence, and viscoelasticity from the energy landscape of human chromosomes. Proc. Natl. Acad. Sci. USA 2018, 115, 7753–7758. [Google Scholar] [CrossRef]
- Hyeon, C.; Thirumalai, D. Capturing the essence of folding and functions of biomolecules using coarse-grained models. Nat. Commun. 2011, 2, 487. [Google Scholar] [CrossRef] [PubMed]
- Chan, H.S.; Zhang, Z.; Wallin, S.; Liu, Z. Cooperativity, local-nonlocal coupling, and nonnative interactions: Principles of protein folding from coarse-grained models. Annu. Rev. Phys. Chem. 2011, 62, 301–326. [Google Scholar] [CrossRef]
- Cho, S.S.; Levy, Y.; Wolynes, P.G. P versus Q: Structural reaction coordinates capture protein folding on smooth landscapes. Proc. Natl. Acad. Sci. USA 2006, 103, 586–591. [Google Scholar] [CrossRef] [PubMed]
- Frauenfelder, H.; Sligar, S.G.; Wolynes, P.G. The energy landscapes and motions of proteins. Science 1991, 254, 1598–1603. [Google Scholar] [CrossRef] [PubMed]
- Sulkowska, J.I. On folding of entangled proteins: Knots, lassos, links and theta-curves. Curr. Opin. Struct. Biol. 2020, 60, 131–141. [Google Scholar] [CrossRef]
- Gosavi, S.; Chavez, L.L.; Jennings, P.A.; Onuchic, J.N. Topological frustration and the folding of interleukin-1 beta. J. Mol. Biol. 2006, 357, 986–996. [Google Scholar] [CrossRef]
- Serwer, P. Proposed ancestors of phage nucleic acid packaging motors (and cells). Viruses 2011, 3, 1249–1280. [Google Scholar] [CrossRef]
- Whitford, P.C.; Miyashita, O.; Levy, Y.; Onuchic, J.N. Conformational transitions of adenylate kinase: Switching by cracking. J. Mol. Biol. 2007, 366, 1661–1671. [Google Scholar] [CrossRef]
- Hyeon, C.; Onuchic, J.N. Mechanical control of the directional stepping dynamics of the kinesin motor. Proc. Natl. Acad. Sci. USA 2007, 104, 17382–17387. [Google Scholar] [CrossRef]
- Givaty, O.; Levy, Y. Protein Sliding along DNA: Dynamics and Structural Characterization. J. Mol. Biol. 2009, 385, 1087–1097. [Google Scholar] [CrossRef]

| Monomer | Number of Events |
|---|---|
| A | 10 |
| B | 70 |
| C | 112 |
| D | 658 |
| E | 845 |
| F | 117 |
| G | 144 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Whitford, P.C.; Jiang, W.; Serwer, P. Simulations of Phage T7 Capsid Expansion Reveal the Role of Molecular Sterics on Dynamics. Viruses 2020, 12, 1273. https://doi.org/10.3390/v12111273
Whitford PC, Jiang W, Serwer P. Simulations of Phage T7 Capsid Expansion Reveal the Role of Molecular Sterics on Dynamics. Viruses. 2020; 12(11):1273. https://doi.org/10.3390/v12111273
Chicago/Turabian StyleWhitford, Paul C., Wen Jiang, and Philip Serwer. 2020. "Simulations of Phage T7 Capsid Expansion Reveal the Role of Molecular Sterics on Dynamics" Viruses 12, no. 11: 1273. https://doi.org/10.3390/v12111273
APA StyleWhitford, P. C., Jiang, W., & Serwer, P. (2020). Simulations of Phage T7 Capsid Expansion Reveal the Role of Molecular Sterics on Dynamics. Viruses, 12(11), 1273. https://doi.org/10.3390/v12111273







