Author Contributions
Conceptualization, S.D., Y.W.,W.H., and J.Z.; methodology, Y.W., W.H., and J.Z.; software, S.D. and W.H.; validation, J.Z.; formal analysis, S.D. and W.H.; investigation, S.D., and W.H.; resources, J.Z.; data curation, F.Q. and Y.W.; writing—original draft preparation, Y.W. and X.Y.; writing—review and editing, Y.W., J.Z., and S.S., and X.Y.; visualization, Y.W., S.S., and F.Q.; supervision, F.Q.; project administration, J.Z.; funding acquisition, Y.W. and S.S. All authors have read and agreed to the published version of the manuscript.
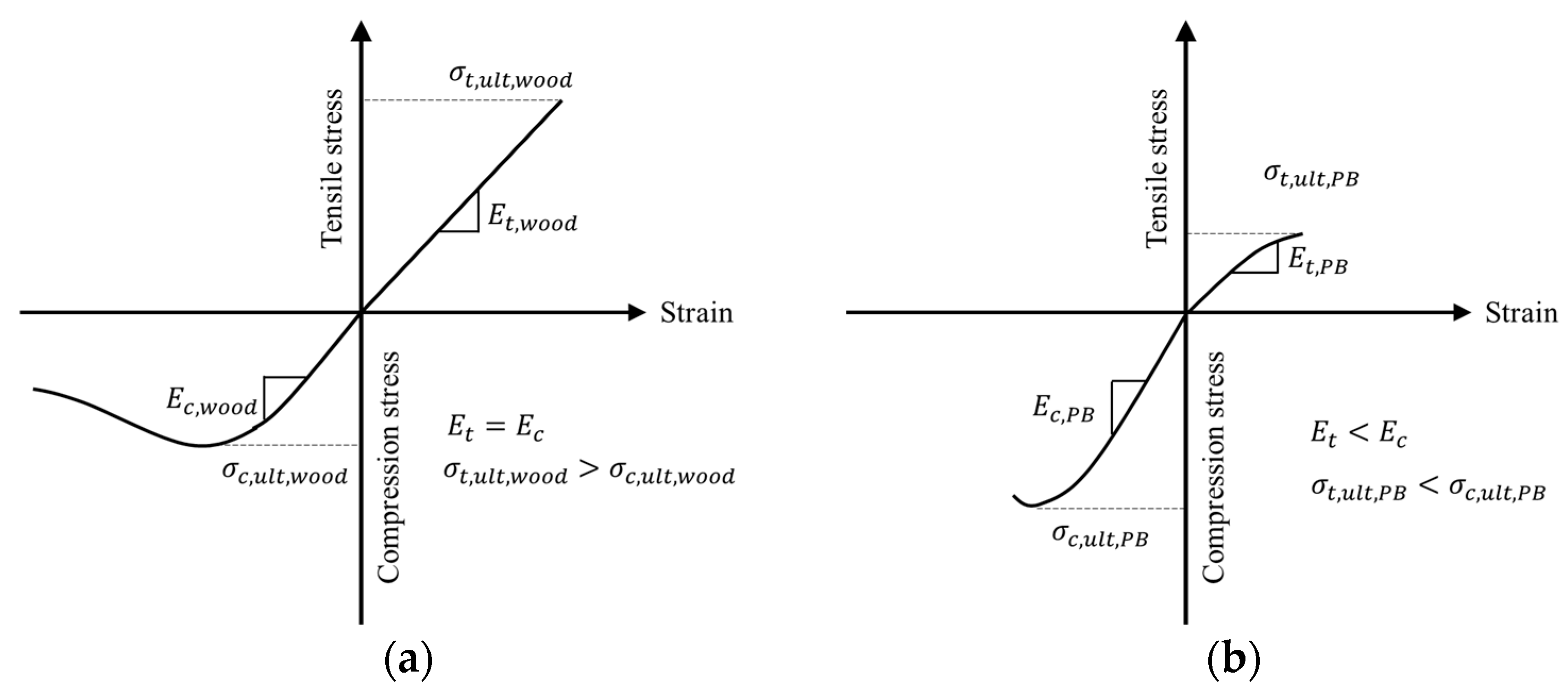
Figure 1.
The general configurations of stress–strain relationship of (a) solid wood timber and (b) PBs, where
is tensile stress, is compressive stress, is tensile modulus, and is compressive modulus.
Figure 1.
The general configurations of stress–strain relationship of (a) solid wood timber and (b) PBs, where
is tensile stress, is compressive stress, is tensile modulus, and is compressive modulus.
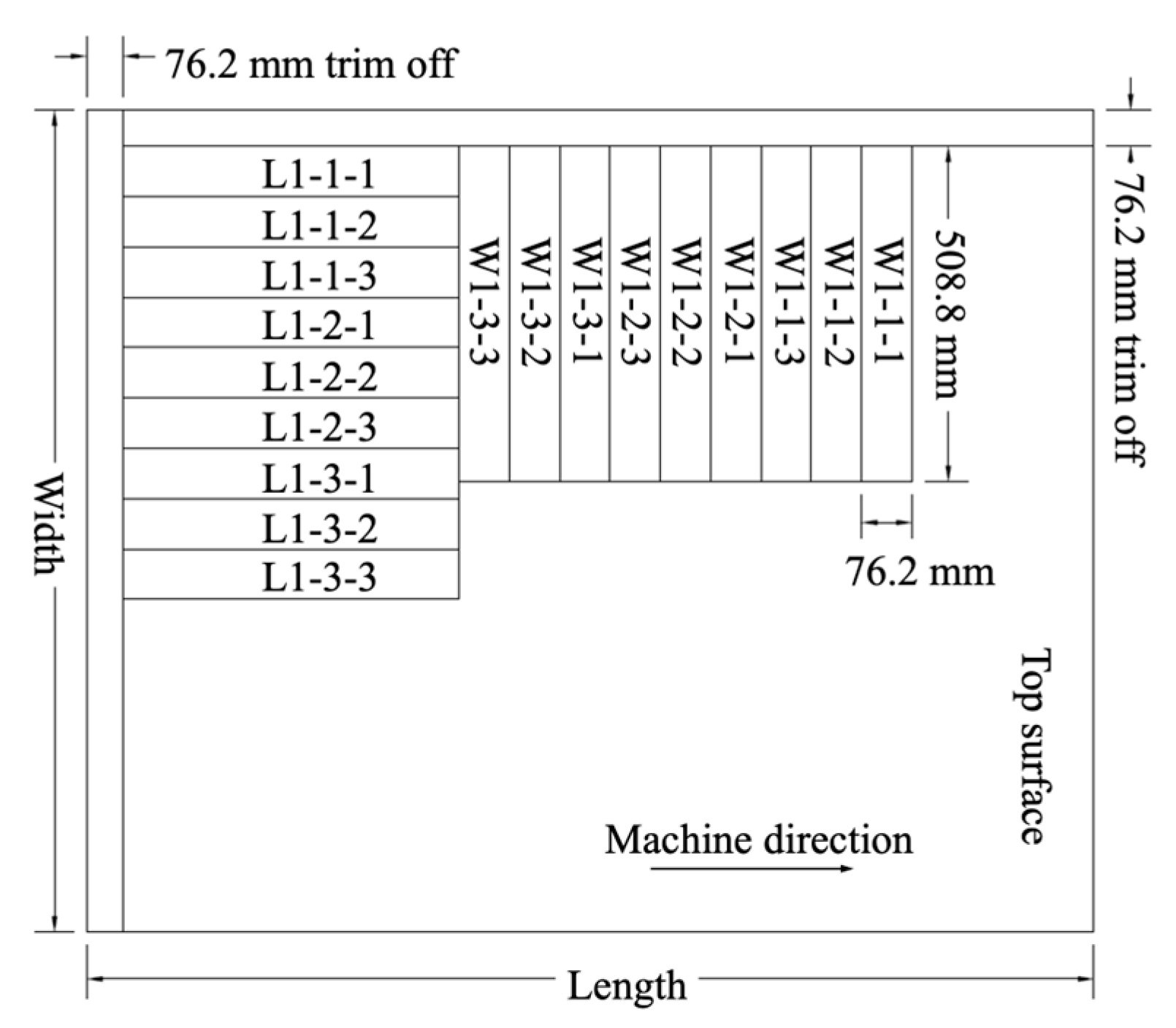
Figure 2.
Cutting pattern showing where particleboard bending strips were cut from a full-size panel.
Figure 2.
Cutting pattern showing where particleboard bending strips were cut from a full-size panel.
Figure 3.
Diagrams illustrate simply supported center-loading conditions designed for the (a) development and (b) validation of the proposed mechanics models.
Figure 3.
Diagrams illustrate simply supported center-loading conditions designed for the (a) development and (b) validation of the proposed mechanics models.
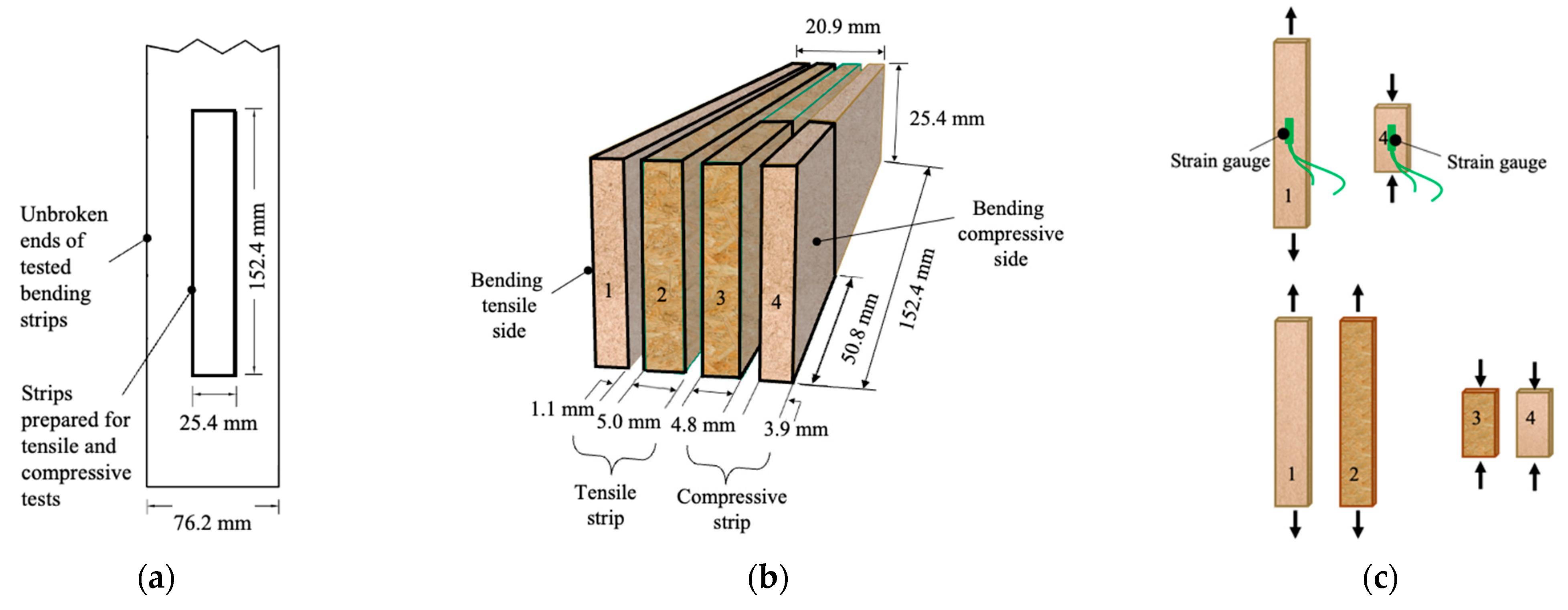
Figure 4.
(a) The process of cutting pure tensile and compressive testing strips from the unbroken end of a previously tested bending strip. (b) The strips then sliced into four layers and (c) subsequently tested in tension and compression.
Figure 4.
(a) The process of cutting pure tensile and compressive testing strips from the unbroken end of a previously tested bending strip. (b) The strips then sliced into four layers and (c) subsequently tested in tension and compression.
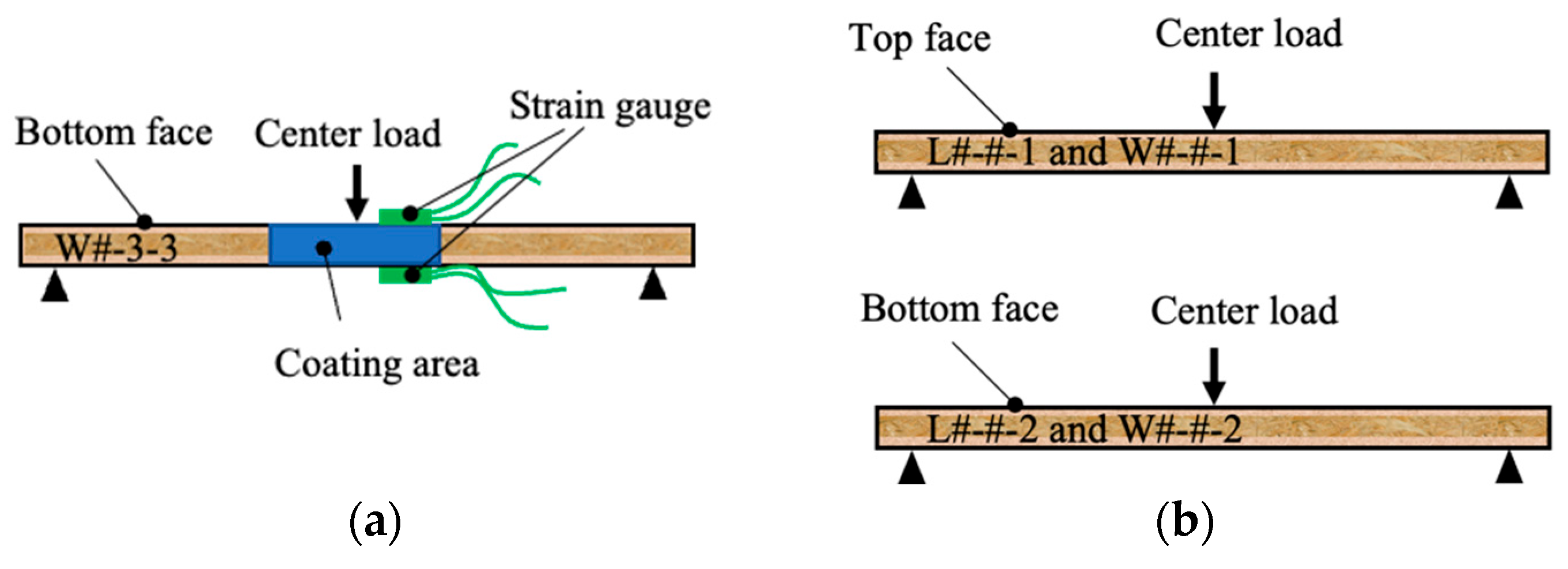
Figure 5.
Photos show (a) the overall appearance of test setup for evaluating neutral axis shifting using photo-coating method and for measuring surface strain of a test particleboard strip under simply supported center-loading in bending; (b) details of a photo-elastic measuring sheet attached to the side of the test strip; and (c) two strain gauges mounted on the top and bottom surfaces of the test strip.
Figure 5.
Photos show (a) the overall appearance of test setup for evaluating neutral axis shifting using photo-coating method and for measuring surface strain of a test particleboard strip under simply supported center-loading in bending; (b) details of a photo-elastic measuring sheet attached to the side of the test strip; and (c) two strain gauges mounted on the top and bottom surfaces of the test strip.
Figure 6.
Testing setups for evaluating (a) pure tensile and (b) compressive properties of particleboard layers at mechanics model development group, and for the (c) pure tensile and (d) compressive properties in the validation group, respectively.
Figure 6.
Testing setups for evaluating (a) pure tensile and (b) compressive properties of particleboard layers at mechanics model development group, and for the (c) pure tensile and (d) compressive properties in the validation group, respectively.
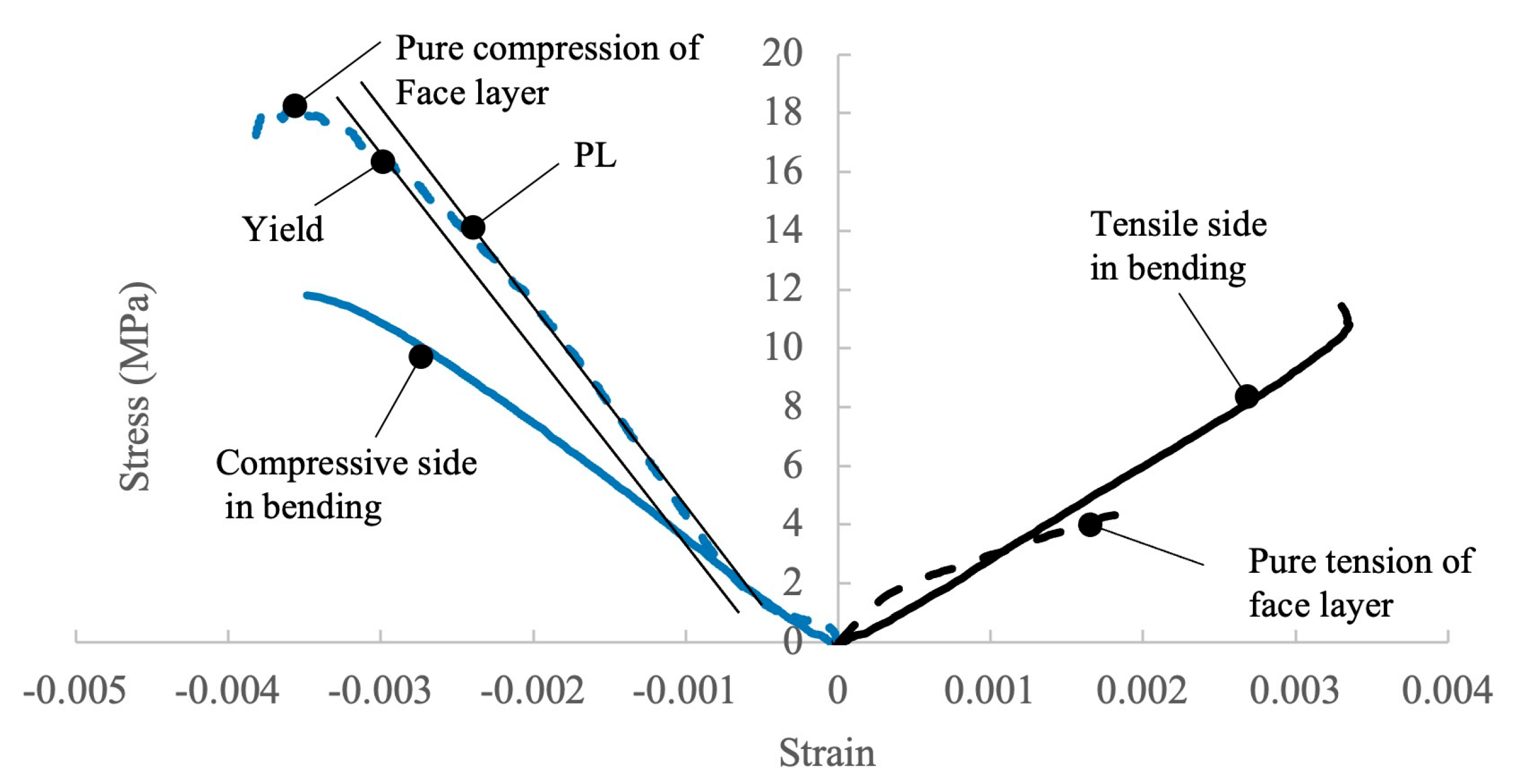
Figure 7.
Typical stress–strain curves of simply supported center-loading bending, face layer pure tension, and face layer pure compression.
Figure 7.
Typical stress–strain curves of simply supported center-loading bending, face layer pure tension, and face layer pure compression.
Figure 8.
Photos recorded during photo-elastic testing show the shift in the neutral axis as the bending load increases at various stages: (a) initial, (b) 1/3 of ultimate, (c) 2/3 of ultimate, and (d) ultimate loads.
Figure 8.
Photos recorded during photo-elastic testing show the shift in the neutral axis as the bending load increases at various stages: (a) initial, (b) 1/3 of ultimate, (c) 2/3 of ultimate, and (d) ultimate loads.
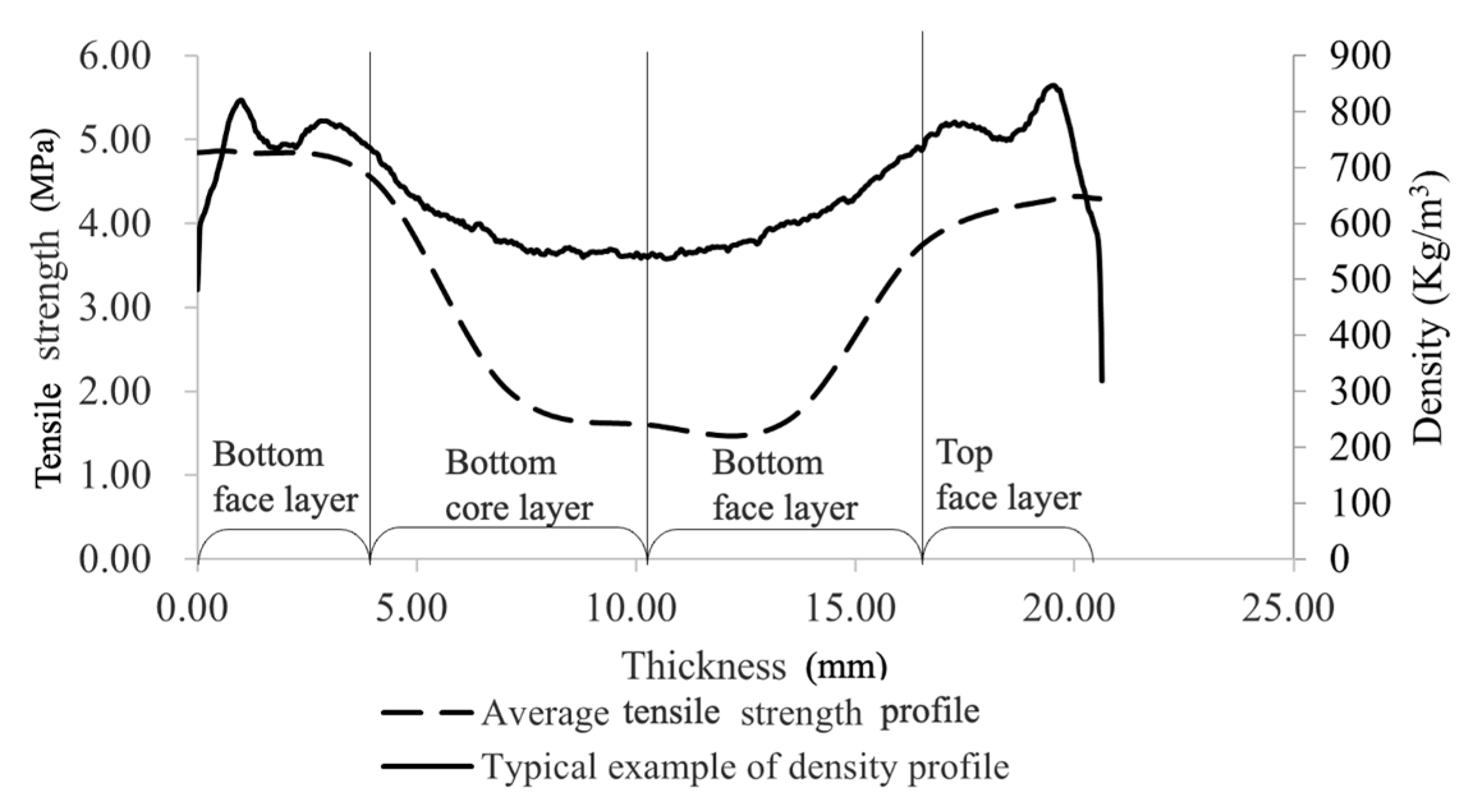
Figure 9.
Average tension strength profile with the center-bending load applied on top face and typical density profile.
Figure 9.
Average tension strength profile with the center-bending load applied on top face and typical density profile.
Figure 10.
Three stages of the bending moment development process proposed to develop mechanics models for predicting the bending moment capacities of particleboard.
Figure 10.
Three stages of the bending moment development process proposed to develop mechanics models for predicting the bending moment capacities of particleboard.
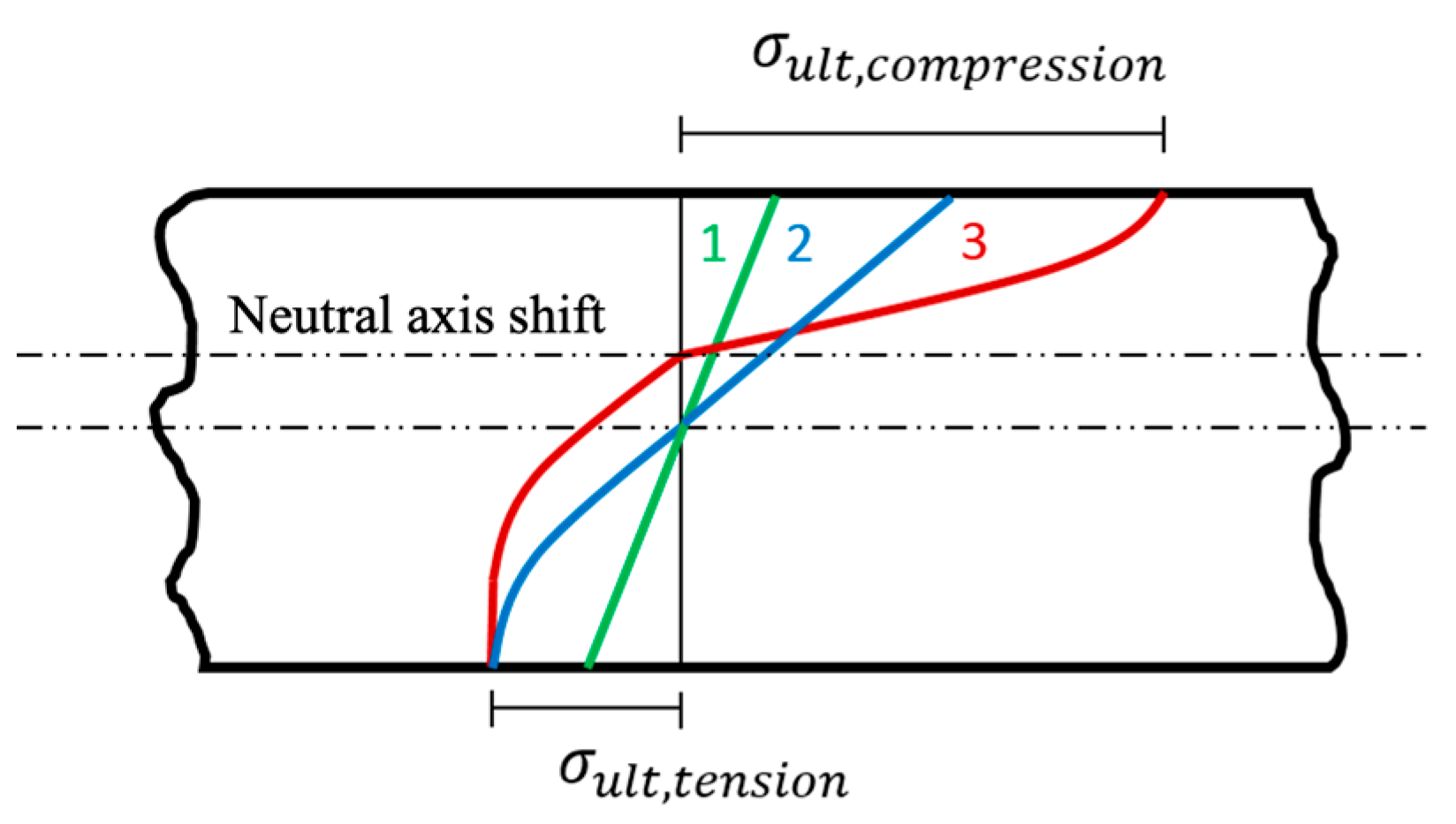
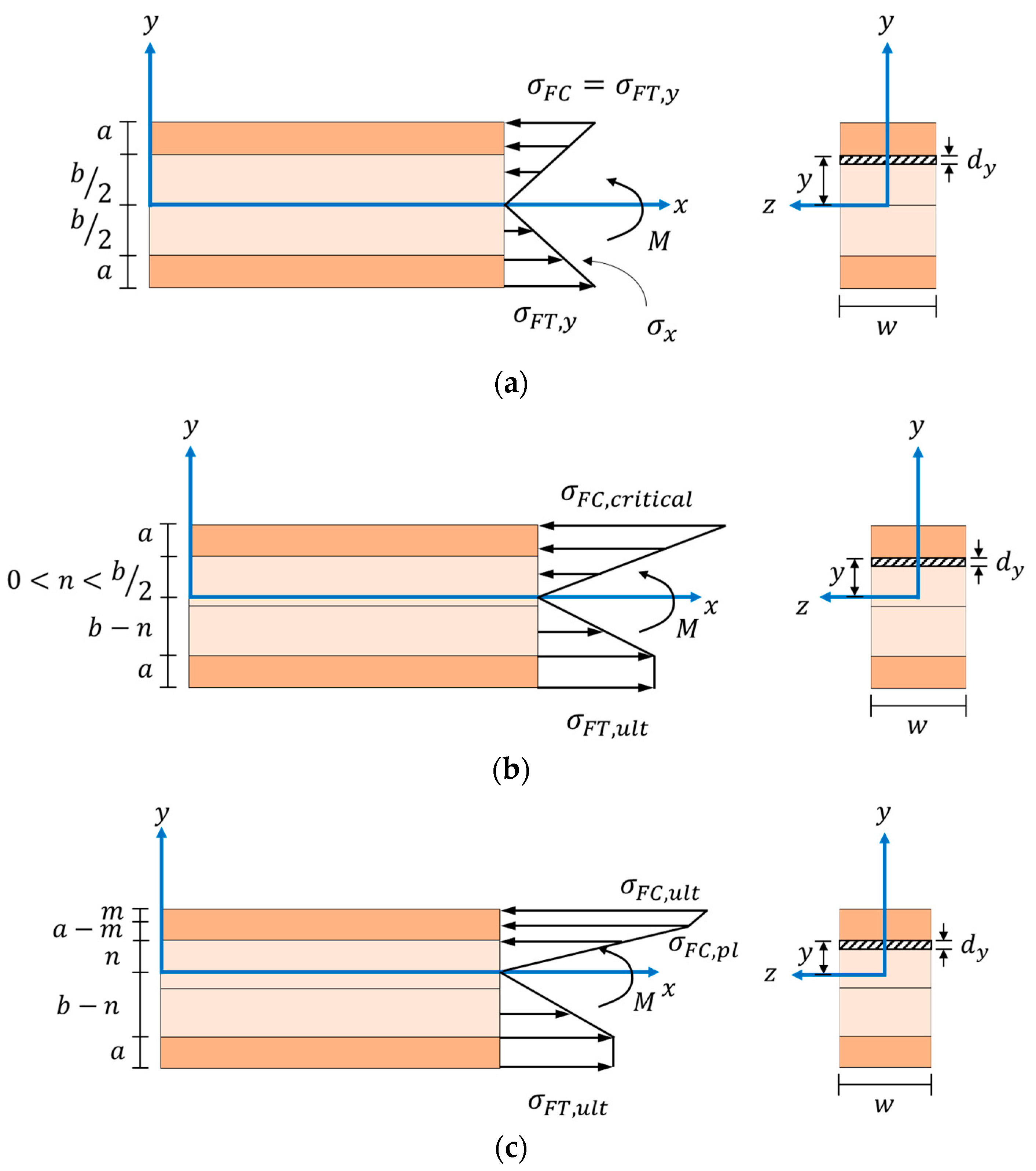
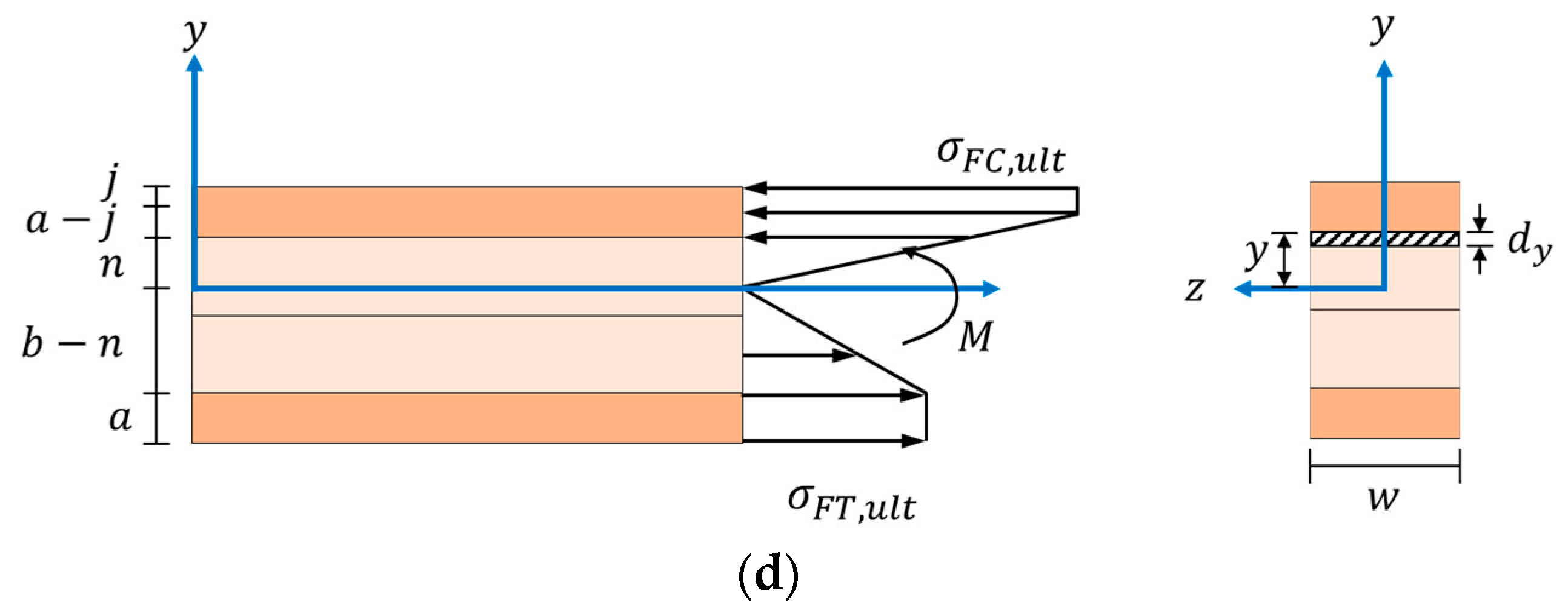
Figure 11.
Illustrations of four proposed stress distributions on the middle cross-section of a four-layered particleboard strip (dark color: for face layers; light color: core layers) at (a) Stage 1, (b,c) Stage 2, and (d) Stage 3 when subjected to simply supported center-loading.
Figure 11.
Illustrations of four proposed stress distributions on the middle cross-section of a four-layered particleboard strip (dark color: for face layers; light color: core layers) at (a) Stage 1, (b,c) Stage 2, and (d) Stage 3 when subjected to simply supported center-loading.
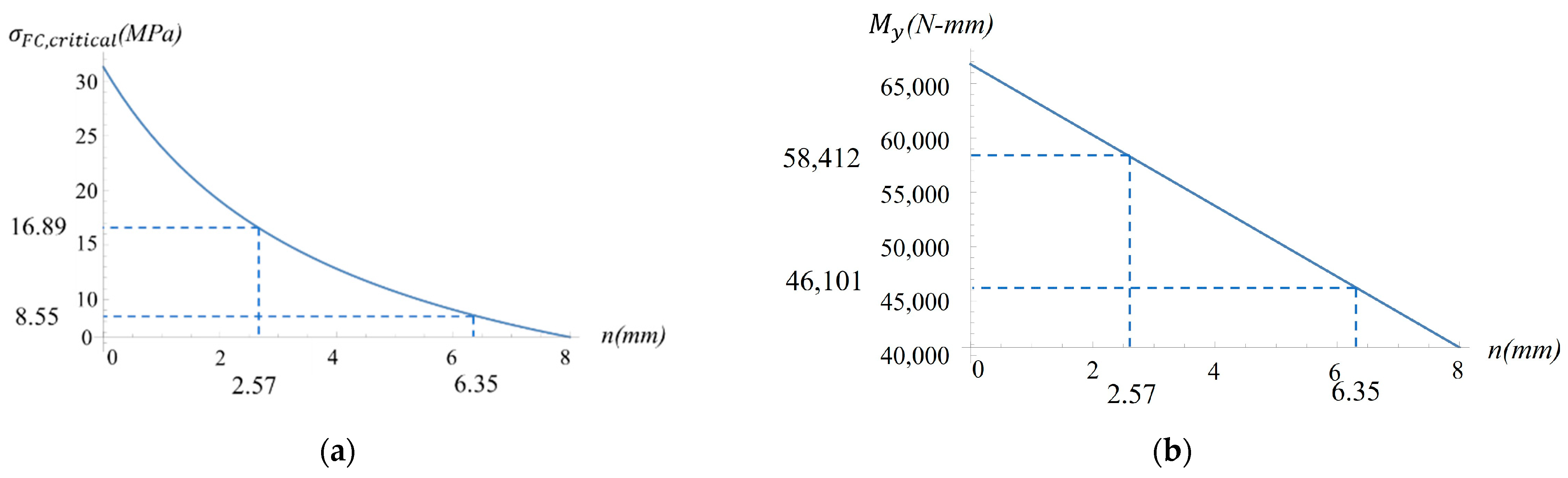
Figure 12.
Plots of (
a) the critical compressive stress in the face layer (
) as a function of
, where
is the distance between the neutral axis and the interface of face and core layers of the compressive side of a test strip (see
Figure 11b), and (
b) the bending moment at the yield point as a function of
.
Figure 12.
Plots of (
a) the critical compressive stress in the face layer (
) as a function of
, where
is the distance between the neutral axis and the interface of face and core layers of the compressive side of a test strip (see
Figure 11b), and (
b) the bending moment at the yield point as a function of
.
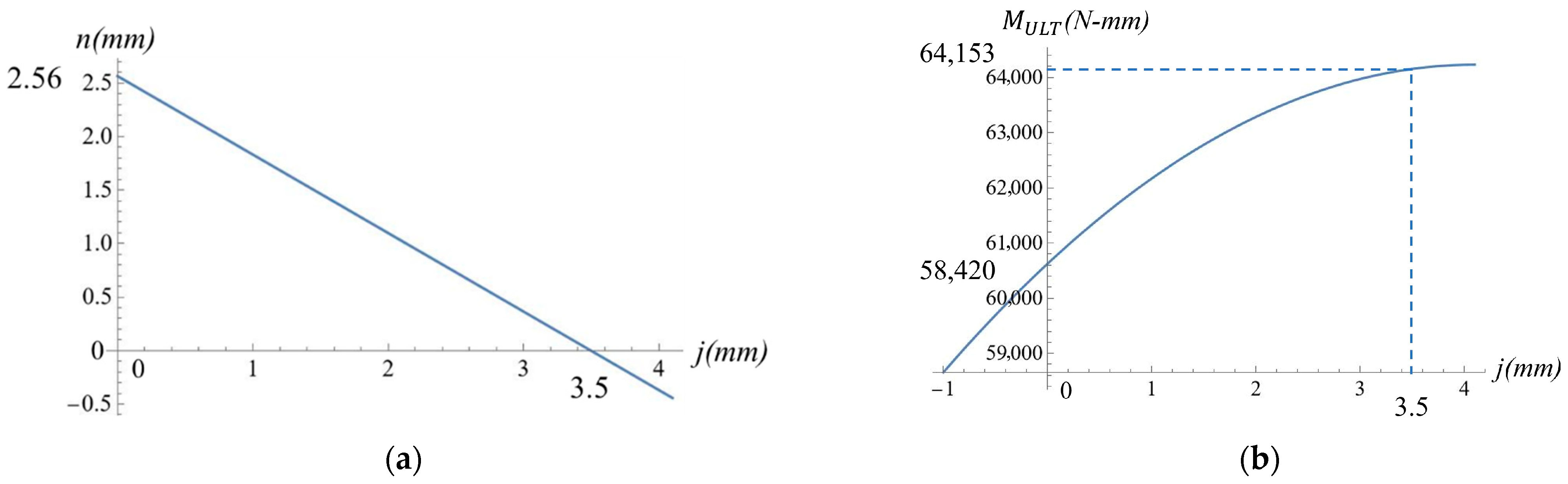
Figure 13.
Plots of (a) the distance between the neutral axis and the interface of face and core layers of the compressive side a test strip (), as a function of , which is the distance from the outer surface of the face layer where its strength reaches its proportional limit, and (b) the bending moment at ultimate point as a function of .
Figure 13.
Plots of (a) the distance between the neutral axis and the interface of face and core layers of the compressive side a test strip (), as a function of , which is the distance from the outer surface of the face layer where its strength reaches its proportional limit, and (b) the bending moment at ultimate point as a function of .
Figure 14.
Plots of (a) the distance between the neutral axis and the interface of face and core layers on the compressive side a test strip () as a function of (the thickness of the face layer in compression reaching its ultimate compressive strength), and (b) the bending moment at ultimate point as a function of .
Figure 14.
Plots of (a) the distance between the neutral axis and the interface of face and core layers on the compressive side a test strip () as a function of (the thickness of the face layer in compression reaching its ultimate compressive strength), and (b) the bending moment at ultimate point as a function of .
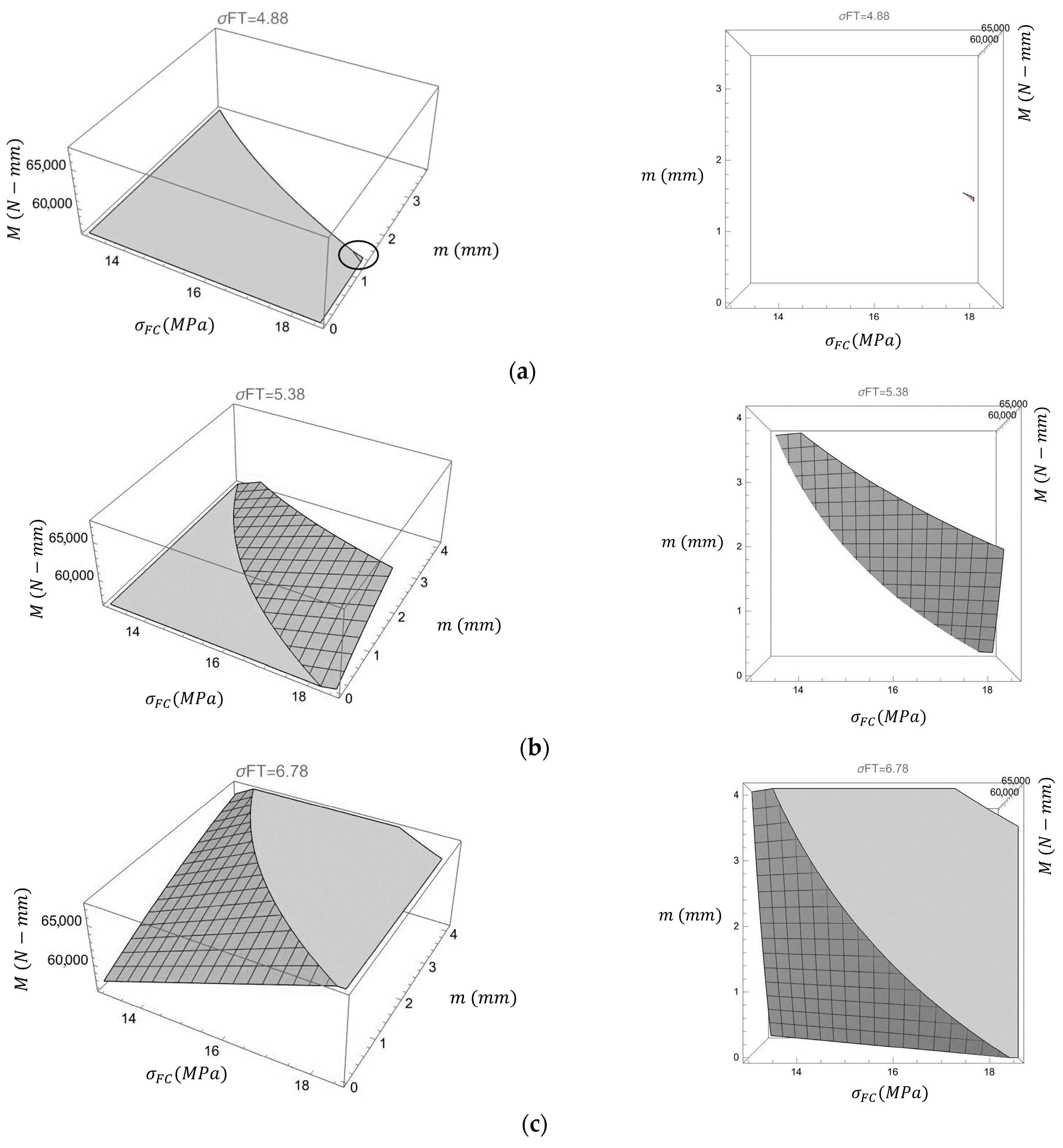
Figure 15.
3D plot of the face tensile and compressive strength with corresponding bending moment (gray grid area), perspective view and front view. (a) Face layer tensile strength is 4.88 MPa. (b) Face layer tensile strength is 5.38 MPa. (c) Face layer tensile strength is 6.78 MPa.
Figure 15.
3D plot of the face tensile and compressive strength with corresponding bending moment (gray grid area), perspective view and front view. (a) Face layer tensile strength is 4.88 MPa. (b) Face layer tensile strength is 5.38 MPa. (c) Face layer tensile strength is 6.78 MPa.
Table 1.
Mean values of ultimate strain and modulus of elasticity for particleboards tested under pure tensile, compressive, and simply supported center-loading (bending) conditions.
Table 1.
Mean values of ultimate strain and modulus of elasticity for particleboards tested under pure tensile, compressive, and simply supported center-loading (bending) conditions.
| Mechanical Property | Loading Condition |
|---|
| Pure | Bending |
|---|
| Tensile | Compressive | Tensile | Compressive |
|---|
| Ultimate strain | 0.00210(11) 1 (B) 2 | 0.00379(9) (A) | 0.00360(5) (A) | 0.00371(4) (A) |
| Modulus of elasticity | 2925(5) (B) | 4487(14) (A) | 3291(4) (B) | 3196(5) (B) |
Table 2.
Mean values of pure tensile and compressive strengths of the face and core layers and bending moment capacity, selected and tested in mechanical model development group.
Table 2.
Mean values of pure tensile and compressive strengths of the face and core layers and bending moment capacity, selected and tested in mechanical model development group.
| Loading Condition | Layer | Strength (MPa) |
|---|
| Proportional Limit | Yield | Ultimate |
|---|
| Pure tension | 1 | 5.20(11) 1 | 5.59(9) | 6.14(10) |
| 2 | 2.27(9) | 2.41(11) | 2.65(10) |
| Pure compression | 3 | 5.83(10) | 6.22(12) | 6.83(15) |
| 4 | 14.60(10) | 15.41(9) | 16.89(10) |
| Bending | Entire piece | Moment (N-mm) |
| 36,215(4) | 55,828(3) | 65,757(3) |
Table 3.
Mean values of ultimate bending moment of sixty particleboard strips evaluated in the mechanics model validation group, along with their corresponding ultimate pure tensile and compressive strengths of face and core layers.
Table 3.
Mean values of ultimate bending moment of sixty particleboard strips evaluated in the mechanics model validation group, along with their corresponding ultimate pure tensile and compressive strengths of face and core layers.
| Center-Loading Direction | Strip Length Orientation | Ultimate Bending Moment (N-mm) | Layer |
|---|
| 1 | 2 | 3 | 4 |
|---|
| Ultimate Pure Tensile Strength (MPa) | Ultimate Pure Compressive Strength (MPa) |
|---|
| Top face | Length | 61,351(5) 1 (A) 2 | 6.09(10) | 2.41(7) | 6.00(11) | 16.44(10) |
| Width | 57,735(4) (B) | 5.67(11) | 2.46(12) | 6.12(14) | 14.61(14) |
| Bottom face | Length | 58,187(4) (B) | 5.14(10) | 2.37(23) | 6.88(21) | 16.73(16) |
| Width | 54,120(3) (C) | 5.09(7) | 2.04(8) | 6.83(19) | 15.07(14) |
Table 4.
Comparisons between predicted and experimental bending moment capacities of particleboard materials evaluated in model development.
Table 4.
Comparisons between predicted and experimental bending moment capacities of particleboard materials evaluated in model development.
| Stage | Experimental (N-mm) | Model | Predicted (N-mm) | Exp./Pre. Ratio |
|---|
| 1 | Proportional limit | 36,215 | 1 | | 1.168 |
| 2 | Yield | 55,928 | 2 | | 0.957 |
| 3 | Ultimate | 65,757 | 3 | | 1.033 |
| 4 | | 1.025 |
Table 5.
Comparisons between predicted and experimental bending moment capacities of four-layered particleboard materials evaluated in model validation group.
Table 5.
Comparisons between predicted and experimental bending moment capacities of four-layered particleboard materials evaluated in model validation group.
| Loading Condition | Experimental (N-mm) | Model | Predicted (N-mm) | Exp./Pre. Ratio |
|---|
| Top length | 61,351 | 4 | | 0.941.04 |
| Top width | 57,735 | | 0.921.02 |
| Bottom length | 58,187 | | 0.880.94 |
| Bottom width | 54,120 | | 0.910.99 |