Modelling Wood Product Service Lives and Residence Times for Biogenic Carbon in Harvested Wood Products: A Review of Half-Lives, Averages and Population Distributions

Abstract

Timber and other biobased materials store carbon that has been captured from the atmosphere during photosynthesis and plant growth. The estimation of these biogenic carbon stocks in the harvested wood products (HWP) pool has received increasing attention since its inclusion in greenhouse gas reporting by the IPCC. It is of particular interest for long service life products such as timber in buildings; however, some aspects require further thought—in particular the handling of service lives as opposed to half-lives. The most commonly used model for calculating changes in the HWP pool uses first order decay based on half-lives. However other approaches are based on average service lives and estimates of residence times in the product pool, enabling different mathematical functions to be used. This paper considers the evolution of the two concepts and draws together data from a wide range of sources to consider service life estimation, which can be either related to design life or practical observations such as local environmental conditions, decay risk or consumer behaviour. As an increasing number of methods emerge for calculating HWP pool dynamics, it is timely to consider how these numerical inputs from disparate sources vary in their assumptions, calculation types, accuracy and results. Two groups are considered: half-lives for first order decay models, and service life and residence time population distributions within models based on other functions. A selection of examples are drawn from the literature to highlight emerging trends and discuss numerical constraints, data availability and areas for further study. The review indicated that issues exist with inconsistent use of nomenclature for half-life, average service life and peak flow from the pool. To ensure better sharing of data between studies, greater clarity in reporting function types used is required.

1. Introduction

Timber, wood products and other bio-based materials store carbon that has been captured from the atmosphere during photosynthesis and plant growth. There is a growing interest in quantifying this biogenic carbon and considering the carbon storage benefits of timber, with many studies considering the carbon in forest products or in buildings [1,2,3]. This is commonly referred to as harvested wood products (HWP) storage. It is widely recognised that the HWP carbon pool is the destination for much of the forest carbon that is harvested during sustainable forest management. Accounting for changes in the HWP pool allows for the storage of carbon in the built environment or technosphere to be acknowledged, while the forest re-starts sequestration within the new generation tree crop. Quantifying this effect is an expanding area of interest.

However, whilst the rate of production of harvested wood products is relatively easily understood and quantified, the duration of the associated carbon storage (and, by extension, any associated climate change mitigation) is more difficult to assess. The rate at which carbon is removed from the storage ‘pool’ is subject to a range of factors, some of them intrinsic to the product itself (e.g., type of product and species of wood) but some of them relating to the uses to which the product is put and societal norms around use and disposal. A variety of models and assumptions have been put forward to assess HWP carbon storage, and these are discussed here, with a view to moving towards more consistent and accurate assessments. The review and discussion presented in this paper will enable the benefit of delaying the re-release of biogenic carbon to the atmosphere to be credibly reported and recognised.

The interest in HWP carbon storage largely follows from the requirement, under the Kyoto Protocol, for Annex 1 countries [4] to report HWP values in the LULUCF (land use land use change and forestry) component of their national inventory reports (NIRs). This has applied since the 2011 decision by the UNFCCC (United Nations Framework Convention on Climate Change) to include HWP in the LULUCF section. Subsequently, the 2013 revision of the IPCC (Intergovernmental Panel on Climate Change) guidance [5] established three tiers of methodologies for assessing HWP storage. IPCC guidelines for reporting were most recently updated in 2019 [6].

In addition to the national reporting aspects covered by the IPCC guidelines [6], there is scope for considering policy options through quantifying different scenarios [7,8] as well as activity at the market level, with organisations seeking to quantify carbon in buildings to use financial methods and carbon credits to promote carbon storage in medium to long term applications. In Europe, the new Carbon Removals and Carbon Farming (CRCF) framework sets out additional criteria to establish transparency in carbon finance [9]. In addition, various organisations in the wood products sector have begun to quantify the storage of carbon in the products they supply, for example within corporate sustainability reporting [10] and [11] (p. 20). This has demonstrated demand for a consistent framework to present such HWP data alongside other carbon metrics such as the carbon emissions or global warming potential (as considered in Life Cycle Assessment (LCA) or product Environmental Product Declarations (EPDs)) and displacement effects. In April 2025, the ISO published a standard series (ISO 13391) which encompasses product value chain emissions, forest carbon balance, HWP storage and displacement for organisational reporting [12]. Developments are still ongoing. There is scope to consider long term storage, for example of wood products within landfill: the IPCC methodology for national greenhouse gas reporting includes quantifying HWPs in service, and for these materials once they enter solid waste disposal sites (SWDS) [6].

The role of the built environment as a store, or a ‘pool’ of carbon, is frequently acknowledged, so many studies consider housing stock [13,14,15,16,17,18,19]. Other wood products may also be studied, most often including wood-based panels [20,21,22] and joinery timber [23]. Early work preferred to consider the longest term stores, as the 100 year time horizon for storage was seen as a target, e.g., [18,24]. However, consideration of stocks and flows into and out of a pool of harvested wood products enables handling of products with a much wider range of life spans [16].

The IPCC 2019 Tier 1 method segregates wood products into three default commodities: solid wood, panel products and paper products, and a half-life value is assigned to each (35 years, 25 years and 2 years, respectively) [6]. These are frequently described as being insufficient [13], and Tier 2 and Tier 3 methodologies are included in the guidelines to allow adjusted half-lives to reflect a given nation’s forest products sector and service lives, or to use different approaches such as flux data methods. In addition, the recent ISO 13391 standard has reflected the Tier 1, 2 and 3 approaches in considering HWPs produced by organisations, opening the question to a wider audience [25]. Therefore, this paper collates and discusses the use of half-lives and service lives.

Various papers have emerged in which harvested wood products’ carbon storage effects have been evaluated alongside current and projected future changes in forest management, wood utilisation and product diversification [8,26,27]. This can lead to evaluation of policy options to promote greenhouse gas mitigation through sustainable forest management, or through greenhouse gas removals in wood in the built environment. It can also support organisational investment and innovation to ensure continued alignment with corporate sustainability ideals.

The effect of recycling within the wood value chain and its impact on carbon storage is also an important consideration [8,28,29,30,31]. Examples include the effect of recycling the biogenic carbon into a second or third life through cascading [32,33,34]. A model for predicting the split of products within a cascading system has explored this for timber in Maine, USA [35]. The additional storage time, or residence time, can be substantial when recycling or cascading is effectively deployed.

This desire to quantify service lives and storage times for biogenic carbon provides the motivation for this paper. Although many authors report that there is a lack of data in this field [16,34,36,37,38], a more pressing issue appears to be a lack of consistency in definitions and approaches. A recent rapid growth in publications in this area means that there are now many articles, using a range of values taken or adapted from multiple sources. These appear to be selected on popularity, geographic relevance, recentness, mathematical basis (goodness of fit) or perceived accuracy of the service life represented. As a result, the aim of this paper is to collate service life information and modelling approaches from different sources, and to review and discuss the purposes for which the models and data have been developed. The paper will also note key trends, the potential of different data types for use in HWP reporting, and the practical issues that arise if transposing it to consider the biogenic carbon storage question.

2. The Origins of Biogenic Carbon Analysis for Harvested Wood Products

2.1. Some Text on History

The concept of HWP storage has been in development for some considerable time, with various phases occurring within IPCC meetings and guidance documents. Marland et al. [13] provide a succinct history of the early stages, from the Dakar IPCC meeting in 1998 through to provision of guidance in an appendix by the IPCC in 2003 [39] and slightly beyond. Before 2003 it was generally assumed that the HWP pool size was stable and not increasing. Early material flows studies used simplified lifespans, or assumed an equilibrium state [40]. Thus, in the earliest guidelines on HWP storage ‘simple decay’ was the Tier 1 method (i.e., instantaneous release of carbon to the atmosphere at the time of harvest). The IPCC (2003) guidance also made it clear that while protocols were available for calculating HWP storage effects, the onus was on the nation concerned to demonstrate that the effect was sufficiently significant [39].

The emphasis of many early discussions was the political and economic implications of the HWP accounting options, as differences mainly related to whose national account the sinks and emissions were credited to, rather than the mathematics. A series of meetings, reports and documents led to consideration of the atmospheric approach, stock change approach and production approach alongside the original simple decay approach [41], so all four ‘approaches’ are set out in the current IPCC guidelines [6]. The ‘simple decay approach’ (in which carbon is assumed to return instantly to the atmosphere at time of harvest) is now relegated to fourth option, and used mainly to handle timber which was not harvested sustainably.

HWP storage was not included within reporting for the first Kyoto commitment period (2008 to 2012) although it became included in the 2nd commitment period after the UNFCCC decision in Durban, South Africa in 2011. This means that each Annex 1 country started to report HWP values for the second Kyoto commitment period (from start of 2013 onwards) [4]. The Durban decision also established the preferred use of the production approach, to allow consistent reporting across all countries without risk of double counting, and set the use of three default categories (Table 1).

Consolidating this, in 2013 further clarification and guidelines were published by the IPCC and the HWP pool became mandatory for reporting in land use, land use change and forestry (LULUCF) activities [5,42]. The first order decay method became the Tier 1 methodology in the 2019 revision [6] (Table 1). The simple decay method became used where the HWPs were deemed to have arisen from deforestation, to avoid creating an incentive for deforestation to achieve carbon storage. Similarly if the wood is not from sustainably managed forests, no claim of HWP storage effect is permitted for national inventory reports. In the IPCC methodology half-lives of 2, 25 and 35 years are applied to pulp and paper, wood-based panels and sawnwood, respectively [5,6]. Where national data is available a country-specific half-life can be calculated in the Tier 2 method option, and data for finished wood products can be used in the Tier 3 method options [6].

Table 1. Evolution of the terminology and half-life values for the default categories in IPCC guidance and revisions.

Category	IPCC 2003 [39] Appendix Only		IPCC 2006 [43] Tier 2		IPCC 2014 [5], Tier 2 and IPCC 2019 [6], Tier 1
Sawnwood	Saw wood	35	Solid wood products	30	Sawnwood	35
Wood-based panels	Veneer, plywood and structural panels	30			Wood-based panels	25
	Non-structural panels	20
Pulp and paper	Paper	2	Paper products	2	Paper and paperboard	2

Table 1. Evolution of the terminology and half-life values for the default categories in IPCC guidance and revisions.

Category	IPCC 2003 [39] Appendix Only		IPCC 2006 [43] Tier 2		IPCC 2014 [5], Tier 2 and IPCC 2019 [6], Tier 1
Sawnwood	Saw wood	35	Solid wood products	30	Sawnwood	35
Wood-based panels	Veneer, plywood and structural panels	30			Wood-based panels	25
	Non-structural panels	20
Pulp and paper	Paper	2	Paper products	2	Paper and paperboard	2

2.2. History of the Maths—First Order Decay

It was the question of mathematical approach, not who gained credit, which was the focus of Marland et al.’s seminal paper [13], and it appears appropriate to revisit this question today, as the uptake of HWP reporting has expanded. So a short historical glimpse at the mathematical basis for the first generation of IPCC methodologies (first order decay and half-life based models) is useful.

In 2003, Pingoud et al. [37] commented on the apparent decay pattern of harvested wood products potentially being described by “linear or exponential functions”, or following “logistic equations, etc.” Logistic equations had been used in 1996 by Row and Phelps [44] and had also been taken up by Skog and co-workers [45] in the USA as well as Eggers [46] in Europe. The IPCC 2006 Guidelines [43] ultimately adopted a first order decay assumption for wood products, but did acknowledge that this was not the only possible model. It was commented that “Different possibilities include linear decay and more detailed approaches based on studies of the real use of these materials.” As a result a Tier 2 and Tier 3 approach were also introduced, to permit country-specific data and more complex detailed methods, or the use of “decay functions other than first order decay.”

First order decay (FOD) uses a decay constant (λ), which is the fraction lost per year. The corresponding half-life t_½ is given by

$$t_{1/2}={\displaystyle \frac{ln\left(2\right)}{\lambda }}$$

(1)

The stock S decays from an initial quantity S₀ at a rate S(t).

$$S(t)=S_0{e}^{-\lambda t}$$

(2)

The first order decay can be used to calculate the change in stock (dS/dt) with the following formula:

$${\displaystyle \frac{dS}{dt}}=J\left(t\right)-\lambda S(t)$$

(3)

where S is stock and J is production in that year; decay (or removal of stock from the pool) is assumed to be proportional to total size of the stock and calculated by λS(t); and change in stock is the difference between production and removal, i.e., J(t) minus λS(t). In IPCC guidance equations are also provided to handle decay within the year, in the case of short half-life products [6].

The half-life approach means that material is modelled as exiting the pool relatively rapidly in the early years after manufacture, slowing over time, and continuing to leave the pool at very low levels into a longer time horizon. This model appears to be intended to take into account the wide range of lifespans of wood products. For example, within the category of solid wood many short life products might exist, as well as medium and long life products. The longer life products might have lifespans which are increasingly dispersed across decades or centuries.

The IPCC’s Good Practice Guide for LULUCF calculations [39], published in 2003, gave a set of example half-lives from the literature in its Table 3A.1.3, presented in

Table 2. Half-life data (as first presented by the IPCC in Appendix 3a.1 in 2003), showing a selection of prior studies as background information. Source: [39].

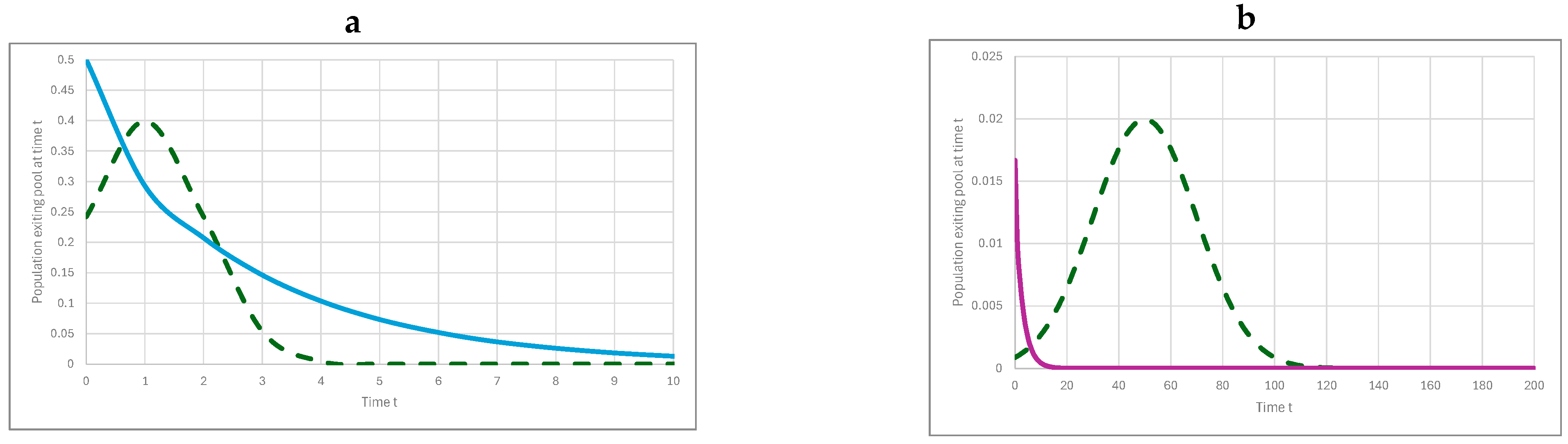
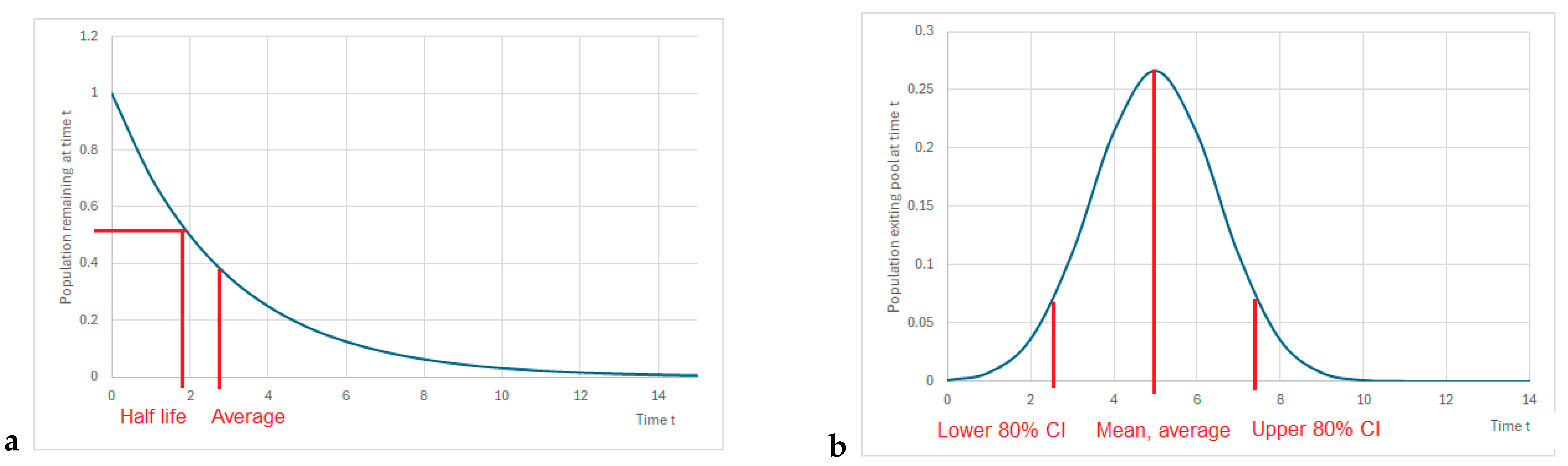
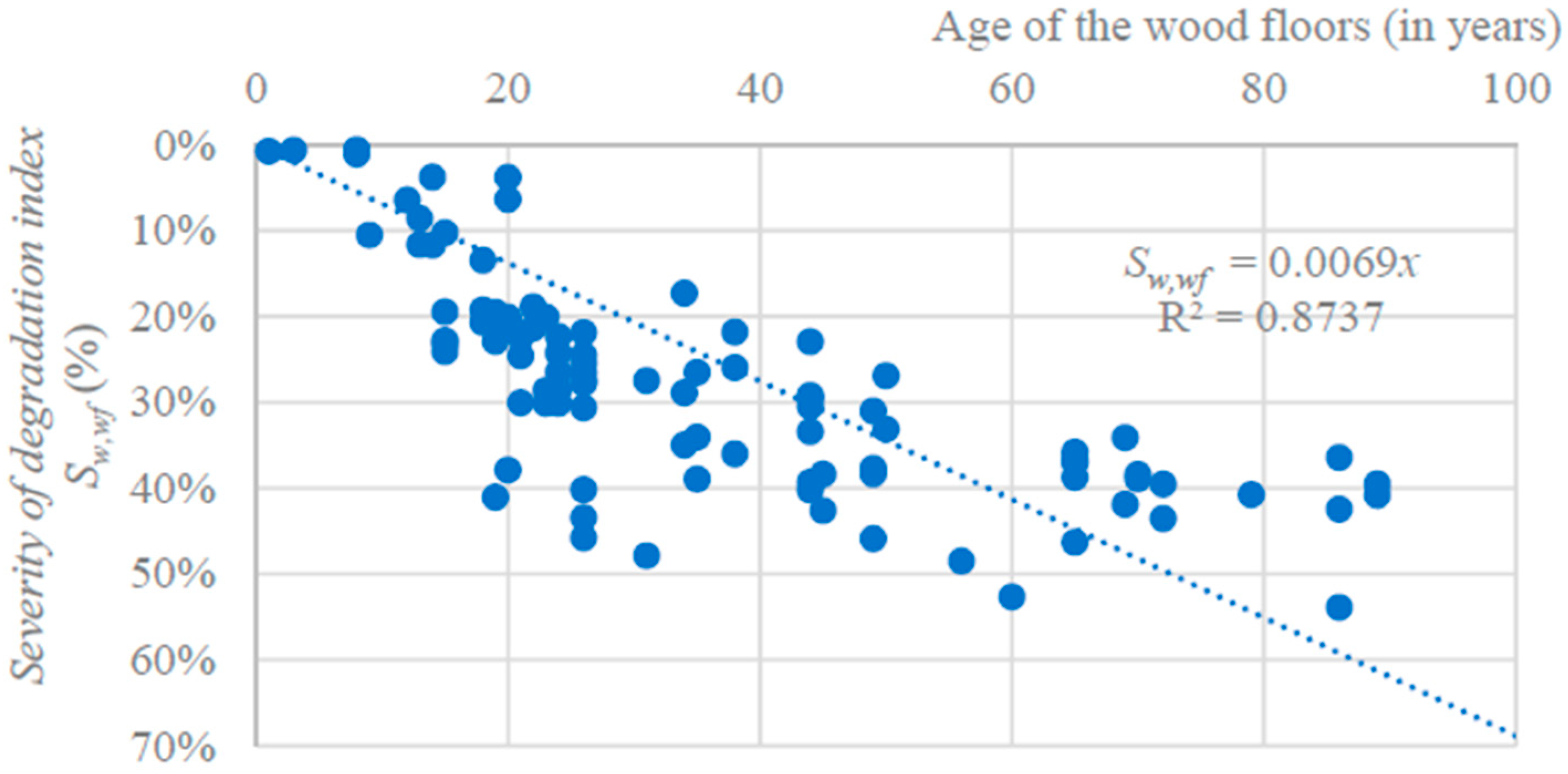
Country/ Region	Reference	HWP Category	Half-Life in Use (Years)	Fraction Loss Each Year (ln(2)/Half-Life)
Defaults	IPCC 2003 [39]	Saw wood	35	0.0198
		Veneer, plywood, structural panels	30	0.0231
		Non-structural panels	20	0.0347
		Paper	2	0.3466
Finland	Pingoud et al., 2001 [47]	Saw wood and plywood (based on change in inventory of products)	30	0.0231
Finland	Karjalainen et al., 1994 [36]	Saw wood and plywood average	50	0.0139
		Paper from mechanical pulp, average	7	0.0990
		Paper from chemical pulp, average	5.3	0.1308
Finland	Pingoud et al., 1996 [48]	Average for paper	1.8	0.3851
		Newsprint, household, sanitary paper	0.5	1.3863
		Linerboard, fluting and folding boxboard	1	0.6931
		80% of printing and writing paper	1	0.6931
		20% of printing and writing paper	10	0.0693
Netherlands	Nabuurs 1996 [49]	Paper	2	0.3466
		Packing wood	3	0.2310
		Particleboard	20	0.0347
		Saw wood average	35	0.0198
		Saw wood spruce and poplar	18	0.0385
		Saw wood oak and beech	45	0.0154
United States	Skog and Nicholson 2000 [50]	Saw wood	40	0.0173
		Structural panels	45	0.0154
		Non structural panels	23	0.0301
		Paper (free sheet)	6	0.1155
		Other paper	1	0.6931

below. This included four suggested ‘default’ values for product categories (as per Table 1), as well as a selection of values taken other studies. In this table the origin of the current three IPCC half-life categories can be seen, but the wood-based panels were initially represented in two sections—the veneer-based and structural panels with a half-life of 30 years, and the non-structural panels with a half-life of 20 years.

Table 2 also included values collated from studies representing a small number of countries (where data was available). These offered slightly more detailed information, for example different types of paper and paper product, and for sawn wood and other wood products. For example, the half-lives for sawn wood of different timber species differed in the data from Nabuurs [49,51], with the value for poplar and spruce being shorter than oak and beech to reflect the perceived typical uses of these species. Even today, many studies cite values from the studies provided in this table. However, the origin of some data in the table is obscure, for example the Skog and Nicholson [50] reference does not contain the values presented, with the exception of the paper (free sheet) and paper (other) values. Other publications have become hard to access. The Skog and Nicholson [50] values in fact influence a different branch of data, which has become firmly established within the USA through development into country specific values in a computer model (see later).

In Table 2 the numbers quoted for Pingoud et al. [48] appear to be based on average values not half-life values, yet the four values given are described as assuming ‘a plausible life age distribution’, and this may be the origin of the half-life concept. Namely an attempt to define a population of products from which much of the material exits the pool quickly, and other categories are retained longer, giving rise to an exponential-type curve, relating to a half-life approach, although this is not specifically mentioned in this paper. Five years later, Pingoud et al. [47] mention the first order decay model for carbon stock, and considered long and medium lifespan scenarios, with half-lives of 48.6 years and 16.2 years, respectively. An average lifetime of 39 years was indicated for construction sawnwood, whereas for sawnwood in buildings and garden construction, an average lifetime of 31 years demonstrated a fit to inventory data.

The IPCC Good Practice Guide in 2003 [39] pointed out that several studies had already considered HWPs using inventory data at different points in time. These included Gjesdal et al. [52] (for Norway) and Karjalainen et al. [36] and Pingoud et al. [47,48] (for Finland). The change in HWP carbon was estimated by noting the change between inventories estimated at different points in time, and was considered to be a stock change method. The purpose of these studies was partially to check the validity of the half-life assumption. Interestingly the findings of Karjalainen and Pingoud differed, with one showing that after 50 years more than 40% of the carbon initially stored in products was still in service or had progressed into storage in landfill [36] and the other suggesting that the half-lives overestimated storage in Finland [47]. These differences may reflect the differences between assumptions, but the findings were sufficient to support the inclusion of a half-life method going forward. The stock change methodology—using national data to assess carbon pool changes continued development, and is still present within Tier 3 options in the IPCC 2019 revision [6]. However it is out of scope for this review.

In 2002 a study by Hashimoto et al. [53] used the two new approaches (flow consumption and flow production) to further consider the effect on reporting. They showed a small but significant improvement in values for the various modifications in method, and the handling of waste wood products moving into solid waste disposal sites. Such work supported the eventual adoption of the production method within more recent iterations of IPCC guidelines [5,6].

2.3. Benefits of Using First Order Decay

The choice of the FOD method permits various attractive simplifications [13,54]. For example, the total stock can be assumed to decay at a rate based on half-life regardless of its age—stock produced last year is just as likely to be removed from service as stock from many years earlier. This means that it is not necessary to segregate by types within that category, or by year of production or differences in service life [54]. This made it an ideal choice for a Tier 1 methodology. It also allowed a coefficient to be provided for each of the default half-life categories, termed ‘fraction loss per year’ and with a value of ln(2)/half-life (Table 2 [39]). There is also simplicity when considering examples where HWP production is growing exponentially and stock is decaying under FOD, the annual increase can simply be assumed to be a fraction of annual production [13]. This approximation is used in the example spreadsheet calculation provided in the IPCC guidance, and utilises the fraction loss per year value.

A characteristic of the first order decay approach is that it models decay rate as being the greatest immediately after production, and thus is likely to suit modelling pools of shorter life products (e.g., fuelwood, and most categories of paper) rather than longer life products [13].

Marland et al. [13] point out that the simple approximation that the assumption that “the change in stocks is a function of the production rate needs to be re-evaluated if the collection of products is not seen as a single, homogeneous pool or if the production cannot reasonably be characterised as exponentially increasing.” Thus, in the shift to measures such as greater use of timber in construction as a greenhouse gas removal (GGR) technology [55], the pool of structural timber products might become sufficiently differentiated from the pool of other general sawnwood usages, that different half-life functions might be required in the two pools [56]. Similarly in situations where production has reached a maximum, for example where throughput reflects a static sustainable quantity (defined based on fixed forest area and sustainable forest management practices) then the pool of HWPs might simply stabilise, and inflow come to directly equal outflow, i.e., J(t) − λS(t) equal to zero. More of a concern is if the HWP production peaks (e.g., if insufficient timber is available, or consumer tastes change leading to a preference for other materials) then pool outflow can exceed inflow. In Japan, the domestic stock of HWP carbon has been projected to become an emission source in the 2020s under a business as usual scenario [57].

2.4. Beyond the IPCC

The USDA and US Department of Energy both utilised the data from Skog and Nicholson [50] in a sequence of computer programme developments and guidance. For example, in 2006 the USDA published methods for calculating ecosystem and harvested carbon (as GTR-343 [58]), while the US Department of Energy published the Technical Guidelines of Voluntary Reporting of Greenhouse Gas Program. The appendix of both documents contained values as shown in

Table 3. Half-life data for the USA from 2006 and 2024 revision [58,59].

End Use or Product	Half-Life (Years)
	Smith et al. (2006) [58]	Murray et al. (2024) [59]
New residential construction
Single family	100	87.8
Multi-family	70	53.7
Mobile homes	12	12
Residential upkeep and improvement	30	30
New non-residential construction
All except railroads	67	67
Railroad ties	12	12
Railcar repair	12	12
Manufacturing
Household furniture	30	30
Commercial furniture	30	30
Other products	12	12
Shipping (wooden containers, pallets, dunnage)	6	6
Other uses for lumber and products	12	12
Solid wood exports	12	12
Paper	2.6	2.6

. Also shown in Table 3 are recent values revised to reflect current market activity and wood usage within the USA [59]. The revision calculation processes are explained by Skog [60].

In the Appendix D of GTR-343, Smith et al. [58] give the data shown in column 2 of Table 3, but in the body of the report they have a table with just 7 categories of wood product, providing values for the percentage remaining in service over time. This had been calculated using the values shown above as input to derive country specific values for use within the national reporting structure. The resulting data does not quite follow a first order decay profile, as it reflects the mix of multiple different products within the categories, altering the profile slightly, but it is a reasonable approximation. From the data it is possible to read off a ‘half-life’ value for the category, by selecting the 50% point, see

Table 4. Half-life values for USA HWP categories derived from data presented in Smith et al. [58].

Wood Product	Calculated From	Year at Which 50% of Stock Remains (Half-Life)
Softwood lumber	Many categories of wood with % in use and specific half-lives	35
Hardwood lumber	Several categories of wood with % in use and half-lives	13
Softwood plywood	Typical applications	38
OSB	Typical applications	60
Non-structural panels	Typical applications	26
Miscellaneous products	As per [58], Table 3	12
Paper	With assumed HL of 2.6 but 48% recovery for recycling and 70% fibre retention during recycling	4

below. Interestingly, as a result of the broad mix of softwood product usages (with wide range of life spans), the half-life for softwood as a whole category is much lower than that for OSB or plywood, where the use types are more restricted to longer-life applications. In contrast the hardwood lumber has an even shorter half-life, possibly reflecting the types of hardwood timber used in different applications in the USA (unlike Nabuurs’ long service life data for oak and beech in the Netherlands, Table 2).

3. History of Other Mathematical Approaches

The point has been made many times that the longer the lifespan of the product, the less likely it is that first order decay will be an appropriate model for its residence time in the pool (Figure 1a,b) [1,13,34]. This has led many researchers to consider alternative mathematical approaches on more differentiated sets of products, as reviewed below. However, even a decade ago some research was still seeking to sideline the question of storage duration within studies, for example by assuming a 100-year service life for buildings to coincide with the 100-year time horizon that is often used within LCA [61]. Some studies also assumed that all previously existing buildings contained no timber, to remove the need to model loss of carbon from the HWP pool [61]. Others have specifically excluded time from models, despite complex analysis of flows and recovery rates [62].

Moving on from FOD models, the probability function for products leaving the pool becomes the focus of study. A product will decay with some probability at various times but with higher probability near the expected lifetime. Much of the thinking has considered building service lives, with observations about the reasons for obsolescence [63] or consideration of hazard rates that relate to the age of the building stock [64] as well as studies on building population data [65,66,67]. The residence time is often plotted as a sigmoidal curve [65,68], which can be translated into a normal, Weibull, gaussian, gamma or chi-squared distribution, as shown in Figure 1 above [13,34,38,69,70]. The use of the Weibull distribution for HWPs was based on this being a common approach in modelling building lifespans for example [30,71,72]. However, some studies have pointed out that validation of these is generally not possible, given the dearth of data [73,74].

One early attempt to consider time-dependent population dynamics was the piecewise decay model demonstrated by Row and Phelps [13,44] in the HarvCarb computer model. The HarvCarb programme is also reported by Heath et al. [75], but the piecewise approach did not progress into later models in the USA [13]. While the original Row and Phelps book chapter [44] is hard to access, Rüter [76] provides the table of median service life values from it in his thesis. The table includes many values which will later be presented as ‘half-lives’ by Skog and Nicholson [50] such as 30 years for residential repairs and maintenance, 12 years for mobile homes, 6 years for packaging timber, 12 years for other uses, 6 years for printing and writing paper, 1 year for paper hygiene products. This confirms that prior to the later developments, the intention of selecting these initial values was as a median, not a half-life. As a result of this difference two of the categories are very different to the values which later emerged as half-lives in Skog and Nicholson’s work [44,50]. The single-family residential value had a median service life of 200 years, and the multi-family house a value of 150 years. Non-residential was expected to have a median service life of 60 years [44,76].

These investigations of other mathematical functions for the population residence time distributions are sometimes called distributed decay models. The population is treated as a series of distinct products, each with its own mathematical function. Most importantly the rate of product loss is dependent on the time since production. A probability function is assigned to the product (Pτ) with τ as the integration variable for the time since production. The integral adds up all the outflow from previous years’ productions, but treats each year separately.

$${\displaystyle \frac{dS}{dt}}=J\left(t\right)-{\int }_0^{t}J\left(t-\tau \right)P\left(\tau \right)d\tau$$

(4)

Marland et al. [13] used the Gamma distribution function to demonstrate this approach, but commented that other functions could also be used. The Gamma distribution has two parameters, the shape parameter (k) and scale parameter (θ). These are calculated based on the peak year and the year by which 95% of decay has occurred.

$${\displaystyle \frac{dS}{dt}}=J\left(t\right)-{\int }_0^{t}J\left(t-\tau \right){\displaystyle \frac{{\tau }^{\left(k-1\right)}}{\Gamma \left(k\right){\theta }^k}} e^{-{\displaystyle \frac{\tau }{\theta }}}d\tau$$

(5)

where Γ(x) is the Gamma function (not Gamma distribution) and is defined as

$$\Gamma \left(x\right)={\int }_0^{\infty }{s}^{x-1}{e}^{-s}ds$$

(6)

Gamma functions were used with the parameters as shown in

Table 5. Year of maximum decay and other parameters necessary to define a gamma distribution, for applications where oak timber would be used in the UK (Source [13]).

Oak Product	Year of Maximum Decay	95% Decay Period	Gamma Parameters
			k	θ
Waste, bark, fuel	2	18	1.305	4.918
Pulpwood	1	5	1.418	1.196
Particleboard	15	40	3.676	5.419
Pallet, packaging	2	5	3.196	0.683
Fencing	40	80	6.662	6.976
Construction	150	300	6.740	26.045
Mining	40	1000	1.128	308.594

, relating to oak in different applications in the UK [13]. The decay function and the residence plots for selected examples are shown in Figure 2.

A key aspect when moving away from FOD to other functions is that the simplification of ‘fraction lost per year’ no longer applies. The population of material from each year that is supplied to the market must be considered, and the cumulative effect modelled. It becomes necessary to consider the total product outflow from all previous years. The growth of the HWP pool is the net value of inflow minus outflow in a given year [6,16]. If the outflow exceeds the inflow of new products, then the HWP pool shrinks and a negative value is recorded. This is a stock change method, based on modelled residence time data or service life data, and is be covered by Tier 3 of the IPCC guidelines [6]. Similar methods are also possible in Tier 3 of the ISO 13391-1 standard [25].

A good example of stock change method to consider HWP stocks is found in Zhang et al. [77], where a Chi-squared function was used for three categories of wood and two categories of paper products. The input data was taken from FAOSTAT for eight leading consumer countries, and considered the global effects. Many other studies have also shown that Chi-squared distributions work well when considering HWPs and building stock [19,67,70,78] and it has been mentioned as a possible method in some guidance for national methods [59].

4. Estimating Product Lifespan

In order to use mathematical functions such as Weibull, Gamma and Chi-squared, it is necessary to obtain lifespan data for each group of wood products. Over the years a great number of values have been put forward for the average life and the half-life of different wood product types. Some have been mentioned already in Table 2, Table 3 and Table 4. Dias et al. [79] observed that the reported average lifespan values fall across a wide range, for example they highlighted that the average lifetime of long-lived sawnwood varies from 15 years if it is used for furniture [80] to 145 years [50] (assuming conversion from half-life to average by dividing by ln(2)) if it is used for residential construction. They also found “long-lived wood-based panels” data spanning the range 15 years [81] to 90 years [36]. For long-lived “other industrial wood”, the average lifetime ranges from 10 years if it is used for fences or gates [82] to 50 years if it is used for poles [83]. Some of the variability within these ranges stems from geographic origin, and a closer look at the Australian study by Jaakko Pöyry Consulting [83] reveals very different results to Europe due to the type of hardwood prevalent in Australia (dense and durable Eucalypts such as Jarrah) and the allowed preservative treatment methods.

It has long been commented that technical lifespan does not necessarily define actual lifespan. For example, Pingoud et al. [37] commented “In real life the decay patterns depend on many socio-economic factors, the true lifetime of HWP can be much shorter than their technical lifetime.” This may certainly be the case for fitted kitchens and consumer goods, where fashion trends and consumer choice may lead to products being replaced before they reach any kind of failure [21]. For building service lives the reverse is often true as building service lives are typically a minimum for performance, whereas demolition rates are typically very low [15]. The greatest activity has looked at products that are building components, as the data is available for other purposes.

4.1. Service Life Values from ISO 15686-1 and Survey Data

The resurgence of interest in establishing service lives has been spurred by desire to define nationally relevant half-life values for wood products in the IPCC Tier 2 methodology [6]. The guidance from IPCC in 2014 [5] highlights the standard ISO 15686-1:2011 as containing reference service life (RSL) values and factors to adjust to gain an adjusted estimated service life (ESL) value that accounts for local conditions [84]. Values from ISO 15686 studies have also been used by the lifecycle assessment community in assessing maintenance and replacement intervals for components in buildings on the same basis [85]. The use of ESL values reflects the ‘factor method’ used in the standard. Factors account for the quality, design, workmanship, interior conditions or exterior conditions, the in-use condition and maintenance activity to adjust the reference value. The use of ESL and RSL was included in the IPCC 2019 revision with greater prominence as part of the Tier 2 methodology for country specific half-lives. In the IPCC guidance the service life can be used to calculate the half-life (t_1/2), based on an assumption of FOD [6].

$$t_{1/2}=service life\times \mathrm{l}\mathrm{n}\left(2\right)$$

(7)

Figure 3a shows the established relationship between average and half-life for FOD. However this assumption may not be valid for other models.

There are a couple of issues to consider in connection with this. The ISO 15686-1 standard was written to establish a method for building component service life prediction, and is widely used in that context. The concept has also been widely taken up for product performance estimation, as reviewed by Aktas and Bilec [85] and Coelho et al. [86]. The Weibull distribution is often used, and different shape and scale parameters can be defined. An 80% confidence interval, when applied to this distribution can provide the average service lifetime and a lower and upper bound to cover the majority of cases (Figure 3b). Aktas and Bilec [85] estimated hardwood in interior finish applications had an average lifespan of 40 years with an 80% confidence interval spanning 15 to 73 years.

Some studies have looked back to the literature from early work and the IPCC guidance from different years, and tables such as Table 2 [39]. For example, Kallio et al. [3] collated a table of half-life values from different sources (

Table 6. Half-lives for various HWPs based on the literature.

HWP Type	Half-Life Range (Years)	Half-Life (Individual Values from Each Source)	Average (Individual Values if Used)	Sources
Sawnwood and plywood	27.7 to 52	35 [6]		[6]
		36, 48.8 ([87] ~ from SI)		[87]
		Mean 31.4 [87]
		30 [36] ~		[36]
		48.6 [47] *	31, 39, 53.8 [47]	[47]
		30 [50] ~		[50]
		27.7, 34.7, 41.6, 42.3, 43.7, 49.2, 52 [90] *	40, 50, 60, 61, 63, 71, 75 [90]	[90]
Panels and boards	0.7 to 45	25 [6]		[6]
		[50] **		[50]
		20 [51]		[51]
		9.7 [21] *	14 [21]	[21]
		0.7, 3.5, 7, 17.3, 20.8 [21] *	1, 5, 10, 25, 30 [21]
Paper	0.5 to 10	2 [6]		[6]
		4 [36]		[36]
		[47] **		[47]
		1, 6 [50]		[50]
		2 [51]		[51]
Some specific HWPs
Packaging and pallets	0.06 to 6.2	1.0, 1.6 [87]		[87]
		Mean 1.5 [87]
		6 [50]		[50]
		3 [51]		[51]
		6 [91] **		[91]
Furniture	8.7 to 30	3.5, 6.9, 17 [87]		[87]
		Mean 8.8 [87]
		30 [50]		[50]
		35 [91] **		[91]
Doors and window frames	6.9 to 45.1	[90] **		[90]
		20, 35, 40 [92]		[92]
		38.8 to 45.1 [88] *	56 to 65;
		[88] ~	68 to 80;
			71 to 83 [88]	[88]
		27.4, 32.4 [89] *	39.6, 46.7 [89]	[89]
Flooring	20.8 to 34.7	20.8 [87]		[87]
		44 [86]		[86]
Exterior cladding and terrace	6.9 to 15.9	6.9 and 15.9 [93] *	10 and 23 decking [93]	[93]
		[93] ~	50 to 60 years cladding [93]
Insulation	27.7 to 42	20.8 [90] ~	30 [90] ~	[90]
		27.7, 31.2, 34.7 [90] *	40, 45, 50 [90]

Note: * indicates that the half-life was calculated from an average value given in the original source publication; ~ indicates other values were available but presumed to have been omitted during compilation; ** indicates no data was found despite being cited. Source: Kallio et al. [3] with modifications.

). These included the original works by Karjalainen et al. [36], Pingoud et al. [47,48] and Skog and Nicholson [50], but also values from more recent sources, including a very detailed analysis of finished product half-lives by Braun et al. [87] and various surveys of flooring condition or component performance [86,88,89]. The data shown in column 2 of Table 6 were reported in [3], while columns 3 and 4 were collated for this current paper by checking the cited sources, as indicated in column 5.

Table 6 and ref. [3] is a good example of assembling the data required to calculate country specific half-lives within IPCC 2019 Tier 2 methodology. Similar examples can be found in Cheng et al. [94], Braun et al. [87], Kers et al. [95]. In order to collate the data it was necessary to check whether values from the source literature were averages or half-lives. It appears from the handling of the values that Kallio et al. [3] were systematic in applying the ln(2) conversion where an average value was imported and used to obtain a half-life, giving rise to the non-integer values in the ranges that they report, this resulted in the inclusion of column 4 to show the average values (prior to conversion) in Table 6.

Analysis of tables such as the one above raise an important question, which pervades this report. The source of the service life data will strongly influence its type. If the data is collated with building design in mind, then the value will reflect some accepted mean or lower confidence interval value to ensure that components exceed it in practice. If data has been imported from ISO 15868 this is likely to be either the lower 80% confidence interval, or from some sources it may be the mean. Other studies based on surveys may consider age when surveyed, or estimated age at removal or use population time series data to determine an average. Thus the data might be an expected lifespan or an average service life duration. Both are different from a half-life. The term ‘average’ can be a further source of confusion, as the mean value differs with mathematical function, and median (often equating to half-life) may lie in a different portion of the population than the mean.

4.2. Half-Life Estimates from Other Sources

Table 6 demonstrates that there are different sources for service life data. ISO 15686 is one source of such reference values, in addition to the half-life data which has been accumulated layer by layer since the initial publication of IPCC guidance concerning half-lives in 2003.

As shown in Equation (7) above, it is possible to define an average (i.e., mean) value for the FOD population, to relate to the half-life (which is the median value), this is average = half-life/ln(2). But this average is not the same as the ‘average’ which occurs in the design-based reference service life data which is based on a different distribution, such as Weibull (Figure 3b). Over many cycles of data collation, comparison and reassembly by different studies, this distinction has become blurred. In some summary tables it is now difficult to discern whether the original values are half-lives or averages. It is often even more difficult to tell whether an average was calculated from a half-life, or modelled based on a population of observations, or a ‘best guess’. If the service life was modelled, for example under ISO 15686, it is not always possible to know whether it was from a Weibull distribution or some other function, and whether the mean was used or a lower confidence interval. This meta-data will become more important if HWP modelling becomes widely used.

As a further layer of confusion, some researchers in the field have taken to assuming that half-lives and averages are the same, as for both it can be said that the median is the point where half of the data points lie below the value and half lie above it. There are even occasions where the mean and the median are the same (e.g., in a normal distribution) but this is not the case for first order decay. The definition that half-life is “the time after which half the carbon placed in use is no longer in use” appears to have initially been used by Skog and Nicholson [45,50] and has continued through the various USA publications. It is also now in embedded in the IPCC 2019 guidelines [6]. However, in the early days it was far from clear whether service life or half-life was intended, for example Eggers [46] uses the two terms interchangeably, even though the mathematical function chosen for that study was the logistic function. The majority of the values used by Skog and Nicholson [50] had been previously proposed as median service life values by Row and Phelps [44].

It should be clear that mathematically speaking, the populations represented by first order decay and the normal distribution are very different (Figure 3a,b). And in the FOD example the ‘average’ value is actually not at the mid-point defined by the ‘half of the values are no longer in use’ criterion. This is a two-directional source of error, as some authors have taken half-lives without conversion and called them average values for other mathematical functions, e.g., [70,96] while others appear to have taken average values and used them without conversion and called them half-lives, e.g., [50] and in some cases values may be called ‘half-lives’ but used in non-FOD models [67]. Superimposed on this are the studies where the conversion according to ln(2) has been used as if the population is FOD, when the average was actually from a different function (e.g., where [3] use Coelho et al. [86] data from ESL analysis) or where FOD half-lives have been used to generate averages for use in other functions, e.g., [1,78].

If a reference service life value is taken as the average of a normal distribution, then it is not possible to calculate the half-life from this, as the distribution does not have FOD properties. As a result, some of the assumptions made in Table 6 would not stand. These sources of error are a particular hazard when assembling data for country specific half-lives, and this paper seeks to assist future researchers by highlighting which function was used for some of the most widely cited values, as well as providing reference information to aid further exploration.

4.3. A Service Life Population Examples—Flooring Products

The paper by Coelho et al. [86] on wooden flooring service lives that was used in Table 6 provides an interesting case for further analysis. The degradation of parquet flooring over time is plotted based on survey data, with a slow increase in scuffing, damage, loosening of blocks or other deterioration. The authors selected 30% degradation as the cut-off point as an end of acceptability of the appearance which, through linear regression analysis was identified as 44 years. This accorded well with literature values for typical service lives of wooden floors [97,98,99]. However, the plot itself demonstrates interesting points around service life definition (Figure 4 [86]). The plot clearly shows the wide scatter of this population of sampled flooring systems, with R² = 0.87. Many floors are of ages considerably greater than the ‘average for wood flooring’ ESL value that was found by the study, and some of considerably younger age have degradation scores of over 30%, so would be removed from service, based on the study’s findings. The study also presented ESL values based on ISO 15686-1 method for many sub-categories of wooden flooring based on wood species, flooring block type, coating type.

The scatter plot of data (Figure 4) could be used to derive a population distribution, if the age at removal were known—however all floors were in service at the time of the surveys, i.e., no data was available for the age at removal or end of life. Figure 5a shows the histograms for population age groups, indicating the full sampled population, then the population which would be removed for exceeding the threshold for degradation (i.e., with degradation 30% or more) and those which are overdue for removal (with degradation 40% or more). A closer analysis reveals that the full sampled population has a left-skewed distribution (Figure 5b), while the 30% and 40% degradation score populations are closer to a normal distribution in shape (Figure 5c,d), indicating different population functions. The age at which they reach or exceed the 30% threshold resembles a Weibull distribution (as is often used in service life modelling). Fitting a regression curve to the 30% threshold data reveals a peak at around 50 to 60 years. Whilst this is not a robust prediction of service life, it hints at the possibility of a slightly longer service life than the 44 years noted [86]. Significantly, there was nothing in the population data to indicate that a first order decay approach would be warranted, or that a half-life could represent the population of floors surveyed.

4.4. Using Service Life Data and ISO 15686

Given that the IPCC Tier 2 method for country-specific half-lives currently suggests the use of nominal product service lives to derive FOD half-life values for use in HWP reporting [6], the observations above raise interesting questions. The method has been widely picked up and used in national inventory reports. The guidance indicates the need to work at the semi-finished product level, defining an average life from which the half-life can be calculated taking into account the proportion of each product group in the market for the country [5,6]. It is suggested that RSL values, from ISO 15686 could be used, or ESL values that are more specific to the local conditions [84]. For example, a product such as cladding has high variability from region to region [100,101,102] with weathering index, and with householder maintenance skills and preferences. As a result, average service life data and RSL and ESL values are most commonly sought for national reporting.

Some studies have found that country specific half-lives decrease rather than increase the default values. Dias et al. [103] compared the IPCC FOD methods (at that time the IPCC 2006 with 2 default values in Tier 2), and the then Tier 3 method for country specific half-lives (

Table 7. Decay rates from linear and first order decay calculations compared by Dias et al. [103], showing the ‘lifespan’ for linear and the half-life for FOD methodologies.

HWP Type	First Order Decay
	Decay Rate Tier 2	Decay Rate Tier 3	Half-Life
Solidwood	0.0231		30
Wood packaging		0.5	1.386
Wood construction		0.033	21
Wood furniture		0.05	13.86
Wood other uses		0.04	17.33
Paper and paperboard	0.3466		2
Paper printing and writing		0.1	6.93
Other paper and paperboard		1.0	0.693

). For the country-specific half-lives in Portugal, construction wood was assumed only to have a half-life of 21 years, and furniture just under 14 years, and the use of country specific half-lives was seen as beneficial, achieving a good fit, but the values were lower than the default values (Table 7).

Analysis by Budzinski et al. [30] used average lifetime values for various wood products from Rüter [76] and proMietrecht [104]. These included values of 40 years for sawnwood, 34 years for fibreboard, 37 years for particleboard, 36 years for plywood. There may be some duplication or ambiguity—for example construction and prefab buildings were 60 years but ‘timber structures’ 35 years. Wooden windows and doors were 45 and 40 years, respectively, whereas furniture was 30 years. Packaging (pallets) was 6 years. The lifespans in [104] reflect values used in the insurance industry, which in turn reflect values expected by consumers. There is no benefit in overestimating service life, just like the other applications in building maintenance scheduling and LCA analysis based on ISO 15686-1 values for RSL, and ESL, based on the typical conditions and practices in a given country. This method can account for differences in weathering intensity in regions with higher wind and rain leading to increased risk of decay for exterior wood; but equally for consumer preferences and biases.

The service life data collated by Vandenbroucke [90] which was used in Table 6 was technical lifespan data, again intended to assist building design and maintenance. Wood elements are listed alongside other material types for a wide range of applications within buildings. Other studies that have considered building components have not differentiated by material type, but may also give indications of expected or reported service life. For example [105] provides detailed statistics from numerous literature sources. The data were found to be well fitted using a log normal distribution, reflecting the skewed nature of the range of lifespans [105]. It then remains to consider how to use service life data from Weibull, log-normal, Gamma or Chi-squared sources within HWP calculations. It becomes useful to look at Tier 3 methodologies, see later.

Other sources that have been used in such studies include data from textbooks on wood technology or preservation [99] or reports collating textbook information for a specific regional market [83]. These remain useful until local data from actual surveys and ISO 15686 type evaluations can be generated. Regional variation in service life can be significant with differences in wood species, product design and usage, weathering and local market expectations. To date the appropriation of data from general lists such as these has often neglected regional effects.

Where data is not yet available for structural elements, the service life of the house or building acts as a good indicator, however predicting building lifespan is also a perennial challenge [15,63]. Changes and trends in building systems used over time can lead to variable percentages of the buildings from a given era being demolished at relatively early or late periods, either due to design faults (such as low energy efficiency or material failure, e.g., concrete carbonation) or built-in short life (for example where prefabricated housing was used to address short term crises).

In fact, building end of life and demolition is even more complex than this. Thomsen and van der Flier [63] reviewed the reasons for building obsolescence and concluded that it could be modelled by physical and behavioural factors, as well as endogenous and exogenous effects. Thus a building may be obsolete due to wear, weathering, fatigue or poor maintenance, but may also become obsolete due to locational factors such as changes in building standards or nearby construction impacts. Further the behavioural factors which are endogenous include misuse, overloading or occupant behaviour while exogenous behavioural factors include social deprivation, criminality and urban blight. Most lifespan models only consider the physical factors.

5. Using Other Methods

5.1. Tier 2 and Tier 3 Methods

The Tier 2 and 3 options outlined by the IPCC [6] for country-specific methods are grouped into (a) flux data methods and (b) combinations of stock inventory and flux data methods. The flux data methods use production data (i.e., the inflow into the HWP pool) with decay or discard rate data (to model the outflow from the HWP pool). The discard rate data relies on reliable estimates of the lifespan of the HWP types as discussed in Section 4. Data from waste statistics or similar sources would overestimate the quantities leaving the HWP pool (by including timber that had not been produced domestically, as this origin information is near impossible to collect at waste disposal sites). Thus the country-specific half-life can be considered to be a Tier 2 flux data method, as are other functions for decay rate. Examples include logarithmic functions [36], retention curves [45], and distribution functions [13].

The combined flux data and stock inventory methods options within Tier 3 are where HWP stock inventory is used for one component of the analysis [6]. This is where data is available for two or more points in time, permitting a change of HWPs in the pool per year to be estimated. Examples include calculations based on change in building stock as a method for evaluating construction timber. The IPCC 2014 guidelines point out that difficulties exist for national reporting based on this method, as the proportion of HWPs in the stock that arise from domestic timber production may not be known [5]. However, interestingly the combined method can be used to consider situations where different building components have different service lives or replacement intervals.

To gather country-specific service life data, or derive half-life values from it, the following comments are useful. RSL and ESL values relating to service lives [84] can be used to consider national level service life and obsolescence, as discussed above. Or an alternative is to use a combination of production and trade statistics data with building inventory information. A third option is national surveys on the final market use of wood.

5.2. Comparing Half-Lives and Other Functions

A study on particleboards (PB) and fibreboards in Japan used methods from the three Tier in IPCC guidance, indicating that Tier 1 tends to underestimate HWP pool values [106]. The work compared the half-life of 25 years (IPCC default for wood-based panels) with a Japan specific half-life (Tier 2) and a log-normal distribution (Tier 3) based on previous analysis which indicated that this gave best estimates for building service lives [67]. The analysis of suitable mathematical functions in [67] considered the lifespan of buildings, so the defined longer average lifespan (38 to 63 years) was only applied to the quantity of PB and fibreboard destined for building applications, with the default half-life of 25 years being used on the other PB and fibreboard components [106]. As a result, the Tier 3 method gave a higher carbon stock in the HWP pool than the Tier 1 and Tier 2 methods. The need for further work on other particleboard and fibreboard applications was identified as removing the long-service life elements for a separate category will alter the half-life of the non-structural panels.

A more general reference [105] showed that building component service lives (all material types) were well fitted using a log normal distribution, reflecting the skewed nature of the range of lifespans. Building components included: electrical installations, heating systems, compact facades (including exterior insulation and rendering), flat roofs, partition walls and doors.

Cherubini et al. [78] compare four approaches to modelling the storage in wood-based panels, see Figure 6. They also commented that a similar result applies for structural timber in housing, but translated over time to model the mean lifetime at 150 years. This value was based on a value from [60]—estimating the half-life of solid wood in a new house in 2010 at 105 years, equating this to an average of 151.5 years but rounded to 150 for their analysis. The Chi-squared distribution was used by this research group in a significant group of papers [91,107]. The Delta function, which is shown as a single pulse, was used for comparison. This was chosen to achieve an effect similar to that which is sometimes used in LCA—assuming all products exit the pool at the specified design life. In addition a ‘uniform distribution’ was also compared—attributing the emissions equally across all years of the product life (in this case 60 years to allow for the range above and below the average of 30 years). They stated that this approach would be more commonly seen in land use change calculations. The study indicated that probability functions for storage effects in HWPs were beneficial, as single pulse approaches typically over-estimated CO₂ emissions. The Chi-squared distribution was most reliable.

Kayo and Tonosaki [67] used six mathematical functions in their analysis, adopting the definition of half-life based on the concept that it was the time at which half of the population remained in service (i.e., in line with the IPCC 2019 definition). The functions were first order decay, logistic, normal, log-normal, Weibull and Gamma. Their results for Japanese wooden buildings indicated that the log-normal distribution was most suitable. Their ‘half-lives’ (maximum release values in log-normal model) for different building ages were 38 years for older stock, 56 years for stock from 1965 to 1996 and 63 years for modern building stock (1997 onward).

A study by Matsumoto et al. [19] also used different functions for building service life and wood residence time in Japan. Analysis of real data for housing stock was used and functions were fitted, to minimise the residual sum of squares (RSS) value. The half-life of 459 was allocated for the exponential function (FOD). The term half-life was used for ‘average’ lifespan in the other functions, as shown in

Table 8. Parameters assigned to models of building stock in Japan, Source: [19].

	Exponential	Logistic	Normal	Log-Normal	Weibull
Half-life (years)	459	66	72	101	79
Parameter a	-	0.09555	22.60593	0.66116	3.14451
Parameter b	-	-	-	-	88.35761
RSS	0.02091	0.00644	0.00565	0.00449	0.00498

. It was acknowledged that the half-life for first order decay was abnormally long, and although 0.02 was the lowest RSS value achieved for this function, it indicates that the function is not a good fit to the data. In addition, the time series itself is considerably shorter than the half-life that has been predicted. The log-normal and the Weibull distributions gave the lowest RSS and appeared to be the most appropriate for modelling building service lives.

5.3. Some Notes on the Gamma Distribution

An interesting study which used the gamma distribution, is the paper by Mason Earles et al. [70]. The six categories from [37] were used with the half-lives assumed as the ‘year of maximum decay’ within a gamma distribution (see

Table 9. Parameters used for gamma distribution considering some common HWP categories. Source: [70].

	Other	Paper	Fiberboard	Sawnwood	Plywood/Veneer Panels
Year of max decay	20	2	20	35	30
95% decay period	50	5	40	150	75
Shape	4.124	3.196	6.557	2.151	4.161
Scale	6.242	0.683	3.509	29.982	9.334
Source	[37]	[43]	[37]	[37]	[37]

), as discussed earlier, this simplification is hard to justify. In the somewhat fatalistic scenario, they assumed clearance of all forests for all nations in FAOSTAT database, and calculated the HWP storage associated with the products, assuming a split based on log size fractions. While it is very hypothetical, it did demonstrate a range of very different residence times for nations with different wood-usage strategies. Cascading was not included, except for recycling of paper, but transfer to SWDS was included as a long-term storage. This led to very long carbon storage time for Germany—which was assumed in the study to have landfill (at that time, despite more recent European policy moving away from this).

The current USDA guidance for calculating HWP carbon, within national greenhouse gas flux calculations acknowledges that research into other distributions, such as the gamma distribution has been undertaken, for example Bates et al. [108] is cited in [59].

5.4. Chi-Squared Distribution

Some authors prefer the Chi-squared distribution to the gamma distribution as it requires fewer parameters, and data on shape of the residence curve is rarely known for products, whereas service life is more likely to be available [77,78]. The Chi-squared distribution is a special case of the Gamma distribution, with α = k/2 and β = 2, where k is a positive integer. The resulting Chi-squared distribution has k degrees of freedom. It has been used by an increasing number of authors in the past decade and a half, and many studies have indicated that Chi-squared distribution is more accurate than the widely used first order decay or exponential distribution [12,78,108].

Cherubini et al. [78] estimated k using the year of maximum oxidation rate, i.e., equivalent to the mean value for service life (ζ). For the wood products the value of k was set to ζ + 2, i.e., 4 years for paper, 32 years for non-structural panels and 152 years for housing construction materials. Guest and Strømman [91] used the Chi-squared distribution to consider the Norwegian HWP sector, assigning each product category a mean lifetime. Lifespan data appears to have been taken from [58] and the Chi-squared method of [78] was cited. The paper goes on to focus in on a single item value chain (glulam beam) and considers issues of attribution for the carbon benefit to the different parties involved in manufacture.

Iordan et al. [1] used a Chi-squared distribution to consider forest products pools in Norway, Sweden and Finland, using historic data series from 1960 to 2015. They commented that the Chi-squared distribution is a special case of the gamma distribution and requires only ‘mean half-life’ of the product to define a bell-shaped curve. Many authors have continued this practice of referring to mean half-life for this distribution, but this has perpetuated potential for misunderstandings when compiling ‘half-life’ data from studies using FOD and other functions.

For six categories of product, they used half-life values (derived from [58]) which they modified to convert to average lifespan, which was then used as the mid-point for the Chi-squared function [1]. These were bioenergy 4 years, paper 4 years, paper and board-based packaging products (9 years), pulp (9 years), furniture and building maintenance (using wood panels such as particleboard, veneer sheets, plywood, fibreboard) 43 years, and buildings (sawnwood) 140 years. The Chi-squared function was used to plot residence times and emissions for a historic timeseries (1960 to 2015) for three countries, in each case showing the residence of HWPs in longer-life products extending beyond the time series period, through to approx. 100 years into the future (2120). The lag (i.e., long term-storage) within buildings and furniture applications were clearly visible. It was commented that 50 years beyond the end of the time series 7% of the biogenic CO₂ from 2015 remained in storage in Norway, 6% in Sweden and 3% in Finland. These differences reflected the profile of product types in each country’s forest products industries. In all cases the storage effect was significant, compared to the instantaneous oxidation approach. An average decrease in the flow of carbon back to the atmosphere of 74%, 64% and 40% was seen for Finland, Sweden and Norway, respectively. A storage function of between 12 and 26 million tC/year, 13–30 million tC/year and 0.2 to 4 million tC/year were seen in Finland, Sweden and Norway. The smaller storage in Norway reflects the product mix [1].

Li et al. [109] built a model of different wood products and service lives for Maine, USA, and appeared to use a Chi-squared distribution to plot these. Using different service life estimates they plotted cumulative HWP pool projections to compare four scenarios in which the service life was extended to prolong carbon storage. They estimated that the net carbon sink for the state of Maine could be increased from 0.44 million tC to 0.63 million tC.

The same model was further developed, also for Maine, USA, with an interface to permit scenarios to be evaluated [35]. Again, the Chi-squared regression calculation was used to consider multiple pools (charcoal, timber in buildings, exterior use, home applications and paper products). The Wood Products Carbon Storage Estimator also included flow paths for recycling and landfilling. The disposal rates of products were based on a model that approximated average disposal rates peaking in year 80 (buildings), 30 years (household wood products), 25 years (exterior products) through to year 1 (packing paper) or 6 months (household paper). The user-friendly interface is intended to increase engagement with carbon calculations—making it quicker and easier to consider activity in a specific region over a given period. They also highlighted the need for ongoing data collection to assist in this.

5.5. Continuing to Use Half-Life Data

Some research groups have engaged in ongoing revision and estimation of half-life values. One example is the USDA forest service, where the initial values defined by Skog and Nicholson [48,50] were used in national methodology [58]. The assumptions and market share data were later revisited [60], producing revised values for the half-lives of residential structures to reflect modern trends. The same process of revision has been undertaken for the more recent publication of data within [59], see Table 3. The result was a decrease in half-life of single-family residential buildings to 87.8 years, and for multi-family residential to 53.7 years.

Dymond [110] incorporated the same root data, and reports that the BC-HWPv1 model uses multiple pools for considering the flow of HWPs over time. Seven of the half-life values directly relate back to the USA values [58] via [60], and the single-family home value has been adapted for the Canadian context. Half-lives range from 2 to 90 years (

Table 10. Half-life values used in Canada (Source: [110]).

HWP Type	Half-Life	References
Single family homes	90	[60,111,112]
Multifamily homes	75	[60,111,113,114]
Commercial buildings	75	[60,111,113,114]
Residential upkeep and moveable homes	30	[60,115,116,117]
Furniture and other manufacturing	38	[60,115,116,117]
Shipping	2	personal communication
Other	38	[60]
Paper	2.5	[60]

). Sources are also given, and intervals which were considered in sensitivity analysis are indicated in the full table in the paper [110]. It is interesting that with the additional sources the values appear to have consolidated at a familiar level.

Values from Table 10 have been used by others. For example, Forster et al. [8,27,118] used the IPCC Tier 1 methodology for HWP calculations, but with adjusted half-lives for the pools taken from [110]. The recycling and disposal of retired HWPs, including via bioenergy were also considered. The developed model was used to consider material flows relating to 2000 ha of commercially managed forests. This was considered in a UK context using data from a combination of forest carbon modelling, harvest data, commercial sawmill data, national recycling data and timber-use statistics. Studies such as this repeatedly demonstrate that the HWP pool has a role in mitigating greenhouse gas emissions [118].

A reference which contains an exhaustive analysis of half-life values, and can shed some light on the European context, is Braun et al. [87].

Table 11. Half-lives for three broad categories of semi-finished product, based on service life data from multiple finished products in Austria. Source: [87].

Category	Subcategory	Sub-Subcategory	Market Share (%)	Half-Life (Years)
Construction	Formwork		7.27	0.75
	Railroad ties		0.19	20.8
	Fences		1.50	16.0
	Poles and posts		1.24	20.8
	Windows		2.02	20.8
	Doors		3.81	19.1
	Floors		4.38	20.8
	Carpenter work	Glue laminated/cross laminated timber	25.1	48.8
		Wall elements	1.93	48.8
		Stairs	0.33	20.8
		Sauna cabinets	0.06	16.0
		Floors	1.84	20.8
		Wood-glass-constructions	0.11	16.0
		Other wooden goods for construction	5.38	36.0
		Other carpenter work	1.99	36.0
	Barracks		2.31	24.3
	Houses		9.75	71.0
	Category half-life 31.4 years
Furniture	Outdoor		0.92	3.5
	Office		4.86	6.9
	Private		3.61	17.0
	Category half-life 8.8 years
Packaging	Boxes/other packaging		3.67	1.0
	Pallets		17.68	1.6
	Category half-life 1.5 years
Total	Total half-life 14.6 years

gives values for semi-finished products, but the entries were taken from multiple sources provided in the supplementary information of [87]. This was because Braun and co-workers set out use service life data for finished products such as window frames or glulam elements to evaluate the semifinished product half-lives. There is a requirement in the IPCC guidelines [5,6] that only semi-finished products should be considered at Tier 2 level, thereby avoiding double counting issues. For example, the carbon in glulam items (a finished product) would be seen as potentially having been already declared in FAOSTAT tables as sawn timber (semi-finished product) so declaring the final product might double count the carbon. In this study the use of market share information for the chosen year (2002) allowed the semi-finished product half-life to be determined for three categories [87].

The semi-finished solid wood products considered were grouped into construction, furniture and packaging, as well as an overall value for all solid wood (Table 11). This was based on production data from 1982 to 2011 in Austria [87]. Solid wood combined sawn wood with wood-based panels, in line with 2006 IPCC defaults [43], rather than the later system. It was found that the half-lives for these categories changed over time, for example construction rose from 27 in 2002 to 39 in 2011, whereas the half-life for packaging was effectively stable and the half-life for furniture decreased from 10 years to 8.5 years on average [87]. These findings are important—if HWP carbon storage is to be well reported in NIRs, then thorough analysis such as this, using national production data give a more realistic estimation of the half-life. The tendency for half-life to fluctuate over time, reflecting in shifts of production and consumption is an important aspect to consider.

Some authors have used the IPCC default half-lives, but looked ahead to consider emerging products. For example, Hurmekoski et al. [26] considered wood plastic composites (WPC) in decking applications and in automotive in their analysis of the Finnish forest sector. In their table an unlikely value of 35 years is applied as half-life for WPC components in cars, but it appears there is no value for extruded WPC planks in exterior applications, possibly as Finland has limited production of this WPC type. It is clear that the choice of 35 years was to reflect the solid wood default half-life which they used for sawnwood and plywood in various applications. Similarly, the 2 year half-life was applied to pulp and paper, and was applied to dissolving pulp for use in regenerated cellulose textile applications.

Two interesting extra choices were made in this study [26]. A half-life of 1 year was applied for heat and power applications, both in CHP and at mills. A half-life of 2 years was applied for biorefining applications (biodiesel, ethanol for transport and ethylene for bioPE and bioPET products). It appears that for the fuel applications the half-life was selected to permit some storage and processing time for the fuel wood or pellets associated with these options, although whether the one-year half-life would be overestimating this residence time is not clear. In the case of the biopolymers derived using ethylene, the service life might approach something similar to paper, also with a 2-year half-life, as target applications would be packaging and short life consumer goods. To handle these emerging product types and low biomass utilisation efficiency a much higher loss level was set than for the more established wood products, (88 and 93% for ethanol and ethylene, respectively, compared to 5% manufacturing loss for all other categories).

5.6. Considerations for Future Work

It appears that the use of a half-life and FOD was initially selected to handle the varying quantities of material with short through longer durations, on the assumption that with machining and processing losses, and a large number of short life product, the resulting population might resemble first order decay or logistic decay. Marland et al. [13] commented “Only a limited fraction of harvested wood products end up in long-term final products due to material losses and residues at every stage in the refining chain, and lifetime estimates of wood products are very uncertain.” As the wood value chain continues to seek efficiency, and to explore solutions to competing sustainability priorities, the assumptions about recycling, waste wood, and offcuts or coproducts, will increasingly influence the HWP pool. This will necessitate revision of the assumptions surrounding half-lives. For example, if bioenergy is sought to achieve substitution benefits, then the HWP pool benefit will diminish, but if the HWP pool is enhanced through policy initiatives such as the New European Bauhaus, then the HWP storage effect may increase. Assessing these aspects requires increasingly accurate modelling of HWP pool dynamics, and may require repeated revision of half-lives, or choice of suitable functions and assignment of population functions.

One aspect in particular is that creating a new sub-pool of HWPs in construction with a suitable half-life value, will require a corresponding sub-pool of non-structural uses for HWPs also with a new half-life value, to avoid biassing results, as has been recognised in many studies [103]. In addition, there is likely to be a limit to the degree to which FOD can be fine-tuned by half-life revisions before different mathematical functions are required, and Tier 2 and 3 methodologies become more widely used. These aspects require ongoing vigilance when reporting values for half-life or service life chosen and mathematical function used, to aid other researchers. Clarity over this meta-data when importing values from studies by other groups will also be essential. This includes meta-data about the boundaries of the pool, the geographic region, the regional market dynamics, and the mathematical approach used. Consistency in naming the parameters, and avoiding misleading usage of names across different model types is urgently needed, especially when translating between FOD and non-exponential populations.

Half-life has become a common way to describe HWP service lives, but the use of this term for FOD and Chi-squared methods simultaneously is a large source of potential confusion. It is as if a shadow half-life concept has emerged which is not related to FOD at all, and where the term ‘half-life’ is being used to imply peak in the population distribution. New terminology such as peak, or median values could rapidly be adopted to avoid mathematical errors and assist future workers.

6. Conclusions

This paper has highlighted the difference between average lifespan, service life, and half-life, with the aim being to improve the consistency in HWP carbon calculations. In particular, an awareness of service life data sources and population models, relative to FOD models and half-lives, will improve the value selection process for future studies. It has also highlighted some common pitfalls and issues in naming, to improve future work.

Half-life and average calculated from FOD are not the same as mean average or peak decay from other functions such as Weibull, log-normal, Gamma and Chi-squared distributions.

Half-life and its fraction loss per year value are useful for simplifying complex maths at the national scale in Tier 1 methodologies, if the half-life is accurately calculated. But they often underestimate storage.

Half-life values and FOD have been widely used and appear to work well for HWP categories containing a mix of products, but they are likely to start to fail if the category is too narrow and where the service life is medium to long in duration, notably in construction applications.

For longer service life product types, time-dependent functions are better. A large interest in the Chi-squared distribution has developed, especially for work considering the built environment as an HWP pool.

Service life estimation for individual products is complex, and population dynamics may use a wide range of mathematical functions. This leads to substantial scope for errors if importing RSL or ESL values (and similar) into HWP calculations based on FOD, even if the mean is transformed to a half-life by the often recommended formula. An additional consideration is that some service life studies consider a lower confidence interval value, not the mean.

As many people seek better values for the half-life and average life of key categories (mainly buildings), there will be a knock-on effect (potential increase in inaccuracy) for the remaining ‘other wood’ category, so a shift to defining accurate service lives for structural timber elements or buildings requires corresponding refinement of the non-structural wood products’ service life data.