Assessing Forest Structure and Biomass with Multi-Sensor Remote Sensing: Insights from Mediterranean and Temperate Forests
Abstract
1. Introduction
- Evaluate the accuracy of different remote sensing sensors when estimating forest variables across a broad climatic gradient, from Mediterranean open woodlands to temperate forests.
- Analyze the contribution of disturbance information on the estimation accuracy.
- Evaluate the model’s temporal inference precision using fully independent datasets.
2. Materials and Methods
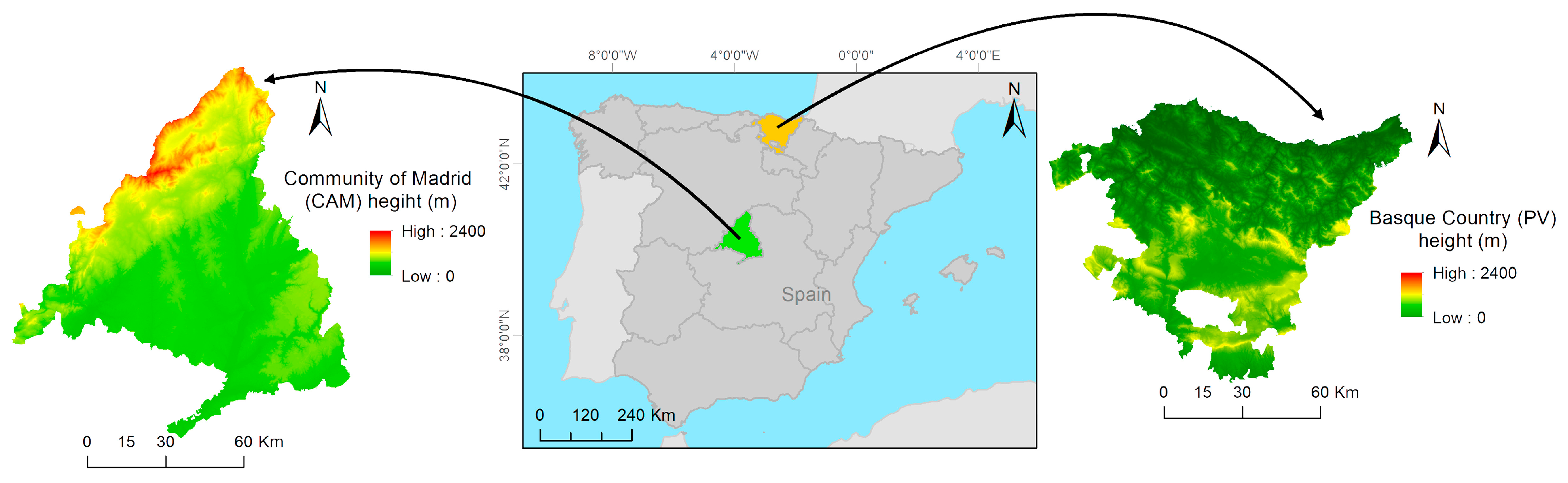
2.1. Study Area
2.2. Remote Sensing Data
2.2.1. Lidar Data
2.2.2. Optical Imagery
2.2.3. Synthetic Aperture Radar Imagery
2.2.4. Ancillary Data
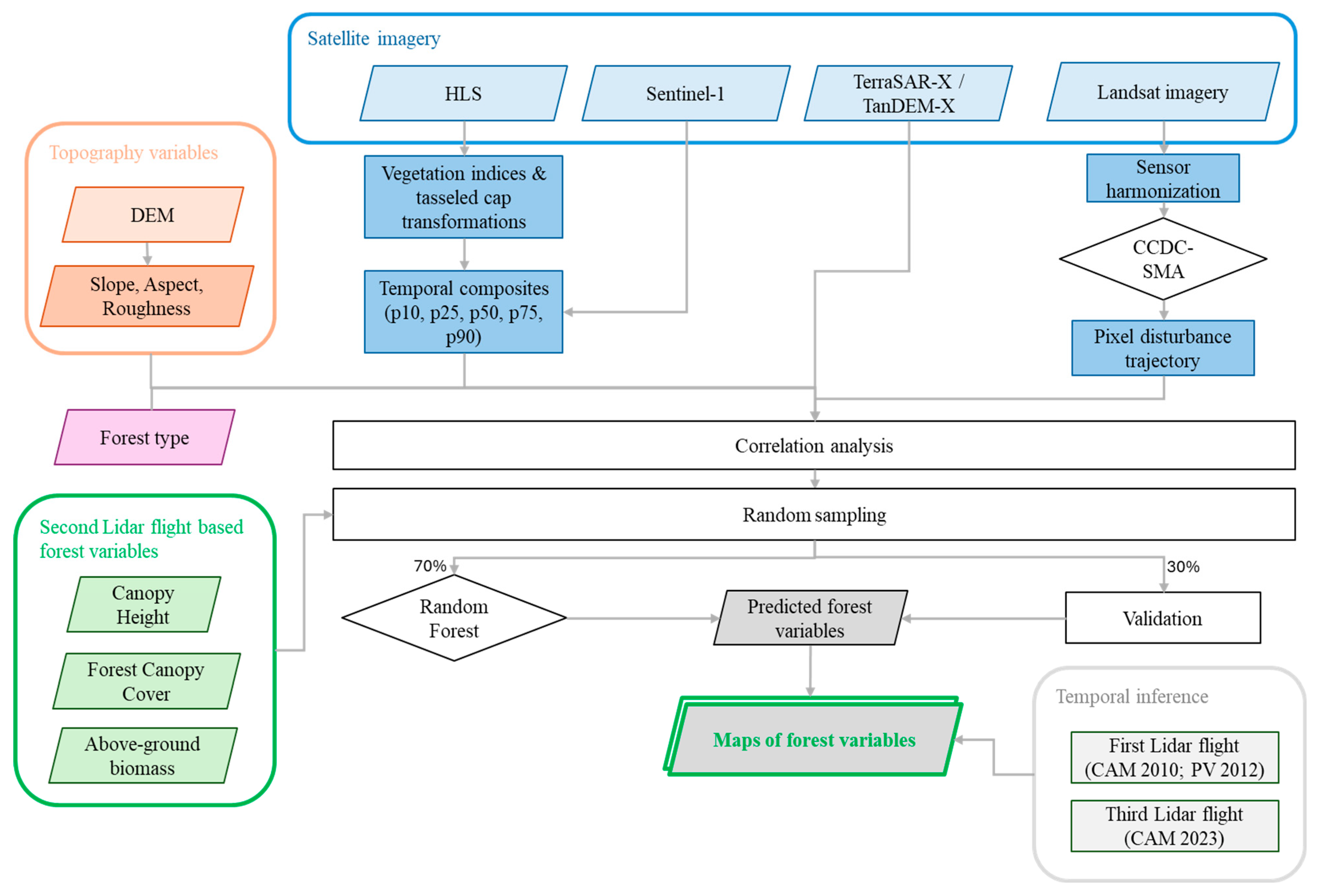
2.3. Modelling and Accuracy Assessment
2.3.1. Forest Variables Estimation
- A model based on HLS optical data (benchmark).
- An extended optical model that incorporated information on disturbances.
- A model based on C-band Sentinel-1 variables (backscatter and coherence).
- A SAR-only model combining Sentinel-1 and TSX/TDX variables.
- A model combining HLS and Sentinel-1 variables.
- A model combining HLS, Sentinel-1, and information on disturbances.
- A ‘full’ model including all the explanatory variables.
2.3.2. Model Evaluation and Performance
3. Results
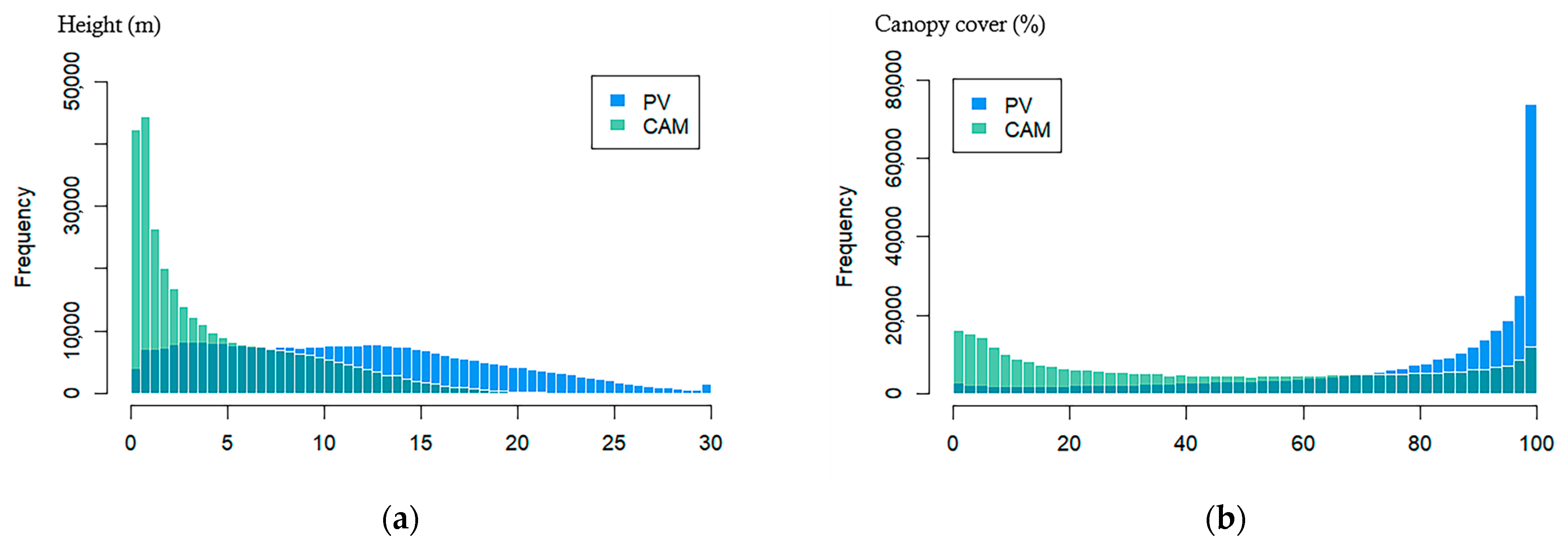
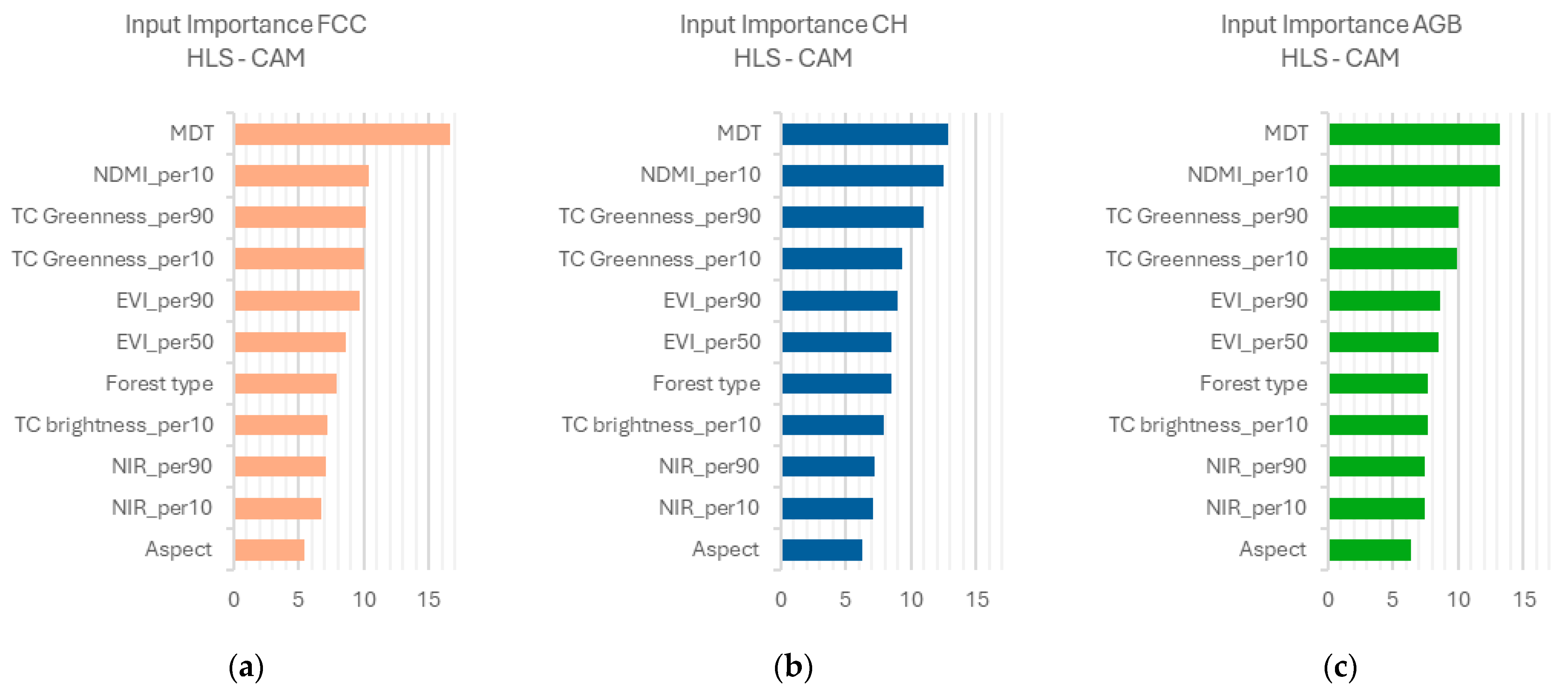
3.1. Mediterranean Forests
3.2. Temperate Forests
3.3. Temporal Inference: HLS Models
4. Discussion
4.1. Mediterranean Forests
4.2. Temperate Forests
4.3. Temporal Inference
4.4. Limitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pan, Y.; Birdsey, R.A.; Phillips, O.L.; Houghton, R.A.; Fang, J.; Kauppi, P.E.; Keith, H.; Kurz, W.A.; Ito, A.; Lewis, S.L.; et al. The enduring world forest carbon sink. Nature 2024, 631, 563–569. [Google Scholar] [CrossRef] [PubMed]
- Keenan, R.J. Climate change impacts and adaptation in forest management: A review. Ann. For. Sci. 2015, 72, 145–167. [Google Scholar] [CrossRef]
- Senf, C.; Pflugmacher, D.; Hostert, P.; Seidl, R. Using Landsat time series for characterizing forest disturbance dynamics in the coupled human and natural systems of Central Europe. ISPRS J. Photogramm. Remote Sens. 2017, 130, 453–463. [Google Scholar] [CrossRef]
- Van Lierop, P.; Lindquist, E.; Sathyapala, S.; Franceschini, G. Global forest area disturbance from fire, insect pests, diseases and severe weather events. For. Ecol. Manag. 2015, 352, 78–88. [Google Scholar] [CrossRef]
- San-Miguel-Ayanz, J.; Durrant, T.; Boca, R.; Maianti, P.; Libertà, G.; Oom, D.; Branco, A.; De Rigo, D.; Ferrari, D.; Roglia, E.; et al. Advance Report on Forest Fires in Europe, Middle East and North Africa; Publications Office of the European Union: Luxembourg, 2023. [Google Scholar]
- FOREST EUROPE; FAO; UNECE. State of Forests and Sustainable Forest Management in Europe 2020; Forest Europe: Zvolen, Slovak Republic, 2020. [Google Scholar]
- Chuvieco, E. Teledetección Ambiental: La Observación de la Tierra Desde el Espacio; Editorial Ariel: Barcelona, Spain, 2010; ISBN 9788434434981. [Google Scholar]
- Ahmed, O.S.; Franklin, S.E.; Wulder, M.A.; White, J.C. Characterizing stand-level forest canopy cover and height using Landsat time series, samples of airborne LiDAR, and the Random Forest algorithm. ISPRS J. Photogramm. Remote Sens. 2015, 101, 89–101. [Google Scholar] [CrossRef]
- Huang, R.; Zhu, J. Using Random Forest to integrate lidar data and hyperspectral imagery for land cover classification. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium—IGARSS, Melbourne, VIC, Australia, 21–26 July 2013; pp. 3978–3981. [Google Scholar] [CrossRef]
- Koetz, B.; Morsdorf, F.; Sun, G.; Ranson, K.J.; Itten, K.; Allgöwer, B. Inversion of a lidar waveform model for forest biophysical parameter estimation. IEEE Geosci. Remote Sens. Lett. 2006, 3, 49–53. [Google Scholar] [CrossRef]
- Hu, X.; Shi, L.; Lin, G.; Lin, L. Comparison of physical-based, data-driven and hybrid modeling approaches for evapotranspiration estimation. J. Hydrol. 2021, 601, 126592. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Jones, S.; Soto-Berelov, M.; Haywood, A.; Hislop, S. Landsat Time-Series for Estimating Forest Aboveground Biomass and Its Dynamics across Space and Time: A Review. Remote Sens. 2020, 12, 98. [Google Scholar] [CrossRef]
- García, M.; Riaño, D.; Chuvieco, E.; Danson, F.M. Estimating biomass carbon stocks for a Mediterranean forest in central Spain using LiDAR height and intensity data. Remote Sens. Environ. 2010, 114, 816–830. [Google Scholar] [CrossRef]
- Senf, C.; Mori, A.S.; Müller, J.; Seidl, R. The response of canopy height diversity to natural disturbances in two temperate forest landscapes. Landsc. Ecol. 2020, 35, 2101–2112. [Google Scholar] [CrossRef]
- Pourshamsi, M.; Xia, J.; Yokoya, N.; Garcia, M.; Lavalle, M.; Pottier, E.; Balzter, H. Tropical forest canopy height estimation from combined polarimetric SAR and LiDAR using machine-learning. ISPRS J. Photogramm. Remote Sens. 2021, 172, 79–94. [Google Scholar] [CrossRef]
- Viana-Soto, A.; García, M.; Aguado, I.; Salas, J. Assessing post-fire forest structure recovery by combining LiDAR data and Landsat time series in Mediterranean pine forests. Int. J. Appl. Earth Obs. Geoinf. 2022, 108, 102761. [Google Scholar] [CrossRef]
- Yu, Y.; Li, M.; Fu, Y. Forest type identification by random forest classification combined with SPOT and multitemporal SAR data. J. For. Res. 2018, 29, 1407–1414. [Google Scholar] [CrossRef]
- Coops, N.C.; Tompalski, P.; Goodbody, T.R.H.; Queinnec, M.; Luther, J.E.; Bolton, D.K.; White, J.C.; Wulder, M.A.; Van Lier, O.R.; Hermosilla, T. Modelling lidar-derived estimates of forest attributes over space and time: A review of approaches and future trends. Remote Sens. Environ. 2021, 260, 112477. [Google Scholar] [CrossRef]
- Woodcock, C.E.; Allen, R.; Anderson, M.; Belward, A.; Bindschadler, R.; Cohen, W.; Gao, F.; Goward, S.N.; Helder, D.; Helmer, E.; et al. Free access to Landsat imagery. Science 2008, 320, 1011. [Google Scholar] [CrossRef]
- Hansen, M.C.; Loveland, T.R. A review of large area monitoring of land cover change using Landsat data. Remote Sens. Environ. 2012, 122, 66–74. [Google Scholar] [CrossRef]
- Claverie, M.; Ju, J.; Masek, J.G.; Dungan, J.L.; Vermote, E.F.; Roger, J.C.; Skakun, S.V.; Justice, C. The harmonized Landsat and Sentinel-2 surface reflectance data set. Remote Sens. Environ. 2018, 219, 145–161. [Google Scholar] [CrossRef]
- Herold, M.; Skutsch, M. Monitoring, Reporting and Verification for National REDD+ Programmes: Two Proposals. Environ. Res. Lett. 2011, 6, 014002. [Google Scholar] [CrossRef]
- Liao, Z.; Liu, X.; van Dijk, A.; Yue, C.; He, B. Continuous Woody Vegetation Biomass Estimation Based on Temporal Modeling of Landsat Data. Int. J. Appl. Earth Obs. Geoinf. 2022, 110, 102811. [Google Scholar] [CrossRef]
- Tanase, M.A.; Villard, L.; Pitar, D.; Apostol, B.; Petrila, M.; Chivulescu, S.; Leca, S.; Borlaf-Mena, I.; Pascu, I.S.; Dobre, A.C.; et al. Synthetic Aperture Radar Sensitivity to Forest Changes: A Simulations-Based Study for the Romanian Forests. Sci. Total Environ. 2019, 689, 1104–1114. [Google Scholar] [CrossRef]
- Hajnsek, I.; Busche, T.; Abdullahi, S.; Bachmann, M.; Baumgartner, S.V.; Bojarski, A.; Bueso-Bello, J.L.; Esch, T.; Fritz, T.; Alonso-Gonzalez, A.; et al. TanDEM-X: The 4D Mission Phase for Earth Surface Dynamics: Science Activities Highlights and New Data Products after 15 Years of Bistatic Operations. IEEE Geosci. Remote Sens. Mag. 2025. [Google Scholar] [CrossRef]
- Gomez, C.; Lopez-Sanchez, J.M.; Romero-Puig, N.; Zhu, J.; Fu, H.; He, W.; Xie, Y.; Xie, Q. Canopy Height Estimation in Mediterranean Forests of Spain with TanDEM-X Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 2956–2970. [Google Scholar] [CrossRef]
- Trier, Ø.D.; Salberg, A.B.; Haarpaintner, J.; Aarsten, D.; Gobakken, T.; Næsset, E. Multi-Sensor Forest Vegetation Height Mapping Methods for Tanzania. Eur. J. Remote Sens. 2018, 51, 587–606. [Google Scholar] [CrossRef]
- Wang, J.; Xiao, X.; Bajgain, R.; Starks, P.; Steiner, J.; Doughty, R.B.; Chang, Q. Estimating Leaf Area Index and Aboveground Biomass of Grazing Pastures Using Sentinel-1, Sentinel-2 and Landsat Images. ISPRS J. Photogramm. Remote Sens. 2019, 154, 189–201. [Google Scholar] [CrossRef]
- Liao, Z.; Van Dijk, A.I.J.M.; He, B.; Larraondo, P.R.; Scarth, P.F. Woody Vegetation Cover, Height and Biomass at 25-m Resolution across Australia Derived from Multiple Site, Airborne and Satellite Observations. Int. J. Appl. Earth Obs. Geoinf. 2020, 88, 102066. [Google Scholar] [CrossRef]
- Tanase, M.A.; Nova, J.P.G.; Marino, E.; Aponte, C.; Tomé, J.L.; Yáñez, L.; Madrigal, J.; Guijarro, M.; Hernando, C. Characterizing Live Fuel Moisture Content from Active and Passive Sensors in a Mediterranean Environment. Forests 2022, 13, 1846. [Google Scholar] [CrossRef]
- Næsset, E. Area-Based Inventory in Norway—From Innovation to an Operational Reality. In Forestry Applications of Airborne Laser Scanning; Maltamo, M., Næsset, E., Vauhkonen, J., Eds.; Springer: Dordrecht, The Netherlands, 2014; Volume 27. [Google Scholar] [CrossRef]
- Magnussen, S.; Nord-Larsen, T.; Riis-Nielsen, T. Lidar supported estimators of wood volume and aboveground biomass from the Danish national forest inventory (2012–2016). Remote Sens. Environ. 2018, 211, 146–153. [Google Scholar] [CrossRef]
- Rivas Martínez, S.; Gandullo, J.M. Memoria del Mapa de Series de Vegetación de España: 1:400.000; ICONA: Madrid, Spain, 1987. [Google Scholar]
- Agencia Estatal de Meteorología (AEMET); Instituto de Meteorologia de Portugal. Atlas Climático Ibérico/Iberian Climate Atlas; AEMET: Madrid, Spain, 2011. [Google Scholar]
- HAZI Fundazioa. El Bosque Vasco en Cifras 2022; HAZI: Vitoria-Gasteiz, Spain, 2022. [Google Scholar]
- Gurrutxaga San Vicente, M. Patrones de Cobertura y Protección de los Bosques en el País Vasco. Geographicalia 2008, 53, 49–72. [Google Scholar] [CrossRef]
- Comunidad de Madrid. El Medio Ambiente de la Comunidad de Madrid 2006–2007; Comunidad de Madrid: Madrid, Spain, 2007. [Google Scholar]
- McGaughey, R.J. FUSION/LDV: Software for LiDAR Data Analysis and Visualization. In F.S. Department of Agriculture, Pacific Northwest Research Station; USDA: Seattle, WA, USA, 2021. [Google Scholar]
- Montero, G.; Ruiz-Peinado, R.; Muñoz, M. Producción de Biomasa y Fijación de CO2 por los Bosques Españoles; Instituto Nacional de Investigación y Tecnología Agraria y Alimentaria (INIA): Madrid, Spain, 2005. [Google Scholar]
- Tanase, M.A.; Mihai, M.C.; Miguel, S.; Cantero, A.; Tijerin, J.; Ruiz-Benito, P.; Domingo, D.; Garcia-Martin, A.; Aponte, C.; Lamelas, M.T. Long-term annual estimation of forest above ground biomass, canopy cover, and height from airborne and spaceborne sensors synergies in the Iberian Peninsula. Environ. Res. 2024, 259, 119432. [Google Scholar] [CrossRef]
- Rouse, J.W., Jr.; Haas, R.H.; Deering, D.W.; Schell, J.A.; Harlan, J.C. Monitoring the Vernal Advancement and Retrogradation (Green Wave Effect) of Natural Vegetation; NASA/GSFC, Final Report: Greenbelt, MD, USA, 1974. [Google Scholar]
- Gao, B.C. NDWI—A Normalized Difference Water Index for Remote Sensing of Vegetation Liquid Water from Space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Key, C.H.; Benson, N.C. Landscape Assessment: Remote Sensing of Severity, the Normalized Burn Ratio. In FIREMON: Fire Effects Monitoring and Inventory System; USDA Forest Service, Rocky Mountain Research Station: Ogden, UT, USA, 2006. [Google Scholar]
- Justice, C.O.; Vermote, E.; Townshend, J.R.G.; Defries, R.; Roy, D.P.; Hall, D.K.; Salomonson, V.V.; Privette, J.L.; Riggs, G.; Strahler, A.; et al. The Moderate Resolution Imaging Spectroradiometer (MODIS): Land Remote Sensing for Global Change Research. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1228–1249. [Google Scholar] [CrossRef]
- Baig, M.H.A.; Zhang, L.; Shuai, T.; Tong, Q. Derivation of a Tasselled Cap Transformation Based on Landsat 8 At-Satellite Reflectance. Remote Sens. Lett. 2014, 5, 423–431. [Google Scholar] [CrossRef]
- Crist, E.P.; Cicone, R.C. A Physically-Based Transformation of Thematic Mapper Data—The TM Tasseled Cap. IEEE Trans. Geosci. Remote Sens. 1984, GE-22, 256–263. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E. Continuous Change Detection and Classification of Land Cover Using All Available Landsat Data. Remote Sens. Environ. 2014, 144, 152–171. [Google Scholar] [CrossRef]
- Soenen, S.A.; Peddle, D.R.; Coburn, C.A. SCS+C: A Modified Sun-Canopy-Sensor Topographic Correction in Forested Terrain. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2148–2159. [Google Scholar] [CrossRef]
- Wegmüller, U.; Werner, C.; Strozzi, T.; Wiesmann, A. Automated and Precise Image Registration Procedures. In Analysis of Multi-Temporal Remote Sensing Images; Bruzzone, L., Smits, P., Eds.; World Scientific Publishing: Singapore, 2002; pp. 37–49. [Google Scholar]
- Frey, O.; Santoro, M.; Werner, C.L.; Wegmüller, U. DEM-Based SAR Pixel-Area Estimation for Enhanced Geocoding Refinement and Radiometric Normalization. IEEE Geosci. Remote Sens. Lett. 2013, 10, 48–52. [Google Scholar] [CrossRef]
- Quegan, S.; Le Toan, T.; Yu, J.J.; Ribbes, F.; Floury, N. Multitemporal ERS SAR Analysis Applied to Forest Mapping. IEEE Trans. Geosci. Remote Sens. 2000, 38, 741–753. [Google Scholar] [CrossRef]
- Goldstein, R.M.; Werner, C.L. Radar Interferogram Filtering for Geophysical Applications. Geophys. Res. Lett. 1998, 25, 4035–4038. [Google Scholar] [CrossRef]
- Werner, C.L.; Wegmüller, U.; Strozzi, T. Processing Strategies for Phase Unwrapping for InSAR Applications. In Proceedings of the 4th European Conference on Synthetic Aperture Radar (EUSAR 2002), Cologne, Germany, 4–6 June 2002; VDE: Cologne, Germany, 2002; pp. 353–356. [Google Scholar]
- Miguel, S.; Ruiz-Benito, P.; Rebollo, P.; Viana-Soto, A.; Mihai, M.C.; García, M.; Tanase, M. Forest Disturbance Regimes and Trends in Continental Spain (1985–2023) Using Dense Landsat Time Series. Environ. Res. 2024, 262, 119802. [Google Scholar] [CrossRef]
- Souza, C.M.; Roberts, D.A.; Cochrane, M.A. Combining Spectral and Spatial Information to Map Canopy Damage from Selective Logging and Forest Fires. Remote Sens. Environ. 2005, 98, 329–343. [Google Scholar] [CrossRef]
- Souza, C.M.; Siqueira, J.V.; Sales, M.H.; Fonseca, A.V.; Ribeiro, J.G.; Numata, I.; Cochrane, M.A.; Barber, C.P.; Roberts, D.A.; Barlow, J. Ten-Year Landsat Classification of Deforestation and Forest Degradation in the Brazilian Amazon. Remote Sens. 2013, 5, 5493–5513. [Google Scholar] [CrossRef]
- Chen, S.; Woodcock, C.E.; Bullock, E.L.; Arévalo, P.; Torchinava, P.; Peng, S.; Olofsson, P.; Weiss, M. Monitoring Temperate Forest Degradation on Google Earth Engine Using Landsat Time Series Analysis. Remote Sens. Environ. 2021, 265, 112648. [Google Scholar] [CrossRef]
- Roberts, D.W.; Cooper, S.V. Concepts and Techniques of Vegetation Mapping. In Land Classifications Based on Vegetation: Applications for Resource Management; Ferguson, D.E., Morgan, P., Johnson, F.D., Eds.; USDA Forest Service, General Technical Report INT-257; Intermountain Research Station: Ogden, UT, USA, 1989; pp. 90–96. [Google Scholar]
- Wilson, M.F.J.; O’Connell, B.; Brown, C.; Guinan, J.C.; Grehan, A.J. Multiscale Terrain Analysis of Multibeam Bathymetry Data for Habitat Mapping on the Continental Slope. Mar. Geod. 2007, 30, 3–35. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Englhart, S.; Keuck, V.; Siegert, F. Aboveground Biomass Retrieval in Tropical Forests—The Potential of Combined X- and L-Band SAR Data Use. Remote Sens. Environ. 2011, 115, 1260–1271. [Google Scholar] [CrossRef]
- Belenguer-Plomer, M.A.; Chuvieco, E.; Tanase, M.A. Temporal Decorrelation of C-Band Backscatter Coefficient in Mediterranean Burned Areas. Remote Sens. 2019, 11, 2661. [Google Scholar] [CrossRef]
- Velasco Pereira, E.A.; Varo Martínez, M.A.; Ruiz Gómez, F.J.; Navarro-Cerrillo, R.M. Temporal Changes in Mediterranean Pine Forest Biomass Using Synergy Models of ALOS PALSAR–Sentinel-1–Landsat-8 Sensors. Remote Sens. 2023, 15, 3430. [Google Scholar] [CrossRef]
- Gao, X.; Huete, A.R.; Ni, W.; Miura, T. Optical–Biophysical Relationships of Vegetation Spectra without Background Contamination. Remote Sens. Environ. 2000, 74, 609–620. [Google Scholar] [CrossRef]
- Gómez, C.; Wulder, M.A.; White, J.C.; Montes, F.; Delgado, J.A. Characterizing 25 years of change in the area, distribution, and carbon stock of Mediterranean pines in Central Spain. Int. J. Remote Sens. 2012, 33, 5546–5573. [Google Scholar] [CrossRef]
- Bolton, D.K.; Tompalski, P.; Coops, N.C.; White, J.C.; Wulder, M.A.; Hermosilla, T.; Queinnec, M.; Luther, J.E.; Van Lier, O.R.; Fournier, R.A.; et al. Optimizing Landsat time series length for regional mapping of lidar-derived forest structure. Remote Sens. Environ. 2020, 239, 111645. [Google Scholar] [CrossRef]
- Anderson-Teixeira, K.J.; Miller, A.D.; Mohan, J.E.; Hudiburg, T.W.; Duval, B.D.; DeLucia, E.H. Altered dynamics of forest recovery under a changing climate. Glob. Chang. Biol. 2013, 19, 2001–2021. [Google Scholar] [CrossRef] [PubMed]
- Baudena, M.; Santana, V.M.; Baeza, M.J.; Bautista, S.; Eppinga, M.B.; Hemerik, L.; Garcia Mayor, A.; Rodriguez, F.; Valdecantos, A.; Vallejo, V.R.; et al. Increased aridity drives post-fire recovery of Mediterranean forests towards open shrublands. New Phytol. 2020, 225, 1500–1515. [Google Scholar] [CrossRef]
- Teijido-Murias, I.; Antropov, O.; López-Sánchez, C.A.; Barrio-Anta, M.; Miettinen, J. Forest Height and Volume Mapping in Northern Spain with Multi-Source Earth Observation Data: Method and Data Comparison. Forests 2025, 16, 563. [Google Scholar] [CrossRef]
- Morin, D.; Planells, M.; Guyon, D.; Villard, L.; Mermoz, S.; Bouvet, A.; Thevenon, H.; Dejoux, J.F.; Le Toan, T.; Dedieu, G. Estimation and mapping of forest structure parameters from open access satellite images: Development of a generic method with a study case on coniferous plantation. Remote Sens. 2019, 11, 1275. [Google Scholar] [CrossRef]
- Pascual, C.; García-Abril, A.; Cohen, W.B.; Martín-Fernández, S.; Garci’a, A.; García-Abril, G.; Marti’n, S.; Marti’n-Ferna’ndez, M.; Ferna’ndez, F.; Montes, T.S.I. Relationship between LiDAR-derived forest canopy height and Landsat images. Int. J. Remote Sens. 2010, 31, 1261–1280. [Google Scholar] [CrossRef]
- Cruz-Alonso, V.; Ruiz-Benito, P.; Villar-Salvador, P.; María Rey-Benayas, J.; Juan Carlos Móstoles, R.; Correspondence Verónica Cruz-Alonso, S. Long-term recovery of multifunctionality in Mediterranean forests depends on restoration strategy and forest type. J. Appl. Ecol. 2019, 56, 745–757. [Google Scholar] [CrossRef]
- Wulder, M.A.; Ortlepp, S.M.; White, J.C.; Maxwell, S. Evaluation of Landsat-7 SLC-off image products for forest change detection. Can. J. Remote Sens. 2008, 34, 93–99. [Google Scholar] [CrossRef]
- Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.A.; Tyukavina, A.; Thau, D.; Stehman, S.V.; Goetz, S.J.; Loveland, T.R.; et al. High-resolution global maps of 21st-century forest cover change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef]
- Potapov, P.V.; Turubanova, S.A.; Tyukavina, A.; Krylov, A.M.; Mccarty, J.L.; Radeloff, V.C.; Hansen, M.C. Eastern Europe’s forest cover dynamics from 1985 to 2012 quantified from the full Landsat archive. Remote Sens. Environ. 2015, 159, 28–43. [Google Scholar] [CrossRef]
- Esteban, J.; McRoberts, R.E.; Fernández-Landa, A.; Tomé, J.L.; Marchamalo, M. A Model-Based Volume Estimator that Accounts for Both Land Cover Misclassification and Model Prediction Uncertainty. Remote Sens. 2020, 12, 3360. [Google Scholar] [CrossRef]
- Roberts, J.W.; Tesfamichael, S.; Gebreslasie, M.; Van Aardt, J.; Ahmed, F.B. Forest structural assessment using remote sensing technologies: An overview of the current state of the art. South. Hemisph. For. J. 2007, 69, 183–203. [Google Scholar] [CrossRef]
- Huang, C.; Zhang, C.; He, Y.; Liu, Q.; Li, H.; Su, F.; Liu, G.; Bridhikitti, A. Land Cover Mapping in Cloud-Prone Tropical Areas Using Sentinel-2 Data: Integrating Spectral Features with Ndvi Temporal Dynamics. Remote Sens. 2020, 12, 1163. [Google Scholar] [CrossRef]
| Model | Forest Variable | CAM | PV | ||||
|---|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | R2 | RMSE | MAE | ||
| Optical-based models | |||||||
| HLS | FCC | 0.77 | 14.47 | 11.08 | 0.58 | 17.28 | 13.30 |
| CH | 0.81 | 1.76 | 1.19 | 0.56 | 4.49 | 3.51 | |
| AGB | 0.77 | 29.44 | 21.58 | 0.49 | 115.60 | 88.97 | |
| HLS and disturbance data | FCC | 0.74 | 13.54 | 10.38 | 0.60 | 17.93 | 14.28 |
| CH | 0.68 | 2.05 | 1.56 | 0.53 | 3.74 | 2.88 | |
| AGB | 0.63 | 34.41 | 27.13 | 0.43 | 95.94 | 70.85 | |
| Radar-based models | |||||||
| Sentinel-1 | FCC | 0.40 | 23.44 | 19.17 | 0.45 | 19.52 | 15.07 |
| CH | 0.47 | 2.94 | 2.10 | 0.51 | 4.72 | 3.64 | |
| AGB | 0.47 | 44.33 | 33.76 | 0.46 | 118.97 | 89.95 | |
| Sentinel-1 and TSX/TDX | FCC | 0.67 | 17.33 | 13.56 | 0.46 | 16.69 | 12.63 |
| CH | 0.80 | 1.79 | 1.22 | 0.68 | 3.65 | 2.72 | |
| AGB | 0.78 | 28.33 | 20.74 | 0.65 | 92.64 | 67.08 | |
| Mixed models | |||||||
| HLS and Sentinel-1 | FCC | 0.77 | 14.55 | 11.15 | 0.61 | 16.70 | 12.79 |
| CH | 0.81 | 1.76 | 1.20 | 0.64 | 4.10 | 3.16 | |
| AGB | 0.77 | 29.26 | 21.49 | 0.58 | 105.76 | 80.09 | |
| HLS, Sentinel-1, and disturbance data | FCC | 0.75 | 13.29 | 10.19 | 0.63 | 17.27 | 13.69 |
| CH | 0.70 | 2.01 | 1.52 | 0.59 | 3.52 | 2.69 | |
| AGB | 0.65 | 33.68 | 26.57 | 0.50 | 99.75 | 76.22 | |
| HLS, Sentinel-1, disturbance data, and TSX/TDX | FCC | 0.76 | 12.90 | 9.90 | 0.61 | 16.31 | 12.94 |
| CH | 0.79 | 1.67 | 1.23 | 0.68 | 3.00 | 2.24 | |
| AGB | 0.75 | 28.47 | 21.75 | 0.62 | 75.86 | 53.87 | |
| Region of Madrid (2010) | |||
| Forest Variable | R2 | RMSE | MAE |
| FCC | 0.51 | 27.86 | 22.90 |
| CH | 0.57 | 2.58 | 2.15 |
| AGB | 0.59 | 45.28 | 36.59 |
| Region of Madrid (2023) | |||
| Forest Variable | R2 | RMSE | MAE |
| FCC | 0.61 | 19.67 | 15.55 |
| CH | 0.55 | 5.41 | 4.04 |
| Region of the Basque Country (2012) | |||
|---|---|---|---|
| Forest Variable | R2 | RMSE | MAE |
| FCC | 0.13 | 32.99 | 28.97 |
| CH | 0.03 | 8.62 | 7.85 |
| AGB | 0.03 | 217.88 | 205.52 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mihai, M.C.; Miguel, S.; Borlaf-Mena, I.; Tijerín-Triviño, J.; Tanase, M. Assessing Forest Structure and Biomass with Multi-Sensor Remote Sensing: Insights from Mediterranean and Temperate Forests. Forests 2025, 16, 1164. https://doi.org/10.3390/f16071164
Mihai MC, Miguel S, Borlaf-Mena I, Tijerín-Triviño J, Tanase M. Assessing Forest Structure and Biomass with Multi-Sensor Remote Sensing: Insights from Mediterranean and Temperate Forests. Forests. 2025; 16(7):1164. https://doi.org/10.3390/f16071164
Chicago/Turabian StyleMihai, Maria Cristina, Sofia Miguel, Ignacio Borlaf-Mena, Julián Tijerín-Triviño, and Mihai Tanase. 2025. "Assessing Forest Structure and Biomass with Multi-Sensor Remote Sensing: Insights from Mediterranean and Temperate Forests" Forests 16, no. 7: 1164. https://doi.org/10.3390/f16071164
APA StyleMihai, M. C., Miguel, S., Borlaf-Mena, I., Tijerín-Triviño, J., & Tanase, M. (2025). Assessing Forest Structure and Biomass with Multi-Sensor Remote Sensing: Insights from Mediterranean and Temperate Forests. Forests, 16(7), 1164. https://doi.org/10.3390/f16071164







