A Critical Review of Methods and Techniques Used for Monitoring Deformations in Wooden Panel Paintings
Abstract
1. Introduction
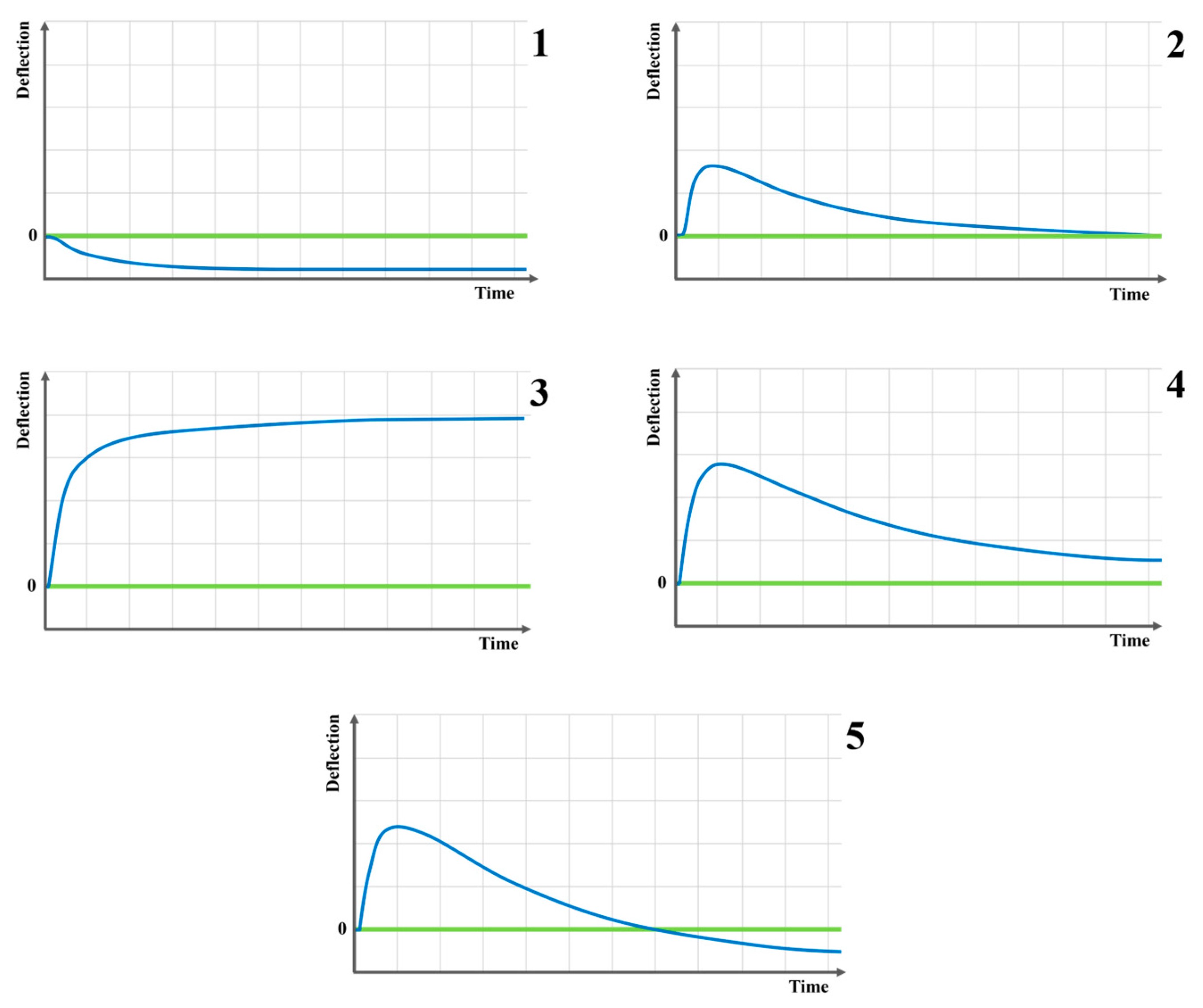
- Non-flying wood monotonic behavior with asymptotic concave deformation relative to the painted face, typical of WPPs painted on the back face with low-stiffness paint layers;
- Flying-wood non-monotonic behavior without residual concavity, characteristic of WPPs painted on a radial board with low-to-high stiffness paint layers;
- Non-flying wood monotonic behavior with asymptotic convex deformation, typical of WPPs painted on a tangential board with high stiffness and low emissivity;
- Flying-wood-type non-monotonic behavior with asymptotic concave deformation, common in WPPs painted on the back side of a tangential board with low emissivity and stiffness paint layers;
- Flying-wood-type non-monotonic behavior with asymptotic convex deformation, typical of WPPs painted on a tangential board with low emissivity and stiffness.
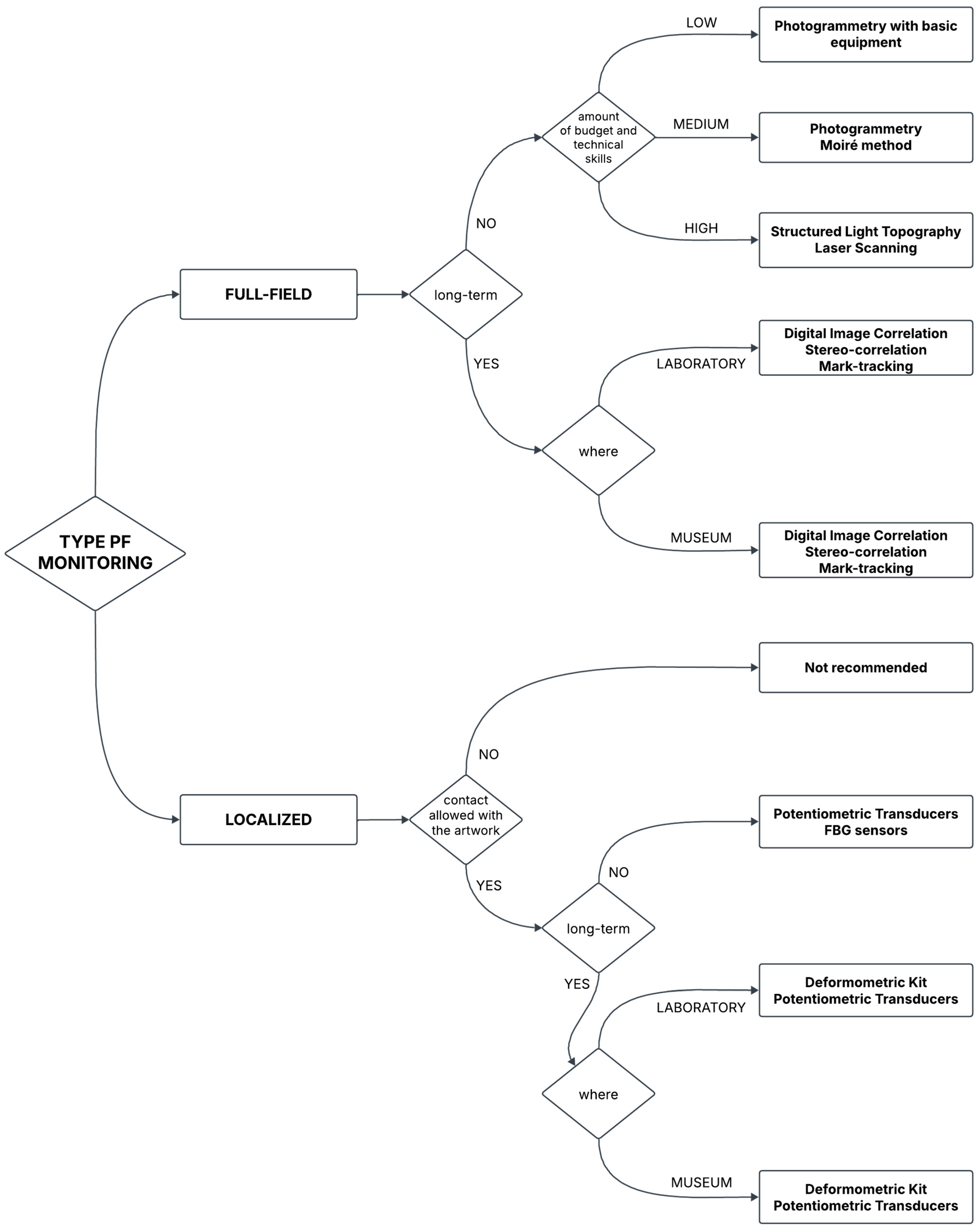
2. Methodological Approach
3. Techniques for Localized Deformations
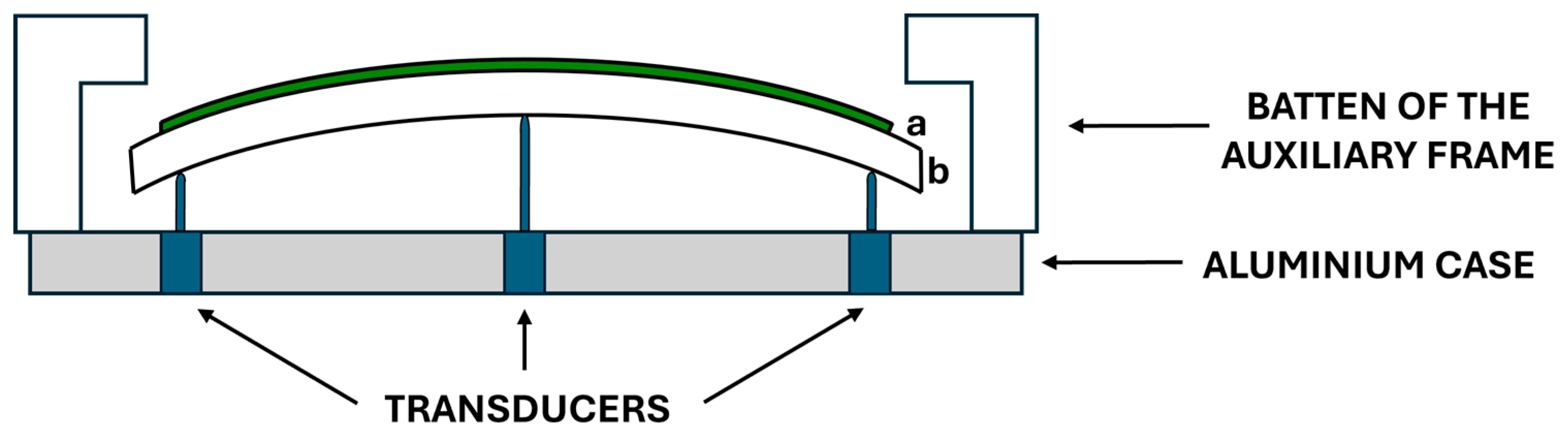
3.1. Linear Potentiometric Transducers
3.2. Deformometric Kit
3.3. Fiber Bragg Grating Sensors
- represents the strain contribution to the Bragg wavelength modulation, with being the photoelastic coefficient accounting for the strain-induced change in the refractive index;
- represents the thermal contribution, where is the thermal expansion coefficient of the fiber and is the thermal modulation of the core refractive index.
3.4. Summary of Localized Deformation Measurement Methods
4. Techniques for Full-Field Deformations
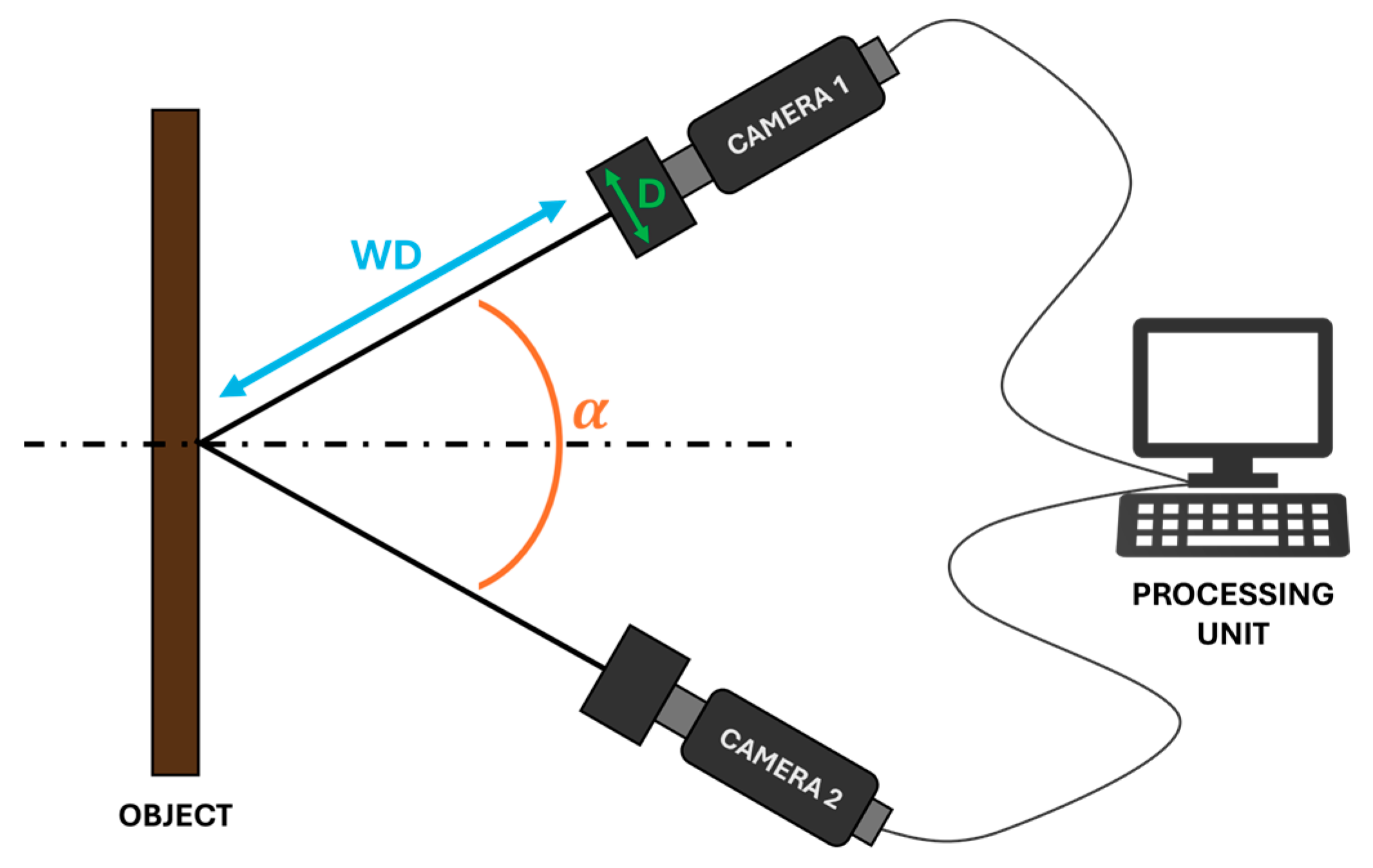
4.1. Digital Image Correlation, Stereo-Correlation, and Mark-Tracking
4.2. Three-Dimensional Models and Their Comparison
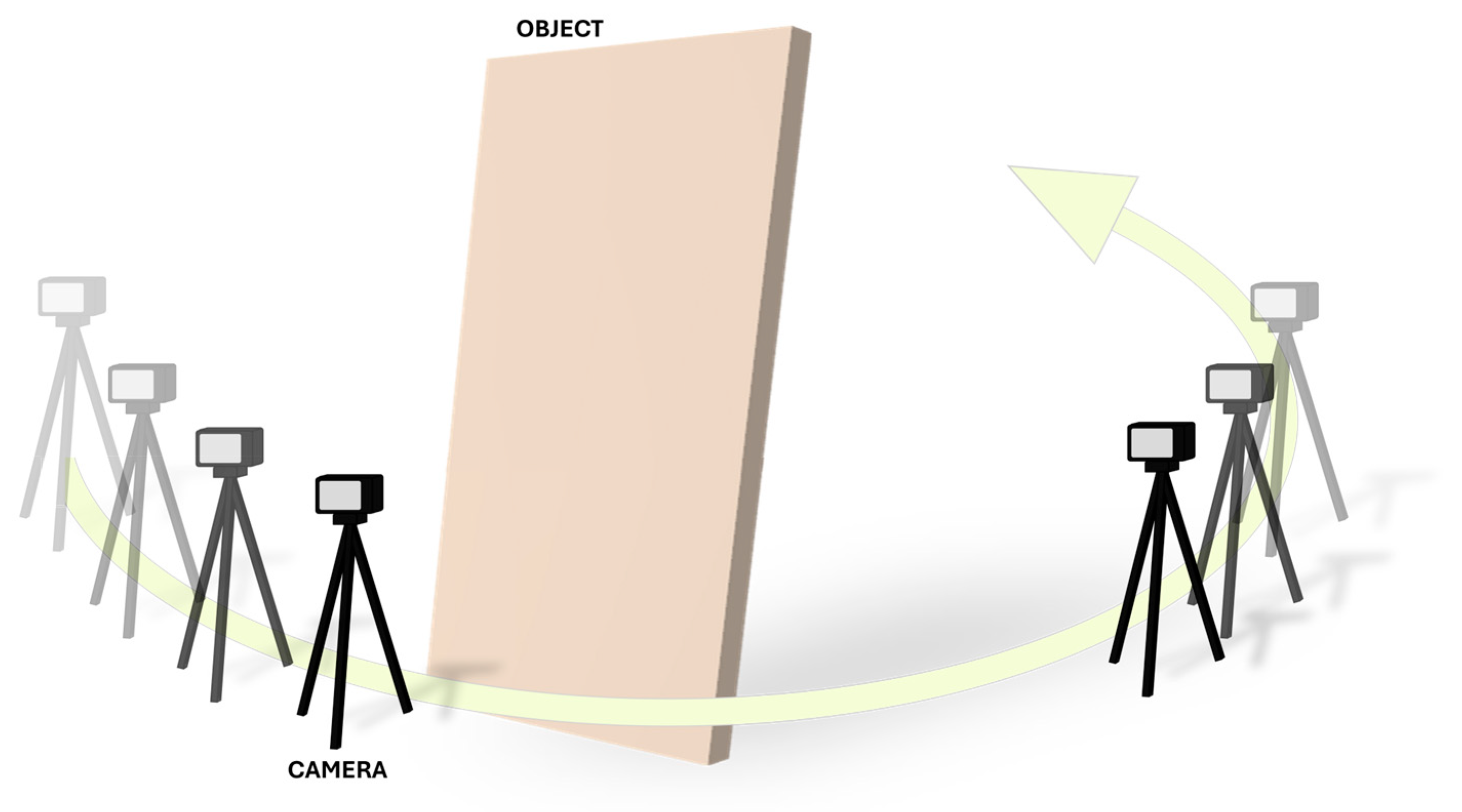
4.2.1. Photogrammetry
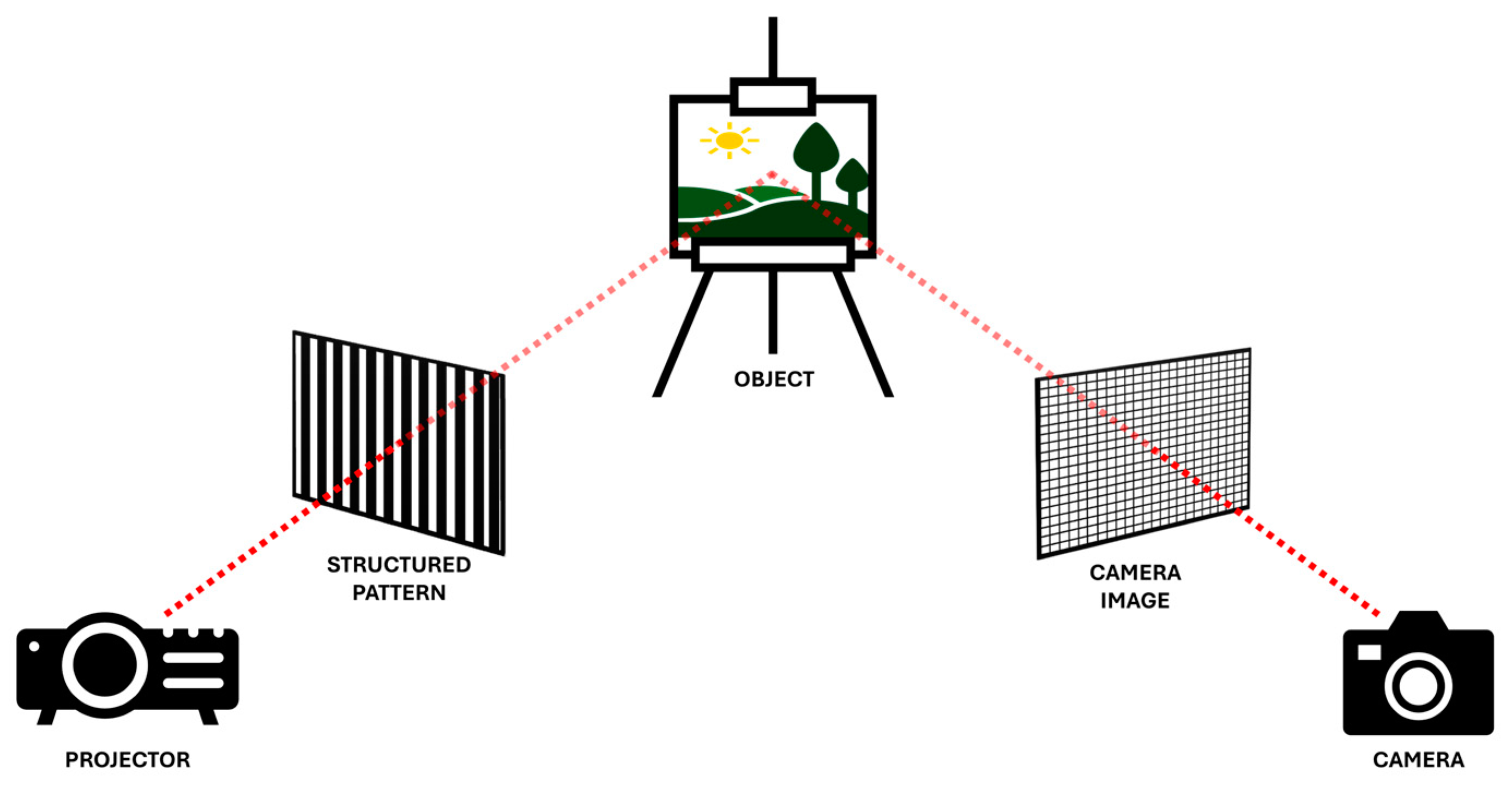
4.2.2. Structured Light Topography
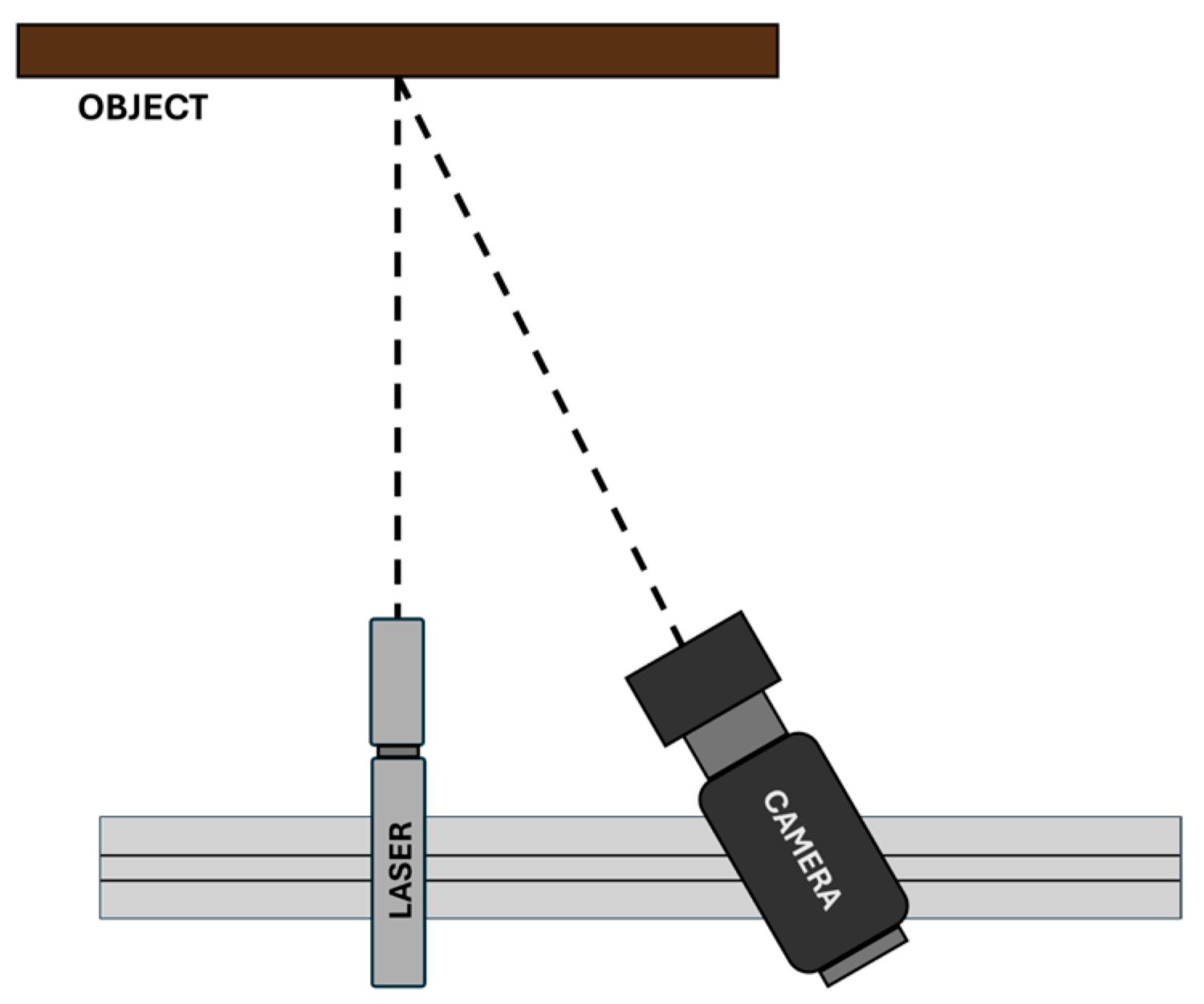
4.2.3. Laser Scanning
4.2.4. Application of Different 3D Modeling Techniques
4.3. Moiré Method
4.4. Summary of Full-Field Deformation Measurement Methods
5. Comparative Analysis of Deformation Monitoring Techniques
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Uzielli, L. Historical Overview of Panel-Making Techniques in Central Italy. In The Structural Conservation of Panel Paintings, Proceedings of the Symposium at the J. Paul Getty Museum, Los Angeles, CA, USA, 24–28 April 1995; Getty Conservation Institute: Los Angeles, CA, USA, 1998; pp. 110–135. [Google Scholar]
- Castelli, C. Techniques of Construction of Wooden Supports for Painting. In Structural Conservation of Panel Paintings at the Opificio Delle Pietre Dure in Florence: Method, Theory, and Practice; Collana dal restauro agli studi; Edifir Edizioni Firenze: Florence, Italy, 2016; pp. 285–349. ISBN 978-88-7970-792-3. [Google Scholar]
- Marette, J. Connaissance Des Primitifs Par L’étude Du Bois. Bull. Monum. 1961, 119-3, 290. [Google Scholar]
- Mecklenburg, M.F.; Tumosa, C.S.; Erhardt, W.D. Structural Response of Painted Wood Surfaces to Changes in Ambient Relative Humidity. In Painted Wood: History and Conservation; Dorge, V., Howlett, F.C., Eds.; The Getty Conservation Institute: Los Angeles, CA, USA, 1998; p. 464. [Google Scholar]
- Fioravanti, M. Le specie legnose dei supporti: Implicazioni per la conoscenza, la conservazione ed il restauro dei dipinti su tavola. In Conservazione dei Dipinti su Tavola; Nardini: Firenze, Italy, 1994; pp. 83–108. ISBN 978-88-404-4027-9. [Google Scholar]
- Cennini, C. Il Libro Dell’arte; Neri Pozza Editore S.p.a.: Vicenza, Italy, 2009. [Google Scholar]
- Federspiel, B. Questions About Medieval Gesso Grounds; The Getty Conservation Institute: Los Angeles, CA, USA; University of Leiden: Leiden, The Netherlands, 1995; pp. 58–64. [Google Scholar]
- Martin, E.; Sonoda, N.; Duval, A. Contribution à l’étude Des Préparations Blanches Des Tableaux Italiens Sur Bois. Stud. Conserv. 1992, 37, 82–92. [Google Scholar] [CrossRef]
- Riparbelli, L. Hygromechanical Behaviour of Wooden Panel Paintings: Classification of Their Deformation Tendencies Based on Numerical Modelling and Experimental Results. Herit. Sci. 2023, 11, 25. [Google Scholar] [CrossRef]
- Blanchette, R.A. A Guide to Wood Deterioration Caused by Microorganisms and Insects. In The Structural Conservation of Panel Paintings, Proceedings of the Symposium at the J. Paul Getty Museum, Los Angeles, CA, USA, 24–28 April 1995; Getty Conservation Institute: Los Angeles, CA, USA, 1998; pp. 55–68. [Google Scholar]
- Hoadley, R.B. Chemical and Physical Properties of Wood. In The Structural Conservation of Panel Paintings, Proceedings of the Symposium at the J. Paul Getty Museum, Los Angeles, CA, USA, 24–28 April 1995; Getty Conservation Institute: Los Angeles, CA, USA, 1998; pp. 2–20. [Google Scholar]
- Uzielli, L.; Fioravanti, M. Il Comportamento Fisico-Meccanico Del Legno Nei Dipinti Su Tavola. In Dipinti su Tavola. La Tecnica e la Conservazione dei Supporti; Edifir: Firenze, Italy, 2000; pp. 37–58. ISBN 978-88-7970-083-2. [Google Scholar]
- Uzielli, L. Danni causati ai dipinti su tavola da variazioni termoigrometriche, e loro prevenzione. In Conservazione dei Dipinti su Tavola; Nardini: Firenze, Italy, 1994; pp. 109–149. ISBN 978-88-404-4027-9. [Google Scholar]
- Riparbelli, L. Modelling of Hygro-Mechanical Behaviour of Wooden Panel Paintings: Model Calibration and Artworks Characterisation. Herit. Sci. 2023, 11, 126. [Google Scholar] [CrossRef]
- Lorenzo, R.; Paola, M.; Thomas, H.; Chiara, M.; Luca, U.; Ciro, C.; Andrea, S.; Luciano, R.; Sandra, R.; Joseph, G.; et al. Exploring the Inner Hygro-Mechanical Behaviour of Historical Panel Paintings: A Novel Approach Using Digital Twins. Herit. Sci. 2024, 12, 27. [Google Scholar] [CrossRef]
- Kránitz, K.; Sonderegger, W.; Bues, C.-T.; Niemz, P. Effects of Aging on Wood: A Literature Review. Wood Sci. Technol. 2016, 50, 7–22. [Google Scholar] [CrossRef]
- Grabner, M.; Kotlinova, M. Ageing of Wood—Described by the Analysis of Old Beams; Firenze University Press: Braga, Portugal, 2010; pp. 42–46. [Google Scholar]
- New, B. The Painted Support: Properties and Behaviour of Wood. In The Conservation of Panel Paintings and Related Objects; NOW: The Hague, The Netherlands, 2014; pp. 19–71. [Google Scholar]
- Inagaki, T.; Yonenobu, H.; Tsuchikawa, S. Near-Infrared Spectroscopic Monitoring of the Water Adsorption/Desorption Process in Modern and Archaeological Wood. Appl. Spectrosc. 2008, 62, 860–865. [Google Scholar] [CrossRef]
- Kawai, S.; Yokoyama, M.; Matsuo, M.; Sugiyama, J. Research on the Ageing of Wood in RISH; Firenze University Press: Braga, Portugal, 2010; pp. 52–56. [Google Scholar]
- Sassoli, M. Characterization of Wood Aging by Means of Volatile Organic Compounds (VOCs) Analysis. Ph.D. Thesis, University of Florence, Firenze, Italy, 2018. [Google Scholar]
- García Esteban, L.; Gril, J.; De Palacios De Palacios, P.; Guindeo Casasús, A. Reduction of Wood Hygroscopicity and Associated Dimensional Response by Repeated Humidity Cycles. Ann. For. Sci. 2005, 62, 275–284. [Google Scholar] [CrossRef]
- Young, C. The Painted Surface and Interface. In The Conservation of Panel Paintings and Related Objects; NOW: The Hague, The Netherlands, 2014; pp. 75–89. [Google Scholar]
- Manfriani, C.; Gualdani, G.; Goli, G.; Carlson, B.; Certo, A.R.; Mazzanti, P.; Fioravanti, M. The Contribution of IoT to the Implementation of Preventive Conservation According to European Standards: The Case Study of the “Cannone” Violin and Its Historical Copy. Sustainability 2021, 13, 1900. [Google Scholar] [CrossRef]
- Mazzanti, P.; Marcon, B.; Cocchi, L.; Goli, G.; Riparbelli, L.; Uzielli, L. An Innovative Method Based on In Situ Deformometric Monitoring to Support Decisions for the Structural Restoration of a Historic Panel Painting. Heritage 2024, 7, 4193–4205. [Google Scholar] [CrossRef]
- Linda, C.; Giacomo, G.; Paola, M.; Bertrand, M.; Luca, U. The Lapidazione di Santo Stefano by Giorgio Vasari: The Study of the Wooden Support’s Deformations as a Contribution to Restoration and Future Conservation. In Proceedings of the VIth European Symposium on Religious Art, Restoration & Conservation, Florence, Italy, 9–11 June 2014. [Google Scholar]
- Uzielli, L.; Cocchi, L. Monitoraggio e analisi dei movimenti del supporto ligneo della Lapidazione di Santo Stefano di Giorgio Vasari. Crit. D’arte 2012, 74, 97–102. [Google Scholar]
- Cocchi, L.; Marcon, B.; Goli, G.; Mazzanti, P.; Castelli, C.; Santacesaria, A.; Uzielli, L. Verifying the Operation of an Elastic Crossbar System Applied to a Panel Painting: The Deposition from the Cross by an Anonymous Artist from Abruzzo, Sixteenth Century. Stud. Conserv. 2017, 62, 150–161. [Google Scholar] [CrossRef]
- Cocchi, L. Tecniche Avanzate per Lo Studio Del Comportamento Strutturale Dei Dipinti Su Tavola. Ph.D. Thesis, University of Florence, Firenze, Italy, 2013. [Google Scholar]
- Mazzanti, P.; Dionisi-Vici, P.; Fioravanti, M.; Cardinali, E.; Mialhe, J.; Togni, M.; Uzielli, L.; Riparbelli, L. The Medusa Parade Shield by Caravaggio: Making Its Structural Replica, Laboratory Testing, and Numerically Modelling Their Hygro-Mechanical Distortion Behaviour. In The Future of Heritage Science and Technologies: Design, Simulation and Monitoring; Lecture Notes in Mechanical Engineering; Springer International Publishing: Cham, Switzerland, 2023; pp. 219–234. ISBN 978-3-031-17593-0. [Google Scholar]
- Uzielli, L.; Cardinali, E.; Dionisi-Vici, P.; Fioravanti, M.; Salvioli, N. Structure, Mock-up Model and Environment-Induced Deformations of Italian Laminated Wood Parade Shields from the 16th Century. In Proceedings of the Wood Science for Conservation of Cultural Heritage-Braga 2008: Proceedings of the International Conference, Braga, Portugal, 5 November 2008; pp. 242–248. [Google Scholar]
- Uzielli, L.; Dionisi-Vici, P.; Mazzanti, P.; Riparbelli, L.; Goli, G.; Mandron, P.; Togni, M.; Gril, J. A Method to Assess the Hygro-Mechanical Behaviour of Original Panel Paintings, through in Situ Non-Invasive Continuous Monitoring, to Improve Their Conservation: A Long-Term Study on the Mona Lisa. J. Cult. Herit. 2022, 58, 146–155. [Google Scholar] [CrossRef]
- Uzielli, L.; Dionisi-Vici, P.; Gril, J. Physical and Mechanical Characterization of the Support. In Mona Lisa Inside the Painting; Abrams: New York, NY, USA, 2006; pp. 43–46. [Google Scholar]
- Riparbelli, L.; Dionisi-Vici, P.; Mazzanti, P.; Brémand, F.; Dupré, J.C.; Fioravanti, M.; Goli, G.; Helfer, T.; Hesser, F.; Jullien, D.; et al. Coupling Numerical and Experimental Methods to Characterise the Mechanical Behaviour of the Mona Lisa: A Method to Enhance the Conservation of Panel Paintings. J. Cult. Herit. 2023, 62, 376–386. [Google Scholar] [CrossRef]
- Riparbelli, L.; Dionisi-Vici, P.; Dupre, J.-C.; Goli, G.; Jullien, D.; Bremand, F.; Mazzanti, P.; Hesser, F.; Marcon, B.; Togni, M.; et al. Mona Lisa’s Digital Twin: Identifying the Mechanical Properties of the Panel Combining Experimental Data and Advanced Finite-Element Modelling; GDR 3544 Sciences du Bois: Cluny, France, 2018; pp. 231–234. [Google Scholar]
- Dionisi Vici, P.; Mazzanti, P.; Uzielli, L. Mechanical Response of Wooden Boards Subjected to Humidity Step Variations: Climatic Chamber Measurements and Fitted Mathematical Models. J. Cult. Herit. 2006, 7, 37–48. [Google Scholar] [CrossRef]
- Rachwał, B.; Bratasz, Ł.; Krzemień, L.; Łukomski, M.; Kozłowski, R. Fatigue Damage of the Gesso Layer in Panel Paintings Subjected to Changing Climate Conditions. Strain 2012, 48, 474–481. [Google Scholar] [CrossRef]
- Rachwał, B.; Bratasz, Ł.; Łukomski, M.; Kozłowski, R. Response of Wood Supports in Panel Paintings Subjected to Changing Climate Conditions. Strain 2012, 48, 366–374. [Google Scholar] [CrossRef]
- Uzielli, L.; Cocchi, L.; Mazzanti, P.; Togni, M.; Jullien, D.; Dionisi-Vici, P. The Deformometric Kit: A Method and an Apparatus for Monitoring the Deformation of Wooden Panels. J. Cult. Herit. 2012, 13, S94–S101. [Google Scholar] [CrossRef]
- Dupre, J.-C. Experimental Study of the Hygromechanical Behaviour of a Historic Painting on Wooden Panel: Devices and Measurement Techniques. J. Cult. Herit. 2020, 46, 165–175. [Google Scholar] [CrossRef]
- Uzielli, L.; Fioravanti, M.; Casazza, O.; Perucca, G. A Technique for Double-Sided Monitoring the Deformations of the Wooden Supports of Panel Paintings: The Experience of Giotto’s “Maestà Di Ognissanti”. In Proceedings of the 3rd International Conference “ART ‘92”; IEEE Computer Society Press: Washington, DC, USA, 1992; Volume 1, pp. 500–514. [Google Scholar]
- Dionisi-Vici, P.; Formosa, M.; Schiro, J.; Uzielli, L. Local Deformation Reactivity of Panel Paintings in an Environment with Random Microclimate Variations: The Maltese Maestro Alberto’s Nativity Case-Study. In Proceedings of the Wood Science for Conservation of Cultural Heritage-Braga 2008: Proceedings of the International Conference, Braga, Portugal, 5 November 2008. [Google Scholar]
- Dionisi-Vici, P.; Bucciardini, I.; Fioravanti, M.; Uzielli, L. Monitoring Climate and Deformation of Panel Paintings in San Marco (Florence) and Other Museums. In Proceedings of the Wood Science for Conservation of Cultural Heritage, Florence 2007: Proceedings of the International Conference, Firenze, Italy, 8–10 November 2009. [Google Scholar]
- Marcon, B. Mechanical Study of a Support System for Cupping Control of Panel Paintings Combining Crossbars and Springs. J. Cult. Herit. 2012, 13, S109–S117. [Google Scholar] [CrossRef]
- Allegretti, O.; Dionisi-Vici, P.; Bontadi, J.; Raffaelli, F. The Case Study of The Daughters of the Emperor Ferdinand I by Jakob Seisenegger, in Trento (Italy): Analytical Hygro-Mechanical Results as a Support in Risk Assessment for Technical Interventions. Appl. Phys. A 2017, 123, 38. [Google Scholar] [CrossRef]
- Allegretti, O.; De Vincenzi, M.; Uzielli, L.; Dionisi-Vici, P. Long-Term Hygromechanical Monitoring of Wooden Objects of Art (WOA): A Tool for Preventive Conservation. J. Cult. Herit. 2013, 14, e161–e164. [Google Scholar] [CrossRef]
- Allegretti, O.; Bontadi, J.; Dionisi-Vici, P. Climate Induced Deformation of Panel Paintings: Experimental Observations on Interaction between Paint Layers and Thin Wooden Supports. IOP Conf. Ser. Mater. Sci. Eng. 2020, 949, 012018. [Google Scholar] [CrossRef]
- Froidevaux, J.; Müller, M.; Kuhnen, R.; Fioravanti, M.; Uzielli, L.; Gril, J.; Navi, P. 3D Modeling of Hydral Deformation of Panel Paintings and Its Confirmation by the Experiments. In Proceedings of the 4th International Conference of COST Action IE0601’Interaction Between Wood Science and Conservation of Cultural Heritage, Florence, Italy, 8–10 November 2007. [Google Scholar]
- Froidevaux, J. Wood and Paint Layers Aging and Risk Analysis of Ancient Panel Painting. Ph.D. Thesis, University of Montpellier 2, Montpellier, France, 2012. [Google Scholar]
- Castelli, C.; Ciatti, M.; Fioravanti, M.; Frosinini, C.; Gualdani, G.; Manfriani, C.; Mazzanti, P.; Ricciardi, L.; Riparbelli, L.; Rossi, S.; et al. Nuove acquisizioni sul comportamento deformativo di dipinti su tavola. OPD Restauro. 2023, 34, 112–119. [Google Scholar]
- Bacci, M. UV-Vis-NIR, FT-IR, and FORS Spectroscopies. In Modern Analytical Methods in Art and Archaeology; Chemical Analysis Series; John Wiley & Sons: New York, NY, USA, 2000; Volume 155. [Google Scholar]
- Meltz, G.; Morey, W.W.; Glenn, W.H. Formation of Bragg Gratings in Optical Fibers by a Transverse Holographic Method. Opt. Lett. 1989, 14, 823–825. [Google Scholar] [CrossRef]
- Kersey, A.D.; Davis, A.D.; Patrick, H.J.; LeBlanc, M.; Koo, K.P.; Askins, C.G.; Putnam, M.A.; Friebele, E.J. Fiber Gratings Sensors. J. Light. Technol. 1997, 15, 1442–1462. [Google Scholar] [CrossRef]
- Falciai, R.; Trono, C.; Lanterna, G.; Castelli, C. Continuous Monitoring of Wooden Works of Art Using FIber Bragg Grating Sensors. J. Cult. Herit. 2003, 4, 285–290. [Google Scholar] [CrossRef]
- Jones, J.D.C. Review of Fibre Sensor Techniques for Temperature-Strain Discrimination. In Optical Fiber Sensors; Optica Publishing Group: Washington, DC, USA, 1997. [Google Scholar]
- Falciai, R.; Trono, C.; Lanterna, G.; Castelli, C. FBG Sensors for Painted Wood Panel Deformation Monitoring. In Smart Structures and Materials 2003: Smart Sensor Technology and Measurement Systems; SPIE: Bellingham, WA, USA, 2003. [Google Scholar]
- Castelli, C.; Falciai, R.; Lanterna, G. Misurazioni non Invasive Delle Deformazioni nei Supporti Lignei. I Primi Dati dal “Tabernacolo dei Linaioli”. OPD Restauro. 2003, 15, 153–160. [Google Scholar]
- Jullien, D. Hygromechanical Study of a 16th Century Painted Wooden Panel: In-Situ Experiments to Quantify the Mechanical Effect of the Frame and the Cradle. J. Cult. Herit. 2023, 64, 266–274. [Google Scholar] [CrossRef]
- Jullien, D.; Bousvarou, M.; Stepanoff, P.; Dupré, J.C.; Gauvin, C.; Lorenzo, R. Monitoring the Deformation of an Historic Painting on a Wooden Panel (16th Century Panel Painting): Effect of the Frame, the Cradle and Microclimate Variations. In Proceedings of the ICOM-CC 20th Triennial Conference-Working Towards a Sustainable Past, Valencia, Spain, 18–22 September 2023. [Google Scholar]
- Sutton, M.A. Experimental Measurements Using Digital Image Correlation Methods: Brief Background and Perspective on Future Developments. J. Eng. Mater. Technol. 2022, 145, 014701. [Google Scholar] [CrossRef]
- Hinsch, K.D. Checkup for Aging Artwork—Optical Tools to Monitor Mechanical Behaviour. Opt. Lasers Eng. 2007, 45, 578–588. [Google Scholar] [CrossRef]
- Hinsch, K.D.; Gulker, G.; Hinrichs, H.; Joost, H. Artwork Monitoring by Digital Image Correlation. In Lasers in the Conservation of Artworks. LACONA V Proceedings; Springer proceedings in physics; Springer: Berlin/Heidelberg, Germany, 2004; p. 528. ISBN 978-3-540-22996-4. [Google Scholar]
- Fricke-Begemann, T. Three-Dimensional Deformation Field Measurement with Digital Speckle Correlation. Appl. Opt. 2003, 42, 6783–6796. [Google Scholar] [CrossRef] [PubMed]
- Dureisseix, D. Follow-up of a Panel Restoration Procedure through Image Correlation and Finite Element Modeling. Int. J. Solids Struct. 2011, 48, 1024–1033. [Google Scholar] [CrossRef]
- Sarvari, E.; Ahadi, A.; Eggeler, G.; Frenzel, J. An Optimized Stereo Digital Image Correlation Setup Based on Parfocal Zoom Lenses for Full-Field Measurements at 0.5–2× Magnification. Exp. Mech. 2024, 64, 1385–1405. [Google Scholar] [CrossRef]
- Garcia, D.; Orteu, J.-J.; Penazzi, L. A Combined Temporal Tracking and Stereo-Correlation Technique for Accurate Measurement of 3D Displacements: Application to Sheet Metal Forming. J. Mech. Work. Technol. 2002, 125–126, 736–742. [Google Scholar] [CrossRef]
- Germaneau, A.; Doumalin, P. Experimental Analysis of Mechanical Response of Stabilized Occipitocervical Junction by 3D Mark Tracking Technique. EPJ Web Conf. 2010, 6, 21004. [Google Scholar] [CrossRef]
- Gauvin, C.; Krekeler, A. Strain Measurements during Structural Conservation Treatment and the Long-Term Monitoring of a 17th-Century Dutch Panel Painting. In Proceedings of the 18th Triennial Conference, Copenhagen, Denmark, 4–7 September 2017. [Google Scholar]
- Colmars, J.; Marcon, B.; Maurin, E.; Remond, R.; Morestin, F.; Mazzanti, P.; Gril, J. Hygromechanical Response of a Panel Painting in a Church, Monitoring and Computer Modeling. In Proceedings of the International Conference on Wooden Cultural Heritage, Evaluation of Deterioration and Management of Change, Hamburg, Germany, 7–10 October 2009. [Google Scholar]
- Gauvin, C. Étude Expérimentale et Numérique Du Comportement Hygromécanique d’un Panneau de Bois. Application à La Conservation Des Tableaux Peints Sur Bois Du Patrimoine. Ph.D. Thesis, University of Montpellier, Montpellier, France, 2015. [Google Scholar]
- Gambino, M.C.; Fontana, R.; Greco, M.; Pampaloni, E.; Pezzati, L.; Pingi, P.; Cignoni, P.; Scopigno, R. Supporting the Restoration of the Minerva of Arezzo. In Proceedings of the Lasers in the Conservation of Artworks: LACONA V Proceedings, Osnabrück, Germany, 15–18 September 2003. [Google Scholar]
- Fontana, R.; Gambino, M.C.; Mazzotta, C.; Greco, M.; Pampaloni, E.; Pezzati, L. High-Resolution 3D Survey of Artworks. In Optical Metrology in Production Engineering; SPIE: Bellingham, WA, USA, 2004. [Google Scholar]
- Carcagnì, P.; Daffara, C.; Fontana, R.; Gambino, M.C.; Mastroianni, M.; Mazzotta, C.; Pampaloni, E.; Pezzati, L. Optical Micro-Profilometry for Archaeology. In Optical Methods for Arts and Archaeology; SPIE: Bellingham, WA, USA, 2005. [Google Scholar]
- Rocchini, C.; Cignoni, P.; Montani, C.; Pingi, P.; Scopigno, R.; Fontana, R.; Greco, M.; Pampaloni, E.; Pezzati, L.; Cygielman, M.; et al. 3D Scanning the Minerva of Arezzo. In Proceedings of the International Cultural Heritage Informatics Meeting, Milan, Italy, 3 September 2001. [Google Scholar]
- Remondino, F.; El-Hakim, S. Image-Based 3D Modelling: A Review. Photogramm. Rec. 2006, 21, 269–291. [Google Scholar] [CrossRef]
- Schenk, T. Introduction to Photogrammetry; The Ohio State University: Columbus, OH, USA, 2005. [Google Scholar]
- Brutto, M.L.; Garraffa, A.; Pellegrino, L.; Natale, B.D. 3D Mosaic Documentation Using Close Range Photogrammetry. In Proceedings of the 1st International Conference on Metrology for Archaeology, Benevento, Italy, 22 October 2015. [Google Scholar]
- Grifoni, E. 3D Multi-Modal Point Clouds Data Fusion for Metrological Analysis and Restoration Assessment of a Panel Painting. J. Cult. Herit. 2024, 66, 356–366. [Google Scholar] [CrossRef]
- Obradović, M.; Mišić, S.; Vasiljević, I.; Ivetić, D.; Obradović, R. The Methodology of Virtualizing Sculptures and Drawings: A Case Study of the Virtual Depot of the Gallery of Matica Srpska. Electronics 2023, 12, 4157. [Google Scholar] [CrossRef]
- Robson, S.; Bucklow, S.; Woodhouse, N.; Papadaki, H. Periodic Photogrammetric Monitoring and Surface Reconstruction of a Historical Wood Panel Painting for Restoration Purposes. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2004, 35, 395–400. [Google Scholar]
- Grifoni, E. Construction and Comparison of 3D Multi-Source Multi-Band Models for Cultural Heritage Applications. J. Cult. Herit. 2018, 34, 261–267. [Google Scholar] [CrossRef]
- Abate, D. Documentation of Paintings Restoration through Photogrammetry and Change Detection Algorithms. Herit. Sci. 2019, 7, 13. [Google Scholar] [CrossRef]
- Angheluță, L.M.; Rădvan, R. Macro Photogrammetry for the Damage Assessment of Artwork Painted Surfaces. ISPRS—Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, XLII-2/W15, 101–107. [Google Scholar] [CrossRef]
- Fantini, F.; Gaiani, M.; Garagnani, S. Knowledge and Documentation of Renaissance Works of Art: The Replica of the “Annunciation” By Beato Angelico. ISPRS—Int. Arch. Photogramm. Remote. Sens. Spat. Inf. Sci. 2023, XLVIII-M-2, 527–534. [Google Scholar] [CrossRef]
- Bornstein, D. New Dimensions in Conservation Imaging: Combining Photogrammetry and Photometric Stereo for 3D Docum. AICCM Bull. 2023, 44, 148–162. [Google Scholar] [CrossRef]
- Gaiani, M. Artworks at Our Fingertips: A Solution Starting from the Digital Replication Experience of the Annunciation in San Giovanni Valdarno. Digit. Appl. Archaeol. Cult. Herit. 2024, 33, e00329. [Google Scholar] [CrossRef]
- Akca, D.; Remondino, F.; Novák, D.; Hanusch, T.; Schrotter, G.; Gruen, A. Performance Evaluation of a Coded Structured Light System for Cultural Heritage Applications. In Proceedings of the Videometrics IX, San Jose, CA, USA, 29–30 January 2007; SPIE: Bellingham, WA, USA, 2007. [Google Scholar]
- Zhang, S. High-Speed 3D Shape Measurement with Structured Light Methods: A Review. Opt. Lasers Eng. 2018, 106, 119–131. [Google Scholar] [CrossRef]
- Bell, T.; Li, B.; Zhang, S. Structured Light Techniques and Applications. In Wiley Encyclopedia of Electrical and Electronics Engineering; Webster, J.G., Ed.; Wiley: Hoboken, NJ, USA, 2016; pp. 1–24. ISBN 978-0-471-34608-1. [Google Scholar]
- Guidi, G.; Atzeni, C.; Seracini, M.; Lazzari, S. Painting Survey by 3D Optical Scanning—The Case of Adoration of the Magi by Leonardo Da Vinci. Stud. Conserv. 2004, 49, 1–12. [Google Scholar] [CrossRef]
- Guidi, G.; Atzeni, C.; Lazzari, S. 3D Optical Scanning Diagnostics for Leonardo Da Vinci’s “Adorazione Dei Magi” Conservation. In Proceedings of the Fourth International Conference on 3-D Digital Imaging and Modeling 2003, Banff, AB, Canada, 6–10 October 2003. [Google Scholar]
- Palma, G. Deformation Analysis of Leonardo Da Vinci’s “Adorazione Dei Magi” through Temporal Unrelated 3D Digitization. J. Cult. Herit. 2019, 38, 174–185. [Google Scholar] [CrossRef]
- Akça, D.; Grün, A.; Breuckmann, B.; Lahanier, C. High Definition 3D-Scanning of Arts Objects and Paintings. Opt. 3-D Meas. Technqiues VIII 2007, 2, 50–58. [Google Scholar]
- Pelagotti, A.; Uccheddu, F.; Massa, E.; Carfagni, M. Comparing Two 3D Measurement Techniques for Documenting Painted Wooden Panels Surface Deformations on a Real Test Case: “Mystical Marriage of Saint Catherine” by Renaissance Artist Piero Di Cosimo. IOP Conf. Ser. Mater. Sci. Eng. 2018, 364, 012090. [Google Scholar] [CrossRef]
- Łukomski, M.; Ziraldo, E.G.; Freeman, A.A.; Cosaert, A.; Taylor, J.; Beltran, V.L. Monitoring Micro-Changes in Wooden Artworks to Support Strategies for Indoor Climate Management; Technical University of Dresden: Dresden, Germany, 2021. [Google Scholar]
- Verykokou, S.; Ioannidis, C. An Overview on Image-Based and Scanner-Based 3D Modeling Technologies. Sensors 2023, 23, 596. [Google Scholar] [CrossRef] [PubMed]
- Altuntas, C. Triangulation and Time-of-Flight Based 3D Digitisation Techniques of Cultural Heritage Structures. ISPRS—Int. Arch. Photogramm. Remote. Sens. Spat. Inf. Sci. 2021, XLIII-B2-2, 825–830. [Google Scholar] [CrossRef]
- Blais, F.; Cournoyer, L. 3D Imaging from Theory to Practice: The Mona Lisa Story. In Proceedings of the Current Developments in Lens Design and Optical Engineering IX, San Diego, CA, USA, 11–12 August 2008; SPIE: Bellingham, WA, USA, 2008. [Google Scholar]
- Blais, F.; Taylor, J.; Cournoyer, L.; Picard, M.; Borgeat, L.; Dicaire, L.G.; Rioux, M.; Lahanier, C.; Aitken, G. Ultra-High Resolution Imaging at 50 Μm Using a Portable XYZ- RGB Color Laser Scanner. In Proceedings of the International Workshop on Recording, Modeling and Visualization of Cultural Heritage, Ascona, Switzerland, 22–27 May 2005; NRC: Ascona, Switzerland, 2005. [Google Scholar]
- Lahanier, C.; Aitken, G.; Taylor, J.; Blais, F.; Borgeat, L.; Beraldin, J.-A.; Rioux, M.; Breuckmann, B.; Colantoni, P.; Cournoyer, L.; et al. The 2D Multi-Spectral Digitisation and the 3D Modelling of Easel Paintings; National Research Council of Canada: Ottawa, ON, Canada, 2005. [Google Scholar]
- Blais, F.; Taylor, J.; Cournoyer, L.; Picard, M.; Borgeat, L.; Godin, G.; Lahanier, C.; Mottin, B. More than a Poplar Plank: The Shape and Subtle Colors of the Masterpiece Mona Lisa by Leonardo. In Proceedings of the Videometrics IX, San Jose, CA, USA, 29–30 January 2007; SPIE: Bellingham, WA, USA, 2007. [Google Scholar]
- Blais, F.; Taylor, J.; Cournoyer, L.; Picard, M.; Borgeat, L.; Godin, G.; Lahanier, C. Ultra High-Resolution 3D Laser Color Imaging of Paintings: The Mona Lisa by Leonardo Da Vinci. In Proceedings of the Lasers in the Conservation of Artworks—Proceedings of the International Conference Lacona VII, Madrid, Spain, 17–21 September 2007. [Google Scholar]
- Remondino, F.; Rizzi, A.; Barazzetti, L.; Scaioni, M.; Fassi, F.; Brumana, R.; Pelagotti, A. Review of Geometric and Radiometric Analyses of Paintings. Photogramm. Rec. 2011, 26, 439–461. [Google Scholar] [CrossRef]
- Barazzetti, L.; Remondino, F.; Scaioni, M.; Brutto, M.L.; Rizzi, A.; Brumana, R. Geometric and Radiometric Analysis of Paintings. ISPRS—Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2010, 38, 5. [Google Scholar]
- Pires, H.; Marques, P.; Henriques, F.; Oliveira, R. Integrating Laser Scanning, Multispectral Imagery and Gis in C&R Documentation Practices: A First Approach Using Two Xvith Century Wood Paintings From Convento de Cristo in Tomar. In Proceedings of the XXI International CIPA Symposium, Athens, Greece, 1–6 October 2007; SPIE: Bellingham, WA, USA, 2007. [Google Scholar]
- Abate, D.; Menna, F.; Remondino, F.; Gattari, M.G. 3D Painting Documentation: Evaluation of Conservation Conditions with 3D Imaging and Ranging Techniques. ISPRS—Int. Arch. Photogramm. Remote. Sens. Spat. Inf. Sci. 2014, XL-5, 1–8. [Google Scholar] [CrossRef]
- Vannini, E.; Lunghi, I.; Grifoni, E.; Farioli, P.; Ginanni, M.; Santacesaria, A.; Fontana, R. Three-Dimensional Analysis for the Documentation of the Restoration of an Earthquake-Damaged Triptych. Heritage 2024, 7, 2176–2194. [Google Scholar] [CrossRef]
- Chen, F.; Brown, G.M.; Way, T.; Song, M. Overview of Three-Dimensional Shape Measurement Using Optical Methods. Opt. Eng. 2000, 39, 10–22. [Google Scholar]
- Creath, K.; Wyant, J.C. Moiré and Fringe Projection Techniques. In Optical Shop Testing; Wiley series in pure and applied optics; Wiley: New York, NY, USA, 1992; p. 773. ISBN 978-0-471-52232-4. [Google Scholar]
- Meadows, D.M.; Johnson, W.O.; Allen, J.B. Generation of Surface Contours by Moiré Patterns. Appl. Opt. 1970, 9, 942–947. [Google Scholar] [CrossRef]
- Takasaki, H. Moiré Topography. Appl. Opt. 1970, 9, 1467–1472. [Google Scholar] [CrossRef]
- Takasaki, H. Moiré Topography. Appl. Opt. 1973, 12, 845–850. [Google Scholar] [CrossRef] [PubMed]
- Breque, C.; Dupre, J.-C.; Bremand, F. Calibration of a System of Projection Moire! For Relief Measuring: Biomechanical Applications. Opt. Lasers Eng. 2004, 41, 241–260. [Google Scholar] [CrossRef]
- Mauvoisin, G.; Brémand, F.; Lagarde, A. Quasi-Heterodyne Shadow Moiré. In Proceedings of the 10th International Conference on Experimental Mechanics, Lisbon, Portugal, 18–22 July 1994; A.A. Balkema: Rotterdam, The Netherlands; Brookfield, VT, USA, 1994; pp. 245–250, ISBN 90 5410 395 7. [Google Scholar]
- Durelli, A.J.; Parks, V.J. Moiré Analysis of Strain; Prentice-Hall: Englewood Cliffs, NJ, USA, 1970. [Google Scholar]
- Pirroda, L. Shadow and Projection Moiré Technique for Absolute or Relative Mapping of Surface Shapes. Opt. Eng. 1982, 21, 640–649. [Google Scholar] [CrossRef]
- Théocaris, P. Isopachic Patterns by the Moiré Method. Exp. Mech. 1964, 4, 153–159. [Google Scholar] [CrossRef]
- Théocaris, P. Moiré Fringes in Strain Analysis; Pergamon Press: Oxford, UK, 1969. [Google Scholar]
- Brewer, A.; Forno, C. Moiré Fringe Analysis of Cradled Panel Paintings. Stud. Conserv. 1997, 42, 211–230. [Google Scholar] [CrossRef]
- Spagnolo, G.S.; Majo, R.; Ambrosini, D.; Paoletti, D. Digital Moire’ by a Diffractive Optical Element for Deformation Analysis of Ancient Paintings. J. Opt. A Pure Appl. Opt. 2003, 5, S146–S151. [Google Scholar] [CrossRef]
- Brémand, F.; Doumalin, P.; Dupré, J.-C.; Hesser, F.; Valle, V. Measuring the Relief of the Panel Support without Contact. In Mona Lisa Inside the Painting; Abrams: New York, NY, USA, 2006; pp. 43–46. [Google Scholar]
- Lunghi, I.; Vannini, E.; Fovo, A.D.; Sarno, V.D.; Rocco, A.; Fontana, R. A Performance Comparison of 3D Survey Instruments for Their Application in the Cultural Heritage Field. Sensors 2024, 24, 3876. [Google Scholar] [CrossRef]
- Buchón-Moragues, F.; Bravo, J.M.; Ferri, M.; Redondo, J.; Sánchez-Pérez, J.V. Application of Structured Light System Technique for Authentication of Wooden Panel Paintings. Sensors 2016, 16, 881. [Google Scholar] [CrossRef]
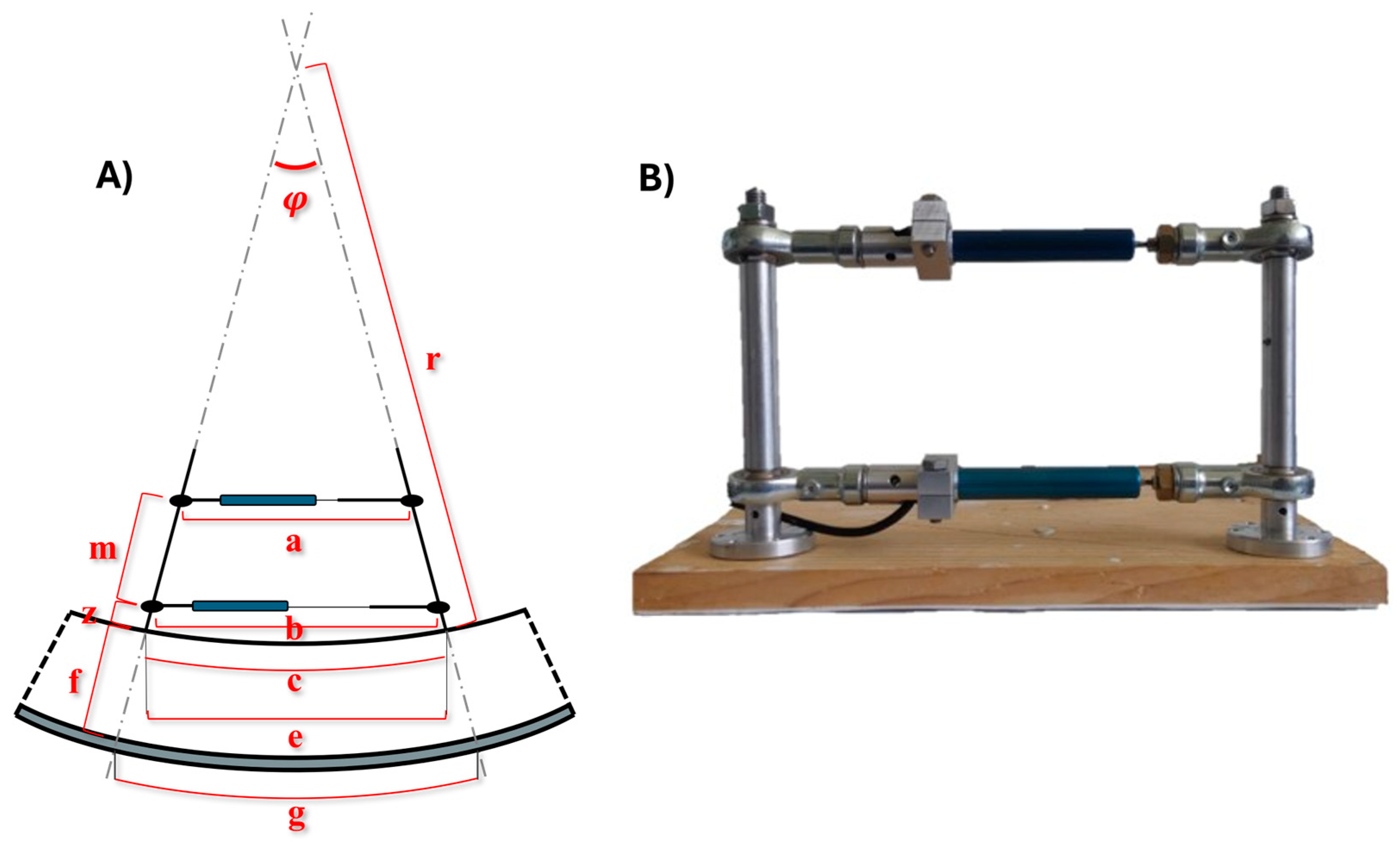


| Cupping curvature | [radians] | (1) | |
| Radius of curvature | [mm] | (2) | |
| Length of the front baseline | [mm] | (3) |
| Type of Monitored Object | Artwork | References | Applied Techniques | Aim |
|---|---|---|---|---|
| Historical artwork | “Lapidazione di Santo Stefano” (Giorgio Vasari) | [25,26,27] | Displacement transducers and DK | Analyzing seasonal behavior of the panel; confirming the effectiveness of the restoration strategies |
| Historical artwork | “Deposizione dalla Croce” (anonymous 16th-century artist) | [28,29] | Displacement transducers | Measuring deformations, forces, and displacements of the panel and the elastic crossbar system |
| Simulacra | Replica of “Medusa” shield (Caravaggio) | [30] | Displacement transducers | Monitoring of the horizontal and vertical shape changes |
| Historical artwork | Shield (inventory no. 408) | [31] | Displacement transducers | Monitoring of the deformation along two diameters; revealing changes in the dimensions |
| Historical artwork | “Mona Lisa” (Leonardo da Vinci) | [32,33,34,35] | Displacement transducers and load cells | Monitoring of the cupping and bowing of the panel; estimation of the panel’s mechanical properties through numerical modeling |
| Simulacra | / | [36] | Displacement transducers and load cells | Monitoring of cupping, swelling/shrinkage deformations, and forces; development of descriptive models of the panel’s mechanical behavior |
| Simulacra | / | [37,38] | Displacement transducers and laser transducers | Tracking the deflection of the panel to validate the numerical model |
| Historical artwork | “Maestà di Ognissanti” (Giotto) | [41,43] | DK | Detection of displacements and cupping related to RH variations |
| Historical artwork | “Madonna con Bambino e Angeli” (Daddi) | [43] | DK | Monitoring the deformations |
| Historical artwork | “Nativity” (Maltese Maestro Alberto) | [42] | DK | Analysis of the board’s deformative response to microclimatic variations |
| Simulacra | Replicas of “Madonna in trono col Bambino e Santi” (Andrea di Giusto) | [44] | DK | Monitoring the panel’s response to humidity change assessing the auxiliary support’s effectiveness |
| Historical artwork | “The daughters of the Emperor Ferdinand I” (Jakob Seisenegger) | [45,46] | DK | Determination of the support’s deformative tendencies in response to microclimatic fluctuations |
| Historical artwork | “Baccanale” (school of Jacob Jordaens) | [47] | DK | Measurement of in-plane and out-of-plane deformations |
| Simulacra | Structural replicas of “Baccanale” school of Jacob Jordaens) | [47] | DK | Isolation of the hygroscopic warping from the mechanical deformation |
| Historical artwork | “La Saint Trinité couronnant la vierge” (anonymous 16th-century artist) | [40,58,59] | DK and mark-tracking technique | Continuous monitoring of the curvature, deformation, stress, and strain; assessment of the impact of physical elements |
| Simulacra | / | [48] | DK | Measurement of cupping to confirm the numerical model |
| Simulacra | / | [49] | DK and fringe projection technique | Comparison of the experimental results with the numerical modeling’s data |
| Historical artwork | Six different WPPs | [9,14,15,50] | DK | Long-term monitoring of deformometric behavior under controlled humidity fluctuations; calibration of digital models; identification of the main variables responsible for a painting’s behavior |
| Simulacra | / | [54,56,57] | FBG sensors | Detection and quantification of deformations during thermo-hygrometric variations; studying the impact of crossbeams |
| Historical artwork | “Tabernacolo dei Linaioli” | [57] | FBG sensors | Tracking strain and cupping during RH fluctuations |
| Type of Monitored Object | Artwork | References | Applied Techniques | Aim |
|---|---|---|---|---|
| Historical artwork | “Le Couronnement d’Epines” (16th-century anonymous painter) | [69] | StereoDIC | Measurement of the shape and observation of different deformations (cupping and twist) |
| Historical artwork | “Baptême du Christ” (anonymous artist) | [64] | StereoDIC | Measurement of displacements during the restoration intervention; employment of finite numerical approach to update the structural model |
| Historical artwork | “Jacob Wrestling with the Angel” (Bartholomeus Breenbergh) | [68,70] | Mark-tracking | Measurement of out-of-plane displacements and strain during structural treatment |
| Historical artwork | “La Saint Trinité couronnant la vierge” (anonymous 16th-century artist) | [40,58,59] | Mark-tracking and DK | Continuous monitoring of the curvature, deformation, stress and strain; assessment of the impact of physical elements |
| Historical artwork | “Westminster Retable” | [80] | Photogrammetry | Study of the panel’s deformometric behavior during environmental fluctuations |
| Historical artwork | “Madonna che allatta il Bambino con Angeli—Annunciazione” (Barnaba da Modena) | [81] | Photogrammetry | Evaluation of qualitative and quantitative differences between the models |
| Historical artwork | “Madonna con Bambino, e la Pentecoste” (15th-century anonymous painter) | |||
| Historical artwork | 18th-century Byzantine icon | [82] | Photogrammetry | Detection of deviations from planarity |
| Historical artwork | “St.Constantine and Helen” and “St. Nicholas” icons | [83] | Macro-photogrammetry | Records of the overall deformations and macro-documentation of damaged areas |
| Historical artwork | “Annunciazione” (Beato Angelico) | [84] | Photogrammetry | Capturing the painting’s deformative state |
| Historical artwork | Nocria Triptych—right panel (anonymous 15th-century artist) | [78] | Photogrammetry | Calculation of the panel’s thickness, quantification of the macro deviations, calculation of the curvature arrow, and evaluation of changes after restoration intervention |
| Historical artwork | “Adorazione dei Magi” (Leonardo da Vinci) | [90,91] | Structured light topography | Quantitative analysis of the painting’s deformations |
| Historical artwork | “Adorazione dei Magi” (Leonardo da Vinci) | [92] | Structured light topography | Analysis of the panel’s deformation over seventeen years |
| Historical artwork | “Lady Praying” (anonymous 16th-century artist) | [93] | Structured light topography | Detection of the painting’s overall shape |
| Historical artwork | “Mystical Marriage of Saint Catherine” (Piero di Cosimo) | [94] | Structured light topography | Assessment of the deviations from planarity, recording of spatial deformations, and monitoring of the painting’s conservation condition |
| Simulacra | / | [49] | Fringe projection technique and DK | Comparison of the experimental results with the numerical modeling’s data |
| Simulacra | / | [95] | Structured light topography | Detection of the overall deformation by comparison of the object’s shape before and after humidity variations |
| Historical artwork | “Dame en Prière” (anonymous artist) | [99,100] | Laser scanning | Capture of the shape and color of the artwork—one of the first applications of a new instrument |
| Historical artwork | “Mona Lisa” (Leonardo da Vinci) | [101,102] | Laser scanning | Documentation and measurement of the distorted shape of the painting |
| Historical artwork | “Giudizio Universale”, “Martirio di S.Pietro”, and “Adorazione dei Magi” (Giorgio Vasari) | [103,104] | Laser scanning | Identification of significant deformation |
| Historical artwork | “Entrance of Christ in Jerusalem” and “Lazarus Resurrection” (Jorge Alfonso) | [105] | Photogrammetry and laser scanning | Quantification of the mechanical deformation |
| Historical artwork | “Saint John the Baptist” (Giacomo Francia) | [106] | Photogrammetry and structured light topography | Measurement of the shape of the support, assessment of deformation, monitoring of shape changes over the medium/long term period |
| Historical artwork | Cretan icon (17th century) | |||
| Historical artwork | Nocria Triptych—central panel (anonymous 15th-century artist) | [107] | Photogrammetry and structured light topography | Comparison of two models, before and after the restoration intervention; documentation and quantification of the shape changes |
| Simulacra | / | [119] | Moiré method | Study the impact of cradling during thermo-hygrometric variations |
| Simulacra | / | [120] | Moiré method | Study and quantification of out-of-plane deformations |
| Historical artwork | “Madonna col bambino, Santi ed Angeli musicanti” (school of Antonio Solario) | |||
| Historical artwork | “Mona Lisa” (Leonardo da Vinci) | [121] | Moiré method | Measurement of the relief of the painting in different situations; calculation of a thickness map; determination of distortion |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gagliardi, C.; Riparbelli, L.; Mazzanti, P.; Fioravanti, M. A Critical Review of Methods and Techniques Used for Monitoring Deformations in Wooden Panel Paintings. Forests 2025, 16, 546. https://doi.org/10.3390/f16030546
Gagliardi C, Riparbelli L, Mazzanti P, Fioravanti M. A Critical Review of Methods and Techniques Used for Monitoring Deformations in Wooden Panel Paintings. Forests. 2025; 16(3):546. https://doi.org/10.3390/f16030546
Chicago/Turabian StyleGagliardi, Claudia, Lorenzo Riparbelli, Paola Mazzanti, and Marco Fioravanti. 2025. "A Critical Review of Methods and Techniques Used for Monitoring Deformations in Wooden Panel Paintings" Forests 16, no. 3: 546. https://doi.org/10.3390/f16030546
APA StyleGagliardi, C., Riparbelli, L., Mazzanti, P., & Fioravanti, M. (2025). A Critical Review of Methods and Techniques Used for Monitoring Deformations in Wooden Panel Paintings. Forests, 16(3), 546. https://doi.org/10.3390/f16030546






