Effects of Plot Size on Airborne LiDAR-Derived Metrics and Predicted Model Performances of Subtropical Planted Forest Attributes
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Field Plot Data
2.3. Lidar Data
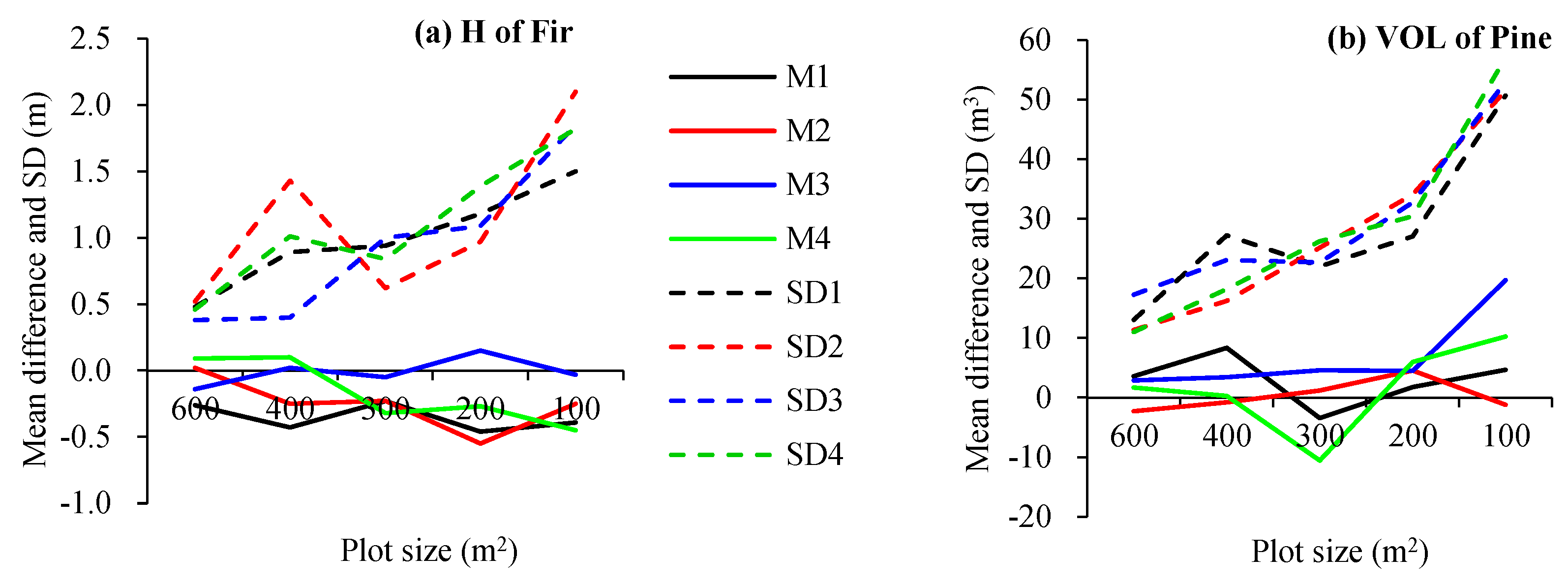
2.4. Comparative Analysis of Plot Size Effects
3. Results
3.1. Plot Size Effects on LiDAR-Derived Metrics
3.1.1. Height Metrics
3.1.2. Density Metrics
3.1.3. Vertical Structure Metrics
3.2. Plot Size Effects on Measured Forest Attributes
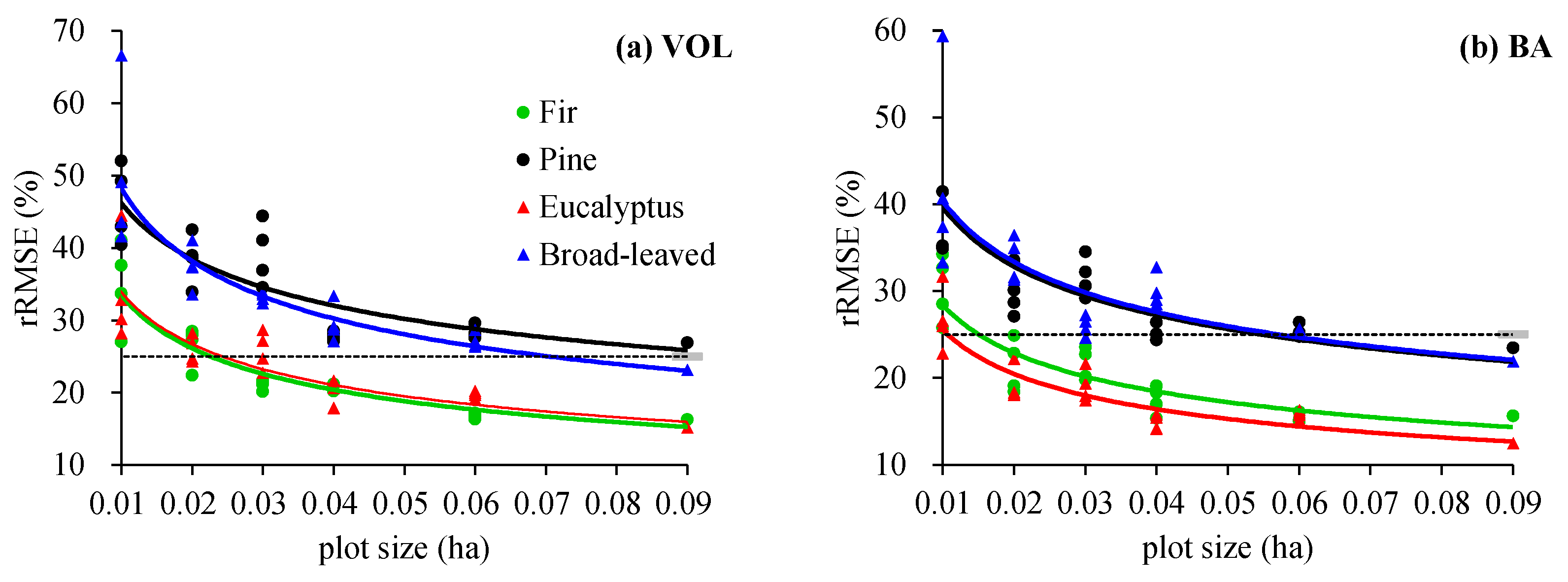
3.3. Plot Size Effects on the Performances of the Predictive Models of Forest Attributes
4. Discussion
5. Conclusions
- (1)
- The means of the 25th, 50th, and 75th height percentiles of laser point clouds, Hmean, Hcv, CC, 25th and 50th density percentiles, and LADcv of plots of different sizes for all four forest types showed irregular differences or no statistically significant difference from that of the 900 m2 plots. However, their standard deviations decreased as the plot size increased. In general, statistically significant differences in the means of Hmax, LADmean, and 75th density percentile were found between plots of various sizes and 900 m2 plots.
- (2)
- Except for the mean Hm, the measured forest attributes of plots of different sizes for all four forest types exhibited irregular variations and no statistically significant difference from those of the 900 m2 plots. However, their standard deviations decreased with the increasing plot size.
- (3)
- As the plot size increased from 100 m2 to 900 m2, the predictive errors (MPE and rRMSE) decreased at approximately the same rate for all forest types, and the model accuracies gradually improved at a similar rate for all forest types. These results were most likely due to the fact that the standard deviations of the LiDAR-derived metrics and measured forest attributes decreased as the plot size increased; that is, the variation in the independent and dependent variables of the model decreased with the increasing plot size, which improved the robustness of the model.
- (4)
- According to this paper, we preliminarily recommend that for a large-scale subtropical planted forest inventory, the plot sizes should be at least 600 m2 for all forest types.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Watt, M.; Adams, T.; Aracil, S.G.; Marshall, H.; Watt, P. The influence of LiDAR pulse density and plot size on the accuracy of New Zealand plantation stand volume equations. N. Z. J. For. Sci. 2013, 43, 15. [Google Scholar] [CrossRef]
- Bouvier, M.; Durrieu, S.; Fournier, R.A.; Renaud, J.-P. Generalizing predictive models of forest inventory attributes using an area-based approach with airborne LiDAR data. Remote Sens. Environ. 2015, 156, 322–334. [Google Scholar] [CrossRef]
- Hyyppä, J.; Yu, X.; Hyyppä, H.; Vastaranta, M.; Holopainen, M.; Kukko, A.; Kaartinen, H.; Jaakkola, A.; Vaaja, M.; Koskinen, J.; et al. Advances in forest inventory using airborne laser scanning. Remote Sens. 2012, 4, 1190–1207. [Google Scholar] [CrossRef]
- Næsset, E. Airborne laser scanning as a method in operational forest inventory: Status of accuracy assessments accomplished in Scandinavia. Scand. J. For. Res. 2007, 22, 433–442. [Google Scholar] [CrossRef]
- Packalen, P.; Maltamo, M. Species-specific management inventory in Finland. In Forestry Applications of Airborne Laser Scanning: Concepts and Case Studies, Managing Forest Ecosystems 27; Maltamo, M., Næsset, E., Vauhkonen, J., Eds.; Springer: Dordrecht, The Netherlands, 2014; pp. 241–252. [Google Scholar] [CrossRef]
- White, J.C.; Tompalski, P.; Vastaranta, M.; Wulder, M.A.; Saarinen, N.; Stepper, C.; Coops, N.C. A Model Development and Application Guide for Generating an Enhanced Forest Inventory Using Airborne Laser Scanning Data and an Area-Based Approach; Canadian Wood Fibre Centre: Victoria, BC, Canada, 2017. [Google Scholar] [CrossRef]
- Lin, C.; Thomson, G.; Popescu, S.C. An IPCC-compliant technique for forest carbon stock assessment using airborne LiDAR-derived tree metrics and competition index. Remote Sens. 2016, 8, 528. [Google Scholar] [CrossRef]
- Lo, C.S.; Lin, C. Growth-competition-based stem diameter and volume modeling for tree-level forest inventory using airborne LiDAR data. IEEE T Geosci. Remote 2012, 51, 2216–2226. [Google Scholar] [CrossRef]
- Pourreza, M.; Moradi, F.; Khosravi, M.; Deljouei, A.; Vanderhoof, M.K. GCPs-free photogrammetry for estimating tree height and crown diameter in Arizona Cypress plantation using UAV-mounted GNSS RTK. Forests 2022, 13, 1905. [Google Scholar] [CrossRef]
- Štroner, M.; Urban, R.; Seidl, J.; Reindl, T.; Brouček, J. Photogrammetry using UAV-mounted GNSS RTK: Georeferencing strategies without GCPs. Remote Sens. 2021, 13, 1336. [Google Scholar] [CrossRef]
- Gobakken, T.; Næsset, E. Assessing effects of laser point density, ground sampling intensity, and field sample plot size on biophysical stand properties derived from airborne laser scanner data. Can. J. For. Res. 2008, 38, 1095–1109. [Google Scholar] [CrossRef]
- Ruiz, L.A.; Hermosilla, T.; Mauro, F.; Godino, M. Analysis of the influence of plot size and LiDAR density on forest structure attribute estimates. Forests 2014, 5, 936–951. [Google Scholar] [CrossRef]
- Singh, K.; Chen, G.; Vogler, J.B.; Meentemeyer, R.K. When big data are too much: Effects of LiDAR returns and point density on estimation of forest biomass. J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3210–3218. [Google Scholar] [CrossRef]
- Næsset, E. Area-based inventory in Norway-From innovation to an operation reality. In Forestry Applications of Airborne Laser Scanning: Concepts and Case Studies, Managing Forest Ecosystems 27; Maltamo, M., Næsset, E., Vauhkonen, J., Eds.; Springer: Dordrecht, The Netherlands, 2014; pp. 215–240. [Google Scholar] [CrossRef]
- Stereńczak, K.; Lisańczuk, M.; Parkitna, K.; Mitelsztedt, K.; Mroczek, P.; Miscicki, S. The influence of number and size of sample plots on modeling growing stock volume based on airborne laser scanning. Drewno 2018, 61. [Google Scholar] [CrossRef]
- Næsset, E. Predicting forest stand characteristics with airborne scanning laser using a practical two-stage procedure and field data. Remote Sens. Environ. 2002, 80, 88–99. [Google Scholar] [CrossRef]
- Næsset, E.; Gobakken, T. Estimation of above- and below-ground biomass across regions of the boreal forest zone using airborne laser. Remote Sens. Environ. 2008, 112, 3079–3090. [Google Scholar] [CrossRef]
- Zolkos, S.G.; Goetz, S.J.; Dubayah, R. A meta-analysis of terrestrial aboveground biomass estimation using lidar remote sensing. Remote Sens. Environ. 2013, 128, 289–298. [Google Scholar] [CrossRef]
- Liao, Z.; Huang, D. Forest inventory handbook of Guangxi, China; Forestry Department of Guangxi Zhuang Autonomous Region: Nanning, China, 1986. (In Chinese)
- Nie, S.; Wang, C.; Zeng, H.; Xi, X.; Li, G. Above-ground biomass estimation using airborne discrete-return andfull-waveform LiDAR data in a coniferous forest. Ecol. Indic. 2017, 78, 221–228. [Google Scholar] [CrossRef]
- Chen, Q.; Laurin, G.V.; Battles, J.J.; Saah, D. Integration of airborne LiDAR and vegetation types derived from aerial photography for mapping aboveground live biomass. Remote Sens. Environ. 2012, 121, 108–117. [Google Scholar] [CrossRef]
- Kim, E.; Lee, W.-K.; Yoon, M.; Lee, J.-Y.; Son, Y.; Abu Salim, K. Estimation of voxel based above-ground biomass using airborne LiDAR data in an intact tropical Rain Forest, Brunei. Forests 2016, 7, 259. [Google Scholar] [CrossRef]
- Silva, V.S.D.; Silva, C.A.; Mohan, M.; Cardil, A.; Rex, F.E.; Loureiro, G.H.; Almeida, D.R.A.D.; Broadbent, E.N.; Gorgens, E.B.; Dalla Corte, A.P.; et al. Combined impact of sample size and modeling approaches for predicting stem volume in Eucalyptus spp. forest plantations using field and LiDAR Data. Remote Sens. 2020, 12, 1438. [Google Scholar] [CrossRef]
- Asner, G.P.; Mascaro, J.; Muller-Landau, H.C.; Vieilledent, G.; Vaudry, R.; Rasamoelina, M.; Hall, J.S.; van Breugel, M. A universal airborne LiDAR approach for tropical forest carbon mapping. Oecologia 2012, 168, 1147–1160. [Google Scholar] [CrossRef]
- Treitz, P.; Lim, K.; Woods, M.; Pitt, D.; Nesbitt, D.; Etheridge, D. LiDAR sampling density for forest resource inventories in Ontario, Canada. Remote Sens. 2012, 4, 830–848. [Google Scholar] [CrossRef]
- Nilsson, M.; Nordkvist, K.; Jonzén, J.; Lindgren, N.; Axensten, P.; Wallerman, J.; Egberth, M.; Larsson, S.; Nilsson, L.; Eriksson, J.; et al. A nationwide forest attribute map of Sweden predicted using airborne laser scanning data and field data from the National Forest Inventory. Remote Sens. Environ. 2017, 194, 447–454. [Google Scholar] [CrossRef]
- Knapp, N.; Fischer, R.; Cazcarra-Bes, V.; Huth, A. Structure metrics to generalize biomass estimation from lidar across forest types from different continents. Remote Sens. Environ. 2020, 237, 111597. [Google Scholar] [CrossRef]
- Li, C.; Li, Z. Generalizing predictive models of sub-tropical forest inventory attributes using an area-based approach with airborne LiDAR data. Sci. Silvae Sin. 2021, 57, 23–35. (In Chinese) [Google Scholar] [CrossRef]
- Zeng, W.; Duo, H.; Lei, X.; Chen, X. Individual tree biomass equations and growth models sensitive to climate variables for Larix spp. in China. Eur. J. For. Res. 2017, 136, 233–249. [Google Scholar] [CrossRef]
- Zeng, W.; Fu, L.; Xu, M.; Wang, X.; Chen, Z.; Yao, S. Developing individual tree-based models for estimating aboveground biomass of five key coniferous species in China. J. For. Res. 2018, 29, 1251–1261. [Google Scholar] [CrossRef]
- Frazer, G.W.; Magnussen, S.; Wulder, M.A.; Niemann, K.O. Simulated impact of sample plot size and co-registration error on the accuracy and uncertainty of LiDAR-derived estimates of forest stand biomass. Remote Sens. Environ. 2021, 115, 636–649. [Google Scholar] [CrossRef]
- Næsset, E.; Bollandsas, O.M.; Gobakken, T.; Solberg, S.; McRoberts, R.E. The effects of field plot size on model-assisted estimation of aboveground biomass change using multitemporal interferometric SAR and airborne laser scanning data. Remote Sens. Environ. 2015, 168, 252–264. [Google Scholar] [CrossRef]
- Asner, G.P.; Mascaro, J. Mapping tropical forest carbon: Calibrating plot estimates to a simple LiDAR metric. Remote Sens. Environ. 2014, 140, 614–624. [Google Scholar] [CrossRef]
- Mauya, E.; Hansen, E.; Gobakken, T.; Bollandsås, O.; Malimbwi, R.; Næsset, E. Effects of field plot size on prediction accuracy of aboveground biomass in airborne laser scanning-assisted inventories in tropical rainforests of Tanzania. Carbon Balance Manag. 2015, 10, 10. [Google Scholar] [CrossRef]
- Kachamba, D.J.; Ørka, H.O.; Næsset, E.; Eid, T.; Gobakken, T. Influence of plot size on efficiency of biomass estimates in inventories of dry tropical forests assisted by photogrammetric data from an unmanned aircraft system. Remote Sens. 2017, 9, 610. [Google Scholar] [CrossRef]
- Hernández-Stefanoni, J.L.; Reyes-Palomeque, G.; Castillo-Santiago, M.Á.; George-Chacón, S.P.; Huechacona-Ruiz, A.H.; Tun-Dzul, F.; Rondon-Rivera, D.; Dupuy, J.M. Effects of sample plot size and GPS location errors on aboveground biomass estimates from LiDAR in tropical dry forests. Remote Sens. 2018, 10, 1586. [Google Scholar] [CrossRef]
- Zenner, E.K. Investigating scale-dependent stand heterogeneity with structure-area-curves. For. Ecol. Manag. 2005, 209, 87–100. [Google Scholar] [CrossRef]
- Flewelling, J.W. Plot size, shape, and co-registration error determine expected overlap. In Proceedings of the International Union of Forest Research Organizations (IUFRO), Division 4, Extending Forest Inventory and Monitoring Over Space and Time, Quebec City, QC, Canada, 19–22 May 2009; Available online: https://blue.for.msu.edu/meeting/proc2/Flewelling.pdf (accessed on 28 April 2010).
- Mitchard, E.T.A.; Saatchi, S.S.; Baccini, A.; Asner, G.P.; Goetz, S.J.; Harris, N.L.; Sandra, B. Uncertainty in the spatial distribution of tropical forest biomass: A comparison of pan-tropical maps. Carbon Balance Manag. 2013, 8, 10. [Google Scholar] [CrossRef] [PubMed]
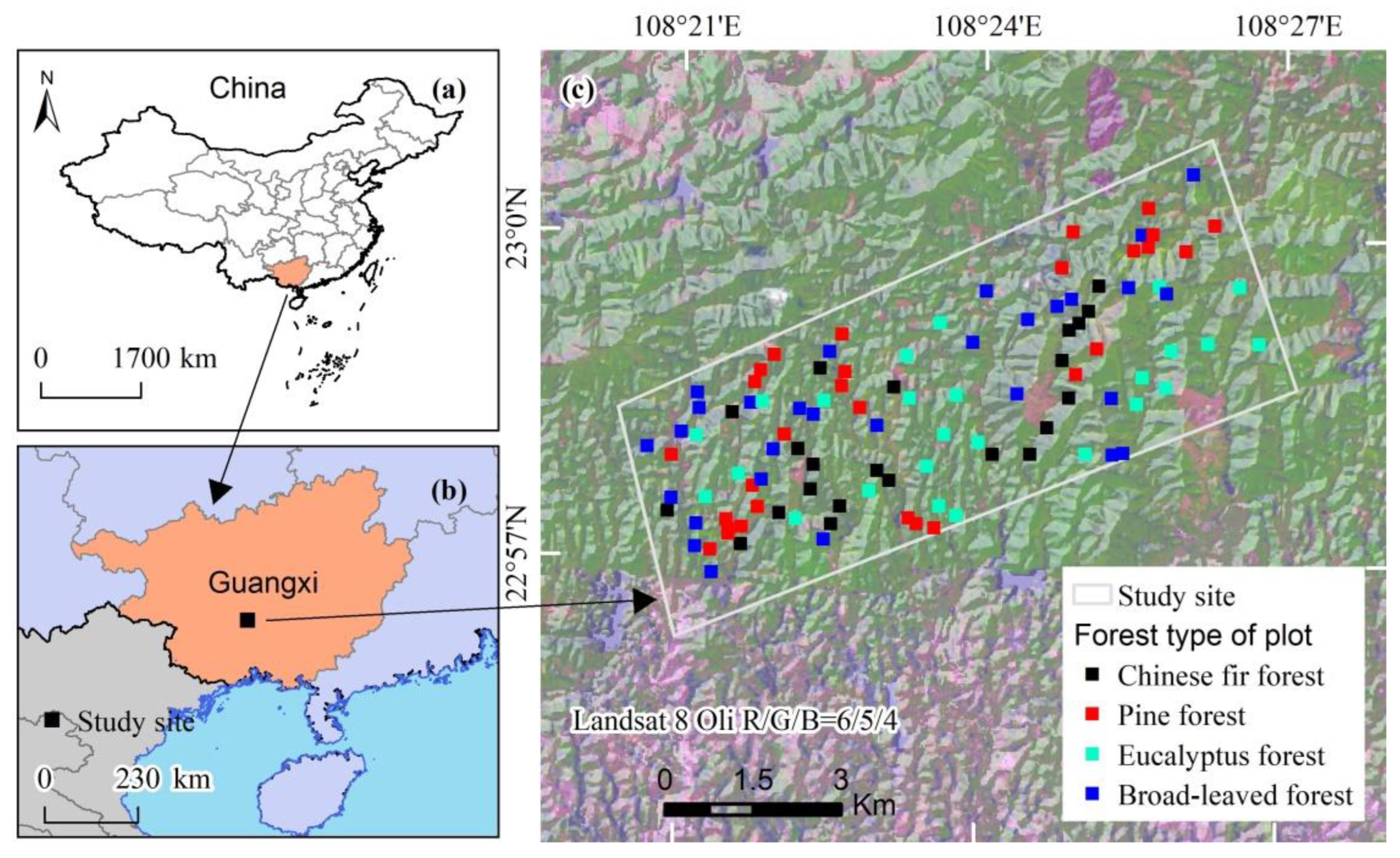


| Stratum | Sample Size | Stand Age (yr) | DBH | Height | Max. Height (m) | BA | Tree Density (Stem ha−1) | VOL | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean (cm) | CV (%) | Mean (m) | CV (%) | Mean (m2 ha−1) | CV (%) | Mean (m3 ha−1) | CV (%) | |||||
| Chinese Fir | 22 | 19–28 | 15.04 | 14.78 | 13.37 | 13.41 | 16.45 | 24.78 | 19.75 | 1536 | 179.87 | 24.39 |
| Pine | 29 | 7–24 | 17.83 | 21.57 | 13.14 | 26.94 | 14.91 | 26.51 | 28.69 | 1166 | 175.86 | 42.34 |
| Eucalyptus | 25 | 2–9 | 11.11 | 15.26 | 16.02 | 20.99 | 18.67 | 17.6 | 35.42 | 1826 | 146.25 | 49.3 |
| Broad-leaved | 28 | 7–56 | 14.35 | 27.36 | 11.37 | 31.84 | 13.7 | 20.44 | 39.28 | 1343 | 128.74 | 59.24 |
| Protocol | 100 m2 | 200 m2 | 300 m2 | 400 m2 | 600 m2 | 900 m2 |
|---|---|---|---|---|---|---|
| 1 | P1 | P1, P2 | P1, P2, P3 | P1, P2, P5, P6 | P1–P6 | P1–P9 |
| 2 | P2 | P2, P5 | P2, P5, P8 | P2-P5 | P2-P5, P8, P9 | P1–P9 |
| 3 | P6 | P6, P7 | P1, P6, P7 | P5-P8 | P1, P2, P5–P8 | P1–P9 |
| 4 | P5 | P4, P5 | P4-P6 | P4, P5, P8, P9 | P4–P9 | P1–P9 |
| Forest Type | Plot Size (m2) | hp50 | Hmean | Hcv | CC | dp50 | LADcv | H | VOL | BA |
|---|---|---|---|---|---|---|---|---|---|---|
| Fir | 100 | 2.50 | 1.93 | 0.16 | 0.15 | 0.17 | 0.37 | 2.62 | 68.49 | 7.35 |
| 200 | 1.92 | 1.62 | 0.15 | 0.13 | 0.17 | 0.29 | 2.18 | 54.82 | 5.91 | |
| 300 | 1.81 | 1.50 | 0.15 | 0.14 | 0.16 | 0.26 | 2.05 | 50.46 | 5.48 | |
| 400 | 1.34 | 1.39 | 0.14 | 0.13 | 0.15 | 0.23 | 1.88 | 45.66 | 5.12 | |
| 600 | 1.31 | 1.36 | 0.14 | 0.13 | 0.15 | 0.23 | 1.81 | 44.73 | 5.01 | |
| 900 | 1.29 | 1.34 | 0.14 | 0.14 | 0.16 | 0.23 | 1.81 | 43.86 | 4.89 | |
| Pine | 100 | 5.08 | 3.88 | 0.19 | 0.17 | 0.22 | 0.45 | 3.67 | 90.63 | 10.43 |
| 200 | 4.46 | 3.80 | 0.17 | 0.15 | 0.21 | 0.36 | 3.55 | 79.54 | 8.48 | |
| 300 | 4.34 | 3.80 | 0.16 | 0.14 | 0.20 | 0.33 | 3.55 | 78.11 | 8.26 | |
| 400 | 4.40 | 3.82 | 0.15 | 0.13 | 0.21 | 0.31 | 3.65 | 75.79 | 7.98 | |
| 600 | 4.38 | 3.80 | 0.15 | 0.13 | 0.20 | 0.30 | 3.54 | 74.80 | 7.75 | |
| 900 | 4.36 | 3.78 | 0.14 | 0.12 | 0.20 | 0.29 | 3.56 | 74.45 | 7.61 | |
| Eucalyptus | 100 | 5.95 | 3.73 | 0.13 | 0.22 | 0.16 | 0.62 | 3.57 | 76.16 | 7.05 |
| 200 | 5.42 | 3.63 | 0.13 | 0.22 | 0.15 | 0.55 | 3.42 | 74.06 | 6.62 | |
| 300 | 5.51 | 3.59 | 0.13 | 0.22 | 0.15 | 0.50 | 3.41 | 73.73 | 6.52 | |
| 400 | 5.24 | 3.59 | 0.13 | 0.21 | 0.15 | 0.46 | 3.56 | 71.80 | 6.22 | |
| 600 | 5.04 | 3.49 | 0.12 | 0.21 | 0.14 | 0.47 | 3.43 | 72.15 | 6.25 | |
| 900 | 4.77 | 3.37 | 0.12 | 0.21 | 0.14 | 0.46 | 3.41 | 72.09 | 6.23 | |
| Broad-leaved | 100 | 5.85 | 5.47 | 0.21 | 0.19 | 0.26 | 0.34 | 4.04 | 93.61 | 9.90 |
| 200 | 5.47 | 5.34 | 0.20 | 0.19 | 0.26 | 0.27 | 3.92 | 83.39 | 8.90 | |
| 300 | 5.50 | 5.36 | 0.20 | 0.19 | 0.27 | 0.25 | 3.85 | 81.65 | 8.44 | |
| 400 | 5.52 | 5.37 | 0.21 | 0.19 | 0.27 | 0.24 | 3.79 | 79.89 | 8.34 | |
| 600 | 5.51 | 5.35 | 0.20 | 0.19 | 0.27 | 0.22 | 3.72 | 77.72 | 8.12 | |
| 900 | 5.51 | 5.34 | 0.20 | 0.18 | 0.28 | 0.22 | 3.66 | 76.25 | 8.03 |
| Stratum | Plot Size (m2) | VOL | BA | ||||
|---|---|---|---|---|---|---|---|
| R2 | rRMSE (%) | MPE (%) | R2 | rRMSE (%) | MPE (%) | ||
| Fir | 100 | 0.390 | 29.31 | 13.93 | 0.313 | 25.00 | 11.88 |
| 200 | 0.433 | 22.38 | 10.64 | 0.310 | 19.77 | 9.40 | |
| 300 | 0.354 | 21.56 | 10.25 | 0.211 | 19.21 | 9.13 | |
| 400 | 0.424 | 19.07 | 9.07 | 0.327 | 17.10 | 8.13 | |
| 600 | 0.467 | 18.11 | 8.61 | 0.337 | 16.55 | 7.87 | |
| 900 | 0.554 | 16.28 | 7.74 | 0.378 | 15.58 | 7.41 | |
| Pine | 100 | 0.327 | 43.69 | 17.48 | 0.098 | 37.88 | 15.15 |
| 200 | 0.445 | 34.13 | 13.66 | 0.172 | 29.34 | 11.74 | |
| 300 | 0.527 | 30.73 | 12.29 | 0.247 | 27.13 | 10.86 | |
| 400 | 0.517 | 30.41 | 12.17 | 0.235 | 26.53 | 10.61 | |
| 600 | 0.572 | 28.06 | 11.23 | 0.302 | 24.51 | 9.81 | |
| 900 | 0.596 | 26.93 | 10.77 | 0.331 | 23.46 | 9.39 | |
| Eucalyptus | 100 | 0.669 | 30.75 | 13.48 | 0.569 | 26.96 | 11.81 |
| 200 | 0.772 | 24.48 | 10.73 | 0.710 | 20.42 | 8.95 | |
| 300 | 0.812 | 22.05 | 9.66 | 0.770 | 17.90 | 7.85 | |
| 400 | 0.864 | 18.26 | 8.00 | 0.823 | 15.03 | 6.59 | |
| 600 | 0.877 | 17.37 | 7.61 | 0.835 | 14.45 | 6.33 | |
| 900 | 0.905 | 15.18 | 6.65 | 0.876 | 12.46 | 5.46 | |
| Broad-leaved | 100 | 0.698 | 38.73 | 15.83 | 0.560 | 31.45 | 12.85 |
| 200 | 0.779 | 30.84 | 12.60 | 0.657 | 25.68 | 10.49 | |
| 300 | 0.788 | 28.89 | 11.81 | 0.668 | 23.46 | 9.59 | |
| 400 | 0.802 | 27.43 | 11.21 | 0.665 | 23.73 | 9.70 | |
| 600 | 0.821 | 25.37 | 10.37 | 0.668 | 22.94 | 9.37 | |
| 900 | 0.847 | 23.13 | 9.45 | 0.690 | 21.89 | 8.94 | |
| Attribute | Forest Type | a0 | a1 | R2 | rRMSE (%) |
|---|---|---|---|---|---|
| VOL | Fir | 6.4570 | −0.3574 | 0.890 | 11.40 |
| Pine | 13.7107 | −0.2637 | 0.772 | 11.02 | |
| Eucalyptus | 7.0049 | −0.3422 | 0.828 | 13.79 | |
| Broad-leaved | 10.2562 | −0.3360 | 0.879 | 13.19 | |
| BA | Fir | 6.7816 | −0.3109 | 0.811 | 11.87 |
| Pine | 11.3946 | −0.2706 | 0.608 | 9.64 | |
| Eucalyptus | 5.8844 | −0.3186 | 0.842 | 11.34 | |
| Broad-leaved | 11.4020 | −0.2745 | 0.735 | 15.85 |
| Plot Size (m2) | rRMSE Difference (%) in VOL Estimation | rRMSE Difference (%) in BA Estimation | ||||||
|---|---|---|---|---|---|---|---|---|
| Fir | Pine | Eucalyptus | Broad-Leaved | Fir | Pine | Eucalyptus | Broad-Leaved | |
| 100 | 119.3 | 78.5 | 112.1 | 109.2 | 98.0 | 83.4 | 101.4 | 82.8 |
| 200 | 71.2 | 48.7 | 67.3 | 65.8 | 59.6 | 51.5 | 61.5 | 51.1 |
| 300 | 48.1 | 33.6 | 45.6 | 44.6 | 40.7 | 35.4 | 41.9 | 35.2 |
| 400 | 33.6 | 23.8 | 32.0 | 31.3 | 28.7 | 25.1 | 29.5 | 24.9 |
| 500 | 23.4 | 16.8 | 22.3 | 21.8 | 20.1 | 17.6 | 20.6 | 17.5 |
| 600 | 15.6 | 11.3 | 14.9 | 14.6 | 13.4 | 11.8 | 13.8 | 11.8 |
| 700 | 9.4 | 6.9 | 9.0 | 8.8 | 8.1 | 7.2 | 8.3 | 7.1 |
| 800 | 4.3 | 3.2 | 4.1 | 4.0 | 3.7 | 3.3 | 3.8 | 3.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Lin, X.; Dai, H.; Li, Z.; Zhou, M. Effects of Plot Size on Airborne LiDAR-Derived Metrics and Predicted Model Performances of Subtropical Planted Forest Attributes. Forests 2022, 13, 2124. https://doi.org/10.3390/f13122124
Li C, Lin X, Dai H, Li Z, Zhou M. Effects of Plot Size on Airborne LiDAR-Derived Metrics and Predicted Model Performances of Subtropical Planted Forest Attributes. Forests. 2022; 13(12):2124. https://doi.org/10.3390/f13122124
Chicago/Turabian StyleLi, Chungan, Xin Lin, Huabing Dai, Zhen Li, and Mei Zhou. 2022. "Effects of Plot Size on Airborne LiDAR-Derived Metrics and Predicted Model Performances of Subtropical Planted Forest Attributes" Forests 13, no. 12: 2124. https://doi.org/10.3390/f13122124
APA StyleLi, C., Lin, X., Dai, H., Li, Z., & Zhou, M. (2022). Effects of Plot Size on Airborne LiDAR-Derived Metrics and Predicted Model Performances of Subtropical Planted Forest Attributes. Forests, 13(12), 2124. https://doi.org/10.3390/f13122124





