Algorithms for Drug Sensitivity Prediction
Abstract
:1. Introduction
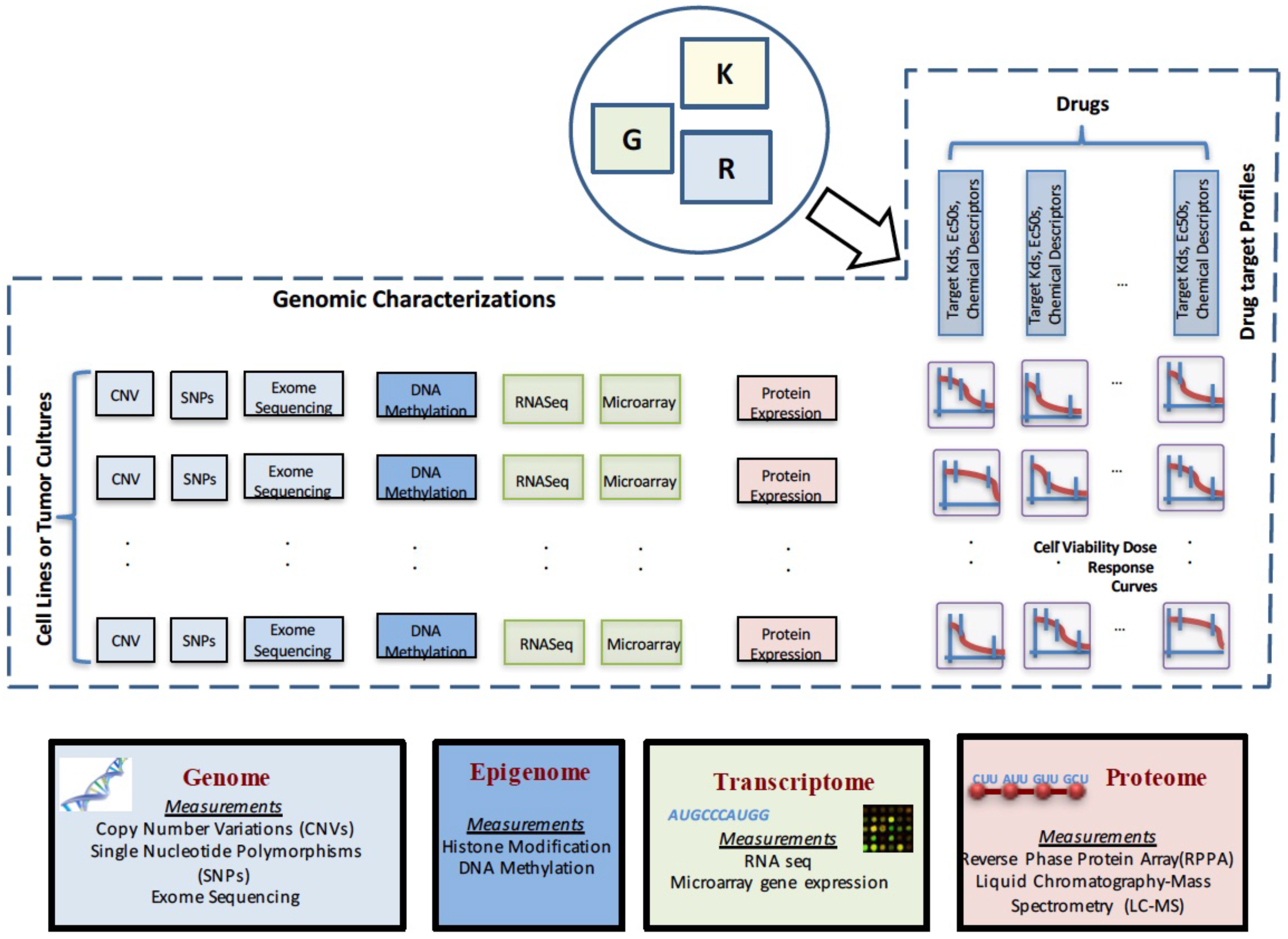
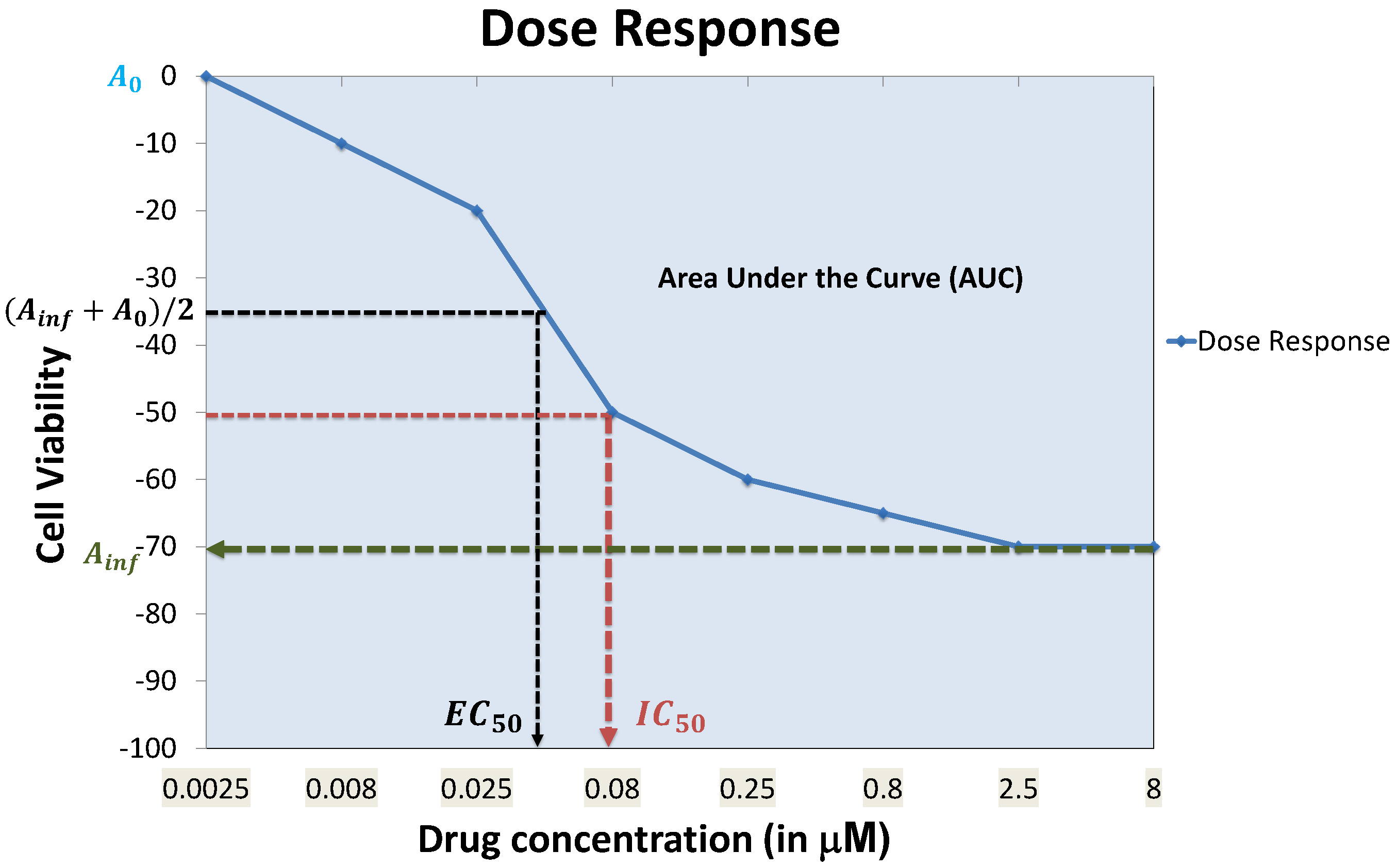
2. Data Characterizations
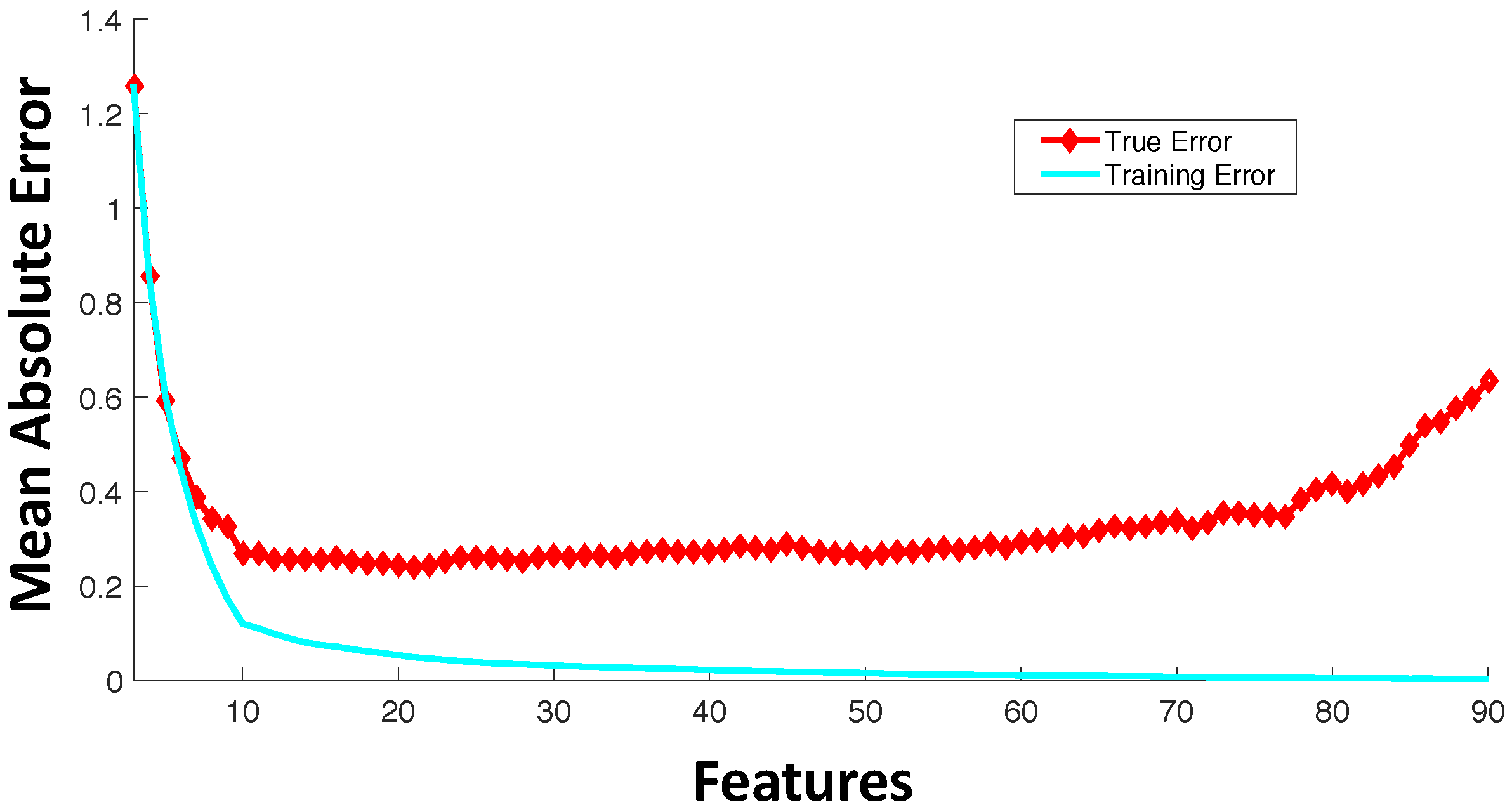
3. Feature Selection
- Filter feature selection: Feature selection refers to selecting a subset of features from the full set of input features based on some design criteria. In filter feature selection, the features are be rated based on general characteristics, such as statistical independence or the correlation of individual features with output response. Some commonly-used filter feature selection approaches in drug sensitivity prediction include: (i) correlation coefficients between genomic features and output responses [25]; (ii) ReliefF [33,34], which is computationally inexpensive, robust and noise tolerant, but does not discriminate between redundant features; (iii) minimum Redundancy Maximum Relevance (mRMR) [35,36,37], which considers features that have highly statistical dependencies with output response, while minimizing the redundancy among selected features.
- Wrapper feature selection: Wrapper techniques evaluate feature subsets based on their predictive accuracy based on a particular model. As compared to wrapper approaches, filter feature selection methods are computationally inexpensive, but they tend to introduce bias and sometimes miss the multivariate relationships among features. A feature may not perform well individually, but in combination with other features, can generate a highly accurate model. Computationally-intensive wrapper methods tend to capture the feature combinations with higher model accuracy, but can potentially overfit the data as compared to filter approaches. In wrapper methods, the goodness of a particular feature subset for feature selection is evaluated using an objective function, , which can model accuracy measured in terms of mean absolute error, root mean square error or the correlation coefficient between predicted and experimental responses. Some commonly-used wrapper feature selection approaches in drug sensitivity prediction include: (i) Sequential Floating Forward Search (SFFS) [32,38], where at each forward iteration, the feature from the remaining features that maximizes the reward or minimizes the cost is selected, and the floating part provides the option to remove an already selected feature if it improves the objective function; (ii) recursive feature elimination [39], which initially involves the ranking of features based on a model fit to all features and recursively eliminating the lowest ranked ones.
- Embedded feature selection: As compared to wrapper feature selection approaches that are evaluated based on objective functions without incorporating the specific structure of the model, embedded feature selection approaches consider the specific structure of the model to select the relevant features, and thus, the feature selection and learning parts cannot be separated. A commonly-used embedded approach is regularization that penalizes the norms of feature weights, such as ridge regression [40,41] penalizing the norm, LASSO [42,43] penalizing the norm and elastic net regularization [23,44] penalizing a mix of and norms.
- Feature extraction: Dimensionality reduction can be approached based on feature extraction from the input data where input data vectors are mapped to new coordinates using different functions. One common example of feature extraction approach is Principal Component Analysis (PCA) [45,46], which maps the input data to a coordinate system that is orthogonal to each other and with the property that the variance along each component projection is maximized.
- Biological knowledge-based feature selection: This approach is based on using prior biological knowledge to reduce the size of the relevant feature set. For instance, if the drugs considered are kinase inhibitors, a potential approach to feature selection might involve modeling from a set of around 500 available kinases [47,48]. Other approaches can include incorporating pathway knowledge in data-driven feature selection, such as pathway-based elastic net regularization [49], biological pathway-based feature selection integrating signalizing and regulatory pathways with gene expression data to select significant features that are minimally redundant [50] or the use of the activation status of signaling pathways as features [51].
4. Predictive Models
4.1. Linear Regression Models
4.2. Logistic Regression and Principal Component Regression-Based Techniques
4.3. Kernel Based Methods
- homogenous polynomial kernels k with and:
- inhomogenous polynomial kernels k with , and:
- radial basis kernels:
4.4. Ensemble Methods
4.5. Deep Neural Networks
4.6. Integrated Functional and Genomic Characterization-Based Models
- C1: If , then
- C2: If , then
4.7. Prediction Performance
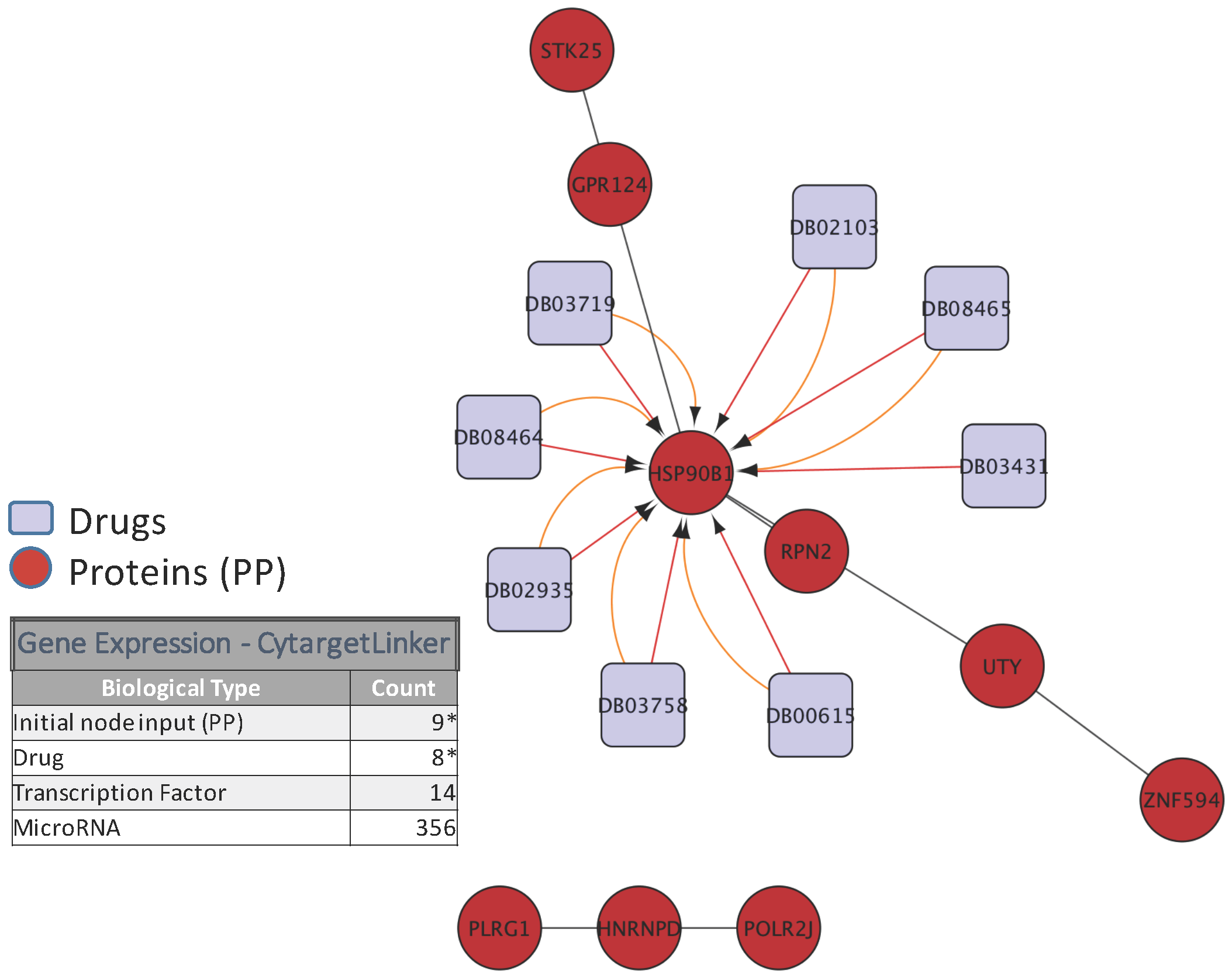
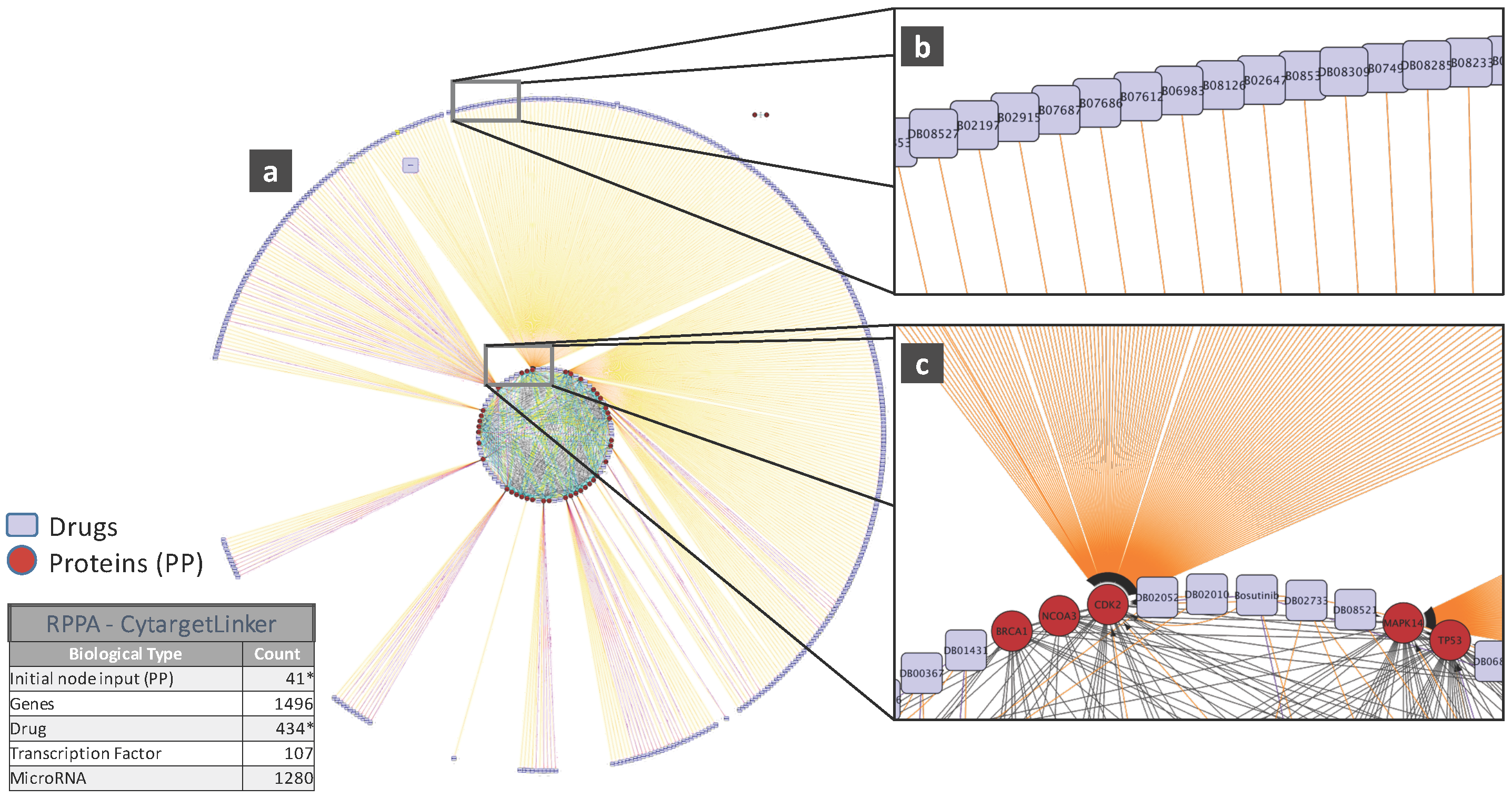
5. Biological Analysis
6. Challenges
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| DNA | Deoxyribonucleic Acid |
| CNV | Copy Number Variation |
| SNP | Single Nucleotide Polymorphism |
References
- Steele, F.R. Personalized medicine: Something old, something new. Future Med. 2009, 6, 1–5. [Google Scholar] [CrossRef]
- Langdon, S.P. Cancer Cell Culture: Methods and Protocols, 1st ed.; Humana Press: New York, NY, USA, 2004. [Google Scholar]
- Masters, J.R. Human cancer cell lines: Fact and fantasy. Nat. Rev. Mol. Cell Biol. 2000, 1, 233–236. [Google Scholar] [CrossRef] [PubMed]
- Gillet, J.; Calcagno, A.M.; Varma, S.; Marino, M.; Green, L.J.; Vora, M.I.; Patel, C.; Orina, J.N.; Eliseeva, T.A.; Singal, V.; et al. Redefining the relevance of established cancer cell lines to the study of mechanisms of clinical anti-cancer drug resistance. Proc. Natl. Acad. Sci. USA 2011, 108, 18708–18713. [Google Scholar] [CrossRef] [PubMed]
- Hudis, C.A. Trastuzumab—Mechanism of Action and Use in Clinical Practice. N. Engl. J. Med. 2007, 357, 39–51. [Google Scholar] [CrossRef] [PubMed]
- Hynes, N.E.; Lane, H.A. ERBB receptors and cancer: The complexity of targeted inhibitors. Nat. Rev. Cancer 2005, 5, 341–354. [Google Scholar] [CrossRef] [PubMed]
- Hoang, M.P.; Sahin, A.A.; Ordonez, N.G.; Sneige, N. HER-2/neu gene amplification compared with HER-2/neu protein overexpression and interobserver reproducibility in invasive breast carcinoma. Am. J. Clin. Pathol. 2000, 113, 852–859. [Google Scholar] [CrossRef] [PubMed]
- Lebeau, A.; Deimling, D.; Kaltz, C.; Sendelhofert, A.; Iff, A.; Luthardt, B.; Untch, M.; Lohrs, U. HER-2/neu analysis in archival tissue samples of human breast cancer: Comparison of immunohistochemistry and fluorescence in situ hybridization. J. Clin. Oncol. 2001, 19, 354–363. [Google Scholar] [PubMed]
- Endo, Y.; Dong, Y.; Kondo, N.; Yoshimoto, N.; Asano, T.; Hato, Y.; Nishimoto, M.; Kato, H.; Takahashi, S.; Nakanishi, R.; et al. HER2 mutation status in Japanese HER2-positive breast cancer patients. Breast Cancer 2015, 23, 902–907. [Google Scholar] [CrossRef] [PubMed]
- Cappuzzo, F.; Hirsch, F.R.; Rossi, E.; Bartolini, S.; Ceresoli, G.L.; Bemis, L.; Haney, J.; Witta, S.; Danenberg, K.; Domenichini, I.; et al. Epidermal growth factor receptor gene and protein and gefitinib sensitivity in non-small-cell lung cancer. J. Natl. Cancer Inst. 2005, 97, 643–655. [Google Scholar] [CrossRef] [PubMed]
- Esteller, M. DNA methylation and cancer therapy: New developments and expectations. Curr. Opin. Oncol. 2005, 17, 55–60. [Google Scholar] [CrossRef] [PubMed]
- Chiappinelli, K.B.; Strissel, P.L.; Desrichard, A.; Li, H.; Henke, C.; Akman, B.; Hein, A.; Rote, N.S.; Cope, L.M.; Snyder, A.; et al. Inhibiting DNA Methylation Causes an Interferon Response in Cancer via dsRNA Including Endogenous Retroviruses. Cell 2015, 162, 974–986. [Google Scholar] [CrossRef] [PubMed]
- Roulois, D.; Loo Yau, H.; Singhania, R.; Wang, Y.; Danesh, A.; Shen, S.Y.; Han, H.; Liang, G.; Jones, P.A.; Pugh, T.J.; et al. DNA-Demethylating Agents Target Colorectal Cancer Cells by Inducing Viral Mimicry by Endogenous Transcripts. Cell 2015, 162, 961–973. [Google Scholar] [CrossRef] [PubMed]
- Heller, M.J. DNA Microarray Technology: Devices, Systems, and Applications. Ann. Rev. Biomed. Eng. 2002, 4, 129–153. [Google Scholar] [CrossRef] [PubMed]
- Velculescu, V.E.; Zhang, L.; Vogelstein, B.; Kinzler, K.W. Serial Analysis of Gene Expression. Science 1995, 270, 484–487. [Google Scholar] [CrossRef] [PubMed]
- Brenner, S.; Johnson, M.; Bridgham, J.; Golda, G.; Lloyd, D.H.; Johnson, D.; Luo, S.; McCurdy, S.; Foy, M.; Ewan, M.; et al. Gene expression analysis by massively parallel signature sequencing (MPSS) on microbead arrays. Nat. Biotechnol. 2000, 18, 630–634. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Gerstein, M.; Snyder, M. RNA-Seq: A revolutionary tool for transcriptomics. Nat. Rev. Genet. 2009, 10, 57–63. [Google Scholar] [CrossRef] [PubMed]
- Rabilloud, T.; Lelong, C. Two-dimensional gel electrophoresis in proteomics: A tutorial. J. Proteom. 2011, 74, 1829–1841. [Google Scholar] [CrossRef] [PubMed]
- Franck, J.; Arafah, K.; Elayed, M.; Bonnel, D.; Vergara, D.; Jacquet, A.; Vinatier, D.; Wisztorski, M.; Day, R.; Fournier, I.; et al. MALDI Imaging Mass Spectrometry. Mol. Cell. Proteom. 2009, 8, 2023–2033. [Google Scholar] [CrossRef] [PubMed]
- Spurrier, B.; Ramalingam, S.; Nishizuka, S. Reverse-phase protein lysate microarrays for cell signaling analysis. Nat. Protoc. 2008, 3, 1796–1808. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Gonzalez, F.J.; Ma, X. LC–MS-based metabolomics in profiling of drug metabolism and bioactivation. Acta Pharm. Sin. B 2012, 2, 118–125. [Google Scholar] [CrossRef]
- Ross, D.T.; Scherf, U.; Eisen, M.B.; Perou, C.M.; Rees, C.; Spellman, P.; Iyer, V.; Jeffrey, S.S.; van de Rijn, M.; Waltham, M.; et al. Systematic variation in gene expression patterns in human cancer cell lines. Nat. Genet. 2000, 24, 227–235. [Google Scholar] [CrossRef] [PubMed]
- Barretina, J.; Caponigro, G.; Stransky, N.; Venkatesan, K.; Margolin, A.A.; Kim, S.; Wilson, C.J.; Lehár, J.; Kryukov, G.V.; Sonkin, D.; et al. The Cancer Cell Line Encyclopedia enables predictive modelling of anticancer drug sensitivity. Nature 2012, 483, 603–607. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.E.A. Genomics of Drug Sensitivity in Cancer (GDSC): A resource for therapeutic biomarker discovery in cancer cells. Nucleic Acids Res. 2013, 41, D955–D961. [Google Scholar] [CrossRef] [PubMed]
- Costello, J.C.; Heiser, L.M.; Georgii, E.; Gönen, M.; Menden, M.P.; Wang, N.J.; Bansal, M.; Ammad-ud-din, M.; Hintsanen, P.; Khan, S.A.; et al. A community effort to assess and improve drug sensitivity prediction algorithms. Nat. Biotechnol. 2014, 32, 1202–1212. [Google Scholar] [CrossRef] [PubMed]
- Weinstein, J.N.; Collisson, E.A.; Mills, G.B.; Shaw, K.R.; Ozenberger, B.A.; Ellrott, K.; Shmulevich, I.; Sander, C.; Stuart, J.M.; Chang, K.; et al. The Cancer Genome Atlas Pan-Cancer analysis project. Nat. Genet. 2013, 45, 1113–1120. [Google Scholar] [PubMed]
- Daemen, A.; Griffith, O.L.; Heiser, L.M.; Wang, N.J.; Enache, O.M.; Sanborn, Z.; Pepin, F.; Durinck, S.; Korkola, J.E.; Griffith, M.; et al. Modeling precision treatment of breast cancer. Genome Biol. 2013, 14, R110. [Google Scholar] [CrossRef] [PubMed]
- Klijn, C.; Durinck, S.; Stawiski, E.W.; Haverty, P.M.; Jiang, Z.; Liu, H.; Degenhardt, J.; Mayba, O.; Gnad, F.; Liu, J.; et al. A comprehensive transcriptional portrait of human cancer cell lines. Nat. Biotechnol. 2015, 33, 306–312. [Google Scholar] [CrossRef] [PubMed]
- Hook, K.E.; Garza, S.J.; Lira, M.E.; Ching, K.A.; Lee, N.V.; Cao, J.; Yuan, J.; Ye, J.; Ozeck, M.; Shi, S.T.; et al. An integrated genomic approach to identify predictive biomarkers of response to the aurora kinase inhibitor PF-03814735. Mol. Cancer Therap. 2012, 11, 710–719. [Google Scholar] [CrossRef] [PubMed]
- Basu, A.; Bodycombe, N.E.; Cheah, J.H.; Price, E.V.; Liu, K.; Schaefer, G.I.; Ebright, R.Y.; Stewart, M.L.; Ito, D.; Wang, S.; et al. An interactive resource to identify cancer genetic and lineage dependencies targeted by small molecules. Cell 2013, 154, 1151–1161. [Google Scholar] [CrossRef] [PubMed]
- Berlow, N.; Haider, S.; Wan, Q.; Geltzeiler, M.; Davis, L.E.; Keller, C.; Pal, R. An integrated approach to anti-cancer drugs sensitivity prediction. IEEE/ACM Trans. Comput. Biol. Bioinform. 2014, 11, 995–1008. [Google Scholar] [CrossRef] [PubMed]
- Berlow, N.; Davis, L.E.; Cantor, E.L.; Seguin, B.; Keller, C.; Pal, R. A new approach for prediction of tumor sensitivity to targeted drugs based on functional data. BMC Bioinform. 2013, 14, 239. [Google Scholar] [CrossRef] [PubMed]
- Robnik-Sikonja, M.; Kononenko, I. Theoretical and empirical analysis of ReliefF and RReliefF. Mach. Learn. 2003, 53, 23–69. [Google Scholar] [CrossRef]
- Haider, S.; Rahman, R.; Ghosh, S.; Pal, R. A Copula Based Approach for Design of Multivariate Random Forests for Drug Sensitivity Prediction. PLoS ONE 2015, 10, e0144490. [Google Scholar] [CrossRef] [PubMed]
- Peng, H.; Long, F.; Ding, C. Feature selection based on mutual information: Criteria of max-dependency, max-relevance, and min-redundancy. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1226–1238. [Google Scholar] [CrossRef] [PubMed]
- De Jay, N.; Papillon-Cavanagh, S.; Olsen, C.; El-Hachem, N.; Bontempi, G.; Haibe-Kains, B. mRMRe: An R package for parallelized mRMR ensemble feature selection. Bioinformatics 2013, 29, 2365–2368. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Chen, L.; Zhang, Y.H.; Wei, L.; Cheng, S.; Kong, X.; Zheng, M.; Huang, T.; Cai, Y.D. Analysis and prediction of drug-drug interaction by minimum redundancy maximum relevance and incremental feature selection. J. Biomol. Struct. Dyn. 2016, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Pudil, P.; Novovicova, J.; Kittler, J. Floating search methods in feature selection. Pattern Recog. Lett. 1994, 15, 1119–1125. [Google Scholar] [CrossRef]
- Dong, Z.; Zhang, N.; Li, C.; Wang, H.; Fang, Y.; Wang, J.; Zheng, X. Anticancer drug sensitivity prediction in cell lines from baseline gene expression through recursive feature selection. BMC Cancer 2015, 15, 489. [Google Scholar] [CrossRef] [PubMed]
- Tikhonov, A. Solution of incorrectly formulated problems and the regularization method. Sov. Math. Dokl. 1963, 4, 1035–1038. [Google Scholar]
- Neto, E.C.; Jang, I.S.; Friend, S.H.; Margolin, A.A. The Stream algorithm: Computationally efficient ridge-regression via Bayesian model averaging, and applications to pharmacogenomic prediction of cancer cell line sensitivity. Pac. Symp. Biocomput. 2014, 27–38. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression Shrinkage and Selection via the Lasso. J. R. Stat. Soc. Ser. B 1994, 58, 267–288. [Google Scholar]
- Park, H.; Imoto, S.; Miyano, S. Recursive Random Lasso (RRLasso) for Identifying Anti-Cancer Drug Targets. PLoS ONE 2015, 10, e0141869. [Google Scholar] [CrossRef] [PubMed]
- Zou, H.; Hastie, T. Regularization and variable selection via the Elastic Net. J. R. Stat. Soc. Ser. B 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Pearson, K. On lines and planes of closest fit to systems of points in space. Philos. Mag. 1901, 2, 559–572. [Google Scholar] [CrossRef]
- Goswami, C.P.; Cheng, L.; Alexander, P.S.; Singal, A.; Li, L. A New Drug Combinatory Effect Prediction Algorithm on the Cancer Cell Based on Gene Expression and Dose-Response Curve. CPT Pharm. Syst. Pharmacol. 2015, 4, e9. [Google Scholar] [CrossRef] [PubMed]
- Pal, R.; Berlow, N. A Kinase inhibition map approach for tumor sensitivity prediction and combination therapy design for targeted drugs. Pac. Symp. Biocomput. 2012, 351–362. [Google Scholar] [CrossRef]
- Wan, Q.; Pal, R. An ensemble based top performing approach for NCI-DREAM drug sensitivity prediction challenge. PLoS ONE 2014, 9, e101183. [Google Scholar] [CrossRef] [PubMed]
- Sokolov, A.; Carlin, D.E.; Paull, E.O.; Baertsch, R.; Stuart, J.M. Pathway-Based Genomics Prediction using Generalized Elastic Net. PLoS Comput. Biol. 2016, 12, e1004790. [Google Scholar] [CrossRef] [PubMed]
- Bandyopadhyay, N.; Kahveci, T.; Goodison, S.; Sun, Y.; Ranka, S. Pathway-BasedFeature Selection Algorithm for Cancer Microarray Data. Adv. Bioinform. 2009, 2009, 532989. [Google Scholar] [CrossRef] [PubMed]
- Amadoz, A.; Sebastian-Leon, P.; Vidal, E.; Salavert, F.; Dopazo, J. Using activation status of signaling pathways as mechanism-based biomarkers to predict drug sensitivity. Sci. Rep. 2015, 5, 18494. [Google Scholar] [CrossRef] [PubMed]
- Jang, I.S.; Neto, E.C.; Guinney, J.; Friend, S.H.; Margolin, A.A. Systematic assessment of analytical methods for drug sensitivity prediction from cancer cell line data. Available online: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3995541/ (accessed on 16 November 2016).
- Kleinbaum, D.G.; Kupper, L.L.; Muller, K.E. (Eds.) Applied Regression Analysis and Other Multivariable Methods; PWS Publishing Co.: Boston, MA, USA, 1988.
- Tikhonov, A.N.; Arsenin, V.Y. Solutions of Ill-Posed Problems; V. H. Winston & Sons: Washington, DC, USA; John Wiley & Sons: New York, NY, USA, 1977. [Google Scholar]
- Zhou, Q.; Chen, W.; Song, S.; Gardner, J.; Weinberger, K.; Chen, Y. A Reduction of the Elastic Net to Support Vector Machines with an Application to GPU Computing. arXiv, 2014; arXiv:1409.1976. [Google Scholar]
- Mermel, C.H.; Schumacher, S.E.; Hill, B.; Meyerson, M.L.; Beroukhim, R.; Getz, G. GISTIC2.0 facilitates sensitive and confident localization of the targets of focal somatic copy-number alteration in human cancers. Genome Biol. 2011, 12, R41. [Google Scholar] [CrossRef] [PubMed]
- Geeleher, P.; Cox, N.J.; Huang, R.S. Clinical drug response can be predicted using baseline gene expression levels and in vitro drug sensitivity in cell lines. Genome Biol. 2014, 15, R47. [Google Scholar] [CrossRef] [PubMed]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Tibshirani, R.; Hastie, T.; Narasimhan, B.; Chu, G. Diagnosis of multiple cancer types by shrunken centroids of gene expression. Proc. Natl. Acad. Sci. USA 2002, 99, 6567–6572. [Google Scholar] [CrossRef] [PubMed]
- Næs, T.; Mevik, B.H. Understanding the collinearity problem in regression and discriminant analysis. J. Chemom. 2001, 15, 413–426. [Google Scholar] [CrossRef]
- pls: Partial Least Squares and Principal Component Regression, R package version 2.5; Available online: https://cran.r-project.org/web/packages/pls/index.html (accessed on 16 November 2016).
- Gonen, M.; Margolin, A.A. Drug susceptibility prediction against a panel of drugs using kernelized Bayesian multitask learning. Bioinformatics 2014, 30, i556–i563. [Google Scholar] [CrossRef] [PubMed]
- Strother, H.; Walker, D.B.D. Estimation of the Probability of an Event as a Function of Several Independent Variables. Biometrika 1967, 54, 167–179. [Google Scholar]
- Freedman, D. Statistical Models: Theory and Practice; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Kim, D.C.; Wang, X.; Yang, C.R.; Gao, J.X. A framework for personalized medicine: prediction of drug sensitivity in cancer by proteomic profiling. Proteome Sci. 2012, 10 (Suppl. 1), S13. [Google Scholar] [CrossRef] [PubMed]
- Hejase, H.A.; Chan, C. Improving Drug Sensitivity Prediction Using Different Types of Data. CPT Pharm. Syst. Pharmacol. 2015, 4, e2. [Google Scholar] [CrossRef] [PubMed]
- Bayer, I.; Groth, P.; Schneckener, S. Prediction errors in learning drug response from gene expression Data—Influence of labeling, sample size, and machine learning algorithm. PLoS ONE 2013, 8, e70294. [Google Scholar] [CrossRef] [PubMed]
- Geladi, P.; Kowalski, B.R. Partial least-squares regression: A tutorial. Anal. Chim. Acta 1986, 185, 1–17. [Google Scholar] [CrossRef]
- Dijkstra, T. Some comments on maximum likelihood and partial least squares methods. J. Econom. 1983, 22, 67–90. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning; Springer Series in Statistics; Springer: New York, NY, USA, 2001. [Google Scholar]
- Ildiko, E.; Frank, J.H.F. A Statistical View of Some Chemometrics Regression Tools. Technometrics 1993, 35, 109–135. [Google Scholar]
- Vapnik, V.; Lerner, A. Pattern Recognition Using Generalized Portrait Method. Autom. Remote Control 1963, 24, 774–780. [Google Scholar]
- Vapnik, V.; Chervonenkis, A. A note on one class of perceptrons. Autom. Remote Control 1964, 25. [Google Scholar]
- Vapnik, V.N. Statistical Learning Theory; Wiley-Interscience: Hoboken, NJ, USA, 1998. [Google Scholar]
- Müller, K.R.; Smola, A.; Rätsch, G.; Schölkopf, B.; Kohlmorgen, J.; Vapnik, V. Predicting time series with support vector machines. In Artificial Neural Networks—ICANN’97; Lecture Notes in Computer Science; Gerstner, W., Germond, A., Hasler, M., Nicoud, J.D., Eds.; Springer: Berlin/Heidelberg, Germany, 1997; Volume 1327, pp. 999–1004. [Google Scholar]
- Mattera, D.; Haykin, S. Support Vector Machines for Dynamic Reconstruction of a Chaotic System. In Advances in Kernel Methods; MIT Press: Cambridge, MA, USA, 1999; pp. 211–241. [Google Scholar]
- Smola, A.J.; Schölkopf, B. A Tutorial on Support Vector Regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Cristianini, N.; Shawe-Taylor, J. An Introduction to Support Vector Machines: And Other Kernel-Based Learning Methods; Cambridge University Press: New York, NY, USA, 2000. [Google Scholar]
- Cherkassky, V.; Ma, Y. Comparison of model selection for regression. Neural Comput. 2003, 15, 1691–1714. [Google Scholar] [CrossRef] [PubMed]
- Freund, Y.; Schapire, R.E. A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef]
- Breiman, L. Bagging Predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Wolpert, D.H. Stacked Generalization. Neural Netw. 1992, 5, 241–259. [Google Scholar] [CrossRef]
- Clarke, B. Comparing Bayes Model Averaging and Stacking When Model Approximation Error Cannot Be Ignored. J. Mach. Learn. Res. 2003, 4, 683–712. [Google Scholar]
- Breiman, L. Stacked Regressions. Mach. Learn. 1996, 24, 49–64. [Google Scholar] [CrossRef]
- Riddick, G.; Song, H.; Ahn, S.; Walling, J.; Borges-Rivera, D.; Zhang, W.; Fine, H.A. Predicting in vitro drug sensitivity using Random Forests. Bioinformatics 2011, 27, 220–224. [Google Scholar] [CrossRef] [PubMed]
- Lunetta, K.L.; Hayward, L.B.; Segal, J.; van Eerdewegh, P. Screening large-scale association study data: Exploiting interactions using random forests. BMC Genet. 2004, 5, 32. [Google Scholar] [CrossRef] [PubMed]
- Bureau, A.; Dupuis, J.; Falls, K.; Lunetta, K.L.; Hayward, B.; Keith, T.P.; Van Eerdewegh, P. Identifying SNPs predictive of phenotype using random forests. Genet. Epidemiol. 2005, 28, 171–182. [Google Scholar] [CrossRef] [PubMed]
- Diaz-Uriarte, R.; Alvarez de Andres, S. Gene selection and classification of microarray data using random forest. BMC Bioinform. 2006, 7, 3. [Google Scholar] [CrossRef] [PubMed]
- Yao, D.; Yang, J.; Zhan, X.; Zhan, X.; Xie, Z. A novel random forests-based feature selection method for microarray expression data analysis. Int. J. Data Min. Bioinform. 2015, 13, 84–101. [Google Scholar] [CrossRef] [PubMed]
- Yu, D.J.; Li, Y.; Hu, J.; Yang, X.; Yang, J.Y.; Shen, H.B. Disulfide Connectivity Prediction Based on Modelled Protein 3D Structural Information and Random Forest Regression. IEEE/ACM Trans. Comput. Biol. Bioinform. 2015, 12, 611–621. [Google Scholar] [PubMed]
- Qi, Y.; Bar-Joseph, Z.; Klein-Seetharaman, J. Evaluation of different biological data and computational classification methods for use in protein interaction prediction. Proteins 2006, 63, 490–500. [Google Scholar] [CrossRef] [PubMed]
- Rahman, R.; Haider, S.; Ghosh, S.; Pal, R. Design of Probabilistic Random Forests with Applications to Anticancer Drug Sensitivity Prediction. Cancer Inform. 2015, 14, 57. [Google Scholar] [PubMed]
- Ho, T.K. Random Decision Forests. In Proceedings of the Third International Conference on Document Analysis and Recognition ICDAR ’95 (Volume 1), Montreal, QC, Canada, 14–15 August 1995; pp. 278–282.
- Ho, T.K. The Random Subspace Method for Constructing Decision Forests. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 832–844. [Google Scholar]
- Amit, Y.; Geman, D. Shape Quantization and Recognition with Randomized Trees. Neural Comput. 1997, 9, 1545–1588. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.; Olshen, R.; Stone, C. Classification and Regression Trees; Wadsworth and Brooks: Monterey, CA, USA, 1984. [Google Scholar]
- Ospina, J.D.; Zhu, J.; Chira, C.; Bossi, A.; Delobel, J.B.; Beckendorf, V.; Dubray, B.; Lagrange, J.L.; Correa, J.C.; Simon, A.; et al. Random forests to predict rectal toxicity following prostate cancer radiation therapy. Int. J. Radiat. Oncol. Biol. Phys. 2014, 89, 1024–1031. [Google Scholar] [CrossRef] [PubMed]
- Hinton, G.E.; Srivastava, N.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Improving neural networks by preventing co-adaptation of feature detectors. CoRR, 2012; arXiv:1207.0580. [Google Scholar]
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed]
- Jaitly, N.; Nguyen, P.; Senior, A.; Vanhoucke, V. Application of pretrained deep neural networks to large vocabulary speech recognition. In Proceedings of the Interspeech 2012, Portland, OR, USA, 9–13 September 2012.
- Dahl, G.; Jaitly, N.; Salakhutdinov, R. Multi-task Neural Networks for QSAR Predictions. arXiv, 2014; arXiv:1406.1231. [Google Scholar]
- Sawyers, C. Targeted Cancer Therapy. Nature 2004, 432, 294–297. [Google Scholar] [CrossRef] [PubMed]
- Green, M.R. Targeting Targeted Therapy. N. Engl. J. Med. 2004, 350, 2191–2193. [Google Scholar] [CrossRef] [PubMed]
- Druker, B.J. Molecularly targeted therapy: Have the floodgates opened? Oncologist 2004, 9, 357–360. [Google Scholar] [CrossRef] [PubMed]
- Hopkins, A.; Mason, J.; Overington, J. Can we rationally design promiscuous drugs? Curr. Opin. Struct. Biol. 2006, 16, 127–136. [Google Scholar] [CrossRef] [PubMed]
- Knight, Z.A.; Shokat, K.M. Features of Selective Kinase Inhibitors. Chem. Biol. 2005, 12, 621–637. [Google Scholar] [CrossRef] [PubMed]
- Tyner, J.W.; Deininger, M.W.; Loriaux, M.M.; Chang, B.H.; Gotlib, J.R.; Willis, S.G.; Erickson, H.; Kovacsovics, T.; O’Hare, T.; Heinrich, M.C.; et al. RNAi screen for rapid therapeutic target identification in leukemia patients. Proc. Natl. Acad. Sci. USA 2009, 106, 8695–8700. [Google Scholar] [CrossRef] [PubMed]
- Berlow, N.; Davis, L.; Keller, C.; Pal, R. Inference of dynamic biological networks based on responses to drug perturbations. EURASIP J. Bioinform. Syst. Biol. 2014, 14. [Google Scholar] [CrossRef]
- Berlow, N.; Pal, R.; Davis, L.; Keller, C. Analyzing Pathway Design From Drug Perturbation Experiments. In Proceedings of the 2012 IEEE Statistical Signal Processing Workshop (SSP), Ann Arbor, MI, USA, 5–8 August 2012; pp. 552–555.
- Berlow, N.; Haider, S.; Pal, R.; Keller, C. Quantifying the inference power of a drug screen for predictive analysis. In Proceedings of the 2013 IEEE International Workshop on Genomic Signal Processing and Statistics (GENSIPS), Houston, TX, USA, 17–19 November 2013; pp. 49–52.
- Haider, S.; Berlow, N.; Pal, R.; Davis, L.; Keller, C. Combination therapy design for targeted therapeutics from a Drug-Protein interaction perspective. In Proceedings of the 2012 IEEE International Workshop on Genomic Signal Processing and Statistics (GENSIPS), Washington, DC, USA, 2–4 December 2012; pp. 58–61.
- Grasso, C.S.; Tang, Y.; Truffaux, N.; Berlow, N.E.; Liu, L.; Debily, M.; Quist, M.J.; Davis, L.E.; Huang, E.C.; Woo, P.J.; et al. Functionally-defined Therapeutic Targets in Diffuse Intrinsic Pontine Glioma. Nat. Med. 2015. [Google Scholar] [CrossRef]
- Menden, M.P.; Iorio, F.; Garnett, M.; McDermott, U.; Benes, C.H.; Ballester, P.J.; Saez-Rodriguez, J. Machine learning prediction of cancer cell sensitivity to drugs based on genomic and chemical properties. PLoS ONE 2013, 8, e61318. [Google Scholar] [CrossRef] [PubMed]
- Yue, Z.; Zhang, W.; Lu, Y.; Yang, Q.; Ding, Q.; Xia, J.; Chen, Y. Prediction of cancer cell sensitivity to natural products based on genomic and chemical properties. PeerJ 2015, 3, e1425. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez, J.J.; Kuncheva, L.I.; Alonso, C.J. Rotation forest: A new classifier ensemble method. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1619–1630. [Google Scholar] [CrossRef] [PubMed]
- Bottou, L. Large-scale machine learning with stochastic gradient descent. In Proceedings of the 19th International Conference on Computational Statistics, Paris, France, 22–27 August 2010.
- Sutskever, I.; Martens, J.; Dahl, G.E.; Hinton, G.E. On the importance of initialization and momentum in deep learning. ICML JMLR Proc. 2013, 28, 1139–1147. [Google Scholar]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Rissanen, J. A Universal Prior for Integers and Estimation by Minimum Description Length. Ann. Stat. 1983, 11, 416–431. [Google Scholar] [CrossRef]
- Tanaka, T.; Tanimoto, K.; Otani, K.; Satoh, K.; Ohtaki, M.; Yoshida, K.; Toge, T.; Yahata, H.; Tanaka, S.; Chayama, K.; et al. Concise prediction models of anticancer efficacy of 8 drugs using expression data from 12 selected genes. Int. J. Cancer 2004, 111, 617–626. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.J.; Litvin, O.; Ungar, L.; Pe’er, D. Context Sensitive Modeling of Cancer Drug Sensitivity. PLoS ONE 2015, 10, e0133850. [Google Scholar] [CrossRef] [PubMed]
- Shoemaker, R.H. The NCI60 human tumour cell line anticancer drug screen. Nat. Rev. Cancer 2006, 6, 813–823. [Google Scholar] [CrossRef] [PubMed]
- Pal, R.; Datta, A.; Fornace, A.; Bittner, M.; Dougherty, E. Boolean relationships among genes responsive to ionizing radiation in the NCI 60 ACDS. Bioinformatics 2005, 21, 1542–1549. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.B.; Stein, R.; O’Hare, M.J. Three-dimensional in vitro tissue culture models of breast cancer—A review. Breast Cancer Res. Treat. 2004, 85, 281–291. [Google Scholar] [CrossRef] [PubMed]
- Gordon, J.W.; Scangos, G.A.; Plotkin, D.J.; Barbosa, J.A.; Ruddle, F.H. Genetic transformation of mouse embryos by microinjection of purified DNA. Proc. Natl. Acad. Sci. USA 1980, 77, 7380–7384. [Google Scholar] [CrossRef] [PubMed]
- Thomas, K.R.; Capecchi, M.R. Site-directed mutagenesis by gene targeting in mouse embryo-derived stem cells. Cell 1987, 51, 503–512. [Google Scholar] [CrossRef]
- Walrath, J.C.; Hawes, J.J.; van Dyke, T.; Reilly, K.M. Genetically engineered mouse models in cancer research. Adv. Cancer Res. 2010, 106, 113–164. [Google Scholar] [PubMed]
- Richmond, A.; Su, Y. Mouse xenograft models vs. GEM models for human cancer therapeutics. Dis. Models Mech. 2008, 1, 78–82. [Google Scholar] [CrossRef] [PubMed]
- Kerbel, R.S. Human tumor xenografts as predictive preclinical models for anticancer drug activity in humans: Better than commonly perceived-but they can be improved. Cancer Biol. Ther. 2003, 2, S134–S139. [Google Scholar] [CrossRef] [PubMed]
- Johnson, J.I.; Decker, S.; Zaharevitz, D.; Rubinstein, L.V.; Venditti, J.M.; Schepartz, S.; Kalyandrug, S.; Christian, M.; Arbuck, S.; Hollingshead, M.; et al. Relationships between drug activity in NCI preclinical in vitro and in vivo models and early clinical trials. Br. J. Cancer 2001, 84, 1424–1431. [Google Scholar] [CrossRef] [PubMed]
- Scholz, C.C.; Berger, D.P.; Winterhalter, B.R.; Henss, H.; Fiebig, H.H. Correlation of drug response in patients and in the clonogenic assay with solid human tumour xenografts. Eur. J. Cancer 1990, 26, 901–905. [Google Scholar] [CrossRef]
- Khanna, C.; Lindblad-Toh, K.; Vail, D.; London, C.; Bergman, P.; Barber, L.; Breen, M.; Kitchell, B.; McNeil, E.; Modiano, J.F.; et al. The dog as a cancer model. Nat. Biotechnol. 2006, 24, 1065–1066. [Google Scholar] [CrossRef] [PubMed]
- Szklarczyk, D.; Franceschini, A.; Wyder, S.; Forslund, K.; Heller, D.; Huerta-Cepas, J.; Simonovic, M.; Roth, A.; Santos, A.; Tsafou, K.P.; et al. STRING v10: Protein-protein interaction networks, integrated over the tree of life. Nucleic Acids Res. 2015, 43, D447–D452. [Google Scholar] [CrossRef] [PubMed]
- Shannon, P.; Markiel, A.; Ozier, O.; Baliga, N.S.; Wang, J.T.; Ramage, D.; Amin, N.; Schwikowski, B.; Ideker, T. Cytoscape: A software environment for integrated models of biomolecular interaction networks. Genome Res. 2003, 13, 2498–2504. [Google Scholar] [CrossRef] [PubMed]
- Kutmon, M.; Kelder, T.; Mandaviya, P.; Evelo, C.T.; Coort, S.L. CyTargetLinker: A cytoscape app to integrate regulatory interactions in network analysis. PLoS ONE 2013, 8, e82160. [Google Scholar] [CrossRef] [PubMed]
- Haibe-Kains, B.; El-Hachem, N.; Birkbak, N.J.; Jin, A.C.; Beck, A.H.; Aerts, H.J.W.L.; Quackenbush, J. Inconsistency in large pharmacogenomic studies. Nature 2013, 504, 389–393. [Google Scholar] [CrossRef] [PubMed]
- Marusyk, A.; Polyak, K. Tumor heterogeneity: Causes and consequences. Biochim. Biophys. Acta 2010, 1805, 105–117. [Google Scholar] [CrossRef] [PubMed]
- Shackleton, M.; Quintana, E.; Fearon, E.R.; Morrison, S.J. Heterogeneity in Cancer: Cancer Stem Cells versus Clonal Evolution. Cell 2009, 138, 822–829. [Google Scholar] [CrossRef] [PubMed]
- Swanton, C.; Burrell, R.; Futreal, P.A. Breast cancer genome heterogeneity: A challenge to personalised medicine? Breast Cancer Res. 2011, 13, 104. [Google Scholar] [CrossRef] [PubMed]
- Gerlinger, M.; Rowan, A.J.; Horswell, S.; Larkin, J.; Endesfelder, D.; Gronroos, E.; Martinez, P.; Matthews, N.; Stewart, A.; Tarpey, P.; et al. Intratumor Heterogeneity and Branched Evolution Revealed by Multiregion Sequencing. N. Engl. J. Med. 2012, 366, 883–892. [Google Scholar] [CrossRef] [PubMed]
- Kuhn, M.; Campillos, M.; Letunic, I.; Jensen, L.J.; Bork, P. A side effect resource to capture phenotypic effects of drugs. Mol. Syst. Biol. 2010, 6, 343. [Google Scholar] [CrossRef] [PubMed]

| Drug Name | Correlation Coefficients | |||
|---|---|---|---|---|
| AZD0530 | 0.2149 | 0.2245 | 0.2577 | 0.1986 |
| Erlotinib | 0.3905 | 0.4100 | 0.4438 | 0.1341 |
| Lapatinib | 0.4758 | 0.4641 | 0.5127 | 0.3667 |
| Crizotinib | 0.3348 | 0.2647 | 0.3622 | 0.2609 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Niz, C.; Rahman, R.; Zhao, X.; Pal, R. Algorithms for Drug Sensitivity Prediction. Algorithms 2016, 9, 77. https://doi.org/10.3390/a9040077
De Niz C, Rahman R, Zhao X, Pal R. Algorithms for Drug Sensitivity Prediction. Algorithms. 2016; 9(4):77. https://doi.org/10.3390/a9040077
Chicago/Turabian StyleDe Niz, Carlos, Raziur Rahman, Xiangyuan Zhao, and Ranadip Pal. 2016. "Algorithms for Drug Sensitivity Prediction" Algorithms 9, no. 4: 77. https://doi.org/10.3390/a9040077
APA StyleDe Niz, C., Rahman, R., Zhao, X., & Pal, R. (2016). Algorithms for Drug Sensitivity Prediction. Algorithms, 9(4), 77. https://doi.org/10.3390/a9040077





