Abstract
Networks constitute powerful means of representing various types of complex systems, where nodes denote the system entities and edges express the interactions between the entities. An important topological property in complex networks is community structure, where the density of edges within subgraphs is much higher than across different subgraphs. Each of these subgraphs forms a community (or module). In literature, a metric called modularity is defined that measures the quality of a partition of nodes into different mutually exclusive communities. One means of deriving community structure is modularity maximisation. In this paper, a novel mathematical programming-based model, DiMod, is proposed that tackles the problem of maximising modularity for directed networks.
1. Introduction
It is increasingly clear that a wide range of systems across different disciplines can be described using network representations. The edges in a network can be binary, weighted, directed and with a positive or negative sign, thus rendering networks a suitable tool to model diverse types of interactions [1]. One common observation is that real world networks are not random graphs with homogeneous edge distribution, rather, a high density of edges exist within subsets of the network, while edge density across these subgraphs is much lower, giving rise to the emergence of a property known as community structure [2].
Community structure detection refers to the procedure of identifying the inherent higher order structure of a network by partitioning nodes into different modules. The modularity metric (Q) was introduced by Newman and Girvan [3] for undirected networks and measures the quality of a network partition into communities. A modularity value close to 1 suggests strong community structure, i.e., a larger proportion of edges falling within modules than at random.
Community detection is often formulated as an optimisation problem, where the partition that yields the maximum modularity for a target network is sought. This metric, however, has been proven to be NP-complete [4], and, therefore, exhaustive search algorithms are only applicable to small networks, as the number of possible partitions increases at least exponentially with the number of nodes. Modularity has also been shown to have a resolution limit [5] and a degenerate solution space [6]. There have been attempts in the literature to address resolution limit issues by adding a resolution parameter, but, as this parameter is hard to determine and increases method complexity, the problem is still not fully resolved [7].
Despite its limitations, modularity is still the most popular community detection metric [7] and it has been used in a variety of applications. Various optimisation algorithms have been proposed in literature that are based on a number of methodologies, including simulated annealing [8,9], greedy algorithm [10], extremal optimisation [11], spectral algorithm [3] and integer programming-based optimisation model [12,13,14,15,16,17].
While modularity optimisation for undirected networks has been well studied over the past decade, little has been done for module detection in directed networks. Many real world networks are inherently directed, including the World Wide Web [18], brain neural networks [19] and metabolic networks, where the directed edge represents material flow from one substrate to a product that may be irreversible [20]. In literature, the conventional manner of tackling the problem of community detection in directed networks is simply to treat the networks as undirected and apply the methods described above [21]; however, such approaches lose valuable information carried in edge directionality. Some algorithms use edge directionality to transform directed graphs to weighted networks or bipartite networks [22]. Recent algorithms propose the use of spectral optimisation [23], local extraction of communities [24] and blockmodeling or statistical inference models [25].
In this study, we use the mathematical description of modularity for directed networks introduced by Leicht and Newman [26] that explicitly considers the in and out-degree distributions of nodes in the network. We propose a two-step algorithm named DiMod composed of two mathematical programming models to detect modules in directed networks by maximising modularity. The two models have equivalent objective functions, but the terms of the equations are rearranged differently to accentuate a desired property of the mathematical model, as described in the section below. We compare the results of our method to three algorithms implemented in the Radatools software (v.4.0, DEIM, Tarragona, Spain) [27] on synthetic and real networks used as test cases.
2. Iterative Mathematical Programming Model for Modularity Optimisation on Directed Networks
We propose an iterative procedure that contains two major mathematical models to optimise modularity for directed networks. The first is a Mixed Integer Non-linear Programming Model (MINLP) that can provide a good partition of the network quickly but is likely to converge to a local optimal region, while the second model, a Mixed Integer Linear Programming Model (MIP), is harder to solve but is capable of finding a solution of higher quality. The algorithm starts by solving the MINLP a number of times, and the best partition is then selected and given as an initial point to the reduced MIP model that will iteratively improve the solution. We reduce the complexity of the MIP by allowing a few nodes to change modules while keeping all other nodes in their initial allocation and we solve each of these reduced MIPs for each module in an iteration.
As mentioned previously, the reason for proposing two different models for solving the same problem is that although a MINLP can find an acceptable solution for a large problem, it often converges to locally optimal solutions, and thus the quality of the solution is hard to guarantee. On the other hand, an MIP model can be solved to global optimality for small problems but consumes large computational resources for larger networks. We combine the best of these two types of models by first solving the MINLP and then the reduced MIPs to improve the acquired solution. The entire computational strategy is named DiMod and the mathematical description follows.
The sets, parameters and variables used in the models are described below:
| Sets | |
| node | |
| m | module |
| directed edge pointing from node n to e | |
| Parameters | |
| weight of edge point from node n to e | |
| sum of weights over all edges points to node n; incoming edge weight | |
| sum of weights over all edges points from node n; outgoing edge weight | |
| L | total amount of weights over all edges in the given network |
| Binary Variables | |
| 1 if node n belongs to module m; 0 otherwise | |
| Free Variables | |
| sum of for all nodes that belong to module m () | |
| sum of for all nodes that belong to module m () | |
| sum of edge weights in module m | |
| a positive intermediate variable. if both nodes n to e belong to module m; 0 otherwise | |
| represent the product of and , used as an intermediate variable for the MIP model | |
| represent the product of and , used as an intermediate variable for the MIP model | |
The next two sections describe the two models, and the following section describes our proposed algorithm and how both stages are employed to find the models of directed networks.
2.1. First Model—MINLP
Modularity is defined as the number of edges that fall within communities minus the expected number of edges that should fall into communities in a null configuration of the equivalent network with edges being placed at random [3]. The modularity for directed networks can be formulated as below [26]:
where represents the fraction of (weighted) edges that fall into module m, while is the expected value for module m.
The sum of weights of edges in module m, , is computed as:
indicating that an edge pointing from node n to node e is included in a module m if and only if both nodes belong to module m, i.e., and .
For a given directed network, the sum of weights of edges coming into node n is denoted as parameter , while the sum of weights of edges pointing from node n is . For an unweighted network, and are simply the in-degree and out-degree of node n. For a module m, the sum of and over all nodes belonging to this module () are, respectively, calculated as below:
We are interested in non-overlapping partitions where each node can only be allocated to exactly one module, and this is modeled via the following constraints:
The first step of the algorithm, the full MINLP model, is summarised below:
2.2. Second Model—MIP
The presence of non-linearity, combined with the use of integer variables, present considerable computational difficulty for finding globally optimal solutions. Solving MINLP problems typically involves repeatedly specifying different initial starting points and solving the model to identify locally optimal solutions, which can generally be realised in affordable computational time. Thus, the MINLP model in the previous section is used to provide an initial network division before a more sophisticated method can be applied to refine the division. In this section, the MINLP model is reformulated as an MIP by redefining the two non-linear constraints (Equation (2) and the multiplication in Equation (1)) as linear constraints.
Firstly, Equation (2) can be replaced by the following three sets of constraints:
where are newly introduced positive intermediate variables. For edges from node n to e, is equal to its weight, , if it belongs to module m; 0, otherwise.
The non-linear term in the objective function, , can be re-written as below:
where is the product of a continuous variable and a binary variable and can be made linear using the following set of equations:
where are introduced as new positive variables to replace the term , the variable is introduced to replace , and U is an arbitrarily large number.
The formulation of the objective function for this model becomes:
and the full model is given by the set of equations below:
2.3. Full Algorithm
The proposed algorithm has three user-defined parameters: , the number of iterations for the MINLP model; , the number of iterations for the MIP model and , the number of nodes to be released for each module at each MIP run. The optimal number of modules is determined by the algorithm itself, but we set a maximum number of modules to generate the set m. After the first model is solved times, the best value of modularity () and its corresponding partition () are selected and used in the second model. At each iteration of the MIP, nodes are allowed to change modules, while the remaining nodes are kept in their previous modules. Each node within the current module is relaxed once only and the procedure of random node selection and re-allocation continues until all the nodes within the current module have been relaxed. In our preliminary tests, we have found that provided the best compromise in calculation time and quality of solution for networks of different sizes. The full proposed model is summarised in Algorithm 1.
| Algorithm 1: Our proposed algorithm DiMod for detecting modules in directed networks. |
 |
Compared to solving one large MIP model that directly optimises the community memberships of all nodes simultaneously, solving a series of reduced models has the advantage of reaching global optimality for each reduced problem at a small computational cost. In the next section, a number of directed networks are used to demonstrate the applicability and efficiency of the proposed community detection algorithm.
3. Results
3.1. Synthetic Networks
The performance of our proposed community detection method is tested against other established methods in literature using synthetic networks generated by the Lancichinetti-Fortunato-Radicchi (LFR) benchmark [28]. We have generated seven non-overlapping directed unweighted networks with the following parameters: 500 nodes; default minus exponent for degree sequence and community size distribution, and , respectively; maximum in-degree ; and minimum and maximum number of nodes per community, and , respectively. Each of the networks had a different mixing parameter (), where larger μ indicates more connections across different communities. Overall, the collection of synthetic networks used allows validating the efficiency of our algorithm in networks with different properties of community structure.
We compare our results to three popular algorithms that optimise modularity for directed networks: extremal optimisation [11], fast algorithm [10] and Tabu search [29], as implemented in Radatools [27]. We have executed each algorithm individually 100 times or until they reach a time limit of 24 h, and the best network division is reported for comparison. In terms of the proposed community detection approach, we solve 10 MINLPs (), we perform 100 iterations on the MIP step of the algorithm () and 60 nodes are relaxed for each solve of the MIP model (). We implemented the models in GAMS [30], we use SBB [31] to solve the MINLP models and CPLEX [32] to solve the MIP models, and the optimality gap is set to 0, i.e., global optimum is achieved if the solver is allowed to run for unlimited time. The CPU time limit for each model was set to 1500 s. The deterministic nature of the proposed approach means only one single execution is required.
Figure 1 shows how the solution compares to the true community structure using the Normalized Mutual Information metric (NMI) [33]. We note that DiMod uncovers the true network communities even in larger mixing parameters. The Extremal Optimisation algorithm performs relatively well, while Fast algorithm and Tabu search fail to identify the ground truth communities before .
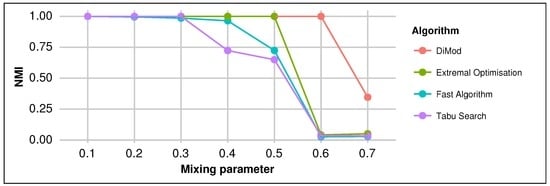
Figure 1.
Performance of algorithms on synthetic directed networks.
3.2. Real Networks
We demonstrate the performance of our proposed method in tests of five real networks. Table 1 shows a summary of the network properties. We include the directed and weighted neural network of Caenorhabditis elegans [34]. Networks for Mycobacterium tuberculosis and Plasmodium falciparum, represent biological pathway interactions as extracted from the Reactome database (May 2014) [35]. The network for Roget’s Thesaurus details cross-references between categories of English words, where one edge points from one category to another if a reference is provided to the latter among the words of the former [36]. In order to show that DiMod can solve larger problems, we include a snapshot of the Gnutella peer-to-peer network, gnutella08, obtained from the Stanford Large Network Dataset Collection (SNAP) [37].

Table 1.
Summary of networks used as benchmarks in this study.
Our tests have shown that the second model (MIP) improves the quality of network division obtained by the MINLP model in the first stage. Table 2 below outlines the improvement in modularity between the more coarse initial network division provided by the MINLP and that of the final solution identified by the MIP step. Roget’s Thesaurus is the network benefiting the most from the iterative procedure, where modularity is improved by about . The iterative algorithm also boosts modularity by nearly for Mycobacterium tuberculosis while improvements of around can be observed in C. elegans and Plasmodium falciparum networks. The gnutella08 network also has an improvement of approximately from the first to the second step and Figure 2 shows how modularity is improved at the end of each MIP iteration.

Table 2.
Modularity improvement achieved by second step of the proposed method over the initial division network given by the MINLP.
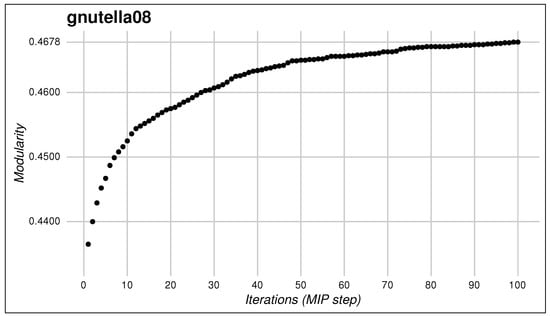
Figure 2.
Improvement of modularity at the end of each MIP iteration for gnutella08 network.
As for synthetic networks, results obtained through DiMod for real networks are compared against modularity maximisation approaches in the literature (extremal optimisation [11], fast algorithm [10] and Tabu search [29]). Overall, the methodology proposed here consistently outperforms other methods, as shown in Table 3, which summarises our computational results.

Table 3.
Comparison of different community detection methods on real networks.
4. Conclusions
This works reports novel mathematical programming formulation to address the problem of community structure detection in directed networks. While modularity optimisation has been extensively studied for undirected networks, there is little research effort to detect modules in directed networks. A mathematical programming-based optimisation approach has been introduced to fill the gap in literature. Modularity optimisation for a directed network can be conveniently formulated as an MINLP model, which can converge to locally optimal solutions quickly even in large networks. The MINLP model is reformulated as an MIP model by re-writing non-linear terms into linear equivalents, which can then be solved to obtain globally optimal solutions for small networks. The novel community detection method proposed consists of two major steps, taking advantage of both models. Firstly, the MINLP model is solved to produce an initial coarse network division. Given the initial network division, the iterative algorithm works by repeatedly removing the community memberships of random sets of nodes, solving the reduced MILP model and re-allocating the relaxed nodes to communities.
Using synthetic and real-world directed networks covering a wide range of node and edge sizes, the proposed iterative algorithm considerably improves the quality of the initial coarse network partition. Compared with three community detection methods in literature, the proposed approach is demonstrated to identify the best network division consistently, yielding the largest modularity value. Another advantage of the proposed approach is its deterministic nature, which means multiple executions are likely to converge into the same network division.
Finally, we note that owing to the nature of the mathematical programming framework used here, modelling can be flexible enough to allow additional constraints and parameters to be easily implemented according to user requirements [38]. Prior knowledge on a particular system can be incorporated, for example in the form of nodes with similar functional annotations that may be constrained to be allocated in the same community [39]. In future work, we plan to study how the density of nodes and distributions of in-degree and out-degree affect the hardness and calculation time of the optimisation problem. We also plan to modify current integer programming models so as to detect and prevent the resolution limit.
Acknowledgments
Lingjian Yang acknowledges funding from the UK Engineering and Physical Sciences Research Council (EPSRC) Centre for Innovative Manufacturing in Emergent Macromolecular Therapies (EP/I033270/1) and Jonathan C. Silva acknowledges funding from Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES), Brasília, Brazil (process number 13312138). Funding from the EU (to Sophia Tsoka, HEALTH-F2-2011-261366), the Leverhulme Trust (to Sophia Tsoka and Lazaros G. Papageorgiou, RPG- 2012-686) and the UK Engineering & Physical Sciences Research Council (to Lazaros G. Papageorgiou, EPSRC Centre for Innovative Manufacturing in Emergent Macromolecular Therapies) is gratefully acknowledged. We gratefully acknowledge Aristotelis Kittas for data preparation.
Author Contributions
Lingjian Yang, Jonathan C. Silva, Lazaros G. Papageorgiou and Sophia Tsoka conceived and designed the experiments. Lingjian Yang and Lazaros G. Papageorgiou designed the computational model. Lingjian Yang and Jonathan C. Silva performed the experiments. Lingjian Yang and Jonathan C. Silva gathered network data. Lingjian Yang, Jonathan C. Silva, Lazaros G. Papageorgiou and Sophia Tsoka analysed the data. Lingjian Yang, Jonathan C. Silva, Lazaros G. Papageorgiou and Sophia Tsoka wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| MINLP | Mixed Integer Non-Linear Programming |
| MIP | Mixed Integer Linear Programming |
References
- Boccaletti, S.; Latora, V.; Moreno, Y.; Chavez, M.; Hwang, D. Complex networks: Structure and dynamics. Phys. Rep. 2006, 424, 175–308. [Google Scholar] [CrossRef]
- Fortunato, S. Community detection in graphs. Phys. Rep. 2010, 486, 75–174. [Google Scholar] [CrossRef]
- Newman, M.E.J. Modularity and community structure in networks. Proc. Natl. Acad. Sci. USA 2006, 103, 8577–8582. [Google Scholar] [CrossRef] [PubMed]
- Brandes, U.; Delling, D.; Gaertler, M.; Gorke, R.; Hoefer, M.; Nikoloski, Z.; Wagner, D. On Modularity Clustering. IEEE Trans. Knowl. Data Eng. 2008, 20, 172–188. [Google Scholar] [CrossRef]
- Lancichinetti, A.; Fortunato, S. Limits of modularity maximization in community detection. Phys. Rev. E 2011, 84, 066122. [Google Scholar] [CrossRef] [PubMed]
- Good, B.H.; De Montjoye, Y.A.; Clauset, A. Performance of modularity maximization in practical contexts. Phys. Rev. E 2010, 81, 046106. [Google Scholar] [CrossRef] [PubMed]
- Fortunato, S.; Hric, D. Community Detection in Networks: A User Guide. Phys. Rep. 2016. [Google Scholar] [CrossRef]
- Danon, L.; Díaz-Guilera, A.; Duch, J.; Arenas, A. Comparing community structure identification. J. Stat. Mech. Theory Exp. 2005, 2005, P09008. [Google Scholar] [CrossRef]
- Medus, A.; Acuña, G.; Dorso, C. Detection of community structures in networks via global optimization. Phys. A Stat. Mech. Appl. 2005, 358, 593–604. [Google Scholar] [CrossRef]
- Newman, M.E.J. Fast algorithm for detecting community structure in networks. Phys. Rev. E 2004, 69, 066133. [Google Scholar] [CrossRef] [PubMed]
- Duch, J.; Arenas, A. Community detection in complex networks using extremal optimization. Phys. Rev. E 2005, 72, 027104. [Google Scholar] [CrossRef] [PubMed]
- Aloise, D.; Cafieri, S.; Caporossi, G.; Hansen, P.; Perron, S.; Liberti, L. Column generation algorithms for exact modularity maximization in networks. Phys. Rev. E 2010, 82, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Xu, G.; Bennett, L.; Papageorgiou, L.G.; Tsoka, S. Module detection in complex networks using integer optimisation. Algorithms Mol. Biol. 2010. [Google Scholar] [CrossRef] [PubMed]
- Bennett, L.; Liu, S.; Papageorgiou, L.G.; Tsoka, S. Detection of Disjoint and Overlapping Modules in Weighted Complex Networks. Adv. Complex Syst. 2012, 15. [Google Scholar] [CrossRef]
- Cafieri, S.; Hansen, P.; Liberti, L. Improving heuristics for network modularity maximization using an exact algorithm. Discret. Appl. Math. 2014, 163, 65–72. [Google Scholar] [CrossRef]
- Bennett, L.; Kittas, A.; Muirhead, G.; Papageorgiou, L.G.; Tsoka, S. Detection of Composite Communities in Multiplex Biological Networks. Sci. Rep. 2015, 5, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Silva, J.C.; Bennett, L.; Papageorgiou, L.G.; Tsoka, S. A mathematical programming approach for sequential clustering of dynamic networks. Eur. Phys. J. B 2016. [Google Scholar] [CrossRef]
- Dourisboure, Y.; Geraci, F.; Pellegrini, M. Extraction and Classification of Dense Communities in the Web. In Proceedings of the 16th International Conference on World Wide Web, Banff, AB, Canada, 8–12 May 2007; pp. 461–470.
- Liu, Y.; Moser, J.; Aviyente, S. Network community structure detection for directional neural networks inferred from multichannel multisubject EEG data. IEEE Trans. Biomed. Eng. 2014, 61, 1919–1930. [Google Scholar] [PubMed]
- Guimerà, R.; Nunes Amaral, L.A. Functional cartography of complex metabolic networks. Nature 2005, 433, 895–900. [Google Scholar] [CrossRef] [PubMed]
- Lai, D.; Lu, H.; Nardini, C. Extracting weights from edge directions to find communities in directed networks. J. Stat. Mech. Theory Exp. 2010, 2010, P06003. [Google Scholar] [CrossRef]
- Satuluri, V.; Parthasarathy, S. Symmetrizations for Clustering Directed Graphs. In Proceedings of the 14th International Conference on Extending Database Technology, Uppsala, Sweden, 21–24 March 2011; pp. 343–354.
- Zheng, Q.; Skillicorn, D.B. Spectral embedding of directed networks. Soc. Netw. Anal. Min. 2016, 6, 1–15. [Google Scholar] [CrossRef]
- Ning, X.; Liu, Z.; Zhang, S. Local community extraction in directed networks. Phys. A Stat. Mech. Appl. 2016, 452, 258–265. [Google Scholar] [CrossRef]
- Malliaros, F.D.; Vazirgiannis, M. Clustering and community detection in directed networks: A survey. Phys. Rep. 2013, 533, 95–142. [Google Scholar] [CrossRef]
- Leicht, E.A.; Newman, M.E.J. Community structure in directed networks. Phys. Rev. Lett. 2008, 100, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Gomez, S. Radatools—Communities Detection in Complex Networks and Other tools. Available online: http://deim.urv.cat/~sergio.gomez/radatools.php (accessed on 20 July 2016).
- Lancichinetti, A.; Fortunato, S. Benchmarks for testing community detection algorithms on directed and weighted graphs with overlapping communities. Phys. Rev. E 2009, 80, 016118. [Google Scholar] [CrossRef] [PubMed]
- Arenas, A.; Fernández, A.; Gómez, S. Analysis of the structure of complex networks at different resolution levels. New J. Phys. 2008, 10, 53039. [Google Scholar] [CrossRef]
- Rosenthal, R.E. GAMS—A User’s Guide; GAMS Development Corporation: Washington, DC, USA, 2016. [Google Scholar]
- Bussieck, M.R.; Drud, A. SBB: A New Solver for Mixed Integer Nonlinear Programming. Available online: http://ww.atlatec.-port.gams.com/presentations/present_sbb.pdf (accessed on 26 October 2016).
- IBM CPLEX Optimizer—United States. Available online: https://www-01.ibm.com/software/commerce/optimization/cplex-optimizer/ (accessed on 27 September 2016).
- Esquivel, A.V.; Rosvall, M. Comparing network covers using mutual information. arXiv, 2012; arXiv:1202.0425. [Google Scholar]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of “small-world” networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
- Kittas, A.; Bennett, L.; Hermjakob, H.; Tsoka, S. Organizational principles of the Reactome human BioPAX model using graph theory methods. J. Complex Netw. 2016. [Google Scholar] [CrossRef]
- Batagelj, V. Pajek Data: Roget’s Thesaurus, 1879. Available online: http://vlado.fmf.uni-lj.si/pub/networks/data/dic/roget/Roget.htm (accessed on 20 July 2016).
- Leskovec, J.; Krevl, A. SNAP Datasets: Stanford Large Network Dataset Collection. Available online: http://snap.stanford.edu/data (accessed on 26 October 2016).
- Xu, G.; Tsoka, S.; Papageorgiou, L.G. Finding community structures in complex networks using mixed integer optimisation. Eur. Phys. J. B 2007, 60, 231–239. [Google Scholar] [CrossRef]
- Bennett, L.; Kittas, A.; Liu, S.; Papageorgiou, L.G.; Tsoka, S. Community Structure Detection for Overlapping Modules through Mathematical Programming in Protein Interaction Networks. PLoS ONE 2014, 9, e112821. [Google Scholar] [CrossRef] [PubMed]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).