Abstract
In this work, a cross-validation procedure is used to identify an appropriate Autoregressive Integrated Moving Average model and an appropriate state space model for a time series. A minimum size for the training set is specified. The procedure is based on one-step forecasts and uses different training sets, each containing one more observation than the previous one. All possible state space models and all ARIMA models where the orders are allowed to range reasonably are fitted considering raw data and log-transformed data with regular differencing (up to second order differences) and, if the time series is seasonal, seasonal differencing (up to first order differences). The value of root mean squared error for each model is calculated averaging the one-step forecasts obtained. The model which has the lowest root mean squared error value and passes the Ljung–Box test using all of the available data with a reasonable significance level is selected among all the ARIMA and state space models considered. The procedure is exemplified in this paper with a case study of retail sales of different categories of women’s footwear from a Portuguese retailer, and its accuracy is compared with three reliable forecasting approaches. The results show that our procedure consistently forecasts more accurately than the other approaches and the improvements in the accuracy are significant.
1. Introduction
Time series often exhibit strong trends and seasonal variations presenting challenges in developing effective forecasting models. How to effectively model time series in order to improve the quality of forecasts is still an outstanding question. State space and Autoregressive Integrated Moving Average (ARIMA) models are the two most widely-used approaches to time series forecasting, and provide complementary methodologies to the problem. While exponential smoothing methods are based on a description of trends and seasonality in the data [1,2,3], ARIMA models aim to describe the autocorrelations in the data [4,5,6,7]. The ARIMA forecasting framework, originally developed by Box et al. [8], involves an iterative three-stage process of model selection, parameter estimation and model checking. A statistical framework for exponential smoothing methods was recently developed based on state space models called ETS (Error, Trend and Seasonality) models [9]. Identifying the proper autocorrelation structure of a time series is not an easy task in ARIMA modeling [10]. Identifying an appropriate state space model for a time series can also be difficult. However, the usual forecast accuracy measures can be used for identifying a model provided the errors are computed from data in a test set that were not used for model estimation. In this work, a cross-validation procedure is used to identify an appropriate state space model and an appropriate ARIMA model for a time series. The data are split into a training set and a test set. The training set is used for estimating the model and the test set is used to measure how well the model is likely to forecast on new data. This approach is exemplified in the paper with a case study of retail sales time series of different categories of women’s footwear from a Portuguese retailer that, by exhibiting complex patterns, present challenges in developing effective forecasting models. Sales forecasting is one of the most important issues that is beyond all strategic and planning decisions in any retail business. The importance of accurate sales forecasts to efficient inventory management at both disaggregate and aggregate levels has long been recognized [11]. Aggregate time series are usually preferred because they contain both trends and seasonal patterns, providing a good testing ground for developing forecasting methods, and because companies can benefit from more accurate forecasts. The remainder of the paper is organized as follows. The next section presents a brief description of the state space models and the ARIMA models and also introduces the usual forecast error measures. Section 3 describes in detail the steps of the model identification procedure and Section 4 presents the results of its application to a case study of retail sales of different categories of women’s footwear. Finally, Section 5 offers the concluding remarks.
2. Forecasting Models
2.1. State Space Models
Exponential smoothing methods have been used with success to generate easily reliable forecasts for a wide range of time series since the 1950s [12]. In these methods, forecasts are calculated using weighted averages where the weights decrease exponentially as observations come from further in the past—the smallest weights are associated with the oldest observations. The most common representation of these methods is the component form. Component form representations of exponential smoothing methods comprise a forecast equation and a smoothing equation for each of the components included in the method. The components that may be included are the level component, the trend component and the seasonal component. By considering all of the combinations of the trend and seasonal components, fifteen exponential smoothing methods are possible. Each method is usually labeled by a pair of letters (T,S) defining the type of ‘Trend’ and ‘Seasonal’ components. The possibilities for each component are: and . For example, denotes the simple exponential smoothing method, denotes Holt’s linear method, denotes the additive damped trend method, denotes the additive Holt–Winters method and denotes the multiplicative Holt–Winters method, to mention the most popular. For illustration, denoting the time series by and the forecast of , based on all of the data up to time t, by , the component form for the method is [13,14]:
where m denotes the period of the seasonality, denotes an estimate of the level (or the smoothed value) of the series at time t, denotes an estimate of the trend (slope) of the series at time t, denotes an estimate of the seasonality of the series at time t and denotes the point forecast for h periods ahead where (which ensures that the estimates of the seasonal indices used for forecasting come from the final year of the sample (the notation means the largest integer not greater than u). The initial states and the smoothing parameters are estimated from the observed data. The smoothing parameters are constrained between 0 and 1 so that the equations can be interpreted as weighted averages. Details about all of the other methods may be found in Makridakis et al. [13]. To be able to generate prediction (or forecast) intervals and other properties, Hyndman et al. [9] (amongst others) developed a statistical framework for all exponential smoothing methods. In this statistical framework, each stochastic model, referred to as a state space model, consists of a measurement (or observation) equation that describes the observed data, and state (or transition) equations that describe how the unobserved components or states (level, trend, seasonal) change over time. For each exponential smoothing method, Hyndman et al. [9] describe two possible state space models, one corresponding to a model with additive random errors and the other corresponding to a model with multiplicative random errors, giving a total of 30 potential models. To distinguish the models with additive and multiplicative errors, an extra letter E was added: the triplet of letters refers to the three components: “Error”, “Trend” and “Seasonality”. The notation ETS(, , ) helps in remembering the order in which the components are specified. For illustration, the equations of the model ETS (additive Holt–Winters’ method with additive errors) are [15]:
and the equations of the model ETS (additive Holt–Winters’ method with multiplicative errors) are [15]:
where
and is a zero mean Gaussian white noise process with variance . Equations (5) and (9) are the measurement equations and Equations (6)–(8) and (10)–(12) are the state equations. The measurement equation shows the relationship between the observations and the unobserved states. The transition equation shows the evolution of the state through time. It should be emphasized that these models generate optimal forecasts for all exponential smoothing methods and provide an easy way to obtain maximum likelihood estimates of the model parameters (for more details about how to estimate the smoothing parameters and the initial states by maximizing the likelihood function, see pp. 68–69 [9]). After identifying an appropriate model, we have to check whether the residuals are statistically insignificant which can be done through a Portmanteau test. According to [16], the most accurate Portmanteau test is the Ljung–Box test. The Ljung–Box test tests whether the first k autocorrelations of the residuals are significantly different from what would be expected from a white noise process. The null-hypothesis is that those first k autocorrelations are null, so large p-values are indicative that the residuals are not distinguishable from a white noise series. Using the usual significance level of 5%, a model passes a Ljung–Box test if the p-value is greater than 0.05 [17]. If the model fails the Ljung–Box test, another one should be tried; otherwise, forecasts can be calculated.
2.2. ARIMA Models
ARIMA is one of the most versatile linear models for forecasting seasonal time series. It has enjoyed great success in both academic research and industrial applications during the last three decades. The class of ARIMA models is broad. It can represent many different types of stochastic seasonal and nonseasonal time series such as pure autoregressive (AR), pure moving average (MA), and mixed AR and MA processes. The theory of ARIMA models has been developed by many researchers and its wide application was due to the work by Box et al. [8] who developed a systematic and practical model building method. Through an iterative three-step model building process—model identification, parameter estimation and model diagnosis—the Box–Jenkins methodology has been proven to be an effective practical time series modeling approach. The multiplicative seasonal ARIMA model, denoted as ARIMA, has the following form [18]:
where
and m is the seasonal frequency, B is the backward shift operator, d is the degree of ordinary differencing, and D is the degree of seasonal differencing, and are the regular autoregressive and moving average polynomials of orders p and q, respectively, and are the seasonal autoregressive and moving average polynomials of orders P and Q, respectively, , where μ is the mean of process and is a zero mean Gaussian white noise process with variance . The roots of the polynomials and should lie outside a unit circle to ensure causality and invertibility [19]. For , is usually assumed because a quadratic or a higher order trend in the forecast function is particularly dangerous. The ARIMA models are useful in describing stationary time series. Although many time series are nonstationary, they can be reduced to stationary time series by taking proper degrees of differencing (regular and seasonal) and making mathematical transformations [20]. The main task in ARIMA forecasting is selecting an appropriate model order, which are the values of and D. Usually, the following steps are used to manually identify a tentative model [20]: (1) plot the time series, identify any unusual observations and choose the proper variance-stabilizing transformation. A series with nonconstant variance often needs a logarithm transformation. Often, more generally to stabilize the variance, a Box–Cox transformation may be applied; (2) compute and examine the sample ACF (autocorrelation function) and the sample PACF (partial autocorrelation function) of the transformed data (if a transformation was necessary) or of the original data to further confirm a necessary degree of differencing (d and D) so that the differenced series is stationary. Because variance-stabilizing transformations such as the Box–Cox transformations require positive values and differencing may create some negative values, variance-stabilizing transformations should always be applied before taking differences. If the data have a strong seasonal pattern, it is recommend that seasonal differencing be done first because sometimes the resulting series will be stationary and there will be no need for a further first difference. If first differencing is done first, there will still be seasonality present; and (3) compute and examine the sample ACF and sample PACF of the properly transformed and differenced series to identify the orders of and Q by matching the patterns in the sample ACF and PACF with the theoretical patterns of known models. After identifying a tentative model, the next step is to estimate the parameters and check whether the residuals are statistically insignificant, which can be done using the procedure described in Section 2.1. If the model fails the Ljung–Box test, another one should be tried; otherwise, forecasts can be calculated.
2.3. Forecast Error Measures
To check the accuracy of a forecasting model, we usually split the data set into a training set and a test set . Then, we estimate the parameters of the model using the training set and use it to forecast the next observations. The forecast errors are the difference between the actual values in the test set and the forecasts produced:
The most commonly used scale-dependent error measures are the mean absolute error (MAE) and the root mean squared error (RMSE) defined as follows:
When comparing the performance of forecast models on a single data set, the MAE is interesting, as it is easy to understand, but the RMSE is more valuable as is more sensitive than other measures to the occasional large error (the squaring process gives disproportionate weight to very large errors). There is no absolute criterion for a ‘good’ value of RMSE or MAE: it depends on the units in which the variable is measured and on the degree of forecasting accuracy, as measured in those units, which is sought in a particular application. Percentage errors have the advantage of being scale-independent, and so are frequently used to compare forecast performance between different data sets. The most commonly used measure is the mean absolute percentage error (MAPE) defined as follows:
Measures based on percentage errors have the disadvantage of being infinite or undefined if and having extreme values when is close to zero. Scaled errors can be used as an alternative to percentage errors when the purpose is to compare the forecast accuracy of time series on different scales [21]. A scaled error is given by , where Q is a scaling statistic computed on the training set. Q can be defined as the MAE of naïve forecasts for nonseasonal time series:
and as the MAE of seasonal naïve forecasts for seasonal time series:
being independent of the scale of the data. Then, the mean absolute scaled error (MASE) is defined as follows:
When comparing several forecasting methods, the accuracy measures frequently lead to different results as to which forecast method is best.
3. Model Identification
As demonstrated in Section 2.1 and Section 2.2, finding appropriate state space and ARIMA models for a time series is not an easy task. Both forecast methodologies are subjective and usually difficult to apply. In this research work, the challenge was to specify a procedure to identify an appropriate state space and an appropriate ARIMA model for a time series. The sample ACFs of seasonal time series typically decay very slowly at regular lags and at multiples of the seasonal period m and the sample PACFs have a large spike at lag 1 and cut off to zero after lag 2 or 3. This behaviour usually suggests seasonal differences and regular differences to achieve stationarity. Therefore, for each seasonal times series , in the case of ARIMA, twelve types of data are considered: raw data , first difference data , second difference data , seasonally difference data , first and seasonally difference data , second and seasonally difference data , log-transformed data , first difference log-transformed data , second difference log-transformed data , seasonally difference log-transformed data , first and seasonally difference log-transformed data , and second and seasonally difference log-transformed data ; higher orders of differencing are unlikely to make much interpretable sense and should be avoided [16]. In the case of ETS, two types of data are considered: raw data and log-transformed data. To be able to explore the forecasting capability of both modeling approaches, for each type of data, all possible ETS models (30 in total) and all ARIMA models, where p and q can take values from 0 to 5, and P and Q can take values from 0 to 2 (324 in total), should be fitted. If the time series is nonseasonal , then, in the case of ARIMA, six types of data are considered (raw data and log-transformed data with regular differencing up to second order differences) and 36 models are fitted to each type; in the case of ETS models, the two types of data are considered (raw data and log-transformed data) and 10 models (“Seasonality” = N) are fitted to each type. To evaluate the forecast accuracy of each model considered, forecasts on a test set should be obtained. For this, the data must be split into a training set and a test set. The size of the test set can be typically about 20%–30% of the data set, although it can be less due to the small size of the sample. In fact, short time series are very common, and, in the case of retail sales, this is usually the case since older data are frequently useless or non-existent due to the changes of consumer demands. To avoid limiting the available data by removing a significant part to the test set and to be able to make multiple rounds of forecasts to obtain more reliable forecast accuracy measures, since the test set is usually small, time series cross-validation instead of conventional validation is performed for the model selection [22]. This procedure is based on one-step forecasts and uses different training sets, each containing one more observation than the previous one. The value of RMSE for each model is calculated averaging the one-step forecasts obtained. The model which has the lowest RMSE value and passes the Ljung–Box test using all the available data with a significance level of 5% is selected among all the ARIMA and ETS models considered. RMSE is used for model selection since it is more sensitive than the other measures to large errors. If the selected model fails the Ljung–Box test, the model with the second lowest RMSE value on the forecasts of the test set is selected, and so on. It should be mentioned that when models are compared using Akaike’s Information Criterion or Bayesian Information Criterion values, it is essential that all models have the same orders of differencing and the same transformation [16]. However, when comparing models using a test set, it does not matter how the forecasts were produced, the comparisons are always valid even if the models have different orders of differencing and/or different transformations. This is one of the advantages of the cross-validation procedure used here— to be able to compare the forecasting performance of models that have different orders of differencing and/or different transformations. The other advantage of the cross-validation procedure used here is that it also tells how accurate the one-step forecasts can be. The procedure based on cross-validation to identify an appropriate state space model and an appropriate ARIMA model for a time series follows these steps:
- Raw data and log-transformed data (to stabilize the variance if necessary) are considered and for each one
- (a)
- in the case of ARIMA,
- if the time series is nonseasonal, the data are differentiated zero, one and two times and for each type of data, p and q vary from 0 to 2 giving 36 models;
- if the time series is seasonal , the data are differentiated considering all of the combinations of with (six in total) and for each type of data, p and q vary from 0 to 5 and P and Q vary from 0 to 2 giving 324 models.
- (b)
- in the case of ETS,
- if the time series is nonseasonal , all of the combinations of (E,T,S), where , and are considered, giving 10 models;
- if the time series is seasonal , all of the combinations of (E,T,S), where , and are considered, giving 30 models.
- The data set is split into a training set and a test set (about 20%–30% of the data set) and time series cross-validation is performed to all ARIMA and ETS models considered in step 1 as follows:
- (a)
- The model is estimated using the observations and then used to forecast the next observation at time . The forecast error for time is computed.
- (b)
- The step (a) is repeated for .
- (c)
- The value of RMSE is computed based on the errors obtained in step (a).
- The model which has the lowest RMSE value and passes the Ljung–Box test using all the available data with a significance level of 5% is selected among all ETS and ARIMA models considered. If none of the fitted models passes the Ljung–Box test, the model with the lowest RMSE value is selected among all considered.
4. Empirical Study
In this section, the application of the model identification procedure described earlier is exemplified through a case study of retail sales of different categories of women’s footwear from a Portuguese retailer.
4.1. Data
The brand Foreva (Portugal) was born in September 1984. Since the beginning, the company is known for offering a wide range of footwear for all seasons. The geographical coverage of Foreva shops in Portugal is presently vast as it has around 70 stores open to the public, with most of them in shopping centers. In this study, monthly sales of the five categories of women’s footwear of the brand Foreva: Boots, Booties, Flats, Sandals and Shoes from January 2007 to April 2012 (64 observations) are analyzed. These times series are plotted in Figure 1. The Boots and Booties categories are sold primarily during the winter season, while the Flats and Sandals categories are sold primarily during the summer season. The Shoes category is sold throughout the year because it comprises the “classic” type of footwear that is used in the hot and cold seasons. As in most of the shops and shopping centers in Portugal, the winter season starts on 30 September of one year and ends on 27 February of the next year; the summer season starts on 28 February and ends on 29 September of each year. With the exception of Flats, the series of all the other footwear present a strong seasonal pattern and are obviously non-stationary. The Boots series remains almost constant in the first two seasons, decreases slightly in 2009–2010, then recovers in 2010–2011, and finally decreases again in 2011–2012. The Booties series also remains fairly constant in the first two seasons and then maintains an upward trend movement in the next three seasons. The Flats series seems more volatile than the other series and the seasonal fluctuations are not so visible. In 2007, the sales are clearly higher than the rest of the years. An exceptional increase of sales is observed in March and April of 2012. The Sandals series increases in 2008 remaining almost constant in the next season, and then increases again in 2010, remaining almost constant in the last season. The Shoes series presents an upward trend in the first two years and then reverses to a downward movement in the last three years. The seasonal behavior of this series shows more variation than the seasonal behavior of the other series.
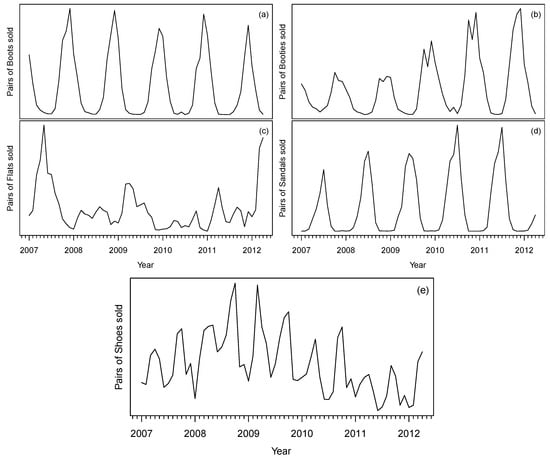
Figure 1.
Monthly sales of the five footwear categories between January 2007 and April 2012: (a) pairs of Boots; (b) pairs of Booties; (c) pairs of Flats; (d) pairs of Sandals; and (e) pairs of Shoes.
4.2. Results
Figure 2 shows the sample ACF and the sample PACF for the five time series. It can be seen that the sample ACFs decay very slowly at regular lags and at multiples of the seasonal period 12 and the sample PACFs have a large spike at lag 1 and cut off to zero after lag 2 or 3 suggesting, possibly, seasonal and regular differencing. A logarithmic transformation might be necessary to stabilize the variance of some times series. In each case, the minimum size of the training set was specified from January 2007 to December 2010 (first 48 observations) while the test set was specified from January 2011 to April 2012 (last 16 observations). The state space model and the ARIMA model with the best performance in the cross-validation procedure were selected as the final models.
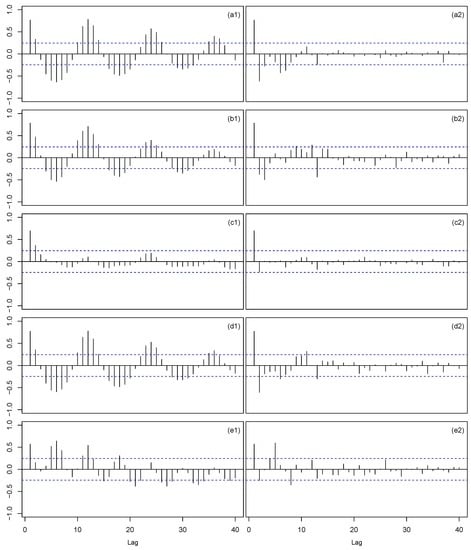
Figure 2.
Sample autocorrelation function (left panels) and sample partial autocorrelation function (right panels) plots for the five footwear categories: Boots (a1,a2); Booties (b1,b2); Flats (c1,c2); Sandals (d1,d2); and Shoes (e1,e2).
To be able to compare the accuracies of the forecasts obtained with the ETS and ARIMA models selected by the cross-validation procedure developed, we also evaluated the forecasts from another three forecasting approaches: the Hyndman and Khandakar [23] algorithm which identifies and estimates ARIMA models, the Hyndman and Athanasopoulos [16] statistical framework which identifies and estimates state space models and the seasonal naïve method which was used as benchmark, despite simple forecasting methods being sometimes surprisingly effective. The Hyndman and Khandakar [23] algorithm identifies an ARIMA model for a time series using the following procedure: first, the user must decide if a Box–Cox transformation should be used to stabilize the variance; then, for non-seasonal data, d is selected based on successive KPSS (Kwiatkowski-Phillips-Schmidt-Shin) unit-root tests [24] and, for seasonal data, D is set to 1 and then d is chosen by applying successive KPSS unit root tests to the seasonally differenced data; once d and D are known, the orders of p, q, P and Q are selected by minimising the Akaike’s Information Criterion (AIC) using a step-wise algorithm: to start, four basic models are considered and the one with the smallest AIC value is selected; then, thirteen variations on this model are considered allowing p, q, P and Q to vary simultaneously by ±1. Whenever a model with a lower AIC value is found, it becomes the new “current” model, and this procedure is repeated. The process finishes when a model close to the current model with a lower AIC cannot be found. The Hyndman and Athanasopoulos [16] statistical framework identifies an ETS model for a time series by selecting the one with the lowest AIC value among all possible ETS models. In the seasonal naïve method, each forecast is equal to the last observed value from the same season of the year (for monthly data, it is the same month of the previous year). Table 1 gives, for each time series, the forecast accuracy measures and the validation performance of each approach. The forecast error measures presented in Table 1 are defined in Section 2.3. The analysis was carried out using the statistical software R programming language (version R-3.3.2 for windows) and the specialized package forecast [25,26]. To be able to compare the forecasting performance of our procedure with the forecasting performance of the other three forecasting approaches, a time series cross-validation based on one-step forecasts was applied to them. Beginning with 48 observations in the training set (data from January 2007 to December 2010) and finishing with 63, a new ARIMA model using the Hyndman and Khandakar [23] algorithm was identified in each step and used to forecast the next observation that is not in the training data. Then, error measures calculated from the 16 one-step forecasts were obtained. The same procedure was applied to the Hyndman and Athanasopoulos [16] statistical framework, i.e., a new ETS model was identified in each step of the time series cross-validation. In the case of the seasonal naïve method, in each step, the forecast of the next observation that was not in the training data was equal to the last observed value from the same month of the previous year. The Ljung–Box test using all of the available data was also performed for these three forecasting approaches and the p-values obtained are shown in Table 1. Since there is no universally agreed-upon performance measure that can be applied to every forecasting situation, multiple criteria are therefore often needed to give a comprehensive assessment of forecasting models [4]. The RMSE, the MAE, and the MAPE are the most commonly used forecast error measures among both academics and practitioners [27]. We also consider the MASE in order to overcome some of the limitations of the MAPE. According to the results for this case study, our procedure to find an ARIMA model produces the most accurate forecasts when judged by the four most common performance measures RMSE, MAE, MAPE and MASE (with the single exception of MAPE for the Sandals time series). The RMSE, MAE and MASE produce the same accuracy ranking, with the exception for the Booties time series—when considering MAE, our procedure to find a state space model is more accurate than the seasonal naïve method, but when considering RMSE, the opposite happens, althoug,h according to MASE, both approaches have the same performance. The MAPE consistently ranks differently, which reinforces the impact that its limitations can have on the results. Our procedure to find a state space model and an ARIMA model consistently forecasts more accurately than the Hyndman and Athanasopoulos [16] statistical framework and the Hyndman and Khandakar [23] algorithm. The improvements in forecast accuracy over the Hyndman and Khandakar [23] algorithm are quite considerable: for Boots time series, the RMSE and the MAE (MASE) are 65% and 70% smaller, respectively; for Booties time series, the RMSE and the MAE (MASE) are 45% and 42% smaller, respectively; for Flats time series, the RMSE and the MAE (MASE) are 29% and 22% smaller, respectively; for Sandals time series, the RMSE and the MAE (MASE) are 69% and 67% smaller, respectively; for Shoes time series, the RMSE and the MAE (MASE) are 36% and 32% smaller, respectively. The improvements in forecast accuracy over the Hyndman and Athanasopoulos [16] statistical framework are also significant: for Boots time series, the RMSE and the MAE (MASE) are 23% and 20% smaller, respectively; for Booties time series, the RMSE and the MAE (MASE) are 30% and 13% smaller, respectively; for Flats time series, the RMSE and the MAE (MASE) are 11% and 7% smaller, respectively; for Sandals time series, the RMSE and the MAE (MASE) are 48% and 33% smaller, respectively; for Shoes time series, the RMSE and the MAE (MASE) are 34% and 35% smaller, respectively. Our procedure to find an ARIMA model also outperforms significantly the seasonal naïve method: for Boots time series, the RMSE and the MAE (MASE) are 55% and 48% smaller, respectively; for Booties time series, the RMSE and the MAE (MASE) are 1% and 11% smaller, respectively; for Flats time series, the RMSE and the MAE (MASE) are 49% and 51% smaller, respectively; for Sandals time series, the RMSE and the MAE (MASE) are 21% and 5% smaller, respectively; for Shoes time series, the RMSE and the MAE (MASE) are 52% and 60% smaller, respectively. In general, our procedure to find a state space model also forecasts more accurately than the seasonal seasonal naïve method: for Boots time series, the RMSE and the MAE (MASE) are 11% and 4% smaller, respectively; for Booties time series, the RMSE is 15% larger, but the MAE is 1% smaller and the MASE is equal; for Flats time series, the RMSE and the MAE (MASE) are 47% and 44% smaller, respectively; for Sandals time series, the RMSE and the MAE (MASE) are 19% and 47% larger, respectively; for Shoes time series, the RMSE and the MAE (MASE) are 49% and 56% smaller, respectively. The seasonal naïve model did not pass the Ljung–Box test in three of the five time series considering the usual significance level of 5%.

Table 1.
Forecast accuracy measures of all forecasting approaches computed using time series cross-validation.
Another observation that can be made from these results is that both transformation and differencing are important for improving ARIMA’s ability to model and forecast time series that contain strong trend and seasonal components. The log transformation was applied to four of the five time series. With the exception of flats, all other time series were differenced: second-order differences were made in Sandals series and first differences were made in Boots, Booties and Shoes series. The Flats, Sandals and Shoes time series were seasonally differenced. Transformation seems not to be significant for state space models. Log transformation was made only on Shoes series.
To see the individual point forecasting behavior, the actual data versus the forecasts from all approaches were plotted (see Figure 3). The ARIMA Cross-Validation and ETS Cross-Validation models selected by our procedure are identified in the legend by ARIMA_CV and ETS_CV, respectively. The forecasts from the Hyndman and Athanasopoulos [16] statistical framework are identified in the legend by ETS_H-A. The forecasts from the Hyndman and Khandakar [23] algorithm are identified in the legend by ARIMA_H-K. In general, it can be seen that both ETS and ARIMA models selected by our cross-validation procedure have the capability to forecast the trend movement and seasonal fluctuations fairly well. As expected, the exceptional increase in the sales of flats observed in March and April 2012 was not predicted by the models that under-forecasted the situation. As mentioned in Section 2.3, one of the limitations of the MAPE is having huge values when data may contain very small numbers. The large values of MAPE for the Boots, Booties and Sandals time series are explained by this fact, since, during some periods, there are almost no sales (close to zero).
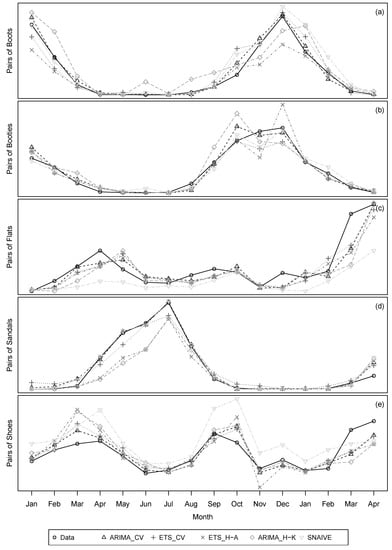
Figure 3.
One-step forecasts from all approaches computed using time series cross-validation (January 2011 to April 2012): (a) pairs of Boots; (b) pairs of Booties; (c) pairs of Flats; (d) pairs of Sandals; and (e) pairs of Shoes.
5. Conclusions
A common obstacle in using ARIMA models for forecasting is that the order selection process is usually considered subjective and difficult to apply. Identifying an appropriate state space model for a time series is also not an easy task. In this work, a cross-validation procedure is used to identify an appropriate ARIMA model and an appropriate state space model for a time series. A minimum size for the training set is specified. The procedure is based on one-step forecasts and uses different training sets, each containing one more observation than the previous one. All possible ETS models and all ARIMA models where the orders are allowed to range reasonably are fitted considering raw data and log-transformed data with regular differencing (up to second order differences) and, if the time series is seasonal, seasonal differencing (up to first order differences). The value of RMSE for each model is calculated averaging the one-step forecasts obtained. The model which has the lowest RMSE value and passes the Ljung–Box test using all of the available data with a reasonable significance level is selected among all the ARIMA and ETS models considered. One of the advantages of this model identification procedure is to be able to compare models that have different orders of differencing and/or different transformations, which is not the case when models are compared using Akaike’s Information Criterion or Bayesian Information Criterion values. The application of the model identification procedure is exemplified in the paper with a case study of retail sales of different categories of women’s footwear from a Portuguese retailer. To be able to compare the accuracies of the forecasts obtained with the ETS and ARIMA models selected by the cross-validation procedure developed, we also evaluated the forecasts from another three forecasting approaches: the Hyndman and Khandakar [23] algorithm for ARIMA models, the Hyndman and Athanasopoulos [16] statistical framework for ETS models and the seasonal naïve method. According to the results, our procedure to find an ARIMA model produces the most accurate forecasts when judged by RMSE, MAE, MAPE and MASE. The RMSE, MAE and MASE produce the same accuracy ranking. The MAPE consistently ranks differently, which reinforces the impact that its limitations can have on the results. Our procedure to find a state space model and an ARIMA model consistently forecasts more accurately than the Hyndman and Athanasopoulos [16] statistical framework and the Hyndman and Khandakar [23] algorithm, and the improvements in the forecast accuracy are significant. Both transformation and differencing were important for improving ARIMA’s ability to model. Transformation did not seem to be significant for accuracy for state space models. Large values of MAPE were found when data contained numbers close to zero, which shows the effect that the limitations of this accuracy measure may have on forecasting results.
Acknowledgments
Project “TEC4Growth-Pervasive Intelligence, Enhancers and Proofs of Concept with Industrial Impact/NORTE-01-0145-FEDER-000020” is financed by the North Portugal Regional Operational Programme (NORTE 2020), under the PORTUGAL 2020 Partnership Agreement, and through the European Regional Development Fund (ERDF).
Author Contributions
Patrícia Ramos designed the cross-validation procedure and José Manuel Oliveira implemented the algorithm and performed the empirical study. Patrícia Ramos wrote the paper and José Manuel Oliveira helped to improve the manuscript. Both authors read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Alon, I. Forecasting aggregate retail sales: The Winters’ model revisited. In Proceedings of the 1997 Midwest Decision Science Institute Annual Conference, Indianapolis, IN, USA, 24–26 April 1997; pp. 234–236.
- Alon, I.; Min, Q.; Sadowski, R.J. Forecasting aggregate retail sales: A comparison of artificial neural networks and traditional method. J. Retail. Consum. Serv. 2001, 8, 147–156. [Google Scholar] [CrossRef]
- Frank, C.; Garg, A.; Sztandera, L.; Raheja, A. Forecasting women’s apparel sales using mathematical modeling. Int. J. Cloth. Sci. Technol. 2003, 15, 107–125. [Google Scholar] [CrossRef]
- Chu, C.W.; Zhang, P.G.Q. A comparative study of linear and nonlinear models for aggregate retail sales forecasting. Int. J. Prod. Econ. 2003, 86, 217–231. [Google Scholar] [CrossRef]
- Aburto, L.; Weber, R. Improved supply chain management based on hybrid demand forecasts. Appl. Soft Comput. 2007, 7, 126–144. [Google Scholar] [CrossRef]
- Zhang, G.; Qi, M. Neural network forecasting for seasonal and trend time series. Eur. J. Oper. Res. 2005, 160, 501–514. [Google Scholar] [CrossRef]
- Kuvulmaz, J.; Usanmaz, S.; Engin, S.N. Time-series forecasting by means of linear and nonlinear models. In Advances in Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Box, G.; Jenkins, G.; Reinsel, G. Time Series Analysis, 4th ed.; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Hyndman, R.J.; Koehler, A.B.; Ord, J.K.; Snyder, R.D. Forecasting with Exponential Smoothing: The State Space Approach; Springer: Berlin, Germany, 2008. [Google Scholar]
- Pena, D.; Tiao, G.C.; Tsay, R.S. A Course in Time Series Analysis; John Wiley & Sons: New York, NY, USA, 2001. [Google Scholar]
- Zhao, X.; Xie, J.; Lau, R.S.M. Improving the supply chain performance: Use of forecasting models versus early order commitments. Int. J. Prod. Res. 2001, 39, 3923–3939. [Google Scholar] [CrossRef]
- Gardner, E.S. Exponential smoothing: The state of the art. J. Forecast. 1985, 4, 1–28. [Google Scholar] [CrossRef]
- Makridakis, S.; Wheelwright, S.; Hyndman, R. Forecasting: Methods and Applications, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1998. [Google Scholar]
- Gardner, E.S. Exponential smoothing: The state of the art-Part II. Int. J. Forecast. 2006, 22, 637–666. [Google Scholar] [CrossRef]
- Aoki, M. State Space Modeling of Time Series; Springer: Berlin, Germany, 1987. [Google Scholar]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice; OTexts: Melbourne, Australia, 2013. [Google Scholar]
- Ljung, G.M.; Box, G.E.P. On a measure of lack of fit in time series models. Biometrika 1978, 65, 297–303. [Google Scholar] [CrossRef]
- Brockwell, P.J.; Davis, R.A. Introduction to Time Series and Forecasting, 2nd ed.; Springer: New York, NY, USA, 2002. [Google Scholar]
- Shumway, R.H.; Stoffer, D.S. Time Series Analysis and Its Applications: With R Examples, 3rd ed.; Springer: New York, NY, USA, 2011. [Google Scholar]
- Wei, W.S. Time Series Analysis: Univariate and Multivariate Methods, 2nd ed.; Addison Wesley: Boston, MA, USA, 2005. [Google Scholar]
- Hyndman, R.J.; Koehler, A.B. Another look at measures of forecast accuracy. Int. J. Forecast. 2006, 22, 679–688. [Google Scholar] [CrossRef]
- Arlot, S.; Alain, C. A survey of cross-validation procedures for model selection. Stat. Surv. 2010, 4, 40–79. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Khandakar, Y. Automatic time series forecasting: the forecast package for R. J. Stat. Softw. 2008, 27, 1–22. [Google Scholar] [CrossRef]
- Kwiatkowski, D.; Phillips, P.C.; Schmidt, P.; Shin, Y. Testing the null hypothesis of stationariry against the alternative of a unit root. J. Econom. 1992, 54, 159–178. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2016. [Google Scholar]
- Hyndman, R.J. Forecast: Forecasting Functions for Time Series and Linear Models. R package Version 7.3. Available online: http://github.com/robjhyndman/forecast (accessed on 7 November 2016).
- Fildes, R.A.; Goodwin, P. Against your better judgment? How organizations can improve their use of management judgment in forecasting. Interfaces 2007, 37, 570–576. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).