1. Introduction
Community detection is one of the classical problems of complex network analysis. A community in a network graph is a subset of the vertices that have a relatively larger density of edges among themselves than to the rest of the vertices [
1]. The quality of the partitioning of a network into communities is evaluated using a metric called the modularity score [
2]; the larger the modularity score, the more appropriate is the partitioning of the vertices into communities. The problem of identifying a partition of the network into communities with the largest modularity score is NP-complete [
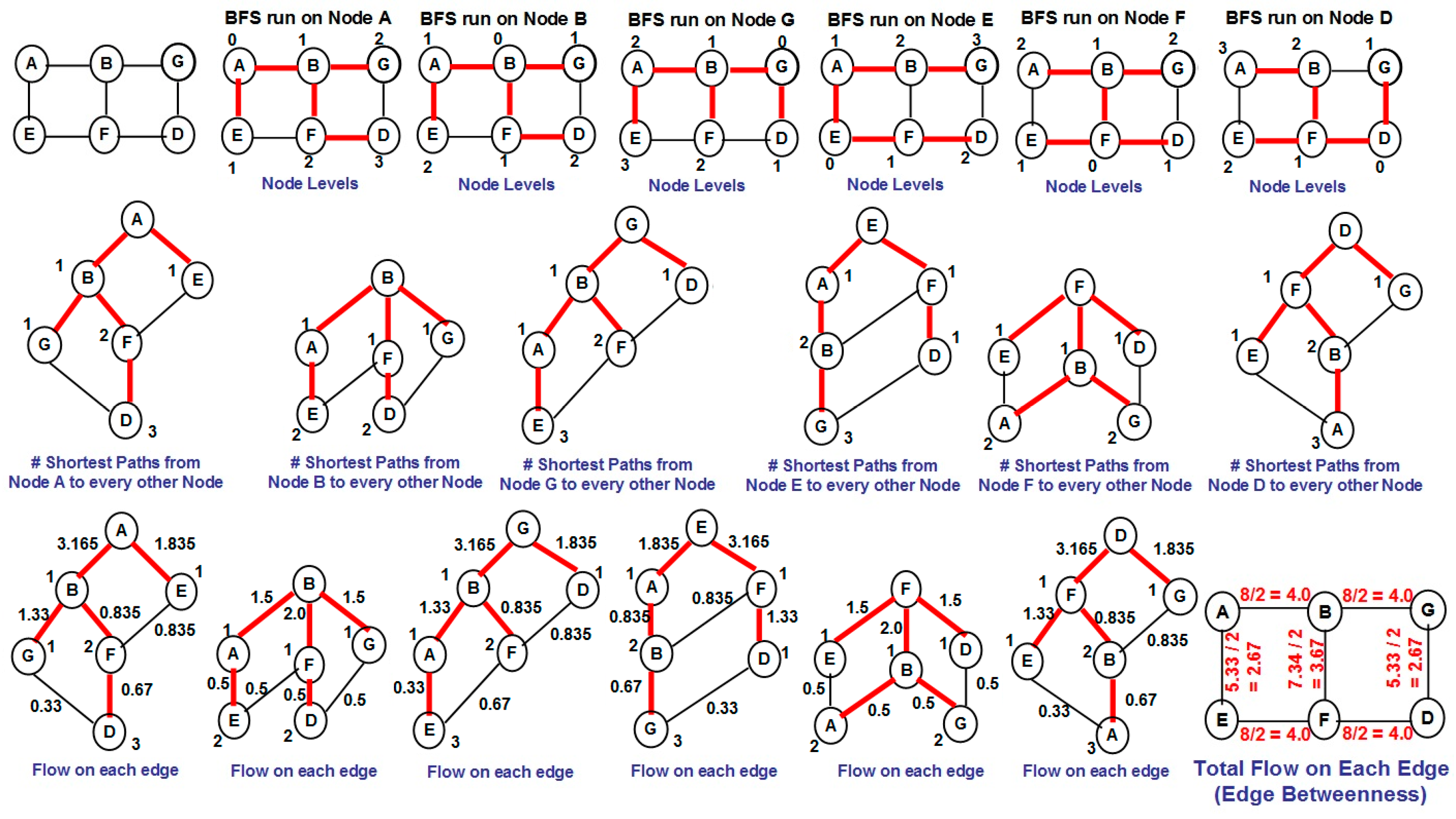
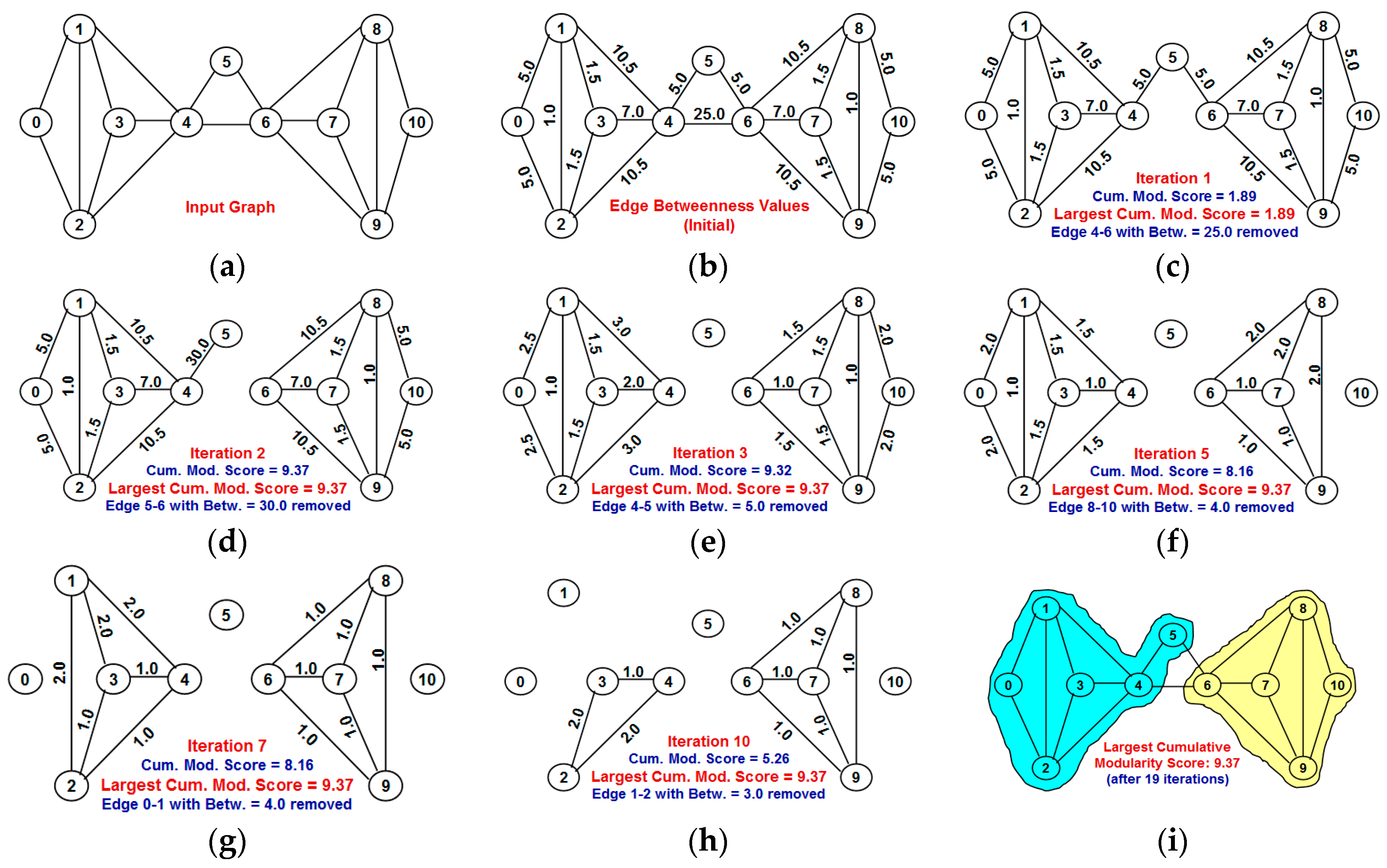
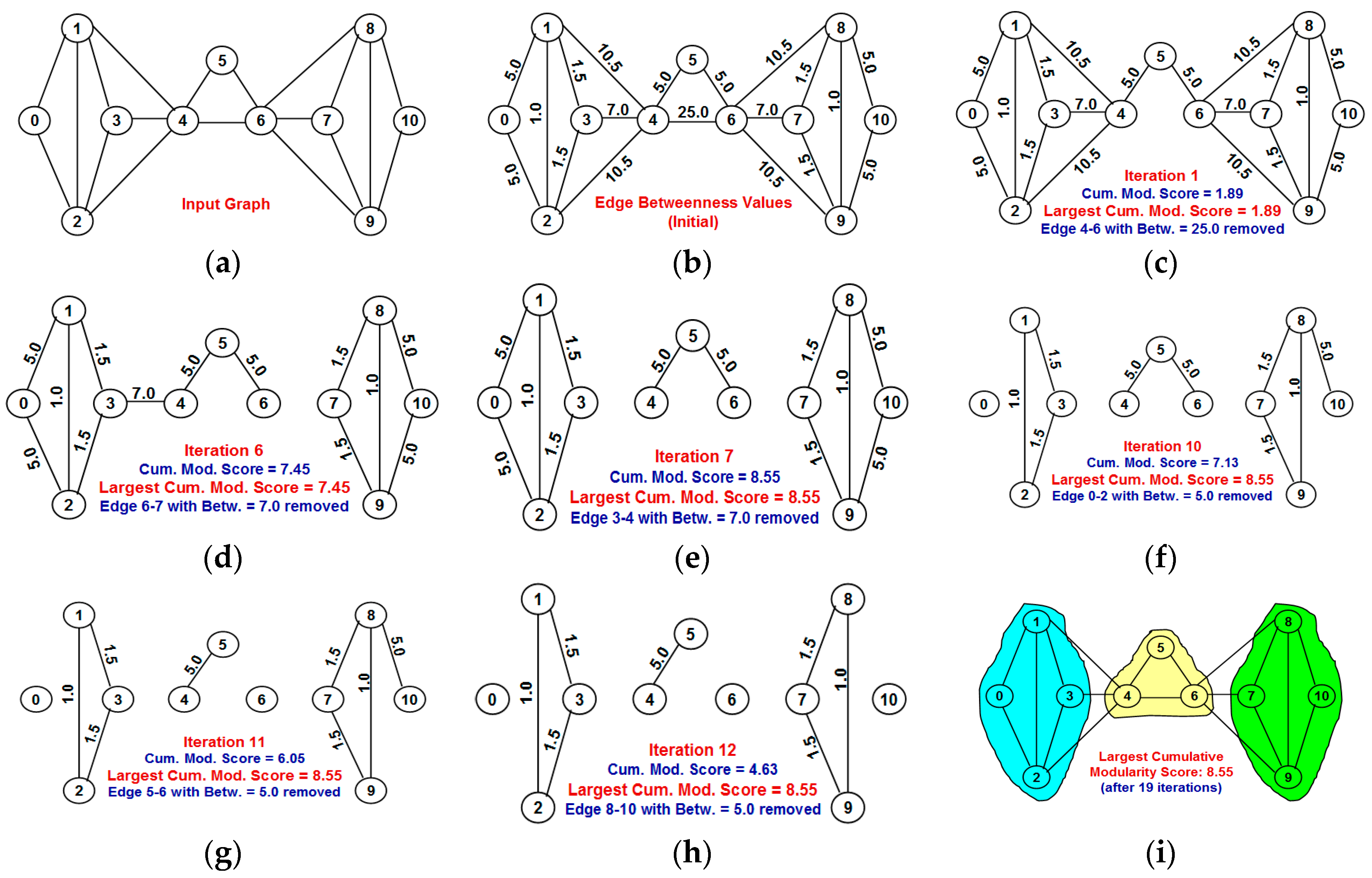
3]. Several algorithms have been proposed in the literature for community detection and a majority of these are based on the notion of betweenness [
4], defined for an edge as the fraction of the shortest paths between any two vertices going through the edge, considered over all pairs of vertices. Edges with high betweenness are typically removed to disintegrate a connected network into two or more components—each of which are considered to form a closely-knit community. Edge betweenness-based algorithms for community detection are typically considered to identify communities with a larger modularity score at the cost of a significantly larger computation time [
5]. Another potential weakness of community detection algorithms could be the inability to detect smaller communities (called the resolution limit problem [
6]); this weakness is more prominent in multi-level aggregation algorithms (like the Louvain algorithm [
7]). To get around this bottleneck, the focus of research in the area of community detection has veered around strategies (e.g., [
8,
9,
10]) that identify the critical edges (the edges that if removed will lead to the identification of closely-knit communities with high modularity score) without essentially running the time-consuming shortest path algorithms for each vertex and for each edge removal [
4,
5] as well as be able to identify smaller communities that indeed exist in the network being analyzed (in such a way that the overall sum of the modularity scores of the communities do not get significantly lowered).
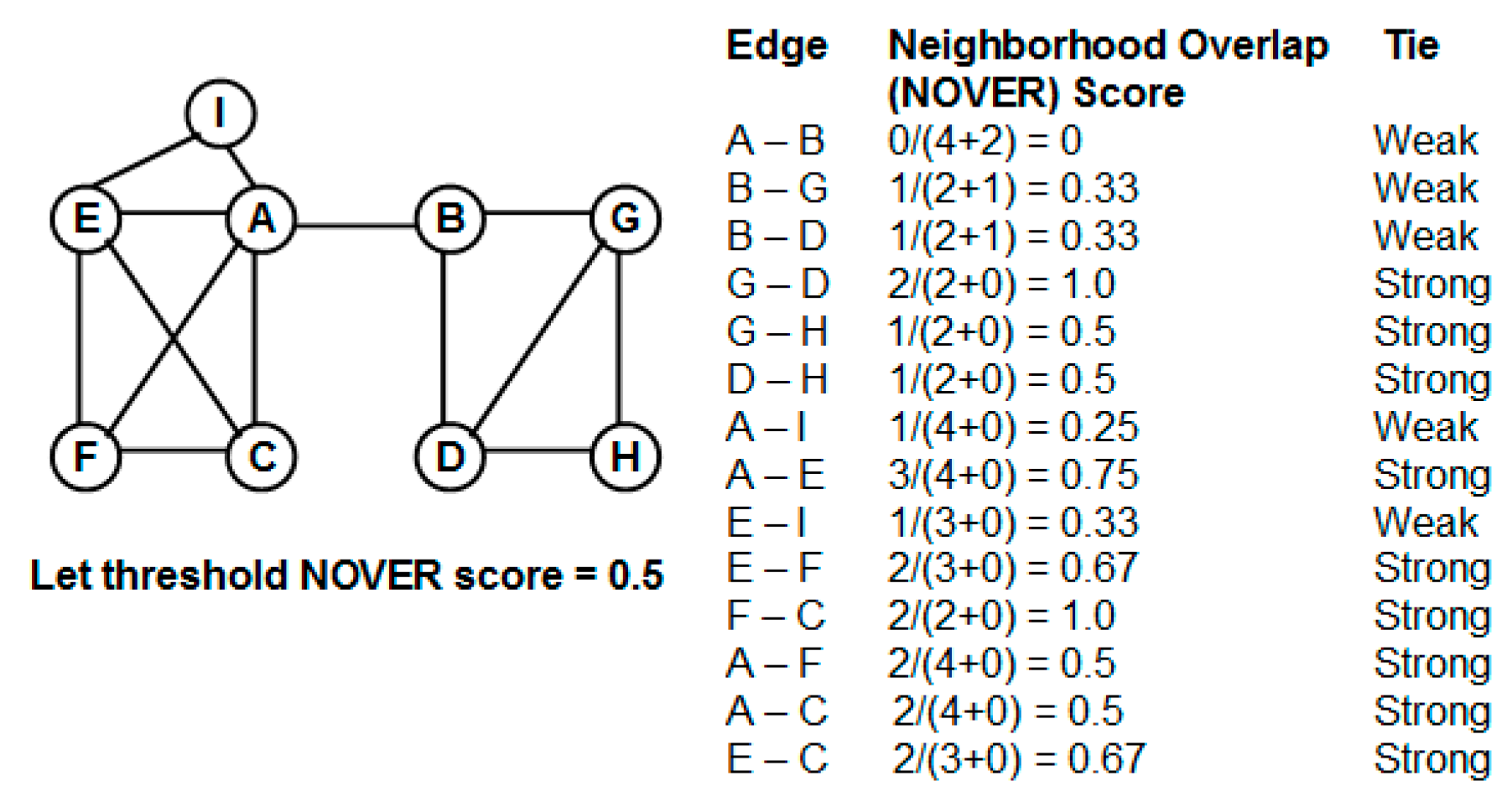
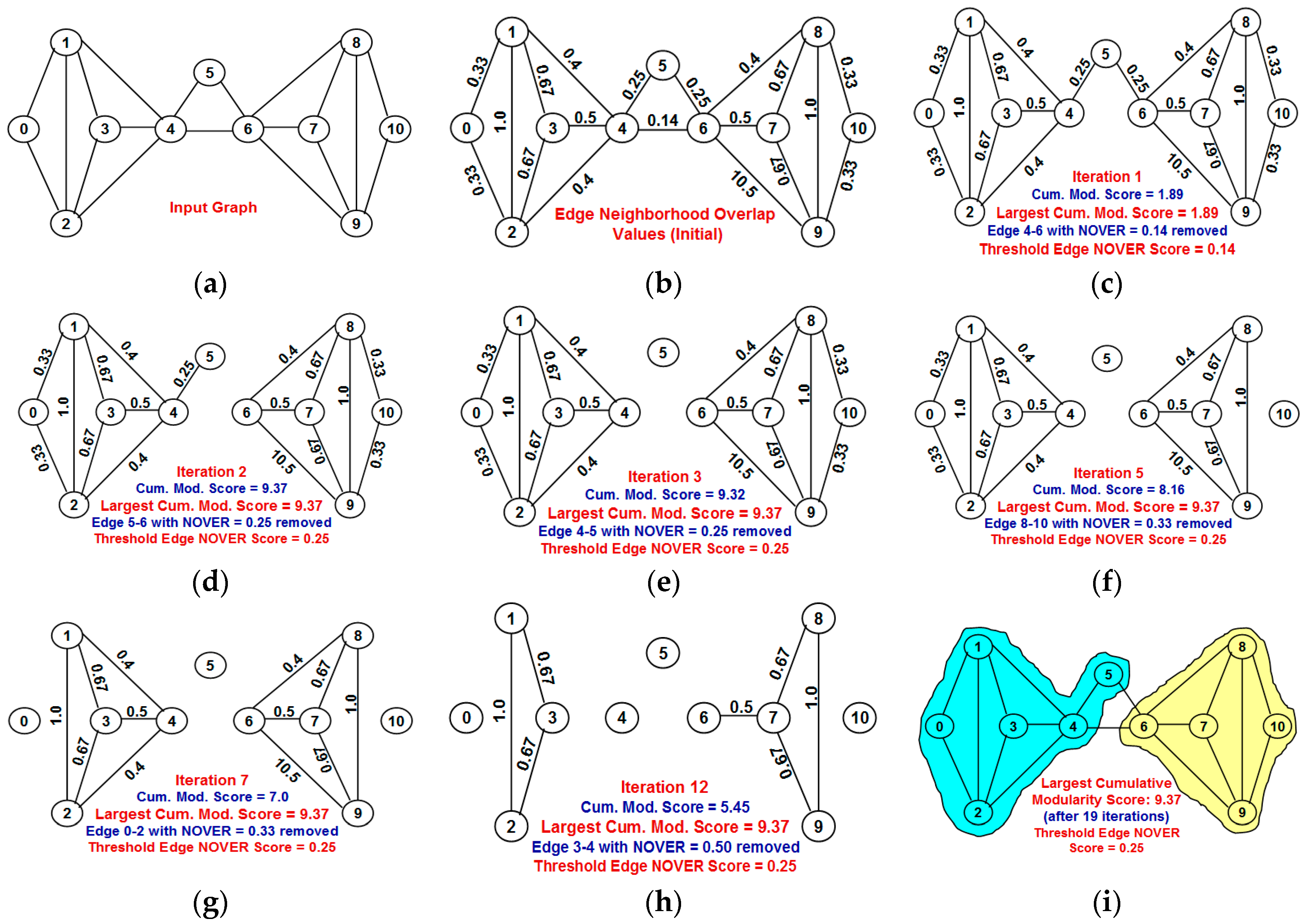
One edge-based criterion that can be quickly computed and at the same time appears to be quite effective for community detection is the “neighborhood overlap”. The neighborhood overlap [
11] for an edge (
u,
v) is defined as the ratio of the number of nodes that are neighbors of both the vertices
u and
v to that of the number of nodes that are neighbors of at least one of the two vertices
u or
v. As one can see from the above definition, the neighborhood overlap of an edge can be computed just based on the local neighborhood information of the end vertices of the edge and no global knowledge is required. An edge (
u,
v) that has a smaller value for the neighborhood overlap is more likely to play a significant role in facilitating communication between
u and
v as well as between vertices that are in the vicinity (
i.e., one or more hops) of
u and vertices that are in the vicinity of
v. The sub graph of vertices involving
u and the sub graph of vertices involving
v are more likely to have fewer edges connecting them; otherwise, the edge (
u,
v) would have had a larger neighborhood overlap. Edges having a lower neighborhood overlap are thus referred to as “weak ties” [
11] and are often considered for removal to disintegrate a connected network to two or more components—each of which form a community.
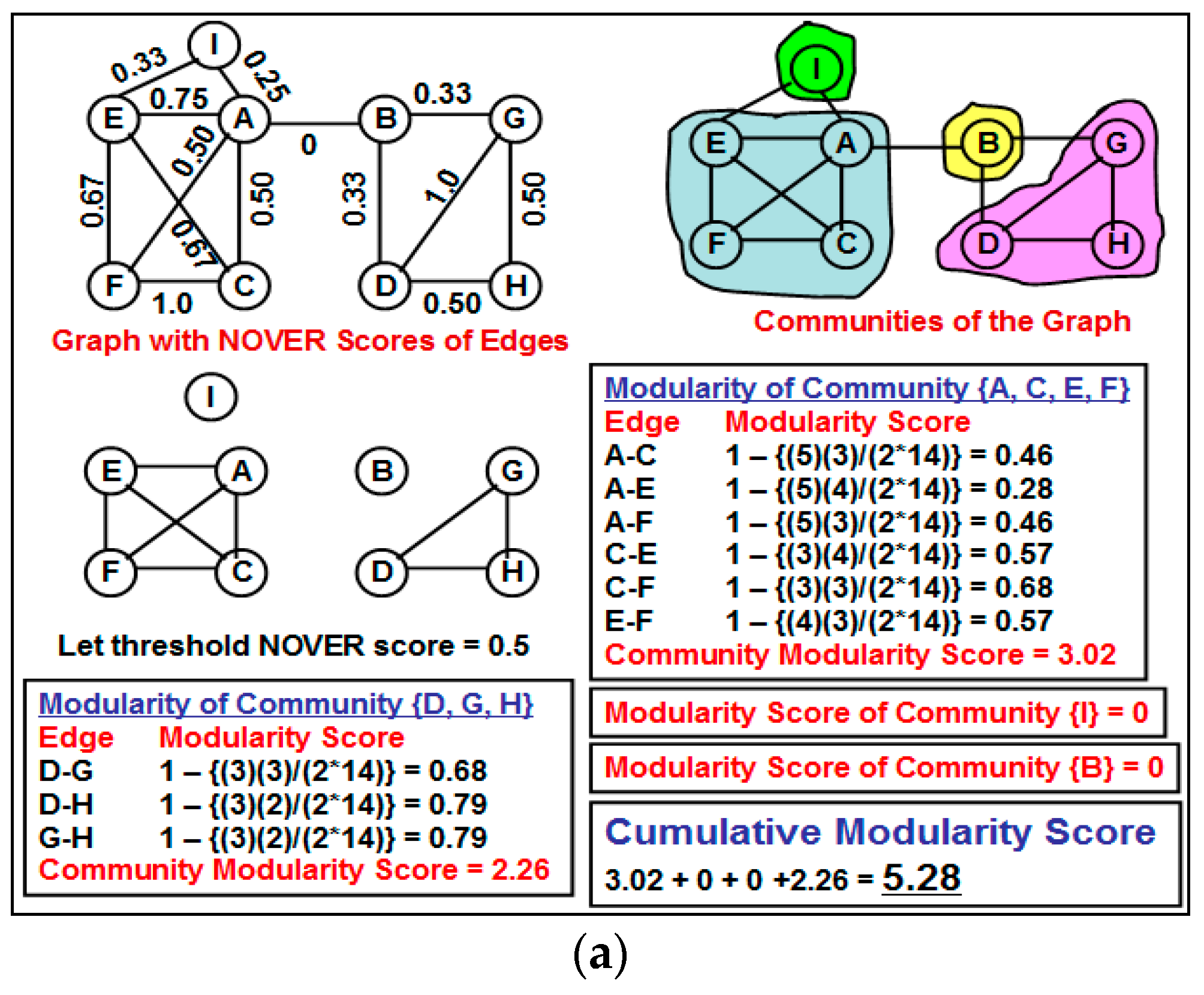
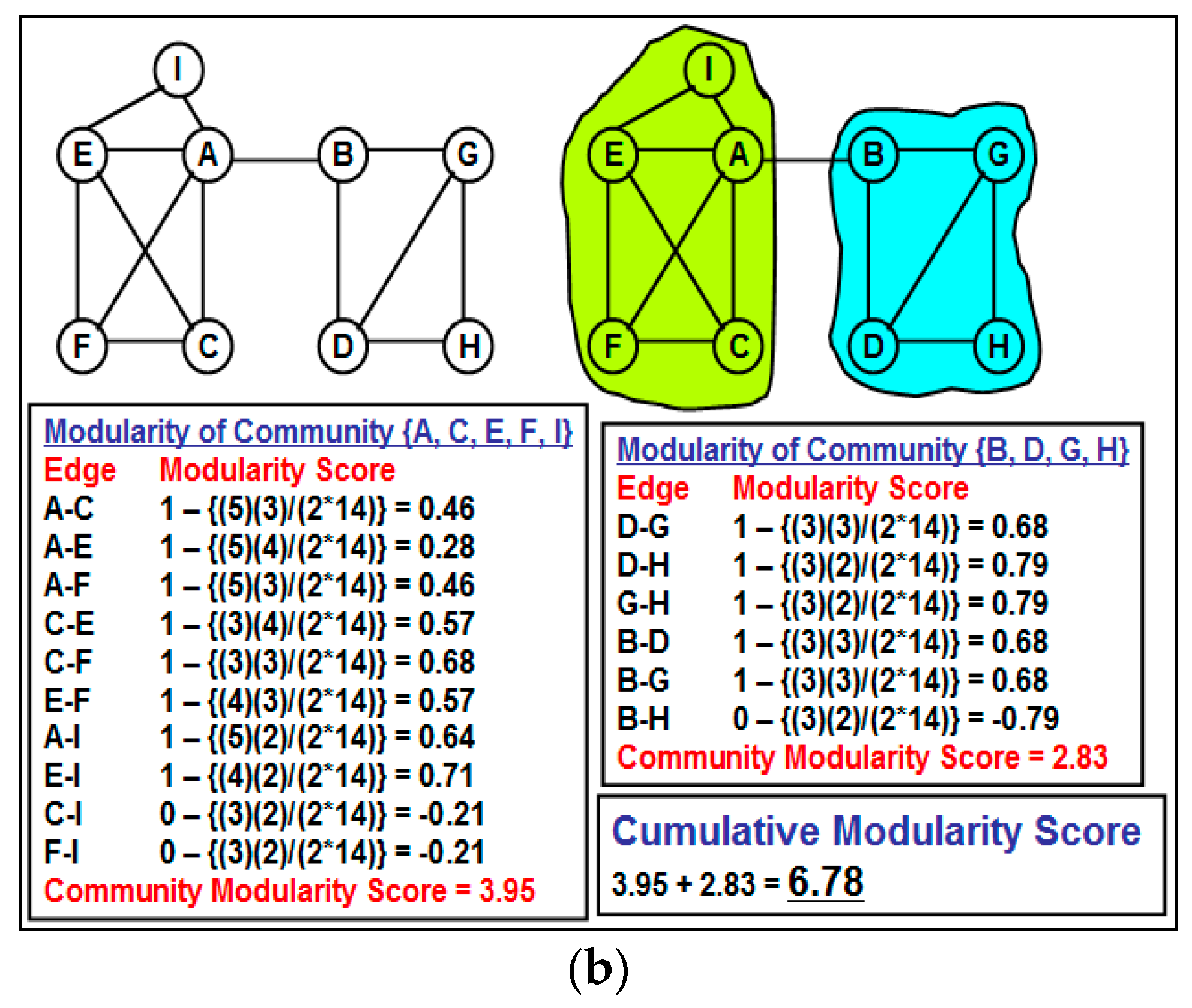
The currently known approach [
11] of utilizing weak ties and neighborhood overlap for community detection involves fixing a threshold value for the neighborhood overlap and all edges in which neighborhood overlap is less than this threshold value are categorized as weak ties and the rest of the edges are categorized as strong ties. All of these weak ties are removed from the network and the resulting network components form the different communities for the network, referred to as the “partition” of the network. The main problem with the above approach is the issue of fixing an appropriate threshold value for the neighborhood overlap of an edge to identify the weak ties. A larger value for the threshold neighborhood overlap could unnecessarily disintegrate the network into several components (most of them being of smaller size), and the cumulative modularity score of the communities (each community has a modularity score; we define the cumulative modularity score as the sum of the modularity scores of all the communities in a network) could be significantly lower than the optimal value. Likewise, a smaller value for the threshold neighborhood overlap could lead to the coexistence of two potentially different communities as one community, leading to a reduction in the cumulative modularity score.
Our contributions in this paper are as follows: (i) We propose a greedy algorithm of iteratively removing the edges in the increasing order of their neighborhood overlap and choosing the partition of communities that sustains the largest cumulative modularity score. The neighborhood overlap of the edge whose removal leads to the identification of the partition with the largest cumulative modularity score is referred to as the threshold neighborhood overlap and the edges removed until then are referred to as weak ties. It is sufficient that the neighborhood overlap of the edges be computed at the beginning of the algorithm and need not be computed after each edge removal. This a characteristic aspect of our proposed algorithm, unlike the well-known edge-betweenness based Girvan-Newman algorithm [
4] and its various improvised versions (e.g., [
8,
9]) that require the betweenness of the edges to be recomputed after each edge removal. The complexity of the Girvan-Newman algorithm is O(|
E| × |
V| × (|
E| + |
V|)) on a graph of |
V| vertices and |
E| edges [
4]. The cumulative modularity score of the communities obtained with our proposed Neighborhood OVERlap-based edge removal (NOVER) algorithm is observed to be only at most 60% lower than the cumulative modularity score obtained with the Girvan-Newman algorithm, whereas the time-complexity of NOVER is O(|
E| × (|
E| + |
V|)) and the actual execution time of the NOVER algorithm has been observed to be as small as just 1% of the execution time of the original Girvan-Newman algorithm on larger real-world networks. The time-complexity of NOVER is thus bound to be significantly smaller than that of the well-known Girvan-Newman algorithm (as large as by a factor of the number of vertices in the graph). Nevertheless, the relative similarity of the communities (quantified on the basis of the Normalized Mutual Information score [
12]) detected by the NOVER algorithm and the Girvan-Newman algorithm is observed to be significantly high; (ii) As part of the performance evaluation studies, we propose a novel metric called the Modularity-Resolution-Execution Time-Nodes (MREN) score—defined quantitatively as the ratio of the product of the cumulative modularity score and the fraction of communities of the smallest size to that of the product of the execution time of the algorithm and the number of nodes in the network. We propose the MREN score to be used as a global metric (irrespective of the number of nodes in the network) for evaluating the effectiveness of an algorithm to detect communities with respect to modularity maximization, resolution limit (detecting smaller communities) and execution time. We claim that larger the MREN score for a community detection algorithm on a real-world network, the more effective is the algorithm with respect to simultaneously satisfying all of the above three performance criteria. We evaluate the MREN scores of the community detection algorithms on nine different real-world networks and observe the NOVER algorithm to incur the largest MREN score for eight of these networks.
To the best of our knowledge, we have not come across such a formal time-efficient and effective algorithm that uses neighborhood overlap as the basis for community detection. The rest of the paper is organized as follows:
Section 2 introduces the terms neighborhood overlap, weak ties and modularity score with appropriate examples.
Section 3 explains in detail the proposed NOVER algorithm with an example.
Section 4 explains the working of the well-known Girvan-Newman (GN) algorithm (both the original and time-efficient versions) for edge betweenness based community detection as well as the working of the Louvain multi-level aggregation algorithm.
Section 5 presents the simulation results evaluating the performance of the NOVER algorithm
vis-à-vis the Louvain, GN-original and GN-efficient versions on real-world network graphs with respect to the cumulative modularity score of the communities detected, resolution limit, execution time and extent of similarity.
Section 6 reviews related work in the literature on community detection using edge betweenness and neighborhood overlap.
Section 7 concludes the paper and outlines ideas for future work. Throughout the paper, the terms “vertex” and “node”, “edge” and “link”, “community” and “component” are used interchangeably. They mean the same.
5. Simulations
In this section, we evaluate the performance of the proposed NOVER algorithm on real-world network graphs and do a comparative analysis with the performance of the original and time-efficient variants of the Girvan-Newman algorithm (GN-original and GN-efficient) as well as with the Louvain algorithm. We consider a total of nine real-world network graphs: The US College Football Network (FN) [
4] is a network of 115 football teams (each team is a node) who competed in the Fall 2000 season and there is a link between any two nodes if the corresponding teams have played against each other at least once in the past. The Dolphin Network (DN) [
16] is a network of 62 dolphins (each dolphin is a node) living in Doubtful Sound, New Zealand; there is a link between any two nodes if the corresponding dolphins were seen together moving around over a period of time. The Karate Network (KN) [
17] is a network of 34 members (each member is a node) of a Karate Club in a US university in the 1970s—there exists a link between two nodes if the corresponding members have been noticed interacting with each other over a period of time. The US Politics Books Network (PN) [
18] is a network of 105 books (each book is a node) related to US politics sold in Amazon.com: there exists a link between any two nodes (
i.e., books, say
u and
v) if customers who bought one book (say book
u) also bought the other book (say book
v) and
vice-
versa. The US Airport Network (AN) [
19] is a network of 332 airports (each airport is a node) and the direct flight connections (edges) between them. The Erdos971 Collaboration Network (EN) [
20] is a network of 472 Collaborators (nodes) who may have either published a paper directly in collaboration with Paul Erdos or through a chain of collaborators leading to Paul Erdos; there exists an edge between two nodes if the corresponding authors have co-authored publications. The Les Miserables Network (LN) [
21] is a network of 77 characters that appeared in the novel Les Miserables; there exists an edge between two nodes (characters) if the corresponding characters appeared together in at least one chapter of the novel. The C. Elegans Neural Network (NN) [
22] is a network of 297 neurons (nodes) in the hermaphrodite Caenorhabditis Elegans; there is an edge between two neurons if they interact with each other in the form of chemical synapses, gap junctions and neuromuscular junctions. The Citation Graph Drawing Network (CN) [
23] is a network of 311 papers (nodes) published in the area of Graph Drawing (GD) in the proceedings of the GD’ 1994 to GD’ 2000 conferences; there exists an edge between two papers if one of the papers has cited the other paper as a reference. Though the CN network is a directed network, we modeled it as an undirected network for consistency with the other real-world networks considered as well as due to the underlying assumption of undirected edges for the community detection algorithms analyzed in this paper.
All the nine real-world networks considered are modeled as undirected network graphs.
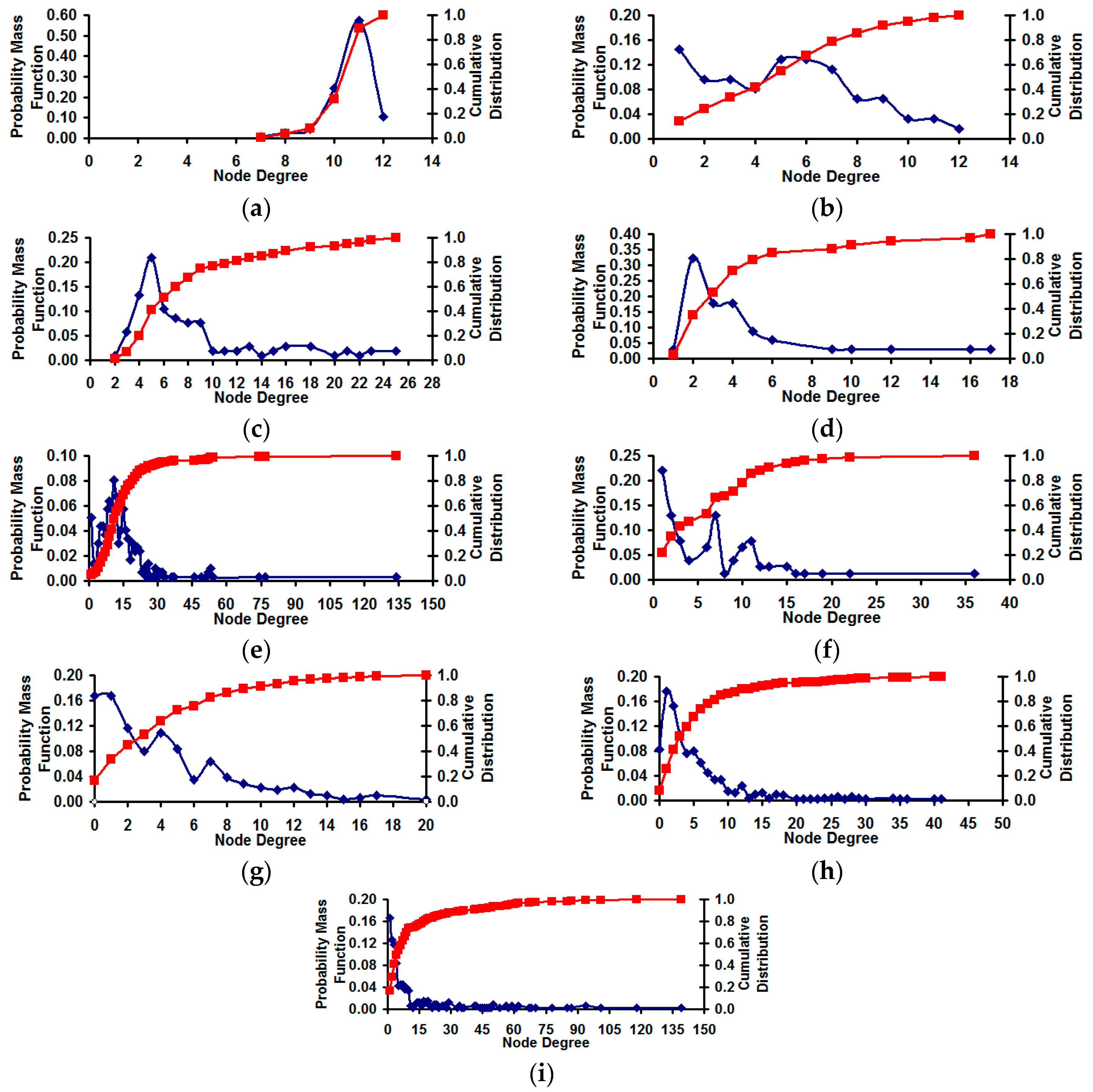
Figure 8 illustrates the degree distribution of the real-world network graphs (both the probability mass function and the cumulative distribution [
24]), listed in the increasing order of the spectral radius ratio for node degree. The spectral radius ratio for node degree (denoted λ
sp) for a graph [
25] captures the extent of variation of the node degree with respect to the average node degree and is calculated as the ratio of the principal eigenvalue of the adjacency matrix of the graph and the average node degree (denoted
kavg). The value for λ
sp is always greater than or equal to 1.0. The farther the λ
sp value from 1.0, the larger the variation in node degree. The US Football Network (FN) has a λ
sp value of 1.01 (vindicating the Poisson-style degree distribution) and the degree distribution of the other real-world networks gradually becomes scale-free [
26], with the US Airports Network (AN) having the largest λ
sp value of 3.22.
Figure 8.
Degree distribution of the real-world Network graphs. (a) US football network (FN): λsp = 1.01; (b) Dolphin Network (DN): λsp = 1.40; (c) US Politics Book Network (PN): λsp = 1.42; (d) Karate Network (KN): λsp = 1.47; (e) C. Elegans Network (NN): λsp = 1.68; (f) Les Miserables Network (LN): λsp = 1.82; (g) Citation GD Network (CN): λsp = 2.24; (h) Erdos971 Network (EN): λsp = 2.28; (i) US Airports Network (AN): λsp = 3.22.
Figure 8.
Degree distribution of the real-world Network graphs. (a) US football network (FN): λsp = 1.01; (b) Dolphin Network (DN): λsp = 1.40; (c) US Politics Book Network (PN): λsp = 1.42; (d) Karate Network (KN): λsp = 1.47; (e) C. Elegans Network (NN): λsp = 1.68; (f) Les Miserables Network (LN): λsp = 1.82; (g) Citation GD Network (CN): λsp = 2.24; (h) Erdos971 Network (EN): λsp = 2.28; (i) US Airports Network (AN): λsp = 3.22.
We measure the following five performance metrics and the probability distribution: (i) Cumulative Modularity Score of the best possible communities detected by each of the algorithms; (ii) Execution time (in milliseconds) for each of the algorithms; (iii) Giant community size—Fraction of the nodes in the largest community among the communities detected; (iv) Resolution limit—Fraction of the communities of the smallest size among all the communities detected; (v) Normalized Mutual Information, NMI: Measure of the extent of similarity (evaluated as a quantitative score from 0 to 1) between the communities detected by two different algorithms; and (vi) Cumulative probability of finding a community of size less than or equal to a certain value. We also introduce a new metric called the MREN score (M-Modularity score; R-Resolution limit; E-Execution time; N-Number of nodes) to evaluate the effectiveness of a community detection algorithm with respect to balancing the tradeoffs among the metrics (modularity score, resolution limit and execution time). Quantitatively, the MREN score for a community detection algorithm run on a particular network is calculated as the ratio of the product of the cumulative modularity score of the communities detected and the Resolution limit to that of the product of the logarithm of the execution time (in milliseconds) and the number of nodes in the network. The inclusion of the number of nodes in the network as part of the calculation of the MREN score facilitates to make the score as a global measure of evaluating the effectiveness of a community detection algorithm. We claim that larger the MREN score (i.e., farther away the score is from 0.0), the larger the effectiveness of the algorithm with respect to balancing the tradeoffs among modularity optimization, resolution limit and execution time. In the case of the NOVER algorithm, we also measure the Threshold NOVER score for weak tie classification.
Figure 9.
Cumulative modularity score vs. execution time for the community detection algorithms on real-world Networks graphs. (a) US FOOTBALL Network (FN); (b) Dolphin Network (DN); (c) US Politics Book Network (PN); (d) Karate Network (KN); (e) C. Elegans Network (NN); (f) Les Miserables Network (LN); (g) Citation GD Network (CN); (h) Erdos971 Collaboration Network (EN); (i) US Airports Network (AN).
Figure 9.
Cumulative modularity score vs. execution time for the community detection algorithms on real-world Networks graphs. (a) US FOOTBALL Network (FN); (b) Dolphin Network (DN); (c) US Politics Book Network (PN); (d) Karate Network (KN); (e) C. Elegans Network (NN); (f) Les Miserables Network (LN); (g) Citation GD Network (CN); (h) Erdos971 Collaboration Network (EN); (i) US Airports Network (AN).
The community detection algorithms were implemented in Java. We take into consideration only the time needed to execute all the steps of the algorithms and not the time incurred to read the network graph file (containing the node and edge information) and print the results. Hence, the execution time measured is a direct measure of the theoretical time-complexity of the algorithms as presented in
Section 4. The simulations were run on a computer with Intel Core i7-2620M CPU @ 2.70 GHz and an installed memory (RAM) of 8 GB.
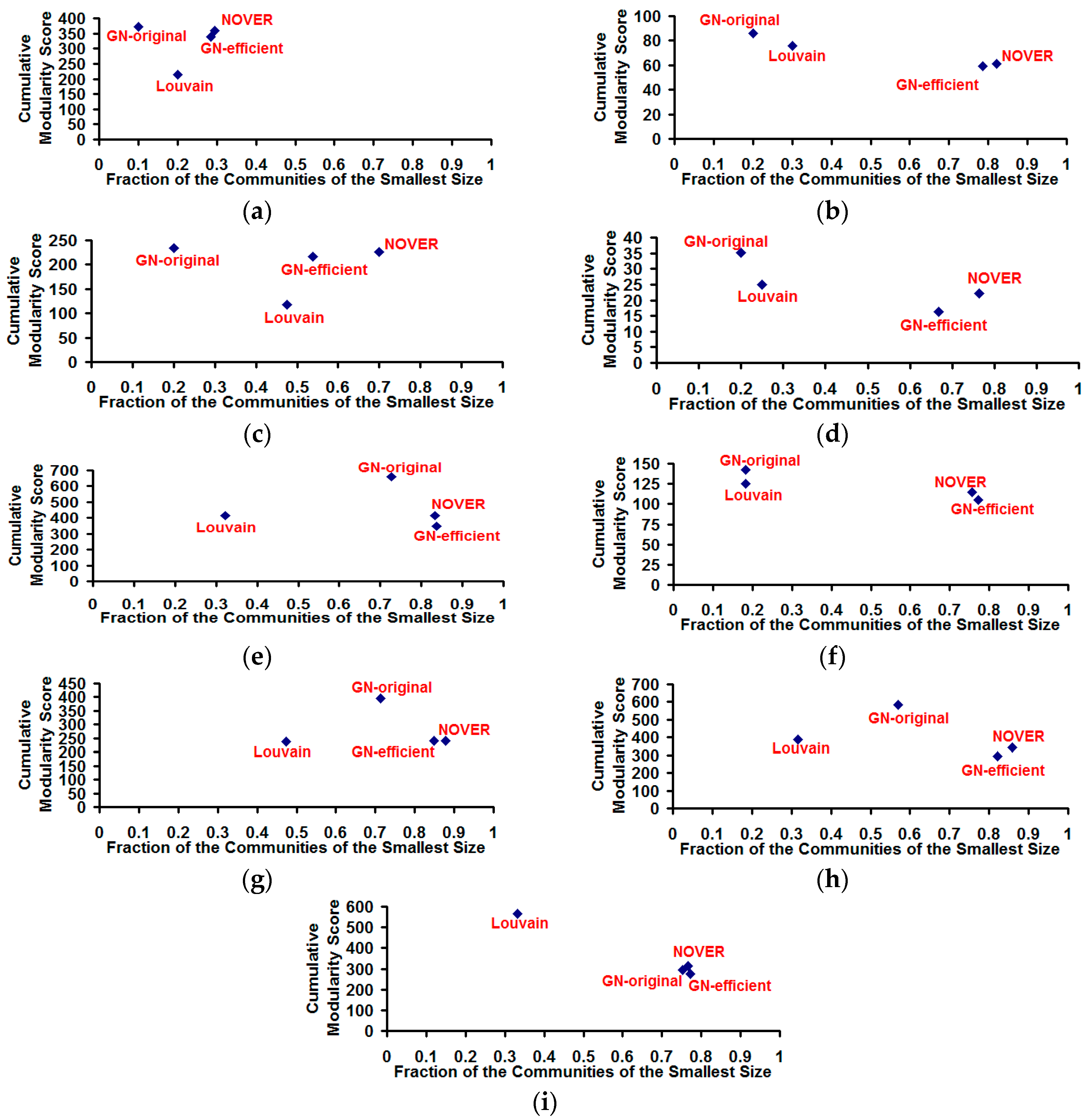
Figure 9 and
Figure 10 respectively present the values for the execution time
vs. cumulative modularity score and fraction of the communities of the smallest size
vs. cumulative modularity score obtained for the community detection algorithms in each of the real-world networks.
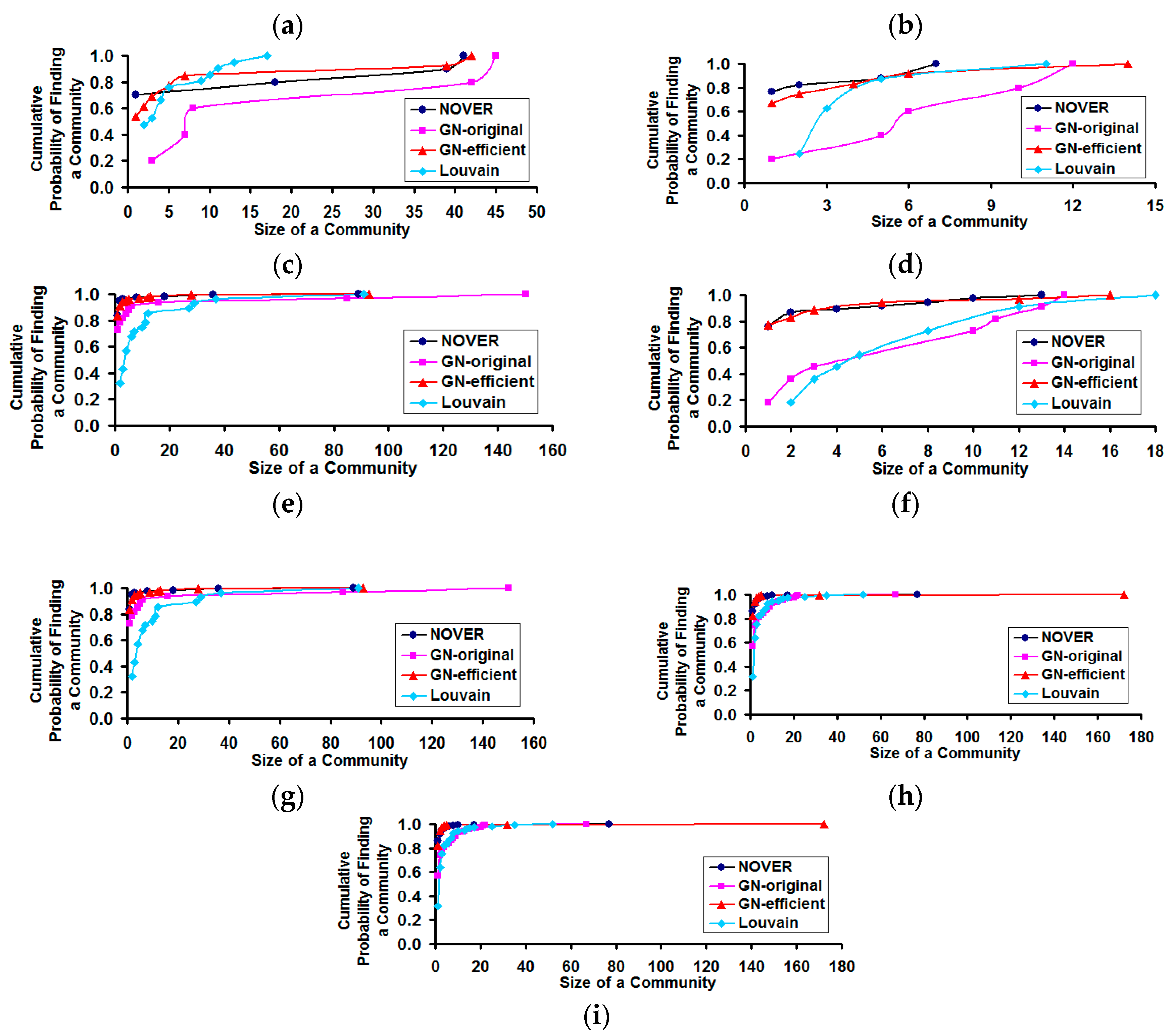
Figure 11 displays the cumulative probability of finding a community of various size under each of the community detection algorithms for the real-world networks studied.
Figure 10.
Cumulative modularity score vs. fraction of the communities of the smallest size for the community detection algorithms on real-world Network graphs. (a) US Football Network (FN); (b) Dolphin Network (DN); (c) US Politics Book Network (PN); (d) Karate Network (KN); (e) C. Elegans Network (NN); (f) Les Miserables Network (LN); (g) Citation GD Network (CN); (h) Erdos971 Collaboration Network (EN); (i) US Airports Network (AN).
Figure 10.
Cumulative modularity score vs. fraction of the communities of the smallest size for the community detection algorithms on real-world Network graphs. (a) US Football Network (FN); (b) Dolphin Network (DN); (c) US Politics Book Network (PN); (d) Karate Network (KN); (e) C. Elegans Network (NN); (f) Les Miserables Network (LN); (g) Citation GD Network (CN); (h) Erdos971 Collaboration Network (EN); (i) US Airports Network (AN).
Figure 11.
Cumulative probability distribution for finding a community of certain size in real-world Network graphs. (a) US Football Network (FN); (b) Dolphin Network (DN); (c) US Politics Book Network (PN); (d) Karate Network (KN); (e) C. Elegans Network (NN); (f) Les Miserables Network (LN); (g) Citation GD Network (CN); (h) Erdos971 Collaboration Network (EN); (i) US Airports Network (AN).
Figure 11.
Cumulative probability distribution for finding a community of certain size in real-world Network graphs. (a) US Football Network (FN); (b) Dolphin Network (DN); (c) US Politics Book Network (PN); (d) Karate Network (KN); (e) C. Elegans Network (NN); (f) Les Miserables Network (LN); (g) Citation GD Network (CN); (h) Erdos971 Collaboration Network (EN); (i) US Airports Network (AN).
The Louvain algorithm incurs the smallest execution time for all the real-world networks, as its execution time is theoretically proportional to Θ(|V| × log|V|) whereas the execution time of the GN-original algorithm is theoretically proportional to Θ(|E| × |V|(|V| + |E|)). The GN-original algorithm takes the longest execution time for all the real-world networks, but at the same time incurs the largest cumulative modularity score for eight of the nine real-world networks. The Louvain algorithm incurs the largest cumulative modularity score for only the US Airports Network. The cumulative modularity score incurred with the NOVER algorithm is significantly larger than that of the Louvain algorithm for two of the nine real-world networks (US Football network and US Politics Book network) whose spectral radius ratio for node degree is in the lower range (λsp ≤ 1.5). For five of the nine real-world networks, the NOVER algorithm incurs a cumulative modularity score that is very much comparable to that of the Louvain algorithm. Only for the US Airports network and Dolphin network, we observe the cumulative modularity score of the Louvain algorithm to be appreciably larger than that of the NOVER algorithm. All of the above observations hold true with the execution time of the NOVER algorithm significantly lower to that of the GN-original algorithm; the difference in execution time increases with increase in the number of nodes and/or the number of edges. The GN-original algorithm is significantly slower for networks with a larger number of nodes and/or edges. The NOVER algorithm incurs an execution time that is either less than or at most equal to that of the GN-efficient algorithm for all the real-world networks, and at the same time incurs a cumulative modularity score that is always either larger or at the worst case equal to that of the GN-efficient algorithm; note that both the NOVER and GN-efficient algorithms have the same theoretical time-complexity of Θ(|E| × (|V| + |E|)).
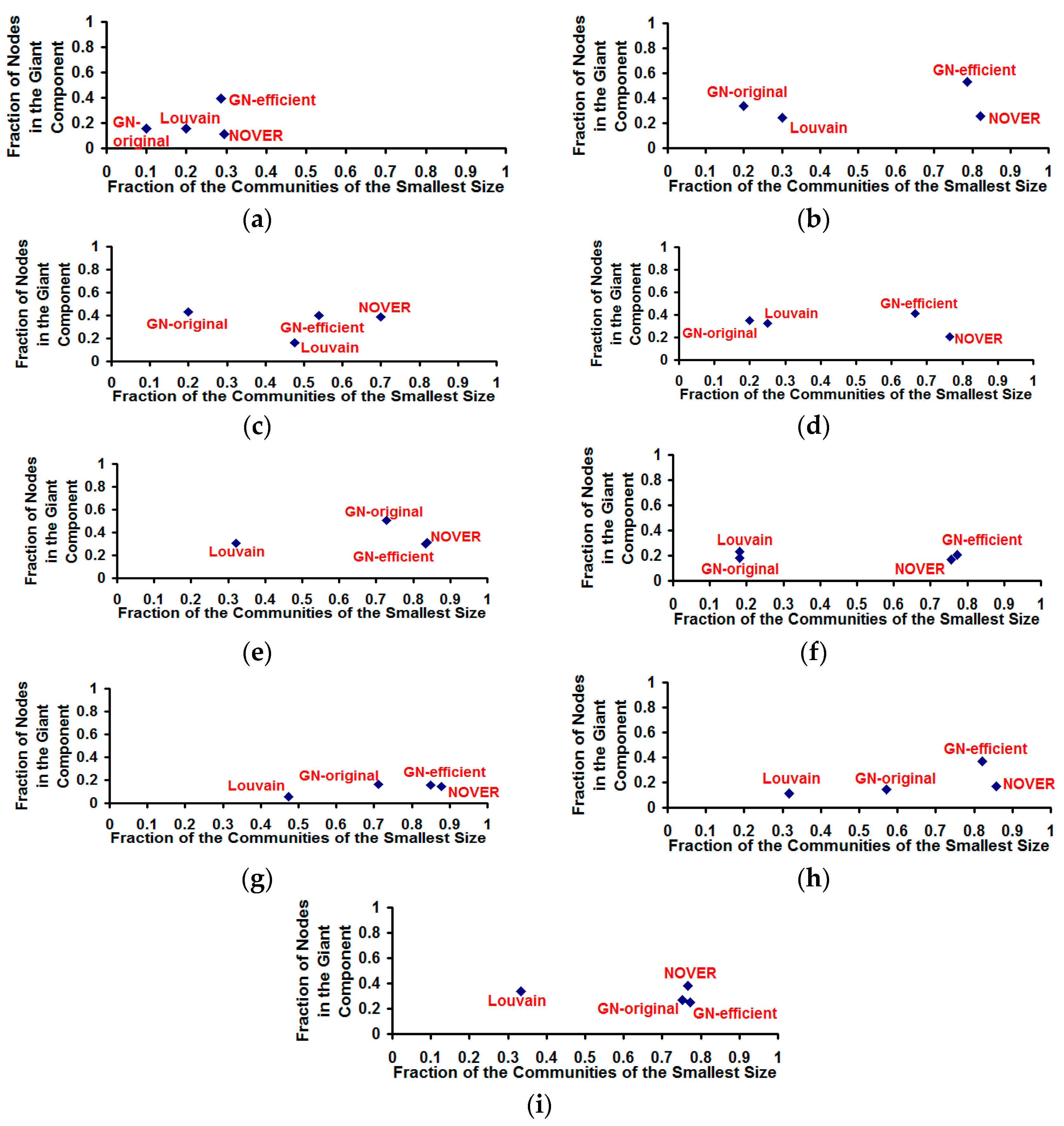
Figure 12.
Fraction of nodes in the giant component vs. fraction of the communities of the smallest size for the community detection algorithms on real-world Network graphs. (a) US Football Network (FN); (b) Dolphin Network (DN); (c) US Politics Book Network (PN); (d) Karate Network (KN); (e) C. Elegans Network (NN); (f) Les Miserables Network (LN); (g) Citation GD Network (CN); (h) Erdos971 Collaboration Network (EN); (i) US Airports Network (AN).
Figure 12.
Fraction of nodes in the giant component vs. fraction of the communities of the smallest size for the community detection algorithms on real-world Network graphs. (a) US Football Network (FN); (b) Dolphin Network (DN); (c) US Politics Book Network (PN); (d) Karate Network (KN); (e) C. Elegans Network (NN); (f) Les Miserables Network (LN); (g) Citation GD Network (CN); (h) Erdos971 Collaboration Network (EN); (i) US Airports Network (AN).
Though the Louvain algorithm and GN-original algorithm appear to be respectively optimal incurring the lowest execution time and largest cumulative modularity score, we observe both these algorithms suffer from the poor resolution problem (incur lower values for the fraction of communities of smaller size), especially the Louvain algorithm. Due to the multi-level aggregation nature of the Louvain algorithm, it becomes difficult to detect communities of size lower than a certain value that could indeed contribute to a larger cumulative modularity score. On the other hand, the NOVER algorithm is able to detect communities of smaller size with an appreciably higher probability and at the same time incurs a larger cumulative modularity score that is very much comparable to that of the Louvain algorithm for seven of the nine real-world networks. Though the GN-efficient algorithm incurs a comparable value (to that of the NOVER algorithm) for the resolution limit for most of the real-world networks, there exists at least a couple of real-world networks for which the fraction of communities of smallest size detected by the GN-efficient algorithm is lower than that of the NOVER algorithm.
With respect to the cumulative probability distribution of the community size (see
Figure 11), we observe the community size distribution to follow a power-law pattern, similar to that of the degree distribution. We observe the NOVER algorithm to incur a larger probability of finding a community of smaller to moderate size for real-world networks with lower variation in node degree (
i.e., spectral radius ratio for node degree ≤1.5). As the spectral radius ratio for node degree increases beyond 1.5, we observe the cumulative probability distribution profiles for the community sizes detected by all the community detection algorithms to overlap with each other. For networks of moderate variation in node degree, the GN-original and Louvain algorithms appear to sustain a relatively lower cumulative probability for finding a community of size less than or equal to a certain value.
The original and time-efficient versions of the Girvan-Newman algorithm appear to detect giant components of relatively larger size (see
Figure 12) compared to that of the Louvain and NOVER algorithms. The GN-efficient algorithm detects communities with a larger resolution limit (fraction of the communities of the smallest size) as well as a larger giant component size (fraction of the nodes in the largest community) for most of the real-world networks. The NOVER algorithm also accomplishes a larger resolution limit that is very much comparable to that of the GN-efficient algorithm, but the giant component size falls short of the GN-efficient algorithm. Nevertheless, the NOVER algorithm detects giant components of relatively larger size than that of the Louvain algorithm for five of the nine real-world networks analyzed. Additionally, we did not observe any ties for the giant component; all the community detection algorithms detected only one single giant component of the largest size on each of the real-world network graphs; on the other hand, there existed several communities of the smallest size in the case of each of the algorithms.
In addition to the modularity score, we also quantitatively compare the NOVER algorithm with the other three algorithms based on a commonly used information-theoretic measure called the Normalized Mutual Information (NMI) score [
12]. The NMI score (0 ... 1) is a quantitative measure of the extent of similarity between the communities detected by any two community detection algorithms. Let
CA and
CB be the sets of communities (identified respectively with indexes
a = 1, ..., |
CA| and
b = 1, ..., |
CB|) detected by two different community detection algorithms A and B on a network graph of
n nodes; let
,
,
be, respectively, the number of vertices in the community of index
a detected by algorithm A, the number of vertices in the community of index
b detected by algorithm B and the number of common vertices in the communities of indexes
a and
b detected by algorithms A and B; then the NMI score for the two algorithms is given by the following formulation:
We use the NMI score as the basis to compare the relative similarity of the communities detected by any two of the four community detection algorithms on each of the nine real-world networks studied in this paper. If the sets of communities detected by two different community detection algorithms are identical, then the NMI score of the two algorithms is 1. Thus, larger the NMI score of two community detection algorithms, the larger is the similarity in the composition of the communities detected by the two algorithms. The results are displayed in
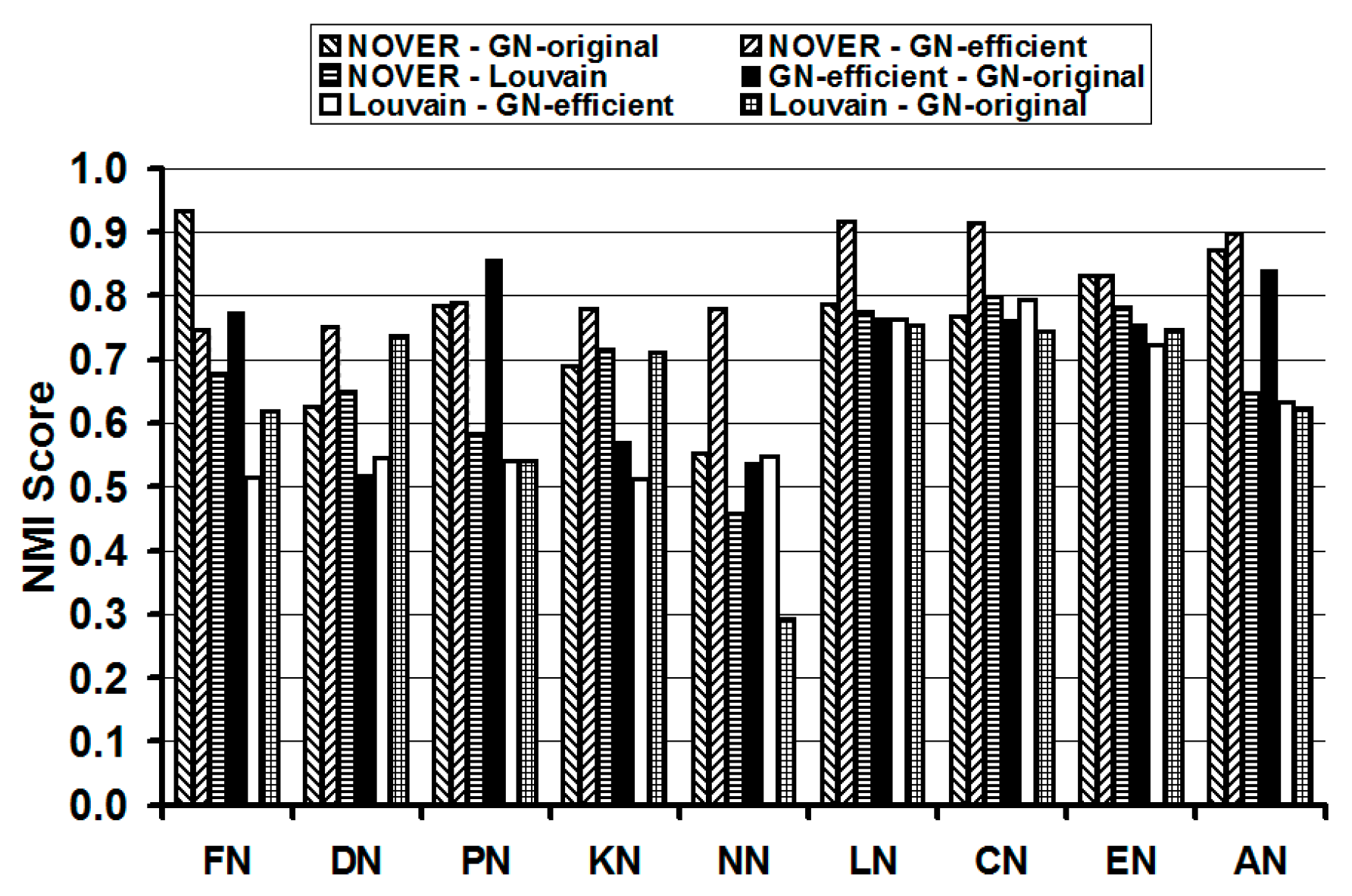
Table 1 and pictorially illustrated in
Figure 13. We color code (the cells in
Table 1 are shaded in gray) the cells corresponding to the pairs of community detection algorithms incurring the top three NMI scores for each real-world network. We observe the NOVER algorithm mutually evaluated with each of the GN-original, GN-efficient and Louvain algorithms to be part of at least two of the top three combinations of the community detection algorithms with larger NMI scores. The NMI values of the NOVER algorithm with each of the other three algorithms are 0.75 or above in 18 of the 27 cells in
Table 1. This indicates that the composition of the communities detected by NOVER algorithm is not vastly different from that of the communities detected by the other three algorithms; but these communities are detected at a much lower execution time (compared to that of the GN-original algorithm) as well as at a relatively higher resolution limit (especially when compared to the communities detected by the Louvain algorithm). The NMI scores of the NOVER-Louvain algorithms are lower than those observed for the NOVER-GN-efficient and NOVER-GN-original algorithms. On this basis, we could say that the composition of the communities detected by NOVER algorithm is relatively more different from that of the Louvain algorithm
vis-à-vis the composition of communities detected by the GN-original and GN-efficient algorithms. For all the nine real-world networks, the NMI scores incurred for NOVER when compared with the GN-efficient algorithm is 0.75 or above. Such a high-level of similarity in the composition of the communities detected by the NOVER and GN-efficient algorithms is also observed in the results displayed in
Figure 9,
Figure 10,
Figure 11 and
Figure 12.
Figure 13.
Illustration of the mutual comparison of the community detection algorithms on real-world Network graphs based on NMI scores.
Figure 13.
Illustration of the mutual comparison of the community detection algorithms on real-world Network graphs based on NMI scores.
Table 1.
A Mutual comparison of the community detection algorithms based on NMI scores.
Table 1.
A Mutual comparison of the community detection algorithms based on NMI scores.
| Network Abbreviation | NOVER-GN-Original | NOVER-GN-Efficient | NOVER-Louvain | GN-Efficient-GN-Original | Louvain-GN-Efficient | Louvain-GN-Original |
|---|
| FN | 0.934 | 0.756 | 0.677 | 0.775 | 0.516 | 0.618 |
| DN | 0.626 | 0.751 | 0.649 | 0.519 | 0.545 | 0.737 |
| PN | 0.785 | 0.789 | 0.583 | 0.859 | 0.541 | 0.540 |
| KN | 0.690 | 0.781 | 0.716 | 0.572 | 0.513 | 0.712 |
| NN | 0.552 | 0.781 | 0.459 | 0.538 | 0.547 | 0.293 |
| LN | 0.786 | 0.918 | 0.776 | 0.766 | 0.763 | 0.754 |
| CN | 0.768 | 0.914 | 0.799 | 0.764 | 0.794 | 0.745 |
| EN | 0.831 | 0.832 | 0.782 | 0.755 | 0.724 | 0.746 |
| AN | 0.873 | 0.899 | 0.647 | 0.841 | 0.633 | 0.624 |
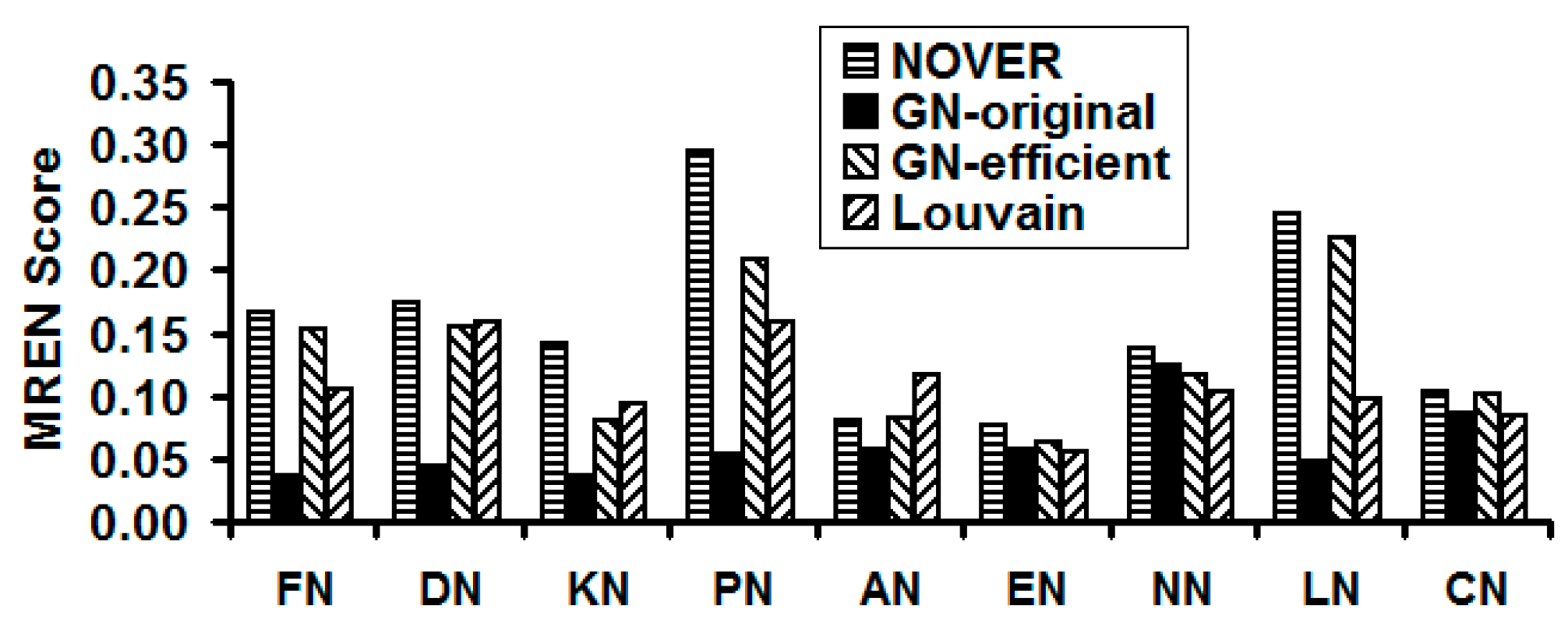
We observe the NOVER algorithm to effectively balance the performance tradeoffs with respect to the cumulative modularity score, execution time and resolution limit. In this pursuit, we observe the MREN score (see
Figure 14) for the NOVER algorithm to be appreciably larger than that of the other three community detection algorithms for eight of the nine real-world networks, except the airport network. The GN-original algorithm incurs the lowest MREN score for eight of the nine real-world networks, except the C. Elegans Neural network (for which we observe the Louvain algorithm to sustain a lower MREN score), attributed to its significantly larger execution time. We propose the MREN score to be a performance measure that is independent of the node size so that we can capture the effectiveness of the community detection algorithms on a comparable globally common scale. For example, in
Figure 14, we observe the MREN scores of the community detection algorithms for the Karate network and the US Airport network to be comparable to each other (even though the two networks are of significantly different sizes).
Figure 14.
Comparison of the MREN scores of the community detection algorithms on real-world Network graphs.
Figure 14.
Comparison of the MREN scores of the community detection algorithms on real-world Network graphs.
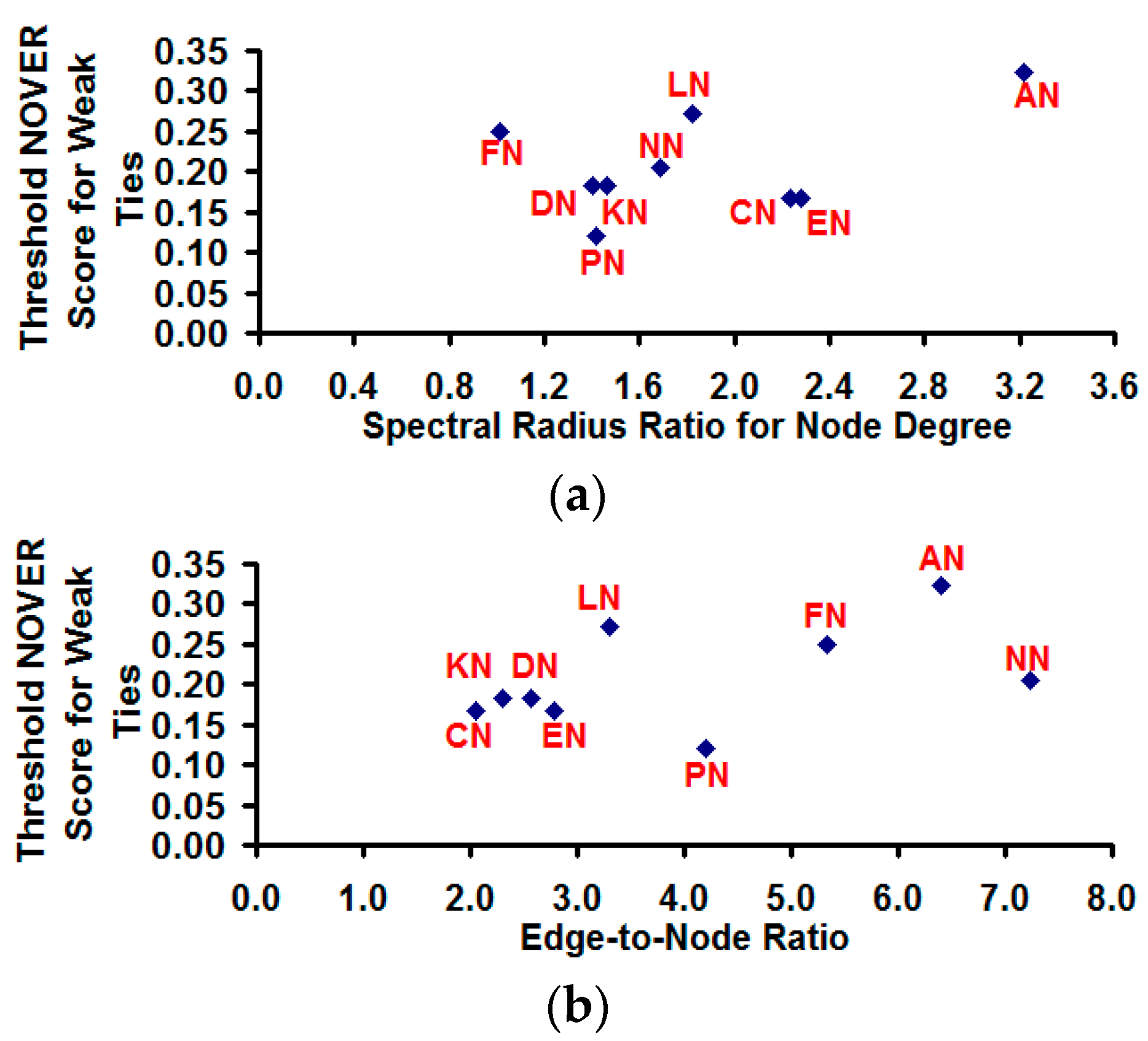
With regards to the threshold NOVER score for community partition, we observe our hypothesis in
Section 2 to be indeed true:
i.e., the threshold NOVER score for classification of edges as weak ties and strong ties for detecting highly modular communities cannot be arbitrarily chosen, and an appropriate value for the threshold NOVER score appears to somewhat depend on the variation in node degree of the vertices as well as on the edge-to-node ratio (see
Figure 15). The overall trend we observe is that the threshold NOVER score is more likely to increase with increase in the spectral radius ratio for node degree (correlation coefficient: 0.44) and with increase in the edge-to-node ratio (correlation coefficient: 0.49).
Figure 15.
Dependence of the threshold NOVER score for weak ties on the spectral radius ratio for node degree and the edge-to-node ratio. (a) Spectral radius ratio for node degree vs. Threshold NOVER score for weak ties; (b) Edge-to-node ratio vs. Threshold NOVER score for weak ties.
Figure 15.
Dependence of the threshold NOVER score for weak ties on the spectral radius ratio for node degree and the edge-to-node ratio. (a) Spectral radius ratio for node degree vs. Threshold NOVER score for weak ties; (b) Edge-to-node ratio vs. Threshold NOVER score for weak ties.
6. Related Work
In this section, we review the related work available in the literature with regards to the use of neighborhood information and edge betweenness for community detection. The importance of using weak ties to analyze relations between disparate groups emanated from the classical work of Granovetter [
27] in which it was observed that the strength of the relationship between any two users in a social network increased with increase in the number of common neighbors. In [
13], it was observed that the NOVER scores of edges (as defined in this paper) connecting two different communities is significantly lower than the NOVER scores of edges within each community. However, the work done in [
13] was just an analytical study of the Facebook network: the NOVER scores were merely computed for the edges and not used as part of a formal algorithm for community detection. Further, as an experimental study, it was stated in [
28] that the average talk time of two users in a telephone network increases with increase in the number of common friends for the two users. All of these support our hypothesis for using edges with low neighborhood overlap as the basis of community detection. If two users had several common neighbors and had a higher neighborhood overlap, then the two users as well as their neighbors belong to one single tightly-knit community. On the other hand, if an edge connecting two users with a lower neighborhood overlap score is removed, it could potentially disconnect the two neighbors from further communication—Indicating that the two nodes belong to two different communities that have relatively fewer edges crossing the two communities, compared to the number of edges within the individual communities.
In [
29], the authors proposed an iterative and hierarchical community detection algorithm that makes use of the neighborhood overlap information of the edges; the idea is to assign each node to a community with which it has strong average aggregated link strength compared to the other communities. Two primary weaknesses of this algorithm are that it partitions a community (to start with all the vertices in the graph are considered to be in one community) into only two communities at a time (irrespective of the modular nature of the network) and assigns the nodes from the original community to one of the two partitions; further the algorithm requires the selection of an appropriate value of a control parameter to stop the partitioning of a community into two communities. On the other hand, our proposed NOVER algorithm does not require the use of any control parameter for its operation; the edges are simply removed in the increasing order of their NOVER values and we observe such a greedy strategy (running at a significantly lower computation time) pays rich dividends by incurring cumulative modularity scores that are only at most 60% of those determined by the Girvan-Newman algorithm for optimal community detection.
With regards to the use of edge betweenness for community detection, several algorithms have been proposed in the literature to detect highly modular communities at a relatively smaller computation time compared to the original Girvan-Newman algorithm for community detection. We discuss some of these algorithms here: In [
10], the authors fix the number of targeted communities (
K) in a network of
N nodes; nodes associated with edges whose betweenness values are lower than (
N/
K) × β (where 0 < β ≤ 1 is a control parameter) are grouped within a community. Tyler
et al. [
8] suggest to run the BFS algorithm on a sample of the vertices (randomly chosen for each iteration) for each edge removal, instead of running the BFS algorithm on all the vertices of the graph in each iteration. Since, we are interested in identifying only the edge with the largest betweenness to be removed in each iteration, the assumption behind the work in [
8] is that as long as the number of samples is sufficiently large, the error introduced due to the random sampling will not make a significant impact on the quality of the partitioning. Radichhi
et al. [
9] observed an inverse correlation between a measure called the edge clustering coefficient and the edge betweenness. The clustering coefficient of an edge (as defined in [
9]) is the ratio of the number of triangles to which the edge belongs to that of the number of triangles that might potentially include it, given the degrees of the adjacent nodes. An edge that has a lower clustering coefficient is likely to be between two communities and an edge that has a higher clustering coefficient is likely to be well-knit within a community. Radicchi
et al. [
9] advocate the removal of an edge with the smallest clustering coefficient per iteration and recalculating the edge clustering coefficient values for each iteration; this is expected to be not that time consuming as that of the procedure to re-compute the edge betweenness values for each iteration.