Data Filtering Based Recursive and Iterative Least Squares Algorithms for Parameter Estimation of Multi-Input Output Systems

Abstract

This paper discusses the parameter estimation problems of multi-input output-error autoregressive (OEAR) systems. By combining the auxiliary model identification idea and the data filtering technique, a data filtering based recursive generalized least squares (F-RGLS) identification algorithm and a data filtering based iterative least squares (F-LSI) identification algorithm are derived. Compared with the F-RGLS algorithm, the proposed F-LSI algorithm is more effective and can generate more accurate parameter estimates. The simulation results confirm this conclusion.

1. Introduction

System modeling and identification of single variable processes have been well studied. However, most industrial processes are multivariable systems [1,2,3], including multiple-input multiple-output (MIMO) systems and multiple-input single-output (MISO) systems. For example, in chemical and process industries, the heat exchangers are MIMO systems, in which the state of a heat exchanger often is represented by four field input variables: the cold inlet temperature, the hot inlet temperature, the cold mass flow and the hot mass flow; the outputs are respectively the cold outlet temperature and hot outlet temperature [4]. In wireless communication systems, the MIMO technology can increase wireless channel capacity and bandwidth by using the multiple antennas without the need of additional power [5]. In computing system technology, the power consumption model for host servers can be identified using a MISO model, in which the system inputs have different forms, such as the rate of the change in the CPU frequency and the rate of the change in the CPU time share, and the system outputs are the changes in power consumption [6]. With the development of the industrial process, the identification of multivariable processes is in great demand. Researchers have studied the problem of identification for multichannel systems from different fields [7,8,9], and many methods have been proposed for multivariable cases [10,11].

Recursive algorithms and iterative algorithms have wide applications in system modeling and system identification [12,13,14]. For example, Wang et al. derived the hierarchical least squares based iterative algorithm for the Box-Jenkins system [15]; and Dehghan and Hajarian presented the iterative method for solving systems of linear matrix equations over reflexive and anti-reflexive matrices [16]. Compared with the recursive identification algorithm, the iterative identification algorithm uses all the measured data to refresh parameter estimation, so the parameter estimation accuracy can be greatly improved, and the iterative identification methods have been successfully applied to many different models [17,18,19].

In the field of system identification, the filtering technique is efficient to improve the computational efficiency [20,21,22], and it has been widely used in parameter estimation of different models [23,24]. Particularly, Basin et al. discussed the parameter estimation for linear stochastic time-delay systems based state filtering [25]; Scarpiniti et al. discussed the identification of Wiener-type nonlinear systems using the adaptive filter [26]; and Wang et al. presented a gradient based iterative algorithm for identification of a class nonlinear systems by filtering the input–output data [27].

This paper combines the filtering technique with the auxiliary model identification idea to estimate parameters of multi-input output error autoregressive (OEAR) systems. By using a linear filter to filter the input-output data, a multi-input OEAR system is transformed into two identification models, and the dimensions of the covariance matrices of the decomposed two models become smaller than that of the original OEAR model. The contributions of this paper are as follows:

• By using the data filtering technique and the auxiliary model identification idea, a data filtering based recursive generalized least squares (F-RGLS) identification algorithm is derived for the multi-input OEAR system.
• A data filtering based iterative least squares (F-LSI) identification algorithm is developed for the multi-input OEAR system.
• The proposed F-LSI identification algorithm updates the parameter estimation by using all of the available data, and can produce highly accurate parameter estimates compared to the F-RGLS identification algorithm.

The rest of this paper is organized as follows: Section 2 gives a description for multi-input OEAR systems. Section 3 gives an F-RGLS algorithm for the multi-input OEAR system by using the data filtering technique. Section 4 derives an F-LSI algorithm by using the data filtering technique and the iterative identification method. Two examples to illustrate the effectiveness of the proposed algorithms are given in Section 5. Finally, Section 6 gives some concluding remarks.

2. The System Description

Consider the following multi-input OEAR system:

$$\begin{array}{ccc}\hfill x_j\left(t\right)& +& a_{j1}{x}_j(t-1)+a_{j2}{x}_j(t-2)+\cdots +a_{j{n}_j}{x}_j(t-n_j)\hfill \\ & =& b_{j1}{u}_j(t-1)+b_{j2}{u}_j(t-2)+\cdots +b_{j{n}_j}{u}_j(t-n_j),\hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill x\left(t\right)& =& \sum _{j=1}^r{x}_j\left(t\right),\hfill \end{array}$$

(2)

$$\begin{array}{ccc}\hfill w\left(t\right)& +& c_{1}w(t-1)+c_{2}w(t-2)+\cdots +c_{n_c}w(t-n_c)=v\left(t\right),\hfill \end{array}$$

(3)

$$\begin{array}{ccc}\hfill y\left(t\right)& =& x\left(t\right)+w\left(t\right),\hfill \end{array}$$

(4)

where $u_j\left(t\right)\in \mathbb{R}$, $j=1,2,\cdots ,r$ are the inputs, $y\left(t\right)\in \mathbb{R}$ is the output, $x\left(t\right)\in \mathbb{R}$ represents the noise-free output, $v\left(t\right)\in \mathbb{R}$ is random white noise with zero mean, and $w\left(t\right)\in \mathbb{R}$ is random colored noise. Assume that the orders $n_j$ and $n_c$ are known, $y\left(t\right)=0$, $u_j\left(t\right)=0$ and $v\left(t\right)=0$ for $t\le 0$. The parameters $a_{ji}$, $b_{ji}$ and $c_i$ are to be identified from input–output data $\{u_j\left(t\right),y\left(t\right),j=1,2,\cdots ,r\}$.

Define the parameter vectors:

$$\begin{array}{ccc}\hfill \mathbf{\theta }& :=& {[{\mathbf{\vartheta }}^{\mathrm{T}},{\mathit{c}}^{\mathrm{T}}]}^{\mathrm{T}}\in {\mathbb{R}}^n,n:=n_0+n_c,\hfill \\ \hfill \mathbf{\vartheta }& :=& {[{\mathbf{\vartheta }}_1^{\mathrm{T}},{\mathbf{\vartheta }}_2^{\mathrm{T}},\cdots ,{\mathbf{\vartheta }}_r^{\mathrm{T}}]}^{\mathrm{T}}\in {\mathbb{R}}^{n_0},n_0:=2n_1+2n_2+\cdots +2n_r,\hfill \\ \hfill \mathit{c}& :=& {[c_1,c_2,\cdots ,c_{n_c}]}^{\mathrm{T}}\in {\mathbb{R}}^{n_c},\hfill \\ \hfill {\mathbf{\vartheta }}_j& :=& {[a_{j1},a_{j2},\cdots ,a_{j{n}_j},b_{j1},b_{j2},\cdots ,b_{j{n}_j}]}^{\mathrm{T}}\in {\mathbb{R}}^{2n_j},\hfill \end{array}$$

and the information vectors as

$$\begin{array}{ccc}\hfill \mathbf{\phi }\left(t\right)& :=& {[{\mathbf{\varphi }}^{\mathrm{T}}\left(t\right),{\mathbf{\psi }}^{\mathrm{T}}\left(t\right)]}^{\mathrm{T}}\in {\mathbb{R}}^n,\hfill \\ \hfill \mathbf{\varphi }\left(t\right)& :=& {[{\mathbf{\varphi }}_1^{\mathrm{T}}\left(t\right),{\mathbf{\varphi }}_2^{\mathrm{T}}\left(t\right),\cdots ,{\mathbf{\varphi }}_r^{\mathrm{T}}\left(t\right)]}^{\mathrm{T}}\in {\mathbb{R}}^{n_0},\hfill \\ \hfill {\mathbf{\varphi }}_j\left(t\right)& :=& {[-x_j(t-1),-x_j(t-2),\cdots ,-x_j(t-n_j),u_j(t-1),u_j(t-2),\cdots ,u_j(t-n_j)]}^{\mathrm{T}}\in {\mathbb{R}}^{2n_j},\hfill \\ \hfill \mathbf{\psi }\left(t\right)& :=& {[-w(t-1),-w(t-2),\cdots ,-w(t-n_c)]}^{\mathrm{T}}\in {\mathbb{R}}^{n_c}.\hfill \end{array}$$

The information vector $\mathbf{\phi }\left(t\right)$ is unknown due to the unmeasured variables $x_j(t-i)$ and $w(t-i)$. By means of the above definitions, Equations (2)–(4) can be expressed as

$$\begin{array}{ccc}\hfill x\left(t\right)& =& \sum _{j=1}^r{x}_j\left(t\right)=\sum _{j=1}^r{\mathbf{\varphi }}_j^{\mathrm{T}}\left(t\right){\mathbf{\vartheta }}_j,\hfill \end{array}$$

(5)

$$\begin{array}{ccc}\hfill w\left(t\right)& =& {\mathbf{\psi }}^{\mathrm{T}}\left(t\right)\mathit{c}+v\left(t\right)=y\left(t\right)-{\mathbf{\varphi }}^{\mathrm{T}}\left(t\right)\mathbf{\vartheta },\hfill \end{array}$$

(6)

$$\begin{array}{ccc}\hfill y\left(t\right)& =& \sum _{j=1}^r{\mathbf{\varphi }}_j^{\mathrm{T}}\left(t\right){\mathbf{\vartheta }}_j+{\mathbf{\psi }}^{\mathrm{T}}\left(t\right)\mathit{c}+v\left(t\right)\hfill \\ & =& {\mathbf{\varphi }}^{\mathrm{T}}\left(t\right)\mathbf{\vartheta }+{\mathbf{\psi }}^{\mathrm{T}}\left(t\right)\mathit{c}+v\left(t\right)\hfill \\ & =& {\mathbf{\phi }}^{\mathrm{T}}\left(t\right)\mathbf{\theta }+v\left(t\right).\hfill \end{array}$$

(7)

Equation (7) is the identification model of the multi-input OEAR system, and the parameter vector $\mathbf{\theta }$ contains all the parameters to be estimated.

3. The Data Filtering Based Recursive Least Squares Algorithm

Define a unit backward shift operator $q^{-1}$ as $q^{-1}u\left(t\right):=u(t-1)$ and a rational function $C\left(q\right):=1+c_1{q}^{-1}+c_2{q}^{-2}+\cdots +c_{n_c}{q}^{-n_c}$. In this section, we use the linear filter $C\left(q\right)$ to filter the input–output data and derive an F-RGLS algorithm.

For the multi-input OEAR system in Equations (1)–(4), we define the filtered input–output data $u_{j\mathrm{f}}\left(t\right)$ and $y_{\mathrm{f}}\left(t\right)$ as

$$\begin{array}{ccc}\hfill u_{j\mathrm{f}}\left(t\right)& :=& C\left(q\right)u_j\left(t\right)=u_j\left(t\right)+c_1{u}_j(t-1)+c_2{u}_j(t-2)+\cdots +c_{n_c}{u}_j(t-n_c),\hfill \end{array}$$

(8)

$$\begin{array}{ccc}\hfill y_{\mathrm{f}}\left(t\right)& :=& C\left(q\right)y\left(t\right)=y\left(t\right)+c_{1}y(t-1)+c_{2}y(t-2)+\cdots +c_{n_c}y(t-n_c).\hfill \end{array}$$

(9)

Multiplying both sides of Equations (1) and (4) by $C\left(q\right)$, we can obtain the following filtered output-error model:

$$\begin{array}{ccc}\hfill y_{\mathrm{f}}\left(t\right)& =& \sum _{j=1}^r{x}_{j\mathrm{f}}\left(t\right)+v\left(t\right):=x_{\mathrm{f}}\left(t\right)+v\left(t\right),\hfill \end{array}$$

(10)

$$\begin{array}{ccc}\hfill x_{j\mathrm{f}}\left(t\right)& =& -\sum _{i=1}^{n_j}{a}_{ji}{x}_{j\mathrm{f}}(t-i)+\sum _{i=1}^{n_j}{b}_{ji}{u}_{j\mathrm{f}}(t-i).\hfill \end{array}$$

(11)

Define the filtered information vectors ${\mathbf{\varphi }}_{\mathrm{f}}\left(t\right)$ and ${\mathbf{\varphi }}_{j\mathrm{f}}\left(t\right)$ as

$$\begin{array}{ccc}\hfill {\mathbf{\varphi }}_{\mathrm{f}}\left(t\right)& :=& {[{\mathbf{\varphi }}_{1\mathrm{f}}^{\mathrm{T}}\left(t\right),{\mathbf{\varphi }}_{2\mathrm{f}}^{\mathrm{T}}\left(t\right),\cdots ,{\mathbf{\varphi }}_{r\mathrm{f}}^{\mathrm{T}}\left(t\right)]}^{\mathrm{T}}\in {\mathbb{R}}^{n_0},\hfill \\ \hfill {\mathbf{\varphi }}_{j\mathrm{f}}\left(t\right)& :=& {[-x_{j\mathrm{f}}(t-1),-x_{j\mathrm{f}}(t-2),\cdots ,-x_{j\mathrm{f}}(t-n_j),u_{j\mathrm{f}}(t-1),u_{j\mathrm{f}}(t-2),\cdots ,u_{j\mathrm{f}}(t-n_j)]}^{\mathrm{T}}\in {\mathbb{R}}^{2n_j}.\hfill \end{array}$$

Equations (10) and (11) can be rewritten as

$$\begin{array}{ccc}\hfill x_{j\mathrm{f}}\left(t\right)& =& {\mathbf{\varphi }}_{j\mathrm{f}}^{\mathrm{T}}\left(t\right){\mathbf{\vartheta }}_j,\hfill \\ \hfill y_{\mathrm{f}}\left(t\right)& =& \sum _{j=1}^r{\mathbf{\varphi }}_{j\mathrm{f}}^{\mathrm{T}}\left(t\right){\mathbf{\vartheta }}_j+v\left(t\right)\hfill \end{array}$$

(12)

$$\begin{array}{ccc}& =& {\mathbf{\varphi }}_{\mathrm{f}}^{\mathrm{T}}\left(t\right)\mathbf{\vartheta }+v\left(t\right).\hfill \end{array}$$

(13)

Taking advantage of the idea in [28] for the filtered identification model in Equation (13), we can get

$$\widehat{\mathbf{\vartheta }}\left(t\right)={\left[\sum _{i=1}^t{\mathbf{\varphi }}_{\mathrm{f}}\left(i\right){\mathbf{\varphi }}_{\mathrm{f}}^{\mathrm{T}}\left(i\right)\right]}^{-1}\sum _{i=1}^t\mathbf{\varphi }\left(i\right)y_{\mathrm{f}}\left(i\right).$$

(14)

Since the information vector ${\mathbf{\varphi }}_{\mathrm{f}}\left(t\right)$ contains the unknown variables $u_{j\mathrm{f}}\left(t\right)$ and $x_{j\mathrm{f}}\left(t\right)$, the algorithm in Equation (14) cannot be applied to estimate $\widehat{\mathbf{\vartheta }}\left(t\right)$ directly. According to the idea in [29], the unknown variables $x_{j\mathrm{f}}\left(t\right)$ are replaced with the outputs of relevant auxiliary model, and the unmeasurable terms $u_{j\mathrm{f}}\left(t\right)$ and $y_{\mathrm{f}}\left(t\right)$ are replaced with their estimates ${\widehat{u}}_{j\mathrm{f}}\left(t\right)$ and ${\widehat{y}}_{\mathrm{f}}\left(t\right)$, respectively. The derivation process is as follows.

Let $\widehat{\mathbf{\vartheta }}\left(t\right)$, $\widehat{\mathit{c}}\left(t\right)$ and ${\widehat{\mathbf{\vartheta }}}_j\left(t\right)$ be the estimates of $\mathbf{\vartheta }$, c and ${\mathbf{\vartheta }}_j$ at time t, respectively. Use the estimates ${\widehat{x}}_j(t-i)$, ${\widehat{x}}_{j\mathrm{f}}(t-i)$ and ${\widehat{u}}_{j\mathrm{f}}(t-i)$ to define the estimates of $\mathbf{\varphi }\left(t\right)$ and ${\mathbf{\varphi }}_{\mathrm{f}}\left(t\right)$ as

$$\begin{array}{ccc}\hfill \widehat{\mathbf{\varphi }}\left(t\right)& :=& {[{\widehat{\mathbf{\varphi }}}_1^{\mathrm{T}}\left(t\right),{\widehat{\mathbf{\varphi }}}_2^{\mathrm{T}}\left(t\right),\cdots ,{\widehat{\mathbf{\varphi }}}_r^{\mathrm{T}}\left(t\right)]}^{\mathrm{T}}\in {\mathbb{R}}^{n_0},\hfill \\ \hfill {\widehat{\mathbf{\varphi }}}_j\left(t\right)& :=& {[-{\widehat{x}}_j(t-1),-{\widehat{x}}_j(t-2),\cdots ,-{\widehat{x}}_j(t-n_j),u_j(t-1),u_j(t-2),\cdots ,u_j(t-n_j)]}^{\mathrm{T}}\in {\mathbb{R}}^{2n_j},\hfill \\ \hfill {\widehat{\mathbf{\varphi }}}_{\mathrm{f}}\left(t\right)& :=& {[{\widehat{\mathbf{\varphi }}}_{1\mathrm{f}}^{\mathrm{T}}\left(t\right),{\widehat{\mathbf{\varphi }}}_{2\mathrm{f}}^{\mathrm{T}}\left(t\right),\cdots ,{\widehat{\mathbf{\varphi }}}_{r\mathrm{f}}^{\mathrm{T}}\left(t\right)]}^{\mathrm{T}}\in {\mathbb{R}}^{n_0},\hfill \\ \hfill {\widehat{\mathbf{\varphi }}}_{j\mathrm{f}}\left(t\right)& :=& {[-{\widehat{x}}_{j\mathrm{f}}(t-1),-{\widehat{x}}_{j\mathrm{f}}(t-2),\cdots ,-{\widehat{x}}_{j\mathrm{f}}(t-n_j),{\widehat{u}}_{j\mathrm{f}}(t-1),{\widehat{u}}_{j\mathrm{f}}(t-2),\cdots ,{\widehat{u}}_{j\mathrm{f}}(t-n_j)]}^{\mathrm{T}}\in {\mathbb{R}}^{2n_j},\hfill \end{array}$$

where the estimates ${\widehat{x}}_j\left(t\right)$ and ${\widehat{x}}_{j\mathrm{f}}\left(t\right)$ can be computed by

$$\begin{array}{c}\hfill {\widehat{x}}_j\left(t\right)={\widehat{\mathbf{\varphi }}}_j^{\mathrm{T}}\left(t\right){\widehat{\mathbf{\vartheta }}}_j\left(t\right),\\ \hfill {\widehat{x}}_{j\mathrm{f}}\left(t\right)={\widehat{\mathbf{\varphi }}}_{j\mathrm{f}}^{\mathrm{T}}\left(t\right){\widehat{\mathbf{\vartheta }}}_j\left(t\right).\end{array}$$

Define the covariance matrix

$${\mathit{P}}_{\mathrm{f}}^{-1}\left(t\right):=\sum _{i=1}^t{\widehat{\mathbf{\varphi }}}_{\mathrm{f}}\left(i\right){\widehat{\mathbf{\varphi }}}_{\mathrm{f}}^{\mathrm{T}}\left(i\right)={\mathit{P}}_{\mathrm{f}}^{-1}(t-1)+{\widehat{\mathbf{\varphi }}}_{\mathrm{f}}\left(i\right){\widehat{\mathbf{\varphi }}}_{\mathrm{f}}^{\mathrm{T}}\left(i\right),$$

(15)

and the gain vector

$${\mathit{L}}_{\mathrm{f}}\left(t\right):={\mathit{P}}_{\mathrm{f}}\left(t\right){\widehat{\mathbf{\varphi }}}_{\mathrm{f}}\left(t\right).$$

Equation (14) can be written as

$$\begin{array}{ccc}\hfill \widehat{\mathbf{\vartheta }}\left(t\right)& =& {\mathit{P}}_{\mathrm{f}}\left(t\right)\sum _{i=1}^t{\widehat{\mathbf{\varphi }}}_{\mathrm{f}}\left(i\right){\widehat{y}}_{\mathrm{f}}\left(i\right)\hfill \\ & =& {\mathit{P}}_{\mathrm{f}}\left(t\right)\left[\sum _{i=1}^{t-1}{\widehat{\mathbf{\varphi }}}_{\mathrm{f}}\left(i\right){\widehat{y}}_{\mathrm{f}}\left(i\right)+{\widehat{\mathbf{\varphi }}}_{\mathrm{f}}\left(t\right){\widehat{y}}_{\mathrm{f}}\left(t\right)\right]\hfill \\ & =& {\mathit{P}}_{\mathrm{f}}\left(t\right)[{\mathit{P}}_{\mathrm{f}}^{-1}(t-1)\widehat{\mathbf{\vartheta }}(t-1)+{\widehat{\mathbf{\varphi }}}_{\mathrm{f}}\left(t\right){\widehat{y}}_{\mathrm{f}}\left(t\right)]\hfill \\ & =& {\mathit{P}}_{\mathrm{f}}\left(t\right)[{\mathit{P}}_{\mathrm{f}}^{-1}(t-1)-{\widehat{\mathbf{\varphi }}}_{\mathrm{f}}\left(t\right){\widehat{\mathbf{\varphi }}}_{\mathrm{f}}^{\mathrm{T}}\left(t\right)]\widehat{\mathbf{\vartheta }}(t-1)+{\mathit{P}}_{\mathrm{f}}\left(t\right){\widehat{\mathbf{\varphi }}}_{\mathrm{f}}\left(t\right){\widehat{y}}_{\mathrm{f}}\left(t\right)\hfill \\ & =& \widehat{\mathbf{\vartheta }}(t-1)+{\mathit{P}}_{\mathrm{f}}\left(t\right){\widehat{\mathbf{\varphi }}}_{\mathrm{f}}\left(t\right)[{\widehat{y}}_{\mathrm{f}}\left(t\right)-{\widehat{\mathbf{\varphi }}}_{\mathrm{f}}^{\mathrm{T}}\left(t\right)\widehat{\mathbf{\vartheta }}(t-1)].\hfill \end{array}$$

Applying the matrix inversion formula ${(\mathit{A}+\mathit{B}\mathit{C})}^{-1}={\mathit{A}}^{-1}-{\mathit{A}}^{-1}\mathit{B}{(\mathit{I}+\mathit{C}{\mathit{A}}^{-1}\mathit{B})}^{-1}\mathit{C}{\mathit{A}}^{-1}$ to Equation (15), we can obtain the following recursive least squares algorithm for estimating $\widehat{\mathbf{\vartheta }}\left(t\right)$:

$$\begin{array}{ccc}\hfill \widehat{\mathbf{\vartheta }}\left(t\right)& =& \widehat{\mathbf{\vartheta }}(t-1)+{\mathit{L}}_{\mathrm{f}}\left(t\right)[y_{\mathrm{f}}\left(t\right)-{\widehat{\mathbf{\varphi }}}_{\mathrm{f}}^{\mathrm{T}}\left(t\right)\widehat{\mathbf{\vartheta }}(t-1)],\hfill \end{array}$$

(16)

$$\begin{array}{ccc}\hfill {\mathit{L}}_{\mathrm{f}}\left(t\right)& =& {\mathit{P}}_{\mathrm{f}}(t-1){\widehat{\mathbf{\varphi }}}_{\mathrm{f}}\left(t\right){[1+{\widehat{\mathbf{\varphi }}}_{\mathrm{f}}^{\mathrm{T}}\left(t\right){\mathit{P}}_{\mathrm{f}}(t-1){\widehat{\mathbf{\varphi }}}_{\mathrm{f}}\left(t\right)]}^{-1},\hfill \end{array}$$

(17)

$$\begin{array}{ccc}\hfill {\mathit{P}}_{\mathrm{f}}\left(t\right)& =& [\mathit{I}-{\mathit{L}}_{\mathrm{f}}\left(t\right){\widehat{\mathbf{\varphi }}}_{\mathrm{f}}^{\mathrm{T}}\left(t\right)]{\mathit{P}}_{\mathrm{f}}(t-1).\hfill \end{array}$$

(18)

Applying the least squares principle to the noise model in Equation (6), we can obtain the following algorithm to estimate the parameter vector c:

$$\begin{array}{ccc}\hfill \widehat{\mathit{c}}\left(t\right)& =& \widehat{\mathit{c}}(t-1)+{\mathit{L}}_{\mathrm{n}}\left(t\right)[w\left(t\right)-{\mathbf{\psi }}^{\mathrm{T}}\left(t\right)\mathit{c}(t-1)],\hfill \end{array}$$

(19)

$$\begin{array}{ccc}\hfill {\mathit{L}}_{\mathrm{n}}\left(t\right)& =& {\mathit{P}}_{\mathrm{n}}(t-1)\mathbf{\psi }\left(t\right){[1+{\mathbf{\psi }}^{\mathrm{T}}\left(t\right){\mathit{P}}_{\mathrm{n}}(t-1)\mathbf{\psi }\left(t\right)]}^{-1},\hfill \end{array}$$

(20)

$$\begin{array}{ccc}\hfill {\mathit{P}}_{\mathrm{n}}\left(t\right)& =& [\mathit{I}-{\mathit{L}}_{\mathrm{n}}\left(t\right){\mathbf{\psi }}^{\mathrm{T}}\left(t\right)]{\mathit{P}}_{\mathrm{n}}(t-1).\hfill \end{array}$$

(21)

The noise information vector $\mathbf{\psi }\left(t\right)$ involves the unknown term $w(t-i)$. From Equations (6) and (7), once the estimate $\widehat{\mathbf{\vartheta }}\left(t\right)$ is obtained, the estimate $\widehat{w}\left(t\right)$ can be computed by

$$\widehat{w}\left(t\right)=y\left(t\right)-{\widehat{\mathbf{\varphi }}}^{\mathrm{T}}\left(t\right)\widehat{\mathbf{\vartheta }}(t-1).$$

Replace the unmeasurable noise terms $w(t-i)$ in $\mathbf{\psi }\left(t\right)$ with estimates $\widehat{w}(t-i)$ and define the estimate of $\mathbf{\psi }\left(t\right)$ as

$$\widehat{\mathbf{\psi }}\left(t\right):=[-\widehat{w}(t-1),-\widehat{w}(t-2),\cdots ,-\widehat{w}(t-n_c)]\in {\mathbb{R}}^{n_c}.$$

Use the estimate $\widehat{\mathit{c}}\left(t\right):={[{\widehat{c}}_1\left(t\right),{\widehat{c}}_2\left(t\right),\cdots ,{\widehat{c}}_{n_c}\left(t\right)]}^{\mathrm{T}}\in {\mathbb{R}}^{n_c}$ to form the estimate of $C\left(q\right)$ as follows:

$$\widehat{C}(t,q):=1+{\widehat{c}}_1\left(t\right)q^{-1}+{\widehat{c}}_2\left(t\right)q^{-2}+\cdots +{\widehat{c}}_{n_c}\left(t\right)q^{-n_c}.$$

The estimates of the filtered input $u_{j\mathrm{f}}\left(t\right)$ and the filtered output $y_{\mathrm{f}}\left(t\right)$ can be computed through

$$\begin{array}{ccc}\hfill {\widehat{u}}_{j\mathrm{f}}\left(t\right)& =& \widehat{C}(t,q)u_j\left(t\right)=u_j\left(t\right)+[u_j(t-1),u_j(t-2),\cdots ,u_j(t-n_c)]\widehat{\mathit{c}}\left(t\right),\hfill \\ \hfill {\widehat{y}}_{\mathrm{f}}\left(t\right)& =& \widehat{C}(t,q)y\left(t\right)=y\left(t\right)+[y(t-1),y(t-2),\cdots ,y(t-n_c)]\widehat{\mathit{c}}\left(t\right).\hfill \end{array}$$

Replacing ${\mathbf{\varphi }}_{\mathrm{f}}\left(t\right)$ and $y_{\mathrm{f}}\left(t\right)$ in Equations (16)–(18) with their estimates ${\widehat{\mathbf{\varphi }}}_{\mathrm{f}}\left(t\right)$ and ${\widehat{y}}_{\mathrm{f}}\left(t\right)$, and replacing $\mathbf{\psi }\left(t\right)$ and $w\left(t\right)$ in Equations (19)–(21) with their estimates $\widehat{\mathbf{\psi }}\left(t\right)$ and $\widehat{w}\left(t\right)$, we can summarize the data filtering based recursive generalized least squares (F-RGLS) algorithm for the multi-input OEAR systems:

$$\begin{array}{ccc}\hfill \widehat{\mathbf{\vartheta }}\left(t\right)& =& \widehat{\mathbf{\vartheta }}(t-1)+{\mathit{L}}_{\mathrm{f}}\left(t\right)[{\widehat{y}}_{\mathrm{f}}\left(t\right)-{\widehat{\mathbf{\varphi }}}_{\mathrm{f}}^{\mathrm{T}}\left(t\right)\widehat{\mathbf{\vartheta }}(t-1)],\hfill \end{array}$$

(22)

$$\begin{array}{ccc}\hfill {\mathit{L}}_{\mathrm{f}}\left(t\right)& =& {\mathit{P}}_{\mathrm{f}}(t-1){\widehat{\mathbf{\varphi }}}_{\mathrm{f}}\left(t\right){[1+{\widehat{\mathbf{\varphi }}}_{\mathrm{f}}^{\mathrm{T}}\left(t\right){\mathit{P}}_{\mathrm{f}}(t-1){\widehat{\mathbf{\varphi }}}_{\mathrm{f}}\left(t\right)]}^{-1},\hfill \end{array}$$

(23)

$$\begin{array}{ccc}\hfill {\mathit{P}}_{\mathrm{f}}\left(t\right)& =& [\mathit{I}-{\mathit{L}}_{\mathrm{f}}\left(t\right){\widehat{\mathbf{\varphi }}}_{\mathrm{f}}^{\mathrm{T}}\left(t\right)]{\mathit{P}}_{\mathrm{f}}(t-1),\hfill \end{array}$$

(24)

$$\begin{array}{ccc}\hfill {\widehat{x}}_{j\mathrm{f}}\left(t\right)& =& {\widehat{\mathbf{\varphi }}}_{j\mathrm{f}}^{\mathrm{T}}\left(t\right){\widehat{\mathbf{\vartheta }}}_j\left(t\right),\hfill \end{array}$$

(25)

$$\begin{array}{ccc}\hfill {\widehat{\mathbf{\varphi }}}_{\mathrm{f}}\left(t\right)& =& {[{\widehat{\mathbf{\varphi }}}_{1\mathrm{f}}^{\mathrm{T}}\left(t\right),{\widehat{\mathbf{\varphi }}}_{2\mathrm{f}}^{\mathrm{T}}\left(t\right),\cdots ,{\widehat{\mathbf{\varphi }}}_{r\mathrm{f}}^{\mathrm{T}}\left(t\right)]}^{\mathrm{T}},\hfill \end{array}$$

(26)

$$\begin{array}{ccc}\hfill {\widehat{\mathbf{\varphi }}}_{j\mathrm{f}}\left(t\right)& =& {[-{\widehat{x}}_{j\mathrm{f}}(t-1),-{\widehat{x}}_{j\mathrm{f}}(t-2),\cdots ,-{\widehat{x}}_{j\mathrm{f}}(t-n_j),{\widehat{u}}_{j\mathrm{f}}(t-1),{\widehat{u}}_{j\mathrm{f}}(t-2),\cdots ,{\widehat{u}}_{j\mathrm{f}}(t-n_j)]}^{\mathrm{T}},\hfill \end{array}$$

(27)

$$\begin{array}{ccc}\hfill {\widehat{u}}_{j\mathrm{f}}\left(t\right)& =& u_j\left(t\right)+{\widehat{c}}_1\left(t\right)u_j(t-1)+{\widehat{c}}_2\left(t\right)u_j(t-2)+\cdots +{\widehat{c}}_{n_c}\left(t\right)u_j(t-n_c),\hfill \end{array}$$

(28)

$$\begin{array}{ccc}\hfill {\widehat{y}}_{\mathrm{f}}\left(t\right)& =& y\left(t\right)+{\widehat{c}}_1\left(t\right)y(t-1)+{\widehat{c}}_2\left(t\right)y(t-2)+\cdots +{\widehat{c}}_{n_c}\left(t\right)y(t-n_c),\hfill \end{array}$$

(29)

$$\begin{array}{ccc}\hfill \widehat{\mathit{c}}\left(t\right)& =& \widehat{\mathit{c}}(t-1)+{\mathit{L}}_{\mathrm{n}}\left(t\right)[\widehat{w}\left(t\right)-{\widehat{\mathbf{\psi }}}^{\mathrm{T}}\left(t\right)\widehat{\mathit{c}}(t-1)],\hfill \end{array}$$

(30)

$$\begin{array}{ccc}\hfill {\mathit{L}}_{\mathrm{n}}\left(t\right)& =& {\mathit{P}}_{\mathrm{n}}(t-1)\widehat{\mathbf{\psi }}\left(t\right){[1+{\widehat{\mathbf{\psi }}}^{\mathrm{T}}\left(t\right){\mathit{P}}_{\mathrm{n}}(t-1)\widehat{\mathbf{\psi }}\left(t\right)]}^{-1},\hfill \end{array}$$

(31)

$$\begin{array}{ccc}\hfill {\mathit{P}}_{\mathrm{n}}\left(t\right)& =& [\mathit{I}-{\mathit{L}}_{\mathrm{n}}\left(t\right){\widehat{\mathbf{\psi }}}^{\mathrm{T}}\left(t\right)]{\mathit{P}}_{\mathrm{n}}(t-1),\hfill \end{array}$$

(32)

$$\begin{array}{ccc}\hfill \widehat{w}\left(t\right)& =& y\left(t\right)-{\widehat{\mathbf{\varphi }}}^{\mathrm{T}}\left(t\right)\widehat{\mathbf{\vartheta }}(t-1),\hfill \end{array}$$

(33)

$$\begin{array}{ccc}\hfill {\widehat{x}}_j\left(t\right)& =& {\widehat{\mathbf{\varphi }}}_j^{\mathrm{T}}\left(t\right){\widehat{\mathbf{\vartheta }}}_j\left(t\right),\hfill \end{array}$$

(34)

$$\begin{array}{ccc}\hfill \widehat{\mathbf{\varphi }}\left(t\right)& =& {[{\widehat{\mathbf{\varphi }}}_1^{\mathrm{T}}\left(t\right),{\widehat{\mathbf{\varphi }}}_2^{\mathrm{T}}\left(t\right),\cdots ,{\widehat{\mathbf{\varphi }}}_r^{\mathrm{T}}\left(t\right)]}^{\mathrm{T}},\hfill \end{array}$$

(35)

$$\begin{array}{ccc}\hfill {\widehat{\mathbf{\varphi }}}_j\left(t\right)& =& {[-{\widehat{x}}_j(t-1),-{\widehat{x}}_j(t-2),\cdots ,-{\widehat{x}}_j(t-n_j),u_j(t-1),u_j(t-2),\cdots ,u_j(t-n_j)]}^{\mathrm{T}},\hfill \end{array}$$

(36)

$$\begin{array}{ccc}\hfill \widehat{\mathbf{\psi }}\left(t\right)& =& {[-\widehat{w}(t-1),-\widehat{w}(t-2),\cdots ,-\widehat{w}(t-n_c)]}^{\mathrm{T}},\hfill \end{array}$$

(37)

$$\begin{array}{ccc}\hfill \widehat{\mathbf{\vartheta }}\left(t\right)& =& {[{\widehat{\mathbf{\vartheta }}}_1^{\mathrm{T}}\left(t\right),{\widehat{\mathbf{\vartheta }}}_2^{\mathrm{T}}\left(t\right),\cdots ,{\widehat{\mathbf{\vartheta }}}_r^{\mathrm{T}}\left(t\right)]}^{\mathrm{T}},\hfill \end{array}$$

(38)

$$\begin{array}{ccc}\hfill {\widehat{\mathbf{\vartheta }}}_j\left(t\right)& =& {[{\widehat{a}}_{j1}\left(t\right),{\widehat{a}}_{j2}\left(t\right),\cdots ,{\widehat{a}}_{j{n}_j}\left(t\right),{\widehat{b}}_{j1}\left(t\right),{\widehat{b}}_{j2}\left(t\right),\cdots ,{\widehat{b}}_{j{n}_j}\left(t\right)]}^{\mathrm{T}},\hfill \end{array}$$

(39)

$$\begin{array}{ccc}\hfill \widehat{\mathit{c}}\left(t\right)& =& {[{\widehat{c}}_1\left(t\right),{\widehat{c}}_2\left(t\right),\cdots ,{\widehat{c}}_{n_c}\left(t\right)]}^{\mathrm{T}}.\hfill \end{array}$$

(40)

The F-RGLS estimation algorithm involves two steps: the parameter identification of the system model—see Equations (22)–(29)—and the parameter identification of the noise model—see Equations (30)–(37). The F-RGLS algorithm can generate the parameter estimation of the multi-input OEAR system; however, the algorithm uses only the measured data $\{u_j\left(i\right),y\left(i\right):i=0,1,2,\cdots ,t\}$ up to time t, not including the data $\left\{u\right(i),y(i):i=t+1,t+2,\cdots ,L\}$. Next, we will make full use of all the measured data to improve the parameter estimation accuracy by adopting the iterative identification approach.

4. The Data Filtering Based Iterative Least Squares Algorithm

Suppose that the data length $L\gg n_0+n_c$. Based on the identification models in Equations (6) and (13), we define two quadratic criterion functions

$$\begin{array}{ccc}\hfill J_1\left(\mathbf{\vartheta }\right)& :=& \sum _{t=1}^L{[y_{\mathrm{f}}\left(t\right)-{\mathbf{\varphi }}_{\mathrm{f}}^{\mathrm{T}}\left(t\right)\mathbf{\vartheta }]}^2,\hfill \\ \hfill J_2\left(\mathit{c}\right)& :=& \sum _{t=1}^L{[w\left(t\right)-{\mathbf{\psi }}^{\mathrm{T}}\left(t\right)\mathit{c}]}^2.\hfill \end{array}$$

Minimizing the above two quadratic criterion functions, we can obtain the estimation algorithm of computing $\widehat{\mathbf{\vartheta }}\left(t\right)$ and $\widehat{\mathit{c}}\left(t\right)$:

$$\begin{array}{ccc}\hfill \widehat{\mathbf{\vartheta }}\left(t\right)& =& {\left[\sum _{t=1}^L{\mathbf{\varphi }}_{\mathrm{f}}\left(t\right){\mathbf{\varphi }}_{\mathrm{f}}^{\mathrm{T}}\left(t\right)\right]}^{-1}\sum _{t=1}^L{\mathbf{\varphi }}_{\mathrm{f}}\left(t\right)y_{\mathrm{f}}\left(t\right),\hfill \end{array}$$

(41)

$$\begin{array}{ccc}\hfill \widehat{\mathit{c}}\left(t\right)& =& {\left[\sum _{t=1}^L\mathbf{\psi }\left(t\right){\mathbf{\psi }}^{\mathrm{T}}\left(t\right)\right]}^{-1}\sum _{t=1}^L\mathbf{\psi }\left(t\right)w\left(t\right).\hfill \end{array}$$

(42)

Because the vectors ${\mathbf{\varphi }}_{\mathrm{f}}\left(t\right)$ and $\mathbf{\psi }\left(t\right)$ are unknown, the parameter estimates $\widehat{\mathbf{\vartheta }}\left(t\right)$ and $\widehat{\mathit{c}}\left(t\right)$ cannot be computed directly. Here, we adopt the iterative estimation theory. Let $k=1,2,3,\cdots$ be an iterative variable, ${\widehat{\mathbf{\vartheta }}}_k$ and ${\widehat{\mathit{c}}}_k$ denote the iterative estimates of $\mathbf{\vartheta }$ and c at iteration k. Let ${\widehat{x}}_{j,k}\left(t\right)$ and ${\widehat{w}}_k\left(t\right)$ be the estimates of $x_j\left(t\right)$ and $w\left(t\right)$ at iteration k. Replacing ${\mathbf{\varphi }}_j\left(t\right)$ and ${\mathbf{\vartheta }}_j$ in Equation (5) with their estimates ${\widehat{\mathbf{\varphi }}}_{j,k}\left(t\right)$ and ${\widehat{\mathbf{\vartheta }}}_{j,k}$ at iteration k, $\mathbf{\varphi }\left(t\right)$ and $\mathbf{\vartheta }$ in Equation (6) with their estimates ${\widehat{\mathbf{\varphi }}}_k\left(t\right)$ at iteration k and the ${\widehat{\mathbf{\vartheta }}}_{k-1}$ at iteration $k-1$, the estimate ${\widehat{x}}_{j,k}\left(t\right)$ and ${\widehat{w}}_k\left(t\right)$ can be calculated by

$$\begin{array}{ccc}\hfill {\widehat{x}}_{j,k}\left(t\right)& =& {\widehat{\mathbf{\varphi }}}_{j,k}^{\mathrm{T}}\left(t\right){\widehat{\mathbf{\vartheta }}}_{j,k},\hfill \end{array}$$

(43)

$$\begin{array}{ccc}\hfill {\widehat{w}}_k\left(t\right)& =& y\left(t\right)-{\widehat{\mathbf{\varphi }}}_k^{\mathrm{T}}\left(t\right){\widehat{\mathbf{\vartheta }}}_{k-1}.\hfill \end{array}$$

(44)

Replacing $x_j(t-i)$ in ${\mathbf{\varphi }}_j\left(t\right)$ with ${\widehat{x}}_{j,k-1}(t-i)$, $w(t-i)$ in $\mathbf{\psi }\left(t\right)$ with ${\widehat{w}}_{k-1}(t-i)$, the estimates ${\widehat{\mathbf{\varphi }}}_k\left(t\right)$, ${\widehat{\mathbf{\varphi }}}_{j,k}\left(t\right)$ and ${\widehat{\mathbf{\psi }}}_k\left(t\right)$ can be obtained by

$$\begin{array}{ccc}\hfill {\widehat{\mathbf{\varphi }}}_k\left(t\right)& =& {[{\widehat{\mathbf{\varphi }}}_{1,k}^{\mathrm{T}}\left(t\right),{\widehat{\mathbf{\varphi }}}_{2,k}^{\mathrm{T}}\left(t\right),\cdots ,{\widehat{\mathbf{\varphi }}}_{r,k}^{\mathrm{T}}\left(t\right)]}^{\mathrm{T}},\hfill \end{array}$$

(45)

$$\begin{array}{ccc}\hfill {\widehat{\mathbf{\varphi }}}_{j,k}\left(t\right)& =& {[-{\widehat{x}}_{j,k-1}(t-1),\cdots ,-{\widehat{x}}_{j,k-1}(t-n_j),u_j(t-1),\cdots ,u_j(t-n_j)]}^{\mathrm{T}},\hfill \end{array}$$

(46)

$$\begin{array}{ccc}\hfill {\widehat{\mathbf{\psi }}}_k\left(t\right)& =& {[-{\widehat{w}}_{k-1}(t-1),-{\widehat{w}}_{k-1}(t-2),\cdots ,-{\widehat{w}}_{k-1}(t-n_c)]}^{\mathrm{T}}.\hfill \end{array}$$

(47)

Using the parameter estimate ${\widehat{\mathit{c}}}_k={[{\widehat{c}}_{1,k},{\widehat{c}}_{2,k},\cdots ,{\widehat{c}}_{n_c,k}]}^{\mathrm{T}}$ to form the estimate of $C\left(q\right)$ at iteration k:

$${\widehat{C}}_k\left(q\right):=1+{\widehat{c}}_{1,k}{q}^{-1}+{\widehat{c}}_{2,k}{q}^{-2}+\cdots +{\widehat{c}}_{n_c,k}{q}^{-n_c}.$$

Filtering the input–output data $u_j\left(t\right)$ and $y\left(t\right)$ by ${\widehat{C}}_k\left(q\right)$, we can obtain the estimates of $u_{j\mathrm{f}}\left(t\right)$ and $y_{\mathrm{f}}\left(t\right)$

$$\begin{array}{ccc}\hfill {\widehat{u}}_{j\mathrm{f},k}\left(t\right)& =& {\widehat{C}}_k\left(q\right)u_j\left(t\right)=u_j\left(t\right)+[u_j(t-1),u_j(t-2),\cdots ,u_j(t-n_c)]{\widehat{\mathit{c}}}_k,\hfill \end{array}$$

(48)

$$\begin{array}{ccc}\hfill {\widehat{y}}_{\mathrm{f},k}\left(t\right)& =& {\widehat{C}}_k\left(q\right)y\left(t\right)=y\left(t\right)+[y(t-1),y(t-2),\cdots ,y(t-n_c)]{\widehat{\mathit{c}}}_k.\hfill \end{array}$$

(49)

Let ${\widehat{x}}_{j\mathrm{f},k}\left(t\right)$ be the estimate of $x_{j\mathrm{f}}\left(t\right)$ at iteration k, replacing ${\mathbf{\varphi }}_{j\mathrm{f}}\left(t\right)$ and ${\mathbf{\vartheta }}_j$ in Equation (12) with their estimates ${\widehat{\mathbf{\varphi }}}_{j\mathrm{f},k}\left(t\right)$ and ${\widehat{\mathbf{\vartheta }}}_{j,k}$ at iteration k, the estimate ${\widehat{x}}_{j\mathrm{f},k}\left(t\right)$ can be computed by

$${\widehat{x}}_{j\mathrm{f},k}\left(t\right)={\widehat{\mathbf{\varphi }}}_{j\mathrm{f},k}^{\mathrm{T}}\left(t\right){\widehat{\mathbf{\vartheta }}}_{j,k}.$$

(50)

Replacing $x_{j\mathrm{f}}(t-i)$ and $u_{j\mathrm{f}}(t-i)$ in ${\mathbf{\varphi }}_{j\mathrm{f}}\left(t\right)$ with their estimates ${\widehat{x}}_{j\mathrm{f},k-1}(t-i)$ at iteration $k-1$ and ${\widehat{u}}_{j\mathrm{f},k}(t-i)$ at iteration k, we can obtain the estimates:

$$\begin{array}{ccc}\hfill {\widehat{\mathbf{\varphi }}}_{\mathrm{f},k}\left(t\right)& =& {[{\widehat{\mathbf{\varphi }}}_{1\mathrm{f},k}^{\mathrm{T}}\left(t\right),{\widehat{\mathbf{\varphi }}}_{2\mathrm{f},k}^{\mathrm{T}}\left(t\right),\cdots ,{\widehat{\mathbf{\varphi }}}_{r\mathrm{f},k}^{\mathrm{T}}\left(t\right)]}^{\mathrm{T}},\hfill \end{array}$$

(51)

$$\begin{array}{ccc}\hfill {\widehat{\mathbf{\varphi }}}_{j\mathrm{f},k}\left(t\right)& =& {[-{\widehat{x}}_{j\mathrm{f},k-1}(t-1),\cdots ,-{\widehat{x}}_{j\mathrm{f},k-1}(t-n_j),{\widehat{u}}_{j\mathrm{f},k}(t-1),\cdots ,{\widehat{u}}_{j\mathrm{f},k}(t-n_j)]}^{\mathrm{T}}.\hfill \end{array}$$

(52)

Replacing ${\mathbf{\varphi }}_{\mathrm{f}}\left(t\right)$ and $y_{\mathrm{f}}\left(t\right)$ in Equation (41) with their estimates ${\widehat{\mathbf{\varphi }}}_{\mathrm{f},k}\left(t\right)$ and ${\widehat{y}}_{\mathrm{f},k}\left(t\right)$, and replacing $\mathbf{\psi }\left(t\right)$ and $w\left(t\right)$ in Equation (42) with their estimates ${\widehat{\mathbf{\psi }}}_k\left(t\right)$ and ${\widehat{w}}_k\left(t\right)$, we can obtain the data filtering based iterative least squares (F-LSI) algorithm of estimating the parameter vectors $\mathbf{\vartheta }$ and c:

$$\begin{array}{ccc}\hfill {\widehat{\mathbf{\vartheta }}}_k& =& {\left[\sum _{t=1}^L{\widehat{\mathbf{\varphi }}}_{\mathrm{f},k}\left(t\right){\widehat{\mathbf{\varphi }}}_{\mathrm{f},k}^{\mathrm{T}}\left(t\right)\right]}^{-1}\sum _{t=1}^L{\widehat{\mathbf{\varphi }}}_{\mathrm{f},k}\left(t\right){\widehat{y}}_{\mathrm{f},k}\left(t\right),k=1,2,3,\cdots \hfill \end{array}$$

(53)

$$\begin{array}{ccc}\hfill {\widehat{\mathit{c}}}_k& =& {\left[\sum _{t=1}^L{\widehat{\mathbf{\psi }}}_k\left(t\right){\widehat{\mathbf{\psi }}}_k^{\mathrm{T}}\left(t\right)\right]}^{-1}\sum _{t=1}^L{\widehat{\mathbf{\psi }}}_k\left(t\right){\widehat{w}}_k\left(t\right).\hfill \end{array}$$

(54)

From Equations (43)–(54), we can summarize the F-LSI algorithm as follows:

$$\begin{array}{ccc}\hfill {\widehat{\mathbf{\vartheta }}}_k& =& {\left[\sum _{t=1}^L{\widehat{\mathbf{\varphi }}}_{\mathrm{f},k}\left(t\right){\widehat{\mathbf{\varphi }}}_{\mathrm{f},k}^{\mathrm{T}}\left(t\right)\right]}^{-1}\sum _{t=1}^L{\widehat{\mathbf{\varphi }}}_{\mathrm{f},k}\left(t\right){\widehat{y}}_{\mathrm{f},k}\left(t\right),k=1,2,3,\cdots \hfill \end{array}$$

(55)

$$\begin{array}{ccc}\hfill {\widehat{\mathbf{\varphi }}}_{\mathrm{f},k}\left(t\right)& =& {[{\widehat{\mathbf{\varphi }}}_{1\mathrm{f},k}^{\mathrm{T}}\left(t\right),{\widehat{\mathbf{\varphi }}}_{2\mathrm{f},k}^{\mathrm{T}}\left(t\right),\cdots ,{\widehat{\mathbf{\varphi }}}_{r\mathrm{f},k}^{\mathrm{T}}\left(t\right)]}^{\mathrm{T}},\hfill \end{array}$$

(56)

$$\begin{array}{ccc}\hfill {\widehat{\mathbf{\varphi }}}_{j\mathrm{f},k}\left(t\right)& =& {[-{\widehat{x}}_{j\mathrm{f},k-1}(t-1),\cdots ,-{\widehat{x}}_{j\mathrm{f},k-1}(t-n_j),{\widehat{u}}_{j\mathrm{f},k}(t-1),\cdots ,{\widehat{u}}_{j\mathrm{f},k}(t-n_j)]}^{\mathrm{T}},\hfill \end{array}$$

(57)

$$\begin{array}{ccc}\hfill {\widehat{u}}_{j\mathrm{f},k}\left(t\right)& =& u_j\left(t\right)+{\widehat{c}}_{1,k}{u}_j(t-1)+{\widehat{c}}_{2,k}{u}_j(t-2)+\cdots +{\widehat{c}}_{n_c,k}{u}_j(t-n_c),\hfill \end{array}$$

(58)

$$\begin{array}{ccc}\hfill {\widehat{y}}_{\mathrm{f},k}\left(t\right)& =& y\left(t\right)+{\widehat{c}}_{1,k}y(t-1)+{\widehat{c}}_{2,k}y(t-2)+\cdots +{\widehat{c}}_{n_c,k}y(t-n_c),\hfill \end{array}$$

(59)

$$\begin{array}{ccc}\hfill {\widehat{x}}_{j\mathrm{f},k}\left(t\right)& =& {\widehat{\mathbf{\varphi }}}_{j\mathrm{f},k}^{\mathrm{T}}\left(t\right){\widehat{\mathbf{\vartheta }}}_{j,k},\hfill \end{array}$$

(60)

$$\begin{array}{ccc}\hfill {\widehat{\mathit{c}}}_k& =& {\left[\sum _{t=1}^L{\widehat{\mathbf{\psi }}}_k\left(t\right){\widehat{\mathbf{\psi }}}_k^{\mathrm{T}}\left(t\right)\right]}^{-1}\sum _{t=1}^L{\widehat{\mathbf{\psi }}}_k\left(t\right){\widehat{w}}_k\left(t\right),\hfill \end{array}$$

(61)

$$\begin{array}{ccc}\hfill {\widehat{\mathbf{\psi }}}_k\left(t\right)& =& {[-{\widehat{w}}_{k-1}(t-1),-{\widehat{w}}_{k-1}(t-2),\cdots ,-{\widehat{w}}_{k-1}(t-n_c)]}^{\mathrm{T}},\hfill \end{array}$$

(62)

$$\begin{array}{ccc}\hfill {\widehat{\mathbf{\varphi }}}_k\left(t\right)& =& {[{\widehat{\mathbf{\varphi }}}_{1,k}^{\mathrm{T}}\left(t\right),{\widehat{\mathbf{\varphi }}}_{2,k}^{\mathrm{T}}\left(t\right),\cdots ,{\widehat{\mathbf{\varphi }}}_{r,k}^{\mathrm{T}}\left(t\right)]}^{\mathrm{T}},\hfill \end{array}$$

(63)

$$\begin{array}{ccc}\hfill {\widehat{\mathbf{\varphi }}}_{j,k}\left(t\right)& =& {[-{\widehat{x}}_{j,k-1}(t-1),\cdots ,-{\widehat{x}}_{j,k-1}(t-n_j),u_j(t-1),\cdots ,u_j(t-n_j)]}^{\mathrm{T}},\hfill \end{array}$$

(64)

$$\begin{array}{ccc}\hfill {\widehat{x}}_{j,k}\left(t\right)& =& {\widehat{\mathbf{\varphi }}}_{j,k}^{\mathrm{T}}\left(t\right){\widehat{\mathbf{\vartheta }}}_{j,k},\hfill \end{array}$$

(65)

$$\begin{array}{ccc}\hfill {\widehat{w}}_k\left(t\right)& =& y\left(t\right)-{\widehat{\mathbf{\varphi }}}_k^{\mathrm{T}}\left(t\right){\widehat{\mathbf{\vartheta }}}_{k-1},\hfill \end{array}$$

(66)

$$\begin{array}{ccc}\hfill {\widehat{\mathbf{\vartheta }}}_k& =& {[{\widehat{\mathbf{\vartheta }}}_{1,k}^{\mathrm{T}},{\widehat{\mathbf{\vartheta }}}_{2,k}^{\mathrm{T}},\cdots ,{\widehat{\mathbf{\vartheta }}}_{r,k}^{\mathrm{T}}]}^{\mathrm{T}},\hfill \end{array}$$

(67)

$$\begin{array}{ccc}\hfill {\widehat{\mathbf{\vartheta }}}_{j,k}& =& {[{\widehat{a}}_{j1,k},{\widehat{a}}_{j2,k},\cdots ,{\widehat{a}}_{j{n}_j,k},{\widehat{b}}_{j1,k},{\widehat{b}}_{j2,k},\cdots ,{\widehat{b}}_{j{n}_j,k}]}^{\mathrm{T}},\hfill \end{array}$$

(68)

$$\begin{array}{ccc}\hfill {\widehat{\mathit{c}}}_k& =& {[{\widehat{\mathit{c}}}_{1,k},{\widehat{\mathit{c}}}_{2,k},\cdots ,{\widehat{\mathit{c}}}_{n_c,k}]}^{\mathrm{T}}.\hfill \end{array}$$

(69)

We list the steps for computing the estimates ${\widehat{\mathbf{\vartheta }}}_k$ and ${\widehat{\mathit{c}}}_k$ as iteration k increases:

• To initialize, let $k=1$, ${\widehat{x}}_{j\mathrm{f},0}\left(t\right)=1/p_0$, ${\widehat{u}}_{j\mathrm{f},0}\left(t\right)=1/p_0$, ${\widehat{y}}_{\mathrm{f},0}\left(t\right)=1/p_0$, ${\widehat{x}}_{j,0}\left(t\right)=1/p_0$, ${\widehat{w}}_0\left(t\right)=1/p_0$, $p_0={10}^6$.
• Collect the input–output data $\{u_1\left(t\right),u_2\left(t\right),\cdots ,u_r\left(t\right),y\left(t\right)$: $t=1,2,\cdots ,L\}$.
• Form ${\widehat{\mathbf{\varphi }}}_{j,k}\left(t\right)$ by Equation (64), ${\widehat{\mathbf{\varphi }}}_k\left(t\right)$ by Equation (63), and ${\widehat{\mathbf{\psi }}}_k\left(t\right)$ by Equation (62).
• Compute ${\widehat{w}}_k\left(t\right)$ by Equation (66), update the parameter estimate ${\widehat{\mathit{c}}}_k$ by Equation (61).
• Read ${\widehat{\mathit{c}}}_k$ by Equation (69), compute ${\widehat{u}}_{j\mathrm{f},k}\left(t\right)$ and ${\widehat{y}}_{\mathrm{f},k}\left(t\right)$ by Equations (58) and (59).
• Form ${\widehat{\mathbf{\varphi }}}_{\mathrm{f},k}\left(t\right)$ and ${\widehat{\mathbf{\varphi }}}_{j\mathrm{f},k}\left(t\right)$ by Equations (56) and (57), update the parameter estimate ${\widehat{\mathbf{\vartheta }}}_k$ by Equation (55).
• Read ${\widehat{\mathbf{\vartheta }}}_{j,k}$ by Equation (68), compute ${\widehat{x}}_{j\mathrm{f},k}\left(t\right)$ and ${\widehat{x}}_{j,k}\left(t\right)$ by Equations (60) and (65).
• Give a small positive ε, compare ${\widehat{\mathbf{\theta }}}_k=\left[\begin{array}{c}{\widehat{\mathbf{\vartheta }}}_k\\ {\widehat{\mathit{c}}}_k\end{array}\right]$ with ${\widehat{\mathbf{\theta }}}_{k-1}$, if $\parallel {\widehat{\mathbf{\theta }}}_k-{\widehat{\mathbf{\theta }}}_{k-1}\parallel \le \epsilon$, obtain the iterative time k and the parameter estimate ${\widehat{\mathbf{\theta }}}_k$, increase k by 1 and go to Step 2; otherwise, increase k by 1 and go to Step 3.

Remark: 

The computational complexity implies the computational amount of multiplications and adds in the algorithm, depending on the sizes and lengths.

5. Examples

Example 1: 

Consider the following multi-input OEAR system:

$$\begin{array}{ccc}\hfill x_1\left(t\right)& +& a_{11}{x}_1(t-1)+a_{12}{x}_1(t-2)=b_{11}{u}_1(t-1)+b_{12}{u}_1(t-2),\hfill \end{array}$$

(70)

$$\begin{array}{ccc}\hfill x_2\left(t\right)& +& a_{21}{x}_2(t-1)+a_{22}{x}_2(t-2)=b_{21}{u}_2(t-1)+b_{22}{u}_2(t-2),\hfill \end{array}$$

(71)

$$\begin{array}{ccc}\hfill w\left(t\right)& +& c_{1}w(t-1)=v\left(t\right),\hfill \end{array}$$

(72)

$$\begin{array}{ccc}\hfill y\left(t\right)& =& x_1\left(t\right)+x_2\left(t\right)+w\left(t\right).\hfill \end{array}$$

(73)

The parameter vector to be estimated is

$$\begin{array}{ccc}\hfill \mathbf{\theta }& =& {[a_{11},a_{12},b_{11},b_{12},a_{21},a_{22},b_{21},b_{22},c_1]}^{\mathrm{T}}\hfill \\ & =& {[0.15,0.25,0.99,-0.78,-0.10,0.35,-0.50,-0.80,0.20]}^{\mathrm{T}}.\hfill \end{array}$$

The inputs $\{u_1\left(t\right),u_2\left(t\right)\}$ are taken as two persistent excitation signal sequences with zero mean and unit variance, and $\left\{v\right(t\left)\right\}$ as a white noise sequence with zero mean and variance ${\sigma }^2=0.{20}^2$ and ${\sigma }^2=0.{60}^2$.

Applying the F-RGLS algorithm to estimate the parameters of this example system, the parameter estimates and their estimation errors $\delta :=\parallel \widehat{\mathbf{\theta }}\left(t\right)-\mathbf{\theta }\parallel /\parallel \mathbf{\theta }\parallel$ are shown in Table 1. Applying the F-LSI algorithm to estimate the parameters of this example system, when the data length $L=2000$ the parameter estimates and their estimation errors $\delta :=\parallel {\widehat{\mathbf{\theta }}}_k-\mathbf{\theta }\parallel /\parallel \mathbf{\theta }\parallel$ are shown in Table 2 with different noise variances. When the data length $L=4000$, the parameter estimates and their errors δ are shown in Table 3 with different noise variances. Under different noise variances and different data lengths, the parameter estimates and their errors δ are shown in Table 4 when the iteration $k=10$. Under different noise variances, the parameter estimation errors δ versus k are shown in Figure 1.

Table 1. The F-RGLS estimates and their errors for Example 1.

${\mathbf{\sigma }}^{\mathbf{2}}$	$\mathit{t}\mathbf{=}\mathit{L}$	${\mathit{a}}_{\mathbf{11}}$	${\mathit{a}}_{\mathbf{12}}$	${\mathit{b}}_{\mathbf{11}}$	${\mathit{b}}_{\mathbf{12}}$	${\mathit{a}}_{\mathbf{21}}$	${\mathit{a}}_{\mathbf{22}}$	${\mathit{b}}_{\mathbf{21}}$	${\mathit{b}}_{\mathbf{22}}$	${\mathit{c}}_{\mathbf{1}}$	$\mathbf{\delta }\mathbf{(}\mathbf{\%}\mathbf{)}$
$0.{20}^2$	100	0.14240	0.23494	0.96900	−0.75613	−0.11071	0.35200	−0.51875	−0.80734	0.00302	12.18486
	200	0.14579	0.25005	0.96382	−0.78341	−0.10189	0.35013	−0.49750	−0.78942	0.11045	5.68913
	500	0.15222	0.26364	0.97647	−0.77308	−0.09060	0.35005	−0.48724	−0.78857	0.13262	4.41957
	1000	0.15892	0.25970	0.98546	−0.76410	−0.10005	0.34897	−0.49297	−0.78559	0.15257	3.28600
	2000	0.15443	0.25820	0.98663	−0.77005	−0.10214	0.34954	−0.49407	−0.79532	0.15569	2.85038
	3000	0.15318	0.25979	0.99026	−0.77528	−0.10025	0.35272	−0.49559	−0.79963	0.15830	2.63155
$0.{60}^2$	100	0.16661	0.22088	0.97687	−0.76637	−0.04796	0.28133	−0.58256	−0.92613	−0.01077	16.67281
	200	0.14230	0.24704	0.95213	−0.83607	−0.06133	0.30376	−0.51120	−0.82406	0.10977	7.91161
	500	0.15181	0.28154	0.96971	−0.78348	−0.06034	0.33148	−0.46893	−0.78559	0.14472	5.25893
	1000	0.17142	0.27161	0.98894	−0.74692	−0.09093	0.33498	−0.48227	−0.76910	0.15722	4.45410
	2000	0.16154	0.27069	0.98704	−0.75643	−0.10049	0.34152	−0.48438	−0.79306	0.16109	3.31329
	3000	0.15847	0.27633	0.99597	−0.76992	−0.09664	0.35335	−0.48844	−0.80372	0.16376	2.95257
True values		0.15000	0.25000	0.99000	−0.78000	−0.10000	0.35000	−0.50000	−0.80000	0.20000

Table 2. The F-LSI parameter estimates and errors for Example 1 ($L=2000$).

${\mathbf{\sigma }}^{\mathbf{2}}$	k	${\mathit{a}}_{\mathbf{11}}$	${\mathit{a}}_{\mathbf{12}}$	${\mathit{b}}_{\mathbf{11}}$	${\mathit{b}}_{\mathbf{12}}$	${\mathit{a}}_{\mathbf{21}}$	${\mathit{a}}_{\mathbf{22}}$	${\mathit{b}}_{\mathbf{21}}$	${\mathit{b}}_{\mathbf{22}}$	${\mathit{c}}_{\mathbf{1}}$	$\mathbf{\delta }\mathbf{(}\mathbf{\%}\mathbf{)}$
$0.{20}^2$	1	−0.02217	−0.02741	0.00000	0.00000	0.00000	0.00000	0.00000	0.00000	−0.04161	100.72791
	2	0.00000	0.00000	0.97952	−0.91091	0.00000	0.00000	−0.49792	−0.86478	0.15858	29.65842
	5	0.15601	0.25797	0.98928	−0.77078	−0.09937	0.34653	−0.49427	−0.79873	0.19811	0.92811
	10	0.15519	0.25727	0.98927	−0.77191	−0.09993	0.34719	−0.49479	−0.79810	0.20207	0.83049
$0.{60}^2$	1	−0.02217	−0.02741	0.00000	0.00000	0.00000	0.00000	0.00000	0.00000	−0.04161	100.72791
	2	0.00000	0.00000	0.97808	−0.90354	0.00000	0.00000	−0.48514	−0.86083	0.16440	29.49952
	5	0.16653	0.27248	0.98778	−0.75450	−0.09914	0.34084	−0.48385	−0.79505	0.20121	2.56878
	10	0.16596	0.27194	0.98782	−0.75539	−0.09986	0.34146	−0.48438	−0.79426	0.20209	2.49317
True values		0.15000	0.25000	0.99000	−0.78000	−0.10000	0.35000	−0.50000	−0.80000	0.20000

Table 3. The F-LSI parameter estimates and errors for Example 1 ($L=4000$).

${\mathbf{\sigma }}^{\mathbf{2}}$	k	${\mathit{a}}_{\mathbf{11}}$	${\mathit{a}}_{\mathbf{12}}$	${\mathit{b}}_{\mathbf{11}}$	${\mathit{b}}_{\mathbf{12}}$	${\mathit{a}}_{\mathbf{21}}$	${\mathit{a}}_{\mathbf{22}}$	${\mathit{b}}_{\mathbf{21}}$	${\mathit{b}}_{\mathbf{22}}$	${\mathit{c}}_{\mathbf{1}}$	$\mathbf{\delta }\mathbf{(}\mathbf{\%}\mathbf{)}$
$0.{20}^2$	1	−0.00166	−0.02686	0.00000	0.00000	0.00000	0.00000	0.00000	0.00000	−0.04216	100.60660
	2	0.00000	0.00000	0.98621	−0.91856	0.00000	0.00000	−0.50246	−0.86196	0.16056	29.74749
	5	0.15307	0.25903	0.99062	−0.77955	−0.09866	0.34570	−0.49802	−0.80145	0.18988	0.89726
	10	0.15239	0.25845	0.99072	−0.78046	−0.09964	0.34658	−0.49821	−0.80051	0.19238	0.74333
$0.{60}^2$	1	−0.00166	−0.02686	0.00000	0.00000	0.00000	0.00000	0.00000	0.00000	−0.04216	100.60660
	2	0.00000	0.00000	0.98710	−0.92316	0.00000	0.00000	−0.49770	−0.86426	0.16301	29.83299
	5	0.15776	0.27565	0.99202	−0.78054	−0.09757	0.33874	−0.49436	−0.80278	0.19163	1.87793
	10	0.15708	0.27501	0.99217	−0.78149	−0.09882	0.33965	−0.49462	−0.80160	0.19240	1.79377
True values		0.15000	0.25000	0.99000	−0.78000	−0.10000	0.35000	−0.50000	−0.80000	0.20000

Table 4. The F-LSI parameter estimates and errors for Example 1 ($k=10$).

${\mathbf{\sigma }}^{\mathbf{2}}$	L	${\mathit{a}}_{\mathbf{11}}$	${\mathit{a}}_{\mathbf{12}}$	${\mathit{b}}_{\mathbf{11}}$	${\mathit{b}}_{\mathbf{12}}$	${\mathit{a}}_{\mathbf{21}}$	${\mathit{a}}_{\mathbf{22}}$	${\mathit{b}}_{\mathbf{21}}$	${\mathit{b}}_{\mathbf{22}}$	${\mathit{c}}_{\mathbf{1}}$	$\mathbf{\delta }\mathbf{(}\mathbf{\%}\mathbf{)}$
$0.{20}^2$	2000	0.15519	0.25727	0.98927	−0.77191	−0.09993	0.34719	−0.49479	−0.79810	0.20207	0.83049
	4000	0.15239	0.25845	0.99072	−0.78046	−0.09964	0.34658	−0.49821	−0.80051	0.19238	0.74333
$0.{60}^2$	2000	0.16596	0.27194	0.98782	−0.75539	−0.09986	0.34146	−0.48438	−0.79426	0.20209	2.49317
	4000	0.15708	0.27501	0.99217	−0.78149	−0.09882	0.33965	−0.49462	−0.80160	0.19240	1.79377
True values		0.15000	0.25000	0.99000	−0.78000	−0.10000	0.35000	−0.50000	−0.80000	0.20000

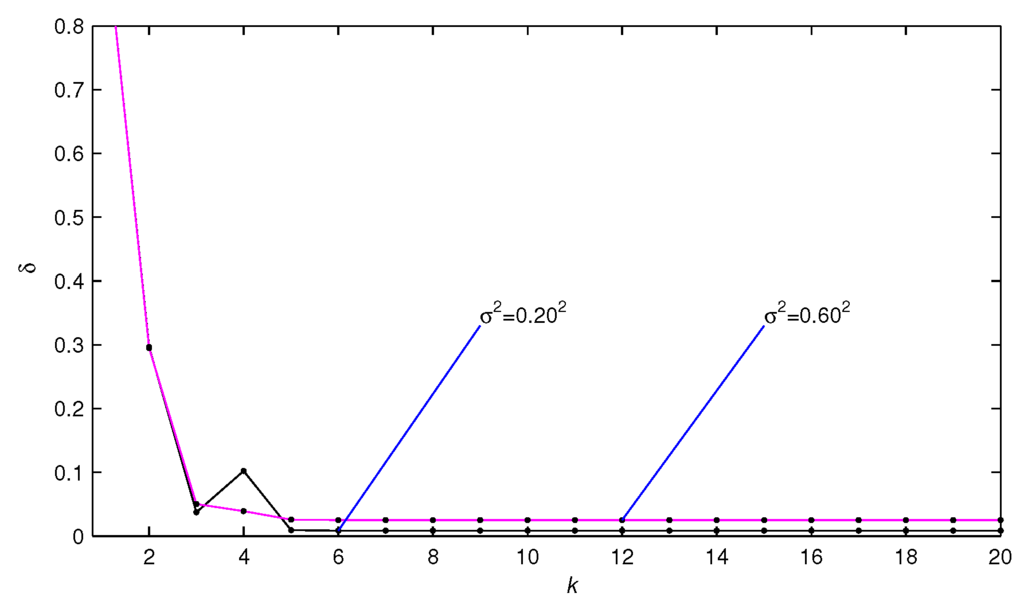
Figure 1. The estimation errors δ versus t.

From Table 1, Table 2, Table 3 and Table 4 and Figure 1, we can draw the following conclusions:

• Increasing the data length L can improve the parameter estimation accuracy of the F-RGLS algorithm and the F-LSI algorithm, and as the data length L increases, the parameter estimates are getting more stationary.
• Under the same data length, the estimation accuracy of the F-RGLS algorithm and the F-LSI algorithm increases as the noise variance decreases.
• Under the same data length and noise variance, the estimation errors of the F-LSI algorithm are smaller than the F-RGLS algorithm.
• The F-LSI algorithm has fast convergence speed, and the parameter estimates only need several iterations close to their true values.

Example 2: 

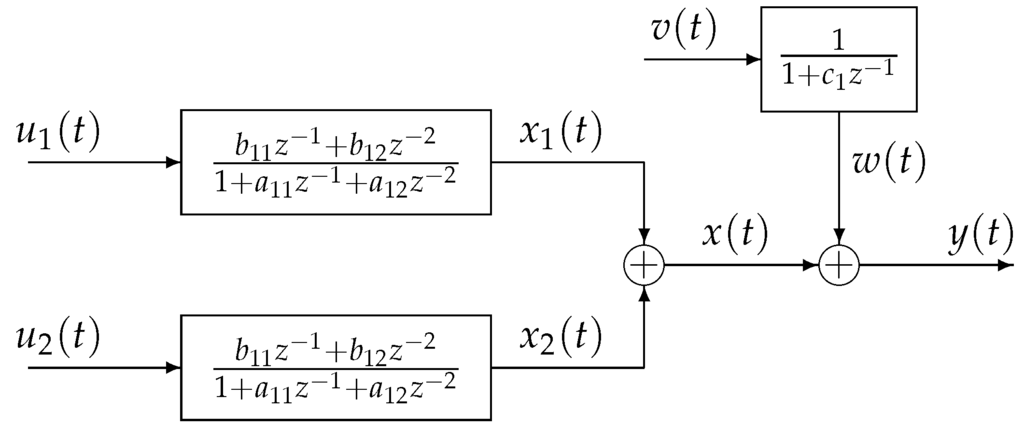
Consider the industrial process with colored noise, which has two inputs and one output as shown in Figure 2 and described as

$$\begin{array}{ccc}\hfill y\left(t\right)& =& G_1\left(z\right)u_1\left(t\right)+G_2\left(z\right)u_2\left(t\right)+H\left(z\right)v\left(t\right)\hfill \\ & =& \sum _{i=1}^2[-a_{1i}{x}_1(t-i)+b_{1i}{u}_1(t-i)]+\sum _{i=1}^2[-a_{2i}{x}_2(t-i)+b_{2i}{u}_2(t-i)]-c_{1}w(t-1)+v\left(t\right),\hfill \end{array}$$

where $G_1\left(z\right)=(b_{11}{z}^{-1}+b_{12}{z}^{-2})/(1+a_{11}{z}^{-1}+a_{12}{z}^{-2})$, $G_2\left(z\right)=(b_{21}{z}^{-1}+b_{22}{z}^{-2})/(1+a_{21}{z}^{-1}+a_{22}{z}^{-2})$ and $H\left(z\right)=1/(1+c_1{z}^{-1})$.

Figure 2. The diagram of a multi-input OEAR system.

The parameters to be estimated are

$$\begin{array}{c}\hfill {[a_{11},a_{12},b_{11},b_{12},a_{21},a_{22},b_{21},b_{22},c_1]}^{\mathrm{T}}={[0.15,0.25,0.99,-0.78,-0.10,0.35,-0.50,-0.80,0.20]}^{\mathrm{T}}.\end{array}$$

The simulation conditions are the same as those of Example 1, and the noise variance ${\sigma }^2=0.{30}^2$. Applying the F-RGLS and the F-LSI algorithms to estimate the parameters of the system, the parameter estimates and their errors are presented in Table 5 and Table 6.

Table 5. The F-RGLS parameter estimates and errors for Example 2.

t	${\mathit{a}}_{\mathbf{11}}$	${\mathit{a}}_{\mathbf{12}}$	${\mathit{b}}_{\mathbf{11}}$	${\mathit{b}}_{\mathbf{12}}$	${\mathit{a}}_{\mathbf{21}}$	${\mathit{a}}_{\mathbf{22}}$	${\mathit{b}}_{\mathbf{21}}$	${\mathit{b}}_{\mathbf{22}}$	${\mathit{c}}_{\mathbf{1}}$	$\mathbf{\delta }\mathbf{(}\mathbf{\%}\mathbf{)}$
100	0.31044	0.27323	0.47823	0.79593	−0.16988	0.31233	0.34733	0.79082	−0.35990	11.48781
200	0.35712	0.26107	0.47534	0.80554	−0.20188	0.32807	0.38468	0.77922	−0.30469	7.07660
500	0.37558	0.30333	0.48485	0.83653	−0.22143	0.30058	0.41246	0.78396	−0.28669	4.56000
1000	0.36022	0.29164	0.49690	0.84216	−0.23072	0.29199	0.40519	0.76406	−0.27138	2.49100
2000	0.36115	0.29540	0.49771	0.84667	−0.24094	0.30037	0.39938	0.74612	−0.27434	2.05076
3000	0.36636	0.30139	0.50263	0.84719	−0.24389	0.30650	0.39658	0.74012	−0.26554	1.89797
True values	0.35000	0.30000	0.50000	0.84000	−0.25000	0.30000	0.40000	0.75000	−0.25000

Table 6. The F-LSI parameter estimates and errors for Example 2.

k	${\mathit{a}}_{\mathbf{11}}$	${\mathit{a}}_{\mathbf{12}}$	${\mathit{b}}_{\mathbf{11}}$	${\mathit{b}}_{\mathbf{12}}$	${\mathit{a}}_{\mathbf{21}}$	${\mathit{a}}_{\mathbf{22}}$	${\mathit{b}}_{\mathbf{21}}$	${\mathit{b}}_{\mathbf{22}}$	${\mathit{c}}_{\mathbf{1}}$	$\mathbf{\delta }\mathbf{(}\mathbf{\%}\mathbf{)}$
1	−0.00611	0.03601	0.00000	0.00000	0.00000	0.00000	0.00000	0.00000	0.00165	99.63926
2	0.00000	0.00000	0.49960	0.67716	0.00000	0.00000	0.41014	0.84617	−0.26452	43.64422
3	0.48512	0.14379	0.50775	0.90619	−0.22359	0.25926	0.39984	0.75210	−0.26452	15.35917
4	0.35231	0.33645	0.50464	0.84218	−0.25181	0.31725	0.39804	0.73802	−0.10385	10.48969
5	0.35968	0.29443	0.50270	0.84889	−0.24823	0.31243	0.39831	0.73841	−0.04162	14.44370
6	0.36474	0.29771	0.50305	0.84987	−0.24911	0.31358	0.39819	0.73823	−0.24951	1.76580
7	0.36336	0.29924	0.50326	0.84956	−0.24869	0.31289	0.39808	0.73850	−0.25696	1.73424
8	0.36328	0.29861	0.50327	0.84966	−0.24868	0.31286	0.39809	0.73855	−0.25698	1.73382
9	0.36336	0.29862	0.50327	0.84967	−0.24865	0.31286	0.39808	0.73856	−0.25703	1.73724
10	0.36335	0.29864	0.50327	0.84966	−0.24865	0.31285	0.39808	0.73856	−0.25702	1.73638
True values	0.35000	0.30000	0.50000	0.84000	−0.25000	0.30000	0.40000	0.75000	−0.25000

From Table 5 and Table 6, we can see that the estimation errors become smaller with the increase of t and the F-LSI algorithm can get accurate parameter estimates by only several iterations, which shows the effectiveness of the proposed algorithms.

The power consumption in host servers can be concerned by the model of Example 2. The two inputs are the changes in CPU frequency of the host server and the changes in the guest server’s time share to use the physical CPU of the host server, and the power consumption is the system output. The configuration and the allocation of memory, storage and network bandwidth for the guest server are the random disturbances of the system.

6. Conclusions

This paper discusses the parameter estimation problem for multi-input OEAR systems. Based on the data filtering technique, an F-RGLS algorithm and an F-LSI algorithm are developed. The proposed methods are effective for estimating the parameters of multi-input OEAR systems. The simulation results indicate that the proposed F-LSI algorithm achieves higher estimation accuracies than the F-RGLS algorithm, and the convergence rate of the proposed methods can be improved by increasing the data length. The methods used in this paper can be extended to study the identification of other linear systems, nonlinear systems, state space systems and time delay systems.