1. Introduction
The stable marriage problem (SM) [
1] is a well-known problem of matching men to women to achieve a certain type of “stability”. Each person expresses a strict preference ordering over the members of the opposite sex. The goal is to match men to women so that there are no two people of the opposite sex who would both rather be matched with each other than with their current partners. The stable marriage problem has a wide variety of practical applications, ranging from matching resident doctors to hospitals, sailors to ships, primary school students to secondary schools, as well as in market trading. Surprisingly, such a stable marriage always exists, and one can be found in polynomial time. Gale and Shapley give an algorithm, which is linear in the size of the input, to solve this problem based on a series of proposals of the men to the women (or
vice versa) [
2].
There are many variants of the traditional formulation of the stable marriage problem. Some of the most useful in practice include incomplete preference lists (SMI), which allow one to model unacceptability for certain members of the other sex, and preference lists with ties (SMT), which model indifference in the preference ordering. With an SMI problem, the goal is to find a stable marriage in which the married people accept each other. It is known that all solutions of an SMI problem have the same size (that is, number of married people) [
3]. In SMT problems, instead, solutions are stable marriages where everybody is married. Both of these variants are polynomial to solve. In real world situations, both ties and incomplete preference lists may be needed. Unfortunately, when we allow both, the problem becomes NP-hard [
4]. In an SMTI (Stable Marriage with Ties and Incomplete lists) problem, there may be several stable marriages of different sizes, and solving the problem means finding a stable marriage of maximum size.
In this paper, we investigate the use of a local search approach to tackle both the classical and the NP-hard variants of the problem. In particular, when we consider the classical problem, we investigate the fairness of stable marriage procedures based on local search, i.e., we investigate how well these procedures sample the lattice of stable marriages. On the other hand, for SMTI problems, we focus on efficiency in terms of time and effectiveness at finding large stable marriages. Our algorithms are based on the same schema: they start from a randomly chosen marriage, and at each step, we move to a neighbor marriage by minimizing the distance to stability, which is measured by the number of unstable pairs. To avoid redundant computation due to the possibly large number of unstable pairs, we consider only those that are undominated, since their elimination minimizes the distance to stability. Random moves are also used, to avoid stagnation in local minima. The algorithms stop when they find a solution or when a given limit on the number of steps is reached. A solution for an SMTI instance is a perfect stable matching (that is, a stable marriage with no singles), whereas, for an SM instance, a solution is just a stable marriage.
For the SM problem, we performed experiments on randomly generated problems with up to 500 men and women. It is interesting to notice that our algorithm always finds a stable marriage. Furthermore, its runtime behavior shows that the number of steps grows as little as
[
5]. We also tested the fairness of our algorithm at generating stable marriages, measuring how well the algorithm samples the set of all stable marriages. As it is non-deterministic, it should ideally return any of the possible stable marriages with equal probability. We measure this capability in the form of an entropy that should be as close to that of a uniform sample as possible. The computed entropy is about 70% of that of a uniform sample, and even higher on problems with small size.
For the SMTI problem, we performed experiments on randomly generated problem instances of size of 90 and, in some cases, also of size of 100. We observe that our algorithm is able to find stable marriages with at most two singles on average in tens of seconds at worst. The SMTI problem has been tackled also in [
6], where the problem is modeled in terms of a constraint optimization problem and solved employing a constraint solver. This systematic approach is guaranteed to always find an optimal solution. However, our experimental results show that our local search algorithm in practice always appears to find optimal solutions. Moreover, it scales well to sizes much larger than those considered in [
6]. An alternative approach to local search is to use approximation methods.
The paper is an extended and revised version of [
7,
8,
9].
2. Related Work
In this paper, we consider the fairness of the methodology to generate stable marriages. Other works have considered the fairness with the meaning of finding stable marriages where the overall happiness of the persons is maximized. One kind of fairer stable marriage that has been considered, is the
minimum regret stable marriage [
5,
10]. The regret for each person is the position in his/her preference list of the persons to whom he/she is married. The regret of a marriage,
M, is the maximum regret of any person. Another way to characterize the overall happiness of a marriage is to consider the sum of the regret of every person. The
egalitarian stable marriage [
11] minimizes the total sum of the regrets. Both minimum regret and egalitarian stable marriage can be found in polynomial time [
10,
11]. In [
12], Roth and Vande Vate show that, beginning from an arbitrary marriage and satisfying a blocking pair at random, we will eventually reach a stable marriage with a probability of one. Our local search approaches exploit this result by building sequences of blocking pair removal that rapidly lead to stability thanks to the use of undominated blocking pairs.
In this paper, we consider also the solution of stable marriage problems with ties and incomplete lists. It is known that weakly stable matchings may have different cardinality. Furthermore, finding the maximum (or minimum) cardinality weak stable matching for a given instance of SMTI is NP-hard. This holds even if the ties are at the tails of lists and on one side only, and each tie has a length of two [
4], though the largest matching is at most twice the size of the smallest [
4]. It has also been established that these problems are not approximable within
δ, unless P= NP, for some
; even if the preference lists are of a constant length, there is at most one tie per list, and the ties occur on one side only [
13]. Above, we noted that a maximum cardinality weak stable matching is at most twice the size of a minimum cardinality weak stable matching. Therefore, if we break all ties in an arbitrary way and apply the GS (Gale and Shapley) algorithm to the resulting instance of SMI, we get what is simultaneously an approximation algorithm for the problem of finding a maximum (resp., minimum) stable matching with a performance ratio of two. In [
13,
14], an improved performance bound is shown for instances of SMTI with sparse ties. Three other pieces of work related to approximating maximum cardinality weak stable matchings have appeared in the literature. In [
15], Halldorsson
et al. present a randomized approximation algorithm with expected performance guarantee
for instances of SMTI in which ties occur on one side only; there is at most one tie per list, and each tie has a length of two. In [
16], the same authors present an approximation algorithm with performance guarantee
for instances of SMTI in which ties occur on one side only and each tie has a length of at most L. Additionally, they show a ratio of
, where ties are allowed on both sides and are of a length of two. In [
17], Iwama
et al. present an approximation algorithm for a general instance of SMTI with guarantee
, for an instance of size
n, where
c is an arbitrary positive constant. Recently, in [
18], Iwama
et al. improve the approximation ratio to
for instances with one-sided ties. This approximation ratio also holds for the hospitals/residents problem (i.e., many-one variant) with one-sided ties (see [
19] for the relationship between the approximability of the stable marriage problem and the hospitals/residents problem). Other approximation results with a higher ratio have been shown in [
20,
21,
22]. A detailed overview of approximation algorithms is presented on pages 136–137 of [
23].
In our paper, we consider a local search approach to solve SMTI instances. Other local search methods have been presented for SMTI instances, but in terms of parameterized complexity in the framework introduced by [
24]. In SMTI instances, the parameter can be the number of ties, the maximum or the overall length of ties [
25]. In [
25], the authors investigate the applicability of a local search algorithm for the problem and they examine the possibilities for giving an FPTalgorithm or an FPT approximation algorithm for finding an egalitarian or a minimum regret stable matching. In general, few papers have investigated the connection of parameterized complexity and local search, although attention to this topic has been increasing recently [
26]. In [
27], the framework of parameterized complexity is used to deal with the hospitals/residents with couples problem, a variant of the classical stable marriage problem. This is the extension of the hospitals/residents problem, where residents are allowed to form pairs and submit joint rankings over hospitals. In this problem, the authors consider the number of couples as a parameter, apply a local search approach and examine the possibilities for giving FPT algorithms applicable in this context.
In [
6], Gent and Prosser give an exhaustive empirical study of the stable marriage problem with ties and incomplete lists, using a constraint programming encoding of the problem. Then, the encoded problem can be solved using off the shelf CPtechnology. They present results for the decision problem “Is there a stable matching of size
n?” and for the optimization problem of finding a maximum or minimum cardinality stable matching. In particular, regarding the optimization problem of finding the largest stable marriage, their complete method (based on the solution of the CP encoding of the problem using the Choco constraint programming toolkit [
28]) finds stable marriages of a size of 9.3 (in average) considering problems of a size of 10 with no ties. When the amount of ties increases, the size increases, as well. Our local search approach obtains very similar results using a test set generated in the same way.
Gent and Prosser in [
29] give a SATencoding of the stable marriage problem with ties and incomplete lists. Using such an encoding, they obtain very good results in the decision problem of whether there is a perfect matching. Even though in our experiments, we often find a perfect matching, we consider a different problem from the one solved in [
29].
In [
30], Brito and Meseguer, propose a distributed approach to the stable marriage problem with ties and incomplete lists with the aim of keeping preference lists private for privacy reasons. They extend some specialized centralized algorithms (such as the Extended Gale Shapley algorithm) to the distributed case. Moreover, they provide a generic distributed constraint programming model. In their experimental evaluation, they consider the communication effort and the computational cost (in terms of constraint checks) which are not applicable to our centralized approach. However, they show also the maximum cardinality of the marriages found by their algorithms considering SMTI instances. Considering problems of the same size, the probability of ties and the incompleteness they used, we obtain marriages of very similar cardinality.
In [
31], Irving and Manlove present two heuristic approaches to find the largest stable matching in the context of the hospital resident-oriented (HR) problems with incomplete lists and ties only in the hospitals’ preference lists. One of the algorithms is based on the hospital-oriented version of the Gale-Shapley algorithm, and the other one is based on the resident version. Heuristics are used to decide how to break ties in order to maximize the size of the returned marriage. In fact, the ways in which ties are broken can significantly affect the size of the stable matching found, and in the extreme case, there may be two matchings differing in size by a factor of two [
4]. When hospitals have a capacity equal to one, the problem becomes an SMTI instance with ties on one side only; thus, the algorithms proposed in [
31] can also be used to solve such restricted SMTIs.
In [
32], the authors give complexity and approximation results regarding the problem of finding a maximum cardinality matching that admits the smallest number of blocking pairs in an SMI instance. They show that such a problem is NP-hard. Our experimental results show that our local search approach is able to find marriages of a large size and with a very small number of blocking pairs within a small number of steps.
In our local search approach, we exploit the Gale-Shapely stable matching procedure. The GS algorithm is computationally easy to manipulate and favors one gender over the other. In [
33,
34], it is shown that there exist stable marriage procedures that are NP-hard to manipulate and that voting rules that are NP-hard to manipulate can be used to define stable marriage procedures, which are themselves NP-hard to manipulate. Moreover, it is shown how to use voting rules to make any stable marriage procedure gender neutral. Manipulation issues have been also considered in the context of stable matching procedures with weighted preferences, where new notions of stability and optimality have been provided [
35,
36,
37]. Besides manipulation, stability, and optimality, also the uniqueness of weakly stable matchings has been studied in the context of stable matching procedures with partially ordered preferences [
38,
39].
3. Background
In this section, we give some basic notions about the stable marriage problem. In addition, we present some basic notions about local search.
3.1. Stable Marriage Problem
A stable marriage (SM) problem instance [
1] consists of matching members of two different sets, usually called men and women. When there are
n men and
n women, the SM problem is said to have size
n. Each person strictly ranks all members of the opposite sex. The goal is to match the men with the women, so that there are no two people of the opposite sex who would both rather marry each other than their current partners. If there are no such pairs (called blocking pairs), the marriage is
“stable”.
Definition 1 (Marriage) Given an SM instance P of size n, a marriage, M, is a one-to-one matching of the men and the women. If a man, m, and a woman, w, are matched in M, we write and .
Definition 2 (Blocking pair) Given a marriage, M, a pair, , where m is a man and w is a woman, is a blocking pair iff m and w are not partners in M, but m prefers w to and w prefers m to .
Definition 3 (Stable Marriage) A marriage, M, is stable iff it has no blocking pairs.
A convenient and widely used SM representation is shown in
Table 1, where each person is followed by his/her preference list in decreasing order.
Table 1.
An example of a stable marriage (SM) instance of a size of eight.
Table 1.
An example of a stable marriage (SM) instance of a size of eight.
| Men’s preference lists | Women’s preference lists |
|---|
| 1: 5 7 1 2 6 8 4 3 | 1: 5 3 7 6 1 2 8 4 |
| 2: 2 3 7 5 4 1 8 6 | 2: 8 6 3 5 7 2 1 4 |
| 3: 8 5 1 4 6 2 3 7 | 3: 1 5 6 2 4 8 7 3 |
| 4: 3 2 7 4 1 6 8 5 | 4: 8 7 3 2 4 1 5 6 |
| 5: 7 2 5 1 3 6 8 4 | 5: 6 4 7 3 8 1 2 5 |
| 6: 1 6 7 5 8 4 2 3 | 6: 2 8 5 4 6 3 7 1 |
| 7: 2 5 7 6 3 4 8 1 | 7: 7 5 2 1 8 6 4 3 |
| 8: 3 8 4 5 7 2 6 1 | 8: 7 4 1 5 2 3 6 8 |
For example,
Table 1 shows that man 1 prefers woman 5 to woman 7 to woman 1, and so on. It is known that at least one stable marriage exists for every SM problem. For a given SM instance, we can define a partial order relation on the set of stable marriages.
Definition 4 (Dominance) Let M and be two stable marriages. M dominates iff every man has a partner in M who is at least as good as the one he has in .
Under the partial order given by the dominance relation, the set of stable marriages forms a distributive lattice [
5]. Gale and Shapley give a polynomial time algorithm (GS) to find the stable marriage at the top (or bottom) of this lattice [
2]. The top of such a lattice is the male optimal stable marriage,
, which is optimal from the men’s point of view. This means that there are no other stable marriages in which each man is married with the same woman or with a woman he prefers to the one in
. The GS algorithm can also be used to find the female optimal stable marriage,
(that is, the bottom of the stable marriage lattice), which is optimal from the women’s perspective, by just replacing men with women (and
vice versa) before applying the algorithm. A clear way to represent this lattice is a Hasse diagram representing the transitive reduction of the partial order relation.
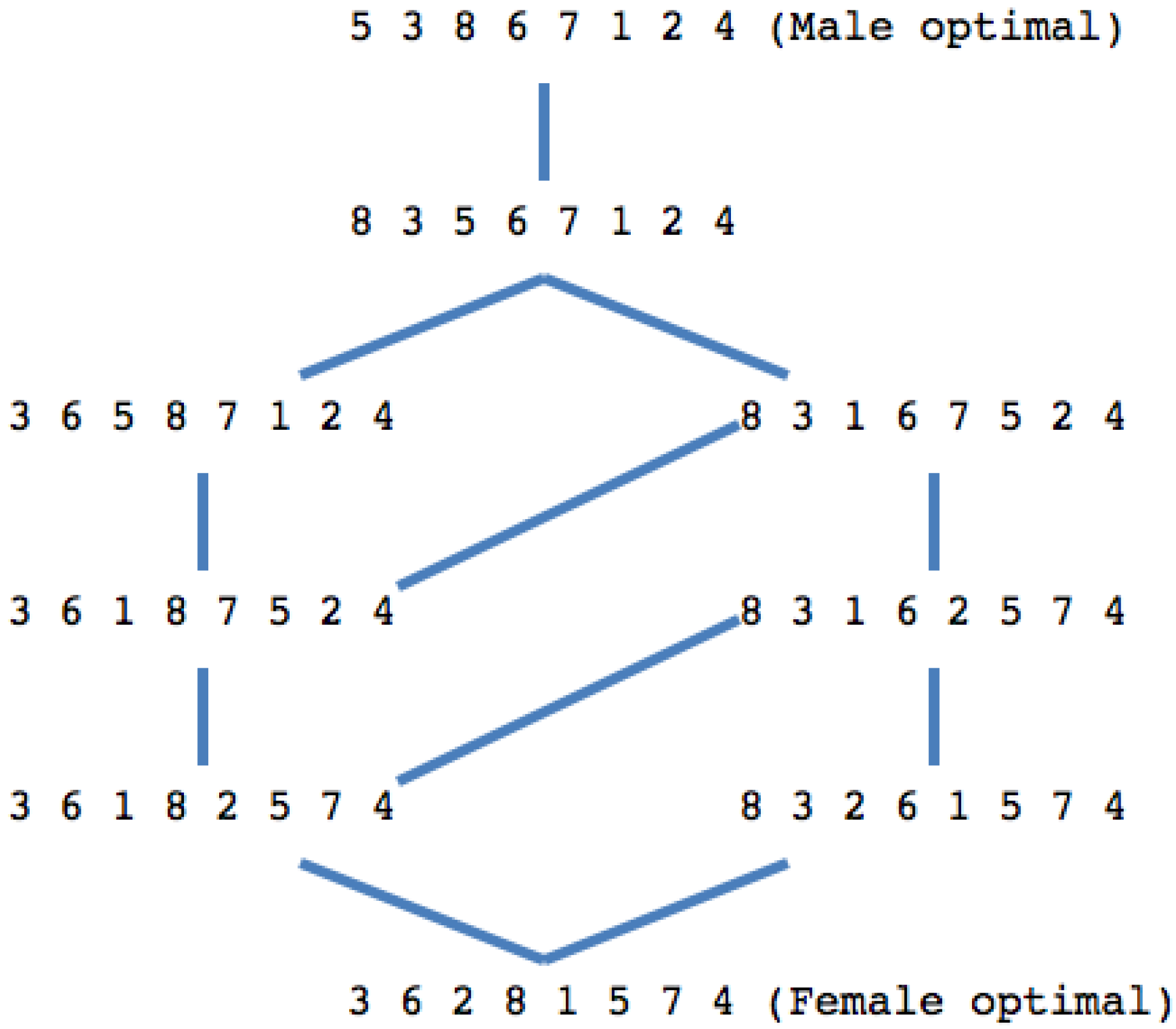
Figure 1 shows the Hasse diagram of the SM in
Table 1.
Figure 1.
The Hasse diagram of the set of all stable marriages for the SM in
Table 1.
Figure 1.
The Hasse diagram of the set of all stable marriages for the SM in
Table 1.
A common concern with the standard Gale-Shapley algorithm is that it unfairly favors one sex at the expense of the other. This gives rise to the problem of finding “fairer” stable marriages. Previous work on finding fair marriages has focused on algorithms for optimizing an objective function that captures the happiness of both genders [
10,
11]. A different approach is to investigate non-deterministic procedures that can generate a random stable marriage from the lattice with a distribution that is as uniform as possible.
In [
40], the authors use a Markov chain approach to sample the stable marriage lattice. More precisely, the edges of the lattice dictate exactly how to formalize the moves to walk from one stable marriage to another one, so that there are at most a linear number of moves at each step, these are easily identifiable and they form reversible moves that connect the state space and converge to the uniform distribution. Unfortunately, Bhatnagar e
t al. show that this random walk has an exponential convergence time, which would appear to suggest that the approach may not be feasible in practice.
In this paper, we also consider a variant of the SM problem, where preference lists may include ties and may be incomplete. This variant is denoted by SMTI [
41]. Ties express indifference in the preference ordering, while incompleteness models unacceptability only for certain partners.
Definition 5 (SMTI marriage) Given an SMTI problem instance with n men and n women, a marriage, M, is a one-to-one matching between men and women, such that the partners accept each other. If a man m and a woman w are matched in M, we write and . If a person, p, is not matched in M, we say that he/she is single.
Definition 6 (Marriage size) Given an SMTI problem instance of size n and a marriage, M, its size is the number of men (or women) that are married.
Definition 7 (Blocking pairs in SMTI problems) Consider a SMTI problem instance, P, a marriage, M, for P, a man, m, and a woman, w. A pair, , is a blocking pair in M iff m and w accept each other and m is either single in M or he strictly prefers w to , and w is either single in M or she strictly prefers m to .
Definition 8 (Weakly stable marriages) Given an SMTI problem instance, P, a marriage, M, for P is weakly stable iff it has no blocking pairs.
As we will consider only weakly stable marriages, we will simply call them stable marriages. Given an SMTI problem instance, there may be several stable marriages of different sizes. If the size of a marriage coincides with the size of the problem, it is said to be a perfect matching. Solving an SMTI problem instance means finding a stable marriage with maximal size. This problem is NP-hard [
4].
3.2. Local Search
Local search [
42] is one of the fundamental paradigms for solving computationally hard combinatorial problems. Local search methods in many cases represent the only feasible way for solving large and complex instances. Moreover, they can naturally be used to solve optimization problems.
Given a problem instance, the basic idea underlying local search is to start from an initial search position in the space of all solutions (typically, a randomly or heuristically generated candidate solution, which may be infeasible, sub-optimal or incomplete) and to iteratively improve this candidate solution by means of typically minor modifications. At each search step, we move to a position selected from a local neighborhood, chosen via a heuristic evaluation function. The evaluation function typically maps the current candidate solution to a number such that the global minima correspond to solutions of the given problem instance. The algorithm moves to the neighbor with the smallest value of the evaluation function. This process is iterated until a termination criterion is satisfied. The termination criterion is usually the fact that a solution is found or that a predetermined number of steps is reached, although other variants may stop the search after a predefined amount of time.
Different local search methods vary in the definition of the neighborhood and of the evaluation function, as well as in the way in which situations are handled when no improvement is possible. To ensure that the search process does not stagnate in unsatisfactory candidate solutions, most local search methods use randomization: at every step, with a certain probability, a random move is performed rather than the usual move to the best neighbor.
4. Local Search on Stable Marriages
We now present an adaptation of the local search schema to deal with the classical stable marriage problem. Then, we will point out the aspects that have to be changed to deal with SMTI problems.
Given an SM instance, P, we start from a randomly generated marriage, M. Then, at each search step, we compute the set, , of blocking pairs in M and compute the neighborhood, which is the set of all marriages obtained by removing one of the blocking pairs in from M. Consider a blocking pair in M, and . Then, removing from M means obtaining a marriage, , in which m is married with w and is married with , leaving the other pairs unchanged. To select the neighbor of M to move to, we use an evaluation function, , where is the set of all possible marriages of size n, and . For each marriage, M, is the number of blocking pairs in M, and we move to one with the smallest value of f.
To avoid stagnation in a local minimum of the evaluation function, at each search step, we perform a random walk with probability p (where p is a parameter of the algorithm), which removes a randomly chosen blocking pair in from the current marriage, M. In this way, we move to a randomly selected marriage in the neighborhood. The algorithm terminates if a stable marriage is found or when a maximal number of search steps or a timeout is reached.
This basic algorithm, called SML, has been improved in the computation of the neighborhood, obtaining SML1. When SML moves from one marriage to another one, it takes as input the current marriage, M, and the list of its blocking pairs and returns the marriage in the neighborhood of M with the best value of the evaluation function, i.e., the one with the fewest blocking pairs. However, the number of such blocking pairs may be very large. Furthermore, some of them may be useless, since their removal would surely lead to new marriages that will not be chosen by the evaluation function. This is the case for the so-called dominated blocking pairs. Algorithm SML1 considers only undominated blocking pairs.
Definition 9 (Dominance in blocking pairs) Let and be two blocking pairs. Then, dominates (from the men’s point of view) iff m prefers w to . There is an equivalent concept from the women’s point of view.
Definition 10 (Undominated blocking pair) A men- (resp., women-) undominated blocking pair is a blocking pair, such that there is no other blocking pair that dominates it from the men’s (resp., women’s) point of view.
It is easy to see that, if M is an unstable marriage, , a men- (resp., women-) undominated blocking pair in M, , and is obtained from M by removing , there are no blocking pairs in in which m (resp., w) is involved. This property would not be true if we removed a dominated blocking pair. This is why we focus on the removal of undominated blocking pairs when we pass from one marriage to another in our local search algorithm.
Considering again the SM in
Table 1 and the marriage 2 7 4 8 6 3 5 1, the blocking pair,
, dominates (from the men’s point of view)
. If we remove
from the marriage,
will remain. On the other hand, removing
also eliminates
. Thus, removing
is more useful than removing
.
By using the undominated blocking pairs instead of all the blocking pairs, we also limit the size of the neighborhood, since each man or woman is involved in at most one undominated blocking pair. Hence, we have at most neighbor marriages to evaluate.
Let us now analyze more carefully the set of blocking pairs considered by SML1. Consider the case in which a man, , is in two blocking pairs, say and , and assume that dominates from the men’s point of view. Then, let be in another blocking pair, say , that dominates from the women’s point of view. In this situation, SML1 returns , because it computes the undominated blocking pairs from the men’s point of view (which are and ) and, among those, maintains the undominated ones from the women’s point of view ( in this case). The removal of automatically eliminates from the set of blocking pairs of the marriage, since it is dominated by . However, the blocking pair, , is still present, because the blocking pair that dominated it (i.e., ) is not a blocking pair any longer. We also consider a procedure that will return, in addition, the blocking pair, , so as to avoid having to consider it again in the subsequent step of the local search algorithm. We call SML2 the algorithm obtained from SML1 by using this new way to compute the blocking pairs.
Since dominance between blocking pairs is defined from one gender’s point of view, at the beginning of our algorithms, we randomly choose a gender and, at each search step, we change the role of the two genders. For example, in SML1, if we start by finding the undominated blocking pairs from the men’s point of view and, among those, we keep only the undominated blocking pairs from the women’s point of view, in the following second step, we do the opposite, and so on. In this way, we ensure that SML1 and SML2 are gender neutral.
Summarizing, we have defined three algorithms, called SML, SML1 and SML2, to find a stable marriage for a given SM instance. Such algorithms differ only by the set of blocking pairs considered to define the neighborhood.
5. Local Search for SMTI Problems
To adapt the SML algorithm to solve problems with ties and incomplete lists, it is important to recall that an SMTI instance may have several stable marriages of different sizes. Thus, solving an SMTI problem instance means finding a stable marriage with maximal size. If the size of the marriage coincides with the size of the problem, it is said to be perfect, and the algorithm can stop before the step limit. Otherwise, the algorithm returns the best marriage found during the search, defined as follows: if no stable marriage has been found, then the best marriage is the one with the smallest value of the evaluation function; otherwise, it is the stable marriage with the fewest singles.
The SML algorithm is therefore modified in the following ways:
the evaluation function has to take into account that some person may be not married; so we use: , where, for each marriage M, is the number of singles in M that are not in any blocking pair.
When we remove a blocking pair, , from a marriage, M, their partners, and , become single.
The algorithm performs a random restart when a stable marriage is reached, since its neighborhood is empty (because it has no blocking pairs).
We call the modified algorithm for SMTI problems LTIU, obtained from SML by the above modifications and by using undominated blocking pairs.
6. Experiments
We tested our algorithms on randomly generated sets of SM and SMTI instances. For SM problems, we generated stable marriage problems of size
n using the impartial culture model (IC) [
43], which assigns to each man and to each woman a preference list uniformly chosen from the
possible total orders of
n persons. This means that the probability of any particular ordering is
.
For SMTI problems, we generated problem instances using the same method as in [
6]. More precisely, the generator takes three parameters: the problem’s size,
n, the probability of incompleteness,
, and the probability of ties,
. Given a triple,
, a SMTI problem instance with
n men and
n women is generated as follows:
For each man and woman, we generate a random preference list of size n, i.e., a permutation of n persons;
We iterate over each man’s preference list: for a man, , and for each women, , in his preference list, with probability , we delete from ’s preference list and from ’s preference list. In this way, we get a possibly incomplete preference list.
If any man or woman has an empty preference list, we discard the problem and go to step 1.
We iterate over each person’s (men and women’s) preference list as follows: for a man, , and for each woman in his preference list, in position , with probability , we set the preference for that woman as the preference for the woman in position (thus, putting the two women in a tie).
Note that this method generates SMTI problem instances in which the acceptance is symmetric.If a man, m, does not accept a woman, w, m is removed from w’s preference list, as well. This does not introduce any loss of generality, because m and w cannot be matched together in any stable marriage.
7. Results on SM Problems
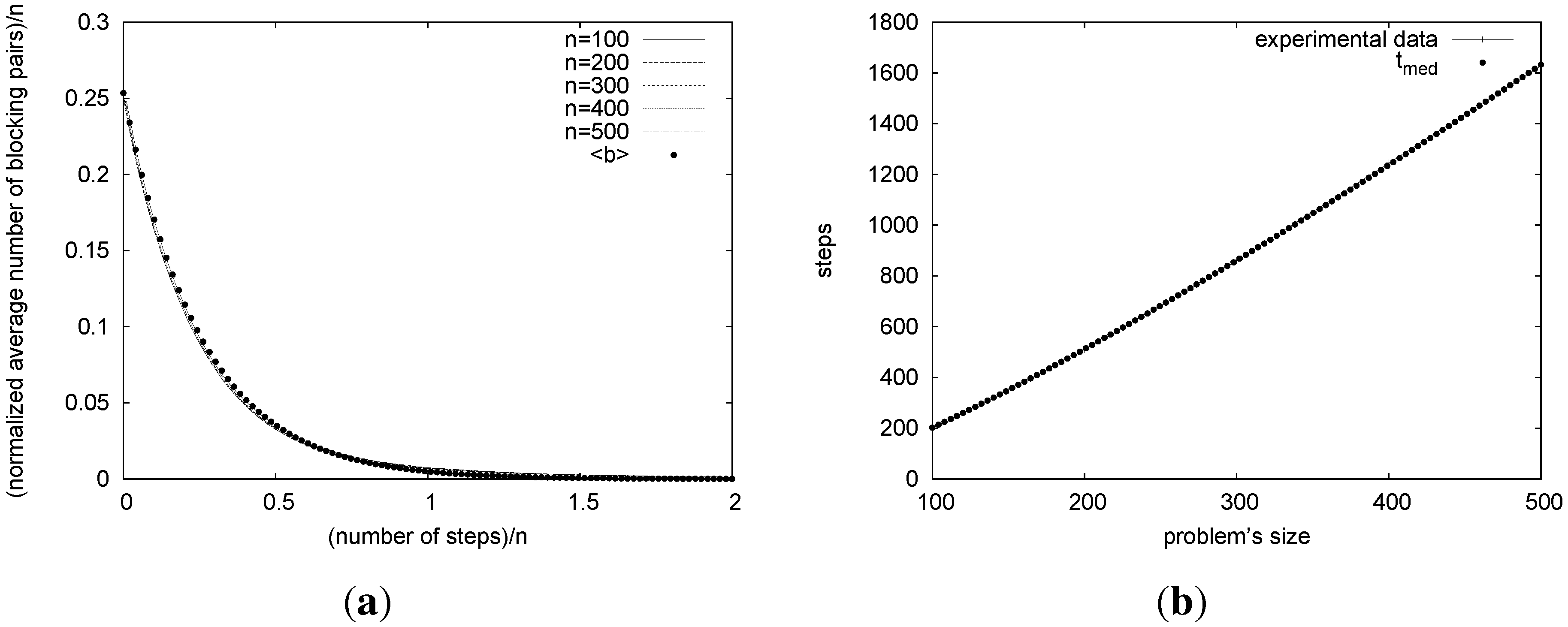
We measured the performance of our algorithms in terms of the number of search steps. For these tests, we generated 100 SM problem instances for each of the following sizes: 100, 200, 300, 400 and 500. In the following, we show only the results of our best algorithm, which is SML2. We studied how fast SML2 converges to a stable marriage, by measuring the ratio between the number of blocking pairs and the size of the problem during the execution.
Figure 2(a) shows that SML2 has a very simple scaling behavior. Let us denote by
the average number of blocking pairs of the marriage found by SML2 for SM problem instances of size
n after
t steps. Then, the experimental results shown in
Figure 2(a) have a very good fit with the function
, where
a and
b are constants computed empirically (
and
).
Figure 2(a) shows that the analytical function
has practically the same curve as the experimental data. The figure shows also that the average number of blocking pairs, normalized by dividing it by
n, decreases during the search process in a way that is independent of the size of the problem.
We can use function to conjecture the runtime behavior of our local search method. Consider the median number of steps, , taken by SML2. Assume this occurs when half the problems have one blocking pair left and the other half have zero blocking pairs. Thus, . Substituting this value in the equation for , taking logs, solving for and grouping constant terms, we get , where c and d are constants. Hence, we can conclude that grows as .
We then fitted this equation for
to the experimental data (using
and
). The result is shown in
Figure 2(b), where we see that the experimental data have the same curve as function
. This suggests that we can use such an equation to predict the number of steps our algorithms needs to solve a given SM instance.
Figure 2.
Results using SML2. (a) Blocking pair ratio during the execution; (b) number of steps necessary to find a stable marriage.
Figure 2.
Results using SML2. (a) Blocking pair ratio during the execution; (b) number of steps necessary to find a stable marriage.
7.1. Sampling the Stable Marriage Lattice
We also evaluated the ability of SML2 to sample the lattice of stable marriages of a given SM problem. To do this, we randomly generated 100 SM problems for each size between 10 and 100, with step 10. Then, we ran the SML2 algorithm 500 times on each instance. To evaluate the sampling capabilities of SML2, we first measured the distance of the found stable marriages (on average) from the male-optimal marriage (the one that would be returned by the GS algorithm).
Given a SM problem instance,
P, consider a stable marriage,
M, for
P. The distance of
M from
is the number of arcs from
M to
in the Hasse diagram of the stable marriage lattice for
P. This diagram can be computed in
time [
10], where
S is the set of all possible stable marriages of a given SM instance. For each SM problem instance, we compute the average normalized distance from the male-optimal marriage considering 500 runs. Notice that normalizations is needed since different SM instances with the same size may have a different number of stable lattices. Then, we compute the average
(With this measure, we want to evaluate how far from the two extremes of the lattice the marriages we find are. However, it is possible to give other definitions of stable matchings that belong to the middle of the lattice, such as the one presented in [
44].) of these distances over all the 100 problems with the same size, which is, therefore, formally defined as
, where
(resp.,
) is the distance of
from the male (resp., female)-optimal marriage in the lattice of an SM instance
. If
, this means that all the stable marriages returned coincide with the male-optimal marriage. On the other extreme, if
, this means that all stable marriages returned coincide with the female-optimal one.
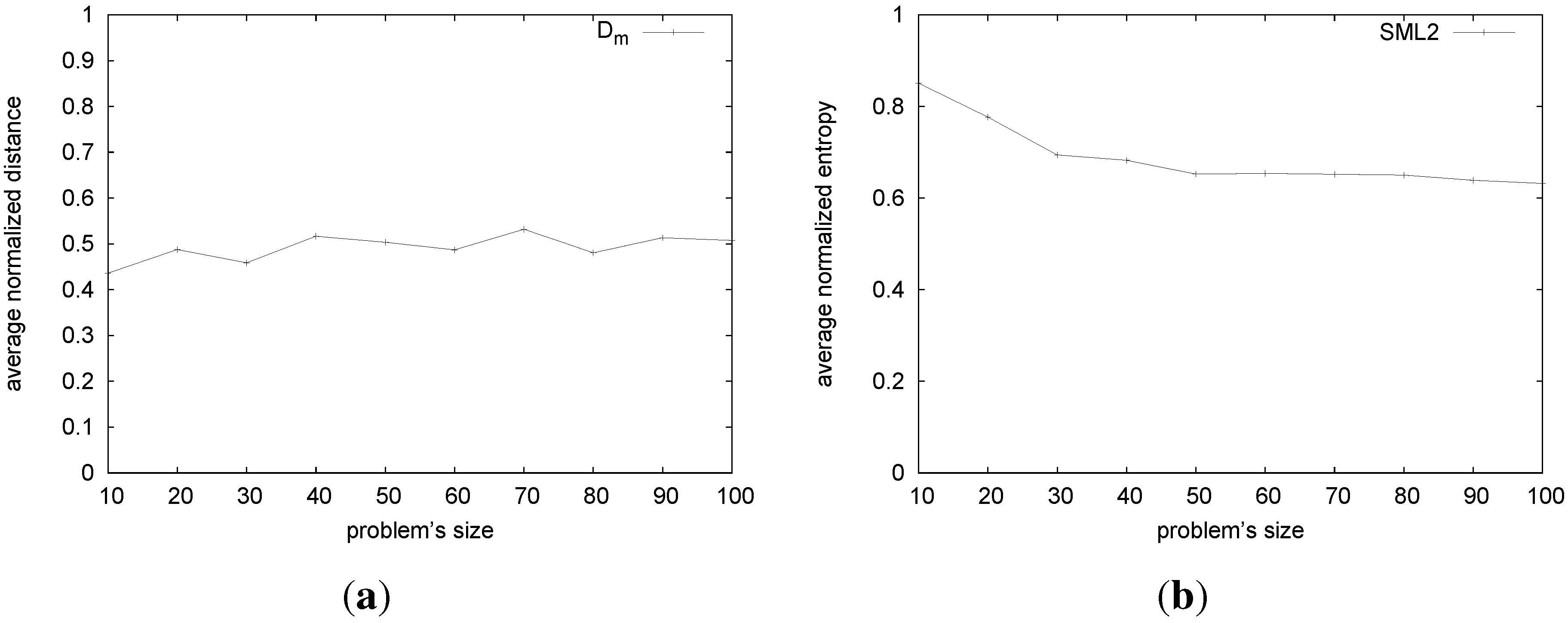
Figure 3(a) shows that, for the stable marriages returned by algorithm SML2, the average distance from the male-optimal is around 0.5.
Figure 3.
Sampling with SML2. (a) Average normalized distance varying n; (b) entropy.
Figure 3.
Sampling with SML2. (a) Average normalized distance varying n; (b) entropy.
This is encouraging, but not completely informative, since an algorithm that returns the same stable marriage all the time, with a distance of 0.5 from the male-optimal would also have . To have more informative results, we consider the entropy of the stable marriages returned by SML2. This measures the randomness in the solutions. Let be the frequency that SML2 finds a marriage, (for i in ), that is: , where is the indicator function that returns one if in the j-th execution the algorithm finds , and zero otherwise. The entropy, , for each SM instance, P (i.e., for each lattice), of the size, k, is then: . In an ideal case, when each stable marriage in the lattice has a uniform probability of to be reached, the entropy is bits. On the other hand, the worst case is when the same stable marriage is always returned, and the entropy is, thus, zero bits. As we want a measure what is independent of the problem’s size, we consider a normalized entropy, that is, , which is in [0,1].
As we have 100 different problems for each size, we compute the average of the normalized entropies for each class of problems with the same size: , where is the set of stable marriages of .
Figure 3(b) shows that SML2 is not far from the ideal behavior. The normalized entropy starts from a value of 0.85 per bit at size 10, decreasing to just above 0.6 per bit as the problem’s size grows.
Considering both
Figure 3(b) and
Figure 3(a), it appears that SML2 samples the stable marriage lattice very well. Considering also the distance,
(
Figure 3(a)), the possible outcomes appear to be equally distributed along the paths from the top to the bottom of the lattice.
To better evaluate the sampling capability of our approach, here, we compare it to a
Markov chain approach (MC) [
40], defined by using rotations exposed in each stable marriage.
More precisely, suppose that
is a current marriage. Then, the next marriage,
, is computed as follows:
(i) with probability 1/3: it randomly chooses a man and, if he is part of a woman-improving rotation ρ, it moves to ;
(ii) with probability 1/3: it randomly chooses a man and, if he is part of a man-improving rotation ρ, it moves to ;
(iii) with probability 1/3, it moves to .
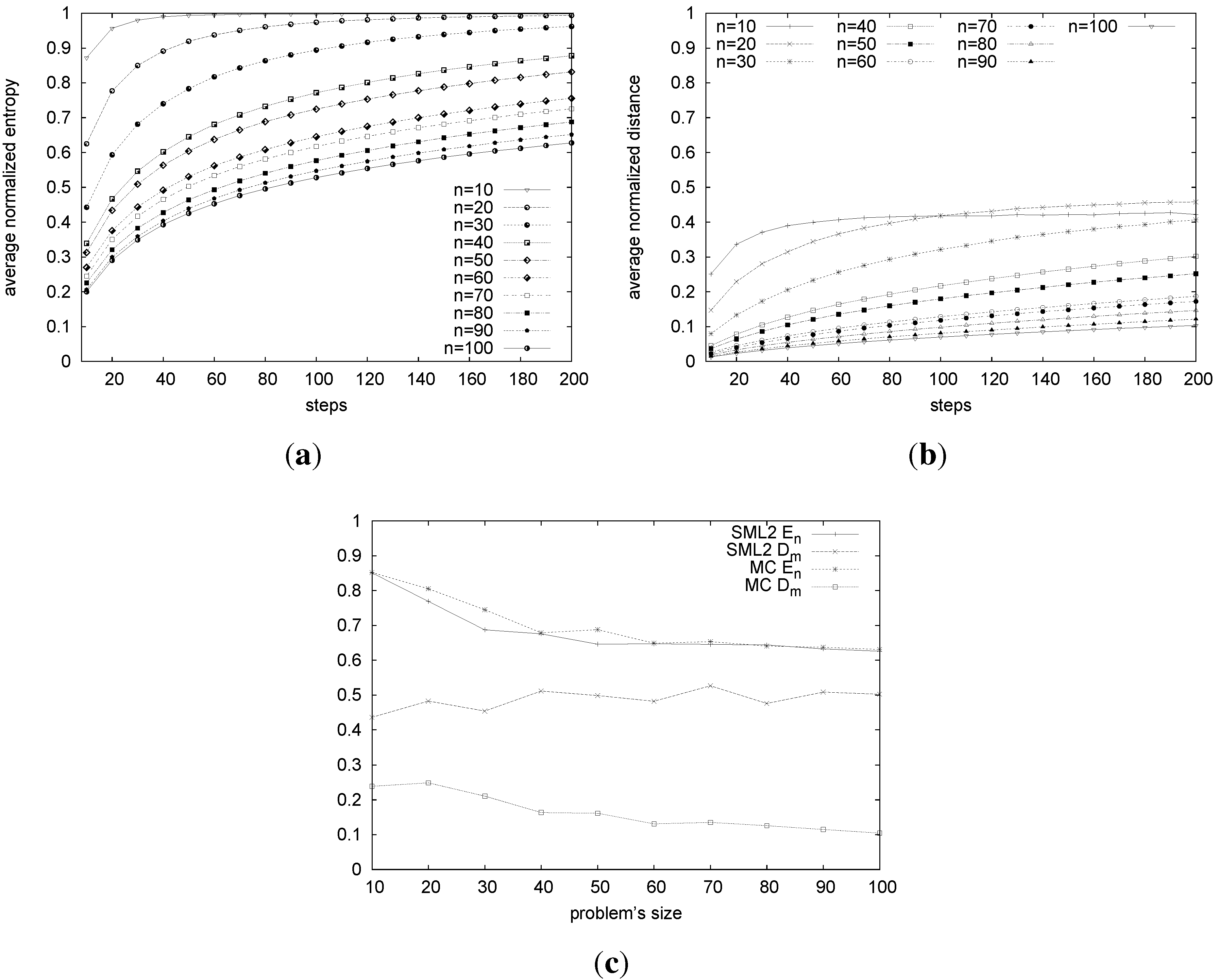
Figure 4.
Average runtime entropy of a Markov chain (MC) (a); average runtime distance from the male-optimal one of the MC (b); local search vs. MC in terms of entropy and distance from the male-optimal one (c).
Figure 4.
Average runtime entropy of a Markov chain (MC) (a); average runtime distance from the male-optimal one of the MC (b); local search vs. MC in terms of entropy and distance from the male-optimal one (c).
Since a rotation and its inverse contain the same people, and the probability of picking a particular rotation is proportional to the number of couples it contains, this Markov chain is reversible. This approach converges in exponential time to the uniform distribution over the stable marriages. We consider the entropy and distance from the male-optimal of MC computed on executions, where we vary the number of steps from 10 to 200. While the entropy of MC increases quite rapidly, the distance from the top of the lattice (i.e., from the male-optimal) increases more slowly (see
Figure 4(a) and
Figure 4(b)). For each problem instance in the test set, we start MC from the male-optimal marriage and take the stable marriage returned by MC after exactly the same number of steps needed by our algorithm to find a stable marriage for that instance. Then, we measure and compare the entropy and the distance from the male-optimal for MC to those of our algorithm (SML2). While the entropy of MC is roughly the same as that of our algorithm, the distance from the male-optimal achieved by our approach (about 0.5) is, on average, higher that that achieved by MC (about 0.2) (see
Figure 4(c)).
Summarizing, our approach is efficient, and it has sampling capabilities comparable with a Markov chain approach considering the same number of steps and may even perform slightly better, considering the distance measured from the top or the bottom of the lattice.
8. Results on SMTI Problems
We generated random SMTI problem instances of a size of 100, by letting vary in [0, 1.0], with step 0.1, and vary in [0.1, 0.8], with step 0.1 (above 0.8, the preference lists start to be empty). For each parameter combination, we generated 100 problem instances. Moreover, the probability of the random walk is set to p = 20%, and the search step limit is s = 50,000.
We start by showing the average size of the marriages returned by LTIU. In
Figure 5(a), we see that LTIU almost always finds a perfect marriage (that is, a stable marriage with no singles). Even in settings with a large amount of incompleteness (that is,
–
), the algorithm finds very many marriages, with only two singles on average.
We also consider the number of steps needed by our algorithm. From
Figure 5(b), we can see that the number of steps is less than 2,000 most of the time, except for problems with a large amount of incompleteness (
i.e.,
). As expected, with
, the algorithm requires more steps. In some cases, it reaches the step limit of 50,000. Moreover, as the percentage of ties rises, stability becomes easier to achieve, and thus, the number of steps tends to decrease slightly. From the results, we see that complete indifference (
= 1) is a special case. In this situation, the number of steps increases for almost every value of
. This is because the algorithm makes most of its progress via random restarts. In these problems, every person (if accepted) is equally preferred to all others accepted. The only blocking pairs are those involving singles who both accept each other. Hence, after a few steps, all singles that can be married are matched; stability is reached, and the neighborhood becomes empty. The algorithm, therefore, randomly restarts. In this situation, it is very difficult to find a perfect matching, and the algorithm, therefore, often reaches the step limit.
Figure 5.
LTIU varying for different values of . (a) Average size of marriages; (b) average number of steps; (c) average execution time; (d) percentage of perfect matchings.
Figure 5.
LTIU varying for different values of . (a) Average size of marriages; (b) average number of steps; (c) average execution time; (d) percentage of perfect matchings.
The algorithm is fast. It takes, on average, less than 40 s to give a result even for very difficult problems (see
Figure 5(c)). As expected, with
, the time increases for the same reason discussed above concerning the number of steps.
Re-considering
Figure 5(a) and the fact that all the marriages the algorithm finds are stable, we notice that most of the marriages are perfect. From
Figure 5(d), we see that the average percentage of matchings that are perfect is almost always 100%, and this percentage only decreases when the incompleteness is large. We compared our local search approach to the one in [
6]. In their experiments, they measured the maximum size of the stable marriages in problems of a size of 10, fixing
to 0.5 and varying
in [0,1]. We did similar experiments and obtained stable marriages of a very similar size to those reported in [
6]. This means that although our algorithm is incomplete in principle, it always appears to find an optimal solution in practice, and for small sizes, it behaves like a complete algorithm in terms of the size of the returned marriage. However, it can also tackle problems of much larger sizes, still obtaining optimal solutions most of the time.
We also considered the runtime behavior of our algorithm. In
Figure 6(a), we show the average normalized number of blocking pairs and, in
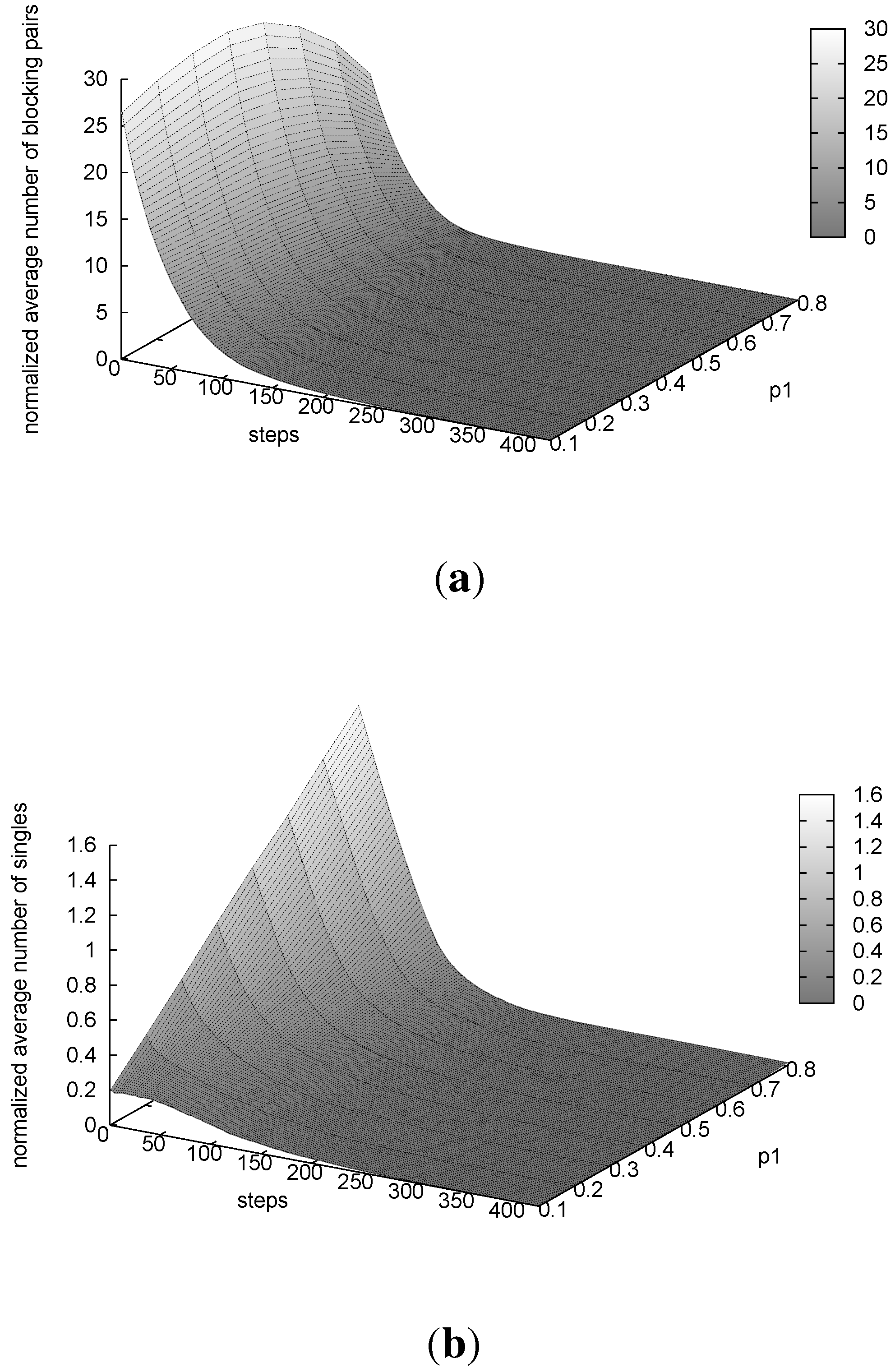
Figure 6(b), the average normalized number of singles of the best marriage as the execution proceeds. Although the step limit is 50,000, we only plot results for the first steps, because the rest is a long plateau that is not very interesting. We show the results only for
= 0.5. However, for a greater (resp., lower) number of ties, the curves are shifted slightly down (resp., up). From
Figure 6(a), we see that the average number of blocking pairs decreases very rapidly, reaching five blocking pairs after only 100 steps. Then, after 300–400 steps, we almost always reach a stable marriage, irrespective of the value of
. Considering
Figure 6(b), we see that the algorithm starts with more singles for greater values of
. This happens because, with more incompleteness, it is more difficult for a person to be accepted. However, after 200 steps, the average number of singles becomes very small no matter the incompleteness in the problem.
Looking at both
Figure 6(a) and
Figure 6(b), we observe that, although we set a step limit
s = 50,000, the algorithm reaches a very good solution after just 300–400 steps. After this number of steps, the best marriage found by the algorithm usually has no blocking pairs nor singles. This appears to be largely independent of the amount of incompleteness and the number of ties in the problems. Hence, for SMTI problem instances of a size of 100, we could set the step limit to just 400 steps and still be reasonably sure that the algorithm will return a stable marriage of a large size, no matter the amount of incompleteness and ties.
Figure 6.
LTIU runtime behavior ( = 0.5). (a) Average normalized number of blocking pairs; (b) average normalized number of singles.
Figure 6.
LTIU runtime behavior ( = 0.5). (a) Average normalized number of blocking pairs; (b) average normalized number of singles.
9. Local Search by Swapping Ties
In previous sections, we have presented two local search algorithms that start from a random marriage and try to converge to a stable marriage with a maximum size by removing blocking pairs. In this section, we present another local search approach suggested by P. Prosser to find the largest stable marriage of a given SMTI instance, I. This approach is based on the observation that, by breaking all ties, I becomes an SMI instance, say , and a stable marriage in is also stable in I, since we are considering weak stability. Furthermore, we recall that all stable marriages of a given SMI have the same size, and one of them can be found in polynomial time using the Gale Shapley algorithm.
More precisely, we consider SMTIs with ties of a length of two (the problem of finding a maximum size stable matching still remains NP-hard in this special case of SMTI [
4]), and we associate a weight in [0,1] to each way of breaking a tie. Initially, such weights are all set to 0.5.
Our method, which is described in Algorithm LST, works as follows. It takes as input an SMTI instance, P, an integer, , and a random walk probability, p. First, it breaks the ties in P, thus obtaining the SMI instance, Q; then, it repeats a sequence of actions as long as the number of steps is lower than . The first of these actions is to compute GS(Q), which finds the male optimal stable matching M of Q by applying the Gale Shapley algorithm to the SMI instance, Q. If the returned marriage, M, is perfect, then the algorithm returns this marriage. Otherwise, if rand(), i.e., if the random number in interval [0,1] generated by the function, rand(), is lower than or equal to the random walk probability, p, then it selects a random tie in P and assigns this tie to tie_neighbest. It applies the procedure, swap_tie(), which returns an SMI instance, Q, that is obtained by Q, where the order of the elements in tie in P is swapped. Then, it finds the male optimal stable matching M of Q, assigns the size of M to max_neigh_size and assigns M to M_neighbest. Otherwise, if rand, for every allowed tie (see the next paragraph) in P, it applies the procedure, swap_tie(), which returns an SMI instance, R, which is obtained by Q, where the order of the elements in tie in P is swapped. Then, it finds the male optimal stable matching M of R. If M is the best stable matching found in the neighborhood, then it recalls that tie as tie_neighbest and that marriage as M_neighbest. After having considered all the allowed ties, it moves to a new SMI instance Q obtained from Q and tie_neighbest by applying the procedure, swap_tie(Q,tie_neighbest). If the size of the obtained stable matching is larger than the overall best one obtained so far, it increases the weight of tie_neighbest by 0.05; otherwise it decreases the weight of tie_neighbest by 0.05.
We can have different versions of the algorithm (Algorithm 1) LST depending on the meaning of the sentence, allowed tie t in P, in line 12. We consider as “allowed” the ties that have a weight greater than a fixed threshold or a certain percentage of ties with the highest weight. In this way, we speed up the search by reducing the size of the neighborhood. We call LSTt (where t is the threshold) the algorithm that limits the neighborhood via a threshold and LSTk (where k is the percentage of best ties considered) the other one.
| Algorithm 1: LST |
![Algorithms 06 00591 i001]() |
9.1. Experimental Evaluation
We generated SMTI problem instances as in the previous section , except for the probability of ties (). For example, if we generate a problem of size n = 100, with a probability of incompleteness = 0.1 and probability of ties = 0.2, then, since = 0.1, the average length of the preference lists will be 90. Additionally, since = 0.2, each preference list will have about nine ties of a length two.
We generated 100 problems for each combination of n, and varying n in {10, 30, 50, 70, 90}, in [0.1, 0.8] and in [0.1, 1.0] and fixing a limit of 20,000 steps.
We ran our algorithms, LSTt and LSTk, on this test set, and we also compared the results against our LTIU algorithm.
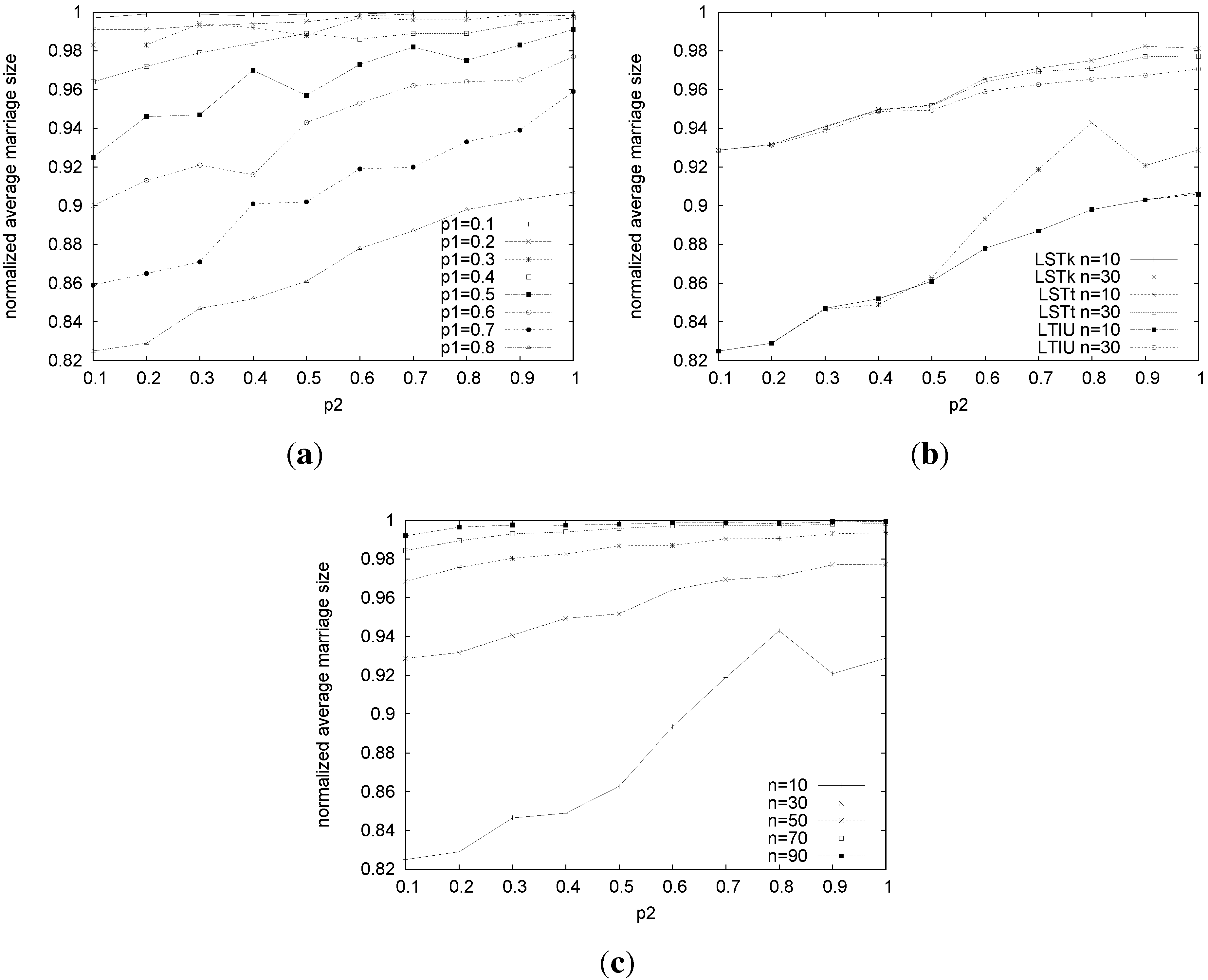
We first measured the average size (normalized w.r.t.the size of the problem) of the stable marriages returned by our algorithms. All three algorithms find larger marriages when the number of ties increases and when the incompleteness in preference lists decreases. In fact, with more ties and longer preference lists, there is less probability of having a blocking pair and more chances for singles to get married.
For instance,
Figure 7(a) shows the results for LSTk when
n = 10 and
k = 50%. The results for LSTt and LTIU are very similar. Only for
= 0.7–0.8 and high values of
, LTIU finds slightly smaller marriages.
Figure 7(b) shows a comparison of the three algorithms on problems of a size of 10 and 30.
For
n = 10, the size of the marriages vary at most only 0.02 comparing LSTk
versus LSTt (LTIU gives practically the same results as LSTt) when we vary the size of the problems. We can also notice that the size of the marriages tends to increase when the size of the problems increases. For instance,
Figure 7(c) shows the results for LSTt, and it easy to see that, for the same values of the other parameters, it finds larger marriages as
n increases. The same results are obtained by the other algorithms. We conjecture that the reason for this behavior is that, considering SMI instances, the probability of having a certain person in at least one preference list, say
, is very high, even with small sizes and a lot of incompleteness. More precisely, the probability of having a person,
p, in at least one preference list in an SMI of size
n, denoted by
, is
. Moreover, the probability to be in exactly
k lists is:
Then, the probability to be in at least
k lists is:
Finally, since our generator rejects problems with empty preference lists, in our test set, each person is always in at least one preference list. Thus, the probability to be in at least
k lists becomes:
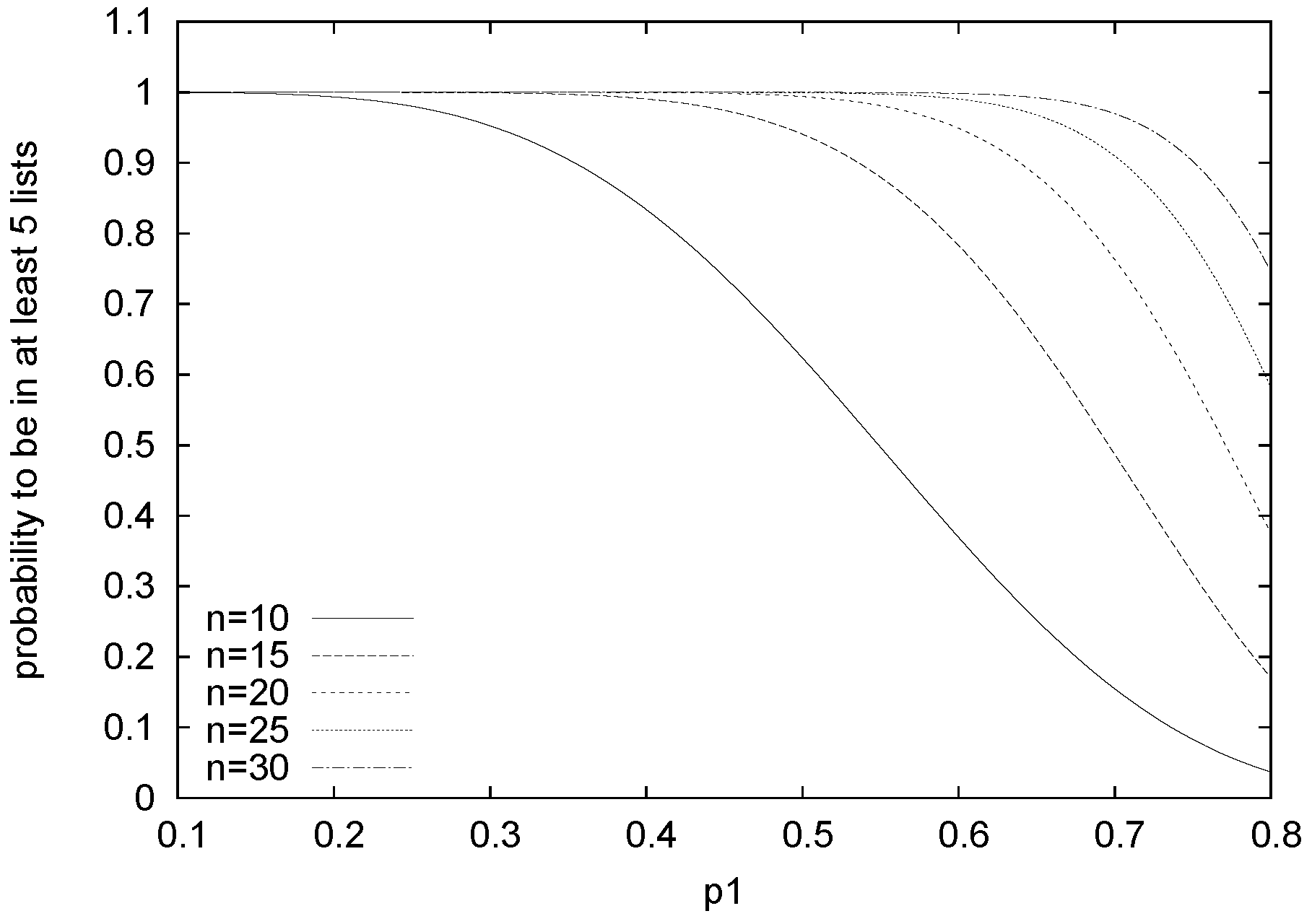
For example,
Figure 8 shows how slowly
decreases when varying
for different values of
n. Thus, in general, the probability for a person to be in more than one preference list rises with the size of the problem. Therefore, having a perfect matching or a marriage with very high cardinality is more probable in bigger problems than in smaller ones.
Figure 7.
Normalized average size of marriages for LSTk, LSTt and LTIU. (a) Normalized average size of marriages found by LSTk using on Stable Marriage with Ties and Incomplete lists (SMTIs) of a size of 10; (b) normalized average size for LSTk, LSTt and LTIU on problems of size 10 and 30. Fixing = 0.8, and ; (c) normalized average size for LSTt varying n and fixing = 0.8 and .
Figure 7.
Normalized average size of marriages for LSTk, LSTt and LTIU. (a) Normalized average size of marriages found by LSTk using on Stable Marriage with Ties and Incomplete lists (SMTIs) of a size of 10; (b) normalized average size for LSTk, LSTt and LTIU on problems of size 10 and 30. Fixing = 0.8, and ; (c) normalized average size for LSTt varying n and fixing = 0.8 and .
Figure 8.
Probability for a person to be in at least five preference lists varying .
Figure 8.
Probability for a person to be in at least five preference lists varying .
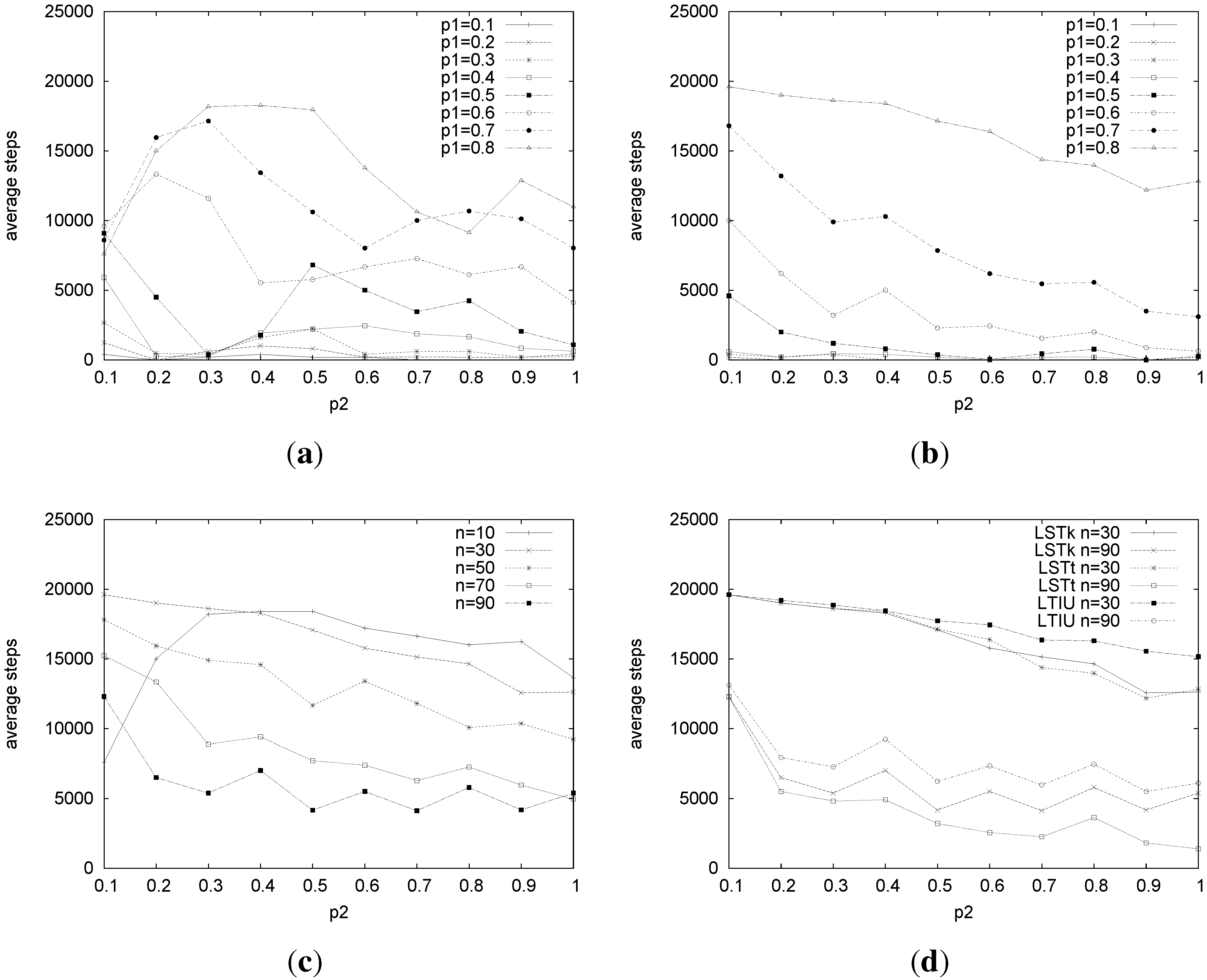
We then considered the average number of steps needed by the algorithms to finish their execution. As can be expected, the number of steps increases as the incompleteness,
, rises. This happens for all algorithms and all problems sizes, and it is more clear as
n increases. This can be seen, for example, in
Figure 9(a), which shows the average number of steps for LSTt on problems of a size of 10 and in
Figure 9(b), which shows the results for
n = 30.
Figure 9.
Average number of steps for LSTt, LSTk and LTIU. (a) Average number of steps for LSTt for n = 10; (b) average number of steps for LSTt for n = 30; (c) average number of steps for LSTt varying n and fixing = 0.8; (d) average number of steps for LSTk, LSTt and LTIU on problems of a size of 30 and 90. Fixing = 0.8, and .
Figure 9.
Average number of steps for LSTt, LSTk and LTIU. (a) Average number of steps for LSTt for n = 10; (b) average number of steps for LSTt for n = 30; (c) average number of steps for LSTt varying n and fixing = 0.8; (d) average number of steps for LSTk, LSTt and LTIU on problems of a size of 30 and 90. Fixing = 0.8, and .
Figure 9(c) shows that the number of steps needed by LSTt for
=0.8 decreases as
n increases. Moreover, it decreases as the amount of ties (
) increases. This behavior is the same for the other algorithms and is due to the increased probability of finding a perfect matching on larger problems. For instance,
Figure 9(d) shows how steps vary considering problems of a size of
n = 30 and
n = 90.
We also measured the execution time of our algorithms. The execution time is mainly influenced by the size and nature of the neighborhood that has to be explored at each search step. The neighborhood used by LTIU depends on blocking pairs, and so, it is larger in problems with few ties. On the other hand, the neighborhoods defined for LSTt and LSTk are bigger as the number of ties rises. For these reasons, the execution time of LTIU tends to slightly decrease as
increases, no matter the size of the problem for fixed values of
(see
Figure 10(a)).
Figure 10(b) and
Figure 10(c) show, respectively, the execution time of LSTk and LSTt. In both cases, the execution is longer as
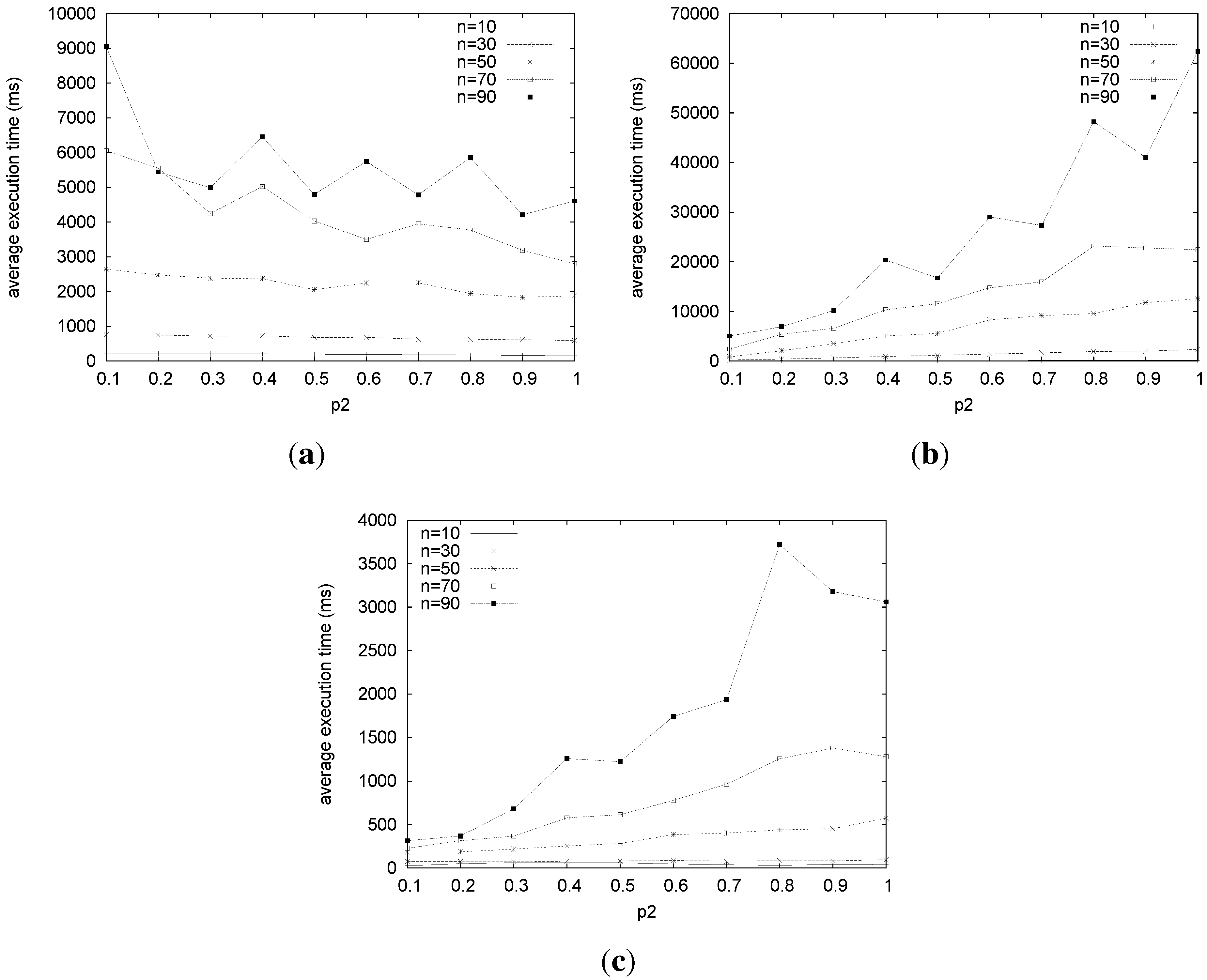
becomes larger. The difference is that the size of the neighborhood in LSTt varies dynamically according to the weights of the ties and the threshold,
t. This speeds up the algorithm drastically, and as we can see, the execution time of LSTt is about half the execution time of LSTk.
Figure 10.
Average execution time for LTIU, LSTk and LSTt. (a) Average execution time for LTIU varying n for = 0.8; (b) average execution time for LSTk varying n for = 0.8 and k = 50%; (c) average execution time for LSTt varying n for = 0.8 and t = 0.5.
Figure 10.
Average execution time for LTIU, LSTk and LSTt. (a) Average execution time for LTIU varying n for = 0.8; (b) average execution time for LSTk varying n for = 0.8 and k = 50%; (c) average execution time for LSTt varying n for = 0.8 and t = 0.5.
Summarizing, both LSTk and LSTt are effective in terms of the size of the returned marriages, but when we also take into account the execution time, LSTt has to be preferred.
10. Conclusions and Future Work
We have presented a local search approach for solving the classical stable marriage (SM) problem instances and its variant with ties and incomplete lists (SMTI). Our algorithm for SM problem instances has a simple scaling and size-independent behavior, and it is able to find a solution in a number of steps, which grows as little as . Moreover, it also samples the stable marriage lattice reasonably well when compared with a Markov chain approach. It is thus a fair method to generate random stable marriages. We also provided an algorithm for SMTI problems, which is both fast and effective at finding large stable marriages for problems of sizes not considered before in the literature. The algorithm was usually able to obtain a very good solution after a small amount of time.
Notice that it is important to validate our local search techniques on larger problem instances. We plan to do that in our future research. Moreover, we intend to compare the algorithms shown in
Section 9 with Algorithm ShiftBrkin [
16]. We plan also to apply a local search approach to the hospital-resident problem and to compare our algorithms to the ones in [
31], where residents express their preferences in strict order and hospitals allow ties in their preferences and each have a finite number of posts.