Multi-Threading a State-of-the-Art Maximum Clique Algorithm

Abstract

We present a threaded parallel adaptation of a state-of-the-art maximum clique algorithm for dense, computationally challenging graphs. We show that near-linear speedups are achievable in practice and that superlinear speedups are common. We include results for several previously unsolved benchmark problems.

1. Introduction

A clique in a graph is a set of vertices, each of which is adjacent to every other vertex in this subset. Deciding whether a graph contains a clique of a given size is one of the archetypal NP-complete problems [1]. We consider the optimisation variant—known as the maximum clique problem—and focus upon dense, computationally challenging graphs [2]. Within computing science, applications include computer vision and pattern recognition; beyond, they extend to mathematics, biology, biochemistry, electrical engineering and communications [3,4].

Multi-core machines are now the norm [5]. Our goal is to adapt a state-of-the-art maximum clique algorithm to make use of the multi-core parallelism offered by today’s processors. We look either to produce a speedup or to allow the tackling of larger problems within a reasonable amount of time [6].

1.1. Preliminaries

We represent a graph as a pair of finite sets, $(V,E)$. The elements of V are known as vertices. The elements of E are edges, represented as pairs, $(v_1,v_2)\in V\times V$. We call vertices $v_1$ and $v_2$ adjacent if $(v_1,v_2)\in E$. Throughout, we assume that our graphs are undirected, that is, $(v_1,v_2)\in E\Rightarrow (v_2,v_1)\in E$, and contain no loops, that is, for all $(v_1,v_2)\in E$, we have $v_1\ne v_2$.

The neighbourhood of a vertex, v, in a graph, G, is the set of vertices adjacent to v, denoted $N(G,v)$. The degree of a vertex is the size of its neighbourhood.

A graph $G^{\prime }=(V^{\prime },E^{\prime })$ is called a subgraph of a graph $G=(V,E)$ if $V^{\prime }\subseteq V$ and $E^{\prime }\subseteq E$. The subgraph induced by $V^{\prime }$ is the subgraph with vertices, $V^{\prime }$, and all edges between those vertices. A graph $G=(V,E)$ is called complete if all its vertices are adjacent—that is, for every distinct pair of vertices, $v_1$ and $v_2$, we have $(v_1,v_2)\in E$. A complete subgraph is known as a clique. We may represent a clique by the vertex set that induces it, and we define the size of the clique to be the size of this vertex set. A clique is maximum if there is no clique with a larger size. We denote the size of a maximum clique in a graph by ω.

A colouring of a graph is an assignment of colours to vertices, such that adjacent vertices are given different colours. Computing a minimal colouring is NP-hard, but a greedy colouring may be obtained in polynomial time.

2. Algorithms for the Maximum Clique Problem

The starting point for our work is a series of algorithms of Tomita [7,8,9]. These are sequential branch and bound algorithms using a greedy graph colouring as a bound and as an ordering heuristic. San Segundo observed that bit parallelism may be used to improve the performance of these algorithms without altering the steps taken [10,11]. A recent computational study analyses these algorithms [12]. We begin by outlining one variant.

Let $G=(V,E)$ be a graph and $v\in V$. We observe that any clique, C, in G either does not contain v or contains only v and possibly vertices adjacent to v. This provides the basis for the branching part of a branch and bound algorithm: incrementally construct the set, C (initially empty), by choosing a candidate vertex, v, from the candidate set, P (initially, all of the vertices in V) and, then, adding v to C. Having chosen a vertex, the candidate set is updated, removing vertices that cannot participate in the evolving clique. If the candidate set is empty, then C cannot grow further, so we backtrack; otherwise, the search continues, selecting from P and adding to C.

We keep track of the largest clique found so far, which we call the incumbent, and denote $C_{max}$. For a bound, we make use of a greedy graph colouring: if we can colour the vertices in P using k colours, we know we cannot extend the size of C by more than k. If this is not enough to unseat the incumbent, we may abandon the search and backtrack.

Producing a new graph colouring at every step is relatively costly. Tomita’s key observation is that if we are given a colouring of a graph, we know not only that we may colour the entire graph using a certain number of colours, but also how to colour certain subgraphs. We demonstrate this in Figure 1 on the following page. Colour classes have been filled greedily: we colour vertex 1 with the first colour, blue, which prevents us from giving vertices 2, 3 or 4 the same colour. We then colour vertex 5 blue, which prevents us from colouring vertex 6 blue. We now start a second colour class (green), and reconsidering uncoloured vertices, we colour vertex 2, then vertex 3. Finally, we colour vertex 4 and, then, vertex 6 in the third colour, yellow. Thus the entire graph can be three-coloured, and we may colour the subgraph induced by $\{1,5,2\}$ or $\{1,5,2,3\}$ using only two colours, the subgraph induced by $\{1,5\}$ using only one colour, and so on. Consequently, as well as a bound, this process gives us an ordering heuristic for selecting a vertex from P: select vertices in non-increasing colour order.

Figure 1. A small graph, together with a constructive colouring.

Figure 1. A small graph, together with a constructive colouring.

We describe this colouring method formally in Algorithm 1. This algorithm produces the same ordering and bounds as the $\mathtt{NUMBER}-\mathtt{SORT}$ procedure from Tomita’s $\mathtt{MCQ}$ [7], but in the manner of San Segundo’s $\mathtt{BBColour}$ procedure in the bitset encoded $\mathtt{BBMC}$ [10]. The algorithm iteratively builds colour classes (lines 9 to 15), where a colour class is an independent set (non-adjacent vertices) of similarly coloured vertices. Line 15 updates the current set of uncoloured vertices, Q, to be the set of vertices not adjacent to the most recently coloured vertex, v. The algorithm delivers as a result a pair $(colour,order)$, where the vertex, $order\left[i\right]$, has been coloured $colour\left[i\right]$ and $colour[i-1]\le colour\left[i\right]$.

Algorithm 1: Sequentially colour vertices and sort into non-decreasing colour order.

We may now discuss Algorithm 2, our baseline sequential algorithm. Following Prosser [12], we opt to order vertices in a non-increasing degree order at the top of the search, use a static ordering throughout, use a bitset encoding and do not include a colour repair mechanism—thus, our algorithm is a bitset encoded version of $\mathtt{MCSa}\mathtt{1}$ (although the techniques presented are not sensitive to this choice).

Algorithm 2: An exact algorithm to deliver a maximum clique.

Procedure $\mathtt{maxClique}$ permutes the graph, such that the vertices are in non-increasing degree order (and this order is exploited by the sequential colouring), then calls the recursive search procedure, $\mathtt{expand}$, on the graph, G, with an initially empty growing clique and a full candidate set. Procedure $\mathtt{expand}$ (lines 7 to 19) searches for cliques. First, the vertices in the candidate set, P, are coloured and sorted (line 9). The procedure then iterates from highest to lowest coloured vertex (line 10). If the size of the growing clique plus the colour number of the current vertex is sufficient to potentially unseat the incumbent, the search progresses (line 11). The ith vertex v, ordered by colour, is selected and added to the growing clique (lines 12 and 13). A new candidate set, $P^{\prime }$, is created, where $P^{\prime }$ is the set of vertices in P adjacent to v. If C cannot grow any further (line 15) and is larger than the incumbent, it is saved (line 16). Otherwise, the search proceeds via a recursive call, with the enlarged clique, C, and reduced candidate set $P^{\prime }$ (line 17). Regardless, having explored the option of taking vertex v (lines 12 to 17), the search then explores the option of not taking vertex v (lines 18 and 19, then iterating back to line 10).

Note that sets are encoded as bit strings, i.e., a bitset encoding similar to San Segundo’s $\mathtt{BBMC}$ [10] is used. This allows the implementation to exploit bit parallelism. The graph should be encoded as an array of n bitsets (this encoding may be done when the graph is permuted). Thus, the call, $N(G,v)$, in line 14 of Algorithm 2 delivers the vth adjacency bitset, and similarly, line 15 of Algorithm 1 delivers the complement of the vth adjacency bitset. To add or remove a vertex from a set, a bit is flipped, and to take the intersection of two sets, a logical-and operation is performed.

Other maximum clique algorithms exist. Recent work by Pattabiraman, Patwary, Rossi et al. [13,14] presents a maximum clique algorithm for sparse graphs and discusses parallelism. Our approach differs in that we primarily consider dense, computationally challenging graphs—on several of the benchmarks where Pattabiraman et al. aborted their run after 10,000 s, our sequential runtime is under one second. Although large sparse graphs have real world applications, we do not wish to neglect the really hard problems [2].

Pattabiraman et al. claim that Tomita’s algorithms are “inherently sequential or otherwise difficult to parallelize”. We agree with the first half of this statement.

3. Parallel Algorithm Design

We may view the branch and bound as being like a depth first search over a tree, where nodes in the tree represent recursive calls. There is a left-to-right dependency between nodes, since we do not know until after we have explored the leftmost subtree whether subtrees further to the right may be eliminated by the bound. However, we may speculatively ignore this dependency and explore subtrees in parallel, sharing the (size of the) incumbent between threads. This technique for branch and bound is generally well known [15,16], and previous experiments by the authors [17], and earlier work by Pardalos [18] suggested that the approach is feasible for a maximum clique.

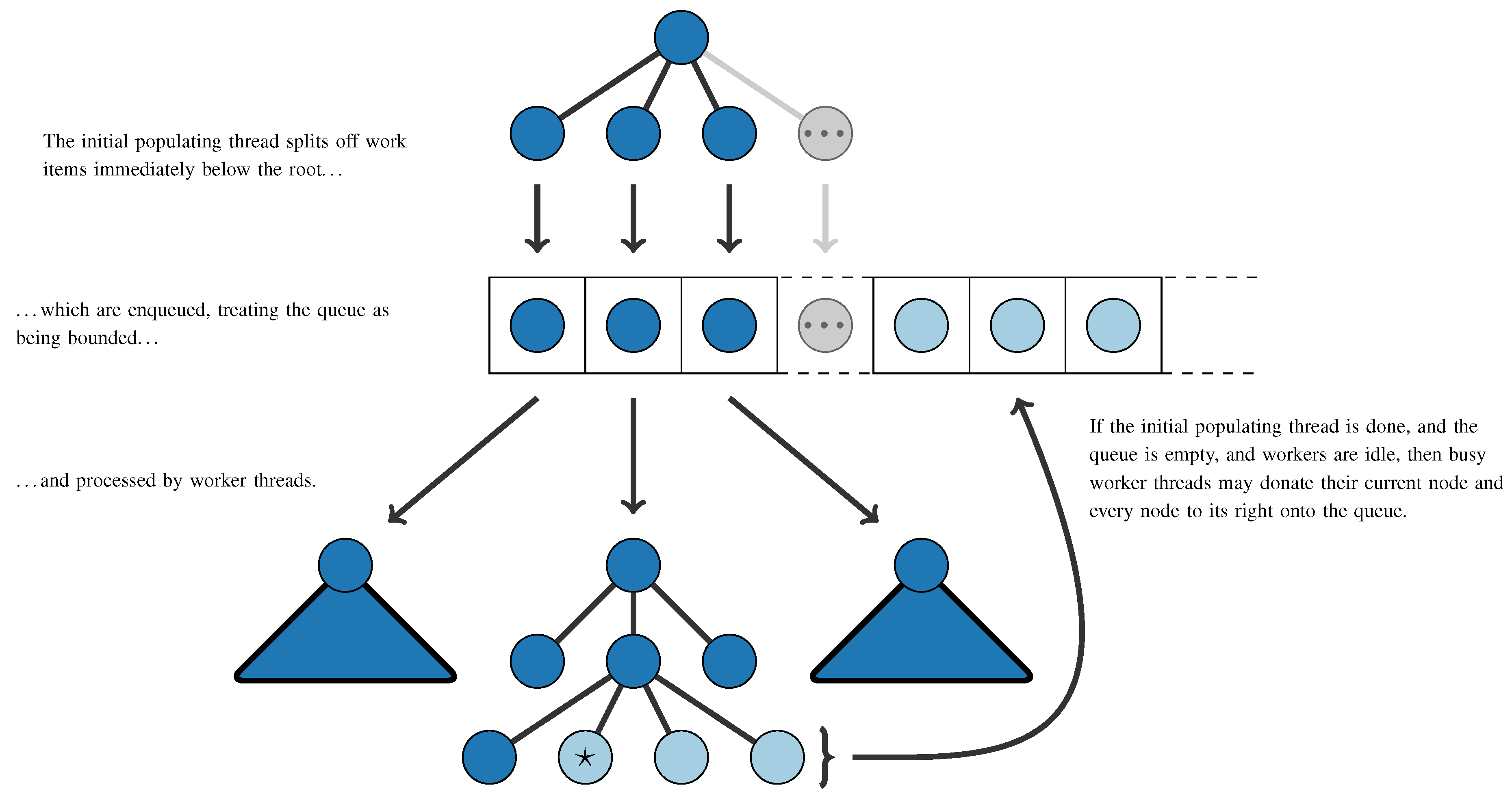
Our parallel version of Algorithm 2 is presented as Algorithm 3 on the next page. We use threads for parallelism; adapting this approach to use message passing is unlikely to be trivial. For work distribution, we use a global queue of work items. Each queue item corresponds to a deferred recursive call to $\mathtt{expand}$. The queue is initially populated by splitting the search tree immediately below the root, in the same order as the sequential algorithm would do. The queue may be treated as bounded when doing so, to avoid excessive memory usage. Worker threads take items from this queue and process them as if they were a sequential subproblem. There is a single variable for the incumbent that must be shared between worker threads—operations involving the incumbent require appropriate synchronisation.

The size of these subtrees can vary dramatically, and we cannot know in advance where the large trees are. Thus, without an additional work splitting mechanism, it is possible that the runtime of a single work item could dominate the overall runtime. We opt for a variation upon work stealing, which we call work donation: if the initial populating has completed, if the queue is empty and if there are idle workers, we set a globally visible flag advising workers that they may choose to place some of their subtrees onto the global queue. We provide a general illustration of this queueing mechanism in Figure 2 on page 624.

The advantage of this method is that it does not require workers to advertise what they are doing and does not require locking, except for rare queue accesses. The success of the sequential algorithm is in part due to its high throughput (we expect to be handling over 100,000 recursive calls per second on modern hardware), and we do not wish to introduce unnecessary overheads. We caution that care must be taken to ensure that worker threads do not exit until no more work can be enqueued (not simply when the queue is empty).

Algorithm 3: A threaded algorithm to deliver a maximum clique

Figure 2. Work splitting and queueing mechanism for our parallel algorithm. Nodes correspond to a call to $\mathtt{expand}$. Work donation occurs once when the donating worker’s position is at the node marked ☆.

Figure 2. Work splitting and queueing mechanism for our parallel algorithm. Nodes correspond to a call to $\mathtt{expand}$. Work donation occurs once when the donating worker’s position is at the node marked ☆.

3.1. Goals of Parallelism

We define the speedup obtained from a parallel algorithm to be the runtime for a good sequential implementation divided by parallel runtime. We call a speedup of n from n cores linear and a speedup of greater than n superlinear.

Intuitively, we may expect that doubling the number of cores available could at best halve the runtime of the algorithm—that is, the speedup we obtain could at best be linear. However, for branch and bound algorithms, this is not the case, and superlinear speedup is possible [19,20,21,22]. This is because we are not simply dividing up a fixed amount of work: if an additional thread finds a better incumbent quickly, we will have less overall work to do. On the flip side, we cannot guarantee that we will produce a speedup at all: it may be that some threads spend all their time exploring parts of the tree, which would have been eliminated in a sequential run, and, so, contribute nothing to the solution.

A parallel algorithm is work efficient if it does “the same amount of work” as a sequential algorithm. We ignore implementation overheads and focus upon a “representative operation”, as is done when considering complexity; here, we count the number of recursive calls to expand. If an algorithm is not work efficient, we define its efficiency to be the ratio of work done by the sequential algorithm to work done by the parallel algorithm, expressed as a percentage. If the time taken to execute each “unit of work” is roughly equivalent, we would expect an efficiency of greater than 100% to be a necessary, but not sufficient, condition for obtaining a superlinear speedup (This is not entirely true, due to cache effects: it could be that the working memory will fit entirely in cache when using multiple cores, but not when using a single core. However, for our purposes, this effect is negligible.).

The goal of parallelisation is not necessarily to produce a speedup. We are also interested in being able to tackle larger problems within a reasonable amount of time [6]. For this work, we consider it more important to be able to reduce a runtime from, say, days to hours, rather than from one second to one tenth of a second.

We must also be careful not to introduce the possibility of a slowdown. Ignoring overheads, this may be done by ensuring that one worker follows “the same path” (or a subset thereof) as the sequential version of the algorithm [23], which our queueing mechanism provides. We must also ensure that newly discovered incumbents are immediately visible to every worker.

3.2. Complications from Hyper-Threading

Hyper-threading “makes a single physical processor appear as two logical processors; the physical execution resources are shared, and the architecture state is duplicated for the two logical processors” [24]. The system we will be using for experimental evaluations is hyper-threaded; this causes complications.

Firstly, this means that when going from using one thread per physical processor to one thread per logical processor, we should not expect to be able to double our speedup. The cited Intel literature suggests a performance increase of “up to 30%”—this figure is derived from benchmarks (which show performance increases of “21%” and “16 to 28%”), not theory. Taken at face value, this means that a speedup of around 15.6 on the 12-core, hyper-threaded system that we describe later should be considered “linear”.

Secondly, and more problematically, this means that if two (software) threads are running on the same physical processing core, each will run more slowly than if it had the core to itself [25]. Because we are not executing a fixed amount of work on each thread, this can lead to a slowdown anomaly—this is a variation of what Bruin et. al. describe as the “[danger of increasing] the processing power of a system by adding a less powerful processing element” [23]. We will assume that so long as the number of threads we use is no greater than the number of physical processing cores, the operating system scheduler will be smart enough to allow us to ignore this issue. For larger numbers of threads, we proceed with the understanding that this could possibly make matters worse, not better (The same problem arises if we use more worker threads than can be executed simultaneously. This, however, is directly under our control.).

4. Experimental Evaluation

4.1. Implementation

We implemented the sequential and threaded algorithms in C++, using C++11 threads [26]. Since we are using shared memory parallelism and since the graph data structure is not modified during execution, we may share the graph between threads to save memory (and improve cache performance). C++ provides us with strong enough guarantees to do this without locking. Sharing the incumbent requires more attention. To avoid the possibility of a slowdown, improved incumbents must be made visible to every worker. To simplify this problem, we note that we only need to share the size of the incumbent, not what its members are. Thus, we need only share a single integer and can retrieve the actual maximum clique when joining threads. We make use of an atomic to do this.

The number of worker threads to use is left as a configuration parameter—this allows experiments to be performed evaluating scalability. We do not count the initial populating thread towards the thread count, as it is expected that the amount of work performed for the population will be a very small part of the overall work. We also do not count the main program thread, which just spawns, then joins, child threads. No attempt was made to parallelise the initial preprocessing and sorting of the graph.

4.2. Experimental Data and Methodology

We work with three sets of experimental data. The first set, from the DIMACS Implementation Challenges [27], contains a smörgåsbord of random and real-world problems of varying difficulty—some can be solved in a few milliseconds, whilst others have not been solved at all. The second set consists of “Benchmarks with Hidden Optimum Solutions for Graph Problems” [28]. Each of these contains a maximum clique of a known size that has been hidden in a way intended to make it exceptionally hard to find. Finally, we consider random graphs.

For timing results, following standard practice, we exclude the time taken to read the graph from the file. We include the time to do preprocessing on the graph (this is not entirely standard, but we consider it the more realistic approach). We measure the wall-clock time until completion of the algorithm. In the case of threaded algorithms, we include the time taken to launch and join threads and to accumulate results as part of the runtime. When giving speedups, we compare threaded runtimes against the sequential algorithm, not against the threaded algorithm running with a single thread, and all experiments have actually been performed on real hardware and are not simulations. We also spend the following section verifying that our implementation of the sequential algorithm is competitive with published results. In other words, our speedup figures measure what we can genuinely gain over a state-of-the-art implementation.

Except where otherwise noted, experiments are performed on a computer with two 2.4 GHz Intel Xeon E5645 processors. Each of these processors has six cores, and hyper-threading is enabled, giving a total of twelve “real” cores or twenty-four hardware threads. To get a better view of scalability, we report results using four, eight, twelve and twenty-four worker threads. Due to the nature of hyper-threading, we should not expect speedup to double when going from twelve to twenty-four threads.

4.3. Comparison of Sequential Algorithm to Published Results

The source code for the implementation by San Segundo [11] is not publicly available. However, we obtained access to a machine with the same CPU model as was used to produce the published results and compared performance for the “brock400” family of graphs from DIMACS. Although our algorithm is not identical, due to differences in initial vertex ordering, we see from Table 1 that runtimes are comparable. The final column presents runtimes using Prosser’s $\mathtt{BMCS}\mathtt{1}$ (which is identical to our sequential algorithm, but coded in Java) on the same machine; we are always faster by a factor of greater than 2.5.

Table 1. Comparison of runtimes (in seconds) for our sequential implementation with San Segundo’s published results for $\mathtt{BBMCI}$ [11] (which differs slightly from our algorithm) and with runtimes using Prosser’s $\mathtt{BBMC}\mathtt{1}$ [12] (which is the same as our algorithm, but in Java). The system used to produce these results has the same model CPU as was used by San Segundo.

Problem	Our runtime (s)	$\mathtt{BBMCI}\left(\mathtt{s}\right)$	$\mathtt{BBMC}\mathtt{1}\left(\mathtt{s}\right)$
brock400_1	198	341	507
brock400_2	144	144	371
brock400_3	114	229	294
brock400_4	56	133	146

Table 1. Comparison of runtimes (in seconds) for our sequential implementation with San Segundo’s published results for $\mathtt{BBMCI}$ [11] (which differs slightly from our algorithm) and with runtimes using Prosser’s $\mathtt{BBMC}\mathtt{1}$ [12] (which is the same as our algorithm, but in Java). The system used to produce these results has the same model CPU as was used by San Segundo.

Problem	Our runtime (s)	$\mathtt{BBMCI}\left(\mathtt{s}\right)$	$\mathtt{BBMC}\mathtt{1}\left(\mathtt{s}\right)$
brock400_1	198	341	507
brock400_2	144	144	371
brock400_3	114	229	294
brock400_4	56	133	146

4.4. Threaded Experimental Results on Standard Benchmarks

Experimental results on graphs from DIMACS are presented in Table 2 and from BHOSLIB in Table 3. The DIMACS benchmarks include a wide variety of problem sizes and difficulties. Problems that took under one second to solve sequentially are omitted. We attempted every DIMACS instance at least with 24 threads. Some problems took over a day to solve with 24 threads, and for these, we indicate the largest clique we found in that time. Blank entries in the table indicate problems that were not attempted with that number of threads.

For four of the problems, we present results that took much longer to calculate. We did not have exclusive access to the machines in question when producing these results, and other CPU-intensive tasks were sometimes being run at the same time. Thus, these runtimes should be considered as an upper bound, rather than an indication of performance. We believe the proofs of optimality for “p_hat1500-3” and “MANN_a81” are new, although in both cases, the maximum clique had already been found (but was not known to be maximum) by heuristic methods. These proofs may be useful to those wishing to evaluate the strength of non-exact algorithms and demonstrate that the tried and tested approach of “throwing more CPU power at a problem” need not be abandoned now that we have more cores rather than more MHz.

Our worst speedups are 3.3 from 4 threads, 6.7 from 8 threads and 7.7 from 12 threads, all from problems where the parallel runtime is under one second. We nearly always produce a near-linear speedup, and we get superlinear speedups for half of the problems. Some of these superlinear speedups are substantial: our best speedups are 19.5 from 4 threads, 75.3 from 8 threads and 102.2 from 12 threads. For the BHOSLIB benchmarks, which are designed to be exceptionally hard to solve, our results are particularly consistent: our speedups are nearly always superlinear, with a speedup of between 11.8 and 15.0 from 12 threads. For the omitted trivial problems, we sometimes got a speedup and sometimes got a slowdown, due to overheads. For larger problems, we do not see any signs of scalability problems when using all of the cores available to us.

Table 2. Experimental results for DIMACS instances. Shown are the size of a maximum clique, then sequential runtimes and the number of search nodes (calls to $\mathtt{expand}$). Next is parallel runtimes, speedups and efficiency using 4 to 24 threads on a 12-core hyper-threaded system. Superlinear speedups and efficiencies greater than 100% are shown in bold; blanks indicate unattempted problems. Problems where the sequential run took under one second are omitted.

Problem	ω	Sequential Runtimes		Threaded Runtimes, Speedups and Efficiency
		and Search Nodes		4			8			12			24
brock400_1	27	274.9s	$2.0\times {10}^8$	69.3 s	4.0	99%	36.0 s	7.6	95%	25.3 s	10.9	90%	11.7 s	23.4	159%
brock400_2	29	200.8 s	$1.5\times {10}^8$	50.7 s	4.0	99%	22.2 s	9.0	117%	16.6 s	12.1	105%	8.9 s	22.5	149%
brock400_3	31	159.4 s	$1.2\times {10}^8$	38.6 s	4.1	106%	17.4 s	9.1	118%	10.6 s	15.1	135%	5.7 s	28.0	193%
brock400_4	33	77.5 s	$5.4\times {10}^7$	17.9 s	4.3	111%	8.5 s	9.1	118%	1.9 s	40.4	477%	1.7 s	45.5	358%
brock800_1	23	4,969.8 s	$2.2\times {10}^9$	1,216.5 s	4.1	104%	587.1 s	8.5	108%	405.6 s	12.3	105%	269.9 s	18.4	122%
brock800_2	24	4,958.2 s	$2.2\times {10}^9$	1,237.8 s	4.0	101%	584.8 s	8.5	109%	386.0 s	12.8	111%	266.7 s	18.6	123%
brock800_3	25	4,590.7 s	$2.1\times {10}^9$	1,125.2 s	4.1	103%	533.2 s	8.6	110%	347.8 s	13.2	114%	222.2 s	20.7	138%
brock800_4	26	1,733.0 s	$6.4\times {10}^8$	408.7 s	4.2	110%	220.3 s	7.9	97%	152.3 s	11.4	96%	131.5 s	13.2	77%
C250.9	44	1,606.8 s	$1.1\times {10}^9$	411.2 s	3.9	98%	228.1 s	7.0	88%	147.8 s	10.9	96%	149.0 s	10.8	97%
C500.9	≥54												>1 day
C1000.9	≥58												>1 day
C2000.5	16	67,058.8 s	$1.8\times {10}^{10}$	17,023.9 s	3.9	100%	8,334.3 s	8.0	100%	5,633.0 s	11.9	100%	4,347.9 s	15.4	100%
C2000.9	≥65												>1 day
C4000.5	18			19 days using 32 threads on a 16-core hyper-threaded dual Xeon E5-2660 shared with other users.
DSJC500_5	13	1.0 s	$1.2\times {10}^6$	266 ms	3.9	101%	152 ms	6.7	101%	130 ms	7.9	99%	89 ms	11.5	99%
DSJC1000_5	15	135.7 s	$7.7\times {10}^7$	34.7 s	3.9	99%	17.4 s	7.8	98%	11.7 s	11.6	99%	9.1 s	15.0	98%
gen200_p0.9_44	44	2.5 s	$1.8\times {10}^6$	654 ms	3.9	100%	109 ms	23.2	471%	100 ms	25.3	316%	95 ms	26.6	540%
gen400_p0.9_55	55			36 h using 32 threads on a 16-core hyper-threaded dual Xeon E5-2660 shared with other users.
gen400_p0.9_65	65	431,310.7 s	$1.8\times {10}^{11}$	96,329.7 s	4.5	114%	38,514.8 s	11.2	140%	16,921.6 s	25.5	216%	17,755.0 s	24.3	162%
gen400_p0.9_75	75	247,538.3 s	$1.0\times {10}^{11}$	22,715.4 s	10.9	309%	17,211.1 s	14.4	214%	11,594.2 s	21.4	200%	3,799.6 s	65.1	445%
hamming10-4	≥40												>1 day
johnson32-2-4	≥16												>1 day
keller5	27	153,970.1 s	$5.1\times {10}^{10}$	38,817.9 s	4.0	100%	19,288.2 s	8.0	100%	12,793.6 s	12.0	100%	10,241.3 s	15.0	100%
keller6	≥55												>1 day
MANN_a45	345	224.8 s	$2.9\times {10}^6$	56.3 s	4.0	100%	27.1 s	8.3	108%	18.2 s	12.3	122%	12.5 s	17.9	161%
MANN_a81	1,100			31 days using 24 threads on a 12-core hyper-threaded dual Xeon E5645 shared with other users.
p_hat300-3	36	1.1 s	$6.2\times {10}^5$	291 ms	3.7	94%	156 ms	7.0	93%	129 ms	8.4	91%	103 ms	10.5	89%
p_hat500-3	50	108.7 s	$3.9\times {10}^7$	29.5 s	3.7	95%	15.1 s	7.2	90%	10.8 s	10.1	86%	8.1 s	13.4	88%
p_hat700-2	44	3.1 s	$7.5\times {10}^5$	946 ms	3.3	102%	402 ms	7.7	103%	403 ms	7.7	100%	270 ms	11.5	93%
p_hat700-3	62	1,627.6 s	$2.8\times {10}^8$	419.9 s	3.9	98%	223.9 s	7.3	91%	156.8 s	10.4	87%	120.4 s	13.5	90%
p_hat1000-2	46	159.2 s	$3.4\times {10}^7$	40.5 s	3.9	98%	20.4 s	7.8	97%	14.3 s	11.1	96%	11.7 s	13.7	92%
p_hat1000-3	68	804,428.9 s	$1.3\times {10}^{11}$	200,853.7 s	4.0	101%	101,303.7 s	7.9	100%	67,659.5 s	11.9	100%	53,424.6 s	15.1	98%
p_hat1500-1	12	3.2 s	$1.2\times {10}^6$	821 ms	3.9	100%	433 ms	7.4	100%	341 ms	9.4	100%	259 ms	12.4	100%
p_hat1500-2	65	24,338.5 s	$2.0\times {10}^9$	6,117.3 s	4.0	99%	3,089.0 s	7.9	98%	2,094.6 s	11.6	96%	1,789.1 s	13.6	91%
p_hat1500-3	94			128 days using 32 threads on a 16-core hyper-threaded dual Xeon E5-2660 shared with other users.
san200_0.9_3	44	8.5 s	$6.8\times {10}^6$	439 ms	19.5	595%	319 ms	26.8	417%	177 ms	48.3	734%	271 ms	31.5	567%
san400_0.7_2	30	2.0 s	$8.9\times {10}^5$	590 ms	3.4	105%	298 ms	6.7	90%	176 ms	11.4	116%	76 ms	26.3	216%
san400_0.7_3	22	1.3 s	$5.2\times {10}^5$	84 ms	15.0	529%	62 ms	20.3	475%	54 ms	23.4	396%	58 ms	21.7	253%
san400_0.9_1	100	23.5 s	$4.5\times {10}^6$	5.3 s	4.4	133%	312 ms	75.3	1,357%	230 ms	102.2	1,353%	191 ms	123.0	1,217%
san1000	15	1.9 s	$1.5\times {10}^5$	488 ms	3.9	101%	281 ms	6.8	107%	173 ms	11.1	108%	108 ms	17.7	139%
sanr200_0.9	42	19.4 s	$1.5\times {10}^7$	5.3 s	3.7	92%	2.8 s	6.8	89%	2.2 s	9.0	85%	3.0 s	6.4	66%
sanr400_0.7	21	72.1 s	$6.4\times {10}^7$	18.1 s	4.0	100%	9.1 s	7.9	100%	6.2 s	11.7	100%	4.6 s	15.7	100%

Table 2. Experimental results for DIMACS instances. Shown are the size of a maximum clique, then sequential runtimes and the number of search nodes (calls to $\mathtt{expand}$). Next is parallel runtimes, speedups and efficiency using 4 to 24 threads on a 12-core hyper-threaded system. Superlinear speedups and efficiencies greater than 100% are shown in bold; blanks indicate unattempted problems. Problems where the sequential run took under one second are omitted.

Problem	ω	Sequential Runtimes		Threaded Runtimes, Speedups and Efficiency
		and Search Nodes		4			8			12			24
brock400_1	27	274.9s	$2.0\times {10}^8$	69.3 s	4.0	99%	36.0 s	7.6	95%	25.3 s	10.9	90%	11.7 s	23.4	159%
brock400_2	29	200.8 s	$1.5\times {10}^8$	50.7 s	4.0	99%	22.2 s	9.0	117%	16.6 s	12.1	105%	8.9 s	22.5	149%
brock400_3	31	159.4 s	$1.2\times {10}^8$	38.6 s	4.1	106%	17.4 s	9.1	118%	10.6 s	15.1	135%	5.7 s	28.0	193%
brock400_4	33	77.5 s	$5.4\times {10}^7$	17.9 s	4.3	111%	8.5 s	9.1	118%	1.9 s	40.4	477%	1.7 s	45.5	358%
brock800_1	23	4,969.8 s	$2.2\times {10}^9$	1,216.5 s	4.1	104%	587.1 s	8.5	108%	405.6 s	12.3	105%	269.9 s	18.4	122%
brock800_2	24	4,958.2 s	$2.2\times {10}^9$	1,237.8 s	4.0	101%	584.8 s	8.5	109%	386.0 s	12.8	111%	266.7 s	18.6	123%
brock800_3	25	4,590.7 s	$2.1\times {10}^9$	1,125.2 s	4.1	103%	533.2 s	8.6	110%	347.8 s	13.2	114%	222.2 s	20.7	138%
brock800_4	26	1,733.0 s	$6.4\times {10}^8$	408.7 s	4.2	110%	220.3 s	7.9	97%	152.3 s	11.4	96%	131.5 s	13.2	77%
C250.9	44	1,606.8 s	$1.1\times {10}^9$	411.2 s	3.9	98%	228.1 s	7.0	88%	147.8 s	10.9	96%	149.0 s	10.8	97%
C500.9	≥54												>1 day
C1000.9	≥58												>1 day
C2000.5	16	67,058.8 s	$1.8\times {10}^{10}$	17,023.9 s	3.9	100%	8,334.3 s	8.0	100%	5,633.0 s	11.9	100%	4,347.9 s	15.4	100%
C2000.9	≥65												>1 day
C4000.5	18			19 days using 32 threads on a 16-core hyper-threaded dual Xeon E5-2660 shared with other users.
DSJC500_5	13	1.0 s	$1.2\times {10}^6$	266 ms	3.9	101%	152 ms	6.7	101%	130 ms	7.9	99%	89 ms	11.5	99%
DSJC1000_5	15	135.7 s	$7.7\times {10}^7$	34.7 s	3.9	99%	17.4 s	7.8	98%	11.7 s	11.6	99%	9.1 s	15.0	98%
gen200_p0.9_44	44	2.5 s	$1.8\times {10}^6$	654 ms	3.9	100%	109 ms	23.2	471%	100 ms	25.3	316%	95 ms	26.6	540%
gen400_p0.9_55	55			36 h using 32 threads on a 16-core hyper-threaded dual Xeon E5-2660 shared with other users.
gen400_p0.9_65	65	431,310.7 s	$1.8\times {10}^{11}$	96,329.7 s	4.5	114%	38,514.8 s	11.2	140%	16,921.6 s	25.5	216%	17,755.0 s	24.3	162%
gen400_p0.9_75	75	247,538.3 s	$1.0\times {10}^{11}$	22,715.4 s	10.9	309%	17,211.1 s	14.4	214%	11,594.2 s	21.4	200%	3,799.6 s	65.1	445%
hamming10-4	≥40												>1 day
johnson32-2-4	≥16												>1 day
keller5	27	153,970.1 s	$5.1\times {10}^{10}$	38,817.9 s	4.0	100%	19,288.2 s	8.0	100%	12,793.6 s	12.0	100%	10,241.3 s	15.0	100%
keller6	≥55												>1 day
MANN_a45	345	224.8 s	$2.9\times {10}^6$	56.3 s	4.0	100%	27.1 s	8.3	108%	18.2 s	12.3	122%	12.5 s	17.9	161%
MANN_a81	1,100			31 days using 24 threads on a 12-core hyper-threaded dual Xeon E5645 shared with other users.
p_hat300-3	36	1.1 s	$6.2\times {10}^5$	291 ms	3.7	94%	156 ms	7.0	93%	129 ms	8.4	91%	103 ms	10.5	89%
p_hat500-3	50	108.7 s	$3.9\times {10}^7$	29.5 s	3.7	95%	15.1 s	7.2	90%	10.8 s	10.1	86%	8.1 s	13.4	88%
p_hat700-2	44	3.1 s	$7.5\times {10}^5$	946 ms	3.3	102%	402 ms	7.7	103%	403 ms	7.7	100%	270 ms	11.5	93%
p_hat700-3	62	1,627.6 s	$2.8\times {10}^8$	419.9 s	3.9	98%	223.9 s	7.3	91%	156.8 s	10.4	87%	120.4 s	13.5	90%
p_hat1000-2	46	159.2 s	$3.4\times {10}^7$	40.5 s	3.9	98%	20.4 s	7.8	97%	14.3 s	11.1	96%	11.7 s	13.7	92%
p_hat1000-3	68	804,428.9 s	$1.3\times {10}^{11}$	200,853.7 s	4.0	101%	101,303.7 s	7.9	100%	67,659.5 s	11.9	100%	53,424.6 s	15.1	98%
p_hat1500-1	12	3.2 s	$1.2\times {10}^6$	821 ms	3.9	100%	433 ms	7.4	100%	341 ms	9.4	100%	259 ms	12.4	100%
p_hat1500-2	65	24,338.5 s	$2.0\times {10}^9$	6,117.3 s	4.0	99%	3,089.0 s	7.9	98%	2,094.6 s	11.6	96%	1,789.1 s	13.6	91%
p_hat1500-3	94			128 days using 32 threads on a 16-core hyper-threaded dual Xeon E5-2660 shared with other users.
san200_0.9_3	44	8.5 s	$6.8\times {10}^6$	439 ms	19.5	595%	319 ms	26.8	417%	177 ms	48.3	734%	271 ms	31.5	567%
san400_0.7_2	30	2.0 s	$8.9\times {10}^5$	590 ms	3.4	105%	298 ms	6.7	90%	176 ms	11.4	116%	76 ms	26.3	216%
san400_0.7_3	22	1.3 s	$5.2\times {10}^5$	84 ms	15.0	529%	62 ms	20.3	475%	54 ms	23.4	396%	58 ms	21.7	253%
san400_0.9_1	100	23.5 s	$4.5\times {10}^6$	5.3 s	4.4	133%	312 ms	75.3	1,357%	230 ms	102.2	1,353%	191 ms	123.0	1,217%
san1000	15	1.9 s	$1.5\times {10}^5$	488 ms	3.9	101%	281 ms	6.8	107%	173 ms	11.1	108%	108 ms	17.7	139%
sanr200_0.9	42	19.4 s	$1.5\times {10}^7$	5.3 s	3.7	92%	2.8 s	6.8	89%	2.2 s	9.0	85%	3.0 s	6.4	66%
sanr400_0.7	21	72.1 s	$6.4\times {10}^7$	18.1 s	4.0	100%	9.1 s	7.9	100%	6.2 s	11.7	100%	4.6 s	15.7	100%

Table 3. Experimental results for BHOSLIB instances. Shown are the size of a maximum clique, then sequential runtimes and the number of search nodes (calls to $\mathtt{expand}$). Next is parallel runtimes, speedups and efficiency using 4 to 24 threads on a 12-core hyper-threaded system. Superlinear speedups and efficiencies greater than 100% are shown in bold.

Problem	ω	Sequential Runtimes and Search Nodes		Threaded Runtimes, Speedups and Efficiency
				4			8			12			24
frb30-15-1	30	657.1 s	2.9 × 108	160.2 s	4.1	102%	76.6 s	8.6	107%	43.9 s	15.0	130%	35.5 s	18.5	127%
frb30-15-2	30	1,183.1 s	5.6 × 108	287.7 s	4.1	102%	141.7 s	8.3	105%	93.6 s	12.6	109%	65.8 s	18.0	131%
frb30-15-3	30	356.7 s	1.7 × 108	80.8 s	4.4	113%	38.8 s	9.2	118%	25.3 s	14.1	125%	19.5 s	18.3	133%
frb30-15-4	30	1,963.2 s	9.9 × 108	496.0 s	4.0	100%	246.1 s	8.0	100%	166.0 s	11.8	100%	124.4 s	15.8	104%
frb30-15-5	30	577.1 s	2.8 × 108	129.2 s	4.5	115%	68.4 s	8.4	109%	44.4 s	13.0	118%	42.1 s	13.7	100%
frb35-17-1	35	51,481.7 s	1.3 × 1010	12,072.8 s	4.3	108%	5,949.7 s	8.7	110%	3,800.8 s	13.5	116%	2,532.0 s	20.3	144%
frb35-17-2	35	91,275.0 s	2.3 × 1010	21,867.3 s	4.2	105%	10,959.2 s	8.3	105%	7,175.1 s	12.7	107%	5,677.3 s	16.1	108%
frb35-17-3	35	33,852.1 s	8.2 × 109	8,278.8 s	4.1	103%	4,063.2 s	8.3	105%	2,813.6 s	12.0	101%	2,349.3 s	14.4	96%
frb35-17-4	35	37,629.2 s	8.9 × 109	9,319.5 s	4.0	101%	4,522.7 s	8.3	105%	2,638.6 s	14.3	122%	2,196.1 s	17.1	111%
frb35-17-5	35	205,356.0 s	5.8 × 1010	49,901.9 s	4.1	103%	25,130.3 s	8.2	102%	16,365.4 s	12.5	105%	10,363.4 s	19.8	137%

Table 3. Experimental results for BHOSLIB instances. Shown are the size of a maximum clique, then sequential runtimes and the number of search nodes (calls to $\mathtt{expand}$). Next is parallel runtimes, speedups and efficiency using 4 to 24 threads on a 12-core hyper-threaded system. Superlinear speedups and efficiencies greater than 100% are shown in bold.

Problem	ω	Sequential Runtimes and Search Nodes		Threaded Runtimes, Speedups and Efficiency
				4			8			12			24
frb30-15-1	30	657.1 s	2.9 × 108	160.2 s	4.1	102%	76.6 s	8.6	107%	43.9 s	15.0	130%	35.5 s	18.5	127%
frb30-15-2	30	1,183.1 s	5.6 × 108	287.7 s	4.1	102%	141.7 s	8.3	105%	93.6 s	12.6	109%	65.8 s	18.0	131%
frb30-15-3	30	356.7 s	1.7 × 108	80.8 s	4.4	113%	38.8 s	9.2	118%	25.3 s	14.1	125%	19.5 s	18.3	133%
frb30-15-4	30	1,963.2 s	9.9 × 108	496.0 s	4.0	100%	246.1 s	8.0	100%	166.0 s	11.8	100%	124.4 s	15.8	104%
frb30-15-5	30	577.1 s	2.8 × 108	129.2 s	4.5	115%	68.4 s	8.4	109%	44.4 s	13.0	118%	42.1 s	13.7	100%
frb35-17-1	35	51,481.7 s	1.3 × 1010	12,072.8 s	4.3	108%	5,949.7 s	8.7	110%	3,800.8 s	13.5	116%	2,532.0 s	20.3	144%
frb35-17-2	35	91,275.0 s	2.3 × 1010	21,867.3 s	4.2	105%	10,959.2 s	8.3	105%	7,175.1 s	12.7	107%	5,677.3 s	16.1	108%
frb35-17-3	35	33,852.1 s	8.2 × 109	8,278.8 s	4.1	103%	4,063.2 s	8.3	105%	2,813.6 s	12.0	101%	2,349.3 s	14.4	96%
frb35-17-4	35	37,629.2 s	8.9 × 109	9,319.5 s	4.0	101%	4,522.7 s	8.3	105%	2,638.6 s	14.3	122%	2,196.1 s	17.1	111%
frb35-17-5	35	205,356.0 s	5.8 × 1010	49,901.9 s	4.1	103%	25,130.3 s	8.2	102%	16,365.4 s	12.5	105%	10,363.4 s	19.8	137%

When using 24 threads, we must worry about hyper-threading; nonetheless, our speedups typically (but not always) improve over those for 12 threads, and even when they do not, a speedup is still obtained. The “gen400_p0.9_75” graph benefits strongly from hyper-threading: with 24 threads, a maximum clique is found (but not proven) after 3,757 s by taking the 17th, 8th, 3rd and 4th choices given by the heuristic, followed by the first choice thereafter. With 12 threads, it takes 11,536 s to find this same maximum, resulting in a lower speedup. On the other hand, “gen400_p0.9_65” is worse with 24 threads: here, it takes 16,288 s rather than 14,868 s to find a maximum, in both cases by taking the 11th, 7th, 3rd and 2nd heuristic choices. This is because hyper-threading provides increased parallelism, at the expense of making each individual thread run more slowly [25], and our additional threads do not reduce the amount of work needed to find a maximum. In the worst case, this property of hyper-threading could even cause a slowdown, although we have never observed this.

As well as speedups, we present efficiencies. We see that, as expected, superlinear speedups are due to efficiencies of greater than 100%. The converse does not always hold, due to overheads.

The “C2000.5” instance from DIMACS provides an indication of how effective our work splitting mechanism is. Here, we see that the efficiency is in each case 100% (at least up to rounding). A speedup of 11.9 from 12 processors would be considered good even for an “embarrassingly parallel” algorithm with a regular work item size, which we do not have. The speedup of 15.4 from 24 threads shows that hyper-threading provides some increase in throughput—in this case, we almost exactly obtain Intel’s claimed benefits of “up to 30%” [24].

4.5. Threaded Experimental Results on Larger Sparse Random Graphs

Experimental results on larger, sparser random graphs are presented in Table 4 on the next page. Here, $G(n,p)$ refers to an Erdős-Réyni random graph with n vertices and edges between each pair of vertices chosen independently with probability p. We see that for $G(1000,0.1)$, where the average sequential runtime is 18 ms, we fail to produce any speedup with 4 threads, and we introduce an increasingly large slowdown as the number of threads rises. With $G(1000,0.2)$, where the average sequential runtime is 65 ms, we do manage to produce a speedup of 2.2 with 4 threads, but this falls to 1.8 with 24 threads. For $G(1000,0.3)$ and $G(3000,0.1)$, where sequential runtimes are under a second, our speedups are modest. This is due to the overheads involved in creating and joining threads and the initial sequential portion of the algorithm whose effects cannot be ignored at this scale. For the remaining problems, where sequential runtimes are longer, our results are better: we achieve average speedups between 3.9 to 4.0 from 4 threads, between 7.1 and 7.9 from 8 threads, between 9.9 and 11.3 from 12 threads and between 11.6 and 15.6 from 24 threads.

We caution that the sequential algorithm we used is not the best choice for sufficiently large and sparse graphs. The benefits of using a bitset encoding decrease as graphs become increasingly sparse, and eventually, it becomes a penalty rather than an improvement [12]. The bitset encoding also forces an adjacency matrix representation of the graph, which requires quadratic memory, even for sparse graphs. For dealing with huge, but very sparse, “real world” graphs, where the difficulty is primarily due to the size of the graphs rather than the computational complexity, we would recommend considering a different algorithm, which can use an adjacent list representation.

Table 4. Experimental results for larger, sparser random graph instances, sample size of 10. Shown are average sequential runtimes and, then, average parallel runtimes and speedups using 4 to 24 threads on a 12-core hyper-threaded system.

Problem	Sequential Runtimes	Average Threaded Runtimes and Speedups
		4		8		12		24
G(1, 000, 0.1)	18 ms	18 ms	1.0	23 ms	0.8	26 ms	0.7	33 ms	0.5
G(1, 000, 0.2)	65 ms	30 ms	2.2	30 ms	2.2	32 ms	2.0	36 ms	1.8
G(1, 000, 0.3)	532 ms	151 ms	3.5	100 ms	5.3	83 ms	6.4	76 ms	7.0
G(1, 000, 0.4)	6.1 s	1.6 s	3.9	860 ms	7.1	585 ms	10.5	439 ms	13.9
G(1, 000, 0.5)	138.6 s	34.9 s	4.0	17.6 s	7.9	12.2 s	11.3	8.9 s	15.6
G(3, 000, 0.1)	640 ms	220 ms	2.9	171 ms	3.7	156 ms	4.1	168 ms	3.8
G(3, 000, 0.2)	11.9 s	3.1 s	3.9	1.7 s	7.0	1.2 s	10.1	900 ms	13.3
G(3, 000, 0.3)	358.5 s	90.3 s	4.0	45.6 s	7.9	30.7 s	11.7	23.2 s	15.4
G(10, 000, 0.1)	84.6 s	21.8 s	3.9	11.5 s	7.3	8.5 s	9.9	7.3 s	11.6
G(15, 000, 0.1)	403.5 s	102.8 s	3.9	53.8 s	7.5	38.1 s	10.6	33.2 s	12.2

Table 4. Experimental results for larger, sparser random graph instances, sample size of 10. Shown are average sequential runtimes and, then, average parallel runtimes and speedups using 4 to 24 threads on a 12-core hyper-threaded system.

Problem	Sequential Runtimes	Average Threaded Runtimes and Speedups
		4		8		12		24
G(1, 000, 0.1)	18 ms	18 ms	1.0	23 ms	0.8	26 ms	0.7	33 ms	0.5
G(1, 000, 0.2)	65 ms	30 ms	2.2	30 ms	2.2	32 ms	2.0	36 ms	1.8
G(1, 000, 0.3)	532 ms	151 ms	3.5	100 ms	5.3	83 ms	6.4	76 ms	7.0
G(1, 000, 0.4)	6.1 s	1.6 s	3.9	860 ms	7.1	585 ms	10.5	439 ms	13.9
G(1, 000, 0.5)	138.6 s	34.9 s	4.0	17.6 s	7.9	12.2 s	11.3	8.9 s	15.6
G(3, 000, 0.1)	640 ms	220 ms	2.9	171 ms	3.7	156 ms	4.1	168 ms	3.8
G(3, 000, 0.2)	11.9 s	3.1 s	3.9	1.7 s	7.0	1.2 s	10.1	900 ms	13.3
G(3, 000, 0.3)	358.5 s	90.3 s	4.0	45.6 s	7.9	30.7 s	11.7	23.2 s	15.4
G(10, 000, 0.1)	84.6 s	21.8 s	3.9	11.5 s	7.3	8.5 s	9.9	7.3 s	11.6
G(15, 000, 0.1)	403.5 s	102.8 s	3.9	53.8 s	7.5	38.1 s	10.6	33.2 s	12.2

4.6. A Detailed Look at a Super-Linear Speedup

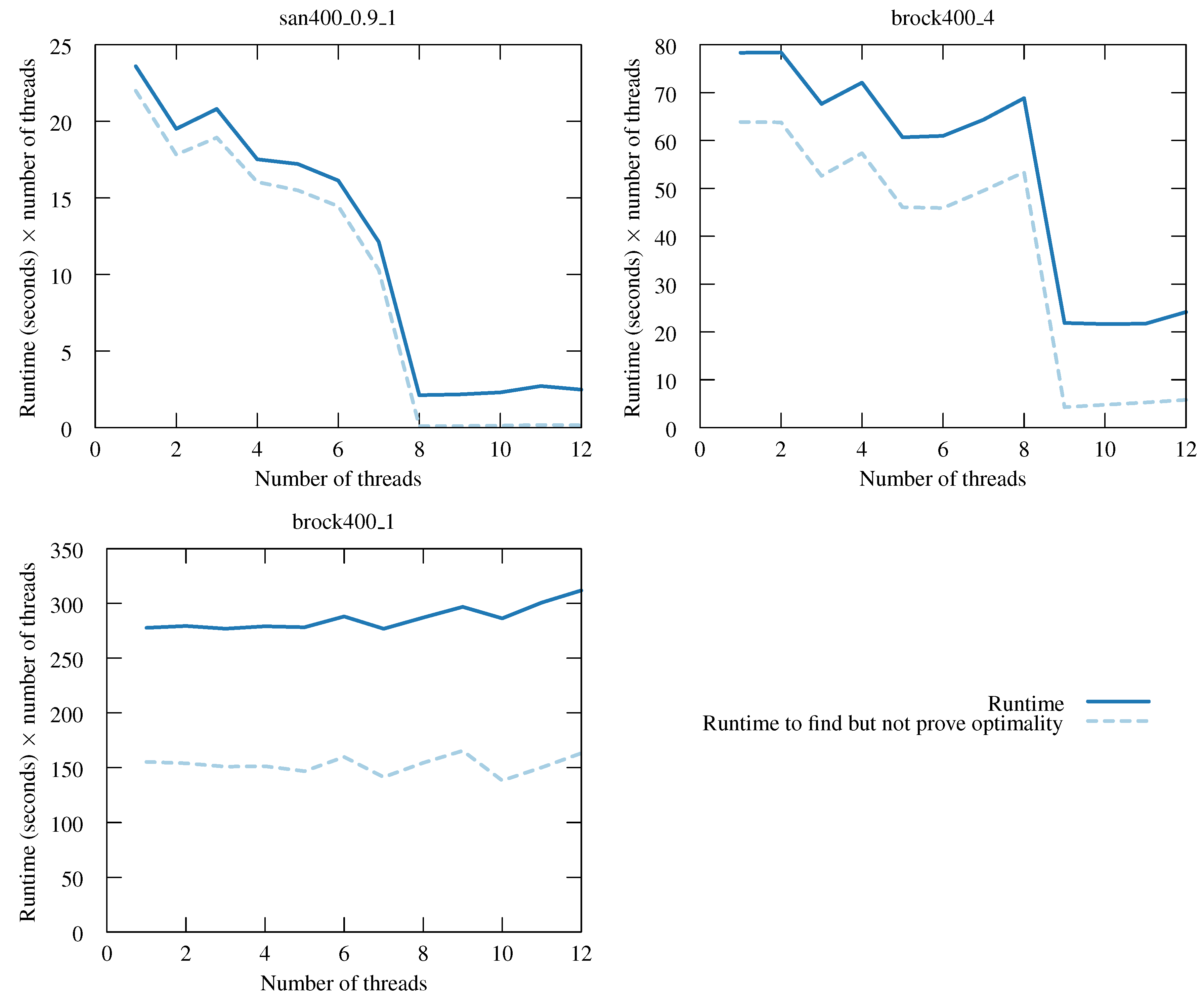
The behaviour seen with the DIMACS instance “san400_0.9_1” is interesting and deserves more attention. We plot runtimes for this instance with varying numbers of threads in Figure 3 on the following page. For the y-axis, we do not plot parallel runtimes; rather, we plot the parallel runtime multiplied by the number of threads—one may think of this as being “total work done”. With such a y-axis, a linear speedup would give a horizontal line. We see a sharp drop as we go to eight threads, after which the line is horizontal.

We can explain this behaviour. Also plotted is the total runtime taken to find a maximum clique, but not proven is its optimality (we rerun the algorithm, telling it to exit as soon as it finds a clique of a size equal to what we now know the maximum to be). We see that with eight threads, a maximum clique is found almost instantly. This is because a maximum clique is located in the part of the search tree given by taking the eighth heuristic choice at the top of search, followed by the first choice at every subsequent depth. The work remaining once such a clique has been found is fixed and consists of exploring every node that cannot be eliminated by the bound regardless of the current incumbent—this explains the linear-like behaviour at over eight threads.

The same behaviour is observed with other “san” graphs and members of the “brock” and “gen” families. The plot of “brock400_4” is similar to that of “san400_0.9_1”, with a drop in work when going to nine threads and, then, a level graph afterwards. Here, a maximum clique is found by taking the ninth heuristic choice, then the third, fourth and third.

For “brock400_1”, we do not see a drop in work done, but we do see an unusually high improvement when going from 12 to 24 threads, despite hyper-threading. Further experiments show that with 20 or more threads, a maximum clique would be found very quickly, and we would get strongly superlinear speedups here, too (One may ask why we do not then use more threads than we have cores, to make this more likely to happen. Such an approach would sometimes be of benefit, but only if we are prepared to accept the possibility of a considerable slowdown in other cases.).

Figure 3. Total CPU time spent (i.e., runtimes multiplied by the number of threads) for “san400_0.9_1” from DIMACS with varying numbers of threads. Also shown is the total CPU time taken to find a maximum clique, but not to prove its optimality. A linear speedup would give a horizontal line, and downwards sloping lines are superlinear.

Figure 3. Total CPU time spent (i.e., runtimes multiplied by the number of threads) for “san400_0.9_1” from DIMACS with varying numbers of threads. Also shown is the total CPU time taken to find a maximum clique, but not to prove its optimality. A linear speedup would give a horizontal line, and downwards sloping lines are superlinear.

5. Conclusion and Future Work

Despite some of the more pessimistic claims that have been made in the literature regarding the suitability of sequential maximum clique algorithms for parallelisation, we have shown that making use of multi-core parallelism for hard clique problems is possible and worthwhile. This is important for two reasons. Firstly, existing work on local parallelism using bitset encodings has produced a speedup of between two and twenty over the basic algorithm [10,12]. We have shown that a further speedup of around the same magnitude is possible by making use of the resources offered by today’s multi-core processors.

Secondly, we have shown that superlinearity can happen in practice and not just as a rare event. Furthermore, when it does happen, the effects can be extremely significant—we are able to make some “hard” instances “easy”. We conjecture that this is due to the method used to split the work, where we use parallelism to avoid an overly strong commitment to an early heuristic. Had we not used this approach, we expect we would be repeating Lai and Sahni’s claim that “our experimental results indicate that such anomalous behaviour will be rarely witnessed in practice” [19].

We expect that this work can be extended in the future. Recently, Batsyn et al. have proposed a number of improvements to Tomita’s algorithms [29]. These changes are all compatible with our approach and also appear to be amenable to bit-parallelisation. We expect that by combining this improved algorithm with bit parallelism and extending our global parallelism approach to be usable with multiple many-core Intel Xeon Phi processors, we may be able to solve yet more of the remaining open DIMACS problems. Additionally, of course, we will be interested to find out whether other hard problems may be tackled using a similar approach.