Abstract
The stable matching problem (also known as the stable marriage problem) is a well-known problem of matching men to women, so that no man and woman, who are not married to each other, both prefer each other. Such a problem has a wide variety of practical applications, ranging from matching resident doctors to hospitals, to matching students to schools or, more generally, to any two-sided market. In the classical stable marriage problem, both men and women express a strict preference order over the members of the other sex, in a qualitative way. Here, we consider stable marriage problems with weighted preferences: each man (resp., woman) provides a score for each woman (resp., man). Such problems are more expressive than the classical stable marriage problems. Moreover, in some real-life situations, it is more natural to express scores (to model, for example, profits or costs) rather than a qualitative preference ordering. In this context, we define new notions of stability and optimality, and we provide algorithms to find marriages that are stable and/or optimal according to these notions. While expressivity greatly increases by adopting weighted preferences, we show that, in most cases, the desired solutions can be found by adapting existing algorithms for the classical stable marriage problem. We also consider the manipulability properties of the procedures that return such stable marriages. While we know that all procedures are manipulable by modifying the preference lists or by truncating them, here, we consider if manipulation can occur also by just modifying the weights while preserving the ordering and avoiding truncation. It turns out that, by adding weights, in some cases, we may increase the possibility of manipulating, and this cannot be avoided by any reasonable restriction on the weights.
1. Introduction
The stable matching problem (SM) [1] is a well-known problem of matching the elements of two sets. It is also called the stable marriage problem, since the standard formulation is in terms of men and women, and the matching is interpreted in terms of a set of marriages. Given n men and n women, where each person expresses a strict ordering over the members of the opposite sex, the problem is to match the men to the women, so that there are no two people of the opposite sex who would both rather be matched with each other than their current partners. If there are no such people, all the marriages are said to be stable. In [2], Gale and Shapley proved that it is always possible to find a stable marriage and provided a polynomial time algorithm, which can be used to find one of two extreme stable marriages, the so-called male-optimal or female-optimal solutions. The Gale–Shapley algorithm has been used in many real-life scenarios [3], such as in matching hospitals to resident doctors [4], medical students to hospitals, sailors to ships [5], primary school students to secondary schools [6], as well as in market trading.
In the classical stable marriage problem, both men and women express a strict preference order over the members of the other sex in a qualitative way. Here, we consider stable marriage problems with weighted preferences. In such problems, each man (resp., woman) provides a score for each woman (resp., man). Stable marriage problems with weighted preferences [7,8] are interesting, since they are more expressive than the classical stable marriage problems, since in the classical stable marriage problem, a man (resp., a woman) cannot express how much he (resp., she) prefers a certain woman (resp., man). Moreover, they are useful in some real-life situations, where it is more natural to express scores that can model notions, such as profit or cost, rather than a qualitative preference ordering. In this context, we define new notions of stability and optimality, we compare such notions with the classical ones and we show algorithms to find marriages that are stable and/or optimal according to these notions. While expressivity increases by adopting weighted preferences, we show that in most cases, the desired solutions can be found by adapting existing algorithms for the classical stable marriage problem.
In this paper, we also study if the stable marriage procedures that return one of these new stable marriages are manipulable. In [9], Roth has shown that, when there are at least three men and three women, every stable marriage procedure is manipulable,i.e., there is a profile in which an agent can mis-report his preferences and obtain a stable marriage that is better than or equal to the one obtained by telling the truth. In this setting, mis-reporting preferences means changing the preference ordering [9] or truncating the preference list [10]. In this paper, we consider a possible additional way of mis-reporting one’s own preferences, which is by just modifying the weights, in a way such that the orderings are preserved and the lists remain complete. We show that it is actually possible to manipulate by just doing this. Thus, in some cases, adding weights makes stable marriage procedures less resistant to manipulation. Moreover, we show that, in these cases, there are no reasonable restrictions on the weights that can prevent such manipulation. As an example of an incentive to manipulate, we can think of an Extreme Programming scenario [11], where we have to match pairs of programmers that must work together. In this scenario, programmers may have an idea of their colleagues preferences and might try to manipulate by lying about their utility or scoring on colleagues to make sure they are paired with their feasible favorite. Moreover, an incentive to manipulate can also be present in the case of matching students to schools.
The paper is organized as follows. In Section 2, we present related research. In Section 3, we give the basic notions of classical stable marriage problems, stable marriage problems with partially ordered preferences and stable marriage problems with weighted preferences (SMWs). In Section 4, we introduce a new notion of stability, called α-stability, for SMWs, which depends on the difference of scores that every person gives to two different people of the other sex, and we compare it with the classical notion of stability. Moreover, we give a new notion of optimality, called lex-optimality, to discriminate among the new stable marriages, which depends on a voting rule. We show that there is a unique optimal stable marriage, and we give an algorithm to find it. In Section 5, we introduce other notions of stability for SMWs that are based on the strength of the link of the pairs (man,woman), we compare them with the classical stability notion and we show how to find marriages that are stable according to these notions with the highest global link. In Section 6, we analyze manipulation issues. In Section 7, we summarize the results contained in the paper, and we give some hints for future work.
This paper is a revised and extended version of the conference papers [12,13,14].
2. Related Work
Stable marriage problems with weighted preferences have been studied also in [7,8]. However, they solve these problems by looking at the stable marriages that maximize the sum of the weights of the married pairs, where the weights depend on the specific criteria used to find an optimal solution, which can be the minimum regret criterion [7], the egalitarian criterion [8] or the Lexcriteria [8]. Therefore, they have considered as stable the same marriages that are stable when we have not considered the weights. We have instead used the weights to define new notions of stability that may lead to stable marriages that are different from the classical case. They may rely on the difference of weights that a person gives to two different people of the other sex or by the strength of the link of the pairs (man,woman),i.e., how much a person of the pair wants to be married with the other person of the pair.
The classical definition of stability for stable marriage problems with weighted preferences has been considered also in [15], which has used a semiring-based soft constraint approach [16] to model and solve these problems. In [15], the authors have modeled such problems as soft constraint problems, and they have used as an optimization criterion a criterion that depends on the chosen semiring (such as Weighted and Fuzzy), thus solving with a unique solver different problems already solved in the literature, also, such as minimizing the egalitarian cost. While in [15], they have considered the classical definition of stability, we have defined more sophisticated notions of stability, and we have presented ad hoc algorithms that are able to find solutions that are stable according to the new notions.
Another encoding of stable marriage problems as constraint problems has been also considered in [17]. In [18], Gent and Prosser provide a constraint programming (CP) encoding to solve a special variant of the stable marriage problem with ties and incomplete lists. Then, the encoded problem is solved using on the shelf CP technology. They provide an empirical study of stable marriage problems with ties and incomplete lists by considering the problem of finding a maximum or minimum cardinality stable marriage. Gent et al. [19] also give a SATencoding of the stable marriage problem with ties and incomplete lists. Using such an encoding, they obtain very good results in the decision problem of whether there is a perfect matching. Many other papers use constraint programming techniques and local search methods to solve classical stable marriage problems and stable marriage problems with ties and incomplete lists [20,21,22,23,24,25]. However, all these papers consider classical notions of stability.
A new notion of stability, that corresponds to our α-stability, has been also considered in [26,27]. In particular, our notion of α-stability corresponds to Definition 2 on page 13 of [27] of additive α-stability in the asymmetric directed case. However, there are some important differences that make our results on α-stability complementary to those in [26,27]. More precisely, we do not restrict our weights to represent utilities, for example; weights may represent the resources a member is willing to make available to the partnership with the other member. Moreover, we do not assume any normalization between zero and one of the weights (called utilities); we do not focus in our results on the global utility of an α-stable marriage, and we do not consider (non-zero) switching costs. Furthermore, the results in Section 5.4 of [27], which are related to the notion of additive α-stability, address the undirected edge-labeled case and, thus, do not apply in our case, since we are in the directed setting. Moreover, we focus on the relation of the weighted problems with respect to the unweighted classical problem, which is a new aspect not considered in [26,27].
Beside the new notions of stability for stable marriage problems with weighted preferences, we have also provided a new way for mis-reporting the preferences by just modifying the weights, in a way such that the orderings are preserved and the lists remain complete. In [9], Roth has shown that, when there are at least three men and three women, every stable marriage procedure is manipulable, i.e., there is a profile in which an agent can mis-report his preferences and obtain a stable marriage that is better than or equal to the one obtained by telling the truth. In their setting, mis-reporting preferences means changing the preference ordering [9] or truncating the preference list [10], while in our setting, mis-reporting the preferences means only modifying the weights, while preserving the ordering and without truncating the preference list.
When we have defined α-stability notion, we have also provided a new definition of optimality, which relies on a voting rule that can be used to provide an ordering over the men and the women on the basis of the given preferences. Voting theory [28] is a wide research area that considers scenarios (elections) in which a collection of voters (or agents) vote by expressing their preferences over a set of candidates (or outcomes) and a voting rule decides the winner. Voting theory provides many voting rules to aggregate agents’ preferences. Each rule takes, as input, a partial or complete preference ordering of the agents and gives, as output, a winner (an outcome that is best according to the rule). If there are only two candidates, the best rule, according to many criteria, is majority voting [29,30]. When there are more than two candidates, there are many voting rules one could use (Plurality, Borda, STV, approval, etc.), each with its advantages and drawbacks. Voting theory provides an axiomatic characterization of voting rules in terms of desirable properties, such as: the absence of a dictator, unanimity, anonymity, neutrality, monotonicity, independence of irrelevant alternatives and resistance to manipulation and bribery. We point the reader to the book by Arrow et al. [28] for an introduction to the other facets and to [29] to a classical impossibility result about some of such properties. While every reasonable voting rule, under some conditions, is manipulable by the Gibbard–Satterthwaite Theorem [31,32], a rule may be said to be resistant to manipulation if it is computationally difficult to decide how to manipulate. This has led to intensive studies of the computational properties of manipulation for a variety of voting rules with complete and incomplete preferences [33,34,35,36,37,38]. This study could be very useful to develop new stable marriage procedures, which are based on voting rules that are computationally difficult to manipulate. Results in this direction have been shown in [39,40], where it is shown that it is computationally difficult to decide if an agent can manipulate the lexicographical minimal regret stable marriage procedure both when such a procedure is based on the hybrid plurality rule and when it is based on the STV rule.
3. Background
We now give some basic notions on various stable marriage problems.
3.1. Stable Marriage Problems
A stable marriage problem (SM) [1] of size n is the problem of finding a stable marriage between n men and n women. Such men and women each have a strict preference ordering over the members of the other sex. A marriage is a one-to-one correspondence between men and women. Given a marriage, M, a man, m, and a woman, w, the pair is a blocking pair for M if m prefers w to his partner in M and w prefers m to her partner in M. A marriage is said to be stable if it does not contain blocking pairs. The sequence of all preference orderings of men and women is usually called a profile. In the case of classical stable marriage problem (SM), a profile is a sequence of strict total orders. Given an SM, P, there may be many stable marriages for P. However, it is interesting to know that there is always at least one stable marriage. Given an SM, P, a feasible partner for a man, m (resp., a woman, w), is a woman, w (resp., a man m), such that there is a stable marriage for P, where m and w are married. We will write for the preference ordering of man or woman x. The set of all stable marriages for an SM forms a lattice, where a stable marriage, , dominates a stable marriage, , iff for every man, m, (where is the woman married to m in ) and there is a man s.t.. The top of this lattice is the stable marriage, where men are most satisfied, and it is usually called the male-optimal stable marriage. Conversely, the bottom is the stable marriage, where men’s preferences are least satisfied (and women are happiest, so it is usually called the female-optimal stable marriage). Thus, a stable marriage is male-optimal, iff every man is paired with his highest ranked feasible partner.
The Gale–Shapley (GS) algorithm [2] (Algorithm 1) is a well-known algorithm to solve the SM problem. This algorithm consists of a number of rounds in which each un-engaged man proposes to the most preferred woman to whom he has not yet proposed. Each woman receiving a proposal becomes “engaged”, provisionally accepting the proposal from her most preferred man. In subsequent rounds, an already engaged woman can “trade up”, becoming engaged to a more preferred man and rejecting a previous proposal, or if she prefers him, she can stick with her current partner. The algorithm takes steps and constructs a matching that is stable and male-optimal, since every man is paired with his highest ranked feasible partner, and female-pessimal, since each woman is paired with her lowest ranked feasible partner.
| Algorithm 1: GS |
 |
3.2. Stable Marriage Problems with Partially Ordered Preferences
In SMs, each preference ordering is a strict total order over the members of the other sex. More general notions of SMs allow preference orderings to be partial [41,42,43,44]. This allows for the modeling of both indifference (via ties) and incomparability (via absence of ordering) between members of the other sex. In this context, a stable marriage problem is defined by a sequence of partial orders, n over the men and n over the women. We will denote with SMP a stable marriage problem with such partially ordered preferences. Given an SMP, we will sometimes use the notion of a linearization of such a problem, which is obtained by linearizing (i.e., ordering in a strict way) the preference orderings of the profile in a way that is compatible with the given partial orders. One way to obtain such a linearization is to consider each partial order in turn and, while there are pairs of incomparable elements, to pick and order one of such pairs and to compute the transitive closure. Another way to obtain the linearization could be to use a topological order on the underlying DAGrepresenting the partial order.
A marriage, M, for an SMP is said to be weakly-stable if it does not contain blocking pairs. Given a man, m, and a woman, w, the pair is a blocking pair, if m and w are not married to each other in M and each one strictly prefers the other to his/her current partner. A weakly stable marriage, , dominates a weakly stable marriage, , iff for every man, m, or (⋈ means incomparable), and there is a man, , s.t. . Notice that there may be more than one undominated weakly stable marriage for an SMP.
3.3. Stable Marriage Problems with Weighted Preferences
A stable marriage problem with weighted preferences (SMW) [8] is a classical SM, where every man/woman gives also a numerical preference value for every member of the other sex, which represents how much he/she prefers such a person. Such preference values are natural numbers and higher preference values denote a more preferred item. Given a man, m, and a woman, w, the preference value for man m (resp., woman w) of woman w (resp., man m) will be denoted by (resp., ).
Example 1 Let and be, respectively, the set of women and men. An instance of an SMW is the following: (i.e., man prefers woman to woman , and he prefers with a value of nine and with a value of one), , , . The numbers written into the round brackets identify the preference values. ☐
We will introduce new notions of stability and optimality for SMWs that have not been considered in [8], and we will show how to find them by adapting the classical Gale–Shapley algorithm for SMs.
4. α-Stability
A simple generalization of the classical notion of stability requires that there are not two people that prefer with at least degree α (where α is a natural number) to be married to each other rather than to their current partners. This notion corresponds to the notion of additive α-stability in the asymmetric directed case presented in [26,27].
Definition 1 (α-stability) Let us consider a natural number, α, with . Given a marriage, M, a man, m, and a woman, w, the pair is an α-blocking pair for M, if it does not belong to M and the following conditions hold:
- m prefers w to his partner in M, say , by at least α (i.e., ) and
- w prefers m to her partner in M, say , by at least α (i.e., ).
A marriage is α-stable if it does not contain α-blocking pairs. A man, m (resp., woman, w), is α-feasible for woman w (resp., man m) if m is married with w in some α-stable marriage.
4.1. Relations with Classical Stability Notions
Given an SMW P, let us denote with the classical SM problem obtained from P by considering only the preference orderings induced by the preference values of P.
The fact that α-stability leads to a larger number of stable marriages w.r.t.the classical case is important to allow new stable marriages where some men, for example, the most popular ones or the least popular ones, may be married with partners better than all the feasible ones according to the classical notion of stability.
denotes the set of the α-stable marriages of P and with , the set of the stable marriages of .
Proposition 1 Given an SMW P, and a natural number, α, with , if , and if , .
Given an SMP, P, the set of α-stable marriages of P contains the set of stable marriages of , since the α-blocking pairs of P are a subset of the blocking pairs of .
Let us denote with the stable marriage problem with incomparable pairs obtained from an SMW, P, by setting as incomparable every pair of people that do not differ for at least α, and with the set of the weakly stable marriages of . It is possible to show that the set of the weakly stable marriages of coincides with the set of the α-stable marriages of P. This means that, given an SMW P, every algorithm that is able to find a weakly stable marriage for provides an α-stable marriage for P.
Theorem 1 Given an SMW P, .
Proof: We first show that . Assume that a marriage , we now show that . If , then there is a pair (man,woman), say , in , such that m prefers w to his partner in M, say , and w prefers m to her partner in M, say . By definition of , this means that m prefers w to by at least degree α and w prefers m to by at least degree α in P, and so, . Similarly, we can show that . In fact, if , then there is a pair (man,woman), say , in P, such that m prefers w to by at least degree α and w prefers m to by at least degree α. By definition of , this means that m prefers w to and w prefers m to in , and so, , i.e., M is not a weakly stable marriage for . ☐
Example 2 Assume that α is two. Let us consider the following instance of an SMW, say P: , , , . The set of the α-stable marriages of P, that coincides with the set of the weakly stable marriages of , by Theorem 1, contains the following marriages: and . ☐
On the other hand, not all stable marriage problems with partially ordered preferences can be expressed as stable marriage problems with weighted preferences, such that the stable marriages in the two problems coincide. More precisely, given any SMP problem, P, we would like to be able to generate a corresponding SMW problem, , and a value, α, such that, in , the weights of elements ordered in P differ more than α, while those of elements that are incomparable in P differ less than α. Consider, for example, the case of a partial order over six elements, defined as follows: and . Then, there is no way to choose a value, α, and a linearization of the partial order such that the weights of and differ for at least α, for any i,j between one and five, while at the same time, the weight of y and each of the ’s differ for less than α.
4.2. Dominance and Lex-Male-Optimality
We recall that in SMPs, a weakly-stable marriage dominates another weakly-stable marriage if men are happier (or equally happy) and there is at least a man that is strictly happier. The same holds for α-stable marriages.
Definition 2 (dominance) Given two α-stable marriages, say M and , M dominates if the following conditions hold:
- ∀ men m,
- ∃ man ,
Example 3 Let us consider the SMW shown in Example 2. We recall that α is two and that the α-stable marriages of this problem are and . It is possible to see that: does not dominate , since, for , and does not dominate , since, for , . ☐
We now discriminate among the α-stable marriages of an SMW, by considering the preference values given by women and men to order pairs that differ for less than α. For example, assume that men are students and women are schools; we want order pairs that differ for less than α among students according to the aggregated opinion the schools have of the students. Then, we want to make sure that best student goes to his favorite (stable) school. To achieve this, in this paper, we will consider a marriage optimal when the most popular men are as happy as possible and they are married with their most popular best α-feasible women (however, we could also consider a marriage optimal when the least popular men are as happy as possible and they are married with their most popular best α-feasible women). To compute a strict ordering on the men where the most popular men (resp., the most popular women) are ranked first, we follow a reasoning similar to the one considered in [39,40], that is, we apply a voting rule [28] to the preferences given by the women (resp., by the men). More precisely, such a voting rule takes as input the preference values given by the women over the men (resp., given by the men over the women) and returns a strict total order over the men (resp., women).
Definition 3 (lex-male-optimal) Consider an SMW, P, a natural number, α, and a voting rule, r. Let us denote with (resp., ) the strict total order over the men (resp., over the women) computed by applying r to the preference values that the women give to the men (resp., the men give to the women). An α-stable marriage, M, is lex-male-optimal w.r.t. and , if, for every other α-stable marriage, , the following conditions hold:
- there is a man, , such that ,
- for every man , .
Proposition 2 Given an SMW, P, a strict total ordering, (resp., ), over the men (resp., women):
- there is a unique lex-male-optimal α-stable marriage w.r.t. and , say L;
- L may be different from the male-optimal stable marriage of ;
- if has a unique undominated weakly stable marriage, say , then L coincides with ; otherwise, L is one of the undominated weakly stable marriages of .
4.3. Finding the Lex-Male-Optimal α-Stable Marriage
It is possible to find optimal α-stable marriages by adapting the Gale–Shapely algorithm. Given an SMW, P, and a natural number, α, by Theorem 1, to find an α-stable marriage, it is sufficient to find a weakly stable marriage of . This can be done by applying the GS algorithm to any linearization of . Given an SMW, P, a natural number, α, and two orderings, and , over men and women computed by applying a voting rule to P, as described in Definition 3, it is possible to find the α-stable marriage that is lex-male-optimal w.r.t and by applying the GS algorithm to the linearization of , where we order incomparable pairs, i.e., the pairs that differ for less than α in P, in accordance with the orderings, and .
Proposition 3 Given an SMW P, a natural number α, (resp., ), an ordering over the men (resp., women), algorithm Lex-male-α-stable-GS returns the lex-male-optimal α-stable marriage of P w.r.t. and .
| Algorithm 2: Lex-male-α-stable-GS |
| Input: P: an SMW, α: a natural number, r: a voting rule Output: μ: a marriage the strict total order over the men obtained by applying r to the preference values given by the women over the men the strict total order over the women obtained by applying r to the preference values given by the men over the women the linearization of obtained by ordering incomparable pairs of in accordance with and ; the marriage obtained by applying the GS algorithm to ; return μ |
5. Link-Based Stability Notions
Until now, we have generalized the classical notion of stability by considering separately the preferences of the men and the preferences of the women. We now intend to define new notions of stability that take into account, simultaneously, the preferences of the men and the women. Such a new notion will depend on the strength of the link of the married people,i.e., how much a man and a woman want to be married with each other. This is useful to obtain a new notion of stable marriage that looks at the happiness of the pairs (man,woman) rather than at the happiness of the members of a single sex. A way to define the strength of the link of two people is the following.
Definition 4 (link additive-strength) Given a man, m, and a woman, w, the link additive-strength of the pair , denoted by , is the value obtained by summing the preference value that m gives to w and the preference value that w gives to m, i.e., .
Notice that we can use other operators beside the sum to define the link strength of a pair, such as, for example, the maximum, the minimum or the product.
Definition 5 (additive-weight) Given a marriage, M, the additive-weight of M, denoted by , is the sum of the links of all its pairs, i.e., .
We now give a notion of stability that exploits the definition of the link additive-strength given above.
Definition 6 (link-additive-stability) Given a marriage, M, a man, m, and a woman, w, the pair is a link-additive-blocking pair for M if it does not belong to M and the following conditions hold:
- ,
- ,
Example 4 Let and be, respectively, the set of women and men. Consider the following instance of an SMW, P: , , , . In this example, there is a unique link-additive-stable marriage, that is , which has additive-weight . Notice that such a marriage has an additive-weight higher than the male-optimal stable marriage of , that is , which has additive-weight . ☐
Link-stability applies anytime there is an incentive to break a partnership to create a new one with an overall larger cumulative worth. This is certainly desirable as it leads to stronger positions in investments or it applies in the case where the benefit will depend on the overall contribution of both partners, but will, for example, benefit a third party. Another motivation is that of considering a man and a women as different sources of resources. For example, assume members of two different groups want to pair up for a project (for example, a grant proposal that allows only two PIs). Each gives a preference to the project by saying how many resources it would be willing to use for a project involving that person. However, the actual number of resources needed for the project to actually happen will be known later, only when the partners sit down and discuss the project. The success of the project strongly depends on the number of resources available to it, and one may prefer to participate in a project that he/she likes less and where he/she will put less resources, but that has a higher overall number of resources available.
5.1. Relations with Other Stability Notions
Given an SMW, P, let us denote with the stable marriage problem with ties obtained from P by changing every preference value that a person, x, gives to a person, y, with the value, , by changing the preference rankings accordingly and by considering only these new preference rankings.
Let us denote with the set of the link-additive-stable marriages of P and with the set of the weakly stable marriages of . It is possible to show that these two sets coincide.
Theorem 2 Given an SMW, P, .
Proof: Let us consider a marriage, M. We first show that if , then . If , there is a pair that is a link-additive-blocking pair, i.e., and , where (resp., ) is the partner of m (resp., w) in M. Since , m prefers w to in the problem, , and, since , w prefers m to in the problem, . Hence, is a blocking pair for the problem, . Therefore, .
We now show that if , then . If , there is a pair that is a blocking pair for ,i.e., m prefers w to in the problem, , and w prefers m to in the problem, . By definition of the problem, , and . Therefore, is a link-additive-blocking pair for the problem, P. Hence, . ☐
When no preference ordering changes in w.r.t. P, then the link-additive-stable marriages of P coincide with the stable marriages of .
Proposition 4 Given an SMW, P, if , then .
If there are no ties in , then there is a unique link-additive-stable marriage with the highest weight.
Proposition 5 Given an SMW, P, if has no ties, then there is a unique link-additive-stable marriage with the highest additive-weight.
If the link strength of a pair is computed by using the maximum of the scores, rather than the sum of the scores, all the results shown above hold, and it is also possible to define a class of SMWs where there is a unique link-maximal stable marriage with the highest weight, where the weight is given by the maximum of the links of its pairs.
Definition 7 (link maximal-strength) Given a man, m, and a woman, w, the link maximal-strength of the pair , denoted by , is the value obtained by taking the maximum between the preference value that m gives to w and the preference value that w gives to m,i.e., .
Definition 8 (max-weight) Given a marriage, M, the max-weight of M, denoted by , is the maximum of the links of all its pairs, i.e., .
Definition 9 (link-maximal-stability) Given a marriage, M, a man, m, and a woman, w, the pair is a link-maximal-blocking pair for M if it does not belong to M and the following conditions hold:
- ,
- ,
Proposition 6 In an SMW, P, where the preference values are all different, there is a unique link-maximal-stable marriage with the highest max-weight.
5.2. Finding Link-Based Stable Marriages with the Highest Weight
We now show that for some classes of preferences it is possible to find optimal link-additive-stable marriages and link-maximal-stable marriages of an SMW by adapting algorithm GS.
5.2.1. Max-Weight
We assume now that the weight of a marriage is computed by taking the maximum of the links of its pairs. We will now provide a general polynomial algorithm that is able to find the link-max stable marriage with the highest max-weight. We will show that this algorithm can be also adapted to find link-additive stable marriage and α-stable marriage with the highest max-weight.
We will first present the Max-link-max algorithm (Algorithm 3). It takes as input an instance, P, of an SMW with n men and n women and returns a marriage, μ. We will show that such a marriage, μ, is the link-max stable marriage of P with the highest max-weight. The algorithm works as follows. First, it initializes μ with the empty set and M with the set of all the pairs (man,woman) that can be built with the men and women of P. Then, it performs the following steps until M is not empty: it looks for the pair with the highest link,i.e., with the highest link-max strength; it adds such a pair, say , to μ; and it removes from M all the pairs containing or . Notice that with a suitable data structure, it is possible to find the pair with the highest link by only saving for every woman and for every man the partner who gives the maximum weight and the value of this maximal weight. This can be done in O() time.
| Algorithm 3: Max-link-max |
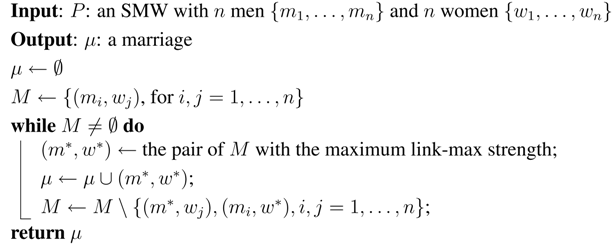 |
Proposition 7 Given an SMW, P, Max-link-max applied to P returns the link-max stable marriage of P with the highest max-weight.
Proof: Let us denote with μ the marriage returned by Max-link-max. We first show that μ is link-max stable, and then, we show that it has the highest max-weight. To show that μ is link-max stable, we have to show that there are no link-max blocking pairs. Assume that there is a link-max blocking pair for μ, say . Then, it must be that . Thus, the pair is picked in the while-loop before and . Thus, if and are in μ, both m and w must have been matched to partners that cannot be and . The link-max stable marriage μ returned by Max-link-max has the highest max-weight, since in the first step, the algorithm puts in μ the pair with the maximum link-max strength, and, by definition, such a value is the max-weight of μ. ☐
Proposition 8 Given an SMW, P, with n men and n women, the complexity of Max-link-max applied to P is .
To find a link-additive stable marriage with the maximum weight, we can adopt an algorithm similar to Max-link-max. In such a case, the link strength of a pair is computed by considering the sum of the scores of the pair elements, rather than their maximum. The only difference in the algorithm is that in the while-cycle, we have to find one of the pairs of M with the maximum link-additive strength, rather than one of the pairs with the maximum link-max strength.
Max-link-max works also for stable marriage procedures that return an α-stable marriage. More precisely, it returns the α-stable marriage with the highest max-weight.
5.3. Additive-Weight
We assume now to compute the link of a marriage as the sum of the links of all its pairs. First, we will show how to find the link-additive stable marriage with the highest additive-weight for some classes of SMWs (i.e., for SMWs P, such that has no ties), and then, we will show a procedure that can be used for any class of SMWs. By Proposition 2, we know that the set of the link-additive-stable (resp., link-maximal-stable) marriages of an SMW, P, coincides with the set of the weakly stable marriages of the SMP, (resp., ). Therefore, to find a link-additive-stable (resp., link-maximal-stable) marriage, we can simply use Algorithm 4 that applies GS to a linearization of (resp., ).
| Algorithm 4: Link-additive-stable-GS (resp., link-maximal-stable-GS) |
| Input: P: an SMW Output: μ: a marriage (resp., ); a linearization of ; the marriage obtained by applying GS algorithm to ; return μ |
Proposition 9 Given an SMW, P, the marriage returned by algorithm link-additive-stable-GS (link-maximal-stable-GS) over P, say M, is link-additive-stable (resp., link-maximal-stable). Moreover, if there are not ties in (resp., ), M is link-additive-stable (resp.,link-maximal-stable), and it has the highest additive-weight.
When there are no ties in (resp., ), the marriage returned by algorithm link-additive-stable-GS (resp., link-maximal-stable-GS) is male-optimal w.r.t. the profile with links. Such a marriage may be different from the classical male-optimal stable marriage of , since it considers the happiness of the men reordered according to their links with the women, rather than according to their single preferences. This holds, for example, when we assume having an SMW with preference values that are all different and we consider the notion of link-maximal-stability.
Proposition 10 Given an SMW P where the preference values are all different, the marriage returned by algorithm link-maximal-stable-GS algorithm over P is link-maximal-stable, and it has the highest additive-weight.
When, instead, there are ties in (resp., ), to find the link-additive stable marriage with the highest additive-weight in SMWs, P, we cannot use Max-link-max, since it may not return the marriage with the highest additive-weight, as shown in the following example.
Example 5 Let and be, respectively, the set of women and men. Consider the following instance, P, of an SMW: , , , . The problem is as follows: , , , . Notice that there is a tie in . Assume applying the algorithm, Max-link-additive. There are two pairs with the maximal link strength, which are and . If the algorithm chooses first the pair , then the returned marriage is , and its additive-weight is . However, if the algorithm chooses first the pair , then the returned marriage is , , which has additive-weight = . Therefore, Max-link-additive may also not return the link-additive stable marriage with the maximum additive-weight. ☐
In [15], the authors have presented an encoding of an SMW as a soft constraint satisfaction problem (soft CSPs) [16]. This encoding is also able to handle SMWs with ties, and it allows, for example, for finding a stable marriage that is optimal in terms of its additive-weight. However, the stability notion that is considered in [15] is the classical one, while we intend to consider α-stability, link-additive stability and link-maximal stability. Our idea is to exploit this encoding to define a general method to find, given an SMW, the link-additive stable marriage and the α-stable marriage with the maximum additive-weight.
Since we have shown that, given an SMW, P, the set of the link-additive (resp., α-) stable marriage of P coincides with the set of the weakly-stable marriages of the stable marriage problem with ties (resp., ), then, to compute one of the link-additive (resp., ) stable marriages, we just need to find a classical weakly stable marriage of (resp., ). Furthermore, since we want to find the link-additive (resp., ) stable marriage with the highest additive-weight, then we can consider the SMW with ties (resp., ), which is obtained by (resp., ) by associating with each pair their link-additive strength (resp., their initial score). Then, we can apply the encoding shown in [15] to this SMW with ties. More precisely, since we want to maximize the sum of the link-additive strengths of the pairs, we must use the encoding shown in [15], which encodes an SMW as a weighted CSP, where the preferences are interpreted as costs, and the goal is to find the solution (i.e., the assignment of values to the variables) with the minimum sum of the costs. The procedure that we propose first computes the SMW with ties . Next, it computes , which is the SMW with ties obtained by by changing the score of every pair, say x, with , and by adapting all the orderings of the pairs. Finally, it encodes the problem obtained so far as a weighted CSPs, and thus, it computes an optimal solution of such a weighted CSP.
The same algorithm can also be used to find the link-max (resp., α) stable marriage of P with the maximum additive-weight. We have only to replace with (resp., α) in our procedure.
6. W-Manipulation
We know that, with at least three men and three women, every stable marriage procedure is manipulable [9], i.e., there is a profile where an agent, mis-reporting his preferences, obtains a stable matching that is better than the one obtained by telling the truth. In stable marriage problems, agents can try to manipulate in two ways: by changing the preference ordering [9] or by truncating the preference list [10].
In SMW problems, there is another way of lying: changing the weights. We show how this gives the agents, in some cases, an additional power to manipulate, even if the manipulator just changes the weights, while preserving the preference ordering and not truncating the preference list.
Definition 10 (w-manipulable (resp., strictly w-manipulable)) A stable marriage procedure, f, is w-manipulable (resp., strictly w-manipulable) if there is a pair of profiles, p and , that contain the same preference orderings, but differ in the weights of an agent, say w, such that is better than or equal to (resp., better than) for w.
6.1. W-Manipulation for α-Stability
We first assume that the agents know the value of α. We show that, when using weights, agents can manipulate by just modifying the weights.
Theorem 3 Let α be any natural number >1. Every procedure that returns an α-stable matching is w-manipulable, and there is at least one procedure that is strictly w-manipulable.
Proof: Let and be, respectively, the set of women and men. Consider the following instance of an SMW, say P:
Let us now see whether there is any syntactical restriction over the profiles that can prevent this additional form of manipulation. First, we may notice that this manipulation is only related to the fact that some distances between adjacent weights are made larger or smaller. This, depending on the chosen α, may imply that some elements are considered in a tie or ordered in . Thus, a manipulator may introduce a tie that was not in its real preference ordering or may eliminate a tie from this ordering. Based on this consideration, we can consider restricting our attention to profiles where ties are not allowed. However, this would simply mean eliminating the weights, since, in this case, the α-stable matchings would coincide with the stable matchings of the SM obtained by just forgetting the weights. We can thus consider what happens if we allow at most one tie (that is, a difference less than α) in each preference ordering. Even this strong restriction does not avoid w-manipulation, since the example in the proof of Theorem 3 respects this restriction. A weaker restriction would be to allow at most one tie in the whole profile, but this would mean requiring coordination between the agents or knowing who is the manipulator. Furthermore, again, the same example obeys this restriction. Summarizing, if agents know the value of α, there is no way to prevent w-manipulation!
Some hope remains for when α is not known by the agents. Assume that this is the case, but agents know that α is bounded by a certain value, say . Unfortunately, again, the example in the proof of Theorem 3 (where we replace every α with ) holds. Thus, every procedure is still w-manipulable, and some are also strictly w-manipulable. Furthermore, restricting to at most one tie per agent will not avoid w-manipulation, since, again, the same example holds.
The most promising case is when agents have no information about α. In this case, we need to define what it means for a procedure to be manipulable.
Definition 11 (α-w-manipulable) A procedure that returns an α-stable matching is α-w-manipulable if it is w-manipulable for all α and it is strictly w-manipulable for at least one α.
Theorem 4 There is a procedure that returns an α-stable matching that is α-w-manipulable.
Proof: Let and be, respectively, the set of women and men. Consider the following instance of an SMW, P: ; ; ; . For every α, P has two α-stable matchings: and . When , is strictly better than for in P, while when , is equally preferred to for in P. Assume that mis-reports her preferences as follows: . Let us denote with the problem obtained from P by using this mis-reported preference for . When , is strictly better than for in , while when , is equally preferred to for in . Let us consider a procedure, which we call mGS, which works as the Gale–Shapley algorithm over all the profiles except on P and , where it works as follows: if a matching is strictly better than another matching in terms of α for , then it returns the best one, while if a matching is equally preferred to another matching in terms of α for , then it returns the worst one for w.r.t. the strict preference ordering induced by the weights. Therefore, when , mGS returns in both P and ; when , mGS returns in P and in , while when , mGS returns in both P and . Therefore, if lies, for every α, he obtains a partner that is better than or equal to the one obtained by telling the truth, and there is a value, α (i.e., α=2), where he obtains a partner that is better than the one obtained by telling the truth. Therefore, the mGS procedure is α-w-manipulable. ☐
As in the case when α is known, we may consider restricting to profiles with at most one tie per agent. However, the example in the above proof satisfies this restriction, so it shows that α-w-manipulability is possible also with such a severe restriction.
It is also possible to give a stronger result that is based on the following notion of manipulation.
Definition 12 (α-strictly-w-manipulable) A procedure that returns an α-stable matching is α-strictly-w-manipulable if it is strictly w-manipulable for all α.
Theorem 5 There is a procedure that returns an α-stable matching that is α-strictly-w-manipulable.
Proof: Let and be, respectively, the set of women and men. Consider the following instance of an SMW, P: . For every α, P has two α-stable matchings: and .
Assume that mis-reports her preferences as follows: . Let us denote with the problem obtained from P by using this mis-reported preference for .
Let us consider a procedure, which we call newGS, which works as the Gale–Shapley algorithm over all the profiles, except on P and , where it works as follows: for every α, it returns in P and in . Therefore, if lies, for every α, he obtains a partner that is better than the one obtained by telling the truth. Therefore, the newGS procedure is α-strictly-w-manipulable. ☐
We may consider restricting to profiles with the same weight for all top choices with at most one tie per agent. However, the example in the above proof satisfies this restriction, so it shows that α-strictly-w-manipulability is possible also with such a severe restriction.
6.2. W-Manipulation for Link-Additive Stability
Every procedure for link-additive stability is strictly w-manipulable.
Theorem 6 Every procedure that returns a link-additive stable matching is strictly w-manipulable.
Proof: Let and be, respectively, the set of women and men. Consider the following instance of an SMW, say P: . P has a unique link-additive stable matching, which is . Assume that mis-reports her preferences as follows: . Then, in the new problem, which we call , there is only one stable matching, which is , and is better than for in P. Since there is only one stable matching in both P and , every procedure that returns a link-additive stable matching will return in P and in , and thus, it is strictly w-manipulable. ☐
The example in the proof of the above theorem shows a very intuitive and dangerous manipulation scheme: the manipulator sets a very high weight (higher than twice the highest of the other weights in the profile) for its top choice. In this way, it will surely be matched to its top choice, no matter the procedure used or the preferences of the other agents over the alternatives that are not their top choices.
This form of manipulation can be avoided by forcing the same weight for all top choices of all agents. This restriction, however, does not prevent all forms of w-manipulation.
Theorem 7 If we restrict to profiles with the same weight for all top choices, every procedure that returns a link-additive stable matching is w-manipulable, and there is at least one procedure that is strictly w-manipulable.
Proof: Let and be, respectively, the set of women and men. Consider the following instance of an SMW, P: . P has an unique link-additive stable matching, which is . Assume that mis-reports her preferences as follows: . Then, in the new problem, that we call , there are only two link-additive stable matchings,i.e., and , where is better than for . Thus, every procedure is w-manipulable. If we consider the procedure that returns matching in , this pair of profiles shows that this procedure is strictly w-manipulable. ☐
Notice that, if we consider profiles where all top choices have the same weight and all differences (of weights of adjacent items in the preference lists) are exactly one, then weights are fixed and are thus irrelevant. Furthermore, obviously, w-manipulation cannot occur, since agents cannot modify the weights. We may wonder whether, by restricting to profiles that are close to this extreme case, we may avoid w-manipulation. Unfortunately, this is not so. In fact, we can consider just profiles with the same weight for all top choices and where at most one difference is two, while all the others are one, for every agent. This holds for the example in the proof of Theorem 7. This shows that even this strong restriction is not enough to avoid w-manipulation.
If we restrict our attention to procedures that return optimal link-additive or link-max stable matchings, we can still prove that all such procedures are strictly w-manipulable, and they are w-manipulable when all top choices have the same weight. In fact, the same examples in the proofs of Theorems 6 and 7 still hold.
We now show that not all the profiles of an SMW can be expressed as a problem, , for some P, and thus, some classical forms of manipulation cannot be adopted in the context of link-based stability.
In particular, we will show that the profiles, P and , which allowed Roth in [9] to state that all the stable marriage procedures are manipulable, cannot be used in our context to prove classical manipulation, since there are no SMWs, P and , such that and .
Theorem 8 Given an SM, P, it may not be possible to find an SMW, , such that .
Proof: Let and be, respectively, the set of women and men. The SMW, P, is as follows: {, , , , , }. Assume that there is an SM, , such that . Then, the following conditions must hold: (1) , (2) , (3) , and (4) . This implies . Thus, we have , which is a contradiction. ☐
Notice that the theorem above holds independently from how the link of a pair is computed. Starting from the above result, we can show that some classical forms of manipulation cannot be adopted in the context of link-based stability.
Theorem 9 The SMs, P and , which allowed Roth in [9] to state that all the stable marriage procedures are manipulable, cannot be used to show classical manipulation when we consider link-based stability notions.
Proof: The SMs, P and , considered in [9], are defined as follows. P coincides with the problem considered in the proof of Theorem 8, and is obtained by P, by replacing the preference of as follows: . is the problem where misreports her preferences and she gets a better result than the one obtained in P by telling the truth. In Theorem 8, we have shown that there is not an SMW , such that . Moreover, by using the same reasoning done in the proof of Theorem 8, we can show that there is not an SMW , such that . ☐
7. Conclusions and Future Work
In this paper, we have considered stable marriage problems with weighted preferences, where both men and women can express a score over the members of the other sex. In particular, we have introduced new stability and optimality notions for such problems, and we have compared them with the classical ones for stable marriage problems with totally or partially ordered preferences. We have also provided algorithms to find marriages that are optimal and stable according to these new notions by adapting the Gale–Shapley algorithm. Moreover, we have investigated manipulation issues in our context. We have shown that, in both cases, adding weights to classical stable marriage problems increases the possibility of manipulating the resulting matching, since agents can manipulate even by just modifying the weights, without changing or truncating the preference lists. We have also shown that reasonable restrictions over the weights do not avoid such additional forms of manipulation. However, in the case of link-additive stability, forcing all top choices to have the same weight for all agents prevents an extreme form of w-manipulation, which would allow the manipulator to dictate its own partner in every link-additive stable matching.
We plan to investigate the computational complexity of w-manipulation. We intend also to use scoring-based voting rules to choose among the stable matchings and to adapt existing results about manipulation complexity for such voting rules to weighted stable marriage problems. We have also considered an optimality notion (that is, lex-male-optimality) that exploits a voting rule to linearize the partial orders. We intend to study if this use of voting rules within stable marriage problems may have other benefits. In particular, we want to investigate if the procedure defined to find such an optimality notion inherits the properties of the voting rule with respect to manipulation: we intend to check whether, if the voting rule is NP-hard to manipulate, then, also, the procedure on SMW that exploits such a rule is NP-hard to manipulate. This would allow us to transfer several existing results on manipulation complexity, which have been obtained for voting rules, to the context of procedures to solve stable marriage problems with weighted preferences.
Acknowledgments
We thank the reviewers for their helpful comments. This work has been partially supported by the MIURPRIN20089M932N project “Innovative and multi-disciplinary approaches for constraint and preference reasoning”.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gusfield, D.; Irving, R.W. The Stable Marriage Problem: Structure and Algorithms; MIT Press: Boston, MA, USA, 1989. [Google Scholar]
- Gale, D.; Shapley, L.S. College admissions and the stability of marriage. Am. Math. Mon. 1962, 69, 9–14. [Google Scholar] [CrossRef]
- Roth, A.E. Deferred acceptance algorithms: History, theory, practice, and open questions. Int. J. Game Theory 2008, 36, 537–569. [Google Scholar] [CrossRef]
- Roth, A.E. The evolution of the labor market for medical interns and residents: A case study in game theory. J. Polit. Econ. 1984, 92, 991–1016. [Google Scholar] [CrossRef]
- Liebowitz, J.; Simien, J. Computational efficiencies for multi-agents: A look at a multi-agent system for sailor assignment. Electon. Gov. Int. J. 2005, 2, 384–402. [Google Scholar] [CrossRef]
- Teo, C.-P.; Sethuraman, J.; Tan, W.P. Gale-shapley stable marriage problem revisited: Strategic issues and applications. Manag. Sci. 2001, 47, 1252–1267. [Google Scholar] [CrossRef]
- Gusfield, D. Three fast algorithms for four problems in stable marriage. SIAM J. Comput. 1987, 16, 111–128. [Google Scholar] [CrossRef]
- Irving, R.W.; Leather, P.; Gusfield, D. An efficient algorithm for the “optimal” stable marriage. J. ACM 1987, 34, 532–543. [Google Scholar] [CrossRef]
- Roth, A.E. The economics of matching: Stability and incentives. Math. Oper. Res. 1982, 7, 617–628. [Google Scholar] [CrossRef]
- Gale, D.; Sotomayor, M. Semiring-based constraint solving and optimization. Am. Math. Mon. 1985, 92, 261–268. [Google Scholar]
- Dawande, M.; Kumar, S.; Mookerjee, V.; Sriskandarajah, C. Maximum commonality problems: Applications and analysis. Manag. Sci. 2008, 54, 194–207. [Google Scholar]
- Pini, M.S.; Rossi, F.; Venable, K.B.; Walsh, T. Stability in Matching Problems with Weighted Preferences. In Proceedings of the ICAART’11, Rome, Italy, 28–30 January 2011; pp. 45–53.
- Pini, M.S.; Rossi, F.; Venable, K.B.; Walsh, T. Weights in Stable Marriage Problems Increase Manipulation Opportunities. In Proceedings of the TARK’11—Best Poster Award, Groningen, The Netherlands, July 2011; pp. 200–204.
- Pini, M.S.; Rossi, F.; Venable, K.B.; Walsh, T. Stability and Optimality in Matching Problems With Weighted Preferences. In Proceedings of the Agents and Artificial Intelligence 2011—ICAART’11— Revised Selected Papers, Rome, Italy, 28–30 January 2011; Springer-Verlag: Berlin Heidelberg, Germany, 2012; Volume 271 CCIS, pp. 319–333. [Google Scholar]
- Bistarelli, S.; Foley, S.N.; O’Sullivan, B.; Santini, F. From Marriages to Coalitions: A Soft CSP Approach. In Proceedings of the CSCLP, Rome, Italy, 18–20 June 2008; pp. 1–15.
- Bistarelli, S.; Montanari, U.; Rossi, F. Semiring-based constraint solving and optimization. J. ACM 1997, 44, 201–236. [Google Scholar] [CrossRef]
- Gent, I.P.; Irving, R.W.; Manlove, D.; Prosser, P.; Smith, B.M. A Constraint Programming Approach to the Stable Marriage Problem. In Proceedings of the CP 2001, Paphos, Cyprus, 26 November–1 December 2001; pp. 225–239.
- Gent, I.; Prosser, P. An Empirical Study of the Stable Marriage Problem with Ties and Incomplete Lists. In Proceedings of the ECAI 2002, Lyon, France, July 2002; pp. 141–145.
- Gent, I.; Prosser, P.; Smith, B.; Walsh, T. Sat Encodings of the Stable Marriage Problem with Ties and Incomplete Lists. In Proceedings of the SAT 2002, Cincinnati, Ohio, USA, May 2002; pp. 133–140.
- Brito, I.; Meseguer, P. Distributed Stable Matching Problems. In Proceedings of the CP 2005, Sitges, Spain, 1–5 October 2005; pp. 152–166.
- Brito, I.; Meseguer, P. Distributed Stable Matching Problems with Ties and Incomplete Lists. In Proceedings of the CP 2006, Nantes, France, 25–29 September 2006; pp. 675–679.
- Gelain, M.; Pini, M.S.; Rossi, F.; Venable, K.B.; Walsh, T. Local search approaches in stable matching problems. Algorithms 2013, 6, 591–617. [Google Scholar] [CrossRef]
- Gelain, M.; Pini, M.S.; Rossi, F.; Venable, K.B.; Walsh, T. Local Search Algorithms on the Stable Marriage Problem: Experimental Studies. In Proceedings of ECAI 2010, Lisbon, Portugal, Lisbon, 16–20 August; IOS Press: Amsterdam, The Netherlands, 2010; Volume 215 Frontiers in Artificial Intelligence and Applications, pp. 1085–1086. [Google Scholar]
- Gelain, M.; Pini, M.S.; Rossi, F.; Venable, K.B.; Walsh, T. Local Search for Stable Marriage Problems With Ties and Incomplete Lists. In Proceedings of the PRICAI 2010, Daegu, Korea, 30 August–2September 2010; Springer: Berlin Heidelberg, Germany, 2010; Volume 6230 LNCS, pp. 64–75. [Google Scholar]
- Gelain, M.; Pini, M.S.; Rossi, F.; Venable, K.B.; Walsh, T. Procedural Fairness in Stable Marriage Problems. In Proceedings of the AAMAS 2011, Taipei, Taiwan, 2–6 May 2011; pp. 1209–1210.
- Anshelevich, E.; Das, S.; Naamad, Y. Anarchy, Stability, and Utopia: Creating Better Matchings. In Proceedings of the SAGT 2009, Paphos, Cyprus, 18–20 October 2009; Springer: Berlin Heidelberg, Germany,, 2009; Volume 5814 LNCS, pp. 159–170. [Google Scholar]
- Anshelevich, E.; Das, S.; Naamad, Y. Anarchy, stability, and utopia: Creating better matchings. Auton. Agents Multi-Agent Syst. 2013, 26, 120–140. [Google Scholar] [CrossRef]
- Arrow, K.J.; Sen, A.K.; Suzumura, K. Handbook of Social Choice and Welfare; North-Holland, Elsevier: Amsterdam, The Netherlands, 2002. [Google Scholar]
- Arrow, K.J. Social Choice and Individual Values; John Wiley and Sons: New York, NY, USA, 1963. [Google Scholar]
- May, K. A set of independent necessary and sufficient conditions for simple majority decisions. Econometrica 1952, 20, 680–684. [Google Scholar] [CrossRef]
- Satterthwaite, M. Strategy-proofness and Arrow’s Conditions: Existence and correspondence theorems for voting procedures and social welfare functions. J. Econ. Theory 1975, 10, 187–216. [Google Scholar] [CrossRef]
- Gibbard, A. Manipulation of voting schemes: A general result. Econometrica 1973, 41, 587–601. [Google Scholar] [CrossRef]
- Conitzer, V.; Sandholm, T.; Lang, J. When are elections with few candidates hard to manipulate? J. ACM 2007, 54, 1–33. [Google Scholar] [CrossRef]
- Pini, M.S.; Rossi, F.; Venable, K.B.; Walsh, T. Incompleteness and incomparability in preference aggregation: Complexity results. Artif. Intell. 2011, 175, 1272–1289. [Google Scholar] [CrossRef]
- Xia, L.; Conitzer, V. Determining possible and necessary winners given partial orders. J. Artif. Intell. Res. (JAIR) 2011, 41, 25–67. [Google Scholar]
- Lang, J.; Pini, M.S.; Rossi, F.; Salvagnin, D.; Venable, K.B.; Walsh, T. Winner determination in voting trees with incomplete preferences and weighted votes. Auton. Agents Multi-Agent Syst. 2012, 25, 130–157. [Google Scholar] [CrossRef]
- Lang, J.; Pini, M.S.; Rossi, F.; Venable, K.B.; Walsh, T. Winner Determination in Sequential Majority Voting. In Proceedings of the IJCAI 2007, Hyderabad, India, 6–12 January 2007; pp. 1372–1377.
- Pini, M.S.; Rossi, F.; Venable, K.B.; Walsh, T. Incompleteness and Incomparability in Preference Aggregation. In Proceedings of the IJCAI 2007, Hyderabad, India, 6–12 January 2007; pp. 1464–1469.
- Pini, M.S.; Rossi, F.; Venable, K.B.; Walsh, T. Manipulation and Gender Neutrality in Stable Marriage Procedures. In Proceedings of the AAMAS 2009, Budapest, Hungary, 10–15 May 2009; Volume 1, pp. 665–672.
- Pini, M.S.; Rossi, F.; Venable, K.B.; Walsh, T. Manipulation complexity and gender neutrality in stable marriage procedures. Auton. Agents Multi-Agent Syst. 2011, 22, 183–199. [Google Scholar] [CrossRef]
- Manlove, D. The structure of stable marriage with indifference. Discret. Appl. Math. 2002, 122, 167–181. [Google Scholar] [CrossRef]
- Irving, R.W. Stable marriage and indifference. Discret. Appl. Math. 1994, 48, 261–272. [Google Scholar] [CrossRef]
- Gelain, M.; Pini, M.S.; Rossi, F.; Venable, K.B.; Walsh, T. Male Optimality and Uniqueness in Stable Marriage Problems with Partial Orders—Extended Abstract. In Proceedings of the AAMAS 2010, Toronto, Canada, 10–14 May 2010.
- Gelain, M.; Pini, M.S.; Rossi, F.; Venable, K.B.; Walsh, T. Male Optimal and Unique Stable Marriages with Partially Ordered Preferences. In Proceedings of the CARE 2009/2010; Springer: Berlin Heidelberg, Germany, 2006; Volume LNAI 6066. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).