Finite Element Quadrature of Regularized Discontinuous and Singular Level Set Functions in 3D Problems
Abstract
:1. Introduction
2. Regularization in the Level Set Context
| weight function | |
|---|---|
| hat function | |
| bell | |
| Laplacian | |
| Gaußian |
3. Error Analysis for Regularized Delta and Heaviside Functions
- the analytical error typically increases with increasing ρ ;
- the numerical error is large for ρ small compared with the mesh size and decreases for increasing ρ.
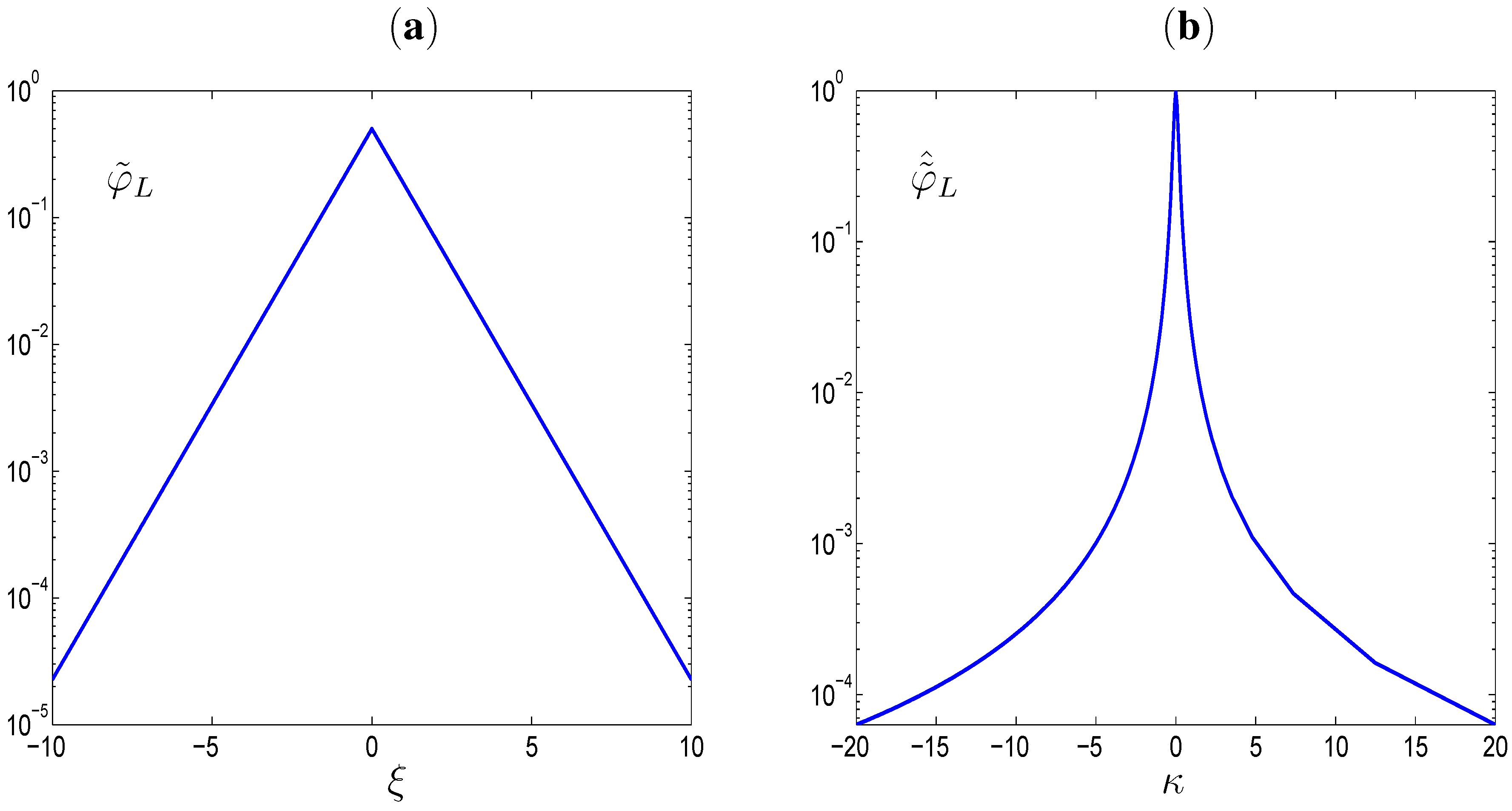
3.1. Fourier Transforms
3.2. Truncation Error
- we choose weight functions with compact support equal to the finite element size multiplied by a suitable integer number m that depends on h, namely [1,3]. This means that whenever the mesh changes, the weight function has to be changed accordingly, otherwise non-vanishing errors for decreasing mesh size are obtained.
- we choose non-compact support weight functions whose Fourier transform satisfies differentiability conditions; the length will denote the truncated support of φ. This makes it possible to have independent of h when , where is the width of the truncated support of the Fourier transform .
3.3. Example
| 1 | 0 | |||
| 1 | 0 |
4. Basic Statements of the Regularized XFEM Formulation
5. Numerical Results
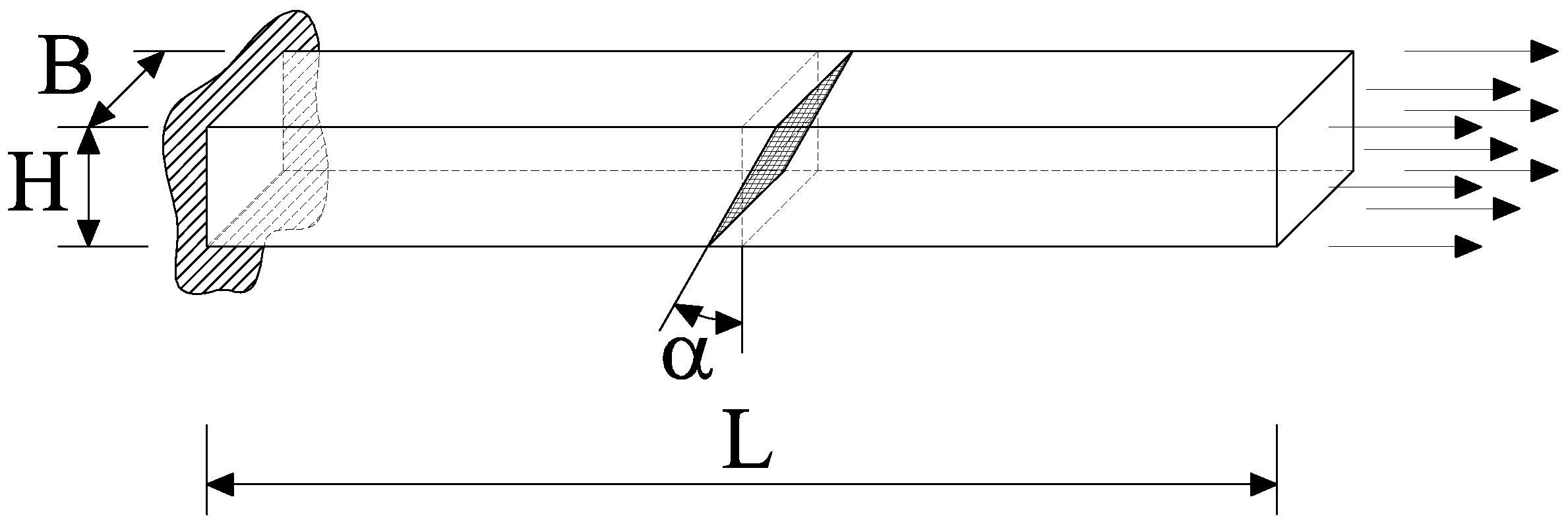

| Mesh | ||
|---|---|---|
| 0.42 | ||
| 0.18 | ||
| 1.0 | ||
| 2.6 | ||
| 5.2 | ||
| 7.8 | ||
| 10.5 | ||
| 16.5 |
| 1 | |
| 2.5 | |
| 4.8 | |
| 7.8 | |
| 17.3 | |
| 37 |
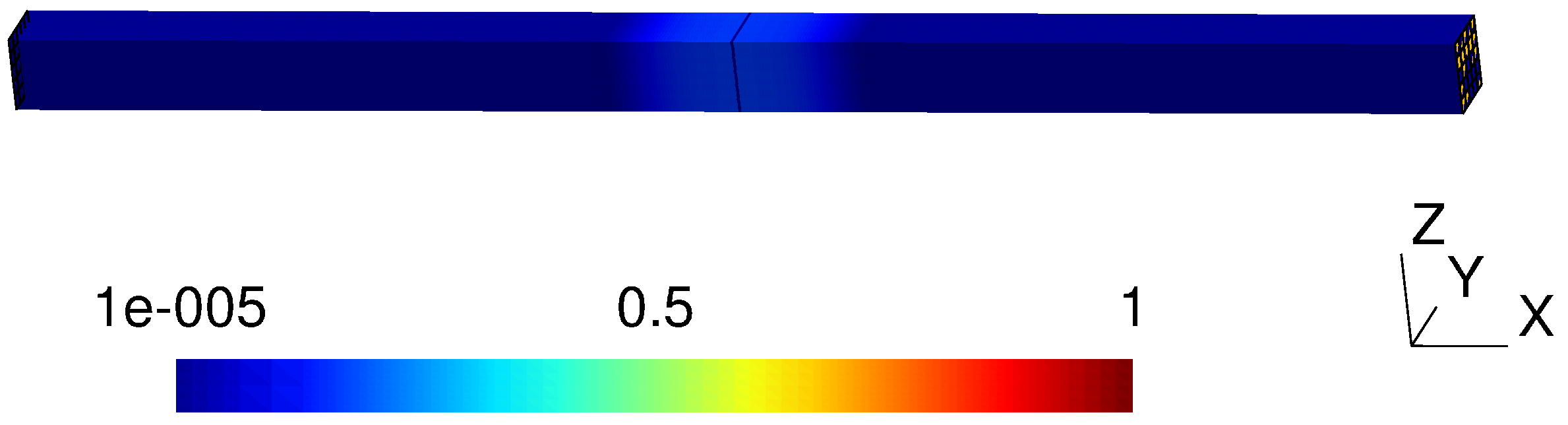
| Mesh | ||
|---|---|---|
| 1.0 | ||
| 2.6 |
| 1 | |||
| 2.5 | |||
| 4.8 | |||
| 7.8 |
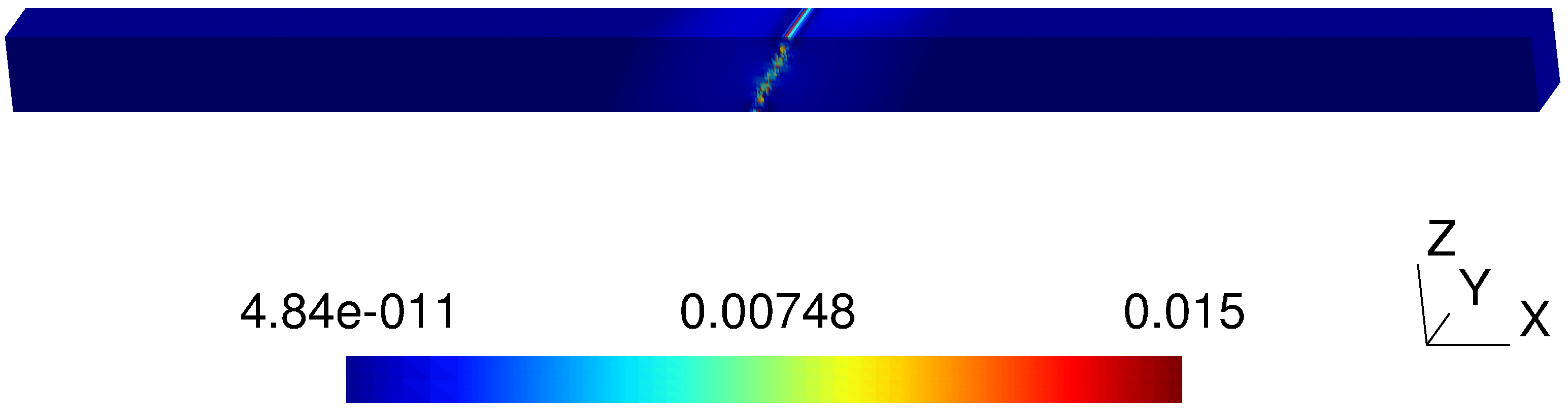
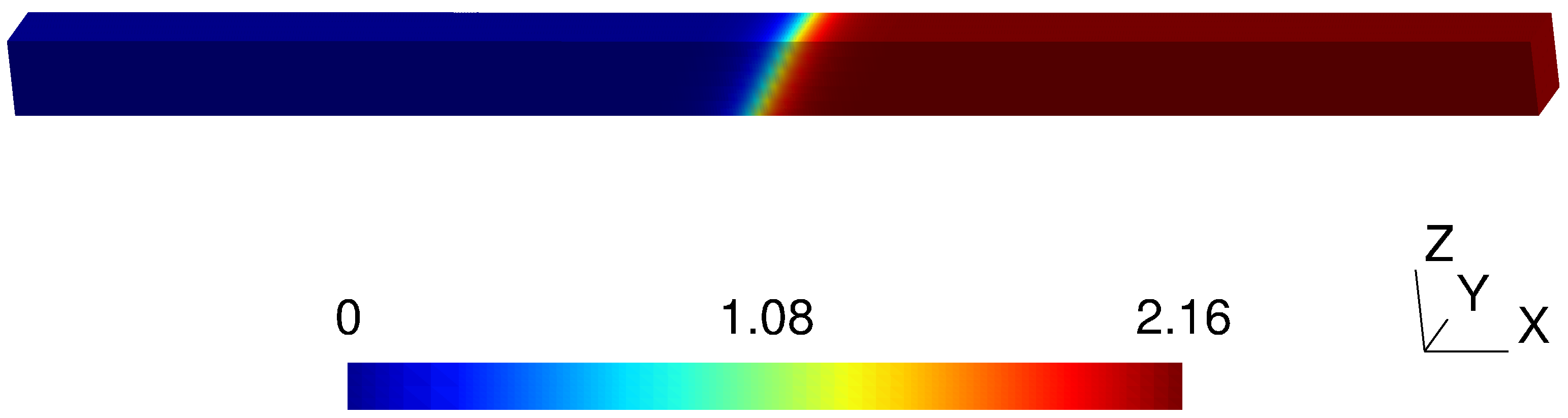
5.1. Algorithm
| Step 1 Fix the tolerance parameters C, |
| Step 2 Evaluate β such that |
| Step 3 Assume , , |
| Step 4 Perform the analysis and evaluate . |
| while |
| set ; |
| . |
| end while |
6. Conclusions
- truncation of the support width influences the analytical error, as the moment conditions (12) are not exactly satisfied;
- the computed error decreases for increasing values of the ratio , that is either increasing ρ for fixed h or decreasing h for fixed ρ;
- discontinuities and singularities along interfaces that are non-aligned with the mesh are prone to severe errors when the support width .
Acknowledgements
References
- Abbas, S.; Alizada, A.; Fries, T. The XFEM for high-gradient solutions in convection-dominated problems. Int. J. Numer. Methods Eng. 2010, 82, 1044–1072. [Google Scholar] [CrossRef]
- Mallardo, V. Integral equations and nonlocal damage theory: A numerical implementation using the BDEM. Int. J. Fract. 2009, 157, 13–32. [Google Scholar] [CrossRef]
- Mousavi, S.; Pask, J.; Sukumar, N. Efficient adaptive integration of functions with sharp gradients and cusps in n-dimensional parallelepipeds. Int. J. Numer. Methods Eng. 2012, 91, 343–357. [Google Scholar] [CrossRef]
- Iarve, E.; Gurvich, M.; Mollenhauer, D.; Rose, C.; Dávila, C. Mesh-Independent matrix cracking and delamination modeling in laminated composites. Int. J. Numer. Methods Eng. 2011, 88, 749–773. [Google Scholar] [CrossRef]
- Xu, J.; Lee, C.; Tan, K. A two-dimensional co-rotational Timoshenko beam element with XFEM formulation. Comput. Mech. 2012, 49, 667–683. [Google Scholar] [CrossRef]
- Belytschko, T.; Gracie, R.; Ventura, G. A review of the extended/generalized finite element methods for material modelling. Modell. Simul. Mater. Sci. Eng. 2009, 17, 1–24. [Google Scholar]
- Fries, T.; Belytschko, T. The extended/generalized finite element method: An overview of the method and its applications. Int. J. Numer. Methods Eng. 2010, 84, 253–304. [Google Scholar] [CrossRef]
- Moës, N.; Dolbow, J.; Belytschko, T. A finite element method for crack growth without remeshing. Int. J. Numer. Methods Eng. 1999, 46, 131–150. [Google Scholar] [CrossRef]
- Mariani, S.; Perego, U. Extended finite element method for quasi-brittle fracture. Int. J. Numer. Methods Eng. 2003, 58, 103–126. [Google Scholar] [CrossRef]
- Nikbakht, M.; Wells, G. Automated modelling of evolving discontinuities. Algorithms 2009, 2, 1008–1030. [Google Scholar] [CrossRef]
- Müller, B.; Kummer, F.; Oberlack, M. Simple multidimensional integration of discontinuous functions with application to level set methods. Int. J. Numer. Methods Eng. 2012, 92, 637–651. [Google Scholar] [CrossRef]
- Ventura, G. On the elimination of quadrature subcells for discontinuous functions in the eXtended Finite-Element Method. Int. J. Numer. Methods Eng. 2006, 66, 761–795. [Google Scholar] [CrossRef]
- Benvenuti, E. A regularized XFEM framework for embedded cohesive interfaces. Comput. Methods Appl. Mech. Eng. 2008, 197, 4367–4378. [Google Scholar] [CrossRef]
- Benvenuti, E.; Tralli, A. Simulation of finite-width process zone for concrete-like materials. Comput. Mech. 2012, 50, 479–497. [Google Scholar] [CrossRef]
- Benvenuti, E.; Tralli, A. Iterative LCP-solvers for non-local loading-unloading conditions. Int. J. Numer. Methods Eng. 2003, 58, 2343–2370. [Google Scholar] [CrossRef]
- Benvenuti, E.; Vitarelli, O.; Tralli, A. Delamination of FRP-reinforced concrete by means of an extended finite element formulation. Compos. Part B 2012, 43, 3258–3269. [Google Scholar] [CrossRef]
- Benvenuti, E.; Tralli, A.; Ventura, G. A regularized XFEM framework for embedded cohesive interfaces. Int. J. Numer. Methods Eng. 2008, 197, 4367–4378. [Google Scholar] [CrossRef]
- Tornberg, A. Multi-Dimensional quadrature of singular and discontinuous functions. BIT Numer. Math. 2002, 42, 644–669. [Google Scholar] [CrossRef]
- Tornberg, A.; Engquist, B. Regularization techniques for numerical approximation of PDEs with singularities. J. Sci. Comput. 2003, 19, 527–552. [Google Scholar] [CrossRef]
- Osher, S.; Sethian, J. Fronts propagating with curvature dependent speed: Algorithms based on Hamilton-Jacobi formulations. J. Comput. Phys. 1988, 79, 12–49. [Google Scholar] [CrossRef]
- Patzák, B.; Jirásek, M. Process zone resolution by extended finite elements. Eng. Fract. Mech. 2003, 70, 957–977. [Google Scholar] [CrossRef]
- Zahedi, S.; Tornberg, A. Delta function approximations in level set methods by distance function extension. J. Comput. Phys. 2010, 229, 2199–2219. [Google Scholar] [CrossRef]
- Discacciati, M.; Quarteroni, A.; Quinodoz, S. Numerical approximation of internal discontinuity interface problems. Math. Tech. Rep. 2011, 9, 1–35. [Google Scholar] [CrossRef]
- Areias, P.; Belytschko, T. Two-Scale method for shear bands: Thermal effects and variable bandwidth. Int. J. Numer. Methods Eng. 2007, 72, 658–696. [Google Scholar] [CrossRef]
- Tornberg, A.; Engquist, B. Numerical approximations of singular source terms in differential equations. J. Comput. Phys. 2004, 200, 462–488. [Google Scholar] [CrossRef]
- Polianin, A.D.; Manzhirov, A.V. Handbook of Integral Equations; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Benvenuti, E. Mesh-Size-Objective XFEM for regularized continuousdiscontinuous transition. Finite Elem. Anal. Des. 2011, 47, 1326–1336. [Google Scholar] [CrossRef]
- Cannarozzi, A.; Ubertini, F. A mixed variational method for linear coupled thermoelastic analysis. Int. J. Solids Struct. 2001, 38, 717–739. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Benvenuti, E.; Ventura, G.; Ponara, N. Finite Element Quadrature of Regularized Discontinuous and Singular Level Set Functions in 3D Problems. Algorithms 2012, 5, 529-544. https://doi.org/10.3390/a5040529
Benvenuti E, Ventura G, Ponara N. Finite Element Quadrature of Regularized Discontinuous and Singular Level Set Functions in 3D Problems. Algorithms. 2012; 5(4):529-544. https://doi.org/10.3390/a5040529
Chicago/Turabian StyleBenvenuti, Elena, Giulio Ventura, and Nicola Ponara. 2012. "Finite Element Quadrature of Regularized Discontinuous and Singular Level Set Functions in 3D Problems" Algorithms 5, no. 4: 529-544. https://doi.org/10.3390/a5040529
APA StyleBenvenuti, E., Ventura, G., & Ponara, N. (2012). Finite Element Quadrature of Regularized Discontinuous and Singular Level Set Functions in 3D Problems. Algorithms, 5(4), 529-544. https://doi.org/10.3390/a5040529







