Alpha-Beta Pruning and Althöfer’s Pathology-Free Negamax Algorithm

Abstract

The minimax algorithm, also called the negamax algorithm, remains today the most widely used search technique for two-player perfect-information games. However, minimaxing has been shown to be susceptible to game tree pathology, a paradoxical situation in which the accuracy of the search can decrease as the height of the tree increases. Althöfer’s alternative minimax algorithm has been proven to be invulnerable to pathology. However, it has not been clear whether alpha-beta pruning, a crucial component of practical game programs, could be applied in the context of Alhöfer’s algorithm. In this brief paper, we show how alpha-beta pruning can be adapted to Althöfer’s algorithm.

1. Introduction

The minimax algorithm remains today the most widely used game tree search technique for two-player perfect-information games. For a given board position, a game tree is built to some depth, a static board-evaluation function is applied to the leaf nodes, and evaluation values are propagated up the tree and used to estimate the evaluation of the root. A criticism of minimaxing is that because the evaluation function applied to the leaf nodes is itself an estimate rather than an exact measurement, evaluation errors introduced at the search frontier can become amplified as they are propagated up the tree, leading to an incorrect root evaluation. Pearl has written [1, p. 427],

Yet, it should come as a surprise that the minimax method works at all. The static evaluation function does not exactly evaluate the positions at the search frontier, but, only provides estimates of their strengths; minimaxing these estimates as if they are true payoffs amounts to committing one of the deadly sins of statistics, computing a function of the estimates instead of an estimate of the function.

Researchers [1,2,3,4,5,6,7,8,9,10,11,12,1314] have found that in models of game trees with an erroneous evaluation function, evaluation errors are not always eliminated by minimaxing and can, in fact, grow with the height of the tree, leading to a situation known as game tree pathology where increasing the depth of search results in loss of accuracy. Recent work [9] suggests that the pathology phenomenon may be even more common than previously thought.

As an alternative to conventional minimaxing, Ingo Althöfer’s [15] alternative minimax algorithm, which uses evaluation values of all nodes in the tree, rather than only leaf nodes, in the evaluation of the root, has been proven not to suffer from pathology. However, one reason why Althöfer’s algorithm has not been used in practical game programs has been the uncertainty regarding the compatibility of the algorithm with alpha-beta pruning: in the conclusion of [15], Althöfer comments that alpha-beta pruning may be “still possible” with his algorithm. Therefore, in the remainder of this paper, we show how full alpha-beta pruning can be adapted to Althöfer’s algorithm.

2. Review of Althöfer’s Algorithm

In the negamax formulation of standard minimaxing, the valuation $V_x$ of a game tree node x is defined as

$$V_x=\left\{\begin{array}{ccc}\underset{y\in \Gamma \left(x\right)}{max}\{-V_y\}\hfill & & x\mathrm{not}\mathrm{a}\mathrm{leaf}\hfill \\ f\left(x\right)\hfill & & \mathrm{otherwise}\hfill \end{array}\right.$$

(1)

where $\Gamma \left(x\right)$ denotes the children of x, and f is the static board-state evaluation function.

In Althöfer’s negamax algorithm, the valuation of a leaf node is also simply its static evaluation, but for a non-leaf node x,

$$W_x=\underset{y\in \Gamma \left(x\right)}{max}\{-W_y\}+f\left(x\right)$$

(2)

assuming that all leaf nodes are at the same depth. Most tournament-oriented programs are based on iterative deepening, which means they already apply the evaluation function to internal nodes as well as leaf nodes. In Althöfer’s algorithm, these evaluation function values for internal nodes are used in addition to those for leaf nodes.

Using an earlier theorem by Karp and Pearl [16], Althöfer showed in [15] that with Equation (2), the probability of an incorrect root evaluation decreases at an exponential rate as the height of the tree increases.

3. Review of Alpha-Beta Pruning

Alpha-Beta pruning [17] is a mathematically sound technique to detect and prune away “dead branches” in a game tree, i.e., branches that cannot have an effect on the outcome of the search. Today, alpha-beta pruning remains a crucial component of any practical game program that uses minimaxing.

Figure 1. Alpha-Beta pruning applied to the standard negamax algorithm.

Figure 1. Alpha-Beta pruning applied to the standard negamax algorithm.

Figure 1 shows alpha-beta pruning applied to the standard negamax formulation of minimax search. If x is a node in a game tree, let $\ell \left(x\right)$ denote its level and let $p\left(x\right)$ denote its parity,

$$p\left(x\right)=\left\{\begin{array}{cc}1\hfill & \mathrm{if}\ell \left(x\right)\mathrm{is}\mathrm{odd}\hfill \\ 0\hfill & \mathrm{if}\ell \left(x\right)\mathrm{is}\mathrm{even}\hfill \end{array}\right.$$

(3)

When the algorithm begins processing a new node x, the parameter α represents the current maximum valuation of any node of x’s parity that is an ancestor of x. The parameter β represents the negative of the current maximum valuation of any node of the opposite parity to x that is an ancestor of x. For example, in Figure 2, x is passed $\alpha =-2$ and $\beta =1$. The $\alpha =-2$ indicates the fact that u has a value of $-2$. The $\beta =1$ represents the fact that y currently has a value of $-\left(1\right)$. When z returns to x a value of $2>\beta$ (note that when we say “return to x” we mean the value returned by z after x has negated it), it becomes clear that the remaining children of x do not need to be examined. This is because the value that x will return to y will be less than or equal to $-2$, which means that y will prefer v over x. Therefore, the remaining children of x become irrelevant and can be safely pruned. When x passes parameters to its own child z, it will pass β equal to the negative of its own α. For x, α represented the highest value of an ancestor of its own parity. Since the child of x will be of opposite parity to x, the value that will be passed for β will correctly be the negative of the maximum value of an ancestor of opposite parity.

When x passes the β parameter to a child, it should pass the negation of the maximum value of an ancestor of the child of opposite parity to the child, i.e., of its own parity. This value will either be the negation of the α that x received from its own parent, or it will be the negation of the value of one of the earlier siblings of z (represented in the algorithm in Figure 1 by the variable m), if that sibling returned a value greater than α. For example, consider the situation illustrated in Figure 3 where x had a child w prior to z. If w returns to x a value less than the α of x (e.g., $-4$), then the maximum value of an ancestor of z of x’s own parity will still be the α that x received from y. If, however, w returns to x a value greater than α (e.g., $-1$), then the maximum value of an ancestor of z of x’s parity will be the current value of x itself. Therefore, z will be passed a value of β equal to the negation of the value x received from w, which is a sibling of z.

In this way, the values of α and β are propagated throughout the tree, where for each node, they represent a window within which the node must score or else it will be irrelevant.

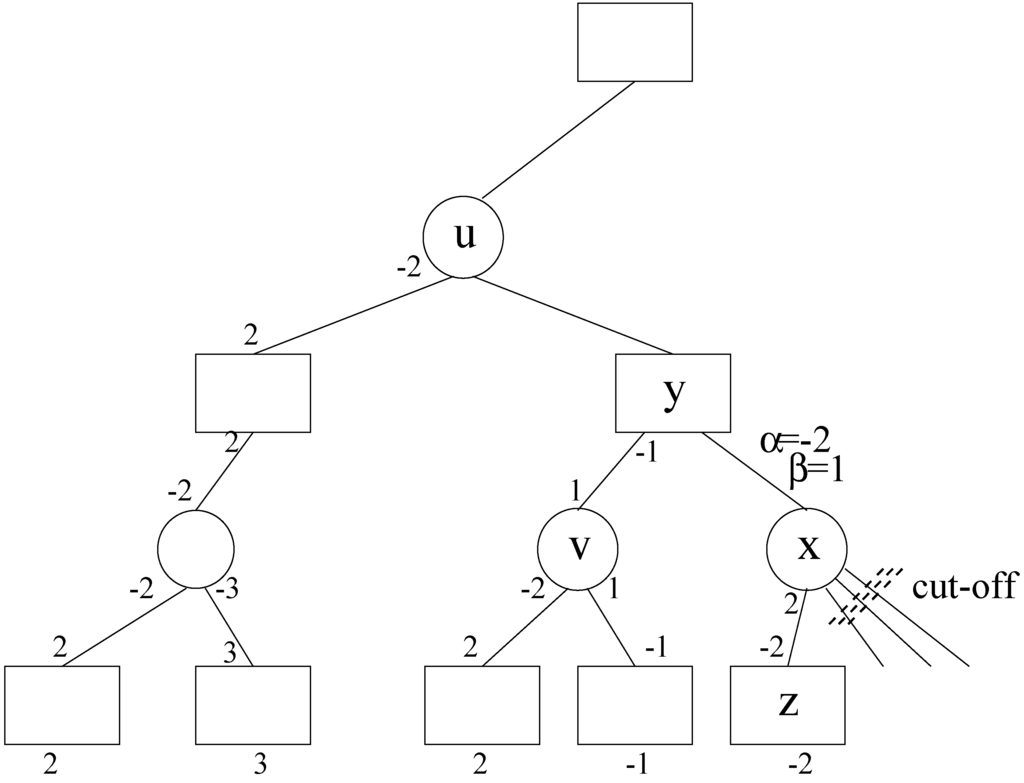
Figure 2. Example of a cut-off in pruning with standard negamax.

Figure 2. Example of a cut-off in pruning with standard negamax.

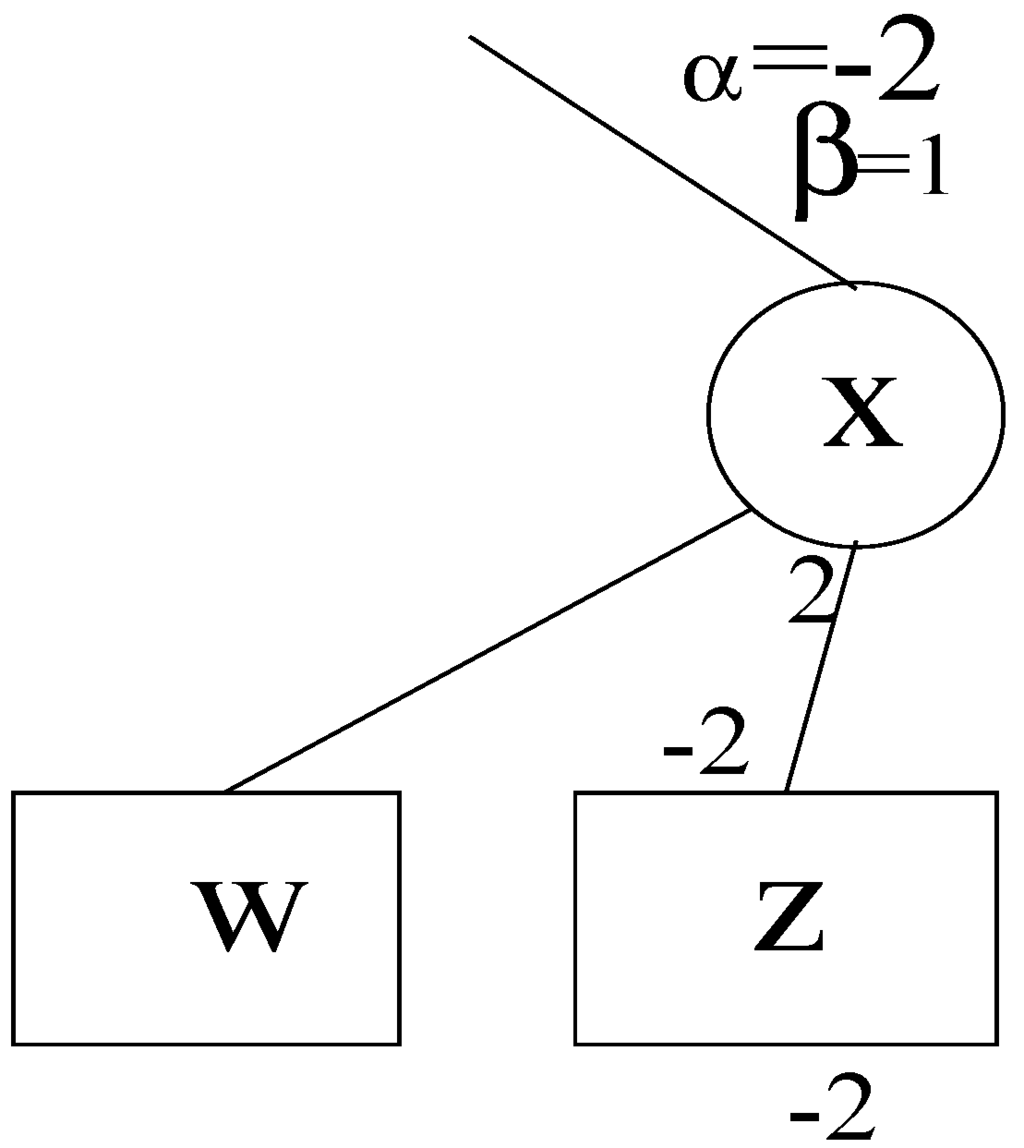
Figure 3. Illustration of parameter-passing in alpha-beta pruning.

Figure 3. Illustration of parameter-passing in alpha-beta pruning.

Figure 4. Our alpha-beta version of Althöfer’s algorithm.

Figure 4. Our alpha-beta version of Althöfer’s algorithm.

4. Applying Alpha-Beta Pruning to Althöfer’s Algorithm

Figure 4 shows our application of alpha-beta pruning to Althöfer’s algorithm. In Althöfer’s algorithm, as described by Equation (2), the valuation of a node u is equal to the value of the optimal path from a leaf node to u. If y is an ancestor of x, we define the value $Q_{x,y}$ of the path $L_{x,y}$ from x to y to be

$$Q_{x,y}=\left[\sum _{z\in L_{x,y}\&p\left(z\right)=p\left(y\right)}f\left(z\right)\right]-\left[\sum _{z\in L_{x,y}\&p\left(z\right)\ne p\left(y\right)}f\left(z\right)\right]$$

(4)

In other words, $Q_{x,y}$ is equal to the sum of the evaluation function applied to the nodes in the path $L_{x,y}$ of the same parity as y minus the sum of the evaluation function applied to the nodes in the path $L_{x,y}$ of the opposite parity to y. The Althöfer valuation $W_u$ of a node u at a given point in the execution of the search is equal to the optimal value of $Q_{x,u}$ such that x belongs to the set of leaf nodes examined thus far,

$$W_u=max\{Q_{x,u}\mid x\mathrm{is}\mathrm{a}\mathrm{leaf}\}$$

(5)

Consider the situation shown in Figure 5 where x is the node that we are currently processing. As soon as it is discovered that $W_z=4$, the remaining children of x are cut off because $-W_z+f\left(x\right)\ge {\beta }_x$.

In the application of alpha-beta pruning to standard negamax, as discussed earlier, the parameters ${\alpha }_x$ and ${\beta }_x$ that are passed to a node x are equal to

$${\alpha }_x=max\{V_u\mid u\mathrm{is}\mathrm{an}\mathrm{ancestor}\mathrm{of}x\mathrm{and}p\left(u\right)=p\left(x\right)\}$$

(6)

$$-{\beta }_x=max\{V_v\mid v\mathrm{is}\mathrm{an}\mathrm{ancestor}\mathrm{of}x\mathrm{and}p\left(v\right)\ne p\left(x\right)\}$$

(7)

where $V_u$ refers to the current valuation of a node u according to Equation (1). In our algorithm, the meanings are

$${\alpha }_x=max\{W_u-Q_{\pi \left(x\right),u}\mid u\mathrm{is}\mathrm{an}\mathrm{ancestor}\mathrm{of}x\mathrm{and}p\left(u\right)=p\left(x\right)\}$$

(8)

$$-{\beta }_x=max\{W_v-Q_{\pi \left(x\right),v}\mid v\mathrm{is}\mathrm{an}\mathrm{ancestor}\mathrm{of}x\mathrm{and}p\left(v\right)\ne p\left(x\right)\}$$

(9)

where $\pi \left(x\right)$ denotes the parent of x. In 18,

$$\begin{array}{ccc}\hfill -{\beta }_x=2& =& W_y-[f\left(y\right)-f\left(u\right)+f\left(v\right)]\hfill \\ & =& -3-\left[\right(-1)-(1)+(-3\left)\right]\hfill \\ & =& -3-[-5]=2\hfill \end{array}$$

(10)

because y is the node that maximizes Equation (9) for x. Similarly,

$$\begin{array}{ccc}\hfill {\alpha }_x=-7& =& W_u-[f\left(u\right)-f\left(v\right)]\hfill \\ & =& -3-[1-(-3\left)\right]\hfill \\ & =& -3-\left[4\right]=-7\hfill \end{array}$$

(11)

because u is the node that maximizes Equation (8) for x.

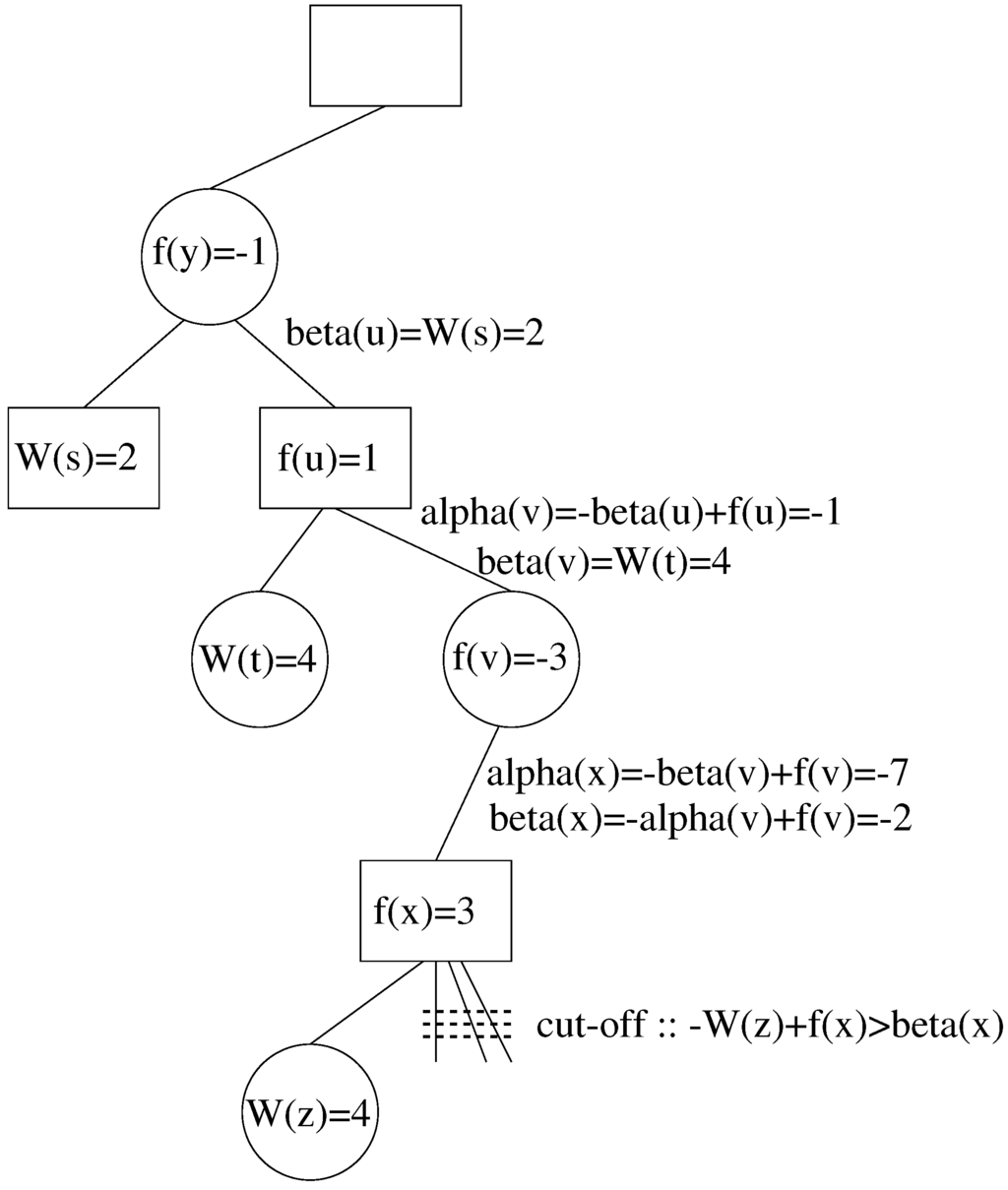
Figure 5. Example of pruning with Althöfer’s algorithm.

Figure 5. Example of pruning with Althöfer’s algorithm.

5. Concluding Remarks

The issue of pathology in game trees might be expected to become more problematic as technological advances allow us to search deeper and deeper game trees. With more difficult games, such as Go [18], game tree pathology could come to the fore as a prohibitive factor. With Althöfer’s algorithm, there is a guarantee that evaluation errors will not grow to dominate the search, and, for programs that use iterative deepening, Althöfer’s algorithm will not add much additional computational burden. In this brief paper, we have shown how alpha-beta pruning, an important component of realistic game programs, can be added to the algorithm, making its practical application more feasible.

The author is indebted to the anonymous reviewers for their useful comments, which substantially improved the paper.