Abstract
Wireless sensor networks are a relatively new area where technology is developing fast and are used to solve a great diversity of problems that range from museums’ security to wildlife protection. The geometric optimisation problem solved in this paper is aimed at minimising the sensors’ range so that every point on a polygonal region R is within the range of at least two sensors. Moreover, it is also shown how to minimise the sensors’ range to assure the existence of a path within R that stays as close to two sensors as possible.
1. Introduction and Related Work
Problems related to wireless ad-hoc networks (or just sensor networks) have emerged in the last few years as a result of the fast development of the associated technology. These networks have great long-term economic potential and pose many new system-building challenges [1]. Sensor networks are used to solve a great diversity of problems that range from battlefield monitoring to weather detection, museums’ security and even wildlife protection [2]. The problems solved in this paper are related to coverage. Since each sensor, antenna (or any device able to send or receive some sort of signal) can be located anywhere within a specific region, coverage measures the quality of this placement. Let R be a region on the plane that is monitored by a given sensor network. Does this network cover R completely? If not, is it still an acceptable coverage? These questions are obviously fundamental issues in this area. Coverage can be seen from two opposite perspectives. In the worst-case coverage there is an attempt to locate the regions of R that are hidden from the sensors, that is, not monitored. These areas are known as breach regions. On the other hand, the best-case coverage is characterised as an attempt to locate the areas that are are within reach of as many sensors as possible, thus identifying the “best” monitored regions of R. The following optimisation problems aim to tune a sensor network so that a given region is well covered and assure the existence of a path between two points within the region that stays as close to the sensors as possible. In other words, a best-coverage path.
Let be a set of n points on the plane that represent the location of n devices that are able to send or receive some sort of signal, like antennas. The devices of S are homogeneous in the sense that they all have the same power transmission range . It is also assumed that they are in general position. Let R be a polygonal region that models a street network (see Figure 1, the background image was taken from Google Maps). People and vehicles can move within R to reach specific locations there.
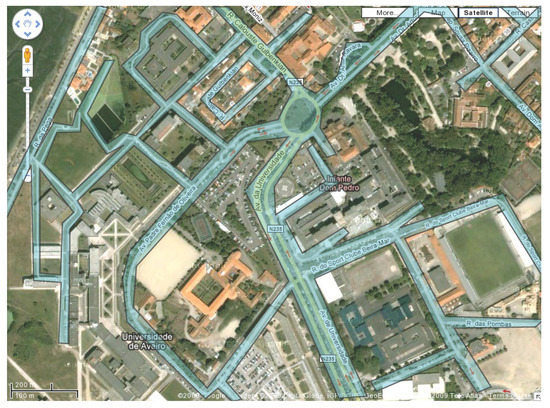
Figure 1.
The blue polygonal region models a street network.
In this example, the set S of antennas is located at the buildings’ tops and not on the streets, so no antennas are found on R. However, the algorithms in this paper work for both cases. The regions within reach of at least two antennas are considered to be well covered. Therefore, the larger these regions the better the coverage of R. This restriction is derived by several real-life problems that may occur in situations where stronger monitoring is needed, such as military applications. This is also the case when multiple sensors are required to detect an event.
In Figure 2 and Figure 3 there are two examples of a polygonal region each with a set of homogeneous antennas (represented by black dots) whose coverage area is shown in white. The antennas’ range in Figure 2 is shorter than in Figure 3. The best covered regions, that is, regions that are within reach of at least two antennas are shown in dark blue. In these zones, any traffic would get a signal transmitted from at least two antennas.
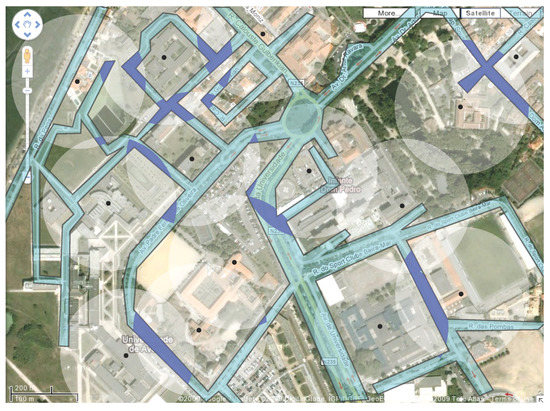
Figure 2.
The areas of the polygonal region that are covered by at least two antennas are shown in dark blue.
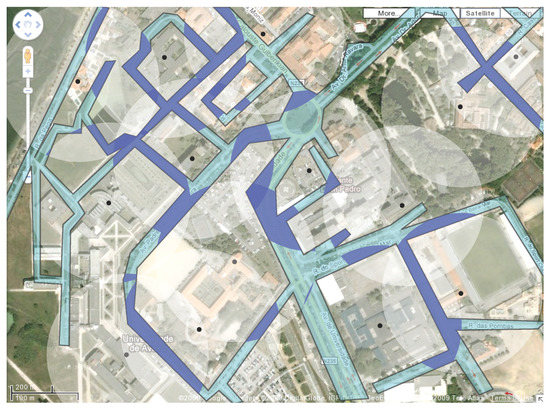
Figure 3.
The areas of the polygonal region that are covered by at least two white antennas are shown in dark blue.
As stated before, it can be seen that larger transmission ranges provide better coverage. However, as larger ranges also result in higher costs, it is appropriate to balance one against the other. Moreover, the optimisation of the antennas’ transmission range also improves the life span of wireless-enabled devices [3]. Consequently, the main problem in this paper is to minimise the antennas’ range in order to provide a good coverage of region R and or to assure the existence of a well covered path within R. What follows is therefore a formal definition of the problem. Assuming all distances are Euclidean, the distance between a point q on the plane and a set S of points is defined as the minimum distance between q and any one point of S. Point q is said to be covered by a set S of antennas with power transmission range r if the distance between q and S is less or equal to r. Therefore, the antennas’ minimum transmission range that covers q is the distance between q and S. A point covered by two or more antennas of S is said to be 2-covered by S (see Figure 4(a)). This definition aims towards quality coverage, as previously explained. The minimum power transmission range of S that 2-covers an object x is denoted by . For example, if the object is a point q, is the minimum power transmission range of S that 2-covers q.
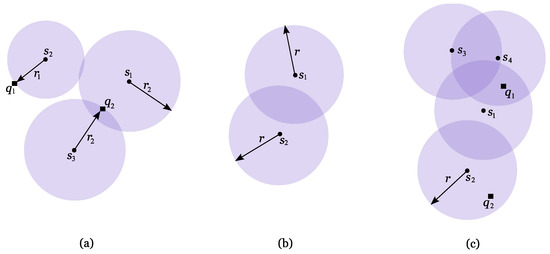
Figure 4.
Set S is represented by dots. (a) Point is covered by antenna with minimum range . Point is 2-covered by S with minimum range . (b) The lens formed by and is shown in dark purple. (c) Regions 2-covered by S with range r are shown in dark purple. Point is 2-covered by S, whilst is not.
Let be the set of discs of radius r each centred at an antenna of S. Each nonempty intersection between two discs of D is called a lens (see Figure 4(b)). The union of these lenses encloses all the points on the plane that are 2-covered by S, thus defining 2-covered regions (see Figure 4(c)). Every point within such regions clearly is 2-covered. The problems presented in the next sections aim to 2-cover a given region while minimising the antennas’ range r. Note that the minimum range of the antennas that covers a point can be easily calculated in time since such range is given by the distance between the point and its closest antenna. However, the Voronoi diagram of S [4] is a useful geometric structure that answers each query in time. This diagram can be constructed in time, so its construction is only justified when the number of queries regarding S is larger than . The two closest antennas to a given point can be found using the second order Voronoi diagram of S, denoted by . The second order Voronoi diagram of S divides the plane into several regions by grouping points that share the same two closest antennas [4]. It has the same complexity as the ordinary Voronoi diagram [5]. This diagram is naturally related to the optimisation problems studied in this paper since a point is 2-covered if it is within range of its two closest antennas.
Following the previous terminology, there are several works related to geometric optimisation using 1-coverage. For example, Abellanas et al. [6] and Mehta et al. [7] study routes that are always close (or always far) to a given set of sensors on the plane. Agnetis et al. [8] compute a subset of a given set of discs with variable radii whose costs depend on their radii, as well as the same subset but with fixed costs to cover a given line segment at minimum cost. After Meguerdichian’s work [1], others followed either by studying different versions of the coverage problem or by improving and proving previous results as are the cases of Boukerche et al. [2], Li et al. [9] and Mehta et al. [7]. Recently, Zhang et al. [10] developed two localised algorithms to identify whether a sensor is on the boundary of the area covered by a sensor network. In this work, one of the proposed algorithms is based on a technique called the localised Voronoi diagram and the other on neighbour embracing polygons. Contrary to some of the previous work, their algorithms can be applied to arbitrary topologies of the sensor network. Using variable radii sensors, Zhou et al. [11] address the problem of selecting a minimum energy-cost coverage, where each sensor can vary its sensing and transmission radius. They propose several centralised and distributed algorithms to compute a small subset sensors that are sufficient to cover the region required to be monitored. Das et al. [12] study efficient location of base stations to cover a convex region when the base stations are interior to the region. Making use of Voronoi diagrams, they developed a fast iterative algorithm to solve this problem. In their paper there are also some citations related to the coverage of a square or an equilateral triangle. Also employing Voronoi diagrams, Stoyan and Patsuk [13] consider the problem of covering a compact polygonal set using identical discs of minimum radius. Boukerche et al. [2] address sensor networks by studying how well a large wireless sensor network can be monitored or tracked while keeping a long lifetime. Their solution outperforms previously known techniques. Bezdek and Kuperberg [14] research an intermediate problem between 1-coverage and 2-coverage. They study the minimum coverage of the plane using homogeneous discs so that the region remains covered even when the radius of one of the discs decreases. This concept provides a continuous transition from 1-coverage to 2-coverage.
This paper is organised as follows: in Section 2 it is shown how to minimise the power transmission range of a set S of antennas to 2-cover a polygonal region R (with or without holes). In Section 3, it is introduced an algorithm to minimise the power transmission range that assures the existence of a 2-covered path between two points on R. This problem is solved using the respective decision problem that is also addressed in this section. The cases where region R is not polygonal are discussed in Section 4, which is followed by a brief discussion of the results.
2. Minimum Transmission Range to 2-Cover a Polygonal Region
Let R be a polygonal region (with or without holes) and S a set of antennas with the same power transmission range. The boundary of R, denoted by , is considered to be part of the region R. Region R is said to be 2-covered by S if every point on R is 2-covered. The algorithm introduced in this section calculates the minimum power transmission range of S to 2-cover R, . Such range is calculated as being the largest distance between a point and its second closest antenna. Let the antennas’ range be large enough to 2-cover R. Now suppose this range is reduced until there is just one point that is no longer 2-covered. The antennas’ minimum range to 2-cover q is exactly . The following proposition characterises the location of point q on R.
Proposition 1
Let R be a polygonal region, q a point on R and S a set of antennas. If for some antenna , then q can only be one of the following:
- (a)
- A vertex of R;
- (b)
- An intersection point between and ;
- (c)
- A vertex of interior to R.
Proof:
Let be such that for some antenna . Given an edge e of R, it is easy to see that is calculated using the intersection points between e and plus the endpoints of e. The minimum range of S that 2-covers all these points is exactly the minimum transmission range needed to 2-cover e (see Figure 5(a)). Consequently, if then q must be a vertex of R or an intersection point between and . If q is an interior point then the situation gets trickier since it does not depend on the shape of R but on the way lenses interact with each other. As the antennas’ range increases, the lenses grow larger and fill the interior of R. The last interior point to be 2-covered must be a point lying in the last “hole” (meaning a region of R not yet 2-covered). These holes are filled when three lenses intersect at a time since not only the intersection point is 2-covered but also its whole neighbourhood (see Figure 5(b)). Since three lenses intersect at a vertex of [15], if q is interior to R then it has to be a vertex of .
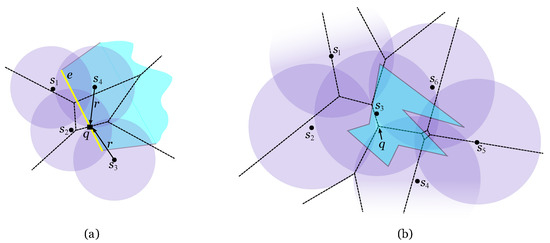
Figure 5.
(a) Line segment e is 2-covered with minimum range . (b) Point q is the last point to be 2-covered on R. It is a vertex of (shown in a dashed line).
According to this proposition, there are several candidates on R to be the point needing the largest range in order to be 2-covered. Since every point on R has to be 2-covered, is calculated as the minimum range to 2-cover every such candidate. Therefore, there is the need to analyse every vertex of R, intersection points between and and vertices of interior to R (see Figure 6(a)). In Figure 6(b) there is an example of a 2-covered polygonal region R with minimum power transmission range. The point of R defining is and so R is 2-covered if the antennas’ transmission range is at least . The following algorithm calculates .
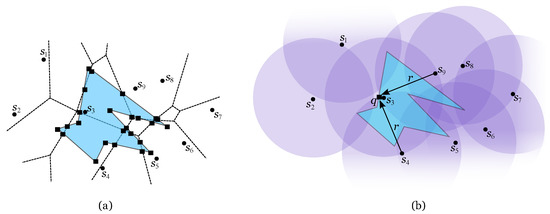
Figure 6.
(a) The candidates are represented by squares: vertices of R, points of and a vertex of interior to R. (b) .
Algorithm Minimum Range to 2-Cover a Region
Input: Set S of n antennas and polygonal region R
Output:
1. Compute , the second order Voronoi diagram of S.
2. Compute the intersection set .
3. Add the vertices of that are interior to R to set I.
4. Add the vertices of R to set I.
5. .
The following result is a direct consequence of the algorithm Minimum Range to 2-Cover a Region.
Theorem 1
Given a set S of n antennas and a polygonal region R with m vertices, can be calculated in time and space.
Proof:
Computing takes time since S is formed by n antennas on the plane [5]. The cardinality of set is at most since has n faces and R has m edges. Adding all the vertices of that are interior to R to set I takes time. The region’s vertices can be added to I in time. For each intersection point , is calculated in constant time using as it is the distance between q and its second closest antenna. The largest of these distances is . Overall, the time complexity of this procedure is . Regarding the space complexity, there is the need to store at most intersection points while can be stored in space [5]. Consequently, this algorithm runs in time and space.
Corollary 1
Given a set S of n antennas and a convex polygonal region R with m vertices, can be calculated in time and space.
Note that, for a convex polygonal region R, can be calculated in time and space if has been previously built.
3. Minimum Transmission Range to 2-Cover a Path on a Polygonal Region
Given two points p and q on a polygonal region R, the objective of this section is to calculate the minimum transmission range of the antennas such that there is a 2-path on R connecting p and q, . In Figure 7(a), the black path connecting p and q is not a 2-path since some of its points are only covered by one antenna. On the other hand, the yellow path in the same figure is a 2-path between p and q. Not only it is 2-covered by S as it exists within R which makes it the interesting type of 2-path for this section. In the following, whenever 2-path is mentioned, it is understood as a 2-path within R.
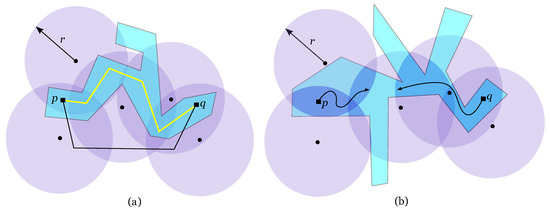
Figure 7.
Region R is shown in blue. (a) The yellow path is a 2-path on R connecting p to q while the black is not. (b) It is not possible to find a 2-path on R between p and q because they lie in different connected component of lenses.
3.1. Decision Problem
In this subsection, it is proposed an algorithm to solve the following decision problem: given a set S of n antennas with power transmission range and two points p and q on R, decide if there is a 2-path connecting p and q. This algorithm will then be used to solve the main problem. As mentioned before, a 2-path from p to q exists if and only if p and q lie in the same connected component of the union of lenses (see Figure 7(b)). If it exists, such 2-path only crosses the regions of R that are 2-covered. With this in mind, let A be the arrangement of the union of lenses confined to region R and intersected by (see Figure 8). If there is a 2-path between p and q on R, then it exists within A. If R is not convex, then there can be more than one face of A per Voronoi region. For example, there are two non-connected faces of A defined by the spikes of R on the lower leftmost Voronoi region in Figure 8.
According to Corollary 1, working with convex regions is easier since the number of intersection points decreases sharply. Moreover, there is only one face of A per Voronoi region. Consequently, the first step to solve this problem is to decompose R in convex pieces (see Figure 9(a)). It can be easily done using Steiner points: for each reflex vertex extend a ray from , which bisects the internal angle of R at , until it reaches or a previous ray. It can be shown that if R has k reflex vertices, then this set of rays divides R into convex pieces. There are some works on the optimisation of the final number of convex pieces, either using Steiner points [16] or diagonals [17]. However, the partition technique used in this paper does not optimise the resulting number of convex pieces.
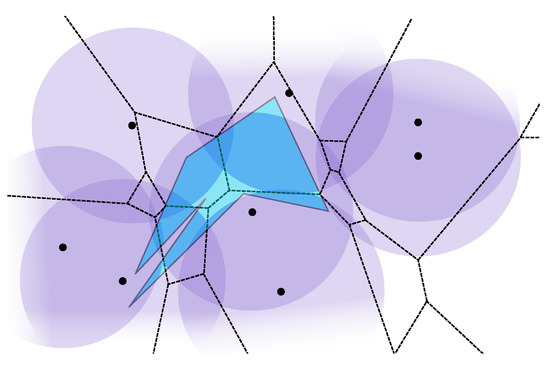
Figure 8.
Polygonal region R is shown in blue and in a dashed line. The arrangement of the union of lenses confined to R and intersected by is shown in dark blue.
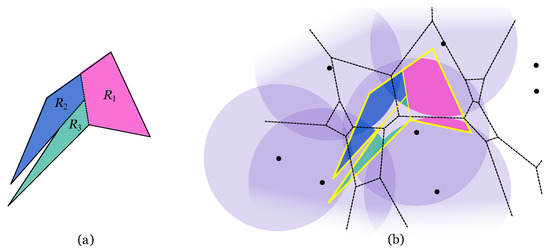
Figure 9.
(a) Polygonal region partitioned in three convex pieces: , and . (b) The arrangements , and are shown in pink, blue and green, respectively.
The strategy to decide if there is there a 2-path between p and q is based on the construction of an intersection graph G of the arrangement A. Since R is partitioned in several convex regions, each will be solved separately. According to this, the following algorithm constructs an intersection graph of the arrangement defined by A restricted to convex piece (see Figure 9(b)). The complete graph G is later constructed by properly uniting these smaller graphs. Let be the second order Voronoi region of antennas and and the lens resulting from the intersection of discs and .
Algorithm Preprocess (PRE)
Input: Set S of n antennas, range r, , convex piece
Output: Arrangement and graph
- Compute the arrangement :For each do
- (a)
- Compute , the lens resulting from
- (b)
- Compute the face of arrangement , which is the region resulting from the non-empty intersection
- Construct graph :For each face do
- (a)
- Add node to
- (b)
- For each neighbouring face of doIf then add edge to
The temporal complexity to construct the restricted arrangement and corresponding graph is given in the following result.
Theorem 2
Let S be a set of n antennas with transmission range r and a convex region with vertices. Arrangement and graph can be constructed in time if has been previously built.
Proof:
Let S be a set of n antennas with range r and a convex region with vertices. Each lens is intersected at most four times by and is convex. Consequently, the intersection between that convex region and also is convex and can be found in time, being the complexity of . As the Voronoi diagram has amortised linear complexity, the arrangement can be found in time. An intersection graph of has n nodes since there is at most one node per Voronoi region that intersects (see Figure 10(a)). Two nodes of are connected if their corresponding faces of intersect. The vertices of each face of can be used to check if it intersects another face of . It suffices that each vertex is identified as an apex of a lens, a point on or a point on a Voronoi edge. The latter is the important type of vertex for this procedure. Suppose face has a vertex v that is a point on a Voronoi edge that separates from . Then v belongs to lenses and , which means faces and intersect each other. Therefore, to construct it suffices to connect the nodes corresponding to the faces of that share at least one vertex on the same Voronoi edge. Overall, this arrangement and corresponding graph can be constructed in time.
Note that has as many edges as the Voronoi diagram and that it may not be connected (see graph on green region in Figure 10(a) Sec:Conclusions). To decide if a 2-path between points p and q exists, there is the need to unite all the restricted graphs to form the final intersection graphs G of arrangement A. Obviously, a node of is merged with another node of if the faces of A they correspond to intersect each other (see Figure 10). The following algorithm solves the decision problem.
Algorithm Power Transmission Range Test (TRT)
Input: Set S of antennas, range r, , region R, points p and q
Output: YES or NO
- Decompose R in convex pieces by adding a set L of rays.
- For each convex piece doPRE()...
- For every ray do.Merge the nodes of G whose corresponding faces of lie on the same lens.
- Assign p to node and q to node .
- Traverse G starting at p using the DFS algorithm [18].
- If node q is found then return YES. Otherwise return NO.
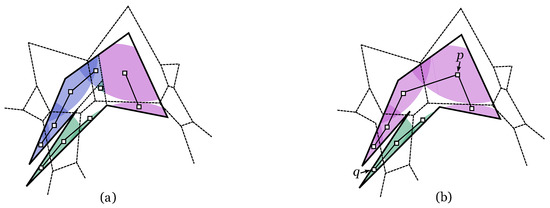
Figure 10.
(a) Three subgraphs corresponding to the three convex pieces, the one in the green region is disconnected. (b) There is not a 2-path between p and q because they lie in different connected components of the complete graph.
Point p is assigned to node that is the node of G whose corresponding face of A contains p. In a similar way, point q is assigned to node . Consequently, the existence of a 2-path connecting p and q depends on and being within the same connected component of G (see Figure 10(b)). The method chosen to traverse G is the Depth-First Search since its complexity is linear on the number of edges of the graph [18].
Theorem 3
Let S be a set of n antennas with transmission range r and R a polygonal region decomposed in convex pieces by adding k rays. Let M be the largest complexity of the convex pieces. Deciding if a 2-path between points p and q exists takes time if has been previously built.
Proof:
Decomposing region R with m vertices in convex pieces by adding a set L of k rays takes time [16]. Consequently, R is decomposed in convex pieces. Supposing each convex piece has vertices, let . According to Theorem 2, constructing for each convex piece takes time, so constructing a first version of G takes time. For the same reason, constructing arrangement A also takes time. Studying the vertices of every face of A on a convex piece takes time. Consequently, finding the sets of faces which have an edge on the same ray of L takes time. Computing the lens that contains a face of A can be done in constant time. Every ray of L can intersect n Voronoi regions and so n faces of A. Therefore, each set of faces has cardinality at most n. The vertices of the rays of L can have degree 3 at most [16], so the number of nodes of G to be merged at a time is at most 3, which can be done in constant time. Consequently, the construction of G is concluded in time. Locating p and q on A can be done in time. In the worst case, the Depth-First Search algorithm has to visit every node of G twice [18]. Therefore, traversing G to decide if there is a 2-path between points p and q takes time. Overall, this decision problem can be solved in time.
Note that if R is a convex polygonal region with m vertices, then deciding if a 2-path between points p and q exists takes time if has been previously built (Theorem 2). It suffices to compute the arrangement and the corresponding graph just for one convex piece.
3.2. Minimising the Antennas’ Transmission Range
The optimisation algorithm presented in this subsection calculates the minimum power transmission range of S that assures the existence of a 2-path on R between p and q. Such range is denoted by . Note that, for , this problem always has a solution because, if the range r is large enough, all discs of radius r centred at points of S contain R. In this case, any path connecting p to q on R is a 2-path. Following the idea presented in Section 2, as the range increases, there is the need to locate point b that is the first intersection between the connected component of lenses containing p and the one containing q. As before, this point can either be on or interior to R. The first case was discussed in Proposition 1 and so b can be a vertex of R or an intersection point between and . The second case is more complicated since now there is no need to completely cover R, in fact, all that is needed is that p and q lie in the same connected component of lenses (see Figure 11). This intersection point is called a bottleneck-point for 2-paths between p and q and it is denoted by .
Definition 1
([15]) Let p and q be two points on the plane and S a set of antennas with range .
- (a)
- A point is a type I bottleneck-point if there is only one antenna such that and there are two other antennas such that .
- (b)
- A point is a type II bottleneck-point if there are exactly three antennas such that and there is no antenna such that .
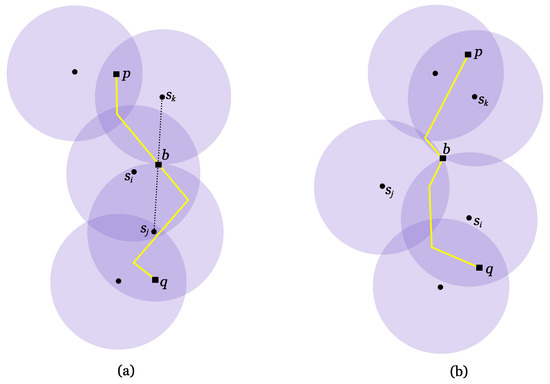
Figure 11.
he antennas’ range is and a 2-path connecting p to q is shown in yellow. (a) Point is a type I bottleneck-point. (b) Point is a type II bottleneck-point.
Without loss of generality, degenerate input data is not considered, so for all purposes, bottleneck-points are regarded as unique for every pair of points. This subject will be further discussed in Section 5. With this in mind, it is clear that every 2-path between p and q has to cross . Moreover, any bottleneck-point falls into one of these categories, that is, it is either a type I or type II bottleneck-point [15]. According to the last definition, it is easy to see that a type I bottleneck-point for 2-paths between p and q is the midpoint of the segment (see Figure 11(a)). The next proposition explains the relation between bottleneck-points and the second order Voronoi diagram of S. This relation helps to locate bottleneck-points on the referred diagram. Let be the triangle formed by the antennas and .
Proposition 2
([15]) Let p and q be two points on the plane and S a set of antennas with range .
- (a)
- If is a type I bottleneck-point covered by and such that , then b is the intersection point between and the second order Voronoi edge that separates from ;
- (b)
- If is a type II bottleneck-point covered by , then b is a vertex of and .
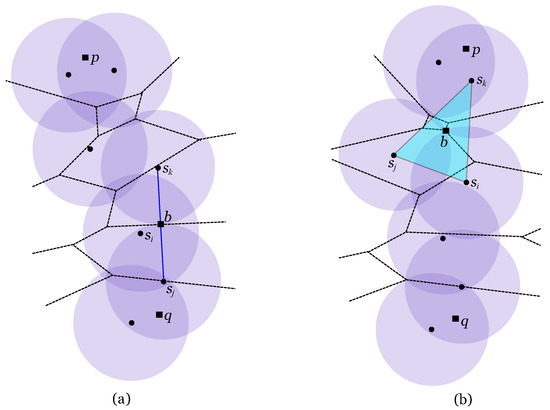
Figure 12.
The antennas’ range is and is shown in a dashed line. (a) Point is a type I bottleneck-point. (b) Point is a type II bottleneck-point.
Algorithm Minimum Transmission Range
Input: Set S of n antennas, points p and q on region R
Output:
- Compute , the second order Voronoi diagram of S.
- Compute set .Add the vertices of R to set I.
- Find set B of candidates for bottleneck-points using Proposition 2.
- .Calculate .
- Perform a binary search on :For the median range doIf TRT() = YES
- Then proceed the search on .
- Otherwise proceed the search on .
- The final range is .
Figure 12 shows the two types of bottleneck-points and their relation to the second order Voronoi diagram of S. According to Proposition 2, candidates to bottleneck-points are found on the edges of that are intersected by the line segment joining the two antennas defining such edge and vertices of that are interior to the triangle of the antennas responsible for them. To conclude, is calculated using a binary search on a list of ranges. Each range of the list is the minimum transmission range needed to 2-cover a candidate and each candidate is either p, q, a vertex of R, a point of or a bottleneck-point. In every step of the binary search, the corresponding range is tested to check if it is large enough to allow a 2-covered path connecting p and q. The algorithm Power Transmission Range Test (TRT) introduced in the last subsection will be used to this end. If the range is indeed large enough then the search proceeds on the lowest half of the ranges. Otherwise, the search continues on the highest half of the ranges.
In Figure 13 there is an example of a 2-path between p and q shown in yellow. Any 2-path between these points only exists if the antennas’ transmission range is at least . This range is represented by . The union of lenses on R is shown in light blue and point b is a type I bottleneck-point for 2-paths between p and q on R. Having this algorithm in mind, the following theorem concludes this subject.
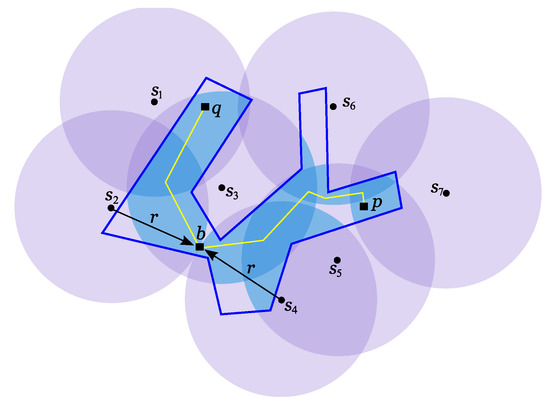
Figure 13.
The yellow 2-path between p and q on R only exists if the antennas’ transmission range is at least . The 2-covered regions of R are shown in light blue.
Theorem 4
Let S be a set of n antennas and R a polygonal region with m vertices decomposed in convex pieces by adding k rays. Let M be the largest complexity of the convex pieces. Given two points p and q on R, can be calculated in time.
Proof:
Computing takes time since S is a set of n antennas on the plane [5]. Set has cardinality since is linear on n and R has m vertices. Adding m vertices to I plus the n candidates to bottleneck-points for 2-paths between p and q takes time. Therefore, the set I can be found in total time. Computing for all also takes time, consequently sorting in ascending order takes time. Supposing each convex piece has vertices, let . Then according to Theorem 3, each step of the binary search runs in time. Consequently, the binary search runs in time, which is the overall complexity to calculate .
4. 2-Covering a Nonpolygonal Region
This work is focused on in the case that the region is a street network, therefore it is modelled by a polygonal region. Nevertheless, this street network can also be modelled by a connected graph that can be seen as a degenerated version of the case presented above. Given a set S of n antennas, calculating the minimum power transmission range to assure the existence of a 2-covered path between two nodes of a street graph takes time, assuming [19].
If an user can move within the whole plane (like an airplane flying through the sky), then region R is actually . This situation has also been addressed before. Calculating the minimum power transmission range to assure the existence of a 2-covered path between two points on the plane can be done in time [15]. This work also shows how to compute a 2-path between two points.
5. Discussion of the Results
This article studies the 2-coverage of a polygonal region R. First it is shown how to completely cover R using a set of n antennas with minimum transmission range and then how to minimise the antennas’ range so that a 2-path between two points exists on R. The first problem is solved using an algorithm that runs in time and space, m being the number of vertices of R. However, this complexity is lowered to time and space if the region is convex. With this in mind, the next problem was solved using a decomposition of R in convex pieces. The minimisation of the antennas’ range to assure the existence of a 2-path between two points on R proved to be harder to solve and so the first approach was directed at the decision problem. Therefore, if the antennas’ power transmission range is then decide if there is a 2-path between two points on R takes time (k is the number of rays added to decompose R in convex pieces and M the complexity of the convex piece with more vertices). Using the decision algorithm together with a binary search finally solves the main problem in time. The binary search is performed on a set of ranges which are needed to 2-cover particular points found on R and .
Although it is assumed throughout the paper that the point defining the minimum range to 2-cover a particular object is unique, this is not true in degenerate cases. The antennas’ distribution might result in a scheme where there can be more than one of these points. However, bottleneck-points can be found using the same technique and they still fall into only two types. The classification of bottleneck-points does not change in the presence of degenerate cases.
Although the antennas’ range is optimised to assure the existence of a 2-path on R, it is never shown how to construct such path. Future work obviously passes through explaining how to construct a 2-path between two points and even how to construct the shortest 2-path between those points. It is not clear how to do this efficiently because the space where the 2-path exists has a shape that is uncommon, some edges are arcs, others are line segments.
Acknowledgements
The fist author is co-supported by Project Consolider Ingenio 2010 i-MATH C3-0159 and MICINN Project MTM2008-05043. The second author is supported by CEOC through Programa POCTI, FCT and co-financed by EC fund FEDER, as well as the third author who also is supported by grant SFRH/BD/28652/2006.
References and Notes
- Meguerdichian, S.; Koushanfar, F.; Potkonjak, M.; Srivastava, M.B. Coverage problems in wireless ad-hoc sensor networks. In Proceedings of the Twentieth Annual Joint Conference of the IEEE Computer and Communications Societies, Anchorage, AK, USA, April 22-26, 2001; Vol. 3, pp. 1380–1387.
- Boukerche, A.; Fei, X.; Araujo, R.B. An energy aware coverage-preserving scheme for wireless sensor networks. In Proocedings of the 2nd ACM international Workshop on Performance Evaluation of Wireless ad hoc, Sensor and Ubiquitous Networks, Montreal, Canada, October 13, 2005; pp. 205–213.
- Gomez, J.; Campbell, A.T.; Naghshineh, M.; Bisdikian, C. Conserving transmission power in wireless ad hoc networks. In Proceedings of the 9th International Conference on Network Protocols, Riverside, CA, USA, November 11-14, 2001; pp. 24–34.
- Aurenhammer, F.; Klein, R. Handbook of Computational Geometry; Sack, J.R., Urrutia, J., Eds.; Elsevier Science: Amsterdam, Holland, 2000; Chapter 5; pp. 201–290. [Google Scholar]
- Lee, D.T. On k-nearest neighbor voronoi diagrams in the plane. IEEE Trans. Comput. 1982, 31, 478–487. [Google Scholar]
- Abellanas, M.; Hernández, G. Optimización de rutas de evacuación. In Proceedings of the XII Encuentros de Geometría Computacional, Valladolid, Spain, June 25-27, 2007; pp. 273–280.
- Mehta, D.P.; Lopez, M.A.; Lin, L. Optimal coverage paths in ad-hoc sensor networks. In Proceedings of the ICC ’03, IEEE International Conference on Communications, Anchorage, Alaska, USA, May 11-15, 2003; Vol. 1, pp. 507–511.
- Agnetis, A.; Grande, E.; Mirchandani, P.B.; Pacifici, A. Covering a line segment with variable radius discs. Comput. Oper. Res. 2009, 36, 1423–1436. [Google Scholar] [CrossRef]
- Li, X.; Wan, P.; Frieder, O. Coverage in wireless ad-hoc sensor networks. IEEE Trans. Comput. 2003, 52, 753–763. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, Y.; Fang, Y. Localized algorithms for coverage boundary detection in wireless sensor networks. Wireless Netw. 2009, 15, 3–20. [Google Scholar] [CrossRef]
- Zhou, Z.; Das, S.R.; Gupta, H. Variable radii connected sensor cover in sensor networks. ACM Trans. Sens. Netw. 2009, 5, 1–36. [Google Scholar] [CrossRef]
- Das, G.K.; Das, S.; Nandy, S.C.; Sinha, B.P. Efficient algorithm for Placing a given number of base stations to cover a convex region. J. Paral. Distrib. Comput. 2006, 66, 1353–1358. [Google Scholar] [CrossRef]
- Stoyan, Y.G.; Patsuk, V.M. Covering a compact polygonal set by identical circles. Comput. Opt. Appl. 2008. [Google Scholar] [CrossRef]
- Bezdek, A.; Kuperberg, W. Circle covering with a margin. Period. Math. Hung. 1997, 34, 3–16. [Google Scholar] [CrossRef]
- Abellanas, M.; Bajuelos, A.L.; Matos, I. 2-Covered paths by a set of antennas with minimum power transmission range. Inf. Processing Lett. 2009, 109, 768–773. [Google Scholar] [CrossRef]
- Chazelle, B. computational geometry and convexity. PhD Thesis, Yale University, New Haven, CT, USA, 1980. [Google Scholar]
- Keil, J.M. Decomposing a polygon into simpler components. SIAM J. Comput. 1985, 14, 799–817. [Google Scholar] [CrossRef]
- Golomb, S.W.; Baumert, L.D. Backtrack programming. JACM 1965, 12, 516–524. [Google Scholar] [CrossRef]
- Abellanas, M.; Bajuelos, A.L.; Matos, I. Safe routes on a street graph with minimum power transmission range. In Proceedings of the 25th European Workshop on Computational Geometry, Brussels, Belgium, March 16-18, 2009; pp. 85–88.
© 2009 by the authors licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).