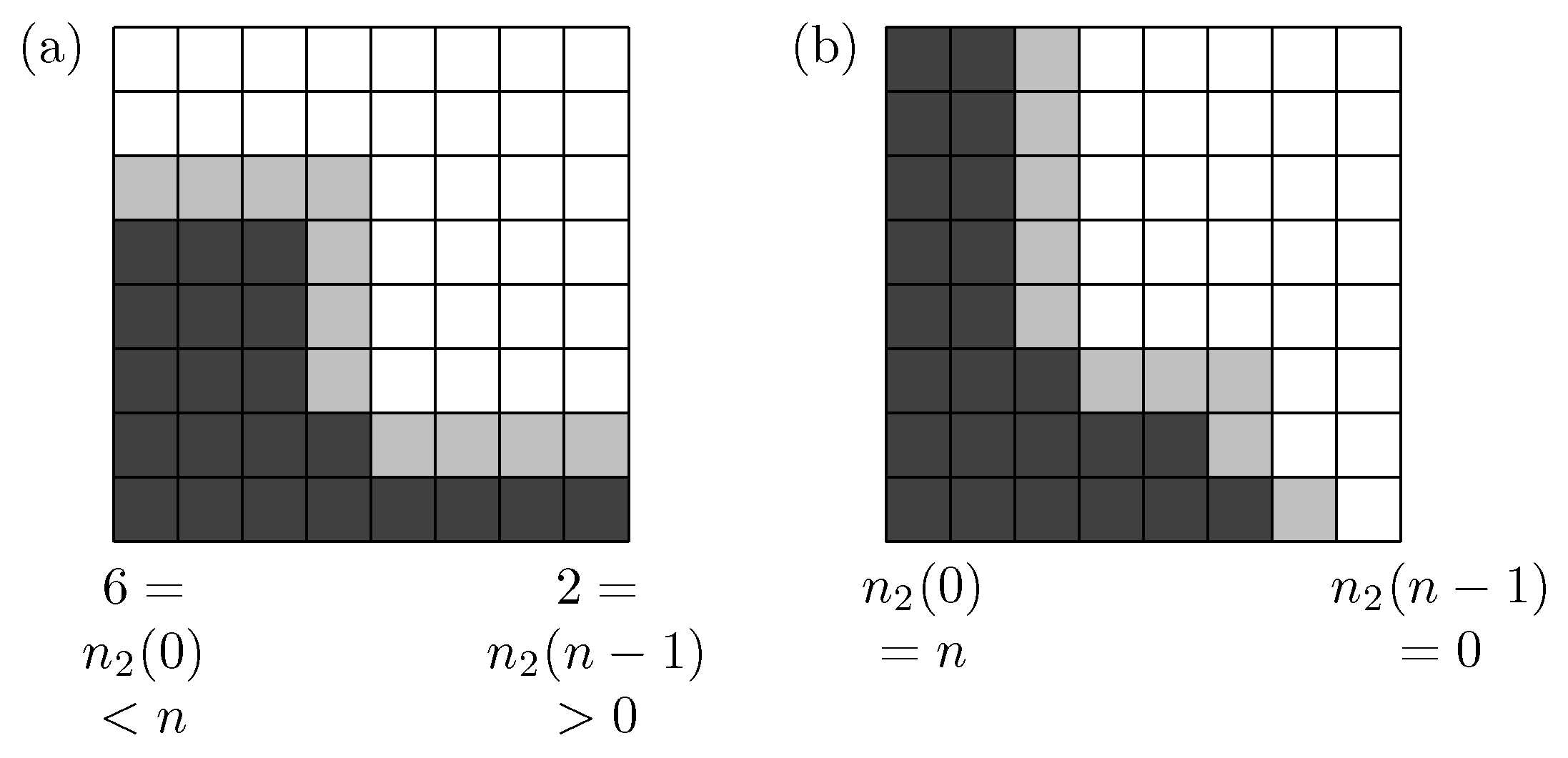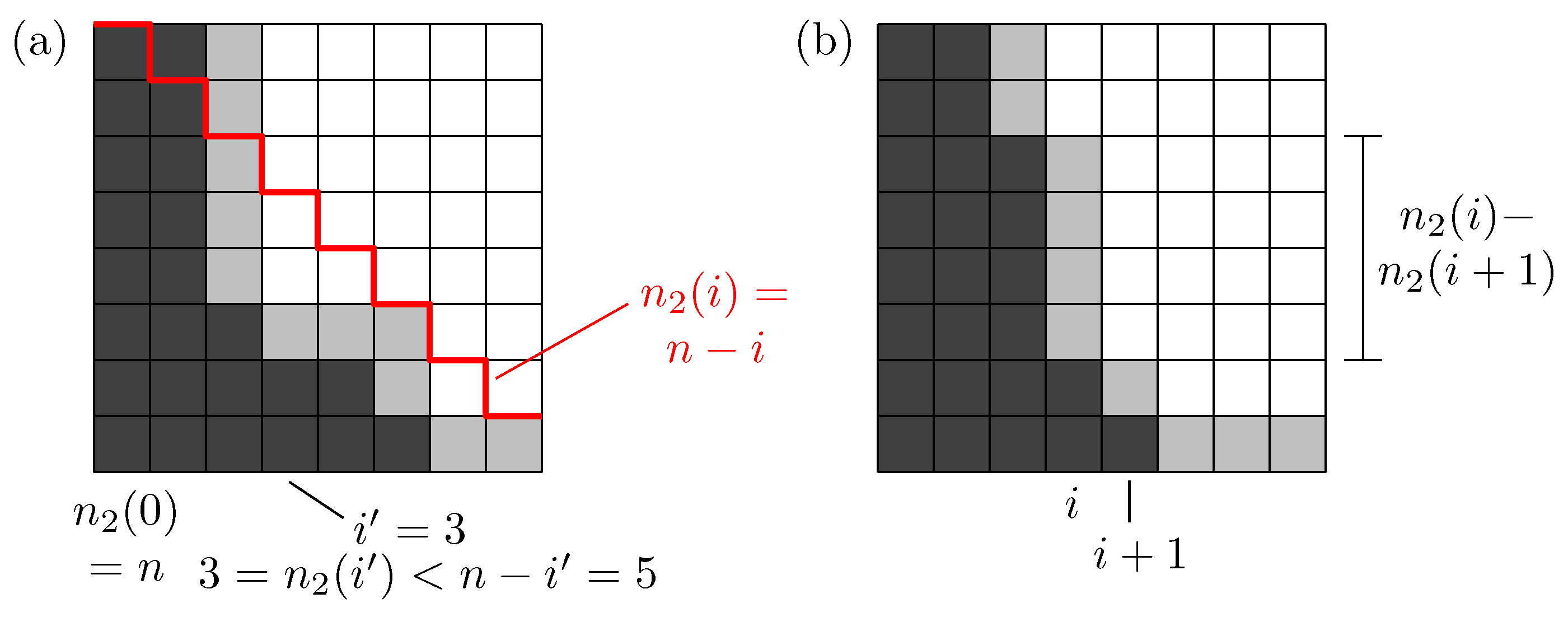4.1. An upper bound
As mentioned in the introduction, one could conjecture
. However, this does not even hold for
, see
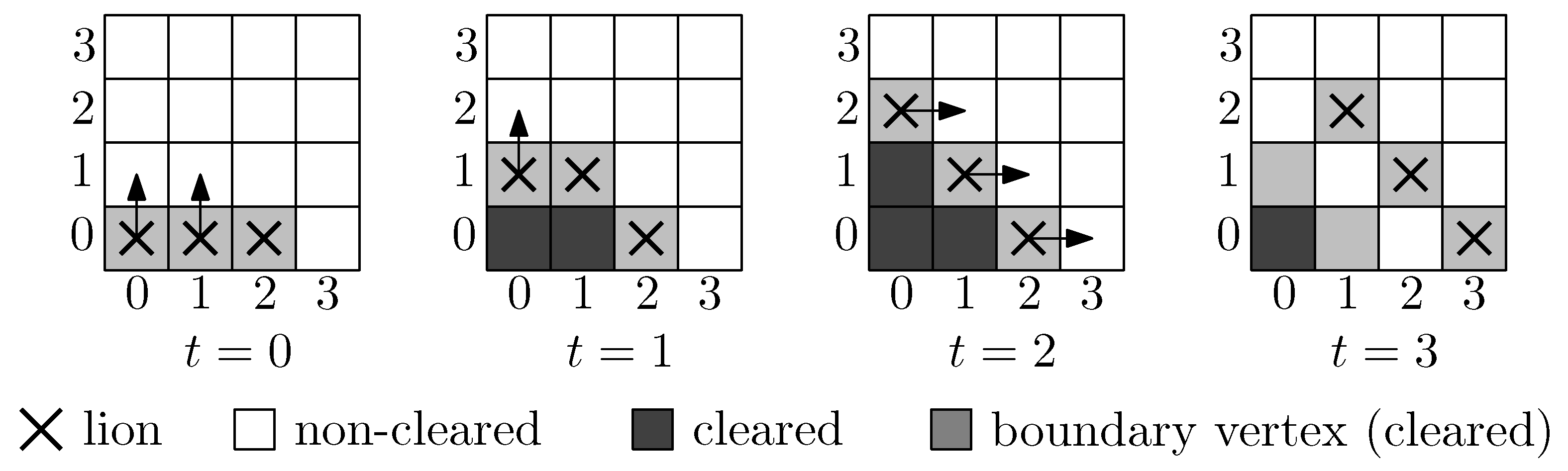
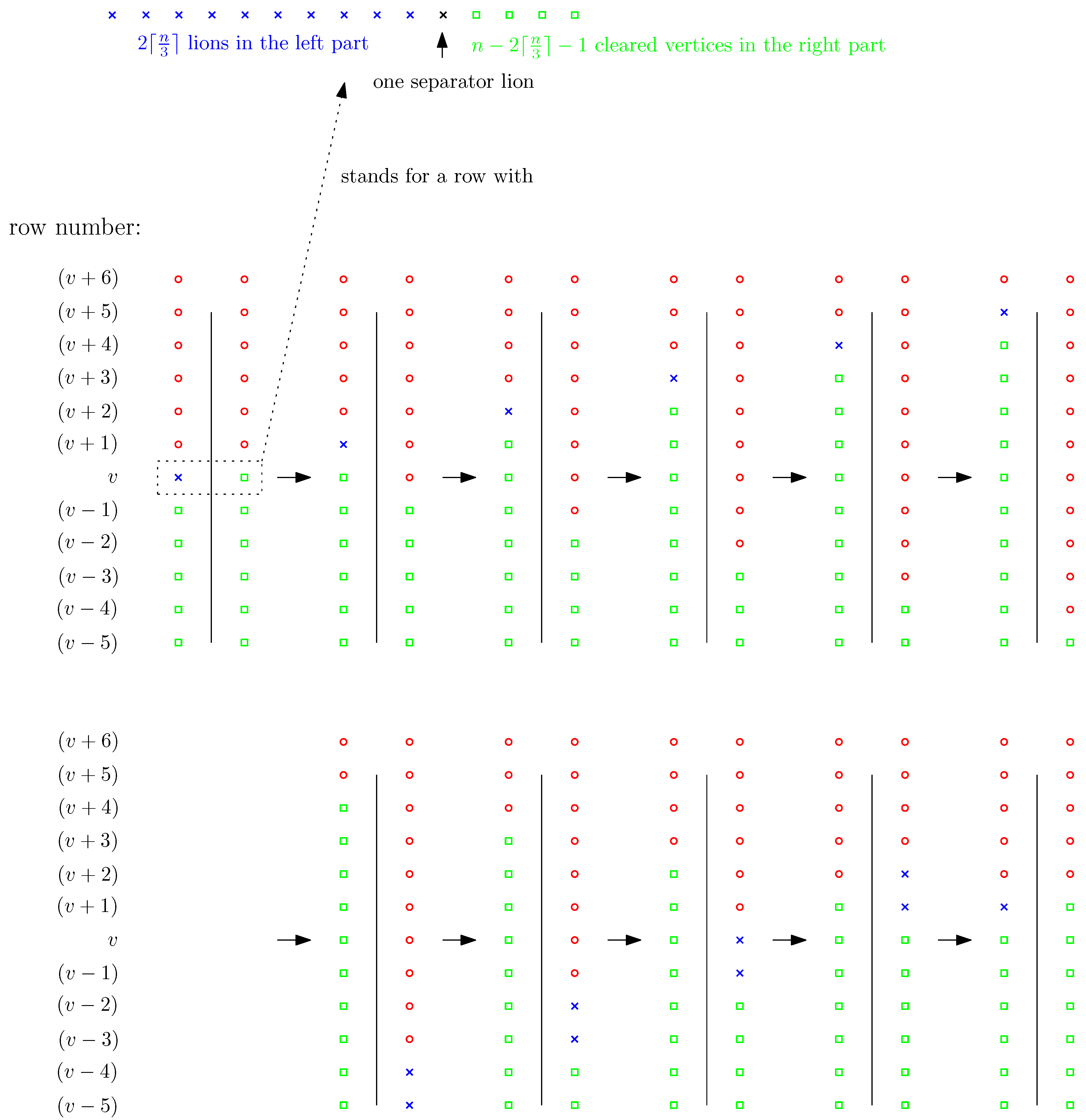
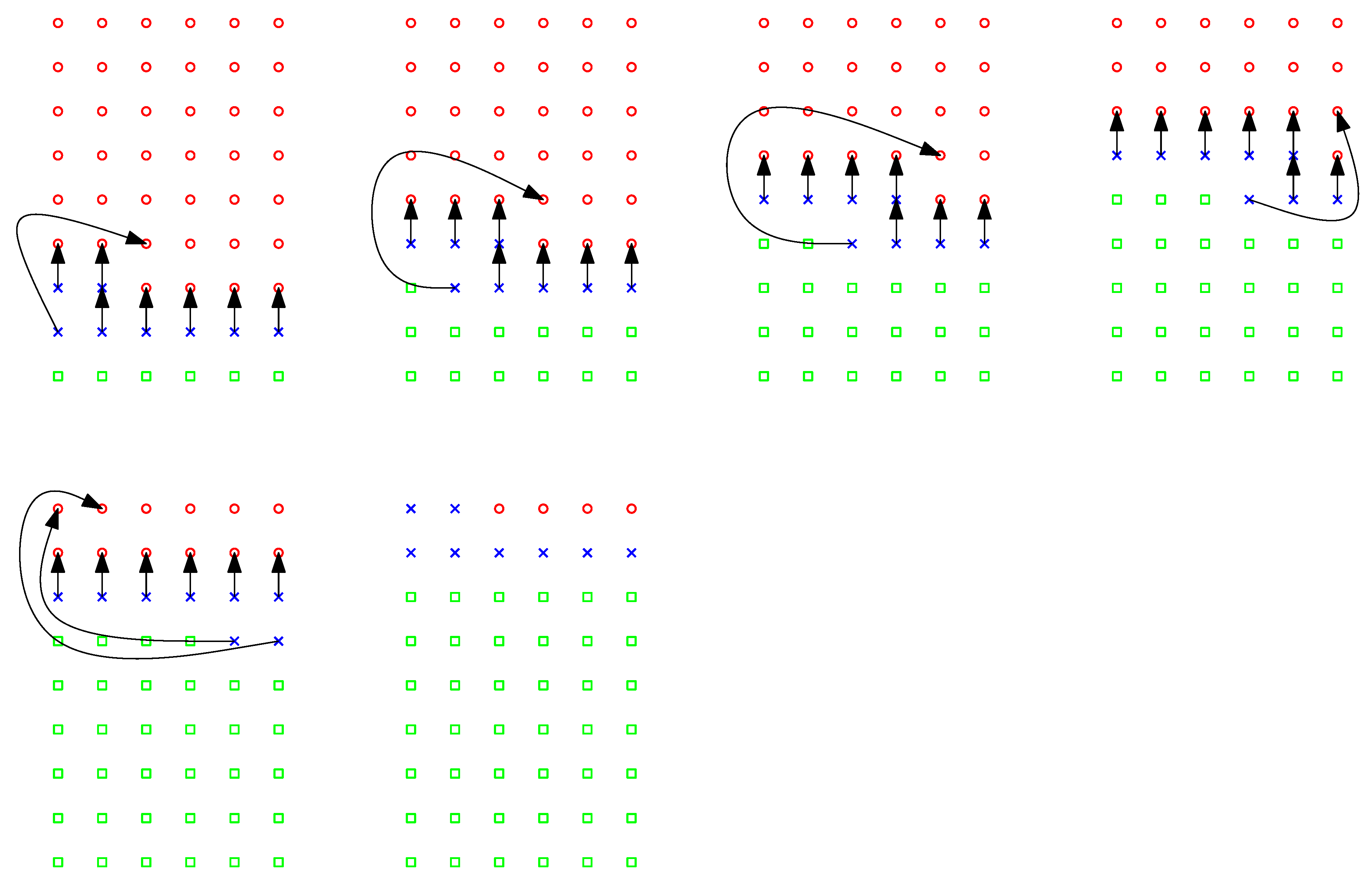
Figure 5. The movement can be done such that only one lion changes its location within each time step. All remaining lions can stay at their current positions and protect the cleared vertices. Even if the moving lion needs several steps to reach its destination, no problem arises.
Figure 5.
Eight lions (rather than ) suffice to clear the -grid. If two lions occupy the same vertex at the same time, this is indicated by two crosses of different orientation.
Figure 5.
Eight lions (rather than ) suffice to clear the -grid. If two lions occupy the same vertex at the same time, this is indicated by two crosses of different orientation.
For any grid vertex v, we denote the -distance from v to the origin 0 as .
The idea is to sweep the vertices layer by layer, where the
r-th layer is the set of vertices of
-distance
r to the origin. It is denoted by
For
the value of
can be computed recursively by:
As start of the recursion, we can use for . To the best of our knowledge, no closed formula is known, but it is not difficult to prove the following Lemma.
Lemma 6. is increasing in r for .
Proof. We use induction on d. For , we have for , which is monotonously increasing.
Now, let us assume, we already showed for dimension d that is increasing in r in the range of . Our task is to prove the monotonicity for dimension .
Due to the symmetry , the induction hypothesis implies that decreases monotonously in r in the range of . The symmetry holds, because all grid points with distance r from the origin have distance from the grid point and vice versa.
Clearly,
is monotonously increasing for
. For the remaining range
, we have
and
. Hence, formula (
3) leads to
We will prove the monotonicity of by showing .
If , then as well as are in the increasing part of , hence and the monotonicity holds. For , the term is monotonously decreasing in r, since is in the decreasing part of , while is still in the increasing part. But even if we chose , which is the maximum value for r we have to consider, we can still show :
If d is odd or n is odd, we obtain , which equals due to the symmetry. This shows that the monotonicity of implies the monotonicity of within the range needed for Lemma 6. Accordingly, if d is even and n is even, we obtain . ☐
This proof shows that the middle layer, , is the biggest, which will be important for our estimates.
The strategy from
Figure 5 can be generalized to grid graphs of arbitrary size and dimension. We sweep the grid
layer after layer. No vertex of
is cleared before the last vertex of
has been.
Let us consider two consecutive layers and , and let us assume that the former has been completely cleared, while the latter is still completely contaminated. Together they form a bipartite graph where every vertex has degree of at most d. How many lions are needed to clear without recontamination?
Lemma 7. Assume that the set is already cleared. At most lions are needed to clear without recontamination, if . In the remaining case, if , we need only lions.
Proof. First, we notice that for every with , lies in . Furthermore, if there is an edge connecting and , and , then .
Now, to clear we proceed as follows: Initially, we place one lion at each vertex of . To do that, we obviously need lions. If , in addition, for every with , we place one lion on a vertex with , so that there exists an edge . For that, lions are needed. The following algorithm shows that no further lion is necessary to clear .
In the first step, each one of the additional lions moves to its assigned vertex . Now all vertices in of this form have been cleared. Because every vertex of is still occupied by a lion, no recontamination has occurred.
Next, we move lions from to without causing any recontamination. Beginning with , we repeat the following action until i equals or r: Move every lion that is placed on a vertex of the form to .
After this loop, every vertex of is occupied, as follows from the remarks at the beginning of this proof. Moreover, no recontamination was possible during the loop, because every lion left his vertex via the only edge that led a contaminated vertex.
Note that in the case of the layer does not contain any vertex v with . We can do the same as above with lions. No additional lions are needed. ☐
As a consequence, we obtain the following upper bounds.
Proof. From Lemma 7 we can conclude
The recursive formula for
implies
We want to establish that
obtains its maximum for
. The above sum contains at most
consecutive elements of the sequence:
By Lemma 6 and its proof, we know that this sequence is monotonously increasing for , monotonously decreasing for and symmetric with respect to . Hence, the sum is maximized if consecutive sequence indices are chosen as symmetrically as possible around .
If is odd and d is odd, a maximum sum arises if . If is odd and d is even, a maximum sum arises if . In the third case, if is even, a maximum sum is obtained for .
In all three cases, the sum obtains its maximum for . This proves the first inequality of the Lemma. The second one is a simple but not very tight estimate. ☐