Abstract
It is crucial to understand how fitness landscape characteristics (FLCs) are associated with the performance and behavior of the differential evolution (DE) algorithm to optimize its application across various optimization problems. Although previous studies have explored DE performance in relation to FLCs, these studies have limitations. Specifically, the narrow range of FLC metrics considered for problem characterization and the lack of research exploring the relationship between the search behavior of the DE algorithm and FLCs represent two major concerns. This study investigates the impact of five FLCs, namely ruggedness, gradients, funnels, deception, and searchability, on DE performance and behavior across various problems and dimensions. Two experiments were conducted: the first assesses DE performance using three performance metrics, i.e., solution quality, success rate, and success speed. The first experiment reveals that DE exhibits stronger associations with FLCs for higher-dimensional problems. Moreover, the presence of multiple funnels and high deception levels are linked to performance degradation, while high searchability is significantly associated with improved performance. The second experiment analyzes the DE search behavior using the diversity rate-of-change (DRoC) behavioral measure. The second experiment shows that the speed at which the DE algorithm transitions from exploration to exploitation varies with different FLCs and the problem dimensionality. The analysis reveals that DE reduces its diversity more slowly in landscapes with multiple funnels and resists deception, but faces excessively slow convergence for high-dimensional problems. Overall, the results elucidate that multiple funnels and high deception levels are the FLCs most strongly associated with the performance and search behavior of the DE algorithm. These findings contribute to a deeper understanding of how FLCs interact with both the performance and search behavior of the DE algorithm and suggest avenues to optimize DE for real-world applications.
1. Introduction
Differential evolution is a well-known evolutionary algorithm proposed by Storn and Price to solve global optimization problems over continuous spaces [1,2,3]. Due to its robustness, efficiency, and simplicity, DE has been successfully applied to address a wide range of optimization problems across various domains, as evidenced by numerous studies highlighting its widespread application and efficacy [4,5,6,7]. Notably, the characteristics of optimization problems play a critical role in determining the effectiveness of search algorithms in solving them [8,9,10,11,12]. Essential to the success of the DE algorithm is its ability to navigate through complex search spaces of various optimization problems [3]. The complexity of the search space of an optimization problem can be effectively characterized using fitness landscape analysis (FLA) [13,14] by examining features such as ruggedness, modality, and the presence of funnels. A thoughtful FLA reveals the intricacies that search algorithms may encounter throughout the search process, thereby facilitating a deeper understanding of the performance and behavior of these algorithms [15].
Recognizing its advantages, FLA has been successfully utilized for problem characterization and performance prediction of optimization algorithms, particularly those involving swarm-based algorithms. For instance, for particle swarm optimization (PSO), Malan and Engelbrecht adapted and proposed metrics to assess and numerically quantify the fitness landscape characteristics (FLCs) of well-known benchmark problems [16,17,18] and used these metrics to predict PSO performance [19]. The outcomes of the research in several studies [16,17,18] led to the design of failure prediction models for the PSO algorithms, demonstrating that failure could be predicted with a high level of accuracy [20]. The resulting prediction models were not only useful in predicting failures, but also offered valuable insights into the PSO algorithms themselves. Drawing on these insights, studies have been conducted to predict optimal values for PSO control parameters based on FLCs [21]. Concerning the DE algorithm, several studies have explored the link between FLCs and the performance of the DE algorithm [22,23,24,25,26,27,28,29,30,31,32,33,34]. However, the majority of these studies adopted only a limited number of FLCs to characterize problems for the DE algorithm [22,23,24,25,26,29,30,31,33,34,35]. Research incorporating more than two FLCs to characterize problems for the DE algorithm has been scarcely reported [27,28,32]. Additionally, while the scope of studies has mainly focused on performance enhancement, important issues such as DE failures and the factors that make specific problems difficult for DE to solve have often been overlooked, with only a few exceptions [32].
The body of literature available on the utilization of FLA for performance and behavior analysis of the PSO algorithm is significantly more advanced compared to what has been reported for the DE algorithm. Engelbrecht et al. [36] utilized several fitness landscape metrics to characterize problems and provided a collection of findings regarding the link between FLCs and the behavior of the PSO algorithms. However, similar research has yet to be reported for the DE algorithm.
Consequently, this paper aims to analyze the influence of various FLCs on the performance and behavior of the DE algorithm across a set of well-known benchmark problems with different complexities. To achieve this, and to specifically understand the influence of various FLCs on DE performance, a set of critical performance metrics and a broader array of FLCs, including those not previously reported in DE-related literature, are considered in this study. Moreover, for the behavioral analysis, a behavioral metric is utilized to quantify and measure the speed at which DE transitions from exploration to exploitation, allowing for an investigation into the impact of various FLCs on DE behavior. This level of behavioral analysis offers a deeper insight into the search dynamics of the DE algorithm, providing a new perspective that has not been previously explored in DE literature. It is important to note that the original DE algorithm, as proposed by Storn and Price [2], is used in this study. The selection of the original DE algorithm allows for a focused investigation without the confounding effects of advanced DE variants. This approach is necessary to facilitate a comprehensive understanding of the impact of various FLCs on DE performance, thereby providing a performance reference for potential future studies involving advanced DE variants. This study provides insights into the design and tuning of adaptive DE algorithms, emphasizing the importance of adapting DE strategies to specific landscape features and problem dimensionality to enhance their efficiency and effectiveness. Subsequently, the main objectives of this research are as follows:
- To investigate the association between various FLCs and DE performance across various optimization problems and dimensions, utilizing critical performance metrics such as solution quality, success rate, and success speed, while considering five key FLCs, namely ruggedness, gradients, funnels, deception, and searchability.
- To investigate the relationship between various FLCs and the search behavior of the DE algorithm across different problems and dimensions, utilizing a behavioral measure to quantify the search behavior of the DE algorithm called the diversity rate-of-change (DRoC).
These objectives directly shape the core contributions of this study, which are twofold. First, this study presents a detailed empirical analysis of how FLCs interacts with DE performance across various problems and dimensionalities, using three critical performance measures, namely accuracy, success rate, and success speed. Second, this study introduces a behavioral investigation of the DE search dynamics using the DRoC measure across multiple landscape types and dimensionalities. To the best of our knowledge, such an analysis is yet to be reported for DE with this breadth of FLC metrics and in conjunction with the DRoC measure. These contributions uncover important insights into the behavior of the DE algorithm and offer valuable guidance for the design of future adaptive DE variants.
The remainder of this paper is organized as follows: Section 2 provides the necessary background of the DE algorithm, FLA, and the DRoC measure. Section 3 outlines the related work in a chronological order. Section 4 provides the empirical analysis, detailing the experimental setup, benchmark problems, performance metrics, and the overall experimental procedure. Section 5 and Section 6 present the results and analysis of Experiment 1 and Experiment 2, respectively. Finally, Section 7 concludes the study by summarizing the key findings and outlining potential directions for future work.
2. Background
This section provides the necessary background on the DE algorithm and FLA, setting the context for the subsequent experimental analysis and conclusions. Section 2.1 discusses the DE algorithm in detail. Section 2.2 focuses on FLCs. Additionally, DRoC, a behavioral metric used to investigate the behavior of the DE algorithm in this study, is discussed in Section 2.3.
2.1. Differential Evolution
The DE algorithm is a well-known population-based optimization algorithm used to solve complex optimization problems. In its basic form, as defined by Storn and Price [1,2], DE starts with a randomly generated population of candidate solutions, which are evolved throughout generations. At each generation, each individual in the population, referred to as a parent, undergoes three evolutionary operations to generate a fitter solution, called an offspring. These operations involve mutation, crossover, and selection. Consequently, each parent is compared to its respective offspring, and the fitter individual is selected to serve as a parent in the next generation. The operators are applied to each individual in the population iteratively, with the aim of generating better offspring, and hence optimize the population. The remainder of this section describes DE, outlining its core principles and evolutionary operators.
- MutationThe mutation operator is applied first to produce a mutant vector for each individual in the current population. That is, for each parent vector xi(t), a mutant vector ui(t) is generated by selecting three distinct individuals from the population. The first selected vector, , serves as the base vector (also called the target vector). The other two vectors, and , are then used to calculate a scaled difference. The vectors are selected such that , with i, i1, i2, i3 ∼ U(1, NP). Here, i denotes the population index and NP represents the population size.The mutant vector is then calculated as follows [2]:where F ∈ (0, ∞) is the scale factor that controls the amplification of the differential variation, . There is no upper limit on F; however, Price et al. advocated that effective values are rarely greater than 1.0 [3].
- CrossoverThe crossover operator in the DE algorithm creates a trial vector, , by recombining components of the parent vector, xi(t), with the mutant vector, ui(t). Each component of the trial vector is assigned as follows:where rj is a random value sampled from a uniform distribution over (0, 1) and xij(t) refers to the jth component of the vector xi(t). The crossover points are uniformly sampled from the dimensional index set . Notably, the crossover rate CR controls the probability of selecting components from the mutant vector CR ∈ (0, 1].
- SelectionThe selection operation in the DE algorithm determines whether the parent vector or its corresponding trial vector proceeds to the next generation based on their fitness in a greedy selection scheme. Specifically, the trial vector, , is compared to the parent vector, xi(t), and the vector which exhibits a better fitness value survives into the next generation.
- Strategy of the Differential Evolution AlgorithmPrice and Storn proposed a naming convention for the DE algorithm based on the applied mutation and crossover operators [2]. This conventional notation, denoted as DE/x/y/z, is widely used to describe different strategies of the DE algorithm. In this notation, x specifies the method used to select the target vector, y indicates the number of difference vectors involved in the mutation operation, and z specifies the crossover technique employed. The basic DE/rand/1/bin strategy is applied in this paper, in which the target vector is randomly selected, a single difference vector is used in the mutation operation, and binomial crossover is performed. A summary of the DE/rand/1/bin strategy is provided in Algorithm 1.
Algorithm 1 DE/rand/1/bin: Differential evolution algorithm with random target vector and binomial crossover. - 1:
- Initialize generation counter: t ← 0
- 2:
- Set control parameters: population size NP, scale factor F, and crossover rate CR
- 3:
- Randomly generate initial population P(0) with NP individuals
- 4:
- while termination criteria not satisfied do
- 5:
- for each candidate solution xi(t) ∈ P(t) do
- 6:
- Evaluate fitness:
- 7:
- Randomly choose distinct indices , , such thatand
- 8:
- Select random dimension
- 9:
- for each dimension j = 1 to D do
- 10:
- Generate trial vector component:
- 11:
- end for
- 12:
- if then
- 13:
- 14:
- else
- 15:
- xi(t + 1) ← xi(t)
- 16:
- end if
- 17:
- end for
- 18:
- 19:
- t ← t + 1
- 20:
- end while
- 21:
- return the individual with the best fitness value in the final population
2.2. Fitness Landscape Analysis
The notion of a fitness landscape was originally proposed by Sewall Wright in 1932 [13,14]. According to the fitness landscape metaphor, optimization problems can be represented as a multi-dimensional terrain, where the coordinates correspond to vectors of candidate solutions, and fitness values of those solutions shape the structure of the landscape, where large values appear like peaks, small values as valleys, and intermediate values as ridges and plateaus. The purpose of FLA is to provide an intuitive picture to analyze optimization problems by visualizing the distribution of fitness values on a landscape grid. In its essence, FLA is concerned with how fitness values of an optimization problem are distributed across the search space. Several metrics have been proposed to provide approximate measures using samples of the search space to predict specific features of the landscape of the problem called fitness landscape characteristics (FLCs). FLCs provide approximate measures that use samples of the search space to predict specific landscape features, thereby providing techniques for predicting problem characteristics. The FLCs considered in this study are listed below and a detailed discussion of the rationale for selecting these particular FLCs is provided in Section 3.
- RuggednessRuggedness refers to the level of variation in fitness values of a particular fitness landscape. A specific landscape is highly rugged if the fitness values of neighboring solutions have extremely different values. For searching algorithms, it is a daunting task to find the global optima for highly rugged problems because of the possibility of getting trapped in numerous local optima. As a measure, ruggedness is directly linked to problem difficulty. The more the ruggedness associated with a specific problem landscape, the more challenging it is to find a global optimum.To measure the ruggedness of an optimization problem, the first entropic measure (FEM) is used. Originally introduced by Vassilev et al. [37] for discrete landscapes and later adapted for continuous ones by Malan and Engelbrecht [16], FEM for macro-scale-ruggedness (denoted by FEM0.1) and for micro-scale-ruggedness (denoted by FEM0.01) are adopted in this research. The FEM metric produces a value in the range [0, 1], where 0 indicates a flat landscape and 1 indicates maximum ruggedness.
- GradientsThe steepness of gradients refers to the magnitude of fitness changes between neighboring solutions or the absolute difference in fitness values between neighboring solutions. A landscape with steep gradients may have a higher probability of being deceptive to search algorithms. Deception occurs when the steepness of gradients guides the algorithm away from a global optimum, causing the algorithm to converge prematurely on a suboptimal solution. In this study, two metrics are used to quantify gradients, as introduced by Malan and Engelbrecht [17]. These are the average gradient, Gavg, and the standard deviation of gradients, Gdev. The Gavg is a positive real number, with larger values indicating greater steepness of gradients. The Gdev is also a positive real number, with larger values indicating greater deviation from the average gradient, which in turn reflects an uneven distribution of gradients across the landscape.
- FunnelsA funnel refers to a global basin shape in the fitness landscape that consists of clustered local optima. Single-funnel landscapes typically guide the search algorithm smoothly toward the global optimum. In contrast, multi-funnel landscapes represent a greater challenge, as they may direct the algorithm toward different competing local optima, which impose increased difficulty and potentially leading to premature convergence.An approach for estimating the presence of multiple funnels in a landscape is the dispersion metric (DM) of Lunacek and Whitley [38]. A problem with small dispersion probably has a single-funneled landscape. In contrast, a high-dispersion problem probably has a multi-funneled landscape. Malan and Engelbrecht proposed an adaptive DM metric and used normalized solution vectors to compare dispersion metric values across problems with different domains [17]. The DM metric produces a value in , where D is the dimensionality of the search space, and dispD is the dispersion of a large uniform random sample of a D-dimensional space normalized to [0, 1] in all dimensions. A positive value for DM indicates the presence of multiple funnels, whereas negative DM values indicate a landscape with a single funnel.
- DeceptionA deceptive landscape provides the search algorithm with false information, guiding the search in the wrong direction. For minimization problems, a landscape is considered easily searchable when fitness values decrease as the distance to the optimum decreases. Deception is primarily attributed to the landscape structure and the distribution of optima. Deceptive landscapes may contain gradients that lead away from the global optima. However, the level of deception is related to the position of suboptimal solutions with reference to the global optima and the presence of isolation. In this paper, the fitness distance correlation (FDC) is used to quantify the deception in a landscape. Jones and Forrest [39] proposed the FDC measure, which was later adapted by Malan and Engelbrecht [18], alleviating the need for prior knowledge of the global optimum. The FDC metric produces a value in the range [−1, 1]. For minimization problems, smaller FDC values indicate a higher degree of deception, making larger values more desirable.
- SearchabilitySearchability (also referred to as the evolvability) of a fitness landscape is defined as the ability of an optimization algorithm to navigate the landscape towards better positions (of fitter solutions) efficiently and effectively. Given the structural characteristics of a fitness landscape, highly searchable landscapes are those with less deceptive terrain allowing the search algorithm to generate fitter offspring in a single move using a specific algorithmic operator. Malan and Engelbrecht [18] introduced the fitness cloud index (FCI) as a metric to measure the searchability in the context of the PSO algorithm, adapted from fitness cloud scatter plots by Verel et al. [40]. The FCI ranges from 0 to 1, where 0 indicates the worst possible searchability, and 1 represents perfect searchability for a given problem concerning a specific search operator of the optimization algorithm. In this study, the FCI is adopted for the DE algorithm, referred to as FCIDE. Specifically, the FCI measure was calculated by comparing each target vector with its corresponding trial vector after one generational step of DE and recording the proportion of instances where the fitness of the trial vector improved upon that of the original target vector. For simplicity, the measure will be termed as FCI, with FCIdev indicating the average standard deviation in searchability.
2.3. Diversity Rate-of-Change
The diversity rate-of-change (DRoC) is a behavioral metric originally proposed to quantify the rate at which the PSO algorithm transitions from exploration to exploitation [41]. The DRoC measure captures how rapidly the population diversity decreases over time, offering insights into the convergence behavior of the algorithm. The DRoC measure is adopted in this study to quantify the search behavior of the DE algorithm. At each iteration, the diversity of the population is calculated during execution as follows [41]:
where xij(t) is the j-th dimensional component of the i-th individual at iteration t, NP is the population size, and is the average of the j-th dimensional component of all individuals at iteration t.
All diversity measurements taken during the execution of the DE algorithm are approximated by a two-piece-wise linear approximation,
where m1 is the gradient of the first line segment, c is the y-intersection of the first line segment, m2 is the gradient of the second line segment, and t′ is the iteration at which the two line segments cross. The values of m1, m2, and t′ are chosen to minimize the least squares error (LSE) between y(t) and D(t), given by
Bosman and Engelbrecht [41] defined the DRoC measure as the slope of the first line of the linear approximation which indicates the rate at which a population decreases its diversity throughout successive iterations. The DRoC measure is, therefore, given by m1, the gradient of the first line. Notably, DRoC is a negative number, where smaller values indicate faster convergence when a population transitions from an explorative state to an exploitative state at a faster rate. The correlation between DRoC and FLCs was previously explored in the context of PSO algorithms by Engelbrecht et al. [36], and for metaheuristic behavior analysis by Hayward and Engelbrecht [42]. However, the influence of DRoC on DE behavior, particularly in relation to FLCs, has yet to be reported in the literature related to DE.
3. Related Work
Fitness landscape analyses of optimization problems and their interaction with the performance of optimization algorithms have received increasing attention in recent years [15,43,44,45,46]. Numerous studies have explored how different landscape features can be efficiently utilized to understand complex optimization problems and to explain and predict the behavior of optimization algorithms [47,48,49]. This provides valuable insights into the performance and efficiency of these algorithms, thereby enabling informed algorithm selection and configuration [15,43,44,50,51,52]. This section reviews and highlights significant studies that involved FLAs and the DE algorithm in a chronological order.
Uludağ et al. [22] proposed a neighborhood definition for adjacent solutions in the DE algorithm and subsequently conducted FLA on a set of benchmark problems. Uludağ et al. [22] used two fitness landscape metrics to characterize these problems, i.e., FDC and correlation length (CL). The results presented in [22] demonstrated that both metrics were effective in explaining DE behavior, except in landscapes with high ruggedness, deceptive features, and unimodal problems with a single large basin of attraction. Uludağ et al. emphasized that FDC and CL alone were insufficient to analyze all types of landscapes and suggested the application of evolvability metrics in future research.
Similarly, utilizing two fitness landscape metrics, Yang et al. [23] analyzed the performance of the DE algorithm. The metrics, dynamic severity (which measures how much the fitness landscape changes over time) and ruggedness, were applied to characterize six benchmark problems of various properties. Yang et al. concluded that DE performed well on simpler benchmark problems but struggled with more complex problems. Specifically, DE exhibited a prolonged convergence speed to navigate highly rugged landscapes with frequent changes in dynamic severity. The study also emphasized that future work should involve using more fitness landscape metrics, analyzing the effect of various DE operators, and investigating control parameter settings with respect to various FLCs. However, the conclusions were limited by the fact that they were based solely on two-dimensional problems.
Zhang et al. [24] investigated the relationship between DE control parameters settings and problem features using FLA. Zhang et al. employed decision tree induction to design performance prediction models to assess the effectiveness of specific DE parameter settings. Linear regression analysis was also conducted to quantify relationships between problem features and DE performance. Two fitness landscape metrics were used to characterize optimization problems, i.e., FDC and the information landscape measure (ILs). The findings suggested that DE performance can be enhanced and potentially optimized by appropriate adjustment of the values of the DE control parameters, namely F and CR based on the problem dimension and the extracted problem features. However, the study was limited to three benchmark problems, i.e., Rosenbrock, Ackley, and Sphere, with dimensions of D = 2, D = 5, and D = 10, which restricts the generalizability of their conclusions. Another limitation of the study is that, while Zhang et al. concluded that a relationship exists between DE control parameters and FLCs, the population size was neglected when analyzing the control parameters of the DE algorithm.
Huang et al. [25] proposed a self-feedback mixed-strategies differential evolution (SFSDE) algorithm to solve the soil water texture optimization problem. The proposed SFSDE algorithm calculates and analyzes the local fitness landscape characteristic (i.e., number of local optima). A self-feedback adaptive mechanism is then iteratively used to evaluate the number of optima and accordingly select a more suitable mutation strategy for the mutation operator. Although the proposed SFSDE strategy demonstrated superiority and outperformed other variants of the DE algorithm, no discussion was provided on the effect of FLCs on the performance of the proposed SFSDE algorithm. Specifically, the selection of a particular mutation strategy concerning a specific problem feature was not justified. Furthermore, the scope of their experimental analysis was limited to six variations of the soil water texture problem, which may limit the generalizability of the conclusions.
Li et al. [26] proposed a self-feedback differential evolution (SFDE) algorithm designed to efficiently adapt according to FLCs. The adaptation mechanism of the proposed SFDE involves analyzing the distribution of optima in the landscape to measure the degree of problem modality at each generation. The probability distribution derived from the local fitness landscape is then used to dynamically adjust the control parameters (F and CR) and to select suitable mutation and crossover strategies for SFDE. A set of 17 benchmark problems of varying modalities and complexities was used to test SFDE algorithm in [26]. Li et al. concluded that SFDE performed well on high-dimensional problems and outperformed other well-known DE variants on most benchmark problems, particularly in terms of local optima avoidance and convergence speed. However, a limitation of SFDE is its high complexity, introducing new control parameters to the original DE. Additional limitations include the use of a single fitness landscape feature to characterize the problems (based on the number of optima) and the exclusion of population size in the analysis of DE control parameters.
Moreover, Li et al. [27] stressed the importance of incorporating several fitness landscape metrics, a point that was also previously acknowledged in [22]. Li et al. [27] analyzed the performance of the DE algorithm with respect to four FLCs, namely dynamic severity, gradients, ruggedness, and FDC. A total of 12 benchmark problems were used, with dimensions ranging from D = 2 to D = 30. The conclusions from Li et al. indicated that solving high-dimensional and highly rugged problems posed a challenge for the DE algorithm. A limitation of this study is that a fixed number of iterations was allowed for the problems in all dimensions, which raises concerns about the credibility of their conclusions. Additionally, the conclusions were drawn based on visual inspection of graphical representations of fitness landscape measures versus DE performance measures, whereas statistical techniques, such as Spearman’s correlation coefficients or linear approximation, would have provided more robust analysis.
Liang et al. [28] proposed an artificial intelligence (AI)-based model [53] for mutation strategy selection in the DE algorithm, guided by FLA. The model accepts four FLCs as inputs, namely the number of optima, basin size ratio, FDC, and keenness (KEE). KEE measures the sharpness of fitness landscapes and was originally used to characterize combinatorial optimization problems [54,55]. It computes a weighted sum of sample points (categorized by fitness difference), with fixed coefficients indicating the contribution of each point type. The KEE indicates how often local fitness changes lead to improvements, thereby reflecting how helpful the landscape is in guiding the search process. The AI-based model then produces a recommended mutation strategy as the output. Classifiers were then utilized to explore the mapping relationships between DE mutation strategies and FLCs. The proposed model produced promising results, with DE achieving better solutions and improved accuracy levels. However, the study did not discuss the correlation between various FLCs and DE performance.
Huang et al. [29] employed machine learning (ML) techniques, specifically reinforcement learning (RL) to propose the fitness landscape ruggedness multi-objective differential evolution (LRMODE) algorithm. The LRMODE algorithm first uses information entropy to assess the ruggedness of the landscape and classify whether the fitness landscape is unimodal or multimodal. This classification is then provided to an RL model, which learns and updates the optimal probability distribution over mutation strategies. The aim is to enable the LRMODE to adaptively select a mutation strategy that aligns with the underlying landscape structure. One limitation of this research is that a single fitness landscape metric was used to characterize problems based on the number of optima similar to [25,26].
At this stage in the development of the literature, AI and ML techniques were employed alongside FLA to guide the adaptive selection of suitable mutation strategies for the DE algorithm. Following this, the adaptation of control parameters based on FLA was increasingly explored to further enhance the performance of the DE algorithm.
Tan et al. [30] proposed a mutation strategy selection mechanism for the DE algorithm based on the local fitness landscape, termed LFLDE. The LFLDE algorithm analyzes local FLCs to guide the selection of a mutation strategy at each generation. Based on the examined roughness of the search space, one of two pre-specified mutation strategies is selected. A notable advancement in [30] over previous studies is the adaptive adjustment of control parameters, along with the application of a population size linear reduction strategy. However, the selection of one mutation strategy over another was never justified, and only a single landscape feature was considered to characterize the problems based on the average distance between each individual and the local optima at each generation. The study also lacks a necessary discussion about the relationship between DE performance and FLCs.
Subsequently, Tan et al. [31] also proposed an advanced fitness landscape differential evolution (FLDE) algorithm. The integration of FLA into the advanced FLDE algorithm involved three main stages. The first stage focused on extracting and analyzing the FLCs of the selected benchmark problems. Notably, two FLCs were adopted in their study, namely FDC and ruggedness. A random forest model was trained to learn the relationships between these FLCs and three predefined mutation strategies in the second stage. The trained model was then employed to predict the optimal mutation strategy for the mutation operator in the third stage. In addition, the FLDE algorithm was equipped with a historical memory parameter adaptation mechanism and population size linear reduction scheme. The FLDE algorithm demonstrated competitive performance, surpassing other well-known DE variants such as the success-history-based adaptive differential evolution (SHADE) algorithm [56] and the linearly decreasing population size SHADE (LSHADE) algorithm [57]. One drawback of FLDE is its high complexity due to the introduction of numerous new control parameters. Furthermore, only two FLCs were considered, and the study did not include a discussion on the link between DE performance and FLCs.
The conclusions from [30,31] also indicated that FLA is beneficial and can be effectively utilized to improve the performance of the DE algorithm, especially for higher-dimensional problems. However, a critical discussion on the link between FLCs and DE performance was notably absent.
Early research by Tan et al. [30,31] laid the groundwork for Zheng and Lou [35] to propose an adaptive DE variant. Zheng and Lou developed an adaptive DE algorithm based on FLCs, called the FL-ADE algorithm. The proportional distribution of optima is used to determine the ruggedness of the fitness landscape at each generation. Based on ruggedness, dynamic adjustments to the population size are made, with the population size increased for more rugged landscapes and decreased for less rugged ones. Additionally, the FL-ADE algorithm is equipped with an archive set to save and retrieve local optimal individuals. An adaptive mutation operator is utilized to randomly select an individual from the archive set to create a mutant vector. The FL-ADE demonstrated superiority over seven high-performing DE variants. However, Zheng and Lou’s research relied on a single fitness landscape feature based on counting the number of optima in the search space to perform the FLA. Notably, the results showed that FLA can effectively guide the adaptive adjustment of the population size in the DE algorithm.
A significant contribution to the literature on FLA for the DE algorithm is attributed to Li et al. [32]. Li et al. adapted the original keenness measure [54,55] to propose a fitness landscape metric for continuous spaces, termed KEEs. KEEs quantifies the sharpness of a fitness landscape by evaluating changes in fitness values using a mirrored random walk, which samples points in both forward and backward directions to capture how clearly the landscape points toward better solutions. Three additional landscape metrics were used alongside KEEs, namely FDC, neutrality, and the DM. Moreover, a prediction model was developed to predict and analyze DE performance. The correlation between landscape features and DE performance, as well as the link between landscape features and the predictive performance of the DE algorithm, were investigated. The results demonstrated the effectiveness of the proposed keenness metric and the feasibility of the performance prediction model. The study by Li et al. [32] is particularly noteworthy because of its in-depth discussion on the link between DE performance and the adopted fitness landscape metrics. The four selected landscape metrics showed a moderate to strong correlation with DE performance. However, the experimentation was conducted on only seven benchmark problems, which may restrict the generalization of their conclusions.
Li et al. [33] proposed an advanced DE variant with a mutation operator selector and a control parameter values specifier (referred to as parameters selector in [33]) based on FLA. The researchers first analyzed the performance of two mutation strategies across various test optimization problems. By identifying the relationship between the FLCs and mutation strategies, they developed a classifier called the mutation operator selector using ensemble learning and decision trees. Similarly, the link between FLCs and various control parameter configurations was established using a neural network to train the parameter selectors. For the experimental study conducted in [33], two fitness landscape metrics were used, i.e., the FDC and ruggedness. Li et al. mentioned that the results of the parameter selector were limited and attributed this limitation to the inclusion of only two FLCs for the analysis, which were found insufficient to fully describe the complexity of the optimization problems. To improve the performance of the DE algorithm, Li et al. suggested incorporation of additional metrics, such as evolvability metrics [58].
Liang et al. [34] proposed an adaptive fitness landscape information differential evolution (FLIDE) algorithm. The proposed FLIDE algorithm employs an adaptive mutation operator based on local fitness landscape information and an adaptive population size linear reduction scheme. A fitness landscape metric, termed population density, was specifically designed for their study. The population density metric calculates the average pairwise Euclidean distance among all individuals every 20 generations. Based on the population density value, one of two mutation strategies is selected, and the population size is linearly reduced. FLIDE demonstrated superior or comparable performance compared to other popular DE variants. However, since only one feature was used for the FLA, Liang et al. concluded that more fitness landscape information needs to be extracted.
An observed trend was the significant increase in literature focusing on the proposal of advanced DE variants based on FLA, particularly those with parameter adaptations and mutation strategy selection, utilizing AI and ML techniques such as random forests, as well as the use of supplementary memory archive sets. Notably, a significant observation from the DE literature is that a limited number of fitness landscape metrics were adopted to characterize problems for the DE algorithm. The majority of the studies utilized only one metric was utilized [25,26,29,30,34,35], while two metrics were employed in some research [22,23,24,31,33]. Fewer studies adopted more than two metrics [27,28,32].
Hu et al. [59] proposed an adaptive DE algorithm, named fitness distance correlation-based adaptive differential evolution (FDCADE), designed for solving nonlinear equation systems. FDCADE incorporates the FDC metric to analyze the underlying landscape structure. Based on their analysis, the algorithm adaptively selects mutation strategies and adapt control parameters to enhance search efficiency. The experimental results in [59] showed that FDCADE achieved improved performance in terms of solution accuracy and success rates. Its robustness was further validated through applications in complex domains such as robot kinematics. However, the research presented in [59] relied solely on a single metric for fitness landscape analysis, potentially overlooking other influential landscape features.
Zhou et al. [60] proposed an adaptive niching DE algorithm for multimodal optimization problems, referred to as the adaptive niching fitness landscape-guided differential evolution (ANFDE) algorithm. The ANFDE integrates the FDC metric to dynamically balance two niching techniques (speciation and crowding) based on the fitness distribution of individuals. Their adaptive strategy aims to enhance convergence while preserving population diversity. Experimental results demonstrated that ANFDE achieved competitive performance on a set of benchmark suite. Nonetheless, the adaptation mechanism in [60] remains confined to strategy allocation and does not extend to broader behavioral analysis or parameter-level adaptation. Furthermore, the landscape characterization is based solely on a single metric (i.e, FDC), potentially overlooking other influential landscape features.
Many FLA metrics have been proposed focusing on measuring various aspects of landscapes [15,43,45]. In this context, it is essential to ensure the appropriate selection of FLA measures that sufficiently characterize problems when analyzing the relationship between problem characteristics and the performance and/or behavior of optimization algorithms. Sun et al. [61] specified two essential criteria that should be considered when selecting a combination of metrics for continuous problem characterization. First, the chosen FLA metrics should capture all relevant problem characteristics. Second, the total computational cost associated with the selected metrics should be minimal. Consequently, the results and conclusions about DE performance using only one or two FLA metrics may lack generalizability, because they may not capture all problem features. Moreover, several studies explicitly stated that two metrics were insufficient to adequately characterize problems and to establish links with DE performance [22,23,58]. The remaining literature on FLA concerning DE that includes more than two FLA metrics is very limited [27,28,32]. Clearly, there remains a need for a comprehensive analysis that adopts multiple FLA metrics and investigates the relationship between FLCs and DE performance, which is the first objective of this research.
In addition to the limited use of FLA metrics, another notable observation in the DE literature is the predominant focus on DE performance enhancement, with less attention paid to understanding DE behavior. Numerous studies have focused on proposing improved variants of the DE algorithm utilizing FLA or designing fitness landscape metrics that better characterize the problems for the DE algorithm [32]. However, further research is needed to investigate how DE performance is affected by various FLCs and how these characteristics correlate with DE convergence behavior.
Furthermore, the impact of specific problem characteristics on DE performance, particularly in cases of DE failure and what makes a problem difficult to solve for the DE algorithm, has yet to be thoroughly investigated. Recently, Li et al. [32] noted that “the research of DE algorithm performance prediction for continuous optimization problems is still in its infancy.”
In light of the gaps identified in the DE literature, particularly the adoption of limited FLA measures and the insufficient focus on DE performance and behavior, contrasted with the advanced research on the PSO algorithm [17,18,20,36], this paper is primarily motivated to fill these gaps. This study also aims to address these issues by analyzing DE performance and behavior with respect to various FLA measures using multiple performance metrics and a behavioral measure over various problems and problem dimensionality.
Moreover, the FLC measures selected for the analysis performed in the present study are well-established in the literature and have been successfully employed for problem characterization and performance prediction in the context of PSO algorithms [36]. While these metrics have proven effective in the context of PSO algorithms, they have not yet been systematically applied to DE in this scope, highlighting the significance of the present work. Furthermore, the selected FLCs align with the two essential criteria proposed in the literature for effective landscape analysis by Sun et al. [61]. Furthermore, the influence of population size on DE performance was investigated across problems with varying FLCs and dimensionalities in prior work, revealing that different population sizes were more effective for different problem modalities and features [62]. The current study builds on that foundation by more directly analyzing the impact of FLCs on DE performance and behavior.
To the best of our knowledge, the analysis presented in this study is the most comprehensive analysis of the FLA for the DE algorithm to date, particularly across various FLC metrics, problem dimensionality, algorithmic performance, and behavioral measures. It is aimed as a foundational seed research that provides a focused and interpretable basis for future exploration. The outcomes of this research are intended to contribute as a milestone toward a deeper understanding of DE behavior in complex search landscapes. Table 1 provides a structured summary of the key studies reviewed, highlighting the fitness landscape metrics employed and the main insights gained.

Table 1.
Summary of studies on DE and FLCs.
As shown in Table 1, recent studies have explored the links between FLCs and DE performance, control parameters, and mutation strategies. However, many of these works focus on a limited set of FLCs (often one or two), lack consistent performance evaluation across dimensions, or use descriptive methods without clear statistical validation. Furthermore, most studies emphasize algorithm design or parameter adaptation without directly analyzing the search behavior of the DE algorithm or convergence dynamics. In contrast, this study aims to provide a more systematic and statistically grounded analysis of the relationship between multiple FLCs and both performance and behavior (via DRoC) of DE/rand/1/bin across various problem dimensions. This fills a gap in understanding the interaction between landscape structure and the effectiveness of the DE algorithm.
4. Empirical Analysis
This section presents the empirical analysis conducted to investigate the performance and behavior of the DE algorithm. First, the experimental setup, including the parameter configurations and algorithmic settings used throughout the study, is outlined in Section 4.1. Next, the benchmark problems utilized in the experiments along with their feasible domains and dimensionality are described in Section 4.2. The performance measures used to assess the performance of the DE algorithm are then detailed in Section 4.3. Finally, Section 4.4 describes the experimental procedure and the statistical analysis approach applied to evaluate the results.
4.1. Experimental Setup
The DE/rand/1/bin strategy was employed as stated in Section 2.1, with thirty independent runs performed for each problem and dimension combination. The DE/rand/1/bin algorithm was configured with the following parameter setup: the population size NP was set to 50 individuals, and both F and CR were set to a moderate value of 0.5 rather than the commonly recommended values (Storn and Price advocated the values for F and CR to be 0.5 and 0.9, respectively). While the value of CR = 0.9 is commonly used in classical benchmark studies and performance optimization applications, several studies have noted that the optimal CR value is highly problem-dependent [63,64]. Large CR values are not always beneficial [65]. A survey by Ahmad et al. mentioned that the most frequently used parameter settings are F = 0.5 and CR = 0.5 [6]. Ali et al. used CR = 0.5 based on the experimental study in [66]. The crossover rate CR = 0.5 is commonly used in DE-related studies due to the balanced exploratory behavior [67,68,69,70,71,72,73,74,75,76,77].
Therefore, in this study, CR = 0.5 was selected to promote a steady and gradual convergence, facilitating a clearer observation of the search behavior of the DE algorithm across various fitness landscapes with different characteristics. Notably, this research aims to analyze the influence of FLCs on the behavior and performance of the DE algorithm. The aim is to enable a more stable and meaningful observation of how the FLCs impact performance across multiple runs. Moreover, the usage of CR = 0.5 thus aligns with the objective of capturing the search dynamics of the DE algorithm rather than accelerating convergence, allowing for a clearer visibility into how the algorithm navigates landscapes with varying structural features. In this study, the control parameters F and CR were fixed across all experiments to ensure consistent conditions for analyzing the relationship between FLCs and DE performance and behavior. This choice allows for a clearer interpretation of performance–landscape associations, without the confounding effects of adaptive or self-adaptive control parameter mechanisms. Exploring such mechanisms represents a promising direction for future research.
For fitness landscape measures, different random sampling approaches were used for various FLC measures, namely progressive random walks of 1000 steps for the ruggedness metric, Manhattan progressive random walks of 1000 steps for the gradient metric, and uniform random samples of 1000 points for the remaining metrics. The fitness landscape metrics used in this study were calculated using sampling configurations consistent with previous work in the relevant literature [32,36]. This setup allows for comparability across studies and aligns with commonly adopted practices.
It is important to note that this study deliberately employed the standard DE/rand/1/bin strategy to maintain methodological clarity and ensure that the observed relationships between DE performance and FLCs were not influenced by adaptive mechanisms. As a widely accepted baseline in evolutionary computation, DE/rand/1/bin provides a transparent and interpretable framework for foundational analysis. While this study focuses exclusively on this variant, future work should investigate more advanced DE algorithms, including adaptive or hybrid variants. The DE algorithm and related experiments were implemented in the C programming language using Microsoft Visual Studio 2019. Statistical analysis were performed in Python 3.10.
4.2. Benchmarks
A set of well-known benchmark problems was utilized in the experimental study, tested across five dimensions, namely 1, 2, 5, 15, and 30 (except for problems that are only defined in a specific dimension). Table 2 provides a detailed description of these benchmark problems. These benchmark problems were carefully selected to exhibit a wide variety of FLCs necessary to investigate the performance of the DE algorithm in the context of the FLCs considered in this study, highlighting key characteristics relevant to the analysis, such as ruggedness, gradients, funnels, deception, and searchability. By selecting these problems, this study ensures a sufficient representation of FLCs, enabling a systematic analysis of how specific features influence the performance of the DE algorithm. Moreover, the selected problems are foundational and have been frequently used in optimization research and align with those commonly adopted in FLA research [17,18,19,32,36], allowing meaningful comparisons and generalizability. The main reason of returning to the foundational problems is to avoid the confounding effects of transformations and hybridization presented in the CEC problems, allowing the study to focus directly on how individual FLCs influence the DE algorithm.

Table 2.
Benchmark functions studied in this paper.
4.3. Performance Measures
This study employs three performance metrics to assess the performance of the DE algorithm. These metrics are defined as follows:
- Quality Metric (QM): The quality metric assesses the quality of the solutions obtained. To calculate the QM, the absolute measure of fitness error is calculated as the difference in fitness between the best solution found in a single run, fmin, and the optimum solution, . The smaller the absolute error, the better the solution quality. Malan and Engelbrecht proposed a method to convert the fitness error into a positive, normalized quality measure, defined as follows [19]:where is an estimation of the maximum fitness value of the function f (calculated by running the function as a maximization problem beforehand). The normalized measure q produces a value in the range [0, 1], where 1 indicates the best possible solution quality and 0 indicates the worst quality. To better distinguish values closer to 1, the value of q is exponentially scaled to obtain the quality metric, QM, as follows [19]:
- Success Rate (SRate): The success rate is defined as the number of successful runs that reach a solution within a fixed accuracy level from the global optimum, divided by the total number of runs. SRate is calculated as follows [19]:
- Success Speed (SSpeed): The speed at which the algorithm finds an acceptable solution is measured by the number of function evaluations consumed to reach that solution. The number of function evaluations required to reach the global optimum or a solution within the fixed accuracy level represents the success speed of a successful run. For unsuccessful runs, SSpeed = 0. The success speed, SSpeed, for a successful run r is calculated as follows [19]:where FESr is the number of function evaluations for a single successful run. The average speed across all runs is then calculated as follows [19]:where ns is the total number of runs. The SSpeed metric produces a value in the range [0, 1]. A larger value of SSpeed indicates the ability of the algorithm to find the solution quickly using a relatively smaller number of function evaluations.
4.4. Experimental Procedure
The DE/rand/1/bin strategy, as outlined in Section 2.1, was executed for each problem and dimensionality, with the maximum number of function evaluations (MaxFES) set to , where D is the dimension of the problem. The results are reported as the average fitness values obtained from 30 independent runs, with a fixed accuracy level of 10−8. In parallel, the specified FLCs were quantified for each problem and dimensionality using the fitness landscape metrics presented in Section 2.2. The online computational intelligence library, CIlib, was used to implement the FLC metrics [85].
To fulfill the objectives outlined in Section 1, two experiments were conducted. The first experiment addresses the first objective by investigating the influence of FLCs on the performance of the DE algorithm, detailed in Section 5. The second experiment corresponds to the second objective, which investigates the impact of FLCs on DE behavior using the DRoC measure, discussed in Section 6. To explore how FLCs relate to the performance and behavior of the DE algorithm, Spearman’s correlation coefficients [86] were used in this study to quantify monotonic associations between FLCs, performance metrics, and the DRoC behavior measure. Spearman’s correlation captures the strength and direction of statistical relationships and serves as a tool to identify general patterns in DE performance and behavior across varying landscape features.
5. Experiment 1: The Association Between Fitness Landscape Characteristics and the Performance of the Differential Evolution Algorithm
Experiment 1 utilizes the experimental setup described in Section 4.1 to specifically investigate the relationship between FLCs and the DE performance metrics, previously defined in Section 2.2 and Section 4.3, respectively. The associations between these metrics and the quantified FLCs were analyzed using Spearman’s correlation coefficients, following the experimental procedures outlined in Section 4.4. The benchmark problems considered for the experiment are detailed in Section 4.2. Through this analysis, the experiment aims to provide insights into how each landscape characteristic is associated with the accuracy, consistency, and speed of the DE algorithm. The results for each problem and dimensionality are presented in Table 3. To simplify the performance assessment, a single performance indicator referred to as “overall” is proposed to represent the overall performance level achieved. The overall performance indicator categorizes the problems based on the DE performance metrics into four classes:

Table 3.
DE performance results across benchmark problems and dimensions D. The column “#f” refers to the benchmark function index. Metrics include QM, SRate, SSpeed, and the overall performance classification.
- Solved and fast (S+): Problems where QM = 1, SRate = 1, and SSpeed > 0.5 indicate that the optimal solution was found for all 30 runs, using less than 50% of the allowed time (i.e., maximum number of function evaluations).
- Solved (S): Problems with QM = 1, SRate = 1, and SSpeed ≤ 0.5 indicate that the optimal solution was found for all 30 runs, but required 50% or more of the allowed time (i.e., maximum number of function evaluations).
- Moderate (M): Problems where 0 < QM < 1 indicate that a near-optimal solution was found.
- Failed (F): Problems where QM = 0 indicate that no solution was found.
Notably, the classifications above are primarily based on the QM value. QM is a vital metric, because it determines whether the problem has been solved or not. A problem is considered solved if a solution within the fixed accuracy level is found (i.e., ). When a solution is found, SRate and SSpeed are used to evaluate the consistency and speed of the DE algorithm, respectively. In the case of finding the optimum (i.e., QM = 1), the overall classification is either S+ or S, based on SSpeed. Similarly, if a non-optimal solution is found (i.e., QM in [0, 1), a moderate performance is reported, and the overall classification is M. The state of failure is indicated by an overall classification of F.
As shown in Table 3, DE generally performs well on lower-dimensional problems (i.e., D = 1, D = 2, and D = 5), with a large proportion of problems falling into the S+ and S categories. However, as the problem dimension increases, there is a noticeable shift in DE performance, with more problems falling into the M and F categories, indicating increased difficulty for the DE algorithm.
Collectively, DE successfully solved 73.9% of the problems, achieving overall classifications of S+ and S, while demonstrating moderate performance on 9.4% of the problems (i.e., overall = M), and reporting failure on only 16.7% of the problems (i.e., overall = F). It is also worth noting that for all S+ and S problems, consistent performance was obtained (i.e., SRate = 1). In summary, DE found the optimal solution across all runs for all S+ and S problems. However, for S+ and S problems, SSpeed shows more variability, particularly as the problem dimensionality increases, indicating that while DE consistently finds high-quality solutions for these problems, the speed of convergence is associated with problem dimensionality and the algorithm requires more function evaluations to approach optimality.
Problems classified as M or F are not exclusively tied to high-dimensional problems and occur across various dimensions, ranging form D = 2 to D = 30, suggesting that the moderate performance or failure is not solely dependent on problem dimension. The SSpeed for M and F classified problems is generally low, often 0.000, since according to Equation (10), the algorithm either failed in all runs or consumed nearly the full function evaluation budget.
The examination of Table 3 was conducted from a dimension-wise perspective, where optimization problems are listed vertically along with their corresponding dimensions. First, DE successfully solved some problems across all dimensions (for, F1). Second, for the other problems, performance degradation was observed as the problem dimension increased (for F14 and F16). Lastly, DE failed to solve certain problems across all dimensions (for F13), which indicates the presence of FLCs that pose particular difficulty for DE on these problems. These observations prompt two critical questions: (1) What makes a problem difficult for DE to solve? (2) Are there specific FLCs that provoke DE failure?
To further investigate the link between DE performance and various problem dimensions, Figure 1 plots the performance metrics across all problems for each dimensionality. Figure 1a clearly shows that the DE algorithm was able to find the optimal solution across all runs for every problem for D = 1 (i.e., QM = SRate = 1), regardless of the FLCs. However, SSpeed shows notable variation, with a minimum value of 0.46 and a maximum value of 0.997 across all problems for D = 1.
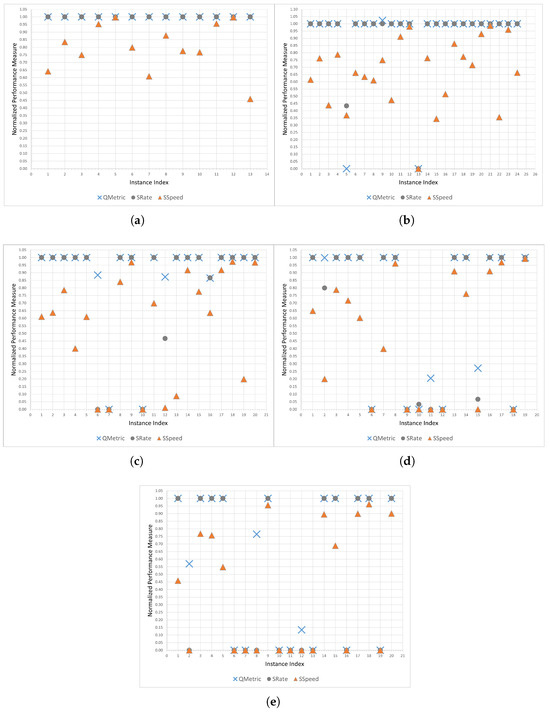
Figure 1.
Performance of the DE algorithm, represented by QM, SRate, and SSpeed, for various problem dimensionalities: (a) D = 1, (b) D = 2, (c) D = 5, (d) D = 15, and (e) D = 30.
For D = 2, as shown in Figure 1b, all but one problem were solved, with approximately one-third of the cases exhibiting moderate QM and SRate values. For D = 5, as shown in Figure 1c, two problems failed, and one was classified at a moderate level. For D = 15, as shown in Figure 1d, five problems failed, whereas for D = 30, as shown in Figure 1e, seven problems failed, and nearly half of the cases resulted in SRate = 0. For three instances of D = 30, DE was able to find a solution of poor quality, though not within the specified accuracy level. In total, for D = 30, only half of the problems were successfully solved.
Figure 1a–e show a significant decline in DE performance as the problem dimensionality increases. The variability in the SRate reflects a decline in the reliability of the DE algorithm in higher-dimensional search spaces. Also, the decline in SSpeed shows that the DE struggled to converge in higher-dimensional search spaces.
SSpeed is the most visually and quantitatively variable performance metric, showing variability even for D = 1. For D = 1, SSpeed generally stays above 0.5 for most problems, indicating relatively quick convergence. However, as the dimensionality increases, SSpeed values progressively decline until reaching their lowest levels for D = 30, indicating that the DE algorithm takes much longer to converge, if it converges at all. For larger dimensional search spaces, even when DE succeeds in finding a solution, it does so much more slowly, indicating increased challenge in such search spaces.
It is also noteworthy that for some instances, QM values were large while SRate values were small, as observed for the Michalewicz problem (i.e., F9) with D = 5. In all cases where QM values are large and SRate values are small, it can be inferred that DE was able to find solutions of high quality, but not precise enough to reach the specified fixed accuracy level.
The experimental results in Table 3 suggest that, generally, SSpeed decreased when problem dimensionality increased. However, for the Griewank problem (i.e., F7), the opposite trend was observed. Specifically, SSpeed decreased with increasing dimensions up to D = 5, but then increased at larger problem dimensionalities (i.e., D = 15 and D = 30). In other words, DE successfully solved all instances of the Griewank problem, achieving larger SSpeed values at D = 30. Interestingly, DE found the optimum with fewer function evaluations for D = 30 for the Griewank problem. This counterintuitive trend was first reported in the context of PSO [87], referring to earlier work discussing that the Griewank function becomes easier as dimensionality increases [88]. The results obtained for the DE algorithm further confirm this behavior.
The preceding discussion highlights that the variation in DE performance is associated with two primary factors: the problem dimensionality and the specific FLCs of the problems.
To relate DE performance to FLCs, the FLC metrics discussed earlier in Section 2.2 were considered, and measurements were reported for each metric across all problems and dimensions. The averages of each fitness landscape metric were calculated for each problem class over the 30 independent runs. For instance, the average of FEM0.01 was calculated for the failed problems (overall F), moderate problems (overall M), and successful problems (overall S+ and S). This was then carried out for all the other FLCs. The averages of each FLC measure and each problem class are visually summarized in Figure 2.
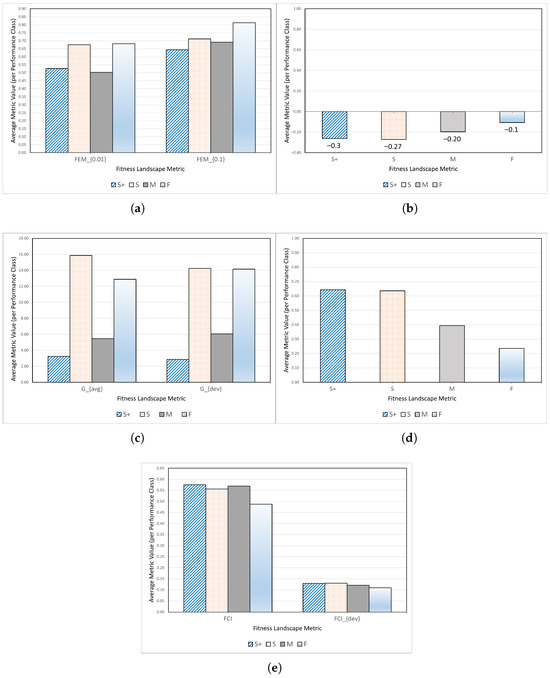
Figure 2.
Average values of fitness landscape metrics across all benchmark problems categorized by DE performance classes. Each subfigure highlights a specific metric: (a) FEM0.01 and FEM0.1, (b) DM, (c) Gavg and Gdev, (d) FDC, and (e) FCI and FCIdev.
Figure 2 reveals that the problems DE failed to solve are characterized by larger average FEM0.1 and FEM0.01, smaller average DM, and the smallest average FDC and FCI, as shown in Figure 2a–e, respectively. The plots in Figure 2 suggest that DE struggled to solve problems with greater ruggedness, multi-funneled, steeper gradients, larger FDC, and smaller FCI. Specifically, DM and FDC demonstrated a consistent influence on the likelihood of DE failure. These initial observations support the earlier findings that different FLCs are associated with varying patterns in DE performance.
To gain further insights into the relationship between DE performance, problem dimensionality, and FLCs, the Spearman’s correlation coefficients for each FLC across dimensions are presented in Table 4. It is observed that for D = 1, all FLCs appear to have no significant association with QM and SRate, while SSpeed exhibited a strong negative correlation with FEM0.01 and Gavg, a moderate negative correlation with FEM0.1, Gdev, DM, and a moderate positive correlation with FCI. Consequently, while DE is expected to find the optimal solution for one-dimensional problems, the convergence speed may be slower for landscapes with high ruggedness and steep gradients. Conversely, faster convergence is anticipated for problem landscapes that facilitate searchability. Moreover, a small positive correlation was observed between SSpeed and FDC.

Table 4.
Spearman’s correlation coefficients between FLCs and DE performance metrics.
Continuing with Table 4, the results for D = 2 indicate that QM, SRate, and SSpeed exhibit a negative correlation of approximately −0.4 with DM and a positive correlation of 0.4 with FDC and FCI. Additionally, QM, SRate, and SSpeed correlated negatively with FEM0.01, FEM0.1, Gavg, and Gdev, though to a lesser extent. These findings suggest that DE performance is associated with DM, FDC, and FCI across all metrics. In other words, DE performance for two-dimensional problems was mainly associated with the presence of funnels, the deception of the search space, and landscape searchability. While ruggedness and gradients may also interact with the performance of the DE algorithm for two-dimensional problems, their interaction appears to be less significant than that of other FLCs.
For problems with dimensionality D = 5, QM exhibited a moderate negative correlation of approximately −0.4 with DM and Gdev, and a positive correlation of about 0.4 with FDC. Similarly, SRate showed a moderate negative correlation of −0.4 with DM and positive correlation with FDC, paralleling the behavior of QM. The speed of convergence, expressed by the SSpead, showed a strong negative correlation of approximately −0.5 with Gavg and Gdev. The performance of the DE algorithm on problems with dimensionality of D = 5 indicates that the quality of the solutions found and the success rate was primarily associated with the presence of funnels and the deception of the landscape (i.e., DM and FDC). However, the convergence speed is expected to be slower in landscapes with steeper gradients (i.e., larger values of Gavg and Gdev).
For problems with dimensionality of D = 15, the correlations are more pronounced. QM, SRate, and SSpeed showed significant negative correlations with FEM0.01, FEM0.1, Gavg, Gdev, and DM. These results suggest that DE performance degrades in highly rugged, steep, multi-funneled landscapes. Conversely, the searchability measures FCI and FCIdev correlated positively with all performance metrics, indicating that DE performance improved in more searchable landscapes and that variations in searchability did not adversely correlate with DE performance.
Furthermore, for larger-dimensional problems, the correlations were even more pronounced, as shown in Table 4 for problems with D = 30: QM, SRate, and SSpeed, exhibited negative correlations with FEM0.01, FEM0.1, DM, Gavg, Gdev, and FCIdev, while positive correlations were observed for all DE performance metrics with FDC and FCI. These findings suggest that the association between DE performance and FLCs becomes stronger for larger-dimensional problems compared to smaller-dimensional ones. The results also imply that the quality of solutions produced by DE in dimension D = 30 was mainly correlated with ruggedness on the macro-scale more than that on the micro-scale, steepness of gradients and variation of these gradients, the presence of funnels, and deception to a lesser extent. However, searchability showed the strongest association with DE performance when D = 30. Notably, FCI emerged as a reliable performance predictor for the DE algorithm across all dimensions, showing a consistent strong correlation with DE performance metrics across all dimensions, and potentially aiding the DE algorithm in exploring and traversing challenging regions of the fitness landscape.
Overall, it can be observed that as the problem dimensionality increased, the FLCs showed stronger correlations with DE performance metrics. Upon careful examination of the entries in Table 4, it can be asserted that for smaller dimensionality (i.e., D = 1, D = 2, and D = 5), DE performance was predominantly associated with DM and FDC. It is noteworthy to mention that Gavg and Gdev showed weaker correlations with DE performance for smaller dimensionality, whereas demonstrating strong negative correlations with DE performance metrics for larger dimensionality (i.e., D = 15 and D = 30). A conclusion could be drawn that DM, FDC, and FCI are the FLCs most strongly associated with DE performance across all problem dimensionalities.
6. Experiment 2: Exploring the Relationship Between Fitness Landscape Characteristics and the Behavior of the Differential Evolution Algorithm
Another key objective of this study is to investigate the relationship between various FLCs and the rate of switching from explorative to exploitative behavior of the DE algorithm. To address this objective, the search behavior of the DE algorithm is quantified using the DRoC measure across all benchmark problems and dimensions. Subsequently, the correlations between FLCs and the DRoC measure were thoroughly analyzed. Spearman’s correlation coefficients [89] were employed to assess the associations between DE performance metrics, the FLC measures, and the DRoC measure.
Table 5 presents the Spearman’s correlation coefficients between the FLC measures and the DRoC measures across all problems and dimensions. It is important to recall that small values for the DRoC measure indicate fast convergence (i.e., smaller negative values with larger magnitude), whereas large DRoC values indicate slow convergence. Thus, a negative correlation between FLC metrics and DRoC measurements suggests that large values for these metrics correspond with small DRoC values, which means faster convergence speed, and therefore, faster transition from exploration to exploitation.

Table 5.
Spearman’s correlation coefficients between FLC metrics and the DRoC measurements across various problems dimensions.
According to the data presented in Table 5, the FEM0.01 metric displayed negative correlations with the DRoC measure in smaller problem dimensionality and positive correlations for larger problem dimensionality. In smaller problem dimensionality (i.e., D = 1 and D = 2), the negative correlations between FEM0.01 and DRoC, particularly for D = 2, suggests that increased micro-level ruggedness is associated with a faster transition from exploration to exploitation for the DE algorithm. Furthermore, for larger dimensionality (i.e., D = 5, D = 15, and D = 30), the correlations between the FEM0.01 metric and the DRoC measure are positive, but are all weak, indicating that increased ruggedness in complex large-dimensional search spaces is associated with slower convergence by the DE algorithm. For FEM0.1, the correlation is weak and negative for D = 1, but becomes moderately positive for D = 2, indicating that as the FEM0.1 value increases, the DE algorithm transitions more slowly to exploitation. In higher dimensions (i.e., D = 5, D = 15, and D = 30), the correlation remains positive and slightly strengthens, indicating that in complex, high-dimensional problems, increased macro-ruggedness is linked to slower transition from exploration to exploitation. Table 5 also shows that the FEM0.01 and FEM0.1 metrics generally exhibited negative correlations in smaller problem dimensionality (i.e., D = 1 and D = 2) and positive correlation in high-dimensional problems. A positive correlation between the FEM metrics and the DRoC measure is logically expected, because landscapes with higher ruggedness, indicated by larger FEM values, are expected to inhibit DE convergence, leading to a slower transition from exploration to exploitation, as observed for D = 5 to D = 30. However, these correlations were generally weak. Furthermore, the negative correlations in smaller problem dimensionality with the DRoC measure suggest that faster diversity reduction can occur in highly rugged problems, highlighting the capability of the DE algorithm to solve highly rugged problems in smaller problem dimensionality. The results in Table 5 indicate that the search behavior of the DE algorithm is linked differently to the micro- and macro-ruggedness, depending on the problem dimensionality. In smaller problem dimensionality, higher ruggedness, especially on micro-scale FEM0.01, seemed to be harmless or even encouraged faster convergence. However, as the dimensionality increases, the ruggedness of both micro- and macro-scales is associated with slower convergence.
The DM measure shows strong positive correlations with the DRoC measurements across most problem dimensionalities, with the largest correlation coefficient (0.477) reported for dimension D = 15, suggesting that for multi-funneled landscapes (indicated by higher DM values), the DE algorithm transitions from exploration to exploitation at a slower rate, particularly in higher dimensions. The positive correlation between the DM measurements and the DRoC measurements highlights a strategic advantage of the DE algorithm: DE tends to slow its convergence speed in the presence of multiple funnels, thereby reducing the risk of premature convergence to suboptimal solutions. This slower transition from exploration to exploitation allows the DE algorithm to explore the fitness landscape more thoroughly, increasing the chances of finding a global optimum or better overall solutions. As anticipated, the DM metric exhibited a positive correlation with the DRoC metric, as smaller DM values indicate single-funneled or less deceptive landscapes. Similarly, smaller DRoC values correspond to faster convergence, facilitating the ability of the DE algorithm to converge without being deceived by multi-funneled landscapes, which is a desirable feature. This behavior is particularly beneficial in avoiding the challenge of complex, multi-funnel landscapes.
However, an excessively slow convergence rate may indicate ineffective convergence behavior or even a state of stagnation [90,91,92], where the algorithm fails to make meaningful progress toward the global optimum, leading to inefficient use of computational resources. The relatively slow convergence behavior exhibited by the conventional DE/rand/1/bin algorithm was highlighted in several studies which proposed advanced DE variants to improve the convergence behavior [67,93,94]. Recall that in Experiment 1, negative correlations were reported between DM and all DE performance metrics across all dimensions, which is linked to the slow convergence rate.
The Gavg metric demonstrated weak and inconsistent correlations with the DRoC measure across various dimensions, indicating that the average steepness of the gradients in the fitness landscape does not significantly correlate with the speed at which the DE algorithm transitions from exploration to exploitation. Moreover, the Gdev metric (which indicates the variability in gradient steepness across the fitness landscape) showed weak correlations with the DRoC measure, indicating that the inconsistency in gradient steepness does not significantly interact with the convergence rate of the DE algorithm. Thus, DE showed consistent performance across landscapes with variable gradient patterns, indicating limited association between gradient variability and its convergence rate. More specifically, the DE algorithm convergence rate was relatively robust to variations in steepness of gradients across the search space. Overall, both Gavg and Gdev show that gradients (whether considering the average steepness of gradients or the variability in steepness) do not significantly correlate with the convergence rate of the DE algorithm. Other FLCs (e.g., ruggedness or the presence of funnels) appear to be more strongly associated with DE search behavior, while gradient-related features show limited association with how quickly the DE algorithm transitions from exploration to exploitation. The correlations between the Gdev metric and the DRoC measure were primarily positive but weak, with the strongest correlation of 0.155 reported for D = 30. A positive correlation between the Gdev metric and the DRoC measure suggests that DE tends to reduce its diversity more quickly in landscapes with an even distribution of gradients. In other words, DE reduces its diversity more rapidly in less-gradient landscapes. Overall, the results in Table 5 show that the correlations between Gavg and Gdev with the DRoC measure are not strongly discernible.
The FDC metric demonstrated a moderate negative correlations with the DRoC measurements across all dimensions, with the strongest negative correlation (−0.373) observed for D = 30. This negative correlation suggests that less deceptive landscapes (indicated by larger FDC values) facilitate faster convergence by consistently guiding the DE algorithm toward fittest regions in the landscape. In contrast, for more deceptive landscapes, DE tends to maintain extensive exploration with a slower transition for a longer period, leading to slower convergence. Larger FDC values signify less deceptive landscapes. The negative correlation between the FDC metric and the DRoC metric is expected and can be explained as follows: For less deceptive landscapes, the individuals within the DE population are more effectively guided towards the fittest regions in the landscape. As a result, for such landscapes, the population is expected to reduce its diversity at a faster rate, leading the individuals to be rapidly clustered in the most promising regions of the search space.
Table 5 reveals that the FCI metric typically exhibited a strong negative correlation with the DRoC measurements across various problem dimensionalities. The strongest correlation for the FCI measure was observed for D = 30, with a correlation coefficient of −0.577, suggesting that as landscape searchability improves (with larger FCI values), the DE algorithm transitions faster from exploration to exploitation, leveraging the ease of finding good solutions. Additionally, weak to moderate correlations were observed between the FCIdev metric and the DRoC measurements, except for D = 5 and D = 30. The FCIdev metric indicates the predictability of a landscape searchability. When the correlation between FCIdev and DRoC is weak, it suggests that variability in searchability does not significantly correlate to DE search transition from exploration to exploitation. In such cases where the correlation is stronger, unpredictable searchability may be associated with variations in the transition speed from exploration to exploitation in the DE algorithm, potentially reflecting how consistently the landscape structure supports the search process. Further analysis concerning the FCI metric and DRoC measures highlights that the strong negative correlations observed between the DRoC measurements and FCI metric (except for D = 2) suggest that faster convergence is associated with more searchable landscapes. This finding aligns with the concept of searchability, which measures the ability of the DE algorithm to find fitter individuals in a single move. In more searchable landscapes, the fittest individuals are expected to rapidly cluster in optimal regions, indicating that DE reduces its diversity at a faster rate in these landscapes. Consequently, for highly searchable landscapes, the speed at which DE loses its diversity and transits from exploration to exploitation occurs more quickly. This study highlighted that the search behavior of the DE algorithm is closely associated with the characteristics of the fitness landscape. In particular, the presence of multiple funnels, deception, and searchability emerged as the most strongly correlated metrics with DE search behavior. The significance of these associations varied across various problem dimensionalities. Higher problem dimensionality is often linked to challenges in exploration, where slow transitions from exploration to exploitation may increase the risk of premature convergence. These findings underscore the importance of tailoring DE strategies to the landscape structure, especially for complex, high-dimensional problems.
7. Conclusions
This research aimed to achieve two main objectives: first, to investigate the correlations between fitness landscape characteristics (FLCs) and the performance of the DE algorithm; and second, to explore their interactions with DE search behavior. To accomplish these objectives, two experiments were conducted. The first experiment focused on the first objective, employing three performance metrics to evaluate DE performance, namely solution quality, success rate, and success speed. For problem characterization, five FLC metrics were utilized, namely ruggedness, gradients, funnels, deception, and searchability.
The findings of the first experiment reveal that DE performance exhibits stronger statistical associations with FLCs in larger-dimensional problems compared to lower-dimensional ones. Among the FLCs analyzed, the presence of multiple funnels, deception, and searchability showed the strongest correlations with DE performance metrics. Specifically, the presence of multiple funnels and higher levels of deception were associated with degraded DE performance, while landscapes with high searchability were strongly correlated with improved performance.
Another key objective of this study was to investigate the search behavior of the DE algorithm in relation to various FLCs, which was addressed in the second experiment. The behavioral measure, DRoC, was adapted and used to quantify the search behavior of the DE algorithm. The results and analysis reveal that the search behavior of the DE algorithm is significantly associated with FLCs, demonstrating that the transition from exploration to exploitation correlates differently with various FLCs and problem dimensionality. The findings from the second experiment align closely with those of the first experiment. The most notable correlations between the search behavior of the DE algorithm and FLCs were observed with the presence of multiple funnels, the level of deception, and searchability, with the presence of funnels registering the highest correlations and appearing most correlated features. Moreover, it was concluded that DE reduces its diversity at a slower rate and resists deception in landscapes with multiple funnels; yet, DE might face the problem of excessively slow convergence in high-dimensional problems.
The findings of this research contribute to a deeper understanding of the interaction between the DE algorithm and complex FLCs, offering valuable insights for the design and adaptation of advanced DE variants. The conclusions drawn from this research improve the understanding of DE behavior and suggest avenues for performance improvement. Future research could further investigate the behavior of the DE algorithm under various control parameter configurations. Specifically, exploring how varying control parameter values influence DE search behavior for specific FLCs, potentially leading to more effective selection of control parameter values based on problem characteristics. For instance, studying the effect of population size on DE search behavior and its correlation with the FLCs of optimization problems could provide a better understanding of how the number of individuals might be utilized to leverage DE performance. The findings from this study could be compared with the existing literature on other swarm-based and evolutionary algorithms utilizing a broader range of optimization problems including real-world optimization problems. Future research should also explore the relationship between FLCs and the performance of more advanced DE variants, including adaptive and hybrid algorithms. Another future research could examine how adaptive or self-adaptive control parameters (guided by landscape features) may enhance performance across diverse problem scenarios.
Further directions for possible future work also include the integration of advanced techniques such as exploratory landscape analysis (ELA) [95,96], which offer broader and more automated characterization of problem structures. Moreover, expanding the range of adopted FLCs and further investigating the influence of sampling approaches and sample sizes used to compute FLCs measures would enrich the analysis. Specifically, Lang and Engelbrecht [97] highlighted the importance of walk length to enhance the robustness of landscape metrics, while their later work [98] emphasized the need for comprehensive decision space coverage in high-dimensional landscapes. These extensions are proposed as future work to build upon the contributions of this study and to support a more nuanced understanding of DE behavior across diverse problem landscapes. Additionally, this study focused on five well-established FLCs (ruggedness, deception, searchability, gradients, and funnels) that have been shown to relate meaningfully to algorithm performance in prior work. Future research could expand on this by incorporating additional landscape metrics, such as neutrality, evolvability, or basin size, or by applying machine learning-based techniques to automatically extract deeper or latent features. These directions may provide complementary insights and further enrich the understanding of how problem structure relates to search behavior and performance.
Finally, the insights gained from this research may also contribute to the development of a performance prediction models for the DE algorithm.
Author Contributions
Formal analysis, A.S., A.P.E. and S.A.K.; Funding acquisition, A.P.E.; Investigation, A.S.; Methodology, A.S. and S.A.K.; Project administration, A.P.E.; Resources, A.P.E. and S.A.K.; Software, A.S.; Supervision, A.P.E. and S.A.K.; Validation, A.P.E. and S.A.K.; Visualization, A.S.; Writing—original draft, A.S.; Writing—review and editing, A.P.E. and S.A.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
The data generated and/or analyzed during the current study are available from the corresponding author on request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Storn, R. On the Usage of Differential Evolution for Function Optimization. In Proceedings of the IEEE International Conference on Fuzzy Systems, New Orleans, LA, USA, 8–11 September 1996; pp. 519–523. [Google Scholar]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for Global Optimization Over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Price, K.; Storn, R.M.; Lampinen, J.A. Differential Evolution: A Practical Approach to Global Optimization, 1st ed.; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Plagianakos, V.P.; Tasoulis, D.K.; Vrahatis, M.N. A Review of Major Application Areas of Differential Evolution. In Advances in Differential Evolution; Chakraborty, U.K., Ed.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 197–238. [Google Scholar]
- Das, S.; Mullick, S.S.; Suganthan, P.N. Recent Advances in Differential Evolution—An Updated Survey. Swarm Evol. Comput. 2016, 27, 1–30. [Google Scholar] [CrossRef]
- Ahmad, M.F.; Isa, N.A.M.; Lim, W.H.; Ang, K.M. Differential Evolution: A Recent Review Based on State-of-the-Art Works. Alex. Eng. J. 2022, 61, 3831–3872. [Google Scholar] [CrossRef]
- Chakraborty, S.P.; Saha, A.K.; Ezugwu, A.E.; Agushaka, J.O.; Zitar, R.A.; Abualigah, L. Differential Evolution and Its Applications in Image Processing Problems: A Comprehensive Review. Arch. Comput. Methods Eng. 2022, 30, 985–1040. [Google Scholar] [CrossRef]
- Langdon, W.B.; Poli, R. Evolving Problems to Learn About Particle Swarm Optimizers and Other Search Algorithms. IEEE Trans. Evol. Comput. 2007, 11, 561–578. [Google Scholar] [CrossRef]
- Talbi, E. Metaheuristics: From Design to Implementation; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Yang, X. Nature-Inspired Metaheuristic Algorithms; Luniver Press: Bristol, UK, 2010. [Google Scholar]
- Gendreau, M.; Potvin, J. (Eds.) Handbook of Metaheuristics, 2nd ed.; Springer: New York, NY, USA, 2010. [Google Scholar]
- Michalewicz, Z.; Fogel, D.B. Tuning the Algorithm to the Problem. In How to Solve It: Modern Heuristics, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 277–298. [Google Scholar]
- Wright, S. The Roles of Mutation, Inbreeding, Crossbreeding, and Selection in Evolution. In Proceedings of the Sixth International Congress on Genetics, Ithaca, NY, USA, 24–31 August 1932; pp. 356–366. [Google Scholar]
- Wright, S. Surfaces of Selective Value Revisited. Am. Nat. 1988, 131, 115–123. [Google Scholar] [CrossRef]
- Zou, F.; Chen, D.; Liu, H.; Cao, S.; Ji, X.; Zhang, Y. A Survey of Fitness Landscape Analysis for Optimization. Neurocomputing 2022, 503, 129–139. [Google Scholar] [CrossRef]
- Malan, K.M.; Engelbrecht, A.P. Quantifying Ruggedness of Continuous Landscapes Using Entropy. In Proceedings of the IEEE Congress on Evolutionary Computation, Trondheim, Norway, 18–21 May 2009; pp. 1440–1447. [Google Scholar]
- Malan, K.M.; Engelbrecht, A.P. Ruggedness, Funnels and Gradients in Fitness Landscapes and the Effect on PSO Performance. In Proceedings of the IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; pp. 963–970. [Google Scholar]
- Malan, K.M.; Engelbrecht, A.P. Characterising the Searchability of Continuous Optimisation Problems for PSO. Swarm Intell. 2014, 8, 275–302. [Google Scholar] [CrossRef]
- Malan, K.M.; Engelbrecht, A.P. Fitness Landscape Analysis for Metaheuristic Performance Prediction. In Recent Advances in the Theory and Application of Fitness Landscapes; Emergence, Complexity and Computation; Richter, H., Engelbrecht, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; Volume 6, pp. 103–132. [Google Scholar]
- Malan, K.M.; Engelbrecht, A.P. Particle Swarm Optimisation Failure Prediction Based on Fitness Landscape Characteristics. In Proceedings of the Symposium on Swarm Intelligence, Orlando, FL, USA, 9–12 December 2014; pp. 1–9. [Google Scholar]
- Dennis, C.; Ombuki-Berman, B.M.; Engelbrecht, A.P. Predicting Particle Swarm Optimization Control Parameters from Fitness Landscape Characteristics. In Proceedings of the IEEE Congress on Evolutionary Computation, Krakow, Poland, 28 June–1 July 2021; pp. 2289–2298. [Google Scholar]
- Uludağ, G.; Uyar, A.Ş. Fitness Landscape Analysis of Differential Evolution Algorithms. In Proceedings of the International Conference on Soft Computing, Computing with Words and Perceptions in System Analysis, Decision and Control, Antalya, Turkey, 9–11 September 2009; pp. 1–4. [Google Scholar]
- Yang, S.; Li, K.; Li, W.; Chen, W.; Chen, Y. Dynamic Fitness Landscape Analysis on Differential Evolution Algorithm. In Proceedings of the Bio-Inspired Computing–Theories and Applications, Xi’an, China, 28–30 October 2016; pp. 179–184. [Google Scholar]
- Zhang, Z.; Duan, N.; Zou, K.; Sun, Z. Predictive Models of Problem Difficulties for Differential Evolutionary Algorithm Based on Fitness Landscape Analysis. In Proceedings of the 37th Chinese Control Conference, Wuhan, China, 25–27 July 2018; pp. 3221–3226. [Google Scholar]
- Huang, Y.; Li, W.; Ouyang, C.; Chen, Y. A Self-Feedback Strategy Differential Evolution with Fitness Landscape Analysis. Soft Comput. 2018, 22, 7773–7785. [Google Scholar] [CrossRef]
- Li, W.; Li, S.; Chen, Z.; Zhong, L.; Ouyang, C. Self-Feedback Differential Evolution Adapting to Fitness Landscape Characteristics. Soft Comput. 2019, 23, 1151–1163. [Google Scholar] [CrossRef]
- Li, K.; Liang, Z.; Yang, S.; Chen, Z.; Wang, H.; Lin, Z. Performance Analyses of Differential Evolution Algorithm Based on Dynamic Fitness Landscape. Int. J. Cogn. Inform. Nat. Intell. 2019, 13, 36–61. [Google Scholar] [CrossRef]
- Liang, J.; Li, Y.; Qu, B.; Yu, K.; Hu, Y. Mutation Strategy Selection Based on Fitness Landscape Analysis: A Preliminary Study. In Bio-Inspired Computing: Theories and Applications; Communications in Computer and Information Science; Pan, L., Liang, J., Qu, B., Eds.; Springer: Singapore, 2020; Volume 1159, pp. 284–298. [Google Scholar]
- Huang, Y.; Li, W.; Tian, F.; Meng, X. A Fitness Landscape Ruggedness Multiobjective Differential Evolution Algorithm with a Reinforcement Learning Strategy. Appl. Soft Comput. 2020, 96, 106693. [Google Scholar] [CrossRef]
- Tan, Z.; Li, K.; Tian, Y.; Al-Nabhan, N. A Novel Mutation Strategy Selection Mechanism for Differential Evolution Based on Local Fitness Landscape. J. Supercomput. 2021, 77, 5726–5756. [Google Scholar] [CrossRef]
- Tan, Z.; Li, K.; Wang, Y. Differential Evolution with Adaptive Mutation Strategy Based on Fitness Landscape Analysis. Inf. Sci. 2021, 549, 142–163. [Google Scholar] [CrossRef]
- Li, Y.; Liang, J.; Yu, K.; Yue, C.; Zhang, Y. Keenness for Characterizing Continuous Optimization Problems and Predicting Differential Evolution Algorithm Performance. Complex Intell. Syst. 2023, 9, 5251–5266. [Google Scholar] [CrossRef]
- Li, S.; Li, W.; Tang, J.; Wang, F. A New Evolving Operator Selector by Using Fitness Landscape in Differential Evolution Algorithm. Inf. Sci. 2023, 624, 709–731. [Google Scholar] [CrossRef]
- Liang, J.; Li, K.; Yu, K.; Yue, C.; Li, Y.; Song, H. A Novel Differential Evolution Algorithm Based on Local Fitness Landscape Information for Optimization Problems. Trans. Inf. Syst. 2023, 106, 601–616. [Google Scholar] [CrossRef]
- Zheng, L.; Luo, S. Adaptive Differential Evolution Algorithm Based on Fitness Landscape Characteristic. Mathematics 2022, 10, 1511. [Google Scholar] [CrossRef]
- Engelbrecht, A.P.; Bosman, P.A.N.; Malan, K.M. The Influence of Fitness Landscape Characteristics on Particle Swarm Optimisers. Nat. Comput. 2022, 21, 335–345. [Google Scholar] [CrossRef]
- Vassilev, V.K.; Fogarty, T.C.; Miller, J.F. Smoothness, Ruggedness and Neutrality of Fitness Landscapes: From Theory to Application. In Advances in Evolutionary Computing: Theory and Applications; Ghosh, A., Tsutsui, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 3–44. [Google Scholar]
- Lunacek, M.; Whitley, D. The Dispersion Metric and the CMA Evolution Strategy. In Proceedings of the 8th Annual Conference on Genetic and Evolutionary Computation, Seattle, WA, USA, 8–12 July 2006; pp. 477–484. [Google Scholar]
- Jones, T.; Forrest, S. Fitness Distance Correlation as a Measure of Problem Difficulty for Genetic Algorithms. In Proceedings of the Sixth International Conference on Genetic Algorithms, Pittsburgh, PA, USA, 15–19 July 1995; pp. 184–192. [Google Scholar]
- Verel, S.; Collard, P.; Clergue, M. Where Are Bottlenecks in NK Fitness Landscapes? In Proceedings of the IEEE Congress on Evolutionary Computation, Canberra, Australia, 8–12 December 2003; pp. 273–280. [Google Scholar]
- Bosman, P.; Engelbrecht, A.P. Diversity Rate of Change Measurement for Particle Swarm Optimisers. In Proceedings of the 9th International Conference on Swarm Intelligence, Brussels, Belgium, 10–12 September 2014; pp. 86–97. [Google Scholar]
- Hayward, L.; Engelbrecht, A. Determining Metaheuristic Similarity Using Behavioral Analysis. IEEE Trans. Evol. Comput. 2025, 29, 262–274. [Google Scholar] [CrossRef]
- Pitzer, E.; Affenzeller, M. A Comprehensive Survey on Fitness Landscape Analysis. In Recent Advances in Intelligent Engineering Systems; Studies in Computational Intelligence; Fodor, J., Klempous, R., Araujo, C.P.S., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; Volume 378, pp. 161–191. [Google Scholar]
- Ochoa, G.; Malan, K. Recent Advances in Fitness Landscape Analysis. In Proceedings of the Genetic and Evolutionary Computation Conference Companion, Prague, Czech Republic, 13–17 July 2019; pp. 1077–1094. [Google Scholar]
- Malan, K.M. A Survey of Advances in Landscape Analysis for Optimisation. Algorithms 2021, 14, 40. [Google Scholar] [CrossRef]
- Malan, K.; Ochoa, G. Landscape Analysis of Optimization Problems and Algorithms. In Proceedings of the Companion Conference on Genetic and Evolutionary Computation, Lisbon, Portugal, 15–19 July 2023; pp. 1416–1432. [Google Scholar]
- Jones, T. Evolutionary Algorithms, Fitness Landscapes and Search. Ph.D. Thesis, University of New Mexico, Albuquerque, NM, USA, 1995. [Google Scholar]
- Barnett, L. Evolutionary Search on Fitness Landscapes with Neutral Networks. Ph.D. Thesis, University of Sussex, East Sussex, UK, 2003. [Google Scholar]
- Derbel, B.; Verel, S. Fitness Landscape Analysis to Understand and Predict Algorithm Performance for Single- and Multi-Objective Optimization. In Proceedings of the Genetic and Evolutionary Computation Conference Companion, Cancun, Mexico, 8–12 July 2020; pp. 993–1042. [Google Scholar]
- Bolshakov, V.; Pitzer, E.; Affenzeller, M. Fitness Landscape Analysis of a Simulation Optimisation Problem with HeuristicLab. In Proceedings of the UKSim 5th European Symposium on Computer Modeling and Simulation, Cambridge, UK, 30 March–1 April 2011; pp. 107–112. [Google Scholar]
- Marmion, M.; Jourdan, L.; Dhaenens, C. Fitness Landscape Analysis and Metaheuristics Efficiency. J. Math. Model. Algorithms Oper. Res. 2013, 12, 3–26. [Google Scholar] [CrossRef]
- Aboutaib, B.; Verel, S.; Fonlupt, C.; Derbel, B.; Liefooghe, A.; Ahiod, B. On Stochastic Fitness Landscapes: Local Optimality and Fitness Landscape Analysis for Stochastic Search Operators. In Proceedings of the 16th International Conference on Parallel Problem Solving from Nature, Leiden, The Netherlands, 5–9 September 2020; Lecture Notes in Computer Science. Bäck, T., Preuss, M., Deutz, A., Wang, H., Kallel, S.A., Juez, J.L., Sim, K., Eds.; Volume 12275, pp. 97–110. [Google Scholar]
- Russell, S.; Norvig, P. Artificial Intelligence: A Modern Approach, 4th ed.; Pearson: Hoboken, NJ, USA, 2020. [Google Scholar]
- Lu, H.; Shi, J.; Fei, Z.; Zhou, Q.; Mao, K. Measures in the Time and Frequency Domains for Fitness Landscape Analysis of Dynamic Optimization Problems. Appl. Soft Comput. 2017, 51, 192–208. [Google Scholar] [CrossRef]
- Lu, H.; Shi, J.; Fei, Z.; Zhou, Q.; Mao, K. Analysis of the Similarities and Differences of Job-Based Scheduling Problems. Eur. J. Oper. Res. 2018, 270, 809–825. [Google Scholar] [CrossRef]
- Tanabe, R.; Fukunaga, A. Success-history Based Parameter Adaptation for Differential Evolution. In Proceedings of the IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 71–78. [Google Scholar]
- Tanabe, R.; Fukunaga, A. Improving the Search Performance of SHADE Using Linear Population Size Reduction. In Proceedings of the IEEE Congress on Evolutionary Computation), Beijing, China, 6–11 July 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1658–1665. [Google Scholar]
- Smith, T.; Husbands, P.; O’Shea, M. Fitness Landscapes and Evolvability. Evol. Comput. 2002, 10, 1–34. [Google Scholar] [CrossRef] [PubMed]
- Xiaowang, H.; Bin, N.; Jicheng, W.; Qiong, G.; Bojun, C. A Fitness Distance Correlation-Based Adaptive Differential Evolution for Nonlinear Equations Systems. Int. J. Swarm Intell. Res. 2024, 15, 1–22. [Google Scholar] [CrossRef]
- Xinyu, Z.; Ningzhi, L.; Long, F.; Hongwei, L.; Bailiang, C.; Mingwen, W. Adaptive niching differential evolution algorithm with landscape analysis for multimodal optimization. Inf. Sci. 2025, 700, 121842. [Google Scholar] [CrossRef]
- Sun, Y.; Halgamuge, S.K.; Kirley, M.; Munoz, M.A. On the Selection of Fitness Landscape Analysis Metrics for Continuous Optimization Problems. In Proceedings of the International Conference on Information and Automation for Sustainability, Colombo, Sri Lanka, 22–24 December 2014; pp. 1–6. [Google Scholar]
- Saad, A.D.; Engelbrecht, A.P.; Khan, S.A. An Analysis of Differential Evolution Population Size. Appl. Sci. 2024, 14, 9976. [Google Scholar] [CrossRef]
- Gämperle, R.; Müller, S.D.; Koumoutsakos, P. A Parameter Study for Differential Evolution. Adv. Intell. Syst. Fuzzy Syst. Evol. Comput. 2002, 10, 293–298. [Google Scholar]
- Ronkkonen, J.; Kukkonen, S.; Price, K. Real-Parameter Optimization with Differential Evolution. In Proceedings of the IEEE Congress on Evolutionary Computation, Edinburgh, Scotland, UK, 2–5 September 2005; Volume 1, pp. 506–513. [Google Scholar]
- Montgomery, J.; Chen, S. An Analysis of the Operation of Differential Evolution at High and Low Crossover Rates. In Proceedings of the IEEE Congress on Evolutionary Computation, Barcelona, Spain, 18–23 July 2010; pp. 1–8. [Google Scholar]
- Ali, M.M.; Törn, A. Population Set-Based Global Optimization Algorithms: Some Modifications and Numerical Studies. Comput. Oper. Res. 2004, 31, 1703–1725. [Google Scholar] [CrossRef]
- Ali, M.; Pant, M. Improving the Performance of Differential Evolution Algorithm Using Cauchy Mutation. Soft Comput. 2011, 15, 991–1007. [Google Scholar] [CrossRef]
- Poikolainen, I.; Neri, F.; Caraffini, F. Cluster-Based Population Initialization for Differential Evolution Frameworks. Inf. Sci. 2015, 297, 216–235. [Google Scholar] [CrossRef]
- Opara, K.; Arabas, J. Comparison of Mutation Strategies in Differential Evolution—A Probabilistic Perspective. Swarm Evol. Comput. 2018, 39, 53–69. [Google Scholar] [CrossRef]
- Guo, S.; Yang, C. Enhancing Differential Evolution Utilizing Eigenvector-Based Crossover Operator. IEEE Trans. Evol. Comput. 2014, 19, 31–49. [Google Scholar] [CrossRef]
- Song, E.; Li, H. A Self-Adaptive Differential Evolution Algorithm Using Oppositional Solutions and Elitist Sharing. IEEE Access 2021, 9, 20035–20050. [Google Scholar] [CrossRef]
- Qiu, X.; Tan, K.C.; Xu, J. Multiple Exponential Recombination for Differential Evolution. IEEE Trans. Cybern. 2016, 47, 995–1006. [Google Scholar] [CrossRef]
- Zhou, Y.; Yi, W.; Gao, L.; Li, X. Adaptive Differential Evolution with Sorting Crossover Rate for Continuous Optimization Problems. IEEE Trans. Cybern. 2017, 47, 2742–2753. [Google Scholar] [CrossRef]
- Sallam, K.M.; Elsayed, S.M.; Sarker, R.A.; Essam, D.L. Landscape-Based Adaptive Operator Selection Mechanism for Differential Evolution. Inf. Sci. 2017, 418, 383–404. [Google Scholar] [CrossRef]
- Tian, M.; Gao, X.; Dai, C. Differential Evolution with Improved Individual-Based Parameter Setting and Selection Strategy. Appl. Soft Comput. 2017, 56, 286–297. [Google Scholar] [CrossRef]
- Zhao, Z.; Yang, J.; Hu, Z.; Che, H. A Differential Evolution Algorithm with Self-Adaptive Strategy and Control Parameters Based on Symmetric Latin Hypercube Design for Unconstrained Optimization Problems. Eur. J. Oper. Res. 2016, 250, 30–45. [Google Scholar] [CrossRef]
- Takahama, T.; Sakai, S. An Adaptive Differential Evolution Considering Correlation of Two Algorithm Parameters. In Proceedings of the 7th International Conference on Soft Computing and Intelligent Systems and 15th International Symposium on Advanced Intelligent Systems, Kitakyushu, Japan, 5–8 December 2014; pp. 618–623. [Google Scholar]
- Yao, X.; Liu, Y.; Lin, G. Evolutionary Programming Made Faster. IEEE Trans. Evol. Comput. 1999, 3, 82–102. [Google Scholar] [CrossRef]
- Rahnamayan, S.; Tizhoosh, H.R.; Salama, M.M.A. A Novel Population Initialization Method for Accelerating Evolutionary Algorithms. Comput. Math. Appl. 2007, 53, 1605–1614. [Google Scholar] [CrossRef]
- Mishra, S.K. Performance of Repulsive Particle Swarm Method in Global Optimization of Some Important Test Functions: A Fortran Program. SSRN Electron. J. 2006. [Google Scholar] [CrossRef]
- Hansen, N.; Kern, S. Evaluating the CMA Evolution Strategy on Multimodal Test Functions. In Proceedings of the International Conference on Parallel Problem Solving from Nature, Birmingham, UK, 18–22 September 2004; pp. 282–291. [Google Scholar]
- Mishra, S.K. Some New Test Functions for Global Optimization and Performance of Repulsive Particle Swarm Method; MPRA Paper 2718; North-Eastern Hill University: Shillong, India, 2006. [Google Scholar]
- Price, K.V.; Storn, R.M.; Lampinen, J.A. Appendix A.1: Unconstrained Uni-modal Test Functions. In Differential Evolution: A Practical Approach to Global Optimization; Natural Computing Series; Springer: Berlin/Heidelberg, Germany, 2005; pp. 514–533. [Google Scholar]
- Jong, K.A.D. An Analysis of the Behavior of a Class of Genetic Adaptive Systems. Ph.D. Thesis, University of Michigan, Ann Arbor MI, USA, 1975. [Google Scholar]
- CIlib Fitness Landscape Analysis. Available online: https://github.com/ciren/fla (accessed on 26 March 2023).
- Spearman, C. The Proof and Measurement of Association Between Two Things. Am. J. Psychol. 1904, 15, 72–101. [Google Scholar] [CrossRef]
- Malan, K.M. Characterising Continuous Optimisation Problems for Particle Swarm Optimisation Performance Prediction. Ph.D. Thesis, University of Pretoria, Pretoria, South Africa, 2014. [Google Scholar]
- Locatelli, M. A Note on the Griewank Test Function. J. Glob. Optim. 2003, 25, 169–174. [Google Scholar] [CrossRef]
- Zar, J.H. Significance Testing of the Spearman Rank Correlation Coefficient. J. Am. Stat. Assoc. 1972, 67, 578–580. [Google Scholar] [CrossRef]
- Lampinen, J.; Zelinka, I. On Stagnation of the Differential Evolution Algorithm. In Proceedings of the 6th International Mendel Conference on Soft Computing, Brno, Czech Republic, 7–9 June 2000; Volume 6, pp. 76–83. [Google Scholar]
- Yu, C.; Jun, H. Average convergence rate of evolutionary algorithms in continuous optimization. Inf. Sci. 2021, 562, 200–219. [Google Scholar] [CrossRef]
- Morales-Castañeda, B.; Maciel-Castillo, O.; Navarro, M.A.; Aranguren, I.; Valdivia, A.; Ramos-Michel, A.; Oliva, D.; Hinojosa, S. Handling stagnation through diversity analysis: A new set of operators for evolutionary algorithms. In Proceedings of the IEEE Congress on Evolutionary Computation, Padua, Italy, 18–23 July 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–8. [Google Scholar]
- Wang, S.; Li, Y.; Yang, H. Self-Adaptive Mutation Differential Evolution Algorithm Based on Particle Swarm Optimization. Appl. Soft Comput. 2019, 81, 105496. [Google Scholar] [CrossRef]
- Xiao, P.; Zou, D.; Xia, Z.; Shen, X. Multi-strategy different dimensional mutation differential evolution algorithm. In Proceedings of the 3rd International Conference on Advances in Materials, Machinery, and Electronics, Wuhan, China, 19–20 January 2019; Volume 2073, p. 020102. [Google Scholar]
- Mersmann, O.; Bischl, B.; Trautmann, H.; Preuss, M.; Weihs, C.; Rudolph, G. Exploratory Landscape Analysis. In Proceedings of the 13th Annual Conference on Genetic and Evolutionary Computation, Dublin, Ireland, 12–16 July 2011; pp. 829–836. [Google Scholar]
- Kerschke, P.; Preuss, M.; Hernández, C.; Schütze, O.; Sun, J.; Grimme, C.; Rudolph, G.; Bischl, B.; Trautmann, H. Cell Mapping Techniques for Exploratory Landscape Analysis. In Advances in Intelligent Systems and Computing; Springer International Publishing: Berlin/Heidelberg, Germany, 2014; pp. 115–131. [Google Scholar]
- Lang, R.D.; Engelbrecht, A.P. On the Robustness of Random Walks for Fitness Landscape Analysis. In Proceedings of the IEEE Symposium Series on Computational Intelligence, Xiamen, China, 6–9 December 2019; pp. 1898–1906. [Google Scholar]
- Lang, R.D.; Engelbrecht, A.P. Decision Space Coverage of Random Walks. In Proceedings of the IEEE Congress on Evolutionary Computation, Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).