Abstract
Synthetic aperture radar (SAR) image classification under limited data conditions faces two major challenges: inter-class similarity, where distinct radar targets (e.g., tanks and armored trucks) have nearly identical scattering characteristics, and intra-class variability, caused by speckle noise, pose changes, and differences in depression angle. To address these challenges, we propose MHD-ProtoNet, a meta-learning framework that extends prototypical networks with two key innovations: margin-aware hard example mining to better separate confusable classes by enforcing prototype distance margins, and dual-loss optimization to refine embeddings and improve robustness to noise-induced variations. Evaluated on the MSTAR dataset in a five-way one-shot task, MHD-ProtoNet achieves accuracy, outperforming the Hybrid Inference Network (HIN) , as well as standard few-shot methods such as prototypical networks , ST-PN , and graph-based models like ADMM-GCN and DGP-NET . By explicitly mitigating inter-class ambiguity and intra-class noise, the proposed model enables robust SAR target recognition with minimal labeled data.
1. Introduction
Synthetic aperture radar (SAR) technology plays a crucial role in defense surveillance, environmental monitoring, and disaster response due to its ability to provide high-resolution images under all weather conditions. However, robust SAR image classification remains challenging due to unique complexities such as speckle noise, variations in target pose, and intra-class variability [1].
Early SAR classification efforts leveraged traditional signal processing techniques and deep learning architectures like CNNs, FCNs, ResNets, and RNNs to improve feature extraction and classification performances [2,3,4,5,6,7,8]. Recent advancements have included the use of Generative Adversarial Networks (GANs) for data augmentation and Siamese Networks for few-shot learning, addressing the challenge of limited labeled data [9,10,11].
To address the persistent challenges of SAR image classification, particularly the scarcity of labeled data and high inter-class similarity, meta-learning has emerged as a promising paradigm. Meta-learning, or “learning to learn,” enables models to adapt quickly to new tasks with minimal data. It is categorized into three main types: learning the initialization, learning the metric, and learning the optimizer [12,13,14]. Among these, metric-based meta-learning has proven particularly effective in SAR applications [1] by learning an embedding space that maximizes class separability while minimizing intra-class distance.
Metric learning techniques, such as ProtoNet [13], are well-suited for SAR applications due to their simplicity and efficiency [15]. ProtoNet learns class prototypes from limited examples, making it ideal for few-shot learning tasks where data is scarce [1]. However, despite its advantages, ProtoNet struggles with misclassification issues in SAR domains due to high inter-class similarity and variations in imaging conditions [16].
In Figure 1, the hard query (pink square) lies closer to an incorrect prototype (BMP2, infantry fighting vehicle) than its correct class prototype (T72, main battle tank), violating the margin condition. Our proposed framework addresses this by adjusting embeddings to reduce the distance to the correct prototype () while increasing the distance to the incorrect one ().
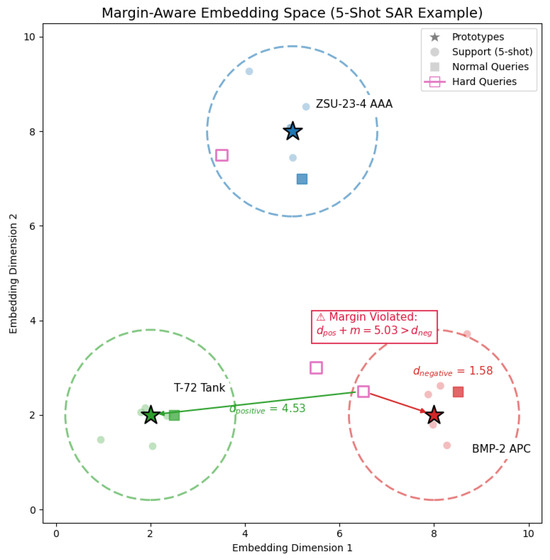
Figure 1.
Embedding space illustration: support prototypes, support samples, and a hard query violating the margin condition.
To overcome these challenges, we propose MHD-Protonet a novel meta-learning framework that enhances prototypical networks through two key innovations: margin-aware hard example mining and dual-loss optimization. This framework is specifically designed to address the complexities of SAR image classification under few-shot learning scenarios.
The main contributions of this work are summarized as follows:
- We introduce a margin-aware hard example mining strategy that dynamically identifies and refines hard queries by enforcing geometric constraints on SAR embeddings, improving class separability in the presence of inter-class similarity.
- We propose a dual-loss optimization approach that combines cross-entropy and margin loss, effectively reducing misclassification errors and enhancing robustness to noise and intra-class variability.
- We provide a comprehensive experimental evaluation on standard SAR datasets under few-shot learning settings, demonstrating that MHD-Protonet achieves significant performance improvements, with an accuracy of 76.80% in five-way one-shot tasks.
- We illustrate the effectiveness and efficiency of MHD-Protonet in real-time SAR classification, showing strong generalization from minimal labeled data while maintaining low computational complexity.
By focusing on metric-based approaches within the prototypical network framework, MHD-Protonet provides a solution that generalizes well from minimal labeled data while ensuring computational efficiency suitable for real-time SAR classification tasks.
2. Related Work
2.1. Meta-Learning and Few-Shot Learning
Few-shot learning (FSL) aims to enable models to generalize effectively from only a few labeled examples per class [17]. This is particularly critical in remote sensing and SAR image classification, where obtaining labeled data is challenging due to high acquisition costs and expert annotation requirements [8,18,19,20]. Conventional deep learning models often fail under such constraints, leading to poor generalization. To overcome this, meta-learning, often described as “learning to learn”, trains models on a distribution of tasks rather than a single one, enabling them to adapt quickly to new tasks using only a few examples [12,21,22]. This approach typically involves three main strategies [12,13,14]: model-based, metric-based, and optimization-based methods. Model-based methods rely on architectures capable of rapid parameter adaptation. Metric-based approaches, such as prototypical networks, learn an embedding space that supports effective few-shot classification through metric comparisons. Optimization-based techniques, like MAML, aim to learn good initial parameters that can be quickly fine-tuned on new tasks. In SAR applications, the ability of meta-learning to extract transferable representations and effective learning strategies is especially valuable due to the small sample sizes, high intra-class variability, and domain-specific noise. These techniques thus help bridge the gap between limited annotated datasets and the performance demands of robust classification systems.
Among the various meta-learning strategies, metric-based methods such as prototypical networks [13] have gained popularity due to their simplicity and effectiveness. These methods aim to learn a shared embedding space, where each class is represented by a prototype, typically computed as the mean of support samples. Classification is then performed by measuring the similarity between the query sample and each class prototype using a distance metric such as Euclidean distance. However, SAR-specific challenges such as speckle noise, geometric distortions, and high inter-class similarity complicate generalization in these settings.
For instance, recent work by Zhang and Luo [23] proposed a feature transformation method to mitigate feature degradation in few-shot class-incremental learning, demonstrating significant improvements in performance across multiple benchmark datasets. This highlights the importance of feature alignment and transformation in enhancing classification accuracy, which is also a key aspect of our proposed MHD-Protonet framework for SAR image classification. By focusing on metric-based approaches within the prototypical network framework, MHD-Protonet provides a solution that generalizes well from minimal labeled data while ensuring computational efficiency suitable for real-time SAR classification tasks.
2.2. Enhancing Prototypes in Few-Shot Learning
Building on prototypical networks, recent research has explored methods to refine prototypes and improve decision boundaries. Li et al. [24] introduced adaptive margins to adjust class boundaries based on semantic similarity, improving inter-class separability. However, such methods often do not account for hard examples near decision boundaries.
Arik and Pfister [25] proposed ProtoAttend, an attention-based framework that dynamically weighs prototypes based on their relevance to the input query. This improved interpretability and performance under distribution shift but remains agnostic to SAR-specific properties such as speckle-induced distortions.
Other enhancements include the Knowledge-Enhanced Prototypical Network (KEPN) [26], which integrates relation networks and class-cluster losses to reinforce intra-class compactness. Despite their promise, these techniques rely on heuristics that may be vulnerable to noise in SAR imagery. Hierarchical prototype structures [27] have also been explored to embed semantic relationships but are less effective for domains like SAR where semantic hierarchies (e.g., tank vs. armored truck) are less clearly defined.
2.3. Adapting Few-Shot Learning to SAR Image Classification
Given the unique challenges of SAR imagery, including viewpoint variation, speckle noise, and inter-class ambiguity, several domain-specific adaptations of few-shot learning have been proposed.
Zhang et al. [28] proposed ST-PN, which integrates a spatial transformer module into prototypical networks to align features across different observation angles. While ST-PN effectively addresses geometric discrepancies, it does not explicitly separate visually similar classes nor handle noise-induced intra-class scatter.
Graph-based deep learning methods have been explored in various remote sensing applications due to their ability to model structural relationships within data. For instance, Patel et al. [29] employed Graph Neural Networks in conjunction with YOLOv7 for ship detection in satellite imagery, achieving high detection accuracy by leveraging both spatial and semantic cues. Li et al. [30] proposed ADMM-GCN, a graph convolutional network that encodes global structure in SAR data and achieves strong performance in few-shot classification scenarios. While these methods differ in task focus and design, both face challenges in scalability and generalization, particularly when relying on predefined graph structures under limited training data conditions.
Generative methods like LST-ACGAN [31] introduce synthetic data augmentation to alleviate data scarcity. By combining label smoothing, auxiliary classification, and triplet loss, this approach attempts to enhance feature discriminability. However, synthetic artifacts, particularly unrealistic speckle patterns, may impair the learning of robust embeddings.
Zhou et al. proposed DGP-Net, a dense graph prototype network that addresses feature deviation in SAR images caused by the special imaging principle (depression angle variation) through learning potential features and feature distribution [32]. DGP-Net demonstrates good classification results for SAR images with different depression angles and outperforms typical FSL methods on the MSTAR dataset.
While these methods address either geometric alignment or data augmentation, two critical challenges remain insufficiently addressed: (1) inter-class ambiguity, where visually similar targets (e.g., tanks and armored vehicles) confuse classifiers; and (2) intra-class scatter, especially due to speckle noise and viewpoint variability.
2.4. Bridging the Gap with MHD-Protonet
To address these challenges, we propose MHD-Protonet, which unifies prototype enhancement and SAR-specific adaptation through two key innovations:
Margin-Aware Hard Example Mining: We explicitly identify hard example queries near decision boundaries and apply a learnable margin constraint to separate them from confusable class prototypes. This enhances the geometric separation of semantically close classes without requiring additional architectural complexity.
Dual-Loss Optimization: Our method combines cross-entropy loss with a geometric margin penalty to handle both inter-class ambiguity and intra-class scatter. This enables learning more robust feature embeddings tailored to the characteristics of SAR data without introducing synthetic artifacts or requiring structured semantic hierarchies.
By integrating these components into a unified meta-learning framework, MHD-Protonet achieves improved generalization in few-shot SAR classification tasks, particularly in scenarios with high noise and class similarity.
3. Methodology
3.1. Proposed Framework: MHD-ProtoNet
The proposed MHD-ProtoNet extends the prototypical network (ProtoNet) framework introduced by Snell et al. [13] by incorporating two key innovations: margin-aware hard example mining and a dual-loss optimization strategy. This design directly addresses the challenges of high inter-class similarity and intra-class variability in SAR image classification. The complete training pipeline is illustrated in Figure 2 The model follows a structured, episodic learning process composed of the following stages:
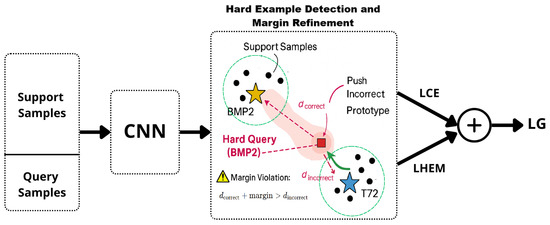
Figure 2.
Flowchart of the MHD-ProtoNet framework illustrating the process from input samples to classification output.
- Input Sampling: Each few-shot learning episode begins with the sampling of a support set (a few labeled examples per class) and a query set (unlabeled examples to be classified). This episodic setup mimics the meta-testing conditions during training and is standard practice in few-shot learning frameworks [13].
- Feature Extraction: All support and query images are passed through a shared ConvNet64 encoder to extract embeddings. This lightweight convolutional architecture has been widely adopted in SAR few-shot learning settings due to its efficiency and effectiveness in representing radar-specific features [13,18].
- Prototype Computation: For each class in the support set, a prototype is computed by averaging the embeddings of its support examples. These prototypes act as reference vectors in the embedding space and serve as the basis for classification.
- Query Evaluation and Distance Computation: Each query embedding is compared to all class prototypes using the Euclidean distance. The closest prototype determines the predicted label for the query.
- Hard Example Detection and Margin Refinement: In the embedding space (as highlighted in Figure 2), the model identifies hard example queries that lie closer to an incorrect prototype than to their true prototype plus a predefined margin. These typically result from class similarity or noise-induced variability. For these hard cases, the model enforces a geometric margin by increasing the distance to the nearest incorrect prototype by a fixed amount. This margin-aware adjustment refines the decision boundary, encouraging separation between confusing classes.
- Loss Computation: MHD-ProtoNet optimizes two loss components:
- –
- Cross-Entropy Loss (): Applied to all query samples to encourage correct classification.
- –
- Hard Example Margin Loss (): Applied only to hard examples that violate the margin condition, encouraging geometric separation by pulling queries closer to their correct prototype and pushing them away from incorrect ones.
- Model Optimization: The two loss terms are combined into a total objective function. The model parameters, including the feature extractor, are updated via backpropagation using gradient-based optimization.
The primary goal of this procedure is to better train the feature extractor by explicitly focusing on hard examples. By refining the embeddings in regions of high ambiguity, the model becomes more robust and achieves improved classification performance during the inference phase. This is particularly valuable under few-shot conditions where data is scarce and hard examples can significantly impact generalization. Further details on the hard example mining and dual-loss components are provided in the following subsections.
3.2. Hard Example Mining and Margin Enforcement
Hard example mining and margin enforcement are integral components of MHD-ProtoNet, working together to enhance the model’s ability to distinguish between visually similar classes and handle intra-class variability. These mechanisms direct the model’s attention to the most challenging instances and ensure clear separability between classes in the embedding space.
3.2.1. Hard Example Mining
Hard example mining is a strategy that focuses model training on the most difficult samples, typically those near class boundaries or those frequently misclassified. These examples are often visually similar to other classes or lie in ambiguous regions of the feature space. Early work such as FaceNet [33] leveraged triplet loss to encourage the model to learn embeddings that maximize inter-class distance while minimizing intra-class variation. This inspired later work like Online Hard Example Mining (OHEM) [34], which actively selected high-loss samples during training, and Focal Loss [35], which down-weights easy examples to focus on difficult ones, particularly in imbalanced datasets. Further, Wu et al. [36] demonstrated that the strategy used to sample hard negatives critically affects the quality of learned embeddings. More recently, SimCLR [37] emphasized the importance of hard negative pairs in contrastive learning, improving representation robustness without supervision. In the context of few-shot learning, where training data is scarce, hard example mining becomes even more critical: the model must generalize from very few support examples, often across visually similar classes. This is especially relevant in SAR image classification, where target classes can have overlapping appearances due to radar imaging geometry and varying aspect angles. Integrating hard example mining into few-shot learning frameworks like prototypical networks [13] can help the model learn more discriminative embeddings, ultimately improving performance on challenging SAR classification tasks. In few-shot learning [1], we define two key sets:
- Support Set: A set of labeled samples used to calculate class prototypes.
- Query Set: A set of unlabeled samples that the model will classify based on the learned prototypes.
The prototypes for each class are computed as the mean embedding of the support samples in that class:
where represents the embedding of the support sample , and is the number of support samples for class c. This approach allows MHD-ProtoNet to focus on class-level representations, enhancing its ability to differentiate between visually similar classes in SAR images.
In the context of MHD-ProtoNet, a hard example is defined as a query sample q whose distance to the correct class prototype is close to or greater than the distance to the nearest incorrect class prototype , violating the margin constraint. These are the instances that the model finds most challenging and that lie near decision boundaries between classes. Hard examples are the ones that are misclassified or classified with low confidence, and the model must learn to adjust the embeddings to improve classification accuracy on these hard examples.
By focusing on hard examples during training, the model can learn more discriminative features that improve its performance on these challenging instances, leading to more robust feature representations.
3.2.2. Margin Enforcement
Margin enforcement ensures clear separability between classes within the embedding space, a core challenge in few-shot learning, especially when dealing with visually similar targets.
Several studies have highlighted the value of enforcing a margin between class prototypes to improve classification performance. Wang et al. [38] demonstrated that incorporating a large margin constraint enhances the generalization of metric-based few-shot models by increasing inter-class distances. Later, Li et al. [24] proposed an adaptive margin loss that adjusts margins based on class similarities, providing dynamic control over class separation. More recently, Liu et al. [39] introduced a negative margin loss, showing that relaxing the margin constraint in specific cases can improve the feature discriminability in few-shot classification.
In the context of synthetic aperture radar (SAR) image classification, margin-based approaches have also proven effective. Liao et al. [40] proposed an adaptive max-margin one-class classifier tailored for SAR target discrimination under complex conditions, highlighting the importance of margin-based constraints in enhancing separability when visual overlap between classes is high. Additionally, Yu et al. [16] introduced an Enhanced Prototypical Network with Customized Region-Aware Convolution specifically for Few-Shot SAR ATR. This work further underscores the importance of refining feature extraction and representation learning in SAR ATR, which complements the role of margin enforcement in creating clear decision boundaries.
Inspired by these works, our method integrates margin enforcement directly into the prototype comparison stage. It ensures that the query embedding is closer to its correct class prototype than to any incorrect prototype by a margin. When this condition is not met, the model adjusts the embeddings during training by attracting the query toward the correct prototype and repelling it from incorrect ones. This combined approach encourages tighter intra-class clusters and clearer inter-class boundaries, which are critical for accurate few-shot SAR classification. This mechanism is a key component of our MHD-ProtoNet framework, enhancing robustness and decision boundaries under limited data conditions. Margin enforcement enhances class separability in the embedding space by enforcing geometric constraints between query samples and class prototypes. For a query embedding with ground-truth class label y, let denote the set of class prototypes (defined earlier). The nearest incorrect prototype is defined as
To ensure adequate separation, we impose the margin constraint
where is a scalar learnable margin parameter, optimized during training to adaptively control the separation between class prototypes in the embedding space.
A violation occurs when
To address violations, we define a margin loss
The subgradient of this loss with respect to is
This update
- Pulls the query embedding closer to the correct prototype ;
- Pushes it away from the nearest incorrect prototype .
This enforcement, combined with hard example mining, encourages the model to form tighter intra-class clusters and clearer inter-class separation a critical factor for accurate few-shot SAR classification. This mechanism is integrated into our MHD-ProtoNet to enhance its robustness and decision boundaries under limited data conditions.
3.3. Dual-Loss Formulation
The dual-loss formulation integrates two crucial loss functions in MHD-ProtoNet: cross-entropy loss and Hard Example Margin (HEM) loss. These losses work in tandem to ensure that the model not only achieves high classification accuracy but also learns robust feature representations, particularly for hard examples near decision boundaries.
3.3.1. Cross-Entropy Loss
The cross-entropy loss drives the model to make accurate predictions for query samples:
where represents the true label and represents the predicted probability for class i. This loss function is widely used in classification tasks due to its effectiveness in measuring the discrepancy between true labels and predicted probabilities [41].
3.3.2. Hard Example Margin (HEM) Loss
The Hard Example Margin (HEM) loss is inspired by the triplet margin loss [33], a classic metric learning objective that enforces a separation between positive and negative examples. It penalizes violations of a margin constraint, encouraging the model to learn more discriminative embeddings by focusing on hard examples. Specifically, Hard Example Margin targets instances where the distance from the query to the correct class prototype plus a predefined margin still does not exceed the distance to an incorrect class prototype. The loss is defined as
This formulation adapts the triplet loss principle to a prototype-based framework [13], where and represent class prototypes. Unlike standard triplet loss, which requires explicit anchor-positive-negative sampling, HEM operates directly on query-to-prototype distances. This inherent focus on hard examples that violate the margin constraint eliminates the need for complex triplet sampling mechanisms.
The total loss L combines the cross-entropy and HEM objectives:
where is a hyperparameter that balances the two components. This dual-loss strategy leverages the strengths of both terms: ensures accurate classification, while refines the embedding space by specifically targeting boundary-violating examples. This addresses a key limitation of vanilla triplet loss, which often struggles with hard example mining without an explicit sampling strategy [42].
By integrating margin enforcement directly into the prototype distance space, HEM avoids the computational overhead of triplet sampling. Moreover, it effectively addresses intra-class variability and inter-class similarity challenges frequently encountered in few-shot learning [13]. A related approach was proposed by Xu et al. [31], who introduced a triplet-loss-based framework for SAR ship classification using an auxiliary classifier GAN. Their results demonstrated that incorporating triplet loss can significantly enhance embedding discriminability, particularly in data-scarce settings like SAR image classification. Our HEM formulation builds upon this idea but removes the need for explicit triplet construction, offering a simpler yet effective alternative tailored for prototype-based few-shot classification.
3.4. MHD-ProtoNet Algorithm
To consolidate the proposed approach, Algorithm 1 presents a structured overview of MHD-ProtoNet, combining training and inference steps. It incorporates hard example mining, margin enforcement, and dual-loss optimization into the standard prototypical network framework.
The pseudocode presented above summarizes the main operations of the proposed MHD-ProtoNet framework. While the detailed steps of the method have already been described and illustrated in Section 3.1, this pseudocode serves to formalize the process and highlight the sequential logic of the margin-based hard query detection mechanism. It is included here to provide a compact and structured overview of the algorithm, thereby supporting both reproducibility and implementation clarity.
| Algorithm 1 MHD-ProtoNet: training and inference |
|
4. Experimental Setup
4.1. Dataset Description
The Moving and Stationary Target Acquisition and Recognition (MSTAR) dataset [43] is a benchmark for evaluating synthetic aperture radar (SAR) Automatic Target Recognition (ATR) algorithms. Developed by the U.S. Air Force Research Laboratory (AFRL) and DARPA, MSTAR provides high-resolution X-band SAR images of military ground targets captured under diverse conditions, including multiple depression angles (15°–17°), complete 360° azimuth coverage, and challenging configurations such as occlusions and structural variations. The dataset is widely used in the research community to evaluate the performance of SAR ATR algorithms and has been used in several few-shot learning studies [1,2].
Each SAR image is a grayscale pixel array acquired in spotlight mode, with a center frequency of 9.59 GHz and a bandwidth of 0.591 GHz, under HH polarization. This setup yields a spatial resolution of 0.3 m in both range and azimuth.
Figure 3 illustrates a comparison of optical and SAR images for representative MSTAR targets, highlighting the perceptual and structural differences between modalities and the difficulty of SAR interpretation. Table 1 provides functional descriptions of the object classes included in the MSTAR dataset. These identifiers correspond to distinct vehicle configurations with varying structural and geometric characteristics relevant to SAR-based recognition tasks.

Figure 3.
Illustration of MSTAR targets in optical and SAR modalities.

Table 1.
Description of vehicle classes in the MSTAR dataset.
To support few-shot learning evaluation, the dataset is partitioned into two mutually exclusive sets:
4.2. Few-Shot Learning Setup
To evaluate model generalization under low-data regimes, we adopt a few-shot learning framework using an N-way K-shot episodic setup [1]:
- A support set with 1 image per class (5 images total);
- A query set with 15 images per class (75 images total).
Few-shot learning is designed to help models learn new tasks quickly when only a few labeled examples are available. To simulate this low-data scenario during training, a special setup called episodic training is used. In episodic training, the learning process is divided into many small tasks, or “episodes,” each resembling a mini classification problem. Each episode consists of two parts: a support set and a query set. The support set contains a small number of labeled images from several classes, which serve as the examples the model learns from in that episode. The query set contains unlabeled images from the same classes, which the model must classify based on what it learned from the support set. By repeatedly training on these episodes, the model learns to quickly adapt to new classes using only a few examples. This episodic approach mimics the real-world situation where new categories appear with very limited data, allowing the model to practice rapid generalization. It also ensures that the model does not simply memorize training data but learns a strategy to identify new classes efficiently.
Figure 4 illustrates the structure of a typical few-shot learning episode, showing the division between the support and query sets for multiple classes.
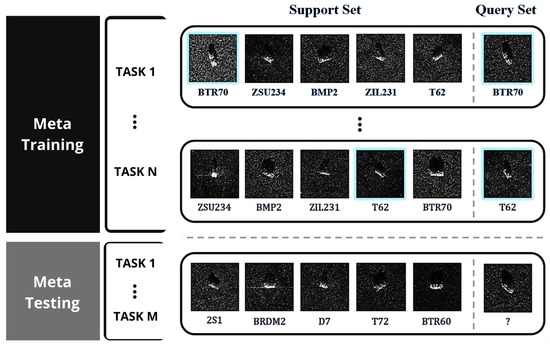
Figure 4.
Visualization of a five-way one-shot episode with one support image and one query image per class.
4.3. Implementation Setup
Experiments are conducted on the MSTAR SAR dataset [43], with preprocessing involving grayscale conversion, center cropping to 84×84 pixels, and intensity normalization (, ). We employ an episodic training framework for 5-way classification under two protocols: (1) 1-shot learning, with 1 support and 15 query examples per class, and (2) 5-shot learning, using 5 support and 15 query examples per class, ensuring matched conditions for both training and testing.
The model architecture combines a Conv64F backbone [13] (four convolutional blocks with 64 filters, BatchNorm, ReLU activation, and max-pooling) with the proposed MHD-ProtoNet classifier, which introduces a learnable margin parameter (initialized to ) and a hybrid loss function () to enhance hard example discrimination. Training is performed over 100 epochs using the Adam optimizer (learning rate ), with gradient clipping (max norm ) and 200 episodes randomly sampled per epoch.
5. Experimental Results
5.1. Main Results
Table 4 presents the comparative results between the standard prototypical network (ProtoNet) and our proposed MHD-ProtoNet across both few-shot settings.

Table 4.
Accuracy (%) of MHD-ProtoNet vs. ProtoNet under few-shot settings (Mean ± Std).
In the five-way one-shot setting, MHD-ProtoNet achieves a significant improvement of 7.42% over ProtoNet. In the five-way five-shot setting, the improvement is 4.20%, demonstrating the consistent effectiveness of our proposed enhancements across different data scarcity scenarios.
5.2. Per-Class Performance
To illustrate a typical classification result of MHD-ProtoNet on the MSTAR dataset, we present predicted class probability distributions for five representative test images, each from a distinct target class (see Table 5). This visual analysis compares the outputs of the standard ProtoNet and the proposed MHD-ProtoNet, highlighting differences in prediction confidence and class separation.

Table 5.
Predicted probability distributions (%) from ProtoNet and MHD-ProtoNet for the same representative test image of each class in the MSTAR dataset. Bold values indicate the ground-truth class.
The BRDM_2 sample illustrates a low-confidence correct classification by ProtoNet, where the ground-truth class receives the highest score (45.97%) but is closely followed by BTR_60 (39.32%), indicating high ambiguity. In contrast, MHD-ProtoNet predicts BRDM_2 with high confidence (84.38%) and reduces the score of BTR_60 to 14.15%, effectively resolving the confusion.
In contrast, a clear misclassification occurs for BTR_60, where ProtoNet incorrectly assigns 96.84% to BRDM_2 and only 0.57% to the correct class. MHD-ProtoNet corrects this error to a large extent, assigning 66.99% to BTR_60 and reducing BRDM_2 to 31.86%.
For simpler cases like 2S1, T72, and D7, both models correctly identify the target class. However, MHD-ProtoNet consistently improves confidence. For instance, in the 2S1 case, ProtoNet predicts with 90.48% confidence, while MHD-ProtoNet raises this to 99.62%.
This performance gap is further illustrated in Figure 5, which compares the predicted class probabilities for the BRDM_2 query using a bar chart. The red bars represent the output of the standard ProtoNet model, while the blue bars correspond to our proposed MHD-ProtoNet. The figure visually confirms how MHD-ProtoNet corrects ProtoNet’s low-confidence prediction by significantly increasing the probability of the correct class and reducing confusion with similar targets.
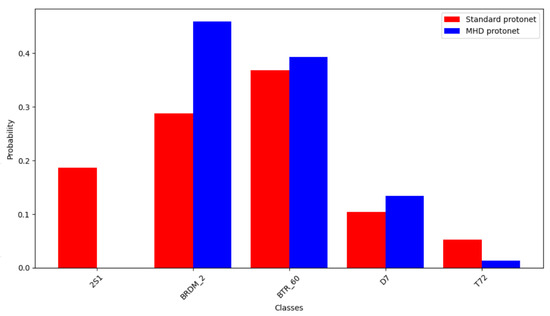
Figure 5.
Class probability distributions of ProtoNet and MHD-ProtoNet for a representative BRDM_2 test image.
Overall, these representative results demonstrate that MHD-ProtoNet enhances prediction confidence and mitigates ambiguity, particularly in scenarios involving visually similar targets where ProtoNet tends to struggle.
To complement these per-sample insights, Figure 6 and Figure 7 present the normalized confusion matrices of ProtoNet and MHD-ProtoNet in the five-way one-shot task across the test classes [‘2S1’, ‘BRDM_2’, ‘BTR_60’, ‘D7’, ‘T72’]. ProtoNet shows significant misclassifications between BRDM_2 and BTR_60, as well as BTR_60 and T72. In contrast, MHD-ProtoNet demonstrates marked improvements. For instance, the classification accuracy for 2S1 improves to from , and D7 achieves accuracy, up from . Overall, MHD-ProtoNet achieves better classification performance across most classes, particularly in distinguishing visually similar targets like BRDM_2 and BTR_60, highlighting the effectiveness of the proposed method in reducing class confusion and enhancing model discriminability. These results demonstrate that MHD-ProtoNet’s margin-aware hard example mining and dual-loss optimization effectively address the inter-class similarity and intra-class variability challenges in SAR image classification, leading to more confident and accurate predictions.
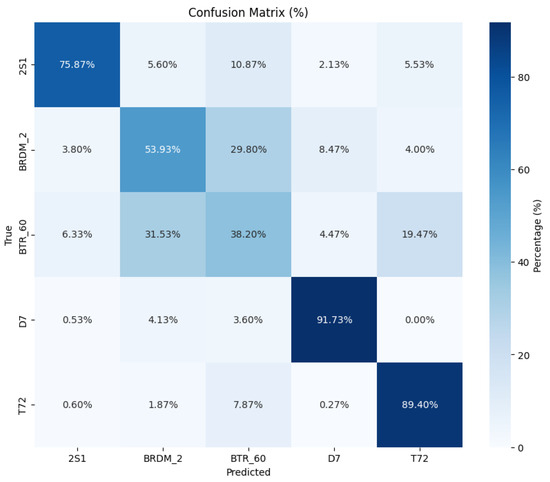
Figure 6.
Normalized confusion matrix for ProtoNet in the five-way one-shot classification task.
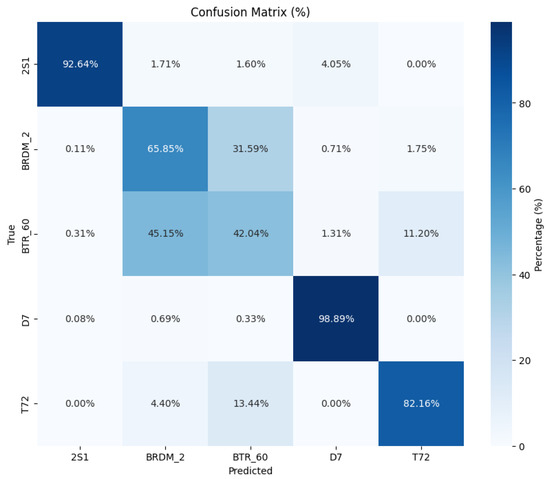
Figure 7.
Normalized confusion matrix for MHD-ProtoNet in the five-way one-shot classification task.
5.3. Embedding Space Visualization (Five-Way One-Shot)
To further demonstrate the effectiveness of our approach, we visualize the learned embedding spaces using t-SNE projections in a five-way one-shot setting with 15 query samples per class.
In Figure 8, ProtoNet yields overlapping clusters, especially for classes with similar scattering patterns. In contrast, Figure 9 shows that MHD-ProtoNet produces tighter intra-class groupings and clearer inter-class margins, confirming that the learned features are more discriminative and robust.
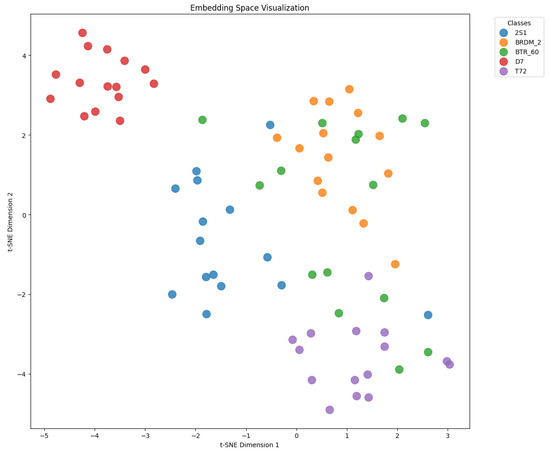
Figure 8.
t-SNE visualization of learned embeddings by ProtoNet in a five-way one-shot task (15 queries/class). The clusters show significant overlap and weak separation between classes.
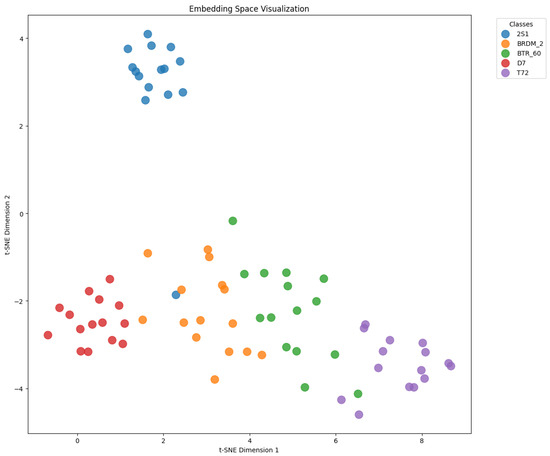
Figure 9.
t-SNE visualization of learned embeddings by MHD-ProtoNet in a five-way one-shot task (15 queries/class). The clusters are more compact and well-separated, indicating better discriminative embedding space.
These visual results highlight MHD-ProtoNet’s ability to address both inter-class similarity and intra-class variability, which are central challenges in SAR few-shot classification.
5.4. Stability Across Episodes
In addition to accuracy, we assess model stability by measuring the standard deviation of accuracy across episodes. To ensure robust evaluation, we use a fixed random seed and repeat each experiment 10 times. This approach allows us to quantify the variance in model performance and ensures reliable comparison between methods.
MHD-ProtoNet consistently demonstrates lower variance than ProtoNet across both few-shot settings. In the five-way one-shot task, the standard deviation for ProtoNet is , while MHD-ProtoNet reduces this to . Similarly, in the five-way one-shot task, the standard deviation decreases from (ProtoNet) to (MHD-ProtoNet). These results confirm that MHD-ProtoNet not only improves accuracy but also enhances stability, making it more reliable for real-world applications where consistent performance across diverse scenarios is crucial.
The improved stability can be attributed to the dual-loss optimization and margin-aware hard example mining components, which help the model learn more robust and generalizable features. This is particularly important in defense-related SAR applications where reliable performance under varying conditions is essential.
5.5. Ablation Study
To evaluate the contribution of each component in the proposed MHD-ProtoNet framework, we conducted a comprehensive ablation study under the five-way (one-shot and five-shot) classification setting on the MSTAR dataset. The study assesses the individual and combined impacts of margin-aware hard example mining and dual-loss optimization, as well as the sensitivity of performance to different fixed margin values and the loss-balancing hyperparameter .
5.5.1. Component-Wise Contributions
We evaluated four model variants to isolate the contributions of each component:
- ProtoNet (Baseline): Standard prototypical network using only cross-entropy loss.
- +Margin Only: Incorporates margin-aware hard example mining with a fixed margin (), but without dual-loss optimization.
- +Dual Loss Only: Applies both cross-entropy and margin loss (), without hard example mining.
- MHD-ProtoNet (Full): The proposed full model combining both margin mining and dual-loss optimization, with a learnable margin parameter.
The results of the ablation study, comparing different components of the proposed framework, are summarized in Table 6.

Table 6.
Ablation study results on MSTAR (five-way one-shot accuracy % ± Std).
Analysis:
- Adding margin-aware hard example mining alone resulted in a improvement over the baseline, demonstrating its effectiveness in separating visually similar classes.
- Dual-loss optimization contributed a +3.44% boost, highlighting its role in learning more stable and noise-resistant embeddings.
- The full MHD-ProtoNet achieved the highest performance at , a gain over the baseline. This underscores the complementary benefits of integrating both mechanisms and the advantage of using a learnable margin parameter.
5.5.2. Margin Parameter Sensitivity
We analyzed the impact of different fixed values of the margin parameter m on classification accuracy. Testing m values of revealed that accuracy increased from (no margin) to at , with a slight decline for larger margins due to over-penalization (see Figure 10). This trend underscores the importance of margin enforcement and supports the use of a learnable margin parameter in the full model, which adapts dynamically to training difficulty and class similarity.
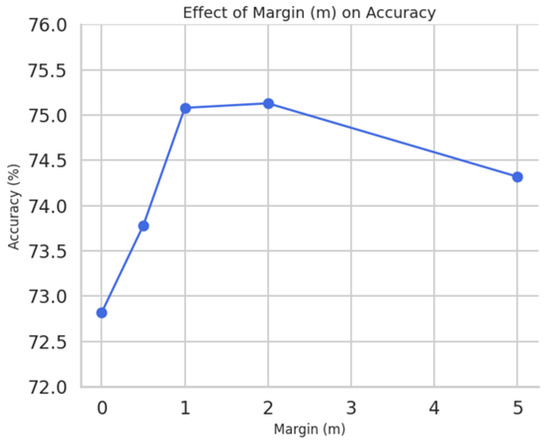
Figure 10.
Effect of fixed margin values on five-way one-shot accuracy. Optimal performance is observed near .
5.5.3. Loss Weight () Sensitivity
We investigated the sensitivity of MHD-ProtoNet to the loss weighting factor , which balances cross-entropy and Hard Example Margin (HEM) loss. Evaluating values across {0, 0.5, 1, 2, 5, 10, 20, 30, 50} showed peak accuracy at (see Figure 11). This indicates that moderate weighting of the margin loss relative to cross-entropy is crucial for optimal performance. Very low underweights the margin constraint, while very high causes excessive penalization, degrading performance.
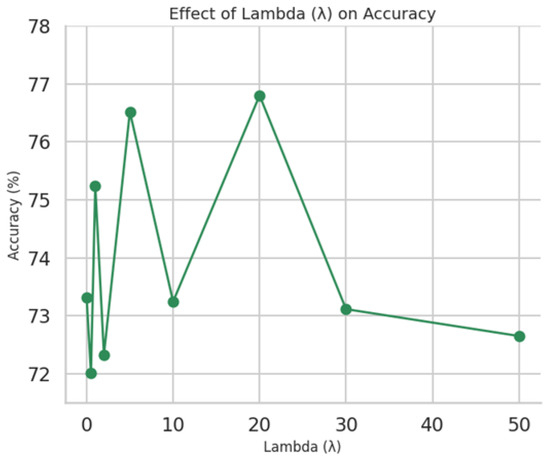
Figure 11.
Accuracy as a function of in the dual-loss formulation. Best results are obtained for between 5 and 20.
The ablation study confirms that each component of MHD-ProtoNet significantly contributes to its performance. Margin-aware mining enhances class separation, dual-loss optimization improves embedding stability, and their integration, coupled with a learnable margin and carefully tuned , maximizes effectiveness in few-shot SAR classification tasks. These findings validate the design choices in MHD-ProtoNet and provide valuable insights for practitioners in the field.
6. Analysis and Discussion
The experimental validation of MHD-ProtoNet underscores its efficacy in addressing the dual challenges of inter-class similarity and intra-class variability inherent to SAR image classification under few-shot conditions. By integrating margin-aware hard example mining and dual-loss optimization, the framework achieves state-of-the-art performance on the MSTAR dataset while maintaining computational efficiency. Below, we dissect these results, contextualize them against existing methods, and critically evaluate the implications for SAR target recognition.
6.1. Key Observations
MHD-ProtoNet demonstrates significant improvements over the baseline ProtoNet, with and accuracy gains in five-way one-shot and five-way one-shot tasks, respectively. These gains stem from its ability to
- Separate visually similar classes (e.g., tanks vs. armored trucks) by enforcing geometric margins between prototypes.
- Suppress intra-class scatter caused by speckle noise and viewpoint variations through dual-loss optimization.
The framework also exhibits enhanced stability, as evidenced by reduced standard deviations across episodes (e.g., vs. ProtoNet’s in 1-shot tasks). This reliability is critical for defense applications, where consistent performance under dynamic imaging conditions such as varying depression angles or occlusions is paramount.
6.2. Component Contributions
The ablation studies reveal the complementary roles of MHD-ProtoNet’s core components. Margin-aware hard example mining contributes a improvement in five-way one-shot accuracy by isolating hard examples near decision boundaries. This mechanism explicitly targets SAR’s high inter-class ambiguity, ensuring prototypes of confusable classes remain separable even under noise.
Dual-loss optimization adds a further improvement by combining cross-entropy and margin loss. This synergy penalizes both classification errors and geometric violations. The margin loss compresses intra-class scatter induced by speckle noise, while cross-entropy refines global decision boundaries.
The full integration of both components results in a improvement over the baseline ProtoNet, underscoring the necessity of addressing both inter-class and intra-class challenges in SAR few-shot learning.
6.3. Comparative Analysis with Existing Methods
The comparative analysis, as summarized in Table 7, reveals that while existing methods such as ST-PN improve geometric alignment, they fail to address speckle-induced intra-class variability. ADMM-GCN and DGP-Net, despite their graph-based architectures, face scalability issues and struggle with high inter-class similarity. RelationNet amplifies noise in SAR’s low signal-to-noise ratio. In contrast, MHD-ProtoNet’s lightweight dual-loss strategy and margin enforcement achieve superior accuracy without sacrificing efficiency, making it ideal for resource-constrained applications.

Table 7.
Comparative accuracy (%) of few-shot learning methods on MSTAR.
MHD-ProtoNet not only outperforms existing methods in accuracy but also maintains computational efficiency. Compared to ADMM-GCN and DGP-Net, which face scalability issues due to their graph-based architectures, MHD-ProtoNet’s training time and memory usage are significantly reduced. This makes it more practical for real-time deployment in defense systems where computational resources are limited.
6.4. Limitations and Future Directions
While MHD-ProtoNet advances SAR few-shot learning, several limitations merit attention:
- Dataset Generalization: Evaluations are confined to MSTAR, which lacks diversity in target types. Testing on datasets like OpenSARShip or SEN1-2 could validate broader applicability.
- Fixed Margin Assumption: The learnable margin adapts to task difficulty but remains global. Class-specific margins, informed by radar cross-section (RCS) signatures, could better capture hierarchical relationships.
- Computational Overhead: Dual-loss optimization increases training complexity. Future work could explore adaptive loss weighting or pruning techniques to reduce inference latency.
To further enhance MHD-ProtoNet and address its limitations, several promising directions are identified:
- Transfer Learning for Feature Enhancement: Utilize pre-trained models on large-scale SAR or related imaging datasets as feature extractors. Fine-tune these models on specific SAR datasets to adapt the features to target recognition tasks. This provides a robust initial set of features and reduces dependency on large amounts of labeled SAR data [45,46].
- Data Augmentation: Increase data diversity through geometric transformations, noise injection, and intensity adjustment. This helps the model learn more robust and invariant features, improving its ability to generalize from limited labeled data [47,48].
- Hybrid Model Integration: Combine MHD-ProtoNet with other meta-learning paradigms such as Model-Agnostic Meta-Learning (MAML) or Meta-SGD. Develop a hybrid framework that leverages the strengths of multiple paradigms to improve adaptability and generalization capabilities [12,14].
MHD-ProtoNet significantly advances few-shot SAR image classification by effectively handling inter-class similarity and intra-class variability. Its success in balancing accuracy, stability, and efficiency paves the way for enhanced target recognition systems in defense and surveillance. The framework’s strategies may also inspire innovations in other noisy data domains. Future work aims to build on these strengths to further improve capabilities and broaden applicability.
7. Conclusions
This paper presents MHD-ProtoNet, a novel extension of prototypical networks designed for few-shot classification in synthetic aperture radar (SAR) imagery. The proposed approach addresses key challenges such as inter-class similarity and intra-class variability through margin-aware hard example mining and a dual-loss optimization scheme. Extensive experiments on the MSTAR dataset demonstrate that MHD-ProtoNet achieves significant performance improvements over baseline methods, with accuracy gains of and in five-way one-shot and five-way one-shot tasks, respectively. The model also exhibits strong stability and computational efficiency, making it suitable for real-time defense applications. Ablation studies and embedding visualizations further confirm the model’s ability to learn robust and discriminative features. Future work will focus on enhancing generalization and adaptability by leveraging transfer learning with large-scale SAR datasets, applying advanced data augmentation strategies to improve robustness under data-scarce conditions, and integrating hybrid meta-learning frameworks such as MAML or Meta-SGD. These directions aim to extend the applicability of MHD-ProtoNet to more complex and diverse SAR-based recognition scenarios.
Author Contributions
Methodology, M.Z., A.T. and A.K.; software, M.Z. and A.T.; validation, M.Z., A.T. and A.K.; formal analysis, M.Z., A.T. and A.K.; supervision, A.T. and A.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding. The APC was funded by the authors.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SAR | Synthetic Aperture Radar |
| ATR | Automatic Target Recognition |
| MSTAR | Moving and Stationary Target Acquisition and Recognition |
| CNN | Convolutional Neural Network |
| ReLU | Rectified Linear Unit |
| PROTONET | Prototypical Network |
| ST-PN | Spatial Transformed Prototypical Network |
| ADMM-GCN | ADMM-based Graph Convolutional Network |
| LST-ACGAN | Label Smoothing and Triplet Loss-based Auxiliary Classification GAN |
| DGP-NET | Dense Graph Prototype Network |
| GANS | Generative Adversarial Networks |
| FSL | Few-Shot Learning |
| MAML | Model-Agnostic Meta-Learning |
| HEM | Hard Example Margin |
| LCE | Cross-Entropy Loss |
| LHEM | Hard Example Margin Loss |
| LG | Global Loss |
| HIN | Hybrid Inference Network |
| t-SNE | t-distributed Stochastic Neighbor Embedding |
| Meta-SGD | Meta-learning with Stochastic Gradient Descent (SGD) |
References
- Zhang, R.; Wang, Z.; Li, Y.; Wang, J.; Wang, Z. FewSAR: A Few-Shot SAR Image Classification Benchmark. arXiv 2023, arXiv:2306.09592. Available online: https://arxiv.org/abs/2306.09592 (accessed on 12 February 2024).
- Li, Y.; Zhang, H.; Xue, X.; Jiang, Y.; Shen, Q. Deep Learning for Remote Sensing Image Classification: A Survey. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2018, 8, e1264. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, X.; Sun, H.; Zhang, Z.; Diao, W.; Fu, K. High Resolution SAR Image Classification with Deeper Convolutional Neural Network. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 2374–2377. [Google Scholar] [CrossRef]
- Geng, J.; Wang, H.; Fan, J.; Ma, X. SAR Image Classification via Deep Recurrent Encoding Neural Networks. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2255–2269. [Google Scholar] [CrossRef]
- El Housseini, A.; Toumi, A.; Khenchaf, A. Deep Learning for Target Recognition from SAR Images. In Proceedings of the 2017 Seminar on Detection Systems Architectures and Technologies (DAT), Algiers, Algeria, 20–22 February 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Toumi, A.; Cexus, J.-C.; Khenchaf, A.; Tartivel, A. Transfer Learning on CNN Architectures for Ship Classification on SAR Images. In Proceedings of the Sea Tech Week—Session Remote Sensing, Brest, France, 12–16 October 2020; Available online: https://hal.science/hal-03109596 (accessed on 5 April 2024).
- Toumi, A.; Cexus, J.-C.; Khenchaf, A. Comparative Performances of CNN Models for SAR Targets Classification. In Proceedings of the 2024 IEEE 7th International Conference on Advanced Technologies, Signal and Image Processing (ATSIP), Sousse, Tunisia, 11–13 July 2024; pp. 122–127. [Google Scholar] [CrossRef]
- Toumi, A.; Cexus, J.-C.; Khenchaf, A.; Abid, M. A Combined CNN-LSTM Network for Ship Classification on SAR Images. Sensors 2024, 24, 7954. [Google Scholar] [CrossRef] [PubMed]
- Kong, J.; Zhang, F. SAR Target Recognition with Generative Adversarial Network (GAN)-Based Data Augmentation. In Proceedings of the 2021 13th International Conference on Advanced Infocomm Technology (ICAIT), Yanji, China, 15–18 October 2021; pp. 215–218. [Google Scholar] [CrossRef]
- Tang, J.; Zhang, F.; Zhou, Y.; Yin, Q.; Hu, W. A Fast Inference Network for SAR Target Few-Shot Learning Based on Improved Siamese Networks. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 1212–1215. [Google Scholar] [CrossRef]
- Khenchaf, Y.; Toumi, A. Siamese Neural Network for Automatic Target Recognition Using Synthetic Aperture Radar. In Proceedings of the IGARSS 2023—2023 IEEE International Geoscience and Remote Sensing Symposium, Pasadena, CA, USA, 16–21 July 2023; pp. 7503–7506. [Google Scholar] [CrossRef]
- Finn, C.; Abbeel, P.; Levine, S. Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks. arXiv 2017, arXiv:1703.03400. Available online: https://arxiv.org/abs/1703.03400 (accessed on 19 April 2024).
- Snell, J.; Swersky, K.; Zemel, R. Prototypical Networks for Few-Shot Learning. arXiv 2017, arXiv:1703.05175. Available online: https://arxiv.org/abs/1703.05175 (accessed on 21 April 2024).
- Li, Z.; Yang, F.; Song, F.; Hou, L.; Wang, K.; Yang, Y. Meta-SGD: Learning to Learn Stochastic Gradient Descent. arXiv 2017, arXiv:1707.09835. Available online: https://arxiv.org/pdf/1707.09835 (accessed on 25 April 2024).
- Zhao, P.; Huang, L.; Xin, Y.; Guo, J.; Pan, Z. Multi-Aspect SAR Target Recognition Based on Prototypical Network with a Small Number of Training Samples. Sensors 2021, 21, 4333. [Google Scholar] [CrossRef]
- Yu, X.; Yu, H.; Liu, Y.; Ren, H. Enhanced Prototypical Network with Customized Region-Aware Convolution for Few-Shot SAR ATR. Remote Sens. 2024, 16, 3563. [Google Scholar] [CrossRef]
- Wang, Y.; Yao, Q.; Kwok, J.T.; Ni, L.M. Generalizing from a Few Examples: A Survey on Few-Shot Learning. ACM Comput. Surv. 2020, 53, 1–34. Available online: https://arxiv.org/pdf/1904.05046 (accessed on 18 August 2024). [CrossRef]
- Wang, N.; Jin, W.; Bi, H.; Xu, C.; Gao, J. A Survey on Deep Learning for Few-Shot PolSAR Image Classification. Remote Sens. 2024, 16, 4632. [Google Scholar] [CrossRef]
- He, K.; Pu, N.; Lao, M.; Lew, M.S. Few-Shot and Meta-Learning Methods for Image Understanding: A Survey. Int. J. Multimed. Inf. Retr. 2023, 12, 14. [Google Scholar] [CrossRef]
- Fu, K.; Zhang, T.; Zhang, Y.; Wang, Z.; Sun, X. Few-Shot SAR Target Classification via Meta-Learning. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Ravi, S.; Larochelle, H. Optimization as a Model for Few-Shot Learning. In Proceedings of the International Conference on Learning Representations (ICLR), Toulon, France, 24–26 April 2017; Available online: https://openreview.net/pdf?id=rJY0-Kcll (accessed on 30 August 2024).
- Demertzis, K.; Iliadis, L. GeoAI: A Model-Agnostic Meta-Ensemble Zero-Shot Learning Method for Hyperspectral Image Analysis and Classification. Algorithms 2020, 13, 61. [Google Scholar] [CrossRef]
- Zhang, X.; Luo, Y. Feature Transformation-Based Few-Shot Class-Incremental Learning. Algorithms 2025, 18, 422. [Google Scholar] [CrossRef]
- Li, A.; Huang, W.; Lan, X.; Feng, J.; Li, Z.; Wang, L. Boosting Few-Shot Learning with Adaptive Margin Loss. arXiv 2020, arXiv:2005.13826. Available online: https://arxiv.org/abs/2005.13826 (accessed on 15 September 2024). [CrossRef]
- Arik, S.O.; Pfister, T. ProtoAttend: Attention-Based Prototypical Learning. arXiv 2019, arXiv:1902.06292. Available online: https://arxiv.org/abs/1902.06292 (accessed on 27 November 2024).
- Liu, T.; Ke, Z.; Li, Y.; Silamu, W. Knowledge-Enhanced Prototypical Network with Class Cluster Loss for Few-Shot Relation Classification. PLoS ONE 2023, 18, e0286915. [Google Scholar] [CrossRef]
- Hamzaoui, M.; Chapel, L.; Pham, M.T.; Lefèvre, S. A Hierarchical Prototypical Network for Few-Shot Remote Sensing Scene Classification. In Proceedings of the International Conference on Pattern Recognition and Artificial Intelligence, Paris, France, 1–3 June 2022; Springer International Publishing: Cham, Switzerland, 2022; pp. 208–220. [Google Scholar] [CrossRef]
- Cai, J.; Zhang, Y.; Guo, J.; Zhao, X.; Lv, J.; Hu, Y. ST-PN: A Spatial Transformed Prototypical Network for Few-Shot SAR Image Classification. Remote Sens. 2022, 14, 2019. [Google Scholar] [CrossRef]
- Patel, K.; Bhatt, C.; Mazzeo, P.L. Improved Ship Detection Algorithm from Satellite Images Using YOLOv7 and Graph Neural Network. Algorithms 2022, 15, 473. [Google Scholar] [CrossRef]
- Jin, J.; Xu, Z.; Zheng, N.; Wang, F. Graph-Based Few-Shot Learning for Synthetic Aperture Radar Automatic Target Recognition with Alternating Direction Method of Multipliers. Remote Sens. 2025, 17, 1179. [Google Scholar] [CrossRef]
- Xu, C.; Gao, L.; Su, H.; Zhang, J.; Wu, J.; Yan, W. Label Smoothing Auxiliary Classifier Generative Adversarial Network with Triplet Loss for SAR Ship Classification. Remote Sens. 2023, 15, 4058. [Google Scholar] [CrossRef]
- Zhou, X.; Wei, Q.; Zhang, Y. DGP-Net: Dense Graph Prototype Network for Few-Shot SAR Target Recognition. arXiv 2023, arXiv:2302.09584. Available online: https://arxiv.org/abs/2302.09584 (accessed on 4 January 2025).
- Schroff, F.; Kalenichenko, D.; Philbin, J. FaceNet: A Unified Embedding for Face Recognition and Clustering. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 815–823. [Google Scholar] [CrossRef]
- Shrivastava, A.; Gupta, A.; Girshick, R. Training Region-Based Object Detectors with Online Hard Example Mining. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 761–769. [Google Scholar] [CrossRef]
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal Loss for Dense Object Detection. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar] [CrossRef]
- Wu, C.Y.; Manmatha, R.; Smola, A.J.; Krahenbuhl, P. Sampling Matters in Deep Embedding Learning. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2840–2848. [Google Scholar] [CrossRef]
- Chen, T.; Kornblith, S.; Norouzi, M.; Hinton, G. A Simple Framework for Contrastive Learning of Visual Representations. In Proceedings of the International Conference on Machine Learning (ICML), Virtual, 13–18 July 2020; pp. 1597–1607, PMLR. Available online: http://proceedings.mlr.press/v119/chen20a.html (accessed on 10 January 2025).
- Wang, Y.; Wu, X.M.; Li, Q.; Gu, J.; Xiang, W.; Zhang, L.; Li, V.O. Large Margin Few-Shot Learning. arXiv 2018, arXiv:1807.02872. Available online: https://arxiv.org/abs/1807.02872 (accessed on 18 January 2025). [CrossRef]
- Liu, B.; Cao, Y.; Lin, Y.; Li, Q.; Zhang, Z.; Long, M.; Hu, H. Negative Margin Matters: Understanding Margin in Few-Shot Classification. arXiv 2020, arXiv:2003.12060. Available online: https://arxiv.org/abs/2003.12060 (accessed on 22 January 2025). [CrossRef]
- Liao, L.; Du, L.; Zhang, W.; Chen, J. Adaptive Max-Margin One-Class Classifier for SAR Target Discrimination in Complex Scenes. Remote Sens. 2022, 14, 2078. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Hermans, A.; Beyer, L.; Leibe, B. In Defense of the Triplet Loss for Person Re-Identification. arXiv 2017, arXiv:1703.07737. Available online: https://arxiv.org/abs/1703.07737 (accessed on 17 September 2024). [CrossRef]
- Defense Advanced Research Project Agency (DARPA); Air Force Research Laboratory (AFRL). The Air Force Moving and Stationary Target Recognition (MSTAR) Database. 2014. Available online: https://www.sdms.afrl.af.mil/index.php?collection=mstar (accessed on 24 May 2025).
- Sung, F.; Yang, Y.; Zhang, L.; Xiang, T.; Torr, P.H.S.; Hospedales, T.M. Learning to Compare: Relation Network for Few-Shot Learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 1199–1208. [Google Scholar] [CrossRef]
- Lu, C.; Li, W. Ship Classification in High-Resolution SAR Images via Transfer Learning with Small Training Dataset. Sensors 2018, 19, 63. [Google Scholar] [CrossRef]
- Huang, Z.; Pan, Z.; Lei, B. Transfer Learning with Deep Convolutional Neural Network for SAR Target Classification with Limited Labeled Data. Remote Sens. 2017, 9, 907. [Google Scholar] [CrossRef]
- Singh, A.; Singh, V.K. Exploring Deep Learning Methods for Classification of SAR Images: Towards NextGen Convolutions via Transformers. arXiv 2023, arXiv:2303.15852. Available online: https://arxiv.org/abs/2303.15852 (accessed on 2 November 2024). [CrossRef]
- Shorten, C.; Khoshgoftaar, T.M. A Survey on Image Data Augmentation for Deep Learning. J. Big Data 2019, 6, 60. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).