Series Arc Fault Detection Method Based on Time Domain Imaging and Long Short-Term Memory Network for Residential Applications
Abstract
1. Introduction
2. Signal Acquisition and Analysis
2.1. Experimental Platform Construction
2.2. Analysis of Typical Appliance Current Waveform
2.3. The Ensemble Empirical Mode Decomposition Method
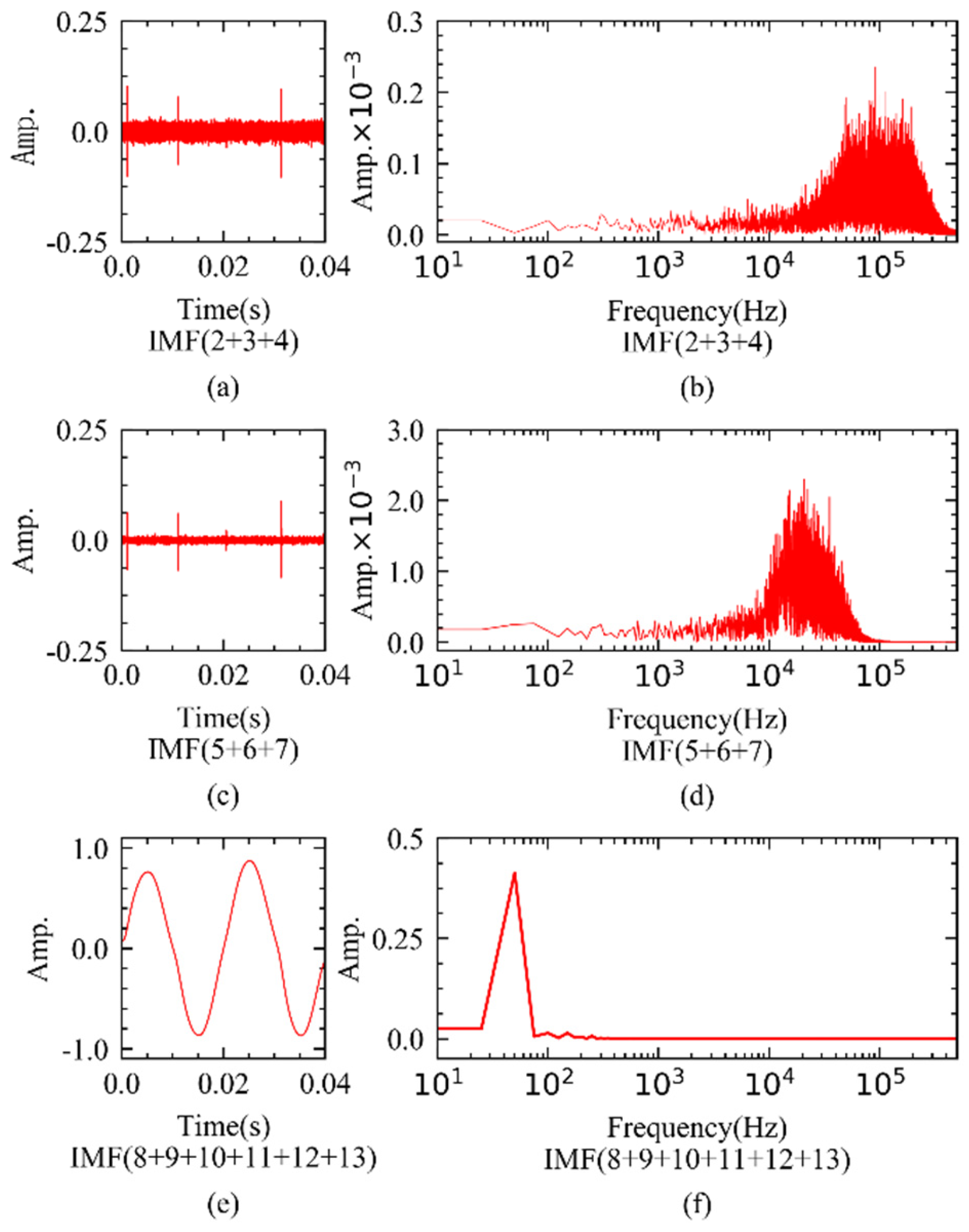
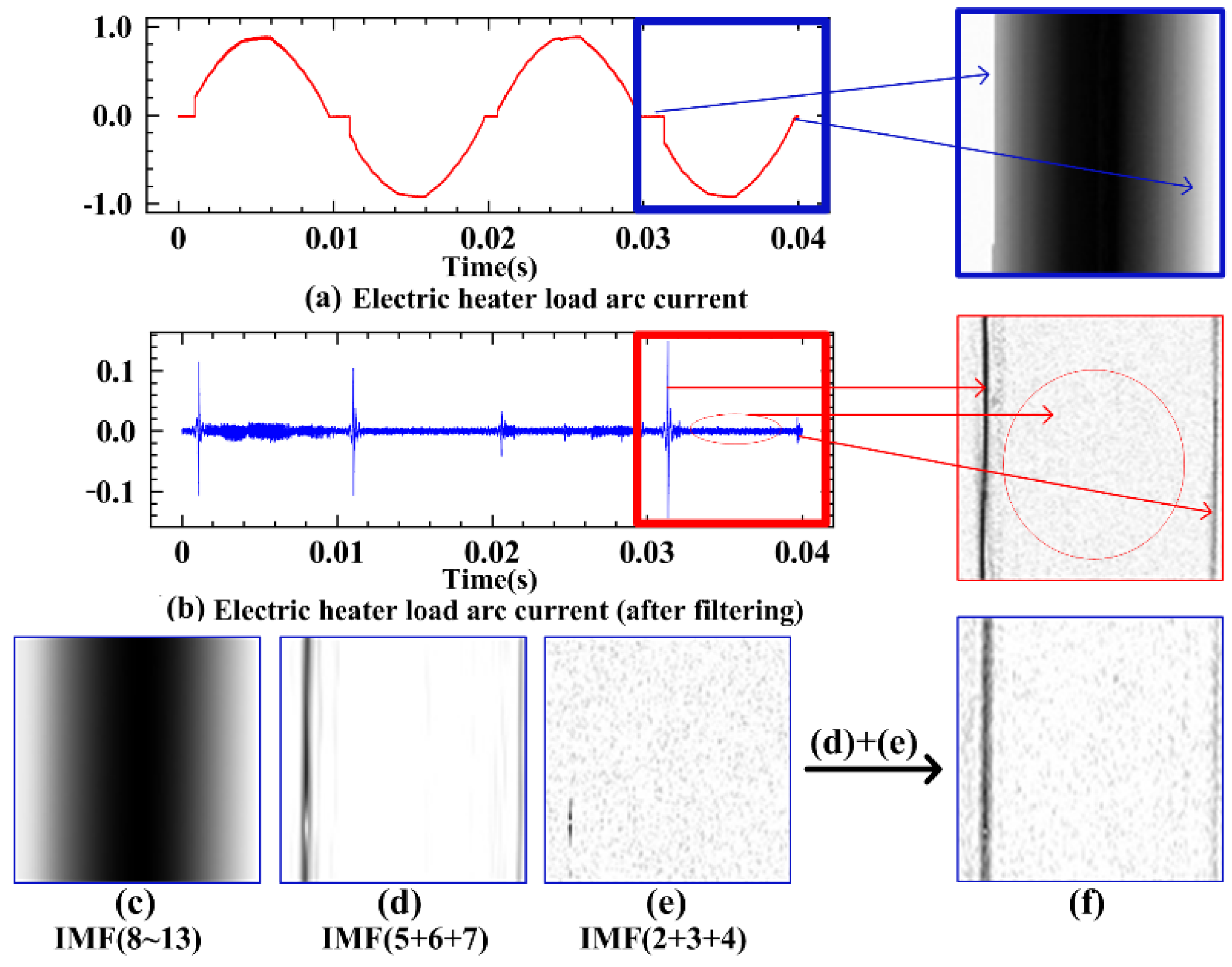
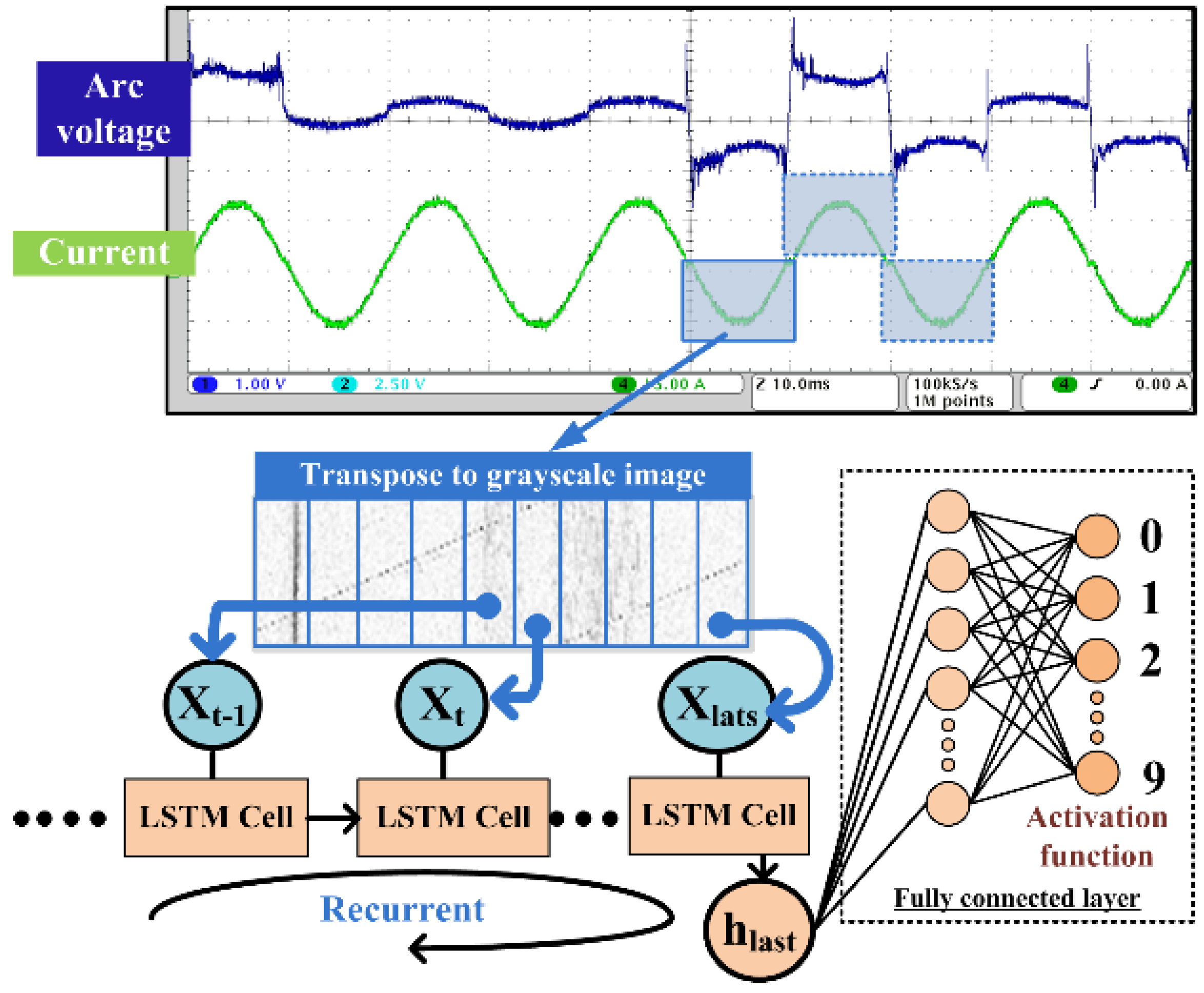
2.4. Empirical Mode Decomposition and Visual Representation of Arc Fault Signal
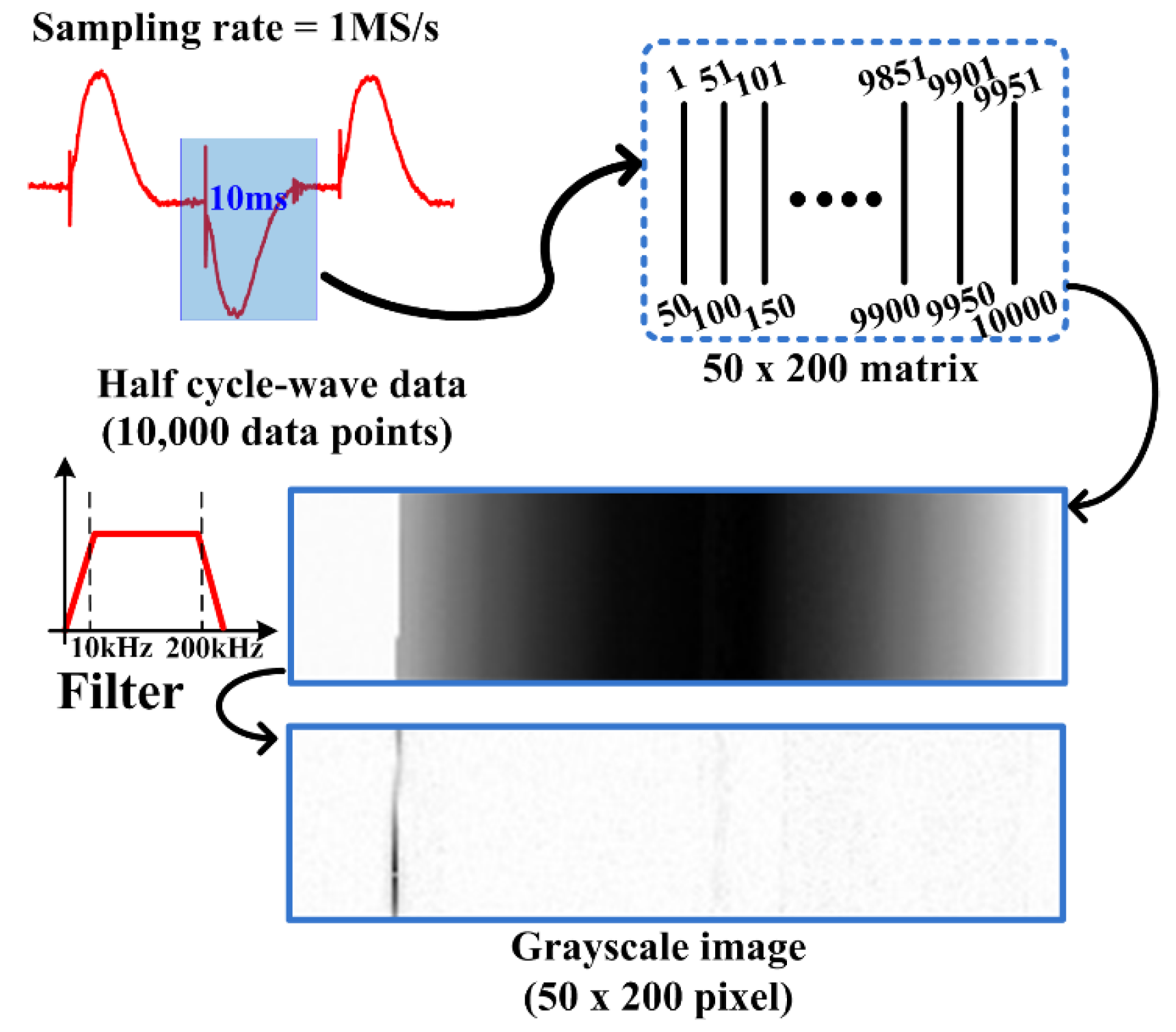
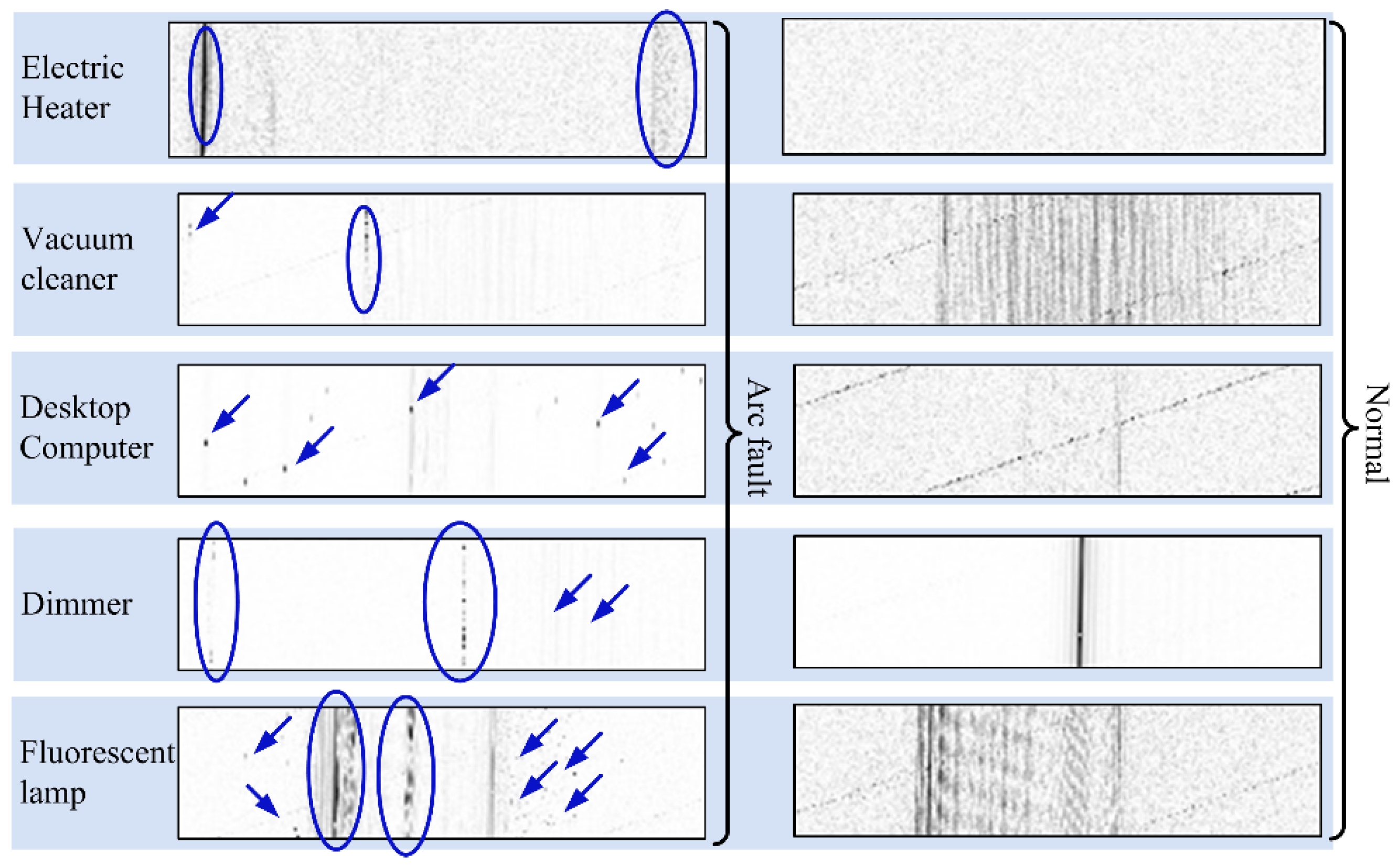
2.5. Utilize the Proposed Method of Generating Grayscale Images to Observe Arc-Fault Characteristics
3. Detection Method of SAFs
3.1. LSTM Background
3.2. Sampling Frequency Selection
3.3. Dataset Construction
3.4. Model Structure and Training
- (1)
- Data Preparation: Define the model’s input and output variables. Preprocess the input dataset and divide it into three subsets: training, validation, and testing.
- (2)
- Model Construction and Training: Build a deep LSTM model for series arc-fault detection. Train the model using the training set, while the validation set is used to assess and optimize the model’s generalization performance during training.
- (3)
- Model Evaluation: Evaluate the trained model using the test dataset to determine its prediction accuracy on unseen data.
- (4)
- Hyperparameter Tuning: Adjust hyperparameters iteratively to minimize the prediction error on the test dataset.
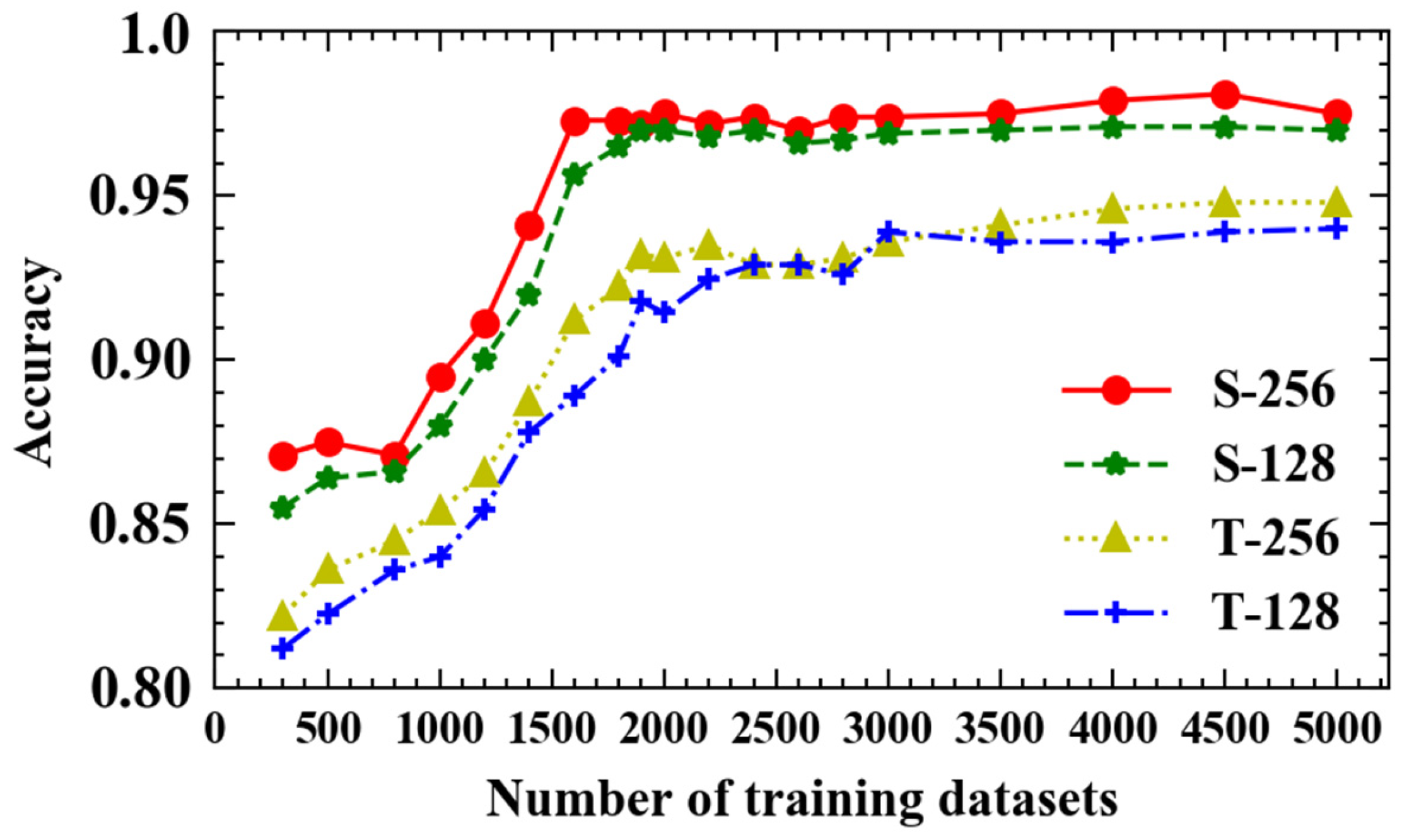
4. TDI-LSTM Performance and Evaluation
- (1)
- Single layer and 128 output neurons (S-128);
- (2)
- Single layer and 256 output neurons (S-256);
- (3)
- Two layers and 128 output neurons (T-128);
- (4)
- Two layers and 256 output neurons (T-256).
4.1. Dimension Reduction Analysis
4.2. Experimental Results
5. Comparison and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fire and Rescue Department Ministry of Emergency Management. “Over 3000 Daily Fires Nationwide in First Half of 2023”. Available online: https://www.119.gov.cn/qmxfgk/sjtj/2023/38420.shtml (accessed on 26 January 2025).
- National Fire Protection Association. “Home Electrical Fires”. Available online: https://www.nfpa.org/education-and-research/research/nfpa-research/fire-statistical-reports (accessed on 6 April 2025).
- Chu, R.; Schweitzer, P.; Zhang, R. Series ac arc fault detection method based on high-frequency coupling sensor and convolution neural network. Sensors 2020, 20, 4910. [Google Scholar] [CrossRef] [PubMed]
- National Fire Protection Association. National Electrical Code; National Fire Protection Association: Quincy, MA, USA, 2014. [Google Scholar]
- GB/T31143-2014; General Requirements for Arc Fault Protection Appliances (AFDD). General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China: Beijing, China, 2014.
- GB14287.4-2014; Electrical Fire Monitoring System-Part 4: Arcing Fault Detectors 2014. General Administration of Quality Supervision. Inspection and Quarantine of the People’s Republic of China: Beijing, China, 2014.
- Underwriters Laboratories Inc. Standard for Safety Arc-Fault Circuit Interrupters, 2nd ed.; UL standard 1699; Underwriters Laboratories Inc.: Northbrook, IL, USA, 2011. [Google Scholar]
- Qu, N.; Wang, J.; Liu, J.; Wu, F. A series arc fault detection method based on Cassie model and L3/4 norm. Dianwang Jishu/Power Syst. Technol. 2018, 42, 3992–3997. [Google Scholar]
- Liu, Y.; Guo, F.; Li, L.; Wang, Z.; Wang, X. A kind of series fault arc mathematical model. Diangong Jishu Xuebao/Trans. China Electrotech. Soc. 2019, 34, 2901–2912. [Google Scholar]
- Kim, J.C. Electromagnetic radiation behavior of low-voltage arcing fault. IEEE Trans. Power Deliv. 2009, 24, 416–423. [Google Scholar] [CrossRef]
- Zhou, N.; Zhou, C.; Wang, Q.; Zhang, J.; Li, T. Improved laplacian score based fault feature selection of switchgear cabinet and its diagnosis. Dianwang Jishu/Power Syst. Technol. 2015, 39, 850–855. [Google Scholar]
- Cudina, M.; Prezelj, J. Evaluation of the sound signal based on the welding current in the gas-metal arc welding process. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2003, 217, 483–494. [Google Scholar] [CrossRef]
- Cai, B.; Chen, D.; Wu, R.; Wang, X.; Gao, D.; Chen, W. Online detecting and protection system for internal faults arc in switchgear. Diangong Jishu Xuebao/Trans. China Electrotech. Soc. 2005, 20, 83–87. [Google Scholar]
- Yang, K.; Chu, R.; Zhang, R.; Xiao, J.; Tu, R. A novel methodology for series arc fault detection by time domain visualization and convolutional neural network. Sensors 2020, 20, 162. [Google Scholar] [CrossRef]
- Wang, W.; Xu, B.; Zou, G.; Liang, D. Arc fault detection method based on voltage characteristic energy amplitude and phase mapping distribution distances. Electr. Power Syst. Res. 2023, 225, 109866. [Google Scholar] [CrossRef]
- Li, J.; Zou, G.; Wang, W.; Shao, N.; Han, B.; Wei, L. Low-voltage series arc fault detection based on ECMC and VB-SCN. Electr. Power Syst. Res. 2023, 218, 109–222. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, F.; Zhang, X.; Zhang, S. Series ac arc fault detection method based on hybrid time and frequency analysis and fully connected neural network. IEEE Trans. Ind. Inform. 2018, 15, 6210–6219. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, F.; Zhang, S. A new methodology for identifying arc fault by sparse representation and neural network. IEEE Trans. Instrum. Meas. 2018, 67, 2526–2537. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, Y.; Cao, Y.; Hou, C. Multi-feature fusion based diagnosis of series arc faults in ac system. Dianwang Jishu/Power Syst. Technol. 2014, 38, 795–801. [Google Scholar]
- Liu, X.; Zhao, Y.; Cao, Y.; Hou, C.; Wang, L. Series arc fault diagnosis based on wavelet transform in ac system. Diangong Jishu Xuebao/Trans. China Electrotech. Soc. 2014, 29, 10–17. [Google Scholar]
- Zhang, S.; Zhang, F.; Wang, Z.; Gu, H.; Ning, Q. Series arc fault identification method based on energy produced by wavelet transformation and neural network. Diangong Jishu Xuebao/Trans. China Electrotech. Soc. 2014, 29, 290–295. [Google Scholar]
- Han, X.; Li, D.; Huang, L.; Huang, H.; Yang, J.; Zhang, Y.; Wu, X.; Lu, Q. Series Arc Fault Detection Method Based on Category Recognition and Artificial Neural Network. Electronics 2020, 9, 1367. [Google Scholar] [CrossRef]
- Yu, Q.; Hu, Y.; Yang, Y. Identification Method for Series Arc Faults Based on Wavelet Transform and Deep Neural Network. Energies 2020, 13, 142. [Google Scholar] [CrossRef]
- Qu, N.; Zuo, J.; Chen, J.; Li, Z. Series arc fault detection of indoor power distribution system based on lvq-NN and PSO-SVM. IEEE Access 2019, 7, 184020–184028. [Google Scholar] [CrossRef]
- Yang, K.; Zhang, R.; Yang, J.; Du, J.; Chen, S.; Tu, R. Series arc fault diagnostic method based on fractal dimension and support vector machine. Diangong Jishu Xuebao/Trans. China Electrotech. Soc. 2016, 31, 70–77. [Google Scholar]
- Le, V.; Yao, X.; Miller, C.; Tsao, B.-H. Series DC Arc Fault Detection Based on Ensemble Machine Learning. IEEE Trans. Power Electron. 2020, 35, 7826–7839. [Google Scholar] [CrossRef]
- Chu, R.; Zhang, R.; Yang, K.; Jinchao, X. A series arc fault detection method based on multi-layer convolutional neural network. Dianwang Jishu/Power Syst. Technol. 2020, 44, 4792–4798. [Google Scholar]
- Chu, R.; Zhang, R.; Huang, Q.; Yang, K. TDI-LSTM: A new methodology for series arc fault detection in low power ac systems. In Proceedings of the 2020 IEEE Sustainable Power and Energy Conference (iSPEC), Chengdu, China, 25 November 2020; pp. 2319–2324. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Maaten, L.V.D.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Siege, J.E.; Pratt, S.; Sun, Y.; Sarma, S.E. Real-time Deep Neural Networks for internet-enabled arc-fault detection. Eng. Appl. Artif. Intell. 2018, 74, 35–42. [Google Scholar] [CrossRef]
- Kim, J.C.; Neacsu, D.O.; Ball, R.; Lehman, B. Clearing Series AC Arc Faults and Avoiding False Alarms Using Only Voltage Waveforms. IEEE Trans. Power Deliv. 2020, 35, 946–956. [Google Scholar] [CrossRef]
- Tisserand, E.; Lezama, J.; Schweitzer, P.; Berviller, Y. Series arcing detection by algebraic derivative of the current. Electr. Power Syst. Res. 2015, 119, 91–99. [Google Scholar] [CrossRef]

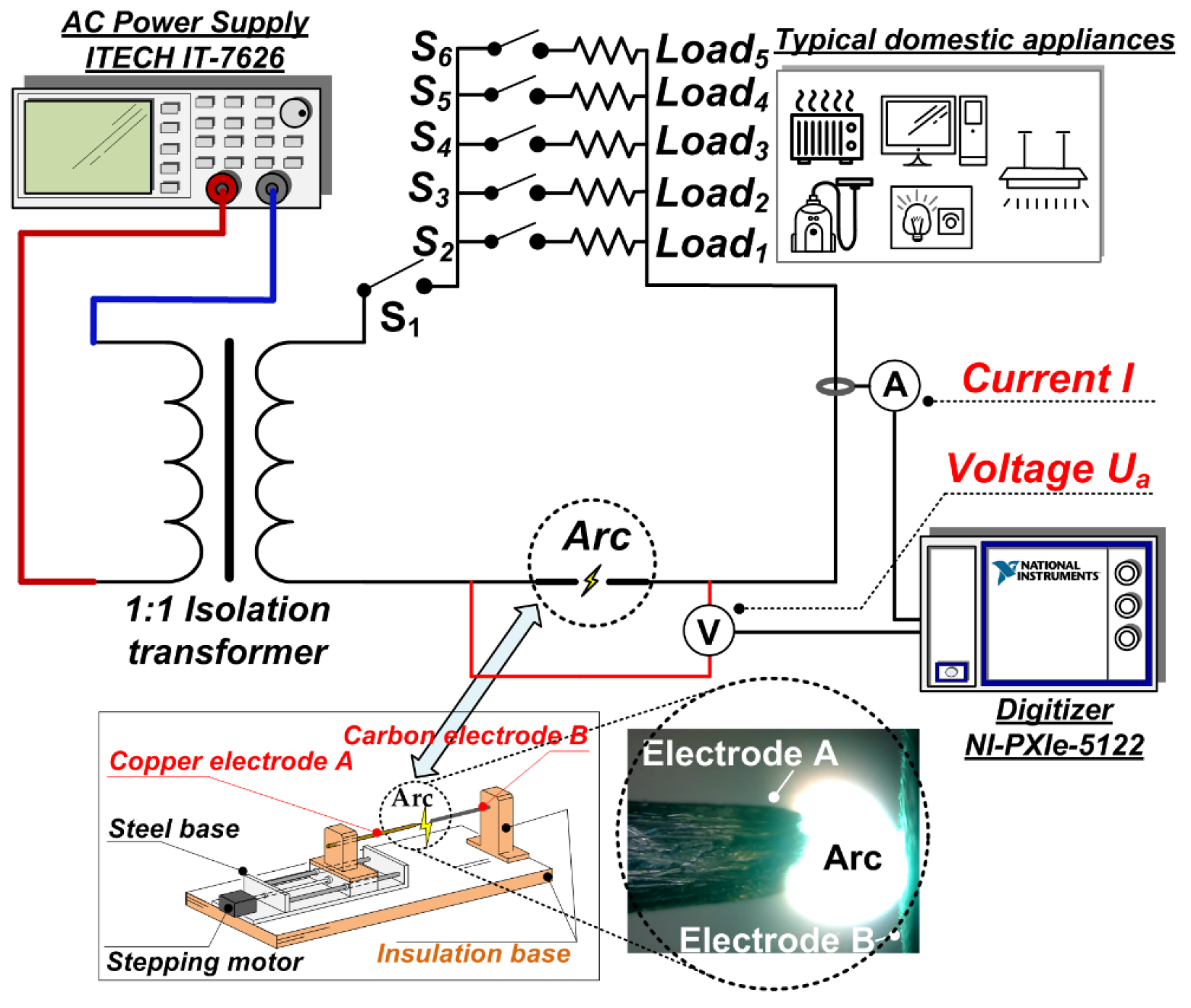

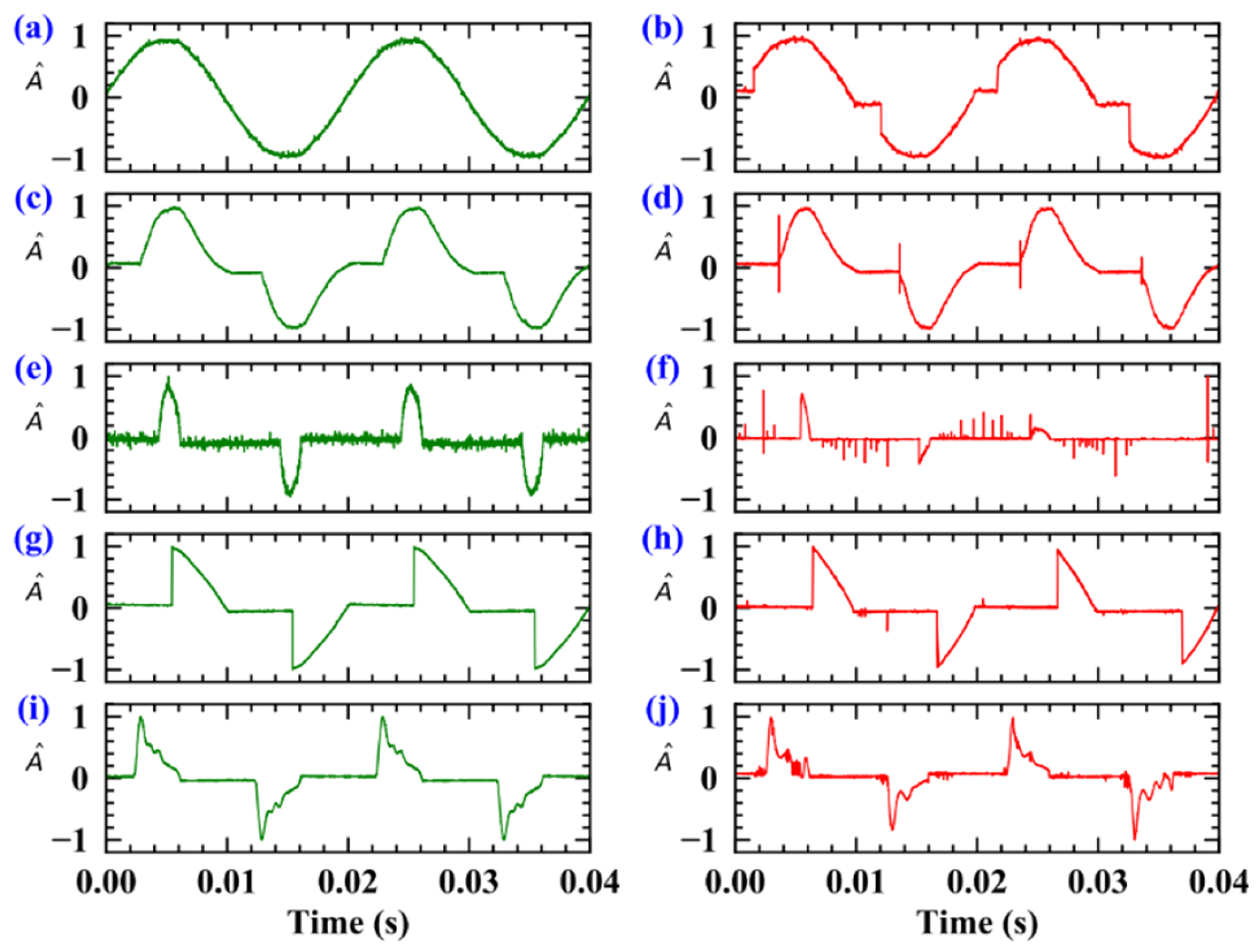
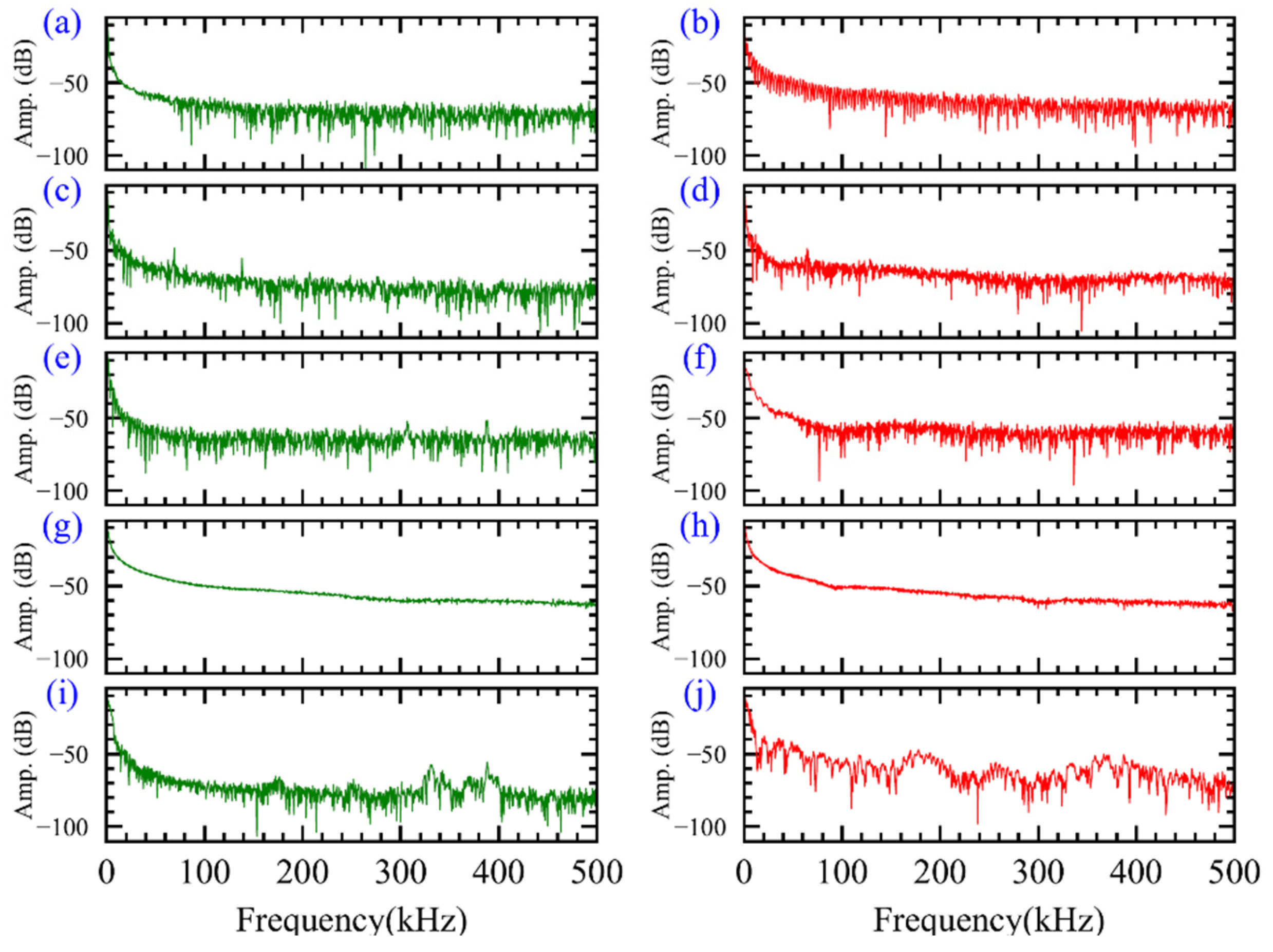
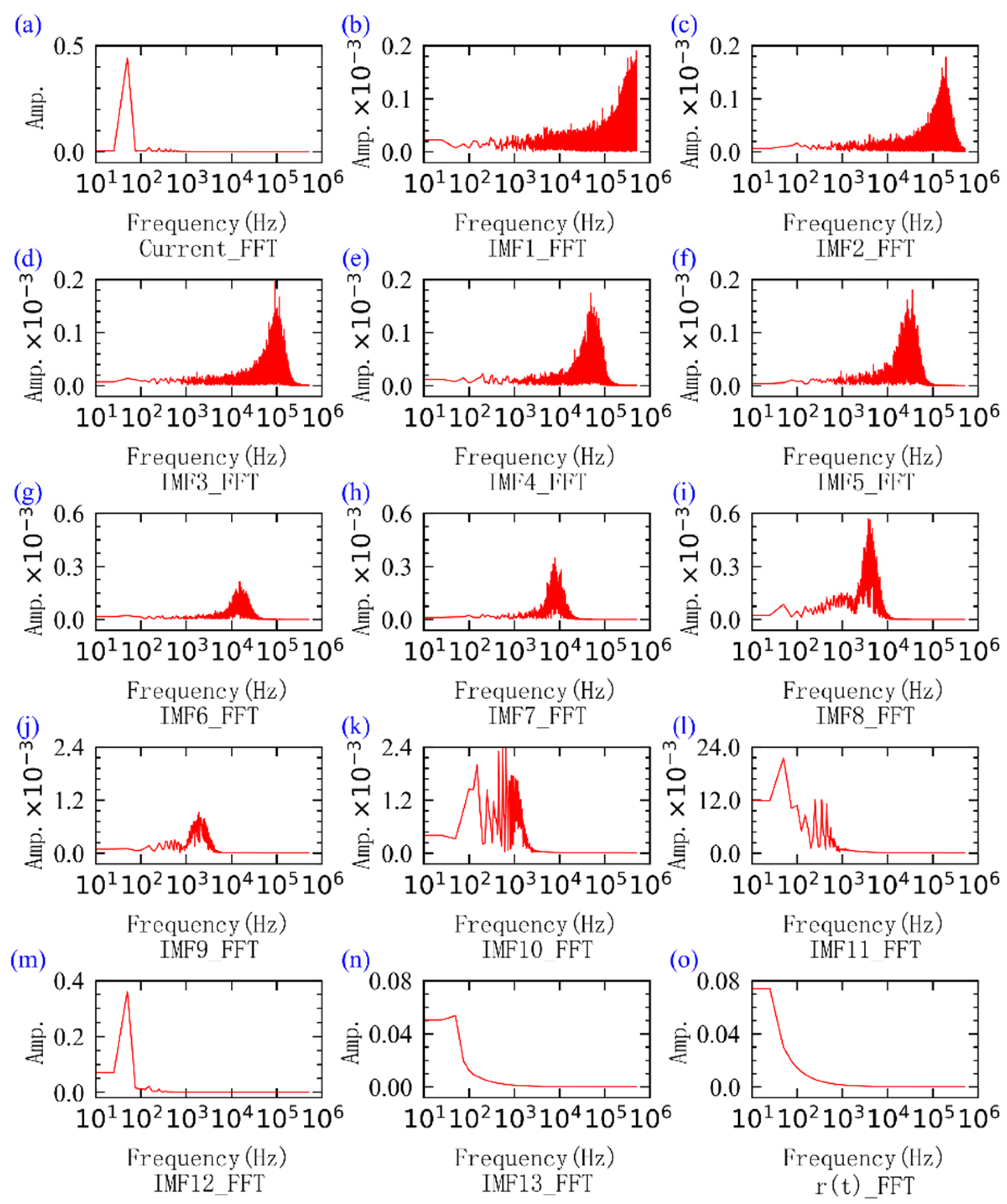





| Main Equipment | Mode | Characteristic | Manufacturer |
|---|---|---|---|
| Digitizer Module | PXIe-5122 | Bandwidth: 100 MHz Maximum sampling rate: 100 MS/s Analog input voltage: −10 V to 10 V Analog input resolution: 14 bits | National Instruments https://www.ni.com/zh-cn.html?srsltid=AfmBOopYU2sJmReat4pDG3KgCF7JxGRmgKKjM1dkenRGpU5pNb67zFzR (accessed on 5 August 2025) |
| Programmable AC Power Supply | IT-7626 | Output frequency: 10~5000 Hz, Output mode: AC, DC, AC+DC, Maximum power: 54 kVA, Voltage: 0~300 V | ITECH https://www.itechate.com/en/ (accessed on 5 August 2025) |
| Adjustable Electronic Load | IT-8616 | Frequency range: 45~450 Hz, Power range: 0–14.4 kVA, Voltage range: 15~260 Vrms, 50~420 Vrms, Current range: 0–160 Arms | ITECH |
| Current Sensor | N2783B | Bandwidth: DC to 100 MHz, Maximum current: 30 Arms, Accuracy: 1% | Keysight Technologies Santa Rosa, CA, USA https://www.keysight.com/us/en/home.html (accessed on 5 August 2025) |
| Label | 0 | 1 | 2 | 3 | 4 |
| Accuracy | 100% | 99% | 100% | 96% | 100% |
| Label | 5 | 6 | 7 | 8 | 9 |
| Accuracy | 96% | 99% | 93% | 100% | 99% |
| Average detection accuracy: 98.1% | |||||
| Ref. | Principle | Sampling Frequency | Application Range | Classify Load Type | Detection Accuracy |
|---|---|---|---|---|---|
| [3] | High-frequency coupling sensor and convolutional neural network. | 1 MHz | Resistive, inductive, capacitive, and switching loads. | ✓ | 99.2% |
| [18] | Apply the sparse coefficients to a single fully connected NN for load type and working state identification. | 25 kHz | Resistive, inductive, capacitive, and switching loads. | ✓ | Above 94.3% |
| [24] | Using the designed LVQ-NN and PSOSVM to detect the load type and arc fault, respectively. | 5 kHz | Resistive, inductive, capacitive, and switching loads. | ✓ | 95.5% |
| [32] | Deep neural networks (DNNs) taking Fourier coefficients, mel-frequency cepstrum data, and wavelet features as inputs. | 48 kHz | Resistive, capacitive, and switching loads, but no capacitive loads. | ✓ | 99.95% (the ozone generator represents a continuous series fault. |
| [33] | Method based only on the voltage waveform measured at the power source. | 500 kHz | Resistive, inductive, capacitive, and switching loads. | ✗ | Not introduced in the paper. |
| [34] | Compare the level of baseline and the output of the derivative estimation filter. | 1 MHz | Resistive and reactive loads, but no switching loads. | ✗ | Not introduced in the paper. |
| This work | TDI-LSTM | 1 MHz | Resistive, inductive, capacitive, and switching loads. | ✓ | 98.9% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chu, R.; Patrick, S.; Yang, K. Series Arc Fault Detection Method Based on Time Domain Imaging and Long Short-Term Memory Network for Residential Applications. Algorithms 2025, 18, 497. https://doi.org/10.3390/a18080497
Chu R, Patrick S, Yang K. Series Arc Fault Detection Method Based on Time Domain Imaging and Long Short-Term Memory Network for Residential Applications. Algorithms. 2025; 18(8):497. https://doi.org/10.3390/a18080497
Chicago/Turabian StyleChu, Ruobo, Schweitzer Patrick, and Kai Yang. 2025. "Series Arc Fault Detection Method Based on Time Domain Imaging and Long Short-Term Memory Network for Residential Applications" Algorithms 18, no. 8: 497. https://doi.org/10.3390/a18080497
APA StyleChu, R., Patrick, S., & Yang, K. (2025). Series Arc Fault Detection Method Based on Time Domain Imaging and Long Short-Term Memory Network for Residential Applications. Algorithms, 18(8), 497. https://doi.org/10.3390/a18080497









