Abstract
To meet the escalating demands of massive data transmission, the next generation of wireless networks will leverage the multi-access edge computing (MEC) architecture coupled with multi-access transmission technologies to enhance communication resource utilization. This paper presents queue stability-constrained reinforcement learning algorithms designed to optimize the transmission control mechanism in MEC systems to improve both throughput and reliability. We propose an analytical framework to model the queue stability. To increase transmission performance while maintaining queue stability, queueing delay model is designed to analyze the packet scheduling process by using the M/M/c queueing model and estimate the expected packet queueing delay. To handle the time-varying network environment, we introduce a queue stability constraint into the reinforcement learning reward function to jointly optimize latency and queue stability. The reinforcement learning algorithm is deployed at the MEC server to reduce the workload of central cloud servers. Simulation results validate that the proposed algorithm effectively controls queueing delay and average queue length while improving packet transmission success rates in dynamic MEC environments.
1. Introduction
With the rapid development of mobile communication technologies, the number of smart terminal devices has experienced exponential growth, posing significant challenges to existing network architectures [1,2]. Traditional centralized network architectures often struggle to meet the quality-of-service (QoS) requirements of low latency and high bandwidth when confronted with massive data transmission demands. Multi-access Edge Computing (MEC) technology effectively alleviates this issue by pushing computing capabilities to the network edge, providing nearby services for terminal devices. However, with the continuous emergence of new application scenarios, transmission stability and low-latency guarantees have become critical bottlenecks restricting the further development of MEC technology [3].
Multi-access data transmission, as a key enabler in MEC systems, significantly enhances system throughput, spectrum effectiveness, and transmission control by coordinatively utilizing the heterogeneous network access links [4]. The core of this technology lies in intelligently integrating various radios, including cellular networks (e.g., 4G/5G/6G) and wireless local area networks (Wi-Fi), to construct composite transmission resources and dynamically use them for data transmission [5].
In MEC environments, end-to-end latency during data exchange between edge servers and terminal devices can be decomposed into three parts: queueing delay (the time data packets wait in buffers for processing), transmission delay (the time data travels through wireless channels), and computation delay (the time edge servers take to execute computational tasks) [6,7]. Santos et al. [8] addressed the challenge of multi-mobile network operator interoperability among multi-access edge servers in MEC. A novel fully decentralized network architecture and orchestration algorithm is designed to reduce transmission latency and energy consumption. Qu et al. [9] introduced a new deep deterministic policy gradient algorithm for the problem of multi-user resource competition in MEC systems, where revenue-driven edge servers might prioritize larger tasks, potentially increasing delays or causing failures for other tasks. Chu et al. [10] tackled the NP-hard problem of maximizing user QoE through joint optimization of service caching, resource allocation, and task offloading/scheduling. A two-stage algorithm was designed to solve the problem efficiently. Zhang et al. [11] addresses computation rate maximization in MEC networks with hybrid access points. The deep reinforcement learning and Lagrangian duality-based method were applied to optimize offloading decisions and resource allocation time. In [12], Zhang et al. proposed a distributed Stackelberg game framework for resource allocation and task offloading in MEC-enabled cooperative intelligent transportation systems. A multi-agent reinforcement learning algorithm was designed to achieve Stackelberg equilibrium in dynamic environments.
Mao et al. [13] applied Lyapunov optimization theory [14] to transform the long-term energy consumption constraints of energy-limited devices into a series of instantaneous optimization problems, achieving latency minimization while ensuring energy efficiency. Ning et al. [15] adopted game-theoretic approaches, constructing Stackelberg game models or auction mechanisms to characterize the interaction between users and edge servers and realizing latency optimization based on Nash equilibrium solutions. Ren et al. [16] approached from the perspective of resource allocation, converting the joint computing and communication resource optimization problem into an equivalent convex optimization form and deriving closed-form optimal solutions. Although these traditional optimization methods can theoretically obtain optimal solutions, their computational complexity often fails to meet real-time requirements in practical dynamic network environments.
In recent years, with the groundbreaking advancements in Deep Reinforcement Learning (DRL), DRL-based optimization methods have demonstrated significant advantages. Wang et al. [17] formulated a latency minimization problem incorporating energy constraints and task deadlines, transformed it into a primal-dual optimization problem through Bellman equations, and implemented a decision-making process using reinforcement learning algorithms. Cui et al. [18] designed a reinforcement learning-based multi-platform intelligent offloading framework for vehicular networks, effectively reducing task processing latency. These innovative works have overcome the real-time limitations of traditional optimization methods.
The consideration of stability in MEC systems is critical due to the inherent challenges posed by dynamic network environments and QoS requirements. MEC systems, which decentralize computing resources to the network edge, must handle bursty traffic patterns, heterogeneous network conditions, and real-time latency constraints. Without stability guarantees, queue lengths in transmission buffers may grow unbounded, leading to increased packet loss, extended queueing delays, and degraded system performance. This paper presents queue stability-constrained deep reinforcement learning algorithms for adaptive transmission control in MEC systems, addressing the dual challenge of optimizing throughput while ensuring queue stability in dynamic network environments. We first develop an analytical framework based on the M/M/c queueing model to estimate packet queueing delay and derive stability conditions, providing a theoretical foundation for transmission control. To adapt to time-varying network conditions, we integrate queue stability constraints into the reinforcement learning reward function, enabling joint optimization of latency and system stability. The proposed algorithm, deployed at the edge server, dynamically manages multi-access transmission without relying on centralized cloud control. Our proposed algorithms share a common theoretical foundation with Lyapunov optimization, as both aim to ensure network stability while optimizing transmission performance. However, our approach differs in its adaptability and scalability in dynamic MEC environments. While Lyapunov optimization relies on analytical derivations to transform long-term constraints into deterministic per-slot problems, our DRL-based algorithms learn optimal control policies directly from environmental interactions, eliminating the need for explicit model knowledge or convexity assumptions.
2. Proposed System Model
2.1. Multi-Access Transmission Scheme
The proposed system architecture, as shown in Figure 1, comprises a hierarchical network structure integrating a core network, backhaul links, multi-radio access points with embedded MEC capabilities, and heterogeneous mobile devices equipped with multiple wireless access links, including 4G, 5G and Wi-Fi [1]. In this framework, mobile devices leverage edge computing resources for both data processing and storage while generating substantial uplink/downlink traffic flows.
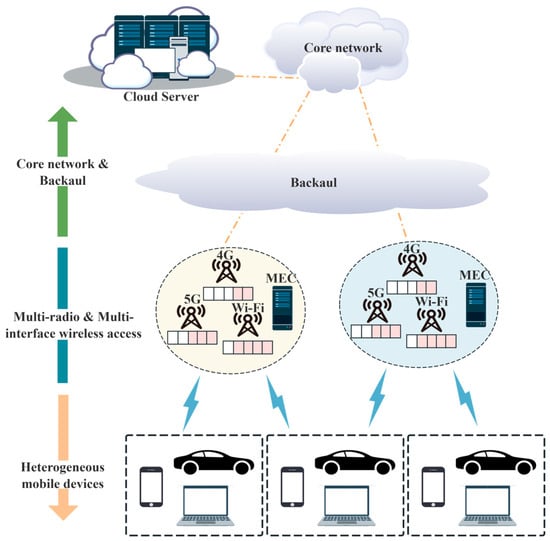
Figure 1.
Multi-access transmission scheme.
To accommodate growing data transmission demands in the edge-device communication path, the system dynamically aggregates bandwidth across multiple available network links (e.g., 5G and Wi-Fi) through simultaneous multi-access transmission [2]. The edge server implements a queue-based control mechanism where each network access link maintains dedicated transmission queues with carefully regulated queue sizes. This integrated approach enables optimization of multiple performance metrics, including queueing delay, transmission reliability, and resource utilization efficiency, particularly crucial when handling bursty traffic patterns across heterogeneous network links.
2.2. Queue Stability and Queueing Delay Model
In the proposed multi-access transmission scheme, improper queue allocation decisions may result in packet assignments exceeding the maximum transmission capacity of the network link, potentially causing packet loss and degraded system performance. To address this challenge, we establish a queue stability model based on queueing theory [19]. Queue stability refers to the condition where the long-term average of queue length remains finite, ensuring the transmission system will not collapse due to task backlogs. By referencing [20], the strong queue stability is defined as follows: A queue is considered strongly stable if its length q(τ) satisfies the condition that its average length remains bounded.
We introduce queue stability constraints into the optimal packet scheduling problem for each network link, aiming to minimize the transmission delay while maintaining queue stability. The optimization problem can be formulated as follows:
where stands for the portions of packet allocation to each queue, and represents the queueing delay of all network links to be optimized. The constraint indicates the requirements for all queues in the system to be strongly stable as an optimization condition. Directly solving this problem presents significant challenges. Traditional methods typically address this by combining the objective function and constraint through weighted factors into a single optimization function, which can be expressed as
where n represents the number of network links. is for the queue length of link i, and the exponential term v adjusts the impact of queue length variations on the optimization function. A and B are positive weighting factors that balance the importance between queue stability and penalty terms. By minimizing this function, we can simultaneously maintain queue stability while minimizing system average penalties. However, solving for the optimal solution at each time step often encounters issues such as high computational complexity, potential non-convex optimization problems making global optima difficult to obtain, and suboptimal performance in dynamic environments. Deep reinforcement learning proves to be an effective tool for addressing such challenges. Below we provide a theoretical explanation for incorporating the optimization function into the reward function of reinforcement learning algorithms.
Assuming all queues start with the length of zero. For finite constants and , the reward function at time satisfies Equation (4). The control policy adopted by the agent will guarantee queue system stability [20].
Furthermore, if the reward function has a lower bound as specified in Equation (5), then queues governed by an agent with such reward function characteristics will be strongly stable.
Thus, the reward function can be reformulated as [19]
where and ; in practical reinforcement learning applications, the discount factor is typically used instead of .
Key components of the queueing delay model include (1) the birth-death process formulation that characterizes state transitions in the multi-access queueing system, (2) the application of Little’s Law to establish the fundamental relationship between average queue length, arrival rate, and waiting time, and (3) the extension of the basic M/M/c model to accommodate time-varying arrival rates and service rates, enabling adaptation to dynamic network conditions. The first-come-first-served (FCFS) is applied for the queue management.
Figure 2 illustrates the birth-death process characterizing packet arrivals and departures in the multi-access queueing system. In the M/M/c model, λ represents the arrival rate as the average number of packets arriving per unit time, μ denotes the service rate that is the average number of packets successfully transmitted per unit time, and their ratio constitutes the traffic intensity [21].

Figure 2.
Birth–death process of the queuing model.
Through cumulative multiplication and summation of probabilities, we obtain the average queue length
According to Little’s Law [22], the average delay can be derived as
Thus, the average queue delay of packets in the entire multi-access data transmission system is given as
3. Queue Stability-Constrained Deep Reinforcement Learning Approach for Adaptive Transmission Control
This section first clarifies the optimization problem to be addressed and formulates it as a Markov Decision Process (MDP) [23]. Subsequently, we present Deep Q-Learning (DQN) and Proximal Policy Optimization (PPO) algorithms specifically designed for multi-access data transmission to solve the packet allocation decision-making problem.
3.1. Description of Optimization Function
The optimization objective is to minimize the average waiting delay of packets in queues while maintaining stability in the multi-access data transmission system. Specifically, the objective function can be expressed as
To simulate packet arrival patterns in networks, we assume the packet size follows a negative exponential distribution, where represents the packet arrival rate of the multi-access transmission system at time t. The bandwidth of network link i is denoted as . The independent variables of the objective function can be represented as the allocation ratio of arrived packets to each network link. The number of packets enqueued and dequeued at link i during time t are denoted as and , respectively. The queue length at the next time step can be expressed by Equation (11).
The average waiting delay of packets in the multi-access transmission system is
Thus, the objective function can be rewritten as
Solving such a complex objective function presents significant challenges. Therefore, the next section will transform this optimization problem into a sequential decision-making formulation and employ deep reinforcement learning algorithms to learn optimal data transmission policies.
3.2. Modeling Data Transmission Control Using Markov Decision Processes
Deep reinforcement learning has been widely employed to address complex problems requiring sequential decision-making. These algorithms typically utilize MDP [23] to simulate the interaction between agents and their environment. Within this framework, agents select actions based on their understanding of the current environmental state and optimize subsequent decisions through environmental feedback, including reward signals and the state transitions. We transform the optimization problem into a sequential decision-making format and employ deep reinforcement learning to train agents in acquiring optimal packet allocation strategies. Specifically, we model the edge server as an agent and formulate the optimization problem as an MDP comprising three key components: state space, action space, and reward function.
State Space : , where is 4G, 5G, Wi-Fi links. represents the queue length of link i, denotes the bandwidth of link i, indicates the delay of link i, signifies the traffic intensity of link i, represents the queue input rate, and represents the queue output rate.
Action Space : , represents the actions executed by the edge server, specifically the packet allocation decisions made based on current environmental states. Formally, it denotes the proportion of arrived packets allocated to each network link at time t. Since all arrived packets at time t must be allocated, the following constraint applies: .
Reward Function reflects the immediate return when the agent takes the action in state , and is directly related to the optimization objective. Given our goal of minimizing data transmission delay under queue stability constraints, we define the reward function as Equation (14):
where represents the average packet waiting delay at current time t, and and denote the reward weights for queue stability and delay, respectively.
3.3. Reinforcement Learning Algorithms for Adaptive Transmission Control
For different types of problems, the reinforcement learning algorithms can be classified for discrete action space and continuous action space. DQN [24] is a representative reinforcement learning algorithm for discrete action spaces, while PPO [25] is designed to address continuous action space problems. To comprehensively analyze algorithm performance, we design DQN and PPO algorithms, respectively, for multi-access data transmission and conduct comparative experiments.
3.3.1. DQN-Based Multi-Access Data Transmission Algorithm
In the multi-access data transmission scenario, the action space is continuous, which represents the proportional allocation of data packets to network links. However, the DQN algorithm is fundamentally designed for discrete action spaces. This problem is addressed by mapping the continuous action space to a finite set of discrete actions, enabling dynamic decision-making for multi-access data transmission.
To accommodate DQN’s discrete action characteristics, we discretize the continuous action space. The system incorporates three network links (4G, 5G, Wi-Fi), with each link’s allocation ratio constrained by . Each link’s allocation proportion is divided into K discrete levels (e.g., K = 30). The global action set is generated by combining all possible discrete levels across network links.
State space includes real-time queue length of each network link, bandwidth, current delay and traffic intensity. The reward function combines queue stability and delay optimization objectives, formulated as Equation (14).
The algorithm procedure begins with initializing parameters for both the main network and target network . Actions are selected according to an ε-greedy policy. After action execution, the agent observes the reward and new state, storing the experience (s, a, r, s’) in the experience replay buffer. When sufficient data accumulates in the buffer, mini-batch samples are drawn to compute target Q-values. The main network parameters are then updated using a mean squared error loss function. Periodically, the target network parameters are synchronized with the main network parameters. The detail of the algorithm is presented in Algorithm 1.
| Algorithm 1. Multi-Access Data Transmission Algorithm Based on DQN |
| Input: State space S, action space A, exploration parameter ε, discount factor γ Output: Packet allocation policy π |
| 1: Initialize: Experience replay buffer, main network weights, target network weights 2: do: do: 4: Select allocation ratios from discretized action space using ε-greedy policy 5: Execute action, observe reward and next state 6: 7: , compute TD target 8: 9: , and update θ 10: Every C steps: Synchronize target network θ′ ← θ 11: end for 12: end for |
3.3.2. PPO-Based Multi-Access Data Transmission Algorithm
For reinforcement learning problems with continuous action spaces, policy gradient methods can directly optimize policy parameters, avoiding the accuracy loss issue caused by action space discretization. As an improved variant of policy gradient algorithms, PPO significantly enhances training stability and sample efficiency through importance sampling and clipping mechanisms, making it particularly suitable for continuous action space optimization in dynamic network environments. We customize the PPO algorithm to achieve an optimal multi-access data transmission strategy.
The core concept of PPO is to constrain policy update steps to prevent training instability caused by abrupt policy changes. It employs an Actor-Critic [26] architecture where the actor network (policy network) generates action distributions. The critic network (value network) evaluates state values to guide policy optimization [27]. In the multi-access data transmission scenario, PPO learns optimal data allocation strategies through environmental interactions, dynamically adjusting allocation ratios across network links to minimize transmission delay while maintaining queue stability.
State space includes real-time queue length per link, bandwidth, current delay and traffic intensity. The reward function combines queue stability and delay optimization objectives, formulated as Equation (14).
The training procedure of the PPO algorithm consists of four key steps. The agent executes its current policy in the environment, collects trajectory samples and stores experiences in a buffer for batch processing. The advantage function is calculated as:
The detail of the algorithm is presented in Algorithm 2.
| Algorithm 2. Multi-Access Data Transmission Algorithm Based on PPO |
for network links |
| 1: Initialize: Policy parameters and value function parameters 2: do: 3: Collect trajectories using current policy 4: Compute advantages function using collected trajectories 5: do: 6: do: 7: 8: 9: Calculate entropy and update parameters 10: end for 11: end for 12: Compute optimal allocation ratio 13: Update old policy parameters 14: end for |
4. Experimental Results and Performance Analysis
In this section, we present the simulation environment configuration and parameters, followed by a detailed analysis of algorithm performance metrics, including convergence behavior, transmission success rate, average transmission delay, and mean queue length. Key simulation parameters are specified in Table 1.

Table 1.
Simulation parameters.
4.1. Simulation Setup
The simulation setup for evaluating the proposed algorithms is configured as follows: The maximum queue length is set to 2000 packets with a tail-drop policy for queue management. Packet arrivals follow a Poisson distribution with an average rate of 500 ± 50 packets per time step to simulate realistic traffic patterns. The service time distribution for each network link (4G, 5G, and Wi-Fi) follows an exponential distribution with mean bandwidths of 150 Mbps, 300 Mbps, and 400 Mbps, respectively, reflecting typical heterogeneous network conditions. The reinforcement learning algorithm employs a discount factor of 0.98 and a learning rate of 0.01, with policy and value networks implemented as 64 × 64 and 16 × 16 fully connected architectures using Tanh activation functions. The PPO algorithm incorporates a clipping range of [0.85, 1.15] to ensure stable policy updates, while the optimization process utilizes mean squared error loss as the loss function for training steps.
4.2. Results and Performance Analysis
Figure 3 compares the total reward of the DQN and PPO algorithms. As the number of iterations increases, the cumulative reward value of the PPO algorithm gradually rises and stabilizes, while the DQN algorithm shows increasing reward values but with lower stability compared to the PPO. The PPO algorithm achieves higher reward values, indicating its superior performance in metrics including transmission success rate, average delay, and average queue length. The fundamental reason lies in their methodological differences in two algorithms. The DQN algorithm discretizes the action space and can only explore coarse-grained actions. The PPO algorithm is able to obtain optimal policy by exploring fine-grained action space. For the DQN algorithm, the optimal action may lie outside the discrete action space. Due to this algorithmic characteristic, the cumulative reward achieved by DQN is lower than that of PPO.
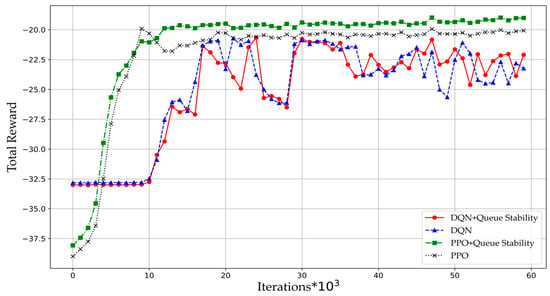
Figure 3.
Total reward of the DQN and PPO algorithms.
Figure 4 shows the variation in average packet queueing delay across different algorithms with increasing iterations. When stabilized, both PPO and PPO with queue stability constraints (PPO-QS) demonstrate significantly lower average delays than DQN and DQN-QS. Specifically, PPO-QS reduces average waiting delay by 16.38% and 15.98% compared to DQN and DQN-QS, respectively, while standard PPO decreases by 13.31% and 12.9% versus DQN and DQN-QS, respectively. Among comparable algorithms, deep reinforcement learning methods with queue stability constraints consistently outperform baseline algorithms. However, for DQN and DQN-QS, the performance difference in average delay is marginal due to the inherent limitations of coarse-grained action space. For PPO algorithms specifically, PPO-QS reduces average waiting delay by 3.62% compared to standard PPO. The queue stability constraint effectively reduces average transmission delay because the constraint makes the agent focus on queue traffic intensity, balances traffic load across queues, consequently improves transmission efficiency, and ultimately reduces overall delay.
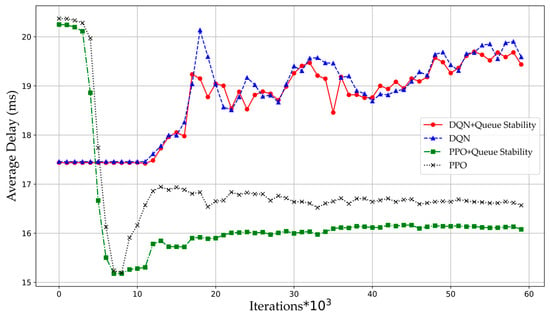
Figure 4.
Average queueing delay between the DQN and PPO algorithms.
Figure 5 illustrates the variation in packet transmission success rates across different algorithms as iterations progress. The PPO and PPO-QS algorithms exhibit a gradual increase in transmission success rates, eventually stabilizing at high performance levels. In contrast, while the DQN and DQN-QS algorithms also show improving success rates with iterations, their performance fails to stabilize due to the inherent limitations of discrete action spaces. This characteristic enables PPO and PPO-QS algorithms to explore a broader range of actions and identify optimal decisions in dynamic network environments. Experimental results demonstrate that PPO and PPO-QS achieve approximately 6.5% higher transmission success rates compared to DQN and DQN-QS.
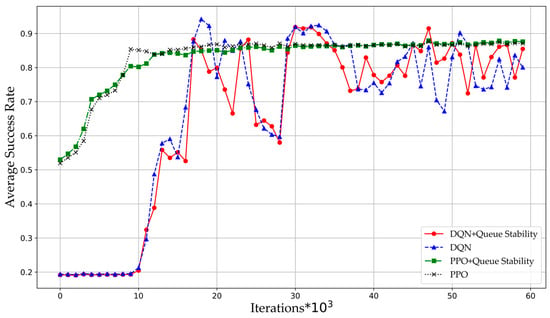
Figure 5.
Average success rate between the DQN and PPO algorithms.
Figure 6 presents the evolution of average queue lengths for different algorithms during experiments. The incorporation of queue stability constraints directs the agent to monitor traffic intensity across transmission queues. By integrating traffic intensity metrics with other state indicators, the agent makes balanced decisions through the reward function to maximize expected returns. Consequently, algorithms with queue stability constraints—both DQN-QS and PPO-QS—consistently maintain shorter average queue lengths than their baseline counterparts. This improvement is further reflected in reduced average packet delays, and ultimately lower end-to-end latency.
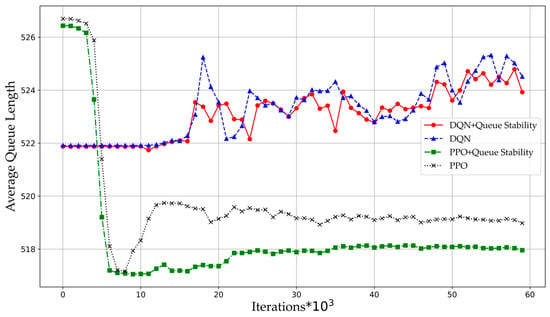
Figure 6.
Average queue length between the DQN and PPO algorithms.
5. Conclusions
This paper presents queue stability-constrained deep reinforcement learning algorithms to optimize multi-access transmission control in MEC systems, effectively addressing the dual challenges of latency minimization and queue stability. By incorporating a queue stability constraint into the DRL reward function and leveraging an M/M/c queueing model for delay estimation, the proposed framework dynamically optimizes link selection while maintaining system stability under time-varying network conditions. Our DRL-based approach enables efficient deployment at MEC servers without relying on centralized load balancing. Simulation results demonstrate that the algorithm achieves a 16.38% reduction in average queueing delay and a 6.5% improvement in transmission success rate compared to conventional methods, while robustly stabilizing queue lengths under dynamic traffic loads. These findings validate the effectiveness of integrating stability constraints into DRL for MEC-based multi-access transmission, offering a scalable solution for future heterogeneous networks. Further research will explore extensions to energy-efficient transmission and ultra-dense network scenarios.
Author Contributions
Conceptualization, L.H. and Y.L.; methodology, T.Z.; software, T.Z.; validation, J.Z.; formal analysis, G.L.; investigation, X.B.; resources, L.H.; data curation, T.Z.; writing—original draft preparation, L.H. and T.Z.; writing—review and editing, G.L.; visualization, J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data sharing is not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sylla, T.; Mendiboure, L.; Maaloul, S.; Aniss, H.; Chalouf, M.A.; Delbruel, S. Multi-Connectivity for 5G Networks and Beyond: A Survey. Sensors 2022, 22, 7591. [Google Scholar] [CrossRef]
- Subhan, F.E.; Yaqoob, A.; Muntean, C.H.; Muntean, G.-M. A Survey on Artificial Intelligence Techniques for Improved Rich Media Content Delivery in a 5G and Beyond Network Slicing Context. IEEE Commun. Surv. Tutor. 2025, 27, 1427–1487. [Google Scholar] [CrossRef]
- He, Z.; Li, L.; Lin, Z.; Dong, Y.; Qin, J.; Li, K. Joint Optimization of Service Migration and Resource Allocation in Mobile Edge–Cloud Computing. Algorithms 2024, 17, 370. [Google Scholar] [CrossRef]
- Jun, S.; Choi, Y.S.; Chung, H. A Study on Mobility Enhancement in 3GPP Multi-Radio Multi-Connectivity. In Proceedings of the 2024 15th International Conference on Information and Communication Technology Convergence (ICTC), Jeju Island, Republic of Korea, 16–18 October 2024; IEEE: Jeju Island, Republic of Korea, 2024; pp. 1347–1348. [Google Scholar]
- Rahman, M.H.; Chowdhury, M.R.; Sultana, A.; Tripathi, A.; Silva, A.P.D. Deep Learning Based Uplink Power Allocation in Multi-Radio Dual Connectivity Heterogeneous Wireless Networks. In Proceedings of the 2024 IEEE 35th International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), Valencia, Spain, 2–5 September 2024; IEEE: Valencia, Spain, 2024; pp. 1–6. [Google Scholar]
- Han, L.; Li, S.; Ao, C.; Liu, Y.; Liu, G.; Zhang, Y.; Zhao, J. MEC-Based Cooperative Multimedia Caching Mechanism for the Internet of Vehicles. Wirel. Commun. Mob. Comput. 2022, 2022, 1–10. [Google Scholar] [CrossRef]
- Zhang, Y.; He, X.; Xing, J.; Li, W.; Seah, W.K.G. Load-Balanced Offloading of Multiple Task Types for Mobile Edge Computing in IoT. Internet Things 2024, 28, 101385. [Google Scholar] [CrossRef]
- Santos, D.; Chi, H.R.; Almeida, J.; Silva, R.; Perdigão, A.; Corujo, D.; Ferreira, J.; Aguiar, R.L. Fully-Decentralized Multi-MNO Interoperability of MEC-Enabled Cooperative Autonomous Mobility. IEEE Trans. Consum. Electron. 2025, 1, 1. [Google Scholar] [CrossRef]
- Qu, B.; Bai, Y.; Chu, Y.; Wang, L.; Yu, F.; Li, X. Resource Allocation for MEC System with Multi-Users Resource Competition Based on Deep Reinforcement Learning Approach. Comput. Netw. 2022, 215, 109181. [Google Scholar] [CrossRef]
- Chu, W.; Jia, X.; Yu, Z.; Lui, J.C.S.; Lin, Y. Joint Service Caching, Resource Allocation and Task Offloading for MEC-Based Networks: A Multi-Layer Optimization Approach. IEEE Trans. Mob. Comput. 2024, 23, 2958–2975. [Google Scholar] [CrossRef]
- Zhang, S.; Bao, S.; Chi, K.; Yu, K.; Mumtaz, S. DRL-Based Computation Rate Maximization for Wireless Powered Multi-AP Edge Computing. IEEE Trans. Commun. 2024, 72, 1105–1118. [Google Scholar] [CrossRef]
- Zhang, S.; Tong, X.; Chi, K.; Gao, W.; Chen, X.; Shi, Z. Stackelberg Game-Based Multi-Agent Algorithm for Resource Allocation and Task Offloading in MEC-Enabled C-ITS. IEEE Trans. Intell. Transport. Syst. 2025, 1–12. [Google Scholar] [CrossRef]
- Mao, Y.; Zhang, J.; Letaief, K.B. Dynamic Computation Offloading for Mobile-Edge Computing with Energy Harvesting Devices. IEEE J. Select. Areas Commun. 2016, 34, 3590–3605. [Google Scholar] [CrossRef]
- Dai, L.; Mei, J.; Yang, Z.; Tong, Z.; Zeng, C.; Li, K. Lyapunov-Guided Deep Reinforcement Learning for Delay-Aware Online Task Offloading in MEC Systems. J. Syst. Archit. 2024, 153, 103194. [Google Scholar] [CrossRef]
- Ning, Z.; Dong, P.; Kong, X.; Xia, F. A Cooperative Partial Computation Offloading Scheme for Mobile Edge Computing Enabled Internet of Things. IEEE Internet Things J. 2019, 6, 4804–4814. [Google Scholar] [CrossRef]
- Ren, J.; Yu, G.; He, Y.; Li, G.Y. Collaborative Cloud and Edge Computing for Latency Minimization. IEEE Trans. Veh. Technol. 2019, 68, 5031–5044. [Google Scholar] [CrossRef]
- Wang, X.; Ning, Z.; Guo, L.; Guo, S.; Gao, X.; Wang, G. Online Learning for Distributed Computation Offloading in Wireless Powered Mobile Edge Computing Networks. IEEE Trans. Parallel Distrib. Syst. 2022, 33, 1841–1855. [Google Scholar] [CrossRef]
- Cui, Y.; Liang, Y.; Wang, R. Resource Allocation Algorithm with Multi-Platform Intelligent Offloading in D2D-Enabled Vehicular Networks. IEEE Access 2019, 7, 21246–21253. [Google Scholar] [CrossRef]
- Bae, S.; Han, S.; Sung, Y. A Reinforcement Learning Formulation of the Lyapunov Optimization: Application to Edge Computing Systems with Queue Stability. arXiv 2020. [Google Scholar] [CrossRef]
- Wu, Q.; Wang, W.; Fan, P.; Fan, Q.; Wang, J.; Letaief, K.B. URLLC-Awared Resource Allocation for Heterogeneous Vehicular Edge Computing. IEEE Trans. Veh. Technol. 2024, 73, 11789–11805. [Google Scholar] [CrossRef]
- Keramidi, I.; Uzunidis, D.; Moscholios, I.; Logothetis, M.; Sarigiannidis, P. Analytical Modelling of a Vehicular Ad Hoc Network Using Queueing Theory Models and the Notion of Channel Availability. AEU-Int. J. Electron. Commun. 2023, 170, 154811. [Google Scholar] [CrossRef]
- Wu, G.; Xu, Z.; Zhang, H.; Shen, S.; Yu, S. Multi-Agent DRL for Joint Completion Delay and Energy Consumption with Queuing Theory in MEC-Based IIoT. J. Parallel Distrib. Comput. 2023, 176, 80–94. [Google Scholar] [CrossRef]
- Zhang, J.; Bao, B.; Wang, C.; Zhu, F. Shapley Value-Driven Multi-Modal Deep Reinforcement Learning for Complex Decision-Making. Neural Netw. 2025, 191, 107650. [Google Scholar] [CrossRef] [PubMed]
- Femminella, M.; Reali, G. Comparison of Reinforcement Learning Algorithms for Edge Computing Applications Deployed by Serverless Technologies. Algorithms 2024, 17, 320. [Google Scholar] [CrossRef]
- Yuan, M.; Yu, Q.; Zhang, L.; Lu, S.; Li, Z.; Pei, F. Deep Reinforcement Learning Based Proximal Policy Optimization Algorithm for Dynamic Job Shop Scheduling. Comput. Oper. Res. 2025, 183, 107149. [Google Scholar] [CrossRef]
- Kumar, P.; Hota, L.; Nayak, B.P.; Kumar, A. An Adaptive Contention Window Using Actor-Critic Reinforcement Learning Algorithm for Vehicular Ad-Hoc NETworks. Procedia Comput. Sci. 2024, 235, 3045–3054. [Google Scholar] [CrossRef]
- Chen, Z.; Maguluri, S.T. An Approximate Policy Iteration Viewpoint of Actor–Critic Algorithms. Automatica 2025, 179, 112395. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).