1. Introduction
Numerous problems in science and engineering can be effectively modeled using linear and nonlinear mathematical equations [
1,
2,
3]. However, unlike linear equations, finding exact solutions to nonlinear equations is not feasible. Therefore, we have to rely on iterative methods to find approximate solutions to such equations. One of the most prominent iterative methods is Newton’s method [
4], which has a quadratic convergence.
In recent years, considerable efforts have been made to improve the convergence properties of iterative methods, aiming for higher convergence rate and better computational efficiency [
1,
5,
6,
7,
8,
9]. Many of these methods are extensions or modifications of Newton’s method [
10,
11,
12] and have been applied to both single-variable and multi-variable nonlinear equations.
The order of convergence of an iterative method is a key measure of its efficiency, which indicates how rapidly the method converges to the solution. We say that a sequence
converges to
with the order of convergence at least
[
13,
14,
15] if there exists a constant
such that
The efficiency index (EI) and informational efficiency (IE) are two metrics to evaluate and compare the performance of iterative methods. Ostrowski [
16] has introduced EI as
and Traub [
14] has introduced IE as
where
p is the order of convergence and
is the total number of functions and derivative evaluations per iteration.
We consider that the primary goal of the iterative method is to improve the convergence speed while enhancing the accuracy and overall efficiency of the method.
In this paper, we focus on the convergence analysis of iterative methods for solving equations of the form
where
is a nonlinear operator from Banach space
X into Banach space
Y, and
is a non-empty open convex set.
The multi-step method for solving nonlinear systems given by Raziyeh and Masoud [
17] is defined for
and
such that
where
The iterative method (
3) has a convergence order 5, which is studied in [
17] using Taylor series expansion, and requires the assumption that the operator F is at least six times differentiable. These restrictions are the motivations for our study. It is shown in [
17] that the method (
3) is highly efficient and superior to the earlier methods. A comparison with other methods in terms of efficiency has been given in [
17]. If we follow the analysis made in [
17], then the method (
3) cannot be used to approximate the solution of (
2) if
F cannot be differentiated six times. For example, consider
defined as
where
and
are real parameters. Notice that
solves the equation
Further, notice the unboundedness of
on the interval
since
does not exists at
Thus, the method (
3) cannot assure the convergence of
to the solution
if we use the analysis in [
17]. However, method (
3) does converge to
if, e.g.,
,
, and
and the initial guess
We have studied the convergence of the method (
3) without using the Taylor series. Thus, our study relaxes the condition that
F has to be six times differentiable and requires
F to be just two times differentiable. The innovative aspects and advantages of our analysis are as follows:
Our analysis is discussed in the Banach space setting.
We have given the semi-local analysis in our studies, which was not given in earlier work [
17].
Earlier studies [
17,
18] rely on assumptions involving the solution for local convergence analysis. However, our assumptions for attaining the convergence order are independent of the solution.
In the existing studies, the assumptions depend on the actual solution , but our assumptions are independent of the solution . Using the information about obtained from semi-local analysis, we study the convergence order using local convergence.
This paper is arranged as follows:
Section 2 contains the semi-local convergence analysis of the method (
3).
Section 3 contains the local convergence of the method (
3) without using the Taylor series expansion.
Section 4 and
Section 5 contain numerical examples and the basins of attraction of the method, respectively. The conclusion is given in
Section 6.
2. Semi-Local Analysis
We will define scalar majorizing sequences for our semi-local analysis [
4].
For
and
define the scalar sequences
and
such that
Lemma 1. Assume there exists such thatThen, the sequences and defined by (4) are convergent to some and Proof. The scalar sequences and are non-decreasing and bounded above . Hence, such that and converges to □
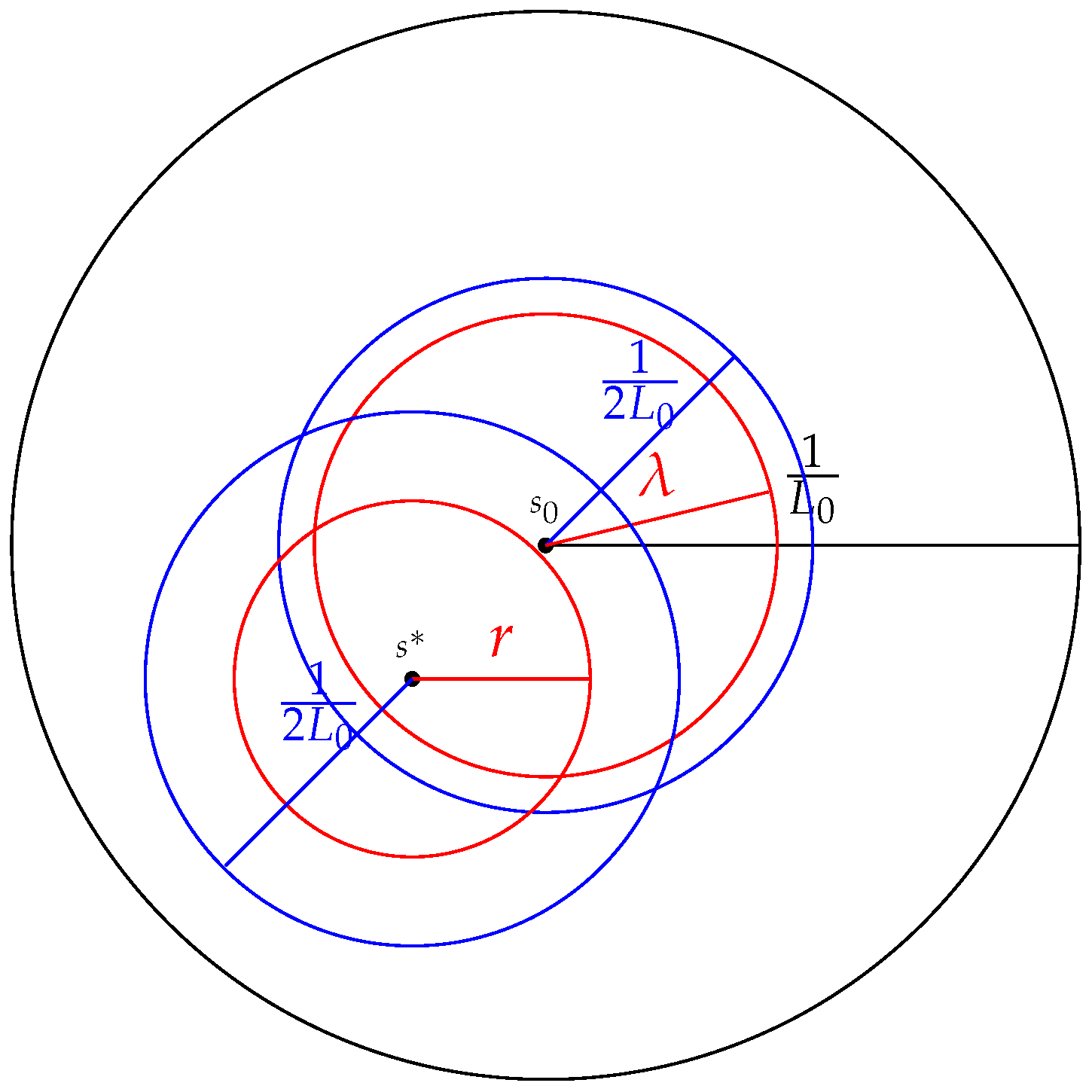
Let be the ball centered at s with radius r and be its closure.
For the convergence analysis, we use the following assumptions.
∃ an initial point such that .
There exist an operator
(the set of all bounded linear operators from
X to
Y) and constant
with
Set .
There exists a constant
with
.
From assumption
, we have
and hence by Banach Lemma (BL) on invertible operators [
4], we get
and
Further, we will be using the following mean value theorem (MVT) [
4]:
Next, the main semi-local result uses the conditions
–
.
Theorem 1. Under the assumptions , the sequence defined by method (3) with satisfiesandMoreover, the sequence converges to some with Proof. We will be using mathematical induction to prove the result.
Using
and first step of (
3),
Thus,
and (
9) is true for
Using MVT, (
8) and the first step of (
3), we have
Using the assumption
and (
7), we get
Similarly,
So, by using assumption (
), (
7) and (
11), we have
where we used
Similarly using assumption
, (
7) and (
11) we get
Next, using (
11)–(
13) in (
3), we get
Note that
Therefore,
and (
10) is true for
Assume that (
9) and (
10) are true for all
This implies that
and
for all
To show that (
9) is true for all
we consider
and using the first step of (
3) and MVT, we have
Using assumptions
in the above equation, we get
Therefore, we have
and
So,
and the inequality (
9) holds for all
The proof is completed by replacing , and with , and , respectively, in the above argument.
Since
and
are Cauchy sequences,
and
are also Cauchy by (
9) and (
10). Hence, we have
as
Now, by (
3) we get
where
for some
. By letting
in (
19), we have
□
Next, we study the uniqueness of the solution.
Proposition 1. Suppose is a simple solution of the Equation (2) for some and such thatSet . Then, d is unique in the region Proof. We can see the proof of the proposition from [
19]. □
3. Local Convergence Analysis
We will be using the following extra assumptions in our local analysis.
The condition (
5) of the lemma holds for
.
- ()
for some and
- ()
for some and
- ()
for some and
We obtained from our semi-local analysis that the solution
. Then, by
, for all
we can get
Now, using BL,
is invertible for all
and
We will use the following inequality in our study. For all
by MVT, we get
Moreover, using assumption
and (
21), for
we obtain
Remark 1. We study the local convergence in the ball which satisfiesHence, hereafter we select from Graphical representation of (23) is given in Figure 1. As a consequence of (
23), all the assumptions we have made remain valid in the local convergence ball. So, we can continue our local analysis independently under the same set of assumptions.
We need the following theorem for our local convergence analysis.
Theorem 2 ([
20]).
Let be twice differentiable at the point then Proposition 2. If , where , is the smallest zero of on , Then, under assumptions , we have with Proof. Note that
are non-decreasing continuous functions (NDCF) on
, with
So, by Intermediate Value Theorem (IVT), there exists a smallest
such that
.
Note that
So, by the assumption
and (
21), we obtain
Thus, the iterate
.
Also, by (
22) and the fact that
we have
Hence, the iterate
. □
Proposition 3. If , where , is the smallest zero of on ,Then, under assumptions we have with Proof. Note that
are NDCF on
, with
So, by IVT, there exists a smallest
such that
.
Using the assumption
and (
21), we obtain
and hence
□
For the next lemma, we introduced NDCF
defined as
and
Notice that
So, by IVT, there exists a smallest
such that
.
Lemma 2. If the assumptions hold and . Then, we have and Proof. Let
. Note that, by adding and subtracting
we have by (
3)
So, by MVT, and the definition of
and
, we have
Then, by rearranging, we get
Combining the first and last terms, and adding and subtracting
appropriately, we have
Next, by applying MVT for first derivatives, we have
Applying MVT on the first term, adding and subtracting
in other terms, we get
Note that
This can be seen by substituting for
and
.
For convenience, let
and
Then, we obtain
where we have used the relation
.
Let
Then, we have
Since
we have
Note that
where
, and hence by (27) we have
Add and subtract
in the last term appropriately to obtain
where
Using Theorem 2, with and , we get
Note that since
we have by (
28)
Add and subtract
in the seventh term appropriately again to get
Using Theorem 2, with
and
, we get
Now, adding and subtracting
in the last term of (30), we get
Combine the terms to get
where
Apply MVT again to get
where
Using the assumptions and inequalities we already have, we calculate as follows.
Using (
21) and assumption
, we get
and
Moreover, using (
2), (
22) and assumption
we get
By (
29), we have
Furthermore, by (
21), (
34) and assumption
,
Similarly, using (
21) and assumption
Then, use (
21), (
22) and assumptions
and
, we get
Then, using (
21), assumptions
and
we get
Using (
21) and assumption
Using (
21), (
34) and the assumptions
and
, we get
Finally, using (
21) and assumption
, we get
Combining the inequalities
we get
Now, since
we have
□
Theorem 3. If the assumptions hold, then the sequence defined by (3) with is well defined andIn particular, for all and converges to with order of convergence five. Proof. Proof of the theorem follows inductively from the previous lemma by replacing and with and , respectively. □
Next, we study the uniqueness of
Proposition 4. Suppose there exists
- (i)
a simple solution of (2) and assumption holds. - (ii)
Set Then (2) has a unique solution in Proof. We can see the proof of the proposition from [
19].
□
4. Numerical Examples
In this section, we examine two examples to calculate the parameters we have discussed in our theoretical part.
Example 1. Let with . is defined for byThe first derivative will beand the second derivative will be Consider the solution . Start with the initial point . Choosing , we have our solution . By comparing with the assumptions and , the constants can be found to be Then the parameters are , , and . Thus,
Example 2. Let us consider the trajectory of an electron in the air gap between two parallel plates, described by the expressionLet the domain be and take the initial point . Choosing the iterated solution is found to be [21]. By comparing with the assumptions and , the constants can be found to be Then the parameters are , , and . Thus . 5. Basins of Attraction
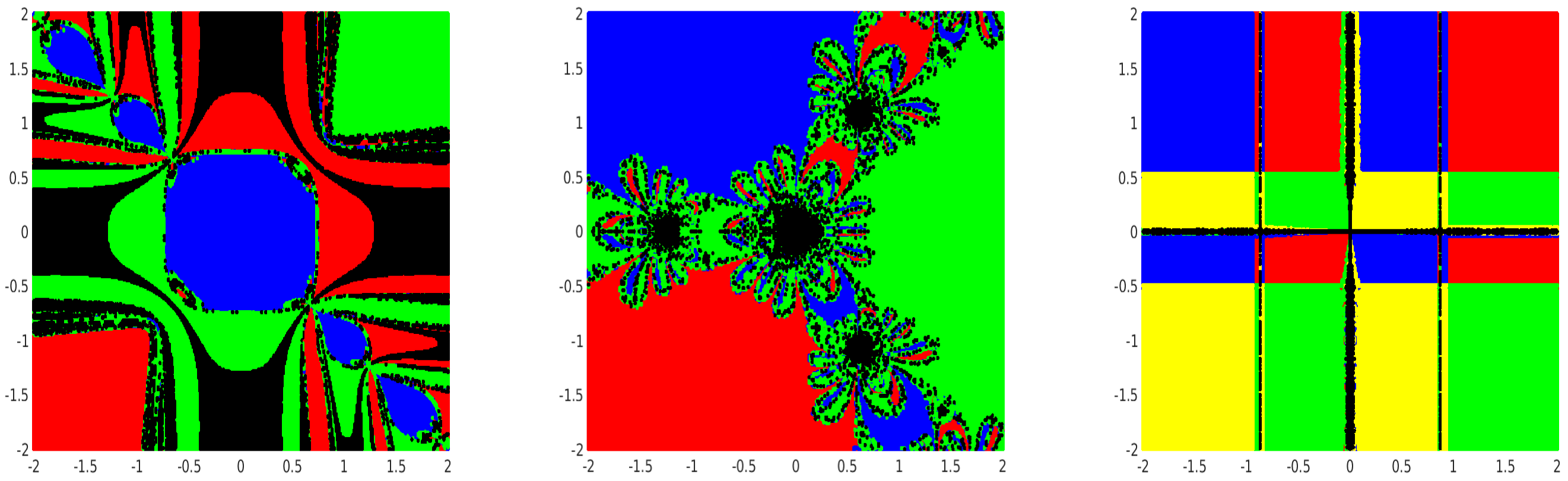
To verify the numerical stability of the method, we analyze the dynamics of the method (
3). The set of all initial points that converge to a specific root is called the Basin of Attraction (BA) [
22].
Example 3.
with roots , .
Example 4.
with roots , .
Example 5.
with roots ,
The BA for the roots of the given nonlinear equations is given (
Figure 2) in a
equidistant grid points within a rectangular domain
Each initial point is given a color corresponding to the root, which the iterative method converges. If the method fails to converge or diverges, the point is marked as black. The BA is shown with a tolerance of
, and a maximum of 45 iterations is considered.