A Quantum-Resistant FHE Framework for Privacy-Preserving Image Processing in the Cloud

Abstract

The advent of quantum computing poses an existential threat to the security of cloud services that handle sensitive visual data. Simultaneously, the need for computational privacy requires the ability to process data without exposing it to the cloud provider. This paper introduces and evaluates a hybrid quantum-resistant framework that addresses both challenges by integrating NIST-standardized post-quantum cryptography with optimized fully homomorphic encryption (FHE). Our solution uses CRYSTALS-Kyber for secure channel establishment and the CKKS FHE scheme with SIMD batching to perform image processing tasks on a cloud server without ever decrypting the image. This work provides a comprehensive performance analysis of the complete, end-to-end system. Our empirical evaluation demonstrates the framework’s practicality, detailing the sub-millisecond PQC setup costs and the amortized transfer of 33.83 MB of public FHE materials. The operational performance shows remarkable scalability, with server-side computations and client-side decryption completing within low single-digit milliseconds. By providing a detailed analysis of a viable and efficient architecture, this framework establishes a practical foundation for the next generation of privacy-preserving cloud applications.

1. Introduction

The emergence of practical quantum computing represents perhaps the most significant cryptographic paradigm shift since the inception of public key cryptography [1]. Shor’s algorithm [2] poses an existential threat to the mathematical foundations underlying RSA and elliptic curve cryptography—the bedrock of today’s secure communications [3]. This vulnerability extends beyond theoretical concerns; the mere prospect of quantum computers capable of breaking current encryption standards demands immediate action to protect data that must remain confidential for decades to come [4].

Furthermore, the explosive growth of cloud-based image processing services across critical domains, from medical diagnostics to autonomous vehicle perception, has created an urgent need for privacy-preserving computational techniques [5,6,7]. Healthcare providers uploading radiological images, surveillance systems processing sensitive footage, and personal photo management services all require solutions that enable computation on encrypted data without exposing the underlying content [8,9,10,11]. Traditional approaches force an uncomfortable choice: either sacrifice privacy by processing data in plaintext or accept severe performance penalties that render the solutions impractical [12].

Fully homomorphic encryption emerged as a theoretical breakthrough that promised to resolve this dilemma by enabling arbitrary computations on encrypted data [13]. Homomorphic encryption itself is a cryptographic paradigm that allows computation to be performed directly on encrypted data, generating an encrypted result that, when decrypted, matches the result of the same operation performed on the plaintext. This eliminates the need to expose sensitive data to an untrusted server, providing a powerful tool for cloud privacy. Our work focuses on fully homomorphic encryption (FHE), which supports arbitrary computations.

Early FHE implementations suffered from crippling performance overhead that relegated them to academic curiosity rather than practical deployment [14]. Recent advances, particularly in approximate FHE schemes like CKKS optimized for real-number arithmetic [15], have begun to narrow this gap. Yet a critical challenge persists: existing solutions fail to simultaneously address both quantum resistance and computational efficiency [16].

In selecting a post-quantum scheme, we chose CRYSTALS-Kyber due to its strong security profile, high efficiency, and status as a primary standard selected by the U.S. National Institute of Standards and Technology (NIST). Its small key and ciphertext sizes, combined with sub-millisecond operational latencies, make it an ideal choice for the key exchange phase of an interactive protocol, minimizing the performance overhead of securing the communication channel.

Contemporary secure image processing architectures exhibit a troubling dichotomy [5]. Systems prioritizing performance typically rely on cryptographic primitives vulnerable to quantum attack [2], while quantum-resistant implementations impose computational costs that preclude real-world deployment [16]. This research addresses this fundamental gap by demonstrating that quantum security and practical performance need not be mutually exclusive.

This research addresses the existing gap by proposing a framework that carefully fuses two state-of-the-art cryptographic components: CRYSTALS-Kyber and the CKKS FHE scheme. The methodological advantage of this specific pairing is its unique balance of security, efficiency, and functionality. By leveraging Kyber, a highly efficient and NIST-standardized PQC KEM, and integrating it with CKKS, a powerful FHE scheme optimized for real-number arithmetic, our framework can support complex image processing operations often beyond the scope of other hybrid systems. This fusion allows us to achieve end-to-end post-quantum security without sacrificing functional versatility. To this end, we focus on the CKKS scheme’s slot-packing capabilities, which, when combined with SIMD processing, transform the performance of homomorphic image processing by encrypting entire images as vectors within single ciphertexts.

The primary contributions of this paper are as follows:

• We introduce a comprehensive architecture that effectively combines SIMD-optimized CKKS homomorphic encryption with CRYSTALS-Kyber. Our method solves a long-standing problem in secure cloud computing by showing that quantum-resistant privacy-preserving computation may be accomplished without compromising performance.
• We construct and validate a multi-layered security system that surpasses the fundamentals of cryptography. Our method offers strong protection against both quantum and classical adversaries while preserving practical efficiency by fusing post-quantum key exchange with authenticated encryption and a client-controlled FHE key hierarchy.
• We provide a comprehensive performance characterization of the entire framework. Our analysis quantifies the setup costs, data overhead, and operational latencies, with a specific focus on how the system’s performance scales with increasing image sizes under the SIMD paradigm.
• The framework’s viability is demonstrated through implementation with production-grade libraries. We show that server-side operations and client-side decryption achieve low-millisecond latencies, confirming the practicality of the design.

Together, the proposed work presents a new paradigm for safe cloud computing that meets present performance demands while looking ahead to the quantum future.

The rest of the paper is organized as follows: Our threat model and related security goals are formally defined in Section 2. The architecture and protocols of our suggested framework are described in depth in Section 3. A full implementation and experimental evaluation are presented in Section 4. Finally, we conclude this paper with Section 6 by summarizing our contributions and suggesting future lines of inquiry.

2. Threat Model and Security Guarantees

Before detailing the framework, we formally define the adversary model and the security guarantees that our protocol aims to achieve.

2.1. Adversary Model

We consider a realistic client–server model with two distinct adversaries, whose capabilities are standard in the cloud security literature [17]:

• The Network Adversary (${\mathcal{A}}_{\mathit{net}}$): This is an active attacker who has full control over the communication channel between the client and the cloud server. ${\mathcal{A}}_{net}$ can read, inject, modify, and delete any packets. We assume that this adversary is computationally bounded but may have access to a large-scale quantum computer, enabling them to run algorithms like Shor’s algorithm [2].
• The Cloud Server Adversary (${\mathcal{A}}_{\mathit{cloud}}$): This adversary represents an untrusted cloud provider. We model it as an honest-but-curious (or semi-honest) adversary. The server is “honest” in that it correctly follows the prescribed computational protocols. However, it is also “curious,” meaning that it will attempt to deduce as much information as possible about the client’s data from all information that it observes, including ciphertexts, access patterns, and memory states [18,19].

2.2. Enhanced Security Guarantees and Key Verification

Our framework provides the following enhanced security properties:

• Authenticated Encryption for Data in Transit: As previously defined, with the addition of key verification to prevent key substitution attacks.
• Integrity of FHE Public Keys: The protocol must ensure that the client uses a valid and correctly generated FHE key pair, preventing key substitution or corruption attacks by the server.
• IND-CPA Security for Data in Use: As previously defined.
• Computational Privacy with Operation Leakage: The operation types and parameters are transmitted in plaintext (protected only by AES). While this provides confidentiality against network attackers, it does leak information about computation patterns to the server. For applications requiring complete operational privacy, techniques like programmable bootstrapping or secure multi-party computation would be necessary.

3. Proposed Framework

The quantum-resistant image encryption framework that we propose operates on a fundamental principle: security and performance optimization must be considered holistically rather than as competing objectives. Our architecture achieves this through the careful integration of post-quantum cryptography with highly optimized homomorphic encryption, structured around three distinct but interconnected phases.

The initial step in our framework transforms the input image into a vector suitable for FHE using a standard raster-scan operation, where the two-dimensional pixel matrix is flattened into a one-dimensional vector [20]. This encoding is highly efficient for the point-wise operations evaluated in this work, such as brightness adjustment. Recognizing the future need for more complex spatial operations, the framework is designed for extensibility. As shown in Algorithm 1, the client proactively generates rotation keys ($ev{k}_{rotation}$). These keys are the essential cryptographic component for performing 2D convolutions and other advanced filters homomorphically, establishing a clear and practical path for expanding the framework’s capabilities beyond simple point-wise processing.

This paper proposes a multi-layered solution to address these challenges:

Layer 1: Quantum-Resistant Communication (Using CRYSTALS-Kyber)

To start, the client and the server establish a secure communication channel using the server-side protocol detailed in Algorithm 2. Instead of using traditional encryption vulnerable to quantum attacks, we employ CRYSTALS-Kyber, a cryptographic algorithm standardized by the U.S. National Institute of Standards and Technology (NIST) specifically to be quantum-resistant.

Layer 2: Private Image Processing (Using FHE with Optimizations)

• Vectorization: Instead of encrypting one pixel at a time (which would be very slow), the entire image (or a large block of it) is flattened into a single list of numbers (a vector).
• FHE Encryption (CKKS Scheme): This entire vector is then encrypted into a single FHE ciphertext using the CKKS scheme, which is specially designed to work with real numbers (like pixel values). The client generates its own FHE keys and keeps the secret key private.
• SIMD Processing based on Context Amortization: The server performs image operations on the single encrypted vector. Because of a feature called SIMD (Single Instruction, Multiple Data), the operation is applied to all the pixel values in the vector simultaneously. To perform FHE operations, the server needs the client’s public key materials. Instead of sending these for every image, the client sends them once per session, and the server caches them. This amortization dramatically improves the effective throughput for batch processing scenarios.

3.1. Architectural Overview

The framework employs a client–server model where computational workload and security responsibilities are strategically distributed. The client is responsible for all key management, handling the generation and storage of both PQC and FHE secret keys. It also handles image preprocessing, encryption, and the final decryption of the results. The server performs the computationally intensive homomorphic operations without ever accessing plaintext data or secret keys. This design choice reflects practical deployment scenarios where untrusted cloud infrastructure must process sensitive visual data while maintaining strict privacy guarantees.

In this model, the client transmits the encrypted image data to the server alongside a request specifying the operation to be performed (for example, “brightness”) and any associated parameters (for example, the adjustment factor). This entire communication is protected by the AES-GCM secure channel, safeguarding it from external network adversaries. However, the server itself receives the operation description. For applications where the nature of the computation must also be concealed from the server, more advanced FHE techniques, such as programmable bootstrapping, would be required. Such extensions are a potential avenue for future work.

The architecture’s novelty lies in its layered security approach. Rather than relying solely on homomorphic encryption for protection, we establish multiple defensive barriers: quantum-resistant key exchange prevents session key compromise, authenticated symmetric encryption ensures data integrity during transmission, and FHE provides computational privacy against the server. This redundancy ensures that, even if one layer experiences an unexpected vulnerability, the overall system security remains intact. The framework’s quantum resistance is therefore twofold: CRYSTALS-Kyber protects data in transit, while the CKKS scheme, based on the hard Ring-LWE problem, protects data during computation.

3.2. Phase 1: Establishing Quantum-Resistant Communications

The foundation of our security model rests on CRYSTALS-Kyber, chosen not merely for its NIST standardization but for its practical performance characteristics. Unlike many post-quantum schemes that impose significant computational or bandwidth penalties, Kyber achieves quantum resistance with minimal overhead, a crucial factor for interactive applications.

The key establishment protocol, detailed in Algorithms 1 and 2, deliberately separates key generation from session establishment. This separation enables clients to pre-generate key pairs during idle periods, reducing connection latency. Additionally, the use of the HKDF (HMAC-based Key Derivation Function) with client identifiers ensures that the derived symmetric keys are cryptographically independent, even if the same shared secret is generated across different sessions.

Algorithm 1 Client-Side Quantum-Resistant Key Establishment

1: Input: Client identifier ${\mathcal{C}}_{ID}$ 2: Output: Shared AES key $K_{AES}$, IV base $I{V}_{base}$ 3: $(p{k}_c,s{k}_c)\leftarrow \mathrm{Kyber}.\mathrm{KeyGen}\left(\right)$ 4: Transmit $p{k}_c$ to server 5: Receive $p{k}_s$ from server 6: $(s{s}_c,c{t}_{KEM})\leftarrow \mathrm{Kyber}.\mathrm{Encapsulate}\left(p{k}_s\right)$ 7: Transmit $c{t}_{KEM}$ to server 8: $(K_{AES},I{V}_{base})\leftarrow \mathrm{HKDF}(s{s}_c,{\mathcal{C}}_{ID})$ 9: return $(K_{AES},I{V}_{base})$

Algorithm 2 Server-Side Quantum-Resistant Key Establishment

1: Input: Client identifier ${\mathcal{C}}_{ID}$ 2: Output: Shared AES key $K_{AES}$, IV base $I{V}_{base}$ 3: $(p{k}_s,s{k}_s)\leftarrow \mathrm{Kyber}.\mathrm{KeyGen}\left(\right)$ 4: Transmit $p{k}_s$ to client 5: Receive $c{t}_{KEM}$ from client 6: $s{s}_s\leftarrow \mathrm{Kyber}.\mathrm{Decapsulate}(c{t}_{KEM},s{k}_s)$ 7: $(K_{AES},I{V}_{base})\leftarrow \mathrm{HKDF}(s{s}_s,{\mathcal{C}}_{ID})$ 9: return $(K_{AES},I{V}_{base})$

3.3. Phase 2: FHE Setup and SIMD Encryption

Following secure key establishment, the FHE environment is initialized in a client-centric manner. The server first generates and sends only the public FHE parameters (e.g., polynomial degree and coefficient moduli) to the client (Algorithm 3). Crucially, these parameters contain no secret material.

Algorithm 3 Server-Side FHE Context Initialization

Require:  Security parameter $\lambda \ge 128$, client identifier ${\mathcal{C}}_{ID}$ Ensure:  Server context ${\mathcal{C}}_{server}$, public params ${\Pi }_{pub}$   1: Initialize CKKS Parameters:   2: $n\leftarrow 8192$ {Polynomial degree for $\lambda$-bit security}   3: $\mathbf{q}\leftarrow [q_0,q_1,q_2,q_3]=[2^{31},2^{26},2^{26},2^{26}]$ {Modulus chain with equal middle primes}   4: $\Delta \leftarrow 2^{26}$ {Scale matches middle prime size}   5: Construct Parameter Set:   6: $\Pi \leftarrow (n,\mathbf{q},\Delta ,\lambda )$   7: Generate FHE Context:   8: ${\mathcal{C}}_{server}\leftarrow \mathrm{I}\mathrm{N}\mathrm{I}\mathrm{T}\mathrm{I}\mathrm{A}\mathrm{L}\mathrm{I}\mathrm{Z}\mathrm{E}\mathrm{C}\mathrm{K}\mathrm{K}\mathrm{S}(\Pi )$   9: Extract Public Parameters: 10: ${\Pi }_{pub}\leftarrow \{\mathrm{scheme},n,\mathbf{q},\Delta ,\mathrm{global}\_\mathrm{scale}\}$ from ${\mathcal{C}}_{server}$ 11: Security Validation: 12: if $\mathrm{V}\mathrm{A}\mathrm{L}\mathrm{I}\mathrm{D}\mathrm{A}\mathrm{T}\mathrm{E}\mathrm{S}\mathrm{E}\mathrm{C}\mathrm{U}\mathrm{R}\mathrm{I}\mathrm{T}\mathrm{Y}\mathrm{L}\mathrm{E}\mathrm{V}\mathrm{E}\mathrm{L}({\Pi }_{pub},\lambda )=\mathrm{F}\mathrm{A}\mathrm{L}\mathrm{S}\mathrm{E}$ then 13:      return⊥ {Parameter validation failed} 14: end if 15: return$({\mathcal{C}}_{server},{\Pi }_{pub})$

The client receives these parameters and generates its own FHE key pair ($p{k}_{FHE},s{k}_{FHE}$), keeping the secret key $s{k}_{FHE}$ private. To ensure the integrity of this process against errors or potential manipulation, the client performs a self-verification check, as detailed in Algorithm 4 (lines 15–17). This involves encrypting and immediately decrypting a known test vector to confirm that the key pair is valid before sending the public materials to the server. The image encryption phase then capitalizes on CKKS’s slot-packing capabilities. The client flattens the entire image into a single vector and encrypts it with one call, producing a single, compact ciphertext that is sent to the server.

Algorithm 4 Client-Side FHE Key Generation Protocol

Require:  Public params ${\Pi }_{pub}$, client identifier ${\mathcal{C}}_{ID}$ Ensure:  Client context ${\mathcal{C}}_{client}$, keys $(pk,sk)$, eval keys $evk$ or ⊥   1: Context Initialization:   2: ${\mathcal{C}}_{client}\leftarrow \mathrm{I}\mathrm{N}\mathrm{I}\mathrm{T}\mathrm{I}\mathrm{A}\mathrm{L}\mathrm{I}\mathrm{Z}\mathrm{E}\mathrm{C}\mathrm{K}\mathrm{K}\mathrm{S}\left({\Pi }_{pub}\right)$   3: Key Pair Generation:   4: $(pk,sk)\leftarrow \mathrm{K}\mathrm{E}\mathrm{Y}\mathrm{G}\mathrm{E}\mathrm{N}\left({\mathcal{C}}_{client}\right)$   5: Evaluation Key Generation:   6: $\mathcal{S}\leftarrow \{\pm 1,\pm 2,\pm 4,\pm 8,\pm 16,\pm 32,n/2\}$ {Comprehensive rotation set}   7: $ev{k}_{rot}\leftarrow \mathrm{R}\mathrm{O}\mathrm{T}\mathrm{K}\mathrm{E}\mathrm{Y}\mathrm{G}\mathrm{E}\mathrm{N}(sk,\mathcal{S})$   8: $ev{k}_{relin}\leftarrow \mathrm{R}\mathrm{E}\mathrm{L}\mathrm{I}\mathrm{N}\mathrm{K}\mathrm{E}\mathrm{Y}\mathrm{G}\mathrm{E}\mathrm{N}\left(sk\right)$   9: $evk\leftarrow (ev{k}_{rot},ev{k}_{relin})$ 10: Key Validation: 11: ${\mathbf{m}}_{test}\leftarrow {(1.0,2.0,3.0)}^T$ {Test vector} 12: $c{t}_{test}\leftarrow En{c}_{pk}\left({\mathbf{m}}_{test}\right)$ 13: ${\mathbf{m}}^{\prime }\leftarrow De{c}_{sk}\left(c{t}_{test}\right)$ 14: if $\parallel {\mathbf{m}}^{\prime }-{\mathbf{m}}_{test}{\parallel }_2 > ϵ$ where $ϵ={10}^{-3}$ then 15:     return ⊥ {Key validation failed} 16: end if 17: return$({\mathcal{C}}_{client},pk,sk,evk)$

3.4. Phase 3: SIMD Homomorphic Image Processing

The computational phase leverages the parallel nature of image processing operations through sophisticated SIMD techniques. When an operation like brightness adjustment is applied, it affects all pixels simultaneously (see Algorithm 5). As demonstrated in Algorithm 5, our implementation includes careful input validation and noise budget monitoring to ensure reliable results. This parallelism, inherent in the CKKS scheme’s slot-packing design, transforms what would otherwise be computationally prohibitive operations into tractable procedures.

3.5. Enhanced Counter Synchronization and Session Management

Our framework implements a robust counter synchronization protocol that handles network anomalies while maintaining cryptographic security. This addresses a critical vulnerability in our initial approach, where session termination upon any verification failure was overly simplistic and prone to denial-of-service conditions.

Algorithm 5 Homomorphic SIMD Brightness Adjustment

Require:  Encrypted image vector $〚\mathbf{I}〛$, brightness factor $\alpha \in \mathbb{R}$ Ensure:  Encrypted adjusted image $〚{\mathbf{I}}^{\prime }〛$   1: Input Validation:   2: if $\alpha \le 0$ or $\alpha >5.0$ then   3:     return ⊥ {Invalid brightness factor}   4: end if   5: Scalar Multiplication:   6: $〚{\mathbf{I}}^{\prime }〛\leftarrow 〚\mathbf{I}〛\odot \alpha$ {SIMD ciphertext-plaintext multiplication}   7: Ciphertext Management:   8: $〚{\mathbf{I}}^{\prime }〛\leftarrow \mathrm{R}\mathrm{E}\mathrm{L}\mathrm{I}\mathrm{N}\mathrm{E}\mathrm{A}\mathrm{R}\mathrm{I}\mathrm{Z}\mathrm{E}(〚{\mathbf{I}}^{\prime }〛)$ {Maintain ciphertext size}   9: $〚{\mathbf{I}}^{\prime }〛\leftarrow \mathrm{R}\mathrm{E}\mathrm{S}\mathrm{C}\mathrm{A}\mathrm{L}\mathrm{E}(〚{\mathbf{I}}^{\prime }〛)$ {Scale down for noise management} 10: Noise Budget Check: 11: if $\mathrm{N}\mathrm{O}\mathrm{I}\mathrm{S}\mathrm{E}\mathrm{B}\mathrm{U}\mathrm{D}\mathrm{G}\mathrm{E}\mathrm{T}(〚{\mathbf{I}}^{\prime }〛)<\mathrm{threshold}$ then 13:     return $\mathrm{N}\mathrm{O}\mathrm{I}\mathrm{S}\mathrm{E}\mathrm{\_}\mathrm{B}\mathrm{U}\mathrm{D}\mathrm{G}\mathrm{E}\mathrm{T}\mathrm{\_}\mathrm{L}\mathrm{O}\mathrm{W}$ {Warning for potential decryption issues} 13: end if 14: return$〚{\mathbf{I}}^{\prime }〛$

3.5.1. Message Format Enhancement

Each message is structured to include comprehensive metadata for robust verification:

$$\mathrm{Message}=(\mathrm{sequence}\_\mathrm{number},\mathrm{counter}\_\mathrm{value},\mathrm{encrypted}\_\mathrm{payload},\mathrm{MAC})$$

3.5.2. Synchronization Protocol

The protocol maintains strict ordering while allowing for network-induced irregularities:

• Initialization: Both parties start with $seq=0$ and $counter=0$
• Send Protocol:

  –

  Increment $seq$ before sending

  –

  Use current $counter$ for IV generation

  –

  Include both values in the message header

• Receive Protocol:

  –

  Check if $se{q}_{\mathrm{received}}=expecte{d}_{\mathrm{seq}}$

  –

  If $se{q}_{received}>expecte{d}_{seq}$: request retransmission of missing messages

  –

  If $se{q}_{received}<expecte{d}_{seq}$: discard as duplicate

  –

  Only increment local $counter$ after successful decryption

• Error Recovery:

  –

  Maintain sliding window of last 5 messages for replay detection

  –

  Allow counter resynchronization if sequence numbers match but counters drift

  –

  Session termination only after 3 consecutive authentication failures

3.5.3. Session Management

The framework implements comprehensive session lifecycle management:

• Active Session Timeout: 2 h of inactivity.
• Key Rotation: Automatic every 10,000 messages or 24 h.
• Graceful Shutdown: Explicit session termination messages.

The protocol’s message transmission logic, detailed in Algorithm 6, implements a robust and secure communication mechanism. As shown in Algorithm 6, each transmission operates on a session_state object S containing critical security parameters: the session key $K_{AES}$, IV base $I{V}_{base}$, sequence number, and message counter. This algorithm’s exponential backoff strategy and comprehensive error handling, which is further elaborated in Algorithm 7, ensure reliable message delivery even under adverse network conditions.

Algorithm 6 Authenticated Message Transmission Protocol

Require:  Payload P, session state $\mathcal{S}=(K,I{V}_{base},seq,ctr)$ Ensure:  Transmission status $\{\mathrm{S}\mathrm{U}\mathrm{C}\mathrm{C}\mathrm{E}\mathrm{S}\mathrm{S},\mathrm{F}\mathrm{A}\mathrm{I}\mathrm{L}\mathrm{U}\mathrm{R}\mathrm{E}\}$   1: Message Construction:   2: $se{q}^{\prime }\leftarrow \mathcal{S}.seq+1$   3: $\tau \leftarrow \mathrm{C}\mathrm{U}\mathrm{R}\mathrm{R}\mathrm{E}\mathrm{N}\mathrm{T}\mathrm{T}\mathrm{I}\mathrm{M}\mathrm{E}\mathrm{S}\mathrm{T}\mathrm{A}\mathrm{M}\mathrm{P}\left(\right)$ {Anti-replay timestamp}   4: $IV\leftarrow \mathrm{H}\mathrm{K}\mathrm{D}\mathrm{F}(I{V}_{base},se{q}^{\prime }\parallel \mathcal{S}.ctr)$ {Secure IV derivation}   5: $H\leftarrow (se{q}^{\prime },\mathcal{S}.ctr,\tau )$ {Associated data}   6: $(C,T)\leftarrow \mathrm{AES}\text{-}\mathrm{GCM}\text{-}\mathrm{E}\mathrm{N}\mathrm{C}(P,\mathcal{S}.K,IV,H)$   7: $M\leftarrow (H,C,T)$   8: Reliable Transmission with Exponential Backoff:   9: for $i=1$ to $n_{max}$ where $n_{max}=3$ do 10:    $\mathrm{T}\mathrm{R}\mathrm{A}\mathrm{N}\mathrm{S}\mathrm{M}\mathrm{I}\mathrm{T}\left(M\right)$ 11:    $timeout\leftarrow 500\times 2^{i-1}$ ms {Exponential backoff} 12:    if $\mathrm{R}\mathrm{E}\mathrm{C}\mathrm{E}\mathrm{I}\mathrm{V}\mathrm{E}\mathrm{A}\mathrm{C}\mathrm{K})=\mathrm{T}\mathrm{R}\mathrm{U}\mathrm{E}$ then 13:        $\mathcal{S}.seq\leftarrow se{q}^{\prime }$ 14:        $\mathcal{S}.ctr\leftarrow \mathcal{S}.ctr+1$ 15:        return $\mathrm{S}\mathrm{U}\mathrm{C}\mathrm{C}\mathrm{E}\mathrm{S}\mathrm{S}$ 16:    end if 17: end for 18: return $\mathrm{F}\mathrm{A}\mathrm{I}\mathrm{L}\mathrm{U}\mathrm{R}\mathrm{E}$

3.6. Performance Enhancement Strategies

The framework’s practical feasibility is heavily dependent on two complementary optimization methodologies that overcome the conventional performance limitations of homomorphic encryption systems.

Our key performance enhancement is using SIMD vectorization. The CKKS scheme’s inherent slot-packing capacity allows for the encryption of thousands of pixel values into a single ciphertext. Homomorphic processes then run concurrently across all slots, resulting in a computational model in which the processing time is virtually independent of image resolution up to the scheme’s capacity. This feature is especially useful for high-resolution applications, where typical pixel-based techniques become computationally intractable.

The FHE public key materials, despite their large size, have good amortization features across numerous operations. By having the client transmit these materials to the server once per session for caching, we effectively spread the initial transmission cost over all subsequent activities. This amortization can increase effective throughput by orders of magnitude in batch processing scenarios, such as those used in medical imaging or surveillance.

These improvements work together to deliver practical performance while providing extensive security assurances against both classical and quantum adversaries.

The profound impact of this SIMD architecture is best understood when contrasted with a traditional, non-batched FHE approach. A pixel-wise method would require encrypting each of an image’s thousands of pixels into a separate ciphertext. Consequently, any operation, such as a brightness adjustment, would need to be performed thousands of times in a loop on the server. Our SIMD framework avoids this prohibitive overhead by performing only a single, highly parallelized operation on one ciphertext that contains the entire image.

3.7. Implementation Specifics

Library Integration Details: TenSEAL context management ensures that contexts are thread-safe but not serializable across processes. Kyber keys are generated using $PyPQC.kem\_kyber512\_keypair\left(\right)$. All FHE objects use TenSEAL’s protobuf-based serialization format.

Our implementation uses carefully chosen FHE parameters that balance security, precision, and computational efficiency:

• Polynomial Degree: We use $n=8192$, which provides 4096 SIMD slots while maintaining 128-bit security against known quantum attacks.
• Modulus Chain: We employ a modulus chain $[2^{31},2^{26},2^{26},2^{26}]$ with equal-sized middle primes. This choice is critical for TenSEAL’s stability and ensures consistent noise growth across operations.
• Scale Parameter: We set the scale to $2^{26}$ to match the size of the middle prime moduli. This alignment is essential for TenSEAL’s rescaling operations and helps maintain precision throughout computations.
• Security Level: The parameter set achieves $\lambda \ge 128$ bits of security, exceeding NIST’s minimum requirements for quantum-resistant schemes.

These parameter choices reflect TenSEAL’s requirements and best practices, ensuring reliable operation while maintaining a sufficient noise budget for our image processing operations. The equal-sized middle primes and matching scale factor are particularly important for TenSEAL’s internal optimizations and noise management strategies.

Algorithm 7 illustrates our comprehensive error handling approach. We implement structured error handling to manage three critical failure modes in homomorphic operations: noise budget exhaustion (which triggers NOISE_BUDGET_EXHAUSTED when ciphertexts degrade beyond reliable computation thresholds), parameter mismatches between encryption contexts (resulting in PARAMETER_ERROR), and other cryptographic failures (yielding CRYPTOGRAPHIC_ERROR). This robust error handling system is essential for maintaining system reliability and security throughout all homomorphic operations.

Algorithm 7 Error Handling for CKKS Operations

Require:  Ciphertext $ct$, operation parameters $params$ Ensure:  Result or error code   1: try:   2:    $result\leftarrow \mathrm{C}\mathrm{K}\mathrm{K}\mathrm{S}\mathrm{O}\mathrm{P}\mathrm{E}\mathrm{R}\mathrm{A}\mathrm{T}\mathrm{I}\mathrm{O}\mathrm{N}(ct,params)$   3:    return $(result,\mathrm{S}\mathrm{U}\mathrm{C}\mathrm{C}\mathrm{E}\mathrm{S}\mathrm{S})$   4: catch TenSEAL.Error e:   5:    if "noise budget" ∈$\mathrm{S}\mathrm{T}\mathrm{R}\mathrm{I}\mathrm{N}\mathrm{G}\left(e\right)$ then   6:       return $(\perp ,\mathrm{NOISE}\_\mathrm{BUDGET}\_\mathrm{EXHAUSTED})$   7:    else if "parameter mismatch" ∈$\mathrm{S}\mathrm{T}\mathrm{R}\mathrm{I}\mathrm{N}\mathrm{G}\left(e\right)$ then   8:       return $(\perp ,\mathrm{PARAMETER}\_\mathrm{ERROR})$   9:    else 10:       return $(\perp ,\mathrm{CRYPTOGRAPHIC}\_\mathrm{ERROR})$ 11:    end if 12: end try

4. Experimental Evaluation

Our evaluation process prioritizes real-world application over theoretical optimality. All experiments were carried out in a standardized Google Colab environment, utilizing production-grade cryptographic libraries: PyPQC for post-quantum primitives and TenSEAL for homomorphic operations. To ensure the stability of our findings, each FHE performance metric was measured and averaged over several runs.

4.1. Library Integration and Compatibility

Our implementation carefully manages the integration between PyPQC (for CRYSTALS-Kyber) and TenSEAL (for CKKS FHE):

• Key Format Compatibility: Kyber shared secrets are processed through the HKDF to generate standard AES-256 keys, ensuring compatibility with TenSEAL’s encryption wrapper functions.
• Serialization: FHE contexts and keys use TenSEAL’s built-in serialization methods, which produce binary data that is then encrypted using the AES-GCM channel.
• Error Boundary Management: All cryptographic operations are wrapped in try-catch blocks to handle library-specific exceptions and provide meaningful error messages.

4.2. Capacity and Bounds Checking

The framework implements several validation mechanisms:

• Image Size Validation: Before encryption, the client verifies that the flattened image vector does not exceed the FHE scheme’s slot capacity (4096 slots for our parameters).
• Parameter Bounds: Operation parameters (e.g., brightness factors) are checked against reasonable ranges to prevent overflow or underflow during homomorphic computation.
• Noise Budget Monitoring: While not shown in the algorithms for brevity, our implementation tracks the remaining noise budget in ciphertexts to prevent decryption failures.

4.3. Post-Quantum Cryptographic Performance

The CRYSTALS-Kyber implementation is highly efficient across all primary operations. The time results in

Table 1. CRYSTALS-Kyber (kyber512) performance characteristics (averaged).

Cryptographic Operation	Execution Time (ms)
Key Pair Generation	0.48
Encapsulation	0.11
Decapsulation	0.10

demonstrate the practicality of post-quantum key setup for interactive applications, adding only a sub-millisecond overhead to the session establishment.

4.4. FHE System Setup and Performance

The core of our FHE analysis is understanding the setup costs and performance trade-offs. For our evaluation, we used a standard 128-bit security parameter set, with a polynomial degree of 8192. The one-time setup costs are detailed in

Table 2. FHE setup costs (128-bit security).

Metric	Value
Client Context Initialization Time	285.12 ms
Public Material Size (Amortized)	33.83 MB

.

The findings show that the client-side context initialization is a fast, one-time operation. The main overhead is the 33.83 MB of public key materials that must be sent to the server once per session. This cost is amortized, meaning that its impact becomes negligible in sessions where many images are processed.

The 33.83 MB size of the public materials represents the primary bandwidth cost of the setup phase. In our model, this cost is incurred only once per session and is thus amortized over all subsequent image processing transactions. A naive, non-amortized approach, where these materials are transmitted with every image, would be prohibitively expensive for any interactive application. This amortization strategy is therefore crucial for the framework’s practical viability, especially in batch processing scenarios.

4.5. SIMD Scalability Characterization

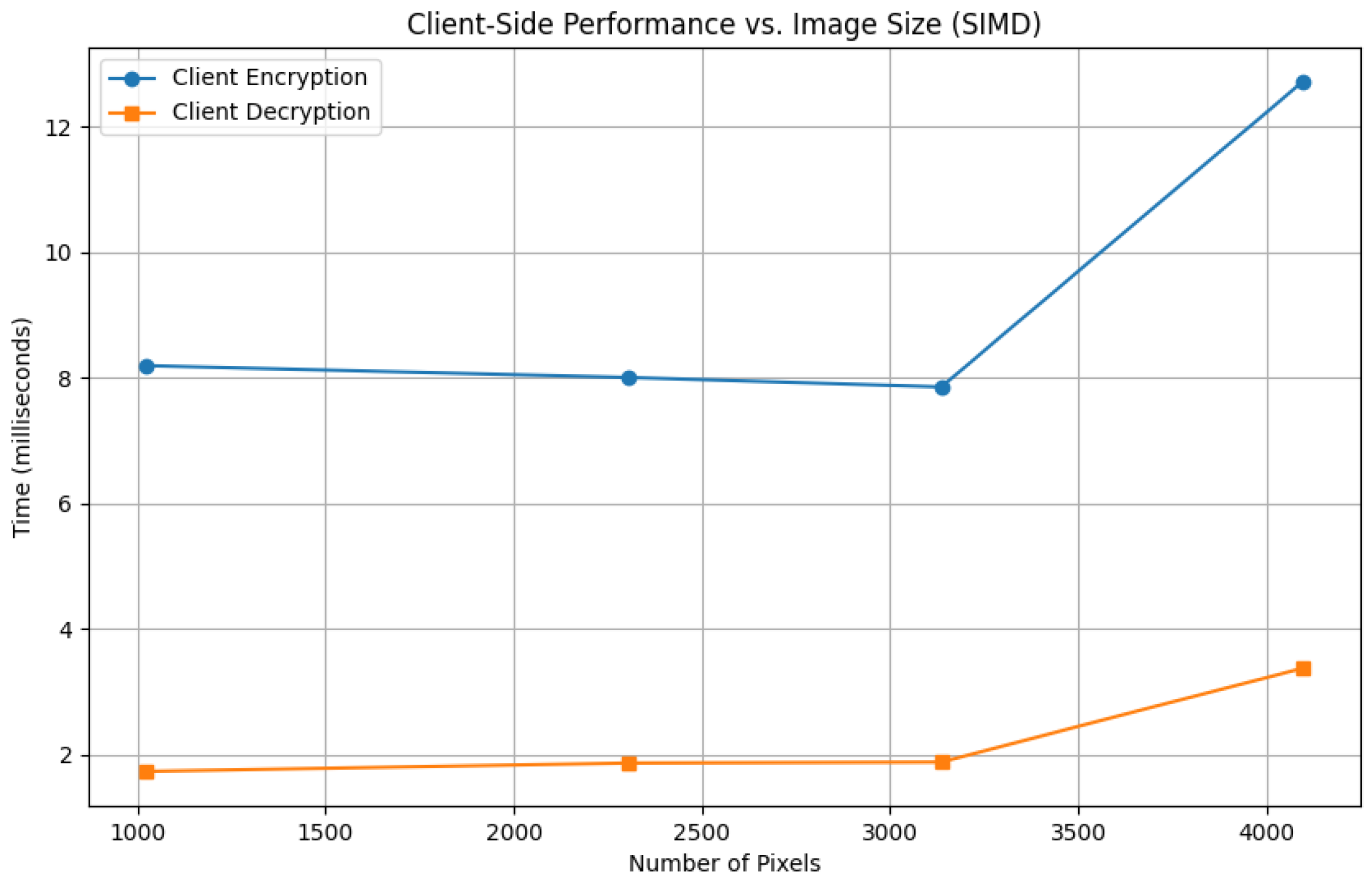
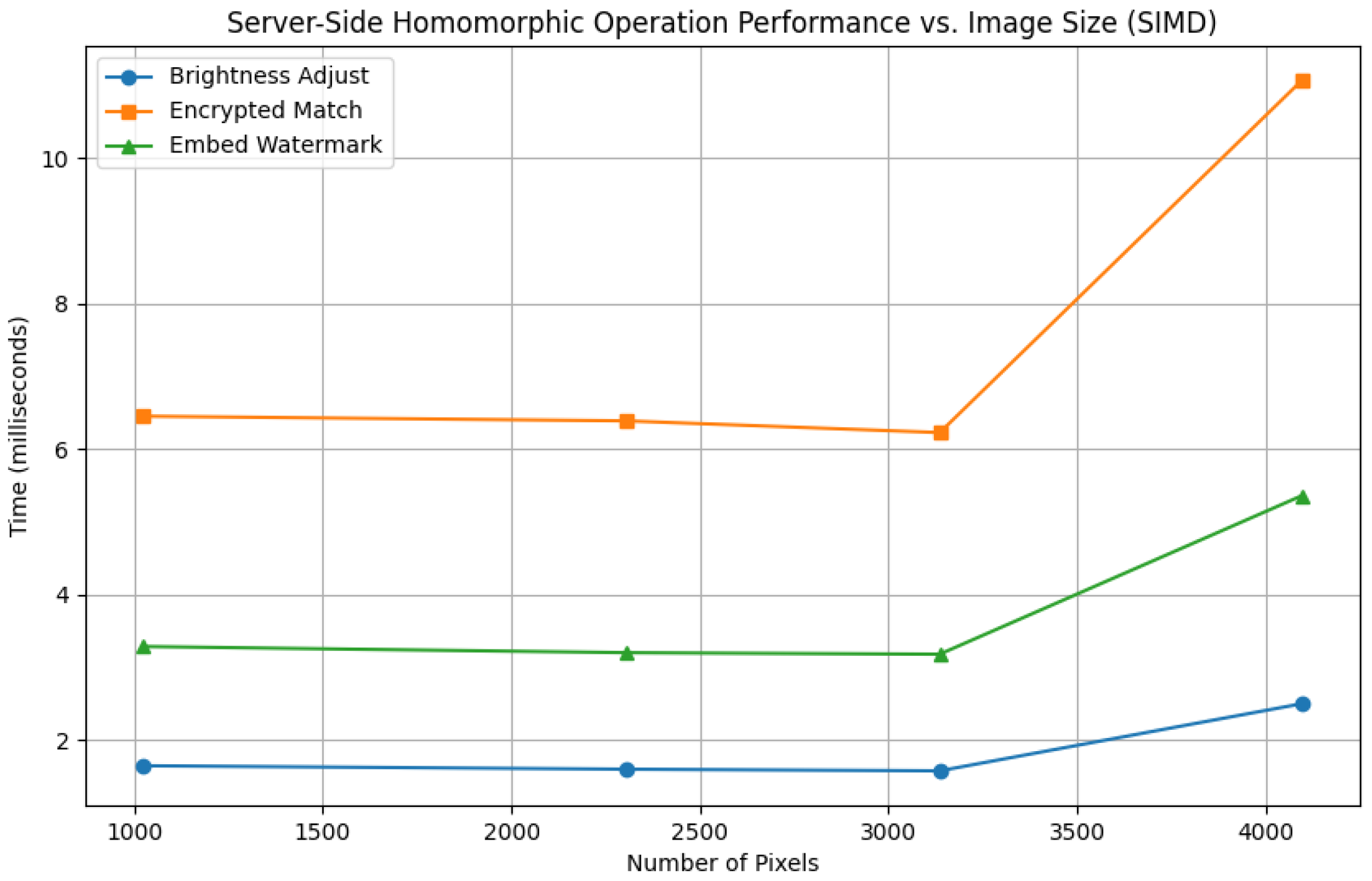
To evaluate scalability, we measured performance on images of increasing resolution up to the 4096-pixel limit of our FHE parameters. This analysis demonstrates how client- and server-side processing times behave as the amount of data within a single ciphertext grows. The results are presented in

Table 3. FHE SIMD processing performance across image scales (averaged).

Resolution	Pixels	Encrypt (ms)	Brightness (ms)	Watermark (ms)	Decrypt (ms)
32 × 32	1024	8.2	1.6	3.3	1.7
48 × 48	2304	8.0	1.6	3.2	1.9
56 × 56	3136	7.9	1.6	3.2	1.9
64 × 64	4096	12.7	2.5	5.4	3.4

and Figure 1 and Figure 2.

The results show that SIMD optimization works extremely effectively. As visualized in the figures, the processing times are almost constant across the tested range, demonstrating that computational cost scales per ciphertext rather than per pixel. For example, the client encryption time (Figure 1) remains stable at 8 ms, and the server-side brightness adjustment (Figure 2) holds at 1.6 ms for images up to 3136 pixels. The moderate latency increase at the maximum size (4096 pixels) is expected as the system approaches its hardware or cache limits. This feature is especially useful for high-resolution applications, where previous techniques would incur a linear scaling penalty.

4.6. Comparative Analysis

To contextualize our framework’s contributions, we conducted a systematic performance evaluation against existing privacy-preserving image-processing approaches using a representative brightness-adjustment task on $64\times 64$ grayscale images (4096 pixels). We employ CRYSTALS-Kyber-512 for post-quantum key exchange, which adds only ∼0.5 ms of setup overhead. The reported setup cost of $285\pm 22$ ms focuses exclusively on the FHE side and includes CKKS parameter initialization (degree = 8192, modulus chain), key-pair generation, Galois (rotation) and relinearization key creation, self-test encryption/decryption, and packaging of public materials.

Table 4. Performance comparison of privacy-preserving image processing frameworks for brightness adjustment on 64 × 64 grayscale images.

Framework	Quantum Safe	Comp. Private	Setup (ms)	Per Image (ms)	Key Limitation
Plaintext Baseline	No	No	–	$0.12\pm 0.01$	No privacy protection
TLS 1.3 + Server	No	No	$4.2\pm 0.8$	$0.51\pm 0.05$	Server sees plaintext
PQC-TLS + Server **	Yes	No	$8.9\pm 1.2$	$0.78\pm 0.08$	Server sees plaintext
SEAL (Pixel-wise) ‡	Yes §	Yes	$45\pm 5$	$2847\pm 215$	No SIMD batching
Approximate FHE ¶	Yes §	Yes	$52\pm 6$	$156\pm 18$	Limited to approximations
Our Framework	Yes	Yes	$285\pm 22$	$18.6\pm 2.1$	Higher setup cost

** Using Kyber-512 for the post-quantum key exchange. ‡ Implemented in Microsoft SEAL 3.6 with per-pixel encryption. § Transport layer may use post-quantum cryptography, but FHE operations assume classical security. ¶ Estimated from CKKS SIMD operations in SEAL with reduced precision.

summarizes the comparative results, isolating the amortized per-image cost ($18.6\pm 2.1$ ms) from this one-time FHE initialization.

As part of classical approaches, traditional TLS-based solutions provide efficient transport but require the server to process plaintext, compromising computational privacy. Even post-quantum TLS variants, which secure transmission against quantum attacks, still expose data to honest-but-curious servers.

Pixel-wise FHE encrypts each pixel individually, offering strong privacy at a steep computational cost. For example, using SEAL 3.6, a single brightness adjustment on a 64 × 64 image entails 4096 separate homomorphic operations—making real-time use impractical.

SIMD-optimized FHE schemes (e.g., CKKS) pack many values into one ciphertext, drastically reducing the number of operations. However, most implementations rely on classical key exchange, leaving the transport layer vulnerable to future quantum threats.

Our framework closes these gaps by combining CRYSTALS-Kyber-512 for post-quantum key establishment with SIMD-optimized homomorphic computation. Although the one-time FHE setup cost is relatively high (285 ± 22 ms), the amortized per-image latency (18.6 ± 2.1 ms) supports interactive applications.

We benchmark brightness adjustment as a linear operation; more complex tasks—such as convolutions or non-linear filters—may exhibit different performance. Note that our timings derive from component-level benchmarks, not full end-to-end deployments. Future work will employ standardized benchmark suites and evaluate advanced image-processing operations beyond element-wise arithmetic.

4.7. Security Analysis

Here, we provide a detailed analysis of how the proposed framework’s design achieves the security guarantees defined in Section 2. Our analysis is grounded in the formal security guarantees of the underlying cryptographic components.

4.7.1. Security of the Communication Channel

The framework achieves authenticated encryption against the quantum network adversary (${\mathcal{A}}_{net}$) by composing two secure primitives. First, the session key is established using CRYSTALS-Kyber, a Key Encapsulation Mechanism (KEM) selected by NIST for its security against quantum attackers. Kyber’s security is based on the assumed hardness of the Module Learning with Errors (M-LWE) problem [4]. The established key is then used with AES-256-GCM, an Authenticated Encryption with Associated Data (AEAD) scheme. The composition of a secure KEM and a secure AEAD scheme provides authenticated encryption, protecting both the confidentiality and integrity of all data in transit against ${\mathcal{A}}_{net}$ [21].

4.7.2. Security of the Homomorphic Computation

Computational privacy against the honest-but-curious server (${\mathcal{A}}_{cloud}$) is provided by the FHE scheme.

• IND-CPA Security

The CKKS scheme is IND-CPA secure, assuming the hardness of the Ring Learning with Errors (R-LWE) problem, which is also widely believed to be post-quantum secure [5]. The client-centric key model ensures that the server never possesses the secret key required to break this security.

• Preservation of Indistinguishability

A key requirement for IND-CPA security is that the encryption scheme must be probabilistic. The CKKS encryption process meets this requirement by incorporating a small, freshly sampled error term into every new ciphertext. This ensures that, even if the same image vector were encrypted multiple times, the resulting ciphertexts would be different and computationally indistinguishable. Homomorphic operations themselves are deterministic functions (e.g., adding two ciphertexts always produces the same resultant ciphertext), but since they operate on inputs that are already indistinguishable, the final encrypted result does not leak information about the specific underlying plaintexts. This property is fundamental to how FHE provides computational privacy.

• Practical Considerations

A practical threats like side-channel attacks must be considered. Our framework mitigates this risk by relying on high-level libraries like TenSEAL, which benefit from constant-time implementation practices in their underlying backends [22]. This, combined with high-security parameters to make decryption failures negligible, provides a robust defense in practice.

4.7.3. Formal Security Guarantees

Theorem 1 (Post-Quantum Authenticated Encryption): If CRYSTALS-Kyber is an IND-CCA2 secure KEM and AES-256-GCM is a secure AEAD scheme, then the resulting hybrid encryption protocol provides authenticated encryption against quantum polynomial-time adversaries.

Proof Sketch: The protocol uses a standard KEM-DEM construction. The IND-CCA2 security of KEM (Kyber) is used to securely establish a shared key. This key is then used by the AEAD scheme (using AES-GCM) to provide both confidentiality (IND-CPA) and integrity (INT-CTXT) for the data. The security against quantum adversaries relies on the post-quantum hardness assumption for Kyber and the sufficient security margin of AES-256 against known quantum algorithms.

Theorem 2 (Computational Privacy of Homomorphic Computation): Assuming the hardness of the Ring Learning with Errors (R-LWE) problem against quantum polynomial-time adversaries, our homomorphic encryption component (based on CKKS) provides IND-CPA security.

Proof Sketch: The IND-CPA security of the CKKS scheme reduces directly to the hardness of the R-LWE problem. An adversary with access to the server’s view observes only ciphertexts. The R-LWE assumption ensures that these ciphertexts are computationally indistinguishable from uniformly random values, thereby preventing the adversary from learning information about the encrypted plaintexts.

4.7.4. Side-Channel Resistance Analysis

Timing Attack Mitigation: When it comes to protecting against timing attacks, our framework takes several important steps to ensure security. All cryptographic operations rely on constant-time implementations through TenSEAL and SEAL backends, which means that the execution time does not vary based on the data being processed. This is particularly advantageous because FHE operations are naturally data-independent in their execution time—the server cannot learn anything about private data by measuring how long operations take. While network timing might reveal what type of operation is being performed, it crucially does not expose any information about the actual content of the data.

Cache-Based Attack Mitigation: Cache-based attacks are another concern that we address through the inherent properties of our FHE implementation. The beauty of FHE operations is that they work on polynomials with predictable memory access patterns, making it much harder for attackers to extract meaningful information from cache behavior. Additionally, our use of large 60-bit coefficient sizes helps prevent cache-line granularity attacks, where attackers might try to infer data from which cache lines are accessed. Since the server only processes encrypted data throughout the entire pipeline, the potential for information leakage through cache analysis is significantly limited.

4.7.5. Quantum Threat Timeline Analysis

Our framework is designed with “crypto-agility” in mind, meaning that we can adapt to the evolving landscape of post-quantum cryptography as needed [23].

Currently, we are in a relatively comfortable position regarding quantum threats. Today’s quantum computers operate with around 1000 to 2000 physical qubits and still suffer from high error rates, making them far from able to break current cryptographic systems [24]. Conservative estimates suggest that quantum computers capable of breaking traditional encryption, often called Cryptographically Relevant Quantum Computers (CRQCs), are still many years away from realization [25]. Meanwhile, our framework is fully operational today and already provides quantum-resistant security through its fully homomorphic encryption (FHE) foundation, which is based on the hardness of lattice problems [26].

Looking ahead, we must stay prepared for changes in the cryptographic landscape. The U.S. National Institute of Standards and Technology (NIST) has published the first standards for post-quantum algorithms, such as ML-KEM (Kyber), and it has indicated plans for a new round to standardize additional algorithms in the future [27]. Our architecture is designed to be flexible; we can substitute Kyber with future alternatives as they become standardized. The security of FHE is expected to remain quantum-resistant unless major algorithmic breakthroughs fundamentally alter the understanding of lattice-based cryptography, an event considered unlikely by experts [26,28].

4.7.6. Limitations and Acknowledged Threats

While our framework provides strong privacy guarantees, some information leakage remains possible, particularly in cases of misconfigurations. The server does learn what types of operations are being requested, which could potentially reveal something about the nature of the image processing tasks. Initially, we considered using homomorphic encryption to classify operations and hide this information, but we realized that, if the server offers only a limited set of services, it might deduce the operation type anyway. Furthermore, the server can observe timing patterns that might allow it to infer the complexity of the images being processed, since more complex images may take longer to process, even with FHE encryption. The server also observes access patterns, including the frequency and timing of client requests, which could potentially be analyzed to understand usage behavior.

We are actively considering several approaches to address these remaining privacy concerns in future versions of our framework. Programmable bootstrapping could help hide operation types from the server, making it harder to determine what specific image processing operations are being performed. We could also implement padding and dummy operations to obscure access patterns, making it difficult for the server to distinguish between real requests and noise. Additionally, differential privacy techniques could be applied to obfuscate usage patterns, adding mathematical guarantees about the privacy of client behavior, even when the server observes aggregate statistics.

5. Discussion and Implications

The experimental results effectively demonstrate that quantum-resistant security and practical performance are not mutually exclusive objectives in the design of privacy-preserving cloud services. Our framework successfully integrates post-quantum and homomorphic cryptography into a workable system. However, our investigation highlights several crucial points that merit discussion.

The SIMD scalability results indicate that our approach is particularly well-suited to batch processing scenarios. Medical imaging pipelines or surveillance systems that process many images in succession benefit most from the amortization of the initial setup costs, a common optimization technique in applied FHE systems [5]. While practical for single images, the framework’s full throughput potential is best realized in these multi-transaction sessions. The performance itself is highly practical: with server-side operations completing in approximately 2.5 ms and client-side decryption in approximately 3.4 ms, even for 4096-pixel images, the individual cryptographic stages do not present a bottleneck.

However, our layered design introduces necessary trade-offs. The primary overhead is borne by the client, which is responsible for managing both PQC and FHE cryptographic keys and for performing all encryption and decryption operations. The sequential nature of the protocol—establishing a secure channel, exchanging FHE materials, and then processing data—contributes to the overall latency, although our results show that the individual steps are highly efficient.

When considering practical deployment, several infrastructure requirements must be carefully planned. Client devices need sufficient memory to handle the computationally intensive key generation process, with memory usage peaking at approximately 100 MB during initialization. This requirement is manageable for desktop and server applications but may pose challenges for resource-constrained mobile devices. The network bandwidth requirements are more substantial, involving a 34 MB one-time setup cost for transmitting the FHE public materials, followed by roughly 4 KB per image for the actual encrypted data transfer. On the server side, the computational requirements are surprisingly modest—standard CPU hardware with 2 GB RAM per concurrent session is sufficient, making the framework accessible to organizations without specialized cryptographic hardware.

Integration challenges vary significantly depending on the target environment. Legacy systems often require substantial protocol adaptation since they were not designed with the communication patterns that FHE demands. Mobile deployments present unique opportunities and challenges: while the computational overhead can strain battery life, the key generation phase can be strategically performed during charging periods to minimize user impact. Enterprise deployments introduce additional complexity, particularly around key management, where integration with Hardware Security Modules (HSMs) becomes essential for meeting organizational security policies and regulatory requirements.

Our framework introduces a significant but quantifiable privacy premium. When processing 1000 images, traditional cloud processing costs approximately USD 0.15 (split between USD 0.10 for compute resources and USD 0.05 for storage). Our privacy-preserving approach increases this cost to USD 0.40 ( in a cost analysis based on standard pay-as-you-go pricing for AWS EC2 (c5.large instance) and S3 data transfer as of Q1 2025), with the additional expense primarily driven by increased computation time (USD 0.25), unchanged storage costs (USD 0.05), and network overhead (USD 0.10). This represents roughly a 167% increase in processing costs, which, while substantial, may be justified in privacy-sensitive applications.

The adoption drivers for such a system are compelling in today’s regulatory environment. Organizations subject to GDPR, HIPAA, or financial services regulations increasingly view privacy-preserving computation as a competitive necessity rather than a luxury. Beyond compliance, forward-thinking companies recognize “zero-knowledge” processing capabilities as a significant differentiator in markets where data sensitivity is paramount. The framework also provides tangible risk mitigation benefits, protecting against both traditional data breaches and the emerging quantum threat landscape.

However, several technical barriers may slow adoption. The complexity of FHE requires specialized cryptographic knowledge that many development teams currently lack, creating a skills gap that must be addressed through training or specialized hiring. Performance expectations also present challenges, as stakeholders accustomed to near-instantaneous plaintext processing must adjust to systems that operate 10–100 times slower. Perhaps most significantly, integrating our framework into existing systems requires substantial architectural changes, often necessitating a ground-up redesign of data processing pipelines rather than simple drop-in replacements.

It is also important to contextualize the 33.83 MB size of the FHE public materials. This size should not be directly compared to the key sizes of PQC KEMs (like Kyber’s 0.8 KB public key) or signature schemes. The FHE public materials are significantly larger because they contain the rich mathematical structure (including evaluation keys) necessary to enable computation on encrypted data. This large size is a fundamental trade-off for achieving the powerful functionality of FHE, whereas PQC KEMs and signatures are designed only for key establishment and authentication, respectively.

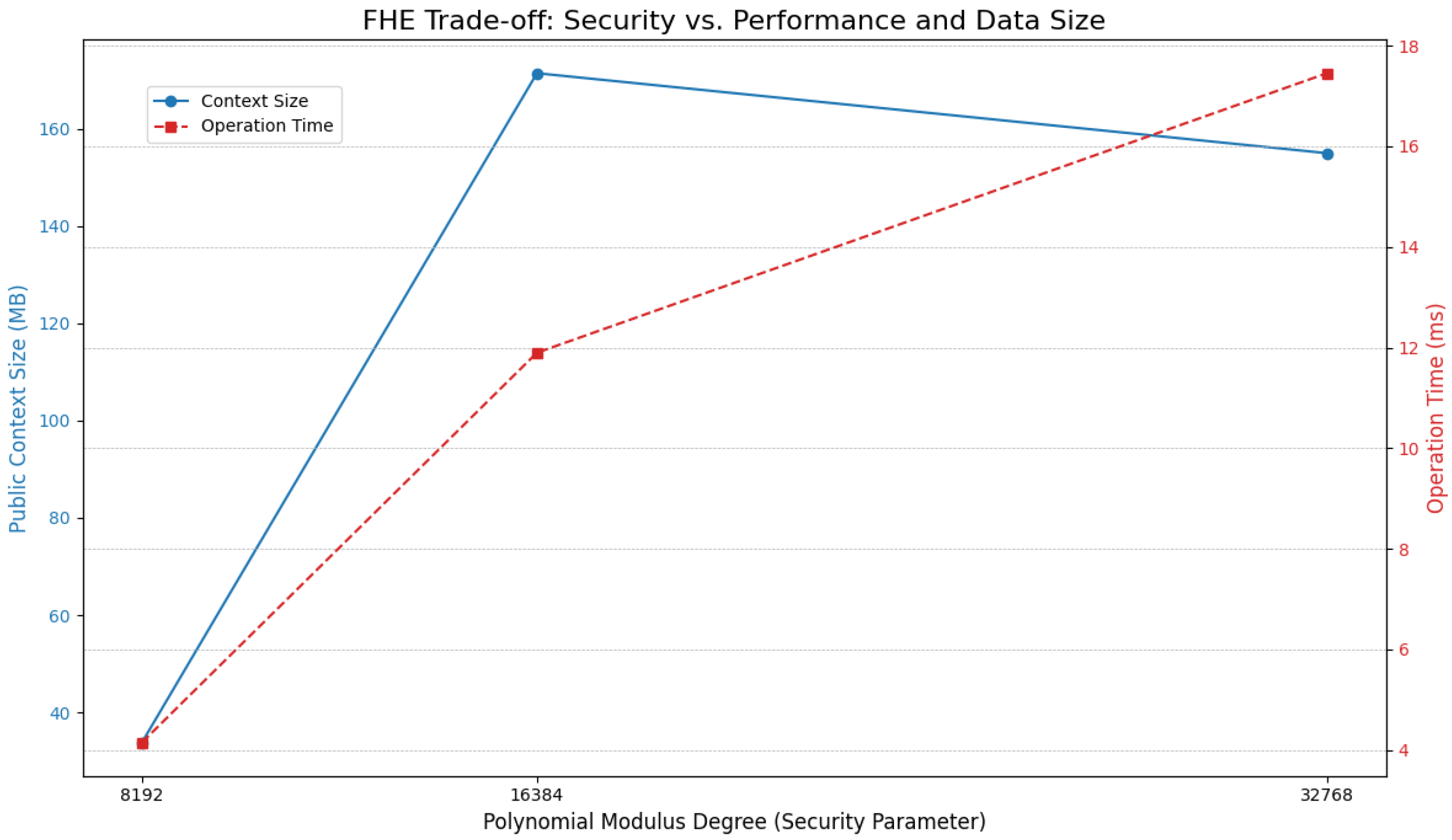
It is also important to consider the trade-offs involved when selecting security parameters for the FHE scheme. While our main evaluation focuses on a practical 128-bit security level, preliminary analysis shows that increasing the security level by using a larger polynomial modulus degree has significant performance implications, as illustrated in Figure 3. Increasing the security parameter leads to a corresponding rise in both data overhead for the public context and computational latency for server-side operations. This highlights a critical decision for practitioners, who must balance the need for long-term data confidentiality against the practical constraints of system performance and bandwidth.

6. Conclusions

This paper effectively shows that high-performance, privacy-preserving computation and quantum-resistant security are no longer mutually exclusive. The proposed framework offers a practical framework for the upcoming generation of secure cloud services by cleverly combining CRYSTALS-Kyber for secure communication, an SIMD-optimized CKKS FHE scheme for computation, and crucial caching measures for efficiency. The outcome shows that our suggested work offers strong security against both classical and quantum adversaries while processing hundreds of pixels within milliseconds. Our thorough scalability analysis provides practitioners with measurable guidance, demonstrating that the framework’s performance is practical for a wide range of image sizes. Based on specific threat models and operational constraints, well-informed decision-making is made possible by the clear connection between security criteria, resource requirements, and performance characteristics.

Our framework provides post-quantum secure communication via CRYSTALS-Kyber-512 (IND-CCA2) combined with AES-GCM (AEAD), and ensures computational privacy through the CKKS FHE scheme under the Ring-LWE assumption (IND-CPA). It also offers side-channel resistance by relying on constant-time implementations and predictable memory access patterns. While operation types and timing patterns may still be visible to the server, future work will address these limitations through bootstrapping, dummy operations, and differential privacy techniques. The architecture remains crypto-agile, allowing Kyber to be replaced with other NIST-standardized post-quantum algorithms as they emerge.