Decision-Time Learning and Planning Integrated Control for the Mild Hyperbaric Chamber
Abstract
1. Introduction
- A decision-time learning and planning integrated framework for MHBC control is established.
- A state context representation learning method is introduced to enable decision-time parameter adaption for modeling environments.
- The dynamic model’s output is optimized compared to PETS algorithm by separately handling epistemic uncertainty and aleatoric uncertainty.
- Value network combined with online policy is applied to guide decision-time planning to optimize the control policy.
2. Problem Formulation
- Decision-time planning generates actions based on the latest state, considering the most up-to-date environmental conditions. In contrast, background planning relies on a pre-trained policy, which may become outdated and require possible retraining upon changing system configuration. In MHBC control, decision-time planning enables adaptive planning based on current conditions, making it more responsive to sudden environmental changes.
- Decision-time planning does not require prior policy learning to take action. As long as an environment model is available, planning can be conducted immediately. In contrast, background planning relies on a policy trained in advance. In MHBC control, decision-time planning directly leverages the environment model trained from previously collected operational data, eliminating the need for further policy learning, which could possibly introduce extra compounding error.
- Decision-time planning performs better in environments that are not visited before. If the system encounters a situation that significantly deviates from the training data distribution, the policy network trained for background planning may struggle to execute tasks efficiently, and in extreme cases may make completely incorrect decisions, leading to out-of-distribution generalization failures. In contrast, decision-time planning uses model-based simulation to explore the best action, making it better suited for handling unexpected situations. In MHBC control, decision-time planning allows the system to adapt dynamically to unforeseen situations.
- While background planning follows a pre-trained policy that does not require significant real-time computation, decision-time planning performs simulation-based optimization at every decision step, which requires more computational resources during deployment. However, computational power in the current computer has improved significantly nowadays, making this concern less relevant in MHBC control scenario.
- Decision-time planning assumes full observability of the environment, which could raise challenges in partially observable situations. If the system cannot fully observe the state of the environment during planning, decision-time planning may suffer to make sub-optimal decisions. To address this, we introduce a state context representation method that captures unobservable system parameters. Additionally, we incorporate uncertainty into the environment model’s output to better handle ambiguities in the state estimation.
- Decision-time planning may result in inconsistent behavior. Since each decision is recomputed independently, the system may exhibit variability in execution trajectories over time. In contrast, background planning learns stable behavioral patterns, leading to more consistent behavior. To mitigate this issue, we integrate a value network to provide extra guidance to the decision-time planning for better performance.
3. Model Learning
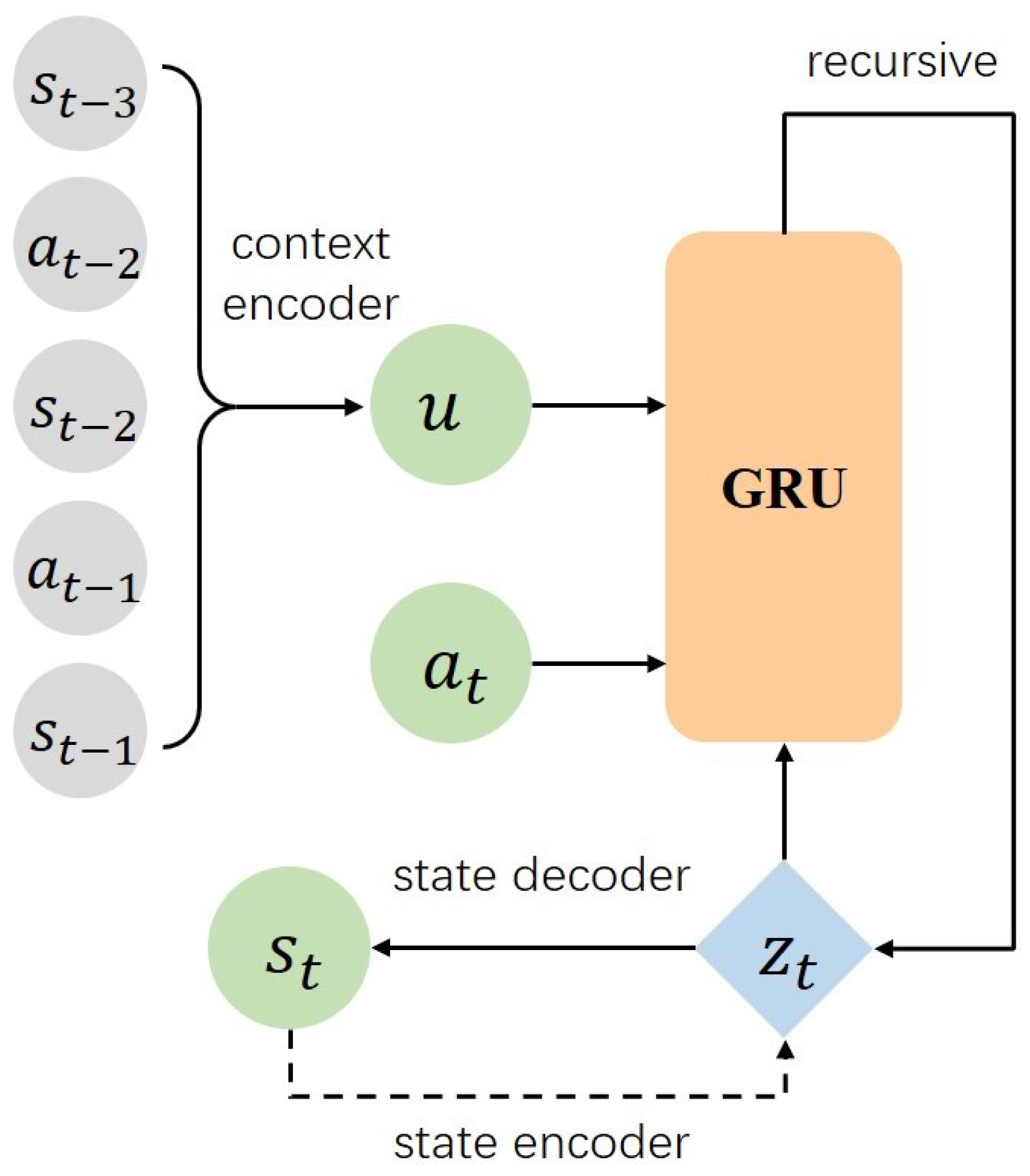
3.1. Decision-Time Learning with State Context Representation
3.2. Model Output Optimization with Separated Uncertainties
4. Control Planning
4.1. Decision-Time Planning with Model Predictive Control
| Algorithm 1: Decision-Time planning with model predictive control |
Input: number of samples N; number of particles P; planning horizon H; initial standard deviation ; model output weights
|
4.2. Policy Strengthening with Value Network
| Algorithm 2: Value network guided Decision-Time planning (VN-DTP) |
Input: learned network parameters ; initial parameters ; number of samples/strategy trajectories ; current state ; planning horizon H; data buffer ; Model-based policy ; online policy ; selection parameter
|
5. Performance Evaluation
5.1. Environment Setup
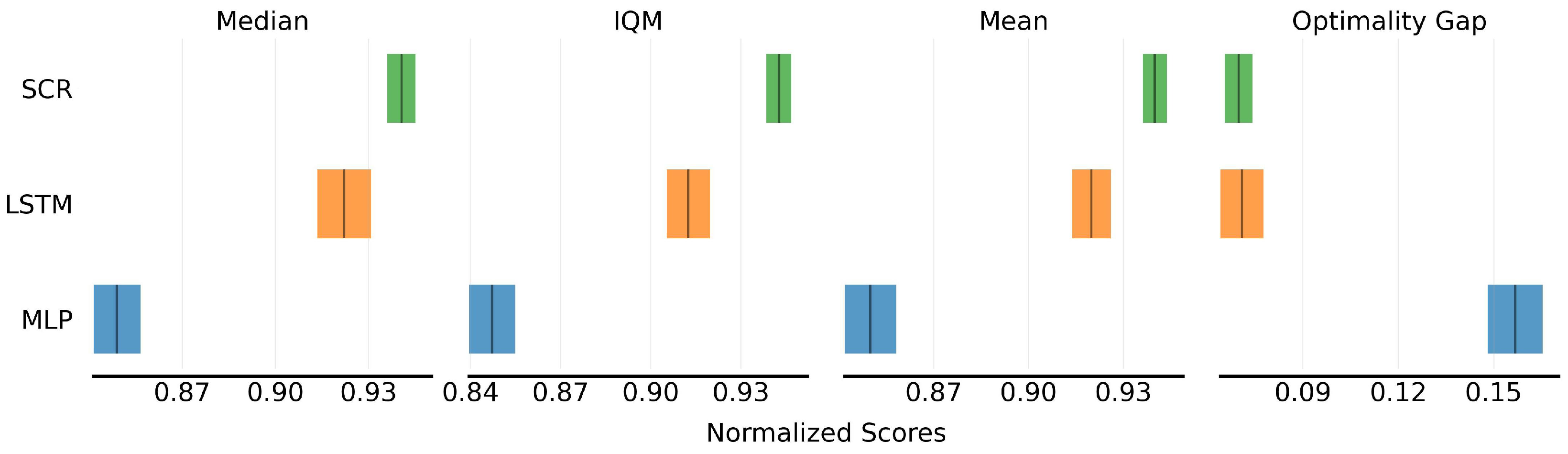
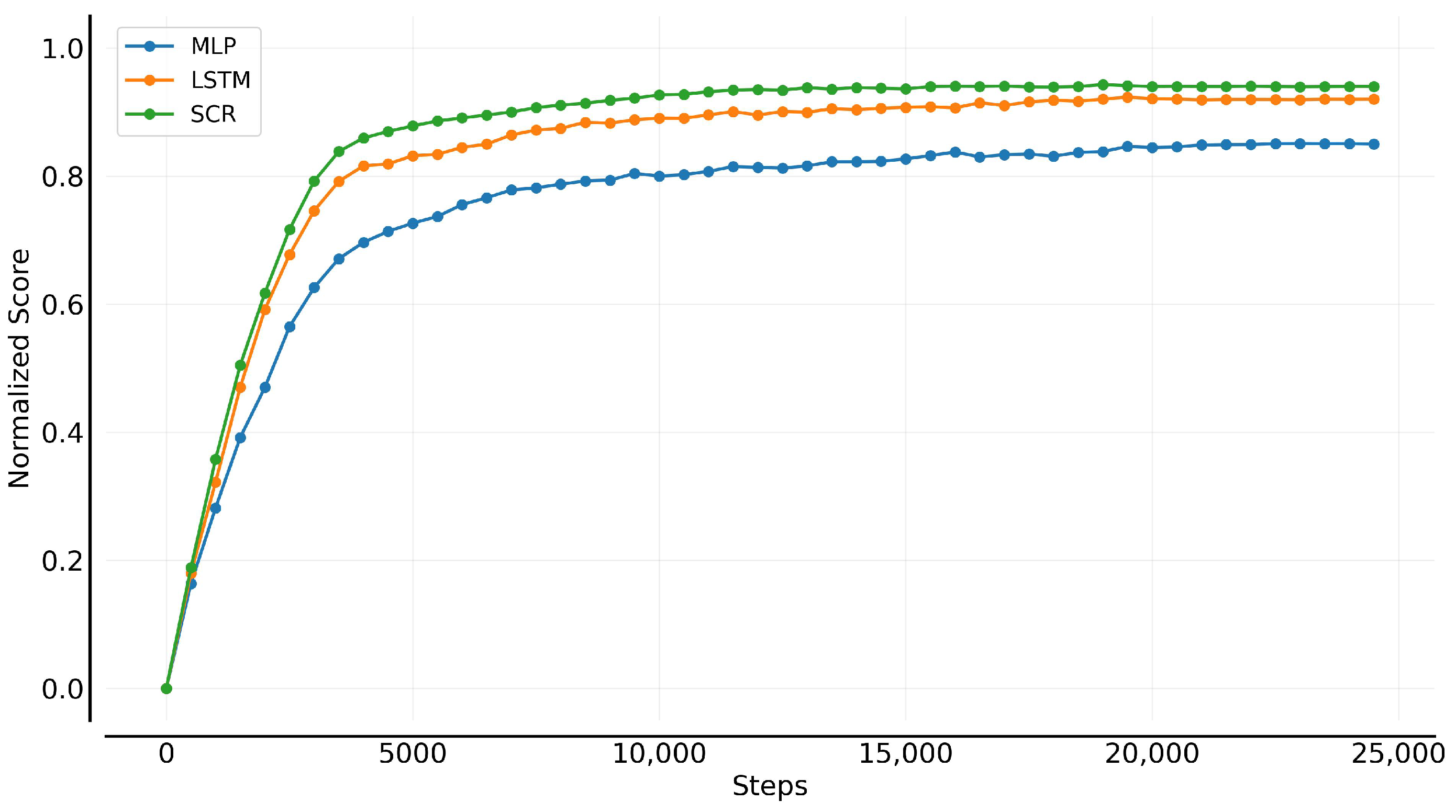
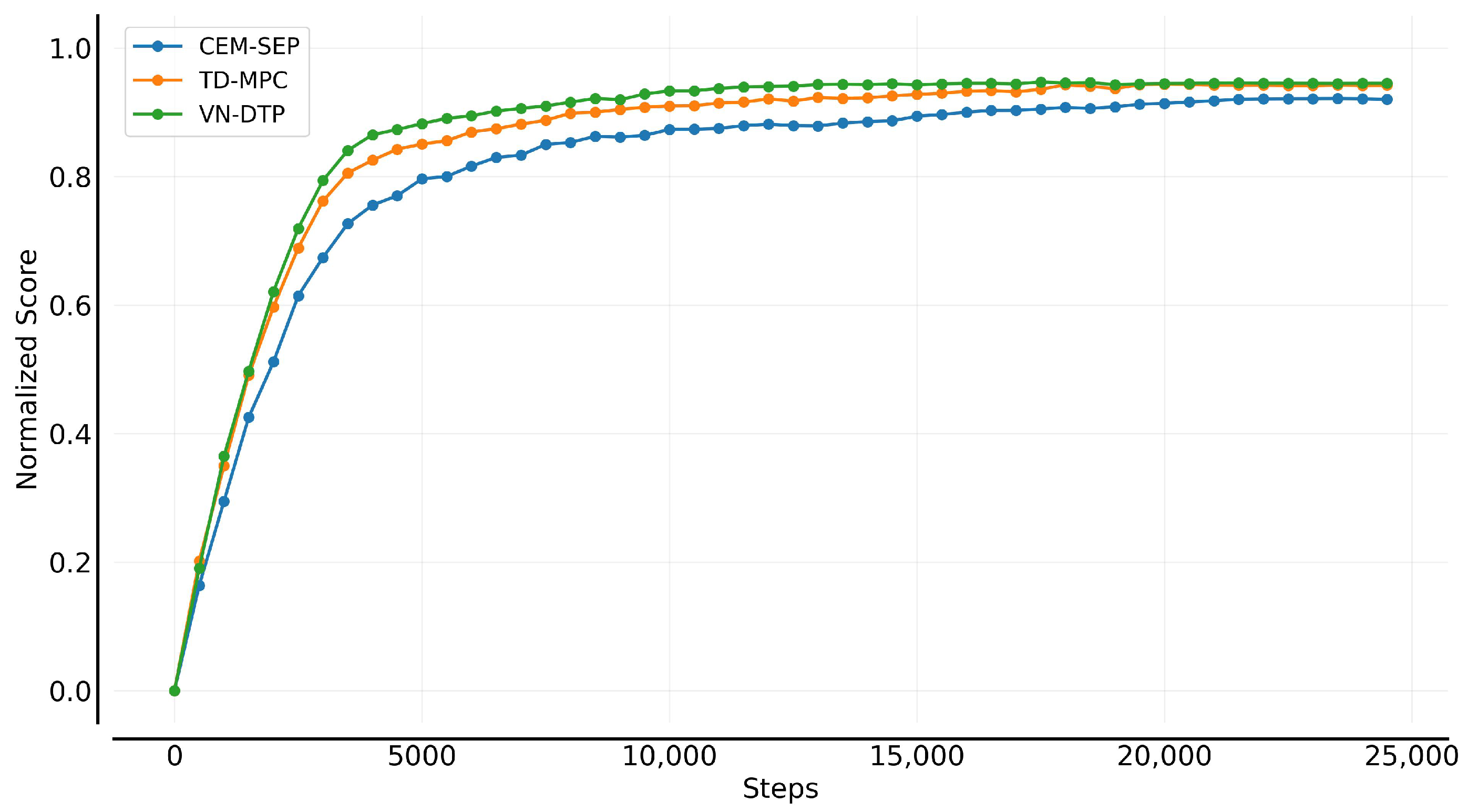
5.2. Model Learning Evaluation
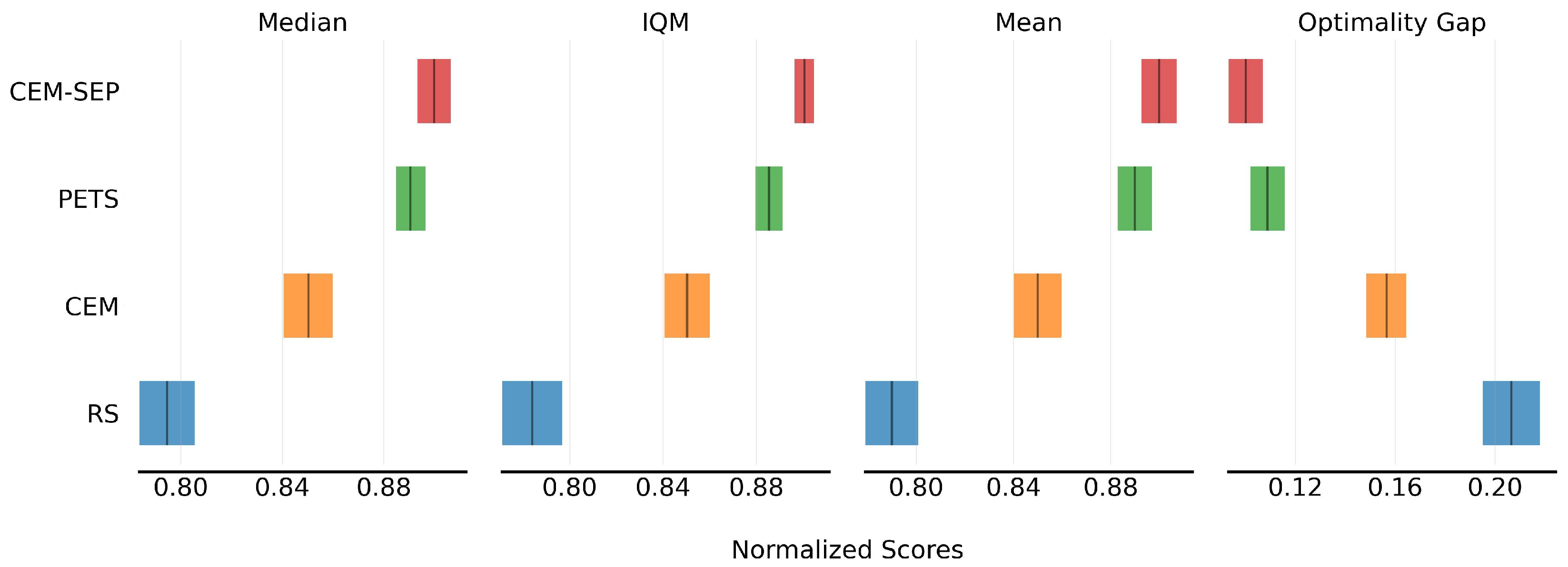
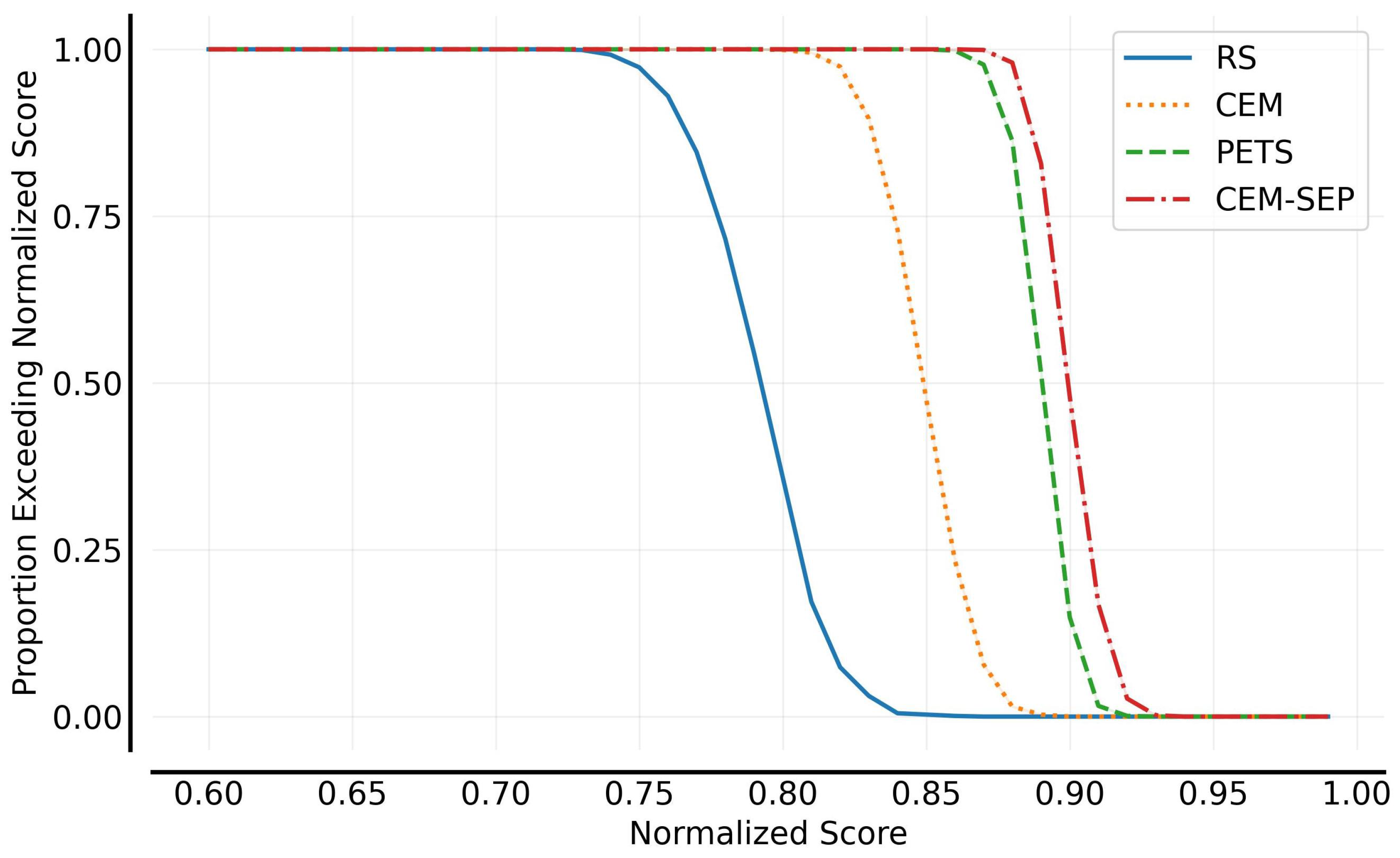
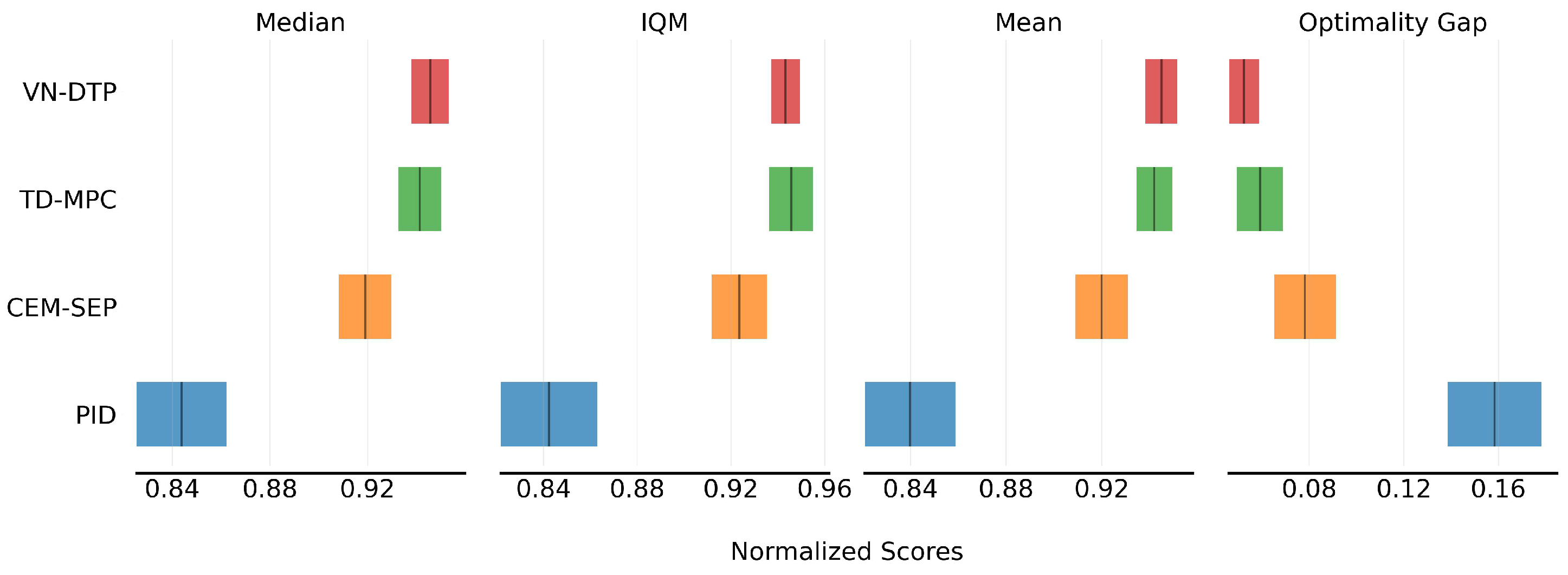
5.3. Control Planning Evaluation
- Valve calibration offset: Simulated by introducing small random disturbances into the valve calibration values.
- Valve failure: Simulated by either setting the valve completely closed or fixing it at a specific opening, with the valve potentially reporting correct or incorrect feedback to the control system.
- Chamber leakage: Simulated by introducing unexpected additional valve openings.
- Valve calibration offset: Originally, the valve opens at a set-point of 5%; due to prolonged usage, it now opens only when the input reaches 6%.
- Valve permanently closed with correct feedback: Valve remains fully closed regardless of inputs, correctly reporting this closed status.
- Valve permanently closed with incorrect feedback: Valve remains fully closed regardless of inputs, incorrectly reporting it as open at the commanded position.
- Valve stuck at fixed opening with correct feedback: Valve remains open at a random fixed opening (2–10%), correctly reporting this actual fixed opening.
- Valve stuck at fixed opening with incorrect feedback: Valve remains open at a random fixed opening (2–10%), incorrectly reporting it as open at the commanded position.
- Simulated chamber leakage: Valve maintains a baseline opening of 1–5%, with additional commanded openings added on top, simulating a chamber leak.
6. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ortega, M.A.; Fraile-Martinez, O.; García-Montero, C.; Callejón-Peláez, E.; Sáez, M.A.; Álvarez-Mon, M.A.; García-Honduvilla, N.; Monserrat, J.; Álvarez-Mon, M.; Bujan, J.; et al. A general overview on the hyperbaric oxygen therapy: Applications, mechanisms and translational opportunities. Medicina 2021, 57, 864. [Google Scholar] [CrossRef] [PubMed]
- Lefebvre, J.C.; Lyazidi, A.; Parceiro, M.; Sferrazza Papa, G.F.; Akoumianaki, E.; Pugin, D.; Tassaux, D.; Brochard, L.; Richard, J.C.M. Bench testing of a new hyperbaric chamber ventilator at different atmospheric pressures. Intensive Care Med. 2012, 38, 1400–1404. [Google Scholar] [CrossRef] [PubMed]
- de Paco, J.M.; Pérez-Vidal, C.; Salinas, A.; Gutiérrez, M.D.; Sabater, J.M.; Fernández, E. Advanced hyperbaric oxygen therapies in automated multiplace chambers. In Proceedings of the 2012 4th IEEE RAS & EMBS International Conference on Biomedical Robotics and Biomechatronics (BioRob), Rome, Italy, 24–27 June 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 201–206. [Google Scholar]
- Wang, B.; Wang, S.; Yu, M.; Cao, Z.; Yang, J. Design of atmospheric hypoxic chamber based on fuzzy adaptive control. In Proceedings of the 2013 IEEE 11th International Conference on Electronic Measurement & Instruments, Harbin, China, 16–19 August 2013; IEEE: Piscataway, NJ, USA, 2013; Volume 2, pp. 943–946. [Google Scholar]
- Gracia, L.; Perez-Vidal, C.; de Paco, J.M.; de Paco, L.M. Identification and control of a multiplace hyperbaric chamber. PLoS ONE 2018, 13, e0200407. [Google Scholar] [CrossRef] [PubMed]
- Motorga, R.M.; Muresan, V.; Abrudean, M.; Valean, H.; Clitan, I.; Chifor, L.; Unguresan, M. Advanced Control of Pressure Inside a Surgical Chamber Using AI Methods. In Proceedings of the 2023 3rd International Conference on Electrical, Computer, Communications and Mechatronics Engineering (ICECCME), Tenerife, Canary Islands, Spain, 19–21 July 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–8. [Google Scholar]
- Ladosz, P.; Weng, L.; Kim, M.; Oh, H. Exploration in deep reinforcement learning: A survey. Inf. Fusion 2022, 85, 1–22. [Google Scholar] [CrossRef]
- Silver, D.; Schrittwieser, J.; Simonyan, K.; Antonoglou, I.; Huang, A.; Guez, A.; Hubert, T.; Baker, L.; Lai, M.; Bolton, A.; et al. Mastering the game of go without human knowledge. Nature 2017, 550, 354–359. [Google Scholar] [CrossRef] [PubMed]
- Wu, T.; He, S.; Liu, J.; Sun, S.; Liu, K.; Han, Q.L.; Tang, Y. A brief overview of ChatGPT: The history, status quo and potential future development. IEEE/CAA J. Autom. Sin. 2023, 10, 1122–1136. [Google Scholar] [CrossRef]
- Tutsoy, O.; Asadi, D.; Ahmadi, K.; Nabavi-Chashmi, S.Y.; Iqbal, J. Minimum distance and minimum time optimal path planning with bioinspired machine learning algorithms for faulty unmanned air vehicles. IEEE Trans. Intell. Transp. Syst. 2024, 25, 9069–9077. [Google Scholar] [CrossRef]
- Afifa, R.; Ali, S.; Pervaiz, M.; Iqbal, J. Adaptive backstepping integral sliding mode control of a mimo separately excited DC motor. Robotics 2023, 12, 105. [Google Scholar] [CrossRef]
- Baillieul, J.; Samad, T. Encyclopedia of Systems and Control; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Borase, R.P.; Maghade, D.; Sondkar, S.; Pawar, S. A review of PID control, tuning methods and applications. Int. J. Dyn. Control 2021, 9, 818–827. [Google Scholar] [CrossRef]
- Luo, F.M.; Xu, T.; Lai, H.; Chen, X.H.; Zhang, W.; Yu, Y. A survey on model-based reinforcement learning. Sci. China Inf. Sci. 2024, 67, 121101. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction. A Bradford Book; The MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Janner, M.; Fu, J.; Zhang, M.; Levine, S. When to trust your model: Model-based policy optimization. In Advances in Neural Information Processing Systems, Proceedings of the 33rd Conference on Neural Information Processing Systems (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019; Curran Associates Inc.: Red Hook, NY, USA, 2019; Volume 32. [Google Scholar]
- Levine, S.; Abbeel, P. Learning neural network policies with guided policy search under unknown dynamics. In Advances in Neural Information Processing Systems, Proceedings of the 28th International Conference on Neural Information Processing Systems, Montréal, QC, Canada, 8–13 December 2014; MIT Press: Cambridge, MA, USA, 2014; Volume 27. [Google Scholar]
- Deisenroth, M.; Rasmussen, C.E. PILCO: A model-based and data-efficient approach to policy search. In Proceedings of the 28th International Conference on Machine Learning (ICML-11), Bellevue, WA, USA, 28 June–2 July 2011; pp. 465–472. [Google Scholar]
- Kahneman, D. A perspective on judgment and choice: Mapping bounded rationality. In Progress in Psychological Science Around the World. Volume 1 Neural, Cognitive and Developmental Issues; Psychology Press: Hove, UK, 2013; pp. 1–47. [Google Scholar]
- Altman, E. Constrained Markov Decision Processes; Routledge: London, UK, 2021. [Google Scholar]
- Kurniawati, H. Partially observable markov decision processes and robotics. Annu. Rev. Control Robot. Auton. Syst. 2022, 5, 253–277. [Google Scholar] [CrossRef]
- Bonassi, F.; Farina, M.; Scattolini, R. On the stability properties of gated recurrent units neural networks. Syst. Control Lett. 2021, 157, 105049. [Google Scholar] [CrossRef]
- Chua, K.; Calandra, R.; McAllister, R.; Levine, S. Deep reinforcement learning in a handful of trials using probabilistic dynamics models. In Advances in Neural Information Processing Systems, Proceedings of the 32nd International Conference on Neural Information Processing Systems, Montréal, QC, Canada, 3–8 December 2018; Curran Associates Inc.: Red Hook, NY, USA, 2018; Volume 31. [Google Scholar]
- Izmailov, P.; Vikram, S.; Hoffman, M.D.; Wilson, A.G.G. What are Bayesian neural network posteriors really like? In Proceedings of the International Conference on Machine Learning, PMLR, Virtual, 18–24 July 2021; pp. 4629–4640. [Google Scholar]
- Hewing, L.; Wabersich, K.P.; Menner, M.; Zeilinger, M.N. Learning-based model predictive control: Toward safe learning in control. Annu. Rev. Control. Robot. Auton. Syst. 2020, 3, 269–296. [Google Scholar] [CrossRef]
- Zhang, Z.; Jin, J.; Jagersand, M.; Luo, J.; Schuurmans, D. A simple decentralized cross-entropy method. In Advances in Neural Information Processing Systems, Proceedings of the 36th International Conference on Neural Information Processing Systems, New Orleans, LA, USA, 28 November–9 December 2022; Curran Associates Inc.: Red Hook, NY, USA, 2022; Volume 35, pp. 36495–36506. [Google Scholar]
- Hansen, N.; Wang, X.; Su, H. Temporal difference learning for model predictive control. arXiv 2022, arXiv:2203.04955. [Google Scholar]
- Agarwal, R.; Schwarzer, M.; Castro, P.S.; Courville, A.C.; Bellemare, M. Deep reinforcement learning at the edge of the statistical precipice. In Advances in Neural Information Processing Systems, Proceedings of the 35th International Conference on Neural Information Processing Systems, Online, 6–14 December 2021; Curran Associates Inc.: Red Hook, NY, USA, 2021; Volume 34, pp. 29304–29320. [Google Scholar]
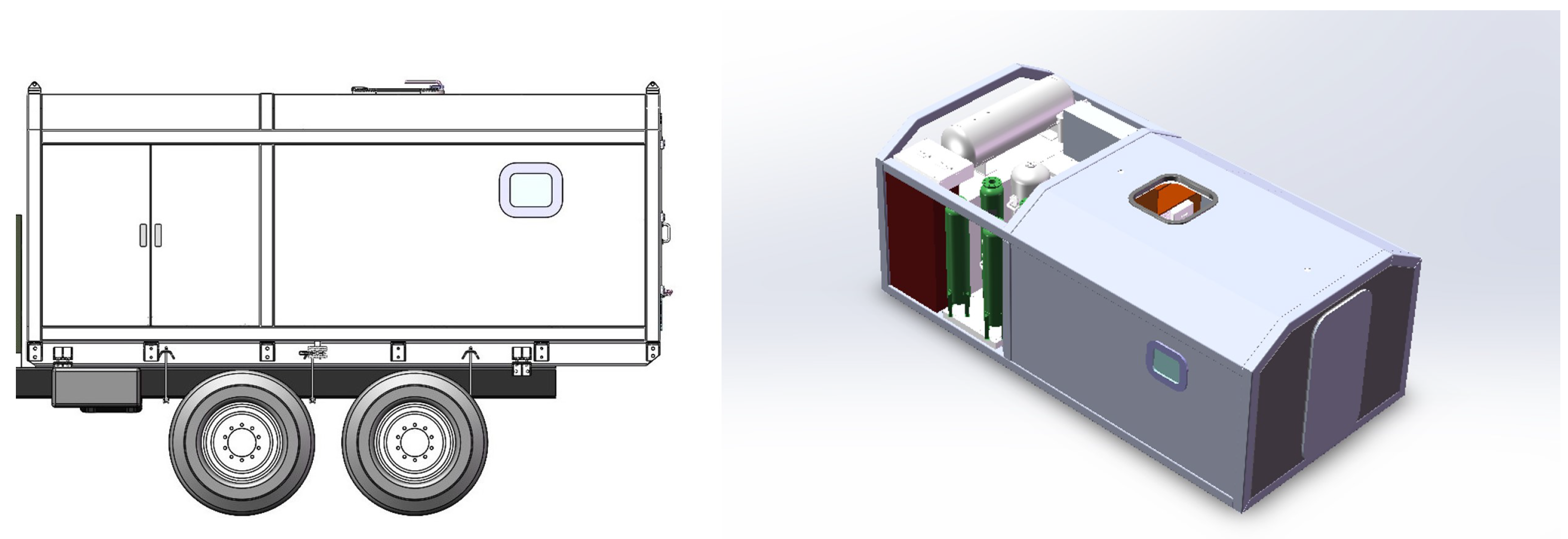
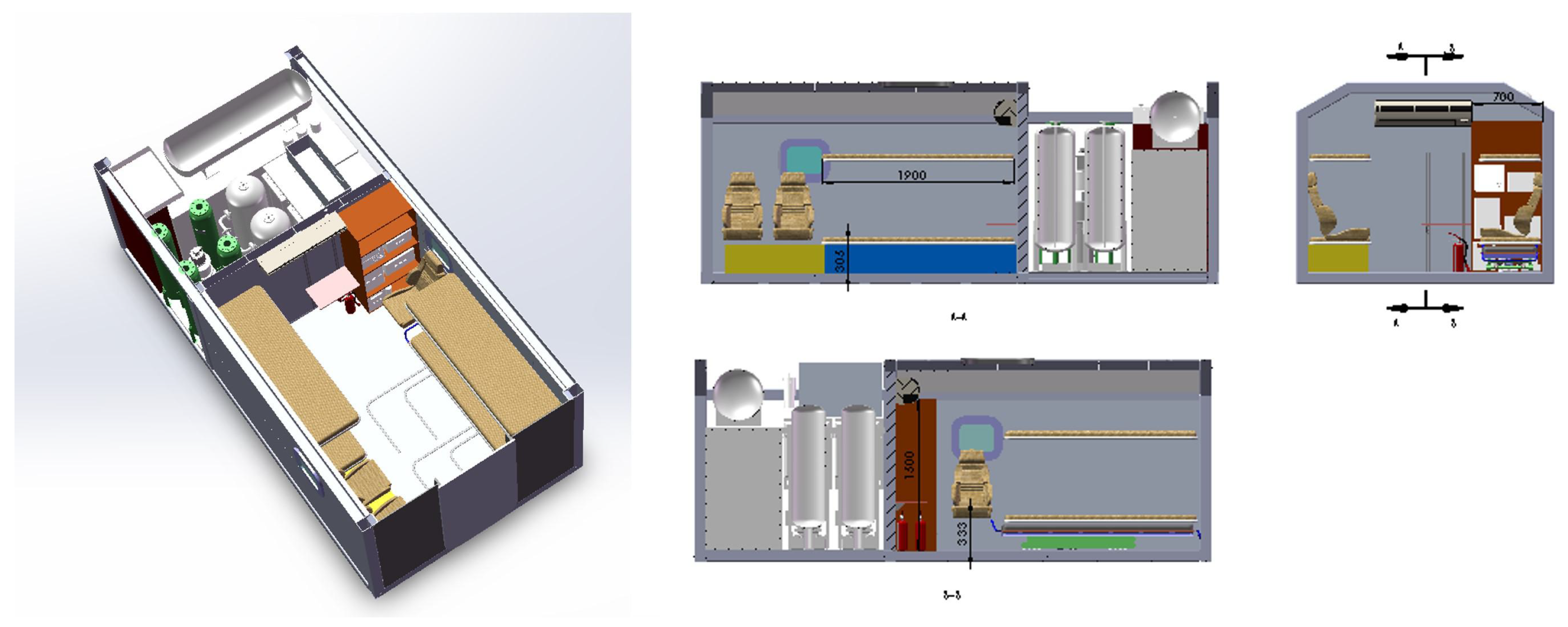
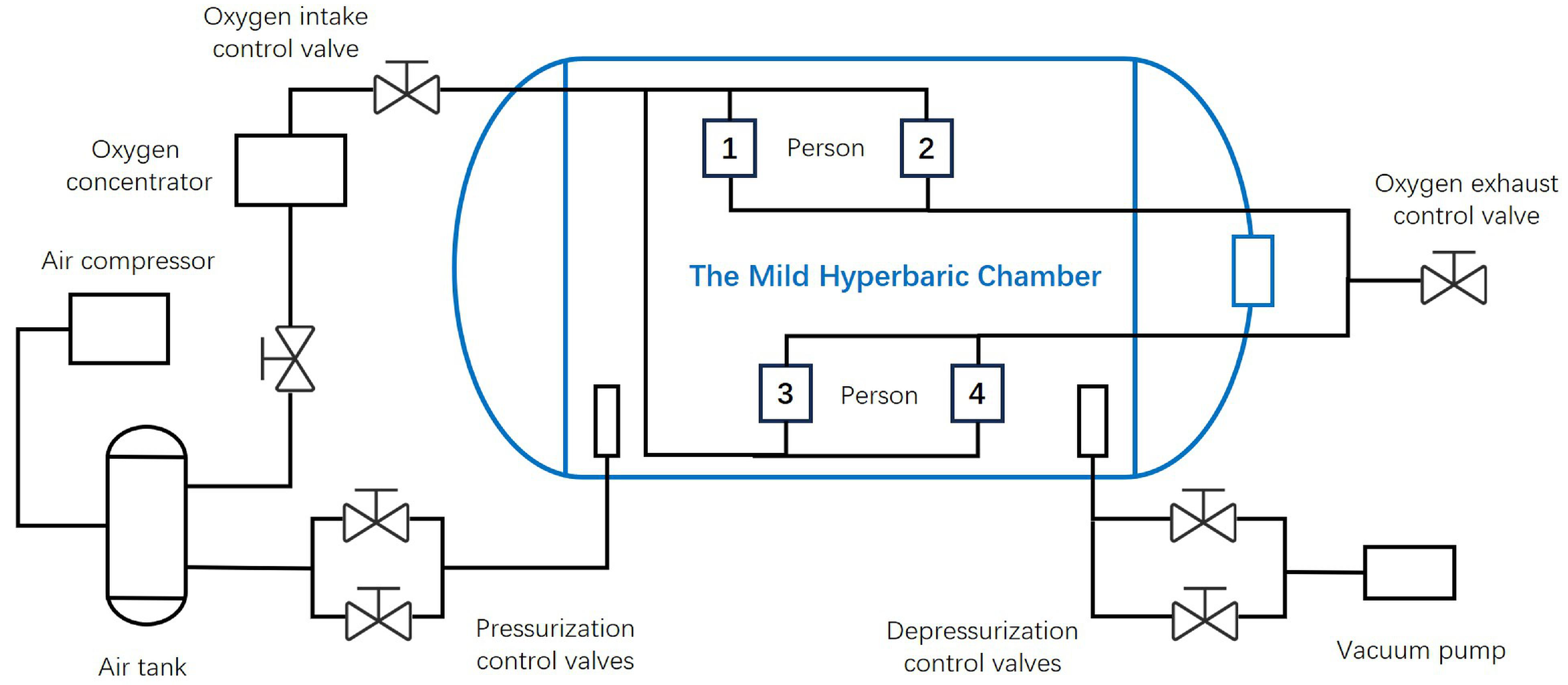
| Technical Specification | MHBC |
|---|---|
| Total chamber volume | |
| Design pressure | 0.155 MPa |
| Maximum operating pressure | 0.150 MPa |
| Cabin temperature | Winter: Summer: |
| Cabin humidity | 40–50% |
| Standard capacity | 4 persons |
| Pressurization rate | |
| Depressurization rate | |
| Oxygen concentration inside | 21–23% |
| Air supply pressure | 0.5 MPa |
| Air storage tank capacity | |
| Air compressor output rate |
| Hyperparameter | Value |
|---|---|
| Discount factor | 0.99 |
| Initial steps | 10 |
| Planning horizon | 30 |
| Initial parameters | (0, 2) |
| Population size | 128 |
| Elite ratio | 16 |
| Iterations | 6 |
| Shrink ratio | 5% |
| Number of particles | 1 |
| Momentum coefficient | 0.1 |
| Learning rate | 3 × 10−4 |
| Optimizer | Adam |
| Temporal coefficient | 0.5 |
| Exploration rate | 0.5 → 0.05 |
| Planning horizon scheduling | |
| Batch size | 128 |
| Momentum coefficient | 0.99 |
| Gradient updates per step | 1 |
| update frequency | 2 |
| Algorithm | Case | Average | |||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| PID | 0.748 | 0.734 | 0.693 | 0.726 | 0.705 | 0.726 | 0.722 |
| CEM-SEP | 0.839 | 0.823 | 0.785 | 0.816 | 0.797 | 0.812 | 0.812 |
| TD-MPC | 0.872 | 0.861 | 0.841 | 0.862 | 0.853 | 0.867 | 0.859 |
| VN-DTP | 0.880 | 0.869 | 0.852 | 0.873 | 0.862 | 0.873 | 0.868 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, N.; Lin, Q.; Jiang, Z. Decision-Time Learning and Planning Integrated Control for the Mild Hyperbaric Chamber. Algorithms 2025, 18, 380. https://doi.org/10.3390/a18070380
Zhang N, Lin Q, Jiang Z. Decision-Time Learning and Planning Integrated Control for the Mild Hyperbaric Chamber. Algorithms. 2025; 18(7):380. https://doi.org/10.3390/a18070380
Chicago/Turabian StyleZhang, Nan, Qijing Lin, and Zhuangde Jiang. 2025. "Decision-Time Learning and Planning Integrated Control for the Mild Hyperbaric Chamber" Algorithms 18, no. 7: 380. https://doi.org/10.3390/a18070380
APA StyleZhang, N., Lin, Q., & Jiang, Z. (2025). Decision-Time Learning and Planning Integrated Control for the Mild Hyperbaric Chamber. Algorithms, 18(7), 380. https://doi.org/10.3390/a18070380







