Abstract
In order to integrate the use of transportation resources, develop a reasonable sea–rail intermodal container transportation plan, and achieve cost reduction and efficiency improvement of the multimodal transportation system, a method for predicting the daily freight volume of sea–rail intermodal transportation based on a convolutional neural network (CNN) algorithm is proposed and a new feature processing method is used: weight assignment (WA). Firstly, we use qualitative methods to preliminarily select the indicators, and then use multiple interpolation to fill in the missing raw data. Next, Pearson and Spearman quantitative analysis methods are used, and the analysis results are grouped using the k-means, with the high correlation groups assigned high weights. Next, we use quadratic interpolation to obtain the daily data. Finally, a weight assignment-enhanced convolutional neural network (WACNN) model and seven other mainstream models are constructed, using the Yingkou port container throughput prediction as a case study. The research results indicate that the WACNN prediction model has the best performance and strong robustness. The research results can provide a reference basis for the planning of sea–rail intermodal container transportation and the allocation of transportation resources, and achieve the overall efficiency improvement of logistics systems.
1. Introduction
1.1. Background and Motivation
Multimodal transport, through the combination of various modes of transport, makes full use of the advantages of multiple modes of transport to complete door-to-door transport services. Sea–rail intermodal transport, an important subset of intermodal transport combining water and rail transportation, can greatly reduce the transit time of goods, simplify the transport process, and improve the efficiency of transport services [1]. In recent years, traffic and transportation networks have been getting better and better, and the mileage of highways and railroads is increasing. At the same time, the container throughput of railroads and waterways is also showing an upward trend, and the market scale of China’s smart port industry is developing rapidly [2,3,4]. The growth volume of the number of containers and public railroad mileage is shown in Figure 1.
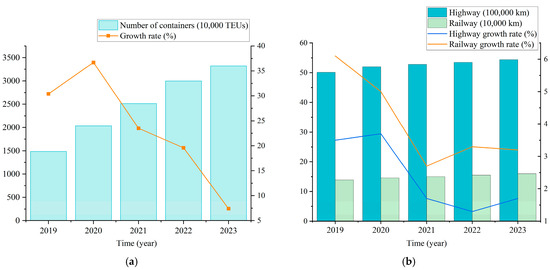
Figure 1.
The growth of number of containers and combined rail mileage. (a) Container throughput quantity and growth rate and (b) rail and road mileage and growth rate.
However, due to weather, policy, and other reasons, sea–rail transportation faces inefficiencies, and these problems lead to the accumulation of cargo in ports and the waste of energy [5]. In response to this problem, a reasonable container throughput forecast could enable a port to layout scheduling in advance and improve the overall efficiency of the port, which could effectively solve this problem. Considering the high-dimensional nonlinear coupling effect and spatiotemporal dynamic characteristics among the multidimensional influencing factors affecting the throughput of sea–rail intermodal containers, traditional time series models that rely solely on historical throughput data have low prediction accuracy. Therefore, this article proposes a prediction method based on multi-indicator feature fusion to improve the accuracy of container throughput prediction.
1.2. Multimethodological Approach and Gaps
The forecasting of container throughput is a typical time series forecasting problem. Changes in a time series are not only influenced by their own historical values, but also closely related to external factors [6]. However, most of the existing studies have focused on the unidimensional correlation between a port’s hinterland economy and the container throughput, and lack a systematic consideration of the synergistic mechanism of multiple factors. But, a reasonable selection of the indicator data can effectively improve the predictive effect of the model [7]. Based on this, how to select suitable index data is one of the problems to be solved. And reasonable data processing is conducive to the improvement of the prediction accuracy of the model. Therefore, after obtaining the indicators, data enhancement methods should be used to improve the data quality.
In the past decade or so, many scholars at home and abroad have tried to use traditional statistical models [8,9], machine learning models [10,11,12,13], and combined models [14,15,16,17] for regression prediction and have achieved fruitful research results. However, statistical models only model linear relationships and are insensitive to nonlinear trends. And they rely on smoothness assumptions and require manual adjustment of the difference and seasonal cycle parameters. Therefore, in recent years, researchers have focused their attention on ML and DL models. For example, Temizceri [18] used various machine learning methods to predict the CO2 emissions from intermodal transport and to optimize transport planning. Bassiouni [19] used four deep learning architectures for recognizing the order status in complex supply chains. It was found that deep learning prediction models work better than machine learning prediction models. Gao [20] used a CNN prediction model and two common machine learning prediction models to predict highway–railway-level crossing accidents, and compared their prediction performances. It was found that the CNN prediction model had a better prediction performance. However, in time series forecasting problems, researchers have focused their goals on traditional forecasting models, and less research has been conducted on deep learning models. Based on this, how to apply deep learning-related models to container throughput forecasting problems is what we need to consider.
In summary, the current research gap can be summarized in two parts. The first is data selection and processing, and the second is the selection of the prediction models. Regarding the data selection and processing, single data decomposition is commonly used for regression prediction. On the contrary, this article uses processing methods, such as multi-index data upsampling and weight assignment. In terms of model selection, unlike previous studies that have used statistical models to predict container throughput, this paper applies a CNN model to time series prediction problems through multi-index time series data.
1.3. Contribution and Paper Organization
Regression prediction using deep learning models can effectively improve prediction accuracy, but there are still some problems. The first is the data level, with a variety of data metrics, and unsuitable data can lead to lower prediction accuracy. Secondly, there is the feature engineering aspect. Considering that deep learning models require more data, we need to choose a suitable method for data enhancement. Finally, the problem of container throughput prediction using DL is faced with a complex network construction and parameter selection, which requires the construction of a suitable structure for the specific problem.
These problems make the container throughput prediction problem difficult to solve. In order to solve these problems and improve the accuracy of container throughput prediction, first of all, for the selection of the data indicators, we summarize the selected indicators in existing container throughput prediction problems and obtain a set of division standards by generalization. Next, we group the indicators and assign weights, and at the same time increase the frequency of the data to achieve the goal of improving the quality of the data. And then, in order to select the appropriate network structure as well as the parameter combinations, we construct multiple sets of network structures as well as parameter combinations. Finally, in order to validate the WACNN model’s effect, multiple mainstream DL and ML models are used for validation and comparison. The main contributions of this study are summarized as follows:
- Firstly, a preliminary screening of the indicators based on qualitative analysis methods, completion of the selection of indicators by formulating scientific division standards, and using missing value analysis to exclude the variables with too high a missing rate; then, using multiple interpolation to fill in the missing data.
- For the feature engineering, we perform a Pearson as well as a Spearman correlation analysis on the selected indicators. Based on the correlation results obtained, the metrics are categorized into multiple groups using a k-means clustering analysis and assigned appropriate weight sizes based on their combined weights. At the same time, the dataset size is increased horizontally using quadratic interpolation.
- In order to select the appropriate model structure, we propose a variety of different network structures and select the most appropriate network structure as well as parameter selection through a comparative analysis. At the same time, in order to verify the prediction effect of the WACNN model, this paper uses a variety of mainstream DL as well as ML models to verify that the WACNN model has the best prediction performance.
The rest of the paper is organized as follows: Section 2 briefly reviews the relevant literature on indicator selection, feature engineering, and DL prediction. Section 3 is an introduction to the methodology, including the indicator selection, feature engineering, WACNN model construction, and evaluation index system selection. The data processing; constructing the complete network structure; and finally, conducting the experiments are shown in Section 4. Finally, in Section 5, the research results are summarized.
2. Literature Review
Through the above analysis of the container throughput forecasting problem, we find that it is very important to improve the accuracy of container forecasting, but there are still some unsolved technical problems. Therefore, we analyze the existing studies in depth by reviewing the literature.
2.1. Indicator Selection
The research on the selection of the indicators for container throughput forecasting has experienced an evolution from a single economic driver to the integration of multiple dimensions [21]. Early studies generally focused on the correlation between macroeconomic indicators and socially productive activities, such as the GDP; the volume of import and export trade; investment in fixed assets; and the output value of secondary industries as the key influencing factors [22]. However, these studies were mostly limited to economic variables, ignoring the impact of other port factors on the throughput. In recent years, scholars have begun to try to construct more complex indicator systems to solve this problem, such as using dimensionality reduction techniques, such as principal component analysis (PCA) and dynamic factor analysis (DFA), to screen the economic indicators with high information density [23,24]. This can significantly reduce the data redundancy while ensuring prediction accuracy. Other researchers have gradually incorporated port-specific operational indicators into the model by studying the port-influencing factors [25], providing a new perspective for explaining throughput differences among ports in the context of regional economic homogenization. Although researchers have started using various indicators for regression prediction, there is no standardized system for the selection of indicators. Therefore, it is not comprehensive enough. In summary, we should summarize the classification criteria in order to select the indicators more reasonably.
2.2. Feature Engineering
For time series forecasting research, the existing methods mostly mine the time series data features through decomposition techniques; for example, decomposing the time series data into multiple sets of feature data and then using correlation regression models for forecasting [26]. However, such methods neglect the optimization value of the data density. Studies have shown that enhancing the temporal frequency can improve the prediction accuracy more effectively than traditional data enhancement means [27]. Based on this, this study proposes to convert low-frequency data into high-frequency sequences by means of a quadratic interpolation algorithm, which directly increases the size of the dataset in order to enhance the data. In terms of feature processing, in addition to increasing the dataset, WA has been proven to improve the prediction accuracy of a model [28]. WA strengthens the impact of the key features and weakens noise interference by quantifying the indicator correlations and setting the weighting coefficients in a hierarchical manner, resulting in higher-quality input data. As for data grouping, correlation analyses, such as Pearson, have commonly been used to detect the magnitude of the correlation between indicators [29]. Meanwhile, a k-means clustering analysis is computationally efficient, works better in low-dimensional grouping problems, and the results can be visualized intuitively [30]. Combining these methods, we first use two correlation indicators, Pearson and Spearman, to check the correlation size between each group of indicators and the container throughput, and then use a k-means to group them together and assign different weights to each group in accordance with the combination of weights. Finally, through the synergistic optimization of data upscaling and feature weighting, a high-quality dataset adapted to this time series prediction task is constructed to provide better input data for the deep learning model.
2.3. Prediction Model Selection Strategy
Deep learning models can not only effectively fit complex nonlinear relationships, but also avoid overfitting problems in shallow structures [31]. In recent years, many researchers have applied deep learning models to time series prediction problems in the transportation field and achieved fruitful results. For example, for traffic flow prediction, Gao introduced a spatiotemporal dynamic model (ST) to integrate the spatial correlation and temporal evolution of traffic flow to capture the dynamic interactions of different nodes in a road network [32]; Pan combined basic graph (FD), Markov, and LSTM models to achieve the progressive prediction of traffic flow [33]; and Zhang designed CASAformer for low-speed congestion scenarios for traffic speed prediction, using a sparse attention mechanism to improve the prediction accuracy [34]. These achievements indicate that the success of deep learning in the field of transportation is due to its ability to mine the complex patterns in high-dimensional spatiotemporal data, especially its ability to dynamically model local features.
However, in the field of container throughput prediction, the application of deep learning has not yet formed a scale. Unlike traffic flow forecasting, container throughput is dominated by long-term global factors, such as macroeconomic cycles and international trade policies, and its data often exhibit strong trends, low-frequency, and high-noise characteristics. Traditional statistical models are still widely used due to their ability to capture the explicit seasonality and linear trends [35]. However, these methods do not take into account the complexity of and variability in the data caused by external environmental changes. Fortunately, deep learning can explore the intrinsic patterns in data and analyze their features [36]. In recent years, scholars have attempted to break through this limitation. For example, Cui [37] and Hirata [38] demonstrated, through comparative experiments, that LSTM outperforms SARIMA and Prophet in most scenarios. Cuong et al. [39] combined a discrete wavelet transform (DWT) with LSTM to validate the effectiveness of deep learning for throughput regression prediction. Liu [40] further introduced the BiLSTM model to improve prediction accuracy using bidirectional time series modeling. However, the existing research has mostly focused on RNNs and their variants, which can capture temporal dependencies but lack the ability to extract local features.
To compensate for this deficiency, some scholars have turned to models with stronger feature extraction capabilities, such as CNNs and GNNs. In practice, Zhang proposed a dynamic graph attention multi-attention network (DGAT-MAN), which significantly improved the prediction performance by modeling the spatiotemporal correlations through graph structures [41]. But such methods rely on precise node relationship definitions. In multi-index time series scenarios, the lack of prior knowledge about node relationships can easily lead to a decrease in model performance. Therefore, this article chooses to apply a CNN model to predict the throughput of sea–rail intermodal containers, as its convolutional kernel can adaptively learn the local correlation patterns between multiple indicators. By extracting the features through a multi-layer network structure, high prediction accuracy can be achieved.
2.4. Summary
Based on the above literature review summary, we use the multiple-input single-output method for container throughput prediction; specifically, by summarizing the indicators used by researchers to derive the division criteria, as a way to select the indicators, and then pre-processing the data. To enhance the data, we use Pearson and Spearman analyses to explore the relationship between each set of metrics and the container throughput, and use this for a k-means grouping of the dataset for a more rational WA. Furthermore, to increase the dataset size, we use the quadratic interpolation method. For model selection, we try to use a CNN model for the container throughput prediction. The following Table 1 shows a comparison between the models that have been used for the container throughput prediction problem and that used in this paper.

Table 1.
Summary of literature containing predictive models.
3. Methodology
3.1. Problem Statement
Accurate prediction of port container throughput is a key link for optimizing intermodal cooperative operation. In order to break through the limitations of traditional forecasting methods, this paper proposes a data-driven forecasting framework to improve the accuracy of throughput prediction by constructing a multidimensional time series regression model, so as to optimize the operational efficiency of ports and promote the efficient collaboration between logistics chains and suppliers. To this end, we design a multidimensional indicator screening framework and innovatively propose a WACNN prediction model. The model takes the screened and data-enhanced multi-source time series indicator data as input, and makes a regression prediction of target data through multiple indicators. The input matrix is shown below:
where ,,, represent sets of indicator data, and represent sets of indicators, each with a total of days of data.
3.2. Feature Selection Method
- Step 1. Preliminary selection of indicators
By summarizing the literature, we systematically categorize and establish four core evaluation dimensions—transportation capacity, infrastructure investment, economic development level, and international openness—thereby constructing a multidimensional assessment framework. Considering regional developmental disparities, we implement a stratified indicator pool strategy for flexible metric adaptation. Specifically, the transportation capacity dimension focuses on freight volume and turnover rates across highway, waterway, and railway networks. Infrastructure investment incorporates fixed-asset indicators from key projects of road, rail, and port construction. Economic development metrics integrate GDP aggregates and industrial structure parameters. International openness evaluation encompasses total import–export volume. Based on this framework, we then collect indicator data.
- Step 2. Data processing
For the collected data, we use a more robust multiple imputation (MI) to complete the data.
The Imputation Phase (IP) is the process of constructing a probability model and generating complete datasets based on observed data. Assuming the interpolation depends on the fully observed covariate and partially observed , the specific formula is as follows:
where is the observed data, is the missing data, is the number of interpolated datasets, and is the model-based predicted distribution. After applying multiple imputation techniques, complete monthly data for multiple indicators are derived. This is subsequently followed by outlier detection via the interquartile range (IQR), calculated as follows:
where is the first quartile, which is the 25th percentile; and is the third or fourth percentile, which is the 75th percentile. From this, it can be concluded that the boundary of outliers is
- Step 3. Correlation analysis
To validate the correlation between the collected data and container throughput, we employ Pearson’s correlation coefficient for the primary correlation analysis and Spearman correlation coefficient for supplementary verification. The formula is as follows:
where represents the sample size; are the observed values of the variables; and are the means of the variables. In the second expression, represents the covariance between and , and and represent the standard deviation of , . Spearman’s rank correlation coefficient is the process of converting raw data into ranks and calculating the Pearson correlation coefficient of ranks. The specific formula is as follows:
where and are the sorted position numbers.
- Step 4. K-means
Next, in this section, in order to more rationally divide the data into multiple groups and give appropriate weights, we use k-means cluster analysis to deal with the correlation of these indicators. Firstly, the objective function of k-means is defined, and here the correlation distance is used with the following formula:
where indicates the total distance within the cluster, which needs to be minimized. denotes the number of clusters. indicates cluster, is a normalized data point, and denotes the mean vector within the cluster. denotes the distance associated with data point from center of mass , which involves the previously mentioned Pearson correlation, and is formulated as follows:
Next, the contour coefficient is chosen as the evaluation criterion, with denoting the contour coefficient of data point , and the overall contour coefficient is the mean of all data points for assessing the clustering quality. The specific formula is as follows:
where denotes the average distance of data point from other points in the same cluster, and denotes the average distance from data point to the nearest other cluster. Using initialization, initialized centers of mass are selected through a probability distribution to maximize the center of mass spacing, where the first center of mass is chosen randomly and the probability of subsequent center of mass selection is inversely proportional to the distance squared with the following formula:
where denotes the minimum distance from the current data point to the selected center of mass and denotes all data points in the data set.
- Step 5. Upsampling
Interpolation, as a meaningful input transformation, is based on the basic principle of using mathematical methods to reasonably infer the values of unknown points between known data points, thereby transforming the data into a form more suitable for model processing. We use the interpolation method to convert monthly data into daily data. Although the statistical characteristics of interpolated data differ from real daily data, its advantages far outweigh the possible disadvantages. The most important aspect is the adaptability of the data. Increasing the amount of data is beneficial for deep learning models and machine learning models to achieve better learning results, while also alleviating the problem of small samples and reducing the risk of overfitting. On the other hand, linear interpolation not only maintains the overall monthly trend but also introduces small fluctuations to simulate natural changes in actual scenarios.
To enhance data diversity and yield more accurate prediction results, quadratic interpolation is applied to the data, transforming the monthly data into daily data. Assuming the time point of monthly data is the first day of each month, the value is ; the corresponding time coordinate is ; and indicates the first day of the first month, indicates the first day of the second month, and so forth. Based on all data points ,,, divided into multiple overlapping three-month windows, with each window containing three consecutive points, the kth window is ,,; and .
Construct a quadratic polynomial——the formula is as follows:
Solve for the coefficient
For any target point , the interpolation result is
After generating daily data using the above formula, calculate the total difference and the corresponding scaling factor for each month to adjust the daily value. Assuming that interval corresponds to raw data , the calibration formula is as follows:
- Step 6. Weight assignment
In neural networks, when the dimensional difference between input data is significant, models tend to focus solely on indicators with large values while overlooking some crucial ones with relatively small values. Data normalization is the process of scaling data proportionally to a specific range, which is mainly used to eliminate dimensional differences and thereby enhance a model’s performance. Therefore, data normalization is generally required before feeding the data into the neural network. Here, the min-max normalization method is adopted and the specific formula is as follows:
where is the normalized value, is the minimum value in a set of data, and is the maximum value in a set of data. The data are effectively linearly mapped onto the [0, 1] interval through Min-Max normalization.
The weight allocation methodology is implemented through correlation-based analysis and k-means. During data normalization, indicators are ranked and grouped according to their correlation coefficients with container throughput, assigning higher weights to strongly correlated groups. The input matrix obtained after assigning weights is as follows:
where represents the number of indicators, represents the number of groups sorted by relevance, represents the indicator and the group, and represents the total number of days of data for each indicator. In the formula, are represented as
where represent the weight multiplied by each group during normalization, from the first group to the group.
For the calculation of weights, we determine the final weight size based on the summed percentage of Pearson as well as Spearman correlations for each group after grouping. The specific formula is as follows:
where is the number of indicators in group and is the total number of indicators. Through the above calculation, we can obtain the specific weights of each correlation group.
3.3. CNN Architecture Design
Convolutional neural network prediction models usually use multiple hidden-layer structures; multiple hidden-layer convolutional neural networks can extract more complex features, and their representation of the input data is stronger. The hidden layers contain multiple convolutional layers and multiple pooling layers, and the pooling operation is chosen here to use maximum pooling. The ReLU activation function is chosen here for the activation function. The dropout function is introduced before full connectivity to prevent overfitting of the model. The construction of the network model is divided into three main parts: the construction of the convolutional layer, the construction of the pooling layer, and the construction of the fully connected layer. The model equations for the construction of each layer are as follows.
where is the feature outputs obtained from the convolution kernel after convolution, represents the convolution operation, is the vector of weights, is the bias vector, and is the activation function.
where is the feature outputs obtained from the convolution kernel after pooling, and represents maximum pooling operations.
where is the feature outputs obtained from the convolution kernel after full connectivity, is the vector of weights, is the bias vector, is the activation function. They use the ReLU activation function. The CNN schematic is shown in Figure 2.
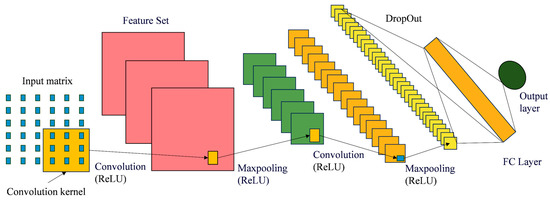
Figure 2.
Schematic diagram of CNN.
3.4. Evaluation
This paper uses five evaluation metrics to comprehensively evaluate the model, namely root mean squared error (RMSE), mean absolute error (MAE), mean bias error (MBE), mean absolute percentage error (MAPE), and r-squared (R2). Among them, RMSE and MAE can measure the size of the error between predicted values and true values. MAPE measures the relative size of prediction error in percentage form. MBE can measure the systematic bias of predicted values. R2 is used to measure the explanatory power of a model for data changes, reflecting the goodness of fit of the model. The five evaluation indicators are as follows.
where is the measured value, is the predicted value, is the mean measured value, and is the number of samples.
3.5. The Framework of This Paper
In this paper, the overall framework of the proposed WACNN model for predicting container throughput is shown in Figure 3.
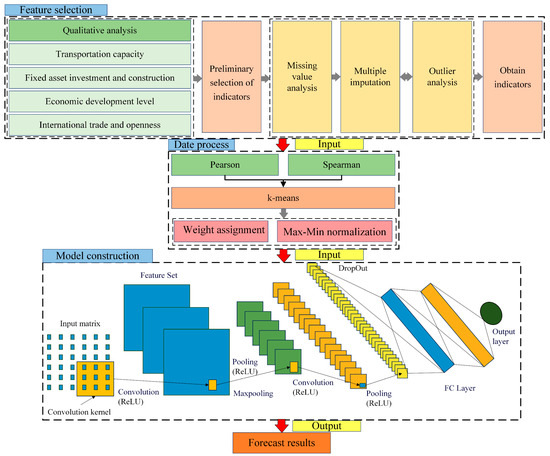
Figure 3.
The overall framework of the proposed WACNN model for predicting container throughput.
- (1)
- The framework starts by using four classification criteria to preliminarily select evaluation indicators. Then, it collects monthly data for each indicator group, conducts missing value analysis and outlier analysis, and uses multiple imputation method to complete the data.
- (2)
- Next, it conducts Pearson and Spearman correlation analyses and uses k-means to group the correlations. Then, it assigns higher weights to the group with higher correlation during normalization.
- (3)
- It uses quadratic interpolation to convert the collected monthly data into daily data.
- (4)
- It builds CNN models separately, and then inputs the WA data into the constructed CNN.
- (5)
- It compares the proposed WACNN with various related models and mainstream models, and validates the analysis using five evaluation criteria.
4. Case Study
In Section 4.1, we analyze and explain the reasons for the selections made in this study. In Section 4.2, we describe the indicator selection methodology, and the specific methods for data processing. In Section 4.3, we detail the overall architecture of and the parameter selection for the seven models. In Section 4.4, we conduct experiments by comparing all the regression models and show the prediction results for each model. Finally, in Section 4.5, we summarize the analysis of the results.
4.1. Data Description
As one of the important ports in China, Yingkou City in Liaoning Province collects and disperses a large number of containers every day. Therefore, container throughput forecasting for Yingkou port is an important logistics and transportation management task. Container transportation involves multiple countries and faces a complex operating environment as well as various uncertainties, which not only increases the complexity of forecasting sea–rail intermodal container transportation for Yingkou port, but also reduces the forecasting performance. Therefore, in order to more accurately predict the container throughput of sea–rail intermodal transportation at Yingkou port, it is necessary to construct a WACNN container throughput prediction model by taking into account the quality of the container throughput data, the correlation between the selected features, and the complexity of the model building to improve the prediction accuracy.
4.2. Data Processing
A combination of quantitative and qualitative analyses was used here for data selection. Qualitative methods were used first. The time series data on sea–rail intermodal container throughput for Yingkou port in Liaoning were selected as the research object for feature selection, and the data were obtained from Liaoning Statistical Yearbook, National Bureau of Statistics, with the relevant statistical data provided by officials for the years from 2014 to 2024. Here, the corresponding evaluation indicators were selected based on four division criteria: the transportation capacity, fixed-asset investment and construction, the economic development level, and international trade and openness. The selection of the evaluation indicators for the four divisional criteria took into account all the public data and indicators for Yingkou City, Liaoning Province, and the whole country, and 33 evaluation indicators were obtained after the statistical organization. The evaluation indicators used under each division standard are shown in Table 2.

Table 2.
Factors affecting container throughput of Yingkou port sea–rail combined transport.
The raw data were analyzed and some missing data were found. For the missing data, multiple interpolation was used to interpolate the missing data values. The fixed-assets investment in road, water, and land transportation in Yingkou and Liaoning, which had more missing values, were eliminated. An outlier analysis was performed on the supplemented data; the outliers were excluded and we continued to use multiple interpolation to make up the difference until there were no outliers in the data.
The Pearson and Spearman correlation coefficients between each factor were obtained through the collated data. Because of the simultaneous use of multiple eigenvalues to predict the sea–rail intermodal container throughput, only the correlation coefficient values of the various influencing factors on the sea–rail intermodal container throughput were screened out, and the correlation coefficients of the influencing factors on the sea–rail intermodal container throughput were obtained after their collation, as shown in Table 3, which can be seen as the degree of influence of the different factors on the sea–rail intermodal container throughput at Yingkou port.

Table 3.
Correlation coefficients of influencing factors on sea–rail intermodal container throughput.
Based on the obtained Pearson and Spearman correlation indices, we grouped them using k-means. To visualize the results, we used a PCA and the results are shown in Figure 4.
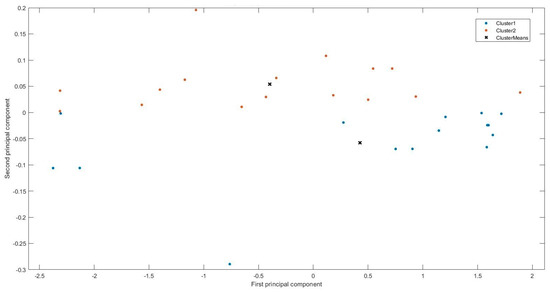
Figure 4.
PCA components of clustered data.
As can be seen in the figure, the 31 sets of indicators are divided into two groups, and the distribution of the two types of data are relatively concentrated, and there is a certain interval between the clusters, indicating that the clustering effectiveness is better. In order to analyze the clustering results in more detail, we plotted the two types of variables and two clusters into a bar chart and a scatter plot, as shown in Figure 5.
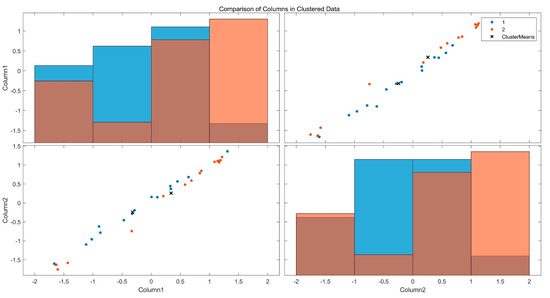
Figure 5.
Comparison of columns in clustered data.
Firstly, in terms of the distribution of variables, there is less overlap in the Pearson correlation distribution in the upper-left corner and the Spearman correlation distribution in the lower-right corner, which indicates that the two clusters have more significant differences in their distribution of the correlation indexes, and that the clustering can effectively differentiate between the data with different correlation characteristics. Second, in terms of the variable correlation, in the scatter plots in the upper-right and lower-left corners, the blue dots and orange dots form relatively independent aggregation areas, indicating that the two clusters, after clustering, have more obvious differences in the association relationship between the Pearson correlation and Spearman correlation, and the clustering is able to effectively differentiate between the different types of data, and the clustering effect is better. The clustering situation is shown in Figure 6.
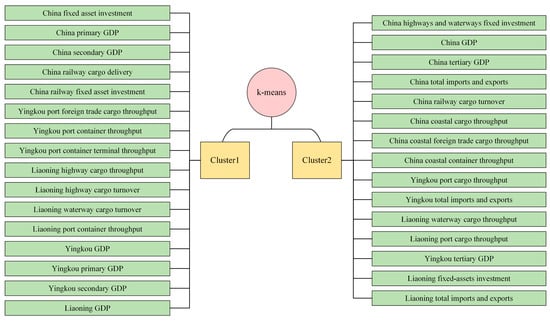
Figure 6.
Grouping results.
Bringing the correlation metrics into the equation yielded a weight ratio of 0.39285:0.60715 for the two groups, which was approximated as 1:1.5. The screened eigenvalues were converted from low frequency to high frequency, using a quadratic interpolation to convert the eigenvalue monthly data into daily data. Finally, a 3834 × 31-sized data set consisting of 3834 days of data for 31 evaluation indexes, including the volume of the sea–rail intermodal container transport at Yingkou hub port, was obtained. The first and second sets of data were imported and the stacked diagrams of the imported data were plotted, as shown in Figure 7 and Figure 8.
Figure 7.
Data stacking chart.
Figure 8.
Data stacking chart.
The following figure shows the second set of stacked data, with the last indicator being the container throughput.
To sum up, the pretreatment in this paper consisted of the following steps. First, 33 indicators were selected according to the classification criteria, and then the indicator data with more missing values were excluded through a missing value analysis, and 31 indicators were obtained. Subsequently, we used multiple imputation and outlier analysis methods many times until there were no outliers in the data. Next, Pearson and Spearman correlation analyses were conducted on the 31 indicators obtained and the container throughput indicators for sea–rail intermodal transport. According to the results obtained, two groups of categories were obtained using k-means clustering. Then, for each group we calculated the sum of the Pearson and Spearman correlations to assign weights. Finally, the monthly data were upsampled into daily data using the quadratic interpolation method to obtain the final input data.
4.3. Parameter Selection
To better test the prediction accuracy and stability of the WACNN model, several models commonly used in regression prediction problems were selected. The CNN, LSTM, BiLSTM, and GRU models for deep learning, and the RF and SVR models for machine learning were used to make a regression prediction of the container throughput of sea–rail intermodal transportation at Yingkou port and compare them at the same time. The structure of the LSTM and BiLSTM models is shown in Figure 9.
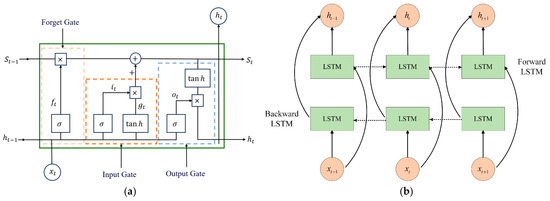
Figure 9.
Model structure. (a) LSTM model structure and (b) BiLSTM model structure.
−Dividing the data into a training set and a test set, using a portion of the data as the training set for training the model, and then comparing the results with those using the remaining portion of the data as the test set, the results predicted by the trained model were used to assess the accuracy of the model’s predictions. To be able to determine better parameters for training the model, several typical values were set as alternative values for each parameter, by referring to the parameter tuning methods in the existing literature. The number of convolutional layers in the CNN model was set as 1, 2, 3, 4, 5, and 6; the number of convolutional kernels per layer were selected as 16-16-16-32-64, 16-16-32-32-64, 16-32-32-32-64, 16-32-64-64-64, and 16-32-64-64-128; and the dropout was selected as 0, 0.1, 0.2, and 0.3. Through numerical experiments, the effects of the model on the RMSE and MAE of the validation set under different parameter configurations were compared, and the values of each parameter corresponding to the optimization of the evaluation index were selected, as shown in Figure 10.
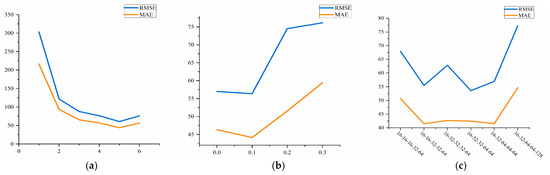
Figure 10.
CNN model parameter tuning diagram. (a) Number of convolutional layers; (b) dropout; and (c) number of convolutional kernels.
Because an increase in the number of layers can lead to overfitting of the model, only a single LSTM layer model and double LSTM layer model were created in the LSTM model. The number of neurons was set to 10, 20, 30, 40, 50, 60, and 70 in the single LSTM; the first layer was set to 10, 20, and 30; and the second layer was set to 10, 20, 30, 40, 50, 60, and 70 in the double LSTM layer. Numerical experiments were conducted to compare the effects of the model on the RMSE and MAE of the validation set under different parameter configurations, and the values of each parameter corresponding to the optimum of the evaluation indexes were selected, as shown in Figure 11.
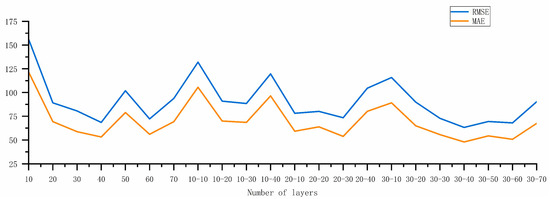
Figure 11.
LSTM model parameter tuning diagram.
In the BiLSTM model, the neurons were set as 10, 20, 30, 40, and 50. The GRU model was set up with two network structures, a single layer and a double layer, and the parameters were set as 16, 32, 64, 128, 16-32, and 32-32, respectively. The comparison of the results is shown in Figure 12 and Figure 13.
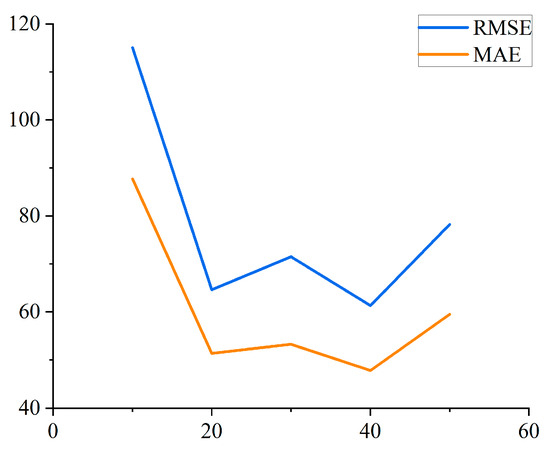
Figure 12.
BiLSTM parameter tuning diagram.
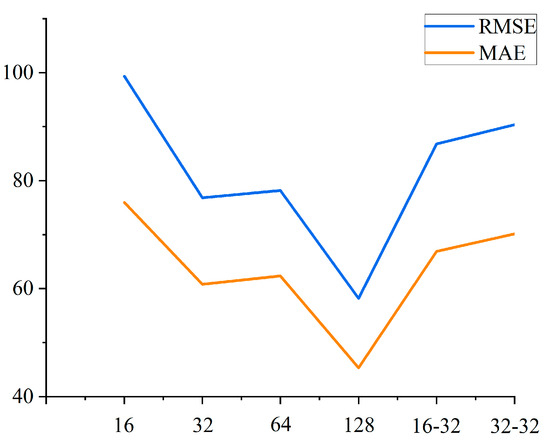
Figure 13.
GRU parameter tuning diagram.
In the RF, the number of decision trees was set to 50, 100, 200, 500, 800, and 1000, and the minimum number of leaves was set to 3, 4, 5, and 6. Numerical experiments were conducted to compare the effects of the model on the validation set’s RMSE and MAE under different parameter configurations and to select the values of each parameter corresponding to the optimization of the evaluation indexes, as shown in Figure 14.
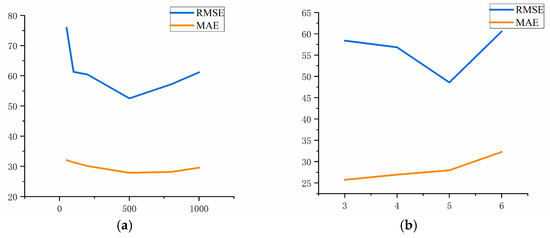
Figure 14.
RF model parameter tuning diagram. (a) Number of decision trees and (b) minimum number of leaves.
In the SVR, the penalty factor was set to 6, 10, 20, 100, 200, and 500, and the parameters of the radial basis function were 0.2, 0.5, 0.8, and 1.0. Through numerical experiments, we compared the effects of the model on the RMSE and MAE of the validation set under different parameter configurations and selected the values of each parameter corresponding to the optimum of the evaluation indexes, as shown in Figure 15.
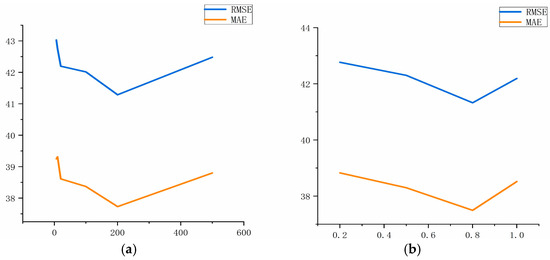
Figure 15.
SVR model parameter tuning diagram. (a) Punishment factor and (b) radial basis function.
In summary, the overall architecture and parameter settings of the CNN model in the experiment are shown in Table 4.

Table 4.
The overall architecture and parameter settings of the CNN model.
As shown in Figure 7, the use of 40 neurons in the single layer model, and 20-30 and 30-40 neurons in the double layer model produced good results. However, it was found in the experiment that if the number of LSTM layers was less, it would result in the model not being able to fully learn the features of the data; so, from an overall consideration, 30-40 neurons in the two-layer model were selected as the optimal parameter here. The overall frameworks and parameter settings of the LSTM, BiLSTM, and GRU models are shown in Table 5.

Table 5.
The overall frameworks and parameter settings of the LSTM, BiLSTM, and GRU models.
The CNN model constructed according to the above process is shown in Figure 16.

Figure 16.
WACNN model.
In the RF model, 2800 sets of data were selected as the training sets, 1034 sets of data were selected as the test sets, the number of decision trees was set to 500, and the minimum number of leaves was set to 5. In the SVR model, 2800 sets of data were selected as the training sets, 1034 sets of data were selected as the test sets, the penalization factor was set to 500, and the parameter of the radial basis function was set to 0.9.
The network training method can be divided into two stages: signal forward propagation and error backpropagation. In the backpropagation process, the gradient descent method gradually approaches the value that minimizes the loss function by calculating the gradient at the current point and then updating the parameters along the opposite direction of the gradient. In this paper, the two most commonly used gradient descent algorithms, Adam and SGDM, are selected and compared. Using the constructed CNN model and the LSTM model, with both models trained 800 times, the two gradient algorithms, SGDM and Adam, are compared. The RMSE using the SGDM is 21.466, and the RMSE value using the Adam is 51.9197, from which can be seen that with the same choice of parameters, the SGDM is more effective than the Adam. In the LSTM model, the RMSE value of the Adam is 74.5857 and the RMSE value of the SGDM is 198.4812, so the SGDM is selected for the WACNN and CNN models and the Adam is selected for the LSTM, BiLSTM, and GRU models. Moreover, the hyperparameter selection of the BiLSTM and GRU is consistent with that of the LSTM.
To verify the stability of the model, we conducted a hyperparameter sensitivity analysis of the proposed model. The stepwise learning rate decay schedule was selected for use. This strategy balanced the need for rapid convergence in the early stages of training with fine tuning in the later stages by reducing the learning rate in stages. Therefore, the batch size, initial learning rate, and learning rate descent factor were selected for the sensitivity analysis. Among them, a batch size that is too small may introduce more noise, while a batch size that is too large may cause the model to become stuck in local solutions or have poor generalization ability. Choosing too small an initial learning rate and learning rate descent factor may lead to slow convergence, while ones too large may cause a sharp drop in the learning rate and miss the optimal solution. Based on the above considerations, the sensitivity analysis range of the selected hyperparameters is shown in Table 6.

Table 6.
Sensitivity analysis.
Based on the above parameter combinations, numerical experiments were conducted to obtain the RMSE under different hyperparameter combinations, as shown in Figure 17.
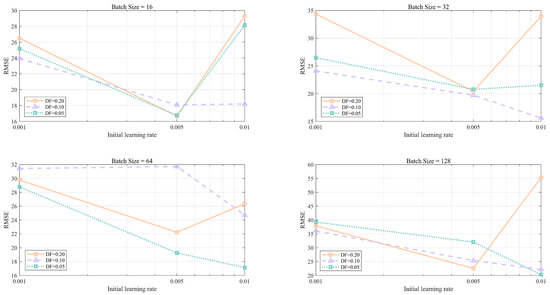
Figure 17.
Sensitivity analysis results.
According to the results in the figure, although the selected hyperparameters have a large range, the overall fluctuation is within an acceptable range. Therefore, the model as a whole has high stability. Finally, we selected the best set of hyperparameter combinations for the WACNN, CNN, and LSTM model hyperparameter settings, as shown in Table 7.

Table 7.
The hyperparameter settings for the WACNN, CNN, and LSTM models.
4.4. Experimental Results
We input the data into the WACNN, CNN, LSTM, BiLSTM, GRU, RF, SVR, and PLS models with the pre-set parameters. In the models used, the PLS serves as the baseline to validate the predictive performance of the various DL and ML methods. The comparison between the predicted values and the true values of each model on the test set is visualized in Figure 18.
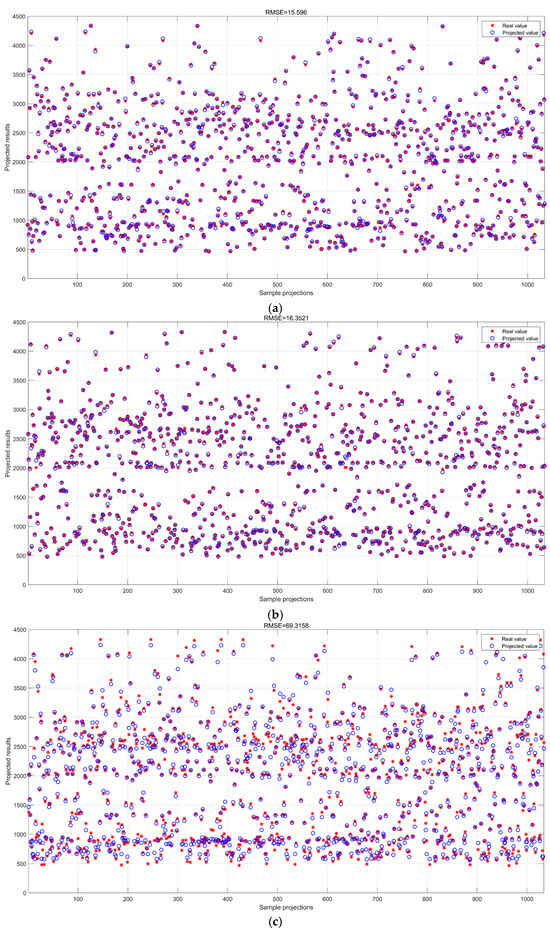
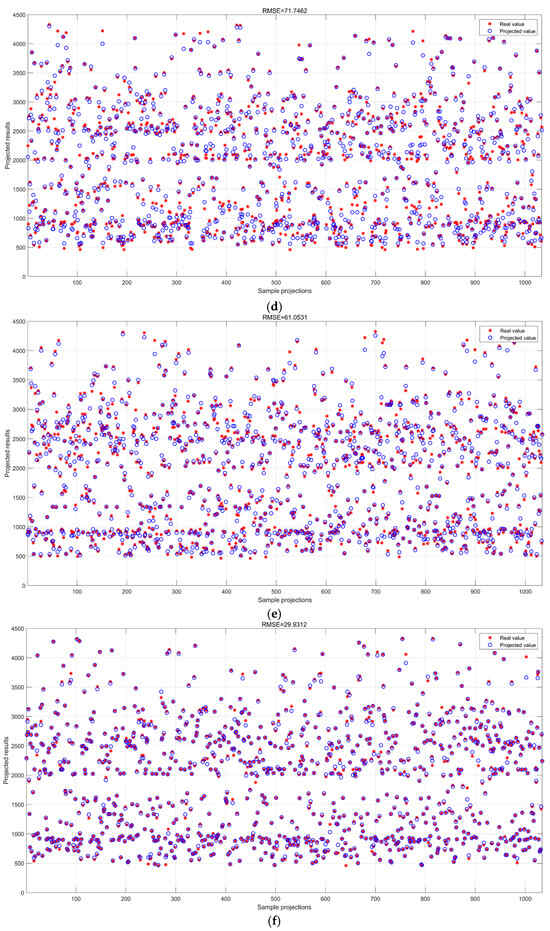
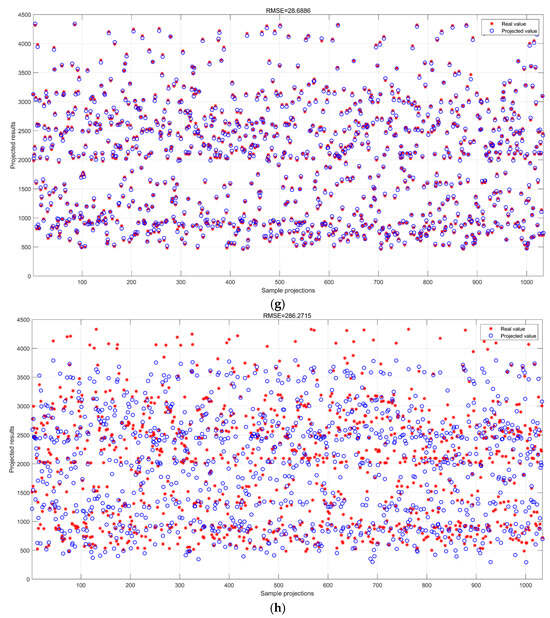
Figure 18.
Test set results. (a) WACNN model test set prediction results; (b) CNN model test set prediction results; (c) LSTM model test set prediction results; (d) BiLSTM model test set prediction results; (e) GRU model test set prediction results; (f) RF model test set prediction results; (g) SVR model test set prediction results; and (h) PLS model test set prediction results.
A comparison of the prediction results of the seven models for the training and test sets is shown in Table 8.

Table 8.
Comparison of model training set and test set prediction results.
From Table 8, the CNN and WACNN performed best on the test set, with RMSEs of 15.596 and 16.3521, respectively, and the WACNN outperformed the CNN, but its training and testing errors were 17.9% and 11.05%, respectively, indicating a certain degree of overfitting. The RF’s overfitting was serious, with a difference of 53.67%, and its generalization ability was poor, whereas the SVR, although stable, with a difference of only 1.04%, had a higher prediction error with an RMSE of 28.6886. The time series models, such as the LSTM, BiLSTM, and GRU, performed worse, with a higher RMSE. The PLS performed the worst.
In order to visualize the predicted values against the true values, we exported the predictions of the seven models and compared them with the true values. As a result of the large amount of data, we zoomed in on the last 100 days of data. The comparison between the predicted and real values of the seven models is shown in Figure 19.
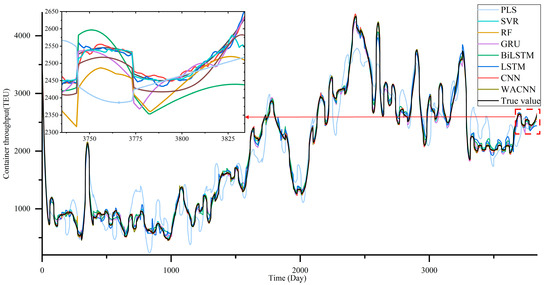
Figure 19.
Comparison between predicted results and actual values.
The figure shows the prediction results of the various models for container throughput compared with the real value. Among them, the WACNN model learned the overall trend of the data very well, and the overall trend of the CNN model was more fitting, but with some fluctuations. Among the three time series models, the LSTM, BiLSTM, and GRU, the BiLSTM model had less fluctuations in relation to the data, and the LSTM and GRU models had more ups and downs and the trend was not very fitting. The two ML results were better than the time series models and their overall trends were smoother. It can be seen that the worst was the PLS, the traditional statistical model. Although the model was consistent with the true values in terms of the overall trend, its predicted results differed significantly from the true values.
The comparison of the values of the RMSE, R2, MAE, MAPE, and MBE for each model on the test set and the improvement rate of the CNN compared to the other models are shown in Table 9.

Table 9.
Comparison of model prediction results.
4.5. Cross-Validation
To further validate the robustness and generalization ability of the WACNN, we used a time series k-fold cross-validation. Choosing 6-fold here meant dividing the original dataset into six cycles of five years. We selected four years of data as the training set and one year of data as the testing set for each cycle, as shown in Table 10.

Table 10.
Cross-validation partitioning strategy.
The partitioned dataset was input into the model, and the results are shown in Table 11.

Table 11.
Cross-validation results.
According to the results of the six-fold cross-validation, it can be seen that the model has good prediction results for the six different datasets, and the errors on the training set and testing machine are within an acceptable range, proving that the proposed model has good stability and generalization ability. Meanwhile, the cross-validation results also demonstrate that the size and volatility of the data have a significant impact on the learning of the model.
4.6. Results Analysis
According to the comparative analysis of the models’ performance in the table, it can be seen that the WACNN and CNN models perform optimally in terms of prediction accuracy, with the WACNN having the highest R2 value of 0.99973, as well as the lowest RMSE and MAE of 15.596 and 11.8649, respectively, with an MBE of 0.1194 and a MAPE as low as 0.0081%, which indicates that the prediction results are close to the true values and have high robustness. The ML models RF and SVR have relatively good performance with a higher prediction accuracy. It is worth noting that the LSTM, BiLSTM, and GRU models have larger prediction errors, with a MAPE over 3%, reflecting that the temporal models may have had insufficient feature capture for this task. The worst performing model is PLS, with a test set RMSE of 286.2715 and a prediction accuracy of only 84%. Compared with the other ML and DL models, there is a significant gap, proving that the performance of these models is indeed better than that of traditional statistical models.
The excellent prediction results of the WACNN and CNN models are due to their convolutional structure that can effectively extract local features and capture spatial correlations in the data, while the WACNN further optimizes the feature learning process by introducing a WA. Unlike traditional CNNs that treat all input data equally, WACNNs focuses models more on the key information that is strongly related to the prediction target because the input data are given different weights. Because in time series or spatial data, certain local segments may contain more significant patterns or trends, the WA mechanism enhances the differentiation of feature representations by increasing the expression weight of these high-value features while weakening the interference of noisy or unimportant regions. In contrast, traditional CNNs lack this explicit weight regulation ability, which may lead to insufficient attention to key features or overfitting of redundant information. Therefore, WACNNs achieve more refined feature filtering and fusion through weight allocation to enhance features.
However, the poor prediction performance of the three time series prediction models is mainly due to the mismatch between their model structure and task characteristics. The core advantage of these three models is their capturing of long-term temporal dependencies, but the input data are relatively large and there are complex nonlinear concerns between the different indicator data, making it difficult for these models to effectively extract valuable information.
The RF and SVR, as traditional machine learning models, perform well on this regression prediction problem. The RF performs better in terms of the error stability, with an MAE and MAPE of 14.0925 and 0.85%, respectively, lower than those of the SVR, thanks to its ensemble learning mechanism’s robustness to noise and outliers. The R2 and RMSE of the SVR are 0.99913 and 28.6886, respectively, slightly better than those of the RF, indicating a strong ability to fit the overall trend of the data. However, its MAE is significantly higher, indicating that there are many large error outliers in the prediction results, which may be related to the sensitivity of the kernel function to high-dimensional features and overfitting to local extrema. The prediction results of both methods are inferior to those of the WACNN model, reflecting the limitations of traditional methods at feature automatic extraction and complex pattern capture, especially when dealing with high-dimensional or implicit spatial correlation data, where the limitations are more pronounced.
Among the compared models, the CNN model and its variants have higher prediction accuracy. Compared to models, such as the LSTM, it has significant improvements, especially for basic statistical models like PLS. Although the improvement of the WACNN is relatively small compared to the CNN, at ports with high container throughput, even a small improvement can have a significant impact due to its large base. On the other hand, even though the CNN model achieves high prediction accuracy, the WACNN can still achieve performance breakthroughs through weight allocation, demonstrating the potential space for model design.
5. Conclusions
This article takes Yingkou port’s sea–rail intermodal container throughput prediction as an example, selects 31 indicators related to sea–rail intermodal container throughput, supplements the collected monthly data using the multiple interpolation method, and then conducts Pearson and Spearman correlation analyses. Based on the correlation indicators, k-means grouping is used, and a WA is performed according to the total weight proportion. Next, the quadratic interpolation method is used to upgrade the monthly data into daily data, which horizontally improves the data quality. The WACNN model is used to solve this prediction problem. Simultaneously, three time series prediction models and two ML models are used for prediction, comparison, and validation, proving that the WACNN model has the best overall prediction performance. The results show that the weight assignment can effectively assist a CNN with capturing and learning local spatial features through feature enhancement. And the WACNN has a strong ability to deal with the regression prediction problem and has strong robustness and strong interpretability.
Traditional time series models typically rely on lagged features as inputs to capture temporal dependencies. However, such methods may result in a systematic bias of the predicted results relative to the true values, due to the time interval between the input features and the target prediction. This model avoids cumulative errors caused by multi-step lag by strictly aligning the time steps of the input and target. The experimental results demonstrate that this prediction method achieves high prediction accuracy. Using the WACNN model to predict the container throughput of the port will help enterprises plan the use of transportation resources and paths to cope with various uncertainties. After predicting the volume of container throughput, the relevant departments will also be able to make appropriate emergency plans to prevent a shortage of capacity caused by a surge in freight volume. In addition, although the prediction results of the model have a certain degree of reference, the accuracy needs further improvement. In order to improve the prediction accuracy, the WACNN model can be combined with other deep learning models so that the accuracy of the prediction results can be improved to a certain extent.
Author Contributions
Y.W.: Writing—original draft preparation, Conceptualization, Data curation, Methodology, Writing—reviewing and editing. W.L.: Supervision, Methodology, Validation, Software, Writing—reviewing and editing. X.Q.: Supervision, Writing—reviewing and editing. Y.Y.: Software and Writing—reviewing and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Hubei Provincial Natural Science Foundation Project–Xiangyang innovation and development joint fund (2025AFD064) and the Philosophy and Social Science Research Project of the Hubei Provincial Department of Education (No. 23Q171).
Data Availability Statement
The data that support the findings of this study are available from the authors on reasonable request.
Acknowledgments
The authors acknowledge the Open Fund of the Hubei Key Laboratory of Power System Design and Test for Electrical Vehicle. Finally, the authors are grateful for the useful contributions made by their project partners.
Conflicts of Interest
Author Yinzhang Yu was employed by the company Xiaohe Lingang Development Group Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Li, B.; Wen, C.; Yang, S.; Ma, M.; Cheng, J.; Li, W. Measuring high-speed train delay severity: Static and dynamic analysis. PLoS ONE 2024, 19, e0301762. [Google Scholar] [CrossRef]
- Guo, J.; Guo, J.; Kuang, T.; Wang, Y.; Li, W. The short-term economic influence analysis of government regulation on railway freight transport in continuous time. PLoS ONE 2025, 20, e0298614. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Zhou, S.; Liu, S. Optimization of Multimodal Transport Paths Considering a Low-Carbon Economy Under Uncertain Demand. Algorithms 2025, 18, 92. [Google Scholar] [CrossRef]
- Pellicer, D.S.; Larrodé, E. Analysis of the Effectiveness of a Freight Transport Vehicle at High Speed in a Vacuum Tube (Hyperloop Transport System). Algorithms 2024, 17, 17. [Google Scholar] [CrossRef]
- Xie, G.; Zhang, N.; Wang, S. Data characteristic analysis and model selection for container throughput forecasting within a decomposition-ensemble methodology. Transp. Res. E Logist. Transp. Rev. 2017, 108, 160–178. [Google Scholar] [CrossRef]
- Milenković, M.; Milosavljevic, N.; Bojović, N.; Val, S. Container flow forecasting through neural networks based on metaheuristics. Oper. Res. 2021, 21, 965–997. [Google Scholar] [CrossRef]
- Dragan, D.; Keshavarzsaleh, A.; Intihar, M.; Popović, V.; Kramberger, T. Throughput forecasting of different types of cargo in the Adriatic seaport Koper. Marit. Policy Manag. 2020, 48, 19–45. [Google Scholar] [CrossRef]
- Homayoonmehr, R.; Rahai, A.; Ramezanianpour, A.A. Predicting the chloride diffusion coefficient and surface electrical resistivity of concrete using statistical regression-based models and its applicationin chloride-induced corrosion service life prediction of RC structures. Constr. Build. Mater. 2022, 357, 1–25. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, J.; Zhang, S.; Li, G.; Jeng, D.S.; Xu, J.; Tian, Z.; Xu, X. An optimal statistical regression model for predicting wave-induced equilibrium scour depth in sandy and silty seabeds beneath pipelines. Ocean Eng. 2022, 258, 1–14. [Google Scholar] [CrossRef]
- Castro-Neto, M.; Jeong, Y.S.; Jeong, M.K.; Han, L.D. Online-SVR for short-term traffic flow prediction under typical and atypical traffic conditions. Expert Syst. Appl. 2009, 36, 6164–6173. [Google Scholar] [CrossRef]
- Zeng, Z.; Ying, G.; Zhang, Y.; Gong, Y.; Mei, Y.; Li, X.; Sun, H.; Li, B.; Ma, J.; Li, S. Classification of failure modes, bearing capacity, and effective stiffness prediction for corroded RC columns using machine learning algorithm. J. Build. Eng. 2025, 102, 111982. [Google Scholar] [CrossRef]
- Tang, L.; Zhao, Y.; Cabrera, J.; Ma, J.; Tsui, K.L. Forecasting Short-Term Passenger Flow: An Empirical Study on Shenzhen Metro. Trans. Intell. Transp. Syst. 2019, 20, 3613–3622. [Google Scholar] [CrossRef]
- Haas, C.; Budin, C.; D’arcy, A. How to select oil price prediction models—The effect of statistical and financial performance metrics and sentiment scores. Energy Econ. 2024, 133, 1–14. [Google Scholar] [CrossRef]
- Zhou, W.; Zhou, Y.; Liu, R.; Yin, H.; Nie, H. Predictive modeling of river blockage severity from debris flows: Integrating statistical and machine learning approaches with insights from Sichuan Province, China. Catena 2025, 248, 1–15. [Google Scholar] [CrossRef]
- Tan, M.C.; Wong, S.C.; Xu, J.M.; Guan, Z.R.; Zhang, P. An aggregation approach to short-term traffic flow prediction. Trans Intell. Transp. Syst. 2009, 10, 60–69. [Google Scholar] [CrossRef]
- Khashei, M.; Bijari, M. A novel hybridization of artificial neural networks and ARIMA models for time series forecasting. Appl Soft Comput. 2011, 11, 2664–2675. [Google Scholar] [CrossRef]
- Ruiz-Aguilar, J.; Turias, I.; Jiménez-Come, M. Hybrid approaches based on SARIMA and artificial neural networks for inspection time series forecasting. Transp. Res. E Logist. Transp. Rev. 2014, 67, 1–13. [Google Scholar] [CrossRef]
- Temizceri, F.T.; Kara, S.S. Towards sustainable logistics in Turkey: A bi-objective approach to green intermodal freight transportation enhanced by machine learning. Res. Transp. Bus. Manag. 2024, 55, 101145. [Google Scholar] [CrossRef]
- Bassiouni, M.M.; Chakrabortty, R.K.; Sallam, K.M.; Hussain, O.K. Deep learning approaches to identify order status in a complex supply chain. Expert Syst. Appl. 2024, 250, 1–28. [Google Scholar] [CrossRef]
- Gao, L.; Lu, P.; Ren, Y. A deep learning approach for imbalanced crash data in predicting highway-rail grade crossings accidents. Reliab. Eng. Syst. Saf. 2021, 216, 108019. [Google Scholar] [CrossRef]
- Zhuang, X.; Li, W.; Xu, Y. Port planning and sustainable development based on prediction modelling of port throughput: A case study of the deep-water Dongjiakou Port. Sustainability 2022, 14, 4276. [Google Scholar] [CrossRef]
- Shankar, S.; Ilavarasan, P.V.; Punia, S.; Singh, S.P. Forecasting container throughput with long short-term memory networks. Ind. Manag. Data Syst. 2020, 120, 425–441. [Google Scholar] [CrossRef]
- Shankar, S.; Punia, S.; Ilavarasan, P.V. Deep learning-based container throughput forecasting: A triple bottom line approach. Ind. Manag. Data Syst. 2021, 121, 2100–2117. [Google Scholar] [CrossRef]
- Awah, P.C.; Nam, H.; Kim, S. Short term forecast of container throughput: New variables application for the Port of Douala. J. Mar. Sci. Eng. 2021, 9, 720. [Google Scholar] [CrossRef]
- Tang, S.; Xu, S.; Gao, J. An optimal model based on multifactors for container throughput forecasting. KSCE J. Civ. Eng. 2019, 23, 4124–4131. [Google Scholar] [CrossRef]
- Li, F.; Tong, W.; Yang, X. Short-term forecasting for port throughput time series based on multi-modal fuzzy information granule. Appl. Soft Comput. 2025, 174, 112957. [Google Scholar] [CrossRef]
- Semenoglou, A.A.; Spiliotis, E.; Assimakopoulos, V. Data augmentation for univariate time series forecasting with neural networks. Pattern Recognit. 2023, 134, 109132. [Google Scholar] [CrossRef]
- Wang, W.; Zhao, C.; Wu, Y. Spatial weighting—An effective incorporation of geological expertise into deep learning models. Geochemistry 2024, 84, 126212. [Google Scholar] [CrossRef]
- Dai, Y.; Yu, W.; Leng, M. A hybrid ensemble optimized BiGRU method for short-term photovoltaic generation forecasting. Energy 2024, 299, 131458. [Google Scholar] [CrossRef]
- Shukla, D.; Chowdary, C.R. A model to address the cold-start in peer recommendation by using k-means clustering and sentence embedding. J. Comput. Sci. 2024, 83, 102465. [Google Scholar] [CrossRef]
- Xiao, J.; Wen, Z.; Liu, B.; Chen, M.; Wang, Y.; Hang, J. A hybrid model based on selective deep-ensemble for container throughput forecasting. Syst. Eng. Theory Pract. 2022, 42, 1107–1128. [Google Scholar] [CrossRef]
- Gao, H.; Jia, H.; Huang, Q.; Wu, R.; Tian, J.; Wang, G.; Liu, C. A hybrid deep learning model for urban expressway lane-level mixed traffic flow prediction. Eng. Appl. Artif. Intell. 2024, 133, 1–21. [Google Scholar] [CrossRef]
- Pan, Y.A.; Guo, J.; Chen, Y.; Cheng, Q.; Li, W.; Liu, Y. A fundamental diagram based hybrid framework for traffic flow estimation and prediction by combining a Markovian model with deep learning. Expert Syst. Appl. 2024, 238, 122219. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, Q.; Wang, J.; Kouvelas, A.; Makridis, M.A. CASAformer: Congestion-aware sparse attention transformer for traffic speed prediction. Commun. Transp. Res. 2025, 5, 100174. [Google Scholar] [CrossRef]
- Nguyen, T.; Cho, G. Forecasting the Busan container volume using XGBoost approach based on machine learning model. J Internet Things Converg. 2024, 10, 39–45. [Google Scholar] [CrossRef]
- Lee, E.; Kim, D.; Bae, H. Container volume prediction using time-series decomposition with a long short-term memory models. Appl. Sci. 2021, 11, 8995. [Google Scholar] [CrossRef]
- Cui, J.; Liu, B.; Xu, Y.; Guo, X. Regional collaborative forecast of cargo throughput in China’s Circum-Bohai-Sea Region based on LSTM model. Comput. Intell. Neurosci. 2022, 2022, 5044926. [Google Scholar] [CrossRef]
- Hirata, E.; Matsuda, T. Forecasting Shanghai Container Freight Index: A deep-learning-based model experiment. J. Mar. Sci. Eng. 2022, 10, 593. [Google Scholar] [CrossRef]
- Cuong, T.N.; Long, L.N.B.; Kim, H.S.; You, S.S. Data analytics and throughput forecasting in port management systems against disruptions: A case study of Busan Port. Marit. Econ. Logist. 2023, 25, 61–89. [Google Scholar] [CrossRef]
- Liu, B.; Wang, X.; Liang, X. Neural network-based prediction system for port throughput: A case study of Ningbo-Zhoushan Port. Res. Transp. Bus. Manag. 2023, 51, 101067. [Google Scholar] [CrossRef]
- Zhang, L.; Schacht, O.; Liu, Q.; Ng, A.K. Predicting inland waterway freight demand with a dynamic spatio-temporal graph attention-based multi attention network. Transp. Res. Part. E Logist. Transp. Rev. 2025, 199, 104139. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).