Patient-Specific Hyperparameter Optimization of a Deep Learning-Based Tumor Autocontouring Algorithm on 2D Liver, Prostate, and Lung Cine MR Images: A Pilot Study
Abstract
1. Introduction
- Patient-specific HPO was performed, tailoring the hyperparameters for each patient dataset to achieve the best possible autocontouring performance.
- The first application of CMA-ES for optimizing the hyperparameters of a U-Net-based autocontouring algorithm is presented.
- The proposed algorithm is the first tumor autocontouring algorithm specifically applicable to the intrafractional MR images of liver and prostate cancer patients for nifteRT.
- A total of 47 in vivo MR image sets were acquired to evaluate the algorithm, which achieved comparable contouring performance to that of human experts.
2. Materials and Methods
2.1. Patient Imaging and Manual Contouring
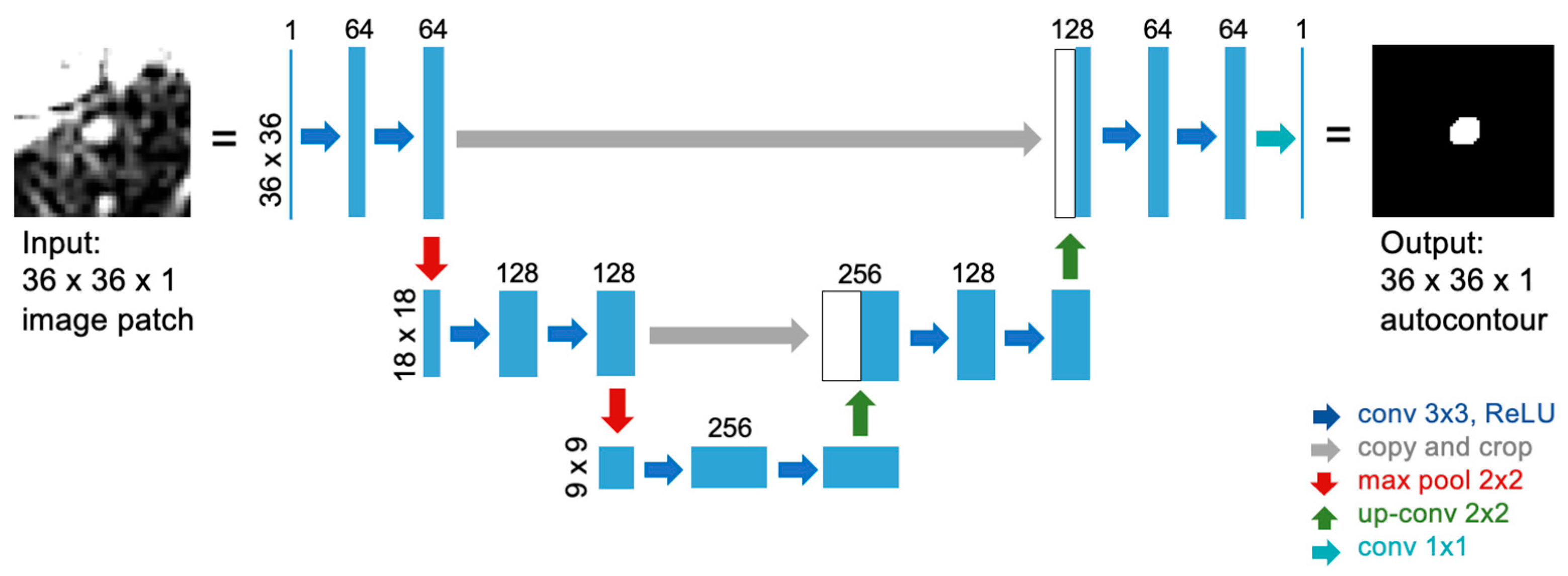
2.2. U-Net Implementation for Autocontouring Algorithm
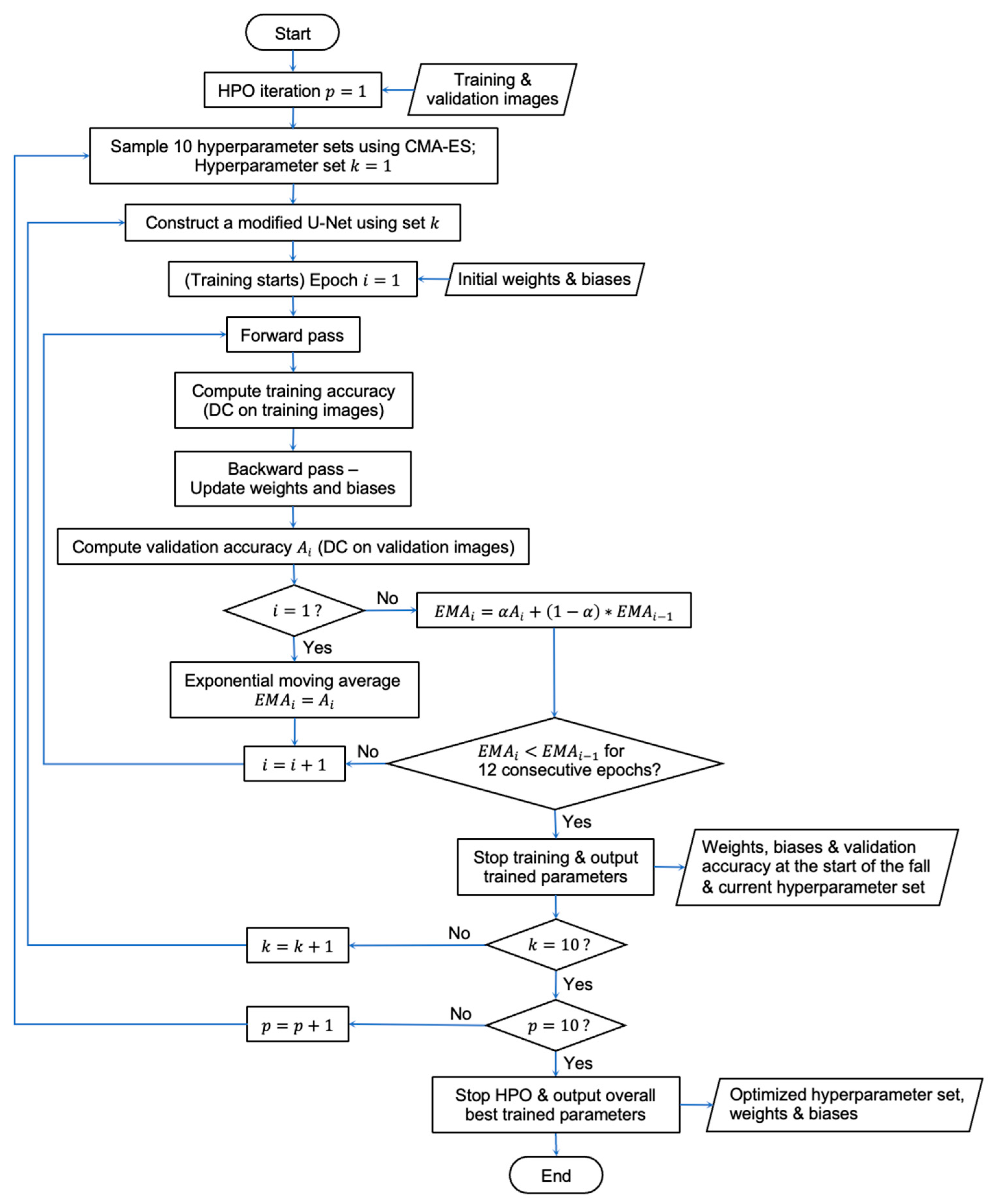
2.3. CMA-ES Implementation for HPO
- Number of consecutive convolutions (1 or 2): As a convolution operation extracts features from the input image, using multiple, consecutive convolutions allows us to extract more complex features that are combinations of simpler features that were previously extracted. As we have a small number of training images (30), a maximum of two convolutions was used to avoid creating too many weight parameters and thereby avoid overfitting.
- Filter size (3 or 5): A smaller filter (e.g., 3 3 matrix) extracts a larger amount of smaller and local features for a given input image, while a larger filter (e.g., 9 9 matrix) extracts a smaller amount of larger and broad features. A maximum of size 5 was used since a larger size may lead to overfitting, and an odd number was used for computational efficiency.
- Number of feature maps ([32, 128]): This refers to the number of filters applied to the input image during convolution. Despite 64 feature maps being used in the original U-Net [31], half of that number was used as the minimum as too small a number may not be sufficient to capture various shapes, and twice that number was used as the maximum as too large a number may cause overfitting.
- Number of poolings (1 or 2): A pooling operation down-samples the input image, reducing the sensitivity of the network to the location of features in the image. As each pooling is followed by convolutions in U-Net, the number of poolings largely affects the number of weight parameters to be used and thus the complexity of the network architecture. A maximum of two poolings was used since small image patches (e.g., 36 36) were used as input.
- Initial learning rate ([10−5, 10−1]): This decides the initial step size the optimizer uses in the search space of weight parameters. With 10−3 being the default value used in the Adam optimizer [62], a range around this value was used since too large a number might cause the network to oscillate in the search space, while too low a number might take too long an execution time.
- Number of training images ([10, 30]): This refers to the number of annotated image pairs used to train the network. The maximum number of training images was set to 30 as it includes approximately two respiratory cycles, which were considered sufficient for the network to learn any respiration-induced tumor motion. Since using a smaller number of training images reduces the amount of labor for manual contouring, 10 was set as the minimum to test whether satisfactory performance can be achieved.
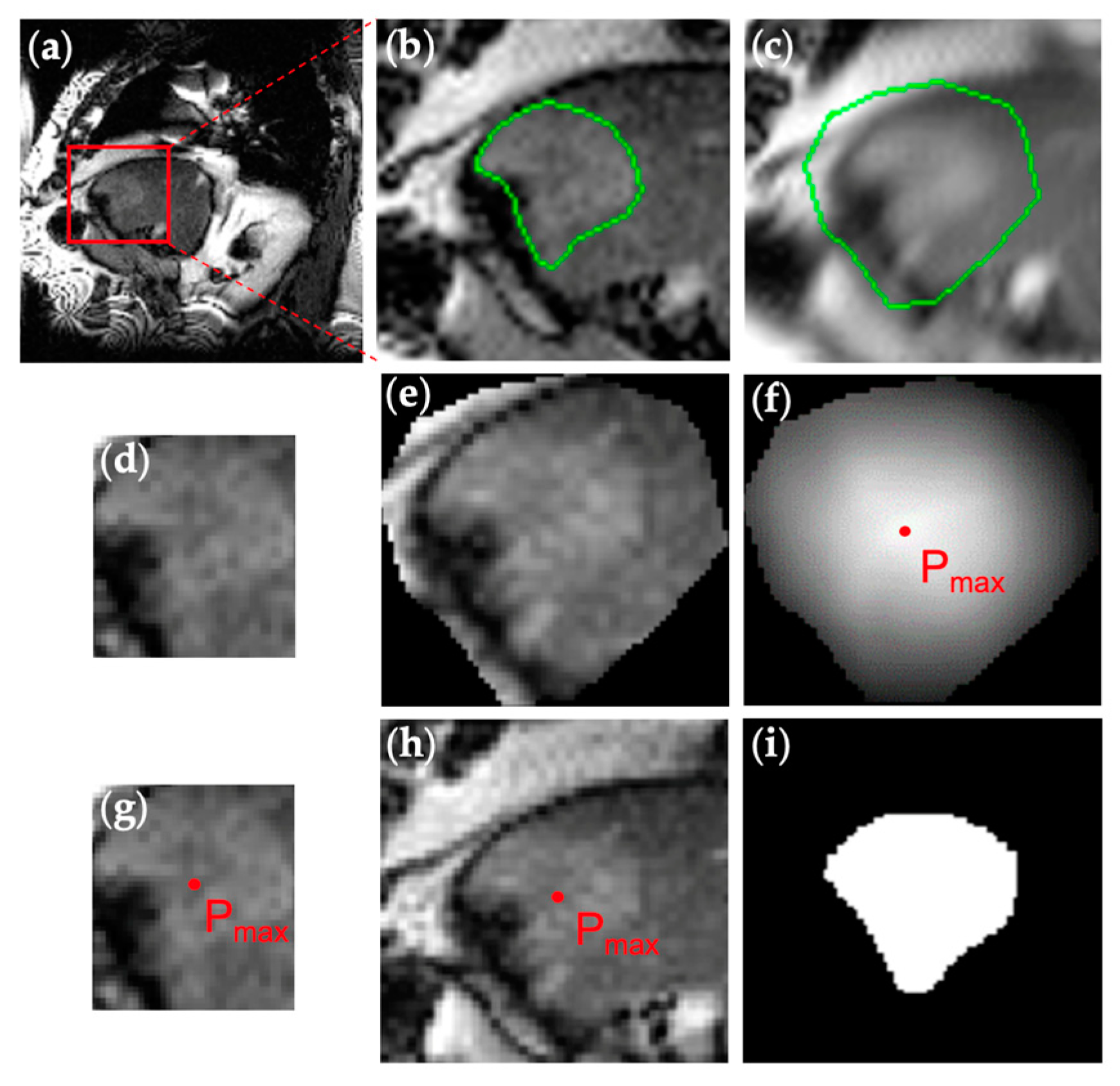
2.4. Performance Evaluation
2.4.1. Non-Optimized U-Net
2.4.2. nnU-Net
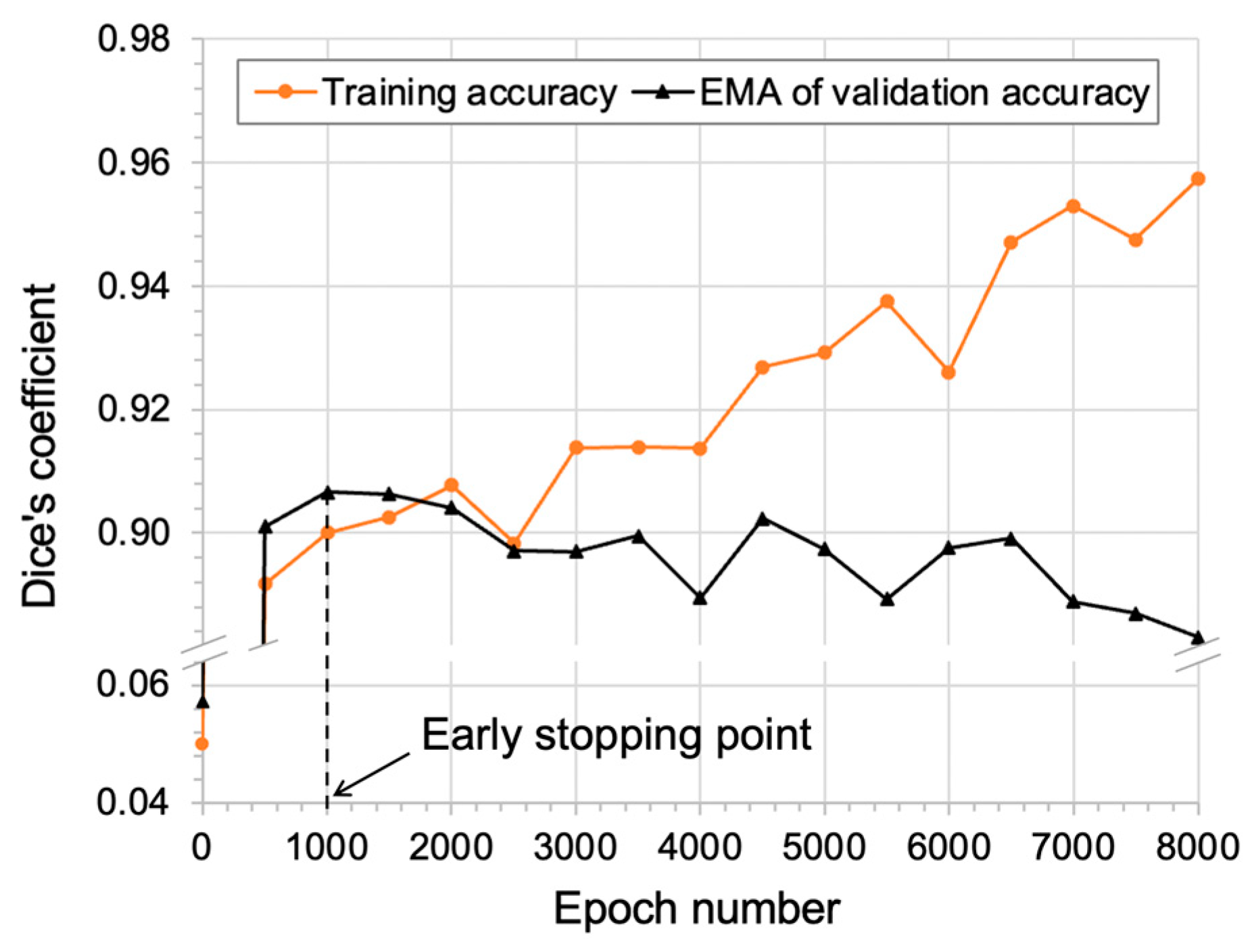
2.5. Overall Workflow
- MR simulation to acquire dynamic images of a patient;
- Manual contouring of the tumor by experts in each dynamic image;
- Patient-specific HPO and training of the algorithm;
- Autocontouring during the actual treatment session.
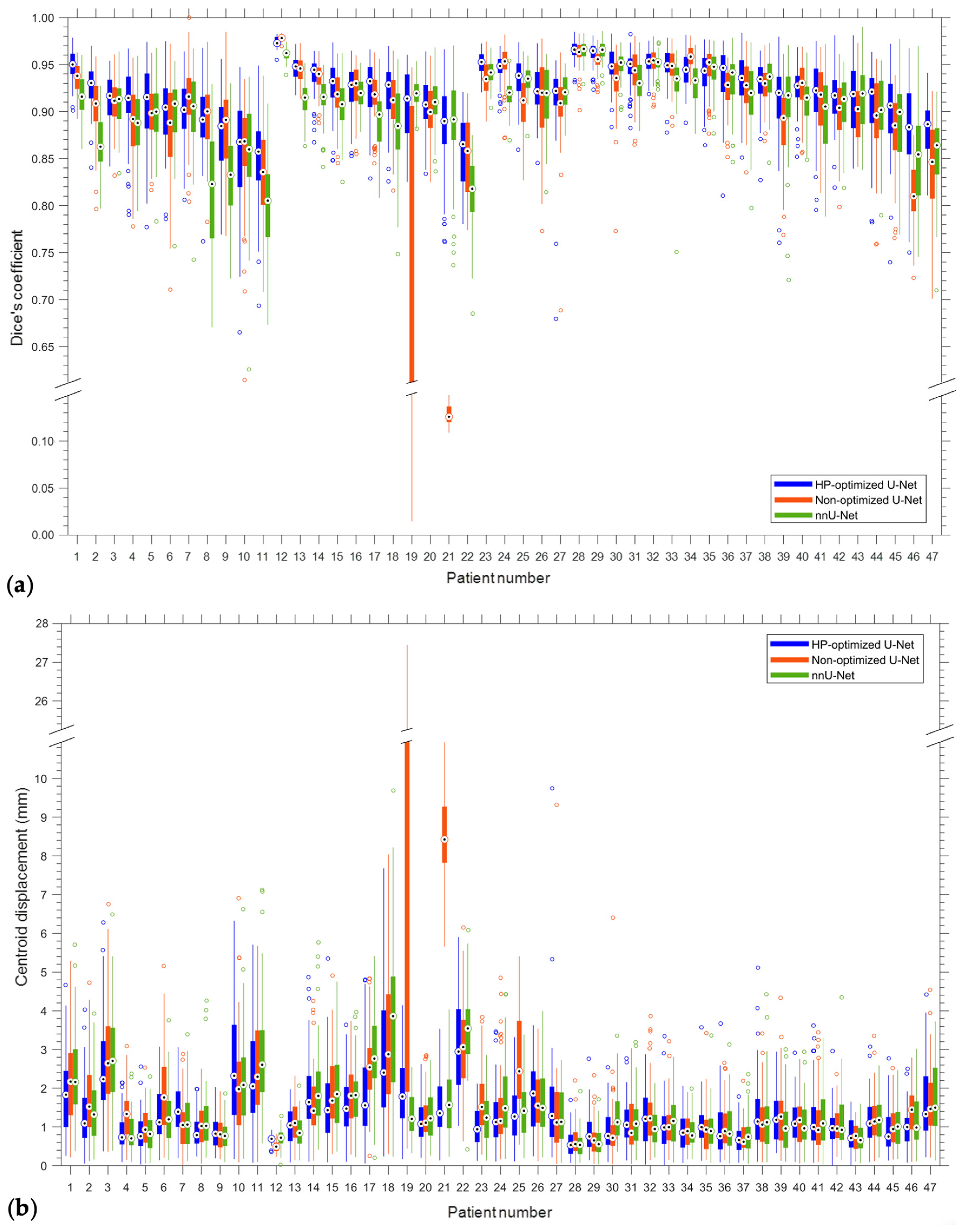
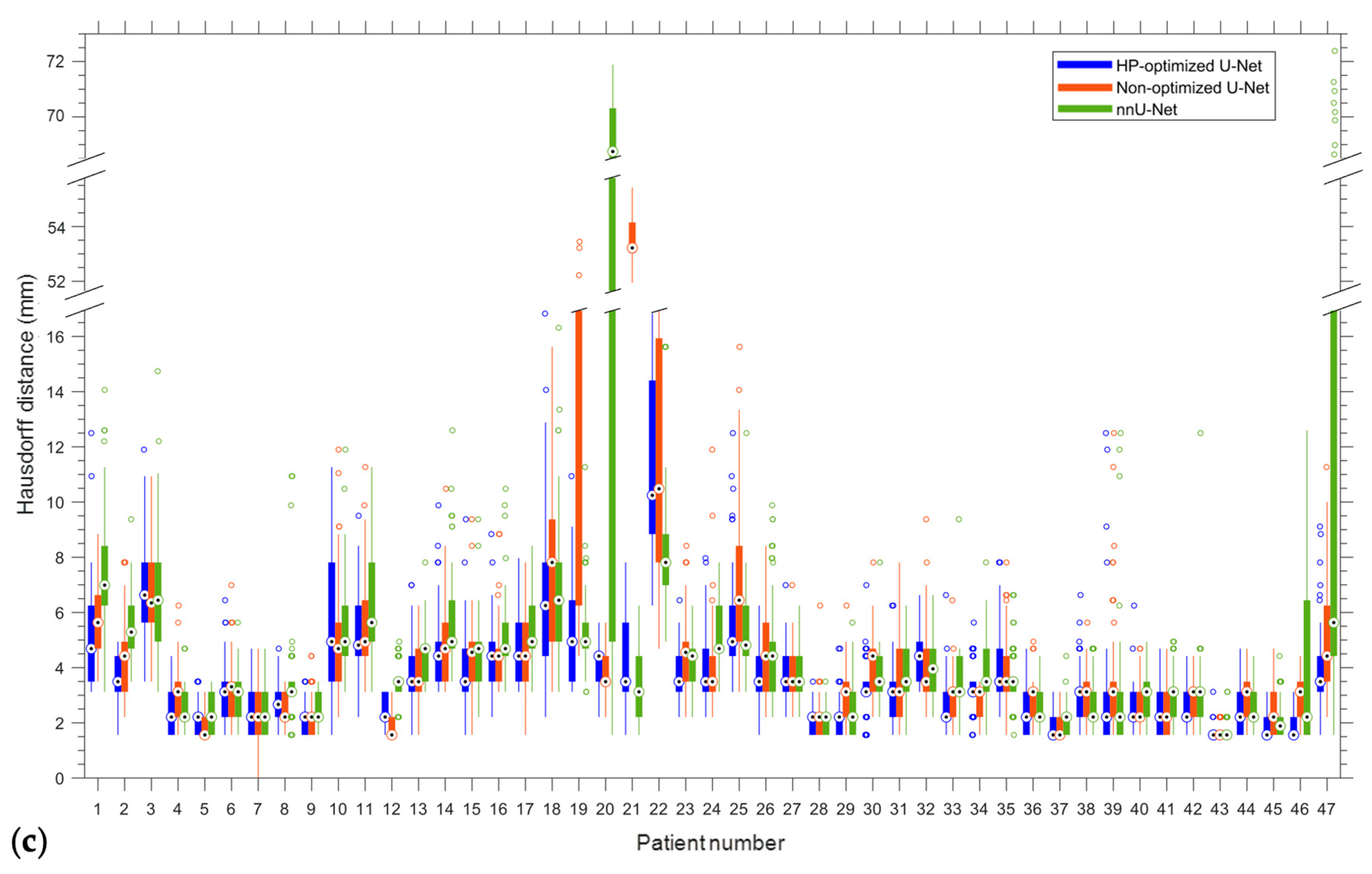
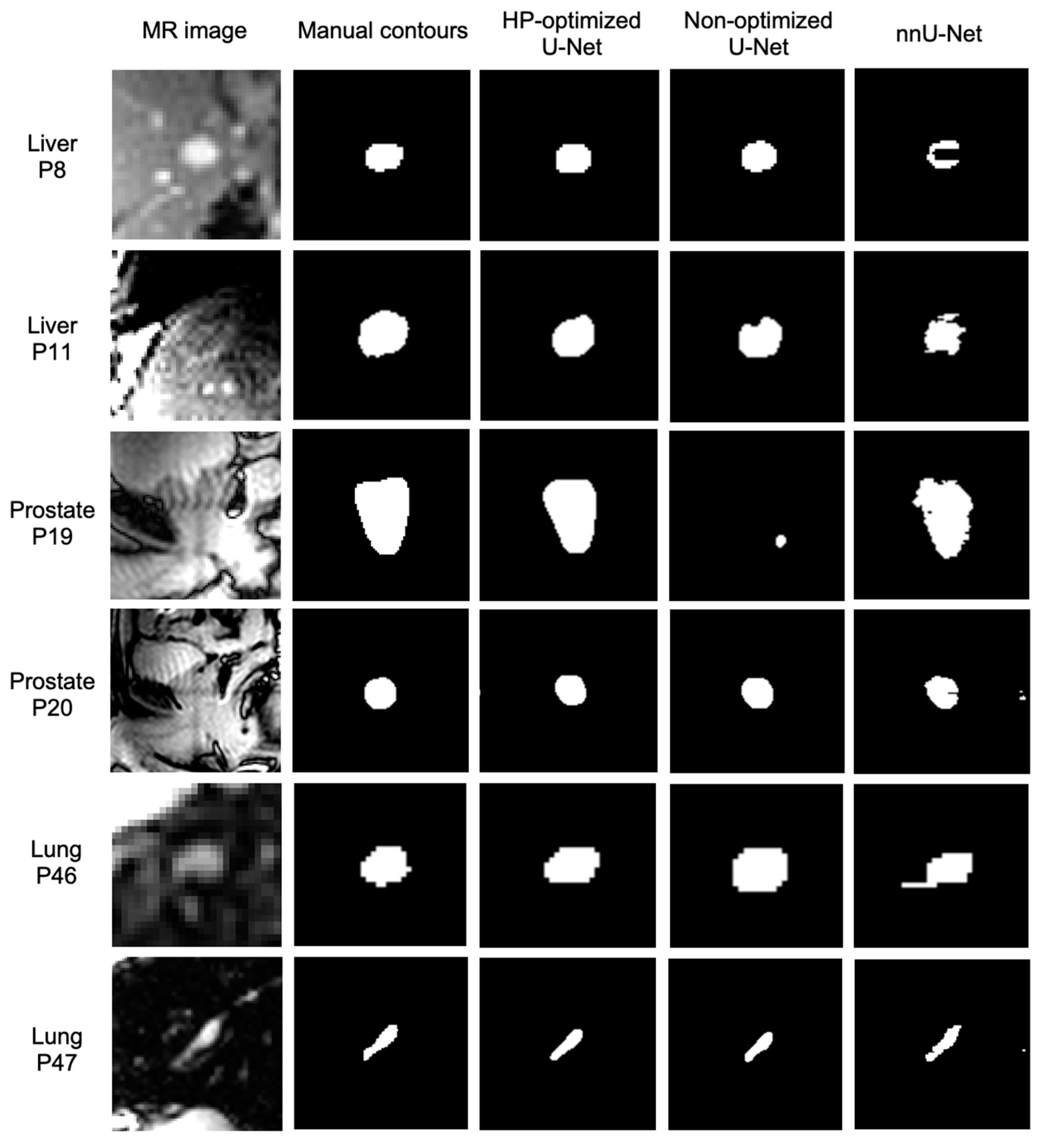
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Patient | # of Convolutions | Filter Size | Feature Map # | # of Poolings | Learning Rate | # of Training Image Pairs | |
|---|---|---|---|---|---|---|---|
| Range: | 1 or 2 | 3 or 5 | [32, 128] | 1 or 2 | [10−5, 10−1] | [10, 30] | |
| 1 | 2 | 5 | 36 | 2 | 2.69 × 10−4 | 30 | |
| 2 | 2 | 5 | 37 | 2 | 3.10 × 10−4 | 23 | |
| 3 | 2 | 3 | 33 | 1 | 1.86 × 10−3 | 10 | |
| 4 | 2 | 3 | 40 | 1 | 6.12 × 10−4 | 21 | |
| 5 | 1 | 3 | 76 | 2 | 1.76 × 10−3 | 24 | |
| 6 | 1 | 5 | 53 | 1 | 3.51 × 10−4 | 30 | |
| 7 | 1 | 5 | 93 | 2 | 1.16 × 10−4 | 11 | |
| 8 | 2 | 5 | 45 | 1 | 2.64 × 10−5 | 18 | |
| 9 | 2 | 5 | 73 | 1 | 3.39 × 10−4 | 30 | |
| 10 | 2 | 5 | 56 | 1 | 4.43 × 10−4 | 30 | |
| 11 | 2 | 5 | 35 | 1 | 1.74 × 10−3 | 27 | |
| 12 | 2 | 5 | 32 | 2 | 3.07 × 10−5 | 23 | |
| 13 | 1 | 5 | 43 | 1 | 8.24 × 10−4 | 29 | |
| 14 | 2 | 5 | 39 | 2 | 1.48 × 10−4 | 21 | |
| 15 | 2 | 5 | 36 | 2 | 5.48 × 10−5 | 29 | |
| 16 | 1 | 3 | 63 | 2 | 4.38 × 10−4 | 29 | |
| 17 | 2 | 5 | 72 | 2 | 4.85 × 10−4 | 11 | |
| 18 | 2 | 5 | 50 | 2 | 1.67 × 10−5 | 30 | |
| 19 | 2 | 5 | 44 | 2 | 2.04 × 10−4 | 23 | |
| 20 | 2 | 5 | 33 | 1 | 1.60 × 10−4 | 30 | |
| 21 | 1 | 5 | 89 | 2 | 8.35 × 10−4 | 10 | |
| 22 | 2 | 5 | 33 | 1 | 2.58 × 10−5 | 10 | |
| 23 | 1 | 5 | 124 | 1 | 3.84 × 10−5 | 11 | |
| 24 | 1 | 3 | 70 | 2 | 3.29 × 10−4 | 18 | |
| 25 | 2 | 5 | 34 | 2 | 8.90 × 10−5 | 29 | |
| 26 | 2 | 5 | 53 | 2 | 1.49 × 10−4 | 30 | |
| 27 | 1 | 5 | 42 | 2 | 1.83 × 10−4 | 28 | |
| 28 | 2 | 5 | 32 | 2 | 8.47 × 10−4 | 23 | |
| 29 | 2 | 5 | 46 | 1 | 4.65 × 10−4 | 24 | |
| 30 | 2 | 5 | 52 | 2 | 1.49 × 10−5 | 18 | |
| 31 | 2 | 5 | 46 | 2 | 1.19 × 10−5 | 14 | |
| 32 | 1 | 5 | 57 | 1 | 9.65 × 10−4 | 15 | |
| 33 | 2 | 5 | 72 | 1 | 5.18 × 10−5 | 28 | |
| 34 | 2 | 3 | 77 | 2 | 2.53 × 10−4 | 16 | |
| 35 | 1 | 5 | 40 | 1 | 7.41 × 10−4 | 29 | |
| 36 | 2 | 3 | 33 | 2 | 9.81 × 10−4 | 28 | |
| 37 | 1 | 5 | 59 | 1 | 1.28 × 10−3 | 24 | |
| 38 | 1 | 3 | 92 | 1 | 1.02 × 10−4 | 28 | |
| 39 | 1 | 5 | 48 | 1 | 9.98 × 10−5 | 23 | |
| 40 | 2 | 5 | 50 | 2 | 6.31 × 10−4 | 17 | |
| 41 | 1 | 5 | 54 | 2 | 3.65 × 10−4 | 15 | |
| 42 | 1 | 5 | 41 | 1 | 2.85 × 10−3 | 29 | |
| 43 | 1 | 5 | 36 | 1 | 5.96 × 10−4 | 15 | |
| 44 | 1 | 5 | 72 | 2 | 3.71 × 10−4 | 29 | |
| 45 | 1 | 5 | 76 | 1 | 2.61 × 10−3 | 18 | |
| 46 | 1 | 5 | 32 | 1 | 3.12 × 10−4 | 30 | |
| 47 | 1 | 5 | 43 | 2 | 2.04 × 10−4 | 27 |
| Patient | DC | IoU | CD (mm) | HD (mm) | ||||
|---|---|---|---|---|---|---|---|---|
| Mean/SD | Max/Min | Mean/SD | Max/Min | Mean/SD | Max/Min | Mean/SD | Max/Min | |
| 1 | 0.95/0.02 | 0.98/0.90 | 0.90/0.03 | 0.96/0.82 | 1.84/1.00 | 4.67/0.25 | 4.96/1.77 | 12.50/3.13 |
| 2 | 0.93/0.02 | 0.97/0.84 | 0.86/0.04 | 0.94/0.72 | 1.29/0.81 | 4.03/0.06 | 3.49/0.75 | 4.94/1.56 |
| 3 | 0.91/0.03 | 0.95/0.84 | 0.84/0.04 | 0.91/0.73 | 2.47/1.29 | 6.28/0.37 | 6.67/1.82 | 11.90/3.49 |
| 4 | 0.91/0.04 | 0.97/0.79 | 0.84/0.06 | 0.94/0.65 | 0.87/0.48 | 2.14/0.09 | 2.25/0.71 | 4.42/1.56 |
| 5 | 0.91/0.04 | 0.97/0.78 | 0.84/0.07 | 0.95/0.64 | 0.85/0.50 | 2.56/0.03 | 2.08/0.61 | 3.49/1.56 |
| 6 | 0.90/0.04 | 0.97/0.79 | 0.82/0.06 | 0.95/0.65 | 1.31/0.74 | 3.07/0.14 | 3.10/1.18 | 6.44/1.56 |
| 7 | 0.90/0.03 | 0.96/0.81 | 0.82/0.05 | 0.93/0.68 | 1.44/0.62 | 3.06/0.20 | 2.31/0.74 | 4.69/1.56 |
| 8 | 0.89/0.04 | 0.97/0.76 | 0.81/0.06 | 0.94/0.62 | 0.88/0.45 | 1.98/0.24 | 2.64/0.81 | 4.69/1.56 |
| 9 | 0.88/0.05 | 0.96/0.77 | 0.79/0.07 | 0.92/0.63 | 0.88/0.42 | 2.03/0.19 | 2.11/0.62 | 3.49/1.56 |
| 10 | 0.86/0.06 | 0.95/0.67 | 0.75/0.09 | 0.90/0.50 | 2.51/1.45 | 6.33/0.17 | 5.58/2.24 | 11.27/1.56 |
| 11 | 0.85/0.05 | 0.95/0.69 | 0.74/0.07 | 0.90/0.53 | 2.30/1.35 | 5.71/0.08 | 5.26/1.58 | 9.50/2.21 |
| 12 | 0.97/0.01 | 0.98/0.96 | 0.95/0.01 | 0.97/0.91 | 0.69/0.11 | 0.93/0.35 | 2.51/0.52 | 3.13/1.56 |
| 13 | 0.95/0.01 | 0.97/0.92 | 0.90/0.02 | 0.95/0.85 | 1.05/0.47 | 1.97/0.08 | 3.84/1.06 | 6.99/1.56 |
| 14 | 0.94/0.02 | 0.96/0.87 | 0.89/0.03 | 0.93/0.77 | 1.82/0.93 | 4.87/0.10 | 4.53/1.37 | 9.88/3.13 |
| 15 | 0.93/0.03 | 0.97/0.85 | 0.87/0.04 | 0.95/0.74 | 1.56/0.96 | 5.35/0.09 | 3.97/1.44 | 9.38/1.56 |
| 16 | 0.92/0.03 | 0.96/0.85 | 0.86/0.04 | 0.93/0.74 | 1.55/0.80 | 3.64/0.10 | 4.43/1.15 | 8.84/2.21 |
| 17 | 0.92/0.03 | 0.97/0.83 | 0.86/0.05 | 0.93/0.71 | 1.88/1.24 | 4.80/0.06 | 4.64/1.33 | 7.97/3.13 |
| 18 | 0.92/0.03 | 0.97/0.83 | 0.86/0.05 | 0.94/0.70 | 2.81/1.68 | 7.68/0.24 | 6.68/2.87 | 16.83/2.21 |
| 19 | 0.91/0.04 | 0.96/0.83 | 0.83/0.06 | 0.92/0.70 | 1.88/0.90 | 4.15/0.17 | 5.30/1.75 | 10.94/3.13 |
| 20 | 0.91/0.03 | 0.96/0.83 | 0.83/0.05 | 0.93/0.72 | 1.14/0.57 | 2.62/0.21 | 3.92/0.91 | 5.63/2.21 |
| 21 | 0.89/0.05 | 0.97/0.76 | 0.80/0.08 | 0.93/0.61 | 1.57/0.85 | 3.53/0.13 | 3.93/1.50 | 7.81/1.56 |
| 22 | 0.86/0.04 | 0.92/0.78 | 0.75/0.06 | 0.85/0.64 | 3.10/1.21 | 5.90/1.03 | 11.52/3.75 | 24.41/6.25 |
| 23 | 0.95/0.01 | 0.97/0.92 | 0.91/0.02 | 0.95/0.85 | 1.02/0.57 | 2.12/0.12 | 3.76/0.82 | 6.44/2.21 |
| 24 | 0.95/0.02 | 0.97/0.90 | 0.90/0.03 | 0.94/0.82 | 1.29/0.77 | 3.46/0.11 | 4.00/1.20 | 7.97/2.21 |
| 25 | 0.94/0.02 | 0.97/0.86 | 0.88/0.04 | 0.95/0.75 | 1.37/0.75 | 3.32/0.11 | 5.38/1.96 | 12.50/3.13 |
| 26 | 0.92/0.02 | 0.97/0.85 | 0.86/0.04 | 0.95/0.73 | 1.82/0.88 | 3.63/0.24 | 3.82/1.13 | 6.25/1.56 |
| 27 | 0.92/0.04 | 0.95/0.68 | 0.84/0.06 | 0.91/0.51 | 1.52/1.33 | 9.75/0.21 | 3.90/1.83 | 17.19/2.21 |
| 28 | 0.97/0.01 | 0.99/0.93 | 0.93/0.02 | 0.97/0.87 | 0.58/0.34 | 1.70/0.07 | 2.13/0.56 | 3.49/1.56 |
| 29 | 0.96/0.01 | 0.98/0.92 | 0.93/0.02 | 0.96/0.86 | 0.84/0.48 | 2.76/0.14 | 2.22/0.77 | 4.69/1.56 |
| 30 | 0.95/0.02 | 0.98/0.88 | 0.90/0.04 | 0.97/0.79 | 0.94/0.56 | 2.54/0.09 | 3.22/0.96 | 6.99/1.56 |
| 31 | 0.95/0.02 | 0.98/0.88 | 0.90/0.04 | 0.97/0.79 | 1.13/0.55 | 2.77/0.13 | 3.21/1.00 | 6.25/1.56 |
| 32 | 0.95/0.01 | 0.98/0.92 | 0.91/0.02 | 0.95/0.85 | 1.28/0.72 | 2.88/0.03 | 4.42/1.06 | 6.63/3.13 |
| 33 | 0.95/0.02 | 0.98/0.88 | 0.90/0.03 | 0.96/0.78 | 0.99/0.59 | 3.34/0.1 | 2.65/0.89 | 6.63/1.56 |
| 34 | 0.94/0.02 | 0.98/0.89 | 0.89/0.03 | 0.96/0.80 | 0.89/0.49 | 2.06/0.07 | 3.30/0.89 | 5.63/1.56 |
| 35 | 0.94/0.03 | 0.98/0.86 | 0.89/0.04 | 0.95/0.76 | 1.07/0.56 | 3.57/0.12 | 4.04/1.26 | 7.81/2.21 |
| 36 | 0.94/0.03 | 0.98/0.81 | 0.88/0.05 | 0.95/0.68 | 0.95/0.68 | 3.67/0.09 | 2.33/0.75 | 4.69/1.56 |
| 37 | 0.93/0.03 | 0.98/0.85 | 0.88/0.05 | 0.97/0.74 | 0.70/0.38 | 1.79/0.08 | 1.86/0.48 | 3.13/1.56 |
| 38 | 0.93/0.03 | 0.97/0.83 | 0.87/0.04 | 0.93/0.71 | 1.34/0.92 | 5.11/0.10 | 2.87/1.00 | 6.63/1.56 |
| 39 | 0.93/0.10 | 0.98/0.76 | 0.84/0.06 | 0.96/0.61 | 1.50/2.31 | 19.85/0.32 | 2.87/2.14 | 12.50/1.56 |
| 40 | 0.92/0.02 | 0.97/0.85 | 0.86/0.04 | 0.94/0.74 | 1.13/0.57 | 2.92/0.09 | 2.63/0.79 | 6.25/1.56 |
| 41 | 0.92/0.04 | 0.98/0.80 | 0.85/0.06 | 0.95/0.66 | 1.18/0.77 | 3.62/0.08 | 2.26/0.73 | 4.69/1.56 |
| 42 | 0.92/0.03 | 0.98/0.82 | 0.85/0.05 | 0.96/0.69 | 1.01/0.50 | 2.96/0.00 | 2.41/0.63 | 4.42/1.56 |
| 43 | 0.91/0.04 | 0.98/0.84 | 0.84/0.07 | 0.96/0.72 | 0.80/0.43 | 1.65/0.00 | 1.60/0.21 | 3.13/1.56 |
| 44 | 0.91/0.04 | 0.96/0.78 | 0.84/0.06 | 0.93/0.64 | 1.14/0.57 | 3.07/0.09 | 2.32/0.80 | 4.69/1.56 |
| 45 | 0.90/0.04 | 0.97/0.74 | 0.82/0.07 | 0.95/0.59 | 0.93/0.57 | 2.77/0.13 | 1.97/0.57 | 3.13/1.56 |
| 46 | 0.88/0.05 | 0.97/0.75 | 0.79/0.08 | 0.95/0.61 | 1.00/0.49 | 2.50/0.08 | 1.81/0.45 | 3.13/1.56 |
| 47 | 0.88/0.03 | 0.94/0.81 | 0.79/0.05 | 0.89/0.68 | 1.60/0.95 | 4.42/0.22 | 3.71/1.52 | 9.11/1.56 |
| Mean | 0.92/0.04 | 0.97/0.83 | 0.85/0.05 | 0.94/0.71 | 1.35/1.03 | 3.95/0.15 | 3.63/2.17 | 7.51/2.01 |
References
- Huang, F.; Ma, C.; Wang, R.; Gong, G.; Shang, D.; Yin, Y. Defining the individual internal gross tumor volume of hepatocellular carcinoma using 4DCT and T2-weighted MRI images by deformable registration. Transl. Cancer Res. 2018, 7, 151–157. [Google Scholar] [CrossRef]
- Feng, M.; Balter, J.M.; Normolle, D.; Adusumilli, S.; Cao, Y.; Chenevert, T.L.; Ben-Josef, E. Characterization of pancreatic tumor motion using cine MRI: Surrogates for tumor position should be used with caution. Int. J. Radiat. Oncol. Biol. Phys. 2009, 74, 884–891. [Google Scholar] [CrossRef]
- Kyriakou, E.; McKenzie, D.R. Changes in lung tumor shape during respiration. Phys. Med. Biol. 2012, 57, 919–935. [Google Scholar] [CrossRef]
- Sawant, A.; Venkat, R.; Srivastava, V.; Carlson, D.; Povzner, S.; Cattell, H.; Keall, P. Management of three-dimensional intrafraction motion through real-time DMLC tracking. Med. Phys. 2008, 35, 2050–2061. [Google Scholar] [CrossRef] [PubMed]
- Willoughby, T.; Lehmann, J.; Bencomo, J.A.; Jani, S.K.; Santanam, L.; Sethi, A.; Solberg, T.D.; Tome, W.A.; Waldron, T.J. Quality assurance for nonradiographic radiotherapy localization and positioning systems: Report of Task Group 147. Med. Phys. 2012, 39, 1728–1747. [Google Scholar] [CrossRef]
- Bertholet, J.; Knopf, A.; Eiben, B.; McClelland, J.; Grimwood, A.; Harris, E.; Menten, M.; Poulsen, P.; Nguyen, D.T.; Keall, P.; et al. Real-time intrafraction motion monitoring in external beam radiotherapy. Phys. Med. Biol. 2019, 64, 15TR01. [Google Scholar] [CrossRef] [PubMed]
- Schweikard, A.; Shiomi, H.; Adler, J. Respiration tracking in radiosurgery. Med. Phys. 2004, 31, 2738–2741. [Google Scholar] [CrossRef]
- Matsuo, Y.; Ueki, N.; Takayama, K.; Nakamura, M.; Miyabe, Y.; Ishihara, Y.; Mukumoto, N.; Yano, S.; Tanabe, H.; Kaneko, S.; et al. Evaluation of dynamic tumour tracking radiotherapy with real-time monitoring for lung tumours using a gimbal mounted linac. Radiother. Oncol. 2014, 112, 360–364. [Google Scholar] [CrossRef]
- Depuydt, T.; Poels, K.; Verellen, D.; Engels, B.; Collen, C.; Buleteanu, M.; Van den Begin, R.; Boussaer, M.; Duchateau, M.; Gevaert, T.; et al. Treating patients with real-time tumor tracking using the Vero gimbaled linac system: Implementation and first review. Radiother. Oncol. 2014, 112, 343–351. [Google Scholar] [CrossRef]
- D’Souza, W.D.; Naqvi, S.A.; Yu, C.X. Real-time intra-fraction-motion tracking using the treatment couch: A feasibility study. Phys. Med. Biol. 2005, 50, 4021–4033. [Google Scholar] [CrossRef]
- Cho, B.; Poulsen, P.R.; Sloutsky, A.; Sawant, A.; Keall, P.J. First demonstration of combined kV/MV image-guided real-time dynamic multileaf-collimator target tracking. Int. J. Radiat. Oncol. Biol. Phys. 2009, 74, 859–867. [Google Scholar] [CrossRef] [PubMed]
- Glitzner, M.; Woodhead, P.L.; Borman, P.T.S.; Lagendijk, J.J.W.; Raaymakers, B.W. Technical note: MLC-tracking performance on the Elekta unity MRI-linac. Phys. Med. Biol. 2019, 64, 15NT02. [Google Scholar] [CrossRef]
- Keall, P.J.; Sawant, A.; Berbeco, R.I.; Booth, J.T.; Cho, B.; Cerviño, L.I.; Cirino, E.; Dieterich, S.; Fast, M.F.; Greer, P.B.; et al. AAPM Task Group 264: The safe clinical implementation of MLC tracking in radiotherapy. Med. Phys. 2021, 48, e44–e64. [Google Scholar] [CrossRef] [PubMed]
- Kitamura, K.; Shirato, H.; Shimizu, S.; Shinohara, N.; Harabayashi, T.; Shimizu, T.; Kodama, Y.; Endo, H.; Onimaru, R.; Nishioka, S.; et al. Registration accuracy and possible migration of internal fiducial gold marker implanted in prostate and liver treated with real-time tumor-tracking radiation therapy (RTRT). Radiother. Oncol. 2002, 62, 275–281. [Google Scholar] [CrossRef] [PubMed]
- Ionascu, D.; Jiang, S.B.; Nishioka, S.; Shirato, H.; Berbeco, R.I. Internal-external correlation investigations of respiratory induced motion of lung tumors. Med. Phys. 2007, 34, 3893–3903. [Google Scholar] [CrossRef]
- Gierga, D.P.; Brewer, J.; Sharp, G.C.; Betke, M.; Willett, C.G.; Chen, G.T. The correlation between internal and external markers for abdominal tumors: Implications for respiratory gating. Int. J. Radiat. Oncol. Biol. Phys. 2005, 61, 1551–1558. [Google Scholar] [CrossRef]
- Fallone, B.G.; Murray, B.; Rathee, S.; Stanescu, T.; Steciw, S.; Vidakovic, S.; Blosser, E.; Tymofichuk, D. First MR images obtained during megavoltage photon irradiation from a prototype integrated linac-MR system. Med. Phys. 2009, 36, 2084–2088. [Google Scholar] [CrossRef]
- Fallone, B.G. The rotating biplanarlinac magnetic resonance imaging system. Semin. Radiat. Oncol. 2014, 24, 200–202. [Google Scholar] [CrossRef]
- Mutic, S.; Dempsey, J.F. The ViewRay system: Magnetic resonance-guided and controlled radiotherapy. Semin. Radiat. Oncol. 2014, 24, 196–199. [Google Scholar] [CrossRef]
- Raaymakers, B.W.; Lagendijk, J.J.W.; Overweg, J.; Kok, J.G.M.; Raaijmakers, A.J.E.; Kerkhof, E.M.; van der Put, R.W.; Meijsing, I.; Crijins, S.P.M.; Benedosso, F.; et al. Integrating a 1.5 T MRI scanner with a 6 MV accelerator: Proof of concept. Phys. Med. Biol. 2009, 54, N229. [Google Scholar] [CrossRef]
- Yun, J.; Wachowicz, K.; Mackenzie, M.; Rathee, S.; Robinson, D.; Fallone, B.G. First demonstration of intrafractional tumor-tracked irradiation using 2D phantom MR images on a prototype linac-MR. Med. Phys. 2013, 40, 051718. [Google Scholar] [CrossRef] [PubMed]
- Cerviño, L.I.; Du, J.; Jiang, S.B. MRI-guided tumor tracking in lung cancer radiotherapy. Phys. Med. Biol. 2011, 56, 3773–3785. [Google Scholar] [CrossRef]
- Uijtewaal, P.; Borman, P.T.S.; Woodhead, P.L.; Hackett, S.L.; Raaymakers, B.W.; Fast, M.F. Dosimetric evaluation of MRI-guided multi-leaf collimator tracking and trailing for lung stereotactic body radiation therapy. Med. Phys. 2021, 48, 1520–1532. [Google Scholar] [CrossRef]
- Yun, J.; Yip, E.; Gabos, Z.; Wachowicz, K.; Rathee, S.; Fallone, B.G. Neural-network based autocontouring algorithm for intrafractional lung-tumor tracking using Linac-MR. Med. Phys. 2015, 42, 2296–2310. [Google Scholar] [CrossRef] [PubMed]
- Hansen, N.; Ostermeier, A. Completely Derandomized Self-Adaptation in Evolution Strategies. Evol. Comput. 2001, 9, 159–195. [Google Scholar] [CrossRef] [PubMed]
- Antonelli, M.; Reinke, A.; Bakas, S.; Farahani, K.; Kopp-Schneider, A.; Landman, B.A.; Litjens, G.; Menze, B.; Ronneberger, O.; Summers, R.M.; et al. The Medical Segmentation Decathlon. Nat. Commun. 2022, 13, 4128. [Google Scholar] [CrossRef]
- Isensee, F.; Jaeger, P.F.; Kohl, S.A.A.; Petersen, J.; Maier-Hein, K.H. nnU-Net: A self-configuring method for deep learning-based biomedical image segmentation. Nat. Methods 2021, 18, 203–211. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar] [CrossRef]
- Minaee, S.; Boykov, Y.; Porikli, F.; Plaza, A.; Kehtarnavaz, N.; Terzopoulos, D. Image segmentation using deep learning: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 3523–3542. [Google Scholar] [CrossRef]
- Liu, W.; Rabinovich, A.; Berg, A.C. ParseNet: Looking wider to see better. arXiv 2015, arXiv:1506.04579. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015; Proceedings, Part III 18. Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar] [CrossRef]
- Bilic, P.; Christ, P.; Li, H.B.; Vorontsov, E.; Ben-Cohen, A.; Kaissis, G.; Szeskin, A.; Jacobs, C.; Mamani, G.E.H.; Chartrand, G.; et al. The Liver Tumor Segmentation Benchmark (LiTS). Med. Image Anal. 2023, 84, 102680. [Google Scholar] [CrossRef]
- Pedrosa, J.; Aresta, G.; Ferreira, C.; Atwal, G.; Phoulady, H.A.; Chen, X.; Chen, R.; Li, J.; Wang, L.; Galdran, A.; et al. LNDb challenge on automatic lung cancer patient management. Med. Image Anal. 2021, 70, 102027. [Google Scholar] [CrossRef] [PubMed]
- Loshchilov, I.; Hutter, F. CMA-ES for hyperparameter optimization of deep neural networks. arXiv 2016, arXiv:1604.07269. [Google Scholar]
- Aggarwal, C.C. Neural Networks and Deep Learning: A Textbook, 1st ed.; Springer International Publishing: Yorktown, VA, USA, 2018; pp. 139–191. [Google Scholar] [CrossRef]
- Loshchilov, I.; Schoenauer, M.; Sebag, M. Bi-population CMA-ES algorithms with surrogate models and line searches. In Proceedings of the 15th Annual Conference on Genetic and Evolutionary Computation, Amsterdam, The Netherlands, 6–10 July 2013; pp. 1177–1184. [Google Scholar] [CrossRef]
- Wollmann, T.; Bernhard, P.; Gunkel, M.; Braun, D.M.; Meiners, J.; Simon, R.; Sauter, G.; Erfle, H.; Rippe, K.; Rohr, K. Black-Box Hyperparameter Optimization for Nuclei Segmentation in Prostate Tissue Images. In Bildverarbeitung Für Die Medizin 2019; Handels, H., Deserno, T., Maier, A., Maier-Hein, K., Palm, C., Tolxdorff, T., Eds.; Springer Vieweg: Wiesbaden, Germany, 2019; pp. 345–350. [Google Scholar] [CrossRef]
- Tsai, Y.L.; Wu, C.J.; Shaw, S.; Yu, P.C.; Nien, H.H.; Lui, L.T. Quantitative analysis of respiration-induced motion of each liver segment with helical computed tomography and 4-dimensional computed tomography. Radiat. Oncol. 2018, 13, 59. [Google Scholar] [CrossRef] [PubMed]
- Shirato, H.; Seppenwoolde, Y.; Kitamura, K.; Onimura, R.; Shimizu, S. Intrafractional tumor motion: Lung and liver. Semin. Radiat. Oncol. 2004, 14, 10–18. [Google Scholar] [CrossRef]
- Plathow, C.; Fink, C.; Ley, S.; Puderbach, M.; Eichinger, M.; Zuna, I.; Schmähl, A.; Kauczor, H.U. Measurement of tumor diameter-dependent mobility of lung tumors by dynamic MRI. Radiother. Oncol. 2004, 73, 349–354. [Google Scholar] [CrossRef]
- Huang, E.; Dong, L.; Chandra, A.; Kuban, D.A.; Rosen, I.I.; Evans, A.; Pollack, A. Intrafraction prostate motion during IMRT for prostate cancer. Int. J. Radiat. Oncol. Biol. Phys. 2002, 53, 261–268. [Google Scholar] [CrossRef]
- Gurjar, O.P.; Arya, R.; Goyal, H. A study on prostate movement and dosimetric variation because of bladder and rectum volumes changes during the course of image-guided radiotherapy in prostate cancer. Prostate Int. 2020, 8, 91–97. [Google Scholar] [CrossRef]
- Deasy, J.O.; Blanco, A.I.; Clark, V.H. CERR: A computational environment for radiotherapy research. Med. Phys. 2003, 30, 979–985. [Google Scholar] [CrossRef]
- Fedorov, A.; Beichel, R.; Kalpathy-Cramer, J.; Finet, J.; Fillion-Robin, J.C.; Pujol, S.; Bauer, C.; Jennings, D.; Fennessy, F.; Sonka, M.; et al. 3D Slicer as an image computing platform for the quantitative imaging network. Magn. Reson. Imaging 2012, 30, 1323–1341. [Google Scholar] [CrossRef]
- Smolders, A.; Lomax, A.; Weber, D.C.; Albertini, F. Patient-specific neural networks for contour propagation in online adaptive radiotherapy. Phys. Med. Biol. 2023, 68, 095010. [Google Scholar] [CrossRef]
- Jansen, M.J.A.; Kuijf, H.J.; Dhara, A.K.; Weaver, N.A.; Jan Biessels, G.; Strand, R.; Pluim, J.P.W. Patient-specific fine-tuning of convolutional neural networks for follow-up lesion quantification. J. Med. Imaging 2020, 7, 064003. [Google Scholar] [CrossRef]
- Fransson, S.; Tilly, D.; Strand, R. Patient specific deep learning based segmentation for magnetic resonance guided prostate radiotherapy. Phys. Imaging Radiat. Oncol. 2022, 23, 38–42. [Google Scholar] [CrossRef] [PubMed]
- Dice, L.R. Measures of the amount of ecologic association between species. Ecology 1945, 26, 297–302. [Google Scholar] [CrossRef]
- Yip, E.; Yun, J.; Gabos, Z.; Baker, S.; Yee, D.; Wachowicz, K.; Rathee, S.; Fallone, B.G. Evaluating performance of a user-trained MR lung tumor autocontouring algorithm in the context of intra- and interobserver variations. Med. Phys. 2018, 45, 307–313. [Google Scholar] [CrossRef] [PubMed]
- Zeng, G.; Yang, X.; Li, J.; Yu, L.; Heng, P.; Zheng, G. 3D U-net with Multi-level Deep Supervision: Fully Automatic Segmentation of Proximal Femur in 3D MR Images. In Machine Learning in Medical Imaging; Wang, Q., Shi, Y., Suk, H.I., Suzuki, K., Eds.; Springer: Cham, Switzerland, 2017; pp. 274–282. [Google Scholar] [CrossRef]
- Jia, S.; Despinasse, A.; Wang, Z.; Delingette, H.; Pennec, X.; Jaïs, P.; Cochet, H.; Sermesant, M. Automatically segmenting the left atrium from cardiac images using successive 3D U-nets and a contour loss. arXiv 2018, arXiv:1812.02518. [Google Scholar]
- Huang, Q.; Sun, J.; Ding, H.; Wang, X.; Wang, G. Robust liver vessel extraction using 3D U-Net with variant dice loss function. Comput. Biol. Med. 2018, 101, 153–162. [Google Scholar] [CrossRef]
- Saleh, H.M.; Saad, N.H.; Isa, N.A.M. Overlapping Chromosome Segmentation using U-Net: Convolutional Networks with Test Time Augmentation. Procedia Comput. Sci. 2019, 159, 524–533. [Google Scholar] [CrossRef]
- Yang, J.; Faraji, M.; Basu, A. Robust segmentation of arterial walls in intravascular ultrasound images using Dual Path U-Net. Ultrasonics 2019, 96, 24–33. [Google Scholar] [CrossRef]
- Tchito Tchapga, C.; Mih, T.A.; Tchagna Kouanou, A.; Fozin Fonzin, T.; Kuetche Fogang, P.; Mezatio, B.A.; Tchiotsop, D. Biomedical Image Classification in a Big Data Architecture Using Machine Learning Algorithms. J. Healthc. Eng. 2021, 2021, 9998819. [Google Scholar] [CrossRef]
- Kim, B.; Yu, K.; Lee, P. Cancer classification of single-cell gene expression data by neural network. Bioinformatics 2020, 36, 1360–1366. [Google Scholar] [CrossRef]
- Siddique, N.; Sidike, P.; Colin, E.; Devabhaktuni, V. U-Net and Its Variants for Medical Image Segmentation: A Review of Theory and Applications. IEEE Access 2021, 9, 82031–82057. [Google Scholar] [CrossRef]
- Feurer, M.; Hutter, F. Chapter 1: Hyperparameter Optimization. In Automated Machine Learning: Methods, Systems, Challenges; Hutter, F., Kotthoff, L., Vanschoren, J., Eds.; Springer: Cham, Switzerland, 2019; pp. 3–33. [Google Scholar]
- Greff, K.; Srivastava, R.K.; Koutník, J.; Steunebrink, B.R.; Schmidhuber, J. LSTM: A Search Space Odyssey. IEEE Trans. Neural Netw. Learn. Syst. 2015, 28, 2222–2232. [Google Scholar] [CrossRef]
- Masood, D.A. Automated Machine Learning Hyperparameter Optimization Neural Architecture Search and Algorithm Selection with Cloud Platforms; Packt Publishing Ltd.: Birmingham, UK, 2021; pp. 27–30. [Google Scholar]
- Wu, J.; Chen, X.Y.; Zhang, H.; Xiong, L.D.; Lei, H.; Deng, S.H. Hyperparameter Optimization for Machine Learning Models Based on Bayesian Optimization. J. Electron. Sci. Technol. 2019, 17, 26–40. [Google Scholar] [CrossRef]
- Kingma, D.; Ba, J.L. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Taha, A.A.; Hanbury, A. Metrics for evaluating 3D medical image segmentation: Analysis, selection, and tool. BMC Med. Imaging 2015, 15, 29. [Google Scholar] [CrossRef] [PubMed]
- Huttenlocher, D.P.; Klanderman, G.A.; Rucklidge, W.J. Comparing images using the Hausdorff distance. IEEE Trans. Pattern Anal. Mach. Intell. 1993, 15, 850–863. [Google Scholar] [CrossRef]
- Yun, J.; Yip, E.; Gabos, Z.; Usmani, N.; Yee, D.; Wachowicz, K.; Fallone, B.G. An AI-based tumor autocontouring algorithm for non-invasive intra-fractional tumor-tracked radiotherapy (nifteRT) on linac-MR. Med. Phys. 2020, 47, e576. [Google Scholar]
- Ma, J. Cutting-edge 3d medical image segmentation methods in 2020: Are happy families all alike? arXiv 2021, arXiv:2101.00232. [Google Scholar]
- Keall, P.J.; Mageras, G.S.; Balter, J.M.; Emery, R.S.; Forster, K.M.; Jiang, S.B.; Kapatoes, J.M.; Low, D.A.; Murphy, M.J.; Murray, B.R.; et al. The management of respiratory motion in radiation oncology report of AAPM Task Group 76. Med. Phys. 2006, 33, 3874–3900. [Google Scholar] [CrossRef]
- Fast, M.F.; Eiben, B.; Menten, M.J.; Wetscherek, A.; Hawkes, D.J.; McClelland, J.R.; Oelfke, U. Tumor auto-contouring on 2d cine MRI for locally advanced lung cancer: A comparative study. Radiother. Oncol. 2017, 125, 485–491. [Google Scholar] [CrossRef]
- Klüter, S. Technical design and concept of a 0.35 T MR-Linac. Clin. Transl. Radiat. Oncol. 2019, 18, 98–101. [Google Scholar] [CrossRef]
- Wachowicz, K.; De Zanche, N.; Yip, E.; Volotovskyy, V.; Fallone, B.G. CNR considerations for rapid real-time MRI tumor tracking in radiotherapy hybrid devices: Effects of B0 field strength. Med. Phys. 2016, 43, 4903. [Google Scholar] [CrossRef] [PubMed]
- Campbell-Washburn, A.E.; Ramasawmy, R.; Restivo, M.C.; Bhattacharya, I.; Basar, B.; Herzka, D.A.; Hansen, M.S.; Rogers, T.; Bandettini, W.P.; McGuirt, D.R.; et al. Opportunities in interventional and diagnostic imaging by using high-performance low-field-strength MRI. Radiology 2019, 293, 384–393. [Google Scholar] [CrossRef]
- Yip, E.; Yun, J.; Wachowicz, K.; Gabos, Z.; Rathee, S.; Fallone, B.G. Sliding window prior data assisted compressed sensing for MRI tracking of lung tumors. Med. Phys. 2017, 44, 84–98. [Google Scholar] [CrossRef]
- Kim, T.; Park, J.C.; Gach, H.M.; Chun, J.; Mutic, S. Technical note: Realtime 3D MRI in the presence of motion for MRI-guided radiotherapy: 3D dynamic keyhole imaging with super-resolution. Med. Phys. 2019, 46, 4631–4638. [Google Scholar] [CrossRef] [PubMed]
- Terpstra, M.L.; Maspero, M.; D’Agata, F.; Stemkens, B.; Intven, M.P.W.; Lagendijk, J.J.W.; van den Berg, C.A.T.; Tijssen, R.H.N. Deep learning-based image reconstruction and motion estimation from undersampled radial k-space for real-time MRI-guided radiotherapy. Phys. Med. Biol. 2020, 65, 155015. [Google Scholar] [CrossRef]
- Ginn, J.S.; Low, D.A.; Lamb, J.M.; Ruan, D. A motion prediction confidence estimation framework for prediction-based radiotherapy gating. Med. Phys. 2020, 47, 3297–3304. [Google Scholar] [CrossRef] [PubMed]
- Bjerre, T.; Crijns, S.; af Rosenschöld, P.M.; Aznar, M.; Specht, L.; Larsen, R.; Keall, P. Three-dimensional MRI-linac intra-fraction guidance using multiple orthogonal cine-MRI planes. Phys. Med. Biol. 2013, 58, 4943–4950. [Google Scholar] [CrossRef]
- Seregni, M.; Paganelli, C.; Lee, D.; Greer, P.B.; Baroni, G.; Keall, P.J.; Riboldi, M. Motion prediction in MRI-guided radiotherapy based on interleaved orthogonal cine-MRI. Phys. Med. Biol. 2016, 61, 872–887. [Google Scholar] [CrossRef]
- Zhou, Z.; Siddiquee, M.M.R.; Tajbakhsh, N.; Liang, J. UNet++: A nested U-Net architecture for medical image segmentation. In Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support; Springer International Publishing: Cham, Switzerland, 2018; Volume 11045, pp. 3–11. [Google Scholar] [CrossRef]
- Huang, H.; Lin, L.; Tong, R.; Hu, H.; Zhang, Q.; Iwamoto, Y.; Han, X.; Chen, Y.W.; Wu, J. UNet 3+: A full-scale connected UNet for medical image segmentation. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 1055–1059. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16 × 16 Words: Transformers for Image Recognition at Scale. In Proceedings of the International Conference on Learning Representations (ICLR), Vienna, Austria, 4 May 2021. [Google Scholar]
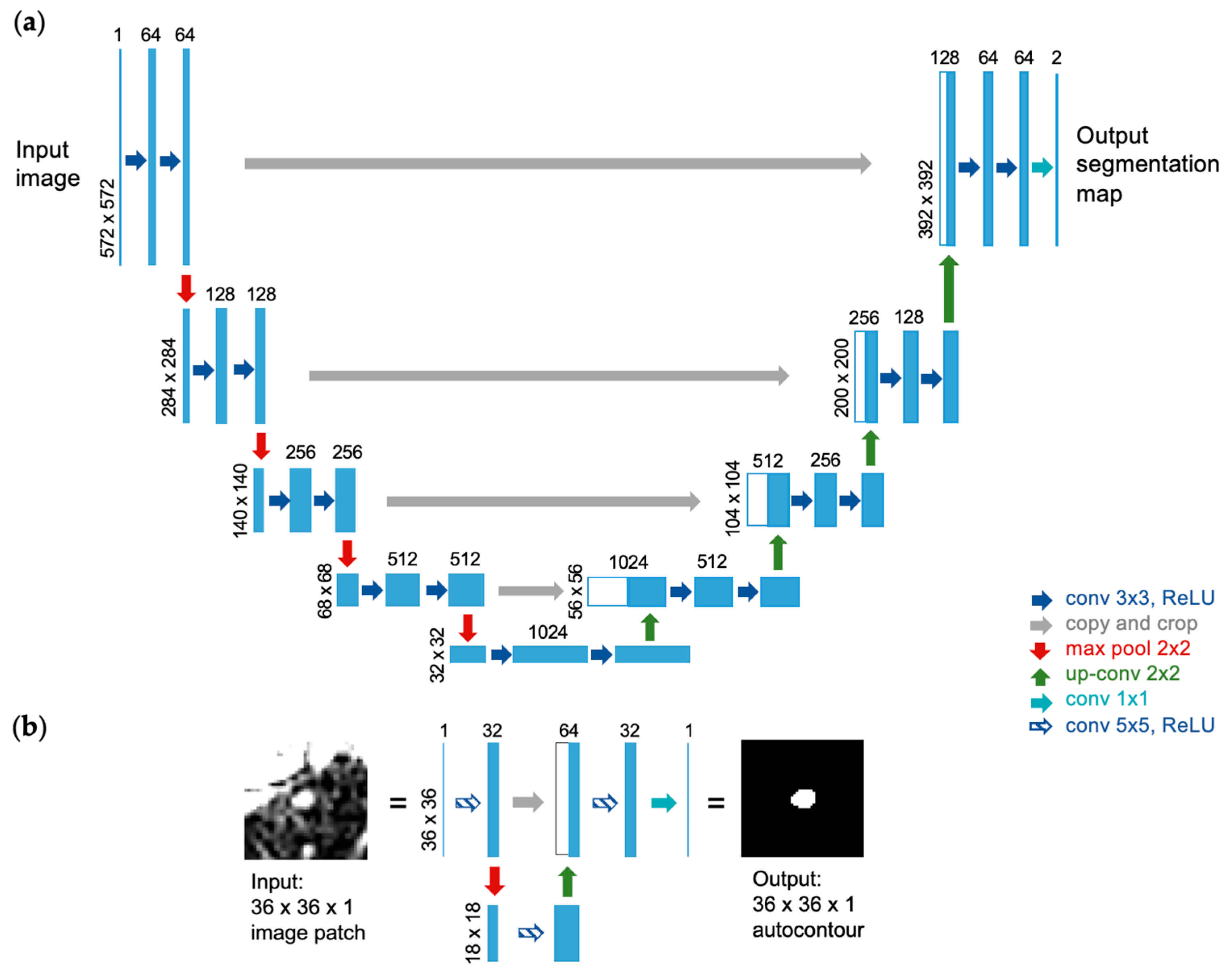
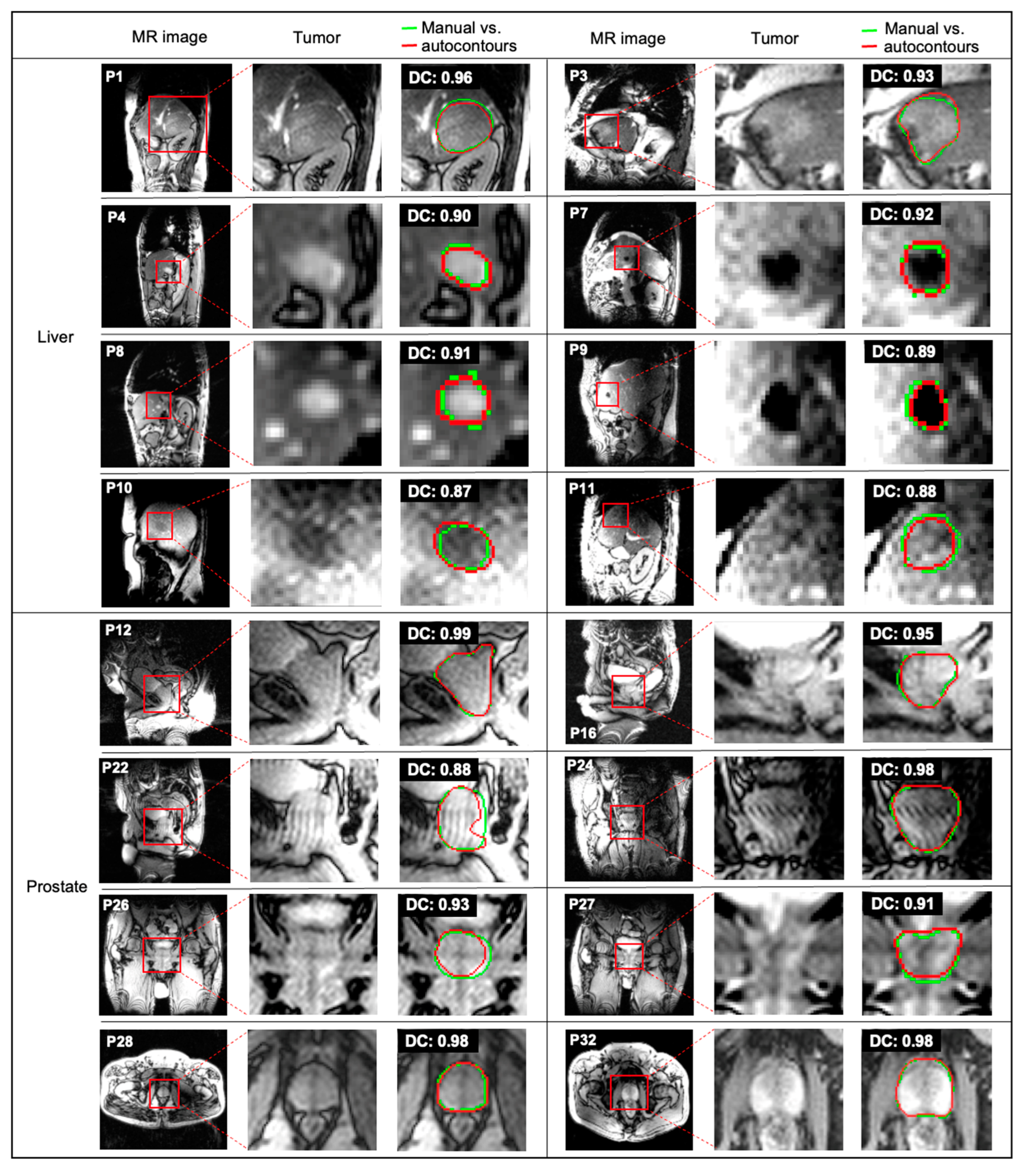
| Site | Patient | Gender | Age | Tumor Area (cm2) | Overall Stage | Cancer Type |
|---|---|---|---|---|---|---|
| Liver | 1 | F | 65 | 36.2 | III | Rectal adenocarcinoma |
| 2 | M | 69 | 11.5 | I | HCC | |
| 3 | M | 70 | 24.2 | IV | Sigmoid colon adenocarcinoma | |
| 4 | M | 57 | 2.8 | I | HCC | |
| 5 | M | 64 | 2.0 | II | HCC | |
| 6 | M | 63 | 3.7 | IVB | Nasopharyngeal carcinoma | |
| 7 | M | 65 | 3.1 | IVA | Colorectal carcinoma | |
| 8 | M | 59 | 2.4 | IV | Adenocarcinoma | |
| 9 | M | 68 | 1.5 | IIB | Rectal adenocarcinoma | |
| 10 | F | 82 | 6.0 | IV | Colorectal cancer | |
| 11 | M | 71 | 6.2 | I | HCC | |
| Prostate | 12 | M | 66 | 23.3 | IIA | Prostatic adenocarcinoma |
| 13 | M | 71 | 14.0 | IIIB | Prostatic adenocarcinoma | |
| 14 | M | 75 | 21.8 | IIB | Prostatic adenocarcinoma | |
| 15 | M | 62 | 12.2 | IIIB | Prostatic adenocarcinoma | |
| 16 | M | 66 | 15.9 | I | Prostatic adenocarcinoma | |
| 17 | M | 76 | 13.7 | I | Prostatic adenocarcinoma | |
| 18 | M | 77 | 24.5 | IIC | Prostatic adenocarcinoma | |
| 19 | M | 70 | 18.7 | IIB | Prostatic adenocarcinoma | |
| 20 | M | 69 | 8.4 | IIIC | Prostatic adenocarcinoma | |
| 21 | M | 63 | 4.7 | IIB | Prostatic adenocarcinoma | |
| 22 | M | 66 | 22.2 | IIC | Prostatic adenocarcinoma | |
| 23 | M | 70 | 20.1 | IIB | Prostatic adenocarcinoma | |
| 24 | M | 66 | 22.8 | IIC | Prostatic adenocarcinoma | |
| 25 | M | 77 | 26.9 | IIC | Prostatic adenocarcinoma | |
| 26 | M | 69 | 13.3 | IIIC | Prostatic adenocarcinoma | |
| 27 | M | 63 | 9.2 | IIB | Prostatic adenocarcinoma | |
| 28 | M | 62 | 11.6 | IIIB | Prostatic adenocarcinoma | |
| 29 | M | 69 | 13.9 | IIIC | Prostatic adenocarcinoma | |
| 30 | M | 66 | 19.7 | IIC | Prostatic adenocarcinoma | |
| 31 | M | 66 | 13.1 | I | Prostatic adenocarcinoma | |
| 32 | M | 75 | 26.4 | IIB | Prostatic adenocarcinoma | |
| 33 | M | 63 | 12.7 | IIB | Prostatic adenocarcinoma | |
| 34 | M | 70 | 14.3 | IIB | Prostatic adenocarcinoma | |
| 35 | M | 77 | 17.7 | IIC | Prostatic adenocarcinoma | |
| Lung | 36 | F | 73 | 6.4 | II | NSCLC |
| 37 | M | 65 | 3.8 | IA | NSCLC | |
| 38 | F | 78 | 7.4 | I | Lung cancer | |
| 39 | M | 79 | 3.8 | I | NSCLC | |
| 40 | M | 65 | 5.1 | I | NSCLC | |
| 41 | M | 90 | 3.9 | I | Squamous cell carcinoma | |
| 42 | M | 75 | 3.7 | I | NSCLC | |
| 43 | M | 81 | 1.3 | I | NSCLC | |
| 44 | M | 75 | 3.0 | IIA | NSCLC | |
| 45 | M | 70 | 1.7 | IB | SCLC | |
| 46 | M | 65 | 1.4 | IA | NSCLC | |
| 47 | M | 72 | 4.8 | IVA | NSCLC | |
| Mean (SD) | 11.6 (8.7) |
| Comparing HP-Optimized U-Net with Non-Optimized U-Net | Comparing HP-Optimized U-Net with nnU-Net | |||||
|---|---|---|---|---|---|---|
| # of Patients with Better Mean Value | # of Patients with p < 0.05 | # of Patients with Better Mean Value | # of Patients with p < 0.05 | |||
| Two-Tailed | One-Tailed | Two-Tailed | One-Tailed | |||
| DC | 36 | 33 | 32 | 37 | 31 | 30 |
| CD | 32 | 25 | 21 | 27 | 26 | 19 |
| HD | 32 | 26 | 24 | 39 | 37 | 33 |
| # of Patients Used for HPO | DC | CD (mm) | HD (mm) | |||
|---|---|---|---|---|---|---|
| Mean/SD | Max/Min | Mean/SD | Max/Min | Mean/SD | Max/Min | |
| (i) Patient-specific HPO | 0.92/0.04 | 0.97/0.83 | 1.35/1.03 | 3.95/0.15 | 3.63/2.17 | 7.51/2.01 |
| (ii) 30 patients (1 training and 1 validation image per patient) | 0.64/0.05 | 0.77/0.53 | 7.34/2.35 | 13.28/3.14 | 15.81/3.53 | 24.31/9.95 |
| (iii) 9 patients (30 training and 30 validation images per patient) | 0.36/0.09 | 0.57/0.17 | 9.44/3.46 | 18.49/2.66 | 19.40/3.81 | 29.64/11.48 |
| (iv) 15 patients (30 training and 30 validation images per patient) | 0.47/0.07 | 0.63/0.33 | 8.54/3.32 | 16.03/3.29 | 17.03/4.09 | 25.96/9.59 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, G.; Wachowicz, K.; Usmani, N.; Yee, D.; Wong, J.; Elangovan, A.; Yun, J.; Fallone, B.G. Patient-Specific Hyperparameter Optimization of a Deep Learning-Based Tumor Autocontouring Algorithm on 2D Liver, Prostate, and Lung Cine MR Images: A Pilot Study. Algorithms 2025, 18, 233. https://doi.org/10.3390/a18040233
Han G, Wachowicz K, Usmani N, Yee D, Wong J, Elangovan A, Yun J, Fallone BG. Patient-Specific Hyperparameter Optimization of a Deep Learning-Based Tumor Autocontouring Algorithm on 2D Liver, Prostate, and Lung Cine MR Images: A Pilot Study. Algorithms. 2025; 18(4):233. https://doi.org/10.3390/a18040233
Chicago/Turabian StyleHan, Gawon, Keith Wachowicz, Nawaid Usmani, Don Yee, Jordan Wong, Arun Elangovan, Jihyun Yun, and B. Gino Fallone. 2025. "Patient-Specific Hyperparameter Optimization of a Deep Learning-Based Tumor Autocontouring Algorithm on 2D Liver, Prostate, and Lung Cine MR Images: A Pilot Study" Algorithms 18, no. 4: 233. https://doi.org/10.3390/a18040233
APA StyleHan, G., Wachowicz, K., Usmani, N., Yee, D., Wong, J., Elangovan, A., Yun, J., & Fallone, B. G. (2025). Patient-Specific Hyperparameter Optimization of a Deep Learning-Based Tumor Autocontouring Algorithm on 2D Liver, Prostate, and Lung Cine MR Images: A Pilot Study. Algorithms, 18(4), 233. https://doi.org/10.3390/a18040233






