Computational Aspects of L0 Linking in the Rasch Model
Abstract
1. Introduction
2. Linking in the Rasch Model
2.1. Identified Item Parameters and Mean–Mean Linking
2.2. Loss Function and Differentiable Approximations
2.3. Linking as a Robust Mean–Mean Linking in the Rasch Model
2.4. Statistical Properties of the Estimated Linking Parameter in Linking
3. Numerical Illustration
3.1. Method
3.2. Results
4. Simulation Study
4.1. Method
4.2. Results
5. Empirical Example
6. Discussion
7. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANOVA | analysis of variance |
| DIF | differential item functioning |
| IRF | item response function |
| IRT | item response theory |
| ML | maximum likelihood |
| MM | mean–mean |
| MSE | mean square error |
| RMSE | root mean square error |
| SD | standard deviation |
References
- Bock, R.D.; Gibbons, R.D. Item Response Theory; Wiley: Hoboken, NJ, USA, 2021. [Google Scholar] [CrossRef]
- Chen, Y.; Li, X.; Liu, J.; Ying, Z. Item response theory—A statistical framework for educational and psychological measurement. arXiv 2021, arXiv:2108.08604. [Google Scholar] [CrossRef]
- Yen, W.M.; Fitzpatrick, A.R. Item response theory. In Educational Measurement; Brennan, R.L., Ed.; Praeger Publishers: Westport, CT, USA, 2006; pp. 111–154. [Google Scholar]
- Van der Linden, W.J. Unidimensional logistic response models. In Handbook of Item Response Theory, Volume 1: Models; van der Linden, W.J., Ed.; CRC Press: Boca Raton, FL, USA, 2016; pp. 11–30. [Google Scholar] [CrossRef]
- Rasch, G. Probabilistic Models for Some Intelligence and Attainment Tests; Danish Institute for Educational Research: Copenhagen, Denmark, 1960. [Google Scholar]
- Bond, T.; Yan, Z.; Heene, M. Applying the Rasch Model; Routledge: New York, NY, USA, 2020. [Google Scholar] [CrossRef]
- Debelak, R.; Strobl, C.; Zeigenfuse, M.D. An Introduction to the Rasch Model with Examples in R; CRC Press: Boca Raton, FL, USA, 2022. [Google Scholar] [CrossRef]
- Bock, R.D.; Aitkin, M. Marginal maximum likelihood estimation of item parameters: Application of an EM algorithm. Psychometrika 1981, 46, 443–459. [Google Scholar] [CrossRef]
- Glas, C.A.W. Maximum-likelihood estimation. In Handbook of Item Response Theory, Volume 2: Statistical Tools; van der Linden, W.J., Ed.; CRC Press: Boca Raton, FL, USA, 2016; pp. 197–216. [Google Scholar] [CrossRef]
- Robitzsch, A. A comprehensive simulation study of estimation methods for the Rasch model. Stats 2021, 4, 814–836. [Google Scholar] [CrossRef]
- Kolen, M.J.; Brennan, R.L. Test Equating, Scaling, and Linking; Springer: New York, NY, USA, 2014. [Google Scholar] [CrossRef]
- Holland, P.W.; Wainer, H. (Eds.) Differential Item Functioning: Theory and Practice; Lawrence Erlbaum: Hillsdale, NJ, USA, 1993. [Google Scholar] [CrossRef]
- Millsap, R.E. Statistical Approaches to Measurement Invariance; Routledge: New York, NY, USA, 2011. [Google Scholar] [CrossRef]
- Penfield, R.D.; Camilli, G. Differential item functioning and item bias. In Handbook of Statistics, Volume 26: Psychometrics; Rao, C.R., Sinharay, S., Eds.; Elsevier: Amsterdam, The Netherlands, 2007; pp. 125–167. [Google Scholar] [CrossRef]
- Lee, W.C.; Lee, G. IRT linking and equating. In The Wiley Handbook of Psychometric Testing: A Multidisciplinary Reference on Survey, Scale and Test; Irwing, P., Booth, T., Hughes, D.J., Eds.; Wiley: New York, NY, USA, 2018; pp. 639–673. [Google Scholar] [CrossRef]
- Sansivieri, V.; Wiberg, M.; Matteucci, M. A review of test equating methods with a special focus on IRT-based approaches. Statistica 2017, 77, 329–352. [Google Scholar] [CrossRef]
- Andrich, D.; Marais, I. A Course in Rasch Measurement Theory; Springer: New York, NY, USA, 2019. [Google Scholar] [CrossRef]
- Lamprianou, I. Applying the Rasch Model in Social Sciences Using R and BlueSky Statistics; Routledge: New York, NY, USA, 2019. [Google Scholar] [CrossRef]
- Robitzsch, A. Extensions to mean–geometric mean linking. Mathematics 2025, 13, 35. [Google Scholar] [CrossRef]
- Von Davier, M.; Bezirhan, U. A robust method for detecting item misfit in large scale assessments. Educ. Psychol. Meas. 2023, 83, 740–765. [Google Scholar] [CrossRef]
- De Boeck, P. Random item IRT models. Psychometrika 2008, 73, 533–559. [Google Scholar] [CrossRef]
- Halpin, P.F. Differential item functioning via robust scaling. Psychometrika 2024, 89, 796–821. [Google Scholar] [CrossRef]
- He, Y.; Cui, Z.; Fang, Y.; Chen, H. Using a linear regression method to detect outliers in IRT common item equating. Appl. Psychol. Meas. 2013, 37, 522–540. [Google Scholar] [CrossRef]
- Magis, D.; De Boeck, P. Identification of differential item functioning in multiple-group settings: A multivariate outlier detection approach. Multivar. Behav. Res. 2011, 46, 733–755. [Google Scholar] [CrossRef]
- Robitzsch, A. Robust and nonrobust linking of two groups for the Rasch model with balanced and unbalanced random DIF: A comparative simulation study and the simultaneous assessment of standard errors and linking errors with resampling techniques. Symmetry 2021, 13, 2198. [Google Scholar] [CrossRef]
- Robitzsch, A. A comparison of linking methods for two groups for the two-parameter logistic item response model in the presence and absence of random differential item functioning. Foundations 2021, 1, 116–144. [Google Scholar] [CrossRef]
- Wang, W.; Liu, Y.; Liu, H. Testing differential item functioning without predefined anchor items using robust regression. J. Educ. Behav. Stat. 2022, 47, 666–692. [Google Scholar] [CrossRef]
- Hu, H.; Rogers, W.T.; Vukmirovic, Z. Investigation of IRT-based equating methods in the presence of outlier common items. Appl. Psychol. Meas. 2008, 32, 311–333. [Google Scholar] [CrossRef]
- Jurich, D.; Liu, C. Detecting item parameter drift in small sample Rasch equating. Appl. Meas. Educ. 2023, 36, 326–339. [Google Scholar] [CrossRef]
- Liu, C.; Jurich, D. Outlier detection using t-test in Rasch IRT equating under NEAT design. Appl. Psychol. Meas. 2023, 47, 34–47. [Google Scholar] [CrossRef] [PubMed]
- Manna, V.F.; Gu, L. Different Methods of Adjusting for Form Difficulty Under the Rasch Model: Impact on Consistency of Assessment Results; (Research Report No. RR-19-08); Educational Testing Service: Princeton, NJ, USA, 2019. [Google Scholar] [CrossRef]
- Oelker, M.R.; Pößnecker, W.; Tutz, G. Selection and fusion of categorical predictors with L0-type penalties. Stat. Model. 2015, 15, 389–410. [Google Scholar] [CrossRef]
- Oelker, M.R.; Tutz, G. A uniform framework for the combination of penalties in generalized structured models. Adv. Data Anal. Classif. 2017, 11, 97–120. [Google Scholar] [CrossRef]
- Atamturk, A.; Gómez, A.; Han, S. Sparse and smooth signal estimation: Convexification of l0-formulations. J. Mach. Learn. Res. 2021, 22, 1–43. [Google Scholar]
- Dai, S. Variable selection in convex quantile regression: L1-norm or L0-norm regularization? Eur. J. Oper. Res. 2023, 305, 338–355. [Google Scholar] [CrossRef]
- Huang, J.; Jiao, Y.; Liu, Y.; Lu, X. A constructive approach to L0 penalized regression. J. Mach. Learn. Res. 2018, 19, 1–37. [Google Scholar]
- Panokin, N.V.; Kostin, I.A.; Karlovskiy, A.V.; Nalivaiko, A.Y. Comparison of sparse representation methods for complex data based on the smoothed L0 norm and modified minimum fuel neural network. Appl. Sci. 2025, 15, 1038. [Google Scholar] [CrossRef]
- Soubies, E.; Blanc-Féraud, L.; Aubert, G. A continuous exact l0 penalty (CEL0) for least squares regularized problem. SIAM J. Imaging Sci. 2015, 8, 1607–1639. [Google Scholar] [CrossRef]
- Yang, Y.; McMahan, C.S.; Wang, Y.B.; Ouyang, Y. Estimation of l0 norm penalized models: A statistical treatment. Comp. Stat. Data Anal. 2024, 192, 107902. [Google Scholar] [CrossRef]
- Liu, W.; Li, Z.; Chen, W. Evaluating model robustness using adaptive sparse L0 regularization. arXiv 2024, arXiv:2408.15702. [Google Scholar] [CrossRef]
- O’Neill, M.; Burke, K. Variable selection using a smooth information criterion for distributional regression models. Stat. Comput. 2023, 33, 71. [Google Scholar] [CrossRef]
- Wang, B.; Wang, L.; Yu, H.; Xin, F. A new regularized reconstruction algorithm based on compressed sensing for the sparse underdetermined problem and applications of one-dimensional and two-dimensional signal recovery. Algorithms 2019, 12, 126. [Google Scholar] [CrossRef]
- Xiang, J.; Yue, H.; Yin, X.; Wang, L. A new smoothed l0 regularization approach for sparse signal recovery. Math. Probl. Eng. 2019, 2019, 1978154. [Google Scholar] [CrossRef]
- Robitzsch, A. L0 and Lp loss functions in model-robust estimation of structural equation models. Psych 2023, 5, 1122–1139. [Google Scholar] [CrossRef]
- Paik, J.W.; Lee, J.H.; Hong, W. An enhanced smoothed L0-norm direction of arrival estimation method using covariance matrix. Sensors 2021, 21, 4403. [Google Scholar] [CrossRef]
- Wang, L.; Yin, X.; Yue, H.; Xiang, J. A regularized weighted smoothed L0 norm minimization method for underdetermined blind source separation. Sensors 2018, 18, 4260. [Google Scholar] [CrossRef]
- Zhu, J.; Li, X. A smoothed l0-norm and l1-norm regularization algorithm for computed tomography. J. Appl. Math. 2019, 2019, 8398035. [Google Scholar] [CrossRef]
- Boos, D.D.; Stefanski, L.A. Essential Statistical Inference; Springer: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Simakhin, V.A.; Shamanaeva, L.G.; Avdyushina, A.E. Robust parametric estimates of heterogeneous experimental data. Russ. Phys. J. 2021, 63, 1510–1518. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Core Team: Vienna, Austria, 2024; Available online: https://www.R-project.org (accessed on 15 June 2024).
- Clausen, A.; Sokol, S. Deriv: Symbolic Differentiation, 2024. R Package Version 4.1.6. Available online: https://cran.r-project.org/web/packages/Deriv/ (accessed on 13 September 2024).
- Robitzsch, A. sirt: Supplementary Item Response Theory Models, 2024. R Package Version 4.2-106. Available online: https://github.com/alexanderrobitzsch/sirt (accessed on 31 December 2024).
- Battauz, M. equateIRT: An R package for IRT test equating. J. Stat. Softw. 2015, 68, 1–22. [Google Scholar] [CrossRef]
- Battauz, M. equateMultiple: Equating of Multiple Forms, 2024. R Package Version 1.0.0. Available online: https://cran.r-project.org/web/packages/equateMultiple/index.html (accessed on 13 September 2024).
- Chen, Y.; Li, C.; Ouyang, J.; Xu, G. DIF statistical inference without knowing anchoring items. Psychometrika 2023, 88, 1097–1122. [Google Scholar] [CrossRef] [PubMed]
- Halpin, P.F.; Gilbert, J. Testing whether reported treatment effects are unduly dependent on the specific outcome measure used. arXiv 2024, arXiv:2409.03502. [Google Scholar] [CrossRef]
- Strobl, C.; Kopf, J.; Kohler, L.; von Oertzen, T.; Zeileis, A. Anchor point selection: Scale alignment based on an inequality criterion. Appl. Psychol. Meas. 2021, 45, 214–230. [Google Scholar] [CrossRef]
- Camilli, G. The case against item bias detection techniques based on internal criteria: Do item bias procedures obscure test fairness issues? In Differential Item Functioning: Theory and Practice; Holland, P.W., Wainer, H., Eds.; Erlbaum: Hillsdale, NJ, USA, 1993; pp. 397–417. [Google Scholar]
- Shealy, R.; Stout, W. A model-based standardization approach that separates true bias/DIF from group ability differences and detects test bias/DTF as well as item bias/DIF. Psychometrika 1993, 58, 159–194. [Google Scholar] [CrossRef]
- De Los Reyes, A.; Tyrell, F.A.; Watts, A.L.; Asmundson, G.J.G. Conceptual, methodological, and measurement factors that disqualify use of measurement invariance techniques to detect informant discrepancies in youth mental health assessments. Front. Psychol. 2022, 13, 931296. [Google Scholar] [CrossRef]
- El Masri, Y.H.; Andrich, D. The trade-off between model fit, invariance, and validity: The case of PISA science assessments. Appl. Meas. Educ. 2020, 33, 174–188. [Google Scholar] [CrossRef]
- Funder, D.C.; Gardiner, G. MIsgivings about measurement invariance. Eur. J. Pers. 2024, 38, 889–895. [Google Scholar] [CrossRef]
- Welzel, C.; Inglehart, R.F. Misconceptions of measurement equivalence: Time for a paradigm shift. Comp. Political Stud. 2016, 49, 1068–1094. [Google Scholar] [CrossRef]
- Zwitser, R.J.; Glaser, S.S.F.; Maris, G. Monitoring countries in a changing world: A new look at DIF in international surveys. Psychometrika 2017, 82, 210–232. [Google Scholar] [CrossRef] [PubMed]



| , | , | |||||||
|---|---|---|---|---|---|---|---|---|
| 250 | 500 | 1000 | 250 | 500 | 1000 | |||
| 10 | 0.900 | 0.065 | 0.030 | 0.150 | 0.100 | 0.090 | ||
| 20 | 0.200 | 0.050 | 0.030 | 0.100 | 0.100 | 0.090 | ||
| 40 | 0.100 | 0.035 | 0.025 | 0.100 | 0.095 | 0.085 | ||
| Ratio Function, | Gaussian Function, | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.25 | 0.10 | 0.05 | 0.01 | 0.25 | 0.10 | 0.05 | 0.01 | |||||||||
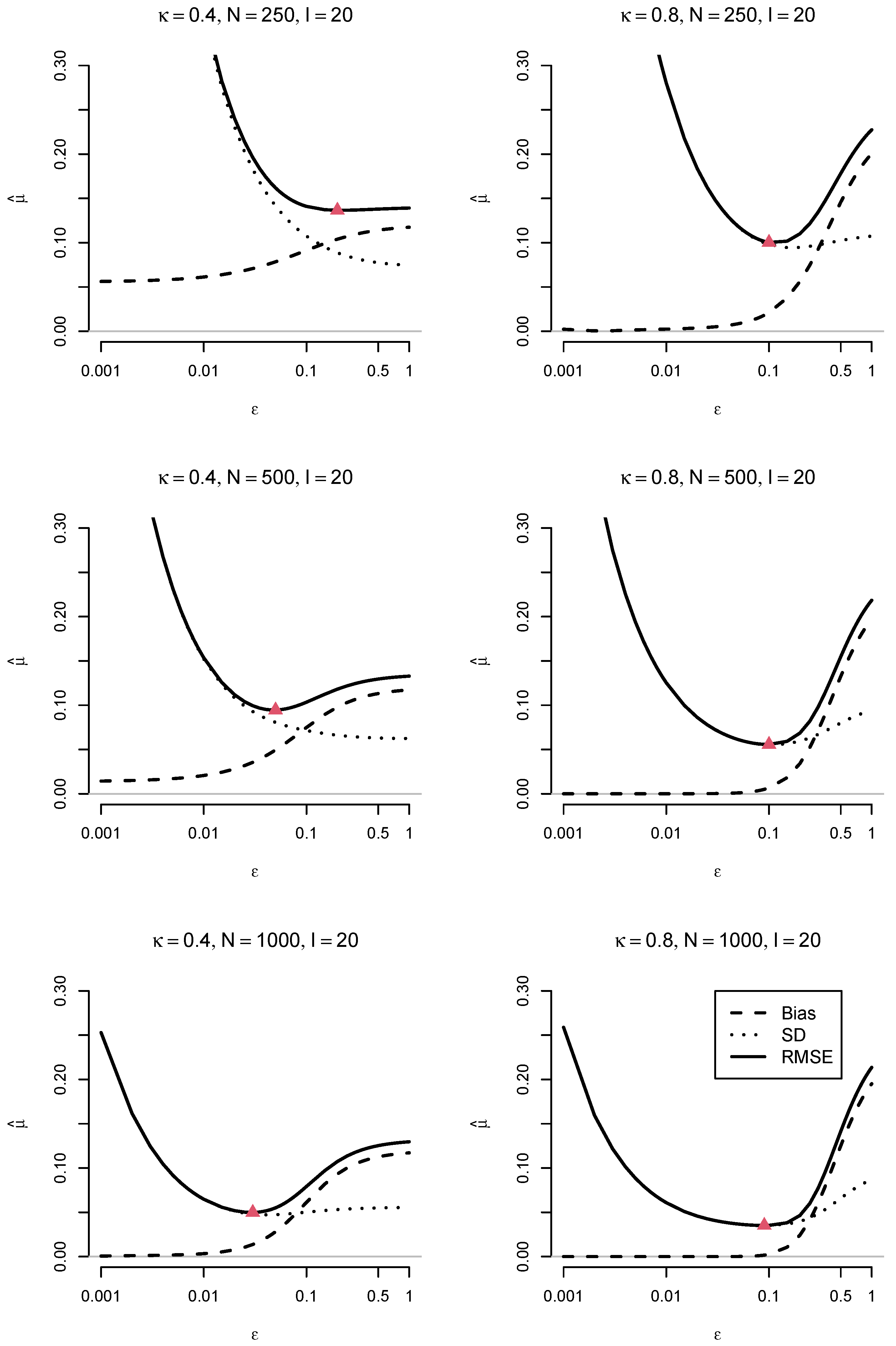
| 0.4 | 10 | 125 | 0.107 | 0.103 | 0.102 | 0.102 | 0.110 | 0.105 | 0.107 | 0.101 | 0.100 | 0.101 | 0.112 | 0.106 | ||
| 250 | 0.098 | 0.087 | 0.082 | 0.079 | 0.096 | 0.085 | 0.101 | 0.086 | 0.080 | 0.078 | 0.101 | 0.087 | ||||
| 500 | 0.088 | 0.066 | 0.052 | 0.041 | 0.068 | 0.049 | 0.097 | 0.067 | 0.046 | 0.033 | 0.075 | 0.048 | ||||
| 1000 | 0.082 | 0.050 | 0.031 | 0.015 | 0.034 | 0.019 | 0.096 | 0.057 | 0.026 | 0.010 | 0.035 | 0.013 | ||||
| 20 | 125 | 0.104 | 0.100 | 0.099 | 0.099 | 0.107 | 0.102 | 0.104 | 0.099 | 0.096 | 0.096 | 0.109 | 0.103 | |||
| 250 | 0.098 | 0.086 | 0.080 | 0.075 | 0.097 | 0.084 | 0.102 | 0.084 | 0.075 | 0.069 | 0.102 | 0.086 | ||||
| 500 | 0.089 | 0.066 | 0.051 | 0.036 | 0.069 | 0.048 | 0.097 | 0.068 | 0.044 | 0.028 | 0.076 | 0.046 | ||||
| 1000 | 0.081 | 0.049 | 0.028 | 0.009 | 0.031 | 0.014 | 0.095 | 0.056 | 0.023 | 0.003 | 0.032 | 0.008 | ||||
| 40 | 125 | 0.105 | 0.101 | 0.098 | 0.096 | 0.108 | 0.103 | 0.106 | 0.099 | 0.096 | 0.096 | 0.110 | 0.105 | |||
| 250 | 0.098 | 0.086 | 0.077 | 0.070 | 0.097 | 0.083 | 0.101 | 0.084 | 0.071 | 0.063 | 0.101 | 0.086 | ||||
| 500 | 0.099 | 0.076 | 0.059 | 0.039 | 0.079 | 0.055 | 0.107 | 0.078 | 0.051 | 0.029 | 0.087 | 0.054 | ||||
| 1000 | 0.087 | 0.054 | 0.033 | 0.012 | 0.036 | 0.018 | 0.100 | 0.062 | 0.027 | 0.006 | 0.036 | 0.012 | ||||
| 0.8 | 10 | 125 | 0.114 | 0.093 | 0.087 | 0.084 | 0.138 | 0.102 | 0.105 | 0.078 | 0.074 | 0.074 | 0.152 | 0.099 | ||
| 250 | 0.069 | 0.037 | 0.027 | 0.023 | 0.064 | 0.033 | 0.066 | 0.021 | 0.015 | 0.015 | 0.067 | 0.023 | ||||
| 500 | 0.048 | 0.017 | 0.008 | 0.003 | 0.019 | 0.006 | 0.047 | 0.004 | 0.000 | 0.001 | 0.009 | 0.000 | ||||
| 1000 | 0.039 | 0.011 | 0.004 | 0.001 | 0.005 | 0.001 | 0.040 | 0.002 | 0.000 | 0.000 | 0.000 | 0.000 | ||||
| 20 | 125 | 0.112 | 0.082 | 0.073 | 0.069 | 0.140 | 0.096 | 0.103 | 0.063 | 0.055 | 0.054 | 0.155 | 0.095 | |||
| 250 | 0.069 | 0.033 | 0.020 | 0.014 | 0.063 | 0.029 | 0.065 | 0.015 | 0.007 | 0.005 | 0.065 | 0.017 | ||||
| 500 | 0.047 | 0.015 | 0.006 | 0.000 | 0.017 | 0.004 | 0.046 | 0.003 | 0.002 | 0.003 | 0.007 | 0.001 | ||||
| 1000 | 0.038 | 0.011 | 0.004 | 0.000 | 0.005 | 0.001 | 0.039 | 0.002 | 0.000 | 0.000 | 0.000 | 0.000 | ||||
| 40 | 125 | 0.109 | 0.075 | 0.061 | 0.054 | 0.140 | 0.092 | 0.099 | 0.052 | 0.041 | 0.036 | 0.156 | 0.090 | |||
| 250 | 0.071 | 0.033 | 0.020 | 0.011 | 0.065 | 0.029 | 0.067 | 0.015 | 0.006 | 0.005 | 0.067 | 0.018 | ||||
| 500 | 0.051 | 0.020 | 0.011 | 0.005 | 0.022 | 0.009 | 0.050 | 0.007 | 0.003 | 0.003 | 0.011 | 0.003 | ||||
| 1000 | 0.039 | 0.012 | 0.005 | 0.001 | 0.006 | 0.002 | 0.040 | 0.002 | 0.001 | 0.001 | 0.001 | 0.001 | ||||
| Ratio Function, | Gaussian Function, | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.25 | 0.10 | 0.05 | 0.01 | 0.25 | 0.10 | 0.05 | 0.01 | |||||||||
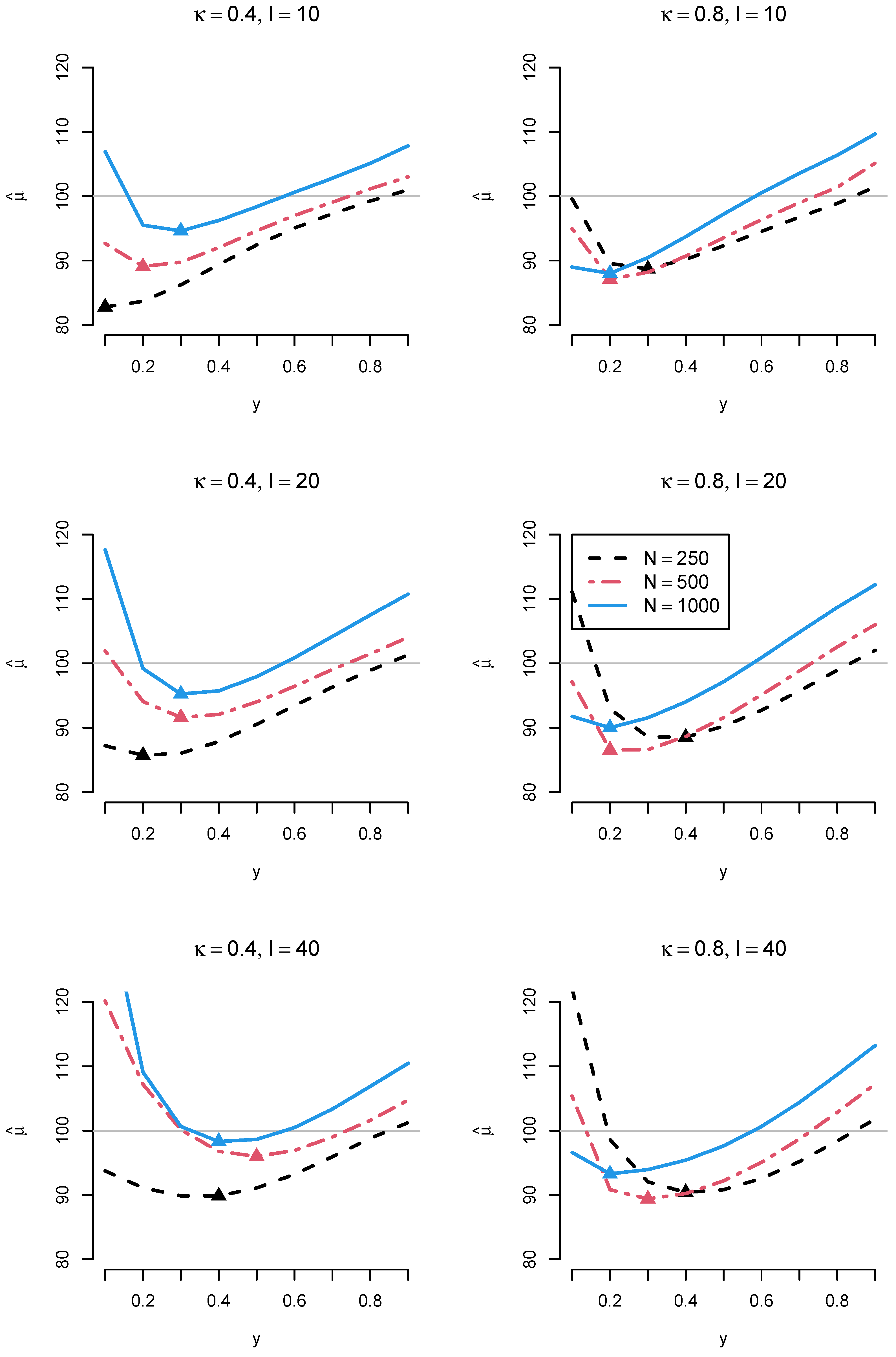
| 0.4 | 10 | 125 | 83.5 | 90.5 | 95.0 | 100 | 80.2 | 86.3 | 83.0 | 92.9 | 99.0 | 105.2 | 79.1 | 84.0 | ||
| 250 | 83.4 | 88.1 | 93.3 | 100 | 83.7 | 89.4 | 83.2 | 89.1 | 96.6 | 105.8 | 83.2 | 88.1 | ||||
| 500 | 92.6 | 89.0 | 91.0 | 100 | 89.1 | 92.0 | 95.6 | 89.8 | 92.3 | 103.8 | 90.5 | 91.6 | ||||
| 1000 | 123.1 | 102.5 | 94.8 | 100 | 95.5 | 96.2 | 134.4 | 108.1 | 94.6 | 102.4 | 97.5 | 94.0 | ||||
| 20 | 125 | 83.2 | 88.6 | 93.8 | 100 | 81.8 | 85.1 | 83.0 | 90.9 | 98.1 | 105.6 | 81.4 | 83.6 | |||
| 250 | 85.9 | 86.9 | 91.3 | 100 | 85.7 | 87.8 | 86.4 | 87.0 | 93.7 | 104.5 | 86.4 | 86.5 | ||||
| 500 | 101.9 | 93.4 | 91.7 | 100 | 94.0 | 92.1 | 106.3 | 94.1 | 91.0 | 103.2 | 96.8 | 90.7 | ||||
| 1000 | 141.1 | 111.1 | 97.7 | 100 | 99.2 | 95.7 | 155.9 | 118.4 | 95.8 | 100.4 | 100.7 | 91.7 | ||||
| 40 | 125 | 85.6 | 88.9 | 93.5 | 100 | 85.2 | 86.5 | 85.4 | 89.8 | 97.1 | 105.9 | 85.2 | 85.6 | |||
| 250 | 91.5 | 89.7 | 91.6 | 100 | 91.1 | 89.9 | 92.4 | 89.3 | 92.5 | 104.4 | 92.4 | 89.3 | ||||
| 500 | 120.2 | 105.7 | 97.9 | 100 | 107.2 | 96.8 | 126.2 | 107.1 | 94.9 | 101.5 | 112.2 | 95.7 | ||||
| 1000 | 169.0 | 127.9 | 106.9 | 100 | 109.1 | 98.3 | 187.6 | 137.6 | 103.0 | 99.7 | 110.8 | 94.2 | ||||
| 0.8 | 10 | 125 | 87.2 | 92.6 | 96.0 | 100 | 85.6 | 89.3 | 87.9 | 95.9 | 100.5 | 106.1 | 86.8 | 88.7 | ||
| 250 | 90.3 | 89.4 | 92.8 | 100 | 89.6 | 90.2 | 91.4 | 89.1 | 94.6 | 106.2 | 91.4 | 89.0 | ||||
| 500 | 94.8 | 87.2 | 89.8 | 100 | 87.1 | 90.7 | 97.7 | 84.0 | 87.5 | 105.3 | 84.6 | 86.6 | ||||
| 1000 | 101.5 | 87.9 | 88.4 | 100 | 88.0 | 93.7 | 106.2 | 85.6 | 86.5 | 102.4 | 87.2 | 91.9 | ||||
| 20 | 125 | 88.7 | 90.9 | 95.0 | 100 | 91.6 | 88.7 | 88.5 | 92.2 | 97.6 | 104.7 | 94.4 | 88.2 | |||
| 250 | 94.6 | 88.3 | 90.9 | 100 | 92.9 | 88.5 | 94.8 | 85.6 | 90.8 | 104.9 | 94.7 | 85.2 | ||||
| 500 | 97.2 | 86.3 | 87.6 | 100 | 86.6 | 88.6 | 99.0 | 83.7 | 86.1 | 104.1 | 84.2 | 85.5 | ||||
| 1000 | 106.8 | 90.5 | 90.2 | 100 | 90.0 | 94.0 | 109.8 | 88.1 | 88.7 | 102.4 | 88.3 | 91.4 | ||||
| 40 | 125 | 92.1 | 90.7 | 94.0 | 100 | 98.3 | 90.2 | 90.2 | 89.4 | 95.3 | 103.8 | 102.7 | 88.8 | |||
| 250 | 101.0 | 90.8 | 91.2 | 100 | 98.6 | 90.4 | 100.3 | 87.5 | 90.1 | 104.0 | 100.1 | 87.6 | ||||
| 500 | 105.4 | 90.3 | 89.7 | 100 | 90.8 | 90.2 | 106.1 | 87.0 | 87.9 | 104.9 | 87.7 | 87.6 | ||||
| 1000 | 116.4 | 94.8 | 93.3 | 100 | 93.3 | 95.4 | 118.6 | 92.0 | 92.2 | 101.8 | 91.9 | 93.7 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Robitzsch, A. Computational Aspects of L0 Linking in the Rasch Model. Algorithms 2025, 18, 213. https://doi.org/10.3390/a18040213
Robitzsch A. Computational Aspects of L0 Linking in the Rasch Model. Algorithms. 2025; 18(4):213. https://doi.org/10.3390/a18040213
Chicago/Turabian StyleRobitzsch, Alexander. 2025. "Computational Aspects of L0 Linking in the Rasch Model" Algorithms 18, no. 4: 213. https://doi.org/10.3390/a18040213
APA StyleRobitzsch, A. (2025). Computational Aspects of L0 Linking in the Rasch Model. Algorithms, 18(4), 213. https://doi.org/10.3390/a18040213







