Abstract
With the escalating environmental crisis, electric vehicles have emerged as a key solution for emission reductions in logistics due to their low-carbon attributes, prompting significant attention and extensive research on the electric vehicle routing problem (EVRP). However, existing studies often overlook charging infrastructure (CI) capacity constraints and fail to fully exploit the synergistic potential of heterogeneous energy replenishment infrastructures (HERIs). This paper addresses the EVRP with HERIs under various capacity constraints (EVRP-HERI-CC), proposing a mixed-integer programming (MIP) model and a hybrid ant colony optimization (HACO) algorithm integrated with a variable neighborhood search (VNS) mechanism. Extensive numerical experiments demonstrate HACO’s effective integration of problem-specific characteristics. The algorithm resolves charging conflicts via dynamic rescheduling while optimizing charging-battery swapping decisions under an on-demand energy replenishment strategy, achieving global cost minimization. Through small-scale instance experiments, we have verified the computational complexity of the problem and demonstrated HACO’s superior performance compared to the Gurobi solver. Furthermore, comparative studies with other advanced heuristic algorithms confirm HACO’s effectiveness in solving the EVRP-HERI-CC. Sensitivity analysis reveals that appropriate CI capacity configurations achieve economic efficiency while maximizing resource utilization, further validating the engineering value of HERI networks.
1. Introduction
Global warming has emerged as a critical climate challenge, prompting nations worldwide to implement tailored energy-saving and emission-reduction policies [1,2,3]. According to a recent report by the European Environment Agency, the transportation sector is a major contributor, accounting for nearly a quarter of total EU-27 emissions in 2024, with over three quarters originating from road transport [4]. As vehicle numbers continue to rise, transportation is expected to remain a primary source of emissions [5]. Recognizing the pivotal role of electric vehicles (EVs) in reducing carbon emissions, an increasing number of governments have introduced favorable policies to incentivize logistics companies to transition from fossil fuel fleets to EVs [6].
Electric logistics vehicles are a category of electric commercial vehicles, which represent an emerging green transportation solution, offering significant environmental and economic benefits due to their electric propulsion, reduced noise, and lower air pollution. As of the end of 2024, EVs have surpassed 40% market penetration in China’s automotive sector, while electric logistics vehicles account for 15% of the logistics vehicle market, with both segments demonstrating sustained year-on-year growth. These advantages and the rapid expansion of EVs have attracted increasing research attention to EVRP in recent years. EVRP traces its origins to Erdogan and Miller-Hooks [7], who first introduced the green vehicle routing problem, emphasizing that fleets with limited range must visit energy replenishment infrastructures mid-route. Current main EVRP variants include EVRP with time windows (EVRP-TWs) [8], EVRP with heterogeneous fleets (EVRP-HFs) [9], and EVRP with multiple depots (EVRP-MDs) [10].
Notably, few studies incorporate the capacity constraints of charging infrastructures (CIs), often assuming infinite capacity where vehicles can immediately start energy replenishment upon arrival. But real-world scenarios differ significantly, as the limited availability of CIs restricts the further adoption and widespread use of electric vehicles. This scarcity is reflected in both the number of CIs and the capacity of their internal charging units. During peak periods or holidays, electric vehicles frequently encounter long queues at CIs. For example, during the 2025 Spring Festival, severe charging congestion occurred on highways near major cities such as Beijing, Shanghai, and Hangzhou, with wait times reaching 1–2 h. For electric logistics vehicles, time-consuming charging queues are particularly detrimental. This hampers the operational efficiency of fleet, presenting a critical challenge that demands urgent resolution.
It is worth noting that the assumption of infinite CI capacity holds partial validity in urban areas with dense charging networks, as illustrated by the node distribution in Figure 1a. In such regions, CIs are distributed among customer points and located relatively close to the depot, providing diverse replenishment options and reducing the likelihood of capacity bottlenecks at individual CIs. Nonetheless, as previously discussed, the capacity limitations of CIs remain a substantial constraint when the energy replenishment demand is high, particularly in scenarios where resource scarcity persists. In suburban or rural areas with sparse energy replenishment infrastructures and customer points far from a depot, these capacity limitations play a decisive role [11]. The smaller the capacity, the higher the probability of charging resource contention among vehicles, as illustrated in Figure 1b.
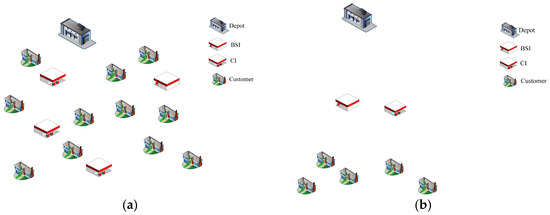
Figure 1.
Impact of CI capacity under different node distributions. (a) CI capacity is not a bottleneck factor, (b) CI capacity is a bottleneck factor.
In addition to insufficient consideration of CI capacity constraints, most existing EVRP studies assume charging as the sole energy replenishment method, with limited exploration of heterogeneous energy replenishment infrastructures (HERIs), which integrate both CIs and battery swapping infrastructures (BSIs) [12]. BSI offers battery-swapping as an energy replenishment option for EVs, which can be completed within 3–10 min using specialized equipment or by trained technicians, significantly reducing energy replenishment times compared to charging. A schematic of this technology is shown in Figure 2. Tesla attempted to deploy battery swapping infrastructures (BSIs) in 2013. However, the project ultimately failed due to financial constraints [13]. In fact, battery swapping solutions for EVs are now predominantly implemented in China. The Chinese EV manufacturer NIO has deployed over 3000 BSIs nationwide since 2018. Therefore, the collaborative use of CIs and BSIs represents an energy replenishment model with both technical feasibility and broad application prospects.
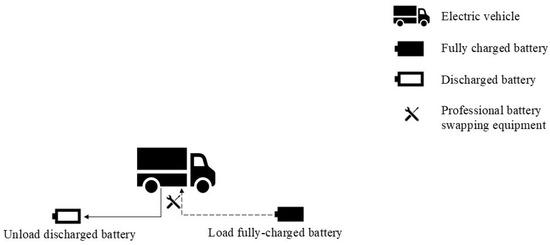
Figure 2.
Schematic diagram of battery swapping technology.
Due to the NP-hard nature of EVRP and the complexity introduced by integrating HERI, vehicle energy replenishment decisions become highly intricate and challenging. Further incorporating the capacity constraints of CI amplifies the heterogeneity among energy replenishment infrastructures, significantly complicating the solution process. In light of the aforementioned challenges, this study introduces a novel variant of EVRP with heterogeneous energy replenishment infrastructures under capacity constraints (EVRP-HERI-CCs). The objective is to minimize the total delivery cost of the electric logistics vehicle fleet with integrated charging and battery swapping capabilities by leveraging HERI under limited charging resources. Here is a brief summary of this paper’s main contributions:
- Extension of EVRP to EVRP-HERI-CCs: Conventional EVRP studies have generally assumed charging-based energy replenishment, overlooking both HERI networks and CI capacity constraints in their problem formulations. By distinguishing the functional independence of CI and BSI and imposing capacity limitations on CI, we extend the classical EVRP into EVRP-HERI-CCs, highlighting the unique characteristics and advantages of heterogeneous energy replenishment networks.
- MIP model and heuristic algorithm: We formulate the MIP model tailored to the problem and design a HACO algorithm integrated with a VNS mechanism. The algorithm incorporates a dynamic rescheduling mechanism that proactively resolves charging conflicts through global optimization during its two-phase solution construction process, thereby maximizing the utilization of available charging resources. Furthermore, it employs an energy management strategy to transition from full charging to partial charging, reducing energy replenishment costs. Extensive numerical experiments validate the algorithm’s effectiveness.
- In-depth analysis of capacity constraints of CI: Computational experiments confirm that the proposed algorithm adaptively optimizes routing plans under CI capacity constraints by leveraging HERI synergies, with comparative cost analyses and large-scale sensitivity studies providing actionable insights for CI capacity deployment.
The remainder of this paper is structured as follows: Section 2 provides a comprehensive review of the relevant literature. Section 3 formulates the problem and develops the mathematical models. The proposed solution methodology is detailed in Section 4. Section 5 discusses the computational experiments and analyzes the results. The paper concludes with key findings and implications in Section 6.
2. Literature Review
This section reviews the existing literature from four perspectives: (1) EVRP research without CI capacity constraints, (2) EVRP research with CI capacity constraints, (3) EVRP research incorporating BSI, and (4) EVRP research under HERI. A detailed review is presented as follows.
2.1. EVRP Research Without CI Capacity Constraints
Traditional EVRP research has predominantly focused on single-type energy replenishment infrastructures, particularly CI. Existing studies often assume homogeneity among these energy replenishment infrastructures, implying uniform attributes such as charging power and service time. For example, Conrad and Figliozzi [14] pioneered the EVRP framework, allowing vehicles to recharge at specific customer nodes with fixed durations. Schneider et al. [15] further integrated standalone CI into EVRPTW, solving it via a hybrid variable neighborhood search-tabu search algorithm. Montoya et al. [16] extended EVRP by incorporating nonlinear charging functions, aiming to minimize total travel and charging time. They proposed a hybrid metaheuristic to solve this problem and introduced new benchmark instances. Froger et al. [17] refined the problem formulation and developed an exact labeling and heuristic algorithm to tackle it. Recently, Bruglieri et al. [18] considered several realistic factors in the energy consumption model, such as payload and vehicle speed. They designed a random kernel search algorithm based on a non-clone MIP formulation to manage EVRPTW. It is evident that CI-based EVRP research initially started with simple assumptions and progressively incorporated additional constraints to reflect real-world complexities.
2.2. EVRP Research with CI Capacity Constraints
In traditional EVRP studies, CI capacity constraints were historically treated as secondary considerations, with early research often assuming infinite capacity to prioritize route optimization and vehicle scheduling. However, growing urban logistics demands and charging needs have highlighted the critical role of capacity constraints on operational efficiency, giving rise to two key research paradigms. The first focuses on capacity constraint modeling and operation research optimization, employing mixed-integer programming and approximate methods. For instance, McCabe and Ban [19] proposed an MIP model for optimizing electric bus CI economics, which are solved via a heuristic algorithm. Froger et al. [20] combined iterative local search and branch-and-cut algorithms to solve EVRP with nonlinear charging and capacity constraints, updating 80 benchmark instances. Lam et al. [21] used a branch-and-price algorithm to solve 34% of 100-customer instances under charger availability and nonlinear charging constraints, while Bruglieri et al. [11] addressed capacity constraints through a charging pump reservation mechanism, which were solved using the cutting-plane method and GRASP algorithm. The second paradigm adopts stochastic and dynamic approaches, integrating queuing theory and Markov decision processes to address random queuing issues. Karimpour et al. [22] embedded charging station queuing models into multi-graph frameworks, showing that alternative routes mitigate cost increases from extended waits. Keskin et al. [23] applied the M/G/1 queuing model and ALNS algorithm to solve EVRP with limited charging capacity. Dastpak et al. [24] proposed a Markov decision process-based framework by using a binary occupancy indicator (OI) to reduce charging wait times by 23.7–95.4% and the total travel time by 1.4–18.5%.
2.3. EVRP Research Incorporating BSI
With the maturation of the battery swapping technology system, concepts related to BSI have gradually permeated research on electric vehicles. Initial investigations primarily focused on battery management strategies and battery swapping pricing. Deng et al. [25] integrated battery degradation into BSI configurations and proposed a charging management strategy that significantly reduced degradation costs. Hu et al. [26] developed a game theory model for the EV battery replenishment market, focusing on optimal pricing for battery swapping. A representative study combining BSI and EVRP is that of Jie et al. [27], who employed a hybrid algorithm of column generation and ALNS to solve a two-stage EVRP based on BSI, exploring the interaction between battery range and vehicle emission reductions. Building on EVRP-BSI, some studies have further expanded the problem to the electric vehicle location routing problem with BSI (ELRP-BSI) by incorporating infrastructure location considerations. The first systematic definition of ELRP-BSI was provided by Yang and Sun [28], who also proposed a multi-phase hybrid heuristic algorithm to solve the problem, simultaneously addressing BSI location strategies and EV fleet routing under a limited range. Hof et al. [29] and Souza et al. [30] applied adaptive variable neighborhood search and variable neighborhood search, respectively, to solve ELRP-BSI.
2.4. EVRP Research Under HERI
Despite the increasing feasibility of deploying combined charging and battery-swapping infrastructures in real-world settings, research on EVRP under this assumption remains significantly less explored compared to studies focusing solely on CI. Existing research often emphasizes energy replenishment heterogeneity by introducing multiple charging technologies to CI, where high-power, high-cost “super-fast charging” is abstracted as analogous to battery swapping due to their similarities in energy replenishment speed and expenses. Felipe et al. [31] and Keskin et al. [32] demonstrated the advantages of fast charging in reducing fleet size and energy costs by incorporating multiple charging technologies into EVRP. Mao et al. [33] independently examined the characteristics of charging and battery-swapping infrastructures, which permitted partial charging at CI and battery swapping at BSI. However, the study separated the usage scenarios of these heterogeneous infrastructures by analyzing route costs under partial charging and battery swapping modes in isolation. Lai and Li [34] proposed an optimization model for ride-hailing services, integrating multi-mode charging and battery swapping networks to enhance fleet utilization and reduce costs. Their non-convex programming and Manhattan case study demonstrated that joint planning increased profits by 11.7% and 17.5% compared to battery swapping-only and charging-only, respectively. However, their work focused on theoretical modeling, which lacked the integration of HERI with EVRP.
In summary, existing research primarily treats charging and battery swapping as separate energy replenishment methods, overlooking the synergistic potential of integrating HERI. The complementary benefits of such integration remain underexplored, and the common assumption of unlimited CI capacity leads to suboptimal conflict resolution strategies, such as the first-in-first-out static scheduling framework, which fails to proactively optimize the utilization of finite charging resources from a global perspective. To overcome these limitations, we propose an EVRP methodology that incorporates the complex characteristics of HERI through an MIP model combined with a heuristic algorithm featuring dynamic rescheduling for charging conflicts. This approach enhances operational efficiency and decision-making in transportation and logistics.
3. Problem Description and Mathematical Modeling
3.1. Problem Description
The problem in our study based on graph theory is described as follows. In the directed graph , is the vertex set containing all customer nodes, HERI with their copies, and the departure and arrival ends of depot with their copies. is the set of arcs, with . Each arc corresponds to a traveling distance of and a travel time of . As the vehicle passes through the arc , the on-board battery discharges at the rate of , with power consumption equal to . Each customer is associated with cargo demand and service time , and the delivery route must cover all customers. The fleet is equipped with homogeneous electric logistics vehicles integrated with both charging and battery swapping capabilities, which have the same maximum load of , and all vehicles start with fully charged batteries from the depot. For all , continuous decision variables , , and represent, respectively, the time the vehicle arrives, the remaining cargo volume, and the state of charge (SOC) of the vehicle at node , while represents the SOC of the vehicle when leaving node . The binary decision variable is if the arc is accessed; otherwise, it is . A set of vertices is determined to minimize the total fleet distribution cost without exceeding the vehicle load , the CI capacity , and the driver shift time .
3.2. Mathematical Formulation
The MIP model based on node clones is described as follows:
Objective Function (1) minimizes the total distribution cost, including vehicle utilization, energy replenishment, and traveling distance expenses. Constraint (2) ensures each customer node is visited exactly once, while Constraint (3) restrict each cloned charging pump and BSI to at most one visit. Constraints (4) and (5) specify that vehicles depart from the depot to a single destination and return from a unique node, respectively. Constraint (6) balances the number of vehicles departing and returning to the depot. Constraint (7) enforces flow conservation to maintain route continuity. Constraints (8) and (9) manage vehicle load capacity, ensuring that loads at subsequent customer points do not exceed previous ones and that total loads do not surpass vehicle capacity. Constraint (10) ensures vehicles return within the driver’s shift time. Constraints (10)–(13) track service durations at customer points, charging pumps, and BSI, respectively. Constraints (14)–(16) define the remaining battery level upon arrival at the next location after departing from customer points, charging pumps, and BSI, respectively. Constraints (17) and (18) specify the remaining battery level when vehicles arrive at and depart from charging pumps and BSI. Constraint (19) ensures vehicles depart the depot with fully charged batteries. Constraint (20) regulates energy replenishment at cloned charge pumps. Constraints (21)–(23) impose capacity limitations on CI. Constraint (21) ensures that the arrival time at a subsequent clone of the same charging pump is at least after the charging duration of the previous clone at the previous arrival time. Constraint (22) enforces the use of cloned charging pumps in ascending numerical order to avoid equivalent solutions. Constraint (23) prioritizes the use of charging pumps with smaller serial numbers within the same CI. Finally, Constraints (24)–(26) define the nature of the decision variables.
4. Algorithm Design
Building upon practical considerations, our research emphasizes capacity-constrained CI operations as a core assumption while addressing CI-BSI coexistence. Given higher per-swap costs reducing BSI utilization frequency and negligible queuing due to rapid battery swapping, we exclude BSI capacity constraints from our analysis. Since the unit charging cost is significantly lower than the unit battery swapping cost, the focus and challenge of algorithm design under the premise of limited capacity of CI is to avoid potential conflicts in charging tasks and maximize the use of existing charging resources to reduce vehicle energy replenishment costs. To this end, we first propose a charging sequence feasibility theorem to determine whether there is a conflict between two charging tasks. Then, based on this, a dynamic rescheduling mechanism is proposed to eliminate conflicts and ensure the global feasibility of charging schedules. Finally, these ideas are incorporated into the initial solution construction phase of the HACO algorithm. After two-phase construction, this approach generates high-quality feasible solutions that comply with the capacity constraints of CI. Additionally, local search operators designed based on the problem characteristics are used to further optimize and improve the quality of the solutions.
4.1. Conflict Resolution Mechanisms for Limited Charging Resources
Existing studies on conflict resolution for charging tasks predominantly adopt the first-in-first-out (FIFO) principle, postponing subsequent energy replenishment tasks based on real-time conditions [11,23,35]. However, this mechanism exhibits a degree of myopia, failing to globally optimize the utilization of limited charging resources to serve the maximum number of vehicles. In this study, we abstract the vehicle charging process as a resource-constrained activity and leverage the critical path method (CPM) from project scheduling. By incorporating path constraints, we propose a charging sequence feasibility theorem and a dynamic rescheduling strategy to eliminate conflicts, thereby enhancing the operation efficiency of capacity-limited CI.
4.1.1. Charging Sequence Feasibility Theorem
This section proposes the charging sequence feasibility theorem by analyzing the time constraints of replenishment for different paths at CI. The theorem establishes the necessary conditions for conflict elimination through charging sequence adjustments between two vehicle paths sharing the same CI, providing a theoretical foundation for the conflict resolution mechanism at energy replenishment.
Assuming that the available internal capacity of the CI is 1, which means only one vehicle is allowed to charge during a specific period. Let denote the earliest start time of charging for vehicle represent the required charging duration, and be the earliest finish time, where . In an ideal scenario without capacity constraints, all vehicles can start charging immediately upon arrival, where and become deterministic values solely dependent on the current route’s structure. represents the longest path duration among all routes, analogous to the total project completion time. represents the time at which vehicle returns to the depot under the current routing plan, allowing for a charging shift time of . Consequently, the latest start time for charging is , and the latest finish time is . Let and denote the actual start and finish times of charging for vehicle , respectively, with . The definitions of the aforementioned time parameters are illustrated in Figure 3.
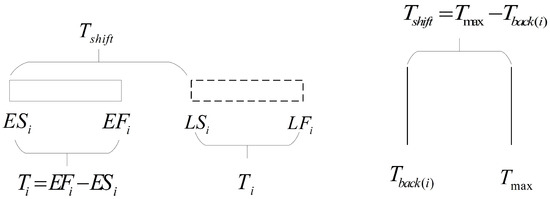
Figure 3.
Schematic diagram of time parameters under CPM.
If vehicles and arrive at the CI sequentially and satisfy , the FIFO principle prioritizes vehicle , requiring vehicle to start charging only after completes its task. This results in a charging delay of . Notably, such a delay occurs if and only if . The mechanism of charging delay for vehicle is shown in Figure 4.
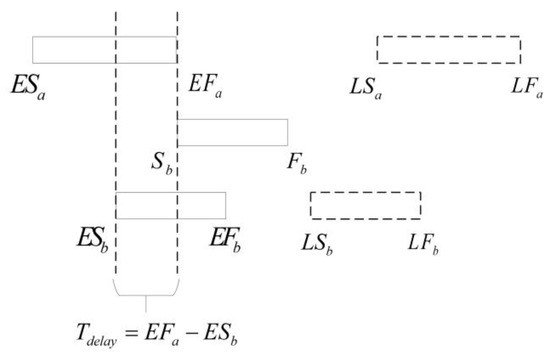
Figure 4.
Deferrable initiation of charging task after the completion of task .
However, if is too small, indicating a narrow charging shift time window for vehicle , there is a probability that . In such cases, adhering to the FIFO principle for vehicle may prevent vehicle from being charged. By reversing the charging order of and , it becomes possible to satisfy both charging demands simultaneously through deferred charging, thereby improving the utilization of capacity-limited CI. Figure 5 depicts charging conflict resolution via this scheduling strategy.
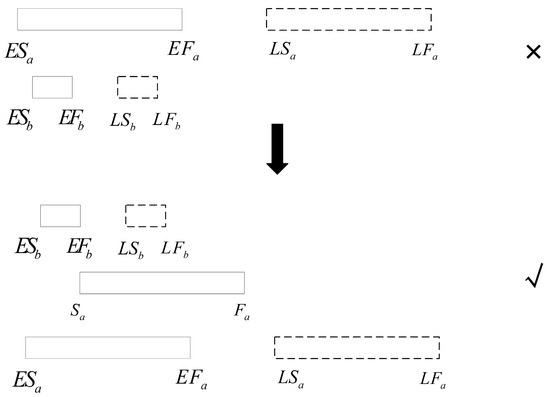
Figure 5.
Charging conflict resolution via task rescheduling at CI.
Based on this insight, the following theorem is proposed.
Theorem 1.
If the internal capacity of the CI is 1 at a given time, and electric logistics vehicle arrives at the CI before vehicle (i.e., ), the following condition on their charging time parameters must be satisfied:
Then, the following is true:
- If the charging task of is an immediate predecessor, the charging demand of cannot be met.
- If the charging task of vehicle is an immediate predecessor, a feasible deferred charging schedule exists to simultaneously satisfy the charging demands of both and .
Proof of Theorem 1.
The charging service interval of vehicle is defined as the closed interval , where .
- (1)
- Scenario 1. Charging task is the immediate predecessor.
Assume that a feasible schedule exists, where the charging interval for vehicle is , thus satisfying
Vehicle starts charging only after the completion of vehicle ’s charging task, implying . Its charging interval must satisfy
From theorem condition , combined with Equation (29) and , we derive the following:
Thus far, , which contradicts in Equation (30). Therefore, no feasible charging scheduling scheme exists.
- (2)
- Scenario 2. Charging task is the immediate predecessor.
By advancing charging task , its charging interval satisfies Equations (30) and (31). Vehicle starts charging after completes its task, implying . Its charging interval must satisfy Equations (28) and (29).
From Equation (28), . To ensure feasibility, we verify the existence of such that
From Equations (30) and (31), , while . Given , it follows that . Thus, , leading to
By theorem condition , the interval is non-empty. Since , the interval is also non-empty. Therefore, a feasible solution exists. In summary, a feasible deferred charging schedule exists to simultaneously satisfy the charging demands of and if and only if the charging task of is the immediate predecessor. This completes the proof of Theorem 1. □
Corollary 1.
At a given time, the internal capacity of the CI is 1. For any two electric logistics vehicles and , if and the following conditions hold:
then the charging order of is feasible. Otherwise, an unresolvable charging conflict arises. The proof follows the same logic as Theorem 1 and is omitted here.
4.1.2. Dynamic Rescheduling Conflict Mitigation
Based on Theorem 1, we conduct conflict detection on path charging tasks accessing the same CI, identifying potential conflicts due to capacity constraints. Through recursive rescheduling, the charging task order is dynamically adjusted to ensure a globally feasible and conflict-free charging sequence.
Assume that the current available capacity of the CI is 1. Define the set of electric logistics vehicles , sorted by their initial arrival times at CI (i.e., ). The charging sequence stores all feasible charging tasks in the actual charging order. represents the set of vehicles charged after in . A conflict pair indicates a charging conflict between and , as defined in Theorem 1. The conflict resolution strategy moves the charging task of ahead of . The dynamic rescheduling mechanism follows the rules below.
Step 1. Initialization. Initialize the scheduling sequence . Then, subsequently add vehicle charging tasks from to .
Step 2. Step-by-step insertion and recalculation. For the current vehicle , detect whether it conflicts with all vehicles in based on Theorem 1. If a conflict exists, insert before the first conflicting vehicle , denoted as . If no conflict exists, append to the end of according to the FIFO principle. After adjusting the task order, dynamically recalculate the actual start time and finish time for in as the following formulas:
Here, represents the immediate predecessor of in the charging schedule, which may result from conflict resolution () or the originally conflict-free .
Step 3. Conflict resolution. If any vehicle satisfies , remove from and recursively regenerate the schedule for the remaining vehicles.
Step 4. Termination condition. The dynamic rescheduling mechanism terminates when all charging tasks are processed and no conflicts remain in .
4.2. Hybrid Ant Colony Optimization Algorithm
The ant colony optimization algorithm has been widely demonstrated as effective for solving VRP and EVRP [36,37,38]. Its core idea simulates the foraging behavior of ants, reinforcing high-quality paths through pheromone evaporation and updates to iteratively converge toward the optimal solution.
In this study, considering the capacity constraints of CI, as well as constraints such as battery level limits, vehicle capacity, and maximum route duration, we design a feasible node access strategy under heterogeneous energy replenishment modes and incorporate problem-specific heuristic information. Furthermore, by integrating the conflict resolution mechanism for energy replenishment resources proposed in Section 3.1, we develop the HACO algorithm for the EVRP-HERI-CC.
Bruglieri et al. [39] employed a biased and randomized greedy randomized adaptive search procedure (BR-GRASP) algorithm with a penalty function to solve the GVRP with private capacity-constrained AFSs, achieving solutions comparable to exact algorithms on benchmark instances and demonstrating higher efficiency on large-scale instances. In the IEEE CEC-12 2020 competition on the electric vehicle routing problem (the CEC-12 competition on the electric vehicle routing problem (https://mavrovouniotis.github.io/EVRPcompetition2020/ (accessed on 2 March 2025)), simulated annealing (SA) and genetic algorithms (GAs) were the winning algorithms [40], highlighting their effectiveness in addressing the EVRP. We also observed that the adaptive gaining–sharing knowledge (AGSK)-based algorithm was a winning method in the IEEE CEC 2020 competition [41], while its canonical form, GSK, has demonstrated strong performance in high-dimensional continuous optimization problems [42]. Although both GA and GSK belong to swarm intelligence algorithms, the latter distinguishes itself by employing a knowledge management strategy that enhances exploration in the junior phase and exploitation in the senior phase. Inspired by this mechanism, we propose integrating GSK principles into GA’s mutation phase to further validate its efficacy. Specifically, we adapt the core GSK formulation to determine the number of individuals in each GA generation that should apply the junior mutation operator (significant path perturbation) versus the senior mutation operator (slight path perturbation). This allocation is governed by Equation (37), where represents the population size, indicates the current generation number, corresponds to the maximum allowed generations, and denotes the knowledge rate.
Based on the above analysis, this study adopts the BR-GRASP, SA, GA, and GA-GSK algorithms as baseline algorithms to solve the same problem and compares their results with those obtained using HACO.
4.2.1. Algorithmic Framework
The overall HACO algorithmic framework is depicted in Figure 6, with the key steps outlined as follows:
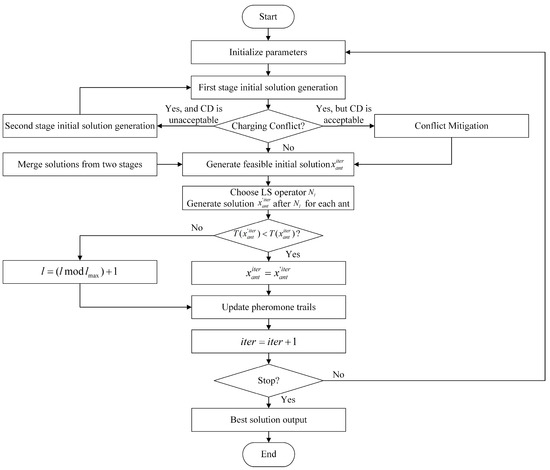
Figure 6.
Flowchart of the HACO algorithm.
Step 1. Initialize the parameters of HACO, including the maximum iteration count , objective value , ant set , neighborhood counter , initial iteration , and the set of unserved customers .
Step 2. Each ant constructs a solution in two stages. The first stage resolves charging conflicts using the dynamic rescheduling mechanism, while paths unable to defer charging proceed to the second stage for supplementary construction, yielding a feasible initial solution ) that adheres to the capacity constraints of CI.
Step 3. Optimize the solution constructed by the ants using the -th local search operator, obtaining .
Step 4. If , update , keep the neighborhood counter unchanged, and proceed to Step 5. Otherwise, update and directly proceed to Step 5.
Step 5. Update the pheromone using the global pheromone update strategy of the ant-cycle model.
Step 6. Check if the termination condition is met. If satisfied, output the optimal solution and terminate. Otherwise, increment iter by 1 and return to Step 2.
4.2.2. Solution Construction
- (1)
- Feasible access node set generation
Given the close relationship between electric vehicles and CI, this paper enhances the initial solution construction method of the classical ant colony algorithm for traditional vehicle routing problems. We propose a feasible access node set that adheres to constraints such as battery capacity, vehicle load, and maximum route duration, storing potential target nodes for subsequent access.
For ant , the feasible access node set is denoted as , which dynamically updates based on the current path construction status. In the EVRP-HERI-CC, nodes are categorized into customer points and energy replenishment infrastructures. Thus, multiple transition scenarios arise between different types of nodes and . Additionally, due to constraints such as limited battery capacity, cargo load, and maximum driver shift duration, the generation of must satisfy multiple conditions to ensure route feasibility. To address this, we systematically decompose the target nodes and transition scenarios by designing three node lists to store different categories of accessible nodes. The complete is then obtained through a concatenation approach.
Define and to represent unserved customer points and the depot, respectively. Let be the last node in the currently constructed partial route , where ,, and represent the remaining battery level upon departure from , the total demand satisfied upon arrival at , and the arrival time at , respectively. The node inserted after may be either a customer point or a CI/BSI . The vehicle may return to the depot from or , provided that all feasibility constraints are satisfied during subsequent route construction. We formally define the node lists as , , and , which collectively constitute the feasible access node set .
We take as an example to explain the meanings of its internal sub-node lists. A vehicle travels from the last point of the current route to an unserved customer point, which is stored in . The distinction lies in the following: for , the vehicle can return directly to the depot after servicing the customer point, whereas for and , the vehicle can proceed to a CI or a BSI, respectively, for energy replenishment before returning to the depot. Similar logic applies to and . The constraints to be satisfied under different conditions are shown in Equations (38)–(40).
Taking the concatenation of the above three sets, we obtain the following:
- (2)
- Heuristic information and state transition probability
When solving the EVRP using the HACO algorithm, the state transition probability represents the probability that ant moves from node to node at time . This probability guides the ant to select the next node from until no unserved customer points remain in . It is calculated as follows:
Here, represents the heuristic information. In TSP and traditional VRP, is typically defined as the reciprocal of the distance, i.e., , reflecting the desirability of transitioning from node to node . denotes the pheromone concentration on the path between nodes and at time . The parameter is the pheromone importance factor, where a higher value emphasizes the role of pheromone concentration in node selection. Similarly, is the heuristic information importance factor, where a higher value prioritizes heuristic information in decision-making.
In real-world distribution scenarios, the remaining battery level of an electric logistics vehicle significantly influences subsequent route planning. A higher remaining battery level increases the likelihood of serving customer points, while a lower level raises the probability of visiting nearby energy replenishment infrastructures. To address this, we redefine the heuristic information based on problem-specific characteristics and update the state transition probability formula accordingly.
By introducing a power threshold of to characterize the critical battery level and to represent the current remaining power, the vehicle can prioritize customer points or energy replenishment infrastructures based on its power status. The updated heuristic information is calculated as follows.
In the above equation, and are heuristic information regulation factors, adjusting the heuristic value when the next node is a customer or an energy replenishment infrastructure, respectively. When , a higher battery level increases the heuristic value for customer points, making the vehicle more likely to select customers. Conversely, when , a lower battery level increases the heuristic value for CI and BSI, prioritizing energy replenishment infrastructures.
- (3)
- Two-stage construction of feasible initial solutions
Due to the limited capacity of CI, a two-stage construction method is adopted to ensure the feasibility of the initial solution (i.e., not exceeding the limited capacity of CI). In the first stage, the HACO algorithm calculates the state transition probability from the current node to the next node using the updated formula, where . However, this approach does not account for the capacity constraints of CI, potentially leading to resource conflicts where multiple electric logistics vehicles compete for the same CI simultaneously, resulting in infeasible solutions.
Therefore, the dynamic rescheduling mechanism is applied to the initial solution obtained in the first stage to resolve conflicting charging tasks, defined as a charging delay (CD). Vehicle routes satisfying the CD condition are retained, while those that cannot are removed, with all associated customer points reclassified as unserved and transferred to the second stage of construction. Assume that the first-stage initial solution involves a single CI, with vehicles requiring charging listed in arrival order as , the set of vehicle routes as , and the set of routes unable to defer charging as . The specific steps are as follows:
Step 1. Charging postponement. Based on the dynamic rescheduling mechanism, the charging scheduling sequence is constructed step by step from , with the aim of maximizing the elimination of charging conflicts. This step may generate vehicle , whose charging task cannot be postponed, and its vehicle path is . Let , , and .
Step 2. Customer degradation. Identify all customer points included in the vehicle paths within , degrade them all to unserved customer points, and then store them in set .
Step 3. Secondary construction. The second stage employs the same initial solution construction approach as the first stage, with the difference that only proper delivery vehicles are arranged for all customer points in obtained from Step 2. Moreover, the node lists are reduced, and , , and related to CI are no longer part of so as to avoid charging conflicts with the feasible solutions after charging postponement. When , the secondary construction is completed, and the new path constructed using the supplemental construction is denoted as .
Step 4. Path merging. Merge the remaining feasible paths in the initial solution of the first stage with the complementary paths generated in the second stage, i.e., .
The proposed two-stage construction method optimizes the utilization of limited charging resources. By incorporating BSI, it enhances energy replenishment efficiency, alleviates capacity pressure on CI, and ensures the feasibility of the initial solution.
4.2.3. Local Search
In this study, the initial solution generated by the HACO algorithm undergoes local search to further optimize the solution. Five local search operators are designed based on the problem and solution characteristics, and the VNS mechanism is employed for operator selection. The process begins by initializing the neighborhood counter to . If a local search with the specific operator improves the current solution, remains unchanged, and the search continues within the same neighborhood. Otherwise, is updated to , and the search transitions to the next neighborhood. This iterative process continues until the termination criterion is satisfied. Each operator is subsequently introduced in the order of their application within the VNS framework.
- (1)
- Destroy Route: Distribution tasks should be accomplished by as few vehicles as possible. Inspired by the destruction and repair operator of the ALNS algorithm [43], this paper introduces a Destroy Route operator. This operator aims to remove one of the shortest routes from the multi-route solution and attempts to reinsert the customer nodes from that route into other routes based on the best improvement rule to minimize the number of vehicles required for the distribution tasks. Following the approach of Vidal et al. [44], we set a granularity threshold to restrict the search to nearby vertices, preventing wasted computation from a full route traversal without finding a feasible insertion point. The schematic diagram of Destroy Route operator is presented in Figure 7.
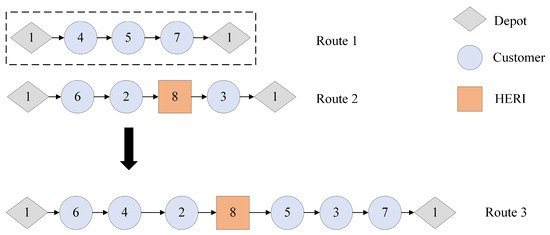 Figure 7. The Destroy Route operator.
Figure 7. The Destroy Route operator. - (2)
- 2P-Swap: The Swap operator has been proven effective in handling EVRP [8], yet existing studies primarily rely on single-phase implementations. To address the unique challenges of this study, where swapping deployed energy replenishment infrastructures with external nodes may cause route infeasibility due to energy constraints, we propose a two-phase Swap operator (2P-Swap). The first phase exchanges customer nodes between routes to generate feasible solutions under load constraints, while the second phase swaps customer nodes and energy replenishment infrastructures within the same route, enhancing exploration while ensuring compliance with energy and time constraints. This approach balances solution quality and feasibility. The schematic diagram of 2P-Swap operator is presented in Figure 8.
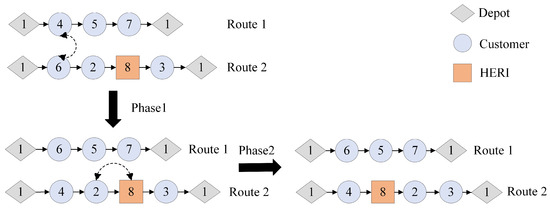 Figure 8. The 2P-Swap operator.
Figure 8. The 2P-Swap operator. - (3)
- 2-opt: Felipe et al. [31] split a complete vehicle route into several segments by setting cut nodes at CI and then perform the best-improvement 2-opt operation on each segment to eliminate intersections. The 2-opt operator used in this study also aims for the best improvement but has a broader scope. It can be applied between any two nodes in a route that meet the criteria for the application of the operator, with the nodes being either customers or energy replenishment infrastructures. The schematic diagram of 2-opt operator is presented in Figure 9.
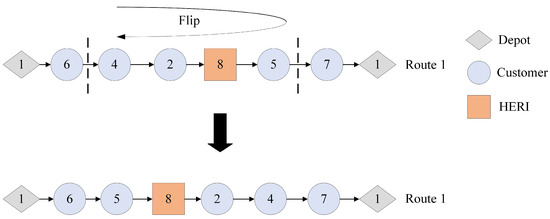 Figure 9. The 2-opt operator.
Figure 9. The 2-opt operator. - (4)
- Remove Infrastructure: The initial solutions generated by the HACO algorithm, driven by pheromone updates and evaporation, exhibit inherent greediness and randomness, potentially leading to redundant energy replenishment infrastructures in the routes. Specifically, if a vehicle’s remaining energy upon arriving at an infrastructure is sufficient for successive infrastructure or to return to the depot, the visit becomes unnecessary, indicating redundancy. Eliminating such infrastructures reduces intermediate energy replenishment costs and prevents unnecessary detours. The schematic diagram of Remove Infrastructure operator is presented in Figure 10.
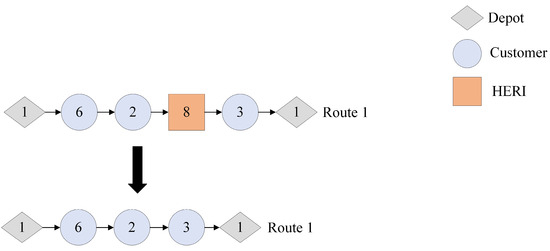 Figure 10. The Remove Infrastructure operator.
Figure 10. The Remove Infrastructure operator. - (5)
- Change Infrastructure: To further leverage the cost advantages of CI, the algorithm first identifies all BSIs along the current route. It then evaluates the feasibility of replacing each BSI with a CI, considering capacity constraints and maximum route duration. If feasible, the replacement is made, and the total route cost is recalculated. The schematic diagram of Change Infrastructure operator is presented in Figure 11.
 Figure 11. The Change Infrastructure operator.
Figure 11. The Change Infrastructure operator.
4.2.4. Pheromone Update
Pheromone update involves both accumulation and evaporation. During their traversal, ants deposit pheromones on paths, while the pheromone concentration gradually evaporates over time. This evaporation mechanism introduces a forgetting effect, preventing the algorithm from prematurely converging to a local optimum and enhancing its exploration capability. Let denote the evaporation factor, representing the rate of pheromone decay. After each iteration, the pheromone concentration on each path is updated, and the concentration at time is given by
In the above equation, represents the pheromone deposited by ant on the path between nodes and . Summing the pheromone contributions from all ants , the total pheromone increment on the path is calculated as . The calculation of is as follows:
This study employs the ant-cycle model, where pheromone updates occur only after ant completes a full route. This approach enhances exploration and prevents premature convergence to local optima by avoiding excessive pheromone accumulation. In the equation above, is a constant, and represents the total cost of the route constructed by the -th ant.
5. Computational Experiments
In this section, extensive numerical experiments were conducted to evaluate the algorithm’s performance. The experiments were performed on a desktop computer equipped with a 4-core Intel Xeon Gold 5218 2.3 GHz processor and 31 GB RAM, with the heuristic algorithm implemented in MATLAB R2019a. To comprehensively evaluate the computational efficiency and practical viability of the proposed HACO algorithm, we designed a series of systematic experiments.
Comparative studies with exact and heuristic approaches validate EVRP-HERI-CC’s NP-hard property while highlighting HACO’s exceptional solution quality through problem-specific adaptations. Capacity-dependent analyses reveal HACO’s robust HERI integration advantages over baseline algorithms, quantifying the substantial impact of CI capacity constraints on algorithmic performance. Furthermore, partial charging strategies significantly reduce operational costs, and sensitivity analyses on large-scale instances provide practical guidelines for optimal CI capacity allocation and route planning optimization.
5.1. Problem Instances
This study adapts the dataset proposed by Bruglieri et al. [39], which includes instances with 15, 25, 50, and 100 customer points, denoted as C15, C25, C50, and C100, respectively. The original dataset assumes a single type of energy replenishment infrastructure, termed an alternative fuel station (AFS), with a constant refueling duration. To emphasize heterogeneity between energy replenishment infrastructures, we modify the instances by introducing CI at the original AFS locations, allowing vehicles to partially charge on demand. Additionally, BSIs are randomly generated within a radius of 2 units around the CI, ensuring proximity between them. Thus, if a vehicle’s current battery level supports visiting one type of infrastructure, it can typically access the other as well. This infrastructure layout enhances the potential for BSI to alleviate the capacity pressure on CI. The instances in this study satisfy the following characteristics:
- The depot is located away from customer points and energy replenishment infrastructures.
- Energy replenishment infrastructures are centrally located among customer points, with a limited capacity of CI.
- A maximum duration limit is imposed on single-vehicle routes, prohibiting service beyond this limit.
Under these conditions, vehicles departing from the depot often require mid-route energy replenishment for distant customer deliveries, typically restricted to a single replenishment due to route duration constraints.
The capacity of CI varies across instances based on their scales. Following Bruglieri et al.’s settings [39], the capacities of CI for C15, C25, C50, and C100 are set to 1, 2, 3, and 8, respectively. Other key parameters are detailed in Table 1.

Table 1.
Parameterization settings for the instances.
5.2. Algorithm Parameter Settings
In the HACO algorithm, several parameters significantly influence search performance and convergence quality. Due to the introduction of the pseudo-random proportional rule and , the most impactful parameters are , , and . Therefore, this study determines the optimal values for these parameters through preliminary experiments. Other parameters, such as the number of ants (ant = 20), maximum iterations (300 or 100, depending on the scales of instances), power threshold , and heuristic information regulation factors ( and ) are set as fixed values.
Following the parameter tuning method described by Miao et al. [45], the experimental ranges for the parameters are set as , , and . Default values are assigned as ,, and . For each experiment on C100, only one parameter is varied while keeping others at their default values. Each parameter combination is tested ten times, and the average results are compared. The cost optimal values in Table 2 have been highlighted in bold.

Table 2.
Experimental results for the HACO algorithm’s parameters.
As shown in Table 2, the HACO algorithm performs best when , , and . These values are adopted for subsequent comparative experiments.
5.3. Experimental Experiments and Comparative Analysis
To evaluate the effectiveness of the HACO algorithm, we compare it with the Gurobi solver, BR-GRASP, SA, GA, and GA-GSK. The experiments are organized into three parts: The first part examines HACO’s solution accuracy and computational efficiency against Gurobi. The second part demonstrates HACO’s ability to generate higher-quality solutions than other baseline algorithms under scenarios with unlimited CI capacity. The third part extends the evaluation to limited CI capacity conditions, where HACO, enhanced by a dynamic rescheduling mechanism for conflict resolution, exhibits superior robustness and adaptability compared to BR-GRASP, SA, GA, and GA-GSK.
For smaller instances (C15 and C25), the HACO algorithm terminates after 300 iterations or 30 consecutive iterations without improvements. For larger-scale instances (C50 and C100), it terminates after 100 iterations or 10 consecutive iterations without improvements. To simplify the presentation, the following terms will be abbreviated in subsequent figures, tables, and texts: number of vehicles (#Veh), times of battery swapping (#BS), charging cost (CC), total cost (TC), and running time (t).
5.3.1. Comparison with the Gurobi Solver on Small-Scale Instances
Based on node replication theory, the mathematical model exhibits an exponential increase in computational complexity with problem size when solved using Gurobi under a one-hour time constraint. To ensure fair heuristic performance evaluations with limited resources, we compare HACO and Gurobi on the small-scale instance set C15 under both unlimited and limited capacities of CI. The capacity constraints in HACO are programmatically adjustable, while in Gurobi, they are tightened or relaxed according to Equations (21)–(23). Table 3 and Table 4 present the performance comparison, with bolded values highlighting the superior results in each case.

Table 3.
Comparison of results obtained with Gurobi under unlimited capacity of CI.

Table 4.
Comparison of results obtained with Gurobi under limited capacity of CI.
- (1)
- The HACO algorithm outperforms Gurobi in 6/10 and 9/10 instances under unlimited and limited capacities of CI, respectively, with solution quality improvements of 3.12% and 4.05%, demonstrating strong optimization capabilities.
- (2)
- Gurobi reaches its time limit on all small-scale instances, failing to obtain optimal solutions within 1 h. In contrast, HACO achieves solutions comparable to or better than Gurobi within 60 s, showing significant computational efficiency.
- (3)
- The HACO algorithm effectively leverages the synergistic advantages of HERI by guiding vehicles to utilize both CI and BSI, achieving overall cost optimization. This is evident in instances C15_2, C15_3, and C15_4, where HACO employs battery swapping, unlike Gurobi, yet achieves lower total costs.
By comparing with the results from Gurobi, the reliability of the HACO algorithm in terms of solution quality and computational efficiency is validated, which can be in part attributed to its problem-specific design. Furthermore, we observe that Gurobi reaches its time limit even when solving only 15 customer node instances, suggesting that the EVRP-HERI-CC is highly complex and may not be effectively solved solely by using exact methods. Given that HACO has been shown to outperform Gurobi in small-scale instances, Section 5.3.2 and Section 5.3.3 further employ the HACO, BR-GRASP, and SA algorithms to solve instances of varying scales, aiming to comparatively analyze the performance of HACO against the other two heuristic methods in solving the EVRP-HERI-CC.
5.3.2. Heuristic Optimization Under Unlimited Capacity of CI
This section eliminates capacity constraints in CI, assuming that both CI and BSI possess infinite service capacity. Table 5 presents the comparative results of four instance types solved using the HACO, BR-GRASP, SA, GA, and GA-GSK algorithms, with optimal solutions emphasized in bold.

Table 5.
Comparison of results obtained with BR-GRASP and SA under unlimited capacity of CI.
Based on the experimental results, we summarize the following conclusions:
- (1)
- The HACO algorithm demonstrates superior performance in solving the EVRP with unlimited capacity of CI, achieving optimal solutions in 35 out of 40 instances and delivering the lowest cost values across all C15 instances. The SA algorithm consistently yields sub-optimal solutions, showing enhanced competitiveness with increasing problem scale and outperforming HACO in five medium-to-large instances. Conversely, the GA algorithm exhibits the least favorable performance.
- (2)
- The BR-GRASP algorithm reveals inherent limitations in its greedy and short-sighted approach. In smaller-scale C15 and C25 instances, it predominantly selects CIs due to their lower energy replenishment costs, neglecting BSI. However, the prolonged duration of CI significantly reduces vehicle availability for customer delivery, necessitating additional vehicle deployment and consequently increasing fixed costs. This ultimately results in total costs that may not be superior to scenarios employing both CIs and BSI. This phenomenon substantiates the cost-effectiveness of HERI in electric logistics fleet management.
- (3)
- GA and GA-GSK exhibit the poorest performance among all algorithms. As the problem scale increases, their excessive reliance on BSI leads to significantly higher energy replenishment costs, as well as total costs. These algorithms first construct a giant tour of customer nodes before inserting CI or BSI to meet energy constraints. However, crossover and mutation operations frequently introduce redundant HERI. Unlike HACO’s Remove Infrastructure operator, they lack mechanisms to eliminate over-replenishment. Notably, GA-GSK consistently outperforms GA across all instances by employing GSK’s balanced exploration–exploitation knowledge management strategy during mutation.
- (4)
- In the majority of instances, the proposed algorithm successfully fulfills all customer delivery requirements with the minimal fleet size. HACO’s ability to minimize vehicle deployment demonstrates its effectiveness in leveraging the complementary advantages of HERI, optimally utilizing BSI when appropriate to achieve total cost minimization, even in scenarios with abundant CI.
5.3.3. Heuristic Optimization Under Limited Capacity of CI
This section presents computational results for CI capacity-limited instances solved using the HACO, BR-GRASP, SA, GA and GA-GSK algorithms, with optimal solutions highlighted in bold in Table 6. The comparative analysis confirms HACO’s superior performance and stability while highlighting the impact of CI capacity constraints on the problem and algorithms.

Table 6.
Comparison of results obtained with BR-GRASP and SA under limited capacity of CI.
The experimental results demonstrate that the HACO algorithm consistently achieves the optimal or near-optimal costs across all instances, indicating its superior performance in objective function optimization. Compared to BR-GRASP, GA, and GA-GSK, HACO exhibits a significant advantage, with performance gaps of 0.16–12.36% (GAP7), 0.45–23.31% (GAP9), and 0.14–15.97% (GAP10), confirming its comprehensive outperformance. While HACO maintains lower total costs than SA in 85% of cases, SA occasionally surpasses HACO in specific instances (e.g., C25_1, C50_1, and C100_10), as indicated by negative GAP8 values, though with less overall stability.
Regarding operational efficiency, HACO demonstrates optimal vehicle utilization with the lowest average fleet size and moderate battery swapping frequency, effectively exploiting the collaborative strengths inherent in HERI. BR-GRASP, GA, and GA-GSK show slightly higher vehicle usage than HACO but compensate through the frequent utilization of BSI. SA, while employing the largest fleet size and minimal times of battery swapping, achieves better total costs than BR-GRASP through optimized routing and energy replenishment strategies.
The study demonstrates that HACO’s performance advantage over BR-GRASP grows significantly with the problem scale, with GAP7 increasing from 4–5% to 8–10%. A parallel trend is observed in the comparative analysis between the HACO and GA/GSK algorithms, with both GAP9 and GAP10 metrics demonstrating progressive escalation as the problem scale increases. In contrast, HACO’s improvement over SA remains stable at 3–4% across most scales, except in large-scale instances with 100 customer points where SA’s performance substantially improves, reducing GAP8 to 0.72%. This enhancement likely stems from SA’s stochastic nature and ability to accept inferior solutions, which proved particularly effective in navigating the complex solution spaces of large-scale problems through improved global search and local optimization capabilities.
Given HACO’s consistent superior performance in both Section 5.3.2 and Section 5.3.3, it is adopted as the reference algorithm for analyzing the impact of CI capacity constraints on EVRP. The accompanying pie charts in Figure 12a,b depict the cost composition of instance set C100 with and without CI capacity constraints, respectively.

Figure 12.
The cost structure of instance set C100. (a) Cost structure of CI with capacity constraints. (b) Cost structure of CI without capacity constraints.
The analysis of the diagram reveals three key insights.
First, the fixed cost and distance cost constitute the primary components of total expenses, collectively accounting for over 90% of the overall cost structure. Given the assumption in this study that the depot is far from customer locations and energy replenishment infrastructures, increasing the number of vehicles can significantly increase travel distances. Under normal circumstances, the fixed cost and distance cost exhibit proportional growth.
Second, while charging and battery swapping costs constitute only about 6% of the total costs, their systematic optimization through heterogeneous energy replenishment strategies significantly influences fixed and distance costs, making them crucial for cost control.
Third, under capacity-constrained CI conditions, the HACO algorithm exhibits adaptive optimization capabilities. The fixed cost, distance cost, and charging cost decreases by 0.42%, 0.32%, and 0.08%, respectively, while the battery swapping cost increases by 0.82%. This cost redistribution reflects the HACO algorithm’s ability to accurately assess the capacity of CI and strategically substitute BSI when charging resources become restricted. The inherent and quick speed of battery swapping implicitly extends the vehicle service duration following energy replenishment, enabling fleet size reduction and contributing to comprehensive cost optimization.
In summary, the capacity allocation of CI significantly impacts the cost structure of EVRP under heterogeneous energy replenishment strategies. Under CI capacity constraints, the algorithm prioritizes BSI for energy replenishment. Although this increases immediate costs, it improves vehicle scheduling efficiency and route compactness, ultimately reducing the total cost. This demonstrates the core value of HERI: the complementary advantages of CI’s cost-effectiveness and BSI’s operational efficiency. By dynamically selecting optimal energy replenishment strategies based on the real-time capacity of CI, the algorithm showcases the adaptability of integrated energy systems in smart logistics networks.
5.4. Cost Performance Differences with Partial and Full Charging
Bruglieri et al. [39] assumed a fixed 30 min replenishment time at AFS, with vehicles leaving fully charged, representing a time-consuming fixed full charging process. In contrast, this study introduces HERI, offering two energy replenishment options: battery swapping and charging. Battery swapping is completed in a short, fixed time, replenishing the entire onboard battery capacity. Charging, however, is more flexible, allowing vehicles to replenish energy partially based on route demands, with both time and energy consumption being variable.
This flexibility is a key advantage of HERI, enabling adaptation to dynamic energy replenishment environments by combining partial charging with battery swapping strategies. Compared to full charging, partial charging offers two main competitive benefits.
- (1)
- Reducing energy costs. When vehicles require only minimal energy for subsequent tasks, partial charging enables on-demand energy replenishment at CI, minimizing unnecessary energy consumption and associated costs.
- (2)
- Alleviating the capacity pressure of CI. By reducing individual charging times, partial charging increases infrastructure turnover rates, effectively easing capacity constraints when serving multiple vehicles.
This study numerically validates the effectiveness of partial charging by comparing energy costs and total costs under full charging and partial charging strategies using the HACO algorithm. The experimental results are presented in Table 7.

Table 7.
Cost distribution patterns under partial and full charging strategies.
The table above demonstrates that partial charging, following the “energy replenishment on demand” principle, effectively reduces charging costs across all instances, as indicated by the positive GAP11 values. Notably, the total cost for instance C25_6 is most significantly impacted by partial charging, with a GAP11 of up to 8.54%. As the instance size increases, the average percentage savings in the total cost under the partial charging strategy, compared to full charging, rises from less than 3% to approximately 4%.
This trend is explained by the metrics. For smaller instances, partial charging costs constitute a higher proportion of full charging costs, reaching up to 0.51. As the instance size grows, this proportion decreases and stabilizes around 0.3, indicating that full charging costs grow faster than partial charging costs. Thus, the cost-saving advantage of partial charging becomes more pronounced with larger problem sizes.
5.5. Sensitivity Analysis
As an emerging energy replenishment infrastructure, BSI can effectively alleviate the replenishment pressure on CI, enabling vehicles to complete energy replenishment tasks under limited charging resources. However, the introduction of battery swapping also increases energy replenishment costs. Through comprehensive CI capacity sensitivity analysis, the HACO algorithm not only quantifies the impact of CI capacity variations on route optimization but also provides strategic insights for leveraging the synergistic advantages of HERI.
The data in Table 5 and Table 6 show that the average times of battery swapping are highest in the large-scale instance set C100, indirectly indicating that CI capacity constraints significantly influence vehicle energy replenishment choices. Therefore, this section conducts a sensitivity analysis on this instance set, exploring vehicle routing planning and cost composition under three scenarios: insufficient, moderate, and sufficient CIs. This analysis provides a theoretical foundation for optimizing electric vehicle energy replenishment strategies.
Figure 13a–d illustrate the trends in the average charging and battery swapping costs, the average number of vehicles in operation, average distance costs, and average total costs, respectively, as the CI capacity varies. The number of CIs increases in increments of two within the range [4,12]. Values of four and six represent insufficient CIs, while eight represents a moderate number, and 10 and 12 represent sufficient CIs.
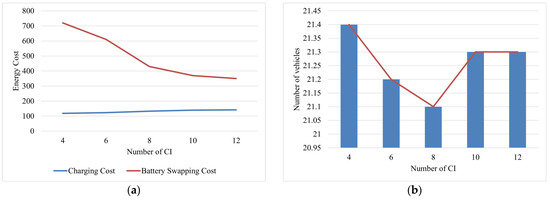
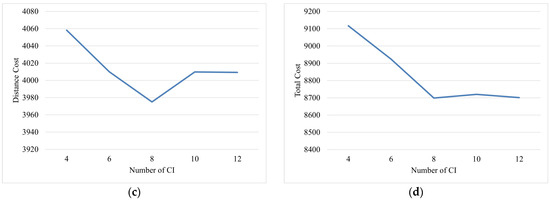
Figure 13.
Sensitivity analysis of the CI capacity for instance set C_100. (a) Energy cost under different CI capacities. (b) Number of vehicles under different CI capacities. (c) Distance cost under different CI capacities. (d) Total cost under different CI capacities.
As shown in Figure 13a, as the capacity of CI increases, the average charging cost rises, while the average battery swapping cost decreases significantly. Specifically, despite a 19.65% increase in charging costs, the 51.39% reduction in battery swapping costs results in a 4.78% decrease in total energy replenishment costs. This trend originates from our algorithm’s design principle of adhering to current economic decision patterns in EV energy replenishment, specifically the charging-priority strategy. Both the dynamic rescheduling conflict mitigation in initial solution construction and the Change Infrastructure operator during local search aim to maximize limited charging resource utilization. Consequently, when HERIs are available, the CI with lower unit costs is prioritized.
Figure 13b reveals that the average number of vehicles in operation decreases as the CI capacity transitions from “insufficient” to “moderate” and then stabilizes as the capacity further increases to “sufficient”. Similarly, Figure 13c shows that the average distance cost follows the same trend, highlighting the coupling relationship between the CI capacity and the operational factors of electric logistics vehicle fleets. These results substantiate that the HACO algorithm’s response to CI capacity fluctuations is not a simplistic unilateral adjustment (either increasing or decreasing specific costs), but rather an intelligent, self-adaptive mechanism that holistically optimizes fleet size, routing plans, and all cost components in a coordinated manner based on operational requirements.
When the CI capacity is limited, increasing the number of operating vehicles becomes an alternative to meet customer distribution demands, alongside battery swapping. As the depot is distant from customer locations and energy replenishment infrastructures, additional vehicle routes inevitably raise distance costs. While the CI capacity expands to an appropriate level, existing vehicles can harness the synergistic benefits of HERI, completing distribution tasks after mid-route energy replenishment. This reduces the need for additional vehicles, thereby simultaneously decreasing both vehicle counts and travel distances.
However, with further increases in CI availability, the algorithm, driven by a greedy attribute, prioritizes the more cost-effective but time-consuming charging method over battery swapping, as the energy replenishment cost is part of the objective function. This decision increases vehicle usage to ensure timely customer service, resulting in a slight rise in vehicle counts () and distance costs (). At this stage, the algorithm achieves dynamic equilibrium through a trade-off between energy replenishment cost-efficiency and delivery timeliness, forming a stable solution set on the Pareto front.
Under the combined effect of these cost changes, the total cost initially decreases rapidly as the CI capacity increases and then stabilizes, exhibiting an L-shaped curve. Figure 13d indicates that once the CI capacity reaches a reasonable threshold, the sensitivity of the electric logistics fleet’s overall distribution cost to capacity changes diminishes. Further capacity expansion beyond this point fails to significantly reduce costs.
This finding provides a reference for optimizing the capacity allocation of CI, aiding in the efficient allocation of heterogeneous energy replenishment resources and reducing fleet operating costs.
6. Conclusions and Future Works
This study addresses the electric vehicle routing problem with limited charging resources, aiming to minimize the total distribution cost of electric logistics fleets by leveraging the complementary advantages of heterogeneous energy replenishment infrastructures. An MIP model is developed, and a HACO algorithm incorporating a VNS mechanism is proposed. During the initial solution construction phase, HACO employs a dynamic rescheduling mechanism to proactively mitigate charging task conflicts induced by CI capacity limitations, thereby optimizing the utilization of constrained charging resources. The effectiveness and stability of HACO are validated through computational experiments on 40 instances of varying sizes by comparing its performance with the Gurobi solver, BR-GRASP, SA, GA, and GA-GSK.
The comparative analysis of HACO results across large-scale instances demonstrates that CI capacity constraints fundamentally reshape cost structures by modulating the operational synergy between CI and BSI. Empirical data reveal that the charging costs via partial charging constitute merely 30–40% of full charging expenditures, yielding a 3–4% reduction in total costs. Sensitivity analysis further identifies moderate CI capacity as the optimal equilibrium point, effectively balancing energy replenishment, fixed vehicle, and distance costs.
This study advances EVRP research by bridging a critical knowledge gap in modeling real-world operational constraints, specifically the simultaneous consideration of HERI and CI capacity limitations, while also yielding practical managerial implications for logistics optimization.
First, the implementation of heterogeneous energy replenishment networks significantly enhances operational flexibility and efficiency. Although electric logistics vehicles with dual charging and battery swapping capabilities require higher initial investment, they substantially reduce long-term operational costs and improve distribution profitability. Therefore, fleet integration strategies should systematically evaluate cost–benefit trade-offs while maintaining service quality.
Second, the partial charging strategy emerges as a cost-effective solution, particularly beneficial in high-demand scenarios or capacity-constrained areas, offering improved route flexibility and fleet efficiency through rapid energy replenishment.
Third, sensitivity analysis underscores the significance of the CI capacity optimization in operational efficiency. Managers should strategically calibrate the CI capacity according to regional demand patterns, establishing an optimal operational range that simultaneously prevents resource underutilization and replenishment constraints while accommodating the heterogeneous energy replenishment demands of vehicle. Such optimization ensures maximal resource efficiency and economic returns.
Finally, the findings provide valuable insights for policy development, suggesting that governments should promote standardized interface protocols for CI and BSI to facilitate the synergistic development of heterogeneous energy replenishment networks.
This study assumes a fixed energy unit price with capacity constraints only for CI. In practice, electricity prices fluctuate throughout the day. Furthermore, the battery inventory at BSI is dynamic, involving both the restocking of fully charged batteries and the recharging of used ones. Future research could explore variable energy replenishment costs under time-of-use tariffs and the limited battery inventory at BSI. Additionally, with the emergence of mobile charging and battery swapping vehicles, which enable electric logistics vehicles to select flexible locations for energy replenishment during transit, future studies could investigate the integration of mobile energy replenishment solutions to address practical EVRP optimization challenges. Lastly, this study’s implications extend beyond logistics. In electric commercial vehicle scenarios like waste collection, medical delivery, and long-distance passenger transport, limited access to energy replenishment resources is still a key challenge. Our proposed framework capitalizes on the synergies of HERI. It shows promise in improving energy replenishment efficiency and operational performance across these sectors, ultimately cutting systemic costs.
Author Contributions
Conceptualization, R.X.; supervision, R.X.; methodology, R.X. and B.S.; validation: B.S.; software: B.S.; writing—original draft preparation, B.S.; formal analysis, R.X.; resources, R.X.; data curation, R.X.; writing—review and editing, R.X. and B.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Natural Science Foundation of China (Grant No. 62106098/62272210), the Fundamental Research Funds for the Central Universities (Grant No. B240207057.423180), and Guangdong Provincial Key Laboratory (Grant No. 2020B121201001).
Data Availability Statement
The data presented in this study are available in article.
Acknowledgments
The authors would like to acknowledge the support and inspiration provided by the Business Data Laboratory at the School of Business, Hohai University.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| Abbreviations | |
| EVRP | Electric vehicle routing problem |
| CI | Charging infrastructure |
| BSI | Battery swapping infrastructure |
| HERIs | Heterogeneous energy replenishment infrastructures |
| MIP | Mixed-integer programming |
| HACO | Hybrid ant colony optimization |
| BR-GRASP | Biased and randomized greedy randomized adaptive search procedure |
| SA | Simulated annealing |
| FIFO | First-in-first-out |
| CC | Charging cost |
| TC | Total cost |
| Sets | |
| Set of customers | |
| Set of CIs | |
| Set of BSIs | |
| Set of BSIs and their copies | |
| Ordered set of all charging pumps in CI c | |
| Ordered set of all cloned charging pumps for charging pump , where | |
| Ordered set of remaining cloned charging pumps without the last one in | |
| Set of depots (departure) | |
| Set of depots (arrival) | |
| Parameters | |
| Vehicle load (kg) | |
| On-board battery capacity (kWh) | |
| Number of charging pumps in | |
| Vehicle speed (km/h) | |
| Distance between nodes and (km) | |
| Travel time from to (min) | |
| Demand of customer (kg) | |
| Service time of customer (min) | |
| Charging speed of the charging pump (min/kWh) | |
| Duration of battery swapping (min) | |
| Energy consumption factor (kWh/km) | |
| Maximum duration per route (min) | |
| Cost of operation per vehicle (CNY/vehicle) | |
| Variable cost per unit distance (CNY/km) | |
| Unit electricity cost of charging (CNY/kWh) | |
| Battery swapping cost (CNY/swap) | |
| Decision variables | |
| Arrival time of the vehicle at node (min) | |
| Load of vehicle upon at node (kg) | |
| Remaining battery level of the vehicle upon arrival at node (kWh) | |
| Remaining battery level of the vehicle upon departure from node (kWh) | |
| One if the vehicle traverses arc (); otherwise, zero | |
| Amount of energy replenished by the vehicle at CI (kWh) | |
| One if the vehicle swaps to battery at BSI ; otherwise, zero | |
References
- European Commission. The European Green Deal Sets Out How to Make Europe the First Climate-Neutral Continent by 2050, Boosting the Economy, Improving People’s Health and Quality of Life, Caring for Nature, and Leaving No One Behind; European Commission: Brussels, Belgium, 2019; Available online: https://ec.europa.eu/commission/presscorner/detail/en/ip_19_6691 (accessed on 2 March 2025).
- PRC State Council. Notice of the State Council on Printing and Distributing the Action Plan for Carbon Peaking Before 2030; PRC State Council: Beijing, China, 2021. Available online: https://www.gov.cn/zhengce/content/2021-10/26/content_5644984.htm (accessed on 2 March 2025).
- U.S. Department of State. The Long-Term Strategy of the United States—Pathways to Net-Zero Greenhouse Gas Emissions by 2050; U.S. Department of State: Washington, DC, USA, 2021. Available online: https://unfccc.int/sites/default/files/resource/US-LongTermStrategy-2021.pdf (accessed on 2 March 2025).
- European Environment Agency. Sustainability of Europe’s Mobility Systems; European Environment Agency: Copenhagen, Denmark, 2024. Available online: https://www.eea.europa.eu/en/analysis/publications/sustainability-of-europes-mobility-systems (accessed on 2 March 2025).
- Liu, Z.; Zhou, S.; Liu, S. Optimization of multimodal transport paths considering a low-carbon economy under uncertain demand. Algorithms 2025, 18, 92. [Google Scholar] [CrossRef]
- Kucukoglu, I.; Dewil, R.; Cattrysse, D. The electric vehicle routing problem and its variations: A literature review. Comput. Ind. Eng. 2021, 161, 107650. [Google Scholar] [CrossRef]
- Erdogan, S.; Miller-Hooks, E. A green vehicle routing problem. Transp. Res. Part E Logist. Transp. Rev. 2012, 48, 100–114. [Google Scholar] [CrossRef]
- Wang, W.Q.; Zhao, J.Y. Partial linear recharging strategy for the electric fleet size and mix vehicle routing problem with time windows and recharging stations. Eur. J. Oper. Res. 2023, 308, 929–948. [Google Scholar] [CrossRef]
- Zhao, M.; Lu, Y. A heuristic approach for a real-world electric vehicle routing problem. Algorithms 2019, 12, 45. [Google Scholar] [CrossRef]
- Diefenbach, H.; Emde, S.; Glock, C.H. Multi-depot electric vehicle scheduling in in-plant production logistics considering non-linear charging models. Eur. J. Oper. Res. 2023, 306, 828–848. [Google Scholar] [CrossRef]
- Bruglieri, M.; Mancini, S.; Pisacane, O. The green vehicle routing problem with capacitated alternative fuel stations. Comput. Oper. Res. 2019, 112, 104759. [Google Scholar] [CrossRef]
- Bezzi, D.; Ceselli, A.; Righini, G. A route-based algorithm for the electric vehicle routing problem with multiple technologies. Transp. Res. Part C Emerging Technol. 2023, 157, 104374. [Google Scholar] [CrossRef]
- Wu, H. A survey of battery swapping stations for electric vehicles: Operation modes and decision scenarios. IEEE Trans. Intell. Transp. Syst. 2022, 23, 10163–10185. [Google Scholar] [CrossRef]
- Conrad, R.G.; Figliozzi, M.A. The recharging vehicle routing problem. In Proceedings of the 2011 Industrial Engineering Research Conference, Norcross, GA, USA, 21–25 May 2011. [Google Scholar]
- Schneider, M.; Stenger, A.; Goeke, D. The electric vehicle-routing problem with time windows and recharging stations. Transp. Sci. 2014, 48, 500–520. [Google Scholar] [CrossRef]
- Montoya, A.; Guéret, C.; Mendoza, J.E.; Villegas, J.G. The electric vehicle routing problem with nonlinear charging function. Transp. Res. Part B Methodol. 2017, 103, 87–110. [Google Scholar] [CrossRef]
- Froger, A.; Mendoza, J.E.; Jabali, O.; Laporte, G. Improved formulations and algorithmic components for the electric vehicle routing problem with nonlinear charging functions. Comput. Oper. Res. 2019, 104, 256–294. [Google Scholar] [CrossRef]
- Bruglieri, M.; Paolucci, M.; Pisacane, O. A matheuristic for the electric vehicle routing problem with time windows and a realistic energy consumption model. Comput. Oper. Res. 2023, 157, 106261. [Google Scholar] [CrossRef]
- McCabe, D.; Ban, X.G. Optimal locations and sizes of layover charging stations for electric buses. Transp. Res. Part C Emerging Technol. 2023, 152, 104157. [Google Scholar] [CrossRef]
- Froger, A.; Jabali, O.; Mendoza, J.E.; Laporte, G. The electric vehicle routing problem with capacitated charging stations. Transp. Sci. 2022, 56, 460–482. [Google Scholar] [CrossRef]
- Lam, E.; Desaulniers, G.; Stuckey, P.J. Branch-and-cut-and-price for the electric vehicle routing problem with time windows, piecewise-linear recharging and capacitated recharging stations. Comput. Oper. Res. 2022, 145, 105870. [Google Scholar] [CrossRef]
- Karimpour, A.; Setak, M.; Hemmati, A. Estimating energy consumption and charging duration of electric vehicle in multigraph. Comput. Oper. Res. 2023, 155, 106216. [Google Scholar] [CrossRef]
- Keskin, M.; Laporte, G.; Catay, B. Electric vehicle routing problem with time-dependent waiting times at recharging stations. Comput. Oper. Res. 2019, 107, 77–94. [Google Scholar] [CrossRef]
- Dastpak, M.; Errico, F.; Jabali, O.; Malucelli, F. Dynamic routing for the electric vehicle shortest path problem with charging station occupancy information. Transp. Res. Part C Emerging Technol. 2024, 158, 104411. [Google Scholar] [CrossRef]
- Deng, Y.L.; Chen, Z.B.; Yan, P.Y.; Zhong, R.X. Battery swapping and management system design for electric trucks considering battery degradation. Transp. Res. Part D Transp. Environ. 2023, 122, 103860. [Google Scholar] [CrossRef]
- Hu, X.; Yang, Z.J.; Sun, J.; Zhang, Y.L. Optimal pricing strategy for electric vehicle battery swapping: Pay-per-swap or subscription? Transp. Res. Part E Logist. Transp. Rev. 2023, 171, 103030. [Google Scholar] [CrossRef]
- Jie, W.C.; Yang, J.; Zhang, M.; Huang, Y.X. The two-echelon capacitated electric vehicle routing problem with battery swapping stations: Formulation and efficient methodology. Eur. J. Oper. Res. 2019, 272, 879–904. [Google Scholar] [CrossRef]
- Yang, J.; Sun, H. Battery swap station location-routing problem with capacitated electric vehicles. Comput. Oper. Res. 2015, 55, 217–232. [Google Scholar] [CrossRef]
- Hof, J.; Schneider, M.; Goeke, D. Solving the battery swap station location-routing problem with capacitated electric vehicles using an AVNS algorithm for vehicle-routing problems with intermediate stops. Transp. Res. Part B Methodol. 2017, 97, 102–112. [Google Scholar] [CrossRef]
- Souza, A.L.S.; Papini, M.; Penna, P.H.V.; Souza, M.J.F. A flexible variable neighbourhood search algorithm for different variants of the electric vehicle routing problem. Comput. Oper. Res. 2024, 168, 106713. [Google Scholar] [CrossRef]
- Felipe, Á.; Ortuño, M.T.; Righini, G.; Tirado, G. A heuristic approach for the green vehicle routing problem with multiple technologies and partial recharges. Transp. Res. Part E Logist. Transp. Rev. 2014, 71, 111–128. [Google Scholar] [CrossRef]
- Keskin, M.; Çatay, B. A matheuristic method for the electric vehicle routing problem with time windows and fast chargers. Comput. Oper. Res. 2018, 100, 172–188. [Google Scholar] [CrossRef]
- Mao, H.T.; Shi, J.M.; Zhou, Y.Z.; Zhang, G.Q. The electric vehicle routing problem with time windows and multiple recharging options. IEEE Access 2020, 8, 114864–114875. [Google Scholar] [CrossRef]
- Lai, Z.J.; Li, S. Towards a multimodal charging network: Joint planning of charging stations and battery swapping stations for electrified ride-hailing fleets. Transp. Res. Part B Methodol. 2024, 183, 102928. [Google Scholar] [CrossRef]
- Maristany de las Casas, P.; Borndörfer, R.; Kraus, L.; Sedeño-Noda, A. An FPTAS for dynamic multiobjective shortest path problems. Algorithms 2021, 14, 43. [Google Scholar] [CrossRef]
- Li, Y.B.; Soleimani, H.; Zohal, M. An improved ant colony optimization algorithm for the multi-depot green vehicle routing problem with multiple objectives. J. Cleaner Prod. 2019, 227, 1161–1172. [Google Scholar] [CrossRef]
- Huang, Y.H.; Blazquez, C.A.; Huang, S.H.; Paredes-Belmar, G.; Latorre-Nuñez, G. Solving the feeder vehicle routing problem using ant colony optimization. Comput. Ind. Eng. 2019, 127, 520–535. [Google Scholar] [CrossRef]
- Lesch, V.; König, M.; Kounev, S.; Stein, A.; Krupitzer, C. Tackling the rich vehicle routing problem with nature-inspired algorithms. Appl. Intell. 2022, 52, 9476–9500. [Google Scholar] [CrossRef]
- Bruglieri, M.; Ferone, D.; Festa, P.; Pisacane, O. A GRASP with penalty objective function for the green vehicle routing problem with private capacitated stations. Comput. Oper. Res. 2022, 143, 105770. [Google Scholar] [CrossRef]
- Hien, V.Q.; Dao, T.C.; Binh, H.T.T. A greedy search based evolutionary algorithm for electric vehicle routing problem. Appl. Intell. 2023, 53, 2908–2922. [Google Scholar] [CrossRef]
- Mohamed, A.W.; Hadi, A.A.; Mohamed, A.K.; Awad, N.H. Evaluating the performance of adaptive gainingsharing knowledge based algorithm on CEC 2020 benchmark problems. In Proceedings of the 2020 IEEE Congress on Evolutionary Computation (CEC), Glasgow, UK, 19–24 July 2020. [Google Scholar]
- Mohamed, A.W.; Hadi, A.A.; Mohamed, A.K. Gaining-sharing knowledge based algorithm for solving optimization problems: A novel nature-inspired algorithm. Int. J. Mach. Learn. Cybern. 2019, 11, 1501–1529. [Google Scholar] [CrossRef]
- Dönmez, S.; Koç, Ç.; Altıparmak, F. The mixed fleet vehicle routing problem with partial recharging by multiple chargers: Mathematical model and adaptive large neighborhood search. Transp. Res. Part E Logist. Transp. Rev. 2022, 167, 102917. [Google Scholar] [CrossRef]
- Vidal, T.; Crainic, T.G.; Gendreau, M.; Lahrichi, N.; Rei, W. A hybrid genetic algorithm for multidepot and periodic vehicle routing problems. Oper. Res. 2012, 60, 611–624. [Google Scholar] [CrossRef]
- Miao, C.W.; Chen, G.Z.; Yan, C.L.; Wu, Y.Y. Path planning optimization of indoor mobile robot based on adaptive ant colony algorithm. Comput. Ind. Eng. 2021, 156, 107230. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
