Abstract
The linking approach replaces the loss function in mean–mean linking under the Rasch model with the loss function. Using the loss function offers the advantage of potential robustness against fixed differential item functioning effects. However, its nondifferentiability necessitates differentiable approximations to ensure feasible and computationally stable estimation. This article examines alternative specifications of two approximations, each controlled by a tuning parameter that determines the approximation error. Results demonstrate that the optimal value minimizing the RMSE of the linking parameter estimate depends on the magnitude of DIF effects, the number of items, and the sample size. A data-driven selection of outperformed a fixed across all conditions in both a numerical illustration and a simulation study.
1. Introduction
Item response theory (IRT) models [1,2,3] are statistical models for multivariate discrete random variables. This article focuses on dichotomous (i.e., binary) random variables and the comparison of two groups through a linking method.
Let denote a vector of random variables , commonly referred to as items or (scored) item responses. A unidimensional IRT model [4] represents the probability distribution for ,
where denotes the density of the normal distribution with mean and standard deviation (SD) . The distribution parameters of the latent variable , often labeled as a trait or ability variable, are collected in the vector . The vector contains the item parameters associated with the item response functions (IRFs) for . The IRF of the Rasch model [5,6,7] is defined as
where denotes the item difficulty , and is the logistic distribution function. In this formulation, the item parameter vector is given as .
For a sample of N individuals with independently and identically distributed observations from the distribution of the random variable , the unknown parameters of the IRT model in (1) can be consistently estimated using maximum likelihood estimation (ML; [8,9,10]).
IRT models are commonly used to compare the performance of two groups on a test by examining differences in the latent variable within the framework of the IRT model in (1). This article focuses on a generalization of the mean–mean linking method [11] based on the Rasch model. The purpose of a linking method is to estimate the difference between the distributions of in the two groups. This difference serves as a summary measure of group performance on the multivariate vector of dichotomous items .
The linking approach consists of two steps. First, the Rasch model is estimated separately for each group, allowing for potential differential item functioning (DIF), where items may function differently across groups [12,13,14]. Second, differences in item parameters are used to estimate group differences in the variable through a linking method [11,15,16].
This article investigates the performance of a generalization of mean–mean (MM; [11]) linking in the presence of fixed uniform DIF [14] in item difficulties. The traditional MM method relies on mean differences in item difficulties, which corresponds to using an loss function. MM linking is a widely used linking or equating method, as discussed in popular textbooks on Rasch modeling [6,7,17,18]. In this study, we investigate a generalization of the MM linking method in the Rasch model using the loss function [19]. Using this robust loss function can essentially remove items with DIF effects from the group comparison directly in the linking method (see also [20,21,22,23,24,25,26,27]). DIF effects can also be treated through the application of robust procedures in MM linking [19,28,29,30,31].
The loss function, being nondifferentiable, requires differentiable approximations to ensure feasible and computationally stable estimation. This article explores alternative specifications of these approximations, which depend on a tuning parameter that controls the approximation error. Previous research relied on fixed values based on prior knowledge or simulation studies. Here, the choice of a fixed parameter is examined and compared with a data-driven approach for determining .
The rest of this article is structured as follows. Section 2 introduces linking in the Rasch model. Section 3 presents a numerical illustration of alternative specifications of linking in a simplified setting. In Section 4, findings from a simulation study are reported. An empirical example is provided in Section 5. This article closes with a discussion in Section 6 and a conclusion in Section 7.
2. Linking in the Rasch Model
This section discusses the linking approach in the Rasch model. Section 2.1 covers item parameter identification and the ordinary MM linking method. Section 2.2 introduces the loss function and presents two differentiable approximations. Section 2.3 applies these approximations to define the linking approach in the Rasch model. Finally, Section 2.4 examines its statistical properties.
2.1. Identified Item Parameters and Mean–Mean Linking
To introduce the linking method as a replacement for ordinary mean–mean linking in the Rasch model, we first outline the identification of item parameters in a group-specific estimation of the Rasch model when no DIF effects are present. In this case, the identified item parameters in the first group are , where represents the invariant item parameters across both groups. For identification, the mean of in the first group is fixed at 0, while the standard deviation remains identifiable within this group.
In the second group, the mean and the SD can be identified when invariant item difficulties are assumed. Thus, and represent group differences in . The identified item parameters in this group, estimated separately under the assumption of a mean of 0 and an estimated SD , are given by
Linking methods aim to recover the group parameter using the group-specific item parameters obtained from separate Rasch model estimations.
The MM linking method estimates the group mean for the second group as
The linking parameter in MM linking is obtained as the minimizer of the squared loss function (i.e., the loss function; [19])
Thus, the estimate satisfies the estimating equation
and denotes the derivative of with respect to x. Clearly, (6) is equivalent to (4).
This paper investigates the computational aspects of MM linking in (5) when the squared loss function is replaced with the loss function, which aims to robustify the linking method in the presence of fixed DIF effects.
2.2. Loss Function and Differentiable Approximations
In this section, we introduce the loss function [32,33], which is defined as
This loss function equals 0 for and 1 for . The loss function has been widely applied in statistical modeling, particularly for obtaining sparse solutions (see, e.g., [34,35,36,37,38,39]).
The exact loss function in (7) has the disadvantage of being nondifferentiable at , making it difficult to use in numerical optimization. To address this, differentiable approximations of the loss function have been proposed.
The ratio loss function, as an approximation of the loss function, is defined as (see [40,41,42,43])
where is a tuning parameter. We have found that performs satisfactorily in applications [19,44].
The linking parameter estimate based on the loss function can be obtained using the approximation (8) with a sufficiently large value, such as . In this case, , and the resulting estimate closely matches the estimate, which is the ordinary MM parameter estimate.
An alternative differentiable approximation of the loss function is based on the Gaussian density function, denoted as the Gaussian function hereafter, and is given by (see [45,46,47])
where is again a tuning parameter.
Figure 1 displays the ratio and the Gaussian loss functions for and . It can be seen that the two loss functions exhibit similar behavior around , which can be explained by the fact that their first two derivatives coincide, with and . For larger values, the Gaussian loss function grows faster toward the upper asymptote of 1 compared to the ratio loss function.
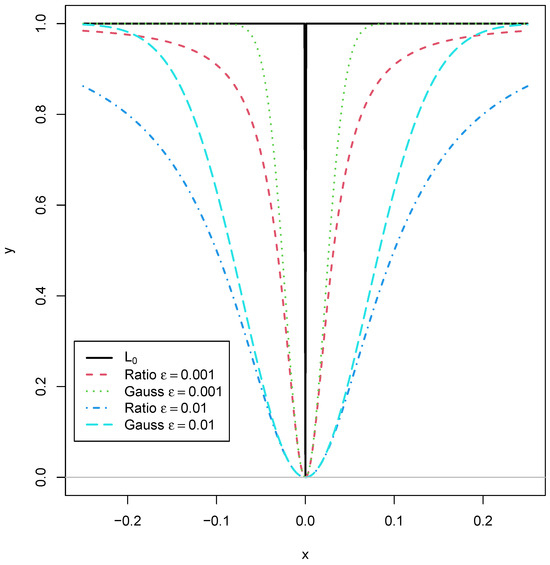
Figure 1.
Ratio loss function and Gaussian loss function for and as differentiable approximations of the loss function.
The ordinary MM parameter estimate can be obtained using the Gaussian loss function approximation, similar to the ratio function, by selecting a sufficiently large value.
2.3. Linking as a Robust Mean–Mean Linking in the Rasch Model
MM linking can be modified by using the loss function instead of the loss function. In the former case, the loss is defined by counting the number of non-vanishing deviations from , which corresponds to the number of non-vanishing DIF effects. To obtain a stable linking parameter estimate in the presence of sampling errors, the loss function is replaced by the differentiable approximation , and the estimated mean is obtained as
This approach can also be referred to as robust MM linking or linking in the Rasch model, where “robust” refers to the linking parameter estimate being resilient to the presence of fixed DIF effects.
Equivalently to (10), the linking parameter estimate solves the estimating equation
Equation (10) represents a one-dimensional optimization problem that can be numerically solved using standard optimizers implemented in statistical software.
2.4. Statistical Properties of the Estimated Linking Parameter in Linking
We now investigate the statistical properties of the linking parameter estimate obtained from (10). The difference in estimated item difficulties required in the linking approach can be written as
with fixed DIF effects and sampling errors , where and . Asymptotic unbiasedness follows from the general properties of ML estimation.
The linking approach is analyzed by starting from the estimating equation
Now, we apply a Taylor expansion with respect to , as in standard M-estimation theory ([48]; see also [25,49]), and obtain
The bias and variance of can be derived from (14) and are given by
where approximate independence of item parameters across items is assumed in (16). As a summary precision measure of the linking parameter estimate, the mean squared error (MSE) can be determined as
Although it might not be immediately evident from Equations (15)–(17), the bias, variance, and MSE depend on the choice of the tuning parameter in the approximation .
In the next two sections, we compare the two differentiable approximations—the ratio and Gaussian loss functions—regarding their statistical properties in a numerical illustration and a simulation study. In particular, we focus on the choice of the tuning parameter .
3. Numerical Illustration
3.1. Method
In this Numerical Illustration, the properties of the estimated linking parameter were studied in a simplified setting in which no item responses were simulated. It was assumed that the difference had a variance of , where N denotes the sample size. Hence, this illustration assumed equal sampling variances of item parameter differences, which might be violated in practice. However, this assumption eases the statistical treatment and aims at yielding clearly interpretable results. Furthermore, we assumed that we had I items, and a proportion of the items had an unbalanced DIF effect , while a proportion of the items did not show DIF.
From Section 2.4, we know that the linking parameter satisfies the estimating equation
where . Because all item parameter differences have equal sampling variances, (18) can be simplified to
assuming that is an integer. By using the bias Formula (15), we obtain
where we use because has a symmetric distribution. The variance can be computed as (see (16))
The root mean square error (RMSE) as the square root of the MSE can be obtained as
The bias, SD, and RMSE are evaluated for for sample sizes N of 250, 500, and 1000, as well as the number of items I as 10, 20, and 40. We simulated fixed DIF effects and , representing small and large DIF. The tuning parameter in the ratio loss function and Gaussian loss function was chosen as 1, 0.95, 0.9, 0.85, 0.8, 0.75, 0.7, 0.65, 0.6, 0.55, 0.5, 0.45, 0.4, 0.35, 0.3, 0.25, 0.2, 0.15, 0.1, 0.095, 0.09, 0.085, 0.08, 0.075, 0.07, 0.065, 0.06, 0.055, 0.05, 0.045, 0.04, 0.035, 0.03, 0.025, 0.02, 0.015, 0.01, 0.009, 0.008, 0.007, 0.006, 0.005, 0.004, 0.003, 0.002, and 0.001. In total, 46 values were evaluated in this Numerical Illustration. We only report results for the ratio loss function because the findings for the Gaussian loss function were very similar. The statistical software R (Version 4.4.1; [50]) was used for the analysis in this study. Symbolic derivatives of the two loss functions were computed with the R package Deriv (Version: 4.1.6; [51]). Replication material for this illustration can be retrieved from https://osf.io/un6q4 (accessed on 20 February 2025).
3.2. Results
Figure 2 displays the absolute bias, the SD, and the RMSE of the estimated mean for items as a function of the DIF effect and the sample size N. The tuning parameter is displayed on a logarithmic scale on the x-axis. The bias increased with increasing values of in the loss function . In contrast, the SD decreased with increasing values of . The RMSE reflects the bias–variance trade-off of the linking parameter estimate. There was an optimal parameter that minimizes the RMSE. This optimal parameter decreased with increasing sample size N. Moreover, the optimal parameter was larger for than for .
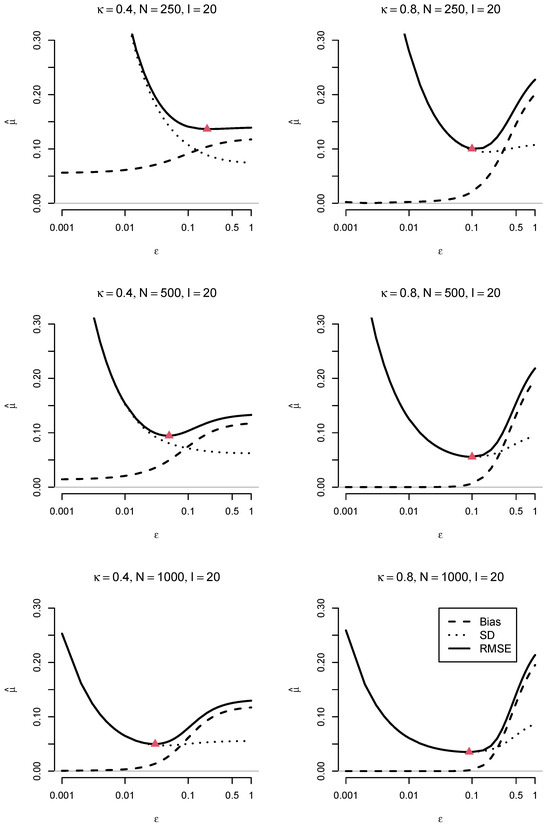
Figure 2.
Numerical Illustration: Absolute bias, standard deviation (SD), and root mean square error (RMSE) of the estimated mean using the ratio loss function for items as a function of sample size N and DIF effect size . The minimum RMSE values are depicted with a triangle. The parameter on the x-axis is displayed on a logarithmic scale.
Table 1 presents the optimal values that minimize the RMSE of the estimated mean under a ratio loss function. These values are reported for different DIF effect sizes , numbers of items I, and sample sizes N. As the sample size N increased, the optimal generally decreased. This pattern was more pronounced for small item numbers (e.g., ), where dropped sharply with increasing N. Larger item numbers I were associated with smaller optimal values, suggesting that when more items were available, the best trade-off under the ratio loss function occurred at a lower value. This effect was particularly evident for , where decreased substantially as I increased from 10 to 40. When the DIF effect size increased from 0.4 to 0.8, the optimal values tended to be slightly higher for the same I and N. This suggests that stronger DIF effects required a higher to achieve the lowest RMSE, likely due to greater bias introduced by DIF at the smaller effect size .

Table 1.
Numerical Illustration: optimal value yielding the minimum root mean square error (RMSE) of the estimated mean using the ratio loss function as a function of the DIF effect size , number of items I, and sample size N.
Overall, the results highlight a trade-off between sample size, the number of items, and DIF effect size in determining the optimal correction for minimizing the RMSE.
4. Simulation Study
4.1. Method
The Rasch model was used as the IRF in the data-generating model for two groups. For identification purposes, the mean of the latent variable in the first group was fixed at 0, with an SD of 1. In the second group, the mean was set to 0.3 to represent the difference in between the groups, while the SD was set to 1.2.
The simulation study was conducted for , 20, and 40 items. In the condition, base item difficulty values were set to −0.314, 0.411, −1.097, −0.542, −1.854, −0.403, −0.895, 0.715, 0.841, and 0.139, resulting in a mean of and an SD of 0.850. These item difficulties were used in the data generation for the first group. In the second group, the same values were applied, except for the first three items, where item difficulties were adjusted to . This introduced fixed DIF in 30% of the items. The DIF effect size was set to 0.4 and 0.8, representing small and large DIF conditions, respectively. For item sets larger than 10, the same 10-item parameter set was repeated accordingly. The item parameters are also available at https://osf.io/un6q4 (accessed on 20 February 2025). Note that item parameters remained fixed across all replications within each condition.
Sample sizes of , 250, 500, and 1000 per group were selected to reflect small- to large-scale applications of the Rasch model.
A total of 5000 replications were conducted for each of the 24 conditions, corresponding to the combinations of 4 sample sizes (N) × 3 item numbers (I) × 2 DIF effect sizes (). For each simulated dataset, linking was performed using various specifications. Both the ratio and Gaussian loss functions (see Section 2.2) were applied. The loss functions were evaluated for a sequence of 11 values: 1, 0.75, 0.50, 0.25, 0.10, 0.075, 0.05, 0.025, 0.01, 0.005, and 0.001.
Additionally, as demonstrated in Section 3, the optimal value corresponding to the minimal RMSE is dependent on the sample size N. To account for this, a data-driven approach for selecting the value was explored. Let denote the average variance of the estimated item difficulty differences . For a fixed , is chosen such that
In the simulation, the following y values were chosen: 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, and 0.9.
The bias, standard deviation (SD), and root mean square error (RMSE) of the estimated mean, , were calculated for all specifications of the linking approach. The relative RMSE of was defined as the ratio of the RMSE for a given specification to the RMSE of a reference method, multiplied by 100. Across all conditions, the reference method was the ratio loss function with a fixed value of 0.01.
All analyses for this simulation study were conducted using the statistical software R (Version 4.4.1; [50]). The Rasch model was fitted with the sirt::xxirt() function from the R package sirt (Version 4.2-106; [52]). The optimization of linking was performed with the stats::nlminb() function. Replication materials for this simulation study can be assessed at https://osf.io/un6q4 (accessed on 20 February 2025).
4.2. Results
Table 2 presents the absolute bias as a function of the DIF effect size , the number of items I, and the sample size N. Overall, the absolute bias generally decreased as increased from 0.4 to 0.8. The bias in the estimated was highest for the smallest number of items () and slightly decreased as the number of items increased. This reduction in bias was more pronounced for smaller sample sizes. As the sample size N increased, the bias systematically decreased, with the lowest bias observed for the largest sample size (). For the data-driven choices and , the bias also decreased as the sample size increased.

Table 2.
Simulation Study: Absolute bias of estimated mean as a function of the DIF effect size , number of items I, and sample size N.
The biases for the ratio and Gaussian loss functions were relatively similar, although the bias was slightly smaller under conditions with a larger DIF effect size () compared to a smaller DIF effect size (). Additionally, the bias decreased as values in the function were reduced. Specifically, the bias was slightly higher for compared to , particularly at smaller N. These findings suggest that while the choice of the loss function influenced estimation accuracy, its effect diminished as I and N increased.
Table 3 presents the relative RMSE of the estimated mean as a function of the DIF effect size , the number of items I, and the sample size N. In general, larger values performed better in smaller samples and with fewer items. Thus, the optimal for minimizing the RMSE depends on , I, and N. The data-driven estimates and generally outperformed the fixed choice based on the loss function . Overall, it can be concluded that was superior to . Although produced a lower RMSE than in many simulation conditions, the differences were typically small. However, in scenarios where performed worse than , its RMSE exceeded the reference value of 100 and was substantially higher than that of . This supports the use of as a conservative default choice. In most conditions, the Gaussian loss function slightly outperformed the ratio loss function. In large samples (), smaller values, such as or , proved effective.

Table 3.
Simulation Study: Relative root mean square error (RMSE) of estimated mean as a function of the DIF effect size , number of items I, and sample size N.
To provide further insight into the absolute bias and relative RMSE, two additional figures are presented below.
Figure 3 presents the absolute bias, SD, and RMSE of the estimated mean using the ratio loss function for items as a function of the DIF effect size and sample size N. The absolute bias increased with larger , while the SD decreased, illustrating a bias–variance trade-off in the RMSE. This trade-off results in an optimal value that minimizes the RMSE. As shown in Figure 3, the optimal was smaller for a larger DIF effect size (i.e., ) than for . Additionally, the optimal decreased with increasing sample size N. As expected, the RMSE was lower for larger sample sizes.
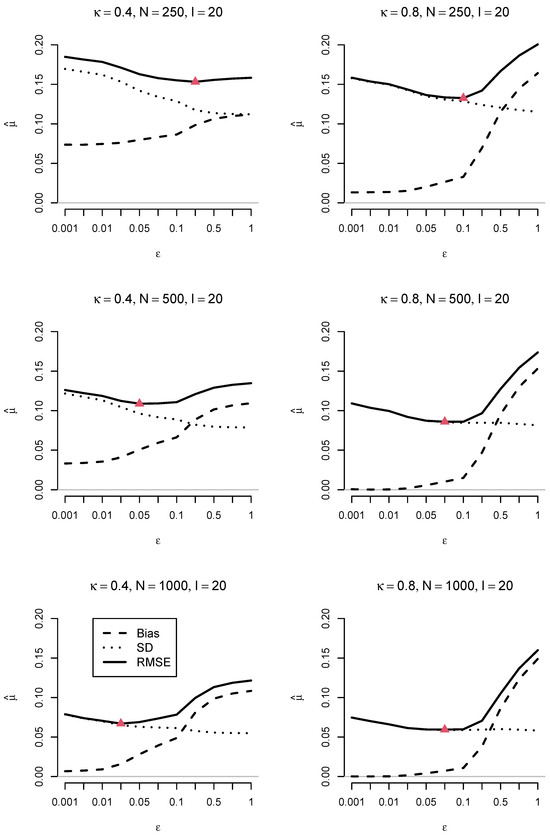
Figure 3.
Simulation Study: Absolute bias, standard deviation (SD), and root mean square error (RMSE) of the estimated mean using the ratio loss function for items as a function of sample size N and DIF effect size . The minimum RMSE values are depicted with a triangle.
Figure 4 presents the relative RMSE of the estimated mean based on data-driven values for the ratio loss function with . The results indicate that an optimal RMSE was achieved for a specific y value, depending on the DIF effect size , the number of items I, and the sample size N. Overall, the findings in Figure 4 support the selection of and , as presented in Table 2 and Table 3.
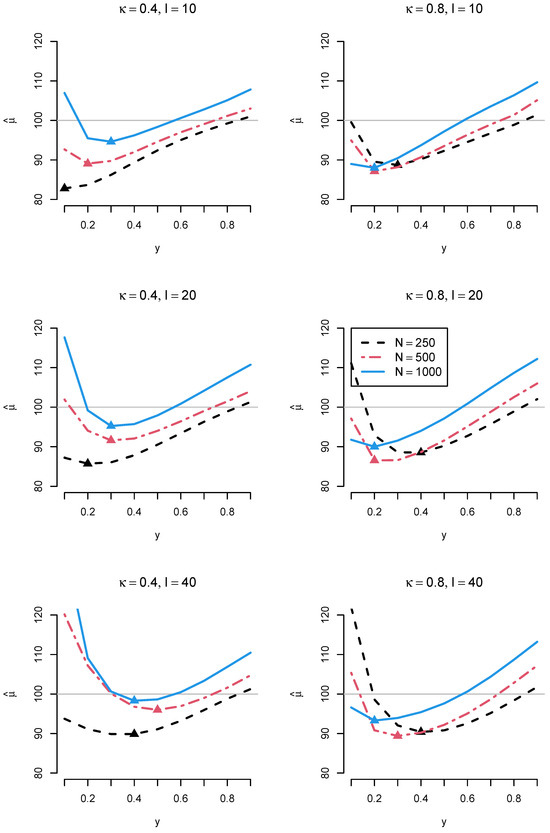
Figure 4.
Simulation Study: Relative root mean square error (RMSE) of the estimated mean using the ratio loss function based on determined through as a function of sample size N, the number of items I, and DIF effect size . The minimum relative RMSE values are depicted with a triangle. The ratio loss function with was chosen as the reference method when computing the relative RMSE.
Following the suggestion of a reviewer, bias and RMSE were regressed onto the simulation factors using a two-way analysis of variance (ANOVA). The factors included sample size N, number of items I, the size of the DIF effect , the type of loss function (i.e., ratio vs. Gaussian function), and the chosen value in the loss function . All simulation factors were treated as categorical factors in the ANOVA. The same item numbers I (e.g., ) and values (i.e., ) as reported in Table 2 and Table 3 were used. The main focus of the analysis was the proportion of variance explained by the main effects and two-way interactions of the factors in the ANOVA.
In the two-way ANOVA with bias as the dependent variable, of the variance was explained by the main factors and their two-way interactions. The largest proportion was attributed to sample size N (), followed by () and (). The number of items I () and the type of loss function () contributed minimally to the variability in bias. Among the two-way interactions, only the interaction between N and (, ) and () accounted for non-negligible proportions of variance.
In the two-way ANOVA with RMSE as the dependent variable, of the variance was explained by the simulation factors and their two-way interactions. As expected, sample size N accounted for the largest proportion of explained variance (), followed by number of items I (), (), (), and the type of loss function (). Among the two-way interactions, (), (), and () contributed with non-negligible amounts to the variance.
5. Empirical Example
We now illustrate linking in the Rasch model using an empirical dataset. The dataDIF dataset from the R package equateIRT (Version 1.0.0; [53,54]) was selected for this purpose. The dataset contains 20 dichotomous items and three groups, each with 1000 subjects. For illustration, only Groups 1 and 2 were linked using the Rasch model.
As in the Simulation Study (see Section 4), the Rasch model was fitted using the sirt::xxirt() function from the R package sirt (Version 4.2-106; [52]). The optimization of linking was performed using the stats::nlminb() function, with R code specifically written for this paper, available at https://osf.io/un6q4 (accessed on 20 February 2025).
The average standard error of item difficulty differences was 0.126. The mean ability difference between Group 1 and Group 2, obtained from MM linking based on the loss function, was 0.482. Slight deviations from this estimate were observed with different specifications of the linking function. For the ratio loss function, the mean estimate based on was 0.535. Empirical choices of the parameter, specifically and , were also explored. For the ratio loss function, the estimates for and yielded mean differences of 0.518 and 0.520, respectively. The mean estimate based on the Gaussian loss function was 0.537, with estimates for and yielding 0.519 and 0.517, respectively.
DIF effects for the 20 items were also computed based on the estimated mean difference of 0.520, obtained with and the ratio loss function. Figure 5 displays the DIF effects along with their 95% confidence intervals. Item 1 exhibited a significantly positive DIF effect (0.798, with a standard error of 0.112), while DIF effects for the remaining 19 items did not significantly differ from 0.
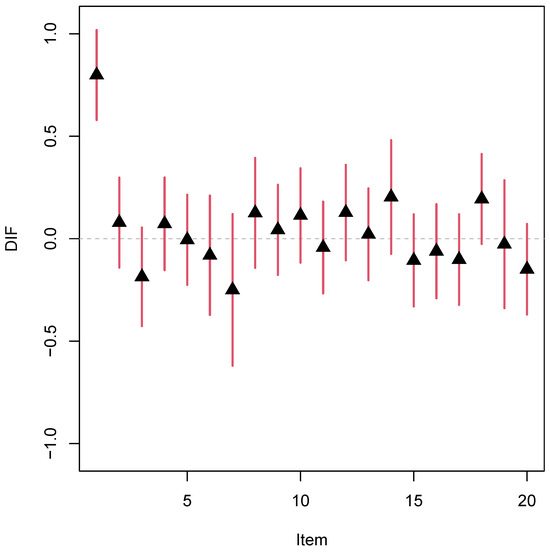
Figure 5.
Empirical example: DIF parameter estimates (displayed with a black triangle) along with their 95% confidence intervals.
6. Discussion
This article examined the computational aspects of linking in the Rasch model. linking serves as a robust alternative to MM linking when fixed DIF effects are present. Since the loss function is not differentiable at , the ratio loss function and the Gaussian loss function were used as differentiable approximations. Both approximations rely on a tuning parameter , which controls the approximation error. A numerical illustration and a simulation study demonstrated that the optimal value minimizing the RMSE of the linking parameter estimate depends on the magnitude of DIF effects, the number of items, and the sample size. A data-driven selection of provided better performance than a fixed across all conditions. Additionally, the Gaussian loss function showed a slight advantage over the ratio loss function, though the differences are likely negligible in practice.
This study aimed to determine group differences in a robust manner, ensuring insensitivity to DIF effects. Detecting DIF items was treated as a nuisance, as the goal was not to identify deviating items but rather to obtain a consistent estimate of the mean difference in ability between the two groups. In contrast, much of the psychometric literature focuses on detecting DIF items [22,27,55,56,57], with group difference estimation being, at best, a by-product of the procedure.
Using the loss function effectively removes items with large DIF effects from the linking process. As a result, the estimated group difference is based solely on items with little to no DIF. This approach may pose a threat to validity, as it alters the construct being measured by treating items with DIF effects as construct-irrelevant [58,59]. Restricting the item set in this way can change the interpretation of the ability variable [60,61,62,63,64].
7. Conclusions
The loss function proved effective in linking two groups based on the Rasch model in the presence of differential item functioning. Two differentiable approximations (i.e., the ratio and Gaussian loss functions) of the nondifferentiable loss function have been proposed. The smoothness of the approximation depends on the tuning parameter . A simulation study demonstrated that a data-driven choice of , based on the average standard error of item difficulty differences, produced estimates with a lower RMSE compared to estimates based on a fixed value, such as .
Funding
This research received no external funding.
Data Availability Statement
This article only uses simulated datasets. Replication material for Section 3 and Section 4 can be found at https://osf.io/un6q4 (accessed on 20 February 2025). The dataset dataDIF used in the empirical example in Section 5 is available from the equateIRT package (https://doi.org/10.32614/CRAN.package.equateIRT; accessed on 20 February 2025).
Conflicts of Interest
The author declares no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ANOVA | analysis of variance |
| DIF | differential item functioning |
| IRF | item response function |
| IRT | item response theory |
| ML | maximum likelihood |
| MM | mean–mean |
| MSE | mean square error |
| RMSE | root mean square error |
| SD | standard deviation |
References
- Bock, R.D.; Gibbons, R.D. Item Response Theory; Wiley: Hoboken, NJ, USA, 2021. [Google Scholar] [CrossRef]
- Chen, Y.; Li, X.; Liu, J.; Ying, Z. Item response theory—A statistical framework for educational and psychological measurement. arXiv 2021, arXiv:2108.08604. [Google Scholar] [CrossRef]
- Yen, W.M.; Fitzpatrick, A.R. Item response theory. In Educational Measurement; Brennan, R.L., Ed.; Praeger Publishers: Westport, CT, USA, 2006; pp. 111–154. [Google Scholar]
- Van der Linden, W.J. Unidimensional logistic response models. In Handbook of Item Response Theory, Volume 1: Models; van der Linden, W.J., Ed.; CRC Press: Boca Raton, FL, USA, 2016; pp. 11–30. [Google Scholar] [CrossRef]
- Rasch, G. Probabilistic Models for Some Intelligence and Attainment Tests; Danish Institute for Educational Research: Copenhagen, Denmark, 1960. [Google Scholar]
- Bond, T.; Yan, Z.; Heene, M. Applying the Rasch Model; Routledge: New York, NY, USA, 2020. [Google Scholar] [CrossRef]
- Debelak, R.; Strobl, C.; Zeigenfuse, M.D. An Introduction to the Rasch Model with Examples in R; CRC Press: Boca Raton, FL, USA, 2022. [Google Scholar] [CrossRef]
- Bock, R.D.; Aitkin, M. Marginal maximum likelihood estimation of item parameters: Application of an EM algorithm. Psychometrika 1981, 46, 443–459. [Google Scholar] [CrossRef]
- Glas, C.A.W. Maximum-likelihood estimation. In Handbook of Item Response Theory, Volume 2: Statistical Tools; van der Linden, W.J., Ed.; CRC Press: Boca Raton, FL, USA, 2016; pp. 197–216. [Google Scholar] [CrossRef]
- Robitzsch, A. A comprehensive simulation study of estimation methods for the Rasch model. Stats 2021, 4, 814–836. [Google Scholar] [CrossRef]
- Kolen, M.J.; Brennan, R.L. Test Equating, Scaling, and Linking; Springer: New York, NY, USA, 2014. [Google Scholar] [CrossRef]
- Holland, P.W.; Wainer, H. (Eds.) Differential Item Functioning: Theory and Practice; Lawrence Erlbaum: Hillsdale, NJ, USA, 1993. [Google Scholar] [CrossRef]
- Millsap, R.E. Statistical Approaches to Measurement Invariance; Routledge: New York, NY, USA, 2011. [Google Scholar] [CrossRef]
- Penfield, R.D.; Camilli, G. Differential item functioning and item bias. In Handbook of Statistics, Volume 26: Psychometrics; Rao, C.R., Sinharay, S., Eds.; Elsevier: Amsterdam, The Netherlands, 2007; pp. 125–167. [Google Scholar] [CrossRef]
- Lee, W.C.; Lee, G. IRT linking and equating. In The Wiley Handbook of Psychometric Testing: A Multidisciplinary Reference on Survey, Scale and Test; Irwing, P., Booth, T., Hughes, D.J., Eds.; Wiley: New York, NY, USA, 2018; pp. 639–673. [Google Scholar] [CrossRef]
- Sansivieri, V.; Wiberg, M.; Matteucci, M. A review of test equating methods with a special focus on IRT-based approaches. Statistica 2017, 77, 329–352. [Google Scholar] [CrossRef]
- Andrich, D.; Marais, I. A Course in Rasch Measurement Theory; Springer: New York, NY, USA, 2019. [Google Scholar] [CrossRef]
- Lamprianou, I. Applying the Rasch Model in Social Sciences Using R and BlueSky Statistics; Routledge: New York, NY, USA, 2019. [Google Scholar] [CrossRef]
- Robitzsch, A. Extensions to mean–geometric mean linking. Mathematics 2025, 13, 35. [Google Scholar] [CrossRef]
- Von Davier, M.; Bezirhan, U. A robust method for detecting item misfit in large scale assessments. Educ. Psychol. Meas. 2023, 83, 740–765. [Google Scholar] [CrossRef]
- De Boeck, P. Random item IRT models. Psychometrika 2008, 73, 533–559. [Google Scholar] [CrossRef]
- Halpin, P.F. Differential item functioning via robust scaling. Psychometrika 2024, 89, 796–821. [Google Scholar] [CrossRef]
- He, Y.; Cui, Z.; Fang, Y.; Chen, H. Using a linear regression method to detect outliers in IRT common item equating. Appl. Psychol. Meas. 2013, 37, 522–540. [Google Scholar] [CrossRef]
- Magis, D.; De Boeck, P. Identification of differential item functioning in multiple-group settings: A multivariate outlier detection approach. Multivar. Behav. Res. 2011, 46, 733–755. [Google Scholar] [CrossRef]
- Robitzsch, A. Robust and nonrobust linking of two groups for the Rasch model with balanced and unbalanced random DIF: A comparative simulation study and the simultaneous assessment of standard errors and linking errors with resampling techniques. Symmetry 2021, 13, 2198. [Google Scholar] [CrossRef]
- Robitzsch, A. A comparison of linking methods for two groups for the two-parameter logistic item response model in the presence and absence of random differential item functioning. Foundations 2021, 1, 116–144. [Google Scholar] [CrossRef]
- Wang, W.; Liu, Y.; Liu, H. Testing differential item functioning without predefined anchor items using robust regression. J. Educ. Behav. Stat. 2022, 47, 666–692. [Google Scholar] [CrossRef]
- Hu, H.; Rogers, W.T.; Vukmirovic, Z. Investigation of IRT-based equating methods in the presence of outlier common items. Appl. Psychol. Meas. 2008, 32, 311–333. [Google Scholar] [CrossRef]
- Jurich, D.; Liu, C. Detecting item parameter drift in small sample Rasch equating. Appl. Meas. Educ. 2023, 36, 326–339. [Google Scholar] [CrossRef]
- Liu, C.; Jurich, D. Outlier detection using t-test in Rasch IRT equating under NEAT design. Appl. Psychol. Meas. 2023, 47, 34–47. [Google Scholar] [CrossRef] [PubMed]
- Manna, V.F.; Gu, L. Different Methods of Adjusting for Form Difficulty Under the Rasch Model: Impact on Consistency of Assessment Results; (Research Report No. RR-19-08); Educational Testing Service: Princeton, NJ, USA, 2019. [Google Scholar] [CrossRef]
- Oelker, M.R.; Pößnecker, W.; Tutz, G. Selection and fusion of categorical predictors with L0-type penalties. Stat. Model. 2015, 15, 389–410. [Google Scholar] [CrossRef]
- Oelker, M.R.; Tutz, G. A uniform framework for the combination of penalties in generalized structured models. Adv. Data Anal. Classif. 2017, 11, 97–120. [Google Scholar] [CrossRef]
- Atamturk, A.; Gómez, A.; Han, S. Sparse and smooth signal estimation: Convexification of l0-formulations. J. Mach. Learn. Res. 2021, 22, 1–43. [Google Scholar]
- Dai, S. Variable selection in convex quantile regression: L1-norm or L0-norm regularization? Eur. J. Oper. Res. 2023, 305, 338–355. [Google Scholar] [CrossRef]
- Huang, J.; Jiao, Y.; Liu, Y.; Lu, X. A constructive approach to L0 penalized regression. J. Mach. Learn. Res. 2018, 19, 1–37. [Google Scholar]
- Panokin, N.V.; Kostin, I.A.; Karlovskiy, A.V.; Nalivaiko, A.Y. Comparison of sparse representation methods for complex data based on the smoothed L0 norm and modified minimum fuel neural network. Appl. Sci. 2025, 15, 1038. [Google Scholar] [CrossRef]
- Soubies, E.; Blanc-Féraud, L.; Aubert, G. A continuous exact l0 penalty (CEL0) for least squares regularized problem. SIAM J. Imaging Sci. 2015, 8, 1607–1639. [Google Scholar] [CrossRef]
- Yang, Y.; McMahan, C.S.; Wang, Y.B.; Ouyang, Y. Estimation of l0 norm penalized models: A statistical treatment. Comp. Stat. Data Anal. 2024, 192, 107902. [Google Scholar] [CrossRef]
- Liu, W.; Li, Z.; Chen, W. Evaluating model robustness using adaptive sparse L0 regularization. arXiv 2024, arXiv:2408.15702. [Google Scholar] [CrossRef]
- O’Neill, M.; Burke, K. Variable selection using a smooth information criterion for distributional regression models. Stat. Comput. 2023, 33, 71. [Google Scholar] [CrossRef]
- Wang, B.; Wang, L.; Yu, H.; Xin, F. A new regularized reconstruction algorithm based on compressed sensing for the sparse underdetermined problem and applications of one-dimensional and two-dimensional signal recovery. Algorithms 2019, 12, 126. [Google Scholar] [CrossRef]
- Xiang, J.; Yue, H.; Yin, X.; Wang, L. A new smoothed l0 regularization approach for sparse signal recovery. Math. Probl. Eng. 2019, 2019, 1978154. [Google Scholar] [CrossRef]
- Robitzsch, A. L0 and Lp loss functions in model-robust estimation of structural equation models. Psych 2023, 5, 1122–1139. [Google Scholar] [CrossRef]
- Paik, J.W.; Lee, J.H.; Hong, W. An enhanced smoothed L0-norm direction of arrival estimation method using covariance matrix. Sensors 2021, 21, 4403. [Google Scholar] [CrossRef]
- Wang, L.; Yin, X.; Yue, H.; Xiang, J. A regularized weighted smoothed L0 norm minimization method for underdetermined blind source separation. Sensors 2018, 18, 4260. [Google Scholar] [CrossRef]
- Zhu, J.; Li, X. A smoothed l0-norm and l1-norm regularization algorithm for computed tomography. J. Appl. Math. 2019, 2019, 8398035. [Google Scholar] [CrossRef]
- Boos, D.D.; Stefanski, L.A. Essential Statistical Inference; Springer: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Simakhin, V.A.; Shamanaeva, L.G.; Avdyushina, A.E. Robust parametric estimates of heterogeneous experimental data. Russ. Phys. J. 2021, 63, 1510–1518. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Core Team: Vienna, Austria, 2024; Available online: https://www.R-project.org (accessed on 15 June 2024).
- Clausen, A.; Sokol, S. Deriv: Symbolic Differentiation, 2024. R Package Version 4.1.6. Available online: https://cran.r-project.org/web/packages/Deriv/ (accessed on 13 September 2024).
- Robitzsch, A. sirt: Supplementary Item Response Theory Models, 2024. R Package Version 4.2-106. Available online: https://github.com/alexanderrobitzsch/sirt (accessed on 31 December 2024).
- Battauz, M. equateIRT: An R package for IRT test equating. J. Stat. Softw. 2015, 68, 1–22. [Google Scholar] [CrossRef]
- Battauz, M. equateMultiple: Equating of Multiple Forms, 2024. R Package Version 1.0.0. Available online: https://cran.r-project.org/web/packages/equateMultiple/index.html (accessed on 13 September 2024).
- Chen, Y.; Li, C.; Ouyang, J.; Xu, G. DIF statistical inference without knowing anchoring items. Psychometrika 2023, 88, 1097–1122. [Google Scholar] [CrossRef] [PubMed]
- Halpin, P.F.; Gilbert, J. Testing whether reported treatment effects are unduly dependent on the specific outcome measure used. arXiv 2024, arXiv:2409.03502. [Google Scholar] [CrossRef]
- Strobl, C.; Kopf, J.; Kohler, L.; von Oertzen, T.; Zeileis, A. Anchor point selection: Scale alignment based on an inequality criterion. Appl. Psychol. Meas. 2021, 45, 214–230. [Google Scholar] [CrossRef]
- Camilli, G. The case against item bias detection techniques based on internal criteria: Do item bias procedures obscure test fairness issues? In Differential Item Functioning: Theory and Practice; Holland, P.W., Wainer, H., Eds.; Erlbaum: Hillsdale, NJ, USA, 1993; pp. 397–417. [Google Scholar]
- Shealy, R.; Stout, W. A model-based standardization approach that separates true bias/DIF from group ability differences and detects test bias/DTF as well as item bias/DIF. Psychometrika 1993, 58, 159–194. [Google Scholar] [CrossRef]
- De Los Reyes, A.; Tyrell, F.A.; Watts, A.L.; Asmundson, G.J.G. Conceptual, methodological, and measurement factors that disqualify use of measurement invariance techniques to detect informant discrepancies in youth mental health assessments. Front. Psychol. 2022, 13, 931296. [Google Scholar] [CrossRef]
- El Masri, Y.H.; Andrich, D. The trade-off between model fit, invariance, and validity: The case of PISA science assessments. Appl. Meas. Educ. 2020, 33, 174–188. [Google Scholar] [CrossRef]
- Funder, D.C.; Gardiner, G. MIsgivings about measurement invariance. Eur. J. Pers. 2024, 38, 889–895. [Google Scholar] [CrossRef]
- Welzel, C.; Inglehart, R.F. Misconceptions of measurement equivalence: Time for a paradigm shift. Comp. Political Stud. 2016, 49, 1068–1094. [Google Scholar] [CrossRef]
- Zwitser, R.J.; Glaser, S.S.F.; Maris, G. Monitoring countries in a changing world: A new look at DIF in international surveys. Psychometrika 2017, 82, 210–232. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).