Abstract
Every year, electric power systems (EPSs) experience accidents resulting in static and dynamic instability, as well as power supply disruptions. Accidents evolve along various trajectories and sometimes can exhibit a cascading effect. In this case, the sequential tripping of generating and/or electric network equipment occurs due to overloads or voltage drops at various nodes of the electric network. This leads to significant losses for industrial and commercial consumers, while also escalating social tensions within the population. This study aims to develop an algorithm for revealing the possibility of cascading failure processes in EPSs and their development trajectories. The use of the algorithm in planning and managing power flows in EPSs facilitates the identification of the boundary between the regions of admissible and inadmissible post-contingency power flows. The algorithm also enables the assessment of the impact of various topology solutions and operational measures on the development of cascading failure processes. This paper presents the results of steady-state calculation for the test schemes of an EPS incorporating 25, 36, and 40 nodes with voltage levels of 6, 35, 110, and 500 kV to illustrate the influence of topology and the non-homogeneity of network parameters on the occurrence and development of cascading failure processes. The deployment of distributed generation facilities of different capacities and FACTS devices, alongside the redistribution of power flows in the network by changing the load of power plants with different electricity generation costs, are considered topology and operational measures that enhance the survivability of the EPS. The performance of the developed algorithm was illustrated through an analysis of the process of the development of a real cascading systemic accident that occurred in the EPS. The proposed algorithm, when utilized in planning and managing power flows in an EPS, facilitates the identification of possibilities for the cascading failure processes and their development pathways to subsequently design and implement the operational measures and topological adjustments to prevent them.
1. Introduction
Emergency disturbances, such as single-phase or multi-phase short circuits (SCs), frequently occur in electric power systems (EPSs). These scenarios result from damage to generating and/or electric network equipment due to external or internal causes, as well as errors made by maintenance personnel [1,2]. The emergency shutdowns of individual types of equipment alter the topology and power flows in an EPS, leading to overloads of the generating and/or network equipment that remains in operation and a decrease in voltage at the nodes of the electric network [3,4,5]. Short circuits are normally localized by the action of protection devices that operate without time delay or with the minimum possible time delay to ensure selectivity. Nevertheless, failures in the operation of individual units of equipment cause systemic accidents, accompanied by significant losses for industrial and commercial consumers of electricity [6,7].
Analysis of the causes of system failures reveals that the EPS structure has “bottlenecks” and the operation planning does not consider the possibility of cascading failure processes. Their likelihood is especially high during periods of extensive repairs of generating and electric network equipment, when EPS topology may change significantly [8,9]. Consequently, to ensure the survivability of the EPS in the event of emergency disturbances during repairs, it is essential to provide appropriate topological and operational strategies [10].
The works addressing the topic at issue indicate that despite the implementation of topological and operational measures in EPSs, many countries experience system-wide accidents, including cascading failures, almost every year [11,12,13]. Below, consideration is given to some examples:
- Massive power outages of more than 30,000 MW that lasted for 7 h in the USA in November 1965 [14,15];
- Massive power outages of more than 1800 MW that lasted for 25 h in the USA (New York) in July 1977 [16];
- Large-scale power outages of approximately 8000 MW that lasted for 4 h in Japan (Tokyo) in July 1987 [17];
- The disconnection of the total capacity of power consumers equal to 11,850 MW that lasted from a few minutes to several hours in July and disconnection of 28,000 MW that lasted from a few minutes to nine hours in the western United States in August, 1996 [18,19,20,21,22];
- The shutdown of intersystem overhead power transmission lines (PTLs) between the northeastern United States and Canada in August 2003, with an outage size of 61,800 MW, that lasted for 42 h (except for consumers with backup power sources) [23];
- Power outages of 724 MW that lasted for 37 min and affected consumers in the UK (London), on 28 August 2003 [24];
- The disconnection of electricity consumers with a total capacity of 20,000 MW that lasted for 20 h in Italy on 28 September 2003 [25];
- System failure accompanied by the disconnection of electricity consumers with a capacity of 2500 MW, with the duration of outages for individual consumers reaching up to 32 h in Russia (Moscow) in May 2005 [26,27,28];
- Power outages of a total capacity of 110,000 MW that lasted for 8 h in India, on 30–31 July 2012 [29];
- Blackout in South America (Argentina, Paraguay, Uruguay) that simultaneously left 48 million people without electricity on 16 June 2019 [30];
- Outages that affected more than 10 million people, lasting for 16 h, in Indonesia (Jakarta) in 2019 [31];
- Power outages that resulted in disconnection of a 973 MW capacity, affecting 1.15 million people in the UK (London) on 9 August 2019 [32].
The considered examples show that despite the evolution of EPSs and the adoption of modern devices designed to control operating conditions, the number of system failures is practically not decreasing, and their consequences are becoming increasingly more significant for consumers of electric power. This stems from the complication of EPS topology; the use of various types of generating equipment at power plants, which have different features and limitations; a decline in the qualifications of repair and maintenance personnel in EPSs; and an increase in the energy availability of consumers [33,34,35].
A cascading failure is defined as a sequence of dependent failures of individual components that gradually weaken an EPS [36].
The study [37] proposes dividing cascading processes into a slow stage (the speed of action of protection devices prevents the development of accidents) and a fast stage (the sequential shutdowns of EPS components with the disruption of power supply to consumers and subsequent operation of emergency control systems to maintain stability in the EPS).
The reliability of power supply to consumers could be improved by dividing large power systems into segments using direct current transmission lines [38]. To minimize consumer outages, the approach presented in the study focused on changing the power flows along DC transmission lines connecting different segments. In this case, the electrical network within individual segments became more independent, which reduced the likelihood of a cascading blackout.
A spectral clustering algorithm was designed to identify EPS components whose disconnection would result in the least damage to electricity consumers in the asynchronous mode [39]. The algorithm relied on assumptions about the coherence of generators in certain clusters. The results of simulation demonstrated that this method could prevent power supply disruptions by islanding EPS parts. However, an analysis of emergency shutdowns revealed that it is extremely difficult to ensure stable operation of generating equipment and consumer power receivers during cascading failures [40].
The paper [41] presented the findings of a reliability assessment for a network when it was transformed into a set of several simple networks. Modeling the cascading failures in the network relied on the developed algorithm consisting of six steps. Changes in the operating conditions were recorded, depending on the disturbance, and a cascading failure was demonstrated in the form of a state transition graph. The presented approach could not provide an analysis of all variations in changes in the states and power flows in the EPS network.
In [42], the results of a study on cascading outages were exemplified by two models of the electric network: ORNL-PSerc-Alaska and Crucitti-Latora-Marchiori. The findings indicated that an increase in the size of the network enhanced its stability under identical emergency disturbances. Calculations proved the influence of network non-homogeneity (differences in the transfer capability of components) on the development of cascading failure processes. At the same time, there was no clear definition and mathematical description of what exactly was meant by non-homogeneity and how the relations for the non-homogeneity factor were obtained.
In [43], reliability is understood as the property of an object of performing specified functions within a specified scope under certain operating conditions. The reliability of an object and its components are complex properties that, depending on the purpose and operating conditions, may include the following (separately or in a certain combination): failure-free operation, recoverability, survivability, (technical) safety, controllability, storability, and stability. In the concept of “reliability”, it is crucial to separately distinguish “survivability”, which is the ability to withstand special disturbances, preventing their development into a chain and cascading process, ending with the complete loss of the functionality of a part or the entire object. In this case, cascading processes are viewed as a sequence of events that culminate in a triggering disturbance, resulting in the sequential disconnection of several components within an EPS. A necessary and sufficient condition for the development of a cascading process is the excess of the admissible current during emergencies in the component being disconnected.
In [44,45], the survivability of technical systems is understood as their ability to maintain their basic functions, even with an acceptable loss in the quality of their performance, under the influence of external factors of an urgent nature, as well as unfavorable operating conditions. With regard to EPSs, the reliability of parallel operation is associated with the ability to maintain stability, which is characterized by the presence/absence of damages and losses for consumers due to the undersupply of electricity for a certain period of time.
Power supply disruptions to consumers can result from large-scale emergency shutdowns that occur in a cascading manner, triggered by a sequence of events that lead to an initiating disturbance [46,47]. In this case, there is no possibility of localizing the initiating disturbance at the place of its origin, which causes it to spread to adjacent fragments of the EPS, leading to failures of other equipment, as well as serious disruptions in the EPS operational conditions.
The cascading development of accidents is caused by the successive tripping of generating and/or power grid equipment by the action of protection devices and/or emergency control systems. It can also be a result of operating conditions that are unacceptable for the specified equipment [48,49]. This definition is of a fairly general nature, since it does not specify the conditions and parameters that influence the development of a cascading failure process.
Cascading failures normally occur due to off-design disturbances and overload failures in electrical grid equipment, followed by its shutdown that leads to power outages affecting vast areas [50,51].
In [52], a systemic failure is understood as a disruption in the stability of the parallel operation of power plants, an unacceptable deviation in frequency in the EPS and voltage at its nodes, current overloads of power grid equipment leading to its cascading shutdown, the emergence of the asynchronous mode, and the division of the EPS into unbalanced parts with a mass shutdown or restriction of electricity consumers across a large area.
A cascading process should be understood as a sequence of quasi-steady states (QSSs) with a transition from one to another as a result of the step-by-step disconnection of EPS components overloaded by current. This process continues until it reaches the region of admissible or inadmissible power flows. In the event that the cascading process terminates in the region of inadmissible power flows, it turns into a cascading system failure.
Evidence indicates that the development of a cascading process with the disconnection of electric grid equipment unfolds over a certain period of time, from several minutes to several days. In this case, there can be no loss of stability in an EPS. Consequently, dispatching personnel can proactively make topological adjustments and implement operational measures to prevent an unfolding failure and its transition to a systemic one.
In recent years, energy storage systems have been increasingly used to enhance the survivability of EPSs. This facilitates preventing unnecessary shutdowns of generating and power grid equipment due to overload [53,54,55]. Energy storage systems have yet to see widespread implementation in EPSs, which is due to their high specific cost relative to the required power and energy capacity [56,57].
The causes of a cascading blackout and its development in the Moscow power system on 25 May 2005 were addressed in [58,59]. During the development of the failure, resulting from overloads, seven 220 kV overhead PTLs were successively disconnected from 09:23 (short circuit in the 220 kV Ochakovo–Choboty overhead PTL) to 10:45 (short circuit in the 220 kV Kedrovo–Ochakovo overhead PTL). Further disconnections of 110–220 kV overhead PTLs triggered a voltage avalanche with the widespread disconnection of consumers [60]. The successive disconnection of 220 kV overhead PTLs until the emergency disconnection of the 220 kV Kedrovo–Ochakovo overhead PTL was not a cascading process. However, it did result in the transition of the EPS to the region of inadmissible power flows.
In [61], the non-homogeneity of an electrical network is understood as the constancy of the value of the ratio of active resistance to inductive resistance (Rij/Xij) for any section of the network (i, j, …, n, i ≠ j). However, this is not enough, since there are other factors that influence the occurrence and development of cascading failure processes.
The study [62] examined the non-homogeneity of EPS parameters by assessing the coherence of generator rotation and identifying the groups of generators that had electrical connections with different inductive resistances. To this end, a mathematical tool, including spectral, singular, and cluster analysis, was utilized. Such calculations require large computational resources and, therefore, are not used in the real-time assessment of EPS reliability.
In [63], the influence of different types of emergency disturbances in a test network circuit, as well as a German 380 kV transmission network, was investigated. The authors took into account the distributed placement of consumers and power plants across the network. The work calculated the probability of the disconnection of a certain number of consumers and its impact on the development of accidents. The authors drew conclusions about the impact of the magnitude of load disconnection on the speed of emergency processes and also found that when one power transmission line failed, a greater number of power receivers were disconnected in large load clusters than in small clusters. The authors noted that with an increase in the EPS size, when critical connections were disconnected (causing cascading shutdowns), the number of critical connections decreased.
The study [64] noted that cascading failures occurred when the load of nodes affected by electrical equipment failures switched part of the load to adjacent nodes. In this case, it was unimportant for what reason the emergency shutdown of the network element occurred. The authors performed modeling in a small-sized test circuit (21 nodes). The article concluded that there was a high probability of node shutdowns due to trigger disturbances at adjacent nodes.
In [65], the authors present an overview of various studies on cascading shutdowns, and in the conclusion, they use the term heterogeneity from the position of the interdependence between electrical networks and cyber networks. The article does not provide a definition of the term “heterogeneity” or a reference to another source.
The work [66] presents a spectral clustering algorithm for developing EPS shutdown decisions, which allows minimizing deviations from planned values of power flows between islands. The developed method allows preventing power supply disruptions by dividing an EPS into stable islands. However, it is not always possible to divide an EPS into balanced islands, especially in the process of developing an emergency cascade process, since individual parts of an EPS, as a rule, contain more power plants, while others contain electricity consumers.
In [67], calculations of modes for assessing the impact of the failure of one power transmission line on flows in other lines were performed using the Moore–Penrose pseudoinverse matrix. The authors used the pseudoinverse matrix of admittances to develop an algorithm for identifying the process of cascade failure development. The article noted that the use of the algorithm was superior to the random enumeration of options and allowed obtaining optimal solutions in simple cases. Evidence from analyzing cascade accidents showed that they could not be classified as simple cases. The authors did not provide a single example of using the developed algorithm to analyze a major cascade accident.
In the study [68], the authors present a dynamic model using Bayes’ theorem to estimate the conditional probability of the failure of power transmission lines and their condition in order to predict potential cascading failures. The authors propose the use of the decision tree method, which allows estimating the probability of the failure of each EPS element and predicting the trajectory of failure development. In large EPSs, even with the availability of statistical data on the parameters of the failure flow for each unit of equipment, it is impossible to guarantee the correctness of the calculation of the probabilities of the occurrence of cascading accidents and the trajectories of their development due to the presence of random factors of natural and human-made natures.
Of interest is the study [69], which examines the efficiency of using protection schemes that implement load shedding when an accident occurs to prevent the development of cascading shutdowns in ring networks. The authors note that cascading shutdowns of elements in an underloaded EPS do not lead to the transition of the mode to an unacceptable region and the development of a cascading accident. At the same time, in an overloaded EPS, additional shutdowns of power grid elements can lead to a significant deterioration in the circuit-mode situation.
In [70], a platform for visualizing the development of cascade outages is presented using the example of the Bay Area (California, USA) power grids. This platform is of interest from the point of view of the visual observation of the development of emergency processes, but it is not intended to assess the possibility of the occurrence and trajectories of emergency cascade processes.
In [71], a computational approach to the analysis of emergency outages according to the N–X and N–1 criteria was proposed. The analysis was performed in Scilab using the Newton–Raphson power flow method for accidents in transmission lines and busbar systems. Examples of its use were presented using the IEEE 14, IEEE 30, and IEEE 57 models. High-performance computing resources were required to calculate modes in on-line and even off-line formats. The authors substantiated the need to implement supercomputers to solve these problems.
Considering that EPSs in different countries were created on the basis of different principles and approaches to the reservation of network elements and power supply to consumers, there are no unified approaches to the analysis of emergency cascade processes. In different EPSs, the probability of occurrence of emergency cascade processes is significantly higher than in others, which is justified by the presence of a large number of heterogeneities. An analysis of the available literature on the study topic indicates that the sources fail to specify the conditions and parameters that drive the emergence of cascading processes. Furthermore, there is a lack of an established algorithm to identify the potential for these cascading processes within EPSs and their development pathways. This allows us to draw a conclusion about the relevance of research on this topic.
This study aimed to design an algorithm for revealing the possibility of cascading failure processes in EPSs and the trajectories of their development. This algorithm, when employed in planning and managing EPS operation, can facilitate assessing the impact of various topology and operational strategies on the development of cascading failure processes and identifying the boundaries of maximum admissible power flows. The timely implementation of topological and operational measures, such as the integration of distributed generation (DG) facilities, FACTS devices, and power flow redistribution in the network by changing the load of power plants with different electricity generation costs, can significantly mitigate the risk of the potential development of cascading failure processes.
The study examines the influence of the topologically non-homogeneous distribution of EPS parameters on the possibility of the occurrence and development of emergency cascade processes. This is due to the fact that, depending on the non-uniformity of the parameters, the boundaries of the region of permissible EPS modes change significantly. This article presents the results of a study of the boundaries of maximum permissible modes for various variants of non-homogeneous EPSs. Emergency shutdowns of individual elements in non-homogeneous EPSs can lead to a cascading development of an accident with the completion of the process in the region of permissible or impermissible modes. This study shows that in EPSs with homogeneous distributed parameters, the occurrence and development of cascade processes is unlikely.
The novelty of the research results is as follows:
- An algorithm for searching for trajectories of emergency cascade processes in EPSs was developed;
- A mathematical tool for determining the values of non-homogeneities in EPSs that affect the occurrence and development of emergency cascade processes was proposed;
- An approach was developed to determine the boundaries of maximum permissible modes taking into account EPSs non-homogeneities;
- A method for 3D graphic analysis of the influence of EPS non-homogeneities on the occurrence and development of emergency cascade processes was proposed.
This paper is organized as follows. Section 2 focuses on the conditions for cascading processes in EPSs and their development trajectories, also providing sources of initial information for the study. Section 3 proposes a cyclic algorithm, discusses the features of its application, and presents the results of steady-state calculations for the test schemes of EPSs that incorporate 25, 36, and 40 nodes operating at voltage levels of 6, 35, 110, and 500 kV and a real EPS scheme. The section highlights the effectiveness of topology and operational measures, including the use of DG facilities of various capacities and FACTS devices, along with power flow redistribution in the network by adjusting the loads of power plants based on their different electricity generation costs to increase the survivability of the EPSs. Section 4 discusses the findings of this research and future areas of work aimed at preventing the development of cascading failure processes in EPSs. The conclusion summarizes the main findings of this study.
2. Materials and Methods
The emergence and subsequent development of a cascading process in an EPS require that Inequality (1) is satisfied in the event of heavy-load conditions with the shutdown of EPS equipment in each step:
where Iij is the current value in the initial state, A; ΔIij is the value of current surge in an analyzed component under the heavy-load conditions, A; and Iprm.ij is the admissible current value during an emergency for the component A.
If Inequality (1) is not met, the cascading failure process ceases. Conversely, if it is met, a series of calculations of steady states, following one after another, is required to determine different development trajectories for the cascading failure process, which has a slow and a fast stage.
The increase in the power flow in each step of the cascading failure process development occurs until the current in one or several network components exceeds the value admissible during emergency Iprm.ij or the critical voltage value (Ucr) at one or several nodes of the EPS.
The impact of non-homogeneous EPS parameters on cascading process development can be effectively assessed utilizing mathematical analysis and 3D graphical representation, which enhance visual comprehension [72,73]. In this case, the EPS under study was represented as a geographically distributed multiparameter system in the form of an i × j matrix A. The non-homogeneity factors of the EPS parameters, i.e., Aij, were presented on a two-dimensional plane of the EPS diagram according to the coordinates i × j.
Analysis of EPSs with non-homogeneous parameters should factor in the following: Xij is the inductive resistance of components; Pijgen is generated active power; Pijload is consumed active power at the load nodes. When constructing a 3D graphic surface of influencing factors, it is essential to determine the value of their maximum distribution, Aijmax. The relative values of the influencing factors are determined by Equation (2):
where A*ij is a relative value of the influencing factor, p.u.; Aij is the actual value of the influencing factor; Aijmax is the maximum value of the influencing factor from the entire series, Aij.
When analyzing EPSs with non-homogeneous parameters, calculations for the factors Xij, Pij gen, and Pij load must be performed by analogy, using Equation (3):
where X*ij, P*ij gen, and P*ij load are the values of the influencing factors in p.u.; Xij, Pijgen, and Pijload are the actual values of the influencing factor; and are the maximum values of the influencing factor from the entire series, Xij, Pij gen, and Pij load.
The values of the non-homogeneity of the EPS parameters for a two-dimensional plane of the scheme had to be determine by simple algebraic addition, provided their influence was equivalent, using Equation (4):
The weighting coefficients were introduced to factor in the significance of each of the analyzed factors. They are given in Equation (5):
where kA, kB, and kC are weighting coefficients (from 0 to 1).
The values of the weighting coefficients had to be determined by the dispatching personnel for each specific EPS based on the experience of maintaining the power flows, given the specific characteristics of the EPS.
The influencing factors X*ij, P*ij gen, and P*ij load were assumed in this study based on the condition that k = 1. However, they could have different values depending on specific topology and operating conditions:
The next stage involved constructing a 3D surface of the change in the specified factors in the coordinates x, y, and z. In this case, the coordinates x, y corresponded to the coordinates i × j of the matrix formalization of the EPS scheme. The value of factor A*ij was distributed along the z coordinate.
This study employed test schemes of EPSs incorporating 25, 36, and 40 nodes with voltage levels of 6, 35, 110, and 500 kV, illustrating the influence of topology features and the non-homogeneity of network parameters on the emergence of cascading processes in EPSs and their development.
The steady states of EPSs in this study were calculated in RastrWin 3 software (version 2.9.0.640). The stable states of EPSs are those states in which all the parameters of the mode are in the range of acceptable values, which allows for the reliable operation of power plants, as well as uninterrupted power supply to consumers in a given volume and with given indicators of power quality.
The performance of the developed algorithm was illustrated by the analysis of a real cascading failure that occurred in one of the EPSs. The initial data for the analysis were taken from the design diagram of an actual EPS where the system accident took place.
3. Results
This study proposes a cyclic algorithm designed to search for the development trajectories of cascading failure processes following the N–X criterion for given EPS power flows. This algorithm can also be used in planning and maintaining EPS power flows.
The N–X criterion is widely used in the analysis of EPS operating modes, as it allows making a decision on the admissibility of a particular mode with the simultaneous disconnection of X elements of the electric grid, when in a normal scheme their number is equal to N. In the calculations of the modes, the results of which are presented in this article, the N–1 criterion was used, while the consequences of an emergency disconnection of one grid element were analyzed. If necessary, analysis could be carried out for the N–X criterion, when the simultaneous emergency disconnection of several grid elements at once was considered.
Here is a detailed step-by-step description of the proposed algorithm, as well as the key features of its utilization:
- Before Step 1 of the algorithm, select a set of components of the studied EPS fragment: generators, Gi, loads, Pi load, and network components, Ln. Calculate the steady state for the studied fragment of the EPS to determine the possibility of its existence.
- Step 1 of the algorithm implementation:
- 2.1.
- Identify the initiating emergency (single) disturbance, leading to the fulfillment of Inequality (1) for one or several network components by alternately disconnecting each generator, Gi, load, Pi load, and network relative to the conditions of aperiodic static stability.
- 2.2.
- If, during the successive disconnection of each generator, Gi, load, Pi load, and network component, Ln, all steady-state calculations are performed and Inequality (1) is not satisfied, then, according to the N–1 criterion, a cascading failure process for the given EPS power flows and network topology is impossible. The check according to the N–1 criterion is completed. The second step of the algorithm is not required.
- 2.3.
- If, during the successive disconnection of each generator, Gi, load, Pi load, and network component, Ln, the check shows that at least one power flow is infeasible in terms of the conditions of static aperiodic stability, then, according to the N–1 criterion, the power flow does not exist and it is not necessary to check for the possibility of a cascading failure process for a given EPS power flow and network topology in the second step.
- 2.4.
- If, with the disconnection of one of the generators, Gi, loads, Pi load, and network components, Ln, Inequality (1) is satisfied for one or several network components, Ln, but the check according to p. 2.3 shows that the obtained power flow is infeasible in terms of static aperiodic stability, then, according to the N–1 criterion, a cascading process for a given power flow and network topology occurs in the first step. Since no power flow meets the conditions of static aperiodic stability, there is no need to check for the possibility of cascading failure process according to the N–1 criterion for a given power flow and network topology in the second step.
- 2.5.
- If, with the disconnection of one of the generators, Gi, the loads, Pi load, and the network components, Ln, Inequality (1) is satisfied for one or several network components, Ln, and the check according to point 2.3 shows the feasibility of the obtained power flow according to the static aperiodic stability, then, according to the N–1 criterion, the cascading failure process is possible. Therefore, the check in the second step of the algorithm needs to be continued.
- 2.6.
- If, according to the N–1 criterion, a cascading failure process for a given power flow and network topology occurs in the first step with the disconnection of different generators, Gi, loads, Pi load, and network components, Ln, i.e., for several options, and the check according to point 2.3 shows the feasibility of the obtained power flows in terms of static aperiodic stability, then, according to the N–1 criterion, the cascading process can develop along several trajectories. Consequently, it is essential to continue checking for the possibility of cascading failure process development in the second step along all the identified trajectories.
- 2.7.
- To prepare for the second step of the algorithm, if the conditions of point 2.5 are met, identify components for which Inequality (1) is satisfied in the first step from the list of generators, Gi, loads, Pi load, and network components, Ln. If the cascading process develops in accordance with point 2.6 along several trajectories, then for each trajectory, determine its list of network components.
- The network components, Ln, for which Inequality (1) is satisfied are considered disconnected in the next step of the algorithm.
- In each subsequent step of the algorithm, perform all actions following the recommendations of points 2.1–2.7.
- In each i-th step of the algorithm, if, during the implementation of points 2.4 and 2.5, the calculations indicate that power flow is inadmissible in terms of the static aperiodic stability, then, following the N–1 criterion, the cascading failure process for the given power flow and network topology exists up to the i-th step. Starting with the i-th step, however, the power flow does not exist according to the conditions of static aperiodic stability. Therefore, there is no need to further check for the possibility of cascading failure process development in step i + 1. This is because along this trajectory, the cascading failure process ends with a loss of stability, and hence, it is inadmissible.
- If point 5 is fulfilled in the first step of the algorithm or Inequality (1) is not satisfied for each of the network components Ln in the first step of the algorithm, then, following the N–1 criterion, there are no conditions for the occurrence of a cascading failure process for the given power flow and network topology.
- If in the i-th step of the algorithm, during the implementation of points 2.4 and 2.5, the power flow is admissible in terms of the static aperiodic stability, then, according to the N–1 criterion, the cascading failure process for the given power flow and topology exist before the i-th step. If, at the same time, in step i, no network components Ln for which Inequality (1) is satisfied are identified, then it is not necessary to check for the possibility of cascading failure process development according to the N–1 criterion for the given power flow and network topology along this trajectory in step i +1. This is because the cascading failure process ends with an admissible post-contingency power flow.
Based on the experience of analyzing steady-state calculations, an algorithm was designed to identify the trajectories of the cascading failure process development for the N–X criterion. For a cascading failure process to develop, the EPS at hand must have the following characteristics:
- The EPS operation must continue in more than one step after an emergency disturbance from the limit power flow in terms of static aperiodic stability;
- The non-homogeneity of the network parameters must be such that in the event of an emergency disturbance (disconnection of generating equipment, network component), a surge in the current ΔIij occurs in the next component, resulting in the current exceeding the limit admissible for emergency and causing its disconnection.
A block diagram of the algorithm built to identify the possibilities of cascading failure processes and their development trajectories in the EPS for the N–X criterion is shown in Figure 1.
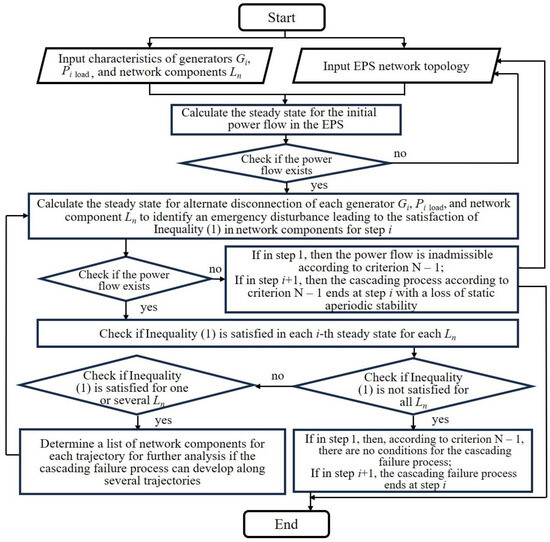
Figure 1.
A block diagram of the algorithm for identifying the possibility of cascading failure processes and their development trajectories in the EPS for the N–X criterion.
We will present the findings from our analysis of the causes behind cascading failure processes and their development in several test schemes and one real-world EPS scheme. The test scheme (N nodes) was understood as a scheme that facilitated establishing the patterns of influence of the topology and parameters of network components on the cascading failure process development.
The EPS schemes considered in the study were as follows:
- The first test scheme contained a 110 kV distribution network (25 nodes), which is shown in Figure 2;
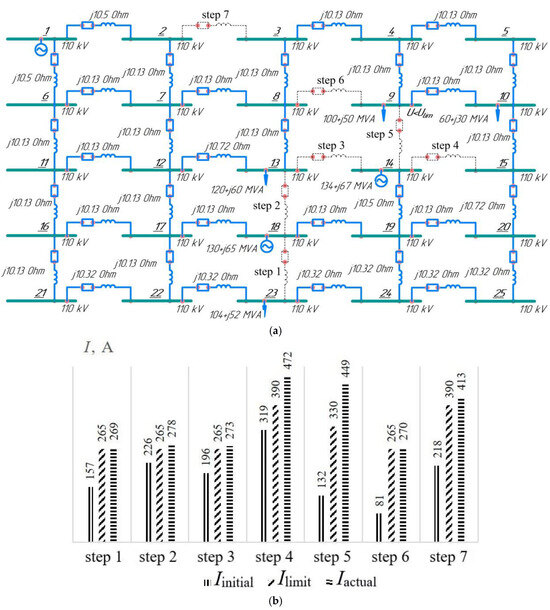 Figure 2. The 110 kV distribution network (25 nodes): (a) the test scheme; (b) a graph of changes in currents in network branches during the cascading failure process development.
Figure 2. The 110 kV distribution network (25 nodes): (a) the test scheme; (b) a graph of changes in currents in network branches during the cascading failure process development. - The second test scheme contained a distribution network with voltage levels of 10, 35, and 110 kV with DG facilities (40 nodes, 67 branches), which is presented in Figure 3;
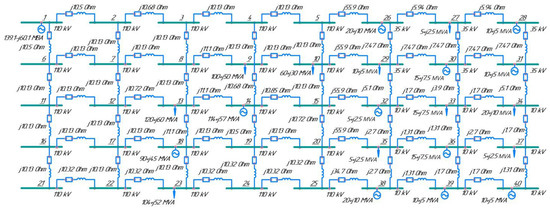 Figure 3. The test scheme of the distribution network with voltage levels of 10, 35, and 110 kV, integrating DG facilities (40 nodes).
Figure 3. The test scheme of the distribution network with voltage levels of 10, 35, and 110 kV, integrating DG facilities (40 nodes). - The third test scheme contained a backbone 500 kV network (36 nodes, 60 branches).;
- The fourth scheme represented a real-world EPS scheme and described the sequence of disconnections for the network components during the cascading failure process development.
The obtained patterns could be employed to analyze the schemes of various EPSs and their operating conditions. At the EPS nodes, one could set the required values of the generated powers (Pi gen and Qi gen) and loads (Pi load, Qi load), as well as branch parameters (R, X, B) to change the network topology and adapt it to the required topology and operational conditions.
The decentralization of energy is leading to a surge in the use of distributed generation facilities relying on both renewable energy sources (RESs), such as wind and solar power plants, and non-renewable energy sources, including gas reciprocating units, gas turbines, and diesel power plants [74,75,76]. This study performed a series of steady-state calculations for various topologies and operating conditions, in which the use of DG facilities was justified by the need to increase the survivability of the EPS.
The first stage of the study involved modeling a cascading failure process for the scheme presented in Figure 2a, which consisted of seven steps, by making changes to the parameters of the network scheme. Figure 2b demonstrates histograms of currents for the EPS components: Iinitial is the current in the network components in the initial conditions before the emergency disturbance, A; Ilimit is the value of the current in the network component allowed in the event of emergency, A; and Iactual is the current in the network component under increased-load conditions, A.
An initiating disturbance in the test scheme (Figure 2a) occurred in the form of a sharp increase in the load at node 23 from 52 + j26 MVA to 72 + j36MVA, which caused overload in branch 18–23 (load 102.2%) and its disconnection. The parameters of branch 18–23 were set for the AC-70/11 steel–aluminum wire: R = 10.7 Ohm; X = 10.13 Ohm; and V = −255∙10−6 Cm.
The second stage of this study examined the feasibility of using DG facilities to increase the EPS survivability in the test scheme of the distribution network with voltage levels of 10, 35, and 110 kV (Figure 3). During the modeling, the power generation from the DG facilities (nodes 26 and 38—20 MW each; nodes 39, 40—10 MW each) enabled the prevention of a cascading failure process development in the EPS. These results proved the efficiency of using DG facilities.
Next, based on Equations (1)–(6), 3D graphic surfaces of network parameter non-homogeneity (Figure 4, Figure 5 and Figure 6) were built for the scheme in Figure 3, which demonstrate the step-by-step development of the cascading failure process.
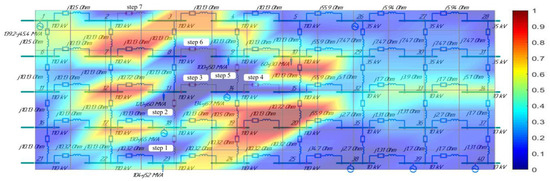
Figure 4.
A 3D graphic surface of the non-homogeneity of parameters of the distribution network with voltage levels of 10, 35, and 110 kV (40 nodes).
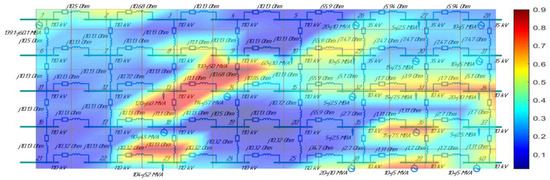
Figure 5.
A 3D graphic surface of the non-homogeneity of parameters for the distribution network when connecting distributed generation facilities and loads (40 nodes).
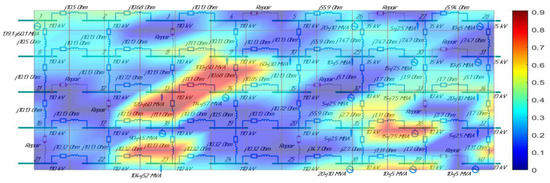
Figure 6.
A 3D graphic surface of parameter non-homogeneity for the distribution network with voltage levels of 10, 35, and 110 kV in the repair scheme (40 nodes).
Analysis of Figure 4 allows us to conclude that in Step 7, the cascading failure process ended with a loss of voltage stability at node 9 at Ucr < 0.7 Urated [77,78]. In this study, one of the criteria for the transition of the mode to an unacceptable area a\z the violation of the conditions for ensuring static voltage stability (voltage avalanche). This was possible in circuit-mode situations when the voltage in one or several network nodes dropped below the critical value. In the calculations, it was assumed that the violation of static voltage stability led to the disconnection of the load in the corresponding EPS nodes.
Figure 5 illustrates a 3D graphic surface of parameter non-homogeneity for the EPS network (40 nodes), in which we have the following:
- Initially, the prevention of a cascading failure process by connecting the DG facilities (nodes 26 and 38—20 MW each; nodes 39, 40—10 MW each) was modeled in the first step. As a result, the current in branch 18–23 went down from 271 A (102.2%) to 249 A (92.9%), which made it possible to prevent its shutdown.
- Power flows in the branches of the distribution network with a voltage of 10 and 35 kV were created by additionally connecting DG facilities and loads in both types of networks at a value of 60 MW each. In the 10 kV network, they were distributed as follows: node 32 (generator)—5 MW; node 36 (generator)—10 MW; node 33 (load)—15 MW; node 34 (load)—20 MW; node 35 (load)—5 MW; node 37 (load)—5 MW. In the 35 kV network, these values were as follows: node 28 (generator)—10 MW; node 29 (generator)—10 MW; node 30 (generator)—15 MW; node 31 (generator)—10 MW; node 27 (load)—15 MW.
Steady states were calculated for the repair scheme of the network, in which eleven components were taken out for repair, including six in the 110 kV network, two in the 10 kV network, two in the 35 kV network, and one 110/10 kV power transformer. In this case, all the operating parameters were within the region of admissible values, as shown in Figure 6.
Next, the topology and operating conditions were analyzed for the zero-power output from renewable energy facilities due to a sharp change in meteorological conditions under the normal operation and repair scheme of the network.
As a result, in the normal 10 kV, 35 kV distribution network scheme, an overload occurred in branch 33–34, and a loss of voltage stability occurred at node 34, at U < Ucr. In this case, the protection device disconnected the overloaded branch 33–34, which sharply increased the current load across the entire adjacent network [79]. Thus, in branch 31–34, the current exceeded the maximum admissible value by 6.18 times (Ilimit = 1920 A; Iactual = 11,876 A).
In the repair 10 kV, 35 kV distribution network scheme, an overload occurred in branches 33–34 and 36–37, while a loss of voltage stability was observed at node 31. After the disconnection of the overloaded branches by the protection devices, the maximum current surge was recorded in branch 31–34, which exceeded Ilimit by a factor of 25.
In the next stage, to increase the survivability of the EPS, we determined the maximum value of the total active power of the DG facilities, necessary to maintain the stability of the EPS. This value for the normal network scheme was 40 MW (DG facilities were connected to nodes 26, 30, 32, 38, and 39). The connection of DG facilities caused overload in branch 18–23, but this shutdown did not lead to further cascading process development, and the voltage remained in the range of admissible values.
The EPS nodes for connecting distributed generation facilities were selected based on the results of mode calculations. The EPS nodes were selected where in the normal mode the load of the branches approaching them was close to the maximum permissible value or the voltage was below the nominal value and approached the limit of −10% Urated.
In the network repair scheme, the connection of DG facilities with a total active power output of 50 MW caused overload in branch 18–23. After its disconnection, a loss of voltage stability occurred at node 34. When the active power output from DG facilities rose to 55 MW, an overload occurred in branch 18–23, but after its disconnection, voltage stability was maintained.
Consequently, DG facilities contributed to the non-homogeneity of the EPS parameters. They can foster cascading failure processes, leading to the disruption of power supply to consumers. However, they can also have the potential to boost the survivability of EPSs and improve the reliability of power supply to consumers [80]. The capacity of DG facilities and their operating conditions should be determined in the planning stage of their construction. The appropriate choice of parameters and operating conditions of DG facilities when integrated into EPSs can provide substantial benefits. However, their operating parameters (output power) should be planned for various topologies and operating conditions.
Figure 7 shows a test scheme of a 500 kV EPS (36 nodes) in which the topology and operating conditions were modeled to ensure an active power flow of 2868 MW between the EPS1 subsystem (the left three columns of network nodes) and the EPS2 subsystem (the right three columns of network nodes).
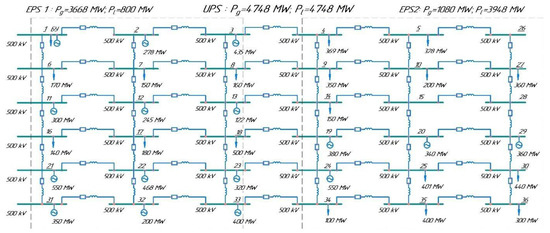
Figure 7.
Test scheme of 500 kV power system (36 nodes).
We will present the results of the steady-state calculation following an emergency disturbance resulting in the disconnection of branch 8–9 under the repair scheme (branch 3–4 was disconnected). This scenario involved an inadmissible overload of the 500 kV intersystem overhead PTL (branch 13–14), resulting in a cascading failure process and its development. It is accompanied by the EPS islanding and the loss of voltage stability. The trajectory along which the cascading process developed in this case and ended in the region of inadmissible power flows with the disconnection of the branches due to the inadmissible overload was as follows: Step 1—8–9; Step 2—9–14, 13–14; Step 3—10–15, 18–19, 33–34, and 34–35. Changes in currents in the branches of the EPS scheme during the development of the cascading failure process are shown in Figure 8.
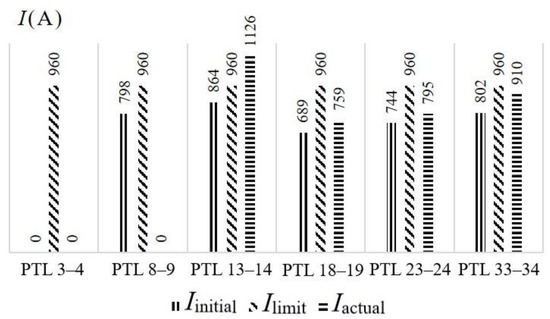
Figure 8.
Graph of changes in currents in EPS branches during cascading failure process development.
To increase survivability and prevent cascading failure development, we explored the installation of various FACTS devices designed to enhance the transfer capability of overhead PTLs [81,82,83]. A series of simplified calculations were conducted as a part of the feasibility study on the implementation of FACTS devices.
The calculated value of the rated power of the FACTS device for the case under consideration, where an overload resulted from a short circuit in the overhead PTLs 8–9, followed by the disconnection of overhead the PTLs 9–14 and 13–14, was 1065 MVA. To unload the specified overhead PTLs, the FACTS device had to be installed in the overhead PTLs 13–14, which had X = 112.8 Ohm.
A simplified feasibility analysis of various technical solutions was based on the specific cost indicators of FACTS devices, specific cost indicators of the 500 kV overhead PTL construction, and the cost of “cheap” and “expensive” electricity from operating power plants [84,85].
The specific costs were employed to calculate the cost of the FACTS devices (Table 1) with a capacity of 1100 MVA, excluding the cost of construction and installation works (CIW), controlled series compensator (CSC), and unified power flow controller (UPFC).

Table 1.
Costs of FACTS devices.
Let us calculate the cost of building a new 500 kV overhead PTL. The size of investment in the construction of 500 kV overhead PTL is determined on the basis of consolidated price standards (CPSs). The cost to construct 1 km of a 500 kV overhead PTL, utilizing wires with a cross-section of 500 mm2 (with three wires per phase), is estimated at USD 0.202 million/km. Then, the cost of the overhead PTLs 8–9 (L8–9 = 900 km), excluding design and survey work, is
For a real-world EPS scheme, studies were conducted to increase its survivability by changing power flows in the 500 kV network by adjusting the load of generating equipment at operating power plants. This facilitated the unloading of branches that had current values approaching the admissible limits during emergencies.
The cost of the generated electricity in the calculations was as follows:
- Electricity generated from power plants with a specific fuel consumption of 310 g.e.f./kWh and a cost of Ccheap = USD 0.039/kWh was considered cheap;
- Electricity generated from power plants with a specific fuel consumption of 650 g.e.f./kWh and a cost of Cexp = USD 0.055/kWh was considered expensive.
Let us determine the total cost of electricity generation within an EPS when loading only power plants producing “cheap” electricity:
where ∑E = 4748 million kWh is the total annual electricity generation from operating power plants in the analyzed EPS.
Throughout the year, power plants producing “expensive” electricity must be loaded during periods of maximum loads in the EPS. According to statistics, the generation of electricity from power plants with “expensive” electricity, which is necessary to prevent the cascading failures and their development, is ∑Eexp = 617 million kWh.
Let us determine the total cost of generating electricity in an EPS given the partial loading of power plants producing “expensive” electricity, whose loading is necessary under certain topologies and operating conditions:
The annual overpayment by consumers in the case of the partial loading of power plants producing “expensive” electricity is
Figure 9 presents the results of a comparative feasibility study for preventing cascading failure processes and their development according to the scenario shown in Figure 7 and Figure 8 in a test scheme of a 500 kV power system.
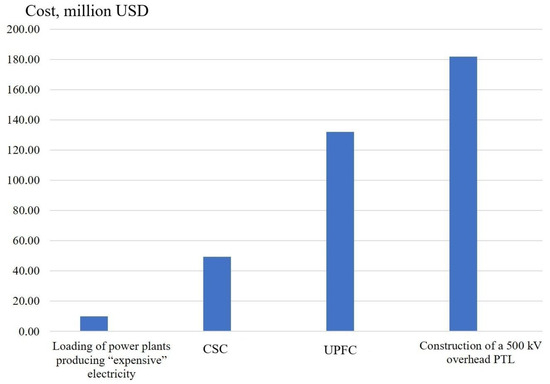
Figure 9.
Comparison of costs for preventing cascading failure process and its development.
Possible options for preventing the first step of the emergency cascade process by implementing circuit-mode measures aimed at increasing the survivability of the EPS were considered. Options for loading power plants with “expensive” electricity, using FACTS devices, and constructing a 500 kV overhead power line were considered measures allowing for the redistribution of power flows in the EPS.
Figure 9 does not show the cost of electricity from renewable energy sources; however, as evidence shows, its cost is 1.2–1.6 times higher than the cost of electricity from power plants producing “expensive” electricity.
As seen in Figure 9, managing the loading of power plants generating “expensive” electricity, along with DG facilities, is the most preferable approach both technically and economically. Meanwhile, the construction of a new 500 kV overhead PTL remains the costliest technical solution. The choice of optimal nodes for connecting DG facilities should rely on the results of multi-variant steady-state calculations in the EPS calculation scheme, with the modeling of all types of emergency disturbances, including double faults.
We analyzed a cascading failure process and its development using the example of a real systemic accident characterized by a cascading nature that took place within one of the EPSs. This was necessary to demonstrate the performance of the algorithm designed to analyze the conditions for the cascading failure process and its development trajectories. Figure 10 demonstrates the superposition of a 3D graphic surface of the network parameter non-homogeneity on the EPS network topology before the moment of a short circuit in a 500 kV overhead PTL 1.
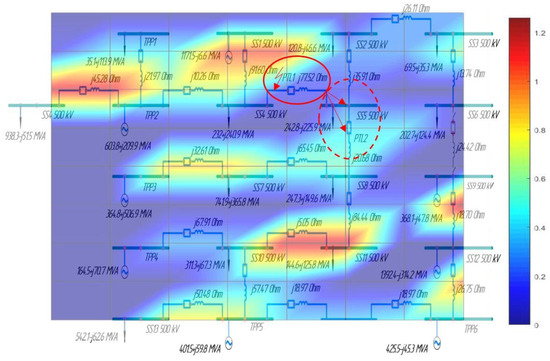
Figure 10.
A 3D graphic surface of the parameter non-homogeneity of the 500 kV network until the moment of short circuit in the 500 kV overhead PTL 1.
The disconnection of the 500 kV overhead PTL 1 by the emergency trip system and by the emergency control devices, AT5 and AT2 (3 × 167 MVA, 500/220/35 kV) and AT6 (250 MVA, 500/110/10 kV) in the 500 kV substation SS8 (Figure 10), resulted in a power surge in the 110–220 kV overhead PTLs. This led to a cascading failure of the overloaded components in the EPS network (Figure 11).
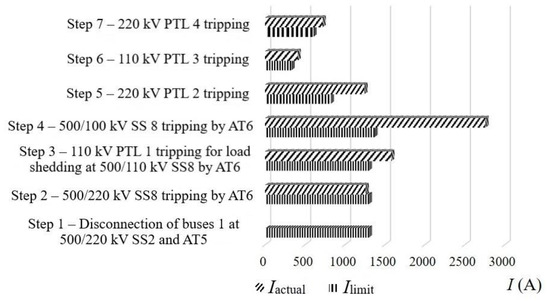
Figure 11.
Diagram of changes in current across branches with cascading tripping of network components under EPS blackout scenario.
Figure 12 shows a 3D graphic surface of the non-uniform distribution of current (I, p.u.) in the EPS components during the development of a cascading systemic failure. In this visualization, branches are replaced by equivalents and the respective rated voltage values are indicated at the network nodes.
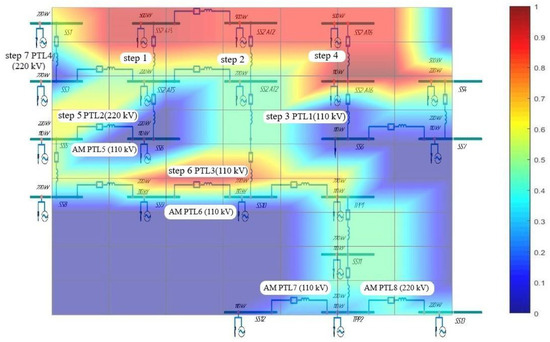
Figure 12.
A 3D graphic surface of non-uniform distribution of current (I, p.u.) in EPS components during cascading systemic failure development.
The overload in the seventh step led to the disconnection of the network components, which caused the asynchronous mode (AM) in four 110–220 kV overhead PTLs. This process was interrupted by the automatic asynchronous mode elimination devices, tripping the PTLs. The active power shortage in the central part of the EPS was 866 MW. Switching to the island mode diminished the frequency to 47.47 Hz, which caused the disconnection of consumers with a total capacity of 967 MW in the analyzed EPS and a capacity of 83 MW in the neighboring EPSs by automatic underfrequency load shedding devices [86,87].
Figure 13 presents a 3D graphic surface of the non-uniform distribution of the current (I, p.u.) after the seventh step of the cascading failure process resulting in the disconnection of the 220 kV overhead PTL 4.
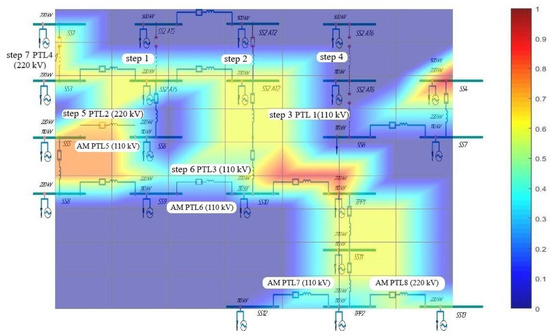
Figure 13.
A 3D graphic surface of the non-uniform distribution of the current (I, p.u.) after Step 7 of the cascading failure process.
Simulation modeling performed for the step-by-step analysis of the sequence of quasi-steady states enabled the prevention of the transition of an emergency process to a cascading systemic failure since, in this case, emergency control devices were activated by unacceptable deviations in the power flow parameters in the EPS, leading to the disconnection of considerable volumes of consumers.
4. Discussion
Cascading systemic accidents lead to the disruption of power supply for a significant number of consumers across vast areas. The restoration of the normal operation of an EPS after such accidents takes from several hours to several days, since such accidents can cause damage to specific components within the EPS, necessitating a thorough emergency restoration effort.
The developed algorithm allows the timely identification of the possibility of cascading failure processes and their development pathways in EPSs with network topologies of varying complexity. This capability of the algorithm was demonstrated by the findings from calculations conducted for three test scenarios and one real-world EPS scheme.
The algorithm can be employed both to plan and manage power flows in EPSs and to strategize about EPS expansion, facilitating the selection of the best technically and economically justified topologies and operational measures. This helps reduce the non-homogeneity of EPS parameters and, accordingly, the possibility of cascading systemic failures.
Simulating possible trajectories for cascading failure development in electric power systems enables dispatching personnel to provide a set of topology and operational strategies in the stage of operation planning to prevent the transition of emergency disturbances into a systemic failure.
The cost indicators of FACTS devices, as well as the cost of electricity, given in this paper, can vary considerably across different countries, exhibiting upward and downward fluctuations. This depends on the availability of in-house developments of FACTS devices and their manufacturers, the performance indicators of generating equipment at operating power plants, and the cost of primary energy resources. Consequently, the decision on the implementation of certain topology and operational measures should be made on the basis of a full-fledged feasibility study relying on comprehensive technical and economic analysis.
The simplified technical and economic calculations provided in this paper did not factor in the costs of design and survey work, the examination of design documentation, and author’s supervision, which can reach 6–8% of the total cost of the equipment. Nor did the calculations consider the cost of land plots for the installation of FACTS devices in substations and overhead PTL supports. The areas of land plots for overhead PTL supports depend on the type and material of supports, span lengths, soil characteristics, and others.
In densely populated areas, there are no opportunities for building new overhead PTLs. In large cities and megalopolises, building new overhead PTLs is generally prohibited by urban planning regulations. The cost of constructing a 500 kV power line in cable design is several times higher; therefore, the use of other measures is more preferable.
The calculation results proved that connecting DG facilities to individual nodes of the EPS network could enhance the survivability of the EPS and boost the reliability of power supply to consumers. However, it is essential for DG facilities to maintain a surplus of power that can be supplied to a network under certain topology and operational conditions, as directed by the EPS dispatching personnel. This capability must be incorporated during the design phase of DG facilities. Based on the steady-state calculations, it is necessary to identify the most advantageous nodes for connecting DG facilities. This is important for developing strategies to encourage the distributed generation owners to build and connect their facilities to these EPS nodes.
While it is clear that consumers benefit from loading power plants that produce “cheap” electricity, there are specific topologies and operational conditions under which it makes sense to load power plants generating “expensive” electricity, as well as DG facilities. In the event of a failure turning into a cascading systemic accident, the losses of consumers due to a systemic power outage lasting several hours will far outweigh any potential overpayment for electricity.
Future Areas of Development
At present, the steady-state simulation and the analysis of all possible trajectories for the development of cascading failure processes are carried out manually. To achieve this, a series of steady-state calculations are conducted for various topologies and operating conditions. This is a fairly labor-intensive process that requires a lot of time and highly qualified personnel. Given that such calculations should be performed daily to plan operations for the day ahead, automation tools are needed. It is crucial to develop tools within software capable of automating the process of searching for trajectories of development of cascading failure processes and calculating series of steady states, when the results of one steady state calculations are the initial data for calculating the steady states in the following steps, as shown in this paper.
The introduction of distributed series compensators (DSCs) suspended on overhead PTL wires—without the need to cut them—enables EPS dispatching personnel to change the resistance of the overhead PTLs and, accordingly, control the power flow throughout the network. There is no need to allocate land for DSCs. The number of DSCs on each of the phase wires of the overhead PTLs is determined by calculations, depending on the required compensation. DSCs are controlled via a radio interface, such as ZigBee. The remote switching on/off of individual units or their groups facilitates avoiding a sharp change in the resistance of overhead PTLs. To date, only pilot projects for the adoption of DSCs have been implemented, demonstrating high technical performance at a low cost, in comparison with other FACTS devices.
5. Conclusions
An algorithm was developed to identify, in a timely manner, the possibility of cascading failure processes and their development trajectory in EPSs with networks characterized by topologies of varying complexity. This algorithm also facilitated the subsequent implementation of effective measures, both topological and operational, to bolster the survivability of the EPSs.
The modeling results for three test schemes of networks operating at voltage levels of 10, 35, 110, and 500 kV proved the effectiveness of the proposed algorithm in finding the boundaries between the regions of admissible and inadmissible post-contingency power flows. A systemic failure that took place in a real-world power system was used as an example to demonstrate the practical application of the developed algorithm for analyzing the causes of the cascading systemic failures and their development.
The use of DG facilities of different capacities and various FACTS devices, alongside the redistribution of power flows in the network by changing the load of power plants with different costs of electricity generation, were considered tools for enhancing the survivability of the EPSs. The results of a simplified technical and economic analysis for the considered topology and operational measures were presented. The loading of existing power plants that generate “expensive” electricity in annual terms is five times cheaper than the installation of CSCs; however, given their long service life, their use can be economically viable. The cost of constructing a new 500 kV overhead PTL is 1.4 times higher than that of UPFCs, making it the most expensive solution. However, if an overhead PTL is necessary for the long-term expansion of an EPS, the choice of this solution can be justified.
The implementation of the developed algorithm in the planning and management of power flows by the dispatching personnel of an EPS will prevent cascading systemic failures and their development causing large-scale disruptions in power supply for consumers and substantial damages.
Author Contributions
Conceptualization, P.I., B.G. and I.S.; methodology, I.S. and B.G.; software, B.G. and P.I.; validation, P.I. and K.S.; formal analysis, I.S. and K.S.; investigation, B.G. and I.S.; resources, P.I. and I.S.; data curation, P.I.; writing—original draft preparation, B.G. and P.I.; writing—review and editing, I.S. and K.S.; visualization, B.G. and P.I.; supervision, I.S.; project administration, P.I.; funding acquisition, P.I. and K.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The funders had no role in the design of this study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Wang, X.; Li, Y.; Yu, Z.; Miao, Y.; Li, P.; Xu, Z. Analysis Method of Transformer Fatigue Life and Damage Under Multiple Short-Circuit Conditions. IEEE Trans. Appl. Supercond. 2024, 34, 5500904. [Google Scholar] [CrossRef]
- Polkovskaya, M.N.; Yakupova, M.A. Analysis of the Causes of Emergency Shutdowns on Electric Networks. J. Phys. Conf. Ser. 2021, 2096, 012130. [Google Scholar] [CrossRef]
- Mohammed, J.; Viswambaran, V. Performance Analysis of Overcurrent Protection Schemes in Power Systems. In Proceedings of the 2024 Advances in Science and Engineering Technology International Conferences (ASET), Abu Dhabi, United Arab Emirates, 3–5 June 2024; pp. 1–7. [Google Scholar] [CrossRef]
- Hemmatpour, M.H. Prediction of voltage stability index in buses without measurement in distribution systems. IET Gener. Transm. Distrib. 2024, 18, 2435–2451. [Google Scholar] [CrossRef]
- Solovyev, I.; Motovilov, A.; Hvijuzov, M.; Emelyanov, A. Improving the reliability of the power system in postfault condition. E3S Web Conf. 2024, 584, 01026. [Google Scholar] [CrossRef]
- Lesnykh, V.; Timofeeva, T. Problems of Assessment of Economic Damage Caused by Power Supply Interruption on Example of Gas Industry Objects. In Proceedings of the 29th European Safety and Reliability Conference (ESREL), Hannover, Germany, 22–26 September 2019. [Google Scholar] [CrossRef]
- El-Bassiouny, A.; El-Shimy, M.; Hammouda, R. Impact of Power Transformer Failures on Customer Interruptions Costs Using Customer Damage Functions. In Proceedings of the 19th International Middle East Power Conference (MEPCON’19), Cairo, Egypt, 19–21 December 2017. [Google Scholar] [CrossRef]
- Voropai, N. Electric Power System Transformations: A Review of Main Prospects and Challenges. Energies 2020, 13, 5639. [Google Scholar] [CrossRef]
- Saleh, S.A.M.; Chowdhury, M.R. Survivability Analysis of Impacts of Load-Side Activities on Power Systems. IEEE Trans. Ind. Appl. 2022, 58, 1869–1878. [Google Scholar] [CrossRef]
- Saleh, S.A.; Betancourt, O.; Ozkop, E.; Ahshan, R.; Zundel, E.; Sanchez, Z.; Meng, J. The Analysis and Modeling of Voltage Survivability in Power Systems. IEEE Trans. Ind. Appl. 2024, 60, 4654–4665. [Google Scholar] [CrossRef]
- Voropai, N.I.; Krupenev, D.S.; Podkovalnikov, S.V.; Senderov, S.M. Two energy collapses—In Texas, USA, and in Primorsky Krai, Russia. Electro-Energy Transm. Distrib. 2021, 4, 166–174. (In Russian) [Google Scholar]
- Harutyunyan, R.V.; Bolshov, L.A.; Borovoy, A.A.; Velikhov, E.P. A Systematic Analysis of the Causes of the Consequences of the Accident at Fukushima-1 Has Been Carried Out; RAS Institute of Problems of Safe Atomic Energy Development: Moscow, Russia, 2018; 408p. (In Russian) [Google Scholar]
- Voropai, N.I.; Chulyukova, M.V. Analysis of the development of a systemic accident in the ECO of the East on 1 August 2017. Electricity 2018, 5, 28–32. (In Russian) [Google Scholar]
- Friedlander, G.D. The Northeast power failure—A blanket of darkness. IEEE Spectr. 1966, 3, 54–73. [Google Scholar] [CrossRef]
- Concordia, C. Performance of interconnected systems following disturbances. IEEE Spectr. 1965, 2, 68–80. [Google Scholar] [CrossRef]
- Wilson, G.L.; Zarakas, P. Anatomy of a blackout: How’s and why’s of the series of events that led to the shutdown of New York’s power in July 1977. IEEE Spectr. 1978, 15, 39–49. [Google Scholar] [CrossRef]
- Kurita, A.; Sakurai, T. The power system failure on 23 July 1987 in Tokyo. In Proceedings of the 27th IEEE Conference on Decision and Control, Austin, TX, USA, 7–9 December 1988; Volume 3, pp. 2093–2097. [Google Scholar] [CrossRef]
- Kosterev, D.N.; Taylor, C.W.; Mittelstadt, W.A. Model validation for the 10 August 1996 WSCC system outage. IEEE Trans. Power Syst. 1999, 14, 967–979. [Google Scholar] [CrossRef]
- Taylor, C.W.; Erickson, D.C. Recording and analyzing the 2 July cascading outage [Western USA power system]. IEEE Comput. Appl. Power 1997, 10, 26–30. [Google Scholar] [CrossRef]
- Liu, C.Q. A discussion of the WSCC 2 July 1996 outages. IEEE Power Eng. Rev. 1998, 18, 60–61. [Google Scholar] [CrossRef]
- Venkatasubramanian, V.; Li, Y. Analysis of 1996 Western American Electric Blackouts. In Proceedings of the Bulk Power System Dynamics and Control—VI, Cortina d’Ampezzo, Italy, 22–27 August 2004; pp. 685–721. Available online: https://www.academia.edu/9198860/Analysis_of_1996_Western_American_Electric_Blackouts (accessed on 12 January 2025).
- Dobson, I.; Carreras, B.A.; Newman, D.E.; Reynolds-Barredo, J.M. Obtaining Statistics of Cascading Line Outages Spreading in an Electric Transmission Network from Standard Utility Data. IEEE Trans. Power Syst. 2016, 31, 4831–4841. [Google Scholar] [CrossRef]
- U.S. Canada Power System Outage Task Force. Interim Report: Causes of the August 14th Blackout in the United States and Canada, November, 2003. Available online: https://eta-publications.lbl.gov/sites/default/files/interim-rpt-aug-14-blkout-03.pdf (accessed on 14 January 2025).
- Investigation Report into the Loss of Supply Incident Affecting Parts of South London at 18:20 on Thursday, 28 August 2003, National Grid Company plc, Volume 43, 10 September 2003. Available online: http://www.g4jnt.com/London28082003.pdf (accessed on 12 January 2025).
- Final Report of the Investigation Committee on the 28 September 2003 Blackout in Italy, UCTE Report, Volume 128, April 2004. Available online: https://eepublicdownloads.entsoe.eu/clean-documents/pre2015/publications/ce/otherreports/20040427_UCTE_IC_Final_report.pdf (accessed on 15 January 2025).
- Kovalev, V.D.; Ivakin, V.N. About a systemic accident in the electrical networks of the central region of Russia on 25 May 2005. Electricity 2006, 9, 52–56. (In Russian) [Google Scholar]
- Smolovik, S.V. Analysis of the accident in the Moscow power grid on 23–25 May 2005. Sci. Tech. Bull. St. Petersburg State Tech. Univ. 2006, 2, 25–32. (In Russian) [Google Scholar]
- Voropai, N.I.; Tomin, N.V.; Sidorov, D.N.; Kurbatsky, V.G.; Panasetsky, D.A.; Zhukov, A.V.; Efimov, D.N.; Osak, A.B. A suite of intelligent tools for early detection and prevention of blackouts in power interconnections. Autom. Remote Control 2018, 79, 1741–1755. [Google Scholar] [CrossRef]
- Report on the Grid Disturbance on 30th July 2012 and Grid Disturbance on 31st July 2012. Submitted in Compliance to CERC Order in Petition No. 167/Suo-Motu/2012 Dated 1st August 2012, Volume 129, 8th August 2012. Available online: https://powermin.gov.in/sites/default/files/uploads/GRID_ENQ_REP_16_8_12.pdf (accessed on 14 January 2025).
- Transmission Failure Causes Nationwide Blackout in Argentina. IEEE Spectrum: Technology, Engineering, and Science News. Retrieved 20 June 2019. Available online: https://spectrum.ieee.org/transmission-failure-causes-nationwide-blackout-in-argentina (accessed on 16 January 2025).
- PLN Corrects Cause of Power Outage in Jakarta and Surrounding Areas. CNN Indonesia. 4 August 2019. Retrieved 4 August 2019. Available online: https://en.tempo.co/read/1232053/pln-power-outage-due-to-disruption-of-electricity-plants-in-java (accessed on 12 January 2025).
- Bialek, J. What does the GB power outage on 9 August 2019 tell us about the current state of decarbonized power systems? Energy Policy 2020, 146, 111821. [Google Scholar] [CrossRef]
- Paul, S.K.; Mohapatra, A.; Das, D.C. Robust network topology for unbalanced active distribution networks with uncertain injections. IET Energy Syst. Integr. 2024, 6, 828–844. [Google Scholar] [CrossRef]
- Ilyushin, P.; Filippov, S.; Kulikov, A.; Suslov, K.; Karamov, D. Specific Features of Operation of Distributed Generation Facilities Based on Gas Reciprocating Units in Internal Power Systems of Industrial Entities. Machines 2022, 10, 693. [Google Scholar] [CrossRef]
- Mohanty, A.; Ramasamy, A.; Verayiah, R.; Bastia, S.; Dash, S.S.; Cuce, E.; Khan, T.Y.; Soudagar, M.E.M. Power system resilience and strategies for a sustainable infrastructure: A review. Alex. Eng. J. 2024, 105, 261–279. [Google Scholar] [CrossRef]
- Baldick, R.; Chowdhury, B.; Dobson, I. Chowdhury Initial review of methods for cascading failure analysis in electric power transmission systems. In Proceedings of the IEEE Power Engineering Society General Meeting, Pittsburgh, PA, USA, 20–24 July 2008; IEEE PES CAMS Task Force on Understanding, Prediction, Mitigation and Restoration of Cascading Failures: Pittsburgh, PA, USA, 2008. Available online: https://www.researchgate.net/publication/303142504_Initial_review_of_methods_for_cascading_failure_analysis_in_electric_power_transmission_systems#fullTextFileContent (accessed on 18 January 2025).
- Wang, J. Power Grid Cascading Failure Blackouts Analysis. AIP Conf. Proc. 2019, 2066, 020046. [Google Scholar] [CrossRef]
- Gomila, D.; Carreras, B.A.; Reynolds-Barredo, J.M.; Colet, P.; Gomis-Bellmunt, O. Analysis of the blackout risk reduction when segmenting large power systems using lines with controllable power flow. Int. J. Electr. Power Energy Syst. 2023, 148, 108947. [Google Scholar] [CrossRef]
- Esmaeilian, A.; Kezunovic, M. Prevention of Power Grid Blackouts Using Intentional Islanding Scheme. IEEE Trans. Ind. Appl. 2017, 53, 622–629. [Google Scholar] [CrossRef]
- Eroshenko, S.A.; Ilyushin, P.V. Features of implementing multi-parameter islanding protection in power districts with distributed generation units. In Proceedings of the 2018 IEEE 59th International Scientific Conference on Power and Electrical Engineering of Riga Technical University (RTUCON), Riga, Latvia, 12–14 November 2018. [Google Scholar] [CrossRef]
- Chang, L.; Wu, Z. Performance and reliability of electrical power grids under cascading failures. Int. J. Electr. Power Energy Syst. 2011, 33, 1410–1419. [Google Scholar] [CrossRef]
- Cupac, V.; Lizier, J.T.; Prokopenko, M. Comparing dynamics of cascading failures between network-centric and power flow models. Int. J. Electr. Power Energy Syst. 2013, 49, 369–379. [Google Scholar] [CrossRef]
- Voropai, N.I.; Stennikov, V.A.; Barakhtenko, E.A. Integrated energy systems: Challenges, trends, philosophy. Stud. Russ. Econ. Dev. 2017, 28, 492–499. [Google Scholar] [CrossRef]
- SEI. Survivability of Energy Systems: Collection of Articles; SEI: Irkutsk, Russia, 1980; 197p. (In Russian) [Google Scholar]
- Guk, Y.B. Reliability Analysis of Electric Power Plants; Energoatomizdat: Leningrad, Russia, 1988; 224p. (In Russian) [Google Scholar]
- Zeylidzon, E.D. On Some Patterns of Chain Development of Accidents in Power Systems; VNIIE: Moscow, Russia, 1978; Volume 55, pp. 17–26. (In Russian) [Google Scholar]
- Motovilov, A.I.; Solovyov, I.I. Prevention of cascade accidents in power system management. Eurasian Union Sci. 2019, 3, 27–31. (In Russian) [Google Scholar]
- Ilyushin, P.; Volnyi, V.; Suslov, K.; Filippov, S. Review of Methods for Addressing Challenging Issues in the Operation of Protection Devices in Microgrids with Voltages of up to 1 kV That Integrates Distributed Energy Resources. Energies 2022, 15, 9186. [Google Scholar] [CrossRef]
- Ilyushin, P.V.; Filippov, S.P. Under-frequency load shedding strategies for power districts with distributed generation. In Proceedings of the 2019 International Conference on Industrial Engineering, Applications and Manufacturing (ICIEAM), Sochi, Russia, 25–29 March 2019. [Google Scholar] [CrossRef]
- Li, B.; Barker, K.; Sansavini, G. Measuring Community and Multi-Industry Impacts of Cascading Failures in Power Systems. IEEE Syst. J. 2018, 12, 3585–3596. [Google Scholar] [CrossRef]
- Rivas-Dávalos, F.; Martínez-Mendoza, J.A.; Martínez-Ceseña, E.A. The effects of load demand uncertainty on cascading overload failures in power systems. Electr. Eng. 2024, 1–14. Available online: https://link.springer.com/article/10.1007/s00202-024-02781-2 (accessed on 18 January 2025). [CrossRef]
- Burman, A.P.; Rozanov, Y.K.; Shakaryan, Y.G. Control of Electric Power Flows and Increasing the Efficiency of Electric Power Systems; Publishing House MEI: Moscow, Russia, 2012; 336p. (In Russian) [Google Scholar]
- Acosta, J.J.S.; Gámez, M.R.; Alaba, L.A.C.; Arauz, W.M.S.; Alvarez, J.R.N.; Pérez, A.V. Energy storage system for increasing electric-power stability. Int. J. Power Electron. Drive Syst. 2024, 15, 2517–2525. [Google Scholar] [CrossRef]
- Ilyushin, P.; Filippov, S.; Kulikov, A.; Suslov, K.; Karamov, D. Intelligent Control of the Energy Storage System for Reliable Operation of Gas-Fired Reciprocating Engine Plants in Systems of Power Supply to Industrial Facilities. Energies 2022, 15, 6333. [Google Scholar] [CrossRef]
- Shamarova, N.; Suslov, K.; Ilyushin, P.; Shushpanov, I. Review of Battery Energy Storage Systems Modeling in Microgrids with Renewables Considering Battery Degradation. Energies 2022, 15, 6967. [Google Scholar] [CrossRef]
- Kobernyk, V.V. Economic Analysis of Electric Energy Storage Technologies. Èlektronnoe Model. 2023, 45, 113–122. [Google Scholar] [CrossRef]
- Dubey, P.K.; Singh, B.; Singh, D.; Verma, P.N.; Verma, K.S.; Jahnavi. Energy Storage Technologies: Types, Recent Trends, and Development. In Proceedings of the 3rd International Conference on Power Electronics and IoT Applications in Renewable Energy and Its Control (PARC), Mathura, India, 23–24 February 2024; pp. 1–7. [Google Scholar] [CrossRef]
- Belyaev, A.N.; Goryunov, Y.P.; Smirnov, A.A.; Smolovik, S.V. Analysis of the Development of Major Systemic Accidents; SPbGPU: St. Petersburg, FL, USA, 2006; 72p. (In Russian) [Google Scholar]
- Gerasimov, A.S.; Esipovich, A.K.; Kosheev, L.A.; Shulginov, N.G. Investigation of the modes of the Moscow power system during the development of the accident in May 2005. Electricity 2008, 1, 2–12. (In Russian) [Google Scholar]
- Kulikov, A.L.; Shepovalova, O.V.; Ilyushin, P.V.; Filippov, S.P.; Chirkov, S.V. Control of electric power quality indicators in distribution networks comprising a high share of solar photovoltaic and wind power stations. Energy Rep. 2022, 8, 1501–1514. [Google Scholar] [CrossRef]
- Ananicheva, S.S.; Myzin, A.L. Methods of Analysis and Calculation of Closed Electric Networks; UrFU: Yekaterinburg, Russia, 2012; 94p. (In Russian) [Google Scholar]
- Voitov, O.N.; Voropai, N.I.; Gamm, A.Z.; Golub, I.I.; Efimov, D.N. Analysis of Heterogeneities of Electric Power Systems; Nauka Publish: Novosibirsk, Russia, 1999; 256p. (In Russian) [Google Scholar]
- Rohden, M.; Jung, D.; Tamrakar, S.; Kettemann, S. Cascading Failures in AC Electricity Grids. Phys. Rev. 2016, 94, 032209. [Google Scholar] [CrossRef]
- Montecchi, L.; Lollini, P.; Ceccarelli, A. Assessing the Impact of Cascading Failures in Urban Electricity Networks. In Proceedings of the 2017 IEEE International Conference on Internet of Things (iThings) and IEEE Green Computing and Communications (GreenCom) and IEEE Cyber, Physical and Social Computing (CPSCom) and IEEE Smart Data (SmartData), Exeter, UK, 21–23 June 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Islam, Z.; Lin, Y.; Vokkarane, V.; Venkataramanan, M. Cyber-physical cascading failure and resilience of power grid: A comprehensive review. Front. Energy Res. 2023, 11, 1–17. [Google Scholar] [CrossRef]
- Ntambara, B.; Umuhoza, R. Optimization of rwanda power system protection in power blackouts and cascading events. SN Appl. Sci. 2022, 4, 296. [Google Scholar] [CrossRef]
- Soltan, S.; Mazauric, D.; Zussman, G. Cascading Failures in Power Grids: Analysis and Algorithms. In Proceedings of the 5th International Conference on Future Energy Systems, Cambridge, UK, 11–13 June 2014; Association for Computing Machinery: New York, NY, USA, 2014; pp. 195–206. [Google Scholar] [CrossRef]
- Ma, R.; Jin, S.; Eftekharnejad, S.; Zafarani, R.; Peter, W.; Philippe, J. A probabilistic cascading failure model for dynamic operating conditions. IEEE Access 2020, 8, 61741–61753. [Google Scholar] [CrossRef]
- Kumar, A.; Shwe, H.Y.; Chong, P.H.J. Protection Strategies Against Cascading Failure for Power Systems of Ring Network. Commun. Netw. 2016, 8, 67–78. [Google Scholar] [CrossRef][Green Version]
- Zhu, Y.; Yan, J.; Sun, Y.; He, H. Visualization of Cascading Failures in Power Grids. 2016, pp. 1–4. Available online: https://sigport.org/sites/default/files/Demo_Cascadingfailure_Zhu_conf_7.pdf (accessed on 14 January 2025).
- Raj, A.; Pattery, J.M.; Hassainar, S. High Performance Computing for Contingency Analysis of Power Systems. Int. J. Eng. Res. Technol. 2013, 2, 1993–1998. [Google Scholar]
- Ismagilov, F.R.; Shahmaev, I.Z.; Gaisin, B.M. The technique to improve the effectiveness of control systems in inhomogeneous electric power grids. In Proceedings of the 2017 International Siberian Conference on Control and Communications (SIBCON), Astana, Kazakhstan, 29–30 June 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Shahmaev, I.Z.; Gaisin, B.M.; Shiryaev, O.V. A new method of taking management decisions at designing and developing electric power systems. In Proceedings of the 2016 2nd International Conference on Industrial Engineering, Applications and Manufacturing (ICIEAM), Chelyabinsk, Russia, 19–20 May 2016; pp. 1–3. [Google Scholar] [CrossRef]
- Panda, A.; Dauda, A.K.; Chua, H.; Tan, R.R.; Aviso, K.B. Recent advances in the integration of renewable energy sources and storage facilities with hybrid power systems. Clean. Eng. Technol. 2023, 12, 100598. [Google Scholar] [CrossRef]
- Klimov, A.; Matrenin, P. Electric Network Topology Optimization with Distributed Generation Using Pandapower Library. J. Mod. Energy Res. 2024, 2, 1–6. [Google Scholar] [CrossRef]
- Ilyushin, P.; Kulikov, A.; Suslov, K.; Filippov, S. Consideration of Distinguishing Design Features of Gas-Turbine and Gas-Reciprocating Units in Design of Emergency Control Systems. Machines 2021, 9, 47. [Google Scholar] [CrossRef]
- Mokred, S.; Wang, Y. Voltage stability assessment and contingency ranking in power systems based on modern stability assessment index. Results Eng. 2024, 23, 102548. [Google Scholar] [CrossRef]
- Baleboina, G.M.; Mageshvaran, R. A survey on voltage stability indices for power system transmission and distribution systems. Front. Energy Res. 2023, 11, 1159410. [Google Scholar] [CrossRef]
- Ilyushin, P.V.; Shepovalova, O.V.; Filippov, S.P.; Nekrasov, A.A. The Effect of Complex Load on the Reliable Operation of Solar Photovoltaic and Wind Power Stations Integrated into Energy Systems and into Off-Grid Energy Areas. Energy Rep. 2022, 8, 1515–1529. [Google Scholar] [CrossRef]
- Boyko, E.; Byk, F.; Ilyushin, P.; Myshkina, L.; Suslov, K. Methods to improve reliability and operational flexibility by integrating hybrid community mini-grids into power systems. Energy Rep. 2023, 9, 481–494. [Google Scholar] [CrossRef]
- Mousaei, A.; Gheisarnejad, M.; Khooban, M.H. Challenges and opportunities of FACTS devices interacting with electric vehicles in distribution networks: A technological review. J. Energy Storage 2023, 73, 108860. [Google Scholar] [CrossRef]
- Zanganeh, M.; Samiei Moghaddam, M.; Azarfar, A.; Vahedi, M.; Salehi, N. Multi-area distribution grids optimization using D-FACTS devices by M-PSO algorithm. Energy Rep. 2023, 9, 133–147. [Google Scholar] [CrossRef]
- Tiwari, V.K.; Gupta, A.R. Application of SVC and STATCOM for Wind Integrated Power System. In Recent Advances in Power Electronics and Drives; Lecture Notes in Electrical, Engineering; Kumar, J., Jena, P., Eds.; Springer: Singapore, 2021; p. 707. [Google Scholar] [CrossRef]
- STO 56947007-29.240.019-2009; Methodology for Assessing the Technical and Economic Efficiency of Using FACTS Devices. UNES: Moscow, Russia, 2009; 35p. (In Russian)
- Ministry of Energy of the Russian Federation. Order of the Ministry of Energy of the Russian Federation Dated 26 February 2024 No. 131 “On Approval of Consolidated Price Standards for Standard Technological Solutions for Capital Construction of Electric Power Facilities in Terms of Electric Grid Facilities”; Ministry of Energy of the Russian Federation: Moscow, Russia, 2024. (In Russian) [Google Scholar]
- Govorun, M.; Satsuk, E.; Luzhkovskiy, Y.; Dubinin, D.; Titov, S.; Khokhrin, A. Experience in implementing the algorithm for emergency control system of unloading in case of overload in terms of power based on synchrophasor angle. E3S Web Conf. 2024, 584, 01039. [Google Scholar] [CrossRef]
- Reese, L.; Rettig, A.; Jauch, C.; Domin, R.J.; Karshüning, T. Joint Frequency Stabilization in Future 100% Renewable Electric Power Systems. Energies 2025, 18, 418. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).